高二【数学(人教A版)】-导数的概念及其几何意义-最新国家级中小学课程全高清
合集下载
高二下学期数学人教A版选择性必修第二册5.1.2第二课时导数的几何意义课件

1.导数的概念
如果当Δx→0
时,平均变化率Δy无限趋近于一个确定的值,即Δy有极限,则称
Δx
Δx
y=
f (x)在 x = x0 处 _可_导__ , 并 把 这个 _确__定_的__值__ 叫 做 y= f (x) 在 x= x0 处 的 导数 ( 也 称 为
_瞬__时_变__化_率___),记作 f
′(x0)或__y_′|x_=__x_0 _,即 f ′(x0)=Δlixm→0
Δy
Δx =
lim
Δx→0
fx0+Δx-fx0 Δx
.
问题2:导数f ′(x0)表示函数y=f (x)在x=x0处
的瞬时变化率,反应函数y=f (x)在x=x0附近的 变化情况.那么导数的几何意义是什么?
二、 新课讲授
5.1.2导数的概念及其几何意义(第二课时)
学科版本:人教A版202X新课标 教材版本:人教A版(202X) 教材章节:选择性必修第二册5.1.2 学段学科:高中数学 年级学期:高二上学期
一、 新课引入
引导语:
问题1:根据平均变化率的概念回顾导数的概念.
二、 新课讲授
[新知初探]
知识点一 导数的几何意义
四、 知识点二
知识点二 导函数的概念 1.定义:当 x 变化时,y= f′(x) 就是 x 的函数,我们称
它为 y=f(x)的导函数(简称导数). lim fx+Δx-fx
2.记法:f′(x)或 y′,即 f′(x)=y′=_Δ_x→__0______Δ_x_____.
五、 例题练习,巩固新知
求曲线的切线方程 [例 1] 已知曲线 C:y=x2,求曲线 C 上的横坐标为 2 的 点处的切线方程.
已知曲线上一点 P(x0,f(x0)),求在该点处切线方程的三个 步骤
高中数学人教A版选择性必修第二册导数的概念及其几何意义完整版课件
的值叫做 y f (x) 在 x x0 处的导数(也称瞬时变化率),
记作 f ' (x0 ) 或 y'|xx0 ,即
:
f
'
(
x0
)
lim
x0
导数的几何意义
y x
f
lim f (x0 x) f (x0
x0
x
'(x0)是函数 y f (x)在
). x
x0
处切线的斜率
典型例题 根据导数定义求函数在某一点处的导数
无限逼近(极限) ★ 答案表示形式具有一致性吗?
平均变化率的极限
4
瞬时变化率的极限
概念生成
1.平均变化率
f(x0+Δx)-f(x0)
fx0+Δx-fx0 Δx
概念生成
2.导数
即
当x 0时,平均变化率 y 有极限,则称 y f (x)在 x
y
x x
无限接近一个确定的值, x0 处可导,并把这个确定
需要对原油进行冷却和加热。已知在第xh时,原油的温 度(单位:。C)为y f (x) x2 7x 15(0 x 8).计算第2h时 与第6h时,原油温度的瞬时变化率,并说明它们的意义.
解 在第2h和第6h时,原油温度的瞬时变化率就是f '2
和 f ' 6.
根据导数的定义, y f 2 x f 2
)
A.f ′(x0) B.2f ′(x0) C.-2f ′(x0) D.0
(2)求函数 y=3x2 在 x=1 处的导数.
解: y f (1 x) f (1)
x
x
f (1) lim y lim ( 1 ) x0 x x0 1 x
典 型 例 题 导数的应用
新教材人教A版高中数学选择性必修第二册5.1导数的概念及其意义 精品教学课件

(2)×.函数y=f(x)从x1到x2的平均变化率
y f(x2) f(x1)公式中Δx与Δy
x
x2 x1
可能同号,也可能异号.
(3)×.物体在某一时刻t的瞬时速度是当Δt➝0时,平均速度的极限.
2.某物体的位移公式为s=s(t),从t0到t0+Δt这段时间内下列理解正确的 是( )
A.(t0+Δt)-t0称为函数值增量 B.t0称为函数值增量 C.Δs=s(t0+Δt)-s(t0)称为函数值增量 D. s 称为函数值增量
x0
x
= lim([ x)2+3x x0
20.+3x
0
x
]=3x
2 0
因为k=3,所以3x20=3,得x0=1或x0=-1,
所以y0=1或y0=-1.
所以点P的坐标为(-1,-1)或(1,1).
2.在抛物线y=x2上求一点P,使在该点处的切线垂直于直线2x-6y+5=0.
【解析】设点P的坐标为(x0,y0),
(2)函数y=f(x)从x1到x2的平均变化率
y x
f(x2) f(x1)公式中Δx与Δy同号.
x2 x1
()
(3)物体在某一时刻t的瞬时速度即在[t,t+Δt]上,当Δt较小时的平均速度.
()
提示:(1)×.在平均变化率的定义中,自变量x在x0处的变化量Δx可以是正数,
也可以是负数,但不能为0.
5.1 导数的概念及其意义
5.1.1 变化率问题 5.1.2 导数的概念及其几何意义 P40
1.瞬时速度 我们把物体在_某__一__时__刻__的速度称为瞬时速度. 【思考】
物体在时间段 1,1 t 的平均速度与在时刻t=1的瞬时速度有什么关系?
导数的概念及其几何意义课件——高二上学期数学人教A版选择性必修第二册

三极(3)取极限 f′(x0)=li m Δx→0
Δy Δx.
例 2.已知函数 f(x)=2x2+4x,若 f′(x0)=12,则 x0=________.
解析:根据导数的定义
f′(x0)=li m Δx→0
ΔΔyx=liΔmx→0
fx0+Δx-fx0 Δx
=li m Δx→0
2x0+Δx2+4x0+Δx-2x20+4x0 Δx
课堂练习
1 根据导数的定义求下列函数的导数. (1)求函数 在x=1处的导数; (2)求函数 在 处的导数.
解:
(2)
(1)
∴
∴
∴
∴
课堂总结
1 平均变化率 2 瞬时变化率 3 导数的概念 4 求函数y=f(x)在点处的导数的三个步骤
板书设计
1 平均变化率 2 瞬时变化率 3 导数的概念 4 例题讲解 5 课堂练习 6 求函数 y=f(x)在点 处的导数的三个步骤
第五章 导数
5.1.2 导数的概念及其几何意义
新知导入
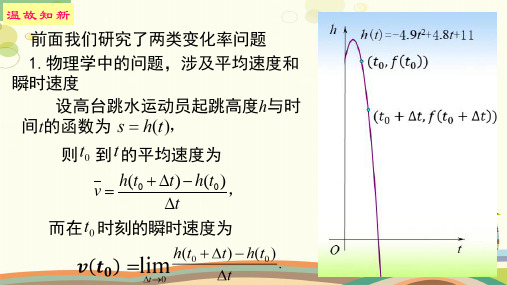
前面我们研究了两类变化率问题:
一类是物理学中的问题,涉及平均速度和瞬时速度; 另一类是几何学中的问题,涉及割线斜率和切线斜率. 这两类问题来自不同的学科领域,但在解决问题时, 都采用了由“平均变化率”逼近“瞬时变化率”的思想方法; 问题的答案也有一样的表示形式.
合作探究
例1 设 ,求 解:
用导数定义求函数在某一点
处的导数的三个步骤
一差(1)作差 Δy=f(x0+Δx)-f(x0). 二比(2)作比ΔΔyx=fx0+ΔΔxx-fx0.
三极(3)取极限 f′(x0)=li m Δx→0
Δy Δx.
巩固练习. 已知函数 f(x)=2x2+4x,则 f′(3)=________.
新教材高中数学第五章第2课时导数的几何意义ppt课件新人教A版选择性必修第二册

解析:因为 y'=
(+) -
=12,
→
故切线的斜率为 12,切线方程为 y-8=12(x-2),即 12x-y-16=0.
答案:A
)
(2)曲线 y=f(x)=x3+2x-1 在点 P(1,2)处的切线方程为
5x-y-3=0
.
解析:由题意,得点 P(1,2)在曲线 y=f(x)上.
=
=f'(1)=-1.
-
→
→
所以所求切线的斜率为-1.
方法规律
1.求曲线上某点处切线方程的步骤
2.已知曲线外的点 P(x1,y1),求曲线过点 P 的切线方程的步骤
(1)设切点为点 Q(x0,y0).
(2)求出函数 y=f(x)在 x0 处的导数 f'(x0).
(3)利用点 Q 在曲线上和 f'(x0)=kPQ,求出 x0,y0 及 f'(x0).
(4)根据直线的点斜式方程,得切线方程为 y-y0=f'(x0)(x-x0),再将其
化为一般式即可.
是
【跟踪训练】
1.若函数 f(x)的图象在点 A(1,2)处的导数是-1,则过点 A 的切线方程
x+y-3=0 .
解析:由题意,得切线的斜率为 k=-1.
所以点 A(1,2)处的切线方程为 y-2=-(x-1),
角形的面积为 ,则
解析:因为
a=
±1
.
(+) -
f'(a)=
=3a2,
→
所以曲线 f(x)在点(a,a3)处的切线方程为 y-a3=3a2(x-a).
(+) -
=12,
→
故切线的斜率为 12,切线方程为 y-8=12(x-2),即 12x-y-16=0.
答案:A
)
(2)曲线 y=f(x)=x3+2x-1 在点 P(1,2)处的切线方程为
5x-y-3=0
.
解析:由题意,得点 P(1,2)在曲线 y=f(x)上.
=
=f'(1)=-1.
-
→
→
所以所求切线的斜率为-1.
方法规律
1.求曲线上某点处切线方程的步骤
2.已知曲线外的点 P(x1,y1),求曲线过点 P 的切线方程的步骤
(1)设切点为点 Q(x0,y0).
(2)求出函数 y=f(x)在 x0 处的导数 f'(x0).
(3)利用点 Q 在曲线上和 f'(x0)=kPQ,求出 x0,y0 及 f'(x0).
(4)根据直线的点斜式方程,得切线方程为 y-y0=f'(x0)(x-x0),再将其
化为一般式即可.
是
【跟踪训练】
1.若函数 f(x)的图象在点 A(1,2)处的导数是-1,则过点 A 的切线方程
x+y-3=0 .
解析:由题意,得切线的斜率为 k=-1.
所以点 A(1,2)处的切线方程为 y-2=-(x-1),
角形的面积为 ,则
解析:因为
a=
±1
.
(+) -
f'(a)=
=3a2,
→
所以曲线 f(x)在点(a,a3)处的切线方程为 y-a3=3a2(x-a).
高二数学课件(人教A版选择性必修第二册)5.1.2导数的概念及其几何意义(2课时)

l
数 = ()在 = 0 附近的变化情况.那么导数 ’ (0 )的几何意义是什么?
l
思考1:观察函数 = ()的图象,平均变化率
∆
∆
=
(0 +∆)−(0 )
∆
∆
∆→0 ∆
’ (0 ) =
表示什么?瞬时变化率
(0 +∆)−(0 )
表示什么?
=
(0 +∆)−(0 )
叫做函数∆=新知探索源自如果当∆∆∆
→l 0时,平均变化率 无限趋近于一个确定的值,即 有极限,则称
∆
∆
= ()在 = 0 处可导,并把这个确定的值叫做
= ()在 = 0 处的导数(也
l
称为瞬时变化率),记作 ’ (0 )或 ’ |=0 ,即 ’ (0 )
瞬时变化率(精确到0.1).
解:血管中某一时刻药物浓度的瞬时变化率,就是药物浓度()在此时刻的导数,
从图象上看,它表示曲线()在此点处的切线的斜率.
例析
l
l
如图,画出曲线上某点处的切线,利用网格估计这条切线的斜率,可以得到此
时药物浓度瞬时变化率的近似值.
作 = 0.8处的切线,并在切线上取两点,如(0.7,0.91),(1.0,0.48),则该切线的
l
l
对原油进行冷却和加热.已知在 ℎ 第时,原油的温度(单位:
℃)为 = () = 2 − 7 + 15(0 ≤ ≤ 8).计算第2 ℎ与第
6 ℎ时,原油温度的瞬时变化率,并说明它们的意义.
同理可得 ’ (6) = 5.
在第2 ℎ和第6 ℎ时,原油温度的瞬时变化率分别为−3℃/ℎ和5℃/ℎ.说明在第
这样,当变化时, = ’ ()就是的函数,我们称它为 = ()的导函数
数 = ()在 = 0 附近的变化情况.那么导数 ’ (0 )的几何意义是什么?
l
思考1:观察函数 = ()的图象,平均变化率
∆
∆
=
(0 +∆)−(0 )
∆
∆
∆→0 ∆
’ (0 ) =
表示什么?瞬时变化率
(0 +∆)−(0 )
表示什么?
=
(0 +∆)−(0 )
叫做函数∆=新知探索源自如果当∆∆∆
→l 0时,平均变化率 无限趋近于一个确定的值,即 有极限,则称
∆
∆
= ()在 = 0 处可导,并把这个确定的值叫做
= ()在 = 0 处的导数(也
l
称为瞬时变化率),记作 ’ (0 )或 ’ |=0 ,即 ’ (0 )
瞬时变化率(精确到0.1).
解:血管中某一时刻药物浓度的瞬时变化率,就是药物浓度()在此时刻的导数,
从图象上看,它表示曲线()在此点处的切线的斜率.
例析
l
l
如图,画出曲线上某点处的切线,利用网格估计这条切线的斜率,可以得到此
时药物浓度瞬时变化率的近似值.
作 = 0.8处的切线,并在切线上取两点,如(0.7,0.91),(1.0,0.48),则该切线的
l
l
对原油进行冷却和加热.已知在 ℎ 第时,原油的温度(单位:
℃)为 = () = 2 − 7 + 15(0 ≤ ≤ 8).计算第2 ℎ与第
6 ℎ时,原油温度的瞬时变化率,并说明它们的意义.
同理可得 ’ (6) = 5.
在第2 ℎ和第6 ℎ时,原油温度的瞬时变化率分别为−3℃/ℎ和5℃/ℎ.说明在第
这样,当变化时, = ’ ()就是的函数,我们称它为 = ()的导函数
第五章5.1.2第2课时 导数的几何意义课件(人教版)

解析 设切点坐标为(x0,y0),
则
y
|x=x0
= lim Δx→0
x0+Δx3-2x0+Δx-x30-2x0 Δx
=3x20-2=tan π4=1,
所以x0=±1, 当x0=1时,y0=-1. 当x0=-1时,y0=1.
当t=t1时,函数的图象在t=t1处的切线l1的斜率h′(t1)<0,这时,在t =t1附近曲线降落,即函数在t=t1附近单调递减. 当t=t2时,函数的图象在t=t2处的切线l2的斜率h′(t2)<0,这时,在t =t2附近曲线降落,即函数在t=t2附近单调递减. 通过研究t=t1和t=t2发现直线l1的倾斜程度小于直线l2的倾斜程度,这 说明函数在t=t1附近比在t=t2附近降落的缓慢.
内容索引
一、导数的几何意义 二、函数的单调性与导数的关系 三、导函数(导数)
随堂演练
课时对点练
一、导数的几何意义
问题1 导数f′(x0)的几何意义是什么? 提示 我们知道导数f′(x0)表示函数y=f(x)在x=x0处的瞬时变化率, 反应了函数y=f(x)在x=x0附近的变化情况,如下图.
容易发现,平均变化率ΔΔyx=fx0+ΔΔxx-fx0表示的是割线 P0P 的斜率,当
跟踪训练 3 已知函数 f(x)=x2-12x.求 f′(x).
解 ∵Δy=f(x+Δx)-f(x)
=(Δx)2+2x·Δx-12Δx,
∴ΔΔyx=2x+Δx-12.
∴f′(x)= lim Δx→0
ΔΔyx=2x-12.
课堂小结
1.知识清单: (1)导数的几何意义. (2)函数的单调性与导数的关系. (3)导函数的概念. 2.方法归纳:方程思想、数形结合. 3.常见误区:切线过某点,这点不一定是切点.
人教A版高中数学选择性必修第二册5.1.2导数的概念及其几何意义课件

解得 x0=-23或 x0=2, ∴切点的坐标为-23,4297或(2,3). 当切点为-23,4297时,有4297=4×-23+a, 解得 a=12271; 当切点为(2,3)时,有 3=4×2+a, 解得 a=-5. ∴当 a=12271时,切点为-23,4297; 当 a=-5 时,切点为(2,3).
=Δlxim→0Δx2Δ-x 3Δx=Δlxim→0(Δx-3)=-3.故选 C.
答案:C
3.如图是函数y=f(x)的图象,则 (1)函数f(x)在区间[-1,1]上的平均变化率为________; (2)函数f(x)在区间[0,2]上的平均变化率为________.
解析:(1)函数 f(x)在区间[-1,1]上的平均变化率为f11--f--11=2-2 1=12. (2)由函数 f(x)的图象知,f(x)=x+2 3,-1≤x≤1,
=x20+x0-1. 又由导数的几何意义知 k=f′(x0)=Δlxim→0fx0+ΔΔxx-fx0 =Δlxim→0x0+Δx3-2x0Δ+x Δx-x30-2x0 =3x20-2, ∴x20+x0-1=3x20-2, ∴2x20-x0-1=0.
∵x0≠1,∴x0=-12. ∴k=x20+x0-1=-54, ∴切线方程为 y-(-1)=-54(x-1), 即 5x+4y-1=0,故选 A. 答案:A
x+1,1<x≤3. 所以函数 f(x)在区间[0,2]上的平均变化率为f22--f00=3-2 32=34. 答案:(1)12 (2)34
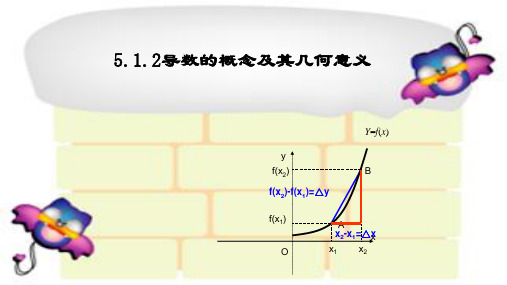
知识点二 导数的几何意义 (一)教材梳理填空
导数的几何意义 函数 y=f(x)在 x=x0 处的导数就是切线 PT 的斜率 k,即 k=_Δlxi_m→_0_f_x_0_+__Δ_Δx_x_-__f_x_0_ =f′(x0).
导数的概念及其几何意义【新教材】人教A版高中数学选择性必修第二册优秀课件

素 养
合 作
沿着曲线 y=f (x)无限趋近于点 P0 时,即当 Δx→0 时,k 无限趋近于
课
探 究
函数 y=f (x)在 x=x0 处的导数,因此,函数 y=f (x)在 x=x0 处的导数
时 分
层
释 疑 难
f ′(x0)就是_切__线___P_0_T__的斜率 k0,即 k0=lim Δx→0
返 首 页
·
第5章 5.1 5.1.2 导数的概念及其几何意义-【新教材】 人教A 版(201 9)高 中数学 选择性 必修第 二册课 件(共60 张PPT)
7
·
情 境
2.导数的几何意义
课 堂
导
小
学
(1)导数的几何意义
探
fx-fx0
·
结 提
新 知
如图,割线 P0P 的斜率 k=___x_-__x_0____.记 Δx=x-x0,当点 P
5
·
情
课
境
堂
导
小
学
1.导数的概念
·
结
探
提
新 知
如果当 Δx→0 时,平均变化率ΔΔyx无限趋近于一个确定的值,即ΔΔyx
素 养
合
作 探
有极限,则称 y=f (x)在 x=x0 处_可__导_,并把这个确__定__的__值__叫做 y=f (x)
课 时
究 释
在 x=x0 处的导数(也称为_瞬__时__变__化_率__),记作 f ′(x0)或__y_′|_x=__x_0_,即
课
探
时
究 术参考?
分 层
释
作
疑 难
思考:什么是平均变化率?如何理解瞬时变化率?
5.1.2导数的概念及其几何意义课件-高二上学期数学人教A版选择性必修第二册

例 5 下图是人体血管中药物浓度 c f (t) (单位: mg / mL )随时间 t(单位:min) 变化的函数图象,根据图象,估计 t 0.2 ,0.4,0.6,0.8 min 时,血管中药物浓度 的瞬时变化率(精确到 0.1).
解:血管中某一时刻药物浓度的瞬吋变化率,就是药物浓度 f (t) 在此时刻的导
从 f (x0 ) 变化到 f (x0 Δx) . 这时,x 的变化量为 Δx ,y 的变化量
为 Δy f (x0 Δx) f (x0 ) .
把比值
Δy Δx
Δy ,即 Δx
f (x0
Δx) Δx
f (x0 )
叫做函数 y
f (x)
从 x0 到
x0 x 的平均变化率.
如果当 Δx 0 时,平均变化率 Δy 无限趋近于一个确定的值, Δx
答案:D 解析:由题意,得 f (5) 5 5 0 , f (5) 1.故选 D.
2.若函数 f (x) 在 x x0 处存在导数,则 lim f x0 h f x0 的值( )
h0
h
A.与 x0 ,h 都有关
B.与 x0 有关,与 h 无关
C.与 h 有关,与 x0 无关
D.与 x0 ,h 都无关
1.4
,所以
f
(0.8)
1.4
.
下表给出了药物浓度的瞬时变化率的估计值.
t
0.2
0.4
0.6
0.
药物浓度的瞬时变化率 f (t)
0.4
0
-0.7
-1
5.导函数的概念
从求函数 y f (x) 在 x x0 处导数的过程可以看到,当 x x0 时, f (x0 ) 是一个
唯一确定的数. 当 x 变化时, y f (x) 就是 x 的函数,称它为 y f (x) 的导函数
高中数学第五章导数的概念及其几何意义第2课时导数的几何意义pptx课件新人教A版选择性必修第二册

()
【答案】(1)A (2)D 【解析】(1)由导数的几何意义知,导函数递增,则说明函数切线斜 率随x增大而变大. (2) 从 导 函 数 的 图 象 可 知 两 个 函 数 在 x0 处 斜 率 相 同 , 可 以 排 除 B , C.再者导函数的函数值反映的是原函数的斜率大小,可明显看出y=f(x) 的导函数的值在减小,所以原函数的斜率慢慢变小,排除A.
【预习自测】
判断正误(正确的画“√”,错误的画“×”)
(1)曲线y=f(x)上的每一点都有切线.
()
(2)直线与曲线相切,则直线与已知曲线只有一个公共点. ( )
【答案】(1)× (2)×
导数的几何意义
(1)函数y=f(x)在x=x0处的导数f′(x0)就是切线P0T的斜率k0,即k0= __Δ_lxi_m→_0_f(_x_0+__Δ_Δ_xx)_-__f_(x_0_)__=f′(x0).
易错警示 混淆曲线“在”或“过”某点的切线致误
求函数y=x3-3x2+x的图象上过原点的切线方程.
【错解】∵Δy=f(Δx+0)-f(0)=(Δx)3-3(Δx)2+Δx, ∴ΔΔyx=1-3Δx+(Δx)2, ∴f′(0)= lim [1-3Δx+(Δx)2]=1.
Δx→0
故所求切线方程为 y=x.
(2)导数f′(x0)的几何意义是曲线 y=f(x)在点(x0,f(x0))处的切线的 ___斜__率___,物理意义是运动物体在x0时刻的__瞬__时__速__度___.
【预习自测】
如果曲线y=f(x)在点(x0,f(x0))处的切线方程为x+2y-3=0,那么 ()
A.f′(x0)>0
B.f′(x0)<0
【答案】3227 -31,2237 【解析】设直线 l 与曲线 C 的切点为(x0,y0), 因为 y′=Δlxi→m0(x+Δx)3-(x+ΔxΔ)2x+1-(x3-x2+1) =3x2-2x,则 y′|x=x0=3x20-2x0=1,解得 x0=1 或 x0=-13,
【答案】(1)A (2)D 【解析】(1)由导数的几何意义知,导函数递增,则说明函数切线斜 率随x增大而变大. (2) 从 导 函 数 的 图 象 可 知 两 个 函 数 在 x0 处 斜 率 相 同 , 可 以 排 除 B , C.再者导函数的函数值反映的是原函数的斜率大小,可明显看出y=f(x) 的导函数的值在减小,所以原函数的斜率慢慢变小,排除A.
【预习自测】
判断正误(正确的画“√”,错误的画“×”)
(1)曲线y=f(x)上的每一点都有切线.
()
(2)直线与曲线相切,则直线与已知曲线只有一个公共点. ( )
【答案】(1)× (2)×
导数的几何意义
(1)函数y=f(x)在x=x0处的导数f′(x0)就是切线P0T的斜率k0,即k0= __Δ_lxi_m→_0_f(_x_0+__Δ_Δ_xx)_-__f_(x_0_)__=f′(x0).
易错警示 混淆曲线“在”或“过”某点的切线致误
求函数y=x3-3x2+x的图象上过原点的切线方程.
【错解】∵Δy=f(Δx+0)-f(0)=(Δx)3-3(Δx)2+Δx, ∴ΔΔyx=1-3Δx+(Δx)2, ∴f′(0)= lim [1-3Δx+(Δx)2]=1.
Δx→0
故所求切线方程为 y=x.
(2)导数f′(x0)的几何意义是曲线 y=f(x)在点(x0,f(x0))处的切线的 ___斜__率___,物理意义是运动物体在x0时刻的__瞬__时__速__度___.
【预习自测】
如果曲线y=f(x)在点(x0,f(x0))处的切线方程为x+2y-3=0,那么 ()
A.f′(x0)>0
B.f′(x0)<0
【答案】3227 -31,2237 【解析】设直线 l 与曲线 C 的切点为(x0,y0), 因为 y′=Δlxi→m0(x+Δx)3-(x+ΔxΔ)2x+1-(x3-x2+1) =3x2-2x,则 y′|x=x0=3x20-2x0=1,解得 x0=1 或 x0=-13,
新教材高中数学第5章导数的概念及其几何意义pptx课件新人教A版选择性必修第二册

根据导数的几何意义,可知函数y=f (x)的切线斜率在[a,b]内单调
递增,观察图象,只有A选项符合.
发现规律 导数几何意义理解中的两个关键点
f ′(x0)>0
关键点一:y=f (x)在点x=x0处的切线斜率为k,则k>0⇔_________;
f ′(x0)<0
f ′(x0)=0
k<0⇔__________;k=0⇔_________.
[解]
Δ
+Δ 3 +1− 3 −1
=
Δ
Δ
3 Δ 2 +3 2 Δ+ Δ 3
=
Δ
=3xΔx+3x2+(Δx)2,
Δ
则 lim =3x2,因此y′=3x2.
Δ→0 Δ
设过点M(1,1)的直线与曲线y=x3+1相切于点(0 ,03 +1),根据
导数的几何意义知曲线在点P处的切线的斜率为k=302 ①,过点M和
如图,割线P0P的斜率k=_____________.记Δx=x-x
0,当点P沿着
曲线y=f (x)无限趋近于点P0时,即当Δx→0时,k无限趋近于函数y=
f (x)在x=x0处的导数,因此,函数y=f (x)在x=x0
切线P0T
处的导数f ′(x0)就是_________的斜率k
0,即
0 +Δ − 0
1
2
3
4
5
2.函数y=f (x)在x=x0处的导数f ′(x0)的几何意义是(
)
A.在点(x0,f (x0))处与y=f (x)的图象只有一个交点的直线的斜率
B.过点(x0,f (x0))的切线的斜率
C.点(x0,f (x0))与点(0,0)的连线的斜率
5.1.2导数的概念及其几何意义课件-高中数学人教A版选择性必修第二册
s
v ;
t
(2)求平均速度
(3)求极限 lim
x 0
s
s(t t ) s (t )
lim
.
t
t
x 0
2由导数的定义可得求导数的一般步骤:
(1)求函数的增量Δy=f(x0+Δt)-f(x0)
y
x
讲
课
人
:
邢
启
强
(2)求平均变化率
(3)求极限 f ' ( x0 ) lim
x 0
y
x
是唯一的;如不存在,则在此点处无切线;
3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个.
10
解:我们用曲线h(t)在t=t0, t1,t2处的切线斜率,刻画曲线h(t)
在上述三个时刻附近的变化情况.
(1)当t=t0时,曲线h(t)在t=t0处的切线l0平行于t轴,h'(t0)=0.
x
1
lim [3 x 2 3 xx ( x ) 2 ] x 2 .
3 x 0
y
4
1
y x3
3
3
P
2
1
-2 -1
O
-1
x
1
2
-2
y | x 2 2 2 4.
即点P处的切线的斜率等于4.
讲
课
人
:
邢
启
强
(2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.
根据导数的定义,
x
x
x
y
4 x x 2 7x
'
lim x 3 3,
v ;
t
(2)求平均速度
(3)求极限 lim
x 0
s
s(t t ) s (t )
lim
.
t
t
x 0
2由导数的定义可得求导数的一般步骤:
(1)求函数的增量Δy=f(x0+Δt)-f(x0)
y
x
讲
课
人
:
邢
启
强
(2)求平均变化率
(3)求极限 f ' ( x0 ) lim
x 0
y
x
是唯一的;如不存在,则在此点处无切线;
3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个.
10
解:我们用曲线h(t)在t=t0, t1,t2处的切线斜率,刻画曲线h(t)
在上述三个时刻附近的变化情况.
(1)当t=t0时,曲线h(t)在t=t0处的切线l0平行于t轴,h'(t0)=0.
x
1
lim [3 x 2 3 xx ( x ) 2 ] x 2 .
3 x 0
y
4
1
y x3
3
3
P
2
1
-2 -1
O
-1
x
1
2
-2
y | x 2 2 2 4.
即点P处的切线的斜率等于4.
讲
课
人
:
邢
启
强
(2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.
根据导数的定义,
x
x
x
y
4 x x 2 7x
'
lim x 3 3,
5.1 导数的概念及其意义(导数的几何意义)课件-高二上学期数学人教A版(2019)选择性必修第二册

(4)曲线的切线不一定与曲线只有一个公共点.(
)
(5)与曲线只有一个公共点的直线一定是曲线的切线.( × )
)
合作探究 释疑解惑
探究一
导数的几何意义与函数图象
【例1】 若函数y=f(x)的导函数在区
间[a,b]上单调递增,则函数y=f(x)在区
间[a,b]上的大致图象可能是(
)
解析:已知函数y=f(x)的导函数y=f'(x)
(2)由直线l1,l2和x轴所围成的三角形的面积.
y
(+Δ)2 +(+Δ)-2-( 2 +-2)
解:(1)y'= lim =
=2x+1.
Δ
Δ→0 x x→0
因为直线l1为曲线y=x2+x-2在点(1,0)处的切线,
所以直线l1的斜率k1=y'|x=1=3,可得直线l1的方程为y=3x-3.
Δ
x→0
= lim (4x+2Δx)=4x.
Δ→0
(1)∵切线的倾斜角为45°,
∴切线的斜率为tan 45°=1.
设切点的坐标为(x0,y0),则 y'|= =4x0=1,解得
0
∴该切点的坐标为
1 9
,
4 8
.
1
x0= ,
4
(2)∵切线平行于直线4x-y-2=0,
∴切线的斜率为4.
则切线的斜率 k=2x0.
切线方程为 y-x02 =2x0(x-x0),将点(-1,0)的坐标代入,
得-x02 =2x0(-1-x0),解得 x0=0 或 x0=-2.
当x0=0时,切线的斜率k=0,过点(-1,0)的切线方程为y=0;
)
(5)与曲线只有一个公共点的直线一定是曲线的切线.( × )
)
合作探究 释疑解惑
探究一
导数的几何意义与函数图象
【例1】 若函数y=f(x)的导函数在区
间[a,b]上单调递增,则函数y=f(x)在区
间[a,b]上的大致图象可能是(
)
解析:已知函数y=f(x)的导函数y=f'(x)
(2)由直线l1,l2和x轴所围成的三角形的面积.
y
(+Δ)2 +(+Δ)-2-( 2 +-2)
解:(1)y'= lim =
=2x+1.
Δ
Δ→0 x x→0
因为直线l1为曲线y=x2+x-2在点(1,0)处的切线,
所以直线l1的斜率k1=y'|x=1=3,可得直线l1的方程为y=3x-3.
Δ
x→0
= lim (4x+2Δx)=4x.
Δ→0
(1)∵切线的倾斜角为45°,
∴切线的斜率为tan 45°=1.
设切点的坐标为(x0,y0),则 y'|= =4x0=1,解得
0
∴该切点的坐标为
1 9
,
4 8
.
1
x0= ,
4
(2)∵切线平行于直线4x-y-2=0,
∴切线的斜率为4.
则切线的斜率 k=2x0.
切线方程为 y-x02 =2x0(x-x0),将点(-1,0)的坐标代入,
得-x02 =2x0(-1-x0),解得 x0=0 或 x0=-2.
当x0=0时,切线的斜率k=0,过点(-1,0)的切线方程为y=0;
高中数学5-1-2导数的概念及其几何意义第1课时导数的概念课件新人教A版选择性必修第二册

【解题探究】利用导数的定义求解.
用导数定义求函数在某一点处的导数的步骤 (1)求函数的增量 Δy=f(x0+Δx)-f(x0); (2)求平均变化率ΔΔyx=f(x0+ΔΔxx)-f(x0); (3)求极限Δlxim→0ΔΔyx.
导数的定义的变形形式 Δlxi→m0f(x0--ΔxΔ)-x f(x0)=Δlxi→m0f(x0+nnΔΔxx)-f(x0)=Δlxi→m0f(x0+Δx)2-Δxf(x0-Δx) =f′(x0).
3.函数y=x2+x在x=1到x=1+Δx之间的平均变化率为 ( )
A.Δx+2
B.Δx+3
C.2Δx+(Δx)2
D.3Δx+(Δx)2
【答案】B 【解析】Δy=(1+Δx)2+(1+Δx)-12-1=(Δx)2+3Δx,所以ΔΔyx=
(Δx)2Δ+x 3Δx=Δx+3.
导数的概念(瞬时变化率)
函数 f(x)在区间[x0,x0+Δx]上的平均变化率为6x0Δx+Δx3(Δx)2=6x0+ 3Δx.
【解题探究】直接利用概念求解.
求平均变化率的策略 (1)求 Δy 时,要把 f(Δx+x)和 f(x)表示出来,再作差. (2)求平均变化率时,先计算自变量和函数值的改变量 Δx=x1-x0,Δy =f(x1)-f(x0),再利用公式ΔΔyx=f(xx1)1- -fx(0x0)求出平均变化率.
lim (6+3Δx)=6.
Δx→0
2.设f(x)=ax3+2,若f′(-1)=3,则a=________. 【答案】1 【解析】Δlxim→0a(-1+Δx)3+Δ2-x [a·(-1)3+2]=Δlxi→ m0(aΔx2-3aΔx+3a) =3a=3,∴a=1.
课堂互动
题型1 求函数的平均变化率
5.1.2导数的概念及其几何意义课件高二上学期数学人教A版选择性

提示 不一定.曲线y=f(x)在点P(x0,f(x0))处的切线l与曲线y=f(x)的交点不一
定只有一个,如图所示.
自主诊断
1.[苏教版教材习题]已知函数y=f(x)的图象在点M(1,f(1))处的切线方程是
1
y=2x+2
,求f(1)+f'(1)的值.
解 由已知点 M(1,f(1))在切线上,所以
应该是
( 0 +Δ)-( 0 )
mΔx,要注意公式的变形.求解时要注意应用 lim
Δ
Δ→0
( 0 +Δ)-( 0 )
m
的应用,这里的
Δ
x→0
m 不等于 0.
=
变式训练 3 若
f(x 0 +3x)-f(x 0 )
f'(x0)=4,则 lim
等于(
x
Δ→0
切点处的导数为切线斜率,所以
1
5
f(1)= +2= ,
2
2
1
f'(1)= ,即
2
f(1)+f'(1)=3.
2.[人教B版教材例题]已知函数
1
f(x)=x
,求曲线y=f(x)在(2,f(2))处切线的方
程.
1 -1
(2+Δ)-(2)
解 f'(2)= lim
= 2+Δ 2 = lim
Δ→0
lim
x
= Δ→0
.
y
'(x0)= x
x→0
导数 (也
2.函数y=f(x)的导函数
对于函数y=f(x),当x=x0时,f'(x0)是一个确定的数,当x变化时,y=f'(x)就是x的
人教版高中数学 选择性必修二 A版5.1.2《导数的概念及其几何意义》课件PPT

作业设计
课本P70.
习题5.1: 1、2、3、4、5、6、7.
在PPT软件中双击图标ห้องสมุดไป่ตู้开配套教案
人教A版高中数学选择性必修二
5.1.2 导数的概念及其
几何意义
第五章 一元函数的导数及其应用
汇报人:XXX
人教A版高中数学选择性必修二
5.1.2 导数的概念及其
几何意义
第五章 一元函数的导数及其应用
汇报人:XXX
目 录
01
学习目标
02
新知讲解
03
课堂练习
04
课程小结
第一部分
学习目标
学习目标
1. 理解函数在0处的瞬时变化率即导数的概念并会求其值.
2.理解导数的几何意义,并会应用之求切线方程.
3.感受新概念的定义、运动变化的数学思想方法,从而
温馨提示:直接利用概念求平均变化率,先求出表达
式,再直接代入数据就可以得出相应的导
数的值.
跟踪练习
解析:当自变量从0变化到0+Δ时,函数的平均变化
Δ+0 − 0
△
率为 =
△
Δ
=
= 30 2 +30 △ + △
2
0 +△ 3 −0 3
Δ
当0=1,Δ → 0时,
1
∆
2
1
∆)=1−2
2
1
2
× 22 )
课堂互动
∴物体在时刻t=2处的瞬时速度是1−2 .
课堂互动
3.已知 =2-3,则 在 = 0处的切线的方程
(
3 + = 0
解析: ′(0)=
)
Δ
导数的概念及其几何意义(第一课时)课件高二上学期数学人教A版选择性

*导数(瞬时变化率)为正,体现了上升的变化趋势.
课堂小结
*
知识层面
➢ 导数的概念; ➢ 根据定义求给定函数在某点处导数的步骤; ➢ 应用导数的意义对实际问题进行了分析和解释.
思想方法层面
➢ 运动变化的观点; ➢ 极限思想 .
*
*
课后作业
必做题
*
3.查阅资料:牛顿是怎样发现导数的
课后作业
选做题
*
课堂练习
思考2
*
在本题中 f (x0 ) (0≤x0≤8) 是原油温度在时刻 x0 的瞬时变化率,它反映的是原油温度在时刻 x0 附近的 变化情况.
导数(瞬时变化率)为负,体现了下降的变化趋势.
f (6) 5 表示在第 6 h 时,原油温度的瞬时变化率为 5℃/h,这说明 在第 6 h 附近,原油温度大约以 5℃/h的速率上升.
*
这个过程中,函数值的
*
单击此处输入你的正文,文字 是您思想的提炼,为了最终演 示发布的良好效果,请尽量言 简意赅的阐述观点;根据需要
可酌情增减文字
*
问题:函数 y = f (x) 在 x = x0 处的瞬时变化率该如何表示呢?
*
*
瞬时变化率 函数 y=f (x)
x
无限趋近于
0
当 无限趋近于 0 时x,0 平均x 变化率无限趋近于
*
人教A版数学选择性必修第二册
5.1.2 导数的概念及其几何意义 (第一课时)
*
*
温故知新
前面
平均变化率 瞬时变化率
*
*
温故知新
前面
平均变化率 瞬时变化率
*
*
温故知新
*
本课内容
单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量 言简意赅的阐述观点;根据需要可酌情增减文字,以便观者可以准确理解您所传达的信 息。单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请 尽量言简意赅的阐述观点;根据需要可酌情增减文字,以便观者可以准确理解您所传达 的信息。
课堂小结
*
知识层面
➢ 导数的概念; ➢ 根据定义求给定函数在某点处导数的步骤; ➢ 应用导数的意义对实际问题进行了分析和解释.
思想方法层面
➢ 运动变化的观点; ➢ 极限思想 .
*
*
课后作业
必做题
*
3.查阅资料:牛顿是怎样发现导数的
课后作业
选做题
*
课堂练习
思考2
*
在本题中 f (x0 ) (0≤x0≤8) 是原油温度在时刻 x0 的瞬时变化率,它反映的是原油温度在时刻 x0 附近的 变化情况.
导数(瞬时变化率)为负,体现了下降的变化趋势.
f (6) 5 表示在第 6 h 时,原油温度的瞬时变化率为 5℃/h,这说明 在第 6 h 附近,原油温度大约以 5℃/h的速率上升.
*
这个过程中,函数值的
*
单击此处输入你的正文,文字 是您思想的提炼,为了最终演 示发布的良好效果,请尽量言 简意赅的阐述观点;根据需要
可酌情增减文字
*
问题:函数 y = f (x) 在 x = x0 处的瞬时变化率该如何表示呢?
*
*
瞬时变化率 函数 y=f (x)
x
无限趋近于
0
当 无限趋近于 0 时x,0 平均x 变化率无限趋近于
*
人教A版数学选择性必修第二册
5.1.2 导数的概念及其几何意义 (第一课时)
*
*
温故知新
前面
平均变化率 瞬时变化率
*
*
温故知新
前面
平均变化率 瞬时变化率
*
*
温故知新
*
本课内容
单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请尽量 言简意赅的阐述观点;根据需要可酌情增减文字,以便观者可以准确理解您所传达的信 息。单击此处输入你的正文,文字是您思想的提炼,为了最终演示发布的良好效果,请 尽量言简意赅的阐述观点;根据需要可酌情增减文字,以便观者可以准确理解您所传达 的信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
瞬时速度——瞬时变化率
lim h(1 t) h(1) 5
t 0
t
问题2 抛物线的切线斜率 f (x) x2在P0 (1,1)处的切线斜率
割线斜率 ——平均变化率
k f (1 x) f (1) x 2 x
切线斜率 ——瞬时变化率
lim f (1 x) f (1) 2
x0
x
高中数学高二上册
当x 0时,y x 1. x x
高中数学
高中数学高二上册
定无限义趋:近如于果一当个确x 无定限的趋值近,于即0时y ,有平极均限变,化我率们称yx
x y = f (x) 在 x = x0 处可导 , 并把这个确定的值叫做
y = f (x) 在 x = x0 处的导数 ( 也称为瞬时变化率 ) ,
lim h(1 t) h(1) 5
t 0
t
问题2 抛物线的切线斜率
f (x) x2
割线斜率 ——平均变化率
k f (1 x) f (1) x 2 x
切线斜率 ——瞬时变化率
lim f (1 x) f (1) 2
x0
x
高中数学高二上册
问题2 一般地,对于函数 y=f (x),你能用 “平均变化率”逼近“瞬时变化率” 的思想方法研究其在某点 (如 x = x0) 处的瞬时变化率吗?
高中数学
为了研究函数 y=f (x) 在 x = x0 处的瞬时 变化率,我们可以选取自变量 x 的一个改变
量x, x 可以是正值,也可以是负值,但不
为 0 . 计算自变量 x 从 x0 变化到 x0 x 这个过 程中函数值的平均变化率.
高中数学高二上册
追问2:自变量 x 从 x0 变化到x0 x 这个过程 中,函数值的平均变化率如何表示呢?
高中数学
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度
h(t) 4.9t2 4.8t 11
平均速度——平均变化率
v h(1 t) h(1) 4.9t 5 t
瞬时速度——瞬时变化率
lim h(1 t) h(1) 5
t 0
t
问题2 抛物线的切线斜率
f (x) x2
割线斜率 ——平均变化率
高中数学
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度
h(t) 4.9t2 4.8t 11
平均速度
v h(1 t) h(1) 4.9t 5 t
瞬时速度
ቤተ መጻሕፍቲ ባይዱ
x0
x
高中数学高二上册
问题1 解决这两类问题时有什么共性? 都采用了由“平均变化率”逼近
“瞬时变化率”的思想方法.
高中数学
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度
h(t) 4.9t2 4.8t 11
平均速度——平均变化率
v h(1 t) h(1) 4.9t 5 t
瞬时速度——瞬时变化率
t
切线斜率 ——瞬时变化率
lim f (1 x) f (1) 2
x0
x
高中数学
高中数学高二上册
函数 y=f (x)
x
无限趋近于
0
x0 x
无限趋近于
x0
y f (x0 x) f (x0 ) 无限趋近于 ?
x
x
高中数学高二上册
追问4:当 x无限趋近于 0 时,平均变化率 y 是否一定会无限趋近于一个确定 x 的值呢?
k f (1 x) f (1) x 2 x
切线斜率 ——瞬时变化率
lim f (1 x) f (1) 2
x0
x
高中数学
高中数学高二上册
函数 y=f (x)
自变量 x : x0
x
x0 x
函数值 y :f (x0 ) y f (x0 x) f (x0) f (x0 x)
函数 y=f (x) 从 x0 到 x0 x 的平均变化率:
高中数学
高中数学高二上册
追问1:为了研究函数 y=f (x) 在 x = x0 处的 瞬时变化率,我们可以研究哪个范围 内函数值的平均变化率呢?
高中数学
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度
h(t) 4.9t2 4.8t 11
平均速度——平均变化率
v h(1 t) h(1) 4.9t 5 t
记作 f (x0 ) 或 y |xx0 . 用极限符号表示这个定义,就是
f
(x0 )
lim
x0
y x
lim
x0
f
( x0
x) x
f
(x0 ) .
导数是平均变化率的极限,是瞬时变化率的数学表达.
高中数学高二上册
问题3 根据导数的定义,你能用导数来重述 跳水运动员速度问题和抛物线切线问 题的结论吗?
y f (x0 x) f (x0 )
x
x
高中数学高二上册
追问3:函数 y = f (x) 在 x = x0 处的瞬时变化 率该如何表示呢?
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度 问题2 抛物线的切线斜率
高中数学
瞬时速度——瞬时变化率
lim h(1 t) h(1) 5
t 0
t 0
t
问题2 抛物线的切线斜率
f (x) x2
割线斜率
k f (1 x) f (1) x 2 x
切线斜率
lim f (1 x) f (1) 2
x0
x
高中数学高二上册
问题1 解决这两类问题时有什么共性?
高中数学
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度
h(t) 4.9t2 4.8t 11
高中数学高二上册
导数的概念及其几何意义(1)
年 级:高二 主讲人:
学 科:数学(人教A版) 学 校:
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度
h(t) 4.9t2 4.8t 11
平均速度
v h(1 t) h(1) 4.9t 5 t
瞬时速度
lim h(1 t) h(1) 5
高中数学
高中数学高二上册
这说明当x 无限趋近于0时,平均变化 率 y 不一定能无限趋近于一个确定的值.
x
高中数学
高中数学
高中数学高二上册
举反例:
考查 f (x)=| x | 在 x=0 附近的变化情况.
y f (0 x) f (0) | x |.
x
x
x
当x 0时,y x 1. x x
平均速度——平均变化率
v h(1 t) h(1) 4.9t 5 t
瞬时速度——瞬时变化率
lim h(1 t) h(1) 5
t 0
t
问题2 抛物线的切线斜率
f (x) x2
割线斜率 ——平均变化率
k f (1 x) f (1) x 2 x
切线斜率 ——瞬时变化率
lim f (1 x) f (1) 2
lim h(1 t) h(1) 5
t 0
t
问题2 抛物线的切线斜率 f (x) x2在P0 (1,1)处的切线斜率
割线斜率 ——平均变化率
k f (1 x) f (1) x 2 x
切线斜率 ——瞬时变化率
lim f (1 x) f (1) 2
x0
x
高中数学高二上册
当x 0时,y x 1. x x
高中数学
高中数学高二上册
定无限义趋:近如于果一当个确x 无定限的趋值近,于即0时y ,有平极均限变,化我率们称yx
x y = f (x) 在 x = x0 处可导 , 并把这个确定的值叫做
y = f (x) 在 x = x0 处的导数 ( 也称为瞬时变化率 ) ,
lim h(1 t) h(1) 5
t 0
t
问题2 抛物线的切线斜率
f (x) x2
割线斜率 ——平均变化率
k f (1 x) f (1) x 2 x
切线斜率 ——瞬时变化率
lim f (1 x) f (1) 2
x0
x
高中数学高二上册
问题2 一般地,对于函数 y=f (x),你能用 “平均变化率”逼近“瞬时变化率” 的思想方法研究其在某点 (如 x = x0) 处的瞬时变化率吗?
高中数学
为了研究函数 y=f (x) 在 x = x0 处的瞬时 变化率,我们可以选取自变量 x 的一个改变
量x, x 可以是正值,也可以是负值,但不
为 0 . 计算自变量 x 从 x0 变化到 x0 x 这个过 程中函数值的平均变化率.
高中数学高二上册
追问2:自变量 x 从 x0 变化到x0 x 这个过程 中,函数值的平均变化率如何表示呢?
高中数学
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度
h(t) 4.9t2 4.8t 11
平均速度——平均变化率
v h(1 t) h(1) 4.9t 5 t
瞬时速度——瞬时变化率
lim h(1 t) h(1) 5
t 0
t
问题2 抛物线的切线斜率
f (x) x2
割线斜率 ——平均变化率
高中数学
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度
h(t) 4.9t2 4.8t 11
平均速度
v h(1 t) h(1) 4.9t 5 t
瞬时速度
ቤተ መጻሕፍቲ ባይዱ
x0
x
高中数学高二上册
问题1 解决这两类问题时有什么共性? 都采用了由“平均变化率”逼近
“瞬时变化率”的思想方法.
高中数学
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度
h(t) 4.9t2 4.8t 11
平均速度——平均变化率
v h(1 t) h(1) 4.9t 5 t
瞬时速度——瞬时变化率
t
切线斜率 ——瞬时变化率
lim f (1 x) f (1) 2
x0
x
高中数学
高中数学高二上册
函数 y=f (x)
x
无限趋近于
0
x0 x
无限趋近于
x0
y f (x0 x) f (x0 ) 无限趋近于 ?
x
x
高中数学高二上册
追问4:当 x无限趋近于 0 时,平均变化率 y 是否一定会无限趋近于一个确定 x 的值呢?
k f (1 x) f (1) x 2 x
切线斜率 ——瞬时变化率
lim f (1 x) f (1) 2
x0
x
高中数学
高中数学高二上册
函数 y=f (x)
自变量 x : x0
x
x0 x
函数值 y :f (x0 ) y f (x0 x) f (x0) f (x0 x)
函数 y=f (x) 从 x0 到 x0 x 的平均变化率:
高中数学
高中数学高二上册
追问1:为了研究函数 y=f (x) 在 x = x0 处的 瞬时变化率,我们可以研究哪个范围 内函数值的平均变化率呢?
高中数学
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度
h(t) 4.9t2 4.8t 11
平均速度——平均变化率
v h(1 t) h(1) 4.9t 5 t
记作 f (x0 ) 或 y |xx0 . 用极限符号表示这个定义,就是
f
(x0 )
lim
x0
y x
lim
x0
f
( x0
x) x
f
(x0 ) .
导数是平均变化率的极限,是瞬时变化率的数学表达.
高中数学高二上册
问题3 根据导数的定义,你能用导数来重述 跳水运动员速度问题和抛物线切线问 题的结论吗?
y f (x0 x) f (x0 )
x
x
高中数学高二上册
追问3:函数 y = f (x) 在 x = x0 处的瞬时变化 率该如何表示呢?
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度 问题2 抛物线的切线斜率
高中数学
瞬时速度——瞬时变化率
lim h(1 t) h(1) 5
t 0
t 0
t
问题2 抛物线的切线斜率
f (x) x2
割线斜率
k f (1 x) f (1) x 2 x
切线斜率
lim f (1 x) f (1) 2
x0
x
高中数学高二上册
问题1 解决这两类问题时有什么共性?
高中数学
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度
h(t) 4.9t2 4.8t 11
高中数学高二上册
导数的概念及其几何意义(1)
年 级:高二 主讲人:
学 科:数学(人教A版) 学 校:
高中数学
高中数学高二上册
问题1 高台跳水运动员的速度
h(t) 4.9t2 4.8t 11
平均速度
v h(1 t) h(1) 4.9t 5 t
瞬时速度
lim h(1 t) h(1) 5
高中数学
高中数学高二上册
这说明当x 无限趋近于0时,平均变化 率 y 不一定能无限趋近于一个确定的值.
x
高中数学
高中数学
高中数学高二上册
举反例:
考查 f (x)=| x | 在 x=0 附近的变化情况.
y f (0 x) f (0) | x |.
x
x
x
当x 0时,y x 1. x x
平均速度——平均变化率
v h(1 t) h(1) 4.9t 5 t
瞬时速度——瞬时变化率
lim h(1 t) h(1) 5
t 0
t
问题2 抛物线的切线斜率
f (x) x2
割线斜率 ——平均变化率
k f (1 x) f (1) x 2 x
切线斜率 ——瞬时变化率
lim f (1 x) f (1) 2
