“胡不归”最值问题
中考数学专题复习38几何最值之胡不归问题(全国通用解析版)
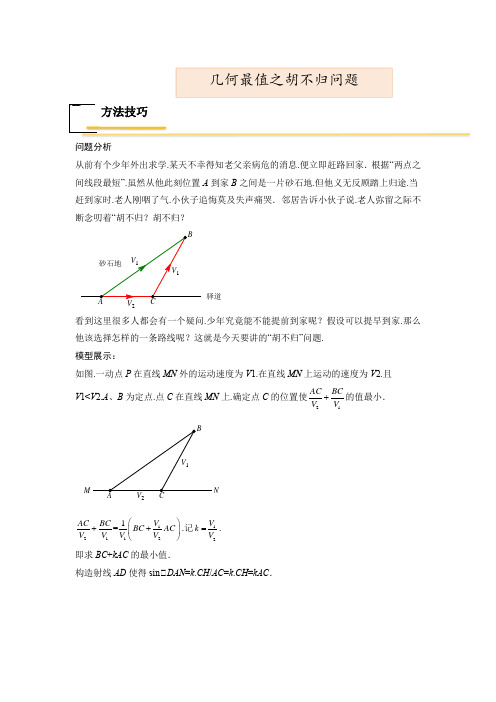
问题分析从前有个少年外出求学.某天不幸得知老父亲病危的消息.便立即赶路回家.根据“两点之间线段最短”.虽然从他此刻位置A 到家B 之间是一片砂石地.但他义无反顾踏上归途.当赶到家时.老人刚咽了气.小伙子追悔莫及失声痛哭.邻居告诉小伙子说.老人弥留之际不断念叨着“胡不归?胡不归?看到这里很多人都会有一个疑问.少年究竟能不能提前到家呢?假设可以提早到家.那么他该选择怎样的一条路线呢?这就是今天要讲的“胡不归”问题. 模型展示:如图.一动点P 在直线MN 外的运动速度为V 1.在直线MN 上运动的速度为V 2.且V 1<V 2.A 、B 为定点.点C 在直线MN 上.确定点C 的位置使21AC BCV V +的值最小.121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭.记12V k V =. 即求BC +kAC 的最小值.构造射线AD 使得sin∠DAN =k .CH /AC =k .CH =kAC .V 1V 2V 1驿道砂石地ABCV 2V 1MNCBA几何最值之胡不归问题方法技巧将问题转化为求BC +CH 最小值.过B 点作BH ∠AD 交MN 于点C .交AD 于H 点.此时BC +CH 取到最小值.即BC +kAC 最小.最值解法:在求形如“P A +kPB ”的式子的最值问题中.关键是构造与kPB 相等的线段.将“P A +kPB ”型问题转化为“P A +PC ”型.【例1】如图.平行四边形ABCD 中.∠DAB =60°.AB =6.BC =2.P 为边CD 上的一动点.则32PB PD的最小值等于________.【解析】已知∠A =60°.且sin60°=32.故延长AD .作PH ∠AD 延长线于H 点. ABCDPMHP DCBAABCDPH M 题型精讲即可得3PH =.∠3PB =PB +PH . 当B 、P 、H 三点共线时.可得PB +PH 取到最小值.即BH 的长.解直角∠ABH 即可得BH 长.【例2】(2021·重庆中考真题)在等边ABC 中.6AB =.BD AC ⊥ .垂足为D .点E 为AB 边上一点.点F 为直线BD 上一点.连接EF .图1 图2图3(1)将线段EF 绕点E 逆时针旋转60°得到线段EG .连接FG .∠如图1.当点E 与点B 重合.且GF 的延长线过点C 时.连接DG .求线段DG 的长; ∠如图2.点E 不与点A .B 重合.GF 的延长线交BC 边于点H .连接EH .求证:3BE BH BF +=;(2)如图3.当点E 为AB 中点时.点M 为BE 中点.点N 在边AC 上.且2DN NC =.点F 从BD 中点Q 沿射线QD 运动.将线段EF 绕点E 顺时针旋转60°得到线段EP .连接FP .当12NP MP +最小时.直接写出DPN △的面积. 【答案】(1)21;∠见解析;(243【分析】(1)∠连接AG .根据题意得出∠ABC 和∠GEF 均为等边三角形.从而可证明∠GBC ∠∠GAC .进一步求出AD =3.AG =BG =23然后利用勾股定理求解即可;∠以点F 为圆心.FB 的长为半径画弧.与BH 的延长线交于点K .连接KF .先证明出∠BFK 是顶角为120°的等腰三角形.然后推出∠FEB ∠∠FHK .从而得出结论即可;(2)利用“胡不归”模型构造出含有30°角的直角三角形.构造出12NP MP NP PJ +=+.当N 、P 、J 三点共线的时候满足条件.然后利用相似三角形的判定与性质分别计算出PN 与DN 的长度.即可得出结论. 【详解】(1)解:∠如图所示.连接AG .由题意可知.∠ABC 和∠GEF 均为等边三角形. ∠∠GFB =60°. ∠BD ∠AC . ∠∠FBC =30°.∠∠FCB =30°.∠ACG =30°. ∠AC =BC .GC =GC . ∠∠GBC ∠∠GAC (SAS ). ∠∠GAC =∠GBC =90°.AG =BG . ∠AB =6.∠AD =3.AG =BG =3 ∠在Rt ∠ADG 中.()222223321DG AD AG =+=+=∠21DG =∠证明:以点F 为圆心.FB 的长为半径画弧.与BH 的延长线交于点K .连接KF .如图. ∠∠ABC 和∠GEF 均为等边三角形. ∠∠ABC =60°.∠EFH =120°. ∠∠BEF +∠BHF =180°. ∠∠BHF +∠KHF =180°. ∠∠BEF =∠KHF .由辅助线作法可知.FB =FK .则∠K =∠FBE . ∠BD 是等边∠ABC 的高. ∠∠K =∠DBC =∠DBA =30°. ∠∠BFK =120°. 在∠FEB 与∠FHK 中.FEB FHK FBE KFB FK ∠=∠⎧⎪∠=∠⎨⎪=⎩∠∠FEB ∠∠FHK (AAS ). ∠BE =KH .∠BE +BH =KH +BH =BK . ∠FB =FK .∠BFK =120°. ∠BK 3BF .即:3BE BH BF +=;(2)如图1所示.以MP 为边构造∠PMJ =30°.∠PJM =90°.则PJ =12MP . ∠求12NP MP +的最小值.即为求NP PJ +的最小值.如图2所示.当运动至N、P、J三点共线时.满足NP PJ+最小.此时.连接EQ.则根据题意可得EQ∠AD.且EQ=12 AD.∠∠MEQ=∠A=60°.∠EQF=90°.∠∠PEF=60°.∠∠MEP=∠QEF.由题意.EF=EP.∠∠MEP∠∠QEF(SAS).∠∠EMP=∠EQF=90°.又∠∠PMJ=30°.∠∠BMJ=60°.∠MJ∠AC.∠∠PMJ=∠DNP=90°.∠∠BDC=90°.∠四边形ODNJ为矩形.NJ=OD.由题.AD=3.BD=33∠MJ∠AC.∠∠BMO∠∠BAD.∠14 BM BO MOBA BD AD===.∠OD=34BD93OM=34AD=94.设PJ=x.则MJ3.OJ3-9 4 .由题意可知.DN =23CD =2. 9324x -=. 解得:113x =. 即:PJ =11312. ∠93113434123PN =-=. ∠11434322233DPNSDN PN ==⨯⨯=. 【例3】已知抛物线2(0)y ax bx c a =++≠过点(1,0)A .(3,0)B 两点.与y 轴交于点C .=3OC .(1)求抛物线的解析式及顶点D 的坐标;(2)过点A 作AM BC ⊥.垂足为M .求证:四边形ADBM 为正方形;(3)点P 为抛物线在直线BC 下方图形上的一动点.当PBC ∆面积最大时.求点P 的坐标; (4)若点Q 为线段OC 上的一动点.问:12AQ QC +是否存在最小值?若存在.求岀这个最小值;若不存在.请说明理由.【答案】(1)抛物线的表达式为:243y x x =-+.顶点(2,1)D -;(2)证明见解析;(3)点33,24P ⎛⎫- ⎪⎝⎭;(4)存在.12AQ QC +的最小值为233+. 【详解】(1)函数的表达式为:()()()2y a x 1x 3a x 4x 3=--=-+.即:3a=3.解得:a=1.故抛物线的表达式为:2y x 4x 3=-+. 则顶点D(2,1)-; (2)OB OC 3==.OBC OCB 45∠∠︒∴==.∠A(1,0).B(3,0).∠ OB=3.OA=1. ∠AB=2.∠AM MB ABsin452︒=== 又∠D(2.-1). ()()2221102-+--=∠AM=MB=AD=BD. ∠四边形ADBM 为菱形. 又∠AMB 90∠︒=.∴菱形ADBM 为正方形;(3)设直线BC 的解析式为y=mx+n.将点B 、C 的坐标代入得:303m n n +=⎧⎨=⎩. 解得:13m n =-⎧⎨=⎩.所以直线BC 的表达式为:y=-x+3. 过点P 作y 轴的平行线交BC 于点N.设点()2P x,x 4x 3-+.则点N (x,x+3)-.则()()22ΔPBC 133S PN OB x 3x 4x 3x 3x 222=⨯=-+-+-=--. 302-<.故ΔPBC S 有最大值.此时3x 2=. 故点33P ,24⎛⎫- ⎪⎝⎭; (4)存在.理由:如图.过点C 作与y 轴夹角为30︒的直线CF 交x 轴于点F.过点A 作AH CF ⊥.垂足为H.交y 轴于点Q. 此时1HQ CQ 2=.则1AQ QC2+最小值=AQ+HQ=AH.在Rt∠COF中.∠COF=90°.∠FOC=30°.OC=3.tan∠FCO=FO CO.3.∠F(3利用待定系数法可求得直线HC的表达式为:y3x3=+…∠.∠∠COF=90°.∠FOC=30°.∠∠CFO=90°-30°=60°.∠∠AHF=90°.∠∠FAH=90°-60°=30°.3∠Q(0,3 ).利用待定系数法可求得直线AH的表达式为:33 y x=+联立∠∠并解得:133 x4-=.故点13333H-+⎝⎭.而点A(1,0).则233+=AH.即1AQ QC2+的最小值为233+.1.如图.△ABC中.AB=AC=10.tanA=2.BE∠AC于点E.D是线段BE上的一个动点.则55CD BD的最小值是______.【答案】B【详解】如图.作DH∠AB于H.CM∠AB于M.提分作业∠BE∠AC. ∠∠AEB=90°. ∠tanA=BEAE=2.设AE=a.BE=2a. 则有:100=a 2+4a 2. ∠a 2=20.5-25. 5∠AB=AC.BE∠AC.CM∠AB.5 ∠∠DBH=∠ABE.∠BHD=∠BEA. ∠5sin DH AE DBH BD AB ∠===. 55BD=CD+DH. ∠CD+DH≥CM. 55 5BD 的最小值为5 故选B .2.在平面直角坐标系中.将二次函数()20y ax a =>的图象向右平移1个单位.再向下平移2个单位.得到如图所示的抛物线.该抛物线与x 轴交于点A 、B (点A 在点B 的左侧).1OA =.经过点A 的一次函数()0y kx b k =+≠的图象与y 轴正半轴交于点C .且与抛物线的另一个交点为D .ABD ∆的面积为5.(1)求抛物线和一次函数的解析式;(2)抛物线上的动点E 在一次函数的图象下方.求ACE ∆面积的最大值.并求出此时点E 的坐标;(3)若点P 为x 轴上任意一点.在(2)的结论下.求35PE PA +的最小值. 【答案】(1)21322y x x =--;1122y x =+;(2)ACE ∆的面积最大值是2516.此时E 点坐标为315,28⎛⎫- ⎪⎝⎭;(3)35PE PA +的最小值是3. 【详解】解:(1)将二次函数()20y ax a =>的图象向右平移1个单位.再向下平移2个单位.得到的抛物线解析式为()212y a x =--. ∠1OA =.∠点A 的坐标为()1,0-. 代入抛物线的解析式得.420a -=.∠12a =. ∠抛物线的解析式为()21122y x =--.即21322y x x =--. 令0y =.解得11x =-.23x =.∠()3,0B . ∠4AB OA OB =+=. ∠ABD ∆的面积为5.∠152ABD D S AB y ∆=⋅=.∠52D y =. 代入抛物线解析式得.2513222x x =--.解得12x =-.24x =.∠54,2D ⎛⎫⎪⎝⎭. 设直线AD 的解析式为y kx b =+.∠5420k b k b ⎧+=⎪⎨⎪-+=⎩.解得:1212k b ⎧=⎪⎪⎨⎪=⎪⎩. ∠直线AD 的解析式为1122y x =+. (2)过点E 作EM y 轴交AD 于M .如图.设213,22E a a a ⎛⎫-- ⎪⎝⎭.则11,22M a a ⎛⎫+ ⎪⎝⎭.∠221113132222222EM a a a a a =+-++=-++. ∠112ACE AME CME S S S EM ∆∆∆=-=⨯⋅()22113121342224a a a a ⎛⎫=-++⨯=--- ⎪⎝⎭.213254216a ⎛⎫=--+⎪⎝⎭. ∠当32a =时.ACE ∆的面积有最大值.最大值是2516.此时E 点坐标为315,28⎛⎫- ⎪⎝⎭.(3)作E 关于x 轴的对称点F .连接EF 交x 轴于点G .过点F 作FH AE ⊥于点H .交x 轴于点P . ∠315,28E ⎛⎫-⎪⎝⎭.1OA =. ∠35122AG =+=.158EG =.∠5421538AG EG ==. ∠90AGE AHP ∠=∠=. ∠3sin 5PH EG EAG AP AE ∠===.∠35PH AP =. ∠E 、F 关于x 轴对称.∠PE PF =.∠35PE AP FP HP FH +=+=.此时FH 最小. ∠1515284EF =⨯=.AEG HEF ∠=∠. ∠4sin sin 5AG FH AEG HEF AE EF ∠=∠===. ∠415354FH =⨯=. ∠35PE PA +的最小值是3.3.已知抛物线2y x bx c =-+(b c ,为常数.0b >)经过点(1,0)A -.点(,0)M m 是x 轴正半轴上的动点.(∠)当2b =时.求抛物线的顶点坐标;(∠)点(,)D D b y 在抛物线上.当AM AD =.5m =时.求b 的值; (∠)点1(,)2Q Q b y +在抛物线上.22AM QM +332.求b 的值. 【答案】(∠)(1,4)-;(∠)321b =-;(∠)4b =. 【详解】解:(∠)∠抛物线2y x bx c =-+经过点(1,0)A -.∠10b c ++=.即1c b =--.当2b =时.2223(1)4y x x x =--=--.∠抛物线的顶点坐标为(1,4)-.(∠)由(∠)知.抛物线的解析式为21y x bx b =---. ∠点(,)D D b y 在抛物线21y x bx b =---上.∠211D y b b b b b =-⋅--=--.由0b >.得02bb >>.10b --<. ∠点(,1)D b b --在第四象限.且在抛物线对称轴2bx =的右侧. 如图.过点D 作DE x ⊥轴.垂足为E .则点(,0)E b . ∠1AE b =+.1DE b =+.得AE DE =. ∠在Rt ADE ∆中.45ADE DAE ︒∠=∠=. ∠2AD AE =. 由已知AM AD =.5m =. ∠5(1)2(1)b --=+. ∠321b =.(∠)∠点1(,)2Q Q b y +在抛物线21y x bx b =---上. ∠2113()()12224Q b y b b b b =+-+--=--. 可知点13(,)224b Q b +--在第四象限.且在直线x b =的右侧. 2222()QM AM QM +=+.可取点(0,1)N . 如图.过点Q 作直线AN 的垂线.垂足为G .QG 与x 轴相交于点M . 有45GAM ︒∠=.2AM GM =. 则此时点M 满足题意. 过点Q 作QHx ⊥轴于点H .则点1(,0)2H b +.在Rt MQH ∆中.可知45QMH MQH ︒∠=∠=.∠QH MH =.2QM MH =. ∠点(,0)M m . ∠310()()242b b m ---=+-.解得124b m =-. 332224AM QM +=. 1113322[()(1)]22[()()]242244b b b ---++--=. ∠4b =.4.如图.已知抛物线y x +2)(x ﹣4)(k 为常数.且k >0)与x 轴从左至右依次交于A.B 两点.与y 轴交于点C.经过点B 的直线y x +b 与抛物线的另一交点为D .(1)若点D 的横坐标为﹣5.求抛物线的函数表达式;(2)若在第一象限内的抛物线上有点P.使得以A.B.P 为顶点的三角形与∠ABC 相似.求k 的值;(3)在(1)的条件下.设F 为线段BD 上一点(不含端点).连接AF.一动点M 从点A 出发.沿线段AF 以每秒1个单位的速度运动到F.再沿线段FD 以每秒2个单位的速度运动到D 后停止.当点F 的坐标是多少时.点M 在整个运动过程中用时最少?【答案】(1);(2)或;(3)当点F 坐标为(﹣)时.点M在整个运动过程中用时最少.【解析】(1)抛物线y=(x+2)(x﹣4).令y=0.解得x=﹣2或x=4.∠A(﹣2.0).B (4.0).∠直线经过点B(4.0).∠×4+b=0.解得b=.∠直线BD解析式为:当x=﹣5时.y=.∠D(﹣).∠点D(﹣)在抛物线y=x+2)(x﹣4)上.∠5+2)(﹣5﹣4)=.∠.∠抛物线的函数表达式为:(x+2)(x﹣4).即.(2)由抛物线解析式.令x=0.得y=﹣k.∠C(0.﹣k).OC=k.因为点P在第一象限内的抛物线上.所以∠ABP为钝角.因此若两个三角形相似.只可能是∠ABC∠∠APB或∠ABC∠∠PAB.∠若∠ABC∠∠APB.则有∠BAC=∠PAB.如答图2﹣1所示.设P(x.y).过点P作PN∠x轴于点N.则ON=x.PN=y.tan∠BAC=tan∠PAB.即:.∠.∠P(+k).代入抛物线解析式y=x+2)(x﹣4).得x+2)(x﹣4x+k.整理得:x2﹣6x﹣16=0.解得:x=8或x=﹣2(与点A重合.舍去).∠P(8.5k).∠∠ABC∠∠APB.∠...∠若∠ABC∠∠PAB.则有∠ABC=∠PAB.如答图2﹣2所示.设P(x.y).过点P作PN∠x轴于点N.则ON=x.PN=y.tan∠ABC=tan∠PAB.即:.∠.∠P(x.x+).代入抛物线解析式y(x+2)(x﹣4).得x+2)(x﹣4x.整理得:x2﹣4x﹣12=0.解得:x=6或x=﹣2(与点A重合.舍去).∠P(6.2k).∠∠ABC∠∠PAB..∠.解得.∠k>0.∠.综上所述.或.(3)作DK∠AB.AH∠DK.AH交直线BD于点F.∠∠DBA=30°.∠∠BDH=30°.∠FH=DF×sin30°.∠当且仅当AH∠DK时.AF+FH 最小.点M在整个运动中用时为:.∠l BD:.∠F X=A X=﹣2.∠F(﹣).。
几何最值之“胡不归”问题(附全国中考真题 解析)

“胡不归”问题属于经典的几何动点最值问题,一直都是中考的热门考点。
该题型因为会涉及到
几何图形、动点问题、最值问题、三角函数等知识点,对于辅助线的构造、求解的计算要求都比较高 ,属于比较难的一类题型。
如果没有进行系统性的学习,考场上遇到该题型往往会容易抓瞎。
在近几年的中考试卷中,天津、四川、江苏、湖北、湖南、山东、贵州、新疆等地,都有该题型的出现。
该题型既有选择题、填空题,比较主流的是和二次函数结合在一起,考察代几综合的内容,综合性非常强。
该题型的特征其实比较明显,当遇到求线段之和的最小值时,而且含有系数时,往往就有可能是胡不归问题。
形如求“ PA + kPB ”这样的式子的最小值,其中 A、B 两点为定值, P 为动点。
当动点 P
在直线上运动时,就是我们今天要说的“胡不归”问题;当动点 P
在圆上运动时,就是另外一个最值问题:阿氏圆问题。
王旭老师总结了“胡不归”问题的背景、模型、解决方案、知识要点,以及近几年中考试卷中出现的“胡不归”真题。
最值模型之胡不归(学生版)-中考数学专题解析

最值模型之胡不归“PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。
1.当k值为1时,即可转化为“PA+PB”之和最短问题,就可用我们常见的“饮马问题”模型来处理,即可以转化为轴对称问题来处理(见专题08);2.当k取任意不为1的正数时,若再以常规的轴对称思想来解决问题,则无法进行,因此必须转换思路。
此类问题的处理通常以动点P所在图像的不同来分类,一般分为2类研究。
即点P在直线上运动和点P 在圆上运动。
(1)其中点P在直线上运动的类型称之为“胡不归”问题;(2)点P在圆周上运动的类型称之为“阿氏圆”问题(见专题11)。
胡不归:【模型建立】如图1:P是直线BC上的一动点,求PA+k·PB的最小值。
【作法】1.作∠CBE=α,使sinα=k,则PD=k·OP(图2)2.当AD最短,AD⊥BE时,则P为要求点。
(图3)AD长即为PA+k·PB的最小值.简记:胡不归,正弦作个角,作高求长即可.特别提醒:当k>1时,kAP+BP=k AP+1k BP按常规模型算即可1∠AOB=30°,OM=2,D为OB上动点,求MD+12OD的最小值.2(1)【问题探究】如图1,点E是等边△ABC高AD上的一定点,请在AB上找一点F,使EF=12AE,并说明理由;(2)【问题解决】如图2,在△ACD中,CO⊥AD,垂足为O,若AD=32,AC=2,OC=3,点P在OC上,求DP+12PC的最小值.(3)【问题拓展】如图3,△ABC中,AB=AC=10,tan∠A=2,BE⊥AC于点E,D是线段BE上的一个动点,求CD+ 55BD的最小值.1.实战训练1一.选择题(共8小题)1如图,在△ABC 中,P 为平面内的一点,连接AP 、PB 、PC ,若∠ACB =30°,AC =8,BC =10,则4PA +2PB +23PC 的最小值是()A.489B.36C.410+25+67D.1610-102如图,△ABC 为等边三角形,BD 平分∠ABC ,AB =2,点E 为BD 上动点,连接AE ,则AE +12BE 的最小值为()A.1B.2C.3D.23如图,在平面直角坐标系中,抛物线y =-49x 2+83x 与x 轴的正半轴交于点A ,B 点为抛物线的顶点,C 点为该抛物线对称轴上一点,则3BC +5AC 的最小值为()A.24B.25C.30D.364如图,在等边△ABC 中,AB =6,点E 为AC 中点,D 是BE 上的一个动点,则CD +12BD 的最小值是()A.3B.33C.6D.3+35如图,在菱形ABCD中,AB=AC=6,对角线AC、BD相交于点O,点M在线段AC上,且AM= 2,点P是线段BD上的一个动点,则MP+12PB的最小值是()A.2B.23C.4D.436如图,在Rt△ABC中,∠ACB=90°,∠A=30°,则AB=2BC.请在这一结论的基础上继续思考:若AC=2,点D是AB的中点,P为边CD上一动点,则AP+12CP的最小值为()A.1B.2C.3D.27如图,△ABC中,AB=AC=10,tan A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD +55BD的最小值是()A.25B.45C.53D.108如图,在菱形ABCD中,∠ABC=60°,E是边BC的中点,P是对角线BD上的一个动点,连接AE,AP,若AP+12BP的最小值恰好等于图中某条线段的长,则这条线段是()A.ABB.AEC.BDD.BE2二.填空题(共9小题)1如图,AC垂直平分线段BD,相交于点O,且OB=OC,∠BAD=120°.(1)∠ABC=.(2)E为BD边上的一个动点,BC=6,当AE+12BE最小时BE=2 .2如图,在△ABC中,∠A=90°,∠C=30°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为.3如图,在平面直角坐标系中,直线y=-x+4的图象分别与y轴和x轴交于点A和点B.若定点P的坐标为(0,63),点Q是y轴上任意一点,则12PQ+QB的最小值为3 .4如图,直线y=x-3分别交x轴、y轴于B、A两点,点C(0,1)在y轴上,点P在x轴上运动,则2PC+PB的最小值为.5如图,抛物线y=x2-2x-3与x轴交于A、B两点,过B的直线交抛物线于E,且tan∠EBA=4 3,有一只蚂蚁从A出发,先以1单位/s的速度爬到线段BE上的点D处,再以1.25单位/s的速度沿着DE爬到E点处觅食,则蚂蚁从A到E的最短时间是 649 s.6如图,在平面直角坐标系中,二次函数y=x2-2x+c的图象与x轴交于A、C两点,与y轴交于点B (0,-3),若P是x轴上一动点,点D(0,1)在y轴上,连接PD,则C点的坐标是,2PD+PC的最小值是.7如图,四边形ABCD是菱形,AB=4,且∠BAD=30°,P为对角线AC(不含A点)上任意一点,则DP+12AP的最小值为.8如图,四边形ABCD中,AB=62,∠ABC=45°,E是BD上一点,若∠ABD=15°,则AE+12BE的最小值为.9如图,矩形OABC中,点A、C分别在x轴,y轴的正半轴上,且OA=3,AB=1,点P为线段OA上一动点,则12OP+PB最小值为.3三.解答题(共5小题)1如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(-1,0),B(0,-3),C(2,0),其对称轴与x轴交于点D.(1)求二次函数的表达式及其顶点坐标;(2)点M为抛物线的对称轴上的一个动点,若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,求点M的坐标;(3)若P为y轴上的一个动点,连接PD,求12PB+PD的最小值.2如图抛物线y=ax2+bx-4与x轴交于A(-1,0),B(4,0)两点,与y轴交于点C.(1)求抛物线解析式.(2)连接BC,点P为BC下方上一动点,连接BP,CP.当△PBC的面积最大时,求点P的坐标和△PBC 面积的最大值.(3)点N为线段OC上一点,连接AN,求AN+12CN的最小值.3如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c与x轴交于点A、B两点,其中A(1,0),与y轴交于点C(0,3).(1)求抛物线解析式;(2)如图1,过点B作x轴垂线,在该垂线上取点P,使得△PBC与△ABC相似,请求出点P坐标;(3)如图2,在线段OB上取一点M,连接CM,请求出CM+12BM的最小值.4(1)【问题探究】如图1,点E是等边△ABC高AD上的一定点,请在AB上找一点F,使EF=12AE,并说明理由;(2)【问题解决】如图2,在△ACD中,CO⊥AD,垂足为O,若AD=32,AC=2,OC=3,点P在OC上,求DP+12PC的最小值.(3)【问题拓展】如图3,△ABC中,AB=AC=10,tan∠A=2,BE⊥AC于点E,D是线段BE上的一个动点,求CD+ 55BD的最小值.。
最值问题之胡不归

《最值问题之----胡不归》【背景知识】有一则历史故事:说的是一个身在他乡的小伙子,得知父亲病危的消息后便日夜赶路回家。
然而,当他气喘吁吁地来到父亲的面前时,老人刚刚咽气了。
人们告诉他,在弥留之际,老人在不断喃喃地叨念:“胡不归?胡不归?”早期的科学家曾为这则古老的传说中的小伙子设想了一条路线。
(如下图)A 是出发地,B 是目的地;AC 是一条驿道,而驿道靠目的地的一侧是沙地。
为了急切回家,小伙子选择了直线路程AB 。
但是,他忽略了在驿道上行走要比在砂土地带行走快的这一因素。
如果他能选择一条合适的路线(尽管这条路线长一些,但是速度可以加快),是可以提前抵达家门的。
那么,这应该是那条路线呢?显然,根据两种路面的状况和在其上行走的速度值,可以在AC 上选定一点D ,小伙子从A 走到D ,然后从D 折往B ,可望最早到达B 。
用现代的科学语言表达,就是:若在驿道上行走的速度为1V ,在沙地上行走的速度为2V ,即求21V BD V AD的最小值.1.如图,平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则的最小值等于________.2.如图,在△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则小值是.3.如图,一条笔直的公路穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是10千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则线段AP+BP+PD的最小值为.4.如图,△ABC在直角坐标系中,AB=AC,,C(1,0),D为射线AO上一点,一动点P从A出发,运动路径为A→D→C,点P在AD上的运动速度是在CD上的3倍,要使整个运动时间最少,则点D的坐标应为()A.(0,)B.(0,C.(0,D.(0,)5.如图,在平面直角坐标系中,二次函数y=ax2+bx+c C(2,0),其对称轴与x轴交于点D(1)求二次函数的表达式及其顶点坐标;(2)若P为y轴上的一个动点,连接PD,则+PD的最小值为;(3)M(x,t)为抛物线对称轴上一动点①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有个;。
胡不归最值问题

“胡不归”最值问题
如图, A是出发点, B是目的地, 直线AC是一条驿道, 而驿道靠目的地一侧全是砂土, 为了选择合适的路线, 根据不同路面速度不同(驿道速度为a米/秒, 砂土速度为b米/秒), 小伙子需要在AC上选取一点D, 再折往至B.
上述数学解释用到了三角函数知识将两个线段的系数权重都化为1, 从而降低了求最值难度。
聪明的同学或许一下就发现转化成了我之前讲过的“将军饮马(小河取水)”模型, 进而作
对称求得最值。
显然线段PA,PB的系数不同, 先要将他们化为1.考虑到本题中有个∠A=30°, 而30°所对的直角边是斜边的一半, 所以可以将二分之一PA转化, 如图
然后问题就明朗了, 系数都是1了, 得到新模型——“将军饮马(小河取水)”模型
剩下的问题就是作对称, 求最值了。
大家思考一下, 该选取哪个点关于AC对称比较好?是D点呢, 还是B点呢?
聪明的你肯定注意到了∠C=90°, 所以我们选取B点关于AC对称比较好, 方便计算。
如下图:。
专题65 胡不归中的双线段模型与最值问题(解析版)

专题65 胡不归中的双线段模型与最值问题【专题说明】胡不归模型问题解题步骤如下;1、将所求线段和改写为“PA+a b PB”的形式(a b <1),若ab >1,提取系数,转化为小于1的形式解决。
2、在PB 的一侧,PA 的异侧,构造一个角度α,使得sinα=a b 3、最后利用两点之间线段最短及垂线段最短解题【模型展示】如图,一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使21AC BC V V +的值最小.121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭,记12V k V =, 即求BC +kAC 的最小值.构造射线AD 使得sin ∠DAN =k ,CH /AC =k ,CH =kAC .2M将问题转化为求BC +CH 最小值,过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC +CH 取到最小值,即BC +kAC 最小.在求形如“P A +kPB ”的式子的最值问题中,关键是构造与kPB 相等的线段,将“P A +kPB ”型问题转化为“P A +PC ”型.【精典例题】1、在平面直角坐标系中,将二次函数()20y ax a =>的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与x 轴交于点A 、B (点A 在点B 的左侧),1OA =,经过点A 的一次函数()0y kx b k =+≠的图象与y 轴正半轴交于点C ,且与抛物线的另一个交点为D ,ABD ∆的面积为5.(1)求抛物线和一次函数的解析式;(2)抛物线上的动点E 在一次函数的图象下方,求ACE ∆面积的最大值,并求出此时点E 的坐标;(3)若点P 为x 轴上任意一点,在(2)的结论下,求35PE PA +的最小值. 【答案】(1)21322y x x =--;1122y x =+;(2)ACE ∆的面积最大值是2516,此时E 点坐标为315,28⎛⎫- ⎪⎝⎭;(3)35PE PA +的最小值是3. 【详解】解:(1)将二次函数()20y axa =>的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为()212y a x =--,∵1OA =,∵点A 的坐标为()1,0-, 代入抛物线的解析式得,420a -=,∵12a =, ∵抛物线的解析式为()21122y x =--,即21322y x x =--. 令0y =,解得11x =-,23x =,∵()3,0B ,∵4AB OA OB =+=,∵ABD ∆的面积为5,∵152ABD D S AB y ∆=⋅=,∵52D y =, 代入抛物线解析式得,2513222x x =--,解得12x =-,24x =,∵54,2D ⎛⎫ ⎪⎝⎭, 设直线AD 的解析式为y kx b =+, ∵5420k b k b ⎧+=⎪⎨⎪-+=⎩,解得:1212k b ⎧=⎪⎪⎨⎪=⎪⎩, ∵直线AD 的解析式为1122y x =+. (2)过点E 作EM y 轴交AD 于M ,如图,设213,22E a a a ⎛⎫-- ⎪⎝⎭,则11,22M a a ⎛⎫+ ⎪⎝⎭, ∵221113132222222EM a a a a a =+-++=-++, ∵112ACE AME CMES S S EM ∆∆∆=-=⨯⋅()22113121342224a a a a ⎛⎫=-++⨯=--- ⎪⎝⎭,213254216a ⎛⎫=--+ ⎪⎝⎭, ∵当32a =时,ACE ∆的面积有最大值,最大值是2516,此时E 点坐标为315,28⎛⎫- ⎪⎝⎭.(3)作E 关于x 轴的对称点F ,连接EF 交x 轴于点G ,过点F 作FH AE ⊥于点H ,交x 轴于点P ,∵315,28E ⎛⎫- ⎪⎝⎭,1OA =, ∵35122AG =+=,158EG =,∵5421538AG EG ==, ∵90AGE AHP ∠=∠=, ∵3sin 5PH EG EAG AP AE ∠===,∵35PH AP =, ∵E 、F 关于x 轴对称,∵PE PF =, ∵35PE AP FP HP FH +=+=,此时FH 最小, ∵1515284EF =⨯=,AEG HEF ∠=∠, ∵4sin sin 5AG FH AEG HEF AE EF ∠=∠===, ∵415354FH =⨯=. ∵35PE PA +的最小值是3.2、如图,△ABC 中,AB =AC =10,tanA =2,BE ∵AC 于点E ,D 是线段BE 上的一个动点,则5CD BD +的最小值是( )【答案】B【详解】如图,作DH∵AB于H,CM∵AB于M.∵BE∵AC,∵∵AEB=90°,∵tanA=BEAE=2,设AE=a,BE=2a,则有:100=a2+4a2,∵a2=20,-,∵AB=AC,BE∵AC,CM∵AB,)∵∵DBH=∵ABE,∵BHD=∵BEA,∵sin DH AE DBH BD AB ∠===,BD ,, ∵CD+DH≥CM ,的最小值为 故选B .3、已知抛物线2(0)y ax bx c a =++≠过点(1,0)A ,(3,0)B 两点,与y 轴交于点C ,=3OC .(1)求抛物线的解析式及顶点D 的坐标;(2)过点A 作AM BC ⊥,垂足为M ,求证:四边形ADBM 为正方形;(3)点P 为抛物线在直线BC 下方图形上的一动点,当PBC ∆面积最大时,求点P 的坐标;(4)若点Q 为线段OC 上的一动点,问:12AQ QC +是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.【答案】(1)抛物线的表达式为:243y x x =-+,顶点(2,1)D -;(2)证明见解析;(3)点33,24P ⎛⎫- ⎪⎝⎭;(4)存在,12AQ QC + 【详解】(1)函数的表达式为:()()()2y a x 1x 3a x 4x 3=--=-+, 即:3a=3,解得:a=1,故抛物线的表达式为:2y x 4x 3=-+, 则顶点D(2,1)-;(2)OB OC 3==,OBC OCB 45∠∠︒∴==,∵A(1,0),B(3,0),∵ OB=3,OA=1,∵AB=2,∵AM MB ABsin45︒===又∵D(2,-1),=∵AM=MB=AD=BD ,∵四边形ADBM 为菱形,又∵AMB 90∠︒=,∴菱形ADBM 为正方形;(3)设直线BC 的解析式为y=mx+n ,将点B 、C 的坐标代入得:303m n n +=⎧⎨=⎩,解得:13m n =-⎧⎨=⎩,所以直线BC 的表达式为:y=-x+3,过点P 作y 轴的平行线交BC 于点N ,设点()2P x,x 4x 3-+,则点N (x,x+3)-, 则()()22ΔPBC 133S PN OB x 3x 4x 3x 3x 222=⨯=-+-+-=--, 302-<,故ΔPBC S 有最大值,此时3x 2=, 故点33P ,24⎛⎫- ⎪⎝⎭; (4)存在,理由:如图,过点C 作与y 轴夹角为30︒的直线CF 交x 轴于点F ,过点A 作AH CF ⊥,垂足为H ,交y 轴于点Q ,此时1HQ CQ 2=,则1AQ QC 2+最小值=AQ+HQ=AH , 在Rt∵COF 中,∵COF=90°,∵FOC=30°,OC=3,tan∵FCO=FO CO ,∵OF=,∵F(0),利用待定系数法可求得直线HC 的表达式为:y 3=+…∵,∵∵COF=90°,∵FOC=30°,∵∵CFO=90°-30°=60°,∵∵AHF=90°,∵∵FAH=90°-60°=30°,∵OQ=AO•tan∵FAQ=3,∵Q(0,),利用待定系数法可求得直线AH 的表达式为:y x 33=-+…∵,联立∵∵并解得:x =,故点H ⎝⎭,而点A(1,0),则AH =,即1AQ QC 2+.4、已知抛物线2y x bx c =-+(b c ,为常数,0b >)经过点(1,0)A -,点(,0)M m 是x 轴正半轴上的动点.(∵)当2b =时,求抛物线的顶点坐标;(∵)点(,)D D b y 在抛物线上,当AM AD =,5m =时,求b 的值;(∵)点1(,)2Q Q b y +2QM +时,求b 的值.【答案】(∵)(1,4)-;(∵)1b =;(∵)4b =.【详解】解:(∵)∵抛物线2y x bx c =-+经过点(1,0)A -,∵10b c ++=.即1c b =--.当2b =时,2223(1)4y x x x =--=--, ∵抛物线的顶点坐标为(1,4)-.(∵)由(∵)知,抛物线的解析式为21y x bx b =---. ∵点(,)D D b y 在抛物线21y x bx b =---上,∵211D y b b b b b =-⋅--=--.由0b >,得02b b >>,10b --<, ∵点(,1)D b b --在第四象限,且在抛物线对称轴2b x =的右侧. 如图,过点D 作DE x ⊥轴,垂足为E ,则点(,0)E b .∵1AE b =+,1DE b =+.得AE DE =.∵在Rt ADE ∆中,45ADE DAE ︒∠=∠=.∵AD =.由已知AM AD =,5m =,∵5(1)1)b --=+.∵1b =.(∵)∵点1(,)2Q Q b y +在抛物线21y x bx b =---上, ∵2113()()12224Q b y b b b b =+-+--=--. 可知点13(,)224b Q b +--在第四象限,且在直线x b =的右侧.2)QM AM QM +=+,可取点(0,1)N , 如图,过点Q 作直线AN 的垂线,垂足为G ,QG 与x 轴相交于点M ,有45GAM ︒∠=AM GM =,则此时点M 满足题意.过点Q 作QH x ⊥轴于点H ,则点1(,0)2H b +. 在Rt MQH ∆中,可知45QMH MQH ︒∠=∠=.∵QH MH =,QM =.∵点(,0)M m , ∵310()()242b b m ---=+-.解得124b m =-.24QM +=111)(1)])()]24224bb b ---++--=. ∵4b =.5、如图,在平面在角坐标系中,抛物线y=x 2-2x -3与x 轴交与点A ,B (点A 在点B 的左侧)交y 轴于点C ,点D 为抛物线的顶点,对称轴与x 轴交于点E .(1)连结BD ,点M 是线段BD 上一动点(点M 不与端点B ,D 重合),过点M 作MN∵BD 交抛物线于点N (点N 在对称轴的右侧),过点N 作NH∵x 轴,垂足为H ,交BD 于点F ,点P 是线段OC 上一动点,当MN 取得最大值时,求HF+FP+13PC 的最小值;(2)在(1)中,当MN 取得最大值HF+FP+1/3PC 取得小值时,把点P 向上平移个2单位得到点Q ,连结AQ ,把∵AOQ 绕点O 瓶时针旋转一定的角度α(0°<α<360°),得到∵AOQ ,其中边AQ 交坐标轴于点C 在旋转过程中,是否存在一点G 使得''Q Q OG ∠=∠?若存在,请直接写出所有满足条件的点Q 的坐标;若不存在,请说明理由.【答案】(1)133+;(2)存在,Q ,﹣5),(5),,5),) 【详解】解:(1)如图1∵抛物线y =x 2﹣2x ﹣3与x 轴交于点A ,B (点A 在点B 的左侧),交y 轴于点C∵令y =0解得:x 1=﹣1,x 2=3,令x =0,解得:y =﹣3,∵A (﹣1,0),B (3,0),C (0,﹣3)∵点D 为抛物线的顶点,且22441(3)41,22441b ac b a a --⨯⨯---=-==⨯﹣4 ∵点D 的坐标为D (1,﹣4)∵直线BD 的解析式为:y =2x ﹣6,由题意,可设点N (m ,m 2﹣2m ﹣3),则点F (m ,2m ﹣6)∵|NF |=(2m ﹣6)﹣(m 2﹣2m ﹣3)=﹣m 2+4m ﹣3∵当m =2b a-=2时,NF 取到最大值,此时MN 取到最大值,此时HF =2, 此时,N (2,﹣3),F (2,﹣2),H (2,0)在x 轴上找一点K (4-,0),连接CK ,过点F 作CK 的垂线交CK 于点J 点,交y 轴于点P ,∵sin∵OCK =13,直线KC 的解析式为:3y =--,且点F (2,﹣2),∵PJ =13PC ,直线FJ 的解析式为:y x =-∵点J (29-, 199--)∵FP +13PC 的最小值即为FJ 的长,且1||3FJ =+∵17|33min HF FP P C +++=;(2)由(1)知,点P (0, 42+-),∵把点P 向上平移2个单位得到点Q ∵点Q (0,﹣2)∵在Rt∵AOQ 中,∵AOG =90°,AQ AQ 的中点G ,连接OG ,则OG =GQ =12AQ ,此时,∵AQO =∵GOQ把∵AOQ 绕点O 顺时针旋转一定的角度α(0°<α<360°),得到∵A ′OQ ′,其中边A ′Q ′交坐标轴于点G ∵如图2G 点落在y 轴的负半轴,则G (0),过点Q '作Q 'I ∵x 轴交x 轴于点I ,且∵GOQ '=∵Q ' 则∵IOQ '=∵OA 'Q '=∵OAQ ,∵sin∵OAQ =OQAQ∵sin 25IQ IQ IOQ OQ '''∠===,解得:|IO |=5∵在Rt∵OIQ '中根据勾股定理可得|OI |∵点Q '的坐标为Q ',﹣5); ∵如图3,当G点落在x轴的正半轴上时,同理可得Q')∵如图4)当G点落在y轴的正半轴上时,同理可得Q',5∵如图5当G点落在x轴的负半轴上时,同理可得Q')综上所述,所有满足条件的点Q′的坐标为:(,﹣),(,),(﹣,),(,﹣)。
2023年中考数学常见几何模型之最值模型胡不归问题

专题10 最值模型---胡不归问题最值问题在中考数学常以压轴题的形式考查,可将胡不归问题看作将军饮马衍生,主要考查转化与化归等的数学思想。
在各类考试中都以高档题为主,中考说明中曾多处涉及。
本专题就最值模型中的胡不归问题进行梳理及对应试题分析,方便掌握。
在解决胡不归问题主要依据是:①两点之间,线段最短;②垂线段最短。
【模型背景】从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A 到家B 之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?看到这里很多人都会有一个疑问,少年究竟能不能提前到家呢?假设可以提早到家,那么他该选择怎样的一条路线呢?这就是今天要讲的“胡不归”问题.【模型解读】一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使21AC BC V V +的值最小.(注意与阿氏圆模型的区分)2驿道2M1)121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭,记12V k V =,即求BC +kAC 的最小值. 2)构造射线AD 使得sin ∠DAN =k ,CH k AC=,CH =kAC ,将问题转化为求BC +CH 最小值. 3)过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC +CH 取到最小值,即BC +kAC 最小.【解题关键】在求形如“P A +kPB ”的式子的最值问题中,关键是构造与kPB 相等的线段,将“P A +kPB ”型问题转化为“P A +PC ”型.(若k >1,则提取系数,转化为小于1的形式解决即可)。
【最值原理】两点之间线段最短及垂线段最短。
例1.(2022·内蒙古·中考真题)如图,在△ABC 中,AB =AC =4,∠CAB =30°,AD ⊥BC ,垂足为D ,P 为线段AD 上的一动点,连接PB 、PC .则P A +2PB 的最小值为 _____.在∠BAC 的外部作∠CAE =15°此时P A +2PB 最小,∴∠AFB ∴∠CAD =∠BAD =12BAC ∠1例2.(2022·湖北武汉·一模)如图,在ACE △中,CA CE =,30CAE ∠=︒,半径为5的O 经过点C ,CE 是圆O 的切线,且圆的直径AB 在线段AE 上,设点D 是线段AC 上任意一点(不含端点),则12OD CD +的最小值为______.//CH AB ,30CAE ∠=︒,OC OA =,sin HCD ∴∠当O ,例3.(2021·眉山市·中考真题)如图,在菱形中,,对角线、相交于点,点在线段上,且,点为线段上的一个动点,则的最小值是______.【分析】过M 点作MH 垂直BC 于H 点,与OB 的交点为P 点,此时的长度最小为MH ,再算出MC 的长度, 在直角三角形MPC 中利用三角函数即可解得MH 【详解】过M 点作MH 垂直BC 于H 点,与OB 的交点为P 点,此时的长度最小∵菱形中,∴AB =BC =AC =10,△ABC 为等边三角形ABCD 10AB AC ==AC BD O M AC 3AM =P BD 12MP PB +12MP PB +12MP PB +ABCD 10AB AC ==∴∠PBC =30°,∠ACB =60°∴在直角△PBH 中,∠PBH =30°∴PH = ∴此时得到最小值, ∵AC =10,AM =3,∴MC =7又∠MPC =60°∴MH =MC【点睛】本题主要考查了菱形的性质与三角函数,能够找到最小值时的P 点是解题关键. 例4.(2022·山东淄博·二模)如图,在平面直角坐标系中,点A 的坐标是(0,2),点C 的坐标是(0,2)−,点(,0)B x 是x 轴上的动点,点B 在x 轴上移动时,始终保持ABP 是等边三角形(点P 不在第二象限),连接PC ,求得12AP PC +的最小值为( )A .B .4C .D .2【答案】C【分析】如图1所示,以OA 为边,向右作等边△AOD ,连接PD ,过点D 作DE ⊥OA 于E ,先求出点D 的坐标,然后证明△BAO ≌△P AD 得到∠PDA =∠BOA =90°,则点P 在经过点D 且与AD 垂直的直线上运动,当点P 运动到y 轴时,如图2所示,证明此时点P 的坐标为(0,-2)从而求出直线PD 的解析式;如图3所示,作点A 关于直线PD 的对称点G ,连接PG ,过点P 作PF ⊥y 轴于F ,设直线PD 与x 轴的交点为H ,先求出点H 的坐1PB 212MP PB +1=2MP PB MP PH MH ++=当点P运动到y轴时,如图2所示,此时点∵△ABP是等边三角形,BO⊥AP,∴例5.(2021·资阳市·中考真题)抛物线与x 轴交于A 、B 两点,与y 轴交于点C ,且.(1)求抛物线的解析式;(2)如图1,点P 是抛物线上位于直线上方的一点,与相交于点E ,当时,求点P 的坐标;(3)如图2,点D 是抛物线的顶点,将抛物线沿方向平移,使点D 落在点处,且,点M 是平移后所得抛物线上位于左侧的一点,轴交直线于点N ,连结.当的值最小时,求的长. 2y x bx c =−++()()1,0,0,3B C −AC BP AC :1:2PE BE =CD D 2DD CD '=D //MN y OD 'CN 5D N CN '+MN【答案】(1);(2)或;(3). 【分析】(1)利用待定系数法即可得;(2)设点的坐标为,先利用待定系数法求出直线的解析式,再根据可得点的坐标,代入直线的解析式求解即可得;(3)先根据求出点的坐标,再根据二次函数图象的平移规律得出平移后的函数解析式,设点的坐标,从而可得点的坐标,然后根据两点之间的距离公式可得,最后根据两点之间线段最短、垂线段最短求解即可得. 【详解】解:(1)由题意,将点代入得:, 解得,则抛物线的解析式为; (2)对于二次函数,当时,,解得或,,设点的坐标为,点的坐标为, ,,解得,2y x 2x 3=−++(1,4)P (2,3)P 34P 2(,23)P a a a −++AC :1:2PE BE =E AC 2DD CD '=D MN 5D N CN '+()()1,0,0,3B C −2y x bx c =−++103b c c −−+=⎧⎨=⎩23b c =⎧⎨=⎩2y x 2x 3=−++2y x 2x 3=−++0y =2230x x −++=1x =−3x =(3,0)A ∴P 2(,23)(03)P a a a a −++<<E 11(,)E x y :1:2,(1,0)PE BE B =−1121111223102a x x a a y y −⎧=⎪+⎪∴⎨−++−⎪=⎪−⎩121213324233x a y a a ⎧=−⎪⎪⎨⎪=−++⎪⎩,设直线的解析式为, 将点代入得:,解得,则直线的解析式为,将点代入得:,解得或,当时,,此时,当时,,此时,综上,点的坐标为或;(3)二次函数的顶点坐标为,设点的坐标为,,,解得,, 则平移后的二次函数的解析式为,设直线的解析式为,将点代入得:,解得, 则直线的解析式为,设点的坐标为,则点的坐标为, 如图,连接,过点作于点,过点作于点,交于点,连接,22124(,2)3333E a a a ∴−−++AC y kx t =+(3,0),(0,3)A C 303k t t +=⎧⎨=⎩13k t =−⎧⎨=⎩AC 3y x =−+22124(,2)3333E a a a −−++22124323333a a a −++=−++1a =2a =1a =2231234a a −++=−++=(1,4)P 2a =22342233a a −++=−+⨯+=(2,3)P P (1,4)P (2,3)P 2223(1)4y x x x =−++=−−+D (1,4)D D 22(,)D x y '2,(0,3),(1,4)DD C D D C '=2212104243x y −⎧=⎪⎪−∴⎨−⎪=⎪−⎩2236x y =⎧⎨=⎩(3,6)D '∴22(3)663y x x x =−−+=−+−OD '0y k x =(3,6)D '036k =02k =OD '2y x =M 2(,63)(3)M m m m m −+−<N (,2)N m m AD 'N NF AD '⊥F C CG AD '⊥G OD 'N 'CF,轴,,, 由两点之间线段最短得:的最小值为,由垂线段最短得:当点与点重合时,取得最小值,此时点与点重合, 则点的纵坐标与点的纵坐标相等,即,解得, 则,,. 【点睛】本题考查了利用待定系数法求二次函数的解析式、二次函数图象的平移规律、垂线段最短等知识点,较难的是题(3),正确求出平移后的抛物线的解析式是解题关键. 例6.(2020·湖南·中考真题)已知直线与抛物线(b ,c 为常数,)的一个交点为,点是x 轴正半轴上的动点.(1)当直线与抛物线(b ,c 为常数,)的另一个交点为该抛物线的顶点E 时,求k ,b ,c 的值及抛物线顶点E 的坐标;(2)点D 在抛物线上,且点D 的横坐标为的最小值多时,求b 的值.【答案】(1)-2,2,-3,;(2)4或6;(3)3 (3,0),(3,6)D A 'AD x '∴⊥3FN m ∴=−35D N CN CN m CN FN CN '+==−+=+FN CN +CF F G CF CG N N 'N 'C 23m =32m =2263243MN m m m m m =−+−−=−+−233()4322=−+⨯−34=2y kx =−2y x bx c =−+0b >(1,0)A −(,0)M m 2y kx =−2y x bx c =−+0b >12b +2DM +4()1,4−【分析】(1)由题意可知直线经过,因而把代入直线即可求出k 的值,然后把代入抛物线得出含b 的代数式表达c ,再根据直线与抛物线(b ,c 为常数,)的另一个交点得出抛物线的顶点坐标E ,并代入直线,解方程即可求出b 的值,代入即可求解;(2)将点D 的横坐标代入抛物线(b ,c 为常数,),根据点A 的坐标得到含b 的代数式表达c ,求出点D 的纵坐标为,可知点D 在第四象限,且在直线的右侧,取点,过点D 作直线AN 的垂线,垂足为G ,DG 与x 轴相交于点M ,过点D 作QH ⊥x 轴于点H ,则点H,在Rt △MDH 中,可知,由题意可知点,用含b 的代数式表示m,可得方程,求解即可得出答案. 【详解】解:(1)∵直线经过,∴把代入直线,可得,解得; ∵抛物线(b ,c 为常数,)经过,∴把代入抛物线,可得,∵当直线与抛物线(b ,c 为常数,)的另一个交点为该抛物线的顶点E ,∴顶点的坐标为,把代入直线,可得,∴,解得,2y kx =−(1,0)A −(1,0)A −2y kx =−(1,0)A −2y kx =−2y xbx c =−+0b >24,24b c b ⎛⎫− ⎪⎝⎭22y x =−−12b +2y x bx c =−+0b >324b −−13,224b b ⎛⎫+−−⎪⎝⎭x b =(0,1)N 1,02b ⎛⎫+⎪⎝⎭45DMH MDH ︒∠=∠=(,0)M m 24DM +=2y kx =−(1,0)A −(1,0)A −2y kx =−02k =−−2k =−2y xbx c =−+0b >(1,0)A −(1,0)A −2y x bx c =−+1c b =−−2y kx =−2y x bx c =−+0b >E 24,24b c b ⎛⎫− ⎪⎝⎭E 24,24b c b ⎛⎫− ⎪⎝⎭22y x =−−242224b c b −−⨯−=()2412224b b b−−−−⨯−=2b =±∵,∴,∴,∴顶点的坐标为. (2)∵点D 在抛物线(b ,c 为常数,)上,且点D 的横坐标为, ∴,∵在抛物线(b ,c 为常数,)上,∴,即,∴,可知点D 在第四象限,且在直线的右侧.,∴可取点,如图2,过点D 作直线AN 的垂线,垂足为G ,DG 与x 轴相交于点M ,∴,得, 则此时点M 满足题意,过点D 作QH ⊥x 轴于点H ,则点H ,在Rt △MDH 中,可知,∴,∵点,∴,解得:,,∴,∴.0b >2b =213c =−−=−E ()1,4−2y xbx c =−+0b >12b +21122D y b b b c ⎛⎫⎛⎫=+−++ ⎪ ⎪⎝⎭⎝⎭(1,0)A −2y x bx c =−+0b >()210b c −+=+1c b =−−21131=2224D b y b b b b ⎛⎫⎛⎫=+−+−−−− ⎪ ⎪⎝⎭⎝⎭13,224b b ⎛⎫+−− ⎪⎝⎭x b =222DM AM DM ⎛⎫+=+ ⎪ ⎪⎝⎭(0,1)N 45GAM ︒∠=2AM GM =1,02b ⎛⎫+⎪⎝⎭45DMH MDH ︒∠=∠=,D DH MH M ==(,0)M m 310242b b m ⎛⎫⎛⎫−−−=+− ⎪ ⎪⎝⎭⎝⎭124b m =−24DM +=111(1)2242244b b b ⎤⎤⎛⎫⎛⎫⎛⎫−−−++−−= ⎪ ⎪ ⎪⎥⎥⎝⎭⎝⎭⎝⎭⎦⎦3b =【点睛】本题是二次函数综合题,主要考查了待定系数法求解析式、二次函数的性质、等腰三角形的性质、三角形的面积公式等知识点,解题的关键是学会使用待定系数法求出抛物线的解析式.例7.(2022·四川成都·中考模拟)6.如图,已知抛物线为常数,且与轴从左至右依次交于,两点,与轴交于点,经过点的直线与抛物线的另一交点为.(1)若点的横坐标为,求抛物线的函数表达式;(2)若在第一象限内的抛物线上有点,使得以,,为顶点的三角形与相似,求的值;(3)在(1)的条件下,设为线段上一点(不含端点),连接,一动点从点出发,沿线段以每秒1个单位的速度运动到,再沿线段以每秒2个单位的速度运动到后停止,当点的坐标是多少时,点在整个运动过程中用时最少?(2)(4)(8ky x x k =+−0)k >x A B y C B y b =+D D 5−P A B P ABC ∆k F BD AF M A AF F FD D F M解:(1)抛物线,令,解得或,,.直线经过点,,解得, 直线解析式为:.当时,,,. 点,在抛物线上,,.抛物线的函数表达式为:.即. (2)由抛物线解析式,令,得,,. 因为点在第一象限内的抛物线上,所以为钝角.因此若两个三角形相似,只可能是或. ①若,则有,如答图所示. 设,过点作轴于点,则,. ,即:,. ,代入抛物线解析式,得,整理得:, 解得:或(与点重合,舍去),.,,即. ②若,则有,如答图所示. 设,过点作轴于点,则,.,即:,. (2)(4)8ky x x =+−0y =2x =−4x =(2,0)A ∴−(4,0)B y b =+(4,0)B 40b +=b ∴BD 33y x =+5x =−y =(5D ∴−(5D −(2)(4)8k y x x =+−∴(52)(54)8k −+−−=k ∴=∴2)(4)y x x +−2y x =0x =y k =−(0,)C k ∴−OC k =P ABP ∠ABC APB ∆∆∽ABC PAB ∆∆∽ABC APB ∆∆∽BAC PAB ∠=∠21−(,)P x y P PN x ⊥N ON x =PN y =tan tan BAC PAB ∠=∠22k y x =+2k y x k ∴=+(,)2k P x x k ∴+(2)(4)8ky x x =+−(2)(4)82k kx x x k +−=+26160x x −−=8x =2x =−A (8,5)P k ∴ABC APB ∆∆∽∴AC AB AB AP ==5k =ABC PAB ∆∆∽ABC PAB ∠=∠22−(,)P x y P PN x ⊥N ON x =PN y =tan tan ABC PAB ∠=∠42k y x =+42k ky x ∴=+,代入抛物线解析式,得,整理得:, 解得:或(与点重合,舍去),. ,,,,综上所述,或(3)方法一:如答图3,由(1)知:,,如答图,过点作轴于点,则,,, ,. 过点作轴,则.过点作于点,则. 由题意,动点运动的路径为折线,运动时间:,,即运动的时间值等于折线的长度值.由垂线段最短可知,折线的长度的最小值为与轴之间的垂线段.(,)42k k P x x ∴+(2)(4)8ky x x =+−(2)(4)842k k kx x x +−=+24120x x −−=6x =2x =−A (6,2)P k ∴ABC PAB ∆∆∽AB CBAP AB=∴=k =0k >k ∴=k =k =(5D −22−D DN x ⊥N DN =5ON =459BN =+=tan DN DBA BN ∴∠===30DBA ∴∠=︒D //DK x 30KDF DBA ∠=∠=︒F FG DK ⊥G 12FG DF =M AF DF +12t AF DF =+t AF FG ∴=+AF FG +AF FG +DK x过点作于点,则,与直线的交点,即为所求之点. 点横坐标为,直线解析式为:,,. 综上所述,当点坐标为,时,点在整个运动过程中用时最少. 方法二:作,,交直线于点, ,,, 当且仅当时,最小,点在整个运动中用时为:, ,, 【点睛】本题考查单动点问题;二次函数和一次函数交点问题;曲线上点的坐标与方程的关系;勾股定理;相似三角形的判定;垂直线段最短的性质;分类思想和数形结合思想的应用.课后专项训练1.(2022·河北·九年级期中)如图,在△ABC 中,∠A =15°,AB =2,P 为AC 边上的一个动点(不与A 、C 重合),连接BP ,则AP +PB 的最小值是( )A AH DK ⊥H t AH =最小AH BD FA 2−BD 33y x =+(2)33y ∴=⨯−+=(2F ∴−F (2−M //DK AB AH DK ⊥AH BD F 30DBA ∠=︒30BDH ∴∠=︒sin302FDFH DF ∴=⨯︒=∴AH DK ⊥AF FH +M 12AF FDt AF FH =+=+:BD l y =+2X X F A ∴==−(F ∴−A.B.C.D.2【解答】解:如图,在△ABC内作∠MBA=30°过点A作AE⊥BM于点E,BM交AC于点P,∵∠BAC=15°,∴∠APE=45°∴EP=AP当BP⊥AE时,则AP+PB=PE+PB的值最小,最小值是BE的长,在Rt△ABE中,∠ABE=30°,AB=2∴BE=AB•cos30°=.∴AP+PB的最小值是.故选:B.2.(2022·江苏·九年级月考)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=4,点D、F分别是边AB,BC上的动点,连接CD,过点A作AE⊥CD交BC于点E,垂足为G,连接GF,则GF+FB的最小值是()A.B.C.D.【解答】解:延长AC到点P,使CP=AC,连接BP,过点F作FH⊥BP于点H,取AC中点O,连接OG,过点O作OQ⊥BP于点Q,∵∠ACB=90°,∠ABC=30°,AB=4∴AC=CP=2,BP=AB=4∴△ABP 是等边三角形∴∠FBH =30°∴Rt △FHB 中,FH =FB ∴当G 、F 、H 在同一直线上时,GF +FB =GF +FH =GH 取得最小值 ∵AE ⊥CD 于点G ∴∠AGC =90°∵O 为AC 中点∴OA =OC =OG =AC ∴A 、C 、G 三点共圆,圆心为O ,即点G 在⊙O 上运动 ∴当点G 运动到OQ 上时,GH 取得最小值 ∵Rt △OPQ 中,∠P =60°,OP =3,sin ∠P =∴OQ =OP =∴GH 最小值为故选:C .3.(2022·山东·九年级月考)如图,在平面直角坐标系中,二次函数y =x 2﹣2x +c 的图象与x 轴交于A 、C 两点,与y 轴交于点B (0,﹣3),若P 是x 轴上一动点,点D (0,1)在y 轴上,连接PD +PC 的最小值是( )A .4B .2+C .D .32∵二次函数y =x 2﹣2x +c 的图象与∴二次函数的解析式为y =x 2解得x =﹣1或3,∴A (﹣1∵∠BOC =90°,∴∠OBC =∵D (0,1),∴OD =1,BD 设DH x =,则BH x =,∵DH4.(2022·重庆·九年级期中)如图所示,菱形ABCO 的边长为5,对角线OB 的长为,P为OB 上一动点,则AP +的最小值为( )A .4B .5C .D .解:如图,过点A 作AH OC ⊥于点H ,过点P 作PF OC ⊥于点F ,连接AC 交OB 于点J .四边形OABC 是菱形,AC OB ∴⊥,OJ JB ∴==,CJ ==2AC CJ ∴==,AH OC ⊥,12OC AH OB AC ∴⋅=⋅⋅,142AH ∴==,sin PF CJ POF OP OC ∴∠==,PF ∴,AP AP PF ∴+=+,AP PF AH +,4AP ∴,AP ∴+的最小值为4,故选:A .5.(2022·浙江宁波·九年级开学考试)如图,在平面直角坐标系中,一次函数y =分别交x 轴、y 轴于A 、B 两点,若C 为x 轴上的一动点,则2BC +AC 的最小值为__________.6.(2022·湖南·九年级月考)如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=6,△BCD为等边三角形点E为△BCD围成的区域(包括各边)的一点过点E作EM∥AB,交直线AC于点M作EN∥AC交直线AB于点N,则AN+AM的最大值为.【解答】解:过E作EH⊥AC交AC的延长线于点H,∵EN∥AC,EM∥AB,∴四边形ANEM是平行四边形,∠HME=∠A=60°,设EM =AN =a ,AM =b ,Rt △HEM 中,∠HEM =30°,∴MH =ME =a ,∴AN +AM =a +b =MH +AM =AH ,当E 在点D 时,AH 的值最大是:3+4.5=7.5,AN +AM 的最大值为7.5,故答案为:7.5.7.(2022·湖北武汉·九年级期末)如图,▱ABCD 中60A ∠=︒,6AB =,2AD =,P 为边CD 2PB +的最小值为______.四边形8.(2022·成都市七中育才九年级期中)如图,在平面直角坐标系中,直线l 分别交x 、y 轴于B 、C 两点,点A 、C 的坐标分别为(3,0)、(0,﹣3),且∠OCB =60°,点P 是直线l 上一动点,连接AP ,则2AP PC +的最小值是______.在Rt △PCG 中,∠PCG =60°,则∠CPG =30°,1PC PG =3PC AP 9.(2022·四川自贡·一模)如图,ABC 中,10AB AC ==,tan 2A =,BE AC ⊥于点E ,D 是线段BE 上的一个动点,则CD 的最小值是__________.DH CM 即可求值.【详解】解:如图,过点∵BE AC ⊥,∴90AEB ∠=︒设AE a =,2BE a =,2AB AE =∴25a =或25−(舍弃),∴∵AB AC =,BE AC ⊥,CM ⊥DH CM ,∴45BD ,∴【点睛】本题主要考查解直角三角形,等腰三角形的性质,勾股定理,垂线段最短等,学会添加辅助线并利用转化的思想是解题的关键.10.(2022·广东·一模)已知抛物线243y x x =−+与x 轴交于A ,B 两点(A 在B 点左侧),与y 轴正半轴交于点C ,点P 是直线BC 上的动点,点Q 是线段OC 上的动点.(1)求直线BC 解析式.(2)如图①,求OP +P A 的和取最小值时点P 的坐标. 12+QC 的最小值. Rt A PB '∵B (3,0),C (0,3),∴又∠BOC =90°,∴∠OCB 由对称性可知OCP DCP ≌,OCB DCB ≌,∴∠DCB =∠OCB =45°,∠CDB =∠COB =90°,∴∠OCD =90°,∴四边形OCDB 为正方形,∴D 坐标为(又A (1,0),∴AB =2,BD =3,则AQ +QP =A Q PQ A '+≥在Rt A PB '中,∠OBP =45°为22;(4)解:如图,在x 轴负半轴上找点∴12HQ CQ =,∴12AQ +∴当A ,Q ,H 三点共线,且∵CO =3,∠COG =90°,∠∴GO =3,∠CGO =60°当AH ⊥CG 时,AH AG =11.(2022·江苏·中考模拟)如图,抛物线与直线交于,两212y x mx n =++132y x =−+A B点,交轴于,两点,连接,,已知,.(Ⅰ)求抛物线的解析式和的值;(Ⅱ)在(Ⅰ)条件下:(1)为轴右侧抛物线上一动点,连接,过点作交轴于点,问:是否存在点使得以,,为顶点的三角形与相似?若存在,请求出所有符合条件的点的坐标;若不存在,请说明理由.(2)设为线段上一点(不含端点),连接,一动点从点出发,沿线段以每秒一个单位速度运动到点,再沿线段个单位的速度运动到后停止,当点的坐标是多少时,点在整个运动中用时最少?解:(Ⅰ)把,代入,得,解得:.抛物线的解析式为联立,解得:或,点的坐标为.如图1.,,,,,,,是直角三角形,,;(Ⅱ)方法一:(1)存在点,使得以,,为顶点的三角形与相似.过点作轴于,则.x D C AC BC(0,3)A(3,0)Ctan BAC∠P y PA P PQ PA⊥y Q P A P QACB∆PE AC DE M D DEE EA A EM(0,3)A(3,0)C212y x mx n=++31902nmx n=⎧⎪⎨⨯++=⎪⎩523mn⎧=−⎪⎨⎪=⎩∴215322y x x=−+213215322y xyx x⎧=−+⎪⎪⎨⎪=−+⎪⎩3xy=⎧⎨=⎩41xy=⎧⎨=⎩∴B(4,1)(3,0)C(4,1)B(0,3)A220AB∴=22BC=218AC=222BC AC AB∴+=ABC∴∆90ACB∴∠=︒1tan3BCBACAC∴∠===P A P Q ACB∆P PG y⊥G90PGA∠=︒设点的横坐标为,由在轴右侧可得,则.,,.若点在点的下方,①如图2①,当时,则. ,,,.. 则.把代入,得 ,整理得:解得:(舍去),(舍去). ②如图2②,当时,则.同理可得:,则, 把代入,得, 整理得:解得:(舍去),,,; 若点在点的上方,①当时,则,同理可得:点的坐标为.②当时,则.同理可得:点的坐标为,. 综上所述:满足条件的点的坐标为、,、,; 方法二:作的“外接矩形” ,易证,, 以,,为顶点的三角形与相似,或, 设,,, ①,,,, ②,,,(舍, 满足题意的点的坐标为、,、,; (2)方法一:过点作轴于,如图3.在中,,即, P x P y 0x >PG x =PQ PA ⊥90ACB ∠=︒90APQ ACB ∴∠=∠=︒G A PAQ CAB ∠=∠PAQ CAB ∆∆∽90PGA ACB ∠=∠=︒PAQ CAB ∠=∠PGA BCA ∴∆∆∽∴13PG BC AG AC ==33AG PG x ∴==(,33)P x x −(,33)P x x −215322y x x =−+21533322x x x −+=−20x x +=10x =21x =−PAQ CBA ∠=∠PAQ CBA ∆∆∽1133AG PG x ==1(,3)3P x x −1(,3)3P x x −215322y x x =−+215133223x x x −+=−21303x x −=10x =2133x =13(3P ∴14)9G A PAQ CAB ∠=∠PAQ CAB ∆∆∽P (11,36)PAQ CBA ∠=∠PAQ CBA ∆∆∽P 17(3P 44)9P (11,36)13(314)917(344)9APQ ∆AQGH AHP QGP ∆∆∽∴AP HP PQ QG=A P Q ACB ∆∴13AP HP BC PQ QG AC ===3AP HP AC PQ QG BC===2(2,253)P t t t −+(0,3)A (2,3)H t 13HP QG =232531||23t t t −−+∴=11323t ∴=21723t =3HP QG =23253||32t t t −−+∴=1211t ∴=221t =−)∴P (11,36)13(314)917(344)9E EN y ⊥N Rt ANE∆sin 452EN AE AE =⋅︒=AE =点在整个运动中所用的时间为. 作点关于的对称点,连接,则有,,,,.根据两点之间线段最短可得:当、、三点共线时,最小.此时,,四边形是矩形,,.对于, 当时,有,解得:,.,, ,,点的坐标为.方法二:作点关于的对称点,交于点,显然,作轴,垂足为,交直线于点,如图4,在中,,即, 当、、三点共线时,最小,,,,,,,,,,,, ∴M 1DE DE EN =+D AC D 'D E 'D E DE '=D C DC '=45D CA DCA ∠'=∠=︒90D CD ∴∠'=︒DE EN D E EN +='+D 'E N DE EN D E EN +='+90D CD D NO NOC ∠'=∠'=∠=︒∴OCD N '3ND OC ∴'==ON D C DC ='=215322y x x =−+0y =2153022x x −+=12x =23x =(2,0)D ∴2OD =321ON DC OC OD ∴==−=−=312NE AN AO ON ∴==−=−=∴E(2,1)D AC D 'DD 'AC M DE D E ='D N y '⊥N AC E Rt ANE∆sin 45EN AE AE =⋅︒=AE =∴D 'E N DE EN D E EN +='+(0,3)A (3,0)C :3AC l y x ∴=−+(,3)M m m ∴−+(2,0)D DM AC ⊥1DM AC K K ∴⨯=−3112m m −+∴−⨯=−−52m ∴=5(2M ∴1)2为的中点,,,.方法三:如图,5,过作射线轴,过作射线轴,与交于点. ,,.,,, ,..当且仅当时,取得最小值,点在整个运动中用时最少为: , 抛物线的解析式为,且,可求得点坐标为 则点横坐标为2,将代入,得.所以.12.(2020·四川乐山市·中考真题)已知抛物线与轴交于,两点,为抛物线的顶点,抛物线的对称轴交轴于点,连结,且,如图所示.(1)求抛物线的解析式;(2)设是抛物线的对称轴上的一个动点.①过点作轴的平行线交线段于点,过点作交抛物线于点,连结、,求的面积的最大值;②连结,求的最小值.【答案】(1);(2)①;②. 【分析】(1)先函数图象与x 轴交点求出D 点坐标,再由求出C 点坐标,用待定系数法设交点式,将C 点坐标代入即可求解;(2)①先求出BC 的解析式M DD '(3,1)D ∴'1Y Y E D ='=(2,1)E ∴A //AF x D //DF y DF AC E (0,3)A (3,0)C :3AC l y x ∴=−+OA OC =90AOC ∠=︒45ACO ∴∠=︒//AF OC 45FAE ∴∠=︒sin 45EF AE ∴=⋅︒∴AF DF ⊥DE EF +M 1DE t DE EF ==+215322y x x =−+(3,0)C ∴D (2,0)E 2x =:3AC l y x =−+1y =(2,1)E 2y ax bx c =++x (1,0)A −(50)B ,C x D BC 4tan 3CBD ∠=P P x BC E E EF PE ⊥F FB FC BCF ∆PB 35PC PB+241620999y x x =−++322454tan 3CBD ∠=,设E 坐标为,则F 点坐标为,进而用t 表示出的面积,由二次函数性质即可求出最大值;②过点作于,由可得,由此可知当BPH 三点共线时的值最小,即过点作于点,线段的长就是的最小值,根据面积法求高即可. 【详解】解:(1)根据题意,可设抛物线的解析式为:,∵是抛物线的对称轴,∴,又∵,∴,即,代入抛物线的解析式,得,解得 , ∴二次函数的解析式为 或; (2)①设直线的解析式为 ,∴ 解得 即直线的解析式为 ,设E 坐标为,则F 点坐标为, ∴, ∴的面积 ∴, 42033=−+y x 420,33t t ⎛⎫−+ ⎪⎝⎭241620999,t t t ⎛⎫ ⎪⎝−+⎭+BCF ∆P PG AC ⊥G 3sin 5PG PC ACD PC =⋅∠=35PC PB PG PB +=+35PC PB +B BH AC ⊥H BH 35PC PB +(1)(5)y a x x =+−CD (20)D ,4tan 3CBD ∠=tan 4CD BD CBD =⋅∠=(24)C ,4(21)(25)a =+−49a =−4(1)(5)9y x x =−+−241620999y x x =−++BC y kx b =+0542.k b k b =+⎧⎨=+⎩,4320.3k b ⎧=−⎪⎪⎨⎪=⎪⎩,BC 42033=−+y x 420,33t t ⎛⎫−+ ⎪⎝⎭241620999,t t t ⎛⎫ ⎪⎝−+⎭+22420341620428409999993EF t t t t t =−++−=−+⎛⎫⎛⎫−+ ⎪ ⎪⎝⎭−⎝⎭BCF ∆21142840322999S EF BD t t ⎛⎫=⨯⨯=−+− ⎪⎝⎭2273()322S t =−−+∴当时,的面积最大,且最大值为; ②如图,连接,根据图形的对称性可知 ,,∴,过点作于,则在中,, ∴,再过点作于点,则, ∴线段的长就是的最小值,∵, 又∵,∴,即,∴的最小值为. 【点睛】此题主要考查了二次函数的综合题型,其中涉及了待定系数法求解析式和三角形的面积最大值求法、线段和的最值问题.解(1)关键是利用三角函数求出C 点坐标,解(2)关键是由点E 、F 坐标表示线段EF 长,从而得到三角形面积的函数解析式,解(3)的难点是将的最小值转化为点B 到AC 的距离. 13.(2021·四川达州市·中考真题)如图,在平面直角坐标系中,抛物线交轴于点和,交轴于点,抛物线的对称轴交轴于点,交抛物线72t =BCF ∆32AC ACD BCD ∠=∠5AC BC ==3sin 5AD ACD AC ∠==P PG AC ⊥G Rt PCG ∆3sin 5PG PC ACD PC =⋅∠=35PC PB PG PB +=+B BH AC ⊥H PG PH BH +≥BH 35PC PB +11641222ABC S AB CD ∆=⨯⨯=⨯⨯=1522ABC S AC BH BH ∆=⨯⨯=5122BH =245BH =35PC PB +24535PC PB +2y x bx c =−++x A ()1,0C y ()0,3B x E于点.(1)求抛物线的解析式;(2)将线段绕着点沿顺时针方向旋转得到线段,旋转角为,连接,,求的最小值.(3)为平面直角坐标系中一点,在抛物线上是否存在一点,使得以,,,为顶点的四边形为矩形?若存在,请直接写出点的横坐标;若不存在,请说明理由;【答案】(1);(2;(3)存在,点的横坐标分别为:2,,或. 【分析】(1)待定系数法求二次函数解析式,设解析式为将,两点代入求得,c的值即可;(2)胡不归问题,要求的值,将折线化为直线,构造相似三角形将转化为,再利用三角形两边之和大于第三边求得最值;(3)分2种情形讨论:①AB 为矩形的一条边,利用等腰直角三角形三角形的性质可以求得N 点的坐标;②AB 为矩形的对角线,设R 为AB 的中点,RN =AB ,利用两点距离公式求解方程可得N 点的坐标. F OE О'OE ()090αα︒<<︒'AE 'BE 13''BE AE +M N A B M N N 223y x x =−−+N 1−12−+12−2y x bx c =−++()1,0C ()0,3B b 13''BE AE +13'AE 13'DE 13''BE AE +12【详解】解:(1)∵过,∴∴,∴抛物线的解析式为: (2)在上取一点,使得,连接,∵对称轴.∴, ,∴,∴ ∴ ∴ 当,,三点在同一点直线上时,最小为.在中,, ∴ 即. (3)情形①如图,AB 为矩形的一条边时,联立得 2y x bx c =−++()1,0C ()0,3B 103b c c −++=⎧⎨=⎩2b =−3c =223y x x =−−+OE D 13OD OE ='AE BD 11'33OD OE OE ==3112x −+==−()1,0E −1OE ='1OE OE ==3OA ='1'3OE OD OA OE ==''DOE E OA ∠=∠''DOE E OA ∆∆∽1''3DE AE =1''''3BE AE BE DE +=+B 'E D ''BE DE +BD Rt BOD ∆13OD =3OB =3BD ===13''BE AE +2023y y x x =⎧⎨=−−+⎩31,00x x y y =−=⎧⎧⎨⎨==⎩⎩是等腰,分别过 两点作的垂线,交于点,过作轴,轴,,也是等腰直角三角形 设,则,所以代入,解得,(不符题意,舍) 同理,设,则 ,所以代入,解得,(不符题意,舍)② AB 为矩形的对角线,设R 为AB 的中点,则 , 设 ,则 整理得: 解得:(不符题意,舍),(不符题意,(3,0),3A OA ∴−=3OB =ABO ∴Rt 45BAO ∠=︒,A B AB 223y x x =−−+12,N N 12,N N 1N Q y ⊥2N P x ⊥1245QBN PAN ∴∠=∠=︒∴1BN Q △2AN P △QB m =1N Q m =1(,3)N m m −+223y x x =−−+11m =20m =∴1(1,4)N −OP n ==3PN n +2(,3)N n n −−223y x x =−−+1n 2=23n =−2(2,-5)N∴12RN AB =()3,0,()0,3A B −33(,)22R ∴−AB ==122RB AB ∴==12RN AB==2RN ∴2(,23)N x x x −−+222233()(2)()222x x x +++−=2(3)(1)0x x x x ++−=1=0x 23x =−舍),, 综上所述:点的横坐标分别为:2,,【点睛】本题考查了二次函数的性质,待定系数法求解析式,三角形相似,勾股定理,二次函数与一次函数交点,矩形的性质,等腰直角三角形性质,平面直角坐标系中两点距离计算等知识,能正确做出辅助线,找到相似三角形是解题的关键.14.(2022·广西·南宁三中一模)如图,二次函数21y ax bx =++的图象交x 轴于点()2,0A −、()10B ,,交y 轴于点C ,点D 是第四象限内抛物线上的动点,过点D 作//DE y 轴交x 轴于点E ,线段CB 的延长线交DE 于点M ,连接OM 、BD 交于点N ,连接AD .(1)求二次函数的表达式;(2)当OEM DBE S S =时,求点D 的坐标及sin DAE ∠;(3)在(2)的条件下,点P 是x 轴上一个动点,求DP 的最小值. 31=2x −+41=2x −∴N 1−12−OEM DBE S S=,∴1BE a =−,EM【点睛】主要考查了待定系数法求函数的解析式,函数图象上点的坐标特征,勾股定理,垂线段最短,轴对称的性质,以及解直角三角形的知识,要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系,解决相关问题.15.(2022·广东·东莞市三模)已知,如图,二次函数2y ax bx c =++图像交x 轴于(1,0)A −,交y 交轴于点(0,3)C ,D 是抛物线的顶点,对称轴DF 经过x 轴上的点(1,0)F .(1)求二次函数关系式;(2)对称轴DF 与BC 交于点M ,点P 为对称轴DF 上一动点.①求AP 的最小值及取得最小值时点P 的坐标; ②在①的条件下,把APF 沿着x 轴向右平移t 个单位长度(04)t ≤≤时,设APF 与MBF 重叠部分面积记为S ,求S 与t 之间的函数表达式,并求出S 的最大值.则sinPH PD FDB=⋅∠=依“垂线段最短”得此时AH∵sinAH DF OBDAB DB ∠==16.(2022·天津·中考模拟)如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.(1)证明:CE是⊙O的切线;(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;(3)设点D是线段AC上任意一点(不含端点),连接OD,当CD+OD的最小值为6时,求⊙O的直径AB的长.【答案】(1)见解析;(2)(3)AB=【解析】(1)连接OC,如图,∵CA=CE,∠CAE=30°,∴∠E=∠CAE=30°,∠COE=2∠A=60°,∴∠OCE=90°,∴CE是⊙O的切线;(2)过点C作CH⊥AB于H,连接OC,如图,由题可得CH=h.在Rt△OHC中,CH=OC•sin∠COH,∴h=OC•sin60°=OC,∴OC=,∴AB=2OC=;(3)作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,如图,则∠AOF=∠COF=∠AOC=(180°﹣60°)=60°.∵OA=OF=OC,∴△AOF、△COF是等边三角形,∴AF=AO=OC=FC,∴四边形AOCF是菱形,∴根据对称性可得DF=DO.过点D作DH⊥OC于H,∵OA=OC,∴∠OCA=∠OAC=30°,∴DH=DC•sin∠DCH=DC•sin30°=DC,∴+OD=DH+FD.根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD CD+OD)最小,此时FH=OF•sin∠FOH==6,则OF=,AB=2OF=8.∴当CD+OD的最小值为6时,⊙O的直径AB的长为8.。
4最值系列之胡不归问题(1)

最值系列之“胡不归”问题在前面的最值问题中往往都是求某个线段最值或者形如P A +PB 最值,除此之外我们还可能会遇上形如“P A +kPB ”这样的式子的最值,此类式子一般可以分为两类问题:(1)胡不归问题;(2)阿氏圆.本文简单介绍“胡不归”模型. 【故事介绍】从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A 到家B 之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?…”(“胡”同“何”)而如果先沿着驿道AC 先走一段,再走砂石地,会不会更早些到家?2驿道【模型建立】如图,一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使21AC BCV V的值最小.2M练习:1.如图,△ABC 中,AB =AC =10,tan A =2,BE ⊥AC 于点E ,D 是线段BE上的一个动点,则CD +的最小值是_______.1题图 2题图2.如图,平行四边形ABCD 中,∠DAB =60°,AB =6,BC =2,P 为边CD上的一动点,则PB +的最小值等于________.3.如图,已知抛物线()()248ky x x =+-(k 为常数,且k >0)与x 轴从左至右依次交于A ,B 两点,与y 轴交于点C ,经过点B的直线y x b =+与抛物线的另一交点为D . (1)若点D 的横坐标为-5,求抛物线的函数表达式;(2)在(1)的条件下,设F 为线段BD 上一点(不含端点),连接AF ,一动点M 从点A出发,沿线段AF 以每秒1个单位的速度运动到F ,再沿线段FD 以每秒2个单位的速度运动到D 后停止,当点F 的坐标是多少时,点M 在整个运动过程中用时最少?ABCDEABCDP4.抛物线2y=与x轴交于点A,B(点A在点B的左边),与y轴交于点C.点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当12PE EC+的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标.(为突出问题,删去了两个小问)。
中考数学最值—胡不归问题(解析+例题)

中考数学最值——胡不归问题(点在直线上运动)(PA+k·PB型最值)【历史典故】从前,有一个小伙子在外地学徒,当他获悉在家的老父亲病危的消息后,便立即启程赶路。
由于思乡心切,他只考虑了两点之间线段最短的原理,所以选择了全是沙砾地带的直线路径A→B(如图所示),而忽视了走折线虽然路程多但速度快的实际情况,当他气喘吁吁地赶到家时,老人刚刚咽了气,小伙子失声痛哭。
邻居劝慰小伙子时告诉说,老人弥留之际不断念叨着“胡不归?胡不归?…”。
这个古老的传说,引起了人们的思索,小伙子能否提前到家?倘若可以,他应该选择一条怎样的路线呢?这就是风靡千百年的“胡不归问题”。
【知识储备】①三角形三边关系:两边之和大于第三边;两边之差小于第三边。
②两点之间线段最短。
③连接直线外一点和直线上各点的所有线段中,垂线段最短。
【模型分析】①条件:已知A、B为定点,P为射线AC上一动点。
②问题:P在何处时,BP+nm AP最短(nm<1)。
③方法:第一步在AC的一侧,PB的异侧构造∠CAE=α,使得sinα=nm 第二步做BH⊥AE,交AC于P,点P就是所求位置,BH就是其最小值。
【模型分析】【问题提出】如图①,已知海岛A到海岸公路BD的距离为AB的长度,C为公路BD上的酒店,从海岛A到酒店C,先乘船到登陆点D,船速为a,再乘汽车,车速为船速的n倍,点D 选在何处时,所用时间最短?个运动过程中用时最少,请求出最少时间和此时点F的坐标。
【巩固训练】练习1:如图,四边形ABCD是菱形,AB=4,且∠ABC=60°,M为对角线BD(不含B点)上BM的最小值为_____。
任意一点,则AM+12练习2:如图,等腰ΔABC中,AB=AC=3,BC=2,BC边上的高为A0,点D为射线A0上一点,一动点P从点A出发,沿AD-DC运动,动点P在AD上运动速度3个单位每秒,动点P在CD上运动的速度为1个单位每秒,则当 AD= 时,运动时间最短为秒。
初中数学最值专题17:胡不归带系数问题

最值系列之“胡不归”问题PA+kPB 解决策略一【故事介绍】 从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A 到家B 之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?…”(“胡”同“何”)而如果先沿着驿道AC 先走一段,再走砂石地,会不会更早些到家?【模型建立】如图,一动点P 在直线MN 外的运动速度为V1,在直线MN 上运动的速度为V2,且V1<V2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使21AC BC V V +的值最小.【问题分析】121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭,记12V k V =, 即求BC+kAC 的最小值.2驿道2M【问题解决】构造射线AD 使得sin ∠DAN=k ,k ACCH ,CH=kAC .将问题转化为求BC+CH 最小值,过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC+CH 取到最小值,即BC+kAC 最小.【模型总结】在求形如“PA+kPB ”的式子的最值问题中,关键是构造与kPB 相等的线段,将“PA+kPB ”型问题转化为“PA+PC ”型.而这里的PB 必须是一条方向不变的线段,方能构造定角利用三角函数得到kPB 的等线段.MM1、如图,△ABC 中,AB=AC=10,tanA=2,BE ⊥AC 于点E ,D 是线段BE上的一个动点,则CD +的最小值是_______.2、如图,平行四边形ABCD 中,∠DAB=60°,AB=6,BC=2,P 为边CD上的一动点,则PB +的最小值等于________.的最小值为_____.4、如图所示,点A 为直线L 外一定点,点B 、C 为直线L 上的两定点,且AB=2,∠ABC=15°,点P 为直线L 上的动点,请确定点P 的位置,使得BP AP 21+最小,并求出这个最小值。
胡不归最值问题

专题十一 胡不归模型【模型总结】在求形如“PB +kP A ”的式子的最值问题中,关键是构造与kP A 相等的线段,将“PB +kP A ”型问题转化为“PB +PC ”型.而这里的P A 必须是一条方向不变的线段,方能构造定角利用三角函数得到kP A 的等线段.【问题】如图,点P 为射线l 上的一动点,A 、B 为定点,求PB +kP A 的最小值.【问题解决】构造射线AD 使得sinα=k ,PC /P A =k ,CP =kAP .l将问题转化为求PB +PC 最小值,过B 点作BC ⊥AD 交l 于点P ,交AD 于C 点,此时PB +PC 取到最小值,即PB +kP A 最小.【例1】如图,⊥ABC 中,AB =AC =10,BE =2AE ,BE ⊥AC 于点E ,D 是线段BE 上的一个动点,则CD +55BD 的最小值是 .【变式1-1】如图,在Rt⊥ABC 中,⊥ACB =90°,⊥A =30°,则AB =2BC .请在这一结论的基础上继续思考:若AC =2,点D 是AB 的中点,P 为边CD 上一动点,则AP +21CP的最小值为.【变式1-3】如图,⊥ABC在直角坐标系中,AB=AC,A(0,22),C(1,0),D为射线AO上一点,一动点P从A出发,运动路径为A→D→C,点P在AD上的运动速度是在CD上的3倍,要使整个运动时间最少,则点D的坐标应为________.【例2】如图, ABCD中,⊥A=60°,AB=6,AD=2,P为边CD上一点,则3PD+2PB最小值为.【变式2-1】如图,在菱形ABCD中,AB=AC=10,对角线AC、BD相交于点O,点M在线段AC上,且1PB的最小值是.AM=3,点P为线段BD上的一个动点,则MP+2巩固练习1.如图,在⊥ABC中,⊥A=90°,⊥B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小值是.2 2.如图,在⊥ABC中,⊥A=15°,AB=2,P为AC边上的一个动点(不与A、C重合),连接BP,则2 AP+PB的最小值是.3.在⊥ABC中,⊥ACB=90°,P为AC上一动点,若BC=4,AC=6,则2BP+AP的最小值为.5OP的最小值为.4.如图,菱形ABCO的边长为5,对角线OB=45,P为OB上一动点,求AP+55.如图,在⊥ABC中,AB=AC=4,⊥CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则P A+2PB的最小值为.6.如图,⊥ABC中,⊥BAC=30°且AB=AC,P是底边上的高AH上一点.若AP+BP+CP的最小值为22,则BC=.7.等边三角形ABC的边长为6,将其放置在如图所示的平面直角坐标系中,其中BC边在x轴上,BC边的高OA在Y轴上.一只电子虫从A出发,先沿y轴到达G点,再沿GC到达C点,已知电子虫在Y 轴上运动的速度是在GC上运动速度的2倍,若电子虫走完全程的时间最短,则点G的坐标为.8.如图,在边长为6的正方形ABCD中,M为AB上一点,且BM=2,N为边BC上一动点,连接MN,点B关于MN对称,对应点为P,连接P A,PC,则P A+2PC的最小值为.9.在菱形ABCD中,⊥DAB=30°.(1)如图1,过点B作BE⊥AD于点E,连接CE,点F是线段CE的中点,连接BF,若ED=2−√3,求线段BF的长度;(2)如图2,过点B作BE⊥AD于点E,连接CE,过点D作DM⊥DC,连接MC,且⊥MCE=15°,连接ME,请探索线段BE,DM,EM之间的数量关系,并证明;(3)如图3,连接AC,点Q是对角线AC上的一个动点,若AB=2√6,求QB+QC+QD的最小值.10.如图1,在平面直角坐标系中将y=2x+1向下平移3个单位长度得到直线l1,直线l1与x轴交于点C;直线l2:y=x+2与x轴、y轴交于A、B两点,且与直线l1交于点D.(1)填空:点A的坐标为,点B的坐标为;(2)直线l1的表达式为;(3)在直线l1上是否存在点E,使S⊥AOE=2S⊥ABO?若存在,则求出点E的坐标;若不存在,请说明理由.(4)如图2,点P为线段AD上一点(不含端点),连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒2个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.。
胡不归最值问题(解析版)

胡不归最值问题【专题说明】胡不归模型问题解题步骤如下;1、将所求线段和改写为“PA +b a PB ”的形式b a <1 ,若b a>1,提取系数,转化为小于1的形式解决。
2、在PB 的一侧,PA 的异侧,构造一个角度α,使得sin α=b a 3、最后利用两点之间线段最短及垂线段最短解题【模型展示】如图,一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使AC V 2+BC V 1的值最小.ACV 2+BC V 1=1V 1BC +V 1V 2AC ,记k =V 1V 2,即求BC +kAC 的最小值.构造射线AD 使得sin ∠DAN =k ,CH /AC =k ,CH =kAC .将问题转化为求BC +CH 最小值,过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC +CH 取到最小值,即BC +kAC 最小.【模型总结】在求形如“PA +kPB ”的式子的最值问题中,关键是构造与kPB相等的线段,将“PA +kPB ”型问题转化为“PA +PC ”型.而这里的PB 必须是一条方向不变的线段,方能构造定角利用三角函数得到kPB 的等线段.【练习】1.如图,AC 是圆O 的直径,AC =4,弧BA =120°,点D 是弦AB 上的一个动点,那么OD +12BD 的最小值为( )A.32B.3C.1+32D.1+3【解答】解:∵BA 的度数为120°,∴∠C =60°,∵AC 是直径,∴∠ABC =90°,∴∠A =30°,作BK ⎳CA ,DE ⊥BK 于E ,OM ⊥BK 于M ,连接OB .∵BK ⎳AC ,∴∠DBE =∠BAC =30°,在Rt ΔDBE 中,DE =12BD ,∴OD +12BD =OD +DE ,根据垂线段最短可知,当点E 与M 重合时,OD +12BD 的值最小,最小值为OM ,∵∠BAO =∠ABO =30°,∴∠OBM =60°,在Rt ΔOBM 中,∵OB =2,∠OBM =60°,∴OM =OB ⋅sin60°=3,∴12DB +OD 的最小值为3,故选:B .2.如图,在ΔABC 中,∠A =15°,AB =10,P 为AC 边上的一个动点(不与A 、C 重合),连接BP ,则22AP +PB 的最小值是( )A.52 B.53 C.1033 D.8【解答】解:如图,以AP 为斜边在AC 下方作等腰Rt ΔADP ,过B 作BE ⊥AD 于E ,∵∠PAD =45°,∴sin ∠PAD =DP AP =22,∴DP =22AP ,∴22AP+PB=DP+PB≥BE,∵∠BAC=15°,∴∠BAD=60°,∴BE=AB sin60°=53,∴22AP+PB的最小值为53.故选:B.3.ΔABC中,∠A=90°,∠B=60°,AB=2,若点D是BC边上的动点,则2AD+DC的最小值为( )A.4B.3+3C.6D.23+3【解答】解:过点C作射线CE,使∠BCE=30°,再过动点D作DF⊥CE,垂足为点F,连接AD,如图所示:在RtΔDFC中,∠DCF=30°,∴DF=12DC,∵2AD+DC=2AD+12DC=2(AD+DF),∴当A,D,F在同一直线上,即AF⊥CE时,AD+DF的值最小,最小值等于垂线段AF的长,此时,∠B=∠ADB=60°,∴ΔABD是等边三角形,∴AD=BD=AB=2,在RtΔABC中,∠BAC=90°,∠B=60°,AB=2,∴BC=4,∴DC=2,∴DF=12DC=1,∴AF=AD+DF=2+1=3,∴2(AD+DF)=2AF=6,∴2AD+DC的最小值为6,故选:C.4.如图所示,菱形ABCO的边长为5,对角线OB的长为45,P为OB上一动点,则AP+55OP的最小值为( )A.4B.5C.25D.35【解答】解:如图,过点A作AH⊥OC于点H,过点P作PF⊥OC于点F,连接AC交OB于点J.∵四边形OABC是菱形,∴AC⊥OB,∴OJ=JB=25,CJ=OC2-OJ2=52-(25)2=5,∴AC=2CJ=25,∵AH⊥OC,∴OC⋅AH=12⋅OB⋅AC,∴AH=12×45×255=4,∴sin∠POF=PFOP=CJOC=55,∴PF=55OP,∴AP+55OP=AP+PF,∵AP+PF≥AH,∴AP+55OP≥4,∴AP+55OP的最小值为4,故选:A.5.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,AB=16,∠ABC=60°,D为弧AC的中点,M是弦AC上任意一点(不与端点A、C重合),连接DM,则12CM+DM的最小值是( )A.43B.33C.23D.4【解答】解:过点M作ME⊥OC于E,过点D作DF⊥OC于F,连接OD,∵AB为⊙O的直径,∴∠ACB=90°,∵∠ABC=60°,∴∠BAC=30°,∵OA=OC,∴∠ACO=∠CAO=30°,∴ME=12MC,∴12CM+DM=ME+DM,∴ME +DM 的最小值为DF 的长,∵D 为弧AC 的中点,∴∠AOD =∠COD =60°,在Rt ΔODF 中,sin ∠DOF =sin60°=DF OD =32,∴DF =32OD =43,∴12CM +DM 的最小值为:43,故选:A .6.在ΔABC 中,∠ACB =90°,P 为AC 上一动点,若BC =4,AC =6,则2BP +AP 的最小值为( )A.5B.10C.52D.102【解答】解:以A 为顶点,AC 为一边在下方作∠CAM =45°,过P 作PF ⊥AM 于F ,过B 作BD ⊥AM 于D ,交AC 于E ,如图:2BP +AP =2BP +22AP ,要使2BP +AP 最小,只需BP +22AP 最小,∵∠CAM =45°,PF ⊥AM ,∴ΔAFP 是等腰直角三角形,∴FP =22AP ,∴BP +22AP 最小即是BP +FP 最小,此时P 与E 重合,F 与D 重合,即BP +22AP 最小值是线段BD 的长度,∵∠CAM =45°,BD ⊥AM ,∴∠AED =∠BEC =45°,∵∠ACB =90°,∴sin ∠BEC =sin45°=BC BE ,tan ∠BEC =BC CE,又BC =4,∴BE =42,CE =4,∵AC =6,∴AE =2,而sin ∠CAM =sin45°=DE AE ,∴DE=2,∴BD=BE+DE=52,∴2BP+AP的最小值是2BD=10,故选:B.7.【问题探究】在等边三角形ABC中,AD⊥BC于点D,AB=2.(1)如图1.E为AD的中点,则点E到AB的距离为 34 ;(2)如图2,M为AD上一动点.则12AM+MC的最小值为 ;【问题解决】如图3,A,B两地相距600km,AC是笔直地沿东西方向向两边延伸的一条铁路,点B到AC的距离为360km.今计划在铁路线AC上修一个中转站M,再在BM间修一条笔直的公路.如果同样的物资在每千米公路上的运费是铁路上的两倍,那么为使通过铁路由A到M再通过公路由M到B的总运费达到最小值,中转站M应修在距A地 km处.【解答】解:(1)∵ΔABC是等边三角形,∴AB=BC=2,∠BAC=∠ACB=∠ABC=60°,∵AD⊥BC,∴∠BAD=30°,BD=1,∴AD=3,过E作EM⊥AB,垂足为M,∵E为AD的中点,∴AE=32,∴EM=12AE=34,故答案为:3 4;(2)如图,作CN⊥AB,垂足为N,此时12AM+MC最小,最小值等于CN,∵在正三角形ABC中,AB=BC=AC=2,CN⊥AB,∴∠ACN=∠BCN=30°,∴AN=12AC=1,由勾股定理得,CN=AC2-AN2=22-12=3,由(1)知,MN=12AM,∴MN+CM=12AM+MC=CN=3,即12AM+MC的最小值为3,故答案为:3;【问题解决】如图,作BD⊥AC,垂足为点D,在AC异于点B的一侧作∠CAN=30°,作BF⊥AN,垂足为点F,交AC于M,则点M即为所求,在RtΔABD中,AB=600km,BD=360km,∴AD=6002-3602=480,易知∠MB D=∠MAF=30°,在RtΔMBD中,∠MB D=30°,BD=360km,则MB=2MD,由勾股定理得MD=1203km,∴AM=AD-MD=(480-1203)km.故答案为(480-1203).8.如图,在菱形ABCD中,AB=AC=10,对角线AC、BD相交于点O,点M在线段AC上,且AM= 3,点P为线段BD上的一个动点,则MP+12PB的最小值是 732 .【解答】解:如图,过点P作PE⊥BC于E,∵四边形ABCD是菱形,AB=AC=10,∴AB=BC=AC=10,∠ABD=∠CBD,∴ΔABC是等边三角形,∴∠ABC=∠ACB=60°,∴∠CBD=30°,∵PE⊥BC,∴PE=12PB,∴MP+12PB=PM+PE,∴当点M,点P,点E共线且ME⊥BC时,PM+PE有最小值为ME,∵AM=3,∴MC=7,∵sin∠ACB=MEMC=3 2,∴ME=732,∴MP+12PB的最小值为732,故答案为73 2.9.如图,直角三角形ABC中,∠A=30°,BC=1,AC=3,BD是∠ABC的平分线,点P是线段BD上的动点,求CP+12BP的最小值 32 .【解答】解:如图,过点P作PE⊥AB于E,∵∠A=30°,BC=1,∠ACB=90°,∴AB=2BC=2,∠ABC=60°,∵BD是∠ABC的平分线,∴∠ABD=∠CBD=30°,∵PE⊥AB,∴PE=12PB,∴CP+12PB=CP+PE,∴当点P,点C,点E三点共线,且CE⊥AB时,CP+12PB有最小值为CE,∴CE=AC×BCAB=1×32=32,故答案为:3 2.10.如图,已知RtΔABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD,且AD=4,点P为线段AC上一动点,连接BP.则2BP+AP的最小值为 43 .【解答】解:如图中,作PF⊥AD于F,BF′⊥AD于F′,交AC于P′.∵∠PAF=30°,∠PFA=90°,∴PF=12PA,∴2BP+AP=2PB+12PA=2(PB+PF),∴当B、P、F共线时,即BF′⊥AD时,PB+PF最短,最小值为线段BF′,在Rt△DF′B中,∵∠D=60°,DB=4,∴BF′=DB∙sin60°=23,∴2BP+AP的最小值为43,故答案为:43.11.如图,▱ABCD 中,∠DAB =60°,AB =6,BC =2,P 为边CD 上的一动点,则PB +32PD 的最小值等于 33 .【解答】解:如图,过点P 作PE ⊥AD ,交AD 的延长线于点E ,∵AB ⎳CD∴∠EDP =∠DAB =60°,∴sin ∠EDP =EP DP =32∴EP =32PD∴PB +32PD =PB +PE ∴当点B ,点P ,点E 三点共线且BE ⊥AD 时,PB +PE 有最小值,即最小值为BE ,∵sin ∠A =BE AB=32∴BE =33故答案为:3312.如图,在平面直角坐标系中,直线y =-x +4的图象分别与y 轴和x 轴交于点A 和点B .若定点P 的坐标为(0,63),点Q 是y 轴上任意一点,则12PQ +QB 的最小值为 53 .【解答】解:过点P 作直线PD 与y 轴的夹角∠OPD =30°,作B 点关于y 轴的对称点B ,过B 点作B E ⊥PD 交于点E 、交y 轴于点Q ,∵B E ⊥PD ,∠OPE =30°,∴QE =12PQ ,∵BQ =B Q ,∴12PQ +QB =QE +B Q =B E ,此时12PQ +QB 取最小值,∵∠OPD =30°,∠POD =90°,∴PD =2OD ,∠ODP =60°,∵P 的坐标为(0,63),∴PO =63,∴OD 2+(63)2=(2OD )2,∴OD =6,∵直线y =-x +4的图象分别与y 轴和x 轴交于点A 和点B ,∴A (0,4),B (4,0),∴OB =4,∴OB =4,∴B D =10,∵B E ⊥PD ,∠ODP =60°,∴∠EB D =30°,∴DE =12B D =5,∴B E =B D 2-DE 2=102-52=53,∴12PQ +QB 取最小值为53,故答案为:53.13.如图,在ΔABC 中,AB =5,AC =4,sin A =45,BD ⊥AC 交AC 于点D .点P 为线段BD 上的动点,则PC +35PB 的最小值为 165 .【解答】解:过点P 作PE ⊥AB 于点E ,过点C 作CH ⊥AB 于点H ,∵BD ⊥AC ,∴∠ADB =90°,∵sin A =BD AB=45,AB =5,∴BD =4,由勾股定理得AD =AB 2-BD 2=52-42=3,∴sin ∠ABD =AD AB =PE BP =35,∴EP =35BP ,∴PC +35PB =PC +PE ,即点C 、P 、E 三点共线时,PC +35PB 最小,∴PC +35PB 的最小值为CH 的长,∵S ΔABC =12×AC ×BD =12×AB ×CH ,∴4×4=5×CH ,∴CH =165.∴PC +35PB 的最小值为165.故答案为:165.14.如图,在ΔABC 中,AB =AC =10,tan A =2,BE ⊥AC 于点E ,D 是线段BE 上的一个动点,那么:(1)AE = 25 ;(2)CD +55BD 的最小值是 .【解答】解:(1)∵tan A =2,BE ⊥AC ,∴BE AE=2,∴设BE =2x ,AE =x ,∴x 2+(2x )2=102,∴x =25(负值舍去),∴AE =25,故答案为25;(2)作DF ⊥AB 于F ,CH ⊥AB 于H ,∵AE =25,AB =10,∴AE AB=2510=55,∴sin ∠ABD =DF BD =55,∴DF =55BD ,∴CD +55BD =CD +DF ,要想CD +DF 最小,只要C 、D 、F 三点共线,即最小值为CH ,∵AB =AC ,根据等积法可知:CH =BE ,由(1)知:BE =2AE =45,∴CD +55BD 的最小值是45,故答案为:45.15.如图,在ΔABC 中,∠A =90°,∠B =60°,AB =2,若D 是BC 边上的动点,则2AD +DC 的最小值为 6 .【解答】解:如图所示,作点A 关于BC 的对称点A ,连接AA ,A D ,过D 作DE ⊥AC 于E ,∵ΔABC 中,∠BAC =90°,∠B =60°,AB =2,∴BH =1,AH =3,AA =23,∠C =30°,∴Rt ΔCDE 中,DE =12CD ,即2DE =CD ,∵A 与A 关于BC 对称,∴AD =A D ,∴AD +DE =A D +DE ,∴当A ,D ,E 在同一直线上时,AD +DE 的最小值等于A E 的长,此时,Rt △AA E 中,A E =sin60°×AA =32×23=3,∴AD +DE 的最小值为3,即2AD +CD 的最小值为6,故答案为:6.16.如图,在平面直角坐标系中,二次函数y =ax 2+bx +c 的图象交x 轴于A 、B 两点,交y 轴于C 点,P 为y 轴上的一个动点,已知A (-2,0)、C (0,-23),且抛物线的对称轴是直线x =1.(1)求此二次函数的解析式;(2)连接PB ,则12PC +PB 的最小值是 33 ;【解答】解:(1)将A ,C 点坐标代入函数解析式,及对称轴,得4a -2b +c =0c =-23-b 2a =1,解得a =34b =-32c =-23,抛物线的解析式为y =34x 2-32x -23,(2)连接AC ,作BH ⊥AC 于H ,交OC 于P ,如图1,此时12PC +PB 最小.理由:当y =0时,34x 2-32x -23=0,解得x =-2(舍)x =4,即B (4,0),AB =4-(-2)=6.∵OA =2,OC =23,∴tan ∠ACO =OA OC=33,∴∠ACO =30°,∴PH =12PC ,∴12PC +PB =PH +PB =BH ,∴此时12PB +PD 最短(垂线段最短).在Rt ΔABH 中,∵∠AHB =90°,AB =4-(-2)=6,∠HAB =60°,∴sin60°=BHAB=3 2,∴BH=6×32=33,∴12PC+PB的最小值为33,故答案为:33.17.已知:如图1,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点D(0,-6),直线y=-13x+2交x轴于点B,与y轴交于点C.(1)求抛物线的函数解析式;(2)在线段OB上有一动点P,直接写出10DP+BP的最小值和此时点P的坐标.【解答】解:(1)∵直线y=-13x+2过点B,C,令y=0,则-13x+2=0,∴x=6,令x=0,则y=2,∴B(6,0),C(0,2),∵抛物线y=x2+bx+c经过点B(6,0)和D(0,-6),∴36+6b+c=0 c=-6,∴b=-5 c=-6 ,∴抛物线的解析式为y=x2-5x-6;(2)如图,以点D为直角顶点作RtΔPDM,使DM=3DP,在RtΔPDM中,根据勾股定理,PM=DM2+DP2=10DP,要使10DP+BP最小,则有点B,P,M在同一条线上,而点B,P在x轴上,所以,点M在x轴上时,10DP+BP最小,此时,点M记作M ,点P记作P ,设P (m,0),∵∠DOP =∠M DP =90°,∠OP D=∠DP M ,∴ΔDOP ∽△M DP ,∴DP P M =OP DP ,∴m DP =DP10DP ,∴DP =10m,在RtΔDOP 中,OD=6,根据勾股定理得,(10m)2-m2=36,∴m=2或m=-2(舍),∴P(2,0),∴10DP+BP=10×210+(6-2)=24,即10DP+BP的最小值为24,此时点P的坐标为(2,0).18.如图,已知抛物线y=k8(x+2)(x-4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=-33x+b与抛物线的另一交点为D.(1)若点D的横坐标为-5,求抛物线的函数表达式;(2)在(1)条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止.当点F的坐标是多少时,点M在整个运动过程中用时最少?【解答】解:(1)将点B(4,0)代入y=-33x+b,得-33×4+b=0,∴b=433,∴BD:y=-33x+433,当x=-5时,y=-33×(-5)+433=33,∴D(-5,33),将点D代入y=k8(x+2)(x-4),得:k8×(-5+2)×(-5-4)=33,∴k=839,∴抛物线的表达式为:y=39(x+2)(x-4)=39x2-239x-839,(2)由题意得:点M的运动时间为AF+12DF,过点D作DE⊥x轴于点E,∵D(-5,33),B(4,0),∴DE=33,EB=9,BD=63,∴∠DBE=30°,过点D和点F分别作x轴的平行线和y轴的平行线,交于点N,∴∠DBE =∠FDN =30°,∴NF =12DF ,∴AF +12DF =AF +NF ,过点A 作AH ⊥DN 于点H ,此时(AF +NF )min =AH ,∴AH 与直线BD 的交点即为所求点F ,∵A (-2,0),∴当x =-2时,y =-33×(-2)+433=23,∴点F 的坐标为(-2,23)时,点M 在整个运动过程中用时最少.19.抛物线y =-x 2+bx +c 与x 轴交于A 、B 两点,与y 轴交于点C ,且B (-1,0),C (0,3).(1)求抛物线的解析式;(2)如图,点D 是抛物线的顶点,将抛物线沿CD 方向平移,使点D 落在点D 处,且DD =2CD ,点M 是平移后所得抛物线上位于D 左侧的一点,MN ⎳y 轴交直线OD 于点N ,连结CN .当55D N +CN 的值最小时,求MN 的长.【解答】解:(1)∵y =-x 2+bx +c 经过B (-1,0),C (0,3),∴c =3-1-b +c =0 ,解得b =2c =3,∴抛物线的解析式为y =-x 2+2x +3.(2)如图,连接AD ′,过点N 作NJ ⊥AD ′于J ,过点C 作CT ⊥AD ′于T .∵抛物线y =-x 2+2x +3=-(x -1)2+4,∴顶点D (1,4),∵C (0,3),∴直线CD 的解析式为y =x +3,CD =2,∵DD ′=2CD ,∵DD ′=22,CD ′=32,∴D ′(3,6),∵A (3,0),∴AD ′⊥x 轴,∴OD ′=OA 2+D ′A 2=32+62=35,∴sin∠OD′A=OAOD′=5 5,∵CT⊥AD′,∴CT=3,∵NJ⊥AD′,∴NJ=ND′⋅sin∠OD′A=55D′N,∴55D N+CN=CN+NJ,∵CN+NJ≥CT,∴55D N+CN≥3,∴55D N+CN的最小值为3,此时N为OD 与CT的交点,∴N(1.5,3),∵平移后抛物线的解析式为y=-(x-3)2+6,MN平行y轴,将x=1.5代入抛物线解析式,∴M(1.5,3.75),∴MN=0.7520.如图,矩形ABCD的对角线AC,BD相交于点O,ΔCOD关于CD的对称图形为ΔCED.(1)求证:四边形OCED是菱形;(2)连接AE,若AB=6cm,BC=5cm.①求sin∠EAD的值;②若点P为线段AE上一动点(不与点A重合),连接OP,一动点Q从点O出发,以1cm/s的速度沿线段OP匀速运动到点P,再以1.5cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动,当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间.【解答】(1)证明:∵四边形ABCD是矩形.∴OD=OB=OC=OA,∵ΔEDC和ΔODC关于CD对称,∴DE=DO,CE=CO,∴DE=EC=CO=OD,∴四边形CODE是菱形.(2)①设AE交CD于K.∵四边形CODE是菱形,∴DE⎳AC,DE=OC=OA,∴DK KC=DEAC=12∵AB =CD =6,∴DK =2,CK =4,在Rt ΔADK 中,AK =AD 2+DK 2=(5)2+22=3,∴sin ∠DAE =DK AK=23,②作PF ⊥AD 于F .易知PF =AP ⋅sin ∠DAE =23AP ,∵点Q 的运动时间t =OP 1+AP 32=OP +23AP =OP +PF ,∴当O 、P 、F 共线时,OP +PF 的值最小,此时OF 是ΔACD 的中位线,∴OF =12CD =3.AF =12AD =52,PF =12DK =1,∴AP =52 2+12=32,∴当点Q 沿上述路线运动到点A 所需要的时间最短时,AP 的长为32cm ,点Q 走完全程所需的时间为3s .。
中考数学几何复习---最值系列之胡不归问题

中考数学几何复习--最值系列之“胡不归”问题在前面的最值问题中往往都是求某个线段最值或者形如P A +PB 最值,除此之外我们还可能会遇上形如“P A +kPB ”这样的式子的最值,此类式子一般可以分为两类问题:(1)胡不归问题;(2)阿氏圆.本文简单介绍“胡不归”模型.【故事介绍】从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A 到家B 之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?…”(“胡”同“何”)而如果先沿着驿道AC 先走一段,再走砂石地,会不会更早些到家?2驿道【模型建立】如图,一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使21AC BCV V +的值最小.2M【问题分析】121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭,记12V k V =, 即求BC +kAC 的最小值.【问题解决】构造射线AD使得sin∠DAN=k,CH/AC=k,CH=kAC.M将问题转化为求BC+CH最小值,过B点作BH⊥AD交MN于点C,交AD于H点,此时BC+CH取到最小值,即BC+kAC最小.M【模型总结】在求形如“P A+kPB”的式子的最值问题中,关键是构造与kPB相等的线段,将“P A+kPB”型问题转化为“P A+PC”型.而这里的PB必须是一条方向不变的线段,方能构造定角利用三角函数得到kPB的等线段.【长沙中考】如图,△ABC 中,AB =AC =10,tan A =2,BE ⊥AC 于点E ,D 是线段BE 上的一个动点,则CD 的最小值是_______.ABCDE【分析】本题关键在于处理”,考虑tan A =2,△ABE三边之比为1:2sin ∠,故作DH ⊥AB 交AB 于H点,则DH =. HEDCBAABCDEH问题转化为CD +DH 最小值,故C 、D 、H共线时值最小,此时CD DH CH BE +===.【小结】本题简单在于题目已经将BA 线作出来,只需分析角度的三角函数值,作出垂线DH ,即可解决问题,若稍作改变,将图形改造如下:EDCB则需自行构造α,如下图,这一步正是解决“胡不归”问题关键所在.αsin α5HEDC BAEDCB【南通中考】如图,平行四边形ABCD 中,∠DAB =60°,AB =6,BC =2,P 为边CD 上的一动点,则PB 的最小值等于________.ABCDP【分析】考虑如何构造”,已知∠A =60°,且sin60°,故延长AD ,作PH ⊥AD 延长线于H 点,即可得PH =,将问题转化为:求PB +PH 最小值. M HPDCBA当B 、P 、H 三点共线时,可得PB +PH 取到最小值,即BH 的长,解直角△ABH 即可得BH 长.ABCDPH M【成都中考】如图,已知抛物线()()248ky x x =+-(k 为常数,且k >0)与x 轴从左至右依次交于A ,B 两点,与y 轴交于点C ,经过点B的直线y b =+与抛物线的另一交点为D . (1)若点D 的横坐标为-5,求抛物线的函数表达式;(2)在(1)的条件下,设F 为线段BD 上一点(不含端点),连接AF ,一动点M 从点A 出发,沿线段AF以每秒1个单位的速度运动到F ,再沿线段FD 以每秒2个单位的速度运动到D 后停止,当点F 的坐标是多少时,点M 在整个运动过程中用时最少?【分析】第一小问代点坐标,求解析式即可,此处我们直接写答案:A (y =+,D 点坐标为(-,故抛物线解析式为)()24y x x +-,化简为:2y =点M 运动的时间为12AF DF ⎛⎫+ ⎪⎝⎭,即求12AF DF ⎛⎫+ ⎪⎝⎭的最小值.接下来问题便是如何构造2DF,考虑BD 与x 轴夹角为30°,且DF 方向不变,故过点D 作DM ∥x 轴,过点F 作FH ⊥DM 交DM 于H 点,则任意位置均有FH =2DF. 当A 、F 、H 共线时取到最小值,根据A 、D 两点坐标可得结果.【重庆中考】抛物线2y x =x 轴交于点A ,B (点A 在点B 的左边),与y 轴交于点C .点P 是直线AC 上方抛物线上一点,PF ⊥x 轴于点F ,PF 与线段AC 交于点E ;将线段OB 沿x 轴左右平移,线段OB 的对应线段是O 1B 1,当12PE EC +的值最大时,求四边形PO 1B 1C 周长的最小值,并求出对应的点O 1的坐标.(为突出问题,删去了两个小问)【分析】根据抛物线解析式得A ()-、B )、C (,直线AC的解析式为:y =+知AC 与x 轴夹角为30°. 根据题意考虑,P 在何处时,PE +2EC取到最大值.过点E 作EH ⊥y 轴交y 轴于H 点,则∠CEH =30°,故CH =2EC,问题转化为PE +CH 何时取到最小值.考虑到PE 于CH并无公共端点,故用代数法计算,设2,P m ⎛- ⎝,则E m ⎛+ ⎝,H ⎛ ⎝,2PE =-,CH =,22=PE CH m +=+sin ABE ∠=当P点坐标为(-时,取到最小值,故确定P 、C 、求四边形面积最小值,运用将军饮马模型解题即可.。
初中数学最值系列之胡不归问题

最值系列之“胡不归”问题在前面的最值问题中往往都是求某个线段最值或者形如P A +PB 最值,除此之外我们还可能会遇上形如“P A +kPB ”这样的式子的最值,此类式子一般可以分为两类问题:(1)胡不归问题;(2)阿氏圆.本文简单介绍“胡不归”模型.【故事介绍】从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A 到家B 之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?…”(“胡”同“何”)而如果先沿着驿道AC 先走一段,再走砂石地,会不会更早些到家?2驿道【模型建立】如图,一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使21AC BCV V +的值最小.2M【问题分析】121121=V AC BC BC AC V V V V ⎛⎫++ ⎪⎝⎭,记12V k V =, 即求BC +kAC 的最小值.【问题解决】构造射线AD使得sin∠DAN=k,CH/AC=k,CH=kAC.M将问题转化为求BC+CH最小值,过B点作BH⊥AD交MN于点C,交AD于H点,此时BC+CH取到最小值,即BC+kAC最小.M【模型总结】在求形如“P A+kPB”的式子的最值问题中,关键是构造与kPB相等的线段,将“P A+kPB”型问题转化为“P A+PC”型.而这里的PB必须是一条方向不变的线段,方能构造定角利用三角函数得到kPB的等线段.【2019长沙中考】如图,△ABC 中,AB =AC =10,tan A =2,BE ⊥AC 于点E ,D 是线段BE 上的一个动点,则CD 的最小值是_______. ABCDE【分析】本题关键在于处理“”,考虑tan A =2,△ABE 三边之比为1:2,sin ∠,故作DH ⊥AB 交AB 于H点,则DH . HEDCB AABCDEH问题转化为CD +DH 最小值,故C 、D 、H共线时值最小,此时CD DH CH BE +===.【小结】本题简单在于题目已经将BA 线作出来,只需分析角度的三角函数值,作出垂线DH ,即可解决问题,若稍作改变,将图形改造如下:EDCB则需自行构造α,如下图,这一步正是解决“胡不归”问题关键所在.αsin α5HEDC BAEDCB【2019南通中考】如图,平行四边形ABCD 中,∠DAB =60°,AB =6,BC =2,P 为边CD 上的一动点,则PB 的最小值等于________. ABCDP【分析】考虑如何构造”,已知∠A =60°,且sin60°,故延长AD ,作PH ⊥AD 延长线于H点,即可得PH ,将问题转化为:求PB +PH 最小值. M HPDCBA当B 、P 、H 三点共线时,可得PB +PH 取到最小值,即BH 的长,解直角△ABH 即可得BH 长.ABCDPH M【2014成都中考】如图,已知抛物线()()248ky x x =+-(k 为常数,且k >0)与x 轴从左至右依次交于A ,B 两点,与y 轴交于点C ,经过点B的直线y b =+与抛物线的另一交点为D .(1)若点D 的横坐标为-5,求抛物线的函数表达式;(2)在(1)的条件下,设F 为线段BD 上一点(不含端点),连接AF ,一动点M 从点A出发,沿线段AF 以每秒1个单位的速度运动到F ,再沿线段FD 以每秒2个单位的速度运动到D 后停止,当点F 的坐标是多少时,点M 在整个运动过程中用时最少?,直线解析式为y x =,D 点坐标为(-,故抛物线解析式为)()24y x x =+-,化简为:2y x 该题的第二小问.点M 运动的时间为12AF DF ⎛⎫+ ⎪⎝⎭,即求12AF DF ⎛⎫+ ⎪⎝⎭的最小值.接下来问题便是如何构造2DF,考虑BD 与x 轴夹角为30°,且DF 方向不变,故过点D 作DM ∥x 轴,过点F 作FH ⊥DM 交DM 于H 点,则任意位置均有FH =2DF. 当A 、F 、H 共线时取到最小值,根据A 、D 两点坐标可得结果.【2018重庆中考】抛物线2y x=x轴交于点A,B(点A在点B的左边),与y轴交于点C.点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当12PE EC+的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标.(为突出问题,删去了两个小问)【分析】根据抛物线解析式得A()-、B)、C(,直线AC的解析式为:y=+AC与x轴夹角为30°.根据题意考虑,P在何处时,PE+2EC取到最大值.过点E作EH⊥y轴交y轴于H点,则∠CEH=30°,故CH=2EC,问题转化为PE+CH何时取到最小值.考虑到PE于CH并无公共端点,故用代数法计算,设2,P m⎛-⎝,则E m⎛⎝,H⎛⎝,2PE=,CH=,22=PE CH m+=+sin ABE∠=当P点坐标为(-时,取到最小值,故确定P、C、求四边形面积最小值,运用将军饮马模型解题即可.。
中考数学经典几何模型之胡不归最值模型(解析版)

中考数学经典几何模型之胡不归最值模型(解析版)在数学中,经典几何模型是考试中经常出现的题型之一。
其中,胡不归最值模型是一种常见的最值问题。
这类问题通常涉及到形如“PA+kP”的式子,可以分为两类问题:胡不归问题和阿氏圆问题。
胡不归问题的故事源于一个少年外出求学,得知父亲病危后,他立即赶回家。
虽然他所在的位置到家的路上有一片砂石地,但他仍然义无反顾地走了这条路。
当他到家时,父亲已经去世了,他深感悔恨并痛哭流涕。
邻居告诉他,父亲在临终前一直念叨着“胡不归?胡不归?……”(“胡”同“何”)。
这个故事启发我们思考如何求解“PA+kP”型问题中的最值。
以胡不归问题为例,我们需要求解一个动点P在直线MN 外的运动速度为V1,在直线MN上运动的速度为V2,且V1<V2,A、B为定点,点C在直线MN上,确定点C的位置使得AC+BC的值最小,即求BC+kAC的最小值。
为了解决这个问题,我们可以构造射线AD使得sin∠DAN=k,即CH=kAC。
这样,我们可以将问题转化为求BC+CH最小值,过B点作BH⊥AD交MN于点C,交AD于H点,此时BC+CH取到最小值,即BC+kAC最小。
在解决“PA+kP”型问题时,关键是构造与kP相等的线段,将“PA+kP”型问题转化为“PA+PC”型。
而这里的P必须是一条方向不变的线段,方能构造定角利用三角函数得到kP的等线段。
举个例子,如图所示,在△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值为5.这个问题的关键在于处理“CD+BD”的式子,考虑tanA=2,△ABE三边之比为1:2:5,sin ABE⊥AB交AB于H点,则DH=BD/5.通过构造HD,我们可以将问题转化为求CD+CH的最小值,其中CH=kAC,k=sin∠DAN=BD/5.过B点作BH⊥AD交MN于点C,交AD于H点,此时BC+CH取到最小值,即CD+BD的最小值为5.综上所述,胡不归最值模型是一类常见的最值问题。
最值模型之胡不归模型(学生版)-2024年中考数学常见几何模型
最值模型之胡不归模型胡不归模型可看作将军饮马衍生,主要考查转化与化归等的数学思想,近年在中考数学和各地的模拟考中常以压轴题的形式考查,学生不易把握。
本专题就最值模型中的胡不归问题进行梳理及对应试题分析,方便掌握。
在解决胡不归问题主要依据是:点到线的距离垂线段最短。
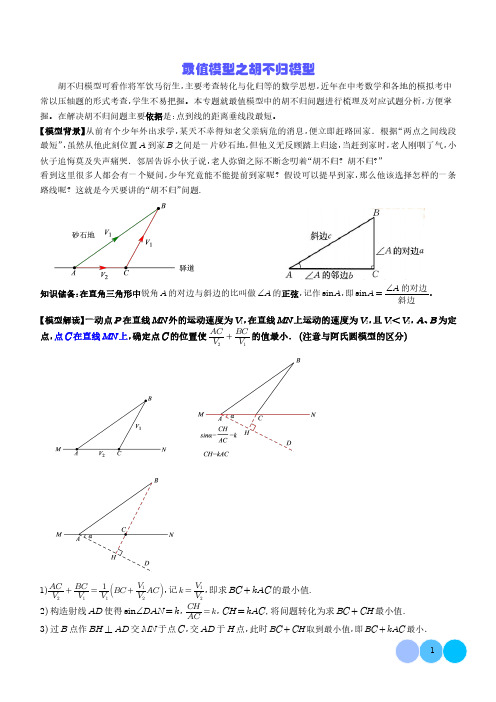
【模型背景】从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A 到家B 之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?”看到这里很多人都会有一个疑问,少年究竟能不能提前到家呢?假设可以提早到家,那么他该选择怎样的一条路线呢?这就是今天要讲的“胡不归”问题.知识储备:在直角三角形中锐角A 的对边与斜边的比叫做∠A 的正弦,记作sin A ,即sin A =∠A 的对边斜边。
【模型解读】一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使AC V 2+BC V 1的值最小.(注意与阿氏圆模型的区分)1)AC V 2+BC V 1=1V 1BC +V 1V 2AC,记k =V 1V 2,即求BC +kAC 的最小值.2)构造射线AD 使得sin ∠DAN =k ,CH AC=k ,CH =kAC ,将问题转化为求BC +CH 最小值.3)过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC +CH 取到最小值,即BC +kAC 最小.【解题关键】在求形如“PA+kPB”的式子的最值问题中,关键是构造与kPB相等的线段,将“PA+kPB”型问题转化为“PA+PC”型.(若k>1,则提取系数,转化为小于1的形式解决即可)。
【最值原理】两点之间线段最短及垂线段最短。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:利用三角函数解决最值问题一、教学内容分析:
本节课以数学史中的一个经典故事——“胡不归问题”为载体开展对“最短路径问题”的研究,让学生经历将实际问题抽象为数学的线段和最小问题,再利用正弦函数将线段和最小问题转化为“直线外一点到直线垂线段最短”的问题.
二、教学目标:
1.能利用垂线段最短解决最短路径问题;
2.在解题过程能总结出解题方法,能进行一定的延伸;
3.体会“正弦函数”的桥梁作用,感悟转化的数学思想.
三、教学重点难点:
重点:利用正弦函数将PA+k·PB问题转化为“直线外一点到直线垂线段最短”问题.
难点:如何找到合理的角将k·PB转化为另一线段.
四、教学过程:
1.【温故知新】
问题:AB、AC有什么数量关系?若∠B不变,移动点C位置,关系改变吗?
设计意图:通过三个图形分析,让学生意识到角固定,它的正弦值就固定,对边和斜边关系就是固定,为后面学习做好准备.
2.【数学问题】
如图,点A是∠MON外部定点,点P是OM上动点,过P作PB ⊥ON ,如何确定点P位置使得 PA+PB 最小?
分析:直线外一点到直线所有连线垂线段最短.(作法如下图)
变式1:如图,点A在∠MON外部,点P是OM上动点,∠MON=30°,如何确定点P位置使得PA+1/2OP 最小?
分析:过P作PQ⊥ON ,则 PQ=1/2OP,那么PA+1/2OP =PA+PQ.利用30°正弦将1/2OP转化为PQ,再利用垂线段最短确定点P.
确定P点位置,使得PB+1/2PA最小?
分析:构造30°角,再利用30°正弦将1/2PA转化为PQ,再利用垂线段最短确定点P.(如下图)
变式3:点P是射线AC上一动点,点B是射线AC外一点,如何确定P点位置,使得 2PA+4PB最小?
点拨:转化为 2PA+4PB=4(PB+1/2PA),变成前一问题.
何确定P点位置,使得 1/4PA+1/2PB 最小?
点拨:1/4PA+1/2PB=1/2(PB+1/2PA),转化为前一问题.
【反思】确定P位置的关键是什么?利用正弦构造1/2PA线段.
一般地:先将问题转化为PB+k·PA,在PB另一侧构造角∂,使得sin∂=k.化折为直,利用垂线段最短.
设计意图:通过一组变式训练,体会这一类问题处理策略,发现总结规律.
三、【模型由来】
历史故事:一个身在他乡的小伙子得知父亲病危后日夜赶路回家。
然而当他气喘吁吁地来到父亲面前时,老人刚刚咽气了.人们告诉他,在临终之际,老人还在不断的念叨:“胡不归?胡不归?……”
早期的科学家曾为这则古老的传说中的小伙子设想了一条路线(如下图)A是出发地,B是目的地,BC是一条驿道,而驿道靠目的地的一侧全是砂土地带.为了急切回家,小伙子选择了直线段AB.
他忽略了在驿道上行走要比在砂土行走快的这一因素.
如果能选合适的路线(这条路线长一些,但速度可以加快),是可以提前抵达家门的.那么这应该是哪条路线呢?
这就是风靡千百年的“胡不归问题”
数学语言表达就是:“已知在驿道和砂地上行走的速度分别为V1 、V2,且V1 =2V2,在BC上求点D,使得A→D→B的行走时间最短.”于是问题在于如何去找出D点.
设计意图:通过历史典故,激发兴趣,体会数学在生活中应用和将实际问题转化为数学问题的分析能力.
四、【模型运用】
如图已知A、B分别坐标轴上定点,且 AB=2,∠BAO=15°,P为y轴上动点。
则PB+1/2PA最小值= .
变式:PB+√2/2PA最小值= .
提示:
设计意图:习题设置让学生进一步巩固解决最短路径问题的基本策略和基本方法.
五、【拓展思维】
已知,正方形ABCD边长为2,P是对角线BD上动点,则PA+PB+PC 最小值= .
思路1:旋转利用两点之间线段最短;
思路2:利用胡不归模型,点线垂线段最短解决问题.
设计意图:发散思维,培养学生一题多解的能力和模型识别能力.
六、【课堂小结】
1.本节课学了将实际问题抽象成数学模型,用数学知识解决实际问题;
2.利用正弦函数将PB+k·PA转化为两条线段,利用垂线段最短解决问题;
3.转化思想;新问题转化为旧问题,复杂问题转化为简单问题.
七、【作业布置】
八、【板书设计】
角固定,它的正弦值就固定.
直线外一点到直线所有连线垂线段最短.
九、【教后反思】。
