常用求导公式矩阵公式数学建模
矩阵运算 梯度和求导公式

∇∇X(:,2) g1(X) ∇∇X(:,2) g2(X) · · · ∇∇X(:,2) gN (X)
...
...
...
∇∇X(:,L) g1(X) ∇∇X(:,L) g2(X) · · · ∇∇X(:,L) gN (X)
= [ ∇2g1(X) ∇2g2(X) · · · ∇2gN (X) ] ∈ RK×N×L×K×L
Mεβoo Publishing USA, 2005, v2010.01.05.
658
APPENDIX D. MATRIX CALCULUS
The gradient of vector-valued function v(x) : R → RN on real domain is a row-vector
∂f(x)
∂x1
∂f(x)
∂x... 2
∈
RK
∂f (x)
∂xK
(1719)
while the second-order gradient of the twice differentiable real function with respect to its vector argument is traditionally called the Hessian ;
= [ ∇g1(X) ∇g2(X) · · · ∇gN (X) ] ∈ RK×N×L
(1727)
while the second-order gradient has a five-dimensional representation;
∇ 2 g(X )
∇∇X(:,1) g1(X) ∇∇X(:,1) g2(X) · · · ∇∇X(:,1) gN (X)
矩阵求导的一些公式

.在网上看到有人贴了如下求导公式:Y = A * X --> DY/DX = A'Y = X * A --> DY/DX = AY = A' * X * B --> DY/DX = A * B'Y = A' * X' * B --> DY/DX = B * A'于是把以前学过的矩阵求导部分整理一下:1. 矩阵Y对标量x求导:相当于每个元素求导数后转置一下,注意M×N矩阵求导后变成N×M了Y = [y(ij)] --> dY/dx = [dy(ji)/dx]2. 标量y对列向量X求导:注意与上面不同,这次括号内是求偏导,不转置,对N×1向量求导后还是N×1向量y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)'3. 行向量Y'对列向量X求导:注意1×M向量对N×1向量求导后是N×M矩阵。
将Y的每一列对X求偏导,将各列构成一个矩阵。
重要结论:dX'/dX = Id(AX)'/dX = A'4. 列向量Y对行向量X’求导:转化为行向量Y’对列向量X的导数,然后转置。
注意M×1向量对1×N向量求导结果为M×N矩阵。
dY/dX' = (dY'/dX)'5. 向量积对列向量X求导运算法则:注意与标量求导有点不同。
d(UV')/dX = (dU/dX)V' + U(dV'/dX)d(U'V)/dX = (dU'/dX)V + (dV'/dX)U'重要结论:d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = A.d(AX)/dX' = (d(X'A')/dX)' = (A')' = Ad(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X6. 矩阵Y对列向量X求导:将Y对X的每一个分量求偏导,构成一个超向量。
2×2矩阵求导法则

2×2矩阵求导法则矩阵求导法则矩阵求导应该分为标量求导、向量求导、矩阵求导三个方面来介绍,公式繁多,但仔细看看其实是有规律可循的。
标量求导无论是矩阵、向量对标量求导,或者是标量对矩阵、向量求导,其结论都是一样的:等价于对矩阵(向量)的每个分量求导,并且保持维数不变。
例如,我们可以计算标量对向量求导:设yy为一个元素,xT=[x1~xq]xT=[x1~xq]是qq维行向量,则:∂y∂xT=[∂y∂x1~∂y∂xq]∂y∂xT=[∂y∂x1~∂y∂xq]向量求导对于向量求导,我们可以先将向量看做一个标量,然后使用标量求导法则,最后将向量形式化为标量进行。
例如,我们可以计算行向量对列向量求导:设yT=[y1~yn]yT=[y1~yn]是nn维行向量,x=[x1,~,xp]x=[x1,~,xp]是pp维列向量,则:∂yT∂x==[∂y1∂x~∂yn∂x]⎡⎡⎡⎡⎡∂y1∂x1~∂y1∂xp~~~∂yn∂x1~∂yn∂xp⎡⎡⎡⎡⎡∂yT∂x=[∂y1∂x~∂yn∂x]=[∂y1∂x1~∂yn∂x1~~~∂y1∂xp~∂yn∂xp]矩阵求导与向量求导类似,先将矩阵化当做一个标量,再使用标量对矩阵的运算进行。
例如,我们可以计算矩阵对列向量求导:设Y=⎡⎡⎡y11~ym1~~~y1n~ymn⎡⎡⎡Y=[y11~y1n~~~ym1~ymn]是m×nm×n矩阵,x=[x1,~,xp]x=[x1,~,xp]是pp维列向量,则:∂Y∂x=[∂Y∂x1,~,∂Y∂xp]∂Y∂x=[∂Y∂x1,~,∂Y∂xp]矩阵微积分常见求导性质实值函数相对于实向量的梯度设f(x)=x=[x1,~,xn]Tf(x)=x=[x1,~,xn]T∂f(x)∂xT=∂x∂xT=In×n∂f(x)∂xT=∂x∂xT=In×n∂(f(x))T∂x=∂xT∂x=In×n∂(f(x))T∂x=∂xT∂x=In×n∂f(x)∂x=∂x∂x=vec(In×n)∂f(x)∂x=∂x∂x=vec(In×n)∂(f(x))T∂xT=∂xT∂xT=vec(In×n)T∂(f(x))T∂xT=∂xT∂xT=vec(In×n)T其中,vecvec表示向量化矩阵,按列将矩阵表示为向量,具体可见Wikipedia。
mathematica 矩阵函数求导

mathematica 矩阵函数求导摘要:一、矩阵求导的重要性二、矩阵求导的基本概念三、Mathematica 软件在矩阵求导中的应用四、常用的矩阵求导公式五、矩阵求导的实际应用案例正文:一、矩阵求导的重要性矩阵在现代数学和物理学等领域具有广泛的应用,而矩阵的导数在很多情况下可以反映出矩阵在某些方面的变化规律。
因此,研究矩阵求导具有重要的理论和实际意义。
二、矩阵求导的基本概念矩阵求导是指对一个矩阵函数进行求导,得到其导数矩阵。
矩阵求导的基本概念包括以下几个方面:1.矩阵的导数:设A 是一个n 阶矩阵,其元素为a_{ij},则A 的导数是一个同维度的矩阵,记作A",其中(A")_{ij}表示矩阵A 第i 行第j 列元素的导数。
2.矩阵求导的运算法则:矩阵求导遵循链式法则和乘法法则。
链式法则指的是对一个矩阵的每个元素求导,然后以矩阵的形式组合起来;乘法法则指的是对两个矩阵的乘积求导,等于其中一个矩阵的导数乘以另一个矩阵加上另一个矩阵的导数乘以第一个矩阵。
3.矩阵求导的常用方法:常用的矩阵求导方法包括高斯消元法、矩阵分解法等。
三、Mathematica 软件在矩阵求导中的应用Mathematica 是一款强大的数学软件,可以方便地用于矩阵求导的计算。
在Mathematica 中,可以使用Grad 函数对矩阵求导,也可以使用矩阵运算函数直接计算导数矩阵。
四、常用的矩阵求导公式在实际应用中,我们常常需要求解一些常见的矩阵函数的导数。
以下是一些常用的矩阵求导公式:1.单位矩阵的导数:单位矩阵的导数仍然是单位矩阵。
2.矩阵乘法的导数:设A 和B 是两个n 阶矩阵,则AB 的导数等于B 的转置乘以A 的导数加上A 的转置乘以B 的导数。
3.矩阵幂的导数:设A 是一个n 阶矩阵,则A^n 的导数等于n*A^(n-1)。
4.矩阵的逆的导数:设A 是一个可逆的n 阶矩阵,则A 的逆的导数等于(-1)^n*A^(n-1)。
矩阵对矩阵求导结论

矩阵对矩阵求导结论
矩阵对矩阵求导是一种矩阵微分运算,也称为矩阵的Jacobi矩阵、矩阵的梯度、矩阵的导数等。
在数学和机器学习领域都有广泛的应用。
假设有两个矩阵A和B,其中A的尺寸为m×n,B的尺寸为p×q。
则矩阵对矩阵求导的结果是一个四维矩阵,其尺寸为m×n×p×q。
对于矩阵A中的每个元素a_ij,其在矩阵对矩阵求导结果中的对应位置是一个p×q的矩阵,记为[dA/dB]_ij。
其中,[dA/dB]_ij表示A对B的第(i,j)个元素求导的结果。
根据矩阵对矩阵求导的定义,可以得到以下结论:
1. 若A和B为两个常数矩阵,则有[dA/dB]_ij = 0,其中i=1,2,...,m,j=1,2,...,n。
2. 若A为常数矩阵,B为可变矩阵,则有[dA/dB]_ij = 0,其中i=1,2,...,m,j=1,2,...,n。
3. 若A和B都为可变矩阵,则有[dA/dB]_ij = ∂a_ij/∂b_kl,其中i=1,2,...,m,j=1,2,...,n,
k=1,2,...,p,l=1,2,...,q。
即矩阵对矩阵求导是指对A中每个元素求对B中每个元素的偏导数。
总结起来,矩阵对矩阵求导的结果是一个四维矩阵,其中每个元素表示A对B的对应元素的偏导数。
具体的求导方法可以使用链式法则或分块矩阵的方法来计算。
矩阵对矩阵求导的应用包括线性回归、逻辑回归、矩阵分解等。
常用求导公式、矩阵公式、数学建模

基本求导公式、矩阵公式、数学建模1.基本求导公式⑴ 0)(='C (C 为常数)⑵ 1)(-='n nnxx ;一般地,1)(-='αααxx 。
特别地:1)(='x ,x x 2)(2=',21)1(x x -=',xx 21)(='。
⑶ x x e e =')(;一般地,)1,0( ln )(≠>='a a a a a xx 。
⑷ x x 1)(ln =';一般地,)1,0( ln 1)(log ≠>='a a ax x a 。
2.求导法则 ⑴ 四则运算法则设f (x ),g (x )均在点x可导,则有:(Ⅰ))()())()((x g x f x g x f '±'='±; (Ⅱ))()()()())()((x g x f x g x f x g x f '+'=',特别)())((x f C x Cf '='(C 为常数); (Ⅲ))0)(( ,)()()()()())()((2≠'-'='x g x g x g x f x g x f x g x f ,特别21()()()()g x g x g x ''=-。
3.微分 函数()y f x =在点x处的微分:()dy y dx f x dx ''== 4、 常用的不定积分公式(1) ⎰⎰⎰⎰⎰+==+=+=-≠++=+c x dx x x dx x c x xdx c x dx C x dx x 43,2,),1( 11433221αααα; (2) C x dx x+=⎰||ln 1; C e dx e x x +=⎰;)1,0( ln ≠>+=⎰a a C a a dx a xx;(3)⎰⎰=dx x f k dx x kf )()((k 为常数) 5、定积分()()|()()bb a af x dx F x F b F a ==-⎰⑴⎰⎰⎰+=+bab abadx x g k dx x f k dx x g k x f k )()()]()([2121⑵ 分部积分法设u (x ),v(x )在[a,b]上具有连续导数)(),(x v x u '',则⎰⎰-=bab abax du x v x v x u x dv x u )()()()()()(6、线性代数 特殊矩阵的概念(1)、零矩阵 ,000022⎥⎦⎤⎢⎣⎡=⨯O (2)、单位矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=100010001 n I 二阶,100122⎥⎦⎤⎢⎣⎡=⨯I (3)、对角矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n a a a A 000000021 (4)、对称矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---==752531212,A a a ji ij (5)、上三角形矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n n a a a a a a A 000022211211 下三角形矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n a a a A 000000021 (6)、矩阵转置⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n n n n a a a a a a a a a A 212222111211转置后⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n nn n T a a a a a a a a a A 2122212121116、矩阵运算 ⎥⎦⎤⎢⎣⎡++++=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=+h d g c f b e a h g f ed c b a B A ⎥⎦⎤⎢⎣⎡++++=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=dh cf dg ce bh af bg ae h gf ed c b a AB 7、MA TLA B软件计算题例6 试写出用M ATLA B软件求函数)e ln(2x x x y ++=的二阶导数y ''的命令语句。
矩阵向量求导法则

矩阵向量求导法则
矩阵向量求导法则是一组规则,用于计算矩阵和向量之间的导数。
以下列出了常见的矩阵向量求导法则:
1. 标量对向量求导:
\frac{d}{dx}(c^{T}x) = c
其中,c是一个常数向量,x是一个列向量。
2. 向量对标量求导:
\frac{d}{dx}(x^{T}c) = c^{T}
其中,c是一个常数向量,x是一个列向量。
3. 向量对向量求导:
\frac{d}{dx}(x^{T}Ax) = (A+A^{T})x
其中,A是一个矩阵,x是一个列向量。
4. 向量对矩阵求导:
\frac{d}{dA}(x^{T}Ax) =
(x^{T}+x)(\frac{dA}{dA}+\frac{dA^{T}}{dA}) = 2x^{T}A
其中,A是一个矩阵,x是一个列向量。
5. 标量对矩阵求导:
\frac{d}{dA}(c^{T}Ax) = c^{T}x^{T}
其中,c是一个常数向量,A是一个矩阵,x是一个列向量。
6. 向量对向量求导(链式法则):
\frac{d}{dx}(f(g(x))) = (\frac{df}{dy})^{T}\frac{dg}{dx}
其中,f(\cdot)和g(\cdot)是两个函数,y=g(x),\frac{df}{dy}是
f(\cdot)对y的导数。
矩阵求导(本质、原理与推导)详解

矩阵求导(本质、原理与推导)详解1.引言矩阵求导是数学分析中重要的一部分,广泛应用于机器学习、数据挖掘和优化问题中。
本文将介绍矩阵求导的本质、原理以及推导过程,为读者提供一个比较全面的了解。
2.矩阵的本质及相关概念在矩阵求导前,我们需要先了解矩阵的本质及相关概念。
矩阵是一个按照规律排列的方阵,其中每个元素通常是实数或者复数。
以$n$行$m$列的矩阵$A$为例,可以表示为:$$A=\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots&a_{1,m}\\a_{2,1}&a_{2,2}&\cdots&a_{2,m}\\\vdots&\vdots&\ddots&\vdots\\a_{n,1}&a_{n,2}&\cdots&a_{n,m}\\\end{bmatrix}$$其中$a_{i,j}$表示矩阵$A$中第$i$行第$j$列的元素。
矩阵还有一些相关的概念,如矩阵的转置、逆矩阵、伴随矩阵等等,这里不一一赘述。
3.标量函数对向量、矩阵的导数在开始矩阵求导之前,我们需要先了解标量函数对向量或矩阵的导数。
设矩阵$A$是一个$m\times n$的矩阵,$x$是一个$n \times1$的向量,函数$f(x)$将$x$映射为一个标量。
我们定义$f(x)$对$x$的导数为:$$\frac{\partial f(x)}{\partial x}=\begin{bmatrix}\frac{\partial f(x)}{\partial x_1}&\frac{\partial f(x)}{\partial x_2}&\cdots&\frac{\partial f(x)}{\partial x_n}\end{bmatrix}$$其中每一项$\frac{\partial f(x)}{\partial x_i}$表示$f(x)$对$x_i$的偏导数。
矩阵内积求导法则

矩阵内积求导法则全文共四篇示例,供读者参考第一篇示例:矩阵内积求导法则是矩阵微积分中非常重要的一个内容,它在机器学习、优化问题、计算机图形学等领域都有着广泛的应用。
本篇文章将详细介绍矩阵内积求导法则的定义、推导过程以及实际应用。
一、定义矩阵内积指的是两个矩阵相乘得到的结果。
设有两个矩阵A和B,它们的内积记为C,记作C=A*B。
在矩阵内积中,两个矩阵的行数和列数要满足一定的要求,具体而言,如果矩阵A的维度为m×n,矩阵B的维度为n×p,那么它们的内积矩阵C的维度为m×p。
二、矩阵内积的求导法则在矩阵微积分中,我们经常需要对矩阵内积进行求导。
矩阵内积的求导法则可以表示为:若有两个矩阵A和B,它们的内积C=A*B,则C对任意一个矩阵的导数可以表示为:∂C/∂A = B^TB^T表示B的转置矩阵。
同理,C对B的导数可以表示为:这个法则的推导过程可以通过矩阵的展开式进行证明,这里不再详述。
这个法则对于矩阵微积分来说是非常重要的,它可以帮助我们快速求解复杂的矩阵导数。
三、实际应用矩阵内积的求导法则在机器学习和优化算法中有着广泛的应用。
在机器学习中,我们经常需要通过梯度下降等方法来最小化损失函数,这就会涉及到对损失函数关于模型参数(矩阵)的导数计算。
利用矩阵内积的求导法则,我们可以快速有效地计算出损失函数对参数的导数,从而完成参数的更新。
在计算机图形学中,矩阵内积求导法则也有着重要的应用。
在图形变换和动画建模等领域,我们经常需要对矩阵进行变换和运动操作,这就需要对矩阵的导数进行计算。
通过矩阵内积的求导法则,我们可以准确地获得矩阵变换的导数,从而实现图形的平移、旋转和缩放等操作。
第二篇示例:矩阵内积是矩阵乘法的一种形式,通常用于描述多个向量之间的关系。
在机器学习和深度学习领域,矩阵内积求导是一项重要的计算任务,它能够帮助我们优化模型并提高模型的性能。
矩阵内积求导法则是求解矩阵内积的导数的规则和方法,其基本原理是通过链式法则和向量微积分等基本数学知识来推导出矩阵内积的导数表达式。
常用的基本求导公式

1.基本求导公式⑴ 0)(='C (C 为常数)⑵ 1)(-='n n nx x ;一般地,1)(-='αααx x 。
特别地:1)(='x ,x x 2)(2=',21)1(x x-=',xx 21)(='。
⑶ x x e e =')(;一般地,)1,0( ln )(≠>='a a a a a x x 。
⑷ x x 1)(ln =';一般地,)1,0( ln 1)(log ≠>='a a ax x a 。
2.求导法则 ⑴ 四则运算法则设f (x ),g (x )均在点x 可导,则有:(Ⅰ))()())()((x g x f x g x f '±'='±; (Ⅱ))()()()())()((x g x f x g x f x g x f '+'=',特别)())((x f C x Cf '='(C 为常数); (Ⅲ))0)(( ,)()()()()())()((2≠'-'='x g x g x g x f x g x f x g x f ,特别21()()()()g x g x g x ''=-。
3.微分 函数()y f x =在点x 处的微分:()dy y dx f x dx ''== 4、 常用的不定积分公式(1) ⎰⎰⎰⎰⎰+==+=+=-≠++=+c x dx x x dx x c x xdx c x dx C x dx x 43,2,),1( 11433221αααα;(2) C x dx x +=⎰||ln 1; C e dx e x x +=⎰; )1,0( ln ≠>+=⎰a a C aa dx a x x; (3)⎰⎰=dx x f k dx x kf )()((k 为常数) 5、定积分()()|()()bb a af x dx F x F b F a ==-⎰⑴⎰⎰⎰+=+bab abadx x g k dx x f k dx x g k x f k )()()]()([2121⑵ 分部积分法设u (x ),v (x )在[a ,b ]上具有连续导数)(),(x v x u '',则⎰⎰-=bab abax du x v x v x u x dv x u )()()()()()(6、线性代数特殊矩阵的概念(1)、零矩阵 ,000022⎥⎦⎤⎢⎣⎡=⨯O (2)、单位矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=100010001 n I 二阶,100122⎥⎦⎤⎢⎣⎡=⨯I (3)、对角矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n a a a A 000000021 (4)、对称矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---==752531212,A a a ji ij (5)、上三角形矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n n a a a a a a A 000022211211下三角形矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n a a a A 000000021 (6)、矩阵转置⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n n n n a a a a a a a a a A 212222111211转置后⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n nn n T a a a a a a a a a A 2122212121116、矩阵运算 ⎥⎦⎤⎢⎣⎡++++=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=+h d g c f b e a h g f ed c b a B A ⎥⎦⎤⎢⎣⎡++++=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=dh cf dg ce bh af bg ae h gf ed c b a AB 7、MATLAB 软件计算题例6 试写出用MATLAB 软件求函数)e ln(2x x x y ++=的二阶导数y ''的命令语句。
矩阵求导的符号推导算法

矩阵求导的符号推导算法在数学和工程中有着广泛的应用。
与普通的标量求导不同,矩阵求导需要特殊的推导策略。
本文将为读者介绍及其应用场景。
一、矩阵求导的基本概念在矩阵求导之前,我们需要先了解矩阵的基本概念。
矩阵是由一组数按一定规律排列成的矩形数组,是线性代数中的基本概念。
矩阵通常用大写字母表示,如A、B、C等。
矩阵中的每个数称为元素,通常用小写字母表示,如a11、a12、a21等。
矩阵求导就是对矩阵中的每个元素求导的过程。
矩阵求导通常用符号∂表示,如∂A/∂x表示对矩阵A中的每个元素对变量x的求导。
二、需要基于矩阵乘法、转置和迹等基本运算符号进行推导。
1. 标量对向量的求导对于标量f对向量x的求导,可以使用以下推导公式:∂f/∂x = [∂f/∂x1, ∂f/∂x2, …, ∂f/∂xn]T其中,T表示矩阵转置。
2. 标量对矩阵的求导对于标量f对矩阵A的求导,可以使用以下推导公式:∂f/∂A = [∂f/∂a11, ∂f/∂a12, …, ∂f/∂a1n; ∂f/∂a21, ∂f/∂a22, …, ∂f/∂a2n; …; ∂f/∂am1, ∂f/∂am2, …, ∂f/∂amn]其中,m是A的行数,n是A的列数。
3. 向量对标量的求导对于向量y对标量x的求导,可以使用以下推导公式:∂y/∂x = [∂y1/∂x, ∂y2/∂x, …, ∂yn/∂x]T其中,T表示矩阵转置。
4. 向量对向量的求导对于向量y对向量x的求导,可以使用以下推导公式:∂y/∂x = [∂y1/∂x1, ∂y1/∂x2, …, ∂y1/∂xn; ∂y2/∂x1, ∂y2/∂x2, …, ∂y2/∂xn; …; ∂yn/∂x1, ∂yn/∂x2, …, ∂yn/∂xn]5. 向量对矩阵的求导对于向量y对矩阵A的求导,可以使用以下推导公式:∂y/∂A = [∂y1/∂a11, ∂y1/∂a12, …, ∂y1/∂a1n; ∂y2/∂a11,∂y2/∂a12, …, ∂y2/∂a1n; …; ∂yn/∂a11, ∂yn/∂a12, …, ∂yn/∂a1n;∂y1/∂a21, ∂y1/∂a22, …, ∂y1/∂a2n; ∂y2/∂a21, ∂y2/∂a22, …,∂y2/∂a2n; …; ∂yn/∂am1, ∂yn/∂am2, …, ∂yn/∂amn]其中,m是A的行数,n是A的列数。
矩阵、向量求导法则
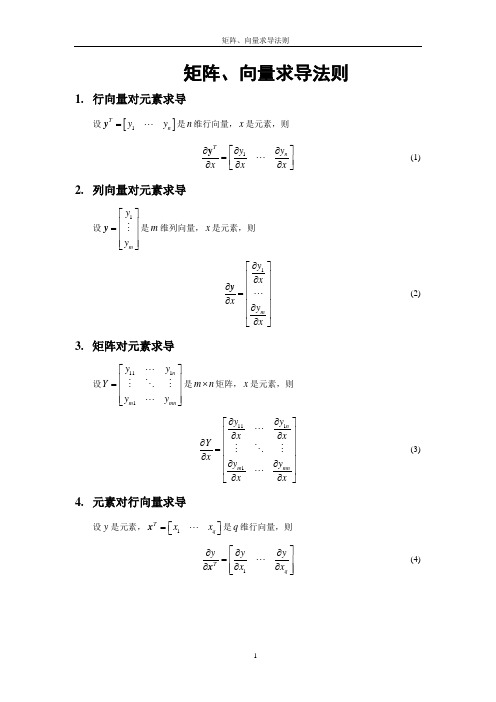
∂yT ∂yT ∂x ∂x1q 11 T ∂y = ∂X T ∂yT ∂y ∂x ∂x pq p1
(13)
14. 列向量对矩阵求导
x11 x1q y1 设 y = 是 m 维列向量, X = 是 p × q 矩阵,则 x p1 x pq ym
矩阵、向量求导法则
矩阵、向量求导法则
1. 行向量对元素求导
设 y = [ y1
T
yn ] 是 n 维行向量, x 是元素,则
∂yn ∂y T ∂y1 = ∂x ∂∂x
(1)
2. 列向量对元素求导
y1 设 y = 是 m 维列向量, x 是元素,则 ym
∂y1 ∂x ∂y = ∂x ∂y m ∂x
(2)
3. 矩阵对元素求导
y11 y1n 设Y = 是 m × n 矩阵, x 是元素,则 ym1 ymn
∂y1n ∂y11 ∂x ∂x ∂Y = ∂x ∂y ∂ymn m1 ∂x ∂x
∂y1 ∂x ∂y = ∂x ∂y m ∂x
(10)
11. 矩阵对行向量求导
y11 y1n T 设Y = 是 m × n 矩阵, x = x1 xq 是 q 维行向量,则 ym1 ymn
∂Y ∂Y ∂Y = T ∂x ∂xq ∂x1
(11)
12. 矩阵对列向量求导
x1 y11 y1n 是 m × n 矩阵, x = 是 p 维列向量,则 设Y = xp ym1 ymn
mathematica 矩阵函数求导

mathematica 矩阵函数求导【实用版】目录一、引言二、矩阵函数求导的重要性三、Mathematica 软件概述四、Mathematica 中矩阵函数求导的方法五、常用的矩阵求导公式六、结论正文一、引言在数学和物理学中,矩阵函数求导是一项重要的研究内容。
对于矩阵函数的求导,我们可以使用 Mathematica 软件来进行操作和计算。
Mathematica 是一款强大的数学软件,可以方便地用于矩阵函数的求导计算。
二、矩阵函数求导的重要性矩阵函数在现代数学和物理学中具有广泛的应用,例如在线性代数、微积分、概率论、量子力学等领域都有矩阵函数的身影。
矩阵函数的求导对于研究矩阵函数的性质和函数图像具有重要意义。
三、Mathematica 软件概述Mathematica 是一款功能强大的数学软件,可以进行各种数学运算和计算。
它支持多种编程语言,如 C、C++、Java、Fortran 等,并具有丰富的函数库和接口,方便用户进行各种计算和操作。
四、Mathematica 中矩阵函数求导的方法在 Mathematica 中,矩阵函数的求导可以通过使用矩阵操作函数和求导函数来实现。
常用的矩阵求导函数包括 Grad、Hessian、Jacobian 等。
此外,Mathematica 还提供了一些专门的矩阵求导函数,如MatrixDerivative、MatrixGradient 等。
五、常用的矩阵求导公式在实际应用中,我们经常会遇到一些常用的矩阵求导公式,如矩阵的梯度、海塞矩阵、雅可比矩阵等。
对于这些常用的矩阵求导公式,我们可以通过 Mathematica 软件来进行快速和准确的计算。
六、结论矩阵函数求导在现代数学和物理学中具有广泛的应用,Mathematica 软件提供了强大的矩阵函数求导功能,可以方便地进行各种矩阵函数的求导计算。
矩阵及向量求导法则

以下是第4种定义的法则!!!矩阵及向量求导法则①元素、列向量、行向量、矩阵;②元素必分其它;求导分子和求导分母皆是元素时便是一般的求导情况;③求导分子为行向量时分配求导分母,除非求导分母为元素;求导分母为列向量时分配求导分子,除非求导分子为元素;④求导分子和求导分母皆是矩阵时,总是化求导分子为列阵,化求导分母为行阵,这样它们就能相互分配彼此。
二元向量值函数的导数与微分m R R A f →⊂2:R x x x x f x x f x x f x x f m ∈⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=212121221121,,),(),(),(),(定义:⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛∂∂+∂∂∂∂+∂∂∂∂+∂∂=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=22211121222121121222211112112121221121),(),(),(),(),(),(),(),(),(),(dx x x x f dx x x x f dx x x x f dx x x x f dx x x x f dx x x x f x x df x x df x x df x x df m m m 利用矩阵乘法:⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂∂∂∂∂∂∂=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂+∂∂∂∂+∂∂=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=21221121221212122211121122211121222121121222211112112121221121),(),(),(),(),(),(),(),(),(),(),(),(),(),(),(),(dx dx x x x f x x x f x x x f x x x f x x x f x x x f dx x x x f dx x x x f dx x x x f dx x x x f dx x x x f dx x x x f x x df x x df x x df x x df m m m m m 于是,将矩阵:),(),(),(),(),(),(),(212211212212121222111211x x Df x x x f x x x f x x x f x x x f x x x f x x x f m m =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂∂∂∂∂∂∂ 称为导数,该矩阵为Jacobi 矩阵。
矩阵导数

t1
t1
t1 t1 t1 [A(t)B]dt = t A(t)dt B,t[AB(t)]dt = A t B(t)dt t0 0 0 0
(3)
(3)
d A(t)dt = A(t), A(t)dt = A(b)- A(a) dt a a
统计系
9
2013-7-8
统计系
10
2013-7-8
统计系
11
2013-7-8
统计系
12
xy x 2 xy 2 e A sin(x y) ln(1 y)
2x y2 ye xy A cos x y 0 dA x 2 xy xe xy dX A 1 y cos x y 1 y 2 y 2 e xy 0 sin( x y ) d dA 2y e xy xye xy dX T dX sin( x y ) 0
一、
矩阵的微分和积分 的每一个元素
a (t) ij
1.矩阵导数定义:若矩阵
A(t)=(aij(t))m×n
是变量t的可微函数,则称A(t)可微,其导数定义为
daij dA = A(t)=( )m×n dt dt
由此出发,函数可以定义高阶导数,类似 地,又可以定义偏导数
2013-7-8
统计系
1
2.矩阵导数性质:
t
b
2013-7-8
统计系
5
二.
一阶线性齐次常系数常微分方程组
设有一阶线性齐次常系数常微分方程组
dx1 dt = a11x1(t)+ a12x2(t)+ + a1nxn(t) dx2 = a x (t)+ a x (t)+ + a x (t) 21 1 22 2 2n n dt dxn = a x (t)+ a x (t)+ + a x (t) n1 1 n2 2 nn n dt
函数对矩阵求偏导公式

函数对矩阵求偏导公式矩阵求偏导是在数学中常见的操作,它在许多领域中都有重要的应用。
这个操作可以通过求解矩阵中每个元素对某个变量的偏导数来实现。
在这篇文章中,我们将详细介绍矩阵求偏导的方法和步骤。
让我们回顾一下矩阵的定义。
矩阵是由行和列组成的二维数组,每个元素都可以用一个下标来表示。
例如,一个3x3的矩阵可以表示为:A = [a11 a12 a13][a21 a22 a23][a31 a32 a33]现在,我们假设这个矩阵A是一个关于变量x的函数,那么我们可以将它表示为A(x)。
要求A(x)对x的偏导数,我们需要分别求解每个元素对x的偏导数。
对于矩阵中的每个元素aij,我们可以使用链式法则来求解它对x的偏导数。
链式法则告诉我们,如果一个函数z是由变量y和变量x 的函数所组成,那么z对x的偏导数可以通过求解z对y的偏导数和y对x的偏导数来计算。
现在,让我们应用这个思想到矩阵中。
对于矩阵A中的每个元素aij,我们可以将它表示为一个关于变量x的函数,即aij(x)。
然后,我们可以通过求解aij(x)对x的偏导数来计算矩阵A(x)对x的偏导数。
具体来说,对于每个元素aij(x),我们可以使用极限的定义来计算它对x的偏导数。
偏导数表示了函数在某个点上的变化率,它可以通过计算邻近点上函数值的差异来近似计算。
为了计算aij(x)对x的偏导数,我们可以选择一个很小的数值h,然后计算aij(x+h)和aij(x)之间的差异。
然后,将这个差异除以h,就可以得到aij(x)对x的近似偏导数。
重复这个过程对矩阵中的每个元素进行计算,我们就可以得到整个矩阵A(x)对x的偏导数。
最后,将这些偏导数组合在一起,就可以得到矩阵A(x)对x的导数矩阵。
总结一下,矩阵求偏导是一个重要的数学操作,它可以帮助我们理解矩阵中每个元素对某个变量的变化率。
通过使用链式法则和极限的定义,我们可以计算矩阵A(x)对x的偏导数。
这个过程需要对矩阵中的每个元素进行计算,然后将这些偏导数组合在一起,得到最终的导数矩阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本求导公式、矩阵公式、数学建模1.基本求导公式⑴ 0)(='C (C 为常数)⑵ 1)(-='n nnxx ;一般地,1)(-='αααxx 。
特别地:1)(='x ,x x 2)(2=',21)1(x x -=',xx 21)(='。
⑶ x x e e =')(;一般地,)1,0( ln )(≠>='a a a a a xx 。
⑷ x x 1)(ln =';一般地,)1,0( ln 1)(log ≠>='a a ax x a 。
2.求导法则 ⑴ 四则运算法则设f (x ),g (x )均在点x 可导,则有:(Ⅰ))()())()((x g x f x g x f '±'='±; (Ⅱ))()()()())()((x g x f x g x f x g x f '+'=',特别)())((x f C x Cf '='(C 为常数); (Ⅲ))0)(( ,)()()()()())()((2≠'-'='x g x g x g x f x g x f x g x f ,特别21()()()()g x g x g x ''=-。
3.微分 函数()y f x =在点x 处的微分:()dy y dx f x dx ''== 4、 常用的不定积分公式(1) ⎰⎰⎰⎰⎰+==+=+=-≠++=+c x dx x x dx x c x xdx c x dx C x dx x 43,2,),1( 11433221αααα; (2) C x dx x+=⎰||ln 1; C e dx e xx +=⎰; )1,0( ln ≠>+=⎰a a C a a dx a x x ; (3)⎰⎰=dx x f k dx x kf )()((k 为常数) 5、定积分()()|()()bb a af x dx F x F b F a ==-⎰⑴⎰⎰⎰+=+bab abadx x g k dx x f k dx x g k x f k )()()]()([2121⑵ 分部积分法设u (x ),v (x )在[a ,b ]上具有连续导数)(),(x v x u '',则⎰⎰-=bab abax du x v x v x u x dv x u )()()()()()(6、线性代数 特殊矩阵的概念(1)、零矩阵 ,000022⎥⎦⎤⎢⎣⎡=⨯O (2)、单位矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=10010001ΛΛO ΛΛΛΛn I 二阶,100122⎥⎦⎤⎢⎣⎡=⨯I(3)、对角矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n a a a A 00000021ΛO ΛΛΛΛ(4)、对称矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---==752531212,A a a ji ij(5)、上三角形矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n n a a a a a a A 000022211211ΛO ΛΛΛΛ下三角形矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n a a a A 00000021ΛO ΛΛΛΛ (6)、矩阵转置⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n n n n a a a a a a a a a A ΛΛO ΛΛΛΛ212222111211转置后⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n nn n T a a a a a a a a a A ΛΛO ΛΛΛΛ2122212121116、矩阵运算 ⎥⎦⎤⎢⎣⎡++++=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=+h d g c f b e a h g f ed c b a B A ⎥⎦⎤⎢⎣⎡++++=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=dh cf dg ce bh af bg ae h gf ed c b a AB 7、MATLAB 软件计算题例6 试写出用MATLAB 软件求函数)e ln(2x x x y ++=的二阶导数y ''的命令语句。
解:>>clear;>>syms x y;>>y=log(sqrt(x+x^2)+exp(x)); >>dy=diff(y,2)例:试写出用MATLAB 软件求函数)e ln(xx y +=的一阶导数y '的命令语句。
>>clear;>>syms x y;>>y=log(sqrt(x)+exp(x)); >>dy=diff(y)例11 试写出用MATLAB 软件计算定积分⎰21d e 13x xx 的命令语句。
解:>>clear;>>syms x y;>>y=(1/x)*exp(x^3); >>int(y,1,2) 例 试写出用MATLAB 软件计算定积分⎰x xx d e 13的命令语句。
解:>>clear;>>syms x y;>>y=(1/x)*exp(x^3); >>int(y)MATLAB 软件的函数命令典型例题例1 设某物资要从产地A 1,A 2,A 3调往销地B 1,B 2,B 3,B 4,运输平衡表(单位:吨)和运价表(单位:百元/吨)如下表所示:(1)用最小元素法编制的初始调运方案,(2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总费用。
解:用最小元素法编制的初始调运方案如下表所示:运输平衡表与运价表找空格对应的闭回路,计算检验数:11λ=1,12λ=1,22λ=0,24λ=-2已出现负检验数,方案需要调整,调整量为1 调整后的第二个调运方案如下表:运输平衡表与运价表销地产地B 1 B 2 B 3 B 4 供应量 B 1B 2 B 3 B 4A 1 5 2 7 3 11 3 11 A 2 3 1 4 1 928A 3 6 3 9 7 4 10 5 需求量365620求第二个调运方案的检验数:11λ=-1已出现负检验数,方案需要再调整,调整量为2 调整后的第三个调运方案如下表:运输平衡表与运价表销地产地B 1 B 2 B 3 B 4 供应量 B 1B 2 B 3 B 4A 1 2 5 7 3 11 3 11 A 2 1 3 4 1 928A 3 6 3 9 7 4 10 5 需求量365620求第三个调运方案的检验数:12λ=2,14λ=1,22λ=2,23λ=1,31λ=9,33λ=12所有检验数非负,故第三个调运方案最优,最低运输总费用为:2×3+5×3+1×1+3×8+6×4+3×5=85(百元)例2 某物流公司下属企业经过对近期销售资料分析及市场预测得知,该企业生产的甲、乙、丙三种产品,均为市场紧俏产品,销售量一直持续上升经久不衰。
今已知上述三种产品的单位产品原材料消耗定额分别为4公斤、4公斤和5公斤;三种产品的单位产品所需工时分别为6台时、3台时和6台时。
另外,三种产品的利润分别为400元/件、250元/件和300A 2 3 1 4 1 9 2 8A 3 6 3 9 7 4 10 5 需求量365620元/件。
由于生产该三种产品的原材料和工时的供应有一定限制,原材料每天只能供应180公斤,工时每天只有150台时。
1.试建立在上述条件下,如何安排生产计划,使企业生产这三种产品能获得利润最大的线性规划模型。
2. 写出用MATLAB 软件计算该线性规划问题的命令语句。
解:1、设生产甲、乙、丙三种产品分别为x 1件、x 2件和x 3件,显然x 1,x 2,x 3≥0线性规划模型为⎪⎩⎪⎨⎧≥≤++≤++++=0150636180544300250400max 321321321321x x x x x x x x x x x x S ,,2.解上述线性规划问题的语句为: >>clear;>>C=-[400 250 300]; >>A=[4 4 5;6 3 6]; >>B=[180;150]; >>LB=[0;0;0];>>[X,fval,exitflag]=linprog(C,A,B,[],[],LB)例3已知矩阵⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-=2101111412210101C B A ,,,求:T C AB + 解:⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎦⎤⎢⎣⎡-=+3612201116012101111412210101C AB 例4 设y =(1+x 2)lnx ,求:y '解:xx x x x x x x y 2221ln 2))(ln 1(ln )1(++='++'+='例5 设xy x+=1e ,求:y '解:22)1(e )1()1(e )1()e (x x x x x y xx x +=+'+-+'='例7 某厂生产某种产品的固定成本为2万元,每多生产1百台产品,总成本增加1万元,销售该产品q 百台的收入为R (q )=4q -0.5q 2(万元)。
当产量为多少时,利润最大?最大利润为多少?解:产量为q 百台的总成本函数为:C (q )=q +2利润函数L (q )=R (q )-C (q )=-0.5q 2+3q -2 令ML (q )=-q +3=0 得唯一驻点 q =3(百台) 故当产量q =3百台时,利润最大,最大利润为L (3)=-0.5×32+3×3-2=2.5(万元)例8 某物流企业生产某种商品,其年销售量为1000000件,每批生产需准备费1000元,而每件商品每年库存费为0.05元,如果该商品年销售率是均匀的,试求经济批量。
解:库存总成本函数qq q C 100000000040)(+=令010********401)(2=-='qq C 得定义域内的唯一驻点q =200000件。
即经济批量为200000件。
例9 计算定积分:⎰+10d )e 3(x x x解:25e 3)e 321(d )e 3(|1021-=+=+⎰x x x x x 例10 计算定积分:⎰+312d )2(x xx解:3ln 2326|)|ln 231(d )2(|313312+=+=+⎰x x x x x教学补充说明1. 对编程问题,要记住函数e x,lnx ,x 在MATLAB 软件中相应的命令函数exp(x),log(x),sqrt(x);2 对积分问题,主要掌握积分性质及下列三个积分公式:c x a x x a a++=+⎰111d (a ≠-1) c x x x +=⎰e d e c x x x +=⎰||ln d 17. 记住两个函数值:e 0=1,ln1=0。
