挠曲线
侧向挠度变形曲线

侧向挠度变形曲线
侧向挠度变形曲线是一种描述结构侧向弯曲程度的曲线。
在建筑、桥梁、高速公路等工程领域中,侧向挠度变形是一个重要的指标,用于评估结构的稳定性和安全性。
侧向挠度变形曲线通常是以结构的高度或跨度为横轴,以结构的侧向位移为纵轴,绘制出的曲线图。
通过观察侧向挠度变形曲线,可以了解结构在不同侧向力作用下的弯曲程度,进而评估结构的承载能力和安全性。
在高速公路工程中,侧向挠度变形曲线可以用于分析桥梁、涵洞等结构物的侧向位移,以确保结构的稳定性和安全性。
如果侧向挠度变形过大,可能会影响结构的承载能力,甚至引发结构倒塌等严重事故。
因此,在工程设计和施工过程中,需要进行详细的侧向挠度变形计算和分析,以确保结构的稳定性和安全性。
同时,对于已经建成的结构物,也需要定期进行侧向挠度变形的监测和维护,以确保其长期安全使用。
讲梁的挠曲线方程与积分解法
②积分常数的确定——边界条件和连续条件:
边界条件:梁在其支承处的挠度或转角是已知的, 这样的已知条件称为边界条件。 连续条件:梁的挠曲线是一条连续、光滑、平坦 的曲线。因此,在梁的同一截面上不可能有两个 不同的挠度值或转角值,这样的已知条件称为连 续条件。
边界条件
积分常数2n个=2n个
连续条件
列出图示结构的边界条件和连续条件。
8
代入(1)(2)得:
1 ( 1 qx3 1 qL3)
EI 6 6
1 ( 1 qx4 qL3 x qL4 )
EI 24
68
将 x 0 代入得:
A
qL3 6EI
(与C比较知E:I A C)
A
qL4 8EI
(与D比较知E:IA )D
因此
常数C表示起始截面的转角×刚度(EI)
常数D表示起始截面的挠度×刚度(EI)
x L
2
2、
d 2
dx 2
M (x) EI z
EI" 1 qx2
2
积分一次: EI' EI 1 qx3 C (1)
积分二次:
6
EI 1 qx4 Cx D (2)
24
B X``
3、确定常数C、D.
由边界条件: x L, 0 代入(1)得: C 1 qL3
6
x L, y 0 代入(2)得: D 1 qL4
支座反力,分段列弯矩方程; 分段的原则:
①凡载荷有突变处(包括中间支座),应作为分段点;
②凡截面有变化处,或材料有变化处,应作为分段点;
③中间铰视为两个梁段间的联系,此种联系体现为两部分之间 的相互作用力,故应作为分段点;
(2)分段列出梁的挠曲线近似微分方程,并对其积分 两次
梁的挠曲线方程 -回复

梁的挠曲线方程
梁的挠曲线方程描述了在受到外力作用下的梁的弯曲形状。
梁的挠曲方程具体形式取决于梁的几何形状、材料性质、荷载情况等因素。
以下是一些常见的梁的挠曲方程:
1.简支梁的挠曲方程:对于简支梁,载荷集中在梁的两端,
其挠曲方程可以用Euler-Bernoulli梁理论描述,其方程形式如下:y(x) = c1x²/2EI - c2x³/6EI + M₀x/2EI
其中,y(x)是弯曲后梁的垂直偏移,x是梁上的位置,E是梁的弹性模量,I是梁的截面惯性矩,M₀是梁上的弯矩。
2.悬臂梁的挠曲方程:对于悬臂梁,悬臂端受到力矩和剪力
的影响,其挠曲方程可以用Timoshenko梁理论描述,其方程形式如下:y(x) = M₀x/GI+ M₁x²/2GI- M₂x⁴/24GI+ θ₀x²/2GJ + V₀x/GJ
其中,y(x)是弯曲后梁的垂直偏移,x是梁上的位置,G是梁的剪切模量,I是梁的截面惯性矩,J是梁的截面极惯性矩,M₀和M₁是梁上的弯矩,M₂是梁上的剪力,θ₀是梁上的旋转角度,V₀是梁上的剪力。
以上方程仅给出了简支梁和悬臂梁的挠曲方程的简化形式,实际情况中还需考虑更多的因素。
对于更复杂的梁形式和加载情况,可能需要采用更复杂的挠曲方程进行描述。
挠曲线近似微分方程

C1
Fb 6l
l2 b2
,
C2
Fab 6l
l
a
Page 14
材料力学 第六章 弯曲变形
四 积分法总结
❖ 优点:适用范围广、精确 ❖ 缺点:计算繁琐
五 刚度条件
w
max ቤተ መጻሕፍቲ ባይዱax
w
练习:写边界条件和连续性条件
A
B
C
D
边界条件 wA 0; wB 0
连续性条件 wC wC;C C 或wC' wC' wD wD;D D 或wD' wD'
Mi EI wi" M EIw" M
w
wi
Page 19
材料力学 第六章 弯曲变形
例一:求图示简支梁C点挠度
y A
l/2
F
C l/2
x B
=
y
y
F
A
C
+ x
B
A
x
C
B
l/2
l/2
l/2
l/2
wC
wC q
wC F
5ql4 384EI
Fl 3 48EI
材料力学 第六章 弯曲变形
Page 20
Page 16
材料力学 第六章 弯曲变形
练习(续)
y
a
x
b
l
边界条件 w 0; 0
x0
x0
连续性条件
w w ;
w w ;
xa
xa xa
xa
xb
xb xb
xb
Page 17
材料力学 第六章 弯曲变形
一 叠加§原理6.4 用叠加法求梁的变形
梁的挠曲线方程 -回复

梁的挠曲线方程 -回复
梁的挠曲线方程是描述梁在受力作用下产生弯曲变形的数学模型。
一般情况下,梁的挠曲线方程是一个二阶常微分方程。
挠曲线方程中通常包含梁的几何参数、受力情况、材料性质等因素。
常见的梁的挠曲线方程包括欧拉-伯努利梁方程、柯西梁方程等。
这些方程描述了梁的弯曲变形行为,可以帮助工程师分析和设计
各种结构工程。
在实际应用中,我们需要根据具体情况选择适合的挠曲线方程。
通常情况下,梁在受力作用下会形成曲线状的挠曲变形。
梁的挠曲线方程可以通过应力、应变关系和受力平衡来推导。
挠曲线方程的求解可以通过不同的数学方法,如变分原理、差分法、有限元法等。
梁的挠曲线方程在结构工程、力学分析等领域具有重要的应用价值。
梁的挠曲线方程可以用来计算梁的挠度、切线和曲率等重要参数。
挠曲线方程还可以用来预测梁的弯曲破坏情况。
根据挠曲线方程,工程师可以优化结构设计,提高梁的强度和稳
定性。
挠曲线方程的解析解通常只适用于简单的几何和边界条件。
对于复杂的问题,需要借助计算机数值模拟进行求解。
梁的挠曲线方程涉及到多个数学和物理学概念,需要深入研究和
理解。
挠曲线方程的求解是工程力学和应用数学的重要课题之一。
有效地求解梁的挠曲线方程对于工程设计和结构分析具有关键意义。
通过挠曲线方程的分析,我们可以了解梁在受力下的变形行为,
为结构设计提供依据。
工程力学第1节 挠曲线近似微分方程

挠曲轴线 近似微分方程 结论
M ( x) y EI
两种情况下弯矩与曲线的二阶导数均同号,微分 方程式应取正号,即: 挠曲轴线 近似微分方程
M ( x) y EI
梁的挠曲轴线近似微分方程的适用条件:梁的变 形是线弹性的小变形。
M ( x) y EI
微分方程弯矩M与曲线的二阶导数 y的正负号关系
1)如图a所示,梁的挠曲轴线是一下凸曲线,梁的下 侧纤维受拉,弯矩 M >0,曲线的二阶导数 y >0;
2)如图b所示,梁的挠曲轴线是一上凸曲线,梁的下 侧纤维受压,弯矩 M <0,曲线的二阶导数 y <0;
第十章
梁的弯曲变形
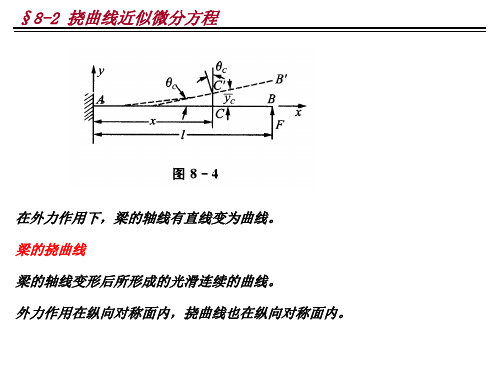
一、挠曲轴线近似微分方程
挠曲轴线:图示悬臂 梁在纵向对称面内的 外力 F 的作用下,将 产生平面弯曲,变形 后梁的轴线将变为一 条光滑的平面曲线, 称梁的挠曲轴线。
挠曲轴线方程
y f ( x)
y f ( x)
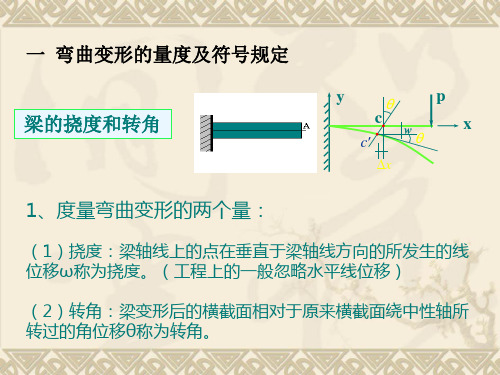
挠度:截面形心线位移的垂直分量称为该截面的 挠度,用 y 表示。
第ቤተ መጻሕፍቲ ባይዱ章
梁的弯曲变形
工程中的很多结构或构件在工作时, 不但要满 足强度条件,同时对于弯曲变形都有一定的要求:
第一类是要求梁的位移不得超过一定的数值。例如 若机床主轴的变形过大,将会影响齿轮的正常啮合 以及轴与轴承的正常配合,造成不均匀磨损、振动 及噪音,缩短了机床的使用寿命,还影响机床的加 工精度。因此,在工程中进行梁的设计时,除了必 须满足强度条件之外,还必须限制梁的变形,使其 不超过许用的变形值。 第二类是要求构件能产生足量的变形。例如车辆钢 板弹簧,变形大可减缓车辆所受到的冲击;跳水起 跳板大变形,以确保运动员被弹起。
转角:横截面绕中性轴转动产生了角位移,此角 位移称转角,用 表示。小变形时,转角 很小, 则有以下关系:
§8 2 挠曲线近似微分方程
§8-2 挠曲线近似微分方程
11 醉翁亭记
1.反复朗读并背诵课文,培养文言语感。
2.结合注释疏通文义,了解文本内容,掌握文本写作思路。
3.把握文章的艺术特色,理解虚词在文中的作用。
4.体会作者的思想感情,理解作者的政治理想。一、导入新课范仲淹因参与改革被贬,于庆历六年写下《岳阳楼记》,寄托自己“先天下之忧而忧,后天下之乐而乐”的政治理想。实际上,这次改革,受到贬谪的除了范仲淹和滕子京之外,还有范仲淹改革的另一位支持者——北宋大文学家、史学家欧阳修。他于庆历五年被贬谪到滁州,也就是今天的安徽省滁州市。也
② 转角
梁横截面绕中性轴转过的角度θ ,逆时针转动为正。
§8-2 挠曲线近似微分方程
③梁的挠曲线方程
y
A
q
x
F
q y
B
x
B1
④转角方程(小变形下):转角与挠度的关系—
y f (x)
q tgq dy y f '(x)
dx 计算位移的目的:校核刚度、解超静定梁。
§8-2 挠曲线近似微分方程 二、梁的挠曲线近似微分方程
环滁/皆山也。其/西南诸峰,林壑/尤美,望之/蔚然而深秀者,琅琊也。山行/六七里,渐闻/水声潺潺,而泻出于/两峰之间者,酿泉也。峰回/路转,有亭/翼然临于泉上者,醉翁亭也。作亭者/谁?山之僧/曰/智仙也。名之者/谁?太守/自谓也。太守与客来饮/于此,饮少/辄醉,而/年又最高,故/自号曰/醉翁也。醉翁之意/不在酒,在乎/山水之间也。山水之乐,得之心/而寓之
§8-2 挠曲线近似微分方程
在外力作用下,梁的轴线有直线变为曲线。 梁的挠曲线 梁的轴线变形后所形成的光滑连续的曲线。 外力作用在纵向对称面内,挠曲线也在纵向对称面内。
第九章梁的弯曲变形-PPT精品文档

第一节
工程中的弯曲变形
梁在外载荷作用下将产生变形,梁不但要满足强 度条件,还要满足刚度条件,即要求梁在工作时的变 形不能超过一定范围,否则就会影响梁的正常工作。 一、挠曲线 挠曲线:图所示悬臂梁在纵向对称面内的外力F的 作用下,将产生平面弯 曲,变形后梁的轴线将变 为一条光滑的平面曲线, 称梁的挠曲线。 挠曲线方程
挠曲轴线 近似微分方程
M ( x) y EI
对梁的挠曲轴线近似微分方程式积分:
积分一次得转角方程:
M ( x ) y x C EI d
积分二次得挠度方程:
M ( x ) y d x d x Cx D EI
第九章 梁的弯曲变形 转角方程 挠度方程
M ( x ) y x C EI d M ( x ) y d x d x Cx D EI
式中积分常数C、D由边界条件(梁中已知的截面 位移)确定:
0 , y 0 简支梁: y A B
悬臂梁: 0 , A
y 0 A
由边界条件、变形连续条件可确定积分常数,通 过上面两个公式可计算梁任一截面的转角与挠度, 这方法称积分法。
第九章 梁的弯曲变形
例9-1 如图所示简支梁,跨度为l,受均布载荷 q作用,梁的抗弯曲刚度EI已知,求跨中截面C的挠 度及截面A处的转角。 解:梁的弯矩方程为:
第九章 梁的弯曲变形 挠曲轴线 近似微分方程 结论 两种情况下弯矩与曲线的二阶导数均同号,微分 方程式应取正号,即: 挠曲轴线 近似微分方程
M(x) y EI
M ( x) y EI
梁的挠曲轴线近似微分方程的适用条件:梁的变 形是线弹性的小变形。
ห้องสมุดไป่ตู้
workbench 挠度曲线

工作台(workbench)是指工程建设、土木工程、机械加工等领域中常用的一种工作评台,用于支撑工作人员、设备和材料。
工作台挠度曲线是对工作台结构进行荷载分析时非常重要的参考曲线,能够直观地反映工作台在荷载作用下的变形情况,对工作台的设计和使用具有重要的指导意义。
1. 工作台挠度曲线的作用工作台挠度曲线是通过对工作台结构进行荷载分析得到的一种曲线图,它能够直观地反映出工作台在荷载作用下的变形情况,包括挠度大小、分布情况等。
工作台挠度曲线的绘制能够帮助工程师和设计人员更好地了解工作台结构的变形特点,为工作台的设计和改进提供重要的参考依据。
通过对工作台挠度曲线的分析,还可以及时发现工作台结构存在的问题,为工程安全和质量提供保障。
2. 工作台挠度曲线的绘制方法工作台挠度曲线的绘制一般需要进行有限元分析,具体步骤包括:a. 建立工作台的有限元模型,确定工作台结构的材料性质、荷载情况等重要参数;b. 进行有限元分析,得到工作台在荷载作用下的变形情况;c. 根据有限元分析结果,绘制工作台挠度曲线。
在进行工作台挠度曲线绘制时,需要结合实际工程情况和设计要求,选择合适的有限元分析软件和绘图工具,确保绘制出准确可靠的挠度曲线。
3. 工作台挠度曲线的分析与应用工作台挠度曲线绘制完成后,需要进行详细的分析与应用,主要包括以下几个方面:a. 分析工作台挠度曲线的形状和变化规律,评估工作台在荷载作用下的变形情况,为工作台的设计、改进和优化提供依据;b. 对比不同荷载下的工作台挠度曲线,找出工作台在不同工况下的变形特点,为工程实际应用提供参考;c. 根据工作台挠度曲线的分析结果,提出改进工作台结构的建议,优化工作台的设计方案,提高工作台的承载能力和使用安全性。
4. 工作台挠度曲线的重要性工作台挠度曲线作为工程结构设计和分析中的重要参考依据,具有以下重要意义:a. 可直观地反映出工作台在荷载作用下的变形情况,为工作台结构的设计和改进提供重要参考;b. 能够及时发现工作台结构存在的问题和隐患,为工程安全和质量提供保障;c. 为工作台的使用和维护提供科学依据,延长工作台的使用寿命,提高工作效率。
材料力学知识点

第六章弯曲变形知识要点1、弯曲变形的概念1)、挠曲线弯曲变形后梁的轴线变为挠曲线。
平面弯曲时,挠曲线为外力作用平面内的平面曲线。
2)、平面弯曲时的变形在小变形情况下,梁的任意二横截面绕各自的中性轴作相对转动,杆件的轴线变为平面曲线,其变形程度以挠曲线的曲率来度量。
1》纯弯曲时,弯矩—曲率的关系(由上式看出,若弯曲刚度EI为常数则曲率为常数,即挠曲线为圆弧线)2》横力弯曲时,弯矩—曲率的关系3)、平面弯曲时的位移1》挠度——横截面形心在垂直于梁轴线方向上的线位移,以表示。
2》转角——横截面绕其中性轴旋转的角位移,以表示。
挠度和转角的正负号由所选坐标系的正方向来确定。
沿y轴正方向的挠度为正。
转角的正负号判定规则为,将x轴绕原点旋转90°而与y轴重合,若转角与它的转向相同,则为正,反之为负。
4)、挠曲线近似微分方程5)、受弯曲构件的刚度条件,2、积分法求梁的挠度和转角由积分常数C、D由边界条件和连续性条件确定。
对于梁上有突变载荷(集中力、集中力偶、间断性分布力)的情况,梁的弯矩M(x)不是光滑连续函数,应用上式时,应分段积分,每分一段就多出现两个积分常数。
因此除了用边界条件外,还要用连续性条件确定所有的积分常数。
边界条件:支座对梁的位移(挠度和转角)的约束条件。
连续条件:挠曲线的光滑连续条件。
悬臂梁边界条件:固定端挠度为0,转角为0连续条件:在载荷分界处(控制截面处)左右两边挠度相等,转角相等简支梁边界条件:固定绞支座或滑动绞支座处挠度为0连续条件:在载荷分界处(控制截面处)左右两边挠度相等,转角相等连接铰链处,左右两端挠度相等,转角不等3、叠加原理求梁的挠度和转角1)、叠加原理各载荷同时作用下梁任一截面的挠度和转角等于各个载荷单独作用时同一截面挠度和转角的代数和。
2)、叠加原理的限制叠加原理要求梁某个截面的挠度和转角与该截面的弯矩成线性关系,因此要求:1》弯矩M和曲率成线性关系,这就要求材料是线弹性材料2》曲率与挠度成线性关系,这就要求梁变形为小变形4、弯曲时的超静定问题——超静定梁1)、超静定梁约束反力数目多于可应用的独立的静力平衡方程数的梁称为超静定梁,它的未知力不能用静力平衡方程完全确定,必须由变形相容条件和力与变形间的物理关系建立补充方程,然后联立静力平衡方程与补充方程,求解所有的未知数。
workbench 挠度曲线

workbench 挠度曲线
摘要:
1.引言
2.什么是挠度曲线
3.挠度曲线的计算方法
4.挠度曲线在工程中的应用
5.总结
正文:
在工程领域,挠度曲线是一个重要的概念,它涉及到结构物的变形和应力分布。
本文将介绍什么是挠度曲线,以及它在工程中的计算方法和应用。
首先,我们需要了解什么是挠度。
挠度是指在受力作用下,结构物发生的弯曲或变形。
挠度曲线则是在一定范围内,描述挠度随伸长量或受力变化的关系曲线。
通过挠度曲线,我们可以了解结构物在不同受力条件下的变形特性。
挠度曲线的计算方法有多种,常见的有欧拉法、瑞利法、特雷斯卡法等。
其中,欧拉法是一种精确度较高的计算方法,适用于任意截面的梁。
瑞利法和特雷斯卡法则适用于简单截面的梁。
这些计算方法都需要考虑材料的弹性模量、截面几何特性、受力条件等因素。
挠度曲线在工程中有着广泛的应用。
在桥梁工程中,挠度曲线可以用于评估桥梁的刚度和稳定性,为设计提供依据。
在房屋建筑中,挠度曲线可以用于分析房屋结构的变形性能,以确保房屋的舒适性和安全性。
此外,在航空航天、汽车制造等领域,挠度曲线也有着重要的应用。
总之,挠度曲线是描述结构物变形特性的重要工具,它在工程设计和分析中具有广泛的应用价值。
挠曲线的近似微分方程

Bx FBy
解:弯矩方程 :
M x 1 qlx 1 qx2
22
挠曲线的近似微分方程:
w
1 EI z
1 2
qlx
1 2
qx2
进行一次积分得:
w
1 EI z
1 4
qlx2
1 6
qx3
C
再进行第二次积分得:
w
1 EI z
1 12
qlx3
Tmax 180 [] GIp
一般传动轴, [φ’] = 0.5 ~1/m
例4 图为一圆截面轴 AC ,受扭转力偶矩MA,MB 与Mc作用。 已知MA =90 N·m , MB =160 N·m , MC =70 N·m , l=2 m, G=80 GPa , IP=3.0×105 mm4 , [φ’] =0.3 (o)/m 。试计算 该轴的总扭转角 φAC (即截面C对截面A的相对转角),并 校核轴的刚度。
F C、D为积分常数,它由位移边界与连续条件确定。
边界条件:梁截面的已知位移条件 固定端的挠度和转角均为零,铰支座处的挠度为零。
A
wA=0 θA=0
F B
A wA=0
F C
B
wC1=wC2 wB=0 θC1=θC2
$ 挠曲轴在C点连续且光滑 连续条件:分段处挠曲轴应满足的连续、光滑条件
例6 如图所示图形为一外伸梁,承受集中载荷作用,试绘制
B
w xl
ql3 6EI z
ql 4
wB
w xl
8EI z
根据挠度和转角的符号规定,上述结果表明转角为顺时针,挠度方 向为向下。
挠曲线的名词解释

挠曲线的名词解释挠曲线是一种数学曲线,它在二维平面上延伸,并具有一定程度的弯曲。
这种曲线的特点是它在任何点上的切线均处于曲线的同一平面内,且切线与曲线之间的夹角保持不变。
挠曲线的概念最早由一位数学家提出,并被广泛应用于物理学、工程学和生物学等领域。
挠曲线的研究可以帮助我们更好地理解曲线的变化规律,并在实际问题中得出相关的结论和解决方案。
挠曲线的定义可以通过数学公式进行表达。
其中,最常见的挠曲线就是悬链线,它是由一根均匀的、自由悬挂的链条所形成的曲线。
悬链线的方程是一个非线性微分方程,需要通过一系列数值方法或近似解法来求解。
值得注意的是,悬链线在物理学和工程学中具有重要的应用,例如桥梁与杆件的设计以及大型吊桥的建造等。
除了悬链线,还存在其他类型的挠曲线。
例如,弧长弯曲度曲线是挠曲线的一种特殊形式,它描述了曲线点的曲率和弧长之间的关系。
这种曲线在地图制作、道路规划和汽车设计中都有广泛的应用。
挠曲线的研究不仅限于平面内,还可以推广到更高维度的空间中。
比如,在三维空间中的挠曲线被称为扭曲线,它在计算机图形学和建筑设计等领域中扮演着重要的角色。
扭曲线的建模和运用可以帮助我们更好地理解三维物体的形态和变化。
挠曲线在现实生活中的应用是广泛而深入的。
例如,工程师们可以利用挠曲线理论来设计建筑物的外形和结构,使其能够抵抗自然灾害和其他不利因素的影响。
同时,在医学领域,挠曲线也被用于研究动脉的流动,以帮助诊断和治疗心血管疾病。
总之,挠曲线是一种数学曲线,具有一定的弯曲特点。
它的研究和应用范围广泛,可以帮助我们更好地理解和解决实际问题。
通过挠曲线的研究,我们可以揭示数学与自然、科学与工程之间的深厚联系,推动科学技术的发展和创新。
结构挠曲线一阶及二阶导数意义

结构挠曲线一阶及二阶导数意义
结构挠曲线的一阶导数和二阶导数在结构工程中具有重要的意义。
一阶导数表示挠曲
线的斜率,二阶导数表示挠曲线的曲率。
在结构工程中,挠曲线的一阶导数表示杆件或梁的弯曲程度,它可以用来计算结构物
的变形情况。
例如,当一个横截面为矩形的杆件受到弯曲作用时,挠曲线的一阶导数表示
沿着杆件的弯曲程度。
如果一阶导数为正,则表示挠曲线向上弯曲;如果一阶导数为负,
则表示挠曲线向下弯曲。
一阶导数的大小表示弯曲的陡峭程度,即斜率的大小。
通过挠曲线的一阶导数和二阶导数,结构工程师可以对结构物的变形和刚度进行评估,从而确定结构物的设计方案,使其能够满足预期的使用要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
主要内容及重点:计算弯曲变形的积分法、叠加法弯曲刚度计算梁的超静定问题1.弯曲变形工程中的弯曲变形问题2.1、挠曲线OB—平面弯曲时,梁变形后轴线。
在xoy 平面内的一条连续、光滑的弹性曲线。
PyxBA(梁弯曲变形的两个基本量)(1)挠度:梁变形后,横截面的形心在垂直于梁轴线(x 轴)方向上所产生的线位移,称为梁在截面的挠度。
一般情况下,不同横截面的挠度值不同。
横截面挠度随截面位置(x 轴)而改变的规律用挠曲线方程表示。
即:)(x f y =y AP x由梁弯曲的平面假设可知:梁的横截面变形前垂直于轴线,变形后仍垂直于挠曲线。
:曲线OAB 在A 点的切线与X 轴间的夹角θABAy AP xθA)挠度与转角的关系挠曲线切线的斜率:θtg dxdy=工程中θ极小:θθtg ≈)(x f dy′==θzEI M =ρ1zEI x M x )()(1=ρOBPyxBPx23222])d d (1[d d )(1xw x w x +±=ρz EI x M xw x w)(])d d (1d d 23222=+zEI x )(ρzEI x M x w )(d d 22=±zEI x M x w )(d d 22=±o>0d 2M>0d 2d 2<0oM<02d zEI Mx w =22d d -挠曲线近似微分方程线弹性范围适用对于等直梁)(x M x w EI z =22d d Cx x M xwEI x EI z z +=∫d )(d d )(=θDCx x x x M x w EI z ++=∫∫d d )()(C 、D :积分常数边界条件已知的挠度及转角光滑连续性PM(x)=F P (L-x)xF L F x L x M xwP P 22))(d −=−=DCx x F x F ++−=3P 2P 6121)θA =0 x =0 时w A =0C=0 D=0)()(x L EI xF x z −22P =θ)3(6)(2P x L EI xF w z−=θEI LF 22P max =θL F w 3P =Pmaxm a xθC x F Lx F x EI P Z +−==2P 21)(θmaxy maxB θ解:建立坐标、写弯矩方程)段:(20lx AC <≤)段:(l x lCB ≤<2BCL/2L/2xxPxx 21)(=)2(21)(lx P Px x M −−=Px1)=)(1)(lx P Px x y EI −−=′′一次:利用边界条件确定积分常数:12141C Px EI Z +=θ1131121D x C Px y EI Z ++=2222)2(241C l x P Px EI Z +−−=θ22332)2(6121D x C l x P Px y EI Z ++−−=⇒==右左右左,C C C C y y θθ2121DDC C ==2100D D y x A =⇒==,02Pl C C y l x B −==⇒==,maxy maxB θBCpL/2164Z 224EI Z )1612(23x Pl Px Z −]16)2(6121[12332x Pl l x P Px EI y Z −−−=max0θ,,l x ==ZEIPl 162max∓=θmax2y lx ,=ZEIPl y 483max−=maxy maxB θBCpx思考:在用积分法求梁的转角和位移过程中,何时需要考虑静力关系、物理关系、变形协调关系?静力关系:支反力、弯矩计算物理关系:挠曲线近似微分方程变形协调关系:积分运算及边界条件图示纯弯曲悬臂梁的挠曲线应为一圆弧线,而由积分法求得的梁挠曲线为二次抛物线为什么?近似微分方程获得的梁挠曲线近似解自由端B 处挠度的精确解:EIxM v e 22=()+−=⎟⎟⎠⎞⎜⎜⎝⎛+−=−=43242!4!2cos 1lM l M v e e BBB θθρθρ1222211)()()(a x m x Lm x M x L mx M −−==2a a 2a x2()2)(452)(2)(222222211a x q a x qa x q x M x q x M −+−+−−==5.用叠加法求弯曲变形叠加法:当梁上同时作用几个荷载时,在小变形情况下,且梁内应力不超过比例极限,则每个荷载所引起的变形(挠度和转角)将不受其它荷载的影响。
梁上任意横截面的总位移等于各荷载单独作用时,在该截面所引起的位移的代数和。
()↵+−==↓+−=+= )2416())(384548(32P 43P EIqL EI L F EI qLEI L F AqAP A CqCP C θθθωωω+ca 2aa 2a f c =f cq + f cma EIqa A θ−−=84EIa qa A 32212=θ()↓−=42411qa EI f zc 逐段刚化EIx x L qx EIx L x x q dw EIxqx EI x x q d B B 6d )3(6)3()d (2d 2)(d 2222−−=−−=−=−=θ)(38441d )3(6)(487d 242322↓−=−↵−=−EIqL x x x L EI q EI qL x x EI q LLLq dx解:采用逐段刚化法首先将AB 段视为刚体,研究BC 段变形:再将BC 段视为刚体,通过外力平移,研究AB 段变形:B CL/2qy 1BCql 2/8/2y 2= y p + y My 3=(θP + θM )L/2EIql EI l q y 1288)2(441==BCL/2qy 1BC ql 2/8/2y 2= y p + y My 3=(θP + θM )L/2EIl ql EI l ql y y y M P 2)2(83)2(2232+=+=2))2(82)2(2(2)(223l EI l ql EI l ql l y M P +=+=θθEIql y 384414=A B CqL/2L/2BC qL/2L/2A B CqL/2L/2常数。
求:使θC =0时,P=?,并求此时的y C解:CM PL/2L/2EIl P EI Ml 2)2(2=lM P 8=EIMl EI Ml EI l P l EI l P 323)2(22)2(2232=−+=P AaEI 1A P y 1P M A y 2x1313EI Pa y =22)(EI a b Pa y ⋅=222)(EI b Pa x =)3(21221I bI a E Pa y y y +=+=6.梁的刚度条件][max w w ≤][max θθ≤-刚度条件截面C 处挠度不超过两轴承间距离的10-4,轴承B 处转角不超过10-3 rad 。
试校核该主轴的刚度。
EIl P B 16221=θEIal P a y B C 162211==θEIal P B 312=θ)(21l a a P y +=P 2P 1B CL/2L/2a P 2B Cy 1y 2P 1BEIa l P EI a l a P 163221−+=)(EI l P EI laP B B 16322112−=−=θθθm 6102−×rad 510−m l y C54100.410][−−×=×=rad 310][−=θ<<满足刚度条件46441088.164m d D I −×=−=)(πL/2L/2a P 2B Cy 1y 2P 1B C(a)(b)RB相当系统w B =0B =w Bq +w BR =0048384534=+EIL F EI qL Rb qL 85=qLF qL F RC RA 163 163==(a)PP(c)(b)PRBBC 的抗拉压刚度为EA 。
试求:BC 杆内力解:(1)选取静定基(2)得相当系统(3)将相当系统变形与原系统比较,得变形协调方程:B/B C LL/2q R BqBCB L y Δ=EIlR EI ql y y y B R q B B3834−=−=l R L B )2(=ΔB /B C LL/2q R BqBCB L y Δ=EA l R EI l R EI ql B B )2(3834=−)32(4323I Al AqlR B +=(b)(a)RB抗弯刚度为EI 。
δ=B w 33LEI F RBδ−=3EIδ/L2试求:经过滚柱所传递的压力。
相当系统确定静定基解:一次超静定B CL/2L/2P PPPL/2R CR C)()(DC C AB C y y =)2(3)2(2)2(23)2)((323EI l R EI L Pl EI l R P C C =+−PR C 35=变形协调方程:120mm 。
求:[P]=?解:一次超静定确定静定基相当系统变形协调方程:补充方程荷载叠加:求B 点挠度B CP2aaB C R B P B C P C BPa P=B y 03)2(2)2)((3)2(323=−+EIa R EIa Pa EI a P B P R B 47=强度条件:求许可荷载B C 2a a EIPa EI a R a EI a R EI a P y B B c 653)2(2)2(3)3(33=−−=PaM =max 62max max1016061×≤==bh Pa W M ZσKNP 4.6≤Pa -CBP PR B 47=解:一次超静定确定取静定基相当系统变形协调方程:2B C a a q BCR B R B/q 3qa /165qa 2/163qa 2/16--右左B B yy =EIaR EI qa y B B 3834−=左EI a R y B B 33=右163qa R B =313qa R qa R ==,3a/16模量均为:E=200GPa ,若P=30KN 。
试求(1)梁和杆内,(2)横截面C 的垂直位移。
解:一次超静定变形协调方程:确定静定基相当系统由于ΔL BC 很小,忽略不计B C DP2m2mB R B R /PC D BCB C L y y Δ+=EIR EI R P y B B C 32484)(33=′−=3345101066.1mmmI Z ×=−mmEIR P y BC 03.8484)(=′−=C DP2mmB R B R B /PC DmKN M GD AB .20max =梁:、MPa W M Z108max max==σMPa AN 8.31max ==σ杆:梁的变形不仅与荷载、支承有关,而且与材料、跨度等也有关。
EIl y n⋅=系数荷载9.1 选择合理的加载方式减小梁变形:(a)P(b)(a)(b)(c)9.3 增大梁的抗弯刚度二梁的受力(包括载荷与约束力)是否相同?二梁的弯矩是否相同?二梁的变形是否相同?二梁的位移是否相同?结论与讨论变形和位移的关系是是是否画出梁的挠度曲线的大致形状+画出梁的挠度曲线的大致形状—。
