暨南大学2010年数学分析考研试题
暨南大学601高等数学2010--2014,2017,2019--2020年考研真题试卷

3.若 y5 2 y x 3x7 0 ,则 dy |x0 __________________________.
4.
lim(
n
n
1 2
1
2 n2 2
...
n ______.
5.以函数 y C2 作为通解的微分方程是_______________________. x C1
____________
(A) 充要条件 (B) 充分不必要条件 (C) 必要不充分条件 (D) 既不充分也不必要
4. 若级数 (an bn ) 收敛,那么说法正确的是___________
n1
(A) an 和 bn 中至少有一个收敛 (B) an 和 bn 有相同的敛散性
n1
n1
n1
n1
(C) an 和 bn 都收敛
D
6.求 4 ln(1 tan x)dx . 0
dx
7. 判断积分 0
(1 x)(1 x2 ) 的收敛,如果收敛,求其值.
8. 求一阶线性微分方程 dy 5y x 的通解. 并求满足初始条件 y(0) 0 的特解. dx
9.求在平面 x y z 1与柱面 x2 y2 1的交线上到 XOY 面的距离最远的点. 345
考试科目:高等数学B
共 4 页,第 3 页
4、证明题 (本题共2小题,每小题5分,共10分)
1. 设函数 f (x) 在 (,) 上可导,证明:若 f ' (x) f (x) 没有实数解,那么曲线
y f (x) 与 x 轴最多只能有一个交点.
df
1 ( dx
x)
|x3
___________
(A) 1 3
(B) 3
(C) 1
暨南大学830数据结构2010,2012--2020年考研真题

考生注意:所有答案必须写在答题纸(卷)上,写在本试题上一律不给分。
一、 单项选择题(每题 2 分,共 30 分)
1. 下述关于顺序存储结构优点的说法,哪个是正确的( )
A. 插入运算方便
B. 可方便地用于各种逻辑结构的存储表示
C. 存储密度大
D. 删除运算方便
2. 假设根结点为第 1 层,深度为 h 层的二叉树至少有( ) 个结点(h>1);
A.3
B.4
C.5
D.6
13. 有一个 100*90 的整数稀疏矩阵,其中非 0 元素个数为 10;设每个整数占用 3 个字节,则
用三元组表示该矩阵时,总共需要的存储空间为( )字节。
A.30
B.33
C.90
D.99
14. 在一个双向链表中,当删除结点 p 时,错误的操作序列为 ( )。
A. p=p->prev; p->next->prev=p; p->next=p->next->next;
2020 年全国硕士研究生统一入学考试自命题试题 B 卷
********************************************************************************************
学科、专业名称:网络空间安全 研究方向:网络空间安全 083900 考试科目名称及代码:数据结构 830
4. 以下关于递归算法的论述,不正确的是( )
A. 递归算法的代码可读性好
B. 递归算法可以提高程序运行效率
C. 递归调用层次太深有可能造成堆栈溢出 D. 递归调用层次太深会占用大量内存
5. 设有字符集合{4,6,3,W,S},将字符序列 6W43S 中的字符按顺序进入堆栈,出栈可发生在任
暨南大学数学分析考研真题试题2015—2020(缺2016)年

********************************************************************************************
招生专业:基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论、统计学 研究方向:各方向 考试科目名称及代码:709 数学分析
********************************************************************************* 题目结束
考试科目: 709 数学分析
共 2 页,第 2 页
2019cçÂôÖa¬Æ ïÄ)\Æ•ÁÁK£Aò¤
*************************************************************************************** Ɖ! ;’¶¡µÄ:êÆ! OŽêÆ! VÇ؆ênÚO! A^êÆ! $ÊƆ››Ø! ÚOÆ ïÄ••µˆ•• •Á‰8¶¡µ709êÆ©Û
n1 n
2.
(10 分)证明:第二型曲线积分
L
xdx ydy ( x2 y2 )3/2
在区域
D
:
x
0
上与路径无关.
3. (11 分)设函数 f (x) 在 [0, 3] 上连续,在 (0, 3) 内可导,且满足 f (0) f (1) f (2) 3 ,
f (0) 1, f (3) 1 ,证明:存在 (0,3) ,使得 f ( ) 0 .
•)5¿µ¤k‰Y7L 3‰K’£ò¤þ§ 3 ÁKþ˜Æ؉©" ˜!OŽK£ 3 K§z K8©§ 24©¤
暨南大学810高等代数2010--2020年考研专业课真题

考试科目名称及代码:810高等代数(A卷)
考生注意:所有答案必须写在答题纸(卷)上,写在本试题上一律不给分。
一、(10分)设 为给定正整数, 为给定常数,计算对角线上元素均为 、其它位置元素均为1的 阶矩阵 的行列式 .
2证明 在某基下的矩阵是
六(15分)1设 ,证明秩 =秩 =秩 。
2设 是实对称矩阵, ,证明 。
七(15分)已知矩阵 是数域 上的一个 级方阵,如果存在 上的一个 级可逆方阵 ,使得 为对角矩阵,那么称 在 上可对角化。分别判断 能否在实数域上和复数域上可对角化,并给出理由。
八(16分)用 表示实数域 上次数小于4的一元多项式组成的集合,它是一个欧几里得空间,内积为 。设 是由零次多项式及零多项式组成的子空间,求 以及它上的一个基。
研究方向:各专业研究方向
考试科目名称:810高等代数
考生注意:所有答案必须写在答题纸(卷)上,写在本试题上一律不给分
一、判断下列命题的正误(只需回答“正确”或“错误”并将你的答案写在答题纸上,不需说明理由,每题2分,共20分):
1唯一解,并求其解;
2无穷多解,给出解的表达式;
3无解。
四(15分)设
1求 的全部特征值;
2对 的每个特征值 ,求 的属于特征值 的特征子空间的维数和一组基;
3求正交矩阵 ,使 是对角矩阵,并给出此对角矩阵。
五(15分)设 是数域 上的一个n维线性空间 ,若有线性变换 与向量 使得 ,但 。
1证明 线性无关;
2020年招收攻读硕士学位研究生入学考试试题
********************************************************************************************
2010-2018研究生考试数学二真题及答案

(13) 已知一个长方形的长 l 以 2 cm/s 的速率增加,宽 w 以 3 cm/s 的速率增加.则当 l 12cm , w 5cm 时,它的
对角线增加的速率为 .
(14)设 A, B 为 3 阶矩阵,且 A 3,B 2, A1 B 2 ,则 A B1 = .
0
1
(C)
1 1
.
0
1
(B)
1 1
.
0
1
(D)
1 1
.
0
二、填空题(9~14 小题,每小题 4 分,共 24 分.请将答案写在答.题.纸.指定位置上.)
(9) 3 阶常系数线性齐次微分方程 y 2 y y 2 y 0 的通解为 y .
x y
2t t (t)
2
,
(t
1) 所确定,其中 (t) 具有
2 阶导数,且
(1)
5 , 2
(1)
6. 已知
d2y dx2
3 4(1 t)
, 求函数
(t)
.
4
(18)(本题满分 10 分)
一个高为 l 的柱体形贮油罐,底面是长轴为 2a ,短轴为 2b 的椭圆.现将贮油罐平放,当油罐中油面高度为 3 b 时 2
1
x 1
y dy
.
2
(C)
1
dx
0
2010年暨南大学803西方经济学 考研真题及答案

暨南大学803西方经济学2010年硕士研究生入学考试试题2010年招收攻读硕士学位研究生入学考试试题学科、专业名称:理论经济学各专业、应用经济学各专业(金融学除外)考试科目名称:803西方经济学考生注意:所有答案必须写在答题纸(卷)上,写在本试题上一律不给分。
一、简答题(共6题,每题10分,共60分)1.列举影响财政政策挤出效应的因素,并解释这些因素如何影响挤出效应。
2.画图简要说明完全竞争厂商短期均衡的形成和条件。
3.简述2009年诺贝尔经济学奖获得者威廉姆森的主要理论贡献。
4.要素使用原则与利润最大化原则有何联系?考试科目:西方经济学共2页,第1页考试科目:西方经济学共2页,第2页4.3.1 暨南大学803西方经济学2010年硕士研究生入学考试试题解析一、简答题(共6题,每题10分,共60分)1、列举影响财政政策挤出效应的因素,并解释这些因素如何影响挤出效应。
【参考答案】:扩张性财政政策导致利率上升,从而“挤出”私人投资,进而对国民收入的增加产生一定程度的抵消作用,这种现象称为挤出效应。
影响挤出效应的因素有:一,支出乘数的大小。
乘数越大,政府支出所引起的产出增加固然越多,但利率提高使投资减少所引起的国民收入减少也越多,即“挤出效应”越大。
二,货币需求对产出变动的敏感程度。
k越大,挤出效应也越大。
三,货币需求对利率变动的敏感程度。
h越大,挤出效应越小。
四,投资需求对利率变动的敏感程度,越敏感,挤出效应越大。
2、画图简要说明完全竞争厂商短期均衡的形成和条件。
【参考答案】:短期内,完全竞争厂商通过对产量的调整来实现MR=SMC的利润最大化的均衡条件的。
首先,在价格依次为P1、P2、P3、P4和P5时,厂商根据MR=SMC的原则依次选择最优产量为Q1、Q2、Q3、Q4和Q5,均衡点分别为E1、E2、E3、E4和E5。
其实,厂商通过比较最优产量水平上的平均收益AR与短期平均成本SAC来确定自己的最大利润是正是负还是零。
2010年全国硕士研究生入学统一考试数学二试题及解析

2010年全国硕士研究生入学统一考试数学二试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内。
(1)函数()f x = (A) 0. (B) 1 (C) 2 (D) 3(2) 设1y ,2y 是一阶线性非齐次微分方程()()y p x y q x '+=的两个特解. 若常数λ, μ使12y y λμ+是该方程的解,12y y λμ-是对应的齐次方程的解, 则 (A )11,22λμ== (B)11,22λμ=-=- (C) 21,33λμ== (D) 22,33λμ== (3) 曲线2y x =与曲线ln (0)y a x a =≠相切,则a =(A)4e (B)3e (C)2e (D)e(4)设,m n 为正整数,则反常积分dx ⎰的收敛性(A)仅与m 取值有关 (B)仅与n 取值有关(C)与,m n 取值都有关(D)与,m n 取值都无关(5)设函数(,)z z x y =由方程(,)0y z F x x=确定,其中F 为可微函数,且20F '≠则z z xy x y∂∂+=∂∂ (A) x(B)z (C) x -(D) z -(6) 2211lim()()nnn i j nn i n j →∞===++∑∑ (A)121(1)(1)xdx dy x y ++⎰⎰(B)11(1)(1)xdx dy x y ++⎰⎰(C) 11001(1)(1)dx dy x y ++⎰⎰ (D)112001(1)(1)dx dy x y ++⎰⎰(7)设向量组12 :, ,, r I ααα⋅⋅⋅可由向量组12II : , ,, s βββ⋅⋅⋅线性表示, 则列命题正确的是(A) 若向量组I 线性无关, 则r s ≤ (B) 若向量组I 线性相关, 则r s >(C) 若向量组II 线性无关, 则r s ≤ (D) 若向量组II 线性相关, 则r s >(8)设A 为4阶对称矩阵,且20A A +=若A 的秩为3,则A 相似于(A)1110⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦(B)1110⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦(C) 1110⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎣⎦(D) 1110-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎣⎦ 二、填空题:9-14 小题,每小题 4分,共 24 分,请将答案写在答题纸指定位置上。
2010年暨南大学803西方经济学-考研专业课真题及答案

考研学习中,专业课占的分值较大。
对于考研专业课复习一定要引起高度的重视,中公考研为大家整理了2010年暨南大学803西方经济学考研专业课真题及答案,并且可以提供暨南大学考研专业课辅导,希望更多考生能够在专业课上赢得高分,升入理想的院校。
暨南大学803西方经济学2010年硕士研究生入学考试试题2010年招收攻读硕士学位研究生入学考试试题学科、专业名称:理论经济学各专业、应用经济学各专业(金融学除外)考生注意:所有答案必须写在答题纸(卷)上,写在本试题上一律不给分。
考试科目:西方经济学共2页,第考试科目:西方经济学共2页,第2页4.3.1 暨南大学803西方经济学2010年硕士研究生入学考试试题解析一、简答题(共6题,每题10分,共60分)1、列举影响财政政策挤出效应的因素,并解释这些因素如何影响挤出效应。
【参考答案】:扩张性财政政策导致利率上升,从而“挤出”私人投资,进而对国民收入的增加产生一定程度的抵消作用,这种现象称为挤出效应。
影响挤出效应的因素有:一,支出乘数的大小。
乘数越大,政府支出所引起的产出增加固然越多,但利率提高使投资减少所引起的国民收入减少也越多,即“挤出效应”越大。
二,货币需求对产出变动的敏感程度。
k越大,挤出效应也越大。
三,货币需求对利率变动的敏感程度。
h越大,挤出效应越小。
四,投资需求对利率变动的敏感程度,越敏感,挤出效应越大。
2、画图简要说明完全竞争厂商短期均衡的形成和条件。
【参考答案】:短期内,完全竞争厂商通过对产量的调整来实现MR=SMC的利润最大化的均衡条件的。
首先,在价格依次为P1、P2、P3、P4和P5时,厂商根据MR=SMC的原则依次选择最优产量为Q1、Q2、Q3、Q4和Q5,均衡点分别为E1、E2、E3、E4和E5。
其实,厂商通过比较最优产量水平上的平均收益AR与短期平均成本SAC来确定自己的最大利润是正是负还是零。
在Q1产量水平上,AR>SAC,因此利润大于0;而在Q2产量水平上,AR=SAC,因此利润等于0;而在Q3产量水平上,AR<SAC,因此利润小于0。
暨南大学2010年招收攻读硕士学位研究生入学考试试题

2010年招收攻读硕士学位研究生入学考试试题******************************************************************************************** 学科、专业名称:081001 通信与信息系统、081002 信号与信息处理、430109电子与通信工程研究方向:01光电子与光通信、02通信网络与信息系统、03微电子器件与集成电路设计、04多媒体技术与信息安全、05无线通信与传感技术;01机器人与测控系统、02量子信息与量子系统、03信息技术与智能仪器、04通信信号处理及SoC设计、05图像处理与应用系统; 01光通信与无线通信、02网络与多媒体技术、03微电子技术与集成电路设计、04测控系统与智能仪器、05信息系统与信息处理技术考试科目:823 电子技术基础共8 页,第 1 页考试科目:823 电子技术基础共8 页,第 2 页考试科目:823 电子技术基础共8 页,第 3 页T2和T3分别构成什么电路?考试科目:823 电子技术基础共8 页,第 4 页考试科目:823 电子技术基础共8 页,第 5 页、如图 求出和表达式,对电流反馈写出20.2sin()k 22sin(10a +∙∙=t v ππ考试科目:823 电子技术基础共8 页,第 6 页考试科目:823 电子技术基础共8 页,第7 页考试科目:823 电子技术基础共8 页,第8 页2010年招收攻读硕士学位研究生入学考试试题********************************************************************************************学科、专业名称:光学工程研究方向:考试科目名称:820 数字电子技术 图2.2 00003210=Q Q Q Q ,则第2个CP 的上升沿到]。
图3四、(10分)用4选1数据选择器实现以下逻辑功能:Y=A⊙B⊙C(要求列出过程)五、(10分)试用ROM实现两个2位二进制数的加法运算(列出过程,用简化阵列图表示)。
2010年考研数学试题详解及评分参考

.
【答】 应填
2 3
.
{ } 【解】 记 D = ( x, y) x2 + y2 £ 1 ,有
òòò òò ò òò ò ò W
dxdydz =
D
dxdy
1 dz
x2 + y2
= (1- x2 - y2 )dxdy =
D
2p dq
0
1(1- r2 )rdr
0
=
p 2
,
òòò òò ò òò ò ò W
.
【答】 应填 -4p .
【解】 令 x = t ,则 dx = 2tdt ,于是有
ò ò ò ò p2 0
x cos
xdx =
p 2t2 costdt = 2t2 sin t
0
p 0
-4
p 0
t sin tdt
=
4t cos
p 0
-4
p 0
cos tdt
=
-4p .
(11) 已知曲线 L 的方程为 y = 1- | x | (x Î[-1,1]) ,起点是 (-1, 0) ,终点为 (1, 0) ,则曲线
【答】 应填 0 .
【解】
因
dy dx
=
dy dx
/ /
dt dt
=
ln(1+ t2 ) -e-t
,
d2y dx2
=
d dt
[
ln(1+t -e-t
2
)
]
1 dx /
dt
=
e2t [ 2t 1+ t
+ ln(1+
t 2 )],
d2y 故 dx2
t=0
2010考研数学一试题

2010年全国硕士研究生入学统一考试数学一试题一、选择题(1~8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上.) (1) 极限2lim ()()xx x x a x b →∞⎡⎤=⎢⎥-+⎣⎦( ) (A) 1. (B) e . (C) a be -. (D) b ae-.(2) 设函数(,)z z x y =,由方程,0y z F x x ⎛⎫=⎪⎝⎭确定,其中F 为可微函数,且20F '≠,则z zxy x y∂∂+=∂∂( ) (A) x . (B) z . (C) x -. (D) z -.(3) 设,m n 是正整数,则反常积分()210ln 1mnx dx x-⎰的收敛性 ( )(A) 仅与m 的取值有关. (B)仅与n 的取值有关. (C) 与,m n 取值都有关. (D) 与,m n 取值都无关. (4) ()()2211limn nn i j nn i n j →∞===++∑∑ ( ) (A)()()120111xdx dy x y ++⎰⎰. (B) ()()100111x dx dy x y ++⎰⎰. (C)()()11111dx dy x y ++⎰⎰. (D) ()()1120111dx dy x y ++⎰⎰. (5) 设A 为m n ⨯矩阵,B 为n m ⨯矩阵,E 为m 阶单位矩阵,若AB E =,则 ( )(A) 秩()r A m =,秩()r B m =. (B) 秩()r A m =,秩()r B n =. (C) 秩()r A n =,秩()r B m =. (D) 秩()r A n =,秩()r B n =. (6) 设A 为4阶实对称矩阵,且2A A O +=,若A 的秩为3,则A 相似于 ( )(A) 1110⎛⎫⎪⎪ ⎪ ⎪⎝⎭. (B) 1110⎛⎫ ⎪ ⎪ ⎪- ⎪⎝⎭.(C) 1110⎛⎫ ⎪- ⎪ ⎪- ⎪⎝⎭. (D) 1110-⎛⎫ ⎪- ⎪ ⎪- ⎪⎝⎭. (7) 设随机变量X 的分布函数0,1(),0121,1x x F x x e x -<⎧⎪⎪=≤<⎨⎪-≥⎪⎩,则{}1P X == ( ) (A) 0. (B)12. (C) 112e --. (D) 11e --. (8) 设1()f x 为标准正态分布的概率密度,2()f x 为[]1,3-上均匀分布的概率密度,若12(),0()(),0af x x f x bf x x ≤⎧=⎨>⎩,(0,0)a b >>为概率密度,则,a b 应满足 ( ) (A) 234a b +=. (B) 324a b +=. (C) 1a b +=. (D) 2a b +=.二、填空题(914小题,每小题4分,共24分.请将答案写在答题纸...指定位置上.) (9) 设()20,ln 1,t tx e y u du -⎧=⎪⎨=+⎪⎩⎰ 求220t d y dx == . (10)2cos x xdx π=⎰.(11) 已知曲线L 的方程为[]{}11,1y x x =- ∈-,起点是()1.0-,终点是()1,0,则曲线积分2Lxydx x dy +=⎰.(12) 设(){}22,,1x y z xy z Ω=+≤≤,则Ω的形心的竖坐标z = .(13) 设()()()1231,2,1,0,1,1,0,2,2,1,1,TTTa ααα=-==,若由123,,ααα生成的向量空间的维数是2,则a = .(14) 设随机变量X 的概率分布为{}!CP X k k ==,0,1,2,k =,则()2E X=.三、解答题(15~23小题,共94分.请将解答写在答题纸...指定位置上.解答应写出文字说明、证明过程或演算步骤.)求微分方程322x y y y xe '''-+=的通解. (16)(本题满分10分)求函数()()2221x t f x xt e dt -=-⎰的单调区间与极值.(17)(本题满分10分)(I)比较()1ln ln 1n t t dt +⎡⎤⎣⎦⎰与10ln nt t dt ⎰()1,2,n =的大小,说明理由;(II)记()1ln ln 1nn u t t dt =+⎡⎤⎣⎦⎰()1,2,n =,求极限lim n n u →∞. (18)(本题满分10分)求幂级数()121121n n n x n -∞=--∑的收敛域及和函数.(19)(本题满分10分)设P 为椭球面222:1S x y z yz ++-=上的动点,若S 在点P 处的切平面与xOy 面垂直,求点P 的轨迹C ,并计算曲面积分()223244x y zI dS y z yz∑+-=++-⎰⎰,其中∑是椭球面S 位于曲线C 上方的部分. (20)(本题满分11分)设110111a A b λλλ ⎛⎫⎛⎫ ⎪ ⎪= - 0= ⎪ ⎪ ⎪ ⎪1 1 ⎝⎭⎝⎭,,已知线性方程组Ax b =存在两个不同的解.( I ) 求λ,a ;( II ) 求方程组Ax b =的通解. (21)(本题满分11 分)已知二次型123(,,)T f x x x x Ax =在正交变换x Qy =下的标准形为2212y y +,且Q 的第三列为22(,0,)22T. ( I ) 求矩阵A ;( II ) 证明A E +为正定矩阵,其中E 为3阶单位矩阵. (22)(本题满分11分)设二维随机变量(,)X Y 的概率密度为2222(,)x xy y f x y Ae -+-=,x -∞<<+∞,y -∞<<+∞,求常数A 及条件概率密度|(|)Y X f y x .设总体X 的概率分布为X 1 2 3P1θ- 2θθ- 2θ其中参数()0,1θ∈未知,以i N 表示来自总体X 的简单随机样本(样本容量为n )中等于i 的个数(1,2,3i =).试求常数123,,a a a ,使31iii T a N ==∑为θ的无偏估计量,并求T 的方差.。
暨南大学数学学科2010年硕士研究生入学考试

暨南大学数学学科2011年硕士研究生入学考试自命题科目《高等代数》考试大纲本《高等代数》考试大纲适用于暨南大学数学学科各专业(基础数学、概率论与数理统计、应用数学)硕士研究生入学考试。
高等代数是大学数学系本科学生的最基本课程之一,也是大多数理工科专业学生的必修基础课。
它的主要内容包括多项式理论、行列式、线性方程组、矩阵理论、二次型理论、线性空间、线性变换、λ-矩阵、欧氏空间。
要求考生熟悉基本概念、掌握基本定理、有较强的运算能力和综合分析解决问题能力。
一、考试的基本要求要求考生比较系统地理解高等代数的基本概念和基本理论,掌握高等代数的基本思想和方法。
要求考生具有抽象思维能力、逻辑推理能力、运算能力和综合运用所学的知识分析问题和解决问题的能力。
二、考试内容(一)多项式1.一元多项式的整除、最大公因式、带余除法公式、互素、不可约、因式分解、重因式、根及重根、多项式函数的概念及判别;2.复根存在定理(代数基本定理);3.根与系数关系;4.一些重要定理的证明,如多项式的整除性质,Eisenstein判别法,不可约多项式的性质,整系数多项式的因式分解定理等;5.运用多项式理论证明有关命题,如与多项式的互素和不可约多项式的性质有关的问题的证明与应用;6.用多项式函数方法证明有关结论。
(二)行列式1.n-级排列、对换、n-级排列的逆序及逆序数和奇偶性;2.n-阶行列式的定义,基本性质及常用计算方法(如三角形法、加边法、降阶法、递推法、按一行或一列展开法、Laplace展开法、Vandermonde行列式法);3.Vandermonde行列式;4.行列式的代数余子式。
(三)线性方程组1.向量组线性相(无)关的判别及相应齐次线性方程组有(无)非零解的相关向量判别法、行列式判别法;2.向量组的极大线性无关组的性质,向量组之间秩的大小关系定理及其三个推论,向量组的秩的概念及计算,矩阵的行秩、列秩、秩概念及其行列式判别法和计算;3.Cramer法则,线性方程组有(无)解的判别定理,齐次线性方程组有(无)非零解的矩阵秩判别法、基础解系的计算和性质、通解的求法;4.非齐次线性方程组的解法和解的结构定理;(四)矩阵理论1.矩阵基本运算、分块矩阵运算及常用分块方法并用于证明与矩阵相关的结论,如有关矩阵秩的不等式;2.初等矩阵、初等变换及其与初等矩阵的关系和应用;3.矩阵的逆和矩阵的等价标准形的概念及计算,矩阵可逆的条件及其与矩阵的秩和初等矩阵的关系,伴随矩阵概念及性质;4.行列式乘积定理;5.矩阵的转置及相关性质;6.一些特殊矩阵的常用性质,如,对角阵、三角阵、三对角阵、对称矩阵、反对称矩阵、幂等矩阵、幂零矩阵、正交矩阵等;7.矩阵的迹、方阵的多项式;8.矩阵的常用分解,如等价分解、满秩分解、实可逆矩阵的正交三角分解、约当分解;9.应用矩阵理论解决一些问题。
暨南大学数学分析考试题

证明: 在 上连Байду номын сангаас.
2010年招收攻读硕士学位研究生入学考试试题(副卷)
*******************************************************************************************
学科、专业名称:数学学科、基础数学专业、概率论与数理统计专业、应用数学专业
(2)求由方程 所确定的函数 的微分.
3.计算积分(第1,2小题每小题7分,第3,4小题每小题10分,总共34分)
(1) ;
(2)瑕积分 是否收敛?若收敛,求其积分值;
(3)设 为连续可微函数,若曲线积分 与路径无关,且 ,求
考试科目:数学分析共2页,第2页
(4)计算 其中 为曲面 上 的那部分取正侧.
研究方向:各方向
考试科目名称:609数学分析
考生注意:所有答案必须写在答题纸(卷)上,写在本试题上一律不给分。
1.求极限(每小题6分,总共36分)
(1) ;(2) ;
(3) ;(4) ;
(5) ;
(6)设函数 在区间 内具有二阶连续的导函数,且
求 .
2.求导数与微分(每小题7分,总共14分)
(1)已知 求 ;
4.求幂级数 的收敛域及和函数.(10分)
5.讨论二元函数
在(0,0)点的可微性. (9分)
6.证明题(第1-3小题每小题12分,第4小题11分,总共47分)
(1)证明不等式:
(2)设函数 在闭区间 上二次可导,且 证明:存在 使得
(3)设函数 满足: 对 在闭区间 上具有连续的导函数; 令
2010年暨南大学考研真题818有机化学B硕士学位研究生入学考试试卷
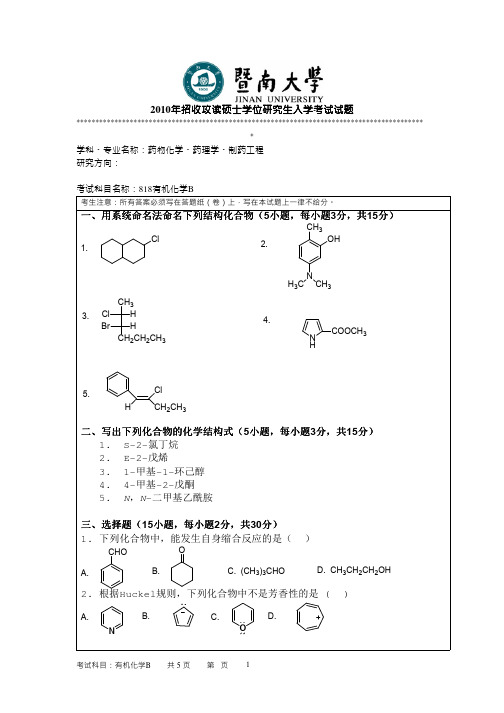
2010年招收攻读硕士学位研究生入学考试试题********************************************************************************************学科、专业名称:药物化学、药理学、制药工程研究方向:考试科目名称:818有机化学B考生注意:所有答案必须写在答题纸(卷)上,写在本试题上一律不给分。
一、用系统命名法命名下列结构化合物一、用系统命名法命名下列结构化合物((5小题小题,,每小题3分,共15分)Cl1. 2.CH3NH3C CH3OH3.CH3Cl HBr HCH2CH2CH34.NHCOOCH35.H CH2CH3Cl二、写出下列化合物的化学结构式二、写出下列化合物的化学结构式((5小题小题,,每小题3分,共15分)1. S-2-氯丁烷2. E-2-戊烯3. 1-甲基-1-环己醇4. 4-甲基-2-戊酮5. N,N-二甲基乙酰胺三、选择题三、选择题((15小题小题,,每小题2分,共30分)1. 下列化合物中,能发生自身缩合反应的是()OCHOA. B. C. (CH3)3CHO D. CH3CH2CH2OH2. 根据Huckel规则,下列化合物中不是芳香性的是 ( )A.N B. C. D.O3. 指出下列结构中最稳定的结构( )OHCH 3CH 3A.B.C.D.4. 下列化合物中,哪一个最容易发生S N 2反应( )FClBrIA.B.C.D.5. 由大到小排列以下化合物与1, 3-丁二烯发生Diels-Alder 反应的活性次序( )I. CH 2=CHCH 2Cl; II. CH 2=CHCH 2CN; III. CH 2=CHCH 2CH 3; IV. CH 2=CHCHO A. I > II > IV > III; B. IV > II > I > III; C. III > II > I > IV; D. IV > I > III > II6.下列化合物中,哪一个最容易发生亲电加成反应( )A. (CH 3)2C=CH-CH 3B. (CH 3)2C=CH 2C. CH 3-CH=CH-CHOD. CH 2=CH-Cl 7. 下列化合物中,能发生碘仿反应的是( )OH OOHCH 3CH 3CH 2CH 2CHOA.B.C.D.8. 下列水溶液中碱性最强的是( )A. 甲乙胺B. 对氨基苯甲酸C. 对氨基苯乙酮D. 苯胺9. 下列化合物中碱性最强的是( )NNNH 2N HA.B.C.D.10. 下列化合物中酸性最强的是( )OHCH 3OHNO 2OHCl OHNO 2NO 2A.B.C.D.11. 下列化合物中最不稳定的是( )O O O OHA. B. C. D.12. 下列化合物中最易发生硝化反应的是()A. 苯B. 溴苯C. 硝基苯D. 甲苯13. 下列化合物中能发生银镜反应的是()A. 环已酮B. 丙醇C. 丙醛D. 异丙醇14. 下列化合物中,不与三氯化铁溶液显色的是()OH OCH3OHA. B. C. D. CH3COCH2COOC2H515. 下列化合物中,有旋光性的是()OH OHOH OHOH OHOHOHA. B. C. D.四、完成下列反应式四、完成下列反应式((每空格2分,共50分)1.+OOO AlCl32.Br2 3.+CH2BrCH2Br ∆COOC2H5COOC2H52 NaOEt(1)H2O/OH-(2) H+ /∆4.CH3CH3NBS过氧化物KCNHCl, H2O SOCl2AlCl3 5.CH3COClAlCl3CHO稀OH-HO OH干HClH2/ Ni H2O/H+∆6.COOC2H5LiAlH4PBr3Mg / ether(1) CO2(2) H3O+7.NH2CH3过量CH3I AgOH∆8.H3C OsO4 , H2O9.OO过量CH2I2Zn(Cu) Ph3P=CH2五、简答题(2小题小题,,共20分)1、(10分)顺-1,2-环戊二醇和丙酮及少量酸的混合物进行回流,用分水器不断除水,获得分子式为C8H14O2的产物(A),(A)对碱稳定,遇稀酸生成原料(即顺-1,2-环戊二醇)。
2010年暨南大学803西方经济学考研真题详解

2010年暨南大学803西方经济学考研真题详解跨考网独家整理最全经济学考研真题资料库,您可以在这里查阅历年经济学考研真题,经济学考研资料,经济学参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行解答。
一、简答题(共6题,每题10分,共60分)1.列举影响财政政策挤出效应的因素,并解释这些因素如何影响挤出效应。
【分析】本题作答可参见高鸿业《西方经济学(宏观部分)》(第5版)教材第十五章“宏观经济政策分析”。
对于教材中标明第一、第二等的知识点,建议掌握,特别容易出简答题。
【答案】挤出效应是指政府支出增加所引起的私人消费或投资降低的效果。
影响财政政策挤出效应的因素有支出乘数的大小、货币需求对产出变动的敏感程度、货币需求对利率变动的敏感程度、投资需求对利率变动的敏感程度。
(1)支出乘数的大小支出乘数越大,政府支出所引起的产出增加越多,但利率提高使投资减少所引起的国民收入减少也越多,即挤出效应越大。
(2)货币需求对产出变动的敏感程度。
货币需求对产出变动的敏感程度即货币需求函数(L ky hr=-)中的k的大小。
k越大,政府支出增加所引起的一定量产出水平增加所导致的对货币的需求(交易需求)的增加也越大,因而使利率上升也越多,从而挤出效应也就越大。
(3)货币需求对利率变动的敏感程度货币需求对利率变动的敏感程度即货币需求函数中h的大小,也就是货币需求的利率系数的大小。
这一系数越小,说明货币需求稍有变动,就会引起利率大幅度变动。
因此,当政府支出增加引起货币需求增加所导致的利率上升就越多,因而对投资的“挤占”也就越多。
相反,如果h越大,则挤出效应就越小。
(4)投资需求对利率变动的敏感程度投资需求对利率变动的敏感程度即投资的利率系数的大小(i e dr=-)。
暨南大学810高等代数历年考研真题专业课考试试题

2016年暨南大学810高等代数考研 真题
2017年暨南大学810高等代数考研 真题
2018年暨南大学810高等代数考研 真题
2019年暨南大学810高等代数考研 真题
2010年暨南大学810高等代数考研 真题
2011年暨南大学810高等代数考研 真题
2012年暨南大学810高等代数考研 真题
2013年暨南大学810高等代数考研 真题
2014年暨南大学810高等代数考研 真题
2015年暨南大学810高等代数考研 真题
目Hale Waihona Puke 录2010年暨南大学810高等代数考研真题 2011年暨南大学810高等代数考研真题 2012年暨南大学810高等代数考研真题 2013年暨南大学810高等代数考研真题 2014年暨南大学810高等代数考研真题 2015年暨南大学810高等代数考研真题 2016年暨南大学810高等代数考研真题 2017年暨南大学810高等代数考研真题 2018年暨南大学810高等代数考研真题 2019年暨南大学810高等代数考研真题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(10
分)
5.
讨论二元函数 f :
x2 y , x2 + y2 ≠ 0 2 2 f ( x, y ) = x + y 0, x 2 + y 2 = 0
6.
在(0,0)点的可微性. (9 分) 证明题 (第 1-3 小题每小题 12 分, 第 4 小题 11 分, 总共 47 分) 1 1 π ≤ +1− (0 < x ≤ ). (1) 证明不等式: sin x x π 2 (2) 设函数 f 在闭区间 [ −1,1] 上二次可导 , 且 f ( −1) = 0, f (0) = 0, f (1) = 1. 证明 : 存在θ ∈ (−1,1) 使得 f ′′(θ ) = 1. (3) 设函数 f 满足 : (i ) 对 ∀x ∈ [ a, b], f ( x) ∈ [a, b]; (ii ) 在闭区间 [ a, b] 上具有连 续的导函数; (iii) | f ′( x) | ≤ 1, x ∈ [a, b]. 令
(1,1)
x
(0,0)
考试科目: 数学分析 (4) 计算 ∫∫ yzdydz + ( x
S
2
+ z 2 ) ydzdx + xydxdy,
其中 S 为曲面 4 − y = x
共 2 页, 第 2 页
2
+ z2
上
y≥0
∞
的那部分取正侧.
n
4.
1 求幂级数 ∑ (nn++2)! x 的收敛域及和函数.
1 x2 lim x → 0 (1 + cos x ) arctan x 2sin x + x 3 cos
lim ∫
y →0 3+ y y 2 +1
; ;
(3)
e x + e− x lim x − x x →+∞ e − e
lim ∑
n →∞ i =1 n
e2 x
;
(4)
x3 ln(e + xy 2 ) dx
2 2 2
xn +1 = f ( xn ) (n = 1, 2,..., x1 ∈ [a, b]).
证明数列{x } 收敛于 α , 其中 α 满足 f (α ) = α . (4) 设函数 z = f ( x, y ) 在矩形闭域 [ a, b] × [c, d ] 上连续 , 上其值含于 [a, b] 内的可微函数. 令
2010 年招收攻读硕士学位 年招收攻读硕士学位研究生 攻读硕士学位研究生入学考试试题 研究生入学考试试题( 入学考试试题(副卷) 副卷)
学科、专业名称:数学学科、基础数学专业、概率论与数理统计专业、应用数学专业 研究方向:各方向 考试科目名称:609 数学分析
考生注意:所有答案必须写在答题纸(卷)上,写在本试题上一律不给分。
1.
*******************************************************************************************
求极限 (每小题 6 分, 总共 36 分)
(1)
lim n a n + bn (a, b > 0)
n →∞
;
(2)
n
x = ϕ (t )
为定义在 [α , β ]
F (t , y ) = ∫
ϕ (t )
a
f ( x, y )dx ((t , y ) ∈ [α , β ] × [c, d ]).
证明: F 在 [α , β ] × [c, d ] 上连续.
(2)
2y
x
求 lim ( g ( 2x )) .
x x →+∞
3.
(1)
∫
2 + x − x 2 dx x
1 0
;
dx
(2)
瑕积分 ∫
x2 1 − x2
是否收敛? 若收敛, 求其积分值;
x C
(3)
设 w = g (u) 为连续可微函数, 若曲线积分 ∫ y(e + 2 g ( x))dx − g ( x)dy 与路径 无关, 且 g (0) = 1 , 求 ∫ y(e + 2 g ( x))dx − g ( x)dy.
(5)
i n + i2
2
;
(6)
设函数 g 在区间 (−∞, +∞) 内具有二阶连续的导函数, 且 g (0) = 1, g ′(0) = 0,
g ′′(0) = −1.
2.
求导数与微分 (每小题 7 分, 总共 14 分) (1) 已知 f ( x ) = (1 − x )(2 − x ) ⋅⋅⋅ (100 − x), 求 f ′(1) ; 求由方程 x − (2 y) = 0 ( x, y > 0) 所确定的函数 y = y( x) 的微分. 计算积分 (第 1,2 小题每小题 7 分, 第 3,4 小题每小题 10 分, 总共 34 分)
