高中数学毕业会考分章节复习练习题精选文档
高中数学毕业会考分章节复习练习题

高中数学毕业会考分章节复习练习题Revised at 2 pm on December 25, 2020.高二数学会考复习练习(1)<集合 简易逻辑 函数>一 选择题(没小题5分,共60分)1 设全集{}{}{}2,3,5,2,5,5U U A a C A ==-=,则a 的值是2 设集合1/2A x x ⎧⎫=<⎨⎬⎩⎭,1/3B x x ⎧⎫=>⎨⎬⎩⎭,则A B = A 11/32x x ⎧⎫<<⎨⎬⎩⎭B 1/2x x ⎧⎫>⎨⎬⎩⎭ C 1/3x x ⎧<-⎨⎩或13x ⎫>⎬⎭ D 1/3x x ⎧<-⎨⎩或12x ⎫>⎬⎭ 3 不等式1273x ≤-<的解集为A {}/45x x ≤<B {/4x x ≥或}5x ≤C {/3x x ≤或}2x >D {/23x x <≤或}45x ≤< 4 若不等式232x x a -++≥-的解集为实数R,则实数a 的取值范围为A 3a -≤B 3a ≤C 32a -≤≤D 5a ≥-5 p :12,x x 是方程2560x x +-=的两根;q :125x x +=-.则p 是q 的A 充分但不必要条件B 必要但不充分条件C 充要条件D 既不充分也不必要条件 6 已知(),x y 在映射f 的作用下的象是(,)x y x y +-,则在f 的作用下()1,2的原象是A ()1,2B ()3,1-C 31,22⎛⎫- ⎪⎝⎭D 13,22⎛⎫- ⎪⎝⎭7 已知函数()22(2)5f x x a x =+-+在区间()4,+∞上是增函数,则实数a 的取值范围是 A 2a ≤- B 2a ≥- C 6a ≤- D 6a ≥-8 若函数()f x 的定义域为[]2,4-,则函数()()()g x f x f x =+-的定义域为A []4,4-B []2,2-C []4,2--D []2,49 已知函数()y f x =的反函数()112x f x -+=,则()1f =A 0B 1C 1-D 410 若2log 15a <,则实数a 的取值范围为A 20,5⎛⎫ ⎪⎝⎭B ()20,1,5⎛⎫+∞ ⎪⎝⎭C 2,15⎛⎫ ⎪⎝⎭D 2,5⎛⎫+∞ ⎪⎝⎭ 11 函数()()212log 2f x x x =-的单调递减区间为A (),0-∞B ()2,+∞C (],1-∞D [)1,+∞12 函数()1log 1a x f x x+=-()0,1a a >≠是 A 非奇非偶函数 B 偶函数 C 奇函数 D 既是奇函数,又是偶函数二 填空题(每题5分共30分)13 集合{}22,a a a -有4个子集,则a 的取值范围为14 若集合{}1,2,3A =则满足A B A =的集合B 的个数是 个15 不等式2312x x ->-的解集为 16 若不等式20x ax b ++>的解集为{/1x x <或}2x >,则a= ,b=17 已知函数()()1,0,1x f x x x -=∈+∞+,则它的反函数()1f x -的定义域为 18 已知()214f x x x +=+,则()f x =三 解答题(每小题10分共60分)19 求下列各不等式的解集: (1) 123x x ->- (2) 22301x x x --≥- 20 求证:()[]22f x x x =-+在区间1,2上是减函数21 设()f x 是定义在R 上的偶函数,且在区间(),0-∞上为增函数,又()()2232121f a a f a a -+>++ 求a 的取值范围.22 求函数()1f x =23 画出下列图象(1) ()22f x x x =- (]2,2x ∈- (2) ()2log f x x =23 已知:22329x y x +=,求22x y +的最大值与最小值高二数学会考复习练习(2)〈数列〉一 选择题(每题5分,共60分)1 已知等比数列{}n a 的公比13q =-,则代数式13572468a a a a a a a a ++++++= A 3- B 13- C 13D 3 2 设等差数列{}n a 的公差为d ,若它的前n 项和2n s n =-则A 21;2n a n d =-=-B 21;2n a n d =-=C 21;2n a n d =-+=-D 21;2n a n d =-+=3 等比数列公比为2,前4项之和为1,则它的前8项之和为A 15B 17C 19D 214 设x y ≠,且两数列12,,,x a a y 及123,,,,x b b b y 都是等差数列,则1212a ab b --= A 34 B 45 C 43 D 54 5 数列{}n a 是公差为2-的等差数列,若1479750a a a a ++++=则36999a a a a ++++等于 A 182- B 78- C 148- D 82-6 公差不为0的等差数列的第2,3,6项组成等比数列,则公比为A 1B 2C 3D 4 7 1111242n ++++= A 11122n +- B 122n - C 112n - D 1122n -- 8 数列{}n a 和{}n b 都是等差数列1110010025,75,100a b a b ==+=则数列{}n n a b +的前100项之和为A 0B 100C 10000D 5050009 数列{}n a 中。
高中毕业会考复习之高二数学排列、组合和概率练习 人教版

高中毕业会考复习之高二数学排列、组合和概率练习 人教版(一)选择题(每小题5分,共60分)1、已知集合A={1,3,5,7,9,11},B={1,7,17}.试以集合A 和B 中各取一个数作为点的坐标,在同一直角坐标系中所确定的不同点的个数是A .32 B.33 C.34 D.362、以1,2,3,…,9这九个数学中任取两个,其中一个作底数,另一个作真数,则可以得到不同的对数值的个数为A 、64B 、56C 、53D 、513、四名男生三名女生排成一排,若三名女生中有两名站在一起,但三名女生不能全排在一起,则不同的排法数有A 、3600B 、3200C 、3080D 、28804、由1003)2x 3(+展开所得x 多项式中,系数为有理项的共有A 、50项B 、17项C 、16项D 、15项5、设有甲、乙两把不相同的锁,甲锁配有2把钥匙,乙锁配有2把钥匙,这4把钥匙与不能开这两把锁的2把钥匙混在一起,从中任取2把钥匙能打开2把锁的概率是A 、4/15B 、2/5C 、1/3D 、2/36、在所有的两位数中,任取一个数,则这个数能被2或3整除的概率是A 、5/6B 、4/5C 、2/3D 、1/27、先后抛掷三枚均匀的硬币,至少出现一次正面的概率是A 、1/8B 、3/8C 、7/8D 、5/88、在四次独立重复试验中,随机事件A 恰好发生1次的概率不大于其恰好发生两次的概率,则事件A 在一次试验中发生的概率中的取值范围是A 、[0.4,1)B 、(0,0.4]C 、(0,0.6)D 、[0.6,1]9、若1001002210100x a x a x a a )3x 2(++++=+ ,则(a 0+a 2+a 4+…+a 100)2-(a 1+a 3+…+a 99)2的值为A 、1B 、-1C 、0D 、210、集合A={x|1≤x ≤7,且x ∈N *}中任取3个数,这3个数的和恰好能被3整除的概率是A 、19/68B 、13/35C 、4/13D 、9/3411、某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘,根据需要至少买3片软件,至少买2盒磁盘,则不同的选购方式共有A 、5种B 、6种C 、7种D 、8种12、已知xy<0,且x+y=1,而(x+y)9按x 的降幂排列的展开式中,T 2≤T 3,则x 的取值范围是A 、)51,(-∞B 、),54[+∞C 、),1(+∞D 、]54,(--∞ (二)填空题(每小题4分,共16分)13、已知A 、B 是互相独立事件,C 与A ,B 分别是互斥事件,已知P(A)=0.2,P(B)=0.6,P(C)=0.14,则A 、B 、C 至少有一个发生的概率P(A+B+C)=____________。
高中数学会考专题训练大全完全版

.高中数学会考函数的概念与性质专题训练一、选择题:Y1fX是定义域到值域的函数,则下面四个结论中正确的是:、映射→YY BX A 中有不同的象中的元素不一定有原象、中不同的元素在、 D CY 、以上结论都不对可以是空集、2、下列各组函数中,表示同一函数的是2xy?lg?y2lgx与2 A B 、、|xy?x与y?|))(2x?3(x?02??xy?与y1?与yy?x C D、、3?x??x1y3 、函数的定义域是) (1,+[0,+] D A(,+) B[1,+ C、)、、、????????)4(fx?f(x)y?y? 4(01), 的反函数的图象必过点、若函数的图象过点则, 4 D141 C14 A41 B),,)),—、(—、(、(、(,—)x)1且a?b(a?y?a0?b与函数y?ax? 5的图像有可能是、函数yyyyxxxxOO O ODC B A2 6的单调递减区间是、函数x?y?1?41111????????,,????,0,?0?? A B C D 、、、、??????2222??????????Rx?y=f(x)f(x) 7图象上的是、函数是偶函数,则下列各点中必在????????)?a,?ffa,?(?a)(a(aa?,f()a?,?fa)? C B A D 、、、、8f(x)[37]5f(x)[73] 上是,那么,-上是增函数且最大值为、如果奇函数在区间在区间,-A5 B5 、增函数且最大值是-、增函数且最小值是-D 55 C 、减函数且最小值是-、减函数且最大值是-y?f(x)[094] 上单调递减,则有、偶函数在区间,;...????)?f(?f()?f(?1f(?1)?f()?f(?))BA 、、33????)()?f(?1)?f(f(?)?f(?1)?f()?f CD 、、33)72?nf()?m,f(3)(ab)?f(a)?f(b)f.(2f(x)f 10的值为满足、若函数,且,则n?m23n?3m3m?2n2 B ACD n?m、、、、2)xf(y?f(x)3?2?xx?f(x)0xx?0?11 的解析式,则当、已知函数时,为奇函数,且当时2232x??x????xf?2x?3(x))f(x B A 、、2232x(fx)?x??2x?3?x??f(x) D C 、、12、某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程。
高中会考练习题及讲解数学

高中会考练习题及讲解数学### 高中数学会考练习题及讲解#### 一、选择题1. 题目:已知函数 \( f(x) = 3x^2 - 4x + 5 \),求导数 \( f'(x) \)。
选项:A. \( 6x - 4 \)B. \( 9x - 4 \)C. \( 3x + 1 \)D. \( 6x + 2 \)2. 题目:已知三角形 ABC 的三边长分别为 a, b, c,且满足\( a^2 + b^2 = c^2 \),该三角形是:选项:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定#### 二、填空题1. 题目:圆的面积公式为 \( A = πr^2 \),如果半径 r = 4,那么圆的面积是 ________。
2. 题目:已知等差数列的首项为 2,公差为 3,求第 10 项的值。
#### 三、解答题1. 题目:解不等式 \( |x - 3| + |x + 2| \geq 5 \)。
2. 题目:已知函数 \( y = x^3 - 3x^2 + 2 \),求函数的极值点。
#### 四、综合题1. 题目:某工厂生产一种产品,其成本函数为 \( C(x) = 1000 +50x \),收入函数为 \( R(x) = 150x - x^2 \)。
求工厂的盈利函数\( P(x) \) 并找出盈利最大时的产量 x。
#### 练习题讲解1. 选择题讲解:- 第一题:求导数,\( f'(x) = 6x - 4 \),故选 A。
- 第二题:根据勾股定理的逆定理,是直角三角形,故选 B。
2. 填空题讲解:- 第一题:将 r = 4 代入面积公式,得 \( A = 16π \)。
- 第二题:等差数列的第 n 项公式为 \( a_n = a_1 + (n - 1)d \),代入得 \( a_{10} = 2 + 3 \times (10 - 1) = 29 \)。
3. 解答题讲解:- 第一题:分情况讨论,当x ≤ -2 时,不等式变为 \( -2x - 1 \geq 5 \);当 -2 < x < 3 时,不等式变为 \( 5 \geq 5 \),恒成立;当x ≥ 3 时,不等式变为 \( 2x + 1 \geq 5 \),解得x ≥ 2。
高中数学会考习题集

高中数学会考练习题集集合与函数(一)1. 已知S ={1,2,3,4,5},A ={1,2},B ={2,3,6},则______=B A ,______=B A ,______)(=B A C S .2. 已知},31|{},21|{<<=<<-=x x B x x A则______=B A ,______=B A .3. 集合},,,{d c b a 的所有子集个数是_____,含有2个元素子集个数是_____.4. 图中阴影部分的集合表示正确的有________.(1))(B A C U (2))(B A C U(3))()(B C A C U U (4))()(B C A C U U5. 已知},6|),{(},4|),{(=+==-=y x y x B y x y x A ________B A =则 .6. 下列表达式正确的有__________.(1)A B A B A =⇒⊆ (2)B A A B A ⊆⇒=(3)A A C A U =)( (4)U A C A U =)(7. 若}2,1{≠⊂}4,3,2,1{⊆A ,则满足A 集合的个数为____.8. 下列函数可以表示同一函数的有________.(1)2)()(,)(x x g x x f == (2)2)(,)(x x g x x f ==(3)x x x g x x f 0)(,1)(== (4))1()(,1)(+=+⋅=x x x g x x x f 9. 函数x x x f -+-=32)(的定义域为________.10. 函数291)(x x f -=的定义域为________.11. 若函数_____)1(,)(2=+=x f x x f 则.12. 已知_______)(,12)1(=-=+x f x x f 则.13. 已知1)(-=x x f ,则______)2(=f .14. 已知⎩⎨⎧≥<=0,20,)(2x x x x f ,则_____)0(=f _____)]1([=-f f .15. 函数xy 2-=的值域为________. 16. 函数R x x y ∈+=,12的值域为________.17. 函数)3,0(,22∈-=x x x y 的值域为________.18. 下列函数在),0(+∞上是减函数的有__________.(1)12+=x y (2)xy 2=(3)x x y 22+-= (4)12+--=x x y 19. 下列函数为奇函数的有________.(1)1+=x y (2)x x y -=2 (3)1=y (4)xy 1-= 20. 将函数xy 1=的图象向左平移2个单位,再向下平移1个单位,则对应 图象的解析式为 .21.已知全集I ={1,2,3,4,5,6},A ={1,2,3,4},B ={3,4,5,6}, 那么C I (A ∩B )=( ).A.{3,4}B.{1,2,5,6}C.{1,2,3,4,5,6}D.Ф22. 设集合M ={1,2,3,4,5},集合N ={9|2≤x x },M ∩N =( ).A.{33|≤≤-x x }B.{1,2}C.{1,2,3}D.{31|≤≤x x }23 设集合M ={-2,0,2},N ={0},则( ).A .N 为空集 B. N ∈M C. N ⊂M D. M ⊂N 24. 函数y =)1lg(2-x 的定义域是__________________.25已知函数f (x )=log 3(8x +7),那么f (21)等于_______________. 26. 与函数y = x 有相同图象的一个函数是( ).A .y =x 2 B. y =x 2x C. y =a log a x (a >0, a ≠1) D. y = log a a x (a>0, a≠1)27. 下列函数中,在区间(0,+∞)上是增函数的是( ).A.y =-x 2B.y = x 2-x +2C.y =(21)xD.y =x 1log 3.0 28. 函数y =)(log 2x -是( ).A. 在区间(-∞,0)上的增函数B. 在区间(-∞,0)上的减函数C. 在区间(0,+∞)上的增函数D. 在区间(0,+∞)上的减函数29. 函数f (x )=3x -13x +1 ( ).A. 是偶函数,但不是奇函数B. 是奇函数,但不是偶函数C. 既是奇函数,又是偶函数D.不是奇函数,也不是偶函数30. 下列函数中为奇函数的是( ).A. f (x )=x 2+x -1B. f (x )=|x |C. f (x )=23x x +D. f (x )=522x x -- 31. 设函数f (x )=(m -1)x 2+(m +1)x +3是偶函数,则m=________.32. 已知函数f (x )=||2x ,那么函数f (x )( ).A. 是奇函数,且在(-∞,0)上是增函数B. 是偶函数,且在(-∞,0)上是减函数C. 是奇函数,且在(0,+∞)上是增函数D. 是偶函数,且在(0,+∞)上是减函数33. 函数y =||log 3x (x ∈R 且x ≠0)( ) .A. 为奇函数且在(-∞,0)上是减函数B. 为奇函数且在(-∞,0)上是增函数C. 是偶函数且在(0,+∞)上是减函数D. 是偶函数且在(0,+∞)上是增函数34. 若f (x )是以4为周期的奇函数,且f (-1)=a (a ≠0),则f (5)的值等于( ).A. 5aB. -aC. aD. 1-a35. 如果函数y =x a log 的图象过点(91,2),则a =___________. 36.下列函数中有2个零点的是 ( )(A) lg y x = (B) 2x y = (C) 2y x = (D) 1y x =-37.函数()lg 27f x x x =+-的零点个数 38. 若1log 21>x ,则x 的取值范围是( ).A. 21<xB.210<<xC.21>x D.0<x 39.若指数函数x a y =在[-1,1]上的最大值与最小值的差是1,则底数a 等于 ( )A .251+B . 251+-C .251±D . 215± 40.函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ,满足1)(>x f 的x 的取值范围( )A .)1,1(-B ),1(+∞-C .}20|{-<>x x x 或D .}11|{-<>x x x 或数列(一)1. 已知数列{n a }中,12=a ,121+=+n n a a ,则=1a ______.2. – 81是等差数列 – 5 , – 9 , – 13 , … 的第( )项.3. 若某一数列的通项公式为n a n 41-=,则它的前50项的和为______.4. 等比数列,271,91,31,1…的通项公式为________. 5. 等比数列,54,18,6,2…的前n 项和公式n S =__________.6. 12-与12+的等比中项为__________.7. 若a ,b ,c 成等差数列,且8=++c b a ,则b = .8. 等差数列{a n }中,a 3+ a 4+ a 5+ a 6+ a 7=150,则a 2+a 8= .9. 在等差数列{a n }中,若a 5=2,a 10=10,则a 15=________.10. 在等差数列{a n }中,,56=a 583=+a a , 则=9S _____.10. 数列1781,1327,99,53,11,…的一个通项公式为________. 11. 在等比数列中,各项均为正数,且962=a a ,则)(log 54331a a a = .12. 等差数列中,2,241-==d a , 则n S =___________.13. 已知数列{ a n }的前项和为S n = 2n 2 – n ,则该数列的通项公式为_______.14. 已知三个数成等比数列,它们的和为14,它们的积为64,则这三个数为 .15. 在等差数列}{n a 中,85=a ,前5项的和105=S ,它的首项是__________,公差是__________.16. 在公比为2的等比数列中,前4项的和为45,则首项为_____.17. 在等差数列}{n a 中,已知1554321=++++a a a a a ,则42a a +=_______.18. 在等差数列}{n a 中,已知前n 项的和n n S n -=24, 则=20a _____.19. 在等差数列}{n a 公差为2,前20项和等于100,那么20642...a a a a ++++等于________.20. 已知数列}{n a 中的3231+=+n n a a ,且2053=+a a ,则=8a _______. 21. 已知数列}{n a 满足n n a a =-+21,且11=a ,则通项公式=n a ______.22. 数列}{n a 中,如果)1(21≥=+n a a n n ,且21=a ,那么数列的前5项和=5S _.23. 两数15-和15+的等比中项是__________________.24. 等差数列}{n a 通项公式为72-=n a n ,那么从第10项到第15项的和为___.25. 在各项均为正数的等比数列中,若551=a a ,则=)(log 4325a a a ________.三角函数1. 下列说法正确的有____________.(1)终边相同的角一定相等(2)锐角是第一象限角(3)第二象限角为钝角(4)小于︒90的角一定为锐角 (5)第二象限的角一定大于第一象限的角2. 已知角x 的终边与角︒30的终边关于y 轴对称,则角x 的集合可以表示为__________________________.3. 终边在y 轴上角的集合可以表示为________________________.4. 终边在第三象限的角可以表示为________________________.5. 在︒︒-720~360之间,与角︒175终边相同的角有__________________.6. 在半径为2的圆中,弧度数为3π的圆心角所对的弧长为________,扇形面积为__________.7. 已知角α的终边经过点(3,-4),则sin α=______ , cos α=______,tan α=_______ .8. 已知0cos 0sin ><θθ且,则角θ一定在第______象限.10. 计算:πππ2cos cos 0tan 20sin 1223cos 7-+++=________. 11. 化简:tan cos ____θθ=.12. 已知,54cos -=α 且α为第三象限角,则_____tan _____,sin ==αα . 13. 已知31tan =α,且23παπ<<,则_____cos _____,sin ==αα .14. 已知2tan =α,则____sin cos cos 2sin =+-αααα. 15. 计算:_____)317sin(=-π, _____)417cos(=-π. 16. 化简:____)cos()sin()2sin()cos(=----++αππαπααπ. 17. 求值: ︒165cos =________,=︒-)15tan(________.18. 已知21cos -=θ,θ为第三象限角,则=+)3sin(θπ________, =+)3cos(θπ________,=+)3tan(θπ________. 19. 已知x tan ,y tan 是方程0762=++x x 的两个根,则=+)tan(y x ______.20. 已知31sin =α,α为第二象限角,则=α2sin ______, =α2cos ______,=α2tan ______.21. 已知21tan =α,则=α2tan ______. 22. 化简或求值:=---y y x y y x cos )cos(sin )sin(______,=︒︒-︒︒170sin 20sin 10cos 70sin ______, =-ααsin 3cos ______, ____15tan 115tan 1=︒-︒+, _____5tan 65tan 35tan 65tan =︒︒-︒-︒, =︒︒15cos 15sin ____, =-2cos 2sin 22θθ______ 15.22cos 22-︒=______, ︒-︒150tan 1150tan 22=______. 23. 已知,3tan ,2tan ==ϕθ且ϕθ,都为锐角,则=+ϕθ______.24. 已知21cos sin =+θθ,则=θ2sin ______. 25. 已知41sin =θ,则=-θθ44cos sin ______. 26. 在ABC ∆中,若,53sin ,135cos =-=B A 则=C sin ________. 27. 函数)4sin(π+=x y 的图象的一个对称中心是( ).A. )0,0(B. )1,4(πC. )1,43(πD. )0,43(π28. 函数)3cos(π-=x y 的图象的一条对称轴是( ).A. y 轴B. 3π-=x C. 65π=x D. 3π=x 29. 函数x x y cos sin =的值域是________,周期是______,此函数的为____函数(填奇偶性).30. 函数x x y cos sin -=的值域是________,周期是______,此函数的为____函数(填奇偶性).31. 函数x x y cos 3sin +=的值域是________,周期是______,此函数的为____函数(填奇偶性).32. 函数)42tan(3π-=x y 的定义域是__________________,值域是________,周期是______,此函数为______函数(填奇偶性).33. 比较大小:︒︒530cos ___515cos , )914sin(____)815sin(ππ-- ︒︒143t a n ____138t a n , ︒︒91tan ___89tan 34. 要得到函数)42sin(2π+=x y 的图象,只需将x y 2sin 2=的图象上各点____35. 将函数x y 2cos =的图象向左平移6π个单位,得到图象对应的函数解析式为________________.36. 已知22cos -=θ,)20(πθ<<,则θ可能的值有_________. 37. 在π2~0范围内,与π310终边相同的角是___________. 38. 若sinα<0且cosα<0 ,则α为第____象限角.39. 在︒︒-360~360之间,与角︒175终边相同的角有_______________.40. 在半径为2的圆中,弧度数为3π的圆心角所对的弧长为______________. 41. 已知角α的终边经过点(3,-4),则cos α=______. 42. sin(π617-)的值等于___________. 43. 设π4 <α<π2 ,角α的正弦. 余弦和正切的值分别为a ,b ,c ,则( ). A. a <b <c B. b <a <c C. a <c <b D. c <b <a44. 已知,54cos -=α 且α为第三象限角,则_____tan =α. 45. 若 tan α=2且sin α<0,则cos α的值等于_____________.46. 要得到函数y =sin(2x -π3 )的图象,只要把函数y =sin2x 的图象( ).A.向左平移π3 个单位B. 向右平移π3 个单位C.向左平移π6 个单位D. 向右平移π6 个单位47. 已知tan α=-3 (0<α<2π),那么角α所有可能的值是___________48. 化简cos x sin(y -x )+cos(y -x )sin x 等于_____________49. cos25o cos35o –sin25o sin35o 的值等于_____________(写具体值).50. 函数y =sin x +cos x 的值域是( )A.[-1,1]B.[-2,2]C.[-1, 2 ]D.[- 2 , 2 ]51. 函数y =cos x - 3 sin x 的最小正周期是( )A.2π B. 4π C. π D.2π 52. 已知sin α=53,90o <α<180o ,那么sin2α的值__________. 53. 函数y=cos 2 x -sin 2x 的最小正周期是( )A. 4πB. 2πC. πD. π254. 函数y =sin x cos x 是( )A.周期为2π的奇函数B. 周期为2π的偶函数C. 周期为π的奇函数D. 周期为π的偶函数55. 已知2tan =α,则=α2tan ________.平面向量1. 下列说法正确的有______________.(1)零向量没有方向 (2)零向量和任意向量平行(3)单位向量都相等 (4)(a ·b )·c =a ·(b ·c )(5)若a ·c = b ·c ,且c 为非零向量,则a =b(6)若a ·b =0,则a,b 中至少有一个为零向量.2. 下列各式的运算结果为向量的有________________.(1)a +b (2)a -b (3)a ·b (4)λa (5)||b a + (6)a ·03 计算:=-++______.4. 如图,在ABC ∆中,BC 边上的中点为M ,设=AB a, =AC b ,用a , b 表示下列向量:=BC ________,=AM ________,=MB ________.5. 在□ABCD 中,对角线AC ,BD 交于O 点,设=AB a,= b ,用a , b 表示下列向量:=________,.=________,=________,=________.6. 已知21,e e 不共线,则下列每组中a , b 共线的有______________.(1)113,2e b e a -== (2)213,2e b e a -==(3)212121,2e e b e e a +-=-= (4)2121,e e b e e a +=-= 7. 已知,4||,3||==b a 且向量b a,的夹角为︒120,则=b a ·________, =-||b a __________.8 已知)1,1(),3,2(-==b a ,则=-b a 2______,=b a ·________, =||a ______,向量b a,的夹角的余弦值为_______.9. 已知)1,2(),2,1(-==b a k ,当b a,共线时,k =____;当b a,垂直时,k =____.10. 已知)4,2(),2,1(B A -,)3,(x C ,且A,B,C 三点共线,则x =______.11. 把点)5,3(P 按向量a =(4,5)平移至点P ’,则P ’的坐标为_______.12. 在ABC ∆中,︒=45A ,︒=105C ,5=a ,则b =_______.13. 在ABC ∆中,2=b ,1=c ,︒=45B ,则C =_______.14. 在ABC ∆中,32=a ,6=b ,︒=30A ,则B =_______.15.在ABC ∆中,3=a ,4=b ,37=c ,则这个三角形中最大的内角为______.16. 在ABC ∆中,1=a ,2=b ,︒=60C ,则c =_______.17. 在ABC ∆中,7=a ,3=c ,︒=120A ,则b =_______.18. 小船以10 3 km/h 的速度向垂直于对岸的方向行驶,同时河水的流速为10km/h ,则小船实际航行速度的大小为( ).A.20 2 km/hB.20km/hC. 10 2 km/hD. 10km/h19. 若向量→a =(1,1),→b =(1,-1),→c =(-1,2),则→c =( ).A. -12 →a +32 →bB. 12 →a -32 →bC. 32 →a -12 →bD.- 32 →a +12 →b20. 有以下四个命题:① 若→a ·→b =→a ·→c 且→a ≠→0,则→b =→c ;② 若→a ·→b =0,则→a =→0或→b =→0;③ ⊿ABC 中,若→AB ·→AC >0,则⊿ABC 是锐角三角形;④ ⊿ABC 中,若→AB ·→BC =0,则⊿ABC 是直角三角形.其中正确命题的个数是( ). A.0 B.1 C.2 D.321. 若|→a |=1,|→b |=2,→c =→a +→b ,且→c ⊥→a ,则向量→a 与→b 的夹角为( ).A.30oB.60oC.120o D150o22. 已知→a . →b 是两个单位向量,那么下列命题中真命题是( ).A. →a =→bB. →a ·→b =0C. |→a ·→b |<1D. →a 2=→b 223. 在⊿ABC 中,AB =4,BC =6,∠ABC =60o ,则AC 等于( ).A. 28B. 76C. 27D. 21924. 在⊿ABC 中,已知a = 3 +1, b =2, c = 2 ,那么角C 等于( ).A. 30oB. 45oC. 60oD. 120o25. 在⊿ABC 中,已知三个内角之比A :B :C =1:2:3,那么三边之比a :b :c =(). A. 1: 3 :2 B. 1:2:3 C. 2: 3 :1 D. 3:2:1不等式1. 不等式3|21|>-x 的解集是__________.2. 不等式2|1|≤-x 的解集是__________.3. 不等式42>x 的解集是__________.4. 不等式022>--x x 的解集是__________.5. 不等式012<++x x 的解集是__________.6. 不等式032≥--xx 的解集是__________. 7. 已知不等式02>++n mx x 的解集是}2,1|{>-<x x x 或,则m 和n 的值分别为__________.8. 不等式042>++mx x 对于任意x 值恒成立,则m 的取值范围为________.10. 已知64,52<<<<b a ,则b a +的取值范围是______________,则a b -的取值范围是______________,ab 的取值范围是___________. 11. 已知0,>b a 且,2=ab 则b a +的最___值为_______.12. 已知0,>b a 且,2=+b a 则ab 的最___值为_______.13. 已知,0>m 则函数mm y 82+=的最___值为_______, 此时m =_______.15. 若0<<b a ,则下列不等关系不能成立的是( ).A. b a 11>B. ab a 11>- C. ||||b a > D. 22b a > 16. 若0>>b a ,0>m ,则下列不等式中一定成立的是( ).A. m a m b a b ++>B. m b m a b a -->C. m a m b a b ++<D. mb m a b a --< 17. 若0>x ,则函数xx y 1+=的取值范围是( ). A.]2,(--∞ B. ),2[+∞ C. ),2[]2,(+∞--∞ D. ]2,2[-18. 若0≠x ,则函数22364x xy --=有( ). A. 最大值264- B. 最小值264-C. 最大值264+D. 最小值264+解析几何1. 已知直线l 的倾斜角为︒135,且过点)3,(),1,4(--m B A ,则m 的值为______.2. 已知直线l 的倾斜角为︒135,且过点)2,1(,则直线的方程为____________.3. 已知直线的斜率为4,且在x .轴.上的截距为2,此直线方程为____________.4. 直线023=+-y x 倾斜角为____________.5. 直线042=+-y x 与两坐标轴围成的三角形面积为__________.6. 直线042=+-y x 关于y 轴对称的直线方程为________________.7. 过点)3,2(P 且在两坐标轴上截距互为相反数的直线方程为_____________.8. 下列各组直线中,互相平行的有____________;互相垂直的有__________.(1)022121=+-+=y x x y 与 (2)0322=-+-=y x x y 与 (3)0322=--=y x x y 与 (4)023=++y x 与33+=x y(5)052052=+=+y x 与 (6)052052=-=+x x 与9. 过点(2,3)且平行于直线052=-+y x 的方程为________________. 过点(2,3)且垂直于直线052=-+y x 的方程为________________.10. 已知直线01:,022:21=--+=--+a y ax l a ay x l ,当两直线平行时, a =______;当两直线垂直时,a =______.11. 直线53=-y x 到直线032=-+y x 的角的大小为__________.12. 设直线0243:,022:,0243:321=+-=++=-+y x l y x l y x l ,则直线 21l l 与的交点到3l 的距离为____________.13. 平行于直线0243=-+y x 且到它的距离为1的直线方程为____________.14. 圆心在)2,1(-,半径为2的圆的标准方程为____________,一般方程为__________,参数方程为______________.15. 圆心在点)2,1(-,与y 轴相切的圆的方程为________________,与x 轴相切的圆的方程为________________,过原点的圆的方程为________________16. 半径为5,圆心在x 轴上且与x =3相切的圆的方程为______________.17. 已知一个圆的圆心在点)1,1(-,并与直线0334=+-y x 相切,则圆的方程为______.18. 点)1,1(-P 和圆024222=--++y x y x 的位置关系为________________.19. 已知4:22=+y x C 圆,(1)过点)3,1(-的圆的切线方程为________________.(2)过点)0,3(的圆的切线方程为________________.(3)过点)1,2(-的圆的切线方程为________________.(4)斜率为-1的圆的切线方程为__________________.20. 已知直线方程为043=++k y x ,圆的方程为05622=+-+x y x(1)若直线过圆心,则k =_________.(2)若直线和圆相切,则k =_________.(3)若直线和圆相交,则k 的取值范围是____________. (4)若直线和圆相离,则k 的取值范围是____________.21. 在圆822=+y x 内有一点)2,1(-P ,AB 为过点P 的弦.(1)过P 点的弦的最大弦长为__________.(2)过P 点的弦的最小弦长为__________.22. 如果直线l 与直线3x -4y +5=0关于y 轴对称,那么直线l 的方程为_____.23. 直线3x + y +1=0的倾斜角的大小是__________.24. 过点(1,-2)且倾斜角的余弦是-35 的直线方程是______________.25. 若两条直线l 1: ax +2y +6=0与l 2: x +(a -1)y +3=0平行,则a 等于_________.26. 过点(1,3)且垂直于直线052=-+y x 的方程为________________.27. 图中的阴影区域可以用不等式组表示为( ).A. ⎪⎩⎪⎨⎧≤+-≤≥0110y x y xB.⎪⎩⎪⎨⎧≤+-≥≤0101y x y x C. ⎪⎩⎪⎨⎧≥+-≥≤0101y x y x D. ⎪⎩⎪⎨⎧≥+-≥≥0101y x y x28. 已知圆的直径两端点为)4,3(),2,1(-,则圆的方程为_____________.29. 圆心在点)2,1(-且与x 轴相切的圆的方程为________________.。
高中数学会考习题集

高中数学会考练习题集集合与函数(一)1. 已知},31|{},21|{<<=<<-=x x B x x A 则______=B A ,______=B A .2. 集合},,,{d c b a 的所有子集个数是_____,含有2个元素子集个数是_____.3. 若}2,1{≠⊂}4,3,2,1{⊆A ,则满足A 集合的个数为____.4. 下列函数可以表示同一函数的有________.(1)2)()(,)(x x g x x f == (2)2)(,)(x x g x x f ==(3)xx x g x x f 0)(,1)(== (4))1()(,1)(+=+⋅=x x x g x x x f5. 函数x x x f -+-=32)(的定义域为________. 6 函数291)(xx f -=的定义域为________..7 已知⎩⎨⎧≥<=0,20,)(2x x x x f ,则_____)0(=f _____)]1([=-f f .8. 下列函数在),0(+∞上是减函数的有__________. (1)12+=x y (2)xy 2=(3)x x y 22+-= (4)12+--=x x y 9. 下列函数为奇函数的有________.(1)1+=x y (2)x x y -=2(3)1=y (4)xy 1-= 10. 将函数xy 1=的图象向左平移2个单位,再向下平移1个单位,则对应 图象的解析式为 .集合与函数(二)1. 已知全集I ={1,2,3,4,5,6},A ={1,2,3,4},B ={3,4,5,6},那么C I (A ∩B )=( ). A.{3,4} B.{1,2,5,6} C.{1,2,3,4,5,6} D.Ф2. 设集合M ={1,2,3,4,5},集合N ={9|2≤x x },M ∩N =( ). A.{33|≤≤-x x } B.{1,2} C.{1,2,3} D.{31|≤≤x x } 3. 函数y =)1lg(2-x 的定义域是__________________. 4. 已知函数f (x )=log 3(8x +7),那么f (21)等于_______________.5. 若f (x )=x + 1x ,则对任意不为零的实数x 恒成立的是( ).A. f (x )=f (-x )B. f (x )=f (x 1) C. f (x )=-f (x 1) D. f (x ) f (x1)=06. 与函数y = x 有相同图象的一个函数是( ).A .y =x 2B. y =x 2xC. y =a log a x (a >0, a ≠1)D. y = log a a x (a>0, a≠1)7. 在同一坐标系中,函数y =x 5.0log 与y =x 2log 的图象之间的关系是( ).A.关于原点对称B.关于x 轴对称C.关于直线y =1对称.D.关于y 轴对称 8. 下列函数中,在区间(0,+∞)上是增函数的是( ). A.y =-x 2 B.y = x 2-x +2 C.y =(21)xD.y =x1log 3.0 9. 函数y =)(log 2x -是( ).A. 在区间(-∞,0)上的增函数B. 在区间(-∞,0)上的减函数C. 在区间(0,+∞)上的增函数D. 在区间(0,+∞)上的减函数 10 设函数f (x )=(m -1)x 2+(m +1)x +3是偶函数,则m=________. 11. 已知函数f (x )=||2x ,那么函数f (x )( ).A. 是奇函数,且在(-∞,0)上是增函数B. 是偶函数,且在(-∞,0)上是减函数C. 是奇函数,且在(0,+∞)上是增函数D. 是偶函数,且在(0,+∞)上是减函数 12. 函数y =||log 3x (x ∈R 且x ≠0)( ) .A. 为奇函数且在(-∞,0)上是减函数B. 为奇函数且在(-∞,0)上是增函数C. 是偶函数且在(0,+∞)上是减函数D. 是偶函数且在(0,+∞)上是增函数 13. 如果函数y =x a log 的图象过点(91,2),则a =___________. 14. 设a =log 26.7, b =log 0.24.3, c =log 0.25.6,则a, b, c 的大小关系为( ) A. b <c <a B. a <c <b C. a <b <c D. c <b <a 15 若1log 21>x ,则x 的取值范围是( ).A. 21<x B.210<<x C.21>x D.0<x数列(一)1. 若某一数列的通项公式为n a n 41-=,则它的前50项的和为______. 2 等比数列,54,18,6,2…的前n 项和公式n S =__________. 312-与12+的等比中项为__________.4. 等差数列{a n }中,a 3+ a 4+ a 5+ a 6+ a 7=150,则a 2+a 8= .5. 在等差数列{a n }中,若a 5=2,a 10=10,则a 15=________.6. 在等差数列{a n }中,,56=a 583=+a a , 则=9S _____.7. 等差数列中,2,241-==d a , 则n S =___________.8 已知数列{ a n }的前项和为S n = 2n 2 – n ,则该数列的通项公式为_______.数列(二)1. 在等差数列}{n a 中,85=a ,前5项的和105=S ,它的首项是_______,公差是______. 2 在等差数列}{n a 中,已知1554321=++++a a a a a ,则42a a +=_______. 3. 在等差数列}{n a 中,已知前n 项的和n n S n -=24, 则=20a _____.4. 已知数列}{n a 中的3231+=+n n a a ,且2053=+a a ,则=8a _______. 5. 已知数列}{n a 满足n n a a =-+21,且11=a ,则通项公式=n a ______. 6 数列}{n a 中,如果)1(21≥=+n a a n n ,且21=a ,那么数列的前5项和=5S _.三角函数(一)1. 终边在y 轴上角的集合可以表示为________________________. 2 终边在第三象限的角可以表示为________________________.3. 在︒︒-720~360之间,与角︒175终边相同的角有__________________.4. 在半径为2的圆中,弧度数为3π的圆心角所对的弧长为________,扇形面积为__________. 5. 已知角α的终边经过点(3,-4),则sin α=______ , cos α=______,tan α=_______ . 6 已知0cos 0sin ><θθ且,则角θ一定在第______象限.7 已知,54cos -=α 且α为第三象限角,则_____tan _____,sin ==αα . 8 已知31tan =α,且23παπ<<,则_____cos _____,sin ==αα . 9. 已知2tan =α,则____sin cos cos 2sin =+-αααα. 10. 计算:_____)317sin(=-π, _____)417cos(=-π. 11 化简:____)cos()sin()2sin()cos(=----++αππαπααπ.三角函数(二) 1. 已知21cos -=θ,θ为第三象限角,则=+)3sin(θπ___, =+)3cos(θπ__,=+)3tan(θπ____.2 已知31sin =α,α为第二象限角,则=α2sin ______,=α2cos _____,=α2tan _____. 3. 化简或求值:=---y y x y y x cos )cos(sin )sin(______, =︒︒-︒︒170sin 20sin 10cos 70sin ______,.4 已知21cos sin =+θθ,则=θ2sin ______. 5. 在ABC ∆中,若,53sin ,135cos =-=B A 则=C sin ________.三角函数(三) 1. 函数)4sin(π+=x y 的图象的一个对称中心是( ).A. )0,0(B. )1,4(π C. )1,43(π D. )0,43(π2. 函数)3cos(π-=x y 的图象的一条对称轴是( ).A. y 轴B. 3π-=xC. 65π=xD. 3π=x3. 函数x x y cos sin =的值域是________,周期是______,此函数的为____函数(填奇偶性).4. 函数x x y cos sin -=的值域是________,周期是______,此函数的为____函数(填奇偶性).5. 函数x x y cos 3sin +=的值域是______,周期是______,此函数的为____函数(填奇偶性).6. 要得到函数)42sin(2π+=x y 的图象,只需将x y 2sin 2=的图象上各点____7. 将函数x y 2cos =的图象向左平移6π个单位,得到图象对应的函数解析式为___________平面向量(一)________________. (1)a +b (2)a -b (3)a ·b (4)λa (5)||b a + (6)a2 计算:=-++______.3. 如图,在ABC ∆中,BC 边上的中点为M ,设=a, = b ,用a , b 表示下列向量:=________,=________,=________.4. 在□ABCD 中,对角线AC ,BD 交于O 点,设=AB a, =AD b ,用a , b 表示下列向量:=AC ________,.=BD ________,=CO ________,=OB ________. 5. 已知21,e e 不共线,则下列每组中a , b 共线的有______________. (1)113,2e b e a -== (2)213,2e b e a -== (3)212121,2e e b e e a +-=-= (4)2121,e e b e e a +=-= 6. 已知,4||,3||==b a 且向量b a,的夹角为︒120,则=b a ·________,=-||b a __________. 7. 已知)1,1(),3,2(-==b a ,则=b a ·________, =||a ______,向量b a,的夹角的余弦值为_______.8. 已知)1,2(),2,1(-==b a k ,当b a,共线时,k =____;当b a,垂直时,k =____. 9. 已知)4,2(),2,1(B A -,)3,(x C ,且A,B,C 三点共线,则x =______. 10 在ABC ∆中,︒=45A ,︒=105C ,5=a ,则b =_______. 11. 在ABC ∆中,2=b ,1=c ,︒=45B ,则C =_______.12. 在ABC ∆中,32=a ,6=b ,︒=30A ,则B =_______. .13 在ABC ∆中,3=a ,4=b ,37=c ,则这个三角形中最大的内角为______.14 在ABC ∆中,1=a ,2=b ,︒=60C ,则c =_______. 中,7=a ,3=c ,︒=120A ,则b =_______.平面向量(二)1. 小船以10 3 km/h 的速度向垂直于对岸的方向行驶,同时河水的流速为10km/h ,则小船实际航行速度的大小为( ). A.20 2 km/h B.20km/h C. 10 2 km/h D. 10km/h2. 若向量→a =(1,1),→b =(1,-1),→c =(-1,2),则→c =( ).A. -12 →a +32 →bB. 12 →a -32 →bC. 32 →a -12 →bD.- 32 →a +12 →b3 已知→a . →b 是两个单位向量,那么下列命题中真命题是( ).A. →a =→bB. →a ·→b =0 C. |→a ·→b |<1 D. →a 2=→b 2 4. 在⊿ABC 中,AB =4,BC =6,∠ABC =60o ,则AC 等于( ).A. 28B. 76C. 27D. 2195 在⊿ABC 中,已知a = 3 +1, b =2, c = 2 ,那么角C 等于( ). A. 30o B. 45o C. 60o D. 120o6. 在⊿ABC 中,已知三个内角之比A :B :C =1:2:3,那么三边之比a :b :c =( ). A. 1: 3 :2 B. 1:2:3 C. 2: 3 :1 D. 3:2:1不等式1. 不等式3|21|>-x 的解集是__________. 2 不等式42>x 的解集是__________. 3不等式022>--x x 的解集是__________. 4. 不等式012<++x x 的解集是__________. 5. 不等式032≥--xx 的解集是__________. 6已知不等式02>++n mx x 的解集是}2,1|{>-<x x x 或,则m 和n 的值分别为__________.7 已知d c b a >>,,下列命题是真命题的有_______________. (1)d b c a +>+ (2)d b c a ->- (3)x b x a ->- (4)bd ac >(5)c bd a > (6)22b a > (7)33b a > (8)33b a > (9)b a 11< (11) 22bx ax > 8 若0<<b a ,则下列不等关系不能成立的是( ).A. b a 11>B.ab a 11>- C. ||||b a > D. 22b a > 9. 若0>>b a ,0>m ,则下列不等式中一定成立的是( ).A. m a m b a b ++>B. m b m a b a -->C. m a m b a b ++<D. mb m a b a --< 10 若0>x ,则函数xx y 1+=的取值范围是( ).A.]2,(--∞B. ),2[+∞C. ),2[]2,(+∞--∞D. ]2,2[- 11. 若0≠x ,则函数22364x xy --=有( ). A. 最大值264- B. 最小值264- C. 最大值264+ D. 最小值264+解析几何(一)1. 已知直线l 的倾斜角为︒135,且过点)3,(),1,4(--m B A ,则m 的值为______.2. 已知直线l 的倾斜角为︒135,且过点)2,1(,则直线的方程为____________.3. 已知直线的斜率为4,且在x .轴.上的截距为2,此直线方程为____________.4. 直线023=+-y x 倾斜角为____________.5. 直线042=+-y x 与两坐标轴围成的三角形面积为__________. 6 过点)3,2(P 且在两坐标轴上截距互为相反数的直线方程为_____________. 7 过点(2,3)且平行于直线052=-+y x 的方程为________________. 过点(2,3)且垂直于直线052=-+y x 的方程为________________. 8. 平行于直线0243=-+y x 且到它的距离为1的直线方程为____________.解析几何(二)1 圆心在点)2,1(-,与y 轴相切的圆的方程为________________,与x 轴相切的圆的方程为________________,过原点的圆的方程为________________2 半径为5,圆心在x 轴上且与x =3相切的圆的方程为______________.3 已知一个圆的圆心在点)1,1(-,并与直线0334=+-y x 相切,则圆的方程为______.4 点)1,1(-P 和圆024222=--++y x y x 的位置关系为________________. 5已知4:22=+y x C 圆,(1)过点)3,1(-的圆的切线方程为________________. (2)过点)0,3(的圆的切线方程为________________. (3)过点)1,2(-的圆的切线方程为________________. (4)斜率为-1的圆的切线方程为__________________. 6 已知直线方程为043=++k y x ,圆的方程为05622=+-+x y x (1)若直线过圆心,则k =_________. (2)若直线和圆相切,则k =_________.(3)若直线和圆相交,则k 的取值范围是____________.(4)若直线和圆相离,则k 的取值范围是____________.7 在圆822=+y x 内有一点)2,1(-P ,AB 为过点P 的弦. (1)过P 点的弦的最大弦长为__________.P 点的弦的最小弦长为__________. 解析几何(四)1. 如果直线l 与直线3x -4y +5=0关于y 轴对称,那么直线l 的方程为_____.2. 直线3x + y +1=0的倾斜角的大小是__________.3. 过点(1,-2)且倾斜角的余弦是-35的直线方程是______________.4. 若两条直线l 1: ax +2y +6=0与l 2: x +(a -1)y +3=0平行,则a 等于_________.5. 过点(1,3)且垂直于直线052=-+y x 的方程为________________.6. 图中的阴影区域可以用不等式组表示为( ).A. ⎪⎩⎪⎨⎧≤+-≤≥0110y x y x B.⎪⎩⎪⎨⎧≤+-≥≤0101y x y x C. ⎪⎩⎪⎨⎧≥+-≥≤0101y x y x D. ⎪⎩⎪⎨⎧≥+-≥≥0101y x y x7. 已知圆的直径两端点为)4,3(),2,1(-,则圆的方程为_____________. 8. 圆心在点)2,1(-且与x 轴相切的圆的方程为________________. 9. 圆x 2+y 2-10x=0的圆心到直线3x +4y -5=0的距离等于___________. 10 过圆x 2+y 2=25上一点P(4, 3),并与该圆相切的直线方程是____________.判断下列说法是否正确:1. 下列条件,是否可以确定一个平面: [ ](1)不共线的三个点 [ ](2)不共线的四个点 [ ](3)一条直线和一个点 [ ](4)两条相交或平行直线2. 关于空间中的直线,判断下列说法是否正确: [ ](1)如果两直线没有公共点,则它们平行[ ](2)如果两条直线分别和第三条直线异面,则这两条直线也异面 [ ](3)分别位于两个平面内的两条直线是异面直线 [ ](4)若βαβα//,,⊂⊂b a ,则a,b 异面 [ ](5)不在任何一个平面的两条直线异面 [ ](6)两条直线垂直一定有垂足 [ ](7)垂直于同一条直线的两条直线平行 [ ](8)若c a b a //,⊥,则b c ⊥[ ](9)过空间中一点有且只有一条直线和已知直线垂直 [ ](10)过空间中一点有且只有一条直线和已知直线平行 3. 关于空间中的直线和平面,判断下列说法是否正确: [ ](1)直线和平面的公共点个数可以是0个,1个或无数 [ ](2)若,,//α⊂b b a 则α//a[ ](3)如果一直线和一平面平行,则这条直线和平面的任意直线平行 [ ](4)如果一条直线和一个平面平行,则这条直线和这个平面内的无数条直线平行[ ](5)若两条直线同时和一个平面平行,则这两条直线平行 [ ](6)过平面外一点,有且只有一条直线和已知平面平行 [ ](7)过直线外一点,有无数个平面和已知直线平行 [ ](8)若共面且b a b a ,,,//αα⊂,则b a // 4. 关于空间中的平面,判断下列说法是否正确: [ ](1)两个平面的公共点的个数可以是0个,1个或无数 [ ](2)若b a b a //,,βα⊂⊂,则βα// [ ](3)若βαβα//,,⊂⊂b a ,则a //b [ ](4)若βαα//,⊂a ,则β//a [ ](5)若αα//,//b a ,则b a // [ ](6)若βα//,//a a ,则βα//[ ](7)若一个平面内的无数条直线和另一个平面平行,则这两个平面平行 [ ](8)若αβα⊂a ,//,则β//a[ ](9)若两个平面同时和第三个平面平行,则这两个平面平行 [ ](10)若一个平面同两个平面相交且它们的交线平行,则两平面平行[ ](11)过平面外一点,有且只有一个平面和已知平面平行 5. 关于直线与平面的垂直,判断下列说法是否正确:[ ](1)如果一直线垂直于一个平面内的所有直线,则这条直线垂直于这个平面 [ ](2)若αα⊂⊥a l ,,则a l ⊥ [ ](3)若m l m ⊥⊂,α,则α⊥l [ ](4)若n l m l n m ⊥⊥⊂,,,α,则α⊥l [ ](5)过一点有且只有一条直线和已知平面垂直 [ ](6)过一点有无数个平面和已知直线垂直 6. 关于平面和平面垂直,判断下列说法是否正确: [ ] (1)若,,βα⊥⊂a a 则βα⊥ [ ] (2)若b a b a ⊥⊂⊂,,βα,则βα⊥ [ ] (3)若,,,βαβα⊂⊂⊥b a ,则b a ⊥ [ ] (4)若,,βαα⊥⊂a 则β⊥a [ ] (6)若γαβα//,⊥,则γβ⊥ [ ] (7)垂直于同一个平面的两个平面平行 [ ] (8)垂直于同一条直线的两个平面平行[ ] (9)过平面外一点有且只有一个平面与已知平面垂直7. 判断下列说法是否正确:[ ] (1)两条平行线和同一平面所成的角相等[ ] (2)若两条直线和同一平面所的角相等,则这两条直线平行 [ ] (3)平面的平行线上所有的点到平面的距离都相等[ ] (4)若一条直线上有两点到一个平面的距离相等,则这条直线和平面平行。
高中数学会考习题集

高中数学会考测试卷练习一集合与函数(一>2. 已知则,.4. 图中阴影部分的集合表示正确的有________.(1>(2>(3>(4>10. 函数的定义域为________.11.17. 函数的值域为________.18. 下列函数在上是减函数的有__________.(1>(2>(3>(4>21. 将函数的图象向左平移2个单位,再向下平移1个单位,则对应图象的解读式为 .练习二集合与函数(二>4. 命题“”是命题“”的____________条件.6. 已知函数f(>=log3(8x+7>,那么f(>等于_______________.9. 在同一坐标系中,函数y=与y=的图象之间的关系是( >.A.关于原点对称B.关于x轴对称C.关于直线y=1对称.D.关于y轴对称12. 函数f(x>=错误!( >.A. 是偶函数,但不是奇函数B. 是奇函数,但不是偶函数C. 既是奇函数,又是偶函数D.不是奇函数,也不是偶函数练习三数列(一>1. 已知数列{}中,,,则______.2. – 81是等差数列– 5 , – 9 , –13 , … 的第< )项.练习四数列(二>3. 在等差数列中,已知,则=_______.4. 在等差数列中,已知前n项的和, 则_____.5. 在等差数列公差为2,前20项和等于100,那么等于________.练习五三角函数(一>1. 下列说法正确的有____________.(1>终边相同的角一定相等(2>锐角是第一象限角(3>第二象限角为钝角(4>小于的角一定为锐角(5>第二象限的角一定大于第一象限的角2. 已知角x的终边与角的终边关于y轴对称,则角x的集合可以表示为__________________________.3. 终边在y轴上角的集合可以表示为________________________. 14. 已知,则.15. 计算:,.练习六三角函数(二>2. 已知,为第三象限角,则________,3. 已知,是方程的两个根,则______.练习七三角函数(三>2. 函数的图象的一条对称轴是( >.A. 轴B.C.D.3. 函数的值域是________,周期是______,此函数的为____函数(填奇偶性>.练习八三角函数(四>2. 在范围内,与终边相同的角是___________.8. sin(>的值等于___________.练习九平面向量(一>1. 下列说法正确的有______________.(1>零向量没有方向(2>零向量和任意向量平行(3>单位向量都相等(4>(a·b>·c=a·(b·c>(5>若a·c= b·c,且c为非零向量,则a=b(6>若a·b=0,则a,b中至少有一个为零向量.2. “”是“∥”的________________条件.12. 已知,当共线时,k=____;当垂直时,k=____.练习十平面向量(二>1. 小船以10错误!km/h的速度向垂直于对岸的方向行驶,同时河水的流速为10km/h,则小船实际航行速度的大小为(>.b5E2RGbCAPA.20错误!km/hB.20km/hC. 10错误!km/hD. 10km/hp1EanqFDPw练习十一不等式1. 不等式的解集是__________.6. 不等式的解集是__________.17. 若,则函数的取值范围是( >.A. B. C. D.19. 解下列不等式:(1> (2>练习十四解读几何(一>1. 已知直线l的倾斜角为,且过点,则m的值为______.4. 直线倾斜角为____________.13. 平行于直线且到它的距离为1的直线方程为____________.练习十五解读几何(二>6. 已知,<1)过点的圆的切线方程为________________.<2)过点的圆的切线方程为________________.<3)过点的圆的切线方程为________________.<4)斜率为-1的圆的切线方程为__________________.练习十六解读几何(三>1. 已知椭圆的方程为,则它的长轴长为______,短轴长为______,焦点坐标为________,离心率为________,准线方程为____________.在坐标系中画出图形.2. 已知双曲线的方程为,则它的实轴长为______,虚轴长为______,焦点坐标为________,离心率为________,准线方程为____________,渐近线方程为__________. 在坐标系中画出图形. DXDiTa9E3d8. 已知双曲线方程为,若P是双曲线上一点,且则.练习十七解读几何(四>1. 如果直线l与直线3x-4y+5=0关于y轴对称,那么直线l的方程为_____.17. 双曲线错误!-错误!=1的渐近线方程是___________. RTCrpUDGiT练习十八立体几何(一>2. 关于空间中的直线,判断下列说法是否正确:[ ](1>如果两直线没有公共点,则它们平行[ ](2>如果两条直线分别和第三条直线异面,则这两条直线也异面3. 关于空间中的直线和平面,判断下列说法是否正确:[ ](1>直线和平面的公共点个数可以是0个,1个或无数[ ](2>若则5. 关于直线与平面的垂直,判断下列说法是否正确:[ ](1>如果一直线垂直于一个平面内的所有直线,则这条直线垂直于这个平面[ ](2>若,则[ ] (7>垂直于同一个平面的两个平面平行练习十九立体几何(二>3. 已知AB为平面的一条斜线,B为斜足,,O为垂足,BC为平面内的一条直线,,则斜线AB与平面所成的角的大小为________. 5PCzVD7HxA4. 观察题中正方体ABCD-A1B1C1D1中, 用图中已有的直线和平面填空:(1> 和直线BC垂直的直线有_________________.(2> 和直线BB1垂直且异面的直线有__________.(3> 和直线CC1平行的平面有________________.(4> 和直线BC垂直的平面有________________.(5> 和平面BD1垂直的直线有________________.9. 在正三棱柱中,底面边长和侧棱长均为a, 取AA1的中点M,连结CM,BM,则二面角的大小为 _________.练习二十立体几何(三>解答题:1. 在四棱锥中,底面是边长为a的正方形,侧棱,.(1> 求证:;(2> 求证:;(3> 求PA与底面所成角的大小;(4> 求PB与底面所成角的余弦值.申明:所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
高三数学会考试题及答案

高三数学会考试题及答案一、选择题(本题共8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一个是正确的。
)1. 若函数f(x) = x^2 - 4x + 3的图象关于x=2对称,则下列说法正确的是:A. f(0) = f(4)B. f(1) = f(3)C. f(-1) = f(5)D. f(2) = f(6)2. 已知等比数列{a_n}的首项为1,公比为2,求该数列前5项的和S_5:A. 31B. 16C. 15D. 31/23. 函数y = x^3 - 6x^2 + 9x + 1的导数为:A. 3x^2 - 12x + 9B. 3x^2 - 6x + 9C. 3x^2 - 12x + 3D. 3x^2 - 6x + 14. 若直线l与直线2x - y + 3 = 0平行,则直线l的斜率为:A. 2B. -2C. -1/2D. 1/25. 已知圆C的方程为(x - 1)^2 + (y + 2)^2 = 9,圆心C到直线2x + y - 3 = 0的距离为:A. √5B. 2√5C. √10D. 2√106. 已知向量a = (3, -2),向量b = (1, 2),则向量a与向量b的数量积为:A. -4B. 4C. -1D. 17. 已知双曲线x^2/a^2 - y^2/b^2 = 1的渐近线方程为y =±(√3/3)x,则双曲线的离心率为:A. √3B. 2C. 3D. √68. 若函数f(x) = ln(x + √(x^2 + 1))的定义域为:A. (-∞, 0)B. (-∞, 0]C. (0, +∞)D. [0, +∞)二、填空题(本题共4小题,每小题4分,共16分。
)9. 若复数z满足|z| = √2,且z的实部为1,则z的虚部为_________。
10. 已知函数f(x) = x^3 - 3x^2 + 2,求f'(x) = 0的根为_________。
11. 已知三角形ABC的三边长分别为a、b、c,且满足a^2 + b^2 = c^2,若a = 3,b = 4,则c的长度为_________。
2023年高中数学会考试卷

2023年高中数学会考试卷第一部分:选择题1. 下列哪个数是一个无理数?A) √4B) πC) 3/4D) 0.252. 已知函数 f(x) = 2x^2 - 3x + 1,求 f(2) 的值是多少?A) 4B) 5C) 6D) 73. 在三角形 ABC 中,∠B = 60°,BC = 8,AC = 10,求 AB 的长度。
A) 2B) 4C) 6D) 84. 一辆汽车以每小时60 公里的速度行驶,行驶3 小时后,行驶的距离是多少?A) 120 公里B) 160 公里C) 180 公里D) 240 公里5. 若 3x - 2y = 4,5x + 2y = 7,则 x 的值是多少?A) 1B) 2C) 3D) 46. 一个边长为 3 的正方形内接于一个圆,这个圆的直径是多少?A) 1B) 2C) 3D) 47. 一根长 20 厘米的杆子,被 3 个点分成 4 个部分,其中相邻两部分的长度比是 2:3:4,求最长的部分的长度。
A) 4 厘米B) 6 厘米C) 8 厘米D) 10 厘米8. 已知 a, b, c 为实数,且a ≠ 0,若方程 ax^2 + bx + c = 0 有两个相等的根,则b 的值是多少?A) 0B) 1C) -1D) 2第二部分:填空题1. 已知函数 f(x) = 2x^2 - 3x + 1,求 f(0) 的值是多少?2. 解方程 2x + 5 = 15 的解是多少?3. 已知等差数列的首项是 2,公差是 3,求第 5 项的值。
4. 一条直线通过点 (2, 4) 和 (5, 10),求这条直线的斜率。
5. 解方程 4x^2 - 16 = 0 的解是多少?6. 一个 45°-45°-90°的直角三角形的斜边长是 8,求直角边的长度。
7. 一辆汽车以每小时 80 公里的速度行驶,行驶 2.5 小时后,行驶的距离是多少?8. 已知 2x - 3y = 7 和 3x + 4y = 5,求 x 和 y 的值。
数学会考高中试题及答案

数学会考高中试题及答案一、选择题(每题3分,共30分)1. 已知函数\( f(x) = 2x^2 - 4x + 3 \),下列说法正确的是:A. 函数的图像是开口向上的抛物线B. 函数的图像是开口向下的抛物线C. 函数的图像与x轴有两个交点D. 函数的图像与x轴没有交点答案:A2. 圆的方程为\( (x-2)^2 + (y-3)^2 = 9 \),圆心坐标为:A. (2, 3)B. (-2, 3)C. (2, -3)D. (-2, -3)答案:A3. 已知等差数列的前三项依次为1,3,5,则该数列的第五项为:A. 7B. 9C. 11D. 13答案:B4. 函数\( y = \log_2(x) \)的定义域是:A. \( x > 0 \)B. \( x < 0 \)C. \( x \geq 0 \)D. \( x \leq 0 \)答案:A5. 集合\( A = \{1, 2, 3\} \)和集合\( B = \{2, 3, 4\} \)的交集为:A. \( \{1\} \)B. \( \{2, 3\} \)C. \( \{2, 4\} \)D. \( \{3, 4\} \)答案:B6. 直线\( y = 2x + 1 \)与直线\( y = -x + 4 \)的交点坐标为:A. (1, 3)B. (-1, 3)C. (1, -1)D. (-1, -1)答案:A7. 已知\( \sin \alpha = \frac{1}{2} \),\( \alpha \)是第二象限角,则\( \cos \alpha \)的值为:A. \( \frac{1}{2} \)B. \( -\frac{1}{2} \)C. \( \frac{\sqrt{3}}{2} \)D. \( -\frac{\sqrt{3}}{2} \)答案:D8. 函数\( f(x) = x^3 - 3x^2 + 3x - 1 \)的单调递增区间为:A. \( (-\infty, 1) \)B. \( (1, +\infty) \)C. \( (-\infty, 2) \)D. \( (2, +\infty) \)答案:B9. 向量\( \vec{a} = (1, 2) \)和向量\( \vec{b} = (2, 1) \)的夹角为:A. \( \frac{\pi}{4} \)B. \( \frac{\pi}{3} \)C. \( \frac{\pi}{2} \)D. \( \frac{2\pi}{3} \)答案:A10. 已知等比数列的前三项依次为2,4,8,则该数列的公比为:A. 2B. 4C. 1D. 0.5答案:A二、填空题(每题4分,共20分)1. 已知\( \tan \theta = 3 \),\( \theta \)是第一象限角,则\( \sin \theta \)的值为______。
(完整word版)高中会考试卷数学试题(word文档良心出品)

高中会考试卷数学试题一、选择题(本题有22小题,每小题2分,共44分.选出各题中一个符合题意的正确选项,不选、多选、错选都不给分)1.数轴上两点A ,B 的坐标分别为2,-1,则有向线段AB 的数量是}}}8.底面半径为3,母线长为4的圆锥侧面积是(A)6π (B)12π (C)15π (D)24π9.下列函数中,在定义域内是增函数的是(A)y =(21)x (B)y =1x(C)y =x 2 (D)y =lg x10.在平行四边形ABCD 中,AB AD +u u u r u u u r 等于11.若一个圆的圆心在直线2y x =上,在y 轴上截得的弦的长度等于2,且与直线0x y -+=相切,则这个圆的方程可能是12.在ΔABC 中,如果sin A cos A =-513,那么ΔABC 的形状是 (D)3a-1,y =(A)向左平移4π个单位(B)向右平移4π个单位 (C)向左平移2π个单位(D)向右平移2π个单位18.已知函数y =f (x )的反函数为y =()1f x -,若f (3)=2,则()12f -为(A)3 (B)31 (C)2(D)21 19.如果函数y =log a x (a >0且a ≠1)在[1,3]上的最大值与最小值的差为2,则满足条件的a 值的集合是(A){3} (B){33}(C){3,33}(D){3,3}20.已知直线m ⊥平面α.直线n 平面β,则下列命题正确(A)α⊥β⇒m ⊥n (B)α⊥β⇒m ∥n (C)m ⊥n ⇒α∥β(D)m ∥n ⇒α⊥β21.一个正方体的表面展开图如图所示,图中的AB ,CD 在原正方体中是两条(A)平行直线 (B)相交直线(C)异面直线且成60°角 (D)异面直线且互相垂直22.已知数列{a n }的前n 项和Sn =q n -1(q >0且q 为常数),某同学研究此数列后,得知如下三个结论:①{a n }的通项公式是a n =(q -1)q n -1;②{a n }是等比数列;③当q ≠1时,221n n n S S S ++•<.其中结论正确的个数有(A)0个 (B)1个 (C)2个(D)3个二、填空题(本题有6小题,每小题3分,共18分) 23.计算:已知向量a r 、b r ,2a =r ,(3,4)b =r ,a r 与b r 夹角等于30︒,则a b⋅r r 等于.24.计算sin 240︒的值为。
高级中学数学会考复习材料

高中数学会考练习题集练习一 集合与函数(一) 1. 已知S ={1,2,3,4,5},A ={1,2},B ={2,3,6},则______=B A I ,______=B A Y ,______)(=B A C S Y .2. 已知},31|{},21|{<<=<<-=x x B x x A则______=B A I ,______=B A Y .3. 集合},,,{d c b a 的所有子集个数是_____,含有2个元素子集个数是_____.4. 图中阴影部分的集合表示正确的有________.(1))(B A C U Y (2))(B A C U I(3))()(B C A C U U Y (4))()(B C A C U U I5. 已知},6|),{(},4|),{(=+==-=y x y x B y x y x A ________B A =则I .6. 下列表达式正确的有__________.(1)A B A B A =⇒⊆I (2)B A A B A ⊆⇒=Y(3)A A C A U =)(I (4)U A C A U =)(Y7. 若}2,1{≠⊂}4,3,2,1{⊆A ,则满足A 集合的个数为____.8. 下列函数可以表示同一函数的有________.(1)2)()(,)(x x g x x f == (2)2)(,)(x x g x x f ==(3)x x x g x x f 0)(,1)(== (4))1()(,1)(+=+⋅=x x x g x x x f 9. 函数x x x f -+-=32)(的定义域为________.10. 函数291)(x x f -=的定义域为________.11. 若函数_____)1(,)(2=+=x f x x f 则.12. 已知_______)(,12)1(=-=+x f x x f 则.13. 已知1)(-=x x f ,则______)2(=f .14. 已知⎩⎨⎧≥<=0,20,)(2x x x x f ,则_____)0(=f _____)]1([=-f f .15. 函数xy 2-=的值域为________. 16. 函数R x x y ∈+=,12的值域为________.17. 函数)3,0(,22∈-=x x x y 的值域为________.18. 下列函数在),0(+∞上是减函数的有__________.(1)12+=x y (2)xy 2=(3)x x y 22+-= (4)12+--=x x y 19. 下列函数为奇函数的有________.(1)1+=x y (2)x x y -=2 (3)1=y (4)x y 1-= 20. 若映射B A f →:把集合A 中的元素(x,y )映射到B 中为),(y x y x +-,则(2, 6)的象是______,则(2, 6)的原象是________.21. 将函数xy 1=的图象向左平移2个单位,再向下平移1个单位,则对应 图象的解析式为 .22. 某厂从1998年起年产值平均每年比上一年增长12.4%,设该厂1998年的产值为a , 则该厂的年产值y 与经过年数x 的函数关系式为________.集合与函数(二)1. 已知全集I ={1,2,3,4,5,6},A ={1,2,3,4},B ={3,4,5,6}, 那么C I (A ∩B )=( ).A.{3,4}B.{1,2,5,6}C.{1,2,3,4,5,6}D.Ф2. 设集合M ={1,2,3,4,5},集合N ={9|2≤x x },M ∩N =( ).A.{33|≤≤-x x }B.{1,2}C.{1,2,3}D.{31|≤≤x x }3. 设集合M ={-2,0,2},N ={0},则( ).A .N 为空集 B. N ∈M C. N ⊂M D. M ⊂N4. 命题“b a >”是命题“22bc ac >”的____________条件.5. 函数y =)1lg(2-x 的定义域是__________________.6. 已知函数f (x )=log 3(8x +7),那么f (21)等于_______________. 7. 若f (x )=x + 1x ,则对任意不为零的实数x 恒成立的是( ). A. f (x )=f (-x ) B. f (x )=f (x 1) C. f (x )=-f (x 1) D. f (x ) f (x1)=0 8. 与函数y = x 有相同图象的一个函数是( ).A .y =x 2B. y =x 2xC. y =a log a x (a >0, a ≠1)D. y = log a a x (a>0, a≠1) 9. 在同一坐标系中,函数y =x 5.0log 与y =x 2log 的图象之间的关系是( ).A.关于原点对称B.关于x 轴对称C.关于直线y =1对称.D.关于y 轴对称10. 下列函数中,在区间(0,+∞)上是增函数的是( ).A.y =-x 2B.y = x 2-x +2C.y =(21)xD.y =x 1log 3.011. 函数y =)(log 2x -是( ).A. 在区间(-∞,0)上的增函数B. 在区间(-∞,0)上的减函数C. 在区间(0,+∞)上的增函数D. 在区间(0,+∞)上的减函数12. 函数f (x )=3x -13x +1 ( ).A. 是偶函数,但不是奇函数B. 是奇函数,但不是偶函数C. 既是奇函数,又是偶函数D.不是奇函数,也不是偶函数13. 下列函数中为奇函数的是( ).A. f (x )=x 2+x -1B. f (x )=|x |C. f (x )=23x x +D. f (x )=522xx --14. 设函数f (x )=(m -1)x 2+(m +1)x +3是偶函数,则m=________.15. 已知函数f (x )=||2x ,那么函数f (x )( ).A. 是奇函数,且在(-∞,0)上是增函数B. 是偶函数,且在(-∞,0)上是减函数C. 是奇函数,且在(0,+∞)上是增函数D. 是偶函数,且在(0,+∞)上是减函数16. 函数y =||log 3x (x ∈R 且x ≠0)( ) .A. 为奇函数且在(-∞,0)上是减函数B. 为奇函数且在(-∞,0)上是增函数C. 是偶函数且在(0,+∞)上是减函数D. 是偶函数且在(0,+∞)上是增函数17. 若f (x )是以4为周期的奇函数,且f (-1)=a (a ≠0),则f (5)的值等于(). A. 5a B. -a C. a D. 1-a18. 如果函数y =x a log 的图象过点(91,2),则a =___________.19. 实数2732–3log 22·log 218 +lg4+2lg5的值为_____________.20. 设a =log 26.7, b =log 0.24.3, c =log 0.25.6,则a, b, c 的大小关系为( )A. b <c <aB. a <c <bC. a <b <cD. c <b <a21. 若1log 21>x ,则x 的取值范围是( ).A. 21<xB.210<<x C.21>x D.0<x数列(一)1. 已知数列{n a }中,12=a ,121+=+n n a a ,则=1a ______.2. – 81是等差数列 – 5 , – 9 , – 13 , … 的第( )项.3. 若某一数列的通项公式为n a n 41-=,则它的前50项的和为______.4. 等比数列,271,91,31,1…的通项公式为________. 5. 等比数列,54,18,6,2…的前n 项和公式n S =__________.6. 12-与12+的等比中项为__________.7. 若a ,b ,c 成等差数列,且8=++c b a ,则b = .8. 等差数列{a n }中,a 3+ a 4+ a 5+ a 6+ a 7=150,则a 2+a 8= .9. 在等差数列{a n }中,若a 5=2,a 10=10,则a 15=________.10. 在等差数列{a n }中,,56=a 583=+a a , 则=9S _____.10. 数列1781,1327,99,53,11,…的一个通项公式为________. 11. 在等比数列中,各项均为正数,且962=a a ,则)(log 54331a a a = .12. 等差数列中,2,241-==d a , 则n S =___________.13. 已知数列{ a n }的前项和为S n = 2n 2 – n ,则该数列的通项公式为_______.14. 已知三个数成等比数列,它们的和为14,它们的积为64,则这三个数为 .数列(二)1. 在等差数列}{n a 中,85=a ,前5项的和105=S ,它的首项是__________,公差是__________.2. 在公比为2的等比数列中,前4项的和为45,则首项为_____.3. 在等差数列}{n a 中,已知1554321=++++a a a a a ,则42a a +=_______.4. 在等差数列}{n a 中,已知前n 项的和n n S n -=24, 则=20a _____.5. 在等差数列}{n a 公差为2,前20项和等于100,那么20642...a a a a ++++等于________.6. 已知数列}{n a 中的3231+=+n n a a ,且2053=+a a ,则=8a _______. 7. 已知数列}{n a 满足n n a a =-+21,且11=a ,则通项公式=n a ______.8. 数列}{n a 中,如果)1(21≥=+n a a n n ,且21=a ,那么数列的前5项和=5S _.9. 两数15-和15+的等比中项是__________________.10. 等差数列}{n a 通项公式为72-=n a n ,那么从第10项到第15项的和为___.11. 已知a, b, c, d 是公比为3 的等比数列,则dc b a ++22=___________. 12. 在各项均为正数的等比数列中,若551=a a ,则=)(log 4325a a a ________.三角函数(一)1. 下列说法正确的有____________.(1)终边相同的角一定相等(2)锐角是第一象限角(3)第二象限角为钝角(4)小于︒90的角一定为锐角 (5)第二象限的角一定大于第一象限的角2. 已知角x 的终边与角︒30的终边关于y 轴对称,则角x 的集合可以表示为__________________________.3. 终边在y 轴上角的集合可以表示为________________________.4. 终边在第三象限的角可以表示为________________________.5. 在︒︒-720~360之间,与角︒175终边相同的角有__________________.6. 在半径为2的圆中,弧度数为3π的圆心角所对的弧长为________,扇形面积为__________.7. 已知角α的终边经过点(3,-4),则sin α=______ , cos α=______, tan α=_______ .8. 已知0cos 0sin ><θθ且,则角θ一定在第______象限.9. “0sin >θ”是“θ是第一或第二象限角”的________条件.10. 计算:πππ2cos cos 0tan 20sin 1223cos 7-+++=________. 11. 化简:tan cos ____θθ=.12. 已知,54cos -=α 且α为第三象限角,则_____tan _____,sin ==αα . 13. 已知31tan =α,且23παπ<<,则_____cos _____,sin ==αα . 14. 已知2tan =α,则____sin cos cos 2sin =+-αααα. 15. 计算:_____)317sin(=-π, _____)417cos(=-π. 16. 化简:____)cos()sin()2sin()cos(=----++αππαπααπ.三角函数(二)1. 求值: ︒165cos =________,=︒-)15tan(________.2. 已知21cos -=θ,θ为第三象限角,则=+)3sin(θπ________, =+)3cos(θπ________,=+)3tan(θπ________. 3. 已知x tan ,y tan 是方程0762=++x x 的两个根,则=+)tan(y x ______. 4. 已知31sin =α,α为第二象限角,则=α2sin ______, =α2cos ______,=α2tan ______.5. 已知21tan =α,则=α2tan ______.6. 化简或求值:=---y y x y y x cos )cos(sin )sin(______,=︒︒-︒︒170sin 20sin 10cos 70sin ______,=-ααsin 3cos ______,____15tan 115tan 1=︒-︒+, _____5tan 65tan 35tan 65tan =︒︒-︒-︒, =︒︒15cos 15sin ____, =-2cos 2sin 22θθ______15.22cos 22-︒=______, ︒-︒150tan 1150tan 22=______. 7. 已知,3tan ,2tan ==ϕθ且ϕθ,都为锐角,则=+ϕθ______.8. 已知21cos sin =+θθ,则=θ2sin ______. 9. 已知41sin =θ,则=-θθ44cos sin ______. 10. 在ABC ∆中,若,53sin ,135cos =-=B A 则=C sin ________.三角函数(三)1. 函数)4sin(π+=x y 的图象的一个对称中心是( ).A. )0,0(B. )1,4(πC. )1,43(πD. )0,43(π 2. 函数)3cos(π-=x y 的图象的一条对称轴是( ).A. y 轴B. 3π-=x C. 65π=x D. 3π=x 3. 函数x x y cos sin =的值域是________,周期是______,此函数的为____函数(填奇偶性).4. 函数x x y cos sin -=的值域是________,周期是______,此函数的为____函数(填奇偶性).5. 函数x x y cos 3sin +=的值域是________,周期是______,此函数的为____函数(填奇偶性).8. 函数)42tan(3π-=x y 的定义域是__________________,值域是________,周期是______,此函数为______函数(填奇偶性).9. 比较大小:︒︒530cos ___515cos , )914sin(____)815sin(ππ-- ︒︒143tan ____138tan , ︒︒91tan ___89tan10. 要得到函数)42sin(2π+=x y 的图象,只需将x y 2sin 2=的图象上各点____11. 将函数x y 2cos =的图象向左平移6π个单位,得到图象对应的函数解析式为________________.12. 已知22cos -=θ,)20(πθ<<,则θ可能的值有_________.三角函数(四)1. 在︒︒360~0范围内,与-1050o 的角终边相同的角是___________.2. 在π2~0范围内,与π310终边相同的角是___________. 3. 若sinα<0且cosα<0 ,则α为第____象限角.4. 在︒︒-360~360之间,与角︒175终边相同的角有_______________.5. 在半径为2的圆中,弧度数为3π的圆心角所对的弧长为______________. 6. 已知角α的终边经过点(3,-4),则cos α=______. 7. 命题 “x = π2 ” 是命题 “sin x =1” 的_____________条件.8. sin(π617-)的值等于___________. 9. 设π4 <α<π2 ,角α的正弦. 余弦和正切的值分别为a ,b ,c ,则( ). A. a <b <c B. b <a <c C. a <c <b D. c <b <a10. 已知,54cos -=α 且α为第三象限角,则_____tan =α. 11. 若 tan α=2且sin α<0,则cos α的值等于_____________.12. 要得到函数y =sin(2x -π3)的图象,只要把函数y =sin2x 的图象( ). A.向左平移π3 个单位 B. 向右平移π3 个单位C.向左平移π6 个单位D. 向右平移π6 个单位13. 已知tan α=-3 (0<α<2π),那么角α所有可能的值是___________14. 化简cos x sin(y -x )+cos(y -x )sin x 等于_____________15. cos25o cos35o –sin25o sin35o 的值等于_____________(写具体值).16. 函数y =sin x +cos x 的值域是( )A.[-1,1]B.[-2,2]C.[-1, 2 ]D.[- 2 , 2 ]17. 函数y =cos x - 3 sin x 的最小正周期是( )A.2π B. 4π C. π D.2π 18. 已知sin α=53,90o <α<180o ,那么sin2α的值__________. 19. 函数y=cos 2 x -sin 2x 的最小正周期是( )A. 4πB. 2πC. πD. π220. 函数y =sin x cos x 是( )A.周期为2π的奇函数B. 周期为2π的偶函数C. 周期为π的奇函数D. 周期为π的偶函数21. 已知2tan =α,则=α2tan ________.练习九 平面向量(一)1. 下列说法正确的有______________.(1)零向量没有方向 (2)零向量和任意向量平行(3)单位向量都相等 (4)(a ·b )·c =a ·(b ·c )(5)若a ·c = b ·c ,且c 为非零向量,则a =b(6)若a ·b =0,则a,b 中至少有一个为零向量.2. “b a =”是“a ∥b ”的________________条件.3. 下列各式的运算结果为向量的有________________.(1)a +b (2)a -b (3)a ·b (4)λa (5)||b a + (6)a ·0 4. 计算:=-++MP MN NQ QP ______.5. 如图,在ABC ∆中,BC 边上的中点为M , 设=AB a, =AC b ,用a , b 表示下列向量: =BC ________,=AM ________,=MB ________.6. 在□ABCD 中,对角线AC ,BD 交于O 点,设=AB a, =AD b ,用a , b 表示下列向量:=AC ________,. =BD ________,=CO ________,=OB ________.7. 已知21,e e 不共线,则下列每组中a , b 共线的有______________.(1)113,2e b e a -== (2)213,2e b e a -==(3)212121,2e e b e e a +-=-= (4)2121,e e b e e a +=-= 8. 已知,4||,3||==b a 且向量b a,的夹角为︒120,则=b a ·________, =-||b a __________.9. 已知)1,1(),3,2(-==b a ,则=-b a 2______,=b a ·________, =||a ______,向量b a,的夹角的余弦值为_______.12. 已知)1,2(),2,1(-==b a k ,当b a,共线时,k =____;当b a,垂直时,k =____.13. 已知)4,2(),2,1(B A -,)3,(x C ,且A,B,C 三点共线,则x =______.14. 把点)5,3(P 按向量a =(4,5)平移至点P ’,则P ’的坐标为_______.15. 将函数22x y =的图象F 按a =(1,-1)平移至F ’, 则F ’的函数解析式为____.16. 将一函数图象按a =(1,2)平移后,所得函数图象所对应的函数解析式为x y lg =,则原图象的对应的函数解析式为_______.17. 将函数x x y 22+=的图象按某一向量平移后得到的图象对应的函数解析式为2x y =,则这个平移向量的坐标为________.18. 已知)3,2(),5,1(B A ,点M 分有向线段的比2-=λ,则M 的坐标为____.19. 已知P 点在线段21P P 上,21P P =5,P P 1=1,点P 分有向线段21P P 的比为__.20. 已知P 点在线段21P P 的延长线上,21P P =5,P P 2=10,点P 分有向线段21P P 的比为_____.21. 在ABC ∆中,︒=45A ,︒=105C ,5=a ,则b =_______.22. 在ABC ∆中,2=b ,1=c ,︒=45B ,则C =_______.23. 在ABC ∆中,32=a ,6=b ,︒=30A ,则B =_______.24. 在ABC ∆中,3=a ,4=b ,37=c ,则这个三角形中最大的内角为______.25. 在ABC ∆中,1=a ,2=b ,︒=60C ,则c =_______.26. 在ABC ∆中,7=a ,3=c ,︒=120A ,则b =_______.平面向量(二)1. 小船以10 3 km/h 的速度向垂直于对岸的方向行驶,同时河水的流速为10km/h ,则小船实际航行速度的大小为( ).A.20 2 km/hB.20km/hC. 10 2 km/hD. 10km/h2. 若向量→a =(1,1),→b =(1,-1),→c =(-1,2),则→c =( ).A. -12 →a +32 →bB. 12 →a -32 →bC. 32 →a -12 →bD.- 32 →a +12 →b3. 有以下四个命题:① 若→a ·→b =→a ·→c 且→a ≠→0,则→b =→c ;② 若→a ·→b =0,则→a =→0或→b =→0;③ ⊿ABC 中,若→AB ·→AC >0,则⊿ABC 是锐角三角形;④ ⊿ABC 中,若→AB ·→BC =0,则⊿ABC 是直角三角形.其中正确命题的个数是( ). A.0 B.1 C.2 D.34. 若|→a |=1,|→b |=2,→c =→a +→b ,且→c ⊥→a ,则向量→a 与→b 的夹角为( ).A.30oB.60oC.120o D150o5. 已知→a . →b 是两个单位向量,那么下列命题中真命题是( ).A. →a =→bB. →a ·→b =0C. |→a ·→b |<1D. →a 2=→b 26. 在⊿ABC 中,AB =4,BC =6,∠ABC =60o ,则AC 等于( ).A. 28B. 76C. 27D. 2197. 在⊿ABC 中,已知a = 3 +1, b =2, c = 2 ,那么角C 等于( ).A. 30oB. 45oC. 60oD. 120o8. 在⊿ABC 中,已知三个内角之比A :B :C =1:2:3,那么三边之比a :b :c =( ).A. 1: 3 :2B. 1:2:3C. 2: 3 :1D. 3:2:1不等式1. 不等式3|21|>-x 的解集是__________.2. 不等式2|1|≤-x 的解集是__________.3. 不等式42>x 的解集是__________.4. 不等式022>--x x 的解集是__________.5. 不等式012<++x x 的解集是__________.6. 不等式032≥--xx 的解集是__________. 7. 已知不等式02>++n mx x 的解集是}2,1|{>-<x x x 或,则m 和n 的值分别为__________.8. 不等式042>++mx x 对于任意x 值恒成立,则m 的取值范围为________.9. 已知d c b a >>,,下列命题是真命题的有_______________.(1)d b c a +>+ (2)d b c a ->- (3)x b x a ->- (4)bd ac >(5)c b d a > (6)22b a > (7)33b a > (8)33b a > (9)ba 11< (11) 22bx ax > 10. 已知64,52<<<<b a ,则b a +的取值范围是______________,则a b -的取值范围是______________,ab 的取值范围是___________. 11. 已知0,>b a 且,2=ab 则b a +的最___值为_______.12. 已知0,>b a 且,2=+b a 则ab 的最___值为_______.13. 已知,0>m 则函数mm y 82+=的最___值为_______, 此时m =_______.14. a >0,b >0是ab >0的( ).A. 充分条件但不是必要条件B. 必要条件但不是充分条件C. 充分必要条件D. 既非充分条件也非必要条件15. 若0<<b a ,则下列不等关系不能成立的是( ).A. b a 11>B. ab a 11>- C. ||||b a > D. 22b a > 16. 若0>>b a ,0>m ,则下列不等式中一定成立的是( ).A. m a m b a b ++>B. m b m a b a -->C. m a m b a b ++<D. mb m a b a --< 17. 若0>x ,则函数xx y 1+=的取值范围是( ). A.]2,(--∞ B. ),2[+∞ C. ),2[]2,(+∞--∞Y D. ]2,2[-18. 若0≠x ,则函数22364x xy --=有( ). A. 最大值264- B. 最小值264-C. 最大值264+D. 最小值264+19. 解下列不等式:(1) 5|32|1<-≤x (2) 6|5|2>-x x(3) 10|83|2<-+x x解析几何(一)1. 已知直线l 的倾斜角为︒135,且过点)3,(),1,4(--m B A ,则m 的值为______.2. 已知直线l 的倾斜角为︒135,且过点)2,1(,则直线的方程为____________.3. 已知直线的斜率为4,且在x .轴.上的截距为2,此直线方程为____________. 4. 直线023=+-y x 倾斜角为____________.5. 直线042=+-y x 与两坐标轴围成的三角形面积为__________.6. 直线042=+-y x 关于y 轴对称的直线方程为________________.7. 过点)3,2(P 且在两坐标轴上截距互为相反数的直线方程为_____________.8. 下列各组直线中,互相平行的有____________;互相垂直的有__________.(1)022121=+-+=y x x y 与 (2)0322=-+-=y x x y 与 (3)0322=--=y x x y 与 (4)023=++y x 与33+=x y(5)052052=+=+y x 与 (6)052052=-=+x x 与9. 过点(2,3)且平行于直线052=-+y x 的方程为________________. 过点(2,3)且垂直于直线052=-+y x 的方程为________________.10. 已知直线01:,022:21=--+=--+a y ax l a ay x l ,当两直线平行时, a =______;当两直线垂直时,a =______.11. 直线53=-y x 到直线032=-+y x 的角的大小为__________.12. 设直线0243:,022:,0243:321=+-=++=-+y x l y x l y x l ,则直线 21l l 与的交点到3l 的距离为____________.13. 平行于直线0243=-+y x 且到它的距离为1的直线方程为____________.解析几何(二)1. 圆心在)2,1(-,半径为2的圆的标准方程为____________,一般方程为__________,参数方程为______________.2. 圆心在点)2,1(-,与y 轴相切的圆的方程为________________,与x 轴相切的圆的方程为________________,过原点的圆的方程为________________3. 半径为5,圆心在x 轴上且与x =3相切的圆的方程为______________.4. 已知一个圆的圆心在点)1,1(-,并与直线0334=+-y x 相切,则圆的方程为______.5. 点)1,1(-P 和圆024222=--++y x y x 的位置关系为________________.6. 已知4:22=+y x C 圆,(1)过点)3,1(-的圆的切线方程为________________.(2)过点)0,3(的圆的切线方程为________________.(3)过点)1,2(-的圆的切线方程为________________.(4)斜率为-1的圆的切线方程为__________________.7. 已知直线方程为043=++k y x ,圆的方程为05622=+-+x y x(1)若直线过圆心,则k =_________.(2)若直线和圆相切,则k =_________.(3)若直线和圆相交,则k 的取值范围是____________. (4)若直线和圆相离,则k 的取值范围是____________.8. 在圆822=+y x 内有一点)2,1(-P ,AB 为过点P 的弦.(1)过P 点的弦的最大弦长为__________.(2)过P 点的弦的最小弦长为__________.解析几何(三)1. 已知椭圆的方程为116922=+x y ,则它的长轴长为______,短轴长为______, 焦点坐标为________,离心率为________,准线方程为____________. 在坐标系中画出图形.2. 已知双曲线的方程为116922=-x y ,则它的实轴长为______,虚轴长为______,焦点坐标为________,离心率为________,准线方程为____________,渐近线方程为__________. 在坐标系中画出图形.3. 经过点)2,0(),0,3(--Q P 的椭圆的标准方程是_____________.4. 长轴长为20,离心率为53,焦点在y 轴上的椭圆方程为__________. 5. 焦距为10,离心率为35,焦点在x 轴上的双曲线的方程为__________. 6. 与椭圆1492422=+y x 有公共焦点,且离心率为45的双曲线方程为________. 7. 已知椭圆的方程为16422=+y x ,若P 是椭圆上一点,且,7||1=PF则________||2=PF .8. 已知双曲线方程为14491622-=-y x ,若P 是双曲线上一点,且,7||1=PF 则________||2=PF .9. 已知双曲线经过)5,2(-P ,且焦点为)6,0(±,则双曲线的标准方程为______10. 已知椭圆12516922=+y x 上一点P 到左焦点的距离为12,则P 点到左准线的距离为__________.11. 已知双曲线1366422=-y x 上点P 到右准线的距离为532,则P 点到右焦点的距离为__________.12. 已知一等轴双曲线的焦距为4,则它的标准方程为____________________.13. 已知曲线方程为14922=-+-k y k x , (1) 当曲线为椭圆时,k 的取值范围是______________.(2) 当曲线为双曲线时,k 的取值范围是______________.14. 方程y 2 = 2px (p >0)中的字母p 表示( ).A .顶点、准线间的距离B .焦点、准线间的距离C .原点、焦点间距离D .两准线间的距离15. 抛物线x y 22=的焦点坐标为__________,准线方程为____________.16. 抛物线y x 212-=的焦点坐标为__________,准线方程为____________. 17. 顶点在原点,对称轴为坐标轴,焦点为)0,2(-的抛物线方程为________.18. 顶点在原点,对称轴为坐标轴,准线方程为81-=y 的抛物线方程为____. 19. 经过点)8,4(-P ,顶点在原点,对称轴为x 轴的抛物线方程为__________.解析几何(四) 1. 如果直线l 与直线3x -4y +5=0关于y 轴对称,那么直线l 的方程为_____.2. 直线3x + y +1=0的倾斜角的大小是__________.3. 过点(1,-2)且倾斜角的余弦是-35的直线方程是______________.4. 若两条直线l 1: ax+2y+6=0与l 2: x+(a-1)y+3=0平行,则a等于_________.5. 过点(1,3)且垂直于直线052=-+yx的方程为________________.6. 图中的阴影区域可以用不等式组表示为().A.⎪⎩⎪⎨⎧≤+-≤≥11yxyxB.⎪⎩⎪⎨⎧≤+-≥≤11yxyxC.⎪⎩⎪⎨⎧≥+-≥≤11yxyxD.⎪⎩⎪⎨⎧≥+-≥≥11yxyx7. 已知圆的直径两端点为)4,3(),2,1(-,则圆的方程为_____________.8. 圆心在点)2,1(-且与x轴相切的圆的方程为________________.9. 已知02024:22=---+yxyxC圆,它的参数方程为_________________.10. 已知圆的参数方程是θθsin2cos2{==yx(θ为参数),那么该圆的普通方程是______11. 圆x2+y2-10x=0的圆心到直线3x+4y-5=0的距离等于___________.12. 过圆x2+y2=25上一点P(4, 3),并与该圆相切的直线方程是____________.13. 已知椭圆的两个焦点是F1(-2, 0)、F2(2, 0),且点A(0, 2)在椭圆上,那么这个椭圆的标准方程是_________.14. 已知椭圆的方程为x29+y225=1,那么它的离心率是__________.15. 已知点P在椭圆x236+y2100=1上,且它到左准线的距离等于10,那么点P 到左焦点的距离等于______.16. 与椭圆x29+y24=1有公共焦点,且离心率e=52的双曲线方程是()A. x2-y24=1 B. y2-x24=1 C.x24-y2=1 D.y24-x2=117. 双曲线x24-y29=1的渐近线方程是___________.18. 如果双曲线x 264 -y 236 =1上一点P 到它的右焦点的距离是5,那么点P 到它的右准线的距离是___________.19. 抛物线x y 22=的焦点坐标为__________.20. 抛物线y x 212-=的准线方程为__________. 21. 若抛物线y 2=2px 上一点横坐标为6,这个点与焦点的距离为10,那么此 抛物线的焦点到准线的距离是_______.立体几何(一)判断下列说法是否正确:1. 下列条件,是否可以确定一个平面:[ ](1)不共线的三个点[ ](2)不共线的四个点[ ](3)一条直线和一个点[ ](4)两条相交或平行直线2. 关于空间中的直线,判断下列说法是否正确:[ ](1)如果两直线没有公共点,则它们平行[ ](2)如果两条直线分别和第三条直线异面,则这两条直线也异面[ ](3)分别位于两个平面内的两条直线是异面直线[ ](4)若βαβα//,,⊂⊂b a ,则a,b 异面[ ](5)不在任何一个平面的两条直线异面[ ](6)两条直线垂直一定有垂足[ ](7)垂直于同一条直线的两条直线平行[ ](8)若c a b a //,⊥,则b c ⊥[ ](9)过空间中一点有且只有一条直线和已知直线垂直[ ](10)过空间中一点有且只有一条直线和已知直线平行3. 关于空间中的直线和平面,判断下列说法是否正确:[ ](1)直线和平面的公共点个数可以是0个,1个或无数[ ](2)若,,//α⊂b b a 则α//a[ ](3)如果一直线和一平面平行,则这条直线和平面的任意直线平行[ ](4)如果一条直线和一个平面平行,则这条直线和这个平面内的无数条直线平行[ ](5)若两条直线同时和一个平面平行,则这两条直线平行[ ](6)过平面外一点,有且只有一条直线和已知平面平行[ ](7)过直线外一点,有无数个平面和已知直线平行[ ](8)若共面且b a b a ,,,//αα⊂,则b a //4. 关于空间中的平面,判断下列说法是否正确:[ ](1)两个平面的公共点的个数可以是0个,1个或无数[ ](2)若b a b a //,,βα⊂⊂,则βα//[ ](3)若βαβα//,,⊂⊂b a ,则a //b[ ](4)若βαα//,⊂a ,则β//a[ ](5)若αα//,//b a ,则b a //[ ](6)若βα//,//a a ,则βα//[ ](7)若一个平面内的无数条直线和另一个平面平行,则这两个平面平行[ ](8)若αβα⊂a ,//,则β//a[ ](9)若两个平面同时和第三个平面平行,则这两个平面平行[ ](10)若一个平面同两个平面相交且它们的交线平行,则两平面平行[ ](11)过平面外一点,有且只有一个平面和已知平面平行5. 关于直线与平面的垂直,判断下列说法是否正确:[ ](1)如果一直线垂直于一个平面内的所有直线,则这条直线垂直于这个平面[ ](2)若αα⊂⊥a l ,,则a l ⊥[ ](3)若m l m ⊥⊂,α,则α⊥l[ ](4)若n l m l n m ⊥⊥⊂,,,α,则α⊥l[ ](5)过一点有且只有一条直线和已知平面垂直[ ](6)过一点有无数个平面和已知直线垂直6. 关于平面和平面垂直,判断下列说法是否正确:[ ] (1)若,,βα⊥⊂a a 则βα⊥[ ] (2)若b a b a ⊥⊂⊂,,βα,则βα⊥[ ] (3)若,,,βαβα⊂⊂⊥b a ,则b a ⊥[ ] (4)若,,βαα⊥⊂a 则β⊥a[ ] (6)若γαβα//,⊥,则γβ⊥[ ] (7)垂直于同一个平面的两个平面平行[ ] (8)垂直于同一条直线的两个平面平行[ ] (9)过平面外一点有且只有一个平面与已知平面垂直7. 判断下列说法是否正确:[ ] (1)两条平行线和同一平面所成的角相等[ ] (2)若两条直线和同一平面所的角相等,则这两条直线平行[ ] (3)平面的平行线上所有的点到平面的距离都相等[ ] (4)若一条直线上有两点到一个平面的距离相等,则这条直线和平面平行练习十九 立体几何(二)1. 若平面的一条斜线长为2,它在平面内的射影的长为3,则这条斜线和平面所成的角为________.2. 在一个锐二面角的一个面内有一点,它到棱的距离是到另一个平面距离的2倍,则这个二面角的大小为________.3. 已知AB 为平面α的一条斜线,B 为斜足,α⊥AO ,O 为垂足,BC 为平面内的一条直线,︒=∠︒=∠45,60OBC ABC ,则斜线AB 与平面所成的角的大小为________.4. 观察题中正方体ABCD-A 1B 1C 1D 1中, 用图中已有的直线和平面填空:(1) 和直线BC 垂直的直线有_________________.(2) 和直线BB 1垂直且异面的直线有__________.(3) 和直线CC 1平行的平面有________________.(4) 和直线BC 垂直的平面有________________.(5) 和平面BD 1垂直的直线有________________.5. 在边长为a 正方体!111D C B A ABCD -中(1)C B C A 111与所成的角为________.(2)1AC 与平面ABCD 所成的角的余弦值为________.(3)平面ABCD 与平面11B BDD 所成的角为________.(4)平面ABCD 与平面11B ADC 所成的角为________.(5)连结11,,DA BA BD ,则二面角1A BD A --的正切值为________.(6)BC AA 与1的距离为________.(7)11BC AA 与的距离为________.6. 在棱长均为a 的正三棱锥ABC S -中,(1) 棱锥的高为______.(2) 棱锥的斜高为________.(3) SA 与底面ABC 的夹角的余弦值为________.(4) 二面角A BC S --的余弦值为________.(5) 取BC 中点M ,连结SM ,则AC 与SM 所成的角的余弦值是_____.(6) 若一截面与底面平行,交SA 于A ’,且SA’:A’A =2:1,则截面的面积为______.7. 在棱长均为a 的正四棱锥ABCD S -中,(1) 棱锥的高为______.(2) 棱锥的斜高为________.(3) SA 与底面ABCD 的夹角为________.(4) 二面角A BC S --的大小为________.8. 已知正四棱锥的底面边长为24,侧面与底面所成的角为︒45,那么它的侧面积为_________.,. 9. 在正三棱柱111C B A ABC -中,底面边长和侧棱长均为a , 取AA 1的中点M ,连结CM ,BM ,则二面角A BC M --的大小为 _________.10.已知长方体的长、宽、高分别是2、3、4,那么它的一条对角线长为_____.11. 在正三棱锥中,已知侧面都是直角三角形,那么底面边长为a 时,它的全面积是______.12. 若球的一截面的面积是π36,且截面到球心的距离为8,则这个球的体积为______,表面积为_________.13. 半径为R 球的内接正方体的体积为__________.14. 已知两个球的大圆面积比为1:4,则它们的半径之比为________,表面积之比为_______,体积之比为______.练习二十 立体几何(三)解答题:1. 在四棱锥ABCD P -中,底面是边长为a 的正方形,侧棱a PD =,a PC PA 2==.(1) 求证:ABCD PD 平面⊥;(2) 求证:AC PB ⊥;(3) 求P A 与底面所成角的大小;(4) 求PB 与底面所成角的余弦值.2. 在正四棱柱1111D C B A ABCD -中,AB =1,21=AA .(1) 求1BC 与ABCD 平面所成角的余弦值;(2) 证明:BD AC ⊥1;(3) 求1AC 与ABCD 平面所成角的余弦值.,.3. 在直三棱柱ABC-A 1B 1C 1中,D 是AB 的中点, AC =BC=2,AA 1=32.(1) 求证:DC D A ⊥1;(2) 求二面角A CD A --1的正切值;(3) 求二面角A BC A --1的大小.4. 四棱锥P -ABCD 的底面是正方形,PD ⊥底面ABCD , 且BD =6, PB 与底面所成角的正切值为66(1) 求证:PB ⊥AC ;(2) 求P 点到AC 的距离.。
高中会考数学练习题及讲解目

高中会考数学练习题及讲解目# 高中会考数学练习题及讲解## 一、选择题1. 题目:已知函数 \(f(x) = 3x^2 - 2x + 1\),求导后得到的导数函数为:- A. \(6x - 2\)- B. \(6x^2 - 4x + 1\)- C. \(f'(x) = 6x - 2\)- D. \(3x - 2\)答案:C解析:根据导数的定义,对于函数 \(f(x) = 3x^2 - 2x + 1\),其导数 \(f'(x)\) 计算如下:\[f'(x) = \frac{d}{dx}(3x^2 - 2x + 1) = 6x - 2\]2. 题目:下列哪个选项是不等式 \(x^2 - 5x + 6 \leq 0\) 的解集? - A. \(x \leq 1\) 或 \(x \geq 6\)- B. \(1 \leq x \leq 6\)- C. \(x \leq 6\) 或 \(x \geq 1\)- D. \(2 \leq x \leq 3\)答案:B解析:首先解方程 \(x^2 - 5x + 6 = 0\),得到 \(x = 2\) 或\(x = 3\)。
由于这是一个开口向上的二次函数,不等式 \(x^2 - 5x + 6 \leq 0\) 的解集是 \(x\) 在两个根之间,即 \(1 \leq x \leq 6\)。
## 二、填空题1. 题目:若 \(\sin(\alpha) = \frac{3}{5}\) 且 \(\alpha\) 在第一象限,求 \(\cos(\alpha)\) 的值。
答案:\(\frac{4}{5}\)解析:根据三角函数的基本关系,\(\sin^2(\alpha) +\cos^2(\alpha) = 1\)。
由于 \(\sin(\alpha) = \frac{3}{5}\),我们可以解出 \(\cos(\alpha)\):\[\cos(\alpha) = \sqrt{1 - \sin^2(\alpha)} = \sqrt{1 -\left(\frac{3}{5}\right)^2} = \frac{4}{5}\]2. 题目:若 \(\log_{10}(100) = 2\),求 \(\log_{10}(0.01)\) 的值。
普通高中数学会考练习题及答案

会考练习二第一部分 选择题(每小题3分,共60分)在每个小题给出的四个备选答案中,只有一个是符合题目要求的. 1. 已知集合{}123A =,,,{}345B =,,,那么集合AB 等于A. {3}B. {}12345,,,,C. {}1245,,,D. ∅2. 不等式2230x x +-<的解集是A. {|31}x x -<<B. {|13}x x -<<C. {|3x x <-,或1}x >D. {|1x x <-,或3}x >3. 如果函数()f x x α=的图象经过点(28),,那么α等于A. 1B. 2C. 3D. 44. 函数sin 2y x =的最小正周期是A.π4B.π2C. πD. 2π5. 已知四个函数 2y x =,||y x =,2xy =,2log y x =,其中偶函数是A. 2y x =B. ||y x =C. 2xy =D. 2log y x =6. 函数()cos f x x x =⋅的一个零点是A. 0B. 1C. πD. 2π7. 已知直线x c =与圆221x y +=相切,那么c 等于A. 1或1-B. 2或2-C. 3或3-D. 08. 在△ABC 中,M 是BC 的中点,设AB =a ,AC =b ,如果用a ,b 表示AM , 那么AM 等于A.()12-a b B. -a b C.1()2+a b D. +a b9. 已知向量(12)=,a ,(12)=-,b ,那么与2-a b 共线的一个向量是A. (64),B. (46),C. (04),D. (16),10. cos80cos 20sin80sin 20︒︒︒︒+的值是A.12B.2C.2D. 111. 设数列{}n a 的前n 项和为n S ,如果15a =-,12n n a a +=+,那么1S ,2S ,3S ,4S 中最小的是A. 1SB. 2SC. 3SD. 4S12. 当[30]x ∈-,时,函数223y x x =++的最小值是A. 1B. 2C. 3D. 413. 如果函数220()log 0xx f x x x ⎧≤⎪=⎨>⎪⎩,,,,那么(2)f 等于A. 0B.14C.12D. 114. 为应对自然灾害,某市应急救援指挥中心筹建医疗专家组. 现要从甲、乙、丙3位脑外科专家中随机选取2位进入专家组,那么甲被选中的概率是 A.14B.13C.12D.2315. 已知圆C 的圆心在y 轴上,半径为1,且经过点(12),,那么圆C 的方程为A. 22(1)1x y +-= B. 22(1)1x y -+= C. 221x y +=D. 22(2)1x y +-=16. 已知两点(00)O ,,(14)P ,,如果直线OP 与直线30ax y --=平行,那么a 等于A. 4-B. 4C. 14-D.1417. 在长度为6的线段AB 上任取一点C ,那么线段AC 的长度不超过2的概率是A.16B.14C.13D.1218. 函数4y x x=+的值域是 A. (,1][1,)-∞-+∞ B. (,2][2,)-∞-+∞C. (,3][3,)-∞-+∞D. (,4][4,)-∞-+∞19. 一个空间几何体的三视图如右图所示, 该几何体的侧面积...为 A. 100 B. 128 C. 144 D. 15220. 已知点()P x y ,的坐标满足||||1x y +≤,那么2x y +的最小值是 A. 3-B. 2-C. 1-D. 2俯视图左(侧)视图主(正)视图0.04分数0.030.020.01第二部分 非选择题(共40分)一、填空题(共4个小题,每小题3分,共12分) 21. 为普及环保知识,某校组织了以“节能减排我能行”为主题的知识竞赛. 经统计,全校500名同学的成绩全部介于60分与100分之间. 将成绩以10为组距分成以下4组:[6070),,[7080),,[8090),,[]90100,,得到如图所示的频率分布直方图,那么成绩大于或等于80分的学生人数为__ . 22. 已知4cos 5α=-,且π(π)2α∈,,那么sin α=__ ,tan (π)α-=__ . 23. 已知函数()2xf x =,如果lg3a =,lg 2b =,那么()f a __()f b (请在横线上填写“>”,“=”或“<”).24. 阅读下面的程序框图,运行相应的程序,输出的结果为__ .二、解答题(共3个小题,共28分) 25.(本小题满分9分)如图,三棱柱111ABC A B C -中,1A A ⊥底面ABC ,AB AC =,D 是BC 的中点 .(Ⅰ)求证 :BC ⊥平面1A AD ; (Ⅱ)若90BAC ∠=,14BC A D ==, 求三棱柱111ABC A B C -的体积 .26.(本小题满分9分)B 1C 1A 1DCBA在直角坐标系xOy 中,已知向量(,)OA k k =,(,)OB m m =-+, 其中00k m >>,.(Ⅰ)当1m k ==时,证明OA AB ⊥; (Ⅱ)求向量OA 和OB 夹角的大小; (Ⅲ)设3AB =,求OA OB +的最大值 .27.(本小题满分10分)已知数列{}n a 的前n 项和31n n S =-,数列{}n b 满足11b =,13(2)n n n b b a n -=+≥,记数列{}n b 的前n 项和为n T .(Ⅰ)证明{}n a 为等比数列 ; (Ⅱ)求n T ;(Ⅲ)设n n n P S T =+,若对于任意*n ∈N ,都有11(1)1(1)n n n n P P λ-+-<+-⋅成立,求实数λ的取值范围 .数学试卷答案及评分参考[说明]1. 第一部分选择题,机读阅卷.2. 第二部分包括填空题和解答题.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解答不同,正确者可参照评分标准给分.解答右端所注分数,表示考生正确做到这一步应得的累加分数.第一部分 选择题(共60分)选择题(每小题3分,共60分)第二部分 非选择题(共40分)一、填空题(每小题3分,共12分) 21. 350 22.35, 3423. > 24. 14二、解答题(共3个小题,共28分) 25.(本小题满分9分)如图,三棱柱111ABC A B C -中,1A A ⊥底面ABC ,AB AC =,D 是BC 的中点.(Ⅰ)求证 :BC ⊥平面1A AD ; (Ⅱ)若90BAC ∠=,14BC A D ==, 求三棱柱111ABC A B C -的体积.(Ⅰ)证明 :因为 1A A ⊥底面ABC ,且BC ⊂底面ABC , 所以 1A A BC ⊥.因为 AB AC =,D 是BC 的中点, 所以 AD BC ⊥. 因为 1A AAD A =,所以 BC ⊥平面1A AD . …………………………… 5分 (Ⅱ)解 :B 1C 1A 1DCBA因为 90BAC ∠=,D 是BC 的中点,4BC =, 所以 122AD BC ==. 所以 142ABCS BC AD ∆=⋅=. 因为 1A A ⊥底面ABC ,且AD ⊂底面ABC , 所以 1A A AD ⊥.在Rt △1A AD 中,14A D =,所以 1A A ==.所以 三棱柱111ABC A B C -的体积1ABC V S A A ∆=⋅=. ……… 9分26.(本小题满分9分)在直角坐标系xOy 中,已知向量(,)OA k k =,(,)OB m m =, 其中00k m >>,.(Ⅰ)当1m k ==时,证明OA AB ⊥; (Ⅱ)求向量OA 和OB 夹角的大小; (Ⅲ)设3AB =,求OA OB +的最大值 . (Ⅰ)证明 : 因为 1m k ==,所以 (11)OA =,,(11OB =.所以 (AB OB OA =-=.因为 30OA AB ⋅=-=,所以 OA AB ⊥. ……………………… 2分 (Ⅱ)解 :因为 ()OA k k =,,()OB m m =+,,且00k m >>,, 所以 2OA =,22OB =,2OA OB km ⋅=.设向量OA 和OB 的夹角为θ,所以 1cos 2OA OB OA OBθ⋅==. 所以向量OA 和OB 的夹角等于π3. …………………… 5分 (Ⅲ)解 :在△OAB 中,由余弦定理得 22π2cos33OA OB OA OB +-=. 因为 ()24OA OB OA OB +≤,所以 ()()()2223334OA OBOA OB OA OB OA OB+=+-≥+-.所以 ()212OA OB+≤,当且仅当3OA OB ==时,等号成立.所以 OA OB +的最大值为…………………… 9分27.(本小题满分10分)已知数列{}n a 的前n 项和31n n S =-,数列{}n b 满足11b =,13(2)n n n b b a n -=+≥,记数列{}n b 的前n 项和为n T .(Ⅰ)证明{}n a 为等比数列 ; (Ⅱ)求n T ;(Ⅲ)设n n n P S T =+,若对于任意*n ∈N ,都有11(1)1(1)n n nn P P λ-+-<+-⋅成立,求实数λ的取值范围 . (Ⅰ)证明 :因为 数列{}n a 的前n 项和31nn S =-, 所以 111(31)(31)23nn n n n n a S S ---=-=---=⋅ (2)n ≥.因为 1n =时,112a S ==,也适合上式, 所以 123n n a -=⋅ *()n ∈N .因为1123323n n n na a +-⋅==⋅,所以 数列{}n a 是首项为2,公比为3的等比数列. ……………… 2分 (Ⅱ)解 :当2n ≥时,11323n n n b b --=+⋅,将其变形为112233n n n n b b ---=+,即112233n n n n b b ----=.所以 数列13n n b -⎧⎫⎨⎬⎩⎭是首项为1013b =,公差为2的等差数列.所以112(1)213n n b n n -=+-=-.所以 1(21)3n n b n -=-⋅ *()n ∈N . 因为 0121133353(21)3n n T n -=⨯+⨯+⨯++-⋅, 所以 1233133353(21)3n n T n =⨯+⨯+⨯++-⋅. 两式相减得 121212(333)(21)3n n n T n -=--++++-⋅.整理得 (1)31n n T n =-⋅+ *()n ∈N . …………………………… 6分 (Ⅲ)解 :由 3nn n n P S T n =+=⋅, 得113(1)333n n n n P n nP n n ++⋅==+⋅+. 于是 11(1)1(1)n n n n P P λ-+-<+-⋅化为 1(1)1(1)33n n nn λ--<+-⋅+. (*) ① 当n 是正奇数时,(*)式可化为21333n λ<++, 显然,133n +大于0,且随着正奇数n 的增大而减小.由于(*)式对任意正奇数n 恒成立,所以 23λ≤. ② 当n 是正偶数时,(*)式可化为41333n λ>-++, 显然,133n +随着正偶数n 的增大而减小.由于(*)式对任意正偶数n 恒成立,所以411133239λ>-+=-⨯+.综上,实数λ的取值范围是112(]93-,.…………………………10分。
高中数学毕业会考分章节复习练习题

高二数学会考复习练习(1)<集合 简易逻辑 函数>一 选择题(没小题5分,共60分)1 设全集{}{}{}2,3,5,2,5,5U U A a C A ==-=,则a 的值是2 设集合1/2A x x⎧⎫=<⎨⎬⎩⎭,1/3B x x ⎧⎫=>⎨⎬⎩⎭,则A B =IA 11/32x x ⎧⎫<<⎨⎬⎩⎭B 1/2x x ⎧⎫>⎨⎬⎩⎭C 1/3x x ⎧<-⎨⎩或13x ⎫>⎬⎭D 1/3x x ⎧<-⎨⎩或12x ⎫>⎬⎭3 不等式1273x ≤-<的解集为A {}/45x x ≤<B {/4x x ≥或}5x ≤C {/3x x ≤或}2x >D {/23x x <≤或}45x ≤< 4 若不等式232x x a -++≥-的解集为实数R,则实数a 的取值范围为 A 3a -≤ B 3a ≤ C 32a -≤≤ D 5a ≥- 5 p :12,x x 是方程2560x x +-=的两根;q :125x x +=-.则p 是q 的A 充分但不必要条件B 必要但不充分条件C 充要条件D 既不充分也不必要条件6 已知(),x y 在映射f 的作用下的象是(,)x y x y +-,则在f 的作用下()1,2的原象是 A ()1,2 B ()3,1- C 31,22⎛⎫- ⎪⎝⎭D 13,22⎛⎫- ⎪⎝⎭7 已知函数()22(2)5f x x a x =+-+在区间()4,+∞上是增函数,则实数a 的取值范围是A 2a ≤-B 2a ≥-C 6a ≤-D 6a ≥-8 若函数()f x 的定义域为[]2,4-,则函数()()()g x f x f x =+-的定义域为 A []4,4- B []2,2- C []4,2-- D []2,4 9 已知函数()y f x =的反函数()112x f x -+=,则()1f =A 0B 1C 1-D 4 10 若2log 15a<,则实数a 的取值范围为 A 20,5⎛⎫⎪⎝⎭B ()20,1,5⎛⎫+∞ ⎪⎝⎭U C 2,15⎛⎫ ⎪⎝⎭D 2,5⎛⎫+∞ ⎪⎝⎭11 函数()()212log 2f x x x =-的单调递减区间为A (),0-∞B ()2,+∞C (],1-∞D [)1,+∞ 12 函数()1log 1axf x x+=-()0,1a a >≠是 A 非奇非偶函数 B 偶函数 C 奇函数 D 既是奇函数,又是偶函数 二 填空题(每题5分共30分)13 集合{}22,a a a -有4个子集,则a 的取值范围为 14 若集合{}1,2,3A =则满足A B A =U 的集合B 的个数是 个 15 不等式2312x x ->-的解集为 16 若不等式20x ax b ++>的解集为{/1x x <或}2x >,则a= ,b= 17 已知函数()()1,0,1x f x x x -=∈+∞+,则它的反函数()1f x -的定义域为 18 已知()214f x x x +=+,则()f x = 三 解答题(每小题10分共60分) 19 求下列各不等式的解集:(1) 123x x ->- (2)22301x x x --≥- 20 求证:()[]22f x x x =-+在区间1,2上是减函数21 设()f x 是定义在R 上的偶函数,且在区间(),0-∞上为增函数,又()()2232121f a a f a a -+>++ 求a 的取值范围.22 求函数()1f x = 23 画出下列图象(1) ()22f x x x =- (]2,2x ∈- (2) ()2log f x x = 23 已知:22329x y x +=,求22x y +的最大值与最小值高二数学会考复习练习(2)〈数列〉一 选择题(每题5分,共60分)1 已知等比数列{}n a 的公比13q =-,则代数式13572468a a a a a a a a ++++++=A 3-B 13- C 13D 32 设等差数列{}n a 的公差为d ,若它的前n 项和2n s n =-则A 21;2n a n d =-=-B 21;2n a n d =-=C 21;2n a n d =-+=-D 21;2n a n d =-+=3 等比数列公比为2,前4项之和为1,则它的前8项之和为 A 15 B 17 C 19 D 214 设x y ≠,且两数列12,,,x a a y 及123,,,,x b b b y 都是等差数列,则1212a ab b --= A 34 B 45 C 43 D 545 数列{}n a 是公差为2-的等差数列,若1479750a a a a ++++=L 则36999a a a a ++++L 等于A 182-B 78-C 148-D 82-6 公差不为0的等差数列的第2,3,6项组成等比数列,则公比为 A 1 B 2 C 3 D 47 1111242n++++=L A 11122n +- B 122n - C 112n - D 1122n --8 数列{}n a 和{}n b 都是等差数列1110010025,75,100a b a b ==+=则数列{}n n a b +的前100项之和为A 0B 100C 10000D 505000 9 数列{}n a 中。
【高中会考】2019年高中数学会考复习 必修2(含答案)
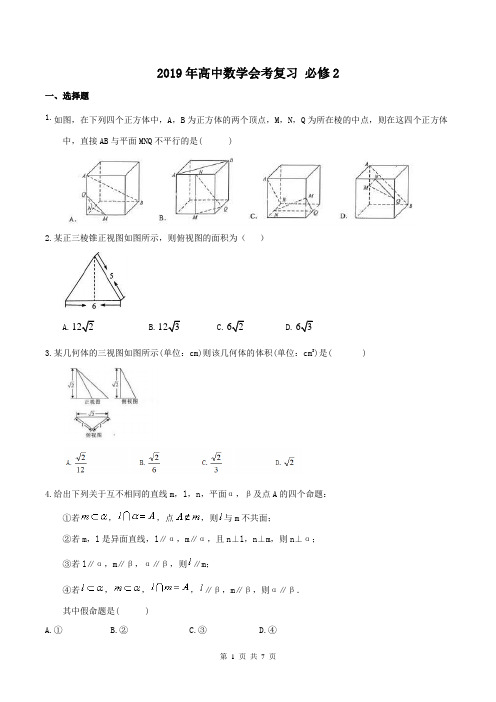
2019年高中数学会考复习必修2一、选择题1.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直接AB与平面MNQ不平行的是( )2.某正三棱锥正视图如图所示,则俯视图的面积为()A. B.3.某几何体的三视图如图所示(单位:cm)则该几何体的体积(单位:cm3)是( )4.给出下列关于互不相同的直线m,l,n,平面α,β及点A的四个命题:①若,,点,则与m不共面;②若m,l是异面直线,l∥α,m∥α,且n⊥l,n⊥m,则n⊥α;③若l∥α,m∥β,α∥β,则∥m;④若,,,∥β,m∥β,则α∥β.其中假命题是( )A.①B.②C.③D.④5.如图,在下列四个正方体图形中,A,B 为正方体的两个顶点,M,N,P 分别为其所在棱的中点,能得出AB//平面MNP 的图形的序号是( ).A.①③B.①④C.②③D.②④6.若m,n 是两条不同的直线,α,β,γ是三个不同的平面,则下列说法中正确的是( )A.α∥β,m ⸦α,n ⸦β→m//nB.α⊥γ,β⊥γ→α//βC.α∥β,m//n,m ⊥α→n ⊥βD.α∩β=m,β∩γ=n,m//n →α//β7.已知点)33,1(),3,1(-B A ,则直线AB 的倾斜角是( )A.3π B.6π C.32π D.65π8.直线l 过点M(-1,2),且与以P(-2,-3),Q(4,0)为端点的线段PQ 相交,则l 的斜率的取值范围是( )A.]5,52[-B.]5,0()0,52[ -C.]5,2()2,52[ππ -D.),5[]52,(+∞--∞ 9.过点(1,0)且与直线x-2y-2=0平行的直线方程是( )A.x-2y-1=0B.x-2y +1=0C.2x +y-2=0D.x +2y-1=0 10.已知直线l 1:(k-3)x +(3-k)y +1=0与直线l 2:2(k-3)x-2y +3=0垂直,则k 的值是( )A.2B.3C.2或3D.2或-311.直线(2k -1)x -(k +3)y -(k -11)=0(k ∈R)所经过的定点是( )A.(5,2)B.(2,3)C.(-0.5,3)D.(5,9) 12.以A(5,5),B(1,4),C(4,1)为顶点的三角形是( )A.直角三角形B.等腰三角形C.等边三角形D.等腰直角三角形 13.两直线2x +3y-k=0和x-ky +12=0的交点在y 轴上,那么k 的值为( )A.-24B.6C.±6D.2414.两条平行线l 1:3x +4y-2=0,l 2:9x +12y-10=0间的距离等于( )A.57 B.157 C.154 D.32 15.方程2x 2+2y 2-4x +8y +10=0表示的图形是( )A.一个点B.一个圆C.一条直线D.不存在16.当a 为任意实数时,直线(a-1)x-y+a+1=0恒过定点C ,则以C 为圆心,5为半径的圆的方程为( )A.(x-1)2+(y+2)2=5 B.(x+1)2+(y+2)2=5 C.(x+1)2+(y-2)2=5 D.(x-1)2+(y-2)2=5 17.圆x 2+y 2=1上的点到点M(3,4)的距离的最小值是( )A.1B.4C.5D.618.圆x 2+y 2-4x +6y-12=0过点(-1,0)的最大弦长为m ,最小弦长为n ,则m-n=( )A.10-27B.5-7C.10-33D.5-223 19.过原点且倾斜角为60°的直线被圆x 2+(y-2)2=4所截得的弦长为( )A.2B.2C.D.20.如果实数x ,y 满足(x ﹣2)2+y 2=2,则xy的范围是( ) A.(﹣1,1) B.[﹣1,1] C.(﹣∞,﹣1)∪(1,+∞) D.(﹣∞,﹣1]∪[1,+∞) 二、填空题21.已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是________.22.设m ,n 是两条不同的直线,α,β是两个不同的平面,下列四个命题:①若m ∥β,m ∥α,α∩β=n ,则m ∥n ; ②若α⊥β,m ∥α,则m ⊥β; ③若α⊥β,m ⊥β,则m ∥α; ④若m ⊥n ,m ⊥α,n ⊥β,则α⊥β. 真命题的有 .(填序号)23.如图,在棱长为1的正方体 ABCD-AB 1C 1D 1 中, M 和 N 分别是 A 1 B 1 和 BB 1 的中点,那么直线1AM 与 CN 所成角的余弦值为________.24.若过点P(1-a,1+a)和Q(3,2a)的直线的倾斜角为钝角,则实数a的取值范围是 .25.经过两直线x–2y+4=0和x+y–2=0的交点,且与直线3x–4y+5=0垂直的直线方程是 .26.圆x2+y2-4x=0在点P(1,3)处的切线方程为______________.三、解答题27.如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明MN∥平面PAB;(2)求四面体N-BCM的体积.28.已知三角形的三个顶点A(0,4),B(-2,6),C(-8,0).(1)求三角形三边所在直线的方程;(2)求AC边上的垂直平分线的方程.29.已知圆C过点A(4,7),B(-3,6),且圆心C在直线l:2x+y-5=0上,求圆C的方程.30.如图,在平面直角坐标系内,已知点A(1,0),B(-1,0),圆C的方程为x2+y2-6x-8y+21=0,点P为圆上的动点.(1)求过点A的圆C的切线方程.(2)求∣AP∣2+∣BP∣2的最大值及此时对应的点P的坐标.答案1. A.2.D.3.B;4.C5.B;6.C;7.C.8.D9.A; 10.C; 11.B. 12.B ; 13.C ; 14.C ; 15.A ; 16.C ; 17.B ; 18.A ; 19.A; 20.B. 21.答案为:38000 cm 322.答案为:①④; 23.答案为:0.4. 24.答案为:-2<a<1. 25.4x+3y-6=026.答案为:x -3y +2=0;27.解析:(1)证明:由已知得AM=AD=2,取BP 的中点T,连接AT,TN,由N 为PC 中点知TN ∥BC,TN=BC=2.又AD ∥BC,故TN ⸦AM,故四边形AMNT 为平行四边形,于是MN ∥AT. 因为AT ⊂平面PAB,MN ⊄平面PAB,所以MN ∥平面PAB.(2)因为PA ⊥平面ABCD,N 为PC 的中点,所以N 到平面ABCD 的距离为PA.取BC的中点E,连接AE.由AB=AC=3得AE⊥BC,AE==.由AM∥BC得M到BC的距离为,故S△BCM=×4×=2.所以四面体N-BCM的体积V N-BCM=·S△BCM·=.28.解:29.解:设圆C:(x-a)2+(y-b)2=r2(r>0),∵A,B∈圆C,C∈l,代入得a=1,b=3,r=5.故圆C的方程为(x-1)2+(y-3)2=25.法二:设圆C:(x-a)2+(y-b)2=r2(r>0),∵C∈l,∴2a+b-5=0,则b=5-2a,∴圆心为C(a,5-2a).由圆的定义得|AC|=|BC|,解得a=1,从而b=3,即圆心为C(1,3),半径r=|CA|=5.故圆C的方程为(x-1)2+(y-3)2=25.30.解:。
高中数学会考练习题

高中数学会考练习题高中数学会考练习题数学作为一门学科,是我们日常生活中不可或缺的一部分。
在高中阶段,数学的学习变得更加深入和复杂。
为了应对高中数学会考,我们需要进行大量的练习,以提高自己的解题能力和应试水平。
一、代数部分代数是数学中的重要分支,也是高中数学会考中的重要考点之一。
在代数部分的练习中,我们需要掌握各种代数式的化简、因式分解、方程的解法等。
例如,下面是一道典型的代数练习题:已知二次方程x²-3x-10=0,求方程的解。
解题思路:首先,我们可以尝试使用因式分解的方法来解这道题。
将方程进行因式分解,得到(x-5)(x+2)=0。
由零乘积法则可知,当(x-5)=0或(x+2)=0时,方程的解分别为x=5和x=-2。
二、几何部分几何是数学中的另一个重要分支,也是高中数学会考中的考点之一。
在几何部分的练习中,我们需要熟练掌握各种几何定理和几何推理方法。
例如,下面是一道典型的几何练习题:已知三角形ABC中,∠B=90°,AB=3,BC=4,求AC的长度。
解题思路:根据勾股定理,可以得到AC的长度为√(AB²+BC²)=√(3²+4²)=√(9+16)=√25=5。
三、概率与统计部分概率与统计是数学中的重要分支之一,也是高中数学会考中的考点之一。
在概率与统计部分的练习中,我们需要理解和应用各种概率和统计的概念和方法。
例如,下面是一道典型的概率与统计练习题:某班级有60人,其中有30人喜欢数学,20人喜欢英语,10人既喜欢数学又喜欢英语。
从班级中随机选取一人,求该人既不喜欢数学也不喜欢英语的概率。
解题思路:根据概率的定义,该人既不喜欢数学也不喜欢英语的概率等于不喜欢数学的人数加上不喜欢英语的人数减去既喜欢数学又喜欢英语的人数,再除以总人数。
即P= (60-30-20+10)/60=20/60=1/3。
通过大量的代数、几何、概率与统计的练习,我们可以提高自己的数学解题能力和应试水平。
高中数学会考试题及答案

高中数学会考试题及答案第一部分:选择题1. 下列哪个不是一次函数?A. f(x) = 2x + 3B. f(x) = 5x^2 - 3C. f(x) = 4x - 1D. f(x) = x/2 + 12. 已知直角三角形ABC,∠A = 90°,AB = 5 cm,AC = 12 cm,求BC的长度。
A. 10 cmB. 11 cmC. 13 cmD. 15 cm3. 解方程2x + 5 = 17的解为:A. x = 6B. x = 7C. x = 8D. x = 94. 已知函数f(x) = 3x - 2,求f(a + b)的值。
A. 4a + b - 2B. 2a + 3b - 2C. 3a + 3b - 2D. 3a + 3b + 25. 若三角形的三边分别为a, b, c,且满足c^2 = a^2 + b^2,这个三角形是:A. 等腰三角形B. 锐角三角形C. 直角三角形D. 钝角三角形第二部分:填空题6. 一个几何中心名为 ____________。
7. 一条直线和一个平面相交,交点个数为 ____________。
8. 未知数的指数为负数,表示 ____________。
9. 若两个角的和等于180°,则这两个角称为 ____________。
10. 在一个等边三角形中,每个内角大小为 ____________。
第三部分:解答题11. 用二分法求方程x^2 - 4x + 3 = 0在区间[1, 3]上的一个根的精确值。
12. 已知函数f(x) = 3x^2 - 12x + 9,求f(x)的最小值。
13. 若平面内通过点A(-2, 3)和点B(4, 1)的直线与x轴交于点C,求直线AC的斜率和方程。
答案:1. B2. C3. A4. B5. C6. 几何中心7. 一个8. 负数9. 互补角10. 60°11. 使用二分法可得根的精确值为2。
12. f(x)的最小值为 0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学毕业会考分章节复习练习题精选文档 TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-高二数学会考复习练习(1)<集合 简易逻辑 函数>一 选择题(没小题5分,共60分)1 设全集{}{}{}2,3,5,2,5,5U U A a C A ==-=,则a 的值是2 设集合1/2A x x ⎧⎫=<⎨⎬⎩⎭,1/3B x x ⎧⎫=>⎨⎬⎩⎭,则A B = A 11/32x x ⎧⎫<<⎨⎬⎩⎭B 1/2x x ⎧⎫>⎨⎬⎩⎭ C 1/3x x ⎧<-⎨⎩或13x ⎫>⎬⎭ D 1/3x x ⎧<-⎨⎩或12x ⎫>⎬⎭3 不等式1273x ≤-<的解集为A {}/45x x ≤<B {/4x x ≥或}5x ≤C {/3x x ≤或}2x >D {/23x x <≤或}45x ≤<4 若不等式232x x a -++≥-的解集为实数R,则实数a 的取值范围为A 3a -≤B 3a ≤C 32a -≤≤D 5a ≥-5 p :12,x x 是方程2560x x +-=的两根;q :125x x +=-.则p 是q 的A 充分但不必要条件B 必要但不充分条件C 充要条件D 既不充分也不必要条件6 已知(),x y 在映射f 的作用下的象是(,)x y x y +-,则在f 的作用下()1,2的原象是A ()1,2B ()3,1-C 31,22⎛⎫- ⎪⎝⎭D 13,22⎛⎫- ⎪⎝⎭7 已知函数()22(2)5f x x a x =+-+在区间()4,+∞上是增函数,则实数a 的取值范围是A 2a ≤-B 2a ≥-C 6a ≤-D 6a ≥-8 若函数()f x 的定义域为[]2,4-,则函数()()()g x f x f x =+-的定义域为A []4,4-B []2,2-C []4,2--D []2,49 已知函数()y f x =的反函数()112x f x -+=,则()1f =A 0B 1C 1-D 410 若2log 15a <,则实数a 的取值范围为A 20,5⎛⎫ ⎪⎝⎭B ()20,1,5⎛⎫+∞ ⎪⎝⎭C 2,15⎛⎫ ⎪⎝⎭D 2,5⎛⎫+∞ ⎪⎝⎭11 函数()()212log 2f x x x =-的单调递减区间为A (),0-∞B ()2,+∞C (],1-∞D [)1,+∞12 函数()1log 1ax f x x +=-()0,1a a >≠是A 非奇非偶函数B 偶函数C 奇函数D 既是奇函数,又是偶函数二 填空题(每题5分共30分)13 集合{}22,a a a -有4个子集,则a 的取值范围为14 若集合{}1,2,3A =则满足A B A =的集合B 的个数是 个15 不等式2312x x ->-的解集为16 若不等式20x ax b ++>的解集为{/1x x <或}2x >,则a= ,b=17 已知函数()()1,0,1x f x x x -=∈+∞+,则它的反函数()1f x -的定义域为18 已知()214f x x x +=+,则()f x =三 解答题(每小题10分共60分)19 求下列各不等式的解集:(1) 123x x ->- (2) 22301x x x --≥-20 求证:()[]22f x x x =-+在区间1,2上是减函数21 设()f x 是定义在R 上的偶函数,且在区间(),0-∞上为增函数,又()()2232121f a a f a a -+>++ 求a 的取值范围.2223 求函数()1f x =+23 画出下列图象(1) ()22f x x x =- (]2,2x ∈- (2) ()2log f x x =2425 已知:22329x y x +=,求22x y +的最大值与最小值高二数学会考复习练习(2)〈数列〉一 选择题(每题5分,共60分)12 已知等比数列{}n a 的公比13q =-,则代数式13572468a a a a a a a a ++++++=A 3-B 13-C 13D 3 34 设等差数列{}n a 的公差为d ,若它的前n 项和2n s n =-则A 21;2n a n d =-=-B 21;2n a n d =-=C 21;2n a n d =-+=-D 21;2n a n d =-+=56 等比数列公比为2,前4项之和为1,则它的前8项之和为A 15B 17C 19D 2178 设x y ≠,且两数列12,,,x a a y 及123,,,,x b b b y 都是等差数列,则1212a ab b --= A 34 B 45 C 43 D 54910 数列{}n a 是公差为2-的等差数列,若1479750a a a a ++++=则36999a a a a ++++等于A 182-B 78-C 148-D 82-1112 公差不为0的等差数列的第2,3,6项组成等比数列,则公比为A 1B 2C 3D 47 1111242n ++++= A11122n +- B 122n - C 112n - D 1122n -- 89 数列{}n a 和{}n b 都是等差数列1110010025,75,100a b a b ==+=则数列{}n n a b +的前100项之和为A 0B 100C 10000D 505000 1011 数列{}n a 中。
111,21,n n a a a n n N *+=-=-∈;则n a =A 101B 121C 122D 25312 13 在等比数列中,首项为98,末项为13,公比为23,则项数为A 4B 3C 5D 61415 一个等差数列共3m 项,若前2m 项的和为200,后2m 项的和为200,那么中间m 项的和为A 50B 75C 100D 2361617 设等差数列{}n a 满足81335a a =且10a >,n S 为前n 项的和;则n S 中最大的是A 10SB 11SC 20SD 21S二 填空题(每题5分,共30分)1819 等比数列{}n a 中,{}0n a >且569a a =,则3132310log log log a a a ++= 2021 在项数为21n +的等差数列中,所有奇数项和与所有偶数项和的比为 2223 数列2211,(12),(122),,(1222)n ++++++++的前99项之和为 2425 已知等差数列{}n a 的公差为正数,且3712a a =-,464a a +=-,则前20项的和20S =2627 等比数列{}n a 中,1234563,9a a a a a a ++=++=则131415a a a ++= 2829 有两个等差数列{}n a ,{}n b ,满足1212n n a a a b b b ++++++=723n n ++则55a b =三 解答题(每小题12分,共60分)19 有四个数,其中前三个成等差数列,后三个成等比数列,且第一个数与第四个数的和为8,第二个数与第三个数的和为4,求这四个数20设n S 是等差数列{}n a 的前n 项和,已知22S 与33S 的等比中项为42,42S S 与33S 的等差中项为1,求等差数列{}n a 的通项21 在数列{}n a 中,113n n na a a +=+,12a =,求{}n a 的通项公式,并求出4a22 在等比数列{}n a 中,前5项之和为531S =,2345662a a a a a ++++=(1)(2) 求{}n a 的首项1a 与公比q(3)(4) 求它的前7项之和7S23 已知等差数列{}n a 中,161,6a a ==,若数列{}n b 满足22n n b a =+(1)(2) 求证:数列{}n b 也是等差数列(3)(4) 求数列{}n b 的通项公式(5)(6) 求1122331111n n a b a b a b a b ++++高二数学会考复习练习(3)三角函数一、二、 选择题(共60分,每小题5分)1.2.若()0,2x π∈,函数y =+( )A .()0,πB .,2ππ⎛⎫ ⎪⎝⎭C .,2ππ⎛⎤ ⎥⎝⎦D .3,22ππ⎛⎫ ⎪⎝⎭3.4.下列函数中,最小正周期为π的偶函数是 ( )A .sin 2y x =B .cos 2x y =C .sin 2cos 2y x x =+D .221tan 1tan x y x-=+ 5. 6.函数22sin 2cos 3y x x =+-的最大值是 ( )A .1-B .12C .12- D .5-7.8.△ABC 中,若2cos sin sin B A C =,则△ABC 的形状一定是 ( )A .等腰直角三角形 B.直角三角形 C.等腰三角形 D.等边三角形 9. 10.一个直角三角形三内角的正弦值成等比数列,其最小角为( )A 1arccos2B1arcsin 2- C D 1arcsin 211. 12. 若3cos 25α=-且0,2πα⎡⎫∈⎪⎢⎣⎭,则sin α= ( ) AB C D .1513.14. 22sin 31tan31tan59sin 59︒+︒⋅︒+︒等于 ( )A .0B .1C .2 D.3 15.16. 若tan()3αβ+=,tan()5αβ-=,则tan 2α=____ ( )A .47B .47-C .12D .12-17. 18.设,(0,)2παβ∈且4tan 3α=,1tan 7β=,则αβ-=__( )A .3π B .4π C .6π D .8π10.下列说法正确的是 ( )A .一条射线绕端点按时针方向旋转形成一个正角;B .11360rad =弧长;C .1︒=周角的360分之一D .任何一个角α都可由公式l rα=计算弧度数(其中l 为以角α为圆心角时所对圆弧的长,r 为圆半径) 11.设sin sin 2x y +=cos cos x y +的取值范围为 ( ) A.⎡⎢⎣⎦B.⎡⎤⎢⎥⎣⎦C.⎡⎢⎣⎦ D .17,22⎡⎤-⎢⎥⎣⎦12.函数2sin cos y x x x =⋅+ ( )A .2πB .πC .2π D .32π二、填空题(共16分,每小题6分)13.若tan 2α=,则22sin 2sin cos 3cos 2αααα+⋅++的值为__________.14.△ABC 若sin()sin()A B C A B C +-=-+,则△ABC 的形状是__________.15.若52sin()2x π+x =_____________.16.给出下列命题①存在实数α,使sin cos 1αα⋅=成立;②在在实数α,使3sin cos 2αα+=成立;③函数5sin(2)2y x =-是偶函数;④方程8x π=是函数5sin(2)4y x π=+的图象的一条对称轴方程。
