万有引力知识点总结23573
高中物理万有引力知识点总结

高中物理万有引力知识点总结1. 牛顿的万有引力定律:任何两个物体间都存在引力,这个引力与它们的质量成正比,与它们之间距离的平方成反比。
这就是牛顿的万有引力定律。
公式表示为:F=G(m1m2)/r^2,其中F是两个物体间的引力,m1和m2分别是两个物体的质量,r是它们之间的距离,G是万有引力常量。
2. 万有引力定律的应用:天体运动:万有引力定律为解释和预测天体运动提供了基础。
例如,行星绕太阳的运动,卫星绕地球的运动等。
重力加速度:在地球表面,万有引力定律可以用来解释重力加速度的存在。
重力加速度是由地球的质量产生的万有引力引起的。
3. 开普勒三定律:第一定律(轨道定律):所有行星绕太阳的轨道都是椭圆,太阳在其中一个焦点上。
第二定律(面积定律):对于任何行星,它与太阳的连线在相同的时间内扫过的面积相等。
第三定律(周期定律):所有行星绕太阳一周的周期的平方与它们轨道半长轴的立方之比是一个常数。
4. 万有引力定律与天体运动的关系:通过万有引力定律和牛顿第二定律(F=ma),我们可以推导出天体运动的规律。
例如,行星的轨道周期与其轨道半径的三次方和质量的二次方之间的关系,这就是开普勒第三定律的来源。
5. 人造卫星:人造卫星是利用万有引力定律进行设计和操作的。
通过调整卫星的轨道和速度,可以实现各种任务,如通信、气象观测、导航等。
6. 逃逸速度:逃逸速度是指一个物体从某天体表面发射出去,要逃离该天体的引力束缚所需要的最小速度。
逃逸速度的计算涉及到万有引力定律和动能定理。
以上就是高中物理中万有引力知识点的主要内容。
掌握这些知识,可以帮助我们更好地理解和预测天体运动,以及设计和操作人造卫星等任务。
物理必修2万有引力知识点总结

物理必修2万有引力知识点总结
万有引力定律揭示了天体运动的规律,在天文学上和宇宙航行计算方面有着广泛的应用。
下面是店铺给大家带来的物理必修2万有引力知识点总结,希望对你有帮助。
物理必修2万有引力知识点
(1)万有引力定律:自然界的一切物体都相互吸引,两个物体间引力的大小跟它们的质量的乘积成正比,跟它们的距离的平方成反比。
万有引力公式:
,其中 r 指球心间的距离。
(2)三种宇宙速度:
① 第一宇宙速度:v 1 =7.9km/s,人造卫星的最小发射速度(此时卫星近表面运行),也是地球卫星的最大环绕速度。
② 第二宇宙速度:v 2 =11.2km/s,使物体挣脱地球引力束缚的最小发射速度。
③ 第三宇宙速度:v 3 =16.7km/s,使物体挣脱太阳引力束缚的最小发射速度。
(3)卫星运行中各物理量与轨道半径的关系:
随着轨道半径的逐渐增大,向心加速度,线速度,角速度将逐渐减小,周期将逐渐增大。
(4)地球同步卫星位于赤道上方某一高度的稳定轨道上,相对于地面静止的,且绕地球运动的周期等于地球的自转周期,离地面高度为:所有地球同步卫星的轨道一定在赤道平面内,并且只有一条。
所有同步卫星都在这条轨道上,以大小相同的线速度,角速度和周期运行。
(5)卫星的超重和失重
“超重”发生在卫星进入轨道的加速上升过程和回收时的减速下降过程。
“失重”发生在卫星进入轨道后正常运转时,并且卫星上的物体完全“失重”,所以在卫星上凡是制造原理与重力有关的仪器都不能
正常使用.。
物理万有引力知识点总结

物理万有引力知识点总结物理万有引力是指物体之间存在的吸引力或引力的力量。
以下是物理万有引力的一些主要知识点总结:1. 万有引力定律:万有引力定律是描述物体之间引力关系的公式,它由牛顿提出。
定律表明,两个物体之间的引力大小与它们质量的乘积成正比,与它们之间的距离的平方成反比。
万有引力定律的公式为F = G * ((m1 * m2) / r^2),其中F表示引力的大小,m1和m2表示两个物体的质量,r表示它们之间的距离,G为引力常数。
2. 引力的性质:物理万有引力具有以下性质:- 引力具有吸引性,它总是指向两个物体之间的中心。
- 引力大小与物体质量成正比,质量越大,引力越大。
- 引力大小与物体距离的平方成反比,距离越近,引力越大。
- 引力作用力对是相互的,即每个物体对另一个物体都有一个相等大小但方向相反的引力。
3. 重力:重力是地球对物体产生的引力。
重力是物体的质量与地球质量之间的吸引力。
重力的大小可以使用万有引力定律计算。
重力使物体朝着地面方向下落,并使物体保持在地球表面。
地球上的物体之间的重力也可以用牛顿的万有引力定律来计算。
4. 行星运动和轨道:根据万有引力定律,行星在太阳的引力作用下绕太阳旋转。
行星的轨道呈椭圆形,太阳位于椭圆的一个焦点上。
行星轨道上离太阳近的部分称为近日点,离太阳远的部分称为远日点。
5. 引力与质量的关系:根据万有引力定律,引力的大小与物体质量成正比。
更大质量的物体将具有更大的引力。
这解释了为什么地球的引力比月球的引力大,因为地球的质量比月球大。
以上是物理万有引力的一些重要知识点总结。
物理万有引力定律是物理学中一个重要的基本定律,它解释了宇宙中物体之间相互吸引的原因,并在天体运动和宇宙学研究中起到关键作用。
(完整版)万有引力定律公式总结

万有引力定律知识点班级: 姓名:一、三种模型1、匀速圆周运动模型:无论自然天体还是人造天体都可以看成质点,围绕中心天体做匀速圆周运动。
2、双星模型:将两颗彼此距离较近的恒星称为双星,它们相互之间的万有引力提供各自转动的向心力.3、“天体相遇"模型:两天体相遇,实际上是指两天体相距最近.二、两种学说1、地心说:代表人物是古希腊科学托勒密2、日心说:代表人物是波兰天文学家哥白尼三、两个定律 第一定律(椭圆定律):所有行星绕太阳的运动轨道都是椭圆,太阳位于椭圆的每一个焦点上。
第二定律(面积定律):对每一个行星而言,太阳和行星的连线,在相等时间内扫过相同的面积。
第三定律(周期定律):所有行星绕太阳运动的椭圆轨道半长轴R 的三次方跟公转周期T 的二次方的比值都相等.(表达式) 四、基础公式线速度:v ==== 角速度:== == 向心力:F=m =m(2r=m (2)2r= m (2)2r=m =m 向心加速度:a== (2r= (2)2r= (2)2r== 五、两个基本思路 1.万有引力提供向心力:ma r T m r m r v m r M G ====222224m πω 2.忽略地球自转的影响:mg RGM =2m (2g R GM =,黄金代换式) 六、测量中心天体的质量和密度测质量: 1.已知表面重力加速度g ,和地球半径R.(mg R GM =2m ,则G gR M 2=)一般用于地球 2.已知环绕天体周期T 和轨道半径r 。
(r T m r Mm G 2224π= ,则2324GTr M π=) 3.已知环绕天体的线速度v 和轨道半径r.(r v m rMm G 22=,则G r v M 2=) 4.已知环绕天体的角速度ω和轨道半径r (r m rMm G 22ω=,则G r M 32ω=) 5.已知环绕天体的线速度v 和周期T (Tr v π2=,r v m r M G 22m =,联立得G T M π2v 3=)测密度:已知环绕天体的质量m 、周期T 、轨道半径r.中心天体的半径R ,求中心天体的密度ρ 解:由万有引力充当向心力r T m r Mm G 2224π= 则2324GTr M π=——① 又334R V M πρρ⋅==—-② 联立两式得:3233R GT r πρ= 当R=r 时,有23GTπρ= 注:R 中心天体半径,r 轨道半径,球体体积公式334R V π=七、星球表面重力加速度、轨道重力加速度问题1.在星球表面: 2RGM mg =(g 为表面重力加速度,R 为星球半径) 2.离地面高h: 2)(h R GM g m +='(g '为h 高处的重力加速度) 联立得g'与g 的关系: 22)('h R gR g += 八、卫星绕行的向心加速度、速度、角速度、周期与半径的关系1.ma r M G =2m ,则2a rM G =(卫星离地心越远,向心加速度越小) 2.r v m rMm G 22=,则r GM v =(卫星离地心越远,它运行的速度越小) 3.r m rMm G 22ω=,则3r GM =ω(卫星离的心越远,它运行的角速度越小) 4.r Tm r Mm G 2224π=,则GMT 32r 4π=(卫星离的心越远,它运行的周期越大) 九、三大宇宙速度 第一宇宙速度(环绕速度):7。
万有引力知识点汇总
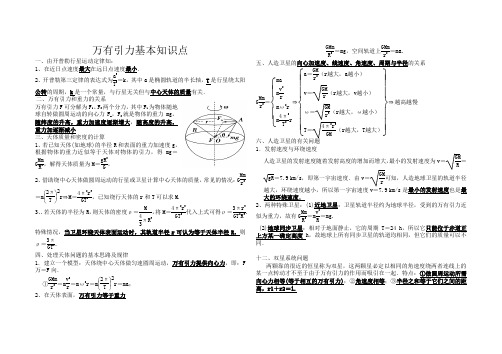
万有引力基本知识点一、由开普勒行星运动定律知:1、在近日点速度最大在远日点速度最小.2、开普勒第三定律的表达式为a 3T2=k ,其中a 是椭圆轨道的半长轴,T 是行星绕太阳公转的周期,k 是一个常量,与行星无关但与中心天体的质量有关. 二、万有引力和重力的关系 万有引力F 可分解为F 1、F 2两个分力,其中F 1为物体随地球自转做圆周运动的向心力F n ,F 2就是物体的重力mg 。
随纬度的升高,重力加速度逐渐增大,随高度的升高,重力加逐渐减小三、天体质量和密度的计算 1、若已知天体(如地球)的半径R 和表面的重力加速度g ,根据物体的重力近似等于天体对物体的引力,得mg =G Mm R 2,解得天体质量为M =gR 2G, 2、借助绕中心天体做圆周运动的行星或卫星计算中心天体的质量,常见的情况:G Mmr2=m ⎝ ⎛⎭⎪⎫2πT 2r ⇒M =4π2r 3GT 2,已知绕行天体的r 和T 可以求M.3、.若天体的半径为R ,则天体的密度ρ=M 43πR 3,将M =4π2r 3GT 2代入上式可得ρ=3πr 3GT 2R 3.特殊情况,当卫星环绕天体表面运动时,其轨道半径r 可认为等于天体半径R ,则ρ=3πGT2.四、处理天体问题的基本思路及规律1.建立一个模型:天体绕中心天体做匀速圆周运动,万有引力提供向心力,即:F 万=F 向.①GMm r 2=m v 2r =m ω2r =m ⎝ ⎛⎭⎪⎫2πT 2r =ma ; 2、在天体表面,万有引力等于重力GMm R 2=mg ,空间轨道上GMmr 2=ma. 五、人造卫星的向心加速度、线速度、角速度、周期与半径的关系G Mmr 2=⎩⎪⎨⎪⎧mam v 2r m ω2rm 4π2T 2r ⇒⎩⎪⎪⎨⎪⎪⎧⎭⎪⎪⎬⎪⎪⎫a =GMr 2(r 越大,a 越小)v =GMr(r 越大,v 越小)ω=GMr 3(r 越大,ω越小)T =4π2r 3GM(r 越大,T 越大)⇒越高越慢 六、人造卫星的有关问题1.发射速度与环绕速度人造卫星的发射速度随着发射高度的增加而增大,最小的发射速度为v =GMR=gR =7.9 km/s ,即第一宇宙速度.由v =GMr可知,人造地球卫星的轨道半径越大,环绕速度越小,所以第一宇宙速度v =7.9 km/s 是最小的发射速度也是最大的环绕速度.2、两种特殊卫星:(1)近地卫星:卫星轨道半径约为地球半径,受到的万有引力近似为重力,故有G Mm R 2=m v 2R=mg.(2)地球同步卫星:相对于地面静止,它的周期T =24 h ,所以它只能位于赤道正上方某一确定高度h ,故地球上所有同步卫星的轨道均相同,但它们的质量可以不同.十二、双星系统问题两颗靠的很近的恒星称为双星,这两颗星必定以相同的角速度绕两者连线上的某一点转动才不至于由于万有引力的作用而吸引在一起.特点:①做圆周运动所需向心力相等(等于相互的万有引力);②角速度相等;③半径之和等于它们之间的距离,r1+r2=l.。
万有引力知识点汇总

万有引力知识点汇总在我们的日常生活中,物体的下落、天体的运行,都离不开万有引力的作用。
万有引力是物理学中一个非常重要的概念,它不仅解释了许多自然现象,也为人类探索宇宙提供了理论基础。
接下来,让我们一起详细了解一下万有引力的相关知识点。
一、万有引力定律的发现万有引力定律是由英国科学家牛顿发现的。
据说,牛顿在看到苹果从树上落下时,开始思考物体下落的原因,并最终得出了万有引力定律。
牛顿的思考是基于对天体运动的观察和研究。
当时,天文学家开普勒已经发现了行星运动的三大定律,但对于行星为什么会按照这样的规律运动,还没有一个合理的解释。
牛顿通过深入的思考和数学推导,得出了万有引力定律,成功地解释了行星的运动规律。
二、万有引力定律的内容万有引力定律的内容是:任何两个物体之间都存在相互吸引的力,这个力的大小与两个物体的质量成正比,与它们之间的距离的平方成反比。
用公式表示为:$F = G\frac{m_1m_2}{r^2}$其中,$F$表示两个物体之间的引力,$G$是万有引力常量,其值约为$667×10^{-11} N·m^2/kg^2$,$m_1$和$m_2$分别表示两个物体的质量,$r$表示两个物体质心之间的距离。
三、万有引力常量的测定万有引力常量$G$的测定是一个非常重要的实验。
英国科学家卡文迪许通过巧妙的实验设计,利用扭秤实验测量出了$G$的值。
卡文迪许的实验装置非常精巧。
他将两个小铅球分别固定在一根轻质横杆的两端,横杆中间用一根细丝悬挂起来,形成一个扭秤。
然后,他再用两个大铅球分别靠近两个小铅球,由于万有引力的作用,横杆会发生扭转。
通过测量横杆的扭转角度,就可以计算出万有引力的大小,从而推算出$G$的值。
四、万有引力定律的适用范围万有引力定律适用于两个质点之间的相互作用。
但在实际情况中,大多数物体都不能看作质点。
对于质量分布均匀的球体,可以将其视为质量集中在球心的质点来计算引力。
当两个物体之间的距离远大于物体的尺寸时,也可以近似地将物体看作质点来计算引力。
万有引力定律知识点总结

万有引力定律知识点总结万有引力定律一.开普勒运动定律 (1)开普勒第一定律:所有的行星绕太阳运动的轨道都是,太阳处在所有椭圆的一个上.相等.D.两个物体间的引力总是大小相等,方向相反的,是一对平衡力:三、万有引力和重力不考虑自转的情况下,F 万=mg(2)开普勒第二定律:对于每一个行星而言,太阳和行星的连线在相等的时间内扫过的 (3)开普勒第三定律:所有行星的轨道的的比值都相等.四.天体表面重力加速度问题)例 1:火星和木星沿各自的椭圆轨道绕太阳运行,根据开普勒行星运动定律可知(A.火星与木星公转周期相等 B.火星和木星绕太阳运行速度的大小始终相等 C.太阳位于木星运行椭圆轨道的某焦点上 D.相同时间内,火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积设天体表面重力加速度为 g,天体半径为 R,由重力加速度的关系为g1 R22 M 1 ? ? g 2 R12 M 2得 g= GM ,由此推得两个不同天体表面 R2例3:据报道,最近在太阳系外发现了首颗“宜居”行星,其质量约为地球质量的 6.4 倍,一个在地球表面重量为 600 N 的人在这个行星表面的重量将变为960 N,由此可推知该行星的半径与地球半径之比约为 A.0.5 B.2. C.3.2 D.4 五.天体质量和密度的计算二.万有引力定律 (1) 公式:F= ,其中 G ? 6.67 ? 10?11 N ? m 2 / kg 2 ,称为为有引力恒量。
间的相互作用,当两个物体间的距离远远大于物体本身间的距离.对于均匀的球体,r 是两1.只能求中心天体的质量2. 只要用实验方法测出卫星做圆周运动的半径 r 及运行周期 T,就可以算出天体的质量 M.若知道行星的半径则可得行星的密度 4? 2 3?r 2 4? 2 r 3 M mM M G 2 =m 2 r,由此可得:M= ;ρ = = = (R 为行星的半径) 2 4 3 GT 2 R 3 V GT T r ?R3(2) 适用条件:严格地说公式只适用于的大小时,公式也可近似使用,但此时 r 应为两物体间的距离对于质量为 m 1 和质量为 m 2 的两个物体间的万有引力的表达式 F=Gm1m2 r2例 2:下()例4:登月火箭关闭发动机在离月球表面112 km 的空中沿圆形轨道运动,周期是 120.5 min,月球的半径是 1740 km,根据这组数据计算月球的质量和平均密度.土星 29.5列说法正确的是公转周期(年)水星 0.241金星 0.615地球 1.0火星 1.88木星 11.86A.公式中的 G 是引力常量,它是人为规定的 B.当两物体间的距离 r 趋于零时,万有引力趋于无穷大 C.两物体间的引力大小一定是相等的六、讨论天体运动规律的基本思路基本方法:把天体的运动看成是匀速圆周运动,其所需向心力由万有引力提供。
万有引力知识点汇总

万有引力开普勒行星运动定律1.所有行星绕太阳运动的轨道都是椭圆;太阳处在椭圆的一个焦点上..2.对任意一个行星来说;它与太阳的连线在相等的时间内扫过相等的面积..3.所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等.此比值的大小只与有关;在不同的星系中;此比值是不同的.错误!=k一、对开普勒三定律的理解1.开普勒第一定律说明了不同行星绕太阳运动时的椭圆轨道是不同的;但有一个共同的焦点.2.行星靠近太阳的过程中都是向心运动;速度增加;在近日点速度最大;行星远离太阳的时候都是离心运动;速度减小;在远日点速度最小.3.开普勒第三定律的表达式为错误!=k;其中a是椭圆轨道的半长轴;T是行星绕太阳公转的周期;k是一个常量;与行星无关但与中心天体的质量有关.二、开普勒三定律的应用1.开普勒定律不仅适用于行星绕太阳的运转;也适用于卫星绕地球的运转.2.表达式错误!=k中的常数k只与中心天体的质量有关.如研究行星绕太阳运动时; 常数k 只与太阳的质量有关;研究卫星绕地球运动时;常数k只与地球的质量有关.三、太阳与行星间的引力1.模型简化:行星以太阳为圆心做匀速圆周运动;太阳对行星的引力提供了行星做匀速圆周运一、太阳与行星间的引力2.万有引力的三个特性1普遍性:万有引力不仅存在于太阳与行星、地球与月球之间;宇宙间任何两个有质量的物体之间都存在着这种相互吸引的力.2相互性:两个有质量的物体之间的万有引力是一对作用力和反作用力;总是满足牛顿第三定律.3宏观性:地面上的一般物体之间的万有引力很小;与其他力比较可忽略不计;但在质量巨大的天体之间或天体与其附近的物体之间;万有引力起着决定性作用.四、万有引力和重力的关系1. 万有引力和重力的关系如图6-2、3-3所示;设地球的质量为M ;半径为R ;A 处物体的质量为m ;则物体受到地球的吸引力为F ;方向指向地心O ;由万有引力公式得F =G 错误!.引力F 可分解为F 1、F 2两个分力;其中F 1为物体随地球自转做圆周运动的向心力F n ;F 2就是物体的重力mg2.近似关系:如果忽略地球的自转;则万有引力和重力的关系为:mg =错误!;g 为地球表面的重力加速度.关系式2G Mm/R mg =即2gr G M =3.随高度的变化:在高空中的物体所受到的万有引力可认为等于它在高空中所受的重力mg ′=G 错误!;在地球表面时mg =G 错误!;所以在距地面h 处的重力加速度g ′=错误!g .五.计算天体的质量行星绕太阳;卫星绕行星做匀速圆周运动;为他们提供向心力的就是他们之间的万有引力;测量出环绕周期和环绕半径..公式:R 22/T 2m GMm/R )(π=即23/GT R 4M π= 观测行星的运动;计算太阳的质量;观测卫星的运动;计算行星的质量..六.天体质量和密度的计算一.“天体自身求解”:若已知天体如地球的半径R 和表面的重力加速度g ;根据物体的重力近似等于天体对物体的引力;得mg =G 错误!;解得天体质量为M =错误!;因g 、R 是天体自身的参量;故称“自力更生法”.2“借助外援法”:借助绕中心天体做圆周运动的行星或卫星计算中心天体的质量;常见的情况:G 错误!=m 错误!错误!r M =错误!;已知绕行天体的r 和T 可以求M .二.若天体的半径为R ;则天体的密度ρ=错误!;将M =错误!代入上式可得ρ=错误!.特殊情况;当卫星环绕天体表面运动时;其轨道半径r 可认为等于天体半径R ;则ρ=错误!.七.天体运动的分析与计算1.基本思路:一般行星或卫星的运动可看作匀速圆周运动;所需向心力由 中心天体对它的万有引力提供.2.常用关系:1G 错误!=ma 向=m 错误!=m ω2r =m 错误!r2mg =G 错误!物体在天体表面时受到的万有引力等于物体重 力;整理可得:gR 2=GM ;该公式通常被称为黄金代换式.八.四个重要结论:设质量为m的天体绕另一质量为M的中心天体做半径为r的匀速圆周运动. 1由G错误!=m错误!得v=错误!;r越大;v越小.2由G错误!=mω2r得ω=错误!;r越大;ω越小.3由G错误!=m错误!错误!r得T=2π错误!;r越大;T越大. 4由G错误!=ma向得a向=错误!;r 越大;a向越小.以上结论可总结为“一定四定;越远越慢”.九.一、处理天体问题的基本思路及规律1.天体问题的两步求解法1建立一个模型:天体绕中心天体做匀速圆周运动;万有引力提供向心力;即:F万=F向.2写出两组式子:①错误!=m错误!=mω2r=m错误!错误!r=ma;②代换关系:天体表面错误!=mg;空间轨道上错误!=ma.十.人造卫星的向心加速度、线速度、角速度、周期与半径的关系G错误!=错误!错误!错误!十一.二、人造卫星的有关问题1.发射速度与环绕速度人造卫星的发射速度随着发射高度的增加而增大;最小的发射速度为v=错误!=错误!=7.9 km/s;即第一宇宙速度.由v=错误!可知;人造地球卫星的轨道半径越大;环绕速度越小;所以第一宇宙速度v=7.9 km/s是最小的发射速度也是最大的环绕速度.2.两类运动——稳定运行和变轨运行卫星绕天体稳定运行时;错误!=m错误!.当卫星速度v突然变化时;F万和m错误!不再相等.当F>m错误!时;卫星做近心运动;当F万<m错误!时;卫星做离心运动.万3.两种特殊卫星:1近地卫星:卫星轨道半径约为地球半径;受到的万有引力近似为重力;故有G错误!=m错误!=mg.2地球同步卫星:相对于地面静止;它的周期T=24 h;所以它只能位于赤道正上方某一确定高度h;故地球上所有同步卫星的轨道均相同;但它们的质量可以不同.十二、双星系统问题两颗靠的很近的恒星称为双星;这两颗星必定以相同的角速度绕两者连线上的某一点转动才不至于由于万有引力的作用而吸引在一起.特点:①做圆周运动所需向心力相等等于相互的万有引力;②角速度相等;③半径之和等于它们之间的距离;r1+r2=l.您好;我是李老师;这是我课前对本次物理课的规划;以上是万有引力部分所有的知识点..望您在王粤回去后;监督他完成相应的作业以及复习功课;并签字..下次课让他把这个带回来;以便我可以第一时间掌握他的复习情况;谢谢..家长签字:。
高考物理万有引力定律知识点总结

高考物理万有引力定律知识点总结万有引力定律是物理学中的一条基础定律,揭示了物体之间的引力相互作用。
下面是对万有引力定律的一些知识点的总结,具体内容如下:1.引力的定义:引力是物体之间由于质量而产生的相互吸引力。
即所有物体都会对其他物体施加引力。
2.万有引力定律的表述:万有引力定律表明,任何两个物体之间的引力大小与它们的质量成正比,与它们之间的距离的平方成反比。
数学表述为F=G*(m1*m2)/r^2,其中F为引力大小,m1和m2分别为两个物体的质量,r为两个物体质心之间的距离,G为万有引力常数。
3. 万有引力定律的量纲:根据万有引力定律的表达式可以得出,引力的量纲为质量的平方与距离的立方的比值。
即[N] = [kg]^2/[m]^35.质心与引力:在万有引力定律中,两个物体之间的引力作用于它们的质心之间的位置。
所以在计算引力大小时,可以将质点近似看作质心。
6.引力与质量的关系:根据万有引力定律可知,引力的大小与物体的质量成正比。
质量越大,引力也越大;质量越小,引力也越小。
7.引力与距离的关系:根据万有引力定律可知,引力的大小与物体之间的距离的平方成反比。
距离越大,引力越小;距离越小,引力越大。
8.万有引力定律的应用:万有引力定律可以用来解释许多物理现象,如行星绕太阳运动、地球上物体的重力、卫星绕地球运动等。
同时,它也是开展天体力学研究的基础,有助于我们对宇宙的理解和天体运行规律的探索。
9.引力的方向:引力的方向始终指向两物体间的质心连线上。
即两物体之间的引力方向与它们质心连线的方向相同。
10.引力的叠加原理:若多个物体同时作用于一个物体上,则它们对该物体的引力按照叠加原理进行叠加。
总结:万有引力定律是物理学中的一条重要定律,揭示了物体之间的引力相互作用规律。
它的数学表达式清晰明确,并可以通过实验求得引力常数G的数值。
万有引力定律对于解释重力现象、天体运行规律等起着重要作用,是天体力学研究的基础。
万有引力知识点总结(必备3篇)

万有引力知识点总结第1篇1.开普勒第三定律:t2/r3=k(=42/gm){r:轨道半径,t:周期,k:常量(与行星质量无关,取决于中心天体的质量)}2.万有引力定律:f=gm1m2/r2(g=,方向在它们的连线上)3.天体上的重力和重力加速度:gmm/r2=mg;g=gm/r2{r:天体半径(m),m:天体质量(kg)}4.卫星绕行速度、角速度、周期:v=(gm/r)1/2;=(gm/r3)1/2;t=2(r3/gm)1/2{m:中心天体质量}5.第一(二、三)宇宙速度v1=(g地r地)1/2=(gm/r地)1/2=;v2=;v3=6.地球同步卫星gmm/(r地+h)2=m42(r地+h)/t2{h36000km,h:距地球表面的高度,r地:地球的半径}注:(1)天体运动所需的xxx力由万有引力提供,f向=f万;(2)应用万有引力定律可估算天体的质量密度等;(3)地球同步卫星只能运行于赤道上空,运行周期和地球自转周期相同;(4)卫星轨道半径变小时,势能变小、动能变大、速度变大、周期变小(一同三反);(5)地球卫星的最大环绕速度和最小发*速度均为。
万有引力知识点总结第2篇定义:万有引力是由于物体具有质量而在物体之间产生的一种相互作用。
它的大小和物体的质量以及两个物体之间的距离有关。
物体的质量越大,它们之间的万有引力就越大;物体之间的距离越远,它们之间的万有引力就越小。
两个可看作质点的物体之间的万有引力,可以用以下公式计算:F=GmM/r^2,即万有引力等于引力常量乘以两物体质量的乘积除以它们距离的平方。
其中G代表引力常量,其值约为×10的负11次方单位N·m2/kg2。
为英国科学家卡文迪许通过扭秤实验测得。
万有引力的推导:若将行星的轨道近似的看成圆形,从开普勒第二定律可得行星运动的角速度是一定的,即:ω=2π/T(周期)如果行星的质量是m,离太阳的距离是r,周期是T,那么由运动方程式可得,行星受到的力的作用大小mrω^2=mr(4π^2)/T^2另外,由开普勒第三定律可得r^3/T^2=常数k'那么沿太阳方向的力为mr(4π^2)/T^2=mk'(4π^2)/r^2由作用力和反作用力的关系可知,太阳也受到以上相同大小的力。
万有引力知识点总结

知识点一 万有引力应用两条线索(1)万有引力=向心力 (2)重力=向心力 G2RMm = mg ⇒GM=gR 2(黄金代换式) 1、(中心天体质量密度)一卫星绕某一行星表面附近做匀速圆周运动,其线速度大小为0v 假设宇航员在该行星表面上用弹簧测力计测量一质量为m 的物体重力,物体静止时,弹簧测力计的示数为N ,已知引力常量为G,则这颗行星的质量为A .GNmv 2B.GNmv4C .GmNv2D.GmNv4【解析】行星对卫星的万有引力提供其做匀速圆周运动的向心力,有Rv m R 22mGM '='① 行星对处于其表面物体的万有引力等于物体重力有,mg R =2GMm② 根据题意有N=mg ③,解以上三式可得GNmv 4M =,选项B 正确。
2、(多天体比较)假设地球是一半径为R 、质量分布均匀的球体。
一矿井深度为d 。
已知质量分布均匀的球壳对壳内物体的引力为零。
矿井底部和地面处的重力加速度大小之比为 A .R d -1 B .R d+1 C .2)(R d R - D .2)(dR R - 【答案】A【解析】在地面上质量为m 的物体根据万有引力定律有:mg RMm G =2 ,从而得R G R RG g πρπρ343423⋅⋅=⋅⋅=。
根据题意,球壳对其内部物体的引力为零,则矿井底部的物体m ′只受到其以下球体对它的万有引力同理有)(34)(2d R G d R M G g -=-'='πρ,式中3)(34d R M -='πρ。
两式相除化简R d R d R g g -=-='1。
答案A 。
3、(多天体比较)火星探测项目我过继神舟载人航天工程、嫦娥探月工程之后又一个重大太空探索项目。
假设火星探测器在火星表面附近圆形轨道运行周期为T ,神州飞船在地球表面附近圆形轨道运行周期为2T ,火星质量与地球质量之比为p ,火星半径与地球半径之比为q ,则T 、2T 之比为222222224[8]2[9]4[10][11][12]Mm v G m m r m r r r Tv mgr m m r m rr Tπωπω======答案:D解析:设中心天体的质量为M ,半径为R ,当航天器在星球表面飞行时,由222M m G m R R T π⎛⎫= ⎪⎝⎭和343M V R ρρπ==,解得23GT πρ=,即T =又因为3343M M M V R R ρπ==∝,所以T ∝12T T =。
物理万有引力知识点总结

物理万有引力知识点总结知识点总结提升成绩的一种有效方法就是从错题入手,将易错题、易错知识点重点掌握,避免再次出错。
以下是小编为大家收集的物理万有引力知识点总结,希望能够帮助到大家。
物理万有引力知识点总结11.开普勒行星运动三定律简介(轨道、面积、比值)丹麦开文学家开普勒信奉日心说,对天文学家有极大的兴趣,并有出众的数学才华,开普勒在其导师弟谷连续20年对行星的位置进行观测所记录的数据研究的基楚上,通过四年多的刻苦计算,最终发现了三个定律。
第一定律:所有行星都在椭圆轨道上运动,太阳则处在这些椭圆轨道的一个焦点上;第二定律:行星沿椭圆轨道运动的过程中,与太阳的连线在单位时间内扫过的面积相等;第三定律:所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。
即开普勒行星运动的定律是在丹麦天文学家弟谷的大量观测数据的基础上概括出的,给出了行星运动的规律。
2.万有引力定律及其应用(1)内容:宇宙间的一切物体都是相互吸引的,两个物体间的引力大小跟它们的质量成积成正比,跟它们的距离平方成反比,引力方向沿两个物体的连线方向。
引力常量,它在数值上等于两个质量都是1kg的物体相距1m时的相互作用力,1798年由英国物理学家卡文迪许利用扭秤装置测出。
万有引力常量的测定——卡文迪许扭秤实验原理是力矩平衡。
实验中的方法有力学放大(借助于力矩将万有引力的作用效果放大)和光学放大(借助于平面境将微小的运动效果放大)。
定律的适用条件:严格地说公式只适用于质点间的相互作用,当两个物体间的距离远远大于物体本身的大小时,公式也可近似使用,但此时r应为两物体重心间的距离。
对于均匀的球体,r是两球心间的距离。
当两个物体间的距离无限靠近时,不能再视为质点,万有引力定律不再适用,不能依公式算出F近为无穷大。
注意:万有引力定律把地面上的运动与天体运动统一起来,是自然界中最普遍的规律之一,式中引力恒量G的物理意义是:G在数值上等于质量均为1kg的两个质点相距1m时相互作用的万有引力。
第六章万有引力定律知识要点

第六章《万有引力定律》知识要点
1、关于天体运动的两种对立看法
•地心说---地球是宇宙的中心,是静止不动的,太阳、月亮及其它行星都绕地球运动。
•日心说---太阳是宇宙的中心,是静止不动的,地球、月亮及其它行星都绕太阳运动。
2、开普勒定律
•开普勒第一定律:所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上。
•开普勒第二定律:对于每一个行星而言,太阳和行星的连线在相等的时间内扫过的面积相等。
•开普勒第三定律:所有的行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。
3、万有引力定律
•文字内容:自然界中任何两个物体都是相互吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比•数学公式:F=Gm1m2/r2
4、宇宙速度
第一宇宙速度
•数值:7.9km/s
•意义:1)人造卫星在地球表面的环绕速度.2)人造卫星的最小发射速度.3)人造卫星的最大环绕速度.
第二宇宙速度
•数值:11.2km/s
•意义:物体脱离地球的引力成为太阳的人造行星所必须具有的最小发射速度,也叫脱离速度.
第三宇宙速度
•数值:16.7km/s
•意义:物体挣脱太阳的束缚,飞到太阳系外的宇宙空间去所必须具有的最小发射速度,也叫逃逸速度.
求解天体运动问题的两个黄金公式。
万有引力知识点汇总

万有引力知识点汇总万有引力是牛顿力学的三大定律之一,是描述物体之间相互作用的重要力量。
它是自然界中普遍存在的力,影响着我们身边的一切。
本文将对万有引力的知识点进行汇总,深入探讨其概念、公式及应用。
一、概念万有引力是指任何两个物体之间都存在着一种吸引力,这种力的大小与两个物体的质量和它们之间的距离有关。
牛顿在其《自然哲学的数学原理》中明确了万有引力的概念,并提出了万有引力定律。
二、公式1. 万有引力定律:牛顿的万有引力定律可以用如下公式表示:F =G * (m1 * m2) / r^2其中,F表示物体之间的引力大小,G表示万有引力常数(近似值为6.67430×10^(-11) N*m^2/kg^2),m1和m2分别是两个物体的质量,r表示它们之间的距离。
2. 引力的方向:根据万有引力定律可知,物体之间的引力方向与它们之间的连线方向相同,即指向对方。
3. 引力的大小与质量和距离的关系:万有引力与物体的质量成正比,与它们之间的距离的平方成反比。
质量越大,引力越大;距离越远,引力越小。
三、应用1. 行星公转:行星绕太阳公转的轨道是由引力保持的。
太阳的质量巨大,因此它对行星的引力也很大,使其保持在固定的轨道上。
2. 卫星运动:人造卫星绕地球运动也是由万有引力来驱动的。
卫星需要以足够高的速度绕地球一周,使其受到的向心力与地球引力相平衡,从而保持在轨道上。
3. 物体自由下落:地球对物体的引力使物体向下运动,这就是我们通常所说的自由下落。
物体的重量实际上就是地球对其施加的引力。
4. 物体的重量:物体在地球上的重量由其质量和地球对其施加的引力决定。
重力加速度约为9.8 m/s^2,利用重力公式可以计算物体在地球上的重量。
5. 星际导航:在星际飞船的导航过程中,万有引力也起到重要的作用。
飞船需要准确计算和使用行星和恒星的引力以调整速度和轨道,从而到达目的地。
四、结语万有引力是牛顿力学的重要内容之一,深入理解万有引力概念、公式及其应用对于理解宇宙运行规律具有重要意义。
物理万有引力知识点

物理万有引力知识点一、万有引力定律万有引力定律是由艾萨克·牛顿在1687年提出的。
它描述了两个物体之间的引力是如何作用的。
定律内容如下:1. 任何两个物体都会相互吸引。
2. 这种吸引力与两个物体的质量的乘积成正比。
3. 吸引力与两个物体之间的距离的平方成反比。
4. 吸引力沿着连接两个物体的直线作用。
数学表达式为:F = G * (m1 * m2) / r^2其中,F 代表万有引力,m1 和 m2 分别代表两个物体的质量,r 代表它们之间的距离,G 是万有引力常数。
二、万有引力常数万有引力常数(G)是一个物理常数,用于计算两个物体之间的引力。
G 的值约为6.67430 × 10^-11 N·(m/kg)^2。
三、引力与质量万有引力与物体的质量直接相关。
质量越大的物体,其引力也越大。
这也是为什么地球和太阳这样的大型天体能够对周围的物体产生显著的引力作用。
四、引力与距离万有引力与物体间距离的平方成反比。
这意味着,当两个物体之间的距离增加时,它们之间的引力会显著减少。
这也是为什么在宇宙尺度上,距离非常遥远的物体之间的引力作用可以忽略不计。
五、引力的方向万有引力总是沿着两个物体之间的直线方向作用。
这意味着,无论物体如何移动或旋转,引力总是指向对方。
六、引力在天体物理中的应用万有引力是天体物理学的基础。
它解释了行星围绕太阳运动的轨道,潮汐现象,以及恒星和星系的形成和演化。
七、引力与其他力的关系在宇宙的四个基本相互作用中,引力是最弱的一种。
然而,由于它的长程特性,即使在微观尺度上,引力也在起着作用,尽管在日常生活中通常被其他力(如电磁力)所掩盖。
八、引力场引力场是一个区域,其中包含一个物体的引力影响。
任何进入该区域的物体都会感受到引力的作用。
引力场的强度与物体的质量和距离有关。
九、引力波根据爱因斯坦的广义相对论,当质量较大的物体加速运动时,它们会在周围的时空中产生涟漪,称为引力波。
万有引力知识点

万有引力知识点万有引力知识点概述1. 万有引力定律的定义万有引力定律是指在宇宙中,任何两个具有质量的物体都会相互吸引。
这种吸引力的大小与两个物体的质量成正比,与它们之间距离的平方成反比。
2. 万有引力公式艾萨克·牛顿在1687年发表的《自然哲学的数学原理》中首次提出了万有引力定律的数学表达式:\[ F = G \frac{{m_1 m_2}}{{r^2}} \]其中,\( F \) 表示两物体之间的引力,\( G \) 是万有引力常数,\( m_1 \) 和 \( m_2 \) 分别是两物体的质量,\( r \) 是它们之间的距离。
3. 万有引力常数万有引力常数 \( G \) 是一个物理常数,用于描述质量之间的引力大小。
其值约为 \( 6.674 \times 10^{-11} \,\text{Nm}^2/\text{kg}^2 \)。
4. 引力与质量的关系万有引力的大小直接取决于两个物体的质量。
质量越大,引力越强。
这也是为什么像地球和太阳这样的大型天体能够对周围的物体产生显著的引力作用。
5. 引力与距离的关系万有引力的强度与物体间距离的平方成反比。
这意味着,当两个物体之间的距离增加时,它们之间的引力会显著减弱。
6. 引力在天体物理学中的应用万有引力是天体物理学的基础,它解释了行星围绕恒星的运动、卫星围绕行星的轨道运动、以及星系内部和星系之间的相互作用。
7. 引力对航天的影响在航天领域,万有引力对于设计和执行太空任务至关重要。
它影响着火箭的发射、卫星的轨道设计以及太空探测器的行进路径。
8. 引力透镜效应由于光在通过强引力场时会发生弯曲,天文学家可以利用这一现象来观察遥远的星系和宇宙的结构。
这种现象被称为引力透镜效应。
9. 引力波当质量较大的物体,如黑洞或中子星合并时,会产生剧烈的引力变化,这些变化以波的形式传播开来,称为引力波。
引力波的直接探测为研究宇宙提供了全新的视角。
10. 万有引力与相对论爱因斯坦的广义相对论提出了一个与牛顿万有引力不同的引力概念,即引力是由物体对周围时空结构的曲率造成的。
万有引力知识点总结

一.万有引力定律1)内容:宇宙间的一切物体都是互相吸引的,两个物体间的引力大小,跟它们的质量的乘积成正比,跟它们的距离的平方成反比.2)公式:F =GMm/r 2其中G=6.67*10-11N.m 2/kg 称为为有引力恒量。
二.万有引力和重力重力是万有引力产生的,由于地球的自转,因而地球表面的物体随地球自转时需要向心力.重力实际上是万有引力的一个分力.重力加速度g 随纬度变化而变化,从赤道到两极逐渐增大.g=GM/r2常用来计算星球表面重力加速度的大小,在地球的同一纬度处,g 随物体离地面高度的增大而减小,即g=GM/(r+h )2地球表面的向心力F 向=mW 2r r=Rcos θ θ为维度角黄金代换 mg=GM/R 2三. 万有引力公式 V=R GM / a=GM/R 2 T=GM R /324π W=3/R GM注意:只有相心加速度与轨道半径成正比四.同步卫星五个“一定”● 周期一定 与天体的周期相同(若天体为地球则T=24h) ● 角速度一定 与天体自转的角速度相同● 高度一定 由GMm/(R+h)=m4π2(R+h)/T 2得同步卫星 的高度h=324/2πGMT -R● 速度一定 v=)/(h R GM● 轨道平面一定 轨道平面与赤道平面共面五.双星问题被相互引力系在一起相互绕转的两颗星就叫物理双星。
双星是绕公共圆心转动的一对恒星。
具有以下特点1. 各自需要的向心力有彼此之间的万有引力相互提供即:Gm1m2/L2=m1w12r1, Gm1m2/L2=m2w22r22. 两颗星的轨道半径及角速度都相同,即T1=T2 w1=w23. 两颗星的轨道半径与他们之间的距离关系为r1 +r2=L4. 两颗星到圆心的距离r1、r2 与星体的质量成反比m1/m2=r2/r15. 双星运动的周期T=2π2GLm/3m(16. 双星的总质量公式m1+m2=4π2L3/T2G。
万有引力 知识要点

万有引力 知识要点一、万有引力定律: F =适用条件:两个质点间(质量均匀分布的球可以看作质量在球心的质点)二、万有引力定律的应用:(天体质量M , 天体半径R, 天体表面重力加速度g )1.万有引力=向心力 (一个天体绕另一个天体作圆周运动时,r=R+h )中心天体的质量: 人造地球卫星的作圆周运动速度大小计算:r GM V r V m r Mm G =⇒=22GM r T Tr m r Mm G 22224ππ=⇒=322r GM r m r Mm G =⇒=ωω22r GM a ma r Mm G =⇒=2.重力=万有引力地面物体的重力加速度:mg = G Mm R 2g =黄金代换式:GM=gR 2高空物体的重力加速度:mg’ = G2)(h R Mm + g’ =3.第一宇宙速度----在地球表面附近(轨道半径可视为地球半径)绕地球作圆周运动的卫星的线速度,在所有圆周运动的卫星中线速度是最大的.由mg = m V R 2或由R GM V R V m R Mm G =⇒=22 =gR =7.9km/s7.9×103m/s 称为第一宇宙速度;11.2×103m/s 称为第二宇宙速度;16.7×103m/s 称为第三宇宙速度。
4.通讯卫星(又称同步卫星)相对于地面静止不动,其圆轨道位于赤道上空,其周期与地球自转周期相同(一天),其轨道半径是一个定值。
5.卫星在发射时加速升高和返回减速的过程中,均发生超重现象,进入圆周运动轨道后,发生完全失重现象,一切在地面依靠重力才能完成的实验都无法做。
机械能和能源知识要点一、功和功率:1.功的计算公式:W=(条件:)2.做功的两个不可缺少的因素:(1);(2);功是标量、是过程量。
功的大小反映了力在使物体发生一段位移的过程中的总效果;同时功又是物理过程中能量转移或转化的量度。
注意:当= π时,W=0。
例如:线吊小球做圆周运动时,线的拉力不做功;当π/2<α≤π时,力对物体做负功,也说成物体克服这个力做了功(取正值)3.功率:定义式物理意义:___________________________;单位及换算:1kW= W其他计算公式:平均功率_____________________;瞬时功率_____________________。
《万有引力定律》 知识清单

《万有引力定律》知识清单一、什么是万有引力定律万有引力定律是艾萨克·牛顿在 1687 年于《自然哲学的数学原理》上发表的。
简单来说,万有引力定律指出:任何两个质点都存在通过其连心线方向上的相互吸引的力。
该引力大小与它们质量的乘积成正比、与它们距离的平方成反比,与两物体的化学组成和其间介质种类无关。
用公式表示就是:F = G (m1 m2) / r²。
其中,F 表示两个物体之间的引力,G 是万有引力常量,数值约为 667×10⁻¹¹ N·m²/kg²,m1 和 m2 分别是两个物体的质量,r 是两个物体质心之间的距离。
二、万有引力定律的发现过程牛顿发现万有引力定律并非一蹴而就,而是经历了一个长期的思考和研究过程。
据说,牛顿是在看到苹果从树上落下时,开始思考重力的作用。
他意识到地球上的物体都会受到指向地心的重力,而月球绕地球运动也可能是受到类似的力的作用。
经过深入的研究和计算,牛顿最终提出了万有引力定律,成功地解释了许多天体的运动现象,包括行星绕太阳的运动、卫星绕行星的运动等。
三、万有引力定律的适用范围万有引力定律适用于宏观物体之间的相互作用。
对于微观粒子,由于它们的运动遵循量子力学规律,万有引力的作用通常非常微弱,可以忽略不计。
在研究天体运动、物体在地球表面的重力等宏观问题时,万有引力定律发挥着重要的作用。
但需要注意的是,当两个物体之间的距离非常小,或者物体的密度非常大时,万有引力定律需要结合相对论进行修正。
四、万有引力常量的测定英国科学家卡文迪许通过扭秤实验,巧妙地测量出了万有引力常量G 的数值。
扭秤实验的基本原理是:利用微小的力通过放大的方法进行测量。
通过实验,卡文迪许得出了 G 的数值,使得万有引力定律能够进行定量的计算和应用。
五、万有引力定律在天文学中的应用1、解释天体的运动万有引力定律能够很好地解释行星绕太阳的椭圆轨道运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识点一 万有引力应用两条线索(1)万有引力=向心力 (2)重力=向心力 G2RMm= mg ⇒GM=gR 2 (黄金代换式) 1、(中心天体质量密度)一卫星绕某一行星表面附近做匀速圆周运动,其线速度大小为假设宇航员在该行星表面上用弹簧测力计测量一质量为m 的物体重力,物体静止时,弹簧测力计的示数为N ,已知引力常量为G,则这颗行星的质量为A .GNmv 2B.GNmv4C .GmNv2D.GmNv4【解析】行星对卫星的万有引力提供其做匀速圆周运动的向心力,有Rv m R 22mGM '='① 行星对处于其表面物体的万有引力等于物体重力有,mg R =2GMm② 根据题意有N=mg ③,解以上三式可得GNmv 4M =,选项B 正确。
2、(多天体比较)假设地球是一半径为R 、质量分布均匀的球体。
一矿井深度为d 。
已知质量分布均匀的球壳对壳内物体的引力为零。
矿井底部和地面处的重力加速度大小之比为 A .R d -1 B .R d+1 C .2)(Rd R - D .2)(d R R - 【答案】A【解析】在地面上质量为m 的物体根据万有引力定律有:mg RMm G =2 ,从而得R G R RG g πρπρ343423⋅⋅=⋅⋅=。
根据题意,球壳对其内部物体的引力为零,则矿井底部的物体m ′只受到其以下球体对它的万有引力同理有)(34)(2d R G d R M G g -=-'='πρ,式中3)(34d R M -='πρ。
两式相除化简R d R d R g g -=-='1。
答案A 。
3、(多天体比较)火星探测项目我过继神舟载人航天工程、嫦娥探月工程之后又一个重大太空探索项目。
假设火星探测器在火星表面附近圆形轨道运行周期为,神州飞船在地球表面附近圆形轨道运行周期为,火星质量与地球质量之比为p ,火星半径与地球半径之比为q ,则、之比为B.C.D.答案:D解析:设中心天体的质量为M ,半径为R ,当航天器在星球表面飞行时,由222M m G m R R T π⎛⎫= ⎪⎝⎭和343M V R ρρπ==,解得23GT πρ=,即T =又因为3343M M M V R R ρπ==∝,222222224[8]2[9]4[10][11][12]Mm v G m m r m r r r Tv mgr m m r m rr Tπωπω======g g所以3R T M ∝,312T q T p=。
4、(中心天体质量密度)若有一艘宇宙飞船在某一行星表面做匀速圆周运动,设其周期为T ,引力常数为G ,那么该行星的平均密度为( B)A. π32GTB. 23GT πC. π42GT D.24GT π5、(多天体比较)近年来,人类发射的多枚火星探测器已经相继在火星上着陆.某火星探测器绕火星做匀速圆周运动,它的轨道距火星表面的高度等于火星的半径,它的运动周期为T ,则火星的平均密度ρ的表达式为(k 为某个常数)( D )A .ρ=kTB .ρ=kTC .ρ=kT 2D .ρ=kT 2 6、(中心天体质量密度)如图K19-3所示,美国的“卡西尼”号探测器经过长达7年的“艰苦”旅行,进入绕土星飞行的轨道.若“卡西尼”号探测器在半径为R 的土星上空离土星表面高h 的圆形轨道上绕土星飞行,环绕n 周飞行时间为t ,已知引力常量为G ,则下列关于土星质量M 和平均密度ρ的表达式正确的是( D )A .M =4π2R +h 3Gt 2,ρ=3πR +h 3Gt 2R 3B .M =4π2R +h 2Gt 2,ρ=3πR +h 2Gt 2R 3C .M =4π2t 2R +h 3gn 2,ρ=3πt 2R +h 3Gn 2R 3 D .M =4π2n 2r +h 3Gt 2,ρ=3πn 2R +h 3Gt 2R 3知识点二 双星模型、多星模型7、两颗靠得较近的天体称为双星,它们以连线上某点为圆心作匀速圆周运动,因而不至于由于引力作用而吸引在一起,以下说法中正确的是( BD ) A .它们作圆周运动的角速度之比与其质量成反比 B .它们作圆周运动的线速度之比与其质量成反比 C .它们所受向心力之比与其质量成反比D .它们作圆周运动的半径与其质量成反比。
8、如右图,质量分别为m 和M 的两个星球A 和B 在引力作用下都绕O 点做匀速 圆周运动,星 A 和B 两者中心之间距离为L 。
已知A 、B 的中心和O 三点始终共线,A 和B 分别在O 的两侧。
引力常数为G 。
(1)求两星球做圆周运动的周期。
(2)在地月系统中,若忽略其它星球的影响,可以将月球和地球看成上述星球A 和B ,月球绕其轨道中心运行为的周期记为T 1。
但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期T 2。
已知地球和月球的质量分别为×1024kg 和 ×1022kg 。
求T 2与T 1两者平方之比。
(结果保留3位小数)解析:⑴A 和B 绕O 做匀速圆周运动,它们之间的万有引力提供向心力,则A 和B 的向心力相等。
且A 和B 和O 始终共线,说明A 和B 有相同的角速度和周期。
因此有R M r m 22ωω=,L R r =+,连立解得L Mm mR +=,L M m M r +=对A 根据牛顿第二定律和万有引力定律得L m M MT m L GMm +=22)2(π 化简得 )(23m M G L T +=π⑵将地月看成双星,由⑴得)(231m M G L T +=π将月球看作绕地心做圆周运动,根据牛顿第二定律和万有引力定律得L T m L GMm 22)2(π=化简得 GML T 322π=所以两种周期的平方比值为01.11098.51035.71098.5)(242224212=⨯⨯+⨯=+=M M m T T9、宇宙中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统,通常可 忽略其它星体对它们的引力作用。
已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R 的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行。
设每个星体的质量均为m 。
(1)试求第一种形式下,星体运动的线速度和周期。
(2)假设两种形式星体的运动周期相同,第二种形式下星体之间的距离应为多少解析:(1)第一种形式下,以某个运动星体为研究对象,由万有引力定律和牛顿第二定律,得:F 1=G 22Rm F 2=G 22)2(R m F 1+F 2=m R v 2运动星体的线速度:v = 周期为T,则有:24R T v ππ== (2)第二种形式星体之间的距离为r ,则三个星体作圆周运动的半径为R /为 R /=︒30cos 2r由于星体作圆周运动所需的向心力靠两个星体的万有引力的合力提供,由万有引力定律和牛顿第二定律,得:F 合=222rGm cos30°F 向=m /224R Tπ222cos30m G l °=2cos30r m o22()Tπ 所以星体之间的距离为:r =知识点三 宇宙速度含义:(1)第一宇宙速度(环绕速度):v 1= km/s ,是人造地球卫星的最小发射速度,最大绕行速度.(2)第二宇宙速度(脱离速度):v 2= km/s ,是物体挣脱地球的引力束缚需要的最小发射速度. (3)第三宇宙速度(逃逸速度):v 3= km/s ,是物体挣脱太阳的引力束缚需要的最小发射速度.环绕速度推算:地gR v = 地R GMv =推导一:物体在地球附近绕地球做匀速圆周运动,万有引力提供向心力即地22地R v m R Mm G =,得地R GM v =。
推导二:物体在地球附近绕地球做匀速圆周运动需要的向心力等于重力,即地2R v m mg =,得地gR v =10、若取地球的第一宇宙速度为8 km/s ,某行星的质量是地球质量的6倍,半径是地球的倍,这顺行星的第一宇宙速度约为( C ) A. 2 km/s B. 4 km/s C. 16 km/s D. 32 km/s11、[2011·杭州检测] 宇航员在一行星上以10 m/s 的初速度竖直上抛一质量为 kg 的物体,不计阻力,经 s 后落回手中,已知该星球半径为7 220 km.(1)该星球表面的重力加速度是多大(2)要使物体沿水平方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大 (3)若物体距离星球无穷远处时其引力势能为零,则当物体距离星球球心r 时其引力势能E p=-G Mm r (式中m 为物体的质量,M 为星球的质量,G 为引力常量).问要使物体沿竖直方向抛出而不落回星球表面,沿星球表面抛出的速度至少是多大11.(1)8 m/s 2 (2)7600 m/s (3)10746 m/s[解析] (1)由匀变速运动规律知星球表面的重力加速度g ′=2v 0t =8 m/s 2. (2)由牛顿第二定律,有mg ′=m v 21R解得v 1=g ′R =7600 m/s. (3)由机械能守恒定律,有 12mv 22+(-G Mm R )=0在该行星表面质量为m 的物体受到的重力等于万有引力,有mg ′=G MmR 2解得v 2=2g ′R =10746 m/s.知识点四 同步卫星与卫星变轨等卫星问题同步卫星:“六同”:即同轨道面(同在赤道的正上方)、同周期(与地球自转的周期相同)、同角速度、同高度、同线速度大小、同向心加速度大小。
“五不同”(通常情况):质量不同、向心力的大小不同、动能、势能、机械能不同。
km R r h 35800=-=环绕模型:不同物理量与半径关系GM r T 32π= 3rGM ω=2r GM a =向 r GM v = 总结:“越高越慢”,只有T 与r 正相关变轨判定:提供的力与所需力比较当F >mv 2/r 时,卫星做近心运动,此时卫星的速度将变大; 当F <mv 2/r 时,卫星做离心运动,此时卫星的速度将变小。
s km rGM v /08.3==12、关于环绕地球运动的卫星,下列说法中正确的是 ( ) A 、分别沿圆轨道和椭圆轨道运行的两颗卫星,不可能具有相同的周期 B 、沿椭圆轨道运行的一颗卫星,在轨道不同位置可能具有相同的速率 C 、在赤道上空运行的两颗地球同步卫星,它们的轨道半径有可能不同 D 、沿不同轨道经过北京上空的两颗卫星,它们的轨道平面一定会重合解析:所有的同步卫星都在同一个赤道轨道上运动,C 错误;沿不同轨道经过北京上空的两颗卫星它们的运行轨道面与赤道面的夹角可以不同,它们的轨道平面就不会重合,D 错误;分别沿圆轨道和椭圆轨道运行的两颖卫星,可能具有相同的周期,A 错误;沿椭圆轨道运行的一颗卫星,在轨道的关于长轴对称的两个位置的速率相等,所以在轨道不同位置可能具有相同的速率是正确的。
