八年级数学上册角度计算中的经典模型(举一反三)(含解析版)
2023学年八年级数学上册高分突破必练专题(人教版)三角形角度计算常考模型(解析版)

三角形角度计算常考模型【考点1 “8字”模型】【结论】∠A+∠B=∠D+∠E.【考点2飞镖模型】【结论】∠BPC=∠A+∠B+∠C.【考点3 “风筝”模型】【考点1 “8字”模型】【典例1】(2021春•鼓楼区校级月考)图1 线段AB、CD相交于点O连接AD、CB我们把形如图1的图形称之为“8字形”.如图2 在图1的条件下∠DAB和∠BCD的平分线AP和CP相交于点P并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中请直接写出∠A、∠B、∠C、∠D之间的数量关系:;(2)图2中当∠D=50度∠B=40度时求∠P的度数.(3)图2中∠D和∠B为任意角时其他条件不变试问∠P与∠D、∠B之间存在着怎样的数量关系.【答案】(1)∠A+∠D=∠C+∠B;(2)∠P=45°(3)2∠P=∠B+∠D【解答】解:(1)由题知∠A+∠D=∠DOB=∠C+∠B∴∠A+∠D=∠C+∠B故答案为:∠A+∠D=∠C+∠B;(2)由(1)可得∠DAO+∠D=∠OCB+∠B①同理可得∠DAM+∠D=∠OCP+∠P∵∠DAB和∠BCD的平分线是AP和CP∴∠DAO+∠D=∠OCB+∠P②由②×2﹣①得∠D=2∠P﹣∠B即2∠P=∠D+∠B∴2∠P=50°+40°故∠P=45°;(3)由(2)可知2∠P=∠B+∠D.【变式1-1】(2020•柯桥区模拟)如图所示∠α的度数是()A.10°B.20°C.30°D.40°【答案】A【解答】解:∵∠A+∠B+∠AOB=∠C+∠D+∠COD∠AOB=∠COD∴∠A+∠B=∠C+∠D∴30°+20°=40°+α∴α=10°故选:A.【变式1-2】(2022春•叙州区期末)如图BP平分∠ABC交CD于点F DP平分∠ADC 交AB于点E若∠A=45°∠P=40°则∠C的度数为()A.30°B.35°C.40°D.45°【答案】B【解答】解:∵∠A+∠ADG+∠AGD=180°∠ABC+∠C+∠BGC=180°∴∠A+∠ADG+∠AGD=∠ABC+∠C+∠BGC.又∵∠AGD=∠BGC∴∠A+∠ADG=∠C+∠GBC.∴∠A﹣∠C=∠GBC﹣∠ADG.同理可得∠A+∠ADE=∠P+∠PBE.∴∠A﹣∠P=∠PBE﹣∠ADE.∵BP平分∠ABC交CD于点F DP平分∠ADC交AB于点E∴∠GBC=2∠PBE∠ADG=2∠ADE.∴∠A﹣∠C=2(∠A﹣∠P).∴∠A+∠C=2∠P.又∵∠A=45°∠P=40°∴∠C=35°.故选:B【变式1-3】(2022春•渝中区校级期中)如图五角星的五个角之和即:∠A+∠B+∠C+∠D+∠E=()A.180°B.90°C.270°D.240°【答案】A【解答】解:连接CD设BD与CE交于点O由∠BOE=∠COD得:∠B+∠E=∠OCD+∠ODC在△ACD中∠A+∠ACD+∠ADC=180°即∠A+∠ACE+∠OCD+∠ODC+∠ADB=180°∴∠A+∠ACE+∠B+∠E+ADB=180°即五角星的五个内角之和为180°.故选:A.【变式1-4】(2021春•玄武区期末)如图∠A+∠B+∠C+∠D+∠E+∠F=°.【答案】360【解答】解:如图延长DE交AB于点G由三角形外角性质可知:∠1=∠F+∠DEF∠2=∠1+∠A∴∠2=∠F+∠DEF+∠A∴在四边形BCDG中由四边形内角和可知:∠B+∠C+∠D+∠2=360°∴∠A+∠F+∠DEF+∠B+∠C+∠D=360°.故答案为:360.【变式1-5】(2020秋•平舆县期末)如图∠A+∠B+∠C+∠D+∠E=°.【答案】180【解答】解:如图设线段BD BE分别与线段AC交于点N M.∵∠AMB=∠A+∠E∠DNC=∠B+∠AMB∠DNC+∠D+∠C=180°∴∠A+∠B+∠D+∠E+∠C=180°故答案为:180.【变式1-6】(2021秋•正阳县期末)图1 线段AB、CD相交于点O连接AD、CB我们把形如图1的图形称之为“8字形”.如图2 在图1的条件下∠DAB和∠BCD的平分线AP和CP相交于点P并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中请直接写出∠A、∠B、∠C、∠D之间的数量关系:;(2)仔细观察在图2中“8字形”的个数:个;(3)图2中当∠D=50度∠B=40度时求∠P的度数.(4)图2中∠D和∠B为任意角时其他条件不变试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结果不必证明).【解答】解:(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°∠AOD=∠BOC ∴∠A+∠D=∠C+∠B故答案为:∠A+∠D=∠C+∠B;(2)①线段AB、CD相交于点O形成“8字形”;②线段AN、CM相交于点O形成“8字形”;③线段AB、CP相交于点N形成“8字形”;④线段AB、CM相交于点O形成“8字形”;⑤线段AP、CD相交于点M形成“8字形”;⑥线段AN、CD相交于点O形成“8字形”;故“8字形”共有6个故答案为:6;(3)∠DAP+∠D=∠P+∠DCP①∠PCB+∠B=∠P AB+∠P②∵∠DAB和∠BCD的平分线AP和CP相交于点P∴∠DAP=∠P AB∠DCP=∠PCB①+②得:∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠P AB+∠P即2∠P=∠D+∠B又∵∠D=50度∠B=40度∴2∠P=50°+40°∴∠P=45°;(4)关系:2∠P=∠D+∠B.∠D+∠1=∠P+∠3①∠B+∠4=∠P+∠2②①+②得:∠D+∠1+∠4+∠B=∠P+∠3+∠2+∠P∵∠DAB和∠DCB的平分线AP和CP相交于点P∴∠1=∠2 ∠3=∠4∴2∠P=∠D+∠B.【考点2 飞镖模型】【典例2】(2019秋•建平县期末)探究与发现:如图(1)所示的图形像我们常见的学习用品一圆规我们不妨把这样图形叫做“规形图(1)观察“规形图(1)”试探究∠BDC与∠A、∠B、∠C之间的数量关系并说明理由;(2)请你直接利用以上结论解决以下问题:①如图(2)把一块三角尺XYZ放置在△AC上使三角尺的两条直角边XY、XZ恰好经过点B、C若∠A=40°则∠ABX+∠ACX=°.②如图(3)DC平分∠ADB EC平分∠AEB若∠DAE=40°∠DBE=130°求∠DCE的度数.【解答】解:(1)如图(1)∠BDC=∠BAC+∠B+∠C理由是:过点A、D作射线AF∵∠FDC=∠DAC+∠C∠BDF=∠B+∠BAD∴∠FDC+∠BDF=∠DAC+∠BAD+∠C+∠B即∠BDC=∠BAC+∠B+∠C;(2)①如图(2)∵∠X=90°由(1)知:∠A+∠ABX+∠ACX=∠X=90°∵∠A=40°∴∠ABX+∠ACX=50°故答案为:50;②如图(3)∵∠A=40°∠DBE=130°∴∠ADE+∠AEB=130°﹣40°=90°∵DC平分∠ADB EC平分∠AEB∴∠ADC=∠ADB∠AEC=∠AEB∴∠ADC+∠AEC==45°∴∠DCE=∠A+∠ADC+∠AEC=40°+45°=85°.【变式2-1】(2020春•沙坪坝区校级期中)如图△ABC中∠A=30°D为CB延长线上的一点DE⊥AB于点E∠D=40°则∠C为()A.20°B.15°C.30°D.25°【答案】A【解答】解:∵DE⊥AB∴∠DEB=90°∵∠D=40°∴∠ABD=180°﹣∠D﹣∠DEB=50°∵∠ABD=∠A+∠C∠A=30°∴∠C=∠ABD﹣∠A=50°﹣30°=20°.故选:A.【变式2-2】(2017•东昌府区一模)如图∠BDC=98°∠C=38°∠A=37°∠B 的度数是()A.33°B.23°C.27°D.37°【答案】B【解答】解:如图延长CD交AB于E∵∠C=38°∠A=37°∴∠1=∠C+∠A=38°+37°=75°∵∠BDC=98°∴∠B=∠BDC﹣∠1=98°﹣75°=23°.故选:B.【变式2-3】(2021春•工业园区校级月考)如图点C是∠BAD内一点连CB、CD∠A=80°∠B=10°∠D=40°则∠BCD的度数是()A.110°B.120°C.130°D.150°【答案】C【解答】解:延长BC交AD于E∵∠BED是△ABE的一个外角∠A=80°∠B=10°∴∠BED=∠A+∠B=90°∵∠BCD是△CDE的一个外角∴∠BCD=∠BED+∠D=130°故选:C.【变式2-4】(2021•碑林区校级二模)如图BE是∠ABD的平分线CF是∠ACD的平分线BE与CF交于G如果∠BDC=140°∠BGC=110°则∠A=.【答案】80°【解答】解:连接BC∵∠BDC=140°∴∠DBC+∠DCB=180°﹣140°=40°∵∠BGC=110°∴∠GBC+∠GCB=180°﹣110°=70°∴∠GBD+∠GCD=70°﹣40°=30°∵BE是∠ABD的平分线CF是∠ACD的平分线∴∠ABG+∠ACG=∠GBD+∠GCD=30°在△ABC中∠A=180°﹣40°﹣30°﹣30°=80°.故答案为:80°.【考点3 “风筝”模型】(2020秋•五华区期末)如图在三角形纸片ABC中∠A=60°∠B=70°将【典例3】纸片的一角折叠使点C落在△ABC外若∠2=18°则∠1的度数为()A.50°B.118°C.100°D.90°【答案】B【解答】解:在△ABC中∠A=60°∠B=70°∴∠C=180°﹣∠A﹣∠B=50°.由折叠可知:∠CDE=∠C′DE∠CED=∠C′ED∴∠CED==99°∴∠CDE=180°﹣∠CED﹣∠C=31°∴∠1=180°﹣∠CDE﹣∠C′DE=180°﹣2∠CDE=118°.故选:B.【变式3-1】(2020秋•潮阳区期中)如图在△ABC中将△ABC沿直线m翻折点B落在点D的位置若∠1﹣∠2=60°则∠B的度数是()A.30°B.32°C.35°D.60°【答案】A【解答】解:如图所示:由折叠的性质得:∠D=∠B根据外角性质得:∠1=∠3+∠B∠3=∠2+∠D∴∠1=∠2+∠D+∠B=∠2+2∠B∴∠1﹣∠2=2∠B=60°.∴∠B=30°故选:A.【变式3-2】(2018•聊城)如图将一张三角形纸片ABC的一角折叠使点A落在△ABC 外的A'处折痕为DE.如果∠A=α∠CEA′=β∠BDA'=γ那么下列式子中正确的是()A.γ=2α+βB.γ=α+2βC.γ=α+βD.γ=180°﹣α﹣β【答案】A【解答】解:由折叠得:∠A=∠A'∵∠BDA'=∠A+∠AFD∠AFD=∠A'+∠CEA'∵∠A=α∠CEA′=β∠BDA'=γ∴∠BDA'=γ=α+α+β=2α+β故选:A.【典例4】(2021春•高州市期末)如图小明从一张三角形纸片ABC的AC边上选取一点N将纸片沿着BN对折一次使得点A落在A′处后再将纸片沿着BA′对折一次使得点C落在BN上的C′处已知∠CMB=68°∠A=18°则原三角形的∠C的度数为()A.87°B.84°C.75°D.72°【答案】A【解答】解:如图由题意得:△ABN≌△A′BN△C′BN≌△CBM.∴∠1=∠2 ∠2=∠3 ∠CMB=∠C′MB=68°.∴∠1=∠2=∠3.∴∠ABC=3∠3.又∵∠3+∠C+∠CMB=180°∴∠3+∠C=180°﹣∠CMB=180°﹣68°=112°.又∵∠A+∠ABC+∠C=180°∴18°+2∠3+(∠3+∠C)=180°.∴18°+2∠3+112°=180°.∴∠3=25°.∴∠C=112°﹣∠3=112°﹣25°=87°.故选:A.【变式4-1】(2021春•济南期中)如图△ABC中∠B=40°∠C=30°点D为边BC上一点将△ADC沿直线AD折叠后点C落到点E处若DE∥AB则∠ADE的度数为()A.100°B.110°C.120°D.130°【答案】B【解答】解:∵∠B=40°∠C=30°∴∠BAC=110°由折叠的性质得∠E=∠C=30°∠EAD=∠CAD∠ADE=∠ADC∵DE∥AB∴∠BAE=∠E=30°∴∠CAD=40°∴∠ADE=∠ADC=180°﹣∠CAD﹣∠C=110°故选:B.【变式4-2】(2021春•滦州市期末)已知:如图所示将△ABC的∠C沿DE折叠点C 落在点C'处若设∠C=α∠AEC′=β∠BDC'=γ则下列关系成立的是()A.2α=β+γB.α=β+γC.α+β+γ=180°D.α+β=2γ【答案】A【解答】解:由折叠的性质知:∠C=∠C′=α.∵∠AEC′+∠CEC′=180°∠BDC′+∠CDC′=180°∴β=180°﹣∠CEC′γ=180°﹣∠CDC′.∴β+γ=360°﹣∠CEC′﹣∠CDC′.∵∠C+∠CEC′+CDC′+∠C′=360°∴2α=360°﹣∠CEC′﹣CDC′.∴β+γ=2α.故选:A.【变式4-3】(2021春•通许县期末)如图所示将△ABC沿着DE折叠使点A与点N重合若∠A=65°则∠1+∠2=()A.25°B.65°C.115°D.130°【答案】D【解答】解:∵△NDE是△ADE翻折变换而成∴∠AED=∠NED∠ADE=∠NDE∠A=∠N=65°∴∠AED+∠ADE=∠NED+∠NDE=180°﹣65°=115°∴∠1+∠2=360°﹣2×115°=130°.故选:D.12.(2021秋•广州期中)如图三角形纸片ABC中∠A=65°∠B=75°将∠C沿DE对折使点C落在△ABC外的点C′处若∠1=20°则∠2的度数为()A.80°B.90°C.100°D.110°【答案】C【解答】解:∵∠A=65°∠B=75°∴∠C=180°﹣65°﹣75°=40°由折叠的性质可知∠C′=∠C=40°∴∠3=∠1+∠C′=60°∴∠2=∠C+∠3=100°故选:C.13.(2022春•晋江市期末)如图把三角形纸片ABC沿DE折叠当点A落在四边形BCDE 外部时则∠A与∠1、∠2之间的数量关系是()A.2∠A=∠1﹣∠2B.3∠A=2(∠1﹣∠2)C.3∠A=2∠1﹣∠2D.∠A=∠1﹣∠2【答案】A【解答】解:∵△A′DE是△ADE沿DE折叠得到∴∠A′=∠A又∵∠ADA′=180°﹣∠1 ∠3=∠A′+∠2∴∠A+∠ADA′+∠3=180°即∠A+180°﹣∠1+∠A′+∠2=180°整理得2∠A=∠1﹣∠2.∴∠A=(∠1﹣∠2)即2∠A=∠1﹣∠2.故选:A.18.(2021春•沙坪坝区校级期中)如图所示∠A+∠B+∠C+∠D+∠E+∠F=度.【答案】360【解答】解:∵∠B+∠C=∠1 ∠A+∠F=∠2∴∠A+∠B+∠C+∠D+∠E+∠F=∠1+∠2+∠E+∠D=360°.故答案为:360.19.(2021秋•海珠区校级期中)如图则∠A+∠B+∠C+∠D+∠E+∠F的度数为.【答案】360°【解答】解:连接AD在△AOD和△BOC中∵∠AOD=∠BOC∴∠B+∠C=∠1+∠2∴∠B+∠C+∠BAF+∠EDF=∠1+∠2+∠BAF+∠EDF=∠EDA+∠F AD∵∠EDA+∠F AD+∠E+∠F=360°∴∠BAF+∠EDF+∠B+∠C+∠E+∠F=360°故答案为:360°.20.(2020•开福区校级开学)如图∠A+∠B+∠C+∠D+E+∠F的度数为.【答案】360°【解答】解:∵∠AIC=∠A+∠B∠EPC=∠C+∠D∠AOE=∠E+∠F∴∠A+∠B+∠C+∠D+∠E+∠F=∠AIC+∠EPC+∠AOE=360°.故答案为:360°.21.(2020春•昌黎县期末)如图∠A+∠B+∠C+∠D+∠E+∠F=度.【答案】360【解答】解:如右图所示∵∠AHG=∠A+∠B∠DNG=∠C+∠D∠EGN=∠E+∠F∴∠AHG+∠DNG+∠EGN=∠A+∠B+∠C+∠D+∠E+∠F又∵∠AHG、∠DNG、∠EGN是△GHN的三个不同的外角∴∠AHG+∠DNG+∠EGN=360°∴∠A+∠B+∠C+∠D+∠E+∠F=360°.故答案为:360°.22.(2017秋•磴口县校级期中)如图∠A=50°∠ABO=28°∠ACO=32°则∠BDC=度∠BOC=度.【答案】78°110°【解答】解:∵∠A=50°∠ABO=28°∠ACO=32°∴∠BDC=∠A+∠ABO=78°∴∠BOC=∠BDC+∠ACO=110°.23.(2021春•江都区校级期末)如图三角形纸片ABC中∠A=63°∠B=77°将纸片一角折叠使点C落在△ABC的内部若∠2=50°则∠1=.【答案】30°【解答】解:设折痕为EF连接CC′.∵∠2=∠ECC′+∠EC′C∠1=∠FCC′+∠FC′C∠ECF=∠EC′F∴∠1+∠2=2∠ECF∵∠C=180°﹣∠A﹣∠B=180°﹣63°﹣77°=40°∴∠1=80°﹣50°=30°故答案为:30°24.(2018春•莘县期末)一个零件的形状如图所示按规定∠A应等于90°∠B、∠D应分别是20°和30°.(1)李叔叔量得∠BCD=142°根据李叔叔量得的结果你能断定这个零件是否合格?请解释你的结论;(2)你知道∠B、∠D、∠BCD三角之间有何关系吗?请写出你的结论.(不需说明理由).【解答】解:(1)不合规格.理由如下:连接AC并延长到点E则∠BCD=∠BCE+∠ECD=∠B+∠BAC+∠CAD+∠D=∠B+∠BAD+∠D=140°故不合格.(2)根据第(1)小题的求解过程不难发现:∠B+∠D+90°=∠BCD.25.(2020秋•郯城县期末)探索归纳:(1)如图1 已知△ABC为直角三角形∠A=90°若沿图中虚线剪去∠A则∠1+∠2等于A.90°B.135°C.270°D.315°(2)如图2 已知△ABC中∠A=40°剪去∠A后成四边形则∠1+∠2=(3)如图2 根据(1)与(2)的求解过程请你归纳猜想∠1+∠2与∠A的关系是(4)如图3 若没有剪掉而是把它折成如图3形状试探究∠1+∠2与∠A的关系并说明理由.【解答】解:(1):∵四边形的内角和为360°直角三角形中两个锐角和为90°∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.∴∠1+∠2等于270°.故选C;(2)∠1+∠2=180°+40°=220°故答案是:220°;(3)∠1+∠2与∠A的关系是:∠1+∠2=180°+∠A(4)∵△EFP是由△EF A折叠得到的∴∠AFE=∠PFE∠AEF=∠PEF∴∠1=180°﹣2∠AFE∠2=180°﹣2∠AEF∴∠1+∠2=360°﹣2(∠AFE+∠AEF)又∵∠AFE+∠AEF=180°﹣∠A∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A.26.(2022春•新野县期末)在学习并掌握了平行线的性质和判定内容后数学老师安排了自主探究内容一利用平行线有关知识探究并证明:三角形的内角和等于180°.小颖通过探究发现:可以将三角形的三个内角之和转化为一个平角来解决也就是可以过三角形的一个顶点作其对边的平行线来证明.请将下面(1)中的证明补充完整:(1)已知:如图1 三角形ABC求证:∠BAC+∠B+∠C=180°证明:过点A作EF ∥BC.(2)如图2 线段AB、CD相交于点O连接AD、CB我们把形如图2这样的图形称之为“8字形”.请利用小颖探究的结论直接写出∠A、∠B、∠C、∠D之间的数量关系:;(3)在图2的条件下∠DAB和∠BCD的平分线AP和CP相交于点P并且与CD、AB分别相交于M、N得到图3 请判断∠P与∠D、∠B之间存在的数量关系并说明理由.【解答】(1)证明:过A作EF∥BC∴∠EAB=∠B∠F AC=∠C又∠EAB+∠BAC+∠F AC=180°∴∠B+∠C+∠BAC=180°;(2)解:根据(1)得∠A+∠D+∠AOD=∠C+∠B+∠COB=180°又∠AOD=∠BOC∴∠A+∠D=∠C+∠B;故答案为:∠A+∠D=∠C+∠B;(3)解:2∠P=∠D+∠B.根据(2)∠D+∠DAP=∠P+∠DCP①∠P AB+∠P=∠B+∠PCB②∵∠DAB和∠BCD的平分线AP和CP相交于点P∴∠DAP=∠P AB∠DCP=∠PCB∴①﹣②得:∠D﹣∠P=∠P﹣∠B∴2∠P=∠D+∠B.27.(2021春•邗江区月考)如图1 已知线段AB、CD相交于点O连接AC、BD则我们把形如这样的图形称为“8字型”.(1)求证:∠A+∠C=∠B+∠D.利用以上结论解决下列问题:(2)如图2所示∠1=130°则∠A+∠B+∠C+∠D+∠E+∠F的度数为.(3)如图3 若∠CAB和∠BDC的平分线AP和DP相交于点P且与CD AB分别相交于点M N.①若∠B=100°∠C=120°求∠P的度数.②若角平分线中角的关系改成“∠CAP=∠CAB∠CDP=∠CDB”试直接写出∠P与∠B∠C之间存在的数量关系并证明理由.【解答】解:(1)证明:在图1中有∠A+∠C=180°﹣∠AOC∠B+∠D=180°﹣∠BOD∵∠AOC=∠BOD∴∠A+∠C=∠B+∠D;(2)如图2所示∵∠DME=∠A+∠E∠3=∠DME+∠D∴∠A+∠E+∠D=∠3∵∠2=∠3+∠F∠1=130°∴∠3+∠F=∠2=∠1=130°∴∠A+∠E+∠D+∠F=130°∵∠B+∠C=∠1=130°∴∠A+∠B+∠C+∠D+∠E+∠F=260°.故答案为:260°.(3)①以M为交点“8字型”中有∠P+∠CDP=∠C+∠CAP 以N为交点“8字型”中有∠P+∠BAP=∠B+∠BDP∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP∵AP、DP分别平分∠CAB和∠BDC∴∠BAP=∠CAP∠CDP=∠BDP∴2∠P=∠B+∠C∵∠B=100°∠C=120°∴∠P=(∠B+∠C)=(100°+120°)=110°;②3∠P=∠B+2∠C其理由是:∵∠CAP=∠CAB∠CDP=∠CDB∴∠BAP=∠CAB∠BDP=∠CDB以M为交点“8字型”中有∠P+∠CDP=∠C+∠CAP以N为交点“8字型”中有∠P+∠BAP=∠B+∠BDP∴∠C﹣∠P=∠CDP﹣∠CAP=(∠CDB﹣∠CAB)∠P﹣∠B=∠BDP﹣∠BAP=(∠CDB﹣∠CAB).∴3(∠C﹣∠P)=∠P﹣∠B∴4∠P=∠B+3∠C.。
八年级上册数学举一反三系列专题06 八年级数学上册期中考试重难点题型(举一反三)(解析版)

专题06 八年级数学上册期中考试重难点题型【举一反三】【人教版】【知识点1】三角形1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2.三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边.3.高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高.钝角三角形三条高的交点在三角形外,直角三角形的三条高的交点在三角形上,锐角三角形的三条高的交点在三角形内,三条高线的交点叫做三角形的垂心4.中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.(三条中线的交点叫重心)5.角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线. (三角形三条角平分线的交点到三边距离相等,三条角平分线的交点叫做内心6.三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性.(例如自行车的三角形车架利用了三角形具有稳定性)7.多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.8.多边形的内角:多边形相邻两边组成的角叫做它的内角.9.多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.10.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.11.正多边形:在平面内,各个角都相等,各条边都相等的多边形叫正多边形.12.平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面,13.公式与性质:⑴三角形的内角和:三角形的内角和为180°⑵三角形外角的性质:性质1:三角形的一个外角等于和它不相邻的两个内角的和.性质2:三角形的一个外角大于任何一个和它不相邻的内角.⑶多边形内角和公式:n 边形的内角和等于(2)n -·180° ⑷多边形的外角和:多边形的外角和为360°. ⑸多边形对角线的条数:①从n 边形的一个顶点出发可以引(3)n -条对角线,把多边形分成(2)n -个三角形.②n 边形共有(3)2n n -条对角线. 【知识点2】全等三角形1.基本定义:⑴全等形:能够完全重合的两个图形叫做全等形.⑵全等三角形:能够完全重合的两个三角形叫做全等三角形.⑶对应顶点:全等三角形中互相重合的顶点叫做对应顶点.⑷对应边:全等三角形中互相重合的边叫做对应边.⑸对应角:全等三角形中互相重合的角叫做对应角.2.基本性质:⑴三角形的稳定性:三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性.⑵全等三角形的性质:全等三角形的对应边相等,对应角相等.3.全等三角形的判定定理:⑴边边边(SSS ):三边对应相等的两个三角形全等.⑵边角边(SAS ):两边和它们的夹角对应相等的两个三角形全等.⑶角边角(ASA):两角和它们的夹边对应相等的两个三角形全等.⑷角角边(AAS):两角和其中一个角的对边对应相等的两个三角形全等.⑸斜边、直角边(HL):斜边和一条直角边对应相等的两个直角三角形全等.4.角平分线:⑴画法:⑵性质定理:角平分线上的点到角的两边的距离相等.⑶性质定理的逆定理:角的内部到角的两边距离相等的点在角的平分线上.(三角形三条角平分线的交点到三边距离相等)【知识点3】轴对称1.基本概念:⑴轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.⑵两个图形成轴对称:把一个图形沿某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称.⑶线段的垂直平分线:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.⑷等腰三角形:有两条边相等的三角形叫做等腰三角形.相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.⑸等边三角形:三条边都相等的三角形叫做等边三角形.2.基本性质:⑴对称的性质:①不管是轴对称图形还是两个图形关于某条直线对称,对称轴都是任何一对对应点所连线段的垂直平分线.②对称的图形都全等.⑵线段垂直平分线的性质:①线段垂直平分线上的点与这条线段两个端点的距离相等.②与一条线段两个端点距离相等的点在这条线段的垂直平分线上.⑷等腰三角形的性质:①等腰三角形两腰相等.②等腰三角形两底角相等(等边对等角).③等腰三角形的顶角角平分线、底边上的中线,底边上的高相互重合.④等腰三角形是轴对称图形,对称轴是三线合一(1条).⑸等边三角形的性质:①等边三角形三边都相等.②等边三角形三个内角都相等,都等于60°③等边三角形每条边上都存在三线合一.④等边三角形是轴对称图形,对称轴是三线合一(3条).3.基本判定:⑴等腰三角形的判定:①有两条边相等的三角形是等腰三角形.②如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边).⑵等边三角形的判定:①三条边都相等的三角形是等边三角形.②三个角都相等的三角形是等边三角形.③有一个角是60°的等腰三角形是等边三角形.4.基本方法:⑴做已知直线的垂线:⑵做已知线段的垂直平分线:⑶作对称轴:连接两个对应点,作所连线段的垂直平分线.⑷作已知图形关于某直线的对称图形:⑸在直线上做一点,使它到该直线同侧的两个已知点的距离之和最短.【考点1 灵活运用三角形三边关系】【例1】(2019秋•洛龙区校级期中)已知△ABC的三边长为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是()A.2b﹣2c B.﹣2b C.2a+2b D.2a【分析】先根据三角形三边关系判断出a+b﹣c与b﹣a﹣c的符号,再把要求的式子进行化简,即可得出答案.【答案】解:∵△ABC的三边长分别是a、b、c,∴a+b>c,b﹣a<c,∴a+b﹣c>0,b﹣a﹣c<0,∴|a+b﹣c|﹣|b﹣a﹣c|=a+b﹣c﹣(﹣b+a+c)=a+b﹣c+b﹣a﹣c=2(b﹣c);故选:A.【点睛】此题考查了三角形三边关系,用到的知识点是三角形的三边关系、绝对值、整式的加减,关键是根据三角形的三边关系判断出a+b﹣c与,b﹣a﹣c的符号.【变式1-1】(2019秋•濉溪县期中)设三角形三边之长分别为3,8,1﹣2a,则a的取值范围为()A.﹣6<a<﹣3B.﹣5<a<﹣2C.﹣2<a<5D.a<﹣5或a>2【分析】根据三角形的三边关系,两边之和大于第三边和两边之差小于第三边列出不等式组求出其解即可.【答案】解:由题意,得8﹣3<1﹣2a<8+3,即5<1﹣2a<11,解得:﹣5<a<﹣2.故选:B.【点睛】本题考查了根据三角形三边关系建立不等式组解实际问题的运用,不等式组的解法的运用,解答时根据三角形的三边关系建立不等式组是关键.【变式1-2】(2019秋•宁都县期中)如图,在△ABC中,AB=5,AC=3,则BC边上的中线AD的取值范围是()A.2<AD<8B.0<AD<8C.1<AD<4D.3<AD<5【分析】先延长AD到E,且AD=DE,并连接BE,由于∠ADC=∠BDE,AD=DE,利用SAS易证△ADC≌△EDB,从而可得AC=BE,在△ABE中,再利用三角形三边的关系,可得2<AE<8,从而易求1<AD<4.【答案】解:延长AD到E,使AD=DE,连接BE,∵AD=DE,∠ADC=∠BDE,BD=DC,∴△ADC≌△EDB(SAS)∴BE=AC=3,在△AEB中,AB﹣BE<AE<AB+BE,即5﹣3<2AD<5+3,∴1<AD<4,∴l的取值范围是1<l<4,故选:C.【点睛】此题主要考查三角形三边关系:两边之和大于第三边,两边之差小于第三边.【变式1-3】(2019•防城港期中)在等腰△ABC中,AB=AC,其周长为20cm,则AB边的取值范围是()A.1cm<AB<4cm B.5cm<AB<10cmC.4cm<AB<8cm D.4cm<AB<10cm【分析】设AB=AC=x,则BC=20﹣2x,根据三角形的三边关系即可得出结论.【答案】解:∵在等腰△ABC中,AB=AC,其周长为20cm,∴设AB=AC=xcm,则BC=(20﹣2x)cm,∴,解得5cm<x<10cm.故选:B.【点睛】本题考查的是等腰三角形的性质、解一元一次不等式组,熟知等腰三角形的两腰相等是解答此题的关键.【考点2 角平分线与多边形内角和】【例2】(2019春•沛县期中)如图,在五边形ABCDE中,∠A+∠B+∠E=α,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是()A.90°+αB.﹣90°C.D.540°【分析】根据五边形的内角和等于540°,由∠A+∠B+∠E=α,可求∠BCD+∠CDE的度数,再根据角平分线的定义可得∠PDC与∠PCD的角度和,进一步求得∠P的度数.【答案】解:∵五边形的内角和等于540°,∠A+∠B+∠E=α,∴∠BCD+∠CDE=540°﹣α,∵∠BCD、∠CDE的平分线在五边形内相交于点O,∴∠PDC+∠PCD=(∠BCD+∠CDE)=270°﹣α,∴∠P=180°﹣(270°﹣α)=α﹣90°,故选:B.【点睛】本题主要考查了多边形的内角和公式,角平分线的定义,熟记公式是解题的关键.注意整体思想的运用.【变式2-1】(2019春•西湖区校级期中)如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=210°,则∠P=()A.10°B.15°C.30°D.40°【分析】利用四边形内角和是360°可以求得∠DAB+∠ABC=150°.然后由角平分线的性质,邻补角的定义求得∠P AB+∠ABP的度数,所以根据△ABP的内角和定理求得∠P的度数即可.【答案】解:如图,∵∠D+∠C=210°,∠DAB+∠ABC+∠C+∠D=360°,∴∠DAB+∠ABC=150°.又∵∠DAB的角平分线与∠ABC的外角平分线相交于点P,∴∠P AB+∠ABP=∠DAB+∠ABC+(180°﹣∠ABC)=90°+(∠DAB+∠ABC)=165°,∴∠P=180°﹣(∠P AB+∠ABP)=15°.故选:B.【点睛】本题考查了三角形内角和定理、多边形的内角与外角.熟知“四边形的内角和是360°”是解题的关键.【变式2-2】(2019秋•香洲区期中)如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD 的平分线交于点P,则∠P=()A.90°﹣αB.αC.90°+αD.360°﹣α【分析】先求出∠ABC+∠BCD的度数,然后根据角平分线的性质以及三角形的内角和定理求解∠P的度数.【答案】解:∵四边形ABCD中,∠ABC+∠BCD=360°﹣(∠A+∠D)=360°﹣α,∵PB和PC分别为∠ABC、∠BCD的平分线,∴∠PBC+∠PCB=(∠ABC+∠BCD)=(360°﹣α)=180°﹣α,则∠P=180°﹣(∠PBC+∠PCB)=180°﹣(180°﹣α)=α.故选:B.【点睛】本题考查了多边形的内角和外角以及三角形的内角和定理,关键是先求出∠ABC+∠BCD的度数.【变式2-3】(2018秋•遵义期中)如图,在四边形ABCD中,∠ABC与∠BCD的平分线的交点E恰好在AD边上,则∠BEC=()A.∠A+∠D﹣45°B.(∠A+∠D)+45°C.180°﹣(∠A+∠D)D.∠A+∠D【分析】根据四边形的内角和和角平分线的定义解答即可.【答案】解:∵四边形的内角和=360°,∴∠ABC+∠BCD=360°﹣(∠A+∠D),∵∠ABC与∠BCD的平分线的交点E恰好在AD边上,∴2∠EBC=∠ABC,2∠ECB=∠BCD,∴∠EBC+∠ECB=,∴∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣=,故选:D.【点睛】本题考查角平分线的定义及四边形的内角和定理,解答的关键是根据四边形的内角和和角平分线的定义解答.【考点3 多边形内角和与外角和】【例3】(2019秋•岳池县期中)一个多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发的对角线的条数是()A.6条B.7条C.8条D.9条【分析】先求出多边形的边数,再求从这个多边形的一个顶点出发的对角线的条数即可.【答案】解:∵多边形的每一个内角都等于140°,∴每个外角是180°﹣140°=40°,∴这个多边形的边数是360°÷40°=9,∴从这个多边形的一个顶点出发的对角线的条数是6条.故选:A.【点睛】本题考查多边形的外角和及对角线的知识点,找出它们之间的关系是本题解题关键.【变式3-1】(2019春•内江期中)马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于830°,则该多边形的边数是()A.7B.8C.7或8D.无法确定【分析】n边形的内角和是(n﹣2)•180°,即为180°的(n﹣2)倍,多边形的内角一定大于0度,小于180度,因而多边形中,除去2个内角外,其余内角和与180度的商加上2,以后所得的数值,比这个数值大1或2的整数就是多边形的边数.【答案】解:设少加的2个内角和为x度,边数为n.则(n﹣2)×180=830+x,即(n﹣2)×180=4×180+110+x,因此x=70,n=7或x=250,n=8.故该多边形的边数是7或8.故选:C.【点睛】本题考查了多边形的内角和定理,正确理解多边形内角的大小的特点,以及多边形的内角和定理是解决本题的关键.【变式3-2】(2019春•诸城市期中)过多边形的一个顶点可以作7条对角线,则此多边形的内角和是外角和的()A.4倍B.5倍C.6倍D.3倍【分析】从多边形一个顶点可作7条对角线,则这个多边形的边数是10,n边形的内角和可以表示成(n ﹣2)•180°,代入公式就可以求出内角和,多边形的外角和为360°,相除即可.【答案】解:∵过多边形的一个顶点共有7条对角线,故该多边形边数为10,∴(10﹣2)•180°=1440°,∴这个多边形的内角和为1440°,又∵多边形的外角和为360°,∴1440÷360=4.故选:A.【点睛】本题主要考查了多边形的对角线、内角和公式.外角和公式,是需要熟记的内容,比较简单.【变式3-3】(2019•凉山州期中)一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为()A.7B.7或8C.8或9D.7或8或9【分析】首先求得内角和为1080°的多边形的边数,即可确定原多边形的边数.【答案】解:设内角和为1080°的多边形的边数是n,则(n﹣2)•180°=1080°,解得:n=8.则原多边形的边数为7或8或9.故选:D.【点睛】本题考查了多边形的内角和定理,一个多边形截去一个角后它的边数可能增加1,可能减少1,或不变.【考点4 三角形全等的条件判断】【例4】(2018秋•利津县期中)如图,AB∥CD,BC∥AD,AB=CD,AE=CF,其中全等三角形的对数是()A.4B.3C.2D.1【分析】根据平行线的性质和全等三角形的判定和性质解答即可.【答案】解:∵AB∥CD,BC∥AD,∴∠BAC=∠ACD,∠DAC=∠ACB.在△ABC和△CDA中,∴△ABC≌△CDA(ASA),∴AD=BC,AB=CD.在△ABE和△CDF中,∴△ABE≌△CDF(SAS),∴BE=DF.∵AE=CF,∴AE+EF=CE+EF,∴AF=CE,在△ADF和△CBE中,∴△ADF≌△CBE(SSS),即3对全等三角形,故选:B.【点睛】本题考查了平行线的性质,全等三角形的性质和判定的应用,能正确根据定理进行推理是解此题的关键,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.【变式4-1】(2018秋•思明区校级期中)如图,已知,∠CAB=∠DAE,AC=AD,增加下列条件:①AB =AE;②BC=ED;③∠C=∠D;④∠B=∠E;⑤∠1=∠2.其中能使△ABC≌△AED的条件有()A.2个B.3个C.4个D.5个【分析】根据已有的条件∠CAB=∠DAE,AC=AD,利用全等三角形的判定定理分别进行分析即可.【答案】解:∵∠CAB=∠DAE,AC=AD,∴①加上条件AB=AE可利用SAS定理证明△ABC≌△AED;②加上BC=ED不能证明△ABC≌△AED;③加上∠C=∠D可利用ASA证明△ABC≌△AED;④加上∠B=∠E可利用AAS证明△ABC≌△AED;⑤加上∠1=∠2不能证明△ABC≌△AED;故选:B.【点睛】此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.【变式4-2】(2018秋•东台市期中)根据下列已知条件,能够画出唯一△ABC的是()A.AB=6,BC=5,∠A=50°B.AB=5,BC=6,AC=13C.∠A=50°,∠B=80°,AB=8D.∠A=40°,∠B=50°,∠C=90°【分析】根据全等三角形的判定方法可知只有C能画出唯一三角形.【答案】解:A、已知AB、BC和BC的对角,不能画出唯一三角形,故本选项错误;B、∵AB+BC=5+6=11<AC,∴不能画出△ABC;故本选项错误;C、已知两角和夹边,能画出唯一△ABC,故本选项正确;D、根据∠A=40°,∠B=50°,∠C=90°不能画出唯一三角形,故本选项错误;故选:C.【点睛】本题考查了全等三角形的判定方法;一般三角形全等的判定方法有SSS、SAS、ASA、AAS,熟练掌握全等三角形的判定方法是解题的关键.【变式4-3】(2018秋•东台市期中)如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,BC=EF,∠B=∠E;③∠B=∠E,∠C=∠F,BC=EF;④AB=DE,AC=DF,∠B=∠E.其中,能使△ABC≌△DEF的条件共有()A.1组B.2组C.3组D.4组【分析】根据全等三角形判定的条件,可得答案.【答案】解:①AB=DE,BC=EF,AC=DF;②AB=DE,BC=EF,∠B=∠E;③∠B=∠E,∠C=∠F,BC=EF;故选:C.【点睛】本题考查了全等三角形的判定,熟记全等三角形的判定是解题关键.【考点5 等腰三角形中的分类讨论思想】【例5】(2018春•鄄城县期中)等腰三角形的周长为15cm,其中一边长为3cm,则该等腰三角形的腰长为()A.3cm B.6cm C.3cm或6cm D.8cm【分析】此题要分情况考虑:3cm是底或3cm是腰.根据周长求得另一边,再进一步根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,判断是否能够组成三角形.【答案】解:当3cm是底时,则腰长是(15﹣3)÷2=6(cm),此时能够组成三角形;当3cm是腰时,则底是15﹣3×2=9(cm),此时3+3<9,不能组成三角形,应舍去.故选:B.【点睛】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.【变式5-1】(2018春•金水区校级期中)已知等腰三角形一腰的垂直平分线与另一腰所在的直线的夹角为40°,则此等腰三角形的顶角是()A.50°B.130°C.50°或140°D.50°或130°【分析】由题意可知其为锐角等腰三角形或钝角等腰三角形,不可能是等腰直角三角形,所以应分开来讨论.【答案】解:当为锐角时,如图:∵∠ADE=40°,∠AED=90°,∴∠A=50°,当为钝角时,如图:∠ADE=40°,∠DAE=50°,∴顶角∠BAC=180°﹣50°=130°.故选:D.【点睛】本题考查了等腰三角形的性质及三角形内角和定理,分类讨论是正确解答本题的关键.【变式5-2】(2019秋•绥棱县期中)已知一个等腰三角形底边的长为5cm,一腰上的中线把其周长分成的两部分的差为3cm,则腰长为()A.2cm B.8cm C.2cm或8cm D.10cm【分析】作出图形,根据三角形的中线的定义可得AD=CD,然后求出两三角形的周长的差等于腰长与底边的差,然后分情况讨论求解即可.【答案】解:如图,∵BD是△ABC的中线,∴AD=CD,∴两三角形的周长的差等于腰长与底边的差,∵BC=5cm,∴AB﹣5=3或5﹣AB=3,解得AB=8或AB=2,若AB=8,则三角形的三边分别为8cm、8cm、5cm,能组成三角形,若AB=2,则三角形的三边分别为2cm、2cm、5cm,∵2+2=4<5,∴不能组成三角形,综上所述,三角形的腰长为8cm.故选:B.【点睛】本题考查了等腰三角形的性质,三角形的中线,难点在于分情况讨论并利用三角形的三边关系判断是否能组成三角形.【变式5-3】(2018秋•沙依巴克区校级期中)等腰三角形一腰上的高等于该三角形某一条边的长度的一半,则其顶角等于()A.30°B.30°或150°C.120°或150°D.30°或120°或150°【分析】题中没有指明等腰三角形一腰上的高是哪边长的一半,故应该分三种情况进行分析,从而不难求解.【答案】解:①如图,∵∠ADB=90°,AD=AB,∴∠B=30°,∵AC=BC,∴∠CAB=30°,∴∠ACB=180°﹣30°﹣30°=120°.②如图,∵∠ADB=90°,AD=AC,∴∠ACD=30°,∵AC=BC,∴∠CAB=∠B=15°,∠ACB=180°﹣30°=150°.③如图,∵∠ADB=90°,AD=BC,∴∠B=30°,∵AB=BC,∴∠CAB=∠C=75°,∴∠B=30°.故选:D.【点睛】此题主要考查等腰三角形的性质,三角形内角和定理及三角形外角性质的综合运用.【考点6 三种双角平分线应用】【例6】(2018春•翠屏区校级期中)已知△ABC,下列说法正确的是(只填序号).①如图(1),若点P是∠ABC和∠ACB的角平分线的交点,则∠P=90°+∠A;②如图(2),若点P是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°﹣∠A;③如图(3),若点P是∠ABC和外角∠ACE的角平分线的交点,则∠P=∠A.【分析】①正确.三角形的内角和为180°,∠ABC+∠ACB=180°﹣∠A,∠P=180°﹣(∠ABC+∠ACB),从而得证;②正确.根据三角形外角平分线的性质可得∠BCP=(∠A+∠ABC)、∠PBC=(∠A+∠ACB);根据三角形内角和定理可得∠P=90°﹣∠A.③正确.根据角平分线的定义可得∠PBC=∠ABC,∠PCE=∠ACE,由外角的性质可得∠ACE=∠ABC+∠A,∠PCE=∠PBC+∠P,等量代换求出结果;【答案】解:①正确.∵P点是∠ABC和∠ACB的角平分线的交点,∴∠PBC+∠PCB=(∠ABC+∠ACB)=(180°﹣∠A)=90°﹣∠A,∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣90°+∠A=90°+∠A;②正确.∵BP、CP为△ABC两外角的平分线,∴∠BCP=∠BCE=(∠A+∠ABC),∠PBC=∠CBF=(∠A+∠ACB),由三角形内角和定理得:∠BPC=180°﹣∠BCP﹣∠PBC=180°﹣[∠A+(∠A+∠ABC+∠ACB)]=180°﹣(∠A+180°)=90°﹣∠A.③正确.∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∴∠PBC=∠ABC,∠PCE=∠ACE,∵∠ACE是△ABC的外角,∠PCE是△BPC的外角,∴∠ACE=∠ABC+∠A,∠PCE=∠PBC+∠P,∴∠ACE=∠ABC+∠A,∴∠ABC+∠A=∠PBC+∠P,∠P=∠A;故答案为①②③.【点睛】此题主要考查了三角形的内角和外角之间的关系.(1)三角形的外角等于与它不相邻的两个内角和;(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.【变式6-1】(2019秋•新洲区期中)如图,△ABC中,∠BAC=70°,∠ABC的平分线与∠ACB的外角平分线交于点O,则∠BOC=度.【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAC+∠ABC=∠ACE,∠BOC+∠OBC=∠OCE,再根据角平分线的定义可得∠OBC=∠ABC,∠OCE=∠ACE,然后整理可得∠D =∠A.【答案】解:由三角形的外角性质,∠BAC+∠ABC=∠ACE,∠BOC+∠OBC=∠OCE,∵∠ABC的平分线与∠ACB的外角平分线交于点O,∴∠OBC=∠ABC,∠OCE=∠ACE,∴(∠BAC+∠ABC)=∠BOC+∠ABC,∴∠BOC=∠A,∵∠BAC=70°,∴∠BOC=35°,故答案为:35°.【点睛】本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,要注意整体思想的利用.【变式6-2】(2019秋•高密市期中)如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BD的平分线与∠A1CD的平分线交于点A2,若∠A=60°,则∠A2的度数为.【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,根据角平分线的定义可得∠A1BC=∠ABC,∠A1CD=∠ACD,然后整理得到∠A1=∠A,同理可得∠A2=∠A1.【答案】解:由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,∵∠ABC的平分线与∠ACD的平分线交于点A1,∴∠A1BC=∠ABC,∠A1CD=∠ACD,∴∠A1+∠A1BC=(∠A+∠ABC)=∠A+∠A1BC,∴∠A1=∠A,同理可得∠A2=∠A1=××60°=15°,故答案为15°.【点睛】本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记性质并准确识图然后求出后一个角是前一个角的是解题的关键.【变式6-3】(2018秋•江汉区校级期中)如图,△ABC中,∠C=104°,BF平分∠ABC与△ABC的外角平分线AE所在的直线交于点F,则∠F=.【分析】根据角平分线的定义的定义可知:∠ABF=∠ABC,∠EAB=∠DAB,根据三角形外角的性质可知:∠EAB﹣∠ABF=52°,进而得到∠F的度数.【答案】解:∵BF平分∠ABC,AE平分∠DAB,∴∠ABF=∠ABC,∠EAB=∠DAB,∵∠DAB﹣∠ABC=∠C=104°,∴∠F=∠EAB﹣∠ABF=(∠DAB﹣∠ABC)=52°,故答案为:52°.【点睛】本题考查的是三角形内角和定理和三角形的外角的性质,掌握三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.【考点7 线段垂直平分线的应用】【例7】(2018春•叶县期中)如图所示,在△ABC中,AB=AC,∠BAC为钝角,BC=6,AB、AC的垂直平分线分别交BC于点D、E,连接AD、AE,那么△ADE的周长为.【分析】根据垂直平分线性质得AD=BD,AE=EC,所以△ADE周长=BC.【答案】解:∵AB、AC的垂直平分线分别交BC于D、E,∴AD=BD,AE=CE,∴L△ADE=AD+DE+AE=BD+DE+CE=BC=6.故答案为:6【点睛】本题主要考查了线段垂直平分线的性质,关键是根据垂直平分线性质得AD=BD,AE=EC.【变式7-1】(2018秋•江都区期中)如图,在△ABC中,DM、EN分别垂直平分AC和BC交AB于M、N,∠ACB=118°,则∠MCN的度数为.【分析】据三角形内角和定理求出∠A+∠B;根据等腰三角形性质得∠ACM+∠BCN的度数,然后求解.【答案】解:∵∠ACB=118°,∴∠A+∠B=62°.∵AM=CM,BN=CN,∴∠A=∠ACM,∠B=∠BCN,∴∠ACM+∠BCN=62°.∴∠MCN=∠ACB﹣(∠ACM+∠BCN)=118°﹣62°=56°.故答案为:56°.【点睛】此题考查了线段垂直平分线性质、三角形内角和定理等知识点,渗透了整体求值的思想方法,难度不大.【变式7-2】(2019秋•新乡期中)如图,在△DAE中,∠DAE=30°,线段AE,AD的中垂线分别交直线DE于B和C两点,则∠BAC的大小是.【分析】由已知条件,利用了中垂线的性质得到线段相等及角相等,再结合三角形内角和定理求解.【答案】解:如图,∵B是AE的中垂线上的点,C是AD的中垂线上的点,∴AB=BE,AC=CD,∴∠AED=∠BAE=∠BAD+∠DAE,∠CDA=∠CAD=∠DAE+∠CAE,∵∠DAE+∠ADE+∠AED=180°,∴∠BAD+∠DAE+∠DAE+∠CAE+∠DAE=3∠DAE+∠BAD+∠EAC=90°+∠BAD+∠EAC=180°,∴∠BAD+∠EAC=90°,∴∠BAC=∠BAD+∠EAC+∠DAE=90°+30°=120°.故答案为:120°.【点睛】本题考查了中垂线的性质、三角形内角和定理及等腰三角形的判定与性质;确定各角的关系利用内角和列式求解是正确解答本题的关键.【变式7-3】(2018秋•老河口市期中)如图,△ABC的边AB,AC的垂直平分线相交于点P,连接PB,PC,若∠A=70°,则∠BPC的度数是.【分析】根据线段的垂直平分线的性质得到P A=PB,根据等腰三角形的性质得到∠P AB=∠PBA,根据三角形内角和定理计算.【答案】解:∠ABC+∠ACB=180°﹣∠A=110°,∵PE是AB的垂直平分线,∴P A=PB,∴∠P AB=∠PBA,同理,∠P AC=∠PCA,∴∠PBA+∠PCA=∠P AB+∠P AC=∠A=70°,∴∠PBC+∠PCB=110°﹣70°=40°,∴∠BPC=180°﹣40°=140°,故答案为:140°.【点睛】本题考查的是线段垂直平分线的性质,等腰三角形的性质,三角形内角和定理,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.【考点8 利用轴对称变换求最值】【例8】(2017秋•襄州区期中)如图,∠AOB=30°,∠AOB内有一定点P,且OP=12,在OA上有一点Q,OB上有一点R,若△PQR周长最小,则最小周长是【分析】先画出图形,作PM⊥OA与OA相交于M,并将PM延长一倍到E,即ME=PM.作PN⊥OB 与OB相交于N,并将PN延长一倍到F,即NF=PN.连接EF与OA相交于Q,与OB相交于R,再连接PQ,PR,则△PQR即为周长最短的三角形.再根据线段垂直平分线的性质得出△PQR=EF,再根据三角形各角之间的关系判断出△EOF的形状即可求解.【答案】解:设∠POA=θ,则∠POB=30°﹣θ,作PM⊥OA与OA相交于M,并将PM延长一倍到E,即ME=PM.作PN⊥OB与OB相交于N,并将PN延长一倍到F,即NF=PN.连接EF与OA相交于Q,与OB相交于R,再连接PQ,PR,则△PQR即为周长最短的三角形.∵OA是PE的垂直平分线,∴EQ=QP;同理,OB是PF的垂直平分线,∴FR=RP,∴△PQR的周长=EF.∵OE=OF=OP=12,且∠EOF=∠EOP+∠POF=2θ+2(30°﹣θ)=60°,∴△EOF是正三角形,∴EF=12,即在保持OP=12的条件下△PQR的最小周长为12.故答案为:12【点睛】本题考查的是最短距离问题,解答此类题目的关键根据轴对称的性质作出各点的对称点,即把求三角形周长的问题转化为求线段的长解答.【变式8-1】(2018秋•洛龙区校级期中)如图,等腰三角形ABC的面积是16,且底边BC长为4,腰AC 的垂直平分线EF分别交边AC,AB于点EF,若点D为边BC的中点,点M为线段EF上一动点,则△CMD周长的最小值是.【分析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再再根据EF是线段AC的垂直平分线可知,点C关于直线EF的对称点为点A,故AD的长为CM+MD的最小值,由此即可得出结论.【答案】解:连接AD,。
浙教版八年级上册求角度中的几个数学模型及习题

浙教版八年级上册求角度中的几个数学模型及习题角平分线的三大模型① 若CE BE 、分别为ACD ABC ∠∠、的角平分线.则E ∠与A ∠的等量关系为 ② 若CO BO 、分别为ACB ABC ∠∠、的平分线.则BOC ∠与A ∠的等量关系为 ③ 若CO BO 、分别为ECB DBC ∠∠、的平分线. 则BOC ∠与A ∠的等量关系为① ②① ② ③单8模型 双8模型多8模型(单8模型与角平分线相结合)结论: 结论:结论:飞镖模型 飞鱼模型断木模型结论: 结论:结论:练习1、如图所示,∠A+∠B+∠C+∠D+∠E=2、如图所示,∠A+∠BCD=140°,∠A BC 、∠A DC 的平分线BO 、CO 交于点O ,则∠BOD=3、如图所示,∠B=90°,∠E=85°,则∠A+∠C+∠D+∠F=4、如图,α=∠CGE ,则F E D C B A ∠+∠+∠+∠+∠+∠的度数为________5、如图,在四边形ABCD 中,F E 、分别是两组对边延长线的交点,EG 、FG 分别平分DFC BEC ∠∠、,若︒=∠︒=∠8060ABC ADC 、,则EGF ∠的大小是6、如图,在ABC ∆中,ECB DCE ACD EBC DBE ABD ∠=∠=∠=∠=∠=∠,若︒=∠145BEC ,则BDC ∠等于( )、A 100° 、B 105° 、C 110° 、D 115°7、如图,BE 平分∠ABD ,CF 平分∠ACD ,BE 与CF 交于点G ,若∠BDC=140°,∠BGC=110°,求∠A 的大小。
8、如图是一个六角星,已知∠AOE=60°求∠A+∠B+∠C+∠D+∠E+∠F的度数。
9、如图,若∠3=40°,∠5=50°,∠7=80°,则∠1+∠2+∠4+∠6+∠8=度.。
[26946616]2020-2021学年八年级数学人教版上册 第11章 与三角形有关的角度计算
![[26946616]2020-2021学年八年级数学人教版上册 第11章 与三角形有关的角度计算](https://img.taocdn.com/s3/m/0102fc6c71fe910ef02df85c.png)
条件:BD 是∠ABC 的角平分线,CD 是∠ACB 的角平分线。
1
结论:∠D=90°+ ∠A。
2 证明:证法一:∵BD 是∠ABC 的角平分线,∴∠1=∠2= 1 ∠ABC,
2
∵CD 是∠ACB 的角平分线,∴∠3=∠4= 1 ∠ACB, 2
1
在△BCD 中,∠D=180°-∠1-∠4=180°- (∠ABC+∠ACB)
4、如图,已知∠ABC 的平分线 BD 与△ACB 的外角平分线 CD 相交于点 D,连接 AD,若 ∠BDC=40°,则∠DAC 的度数为_______.
5、如图,在△ABC 中,∠ABC 与∠ACB 的角平分线交于 I,根据下列条件填空 (1)若∠ABC=50°,∠ACB=80°,则∠BIC=______。 (2)若∠ABC+∠ACB=120°,则∠BIC=_______。 (3)若∠A=56°,则∠BIC=______; (4)若∠BIC=120°,则∠A=______; (5)若∠A=α,请将∠BIC 用α的代数式表示。
M
D
N
7、如图,在△ABC 中,∠ABC 的角平分线与∠ACD 的角平分线交于同一点 P,根据下列条件 填空: (1) 若∠A=50°,则∠P=______;
(2)若∠ABC+∠ACB=135°,则∠P=______;
(3)若∠BPC=34°,则∠A=______;
(4)若∠A=α,请将∠P 用α的代数式表示。
9、如图,∠DBC 和∠ECB 的角平分线相交于点 O,∠A=α,
(1)若∠CBO= 1 ∠DBC,∠BCO= 1 ∠ECB,请将∠BOC 用α的代数式表示.
3
3
八年级上册数学举一反三系列专题02 角度计算中的经典模型(举一反三)(解析版)

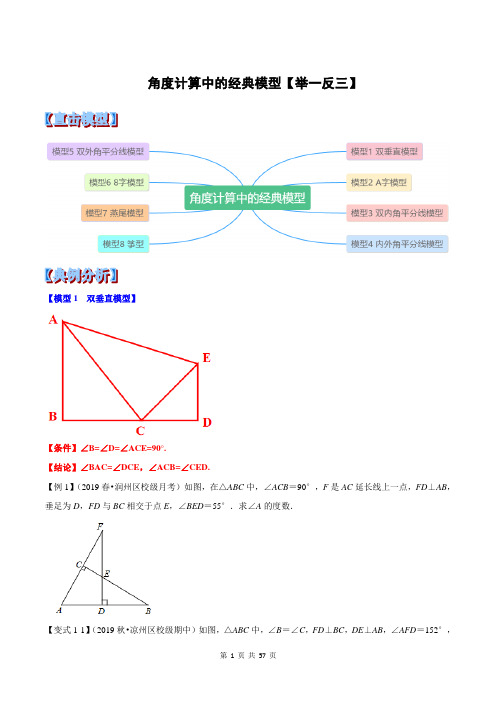
专题02 角度计算中的经典模型【举一反三】【模型1 双垂直模型】【条件】∠B=∠D=∠ACE=90°.【结论】∠BAC=∠DCE,∠ACB=∠CED.【例1】(2019春•润州区校级月考)如图,在△ABC中,∠ACB=90°,F是AC延长线上一点,FD⊥AB,垂足为D,FD与BC相交于点E,∠BED=55°.求∠A的度数.【分析】首先由FD⊥AB于D,根据直角三角形两锐角互余得出∠BED+∠B=90°,同理,由∠ACB=90°,得出∠A+∠B=90°,然后根据同角的余角相等得出∠A=∠BED=55°.【答案】解:∵FD⊥AB于D,∴∠BED+∠B=90°,∵∠ACB=90°,∴∠A+∠B=90°,∴∠A=∠BED=55°.【点睛】本题主要考查了直角三角形的性质以及余角的性质,比较简单.【变式1-1】(2019秋•凉州区校级期中)如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠A的度数.【分析】利用外角性质可求得∠C,在△ABC中利用三角形内角和定理可求得∠A.【答案】解:∵DF⊥BC,∴∠FDC=90°,∵∠AFD=152°,∴∠C=∠AFD﹣∠FDC=152°﹣90°=62°,∵∠B=∠C,∴∠A=180°﹣∠B﹣∠C=180°﹣62°﹣62°=56°.【点睛】本题主要考查三角形内角和定理,掌握三角形三个内角和为180°是解题的关键.【变式1-2】(2019春•莲湖区期中)如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.(1)求证:∠ACD=∠B;(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.【分析】(1)由于∠ACD与∠B都是∠BCD的余角,根据同角的余角相等即可得证;(2)根据直角三角形两锐角互余得出∠CF A=90°﹣∠CAF,∠AED=90°﹣∠DAE,再根据角平分线的定义得出∠CAF=∠DAE,然后由对顶角相等的性质,等量代换即可证明∠CEF=∠CFE.【答案】证明:(1)∵∠ACB=90゜,CD⊥AB于D,∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,∴∠ACD=∠B;(2)在Rt△AFC中,∠CF A=90°﹣∠CAF,同理在Rt△AED中,∠AED=90°﹣∠DAE.又∵AF平分∠CAB,∴∠CAF=∠DAE,∴∠AED=∠CFE,又∵∠CEF=∠AED,∴∠CEF=∠CFE.【点睛】本题考查了直角三角形的性质,三角形角平分线的定义,对顶角的性质,余角的性质,难度适中.【变式1-3】(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,∠ACD与∠B有什么关系?为什么?(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状是什么?为什么?(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,AB⊥BD,点C,B,E在同一直线上,∠A与∠D有什么关系?为什么?【分析】(1)根据直角三角形的性质得出∠ACD+∠A=∠B+∠DCB=90°,再解答即可;(2)根据直角三角形的性质得出∠ADE+∠A=∠A+∠B=90°,再解答即可;(3)根据直角三角形的性质得出∠ABC+∠A=∠ABC+∠DBE=∠DBE+∠D=90°,再解答即可.【答案】解:(1)∠ACD=∠B,理由如下:∵在Rt△ABC中,∠ACB=90°,CD⊥AB,∴∠ACD+∠A=∠B+∠DCB=90°,∴∠ACD=∠B;(2)△ADE是直角三角形.∵在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,∠A为公共角,∴∠AED=∠ACB=90°,∴△ADE是直角三角新;(3)∠A+∠D=90°.∵在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,AB⊥BD,∴∠ABC+∠A=∠ABC+∠DBE=∠DBE+∠D=90°,∴∠A+∠D=90°.【点睛】此题考查直角三角形的性质,关键是根据直角三角形的性质得出两锐角互余.【模型2 A字模型】【结论】∠BDE+∠CED=180°+∠A【例2】(2019春•资中县月考)如图所示,△ABC中,∠C=75°,若沿图中虚线截去∠C,则∠1+∠2等于多少度?【分析】根据三角形内角和定理求出∠A+∠B,根据多边形的内角和公式求出即可.【答案】解:∵∠A+∠B+∠C=180°,∴∠A+∠B=180°﹣∠C,∵∠C=75°,∴∠A+∠B=180°﹣75°=105°,∵∠1+∠2+∠A+∠B=360°,∴∠1+∠2=360°﹣(∠A+∠B),∴∠1+∠2=360°﹣105°=255°.【点睛】本题考查了三角形的内角和定理和多边形的内角和公式,能熟记定理是解此题的关键.【变式2-1】(2019春•长沙县校级期中)如图,已知∠A=40°,求∠1+∠2+∠3+∠4的度数.【分析】根据三角形的内角和定理分别求得∠1+∠2,∠3+∠4,就可求得最后结果.【答案】解:∵∠A=40°,∴∠1+∠2=∠3+∠4=180°﹣∠A=140°.∴∠1+∠2+∠3+∠4=280°.【点睛】此题主要是三角形内角和定理的运用.【变式2-2】(2019春•盱眙县期中)我们容易证明,三角形的一个外角等于它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?Ⅰ.尝试探究:(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?Ⅱ.初步应用:(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2﹣∠C=;(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案.【分析】(1)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠DBC+∠ECB,再利用三角形内角和定理整理即可得解;(2)根据(1)的结论整理计算即可得解;(3)表示出∠DBC+∠ECB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形内角和定理列式整理即可得解;【答案】解:(1)∠DBC+∠ECB=180°﹣∠ABC+180°﹣∠ACB=360°﹣(∠ABC+∠ACB)=360°﹣(180°﹣∠A)=180°+∠A;(2)∵∠1+∠2=∠180°+∠C,∴130°+∠2=180°+∠C,∴∠2﹣∠C=50°;(3)∠DBC+∠ECB=180°+∠A,∵BP、CP分别平分外角∠DBC、∠ECB,∴∠PBC+∠PCB=(∠DBC+∠ECB)=(180°+∠A)在△PBC中,∠P=180°﹣(180°+∠A)=90°﹣∠A;即∠P=90°﹣∠A;故答案为:50°,∠P=90°﹣∠A.【点睛】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,角平分线的定义,熟记性质并读懂题目信息是解题的关键.【变式2-3】(2019春•盐都区期中)(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于A.90°B.135°C.270°D.315°(2)如图2,已知△ABC中,∠A=50°,剪去∠A后成四边形,则∠1+∠2=°.(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是.(4)如图3,若∠A没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.【分析】(1)利用了四边形内角和为360°和直角三角形的性质求解;(2)根据三角形的外角等于与它不相邻的两个内角和求解;(3)根据(1)(2)可以直接写出结果;(4)根据折叠的性质,对应角相等,以及邻补角的性质即可求解.【答案】解:(1)∵四边形的内角和为360°,直角三角形中两个锐角和为90°∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.∴∠1+∠2等于270°.故选C;(2)∠1+∠2=180°+50°=230°.故答案是:230;(3)∠1+∠2与∠A的关系是:∠1+∠2=180°+∠A;故答案是:∠1+∠2=180°+∠A;(4)∵△EFP是由△EF A折叠得到的,∴∠AFE=∠PFE,∠AEF=∠PEF∴∠1=180°﹣2∠AFE,∠2=180°﹣2∠AEF∴∠1+∠2=360°﹣2(∠AFE+∠AEF)又∵∠AFE+∠AEF=180°﹣∠A,∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A,即∠1+∠2=2∠A.【点睛】主要考查了三角形的内角和外角之间的关系.(1)三角形的外角等于与它不相邻的两个内角和.(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.【模型3 双内角平分线模型】【条件】BP、CP分别为∠ABC、∠ACB的角平分线.1∠A.【结论】∠P=90°+2【例3】(2018秋•开封期中)如图,△ABC中,(1)若∠B=70°,点P是△ABC的∠BAC和∠ACB的平分线的交点,求∠APC的度数.(2)如果把(1)中∠B=70°这个条件去掉,试探索∠APC和∠B之间有怎样的数量关系.【分析】(1)依据点P是△ABC的∠BAC和∠ACB的平分线的交点,即可得到∠P AC=∠BAC,∠PCA =∠BCA,再根据三角形内角和定理,即可得到∠APC的度数.(2)依据点P是△ABC的∠BAC和∠ACB的平分线的交点,即可得到∠P AC=∠BAC,∠PCA=∠BCA,进而得出∠P AC+∠PCA=(∠P AC+∠PCA),再根据∠P=180°﹣(∠P AC+∠PCA)进行计算即可.【答案】解:(1)∵∠B=70°,∴∠BAC+∠BCA=110°,∵点P是△ABC的∠BAC和∠ACB的平分线的交点,∴∠P AC=∠BAC,∠PCA=∠BCA,∴∠P AC+∠PCA=(∠P AC+∠PCA)=×110°=55°,∴∠P=180°﹣55°=125°;(2)∵点P是△ABC的∠BAC和∠ACB的平分线的交点,∴∠P AC=∠BAC,∠PCA=∠BCA,∴∠P AC+∠PCA=(∠P AC+∠PCA),∴∠P=180°﹣(∠P AC+∠PCA)=180°﹣(∠BAC+∠BCA)=180°﹣(180°﹣∠B)=90°+∠B.【点睛】本题主要考查了三角形内角和定理以及角平分线的定义,解决问题的关键是掌握三角形内角和定理:三角形内角和是180°.【变式3-1】(2018秋•徐闻县期中)如图,在△ABC中,∠ABC与∠ACB的平分线交于点O.(1)如图1,已知∠ABC=40°,∠ACB=60°,求∠BOC的度数.(2)如图2,已知∠A=90°,求∠BOC的度数.(3)如图1,设∠A=m°,求∠BOC的度数.【分析】根据三角形内角和定理以及角平分线的定义求解即可;【答案】解:(1)∵BC平分∠ABC,∠ABC=40°,∴∠OBC=∠ABC=20°,∵CO平分∠ACB,∠ACB=60°,∴∠OCB=∠ACB=30°,∴∠BOC=180°﹣20°﹣30°=130°.(2)∵∠A=90°,∴∠ABC+∠ACB=180°﹣90°=90°,又∵∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=45°,∴∠BOC=180°﹣45°=135°.(3)∵∠A=m°∴∠ABC+∠ACB=180°﹣m°,又∵∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=90°﹣m°,∴∠BOC=90°+m°.【点睛】本题考查三角形内角和定理,角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.【变式3-2】(2019春•南岗区期末)已知在△ABC中,∠A=100°,点D在△ABC的内部连接BD,CD,且∠ABD=∠CBD,∠ACD=∠BCD.(1)如图1,求∠BDC的度数;(2)如图2,延长BD交AC于点E,延长CD交AB于点F,若∠AED﹣∠AFD=12°,求∠ACF的度数.【分析】(1)依据三角形内角和定理以及角平分线的定义,即可得到∠BDC的度数;(2)设∠ACF=α,则∠BCD=α,∠CBD=40°﹣α=∠ABD,依据三角形外角性质,即可得到∠AED =∠ACF+∠CDF,∠AFD=∠ABE+∠BDF,再根据∠AED﹣∠AFD=12°,即可得到α的值.【答案】解:(1)∵∠A=100°,∴∠ABC+∠ACB=80°,又∵∠ABD=∠CBD,∠ACD=∠BCD,∴∠CBD=∠ABC,∠BCD=∠ACB,∴∠CBD+∠BCD=(∠ABC+∠ACB)=40°,∴∠BDC=180°﹣40°=140°;(2)设∠ACF=α,则∠BCD=α,∵∠BDC=140°,∴∠CBD=40°﹣α=∠ABD,∵∠AED是△DCE的外角,∠AFD是△BDF的外角,∴∠AED=∠ACF+∠CDF,∠AFD=∠ABE+∠BDF,∴∠AED﹣∠AFD=∠ACF+∠CDF﹣∠ABE﹣∠BDE=α﹣(40°﹣α)=12°,解得α=26°,∴∠ACF =26°.【点睛】本题主要考查了三角形内角和定理以及三角形外角性质的运用,解题时注意:三角形内角和是180°.【变式3-3】(2019春•东阿县期末)已知任意一个三角形的三个内角的和是180°.如图1,在△ABC 中, ∠ABC 的角平分线BO 与∠ACB 的角平分线CO 的交点为O(1)若∠A =70°,求∠BOC 的度数;(2)若∠A =a ,求∠BOC 的度数;(3)如图2,若BO 、CO 分别是∠ABC 、∠ACB 的三等分线,也就是∠OBC=31∠ABC ,∠OCB=31∠ACB ,∠A =a ,求∠BOC 的度数.【分析】(1)根据三角形的内角和定理求出∠ABC +∠ACB ,根据角平分线的定义求出∠OBC +∠OCB ,根据三角形内角和定理求出即可;(2)根据三角形的内角和定理求出∠ABC +∠ACB ,根据角平分线的定义求出∠OBC +∠OCB ,根据三角形内角和定理求出即可;(3)根据三角形的内角和定理求出∠ABC +∠ACB ,求出∠OBC +∠OCB ,根据三角形内角和定理求出即可.【答案】解:(1)∵∠A =70°,∴∠ABC +∠ACB =180°﹣∠A =110°,∵在△ABC 中,∠ABC 的角平分线BO 与∠ACB 的角平分线CO 的交点为O ,∴∠OBC =∠ABC ,∠OCB =ACB ,∴∠OBC +∠OCB =(∠ABC +∠ACB )=55°,∴∠BOC =180°﹣(∠OBC +∠OCB )=125°;(2)∵∠A =α,∴∠ABC +∠ACB =180°﹣∠A =180°﹣α,∵在△ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O,∴∠OBC=∠ABC,∠OCB=ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣α)=90°﹣,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(90°﹣)=90°+;(3)∵∠A=α,∴∠ABC+∠ACB=180°﹣∠A=180°﹣α,∵∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣α)=60°﹣,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(60°﹣)=120°+.【点睛】本题考查了三角形的内角和定理和角平分线的定义,能求出∠OBC+∠OCB是解此题的关键,求解过程类似.【模型4 内外角平分线模型】【条件】BP、CP分别为∠ABC、∠ACD的角平分线.1∠P.【结论】∠A=2【例4】(2018秋•江岸区期中)如图,△ABC中,∠ABC与∠ACB的外角的平分线相交于点E.(1)已知∠A=60°,求∠E的度数;(2)直接写出∠A与∠E的数量关系:.【分析】(1)根据角平分线的定义得到∠ECD=∠ACD,∠EBC=∠ABC,根据三角形的外角的性质计算;(2)仿照(1)的计算过程证明.【答案】解:(1)∵CE、BE分别平分∠ACD、∠ABC,∴∠ECD=∠ACD,∠EBC=∠ABC,∴∠E=∠ECD﹣∠EBD=(∠ACD﹣∠ABC)=∠A=30°;(2)由(1)得,∠E=∠A,∴∠A=2∠E故答案为:∠A=2∠E.【点睛】本题考查的是角平分线的定义,三角形的外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.【变式4-1】(2019秋•卫滨区校级期中)如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP 交于点P,若∠BPC=40°,求∠CAB的度数.【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠BAC+∠ABC,∠PCD=∠P+∠PCB,根据角平分线的定义可得∠PCD=∠ACD,∠PBC=∠ABC,然后整理得到∠PCD=40°+∠ABC,再代入数据计算即可得解.【答案】解:在△ABC中,∠ACD=∠BAC+∠ABC,在△PBC中,∠PCD=∠BPC+∠PBC,∵PB、PC分别是∠ABC和∠ACD的平分线,∴∠PCD=∠ACD,∠PBC=∠ABC,∴∠PCD=∠BPC+∠PBC=40°+∠ABC,∴∠ACD=∠ABC+40°,∴∠ACD﹣∠ABC=80°,∴∠BAC=∠ACD﹣∠ABC=80°,即∠CAB=80°.【点睛】本题考查了三角形内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记定理与性质并求出∠PCD=40°+∠ABC是解题的关键.【变式4-2】(2019秋•莆田校级期中)如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE 的平分线,且与BD交于点D;(1)若∠ABC=60°,∠DCE=70°,则∠D=°;(2)若∠ABC=70°,∠A=80°,则∠D=°;(3)当∠ABC和∠ACB在变化,而∠A始终保持不变,则∠D是否发生变化?为什么?由此你能得出什么结论?(用含∠A的式子表示∠D)【分析】(1)根据三角形内角和定理和三角形外角的性质即可求得;(2)根据三角形内角和定理和三角形外角的性质即可求得;(3)根据三角形内角和定理以及角平分线性质,先求出∠D、∠A的等式,推出∠D=∠A,即可求得结论.【答案】解:(1)∵BD为△ABC的角平分线,∠ABC=60°,∴∠DBC=30°,∵∠DCE=70°,∴∠D=∠DCE﹣∠DBC=70°﹣30°=40°;(2)∵∠ABC=70°,∠A=80°,∴∠ACE=150°∵BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,∴∠DBC=∠ABC=35°,∠DCE=∠ACE=75°,∴∠D=∠DCE﹣∠DBC=75°﹣35°=40°;(3)不变化,理由:∵∠DCE=∠DBC+∠D,∴∠D=∠ACE﹣∠ABC=(∠A+∠ABC)﹣∠ABC=∠A.故答案为40;40.【点睛】此题考查三角形内角和定理以及三角形外角的性质的综合运用,解此题的关键是求出∠D=∠A.【变式4-3】(2018秋•彭水县校级月考)如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE 的外角平分线,CD与BD交于点D.(1)若∠A=50°,则∠D=;(2)若∠A=80°,则∠D=;(3)若∠A=130°,则∠D=;(4)若∠D=36°,则∠A=;(5)综上所述,你会得到什么结论?证明你的结论的准确性.【分析】先根据角平分线定义得到∠ACE=2∠2,∠ABC=2∠1,再根据三角形外角性质得∠ACE=∠ABC+∠A,则2∠2=2∠1+∠A,接着再根据三角形外角性质得∠2=∠1+∠D,易得∠A=2∠D,即∠D =∠A,然后利用此结论分别解决(1)、(2)、(3)(4)(5).【答案】解:如图,∵BD是△ABC的角平分线,CD是△ABC的外角∠ACE的平分线,∴∠ACE=2∠2,∠ABC=2∠1,∵∠ACE=∠ABC+∠A,∴2∠2=2∠1+∠A,而∠2=∠1+∠D,∴2∠2=2∠1+2∠D,∴∠A=2∠D,即∠D=∠A,(1)当若∠A=50°,则∠D=25°;(2)若∠A=80°,则∠D=40°;(3)若∠A=130°,则∠D=65°.(4)若∠D=36°,则∠A=72°,故答案为25°,40°,65°,72°;(5)综上所述,∠D=∠A;【点睛】本题考查了三角形内角和定理:三角形内角和是180°.主要用在求三角形中角的度数:①直接根据两已知角求第三个角;②依据三角形中角的关系,用代数方法求三个角;③在直角三角形中,已知一锐角可利用两锐角互余求另一锐角.也考查了三角形外角性质.【模型5 双外角平分线模型】【条件】BP、CP分别为∠EBC、∠BCD的角平分线.1∠A.【结论】∠P=90°-2【例5】(2018秋•鄂伦春自治旗月考)如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD 与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:(1)若∠A=60°,则∠P=°;(2)若∠A=40°,则∠P=°;(3)若∠A=100°,则∠P=°;(4)请你用数学表达式归纳∠A与∠P的关系.【分析】(1)若∠A=60°,则有∠ABC+∠ACB=120°,∠DBC+∠BCE=360°﹣120°=240°,根据角平分线的定义可以求得∠PBC+∠PCB的度数,再利用三角形的内角和定理即可求得∠P的度数.(2)(3)和(1)的解题步骤相似.(4)利用角平分线的性质和三角形的外角性质可求出∠BCP=(∠A+∠ABC),∠CBP=(∠A+∠ACB);再利用三角形内角和定理便可求出∠A与∠P的关系.【答案】解:(1)∵∠A=60°,∴∠ABC +∠ACB =180°﹣60°=120°,∠DBC +∠BCE =360°﹣120°=240°,又∵∠CBD 与∠BCE 的平分线相交于点P ,∴∠PBC =∠DBC ,∠PCB =∠BCE ,∴∠PBC +∠PCB =(∠DBC +∠ECB )=120°,∴∠P =60°.同理得:(2)70°;(3)40°(4)∠P =90°﹣∠A .理由如下:∵BP 平分∠DBC ,CP 平分∠BCE ,∴∠DBC =2∠CBP ,∠BCE =2∠BCP又∵∠DBC =∠A +∠ACB ∠BCE =∠A +∠ABC ,∴2∠CBP =∠A +∠ACB ,2∠BCP =∠A +∠ABC ,∴2∠CBP +2∠BCP =∠A +∠ACB +∠A +∠ABC =180°+∠A ,∴∠CBP +∠BCP =90°+∠A又∵∠CBP +∠BCP +∠P =180°,∴∠P =90°﹣∠A .故答案为:60,70,40,90°﹣∠A .【点睛】本题主要考查三角形的一个外角等于和它不相邻的两个内角的和的性质以及角平分线的定义,熟练掌握性质和定义是解题的关键.【变式5-1】(2019秋•团风县校级月考)BD 、CD 分别是△ABC 的两个外角∠CBE 、∠BCF 的平分线, 求证:∠BDC =90°21∠A .【分析】先根据BD 、CD 分别是∠CBE 、∠BCF 的平分线可知∠DBC =∠EBC ,∠BCD =∠BCF ,再由∠CBE、∠BCF是△ABC的两个外角得出∠CBE+∠BCF=360°﹣(180°﹣∠A)=180°+∠A,故∠DBC+∠BCD=(∠EBC+∠BCF)=(180°+∠A)=90°+∠A,根据在△DBC中∠BDC=180°﹣(∠DBC+∠BCD)即可得出结论.【答案】证明:∵BD、CD分别是∠CBE、∠BCF的平分线∴∠DBC=∠EBC,∠BCD=∠BCF,∵∠CBE、∠BCF是△ABC的两个外角∴∠CBE+∠BCF=360°﹣(180°﹣∠A)=180°+∠A∴∠DBC+∠BCD=(∠EBC+∠BCF)=(180°+∠A)=90°+∠A,在△DBC中,∠BDC=180°﹣(∠DBC+∠BCD)=180°﹣(90°+∠A)=90°﹣∠A.【点睛】本题考查的是三角形内角和定理及三角形外角的性质,熟知三角形的内角和等于180°是解答此题的关键.【变式5-2】(2019春•雨城区校级期中)如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,(1)若∠ABC=40°,∠ACB=36°,求∠BIC的大小;(2)若∠A=96°,试求∠BIC;(3)根据前面问题的求解,请归纳∠BIC和∠A的数量关系并进行证明.【分析】(1)运用三角形的内角和定理及角平分线的定义,求出∠IBC+∠ICB的值,即可解决问题.(2)先根据∠A=96°,得出∠1+∠2=84°,再运用(1)中的方法即可解决问题.(3)证明思路方法即(2)中的方法.【答案】解:(1)如图所示,∵∠ABC=40°,∠ACB=36°,∴∠DBC=140°,∠ECB=144°,又∵BI,CI分别平分△ABC的外角∠DBC和∠ECB,∴∠3=∠DBC=70°,∠4=∠ECB=72°,∴△BCI中,∠I=180°﹣70°﹣72°=38°;(2)∵∠A=96°,∴∠1+∠2=84°,∴∠DBC+∠ECB=276°,又∵BI,CI分别平分△ABC的外角∠DBC和∠ECB,∴∠3+∠4=(∠DBC+∠ECB)=×276°=138°,∴△BCI中,∠I=180°﹣138°=42°;(3)∠BIC=90°﹣∠A.证明:△ABC中,∠1+∠2=180°﹣∠A,∴∠DBC+∠ECB=360°﹣(180°﹣∠A)=180°+∠A,又∵BI,CI分别平分△ABC的外角∠DBC和∠ECB,∴∠3+∠4=(∠DBC+∠ECB)=×(180°+∠A)=90°+∠A,∴△BCI中,∠I=180°﹣(∠3+∠4)=180°﹣(90°+∠A)=90°﹣∠A.【点睛】本题主要考查了三角形的内角和定理及角平分线的定义的运用;解题的关键是灵活运用三角形内角和为180°.【变式5-3】如图,在△ABC中,BD,CD是内角平分线,BP,CP是∠ABC,∠ACB的外角平分线,分别交于点D,P.(1)若∠A=30°,求∠BDC,∠BPC的度数.(2)若∠A=m°,求∠BDC,∠BPC的度数(直接写出结果,不必说明理由)(3)想一想,∠A的大小变化,对∠D+∠P的值是否有影响,若有影响,请说明理由,若无影响,直接求出其值.【分析】(1)通过角的平行线的定义以及三角形的内角和可得出∠CBD+∠BCD=75°,再利用三角形的内角和为180°即可得出∠BDC的度数,同理可求出∠BPC的度数;(2)根据(1)的求角过程将30换成m,即可得出结论;(3)由(2)的结论,将两角相加即可得出结论.【答案】解:(1)∵BD,CD是内角平分线,∴∠CBD+∠BCD=(∠ABC+∠ACB),∵∠A+∠ABC+∠ACB=180°,∠A=30°,∴∠ABC+∠ACB=150°,∴∠CBD+∠BCD=75°.又∵∠BDC+∠CBD+∠BCD=180°,∴∠BDC=105°.∵∠CBE+∠BCF=360°﹣(∠ABC+∠ACB)=210°,BP,CP是∠ABC,∠ACB的外角平分线,∴∠CBP+∠BCP=(∠CBE+∠BCF)=105°,∵∠BPC+∠CBP+∠BCP=180°,∴∠BPC=75°.(2)根据(1)的求角过程可知:∠BDC=90°+°,∠BPC=90°﹣°.(3)∵∠D+∠P=90°+°+90°﹣°=180°为定值,∴∠A的大小变化,对∠D+∠P的值无影响.【点睛】本题考查了三角形外角性质、三角形内角和定义以及角平分线的定义,解题的关键是熟练掌握三角形内角和定理是关键.【模型6 8字模型】【结论】∠A+∠B=∠D+∠E.【例6】(2019春•辉县市期末)图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:;(2)仔细观察,在图2中“8字形”的个数:个;(3)图2中,当∠D=50度,∠B=40度时,求∠P的度数.(4)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结果,不必证明).【分析】(1)根据三角形内角和定理即可得出∠A+∠D=∠C+∠B;(2)根据“8字形”的定义,仔细观察图形即可得出“8字形”共有6个;(3)先根据“8字形”中的角的规律,可得∠DAP+∠D=∠P+∠DCP①,∠PCB+∠B=∠P AB+∠P②,再根据角平分线的定义,得出∠DAP=∠P AB,∠DCP=∠PCB,将①+②,可得2∠P=∠D+∠B,进而求出∠P的度数;(4)同(3),根据“8字形”中的角的规律及角平分线的定义,即可得出2∠P=∠D+∠B.【答案】解:(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,∴∠A+∠D=∠C+∠B;(2)①线段AB、CD相交于点O,形成“8字形”;②线段AN、CM相交于点O,形成“8字形”;③线段AB、CP相交于点N,形成“8字形”;④线段AB、CM相交于点O,形成“8字形”;⑤线段AP、CD相交于点M,形成“8字形”;⑥线段AN、CD相交于点O,形成“8字形”;故“8字形”共有6个;(3)∠DAP+∠D=∠P+∠DCP,①∠PCB+∠B=∠P AB+∠P,②∵∠DAB和∠BCD的平分线AP和CP相交于点P,∴∠DAP=∠P AB,∠DCP=∠PCB,①+②得:∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠P AB+∠P,即2∠P=∠D+∠B,又∵∠D=50度,∠B=40度,∴2∠P=50°+40°,∴∠P=45°;(4)关系:2∠P=∠D+∠B.由∠D+∠1+∠2=∠B+∠3+∠4①由∠ONC=∠B+∠4=∠P+∠2,②①+②得:∠D+2∠B+2∠1+2∠3=∠B+2∠3+2∠P+2∠1,∠D+2∠B=2∠P+∠B,即2∠P=∠D+∠B.【点睛】本题主要考查了三角形内角和定理,角平分线的定义及阅读理解与知识的迁移能力.(1)中根据三角形内角和定理得出“8字形”中的角的规律;(2)是考查学生的观察理解能力,需从复杂的图形中辨认出“8字形”;(3)(4)直接运用“8字形”中的角的规律解题.【变式6-1】(2018春•新泰市期中)已知:如图,AM,CM分别平分∠BAD和∠BCD.①若∠B=32°,∠D=38°,求∠M的度数;②探索∠M与∠B、∠D的关系并证明你的结论.【分析】①根据三角形内角和定理用∠B、∠M表示出∠BAM﹣∠BCM,再用∠B、∠M表示出∠MAD ﹣∠MCD,再根据角平分线的定义可得∠BAM﹣∠BCM=∠MAD﹣∠MCD,然后求出∠M与∠B、∠D 关系,代入数据进行计算即可得解;②根据三角形内角和定理用∠B、∠M表示出∠BAM﹣∠BCM,再用∠B、∠M表示出∠MAD﹣∠MCD,再根据角平分线的定义可得∠BAM﹣∠BCM=∠MAD﹣∠MCD,然后求出∠M与∠B、∠D关系.【答案】解:①根据三角形内角和定理,∠B+∠BAM=∠M+∠BCM,∴∠BAM﹣∠BCM=∠M﹣∠B,同理,∠MAD﹣∠MCD=∠D﹣∠M,∵AM、CM分别平分∠BAD和∠BCD,∴∠BAM=∠MAD,∠BCM=∠MCD,∴∠M﹣∠B=∠D﹣∠M,∴∠M=(∠B+∠D)=(32°+38°)=35°;②根据三角形内角和定理,∠B+∠BAM=∠M+∠BCM,∴∠BAM﹣∠BCM=∠M﹣∠B,同理,∠MAD﹣∠MCD=∠D﹣∠M,∵AM、CM分别平分∠BAD和∠BCD,∴∠BAM=∠MAD,∠BCM=∠MCD,∴∠M﹣∠B=∠D﹣∠M,∴∠M=(∠B+∠D).【点睛】本题考查了三角形的内角和定理,角平分线的定义.注意利用“8字形”的对应角相等求出角的关系是解题的关键,要注意整体思想的利用.【变式6-2】(2018秋•南昌期中)如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.(1)求证:∠A +∠C =∠B +∠D ;(2)如图2,若∠CAB 和∠BDC 的平分线AP 和DP 相交于点P ,且与CD 、AB 分别相交于点M 、N . ①以线段AC 为边的“8字型”有 个,以点O 为交点的“8字型”有 个;②若∠B =100°,∠C =120°,求∠P 的度数;③若角平分线中角的关系改为“∠CAP=31∠CAB ,∠CDP=31∠CDB ”,试探究∠P 与∠B 、∠C 之间存在的数量关系,并证明理由.【分析】(1)根据三角形的内角和即可得到结论; (2)①以线段AC 为边的“8字型”有3个,以点O 为交点的“8字型”有4个;②根据角平分线的定义得到∠CAP =∠BAP ,∠BDP =∠CDP ,再根据三角形内角和定理得到∠CAP +∠C =∠CDP +∠P ,∠BAP +∠P =∠BDP +∠B ,两等式相减得到∠C ﹣∠P =∠P ﹣∠B ,即∠P =(∠C +∠B ),然后把∠C =120°,∠B =100°代入计算即可;③与②的证明方法一样得到3∠P =∠B +2∠C .【答案】(1)证明:在图1中,有∠A +∠C =180°﹣∠AOC ,∠B +∠D =180°﹣∠BOD ,∵∠AOC =∠BOD ,∴∠A +∠C =∠B +∠D ;(2)解:①3;4;故答案为:3,4;②以M 为交点“8字型”中,有∠P +∠CDP =∠C +∠CAP ,以N 为交点“8字型”中,有∠P +∠BAP =∠B +∠BDP∴2∠P +∠BAP +∠CDP =∠B +∠C +∠CAP +∠BDP ,∵AP 、DP 分别平分∠CAB 和∠BDC ,∴∠BAP =∠CAP ,∠CDP =∠BDP ,∴2∠P =∠B +∠C ,∵∠B =100°,∠C =120°,∴∠P=(∠B+∠C)=(100°+120°)=110°;③3∠P=∠B+2∠C,其理由是:∵∠CAP=∠CAB,∠CDP=∠CDB,∴∠BAP=∠CAB,∠BDP=∠CDB,以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP∴∠C﹣∠P=∠CDP﹣∠CAP=(∠CDB﹣∠CAB),∠P﹣∠B=∠BDP﹣∠BAP=(∠CDB﹣∠CAB).∴2(∠C﹣∠P)=∠P﹣∠B,∴3∠P=∠B+2∠C.【点睛】本题考查了三角形内角和定理:三角形内角和是180°.也考查了角平分线的定义.【变式6-3】(2018秋•青岛期末)【问题背景】(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B=∠C+∠D【简单应用】(2)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=20°,∠ADC=26°,求∠P的度数(可直接使用问题(1)中的结论)【问题探究】(3)如图3,直线AP平分∠BAD的外角∠F AD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,猜想∠P 的度数为【拓展延伸】(4)在图4中,若设∠C =x ,∠B =y ,∠CAP=31∠CAB ,∠CDP=31∠CDB ,试问∠P 与∠C 、∠B 之间的数量关系为 (用x 、y 表示∠P )(5)在图5中,AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、∠D 的关系,直接写出结论 .【分析】(1)根据三角形内角和定理即可证明;(2)如图2,根据角平分线的性质得到∠1=∠2,∠3=∠4,列方程组即可得到结论;(3)由AP 平分∠BAD 的外角∠F AD ,CP 平分∠BCD 的外角∠BCE ,推出∠1=∠2,∠3=∠4,推出∠P AD =180°﹣∠2,∠PCD =180°﹣∠3,由∠P +(180°﹣∠1)=∠D +(180°﹣∠3),∠P +∠1=∠B +∠4,推出2∠P =∠B +∠D ,即可解决问题;(4)(5)同法列出方程组即可解决问题.【答案】(1)证明:在△AOB 中,∠A +∠B +∠AOB =180°,在△COD 中,∠C +∠D +∠COD =180°,∵∠AOB =∠COD ,∴∠A +∠B =∠C +∠D ;(2)解:如图2,∵AP 、CP 分别平分∠BAD ,∠BCD ,∴∠1=∠2,∠3=∠4,由(1)的结论得:, ①+②,得2∠P +∠2+∠3=∠1+∠4+∠B +∠D ,∴∠P =(∠B +∠D )=23°;(3)解:如图3,∵AP 平分∠BAD 的外角∠F AD ,CP 平分∠BCD 的外角∠BCE ,∴∠1=∠2,∠3=∠4,∴∠P AD=180°﹣∠2,∠PCD=180°﹣∠3,∵∠P+(180°﹣∠1)=∠D+(180°﹣∠3),∠P+∠1=∠B+∠4,∴2∠P=∠B+∠D,∴∠P=(∠B+∠D)=×(36°+16°)=26°;故答案为:26°;【拓展延伸】(4)同法可得:∠P=x+y;故答案为:∠P=x+y,(5)同法可得:∠P=.故答案为:∠P=.【点睛】本题考查三角形内角和,三角形的外角的性质、多边形的内角和等知识,解题的关键是学会用方程组的思想思考问题,属于中考常考题型.【模型7 燕尾模型】【结论】∠BPC=∠A+∠B+∠C.【例7】(2019春•冠县期末)(1)探究:如图1,求证:∠BOC=∠A+∠B+∠C.(2)应用:如图2,∠ABC=100°,∠DEF=130°,求∠A+∠C+∠D+∠F的度数.【分析】(1)连接OA,由三角形外角的性质可知∠1+∠B=∠3,∠2+∠C=∠4,两式相加即可得出结论;(2)连接AD,由(1)的结论可知∠F+∠2+∠3=∠DEF,∠1+∠4+∠C=∠ABC,两式相加即可得出结论.【答案】解:(1)连接OA,∵∠3是△ABO的外角,∴∠1+∠B=∠3,①∵∠4是△AOC的外角,∴∠2+∠C=∠4,②①+②得,∠1+∠B+∠2+∠C=∠3+∠4,即∠BOC=∠A+∠B+∠C;(2)连接AD,同(1)可得,∠F+∠2+∠3=∠DEF③,∠1+∠4+∠C=∠ABC④,③+④得,∠F+∠2+∠3+∠1+∠4+∠C=∠DEF+∠ABC=130°+100°=230°,即∠A+∠C+∠D+∠F=230°.【点睛】本题考查的是三角形外角的性质及三角形内角和定理,根据题意作出辅助线,构造出三角形是解答此题的关键.【变式7-1】(2019秋•平度市期末)材料阅读:如图①所示的图形,像我们常见的学习用品﹣圆规.我们不妨把这样图形叫做“规形图”.解决问题:(1)观察“规形图”,试探究∠BDC与∠A,∠B,∠C之间的数量关系,并说明理由;(2)请你直接利用以上结论,解决以下两个问题:Ⅰ.如图②,把一块三角尺DEF放置在△ABC上,使三角尺的两条直角边DE,DF恰好经过点B,C,若∠A=40°,则∠ABD+∠ACD=°.Ⅱ.如图③,BD平分∠ABP,CD平分∠ACP,若∠A=40°,∠BPC=130°,求∠BDC的度数.【分析】(1)连接AD并延长至点F,根据三角形外角性质即可得到∠BDC与∠A,∠B,∠C之间的数量关系;(2)Ⅰ、由(1)可得,∠BDC=∠ABD+∠ACD+∠A,再根据∠A=40°,∠D=90°,即可得出∠ABD+∠ACD的度数;Ⅱ、根据(1),可得∠BPC=∠BAC+∠ABP+∠ACP,∠BDC=∠BAC+∠ABD+∠ACD,再根据BD平分∠ABP,CD平分∠ACP,即可得出∠BDC的度数.【答案】解:(1)如图①,连接AD并延长至点F,根据外角的性质,可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD,又∵∠BDC=∠BDF+∠CDF,∠BAC=∠BAD+∠CAD,∴∠BDC=∠A+∠B+∠C;(2)Ⅰ.由(1)可得,∠BDC=∠ABD+∠ACD+∠A;又∵∠A=40°,∠D=90°,∴∠ABD+∠ACD=90°﹣40°=50°,故答案为:50;Ⅱ.由(1),可得∠BPC=∠BAC+∠ABP+∠ACP,∠BDC=∠BAC+∠ABD+∠ACD,∴∠ABP+∠ACP=∠BPC﹣∠BAC=130°﹣40°=90°,又∵BD平分∠ABP,CD平分∠ACP,∴∠ABD+∠ACD=(∠ABP+∠ACP)=45°,∴∠BDC=45°+40°=85°.【点睛】本题考查的是三角形内角和定理以及三角形外角性质的运用,熟知三角形的内角和等于180°是解答此题的关键.【变式7-2】(2019秋•阜阳月考)在数学学习中整体思想与转化思想是我们常用到的数学思想.如图(1)中,求∠A+∠B+∠C+∠D+∠E的度数等于多少时,我们可以连接CD,利用三角形的内角和则有∠B+∠E =∠ECD+∠BDC,这样∠A、∠B、∠C、∠D、∠E的和就转化到同一个△ACD中,即∠A+∠B+∠C+∠D+∠E=180°.尝试练习:图(2)中∠A+∠B+∠C+∠D+∠E的度数等于.图(3)中∠A+∠B+∠C+∠D+∠E的度数等于.图(4)中∠A+∠B+∠C+∠D+∠E+∠F的度数等于.【分析】仿照材料、根据三角形内角和定理计算即可.【答案】解:如图(2),连接CE,则有∠A+∠B=∠AEC+∠BCE,∴∠A+∠B+∠DCB+∠D+∠DEA=180°;同理,图(3)中∠A+∠B+∠C+∠D+∠E=180°;图(4)中∠A+∠B+∠C+∠D+∠E+∠F=360°.故答案为:180°;180°;360°.【点睛】本题考查的是三角形内角和定理,掌握三角形内角和等于180°是解题的关键.【变式7-3】(2019秋•襄城区期中)已知:点D是△ABC所在平面内一点,连接AD、CD.(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;(3)如图3,在(2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.【分析】(1)如图1,延长AD交BC于E.利用三角形的外角的性质即可解决问题;(2)∠A﹣∠C=2∠P,利用三角形的外角的性质可以推出:∠A+∠1=∠P+∠3,由∠1=∠2,∠3=∠4,推出∠A+∠2=∠P+∠4,由(1)知∠4=∠2+∠P+∠C,可得∠A+∠2=∠P+∠2+∠P+∠C即可解决问题;(3)∠A+∠C=2∠P,证明方法类似;【答案】解:(1)如图1,延长AD交BC于E.在△ABE中,∠AEC=∠A+∠B=28°+72°=100°,在△DEC中,∠ADC=∠AEC+∠C=100°+11°=111°.(2)∠A﹣∠C=2∠P,理由如下:如图2,∠5=∠A+∠1,∠5=∠P+∠3,∴∠A+∠1=∠P+∠3,∵PB平分∠ABC,PD平分∠ADC,∴∠1=∠2,∠3=∠4,∴∠A+∠2=∠P+∠4,由(1)知∠4=∠2+∠P+∠C,∴∠A+∠2=∠P+∠2+∠P+∠C,∴∠A﹣∠C=2∠P.(3)∠A+∠C=2∠P,理由如下:同(2)理知∠A+∠1=∠P+∠3,∠C+∠4=∠P+∠2,∴∠A+∠C+∠1+∠4=2∠P+∠2+∠3,∵PB平分∠ABC,PD平分∠ADC,∴∠1=∠2,∠3=∠4,∴∠1+∠4=∠2+∠3,∴∠A+∠C=2∠P.【点睛】本题考查三角形的外角的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.【模型8 筝型】【结论】∠PBD+∠PCD=∠A+∠P【例8】(2019春•邳州市校级月考)如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合.(1)若∠A=75°,则∠1+∠2=.(2)若∠A=n°,则∠1+∠2=.(3)由(1)(2)探索∠A与∠1+∠2之间的数量关系,并说明理由.【分析】(1)先根据图形翻折变化的性质得出△ADE≌△A′DE,∠AED=∠A′ED,∠ADE=∠A′DE,再根据三角形内角和定理求出∠AED+∠ADE及∠A′ED+∠A′DE的度数,然后根据平角的性质即可求出答案;(2)同(1);(3)根据(1)、(2)的规律即可得出结论.【答案】解:(1)∵△A′DE是△ABC翻折变换而成,∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′=75°,∴∠AED+∠ADE=∠A′ED+∠A′DE=180°﹣75°=105°,∴∠1+∠2=360°﹣2×105°=150°.故答案为:150°;(2)∵△A′DE是△ABC翻折变换而成,∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′=n°,∴∠AED+∠ADE=∠A′ED+∠A′DE=180°﹣n°,∴∠1+∠2=360°﹣2(180°﹣n°)=2n°,∴∠1+∠2=2n°;(3)由(1)、(2)可知,2∠A=∠1+∠2.【点睛】本题考查的是图形翻折变换的性质,即折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.【变式8-1】(2018春•迁安市期末)动手操作:一个三角形的纸片ABC,沿DE折叠,使点A落在点Aˊ处.观察猜想(1)如图1,若∠A=40°,则∠1+∠2=°;若∠A=55°,则∠1+∠2=°;若∠A=n°,则∠1+∠2=°.探索证明:(2)利用图1,探索∠1、∠2与∠A有怎样的关系?请说明理由.拓展应用:(3)如图2,把△ABC折叠后,BA′平分∠ABC,CA′平分∠ACB,若∠1+∠2=108°,利用(2)中结论求∠BA′C的度数.【分析】(1)根据翻折变换的性质用∠1、∠2表示出∠ADE和∠AED,再根据三角形的内角和定理列式整理即可得解;根据翻折变换的性质用∠1、∠2表示出∠ADE和∠AED,再根据三角形的内角和定理列式整理即可得解;(2)由∠BDE、∠CED是△ADE的两个外角知∠BDE=∠A+∠AED、∠CED=∠A+∠ADE,据此得∠BDE+∠CED=∠A+∠AED+∠A+∠ADE,继而可得答案;(3)由(1)∠1+∠2=2∠A知∠A=54°,根据BA'平分∠ABC,CA'平分∠ACB知∠A'BC+∠A'CB=(∠ABC+∠ACB)=90°﹣∠A.利用∠BA'C=180°﹣(∠A'BC+∠A'CB)可得答案.【答案】解:(1)∵点A沿DE折叠落在点A′的位置,∴∠ADE=∠A′DE,∠AED=∠A′ED,∴∠ADE=(180°﹣∠1),∠AED=(180°﹣∠2)在△ADE中,∠A+∠ADE+∠AED=180°,∴40°+(180°﹣∠1)+(180°﹣∠2)=180°,整理得∠1+∠2=80°;同理∠A=55°,则∠1+∠2=110°;∠A=n°,则∠1+∠2=2n°;故答案为:80°;110°;2n°;(2)∠1+∠2=2∠A,理由:∵∠BDE、∠CED是△ADE的两个外角,∴∠BDE=∠A+∠AED,∠CED=∠A+∠ADE,。
数学北师大版八年级上册举一反三

举一反三
2.在我国古代数学著作《九章算 术》中记载了一道有趣的问题,这 个问题的意思是:有一个水池,水
பைடு நூலகம்
中国古代人民 的聪明才智真 是令人赞叹 !
面是一个边长为10尺的正方形,在
水池的中央有一根新生的芦苇,它
高出水面1尺,如果把这根芦苇垂
直拉向岸边,它的顶端恰好到达岸
边的水面,请问这个水池的深度和
这根芦苇的长度各是多少?
举一反三
解:设水池的水深AC为x尺,则这根芦苇 长为AD=AB=(x+1)尺, 在直角三角形ABC中,BC=5尺 由勾股定理得:BC2+AC2=AB2 即 52+x2=(x+1)2 25+x2= x2+2x+1, 2x=24, ∴ x=12, x+1=13 . 答:水池的水深12尺,这根芦苇长13尺.
八年级数学上册质量计算中的经典模型(举一反三)(含解析版)

八年级数学上册质量计算中的经典模型(举一反三)(含解析版)数学上册的质量计算是一个重要且具有挑战性的领域。
在本文档中,我们将介绍八年级数学上册中的经典模型,并附上详细的解析,以帮助学生更好地理解和应用这些模型。
目录1. 体积计算模型- 立方体的体积计算- 柱体的体积计算- 圆柱的体积计算2. 相似形状模型- 相似三角形的性质和应用- 相似图形的比例应用- 相似形状的面积和体积计算3. 百分数模型- 百分比的表示与计算- 百分数在实际问题中的应用4. 比例模型- 比例的性质和简化- 比例在实际问题中的应用- 比例方程的解法与应用5. 方程模型- 一元一次方程的概念和解法- 一元一次方程在实际问题中的应用- 解方程后的验证与解释体积计算模型立方体的体积计算立方体是一个六个面都是正方形的特殊几何体。
计算立方体的体积,只需将边长的立方作为结果即可。
例如,一个边长为3厘米的立方体,其体积为3^3 = 27立方厘米。
柱体的体积计算柱体是一个上下底面相等、侧面为矩形的几何体。
计算柱体的体积,需将底面积与高相乘。
例如,一个底面半径为4厘米,高度为6厘米的柱体,其体积为π * 4^2 * 6 ≈ 301.59立方厘米。
圆柱的体积计算圆柱是一个上下底面相等、侧面为圆柱面的几何体。
计算圆柱的体积,同样需要将底面积与高相乘。
例如,一个底面半径为5厘米,高度为8厘米的圆柱,其体积为π * 5^2 * 8 ≈ 628.32立方厘米。
相似形状模型相似三角形的性质和应用相似三角形指的是具有相同形状但大小不同的三角形。
它们的对应角度相等,对应边长成比例。
在实际问题中,我们可以利用相似三角形的性质来解决各种测量和计算问题。
相似图形的比例应用相似图形指的是形状相同但大小不同的图形。
我们可以通过比较它们的对应边长,得到它们的比例关系。
应用相似图形的比例关系,可以解决一些有关长度、面积和体积的计算问题。
相似形状的面积和体积计算利用相似图形的比例关系,我们可以计算相似形状的面积和体积。
部编数学八年级上册专题01三角形边或角关系的三种模型(解析版)(人教版)含答案

专题01 三角形边或角关系的三种模型几何探究类问题一直属于考试压轴题范围,在三角形这一章,压轴题主要考查是证明角的数量关系,或者三角形的三边和差关系等,接来下我们针对这两个版块做出详细分析与梳理。
类型一、燕尾角模型例1.在社会实践手工课上,小茗同学设计了一个形状如图所示的零件,如果52,25A B °°Ð=Ð=,30,35,72C D E °°°Ð=Ð=Ð=,那么F Ð的度数是( ).A .72°B .70°C .65°D .60°【答案】A 【详解】延长BE 交CF 的延长线于O ,连接AO ,如图,∵180,OAB B AOB Ð+Ð+Ð=° ∴180,AOB B OAB Ð=°-Ð-Ð同理得180,AOC OAC C Ð=°-Ð-Ð∵360,AOB AOC BOC Ð+Ð+Ð=°∴360BOC AOB AOC Ð=°-Ð-Ð 360(180)(180)B OAB OAC C =°-°-Ð-Ð-°-Ð-Ð107,B C BAC =Ð+Ð+Ð=°∵72,BED Ð=°∴180108,DEO BED Ð=°-Ð=°∴360DFO D DEO EOF Ð=°-Ð-Ð-Ð 36035108107110,=°-°-°-°=°∴180********DFC DFO Ð=°-Ð=°-°=°,故选:A .【变式训练1】如图,若115EOC Ð=°,则A B C D E F Ð+Ð+Ð+Ð+Ð+Ð=____________.【答案】230°【详解】解:如图∵∠EOC =∠E +∠2=115°,∠2=∠D +∠C , ∴∠E +∠D +∠C =115°,∵∠EOC =∠1+∠F =115°,∠1=∠A +∠B , ∴∠A +∠B +∠F =115°,∴∠A +∠B +∠C +∠D +∠E +∠F =230°, 故答案为:230°.【变式训练2】如右图,∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H =__.【答案】360°【详解】解:由图形可知:∠BNP =∠A +∠B ,∠DPQ =∠C +∠D ,∠FQM =∠E +∠F ,∠HMN =∠G +∠H ,∵∠BNP +∠DPQ +∠FQM +∠HMN =360°,∴∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H =∠BNP +∠DPQ +∠FQM +∠HMN =360°.故答案为:360°.【变式训练3】如图,求∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H +∠I =__.【答案】900°【详解】解:连EF ,GI ,如图,∵6边形ABCDEFK 的内角和=(6-2)×180°=720°,∴∠A +∠B +∠C +∠D +∠E +∠F =720°-(∠1+∠2),即∠A +∠B +∠C +∠D +∠E +∠F +(∠1+∠2)=720°,∵∠1+∠2=∠3+∠4,∠5+∠6+∠H =180°,∴∠A +∠B +∠C +∠D +∠E +∠F ∠H +(∠3+∠4)=900°,∴∠A +∠B +∠C +∠D +∠E +∠F (∠3+∠4)+∠5+∠6+∠H =720°+180°,∴∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H +∠I =900°,故答案为:900°.【变式训练4】模型规律:如图1,延长CO 交AB 于点D ,则1BOC B A C B Ð=Ð+Ð=Ð+Ð+Ð.因为凹四边形ABOC 形似箭头,其四角具有“BOC A B C Ð=Ð+Ð+Д这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用(1)直接应用:①如图2,60,20,30A B C Ð=°Ð=°Ð=°,则BOC Ð=__________°;②如图3,A B C D E F Ð+Ð+Ð+Ð+Ð+Ð=__________°;(2)拓展应用:①如图4,ABO Ð、ACO Ð的2等分线(即角平分线)1BO 、1CO 交于点1O ,已知120BOC Ð=°,50BAC Ð=°,则1BO C Ð=__________°;②如图5,BO 、CO 分别为ABO Ð、ACO Ð的10等分线1,2,3,,(,)89i =¼.它们的交点从上到下依次为1O 、2O 、3O 、…、9O .已知120BOC Ð=°,50BAC Ð=°,则7BO C Ð=__________°;③如图6,ABO Ð、BAC Ð的角平分线BD 、AD 交于点D ,已知120,44BOC C Ð=°Ð=°,则ADB =∠__________°;④如图7,BAC Ð、BOC Ð的角平分线AD 、OD 交于点D ,则B Ð、C Ð、D Ð之同的数量关系为__________.【答案】(1)①110;②260;(2)①85;②110;③142;④∠B -∠C +2∠D =0【详解】解:(1)①∠BOC =∠A +∠B +∠C =60°+20°+30°=110°;②∠A +∠B +∠C +∠D +∠E +∠F =∠BOC +∠DOE =2×130°=260°;(2)①∠BO 1C =∠BOC -∠OBO 1-∠OCO 1=∠BOC -12(∠ABO +∠ACO )=∠BOC -12(∠BOC -∠A )=∠BOC -12(120°-50°)=120°-35°=85°;②∠BO 7C =∠BOC -17(∠BOC -∠A )=120°-17(120°-50°)=120°-10°=110°;③∠ADB =180°-(∠ABD +∠BAD )=180°-12(∠BOC -∠C )=180°-12(120°-44°)=142°;④∠BOD =12∠BOC =∠B +∠D +12∠BAC ,∠BOC =∠B +∠C +∠BAC ,联立得:∠B -∠C +2∠D =0.类型二、折叠模型例1.如图,在ABC V 中,46C Ð=°,将ABC V 沿直线l 折叠,点C 落在点D 的位置,则12Ð-Ð的度数是( ).A .23°B .92°C .46°D .无法确定【答案】B 【详解】解:由折叠的性质得:46D C Ð=Ð=°,根据外角性质得:13C Ð=Ð+Ð,32D Ð=Ð+Ð,则1222292C D C Ð=Ð+Ð+Ð=Ð+Ð=Ð+°,则1292Ð-Ð=°.故选:B .【变式训练1】如图,将△ABC 纸片沿DE 折叠,使点A 落在点A '处,且A 'B 平分∠ABC ,A 'C 平分∠ACB ,若∠BA 'C =120°,则∠1+∠2的度数为( )A .90°B .100°C .110°D .120°【答案】D【详解】解:如图,连接AA',∵A'B平分∠ABC,A'C平分∠ACB,∴∠A'BC=12∠ABC,∠A'CB=12∠ACB,∵∠BA'C=120°,∴∠A'BC+∠A'CB=180°-120°=60°,∴∠ABC+∠ACB=120°,∴∠BAC=180°-120°=60°,∵沿DE折叠,∴∠DAA'=∠DA'A,∠EAA'=∠EA'A,∵∠1=∠DAA'+∠DA'A=2∠DAA',∠2=∠EAA'+∠EA'A=2∠EAA',∴∠1+∠2=2∠DAA'+2∠EAA'=2∠BAC=2×60°=120°,故选:D.【变式训练2】如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=55°,∠1=95°,则∠2的度数为().A.14°B.15°C.28°D.30°【答案】B【详解】解:∵∠A=55°,∴∠AEF+∠AFE=180°-55°=125°,∴∠FEB+∠EFC=360°-125°=235°,由折叠可得:∠B′EF+∠EFC′=∠FEB+∠EFC=235°,∴∠1+∠2=235°-125°=110°,∵∠1=95°,∴∠2=110°-95°=15°,故选:B .【变式训练3】如图,将△ABC 沿着DE 翻折,使B 点与B'点重合,若∠1+∠2=80°,则∠B 的度数为( )A .20°B .30°C .40°D .50°【答案】C 【详解】由折叠的性质可知','BED B ED BDE B DEÐ=ÐÐ=Ð∵1'180,2'180BED B ED BDE B DE Ð+Ð+Ð=°Ð+Ð+Ð=°∴11(36012)(36080)14022BED BDE Ð+Ð=°-Ð-Ð=´°-°=°∴180()18014040B BED BDE Ð=°-Ð+Ð=°-°=°故选C【变式训练4】如图,将矩形纸片ABCD 沿EF 折叠,点C 落在边AB 上的点H 处,点D 落在点G 处,若111GEF Ð=°,则AHG ∠的度数为( ).A .42°B .69°C .44°D .32°【答案】A 【详解】由图形翻折的性质可知,111GEF DEF Ð=Ð=°,180111AEF \Ð=°-°=69°,1116942AEG GEF AEF Ð=Ð-Ð=°-°=°,90A G Ð=Ð=°Q ,利用“8”字模型,42AHG AEG \Ð=Ð=°,故选:A .类型三、“8”字模型例1.如图,BP 平分ABC Ð,交CD 于点F ,DP 平分ADC Ð交AB 于点E ,AB 与CD 相交于点G ,42A Ð=°.(1)若60ADC Ð=°,求AEP Ð的度数;(2)若38C Ð=°,求P Ð的度数.【答案】(1)72°;(2)40°.【详解】解:(1)∵DP 平分∠ADC ,∴∠ADP=∠PDF=12ADC Ð,∵60ADC Ð=°,∴30ADP Ð=°,∴304272AEP ADP A Ð=Ð+Ð=°+°=°;(2)∵BP 平分∠ABC ,DP 平分∠ADC ,∴∠ADP=∠PDF ,∠CBP=∠PBA ,∵∠A+∠ADP=∠P+∠ABP ,∠C+∠CBP=∠P+∠PDF ,∴∠A+∠C=2∠P ,∵∠A=42°,∠C=38°,∴∠P=12(38°+42°)=40°.【变式训练1】如图,求∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H +∠K 的度数.【答案】540°【详解】解:如图所示:由三角形的外角的性质可知:∠A +∠B =∠IJL ,∠C +∠D =∠MLJ ,∠H +∠K =∠GIJ ,∠E +∠F =∠GML ,∴∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H +∠K =∠IJL +∠MLJ +∠GML +∠G +∠GIJ =(5-2)×180°=3×180°=540°.【变式训练2】(1)已知:如图①的图形我们把它称为“8字形”,试说明:A B C D Ð+Ð=Ð+Ð.(2)如图②,AP ,CP 分别平分BAD Ð,BCD Ð,若36ABC Ð=°,16ADC Ð=°,求P Ð的度数.(3)如图(3),直线AP 平分BAD Ð,CP 平分BCD Ð的外角BCE Ð,猜想P Ð与B Ð、D Ð的数量关系是__;(4)如图(4),直线AP 平分BAD Ð的外角FAD Ð,CP 平分BCD Ð的外角BCE Ð,猜想P Ð与B Ð、D Ð的数量关系是________.【答案】(1)见解析;(2)26°;(3)()1902P B D Ð=°+Ð+Ð;(4)()11802P B D Ð=°-Ð+Ð【详解】解:(1)A B AOB Ð+Ð+Ð=Q 180°,C D COD Ð+Ð+Ð=180°,A B AOB C D COD \Ð+Ð+Ð=Ð+Ð+Ð.AOB COD Ð=ÐQ ,A B C D \Ð+Ð=Ð+Ð;(2)AP Q ,CP 分别平分BAD Ð,BCD Ð,设BAP PAD x Ð=Ð=,BCP PCD y Ð=Ð=,则有x ABC y P x P y ADC +Ð=+Ðìí+Ð=+Ðî, ABC P P ADC \Ð-Ð=Ð-Ð,()1122P ABC ADC \Ð=Ð+Ð=(36°+16°)=26°(3)Q 直线AP 平分BAD Ð,CP 平分BCD Ð的外角BCE Ð,1=2PAB PAD BAD \Ð=Ð∠,1=2PCB PCE BCE Ð=ÐÐ,∴2PAB B Ð+Ð=180°-2PCB D Ð+Ð,∴180°()2PAB PCB D B-Ð+Ð+Ð=Ð∵∠P +∠PAD =∠PCD +∠D ,∠BAD +∠B =∠BCD +∠D ,∴=P PAD BAD B PCD BCD Ð+---∠∠∠∠∠,P PAB B PCB \Ð-Ð-Ð=Ð∴P B PAB PCBÐ-=Ð+Ð∠∴180°()2P B D B -Ð-Ð+Ð=Ð,即P Ð=90°()12B D +Ð+Ð.(4)连接PB ,PDQ 直线AP 平分BAD Ð的外角FAD Ð,CP 平分BCD Ð的外角BCE Ð,FAP PAO \Ð=Ð,PCE PCB Ð=Ð,∵APB PBA PAB +Ð+Ð=∠180°,PCB PBC BPC +Ð+Ð=∠180°∴APC ABC PCB PAB Ð+Ð+Ð+=∠360°同理得到:APC ADC PCD PAD Ð+Ð+Ð+=∠360°∴2APC ABC ADC PCB PAB PCD PAD Ð+Ð+Ð+Ð++Ð+=∠∠720°∴2APC ABC ADC PCE PAB PCD PAF Ð+Ð+Ð+Ð++Ð+=∠∠720°∵=PCE PCD Ð+Ð180°,=PAB PAF +∠∠180°∴2APC ABC ADC Ð+Ð+Ð=360°,APC \Ð=180°-()12ABC ADC Ð+Ð。
八年级数学上册全等三角形章末重难点题型(举一反三)(含解析版)

专题01 全等三角形章末重难点题型汇编【举一反三】【考点1 利用全等三角形的性质求角】【方法点拨】全等三角形的性质:(1)全等三角形的对应边相等、对应角相等;(2)全等三角形的周长相等、面积相等;(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
【例1】(2019春•临安区期中)如图,△ACB≌△A′CB′,∠ACB=70°,∠ACB′=100°,则∠BCA′的度数为()A.30°B.35°C.40°D.50°【变式1-1】(2018秋•绍兴期末)如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,∠ACB =20°,则∠ADC的度数是()A.55°B.60°C.65°D.70°【变式1-2】(2018秋•厦门期末)如图,点F,C在BE上,△ABC≌△DEF,AB和DE,AC和DF是对应边,AC,DF交于点M,则∠AMF等于()A.2∠B B.2∠ACB C.∠A+∠D D.∠B+∠ACB【变式1-3】(2018秋•桐梓县校级期中)如图,△ABC≌△A′B′C,∠ACB=90°,∠B=50°,点B′在线段AB上,AC,A′B′交于点O,则∠COA′的度数是()A.50°B.60°C.70°D.80°【考点2 全等三角形的判定条件】【方法点拨】寻找并证明全等三角形还缺少的条件,其基本思路是:(1)有两边对应相等,找夹角对应相等,或第三边对应相等.前者利用SAS判定,后者利用SSS判定. (2)有两角对应相等,找夹边对应相等,或任一等角的对边对应相等.前者利用ASA判定,后者利用AAS 判定.(3)有一边和该边的对角对应相等,找另一角对应相等.利用AAS判定.(4)有一边和该边的邻角对应相等,找夹等角的另一边对应相等,或另一角对应相等.前者利用SAS判定,后者利用AAS判定.【例2】(2019春•沙坪坝区校级期中)如图,在△ABC和△AED中,已知∠1=∠2,AC=AD,添加一个条件后,仍然不能证明△ABC≌△AED,这个条件是()A.AB=AE B.BC=ED C.∠C=∠D D.∠B=∠E【变式2-1】(2019秋•潘集区期中)在△ABC与△DEF中,给出下列四组条件:(1)AB=DE,AC=DF,BC=EF(2)AB=DE,∠B=∠E,BC=EF(3)∠B=∠E,BC=EF,∠C=∠F(4)AB=DE,∠B=∠E,AC=DF,其中能使△ABC≌△DEF的条件共有()A.1组B.2组C.3组D.4组【变式2-2】(2018春•渝中区校级期中)如图,点B、F、C、E在一条直线上,∠A=∠D,∠B=∠E,再添一个条件仍不能证明△ABC≌△DEF的是()A.AB=DE B.BC=EF C.∠ACB=∠DFE D.AC=DF【变式2-3】(2018秋•鄂尔多斯期中)如图,已知AB=AC,AD=AE,若要得到“△ABD≌△ACE”,必须添加一个条件,则下列所添条件不恰当的是()A.BD=CE B.∠ABD=∠ACE C.∠BAD=∠CAE D.∠BAC=∠DAE【考点3 全等三角形判定的应用】【方法点拨】解决此类题型的关键是理解题意,利用全等三角形的判定.【例3】(2019春•郓城县期末)如图所示,要测量河两岸相对的两点A、B的距离,因无法直接量出A、B 两点的距离,请你设计一种方案,求出A、B的距离,并说明理由.【变式3-1】(2019春•峄城区期末)如图,点C、E分别在直线AB、DF上,小华想知道∠ACE和∠DEC 是否互补,但是他没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连结CF,再找出CF的中点O,然后连结EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.小华的想法对吗?为什么?【变式3-2】(2019春•槐荫区期末)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.【变式3-3】如图,两根长12m的绳子,一端系在旗杆上的同一位置,另一端分别固定在地面上的两个木桩上(绳结处的误差忽略不计),现在只有一把卷尺,如何来检验旗杆是否垂直于地面?请说明理由.【考点4 利用AAS证明三角形全等】【方法点拨】两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”)【例4】(2018秋•仙游县期中)如图,△ABC的两条高AD,BE相交于点F,请添加一个条件,使得△ADC ≌△BEC(不添加其他字母及辅助线),你添加的条件是.并证明结论.【变式4-1】(2018春•揭西县期末)如图,∠ABC=∠ACB,∠ADE=∠AED,BE=CD,试说明:△ABD ≌△ACE.【变式4-2】(2018秋•杭州期中)如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE.求证:△ACD≌△CBE.【变式4-3】(2018•雁塔区校级二模)如图,在四边形ABCD中,点E在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC≌△DEC.【考点5 利用SAS证明三角形全等】【方法点拨】两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)【例5】(2018春•金山区期末)如图,已知CA=CD,CB=CE,∠ACB=∠DCE,试说明△ACE≌△DCB 的理由.【变式5-1】(2018春•黄岛区期末)如图,点E在AB上,AC=AD,∠CAB=∠DAB,那么△BCE和△BDE 全等吗?请说明理由.【变式5-2】(2018秋•仪征市校级月考)如图,已知点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE,说明△ABC与△DEF全等的理由.【变式5-3】(2019秋•东莞市校级月考)如图:△ABC和△EAD中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE.求证:△ABD≌△AEC.【考点6 利用ASA证明三角形全等】【方法点拨】两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”)【例6】(2019秋•利辛县期末)如图,已知AB=AC,∠ABE=∠ACD,BE与CD相交于O,求证:△ABE ≌△ACD.【变式6-1】(2018•双柏县二模)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.求证:△AEC≌△BED;【变式6-2】(2019•陕西模拟)如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC≌△DEC.【变式6-3】(2019秋•乐清市校级期中)如图,△ABC的两条高AD、BE相交于点H,且AD=BD,求证:△BDH≌△ADC.【考点7 利用SSS证明三角形全等】【方法点拨】三边对应相等的两个三角形全等(可简写成“SSS”)【例7】(2019春•渝中区校级月考)如图,AB=CD,AE=CF,E、F是BD上两点,且BF=DE.求证:△ABE≌△CDF.【变式7-1】(2019秋•扶余县校级月考)如图,在△ABC中,AD=AE,BE=CD,AB=AC.(1)求证:△ABD≌△ACE;(2)求证:∠BAE=∠CAD.【变式7-2】(2019秋•保亭县校级月考)如图,AB=AD,DC=BC,∠B与∠D相等吗?为什么?【变式7-3】(2019秋•蓬江区校级期末)如图,在△ABC中,∠C=90°,D、E分别为AC、AB上的点,且AD=BD,AE=BC,DE=DC,求证:DE⊥AB.【考点8 利用HL证明三角形全等】【方法点拨】对于特殊的直角三角形,判定它们全等时,还有HL定理(斜边、直角边定理):有斜边和一条直角边对应相等的两个直角三角形全等(可简写成“斜边、直角边”或“HL”)【例8】(2018秋•思明区校级月考)如图,在四边形ABCD中,AD⊥BD,AC⊥CB,BD=AC.求证:△ABD≌△BAC;【变式8-1】(2019秋•睢宁县校级月考)如图,Rt△ABC中,∠C=90°,BC=2,一条直线MN=AB,M、N分别在AC和过点A且垂直于AC的射线AP上运动.问点M运动到什么位置,才能使△ABC和△AMN 全等?并证明你的结论.【变式8-2】(2019秋•合浦县期末)如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:Rt△ABF≌Rt△DCE.【变式8-3】(2019春•醴陵市期末)如图,在四边形ABCD中,AB=AD,CA平分∠BCD,AE⊥BC于点E,AF⊥CD交CD的延长线于点F.求证:△ABE≌△ADF.【考点9 全等三角形的判定与性质综合】【例9】(2019•南岸区)如图,在△ABC和△ABD中,∠BAC=∠ABD=90°,点E为AD边上的一点,且AC=AE,连接CE交AB于点G,过点A作AF⊥AD交CE于点F.(1)求证:△AGE≌△AFC;(2)若AB=AC,求证:AD=AF+BD.【变式9-1】(2019•福州模拟)(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE.(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由.【变式9-2】(2018秋•天台县期末)如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,若AD=a,DE=b,(1)如图1,求BE的长,写出求解过程;(用含a,b的式子表示)(2)如图2,点D在△ABC内部时,直接写出BE的长.(用含a,b的式子表示)【变式9-3】(2019春•道外区期末)如图,四边形ABCD中,∠ABC=∠BCD=90°,点E在BC边上,∠AED=90°(1)求证:∠BAE=∠CED;(2)若AB+CD=DE,求证:AE+BE=CE;(3)在(2)的条件下,若△CDE与△ABE的面积的差为18,CD=6,求BE的长.【考点10 动点问题中的全等三角形应用】【例10】(2019春•平川区期末)如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP 全等?【变式10-1】(2019春•永新县期末)△ABC中,AB=AC,∠A=40°,D、E分别是AB,AC上的不动点.且BD+CE=BC,点P是BC上的一动点.(1)当PC=CE时(如图1),求∠DPE的度数;(2)若PC=BD时(如图2),求∠DPE的度数还会与(1)的结果相同吗?若相同,请写出求解过程;若不相同,请说明理由.【变式10-2】(2019春•宝安区期中)如图,在四边形ABCD中,AD=BC=10,AB=CD,BD=14,点E 从D点出发,以每秒2个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒5个单位的速度沿C→B→C,作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.(1)试证明:AD∥BC;(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.【变式10-3】(2018秋•十堰期末)在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.(1)如图,当点D在BC延长线上移动时,若∠BAC=25°,则∠DCE=.(2)设∠BAC=α,∠DCE=β.①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;②当点D在直线BC上(不与B,C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.专题01 全等三角形章末重难点题型汇编【举一反三】【考点1 利用全等三角形的性质求角】【方法点拨】全等三角形的性质:(1)全等三角形的对应边相等、对应角相等;(2)全等三角形的周长相等、面积相等;(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
八年级数学上册角度计算中的经典模型(举一反三)(含解析版)
角度计算中的经典模型【举一反三】【模型1 双垂直模型】【条件】∠B=∠D=∠ACE=90°.【结论】∠BAC=∠DCE,∠ACB=∠CED.【例1】(2019春•润州区校级月考)如图,在△ABC中,∠ACB=90°,F是AC延长线上一点,FD⊥AB,垂足为D,FD与BC相交于点E,∠BED=55°.求∠A的度数.【变式1-1】(2019秋•凉州区校级期中)如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠A的度数.【变式1-2】(2019春•莲湖区期中)如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.(1)求证:∠ACD=∠B;(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.【变式1-3】(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,∠ACD与∠B有什么关系?为什么?(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状是什么?为什么?(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,AB⊥BD,点C,B,E在同一直线上,∠A与∠D有什么关系?为什么?【模型2 A字模型】【结论】∠BDE+∠CED=180°+∠A【例2】(2019春•资中县月考)如图所示,△ABC中,∠C=75°,若沿图中虚线截去∠C,则∠1+∠2等于多少度?【变式2-1】(2019春•长沙县校级期中)如图,已知∠A=40°,求∠1+∠2+∠3+∠4的度数.【变式2-2】(2019春•盱眙县期中)我们容易证明,三角形的一个外角等于它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?Ⅰ.尝试探究:(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?Ⅱ.初步应用:(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2﹣∠C=;(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案.【变式2-3】(2019春•盐都区期中)(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于A.90°B.135°C.270°D.315°(2)如图2,已知△ABC中,∠A=50°,剪去∠A后成四边形,则∠1+∠2=°.(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是.(4)如图3,若∠A没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.【模型3 双内角平分线模型】【条件】BP、CP分别为∠ABC、∠ACB的角平分线.1∠A.【结论】∠P=90°+2【例3】(2018秋•开封期中)如图,△ABC中,(1)若∠B=70°,点P是△ABC的∠BAC和∠ACB的平分线的交点,求∠APC的度数.(2)如果把(1)中∠B=70°这个条件去掉,试探索∠APC和∠B之间有怎样的数量关系.【变式3-1】(2018秋•徐闻县期中)如图,在△ABC 中,∠ABC 与∠ACB 的平分线交于点O . (1)如图1,已知∠ABC =40°,∠ACB =60°,求∠BOC 的度数. (2)如图2,已知∠A =90°,求∠BOC 的度数. (3)如图1,设∠A =m °,求∠BOC 的度数.【变式3-2】(2019春•南岗区期末)已知在△ABC 中,∠A =100°,点D 在△ABC 的内部连接BD ,CD , 且∠ABD =∠CBD ,∠ACD =∠BCD . (1)如图1,求∠BDC 的度数;(2)如图2,延长BD 交AC 于点E ,延长CD 交AB 于点F ,若∠AED ﹣∠AFD =12°,求∠ACF 的度数.【变式3-3】(2019春•东阿县期末)已知任意一个三角形的三个内角的和是180°.如图1,在△ABC 中, ∠ABC 的角平分线BO 与∠ACB 的角平分线CO 的交点为O (1)若∠A =70°,求∠BOC 的度数; (2)若∠A =a ,求∠BOC 的度数;(3)如图2,若BO 、CO 分别是∠ABC 、∠ACB 的三等分线,也就是∠OBC=31∠ABC ,∠OCB=31∠ACB ,∠A =a ,求∠BOC 的度数.【模型4 内外角平分线模型】【条件】BP、CP分别为∠ABC、∠ACD的角平分线.1∠P.【结论】∠A=2【例4】(2018秋•江岸区期中)如图,△ABC中,∠ABC与∠ACB的外角的平分线相交于点E.(1)已知∠A=60°,求∠E的度数;(2)直接写出∠A与∠E的数量关系:.【变式4-1】(2019秋•卫滨区校级期中)如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP 交于点P,若∠BPC=40°,求∠CAB的度数.【变式4-2】(2019秋•莆田校级期中)如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE 的平分线,且与BD交于点D;(1)若∠ABC=60°,∠DCE=70°,则∠D=°;(2)若∠ABC=70°,∠A=80°,则∠D=°;(3)当∠ABC和∠ACB在变化,而∠A始终保持不变,则∠D是否发生变化?为什么?由此你能得出什么结论?(用含∠A的式子表示∠D)【变式4-3】(2018秋•彭水县校级月考)如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE 的外角平分线,CD与BD交于点D.(1)若∠A=50°,则∠D=;(2)若∠A=80°,则∠D=;(3)若∠A=130°,则∠D=;(4)若∠D=36°,则∠A=;(5)综上所述,你会得到什么结论?证明你的结论的准确性.【模型5 双外角平分线模型】【条件】BP 、CP 分别为∠EBC 、∠BCD 的角平分线. 【结论】∠P=90°-21∠A.【例5】(2018秋•鄂伦春自治旗月考)如图,△ABC 中,分别延长△ABC 的边AB 、AC 到D 、E ,∠CBD 与∠BCE 的平分线相交于点P ,爱动脑筋的小明在写作业的时发现如下规律: (1)若∠A =60°,则∠P = °; (2)若∠A =40°,则∠P = °; (3)若∠A =100°,则∠P = °;(4)请你用数学表达式归纳∠A 与∠P 的关系 .【变式5-1】(2019秋•团风县校级月考)BD 、CD 分别是△ABC 的两个外角∠CBE 、∠BCF 的平分线, 求证:∠BDC =90°21∠A .【变式5-2】(2019春•雨城区校级期中)如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,(1)若∠ABC=40°,∠ACB=36°,求∠BIC的大小;(2)若∠A=96°,试求∠BIC;(3)根据前面问题的求解,请归纳∠BIC和∠A的数量关系并进行证明.【变式5-3】如图,在△ABC中,BD,CD是内角平分线,BP,CP是∠ABC,∠ACB的外角平分线,分别交于点D,P.(1)若∠A=30°,求∠BDC,∠BPC的度数.(2)若∠A=m°,求∠BDC,∠BPC的度数(直接写出结果,不必说明理由)(3)想一想,∠A的大小变化,对∠D+∠P的值是否有影响,若有影响,请说明理由,若无影响,直接求出其值.【模型6 8字模型】【结论】∠A+∠B=∠D+∠E.【例6】(2019春•辉县市期末)图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:;(2)仔细观察,在图2中“8字形”的个数:个;(3)图2中,当∠D=50度,∠B=40度时,求∠P的度数.(4)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结果,不必证明).【变式6-1】(2018春•新泰市期中)已知:如图,AM,CM分别平分∠BAD和∠BCD.①若∠B=32°,∠D=38°,求∠M的度数;②探索∠M与∠B、∠D的关系并证明你的结论.【变式6-2】(2018秋•南昌期中)如图1,已知线段AB 、CD 相交于点O ,连接AC 、BD ,则我们把形如这 样的图形称为“8字型”. (1)求证:∠A +∠C =∠B +∠D ;(2)如图2,若∠CAB 和∠BDC 的平分线AP 和DP 相交于点P ,且与CD 、AB 分别相交于点M 、N . ①以线段AC 为边的“8字型”有 个,以点O 为交点的“8字型”有 个; ②若∠B =100°,∠C =120°,求∠P 的度数;③若角平分线中角的关系改为“∠CAP=31∠CAB ,∠CDP=31∠CDB ”,试探究∠P 与∠B 、∠C 之间存在的数量关系,并证明理由.【变式6-3】(2018秋•青岛期末)【问题背景】(1)如图1的图形我们把它称为“8字形”,请说理证明∠A +∠B =∠C +∠D【简单应用】(2)如图2,AP 、CP 分别平分∠BAD 、∠BCD ,若∠ABC =20°,∠ADC =26°,求∠P 的度数(可直接使用问题(1)中的结论) 【问题探究】(3)如图3,直线AP 平分∠BAD 的外角∠F AD ,CP 平分∠BCD 的外角∠BCE ,若∠ABC =36°,∠ADC =16°,猜想∠P 的度数为【拓展延伸】(4)在图4中,若设∠C =x ,∠B =y ,∠CAP=31∠CAB ,∠CDP=31∠CDB ,试问∠P 与∠C 、∠B 之间的数量关系为 (用x 、y 表示∠P )(5)在图5中,AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、∠D 的关系,直接写出结论 . 【模型7 燕尾模型】【结论】∠BPC=∠A+∠B+∠C.【例7】(2019春•冠县期末)(1)探究:如图1,求证:∠BOC =∠A +∠B +∠C .(2)应用:如图2,∠ABC =100°,∠DEF =130°,求∠A +∠C +∠D +∠F 的度数.【变式7-1】(2019秋•平度市期末)材料阅读:如图①所示的图形,像我们常见的学习用品﹣圆规.我 们不妨把这样图形叫做“规形图”. 解决问题:(1)观察“规形图”,试探究∠BDC与∠A,∠B,∠C之间的数量关系,并说明理由;(2)请你直接利用以上结论,解决以下两个问题:Ⅰ.如图②,把一块三角尺DEF放置在△ABC上,使三角尺的两条直角边DE,DF恰好经过点B,C,若∠A=40°,则∠ABD+∠ACD=°.Ⅱ.如图③,BD平分∠ABP,CD平分∠ACP,若∠A=40°,∠BPC=130°,求∠BDC的度数.【变式7-2】(2019秋•阜阳月考)在数学学习中整体思想与转化思想是我们常用到的数学思想.如图(1)中,求∠A+∠B+∠C+∠D+∠E的度数等于多少时,我们可以连接CD,利用三角形的内角和则有∠B+∠E =∠ECD+∠BDC,这样∠A、∠B、∠C、∠D、∠E的和就转化到同一个△ACD中,即∠A+∠B+∠C+∠D+∠E=180°.尝试练习:图(2)中∠A+∠B+∠C+∠D+∠E的度数等于.图(3)中∠A+∠B+∠C+∠D+∠E的度数等于.图(4)中∠A+∠B+∠C+∠D+∠E+∠F的度数等于.【变式7-3】(2019秋•襄城区期中)已知:点D是△ABC所在平面内一点,连接AD、CD.(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;(3)如图3,在(2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.【模型8 筝型】【结论】∠PBD+∠PCD=∠A+∠P【例8】(2019春•邳州市校级月考)如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合.(1)若∠A=75°,则∠1+∠2=.(2)若∠A=n°,则∠1+∠2=.(3)由(1)(2)探索∠A与∠1+∠2之间的数量关系,并说明理由.【变式8-1】(2018春•迁安市期末)动手操作:一个三角形的纸片ABC,沿DE折叠,使点A落在点Aˊ处.观察猜想(1)如图1,若∠A=40°,则∠1+∠2=°;若∠A=55°,则∠1+∠2=°;若∠A=n°,则∠1+∠2=°.探索证明:(2)利用图1,探索∠1、∠2与∠A有怎样的关系?请说明理由.拓展应用:(3)如图2,把△ABC折叠后,BA′平分∠ABC,CA′平分∠ACB,若∠1+∠2=108°,利用(2)中结论求∠BA′C的度数.【变式8-2】(2019春•宿城区校级月考)Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图(1)所示,且∠α=50°,求∠1+∠2的度数;(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由;(3)若点P运动到边AB的延长线上,如图(3)所示,直接写出∠α、∠1、∠2之间关系为:.(不需说明理由).。
八年级上册数学举一反三系列专题10 分式章末重难点题型(举一反三)(人教版)(解析版)

专题10 分式章末重难点题型【举一反三】【人教版】【考点1 分式及最简分式的概念】 【方法点拨】1.分式:形如AB,A B 、是整式,B 中含有字母且B 不等于0的整式叫做分式.其中A 叫做分式的分子,B 叫做分式的分母.2. 最简分式:若分式的分子和分母没有公因式,这个分式称为最简分式,约分时,一般将一个分式化为最简 分式.【例1】(2019秋•泰安期中)下列各式2a b -,3x x +,5y π+,a b a b +-,1()x y m -,xyx中,分式的个数共有( )A .2个B .3个C .4个D .5个【分析】一般地,如果A ,B 表示两个整式,并且B 中含有字母,那么式子叫做分式. 【答案】解:由题可得,是分式的有:,,(x ﹣y ),,共4个,故选:C .【点睛】本题主要考查了分式的定义,分式的分母必须含有字母,而分子可以含字母,也可以不含字母.【变式1-1】(2018春•沈北校级期中)代数式2232212124513,(2),,,,2,,,3123213x x x x a x x a a x m t x x b x x aπ-+++-++---中分式的个数为( ) A .6个B .5个C .1个D .3个【分析】根据分式的定义,可得答案. 【答案】解:代数式、、、、、的分母中含有字母,属于分式,共有6个. 故选:A .【点睛】本题考查了分式的定义,分母中含有字母的式子是分式,注意π是常数不是字母.【变式1-2】(2019春•温江区期末)下列分式2410xyx ,22a b a b ++,22x y x y -+,221a a a +-最简分式的个数有( )A .4个B .3个C .2个D .1个【分析】直接利用分式的基本性质化简得出答案. 【答案】解:=,,=x ﹣y ,==,故只有是最简分式.故选:D .【点睛】此题主要考查了最简分式,正确化简分式是解题关键.【变式1-3】(2018秋•任城区期中)下列分式23bcab c-,2242x x x --,2222x xy xy y +-,211m m ++中,最简分式有( ) A .1个B .2个C .3个D .4个【分析】根据最简分式的定义,逐个判断即可得结论. 【答案】解:∵=,故A 不是最简分式;==,故B 不是最简分式;=,故C 是最简分式;分式的分子分母没有公因式,故D 最是简分式.故选:B .【点睛】本题考查了最简分式的判断,掌握最简分式的定义是解决本题的关键.【考点2 分式有意义条件】【方法点拨】分式有意义的条件:分母不等于0.【例2】(2019秋•夏津县校级月考)x取何值时,下列分式有意义:(1)2 23 xx+-(2)6(3) ||12 xx+-(3)26 1x x ++.【分析】(1)根据分式的分母不为零分式有意义,可得答案;(2)根据分式的分母不为零分式有意义,可得答案;(3)根据分式的分母不为零分式有意义,可得答案.【答案】解:(1)要使有意义,得2x﹣3≠0.解得x≠,当x≠时,有意义;(2)要使有意义,得|x|﹣12≠0.解得x≠±12,当x≠±12时,有意义;(3)要使有意义,得x2+1≠0.x为任意实数,有意义.【点睛】本题考查了分式有意义,分式的分母不为零分式有意义.【变式2-1】下列分式中的字母满足什么条件时,分式有意义.(1)21mm+-;(2)123xx+-;(3)211xx--;(4)293xx--.【分析】(1)利用分式有意义的条件是分母不等于零,进而求出即可;(2)利用分式有意义的条件是分母不等于零,进而求出即可;(3)利用分式有意义的条件是分母不等于零,进而求出即可;(4)利用分式有意义的条件是分母不等于零,进而求出即可.【答案】解:(1)m﹣1≠0时,分式有意义,故m≠1;(2)2﹣3x≠0时,分式有意义,故x≠;(3)x﹣1≠0时,分式有意义,故x≠1;(4)x﹣3≠0时,分式有意义,故x≠3.【点睛】此题主要考查了分式有意义的条件,利用分母不等于零求出是解题关键.【变式2-2】(2019秋•夏津县校级月考)若分式1324x xx x++÷++有意义,求x的取值范围.【分析】先把除法化为乘法,再根据分式有意义的条件即可得到结果.【答案】解:∵,∴x+2≠0且x+4≠0且x+3≠0解得x≠﹣2、﹣3、﹣4.【点睛】本题主要考查了分式有意义的条件,关键是注意分式所有的分母部分均不能为0,分式才有意义.【变式2-3】(2018秋•宜都市期末)若式子2131xy+-无意义,求代数式2()()y x y x x+-+的值.【分析】根据式子无意义可确定y的值,再化简代数式(y+x)(y﹣x)+x2,最后代入求值.【答案】解:∵式子无意义,∴3y﹣1=0,解得y=,原式=y2﹣x2+x2=y2=()2 =.【点睛】本题考查了分式无意义的条件和多项式的化简求值.当分母等于0时,分式无意义. 【考点3 分式值为0的条件】【方法点拨】满足分式的值为0的条件:分子为0分母不为0.【例3】(2018秋•大荔县期末)如果分式2122x x -+的值为0,求x 的值是多少?【分析】根据分式值.为0的条件:分子为0,分母不为0,求出x 的值即可 【答案】解:依题意得:x 2﹣1=0且2x +2≠0, 解得x =1, 即分式的值为0时,x 的值是1.【点睛】此题考查了解一元二次方程﹣因式分解法,以及分式值为零的条件,做题时注意分母不为0的条件.【变式3-1】(2019秋•东莞市校级期中)当a 取何值时,分式3||62a a-+的值为零. 【分析】分式的值为0的条件是:(1)分子为0;(2)分母不为0.两个条件需同时具备,缺一不可.据此可以解答本题. 【答案】解:由分式的值为零,得3﹣|a |=0,且6+2a ≠0. 解得a =3, 当a =3时,分式的值为零.【点睛】此题主要考查了分式值为零的条件,关键是掌握分式值为零的条件是分子等于零且分母不等于零.注意:“分母不为零”这个条件不能少.【变式3-2】(2019秋•北湖区校级月考)当x 取何值时,分式2(3)(2)9x x x +--(1)有意义;(2)分式的值为0.【分析】(1)分式有意义,分母不为零;(2)分式的值为零时,分子为零,但是分母不为零. 【答案】解:(1)根据题意,得 x 2﹣9≠0,解得,x ≠±3, 即当x ≠±3时,分式有意义;(2)根据题意,得(x +3)(x ﹣2)=0,且x 2﹣9≠0, 解得,x =2, 即当x =2时,分式的值为零. 【点睛】本题考查了分式的值为零的条件、分式有意义的条件.若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可. 【变式3-3】对于分式23x a ba b x++-+,当1x =时,分式的值为零,当2x =-时,分式无意义,试求a 、b 的值.【分析】根据分式的值为零的条件为0的条件可得1+a +b =0且a ﹣2b +3≠0,根据分式无意义的条件可得a ﹣2b ﹣6=0,两者联立可求a 、b 的值. 【答案】解:∵分式,当x =1时,分式的值为零,∴1+a +b =0且a ﹣2b +3≠0, 当x =﹣2时,分式无意义, ∴a ﹣2b ﹣6=0, 联立可得,解得.故a 的值是、b 的值是﹣.【点睛】此题主要考查了分式无意义的条件和分式值为零的条件,关键是掌握分式值为零的条件是分子等于零且分母不等于零.注意:“分母不为零”这个条件不能少. 【考点4 分式的基本性质】【方法点拨】分式的基本性质:分式的分子和分母同时乘以(或除以)同一个不为0的整式,分式的值 不变.【例4】(2019春•稷山县期末)若A ,B 为不等于0的整式,则下列各式成立的是( )A .(A A E E B B E=g g 为整式) B .(A A E E B B E+=+为整式)C .22(1)(1)A A x B B x +=+g gD .22(1)(1)A A xB B x +=+g g【分析】分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变. 【答案】解:A .E 可能为0,故不成立; B .不符合分式性质,故错误; C .(x +1)2≥0,故错误; D .x 2+1>0,故正确. 故选:D .【点睛】本题考查了分式的性质,正确理解分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变是解题的关键,【变式4-1】(2019秋•龙口市期中)下列各式从左到右变形正确的是( ) A .0.220.22a b a ba b a b++=++B .231843214332x yx y x y x y ++=--C .n n am m a -=- D .221a b a b a b+=++ 【分析】根据分式的基本性质,依次分析各个选项,选出正确的选项即可. 【答案】解:A .分式的分子和分母同时乘以10,应得,即A 不正确,B .,故选项B 正确,C .分式的分子和分母同时减去一个数,与原分式不相等,即C 项不合题意,D .不能化简,故选项D 不正确.故选:B .【点睛】本题考查了分式的基本性质,正确掌握分式的基本性质是解题的关键. 【变式4-2】(2019秋•大名县期中)下列各式中,正确的是( )A .3355x xy y--=- B .a b a bc c+-+-=C .a b a bc c---=D .a ab a a b-=-- 【分析】根据分式的基本性质即可求出答案. 【答案】解:(A )原式=,故选项A 错误;(B )原式=,故选项B 错误; (C )原式=,故选项C 错误;故选:D .【点睛】本题考查分式的基本性质,解题的关键是熟练运用分式的基本性质,本题属于基础题型. 【变式4-3】(2018秋•奉贤区期末)若分式22xyx y+中的x ,y 的值同时扩大到原来的2倍,则此分式的值( )A .扩大到原来的4倍B .扩大到原来的2倍C .不变D .缩小到原来的12【分析】根据分式的基本性质即可求出答案. 【答案】解:=,故选:C .【点睛】本题考查分式的基本性质,解题的关键是熟练运用分式的基本性质,本题属于基础题型. 【考点5 利用分数的基本性质求值】 【例5】若a 、b 都是正实数,且112a b a b-=+,求22ab a b -的值. 【分析】已知等式左边通分并利用同分母分式的减法法则计算,整理后得到一个关系式,代入所求式子中计算即可求出值. 【答案】解:∵﹣==,∴﹣(a ﹣b )(a +b )=2ab ,即a 2﹣b 2=﹣2ab , 则==﹣.【点睛】此题考查了分式的化简求值,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时分式的分子分母出现多项式,应将多项式分解因式后再约分.【变式5-1】(2019春•禅城区校级月考)已知:0234x y z==≠,求代数式2x y z x y z +-++的值. 【分析】设t =,则x 、y 、z 可以用同一个字母来表示,然后将其代入代数式,然后将代数式化简即可. 【答案】解:设t =,则x =2t ① y =3t ② z =4t ③将①②③代入代数式,得 ==, 所以,代数式的值是.【点睛】本题体现了转化思想,将未知数x 、y 、z 转化为含有相同字母的量,然后代入所求代数式,只要将代数式化简即可.【变式5-2】(2019秋•高唐县期末)已知113a b-=,求分式232a ab ba ab b +---的值.(提示:分式的分子与分母同除以)ab .【分析】根据分式的基本性质,分式的分子分母都除以ab ,分式的值不变,再把换成3计算即可.【答案】解:分式的分子分母都除以ab ,得==,∵=3, ∴=﹣3,所以原式==.【点睛】本题利用分式的基本性质,分子分母都除以ab ,巧妙运用已知条件是解本题的关键,也是解本题的突破口.【变式5-3】已知实数a 满足2310a a -+=,求下列各式的值: (1)21()a a+的值;(2)221a a +; (3)441a a +的值; (4)225121a a a a ++-+的值.【分析】(1)已知等式两边除以a ,求出a +的值,即可确定出原式的值; (2)原式利用完全平方公式变形,把a +的值代入计算即可求出值; (3)原式利用完全平方公式变形,把(2)结论代入计算即可求出值; (4)把已知等式变形后代入计算即可求出值. 【答案】解:(1)已知等式变形得:a +=3, 则原式=9;(2)原式=(a +)2﹣2=9﹣2=7; (3)原式=(a 2+)2﹣2=49﹣2=47;(4)由a 2﹣3a +1=0,得到a 2=3a ﹣1, 则原式==8.【点睛】此题考查了分式方程混合运算,熟练掌握运算法则是解本题的关键. 【考点6 分式的化简求值】【例6】(2019春•潜山市期末)先化简,再求值:2292(3)693x x x x x x -+--+++,其中1x =-.【分析】根据分式的加法和减法可以化简题目中的式子,然后将x =﹣1代入化简后的式子即可解答本题. 【答案】解:+(x ﹣3﹣)======x ﹣4, 当x =﹣1时,原式=﹣1﹣4=﹣5.【点睛】本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.【变式6-1】(2019春•合肥期末)先化简,再求值:3(2)(1)2m m m ++÷+-.其中﹣2≤m ≤2且m 为整数,请你从中选取一个喜欢的数代入求值.【分析】根据分式的加法和除法可以化简题目中的式子,然后从﹣2≤m ≤2且m 为整数中选取一个使得原分式有意义的整数代入化简后的式子即可解答本题.【答案】解:(m +2+)÷(m +1) ====, ∵﹣2≤m ≤2且m 为整数,∴当m =0时,原式==.【点睛】本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.【变式6-2】(2019春•卫辉市期末)先化简:223626699a a a a a a +-+++-g ,然后从﹣3≤a ≤3的范围内选取一个合适的整数作为a 的值代入求值.【分析】根据分式的运算法则进行化简,然后根据分式有意义的条件找出a 的值代入原式即可求出答案.【答案】解:•+ =×… ==∵a≠±3,0∴取a=1,原式==2【点睛】本题考查分式,解题的关键是熟练运用分式的运算法则,本题属于中等题型.【变式6-3】(2018秋•长安区校级月考)(1)先化简:2344(1)11a aaa a-+-+÷++,并从0,1-,2中选一个合适的数,作为a的值代入求值.(2)先化简后求值:2221412211a aa a a a--÷+-+-g,其中a满足20a a-=.【分析】(1)根据分式的混合计算的法则进行计算,先算括号内的,除以一个数等于乘以这个数的倒数,分式乘法先约分,再相乘,x只能取0,而不能取﹣1,2,应注意.(2)先将各自的分子、分母进行因式分解,再转化为乘法,约分后,整体代入即可求出结果.【答案】解:(1)=(﹣)×=×=;∵x≠﹣1,x≠2,∴x=0,当x=0时,原式==1.(2)=××=(a﹣2)(a+1)=a2﹣a﹣2;当a2﹣a=0时,原式=﹣2.【点睛】本题考查了分式的混合运算,掌握计算法则、熟练进行分解因式是解题的关键.【考点7 解分式方程】【方法点拨】分式方程的解法:①去分母(方程两边同时乘以最简公分母,将分式方程化为整式方程);②按解整式方程的步骤求出未知数的值;③检验(求出未知数的值后必须验根,因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根).【例7】(2019秋•武冈市期中)解方程:(1)3222x x x --=-- (2)22510111x x x -+=+-- 【分析】(1)根据解分式方程的过程进行计算即可;(2)先确定公分母,再进行计算即可.【答案】解:(1)3﹣2(x ﹣2)=﹣x解得x =7经检验:x =7是原方程的根∴原方程的解是x =7.(2)2(1﹣x )+5(1+x )=10解得x =1检验:把x =1代入到(x +1)(x ﹣1)中,得:(1+1)×(1﹣1)=0∴原分式方程无解.【点睛】本题考查了解分式方程,解决本题的关键是解分式方程要进行验根.【变式7-1】(2019秋•临淄区期中)解分式方程(1)22411x x =-- (2)2113222x x x x+=++ 【分析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解;(2)分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【答案】解:(1)去分母得:2x +2=4,解得:x =1,经检验x =1是增根,分式方程无解;(2)去分母得:x +x +2=32,经检验x =15是分式方程的解.【点睛】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.【变式7-2】(2019秋•岱岳区期中)解方程:(1)31144x x x --=-- (2)213242x x x=+-- 【分析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解;(2)分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【答案】解:(1)去分母得:3﹣x +1=x ﹣4,解得:x =4,经检验x =4是增根,分式方程无解;(2)去分母得:4x =6x ﹣12﹣1,解得:x =6.5,经检验x =6.5是分式方程的解.【点睛】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.【变式7-3】(2019秋•泰安期中)解下列分式方程:(1)2214111x x x +=+-- (2)29472393x x x x +-=+-- 【分析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解;(2)分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【答案】解:(1)方程两边同乘(x +1)(x ﹣1)得:2(x ﹣1)﹣(x +1)=4,去括号得:2x ﹣2﹣x ﹣1=4,解得:x =7,检验:当x =7时,(x +1)(x ﹣1)≠0,∴x =7是原方程的解;(2)方程两边同乘3(x ﹣3)得:2x +9=3(4x ﹣7)+6(x ﹣3)检验:当x =3时,3(x ﹣3)=0,∴x =3是原方程的增根∴原方程无解.【点睛】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.【考点8 分式方程的增根】【例8】(2019•大城县一模)小华想复习分式方程,由于印刷问题,有一个数“?”看不清楚:?1322x x+=--. (1)她把这个数“?”猜成5,请你帮小华解这个分式方程;(2)小华的妈妈说:“我看到标准答案是:方程的增根是2x =,原分式方程无解”,请你求出原分式方程中“?”代表的数是多少?【分析】(1)把?=5代入方程,进而利用解分式方程的方法解答即可;(2)设?为m ,利用分式方程的增根解答即可.【答案】解:(1)方程两边同时乘以(x ﹣2)得5+3(x ﹣2)=﹣1解得x =0经检验,x =0是原分式方程的解.(2)设?为m ,方程两边同时乘以(x ﹣2)得m +3(x ﹣2)=﹣1由于x =2是原分式方程的增根,所以把x =2代入上面的等式得m +3(2﹣2)=﹣1,m =﹣1所以,原分式方程中“?”代表的数是﹣1.【点睛】此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.【变式8-1】(2018春•安岳县期末)关于x 的方程:12111ax x x+-=--. (1)当3a =时,求这个方程的解;(2)若这个方程有增根,求a 的值.【分析】(1)把a 的值代入分式方程,去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解;(2)由分式方程有增根,得到最简公分母为0,求出x 的值,代入整式方程即可求出a 的值.【答案】解:(1)当a =3时,原方程为﹣=1,方程两边同时乘以(x ﹣1)得:3x +1+2=x ﹣1,解这个整式方程得:x =﹣2,检验:将x =﹣2代入x ﹣1=﹣2﹣1=﹣3≠0,∴x =﹣2是原方程的解;(2)方程两边同时乘以(x ﹣1)得ax +1+2=x ﹣1,若原方程有增根,则x ﹣1=0,解得:x =1,将x =1代入整式方程得:a +1+2=0,解得:a =﹣3.【点睛】此题考查了分式方程的增根,增根确定后可按如下步骤进行:①化分式方程为整式方程;②把增根代入整式方程即可求得相关字母的值.【变式8-2】(2018春•洛宁县期中)m 为何值时,关于x 的方程223242mx x x x +=--+会产生增根? 【分析】先去分母得2(x +2)+mx =3(x ﹣2),整理得(m ﹣1)x +10=0,由于关于x 的方程+=会产生增根,则(x +2)(x ﹣2)=0,解得x =﹣2 或x =2,然后把x =﹣2 和x =2分别代入(m ﹣1)x +10=0即可得到m 的值. 【答案】解:原方程化为+=,方程两边同时乘以(x +2)(x ﹣2)得2(x +2)+mx =3(x ﹣2),整理得(m ﹣1)x +10=0,∵关于x 的方程 +=会产生增根,∴(x +2)(x ﹣2)=0,∴x =﹣2 或x =2,∴当x =﹣2时,(m ﹣1)×(﹣2)+10=0,解得m =6,当x =2时,(m ﹣1)×2+10=0,解得m =﹣4,∴m =﹣4或m =6时,原方程会产生增根.【点睛】本题考查了分式方程的增根:先把分式方程转化为整式方程,解整式方程,若整式方程的解使分式方程的分母为0,则这个整式方程的解就是分式方程的增根.【变式8-3】(2018秋•克东县期末)若关于x的方程322133x mxx x---=---无解,求m的值.【分析】方程去分母转化为整式方程,根据分式方程无解可得m﹣1=0或将x=3代入整式方程,即可求出m的值.【答案】解:去分母得:3﹣2x+mx﹣2=﹣x+3,整理得:(m﹣1)x=2,当m﹣1=0,即m=1时,方程无解;当m﹣1≠0时,x﹣3=0,即x=3时,方程无解,此时=3,即m=,所以m=1或m=.【点睛】此题考查了分式方程的解,分式方程的解即为能使分式方程左右两边相等的未知数的值,且分式方程分母不为0.【考点9 分式方程的应用之行程问题】【例9】(2019秋•正定县期中)A市到B市的距离约为210km,小刘开着小轿车,小张开着大货车,都从A 市去B市.小刘比小张晚出发1小时,最后两车同时到达B市,已知小轿车的速度是大货车速度的1.5倍.(1)求小轿车和大货车的速度各是多少.(列方程解答)(2)当小刘出发时,求小张离B市还有多远.【分析】(1)设大货车的速度为x千米/小时,则小轿车的速度为1.5x千米/小时,根据时间=路程÷速度结合小轿车比大货车少用1小时,即可得出关于x的分式方程,解之经检验后即可得出结论;(2)根据小张离B市的距离=A,B两市间的距离﹣小张的速度×小张出发的时间,即可求出结论.【答案】解:(1)设大货车的速度为x千米/小时,则小轿车的速度为1.5x千米/小时,依题意,得:﹣=1,解得:x=70,经检验,x=70是原方程的解,且符合题意,∴1.5x=105.答:大货车的速度为70千米/小时,小轿车的速度为105千米/小时.(2)210﹣70×1=140(千米).答:当小刘出发时,小张离B市还有140千米.【点睛】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.【变式9-1】(2019•云南模拟)在“要致富先修路”的思想指导下,近几年云南的交通有了快速的变化,特别是“高铁网络”延伸到云南以后,许多地区的经济和旅游发生了翻天覆地的变化,高铁列车也成为人们外出旅行的重要交通工具.假期里小明和爸爸从昆明到某地去旅游,从昆明到该地乘汽车行驶的路程约为800km,高铁列车比汽车行驶的路程少50km,高铁列车比汽车行驶的时间少5h.已知高铁列车的平均时速是汽车平均时速的2.5倍,求高铁列车的平均时速.【分析】设汽车的平均时速为xkm/h,则高铁列车的平均时速为2.5xkm/h,根据时间=路程÷速度结合高铁列车比汽车行驶的时间少5h,即可得出关于x的分式方程,解之经检验后即可得出结论.【答案】解:设汽车的平均时速为xkm/h,则高铁列车的平均时速为2.5xkm/h,依题意,得:﹣=5,解得:x=100,经检验,x=100是原分式方程的解,且符合题意,∴2.5x=250.答:高铁列车的平均时速为250km/h.【点睛】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.【变式9-2】(2019•宜宾)甲、乙两辆货车分别从A、B两城同时沿高速公路向C城运送货物.已知A、C 两城相距450千米,B、C两城的路程为440千米,甲车比乙车的速度快10千米/小时,甲车比乙车早半小时到达C城.求两车的速度.【分析】设乙车的速度为x千米/时,则甲车的速度为(x+10)千米/时,路程知道,且甲车比乙车早半小时到达C城,以时间做为等量关系列方程求解.【答案】解:设乙车的速度为x千米/时,则甲车的速度为(x+10)千米/时.根据题意,得:+=,解得:x=80,或x=﹣110(舍去),∴x=80,经检验,x=80是原方程的解,且符合题意.当x=80时,x+10=90.答:甲车的速度为90千米/时,乙车的速度为80千米/时.【点睛】本题考查分式方程的应用、分式方程的解法,分析题意,找到合适的等量关系是解决问题的关键.根据时间=,列方程求解.【变式9-3】(2019•高淳区二模)甲、乙两同学的家与学校的距离均为3200米.甲同学先步行200米,然后乘公交车去学校,乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的13,公交车的速度是乙骑自行车速度的3倍.甲、乙两同学同时从家出发去学校,结果甲同学比乙同学早到8分钟.(1)求乙骑自行车的速度;(2)当甲到达学校时,乙同学离学校还有多远?【分析】(1)设乙骑自行车的速度为xm/min,则公交车的速度是3xm/min,甲步行速度是xm/min,根据题意列方程即可得到结论;(2)8×200=1600米即可得到结果.【答案】解:(1)设乙骑自行车的速度为xm/min,则公交车的速度是3xm/min,甲步行速度是xm/min,由题意得:﹣8=+.解得x=200.经检验x=200原方程的解答:乙骑自行车的速度为200m/min.(2)当甲到达学校时,乙同学还要继续骑行8分钟,所以8×200=1600(m).答:乙同学离学校还有1600m.【点睛】此题主要考查了分式方程的应用,根据题意得到甲的运动速度是解题关键.【考点10 分式方程的应用之工程问题】【例10】(2019秋•滦州市期中)列方程解应用题某工程队修建一条1200m的道路,由于施工过程中采用了新技术,所以工作效率提高了50%,结果提前4天完成任务.(1)求这个工程队原计划每天修建道路多少米?(2)这项工程,如果要求工程队提前两天完成任务,那么实际的工作效率比原计划增加百分之几?【分析】(1)设这个工程队原计划每天修建道路x米,则实际每天修建道路(1+50%)x米,根据工作时间=工作总量÷工作效率结合实际比原计划提前4天完成任务,即可得出关于x的分式方程,解之经检验后即可得出结论;(2)设实际的工作效率比原计划增加的百分比为y,根据工作时间=工作总量÷工作效率结合实际比原计划提前2天完成任务,即可得出关于y的分式方程,解之经检验后即可得出结论.【答案】解:(1)设这个工程队原计划每天修建道路x米,则实际每天修建道路(1+50%)x米,依题意,得:﹣=4,解得:x=100,经检验,x=100是原方程的解,且符合题意.答:这个工程队原计划每天修建道路100米.(2)设实际的工作效率比原计划增加的百分比为y,依题意,得:﹣=2,解得:y=0.2=20%.经检验,y=20%是原方程的解,且符合题意.答:实际的工作效率比原计划增加20%.【点睛】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键【变式10-1】(2018秋•徽县期末)某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成:若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.(1)这项工程的规定时间是多少天?(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲乙两队合作完成该工程需要多少天?【分析】(1)设这项工程的规定时间是x天,则甲队单独施工需要x天完工,乙队单独施工需要1.5x天完工,根据甲队完成的工作量+乙队完成的工作量=总工作量(单位1),即可得出关于x的分式方程,解之经检验后即可得出结论;(2)由(1)可求出甲、乙单独施工所需天数,再利用两队合作完工所需时间=总工作量÷(甲队一天完成的工作量+乙队一天完成的工作量),即可求出结论.【答案】解:(1)设这项工程的规定时间是x天,则甲队单独施工需要x天完工,乙队单独施工需要1.5x天完工,依题意,得:+=1,解得:x=30,经检验,x=30是原方程的解,且符合题意.答:这项工程的规定时间是30天.(2)由(1)可知:甲队单独施工需要30天完工,乙队单独施工需要45天完工,1÷(+)=18(天).答:甲乙两队合作完成该工程需要18天.【点睛】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.【变式10-2】(2018秋•江北区期末)在我市区某中学美化校园招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要30天,若由甲队先做10天,剩下的工程由甲、乙合做12天可完成.(1)乙队单独完成这项工程需要多少天?(2)甲队施工一天,需付工程款3.5万元,乙队施工一天,需付工程款2万元.若该工程计划在35天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱,还是由甲乙两队全程合作完成该工程省钱?【分析】(1)设乙队单独完成这项工程需要x天,根据甲完成的部分+乙完成的部分=总工程量(单位1),即可得出关于x的分式方程,解之经检验后即可求出结论;(2)设甲、乙两队全程合作需要y天完成该工程,根据甲完成的部分+乙完成的部分=总工程量(单位1),即可得出关于y的一元一次方程,解之即可得出y值,再分别求出甲队单独完成以及甲、乙两队全程合作完成该工程所需费用,比较后即可得出结论.【答案】解:(1)设乙队单独完成这项工程需要x天,依题意,得:+=1,解得:x=45,经检验,x=45是所列分式方程的解,且符合题意.答:乙队单独完成这项工程需要45天.(2)设甲、乙两队全程合作需要y天完成该工程,依题意,得:+=1,解得:y=18.。
专题02全等模型一线三等角(K字)模型(解析版)八年级数学上册常见几何模型全归纳之模型解读与提分精练

专题02全等模型--一线三等角(K 字)模型全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(一线三等角(K 字)模型)进行梳理及对应试题分析,方便掌握。
模型1.一线三等角(K 型图)模型(同侧型)【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】同侧型一线三等角(常见):锐角一线三等角直角一线三等角(“K 型图”)钝角一线三等角条件:A CED B ∠=∠=∠+CE=DE证明思路:,A B C BED ∠=∠∠=∠+任一边相等BED ACE⇒≅ 例1.(2022·河南濮阳市·八年级期末)已知:D ,A ,E 三点都在直线m 上,在直线m 的同一侧作ABC ,使AB AC =,连接BD ,CE .(1)如图①,若90BAC ∠=︒,BD m ⊥,CE m ⊥,求证ABD ACE ≅ ;(2)如图②,若BDA AEC BAC ∠=∠=∠,请判断BD ,CE ,DE 三条线段之间的数量关系,并说明理由.【答案】(1)见详解;(2)DE =BD +CE .理由见详解【分析】(1)根据BD ⊥直线m ,CE ⊥直线m 得∠BDA =∠CEA =90°,而∠BAC =90°,根据等角的余角相等,得∠CAE =∠ABD ,然后根据“AAS”可判断△ABD ≌△CAE ;(2)由∠BDA =∠AEC =∠BAC ,就可以求出∠BAD =∠ACE ,进而由ASA 就可以得出△ABD ≌△CAE ,就可以得出BD =AE ,DA =CE ,即可得出结论.【详解】(1)证明:如图①,∵D ,A ,E 三点都在直线m 上,∠BAC =90°,∴∠BAD +∠CAE =90°,∵BD ⊥m ,CE ⊥m ,∴∠ADB =∠CEA =90°,∴∠BAD +∠ABD =90°,∴∠ABD =∠CAE ,在△ABD 和△CAE 中,ADB AEC ABD CAE AB AC ∠∠⎧⎪∠∠⎨⎪⎩===,∴△ABD ≌△CAE (AAS );(2)DE =BD +CE .理由如下:如图②,∵∠BDA =∠AEC =∠BAC ,∴由三角形内角和及平角性质,得:∠BAD +∠ABD =∠BAD +∠CAE =∠CAE +∠ACE ,∴∠ABD =∠CAE ,∠BAD =∠ACE ,在△ABD 和△CAE 中,ABD CAE AB AC BAD ACE ∠∠⎧⎪⎨⎪∠∠⎩===,∴△ABD ≌△CAE (ASA ),∴BD =AE ,AD =CE ,∴DE =AD +AE =BD +CE .【点睛】本题考查了全等三角形的判定与性质以及三角形内角和定理的综合应用,解题的关键是熟练掌握全等三角形的判定方法,灵活运用所学知识解决问题.例2.(2022·绵阳市·八年级课时练习)(1)如图1,在△ABC 中,∠BAC =90°,AB =AC ,直线m 经过点A ,BD ⊥直线m ,CE ⊥直线m ,垂足分别为点D 、E .求证:△ABD ≌△CAE ;(2)如图2,将(1)中的条件改为:在△ABC 中,AB =AC ,D 、A 、E 三点都在直线m 上,并且有∠BDA =∠AEC =∠BAC =α,其中α为任意锐角或钝角.请问结论△ABD ≌△CAE 是否成立?如成立,请给出证明;若不成立,请说明理由.(3)拓展应用:如图3,D ,E 是D ,A ,E 三点所在直线m 上的两动点(D ,A ,E 三点互不重合),点F 为∠BAC 平分线上的一点,且△ABF 和△ACF 均为等边三角形,连接BD ,CE ,若∠BDA =∠AEC =∠BAC ,求证:△DEF是等边三角形.【答案】(1)见详解;(2)成立,理由见详解;(3)见详解【分析】(1)根据BD ⊥直线m ,CE ⊥直线m 得90BDA CEA ∠=∠=︒,而90BAC ∠=︒,根据等角的余角相等得CAE ABD ∠=∠,然后根据“AAS ”可判断ADB CEA ∆∆≌;(2)利用BDA BAC α∠=∠=,则180DBA BAD BAD CAE ∠∠∠∠α+=+=︒-,得出CAE ABD ∠=∠,然后问题可求证;(3)由题意易得,60BF AF AB AC ABF BAF FAC ===∠=∠=∠=︒,由(1)(2)易证ADB CEA ∆∆≌,则有AE BD =,然后可得FBD FAE ∠=∠,进而可证DBF EAF ∆∆≌,最后问题可得证.【详解】(1)证明:BD ⊥ 直线m ,CE ⊥直线m ,90BDA CEA ∴∠=∠=︒,90BAC ∠=︒ ,90BAD CAE ∴∠+∠=︒,90BAD ABD ∠+∠=︒ ,CAE ABD ∴∠=∠,在ADB ∆和CEA ∆中,ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ADB CEA AAS ∴∆∆≌;解:(2)成立,理由如下:α∠=∠= BDA BAC ,180α∴∠+∠=∠+∠=︒-DBA BAD BAD CAE ,CAE ABD ∴∠=∠,在ADB ∆和CEA ∆中,ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ADB CEA AAS ∴∆∆≌;(3)证明:∵△ABF 和△ACF 均为等边三角形,∴,60BF AF AB AC ABF BAF FAC ===∠=∠=∠=︒,∴∠BDA =∠AEC =∠BAC =120°,∴180120DBA BAD BAD CAE ∠+∠=∠+∠=︒-︒,∴CAE ABD ∠=∠,∴()ADB CEA AAS ∆∆≌,∴AE BD =,∵,FBD FBA ABD FAE FAC CAE ∠=∠+∠∠=∠+∠,∴FBD FAE ∠=∠,∴DBF EAF ∆∆≌(SAS ),∴,FD FE BFD AFE =∠=∠,∴60BFA BFD DFA AFE DFA DFE ∠=∠+∠=∠+∠=∠=︒,∴△DFE 是等边三角形.【点睛】本题主要考查全等三角形的判定与性质及等边三角形的性质与判定,熟练掌握全等三角形的判定与性质及等边三角形的性质与判定是解题的关键.例3.(2022秋·河北张家口·八年级校考期中)如图1,在长方形ABCD 中,4AB cm =,3BC cm =,点P 在线段AB 上以1/cm s 的速度由A 向终点B 运动,同时,点Q 在线段BC 上由点B 向终点C 运动,它们运动的时间为()t s .【解决问题】若点Q 的运动速度与点P 的运动速度相等,当1t =时,回答下面的问题:(1)_________AP cm =;(2)此时ADP ∆与BPQ ∆是否全等,请说明理由;(3)求证:DP PQ ⊥;【变式探究】若点Q 的运动速度为 /x cm s ,是否存在实数x ,使得ADP ∆与BPQ ∆全等?若存在,请直接【答案】解决问题(1)1;(2)全等;【分析】解决问题(1)当t=1时,AP 判定;(3)利用同角的余角相等证明∠①ADP ∆≌BPQ ∆②ADP ∆≌BQP ∆【详解】解:解决问题(1)∵t=1,点P 的运动速度为1cm (2)全等,理由是:当t=1时,可知在△ADP 与△BPQ 中,AD PB A B AP BQ =⎧⎪∠=∠⎨⎪=⎩,∴△(3)∵△ADP ≌△BPQ ,∴∠APD=∠②若ADP ∆≌BQP ∆,AP=BP ,即点AB 中点,此时AP=2,t=2÷1=2s ,AD=BQ=3综上:当ADP ∆与BPQ ∆全等时,x 的取值为1或32.【点睛】本题考查了全等三角形的判定和性质,注意在运动中对三角形全等进行分类讨论,从而得出不同情况下的点Q 速度.例4.(2023·湖南岳阳·统考一模)如图,在与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.(1)当∠BDA=115°时,∠EDC=______°,∠AED=______°;(2)线段DC的长度为何值时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,求∠BDA的度数;若不可以,请说明理由.【答案】(1)25°,65°;(2)2,理由见详解;(3)可以,110°或80°.【分析】(1)利用邻补角的性质和三角形内角和定理解题;(2)当DC=2时,利用∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,求出∠ADB=∠DEC,再利用AB=DC=2,即可得出△ABD≌△DCE.(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形.【详解】解:(1)∵∠B=40°,∠ADB=115°,∴∠BAD=180°-∠B-∠ADB=180°-115°-40°=25°,∵AB=AC,∴∠C=∠B=40°,∵∠EDC=180°-∠ADB-∠ADE=25°,∴∠DEC=180°-∠EDC-∠C=115°,∴∠AED=180°-∠DEC=180°-115°=65°;(2)当DC=2时,△ABD≌△DCE,理由:∵∠C=40°,∴∠DEC+∠EDC=140°,又∵∠ADE=40°,∴∠ADB+∠EDC=140°,∴∠ADB=∠DEC,又∵AB=DC=2,在△ABD和△DCE中,ADB DECB CAB DC∠∠⎧⎪∠∠⎨⎪⎩===∴△ABD≌△DCE(AAS);(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,∵∠BDA=110°时,∴∠ADC=70°,∵∠C=40°,∴∠DAC=70°,∴△ADE的形状是等腰三角形;∵当∠BDA的度数为80°时,∴∠ADC=100°,∵∠C=40°,∴∠DAC=40°,∴△ADE的形状是等腰三角形.【点睛】本题主要考查学生对等腰三角形的判定与性质,全等三角形的判定与性质,三角形外角的性质等知识点的理解和掌握,此题涉及到的知识点较多,综合性较强,但难度不大,属于基础题.模型2.一线三等角(K 型图)模型(异侧型)【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
八年级上册数学重点模型

八年级上册数学重点模型一、三角形全等模型。
1. 平移型。
- 模型特点:两个三角形通过平移可以完全重合。
- 示例:在△ABC和△DEF中,AB = DE,BC = EF,AC = DF,且∠A = ∠D,∠B = ∠E,∠C = ∠F。
这是因为将△ABC沿着某一方向平移一定距离后可与△DEF重合。
- 解题思路:当遇到此类图形时,可直接利用全等三角形的判定定理(SSS、SAS、ASA、AAS、HL)来证明两个三角形全等,进而得出对应边相等、对应角相等的结论。
例如,若已知AB = DE,BC = EF,AC = DF,可直接根据SSS判定△ABC≌△DEF。
2. 旋转型。
- 模型特点:一个三角形绕着某一点旋转一定角度后与另一个三角形重合。
- 示例:在等腰△ABC中,AB = AC,将△ABC绕点A逆时针旋转一定角度得到△ADE,此时AB与AD重合,AC与AE重合,∠BAC = ∠DAE。
- 解题思路:首先要找到旋转中心和旋转角度,然后根据旋转的性质(对应边相等,对应角相等),再结合全等三角形的判定条件来证明三角形全等。
如在上述例子中,因为AB = AD,AC = AE,∠BAC = ∠DAE,根据SAS可判定△ABC≌△ADE。
3. 翻折型(对称型)- 模型特点:一个三角形沿着某一条直线翻折后与另一个三角形重合,这条直线就是对称轴。
- 示例:在△ABC中,AD是BC边上的高,将△ABD沿AD翻折得到△AED,则△ABD≌△AED。
- 解题思路:根据翻折的性质,即翻折前后的图形全等,得到对应边相等和对应角相等。
在这个例子中,BD = ED,AB = AE,∠B = ∠AED等,再根据这些条件来解决相关问题,如求线段的长度或角的大小等。
二、等腰三角形模型。
1. “三线合一”模型。
- 模型特点:在等腰三角形中,底边上的高、底边上的中线、顶角平分线互相重合。
- 示例:在等腰△ABC中,AB = AC,AD是BC边上的中线,则AD也是BC边上的高和∠BAC的平分线。
八年级数学上册角度计算中的经典模型(举一反三)(含解析版)

八年级数学上册角度计算中的经典模型(举一反三)(含解析版)八年级数学上册角度计算中的经典模型(举一反三)(含解析版)角度计算是数学中非常重要的一部分,它与几何形状、图形关系等有着密切的联系。
在八年级数学上册中,我们学习到了一些经典的角度计算模型,通过举一反三的方法,我们可以进一步应用这些模型去解决更加复杂的问题。
本文将介绍并解析其中的经典模型。
一、等腰三角形内角计算模型等腰三角形是指两边长度相等的三角形,它具有一些特殊的性质。
在角度计算中,我们可以利用等腰三角形内角的关系来求解未知角度。
假设等腰三角形两边的夹角为x度,那么根据等腰三角形的性质,其他两个角度也是x度。
因此,我们可以通过等腰三角形的内角关系求解未知角度。
示例:已知一个等腰三角形的两边夹角为45度,求其他两个角度。
解析:根据等腰三角形的性质,其他两个角度也是45度。
因此,该等腰三角形的三个角度均为45度。
二、垂直直角三角形内角计算模型垂直直角三角形是指其中一个内角为90度的三角形,也被称为直角三角形。
在角度计算中,我们可以利用直角三角形的内角关系来求解未知角度。
通过观察直角三角形的角度特点,我们可以利用已知角度和直角的关系来求解其他未知角度。
示例:已知一个直角三角形的一个内角为30度,求其他两个角度。
解析:由于直角三角形的角度和为180度,其中一个内角为90度,已知另一个内角为30度,那么第三个角度为180度减去90度和30度得到的60度。
三、平行线夹角计算模型平行线是指在同一个平面上不相交且始终保持相同距离的两条直线。
在角度计算中,我们可以利用平行线夹角的关系来求解未知角度。
根据平行线的性质,夹在同一边的两个角互补,它们的和为180度。
因此,我们可以通过已知角度和平行线的夹角关系求解其他未知角度。
示例:已知一对平行线之间的夹角为60度,求其余两个夹角。
解析:根据平行线夹角的关系可知,其余两个夹角的和为180度减去已知的60度,即120度。
2024年初中数学《角度计算的经典模型》及答案解析

角度计算的经典模型(八大题型)【题型01:双垂直模型】【题型02:A字模型】【题型03:8字模型】【题型04:飞镖模型】【题型05:风筝模型】【题型06:两内角角平分线模型】【题型07:两外角角平分线模型】【题型08:内外角平分线模型】【题型01:双垂直模型】【条件】∠B=∠D=∠ACE=90°.【结论】∠BAC=∠DCE,∠ACB=∠CED.1.AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.2.如图,在△ABC中,∠BAC=80°,∠B=60°,AD是BC边上的高,∠ACB的平分线CF交AD于点E.求∠AEC的度数.3.如图,在△ABC中,AD⊥BC,垂足为D,E是AC边上一点,BE与AD交于点F,若∠ABC=45°,∠BAC=75°,∠BFD=60°,求∠BEC的度数.【题型02:A字模型】图1【条件】图1中三种情况【结论】∠1=∠2【证明】略图2【结论】∠1+∠2=∠3+∠4【证明】根据内角和定理,∠1+∠2+∠A=∠3+∠4+∠A=180°∴∠1+∠2=∠3+∠4图3【结论】∠1+∠2=180°+∠A【证明】∠1+∠2=(∠AED+∠A)+(∠ADE+∠A)=180°+∠A4.探索归纳:(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2=.(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=.(3)如图2,根据(1)与(2)的求解过程,你归纳猜想∠1+∠2与∠A的关系是.(4)如图3,若没有剪掉∠A,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系,并说明理由.5.如图,在△ABC中,BD平分∠ABC,DE∥BC交AB于点E.若∠A=70°,∠BDC=100°,则∠BED的度数为()A.120°B.130°C.140°D.150°6.如图,已知:AD∥EF,∠CAD+∠DEF=180°.(1)证明:AC∥DE;(2)若AC平分∠BAD,∠ADC=35°,∠ACD=∠ADE+45°.求∠G的度数.7.在△ABC中,已知∠A=80°,∠C=30°,现把△CDE沿DE进行不同的折叠得△C DE,对折叠后产生的夹角进行探究:(1)如图(1)把△CDE沿DE折叠在四边形ADEB内,则求∠1+∠2的和;(2)如图(2)把△CDE沿DE折叠覆盖∠A,则求∠1+∠2的和;(3)如图(3)把△CDE沿DE斜向上折叠,探求∠1、∠2、∠C的关系.【题型03:8字模型】【条件】AE、BD相交于点C【结论】∠A+∠B=∠D+∠E.8.(1)已知:如图(1)的图形我们把它称为“8字形”,试说明:∠A+∠B=∠C+∠D.(2)如图(2),AP,CP分别平分∠BAD,∠BCD,若∠ABC=36°,∠ADC=16°.求∠P的度数.(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是;(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是.9.如图,∠1=60°,则∠A+∠B+∠C+∠D+∠E+∠F=()A.240°B.280°C.360°D.540°10.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=.11.如图,已知AB∥CD,∠B=∠D,CD与AE相交于F.(1)求证:AD∥BC;(2)若∠B=50°,AE平分∠BAD,求∠DFE的度数.12.已知:如图,FE∥OC,AC和BD相交于点O,F是OD上一点,且∠1=∠A.(1)求证:AB∥DC;(2)若∠B=30°,∠1=65°,求∠OFE的度数.13.如图,BP平分∠ABC,交CD于点F,DP平分∠ADC交AB于点E,AB与CD相交于点G,∠A=42°.(1)若∠ADC=60°,求∠AEP的度数;(2)若∠C=38°,求∠P的度数.【题型04:飞镖模型】图1图2图3【条件】四边形ABPC如图1所示【结论】∠BPC=∠A+∠B+∠C.14.探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图(1)观察“规形图(1)”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;(2)请你直接利用以上结论,解决以下问题:①如图(2),把一块三角尺XYZ放置在△AC上使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=40°,则∠ABX+∠ACX=°.②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.15.一个零件的形状如图,按要求∠A=90°,∠B=32°,∠C=21°,检验工人量得∠CDB=148°,就断定这个零件不合格,运用三角形的有关知识说明零件不合格的理由.16.附加题:如图,试说明:①∠BDC>∠A;②∠BDC=∠B+∠C+∠A.如果点D在线段BC的另一侧,结论会怎样?17.如图,△ABC中,∠A=30°,D为CB延长线上的一点,DE⊥AB于点E,∠D=40°,则∠C为()A.20°B.15°C.30°D.25°18.如图,点E在BC上,ED⊥AC于F,交BA的延长线于D,已知∠D=30°,∠C=20°,则∠B的度数是()A.20°B.30°C.40°D.50°19.如图,已知在△ABC中,∠A=40°,现将一块直角三角板放在△ABC上,使三角板的两条直角边分别经过点B,C,直角顶点D落在△ABC的内部,则∠ABD+∠ACD=( ).A.90°B.60°C.50°D.40°20.如图,若∠EOC=115°,则∠A+∠B+∠C+∠D+∠E+∠F=.【题型05:风筝模型】21.如图1和图2,在三角形纸片ABC中,点D,E分别在边AC,AB上,沿DE折叠,点A落在点A'的位置.(1)如图1,当点A′落在CD边上时,∠DAE与∠1之间的数量关系为(只填序号),并说明理由;①∠DAE=∠1②∠DAE=2∠1③∠1=2∠DAE(2)如图2,当点A落在△ABC内部时,直接写出∠DAE与∠1,∠2之间的数量关系.22.如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是()A.40°B.80°C.90°D.140°23.将纸片△ABC沿DE折叠使点A落在A′处的位置.(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是.(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.【题型06:两内角角平分线模型】双内角平分线模型【条件】BP 、CP 分别为∠ABC 、∠ACB 的角平分线.【结论】∠P =90°+12∠A .24.如图1,点A 、B 分别在射线OM 、ON 上运动(不与点O 重合),AC 、BC 分别是∠BAO 和∠ABO 的角平分线,BC 延长线交OM 于点G .(1)若∠MON =60°,则∠ACG =;(直接写出答案)(2)若∠MON =n °,求出∠ACG 的度数;(用含n 的代数式表示)(3)如图2,若∠MON =80°,过点C 作CF ∥OA 交AB 于点F ,求∠BGO 与∠ACF 的数量关系.25.如图,BE 平分∠ABD ,CF 平分∠ACD ,BE 与CF 交于点G ,若∠BDC =140°,∠BGC =100°,则∠A =()A.80°B.75°C.60°D.45°26.如图,在△ABC 中,已知∠A =70°,∠ABC 、∠ACB 的平分线OB 、OC 相交于点O ,则∠BOC 的度数为.27.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P.(1)若∠ABC+∠ACB=130°,求∠BPC的度数.(2)当∠A为多少度时,∠BPC=3∠A?【题型07:两外角角平分线模型】双外角平分线模型【条件】BP、CP分别为∠EBC、∠BCF的角平分线.【结论】∠P=90°-12∠A.28.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=70°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q,∠A之间的数量关系.(3)如图③,延长线段BP,QC交于点E,在△BQE中,存在一个内角等于另一个内角的3倍,求∠A的度数.29.如图,在△ABC中,∠B=58°,三角形两外角的角平分线交于点E,则∠AEC=.30.如图,△ABC两个外角∠CBD、∠BCE的平分线相交于点O,∠A=40°,求∠BOC的度数.31.如图,在△ABC中,BO、CO分别平分∠ABC,∠ACB,BO的延长线交外角∠ACD的角平分线于点E.以下结论:①∠1=2∠2;②∠BOC=3∠2;③∠BOC=90°+∠2;④∠BOC=90°+∠1.其中正确的结论有(填序号).32.如图,在△ABC中,∠A=α,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得A2;⋯;∠A2019BC与∠A2019CD的平分线相交于点A2020,得∠A2020,则∠A2020=.33.【初步认识】(1)如图1,BM平分∠ABC,CM平分外角∠ACD,若∠A=80°,则∠M=°.【变式探究】(2)已知ABCD为四边形,E为边AB延长线上一点,如图2,∠ADC=110°,∠BCD=120°,∠DAB和∠CBE的平分线交于点F,则∠F=°.【继续探索】(3)已知ABCD为四边形,E为边AB延长线上一点,如图3,∠ADC=α,∠BCD=β,且α+β>180°,∠DAB和∠CBE的平分线交于点F,求∠F与α、β之间的数量关系,并说明理由;【终极挑战】(4)如果将(3)中的条件α+β>180°改为α+β<180°,再分别作∠DAB和∠CBE的平分线,且两平分线所在的直线交于点F,那么∠F与α、β又有怎样的数量关系?请直接写出结论.(不用说明理由)角度计算的经典模型(八大题型)【题型01:双垂直模型】【题型02:A字模型】【题型03:8字模型】【题型04:飞镖模型】【题型05:风筝模型】【题型06:两内角角平分线模型】【题型07:两外角角平分线模型】【题型08:内外角平分线模型】【题型01:双垂直模型】【条件】∠B=∠D=∠ACE=90°.【结论】∠BAC=∠DCE,∠ACB=∠CED.1.AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.【答案】见试题解答内容【解答】解:∵AD是△ABC的高,∴∠BHD+∠HBD=90°,∵BE是△ABC的高,∴∠HBD+∠C=90°,∴∠BHD=∠C,∵∠C=50°,∴∠BHD=50°.2.如图,在△ABC中,∠BAC=80°,∠B=60°,AD是BC边上的高,∠ACB的平分线CF交AD于点E.求∠AEC的度数.【答案】110°【分析】本题考查三角形的内角和定理,角平分线的定义,三角形外角的性质.先根据三角形的内角和定理得到∠ACB 的度数,然后根据角平分线的定义得到∠ECD 的值,然后利用三角形的外角等于与它不相邻的两个内角的和解题即可.【详解】解:∵在△ABC 中,∠BAC =80°,∠B =60°,∴∠ACB =180°-∠CAB =∠B =180°-80°-60°=40°,∵CF 是∠ACB 的平分线,∴∠ECD =12∠ACD =12×40°=20°,∵AD 是BC 边上的高,∴∠ADC =90°,∴∠AEC =∠ADC +∠ECD =90°+20°=110°.3.如图,在△ABC 中,AD ⊥BC ,垂足为D ,E 是AC 边上一点,BE 与AD 交于点F ,若∠ABC =45°,∠BAC =75°,∠BFD =60°,求∠BEC 的度数.【答案】90°【分析】本题主要考查了三角形内角和定理,先根据三角形内角和定理求出∠C ,然后求出∠DBF ,进而得出答案.【详解】∵∠ABC =45°,∠BAC =75°,∴∠C =180°-45°-75°=60°.∵AD ⊥BC ,∴∠ADB =90°.∵∠BFD =60°,∴∠DBF =90°-60°=30°,∴∠BEC =180°-∠EBC -∠C =180°-60°-30°=90°.【题型02:A 字模型】图1【条件】图1中三种情况【结论】∠1=∠2【证明】略图2【结论】∠1+∠2=∠3+∠4【证明】根据内角和定理,∠1+∠2+∠A=∠3+∠4+∠A=180°∴∠1+∠2=∠3+∠4图3【结论】∠1+∠2=180°+∠A【证明】∠1+∠2=(∠AED+∠A)+(∠ADE+∠A)=180°+∠A4.探索归纳:(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2=270°.(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=220°.(3)如图2,根据(1)与(2)的求解过程,你归纳猜想∠1+∠2与∠A的关系是180°+∠A.(4)如图3,若没有剪掉∠A,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系,并说明理由.【答案】见试题解答内容【解答】解:(1):∵四边形的内角和为360°,直角三角形中两个锐角和为90°∴∠1+∠2=360°-(∠A+∠B)=360°-90°=270°.∴∠1+∠2等于270°.故答案为:270°;(2)∠1+∠2=180°+40°=220°,故答案是:220°;(3)∠1+∠2与∠A的关系是:∠1+∠2=180°+∠A;故答案为:180°+∠A;(4)∵△EFP是由△EFA折叠得到的,∴∠AFE=∠PFE,∠AEF=∠PEF∴∠1=180°-2∠AFE,∠2=180°-2∠AEF∴∠1+∠2=360°-2(∠AFE+∠AEF)又∵∠AFE+∠AEF=180°-∠A,∴∠1+∠2=360°-2(180°-∠A)=2∠A.5.如图,在△ABC中,BD平分∠ABC,DE∥BC交AB于点E.若∠A=70°,∠BDC=100°,则∠BED的度数为()A.120°B.130°C.140°D.150°【答案】A【分析】本题考查三角形内角和定理,角平分线的定义,平行线的性质等知识.求出∠EBD,∠EDB,再利用三角形内角和定理即可解决问题.【详解】解:∵∠A+∠ABD=∠BDC,∠A=70°,∠BDC=100°,∴∠ABD=30°,∵BD平分∠ABC,∴∠ABD=∠CBD=30°,又∵DE∥BC,∴∠BDE=∠CBD=30°,∴∠BED=180°-∠ABD-∠BDE=120°.故选:A.6.如图,已知:AD∥EF,∠CAD+∠DEF=180°.(1)证明:AC∥DE;(2)若AC平分∠BAD,∠ADC=35°,∠ACD=∠ADE+45°.求∠G的度数.【答案】(1)见解析(2)∠G=50°【分析】本题考查平行线的判定与性质,三角形内角和定理,角平分线的定义等知识点,解题的关键是熟练掌握平行线的判定与性质.(1)由平行线的性质可得∠DEF+∠ADG=180°,由∠CAD+∠DEF=180°可得∠CAD=∠ADG,即可证明;(2)首先利用已知条件可以去求出∠BAC=∠ADE=50°,然后利用三角形的外角求出∠BDG,解答即可.【详解】(1)证明:∵AD∥EF,∴∠DEF+∠ADG=180°.∵∠CAD+∠DEF=180°.∴∠CAD=∠ADG.∴AC∥DE;(2)解:∵AC是∠BAD的平分线,且AC∥DE,∴∠BAC=∠CAD,∠CAD=∠ADE,∴∠BAC=∠ADE,∵∠ACD=∠ADE+45°,∠ACD=∠B+∠BAC,∴∠B=45°,∵∠ADC=35°,∴∠BAD=180°-∠B-∠ADC=180°-45°-35°=100°.∵AC是∠BAD的平分线,∠BAD=50°,∴∠CAD=∠ADE=12∴∠G=∠BAD-∠ADE=100°-50°=50°.7.在△ABC中,已知∠A=80°,∠C=30°,现把△CDE沿DE进行不同的折叠得△C DE,对折叠后产生的夹角进行探究:(1)如图(1)把△CDE沿DE折叠在四边形ADEB内,则求∠1+∠2的和;(2)如图(2)把△CDE沿DE折叠覆盖∠A,则求∠1+∠2的和;(3)如图(3)把△CDE沿DE斜向上折叠,探求∠1、∠2、∠C的关系.【答案】(1)60°(2)50°(3)∠2-∠1=2∠C【分析】本题考查折叠性质,三角形内角和定理,解答此题时要充分利用折叠部分折叠前后形成的图形为全等形的性质,并且解答该题时要充分利用三角形的性质.(1)根据折叠前后的图象全等可知,∠1=180°-2∠CDE,∠2=180°-2∠CED,再根据三角形内角和定理比可求出答案;(2)连接DG,将∠ADG+∠AGD作为一个整体,根据三角形内角和定理来求;(3)将∠2看作180°-2∠CED,∠1看作2∠CDE-180°,再根据三角形内角和定理求解,即可解题.【详解】(1)解:由折叠性质可知:∠CDC =2∠CDE,∠CEC =2∠CED,∵∠C=30°,∴∠1+∠2=180°-2∠CDE+180°-2∠CED=360°-2∠CDE+∠CED=360°-2180°-∠C=2∠C=60°;(2)解:连接DG,∵∠A=80°,∴∠1+∠2=180°-∠C -∠ADG+∠AGD=180°-30°-180°-80°=50°;(3)解:∠2-∠1=180°【题型03:8字模型】【条件】AE、BD相交于点C【结论】∠A +∠B =∠D +∠E .8.(1)已知:如图(1)的图形我们把它称为“8字形”,试说明:∠A +∠B =∠C +∠D .(2)如图(2),AP ,CP 分别平分∠BAD ,∠BCD ,若∠ABC =36°,∠ADC =16°.求∠P 的度数.(3)如图(3),直线AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、∠D 的数量关系是;(4)如图(4),直线AP 平分∠BAD 的外角∠FAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、∠D 的数量关系是.【答案】(1)见解析;(2)26°;(3)∠P =90°+12∠B +∠D ;(4)∠P =180°-12∠B +∠D 【分析】(1)根据三角形的内角和等于180°和对顶角的性质即可得证;(2)设∠BAP =∠P AD =x ,∠BCP =∠PCD =y ,x +∠ABC =y +∠P x +∠P =y +∠ADC 解方程即可得到答案;(3)根据直线AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,得到∠P AB =∠P AD =12∠BAD ,∠PCB =∠PCE =12∠PCD 从而可以得到180°-2∠P AB +∠PCB +∠D =∠B ,再根据∠P +∠P AD =∠PCD +∠D ,∠BAD +∠B =∠BCD +∠D 得到∠P -∠B =∠P AD +∠PCB =∠P AB +∠PCB 即可求解;(4)连接PB ,PD ,求得∠APC +∠ABC +∠PCB +∠P AB =360°,∠APC +∠ADC +∠PCD +∠P AD =360°,再根据∠PCE +∠PCD =180°,∠P AB +∠P AF =180°,∠FAP =∠P AO ,∠PCE =∠PCB ,即可求解.【详解】解:(1)如图.∵∠A +∠B +∠AOB =180°,∠C +∠D +∠COD =180°,∴∠A +∠B +∠AOB =∠C +∠D +∠COD .∵∠AOB =∠COD ,∴∠A +∠B =∠C +∠D ;(2)如图.∵AP ,CP 分别平分∠BAD ,∠BCD ,设∠BAP =∠P AD =x ,∠BCP =∠PCD =y ,则有x +∠ABC =y +∠P x +∠P =y +∠ADC ,∴∠ABC -∠P =∠P -∠ADC ,∴∠P =12∠ABC +∠ADC =1236°+16° =26°(3)如图.∵直线AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,∴∠P AB =∠P AD =12∠BAD ,∠PCB =∠PCE =12∠BCE ,∴2∠P AB +∠B =180°-2∠PCB +∠D ,∴180°-2∠P AB +∠PCB +∠D =∠B∵∠P +∠P AD =∠PCD +∠D ,∠BAD +∠B =∠BCD +∠D∴∠P +∠P AD -∠BAD -∠B =∠PCD -∠BCD∴∠P -∠P AB -∠B =∠PCB ,∴∠P -∠B =∠P AB +∠PCB∴180°-2∠P -∠B +∠D =∠B ,即∠P =90°+12∠B +∠D .(4)连接PB ,PD∵直线AP 平分∠BAD 的外角∠FAD ,CP 平分∠BCD 的外角∠BCE ,∴∠FAP =∠P AO ,∠PCE =∠PCB ,∵∠APB +∠PBA +∠P AB =180°,∠PCB +∠PBC +∠BPC =180°∴∠APC +∠ABC +∠PCB +∠P AB =360°同理得到:∠APC +∠ADC +∠PCD +∠P AD =360°∴2∠APC +∠ABC +∠ADC +∠PCB +∠P AB +∠PCD +∠P AD =720°∴2∠APC +∠ABC +∠ADC +∠PCE +∠P AB +∠PCD +∠P AF =720°∵∠PCE +∠PCD =180°,∠P AB +∠P AF =180°∴2∠APC +∠ABC +∠ADC =360°,∴∠APC =180°-12∠ABC +∠ADC 【点睛】本题主要考查了角平分线的定义,三角形内角和定理,解题的关键在于能够熟练掌握相关知识进行求解.9.如图,∠1=60°,则∠A +∠B +∠C +∠D +∠E +∠F =()A.240°B.280°C.360°D.540°【答案】A 【分析】根据三角形内角和定理得到∠B 与∠C 的和,然后在五星中求得∠1与另外四个角的和,加在一起即可.【详解】解:由三角形外角的性质得:∠3=∠A +∠E ,∠2=∠F +∠D ,∵∠1+∠2+∠3=180°,∠1=60°,∴∠2+∠3=120°,即:∠A+∠E+∠F+∠D=120°,∵∠B+∠C=120°,∴∠A+∠B+∠C+∠D+∠E+∠F=240°.故选A.【点睛】本题考查了三角形的外角和三角形的内角和的相关知识,解决本题的关键是将题目中的六个角分成两部分来分别求出来,然后再加在一起.10.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=.【答案】900°【分析】根据多边形的内角和,可得答案.【详解】解:连EF,GI,如图∵6边形ABCDEFK的内角和=(6-2)×180°=720°,∴∠A+∠B+∠C+∠D+∠E+∠F=720°-(∠1+∠2),即∠A+∠B+∠C+∠D+∠E+∠F+(∠1+∠2)=720°,∵∠1+∠2=∠3+∠4,∠5+∠6+∠H=180°,∴∠A+∠B+∠C+∠D+∠E+∠F∠H+(∠3+∠4)=900°,∴∠A+∠B+∠C+∠D+∠E+∠F(∠3+∠4)+∠5+∠6+∠H=720°+180°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=900°,故答案为:900°.【点睛】本题考查了n边形的内角和定理:n边形的内角和为(n-2)×180°(n≥3的整数).11.如图,已知AB∥CD,∠B=∠D,CD与AE相交于F.(1)求证:AD∥BC;(2)若∠B=50°,AE平分∠BAD,求∠DFE的度数.【答案】(1)见解析;(2)115°.【分析】本题考查平行线的判定和性质,与角平分线有关的计算:(1)AB∥CD,得到∠B=∠DCE,推出∠D=∠DCE,即可得证;(2)平行线的性质求出∠BAD的度数,角平分线求出∠DAE=65°,再利用三角形的外角求解即可.【详解】(1)证明:∵AB∥CD,∴∠B=∠DCE,∵∠B=∠D,∴∠D=∠DCE,∴AD∥BC,(2)∵AD∥BC,∴∠BAD=180°-∠B=180°-50°=130°,∵AE平分∠BAD,∴∠DAE=65°,∵∠D=∠B=50°,∴∠DFE=∠D+∠EAD=50°+65°=115°.12.已知:如图,FE∥OC,AC和BD相交于点O,F是OD上一点,且∠1=∠A.(1)求证:AB∥DC;(2)若∠B=30°,∠1=65°,求∠OFE的度数.【答案】(1)见解析(2)95°【分析】本题考查了平行线的性质和判定,三角形外角的性质的应用:(1)根据平行线的性质和已知得出∠A=∠C,根据平行线的判定推出即可;(2)根据平行线的性质求出∠D,根据三角形的外角性质推出即可.【详解】(1)证明:∵FE∥OC,∴∠1=∠C,∵∠1=∠A,∴∠A=∠C,∴AB∥DC;(2)解:∵AB∥DC,∴∠D=∠B,∵∠B=30°,∴∠D=30°,∵∠OFE是△DEF的外角,∴∠OFE=∠D+∠2,∵∠1=65°,∴∠OFE=30°+65°=95°.13.如图,BP平分∠ABC,交CD于点F,DP平分∠ADC交AB于点E,AB与CD相交于点G,∠A=42°.(1)若∠ADC=60°,求∠AEP的度数;(2)若∠C=38°,求∠P的度数.【答案】(1)72°;(2)40°.【分析】(1)根据角平分线的定义可得∠ADP=12∠ADC,然后利用三角形外角的性质即可得解;(2)根据角平分线的定义可得∠ADP=∠PDF,∠CBP=∠PBA,再根据三角形的内角和定理可得∠A+∠ADP=∠P+∠ABP,∠C+∠CBP=∠P+∠PDF,所以∠A+∠C=2∠P,即可得解.【详解】解:(1)∵DP平分∠ADC,∴∠ADP=∠PDF=12∠ADC,∵∠ADC=60°,∴∠ADP=30°,∴∠AEP=∠ADP+∠A=30°+42°=72°;(2)∵BP平分∠ABC,DP平分∠ADC,∴∠ADP=∠PDF,∠CBP=∠PBA,∵∠A+∠ADP=∠P+∠ABP,∠C+∠CBP=∠P+∠PDF,∴∠A+∠C=2∠P,∵∠A=42°,∠C=38°,∴∠P=12(38°+42°)=40°.【点睛】本题考查了三角形的内角和定理及三角形外角的性质,角平分线的定义,熟记定理并理解“8字形”的等式是解题的关键.【题型04:飞镖模型】图1图2图3【条件】四边形ABPC如图1所示【结论】∠BPC=∠A+∠B+∠C.14.探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图(1)观察“规形图(1)”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;(2)请你直接利用以上结论,解决以下问题:①如图(2),把一块三角尺XYZ放置在△AC上使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=40°,则∠ABX+∠ACX=50°.②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.【答案】见试题解答内容【解答】解:(1)如图(1),∠BDC=∠BAC+∠B+∠C,理由是:过点A、D作射线AF,∵∠FDC=∠DAC+∠C,∠BDF=∠B+∠BAD,∴∠FDC+∠BDF=∠DAC+∠BAD+∠C+∠B,即∠BDC=∠BAC+∠B+∠C;(2)①如图(2),∵∠X=90°,由(1)知:∠A+∠ABX+∠ACX=∠X=90°,∵∠A=40°,∴∠ABX+∠ACX=50°,故答案为:50;②如图(3),∵∠A=40°,∠DBE=130°,∴∠ADE+∠AEB=130°-40°=90°,∵DC平分∠ADB,EC平分∠AEB,∴∠ADC=12∠ADB,∠AEC=12∠AEB,∴∠ADC+∠AEC=12∠ADB+∠AEB=45°,∴∠DCE=∠A+∠ADC+∠AEC=40°+45°=85°.15.一个零件的形状如图,按要求∠A=90°,∠B=32°,∠C=21°,检验工人量得∠CDB=148°,就断定这个零件不合格,运用三角形的有关知识说明零件不合格的理由.【答案】见试题解答内容【解答】解:如图,延长CD交AB于E,∵∠A=90°,∠C=21°,∴∠1=∠A+∠C=90°+21°=111°,∵∠B=32°,∴∠BDC=∠B+∠1=32°+111°=143°.又∵∠BDC=148°,∴这个零件不合格.16.附加题:如图,试说明:①∠BDC>∠A;②∠BDC=∠B+∠C+∠A.如果点D在线段BC的另一侧,结论会怎样?【答案】见试题解答内容【解答】解:①延长BD交AC于E,则∠BDC>∠DEC,而∠DEC>∠A,所以∠BDC>∠A;②由∠BDC=∠C+∠DEC,而∠DEC=∠A+∠B,所以∠BDC=∠A+∠B+∠C.如果点D在线段BC的另一侧,如图所示:结论:①∠BDC与∠A无法比较大小;②∠BDC=360°-(∠A+∠B+∠C),17.如图,△ABC中,∠A=30°,D为CB延长线上的一点,DE⊥AB于点E,∠D=40°,则∠C为()A.20°B.15°C.30°D.25°【答案】A【解答】解:∵DE⊥AB,∴∠DEB=90°,∵∠D=40°,∴∠ABD=180°-∠D-∠DEB=50°,∵∠ABD=∠A+∠C,∠A=30°,∴∠C=∠ABD-∠A=50°-30°=20°.故选:A.18.如图,点E在BC上,ED⊥AC于F,交BA的延长线于D,已知∠D=30°,∠C=20°,则∠B的度数是()A.20°B.30°C.40°D.50°【答案】C【解答】解:∵ED⊥AC,∠D=30°,∠C=20°,又∵∠DEC=∠B+∠D,∴∠C+∠DEC=∠C+∠D+∠B=90°,∴∠B=40°.故选:C.19.如图,已知在△ABC中,∠A=40°,现将一块直角三角板放在△ABC上,使三角板的两条直角边分别经过点B,C,直角顶点D落在△ABC的内部,则∠ABD+∠ACD=( ).A.90°B.60°C.50°D.40°【答案】C【分析】由三角形内角和定理可得∠ABC+∠ACB+∠A=180°,即∠ABC+∠ACB=180-∠A=140°,再说明∠DBC+∠DCB=90°,进而完成解答.【详解】解:∵在△ABC中,∠A=40°∴∠ABC+∠ACB=180-∠A=140°∵在△DBC中,∠BDC=90°∴∠DBC+∠DCB=180°-90°=90°∴∠ABD+∠ACD=40°-90°=50°故选C.【点睛】本题主要考查三角形内角和定理,灵活运用三角形内角和定理成为解答本题的关键.20.如图,若∠EOC=115°,则∠A+∠B+∠C+∠D+∠E+∠F=.【答案】230°【分析】根据三角形外角的性质,得到∠EOC=∠E+∠2=115°,∠2=∠D+∠C,∠EOC=∠1+∠F=115°,∠1=∠A+∠B,即可得到结论.【详解】解:如图∵∠EOC=∠E+∠2=115°,∠2=∠D+∠C,∴∠E+∠D+∠C=115°,∵∠EOC=∠1+∠F=115°,∠1=∠A+∠B,∴∠A+∠B+∠F=115°,∴∠A+∠B+∠C+∠D+∠E+∠F=230°,故答案为:230°.【点睛】本题主要考查三角形内角和定理和三角形外角的性质,解决本题的关键是要熟练掌握三角形外角性质.【题型05:风筝模型】21.如图1和图2,在三角形纸片ABC中,点D,E分别在边AC,AB上,沿DE折叠,点A落在点A'的位置.(1)如图1,当点A′落在CD边上时,∠DAE与∠1之间的数量关系为③(只填序号),并说明理由;①∠DAE=∠1②∠DAE=2∠1③∠1=2∠DAE(2)如图2,当点A落在△ABC内部时,直接写出∠DAE与∠1,∠2之间的数量关系.【答案】(1)③,理由详见解答过程.(2)∠1+∠2=2∠DAE.【解答】解:(1)由题意得:∠DAE=∠DA′E.∵∠1=∠EAD+∠EA′D=2∠DAE.故答案为:③.(2)∠1+∠2=2∠DAE,理由如下:如图2,连接AA′.由题意知:∠EAD=∠EA′D.∵∠1=∠A′AE+∠AA′E,∠2=∠A′AD+∠AA′D,∴∠1+∠2=∠EAA′+∠A′AD+∠EA′A+∠AA′D=∠EAD+∠EA′D=2∠EAD.22.如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是()A.40°B.80°C.90°D.140°【答案】B【解答】解:由折叠的性质得:∠D=∠C=40°,根据外角性质得:∠1=∠3+∠C,∠3=∠2+∠D,则∠1=∠2+∠C+∠D=∠2+2∠C=∠2+80°,则∠1-∠2=80°.故选:B.23.将纸片△ABC沿DE折叠使点A落在A′处的位置.(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是2∠A=∠2.(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.【答案】见试题解答内容【解答】解:(1)图1中,2∠A=∠1+∠2,理由是:∵延DE折叠A和A′重合,∴∠AED=∠A′ED,∠ADE=∠A′DE,∵∠AED+∠ADE=180°-∠A,∠1+∠2=180°+180°-2(∠AED+∠ADE),∴∠1+∠2=360°-2(180°-∠A)=2∠A;(2)2∠A=∠2,如图∠2=∠A+∠EA′D=2∠A,故答案为:2∠A=∠2;(3)如图2,2∠A=∠2-∠1,理由是:∵延DE折叠A和A′重合,∴∠A=∠A′,∵∠DME=∠A′+∠1,∠2=∠A+∠DME,∴∠2=∠A+∠A′+∠1,即2∠A=∠2-∠1.【题型06:两内角角平分线模型】双内角平分线模型【条件】BP 、CP 分别为∠ABC 、∠ACB 的角平分线.【结论】∠P =90°+12∠A .24.如图1,点A 、B 分别在射线OM 、ON 上运动(不与点O 重合),AC 、BC 分别是∠BAO 和∠ABO 的角平分线,BC 延长线交OM 于点G .(1)若∠MON =60°,则∠ACG =;(直接写出答案)(2)若∠MON =n °,求出∠ACG 的度数;(用含n 的代数式表示)(3)如图2,若∠MON =80°,过点C 作CF ∥OA 交AB 于点F ,求∠BGO 与∠ACF 的数量关系.【答案】(1)60°;(2)90°-12n °;(3)∠BGO -∠ACF =50°【分析】(1)根据三角形内角和定理求出∠BAO +∠ABO ,根据角平分线的定义、三角形的外角性质计算,得到答案;(2)仿照(1)的解法解答;(3)根据平行线的性质得到∠ACF =∠CAG ,根据(2)的结论解答.【详解】解:(1)∵∠MON =60°,∴∠BAO +∠ABO =120°,∵AC 、BC 分别是∠BAO 和∠ABO 的角平分线,∴∠CBA =12∠ABO ,∠CAB =12∠BAO ,∴∠CBA +∠CAB =12(∠ABO +∠BAO )=60°,∴∠ACG =∠CBA +∠CAB =60°,故答案为:60°;(2)∵∠MON =n °,∴∠BAO +∠ABO =180°-n °,∵AC 、BC 分别是∠BAO 和∠ABO 的角平分线,∴∠CBA =12∠ABO ,∠CAB =12∠BAO ,∴∠CBA+∠CAB=12(∠ABO+∠BAO)=90°-12n°,∴∠ACG=∠CBA+∠CAB=90°-12n°;(3)∵CF∥OA,∴∠ACF=∠CAG,∴∠BGO-∠ACF=∠BGO-∠CAG=∠ACG,由(2)得:∠ACG=90°-12×80°=50°.∴∠BGO-∠ACF=50°.【点睛】本题考查的是角平分线的定义、平行线的性质、三角形的外角性质,掌握两直线平行、内错角相等是解题的关键.25.如图,BE平分∠ABD,CF平分∠ACD,BE与CF交于点G,若∠BDC=140°,∠BGC=100°,则∠A=()A.80°B.75°C.60°D.45°【答案】C【分析】连接BC,先求解∠DBC+∠DCB,再求解∠GBC+∠GCB,可得∠GBD+∠GCD,再利用角平分线的定义可得:∠ABD+∠ACD,从而可得:∠ABC+∠ACB,再利用三角形的内角和定理可得∠A的大小.【详解】解:连接BC,∵∠BDC=140°,∴∠DBC+∠DCB=180°-140°=40°,∵∠BGC=100°,∴∠GBC+∠GCB=180°-100°=80°,∴∠GBD+∠GCD=∠GBC+∠GCB-∠DBC-∠DCB=40°,∵BE平分∠ABD,CF平分∠ACD,∴∠ABD+∠ACD=2(∠GBD+∠GCD)=80°,∴∠ABC+∠ACB=∠ABD+∠ACD+∠DBC+∠DCB=80°+40°=120°,∴∠A=180°-(∠ABC+∠ACB)=60°.故选:C.【点睛】本题考查的是三角形的内角和定理的应用,角平分线的定义,熟练利用三角形的内角和定理求解与之相关的角的大小是解题的关键.26.如图,在△ABC中,已知∠A=70°,∠ABC、∠ACB的平分线OB、OC相交于点O,则∠BOC的度数为.【答案】125°【分析】根据三角形的内角和定理求出∠ABC +∠ACB ,再根据角平分线的定义求出∠OBC +∠OCB ,然后利用三角形的内角和定理列式计算即可得解.【详解】在△ABC 中,∠ABC +∠ACB =180°-∠A =180°-70°=110°,∵∠ABC 与∠ACB 的角平分线BO ,CO 相交于点O ,∴∠OBC +∠OCB =12∠ABC +∠ACB =12×110°=55°,在△BOC 中,∠BOC =180°-(∠OBC +∠OCB )=180°-55°=125°,故答案为:125°.【点睛】本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.27.如图,在△ABC 中,∠ABC 和∠ACB 的平分线相交于点P .(1)若∠ABC +∠ACB =130°,求∠BPC 的度数.(2)当∠A 为多少度时,∠BPC =3∠A ?【答案】(1)115°;(2)∠A =36°【分析】(1)根据角平分线的定义,求得∠PBC ,∠PCB ,再根据三角形内角和定理即可求得∠BPC ;(2)根据(1)的方法求得∠BPC ,再结合条件∠BPC =3∠A ,解方程即可求得∠A .【详解】(1)∵PB 平分∠ABC ,PC 平分∠ACB ,∴∠PBC =12∠ABC ,∠PCB =12∠ACB ,∵∠ABC +∠ACB =130°,∴∠PBC +∠PCB =12(∠ABC +∠ACB )=65°,∴∠BPC =180°-(∠PBC +∠PCB )=180°-65°=115°,(2)∵PB 平分∠ABC ,PC 平分∠ACB ,∴∠PBC =12∠ABC ,∠PCB =12∠ACB ,∴∠PBC+∠PCB=12(∠ABC+∠ACB),∵∠ABC+∠ACB=180°-∠A,∴∠PBC+∠PCB=90°-12∠A,∠BPC=180°-(∠PBC+∠PCB)=180°-90°-12∠A=90°+12∠A∵∠BPC=3∠A∴3∠A=90°+12∠A,∴∠A=36°.【点睛】本题考查了与角平分线有关的角度计算,三角形内角和定理,掌握三角形内角和定理是解题的关键.【题型07:两外角角平分线模型】双外角平分线模型【条件】BP、CP分别为∠EBC、∠BCF的角平分线.【结论】∠P=90°-12∠A.28.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=70°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q,∠A之间的数量关系.(3)如图③,延长线段BP,QC交于点E,在△BQE中,存在一个内角等于另一个内角的3倍,求∠A的度数.【答案】(1)125°(2)∠Q=90°-12∠A(3)∠A的度数是45°或60°或120°或135°【分析】(1)在△ABC中,根据三角形内角和定理求出∠ABC+∠ACB=110°,根据角平分线的定义得出∠PBC=12∠ABC,∠PCB=12∠ACB,求出∠PBC+∠PCB=55°,再在△BPC中,根据三角形内角和定理求出即可;(2)根据三角形外角性质得出∠MBC=∠ACB+∠A,∠NCB=∠ABC+∠A,求出∠MBC+∠NCB=∠ACB+∠A+∠ABC+∠A=180°+∠A,根据角平分线的定义得出QBC=12∠MBC,∠QCB=12∠NCB,求出∠QBC+∠QCB=90°+12∠A,根据三角形内角和定理求出即可;(3)根据角平分线的定义得出∠ACF=2∠BCF,∠ABC=2∠EBC,根据三角形外角性质得出∠ECF=∠EBC+∠E,求出∠A=2∠E,求出∠EBQ=90°,分为四种情况:①∠EBQ=3∠E=90°,②∠EBQ=3∠Q,③∠Q=3∠E,④∠E=3∠Q,再求出答案即可【详解】(1)∵∠A=70°,∴∠ABC+∠ACB=180°-∠A=110°,∵点P是∠ABC和∠ACB的角平分线的交点,∴∠PBC=12∠ABC,∠PCB=12∠ACB,∴∠PBC+∠PCB=55°,∴∠BPC=180°-(∠PBC+∠PCB)=125°;(2)∵∠MBC=∠ACB+∠A,∠NCB=∠ABC+∠A,∴∠MBC+∠NCB=∠ACB+∠A+∠ABC+∠A=180°+∠A,∵点Q是∠MBC和∠NCB的角平分线的交点,∴∠QBC=12∠MBC,∠QCB=12∠NCB,∴∠QBC+∠QCB=12(∠MBC+∠NCB)=12(180°+∠A)=90°+12∠A,∴∠Q=180°-(∠QBC+∠QCB)=180°-90°+12∠A=90°-12∠A;(3)∵CQ为△ABC的外角∠NCB的角平分线,∴CE是△ABC的外角∠ACF的平分线,∴∠ACF=2∠BCF,∵BE平分∠ABC,∴∠ABC=2∠EBC,∵∠ECF=∠EBC+∠E,∴2∠ECF=2∠EBC+2∠E,即∠ACF=∠BC+2∠E,∵∠ACF=∠ABC+∠A,∴∠A=2∠E,即∠E=12∠A,∵∠EBQ=∠EBC+∠CBQ=12∠ABC+12∠MBC=12(∠ABC+∠A+∠ACB) =90°,如果△BQE中,存在一个内角等于另一个内角的3倍,那么分为四种情况:①∠EBQ=3∠E=90°,则∠E=30°,∠A=2∠E=60°;②∠EBQ=3∠Q,则∠Q=30°,∠E=60°,∠A=2∠E=120°;③∠Q=3∠E,则∠E=22.5°,∠A=2∠E=45°;④∠E=3∠Q,则∠E=67.5°,∠A=2∠E=135°,综合上述,∠A的度数是45°或60°或120°或135°.【点睛】本题考查了三角形的外角性质,三角形内角和定理,角平分线的定义等知识点,熟练掌握知识点及运用分类讨论思想是解题的关键.29.如图,在△ABC中,∠B=58°,三角形两外角的角平分线交于点E,则∠AEC=.【答案】61°【分析】先根据三角形的内角和定理和平角定义求得∠DAC+∠ACF的度数,再根据角平分线的定义求得∠EAC+∠ECA的度数,即可解答.【详解】解:∵∠B+∠BAC+∠BCA=180°,∠B=58°,∴∠BAC+∠BCA=180°-∠B=180°-58°=122°,∵∠BAC+∠DAC=180°,∠BCA+∠ACF=180°,∴∠DAC+∠ACF=360°-(∠BAC+∠BCA)=360°-122°=238°,∵AE平分∠DAC,CE平分∠ACF,∴∠EAC=12∠DAC,∠ECA=12∠ACF,∴∠EAC+∠ECA=12(∠DAC+∠ACF)=119°,∵∠EAC+∠ECA+∠AEC=180°,∴∠AEC=180°-(∠EAC+∠ECA)=180°-119°=61°,故答案为:61°.【点睛】本题考查三角形的内角和定理、角平分线的定义、平角定义,熟练掌握三角形的内角和定理和角平分线的定义是解答的关键.30.如图,△ABC两个外角∠CBD、∠BCE的平分线相交于点O,∠A=40°,求∠BOC的度数.【答案】见试题解答内容【解答】解:∵∠CBD、∠BCE的平分线相交于点O,∴∠OBC=12(∠A+∠ACB),∠OCB=12(∠A+∠ABC),∴∠OBC +∠OCB =12(∠A +∠ACB +∠ABC +∠A ),∵∠A +∠ACB +∠ABC =180°,∴∠OBC +∠OCB =90°+12∠A ,在△OBC 中,∠BOC =180°-(∠OBC +∠OCB )=180°-(90°+12∠A )=90°-12∠A ,∵∠A =40°,∴∠BOC =90°-12×40°=90°-20°=70°.【题型08:内外角平分线模型】内外角平分线模型【条件】BP 、CP 分别为∠ABC 、∠ACE 的角平分线【结论】∠P =12∠A 【典例8】(1)如图1,在△ABC 中,BP 平分∠ABC ,CP 平分∠ACB ,求证:∠P =90°+12∠A ;(2)如图2,在△ABC 中,BP 平分∠ABC ,CP 平分外角∠ACE ,猜想∠P 和∠A 有何数量关系,并证明你的结论.【答案】(1)证明过程见解答;(2)∠P =12∠A .【解答】(1)证明:∵A +∠ABC +∠ACB =180°,∴∠ABC +∠ACB =180°-∠A ,∵BP 平分∠ABC ,CP 平分∠ACB ,∴∠PCB =12∠ACB ,∠PBC =12∠ABC ,∴∠P =180°-(∠PCB +∠PBC )=180°-12(∠ACB +∠ABC )=180°-12(180°-∠A )=90°+12∠A ;(2)猜想:∠P=12∠A证明:∵∠ACE=∠A+∠ABC,∴∠A=∠ACE-∠ABC,∵∠PCE=∠P+∠PBC,∴∠P=∠PCE-∠PBC,又∵BP平分∠ABC,CP平分∠ACE,∴∠PBC=12∠ABC,∠PCE=12∠ACE,∴∠P=12∠ACE-12∠ABC=12(∠ACE-∠ABC)=12∠A.31.如图,在△ABC中,BO、CO分别平分∠ABC,∠ACB,BO的延长线交外角∠ACD的角平分线于点E.以下结论:①∠1=2∠2;②∠BOC=3∠2;③∠BOC=90°+∠2;④∠BOC=90°+∠1.其中正确的结论有(填序号).【答案】①③/③①【分析】依据角平分线的性质以及三角形外角性质,即可得到∠1=2∠2,∠BOC=90°+12∠1,∠BOC=90°+∠2,即可得出答案.【详解】解:∵CE为外角∠ACD的平分线,BE平分∠ABC,∴∠DCE=12∠ACD,∠DBE=12∠ABC,又∵∠DCE是△BCE的外角,∴∠2=∠DCE-∠DBE=12∠ACD-∠ABC=12∠1,即∠1=2∠2,故①正确;∵BO、CO分别平分∠ABC,∠ACB,∴∠OBC=12∠ABC,∠OCB=12∠ACB,∴∠BOC=180°-∠OBC+∠OCB=180°-12∠ABC+∠ACB=180°-12180°-∠1=90°+12∠1,故④错误;∵CO平分∠ACB,CE平分∠ACD,∴∠ACO=12∠ACB,∠ACE=12ACD,∴∠OCE =12∠ACB +∠ACD =12×180°=90°,∵∠BOC 是△COE 的外角,∴∠BOC =∠OCE +∠2=90°+∠2,故②错误、③正确;综上,正确的有①③.故答案为:①③.【点睛】本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,以及角平分线的定义.32.如图,在△ABC 中,∠A =α,∠ABC 与∠ACD 的平分线交于点A 1,得∠A 1;∠A 1BC 与∠A 1CD 的平分线相交于点A 2,得A 2;⋯;∠A 2019BC 与∠A 2019CD 的平分线相交于点A 2020,得∠A 2020,则∠A 2020=.【答案】α22020【分析】结合题意,根据角平分线、三角形外角、三角形内角和的性质,得∠A 1=12∠A ,同理得∠A 2=12∠A 1=α22;再根据数字规律的性质分析,即可得到答案.【详解】根据题意,∠A =α,∠ABC 与∠ACD 的平分线交于点A 1∴∠A 1=180°-12∠ABC -∠ACB -12∠ACD ∵∠ACD =∠A +∠ABC∴∠A 1=180°-∠ABC -∠ACB -12∠A ∵∠A +∠ABC +∠ACB =180°∴∠A 1=12∠A 同理,得∠A 2=12∠A 1=12×12∠A =α22;∠A 3=12∠A 2=12×12×12∠A =α23;∠A 4=12∠A 3=12×12×12×12∠A =α24;⋯∠A n =12∠A n -1=α2n ∴∠A 2020=α22020故答案为:α22020.【点睛】本题考查了三角形和数字规律的知识;解题的关键是熟练掌握三角形内角和、三角形外角、角平分线、数字规律的性质,从而完成求解.33.【初步认识】(1)如图1,BM 平分∠ABC ,CM 平分外角∠ACD ,若∠A =80°,则∠M =°.【变式探究】(2)已知ABCD 为四边形,E 为边AB 延长线上一点,如图2,∠ADC =110°,∠BCD =120°,∠DAB 和∠CBE 的平分线交于点F ,则∠F =°.【继续探索】(3)已知ABCD 为四边形,E 为边AB 延长线上一点,如图3,∠ADC =α,∠BCD =β,且α+β>180°,∠DAB 和∠CBE 的平分线交于点F ,求∠F 与α、β之间的数量关系,并说明理由;【终极挑战】(4)如果将(3)中的条件α+β>180°改为α+β<180°,再分别作∠DAB 和∠CBE 的平分线,且两平分线所在的直线交于点F ,那么∠F 与α、β又有怎样的数量关系?请直接写出结论.(不用说明理由)【答案】(1)40;(2)25;(3)∠F =12α+12β-90°,理由见解析;(4)∠F =90°-12α-12β【分析】本题考查了角平分线的定义,三角形外角的性质,三角形内角和定理等知识,解题的关键是:(1)利用角平分线定义和三角形外交的性质可探究出∠M =12∠A ,即可求解;(2)延长AD 、BC 相交于G ,先求出∠G 的度数,然后同(1)得出∠F =12∠G ,即可求解;(3)类似(2)探究即可;(4)延长DA ,CB 相交于G ,延长BA ,先求出∠G =180°-α-β,再判断AF 平分∠NAG ,FB 平分∠ABG ,然后同(1)得出∠F =12∠G ,即可求解.【详解】解:∵BM 平分∠ABC ,CM 平分外角∠ACD ,∴∠MBC =12∠ABC ,∠MCD =12∠ACD ,∵∠A =∠ACD -∠ABC ,∠M =∠MCD -∠MBD ,∴∠M =12∠ACD -12∠ABC =12∠A ,∵∠A =80°,∴∠M =40°,故答案为:40;(2)延长AD 、BC 相交于G ,∵∠ADC =110°,∠BCD =120°,∴∠GDC =70°,∠GCD =60°,∴∠G =50°,同(1)可证∠F =12∠G ,∴∠F =25°,故答案为:25;(3)∠F =12α+12β-90°理由:延长AD 、BC 相交于G ,∵∠ADC =α,∠BCD =β,。
专题9.6 角度计算中的经典模型【八大题型】(华东师大版)(解析版)

专题9.6角度计算中的经典模型【八大题型】【华东师大版】【题型1双垂直模型】 (1)【题型2A字模型】 (6)【题型38字模型】 (10)【题型4飞镖模型】 (16)【题型5风筝模型】 (23)【题型6两内角角平分线模型】 (29)【题型7两外角角平分线模型】 (35)【题型8内外角角平分线模型】 (39)【知识点1双垂直模型】【条件】∠B=∠D=∠ACE=90°.【结论】∠BAC=∠DCE,∠ACB=∠CED.【证明】∵∠B=∠D=∠ACE=90°;∴∠BAC+∠ACB=90°;又∠ECD+∠ACB=90°;∴∠BAC=∠DCE同理,∠ACB+∠DCE=90°,且∠CED+∠DCE=90°;∴∠ACB=∠CED,得证.【题型1双垂直模型】【例1】(2022春•建邺区期末)如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.(1)求证:CD⊥AB证明:在Rt△ABC中,∵∠ACB=90°(已知)∴∠A+∠B=90°(直角三角形两锐角互余)又∵∠ACD=∠B(已知)∴∠A+∠ACD=90°(等量代换)∴∠ADC =90°(三角形内角和定理)∴CD ⊥AB .(2)如图②,若∠BAC 的平分线分别交BC ,CD 于点E ,F ,求证:∠AEC =∠CFE ;(3)如图③,若E 为BC 上一点,AE 交CD 于点F ,BC =3CE ,AB =4AD ,S △ABC =36.①求S △CEF ﹣S △ADF 的值;②四边形BDFE 的面积是21.【分析】(1)根据直角三角形的性质、三角形内角和定理解答即可;(2)根据角平分线的定义得到∠CAE =∠BAE ,根据三角形的外角性质计算,证明结论;(3)①根据三角形的面积公式分别求出S △ACD 、S △ACE ,结合图形计算即可;②连接BF ,设S △ADF =x ,根据三角形的面积公式列出方程,求出x ,把x 代入计算得到答案.【解答】(1)证明:在Rt △ABC 中,∵∠ACB =90°(已知)∴∠A +∠B =90°(直角三角形两锐角互余)又∵∠ACD =∠B (已知)∴∠A +∠ACD =90°(等量代换)∴∠ADC =90°(三角形内角和定理),∴CD ⊥AB .故答案为:直角三角形两锐角互余;三角形内角和定理;(2)证明:∵AE 平分∠BAC ,∴∠CAE =∠BAE ,∵∠AEC =∠BAE +∠B ,∠CFE =∠ACD +∠CAE ,∴∠AEC =∠CFE ;(3)解:①∵BC =3CE ,AB =4AD ,S △ABC =36,∴S △ACD =14S △ABC =9,S △ACE =13S △ABC =12,∴S △CEF ﹣S △ADF =S △ACE ﹣S △ACD =12﹣9=3;②连接BF ,设S △ADF =x ,则S △CFE =3+x ,∵AB=4AD,=3x,∴S△BDF∵BC=3CE,=2(x+3)=2x+6,∴S△BEF∴x+3+2x+6+3x=34×36,解得,x=3,∴四边形BDFE的面积=3x+2x+6=21,故答案为:21.【变式1-1】(2022春•润州区期末)已知△ABC中,∠ABC=90°,BD是AC边上的高,AE平分∠BAC,分别交BC、BD于点E、F.求证:∠BFE=∠BEF.【分析】根据角平分线的定义可得∠BAE=∠CAE,再根据等角的余角相等求出∠BEF=∠AFD,然后根据对顶角相等可得∠BFE=∠AFD,等量代换即可得解.【解答】证明:∵AE平分∠BAC,∴∠BAE=∠CAE,∵BD⊥AC,∠ABC=90°,∴∠BAE+∠BEF=∠CAE+∠AFD=90°,∴∠BEF=∠AFD,∵∠BFE=∠AFD(对顶角相等),∴∠BEF=∠BFE【变式1-2】(2022•绥棱县校级期中)(1)如图①,△ABC是锐角三角形,高BD、CE相交于点H,找出∠BHC和∠A之间存在何种等量关系;(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD、CE所在的直线相交于点H,把图②补充完整,并指出此时(1)中的等量关系是否仍然成立?【分析】(1)根据对顶角的性质,可得∠BHC与∠EHD的关系,根据四边形的内角和定理,可得答案;(2)根据对顶角的性质,可得∠BHC与∠EHD的关系,根据四边形的内角和定理,可得答案.【解答】解:(1)由∠BHC与∠EHD是对顶角,得∠BHC=∠EHD.由高BD、CE相交于点H,得∠ADH=∠AEH=90°.由四边形内角和定理,得∠A+∠AEH+∠EHD+∠HDA=360°,∠A+∠EHD=360°﹣∠AEH﹣∠HDA=360°﹣90°﹣90°=180°,∴∠BHC+∠A=180°;(2)如图,由∠BHC与∠EHD是对顶角,得∠BHC=∠EHD.由高BD、CE相交于点H,得∠ADH=∠AEH=90°.由四边形内角和定理,得∠H+∠AEH+∠EAD+∠HDA=360°,∠H+∠DAE=360°﹣∠AEH﹣∠HDA=360°﹣90°﹣90°=180°,∴∠BHC+∠BAC=180°.【变式1-3】(2022春•香洲区期末)如图1,线段AB⊥BC于点B,CD⊥BC于点C,点E在线段BC上,且AE⊥DE.(1)求证:∠EAB=∠CED;(2)如图2,AF、DF分别平分∠BAE和∠CDE,EH平分∠DEC交CD于点H,EH的反向延长线交AF于点G.①求证EG⊥AF;②求∠F的度数.【提示:三角形内角和等于180度】【分析】(1)利用同角的余角相等即可证明;(2)①想办法证明∠EAG+∠AEG=90°即可解决问题;②利用∠DFA=∠DFM+∠AFM=12∠CDE+12∠EAB=12(∠CDE+∠EAB)即可解决问题;【解答】解:(1)∵AB⊥BC,∴∠EAB+∠AEB=90°,∵AE⊥ED,∴∠CED+∠AEB=90°,∴∠EAB=∠CED.(2)①∵AF平分∠BAE,∴∠EAG=12∠EAB,∵EH平分∠CED,∴∠HED=12∠CED,∵∠EAB=∠CED,∴∠HED=∠EAG,∴∠HED+∠AEG=90°,∴∠EAG+∠AEG=90°,∴∠EGA=90°,∴EG⊥AF.②作FM∥CD.∵AB⊥BC,CD⊥BC,∴AB∥CD,∴FM∥AB,∴∠DFM=∠CDF=12∠CDE,∠AFM=∠FAB=12∠EAB,∵∠CDE+∠CED=90°,∴∠CDE+∠EAB=90°,∴∠DFA=∠DFM+∠AFM=12∠CDE+12∠EAB=12(∠CDE+∠EAB)=45°.【知识点2A字模型】【条件】△ADE与△ABC.【结论】∠AED+∠ADE=∠B+C.【证明】根据三角形内角和可得,∠AED+∠ADE=180°-∠A,∠B+C=180°-∠A,∴∠AED+∠ADE=∠B+C,得证.【题型2A字模型】【例2】(2022•江阴市校级月考)如图是某建筑工地上的人字架.这个人字架夹角∠1=120°,那么∠3﹣∠2的度数为60°.【分析】根据平角的定义求出∠4,再利用三角形的外角的性质即可解决问题;【解答】解:如图∵∠1+∠4=180°,∠1=120°,∴∠4=60°,∵∠3=∠2+∠4,∴∠3﹣∠2=∠4=60°,故答案为60°.【变式2-1】(2022春•道里区期末)如图,△ABC中∠A=115°,若图中沿虚线剪去∠A,则∠1+∠2等于()A.180°B.230°C.290°D.295°【分析】根据题意由三角形内角和可得出∠B+∠C=65°,再根据四边形的内角和可求出∠1+∠2.【解答】解:∵∠A=115°,∴∠B+∠C=65°,∵∠1+∠2+∠B+∠C=360°,∴∠1+∠2=360°﹣65°=295°.故选:D.【变式2-2】(2022武功县期末)如图,点D、E分别在△ABC的边AB、AC上,连接DC、DE,在CD上取一点F,连接EF,若∠1+∠2=180°,∠3=∠B,求证:DE∥BC.【分析】先利用平行线的判定定理判定AB∥EF,利用平行线的性质定理得到∠3=∠ADE,利用等量代换得到∠B=∠ADE,最后利用同位角相等,两直线平行判定即可.【解答】证明:∵∠1+∠DFE=180°,∠1+∠2=180°,∴∠2=∠DFE.∴AB∥EF.∴∠3=∠ADE.∵∠3=∠B,∴∠B=∠ADE.∴DE∥BC.故答案为:240°.【变式2-3】(2022春•新野县期末)旧知新意:我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?尝试探究:(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?初步应用:(2)如图2,在△ABC纸片中剪去△CDE,得到四边形ABDE,∠1=130°,则∠2﹣∠C=50°;(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案∠P=90°−12∠A.拓展提升:(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由.)【分析】(1)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠DBC+∠ECB,再利用三角形内角和定理整理即可得解;(2)根据(1)的结论整理计算即可得解;(3)表示出∠DBC+∠ECB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形内角和定理列式整理即可得解;(4)延长BA、CD相交于点Q,先用∠Q表示出∠P,再用(1)的结论整理即可得解.【解答】解:(1)∠DBC+∠ECB=180°﹣∠ABC+180°﹣∠ACB=360°﹣(∠ABC+∠ACB)=360°﹣(180°﹣∠A)=180°+∠A;(2)∵∠1+∠2=∠180°+∠C,∴130°+∠2=180°+∠C,∴∠2﹣∠C=50°;(3)∠DBC+∠ECB=180°+∠A,∵BP、CP分别平分外角∠DBC、∠ECB,∴∠PBC+∠PCB=12(∠DBC+∠ECB)=12(180°+∠A),在△PBC中,∠P=180°−12(180°+∠A)=90°−12∠A;即∠P=90°−12∠A;故答案为:50°,∠P=90°−12∠A;(4)延长BA、CD于Q,则∠P=90°−12∠Q,∴∠Q=180°﹣2∠P,∴∠BAD+∠CDA=180°+∠Q,=180°+180°﹣2∠P,=360°﹣2∠P.【知识点38字模型】【条件】AD、BC相交于点O.【结论】∠A+∠B=∠C+∠D.(上面两角之和等于下面两角之和)【证明】在△ABO中,由内角和定理:∠A+∠B+∠BOA=180°,在△CDO中,∠C+∠D+∠COD=180°,∴∠A+∠B+∠BOA=180°=∠C+∠D+∠COD,由对顶角相等:∠BOA=∠COD∴∠A+∠B=∠C+∠D,得证.【题型38字模型】【例3】(2022春•叙州区期末)如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,若∠A =45°,∠P=40°,则∠C的度数为()A.30°B.35°C.40°D.45°【分析】根据三角形内角和定理,得∠A+∠ADG=∠C+∠GBC,∠A+∠ADE=∠P+∠PBE.根据角平分线的定义,得到∠GBC=2∠PBE,∠ADG=2∠ADE,进而推断出∠A+∠C=2∠P,从而解决此题.【解答】解:∵∠A+∠ADG+∠AGD=180°,∠ABC+∠C+∠BGC=180°,∴∠A+∠ADG+∠AGD=∠ABC+∠C+∠BGC.又∵∠AGD=∠BGC,∴∠A+∠ADG=∠C+∠GBC.∴∠A﹣∠C=∠GBC﹣∠ADG.同理可得,∠A+∠ADE=∠P+∠PBE.∴∠A﹣∠P=∠PBE﹣∠ADE.∵BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,∴∠GBC=2∠PBE,∠ADG=2∠ADE.∴∠A﹣∠C=2(∠A﹣∠P).∴∠A+∠C=2∠P.又∵∠A=45°,∠P=40°,∴∠C=35°.故选:B.【变式3-1】(2022春•靖江市校级月考)已知,如图,线段AD、CB相交于点O,连结AB、CD,∠DAB 和∠BCD的平分线AP和CP相交于点P.试问∠P与∠D、∠B之间存在着怎样的数量关系,请说明理由.【分析】根据“8字形”可得∠OAB+∠B=∠OCD+∠D,∠1+∠P=∠2+∠D,由角平分线的定义可得∠OAB=2∠1,∠OCD=2∠2,整理可得结论.【解答】解:2∠P=∠B+∠D,理由如下:如图,在△AOB和△COD中,∵∠AOB=∠COD,∴∠OAB+∠B=∠OCD+∠D,在△AEP和△CED中,∵∠AEP=∠CED,∴∠1+∠P=∠2+∠D,∵AP、CP分别是∠DAB和∠BCD的角平分线,∴∠OAB=2∠1,∠OCD=2∠2,∴2∠P﹣∠B=2∠D﹣∠D,整理得,2∠P=∠B+∠D.【变式3-2】(2022春•新野县期末)在学习并掌握了平行线的性质和判定内容后,数学老师安排了自主探究内容一利用平行线有关知识探究并证明:三角形的内角和等于180°.小颖通过探究发现:可以将三角形的三个内角之和转化为一个平角来解决,也就是可以过三角形的一个顶点作其对边的平行线来证明.请将下面(1)中的证明补充完整(1)已知:如图1,三角形ABC,求证:∠BAC+∠B+∠C=180°,证明:过点A作EF∥BC.(2)如图2,线段AB、CD相交于点O,连接AD、CB,我们把形如图2这样的图形称之为“8字形”.请利用小颖探究的结论直接写出∠A、∠B、∠C、∠D之间的数量关系:∠A+∠D=∠C+∠B;(3)在图2的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,得到图3,请判断∠P与∠D、∠B之间存在的数量关系,并说明理由.【分析】(1)通过作平行线把三角形的内角转移到同一个顶点,然后利用平角的定义解决问题;(2)利用(1)的结论即可求解;(3)利用(2)的结论即可求解.【解答】(1)证明:过A作EF∥BC,∴∠EAB=∠B,∠FAC=∠C,又∠EAB+∠BAC+∠FAC=180°,∴∠B+∠C+∠BAC=180°;(2)解:根据(1)得∠A+∠D+∠AOD=∠C+∠B+∠COB=180°,又∠AOD=∠BOC,∴∠A+∠D=∠C+∠B;故答案为:∠A+∠D=∠C+∠B;(3)解:2∠P=∠D+∠B.根据(2)∠D+∠DAP=∠P+∠DCP①,∠PAB+∠P=∠B+∠PCB②,∵∠DAB和∠BCD的平分线AP和CP相交于点P,∴∠DAP=∠PAB,∠DCP=∠PCB,∴①﹣②得:∠D﹣∠P=∠P﹣∠B,∴2∠P=∠D+∠B.【变式3-3】(2022春•石家庄期中)如图1至图2,在△ABC中,∠BAC=α°,点D在边AC所在直线上,作DE垂直于直线BC,垂足为点E;BM为△ABC的角平分线,∠ADE的平分线交直线BC于点G.特例感悟:(1)如图1,延长AB交DG于点F,若BM∥DG,∠F=30°.解决问题:①∠ABC=60°;②求证:AC⊥AB;深入探究;(2)如图2,当α<90,DG与BM反向延长线交于点H,用含α的代数式表示∠BHD=45°−12;拓展延伸:(3)当点D在直线AC上移动时,若射线DG与射线BM相交,设交点为N,直接写出∠BND与α的关系式.【分析】(1)①根据平行线的性质和角平分线的定义可得答案;②根据平行线的性质得∠DGC=∠CBM =30°,再根据垂直的定义和角平分线的定义可得结论;(2)由八字模型可得,△BHG和△DEG中,∠BHD=∠EDG+90°﹣∠HBG,再整理可得答案;(3)分情况讨论,分别画出对应图形,再整理即可.【解答】解:(1)①∵BM∥DG,∴∠ABM=∠F=30°,∵BM为△ABC的角平分线,∴∠ABC=2∠ABM=60°,故答案为:60°;②证明:由①得,∠CBM=∠ABM=30°,∵BM∥DG,∴∠DGC=∠CBM=30°,∵DE⊥BC,∴∠EDG=60°,∵DG平分∠ADE,∴∠ADF=60°,∴∠A=180°﹣30°﹣60°=90°,∴AC⊥AB;(2)由八字模型可得,△BHG和△DEG中,∠BHD=∠EDG+90°﹣∠HBG=12∠ADE+90°﹣(180°−12∠ABC)=12(∠ADE+∠ABC)﹣90°=45°−12.故答案为:45°−12;(3)①如图,由八字模型可得,△ABM和△NMD中,∠BND=∠ABN+∠A﹣∠MDN=12∠ABC+α−12(90°﹣∠ACB)=12(∠ABC+∠ACB)+α﹣45°=45°+12;②如图,由四边形的内角和得,∠BND=360°﹣90°−12∠ABC−12∠ADE=270°−12(270°﹣α)=135°+12;③如图,由八字模型可得,∠BND+∠ABM=∠ADG+∠DAB,∴∠BND=12∠ADE+(180°﹣α)−12∠ABC=12(90°﹣∠ACB)+(180°﹣α)−12∠ABC=135°−12;综上,∠BND=45°+12或135°±12.【知识点4飞镖模型】【条件】四边形ABDC如上左图所示.【结论】∠D=∠A+∠B+∠C.(凹四边形凹外角等于三个内角和)【证明】如上右图,连接AD并延长到E,则:∠BDC=∠BDE+∠CDE=(∠B+∠1)+(∠2+∠C)=∠B+∠BAC+∠C.本质为两个三角形外角和定理证明.【题型4飞镖模型】【例4】(2022春•三明期末)探究与思考:(1)如图①,∠BPC是△ABP的一个外角,则有结论:∠BPC=∠A+∠B成立.若点P沿着线段PB向点B运动(不与点B重合),连接PC形成图形②,我们称之为“飞镖”图形,那么请你猜想“飞镖”图形中∠BPC与∠A、∠B、∠C之间存在的数量关系?并证明你的猜想;(2)利用(1)的结论,请你求出五角星(如图③)中∠A+∠B+∠C+∠D+∠E的值,说明你的理由;(3)若五角星中的点B向右运动,形成如图④⑤形状,(2)中的结论还成立吗?请从图④⑤中任选一个图形说明理由.【分析】(1)连接AP并延长至F,将“飞镖”图形转化为两个三角形,再根据三角形的外角的性质进行解答;(2)两次运用三角形外角的性质得到∠C+∠E=∠1,∠B+∠D=∠2,相加即可得到∠A+∠B+∠C+∠D+∠E=180°;(3)根据三角形外角的性质可知,在△ACG中,∠AGE=∠A+∠C,在△BDF中,∠DFE=∠DBF+∠D,所以,∠A+∠C+∠DBF+∠D+∠E=180°.【解答】解:(1)如图②,∠BPC=∠A+∠B+∠C,连接AP并延长至F,则有∠B+∠BAP=∠BPF,∠C+∠CAP=∠CPF,所以∠B+∠C+∠CAP+∠BAP=∠BPF+∠CPF=∠BPC,即∠B+∠C+∠A=∠BPC,(2)如图③,∠C+∠E=∠1,∠B+∠D=∠2,则∠A+∠B+∠C+∠D+∠E=∠A+∠1+∠2=180°.(3)如图④,在△ACG中,∠AGE=∠A+∠C,在△BDF中,∠DFE=∠DBF+∠D,所以,∠A+∠C+∠DBF+∠D+∠E=∠AGE+∠DFE+∠E=180°.【变式4-1】(2022春•井研县期末)Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=α.(1)若点P在线段AB上,如图(1)所示,且∠α=60°,则∠1+∠2=150°;(2)若点P在线段AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为90°+α;(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由;(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.【分析】(1)由平角的定义得出,∠CDP=180﹣∠1,∠CEP=180﹣∠2,最后用四边形CDPE的内角和是360°即可求得∠1+∠2.(2)同(1)的方法.(3)利用三角形的外角的性质即可得出结论.(4)利用外角的性质和对顶角相等即可得出结论.【解答】解:(1)由平角的定义知,∠1+∠CDP=180°,∠2+∠CEP=180°,在四边形CDPE中,∠CDP+∠α+∠PEC+∠C=360°,即(180°﹣∠1)+∠α+(180°﹣∠2)+∠C=360°,180°﹣∠1+∠α+180°﹣∠2+90°=360°,∴∠1+∠2=90°+α.当α=60°时,∠1+∠2=150°.故答案为:150°.(2)由(1)知,∠1+∠2=90°+α.故答案为:90°+α.(3)∠1=90°+∠2+∠α.理由如下:由三角形的外角的性质知,∠DMC=∠2+∠α,∠1=∠C+∠DMC,∴∠1=∠C+(∠2+∠α),即∠1=90°+∠2+∠α.(4)∠2=90°+∠1﹣∠α.理由如下:由三角形的外角的性质知,∠2=∠CFE+∠C,∠1=∠PFD+∠α,∵∠CFE=∠PFD,∴∠2﹣∠C=∠1﹣∠α,∴∠2=∠C+∠1﹣∠α,即∠2=90°+∠1﹣∠α.【变式4-2】(2022春•深圳校级期中)平面内的两条直线有相交和平行两种位置关系(1)已知AB平行于CD,如a图,当点P在AB、CD外部时,∠BPD+∠D=∠B即∠BPD=∠B﹣∠D,为什么?请说明理由.如b图,将点P移动到AB、CD内部,以上结论是否仍然成立?若不成立,则∠BPD、∠B、∠D之间有何数量关系?请说明结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.【分析】(1)①利用平行线的性质和三角形的外角即可;②利用平行线的特点作出平行线,再利用平行线的性质即可;(2)利用三角形的外角等于与它不相邻的两内角的和即可;(3)利用三角形的外角的性质把角转化到四边形CDHM中,用四边形的内角和即可.【解答】解:(1)①∵AB∥CD,∴∠B=∠COP,∵∠COP=∠BPD+∠D,∴∠B=∠BPD+∠D,即:∠BPD=∠B﹣∠D,②不成立,结论:∠BPD=∠B+∠D,理由:如图b,过点P作PG∥AB,∴∠B=∠BPG,∵PG∥AB,CD∥AB,∴PG∥CD,∴∠DPG=∠D,∴∠BPD=∠BPG+∠DPG=∠B+∠D;(2)结论:∠DPQ=∠B+∠BQD+∠D,理由:如图c,连接QP并延长,∵∠BP∠G是△BPQ的外角,∴∠BPG=∠B+∠BQP,同理:∠DPG=∠D+∠DQP,∴∠BPD=∠BPG+∠DPG=∠B+∠BQP+∠DQP+∠D=∠B+∠BQD+∠D;(3)如图d,∵∠DHM是△BFH的外角,∴∠DHM=∠B+∠F,同理:∠CMH=∠A+∠E,∴∠A+∠B+∠C+∠D+∠E+∠F=∠DHM+∠CMH+∠C+∠D=360°.【变式4-3】(2022•吉州区期末)探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”,(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;(2)请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX=50°;②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.【分析】(1)首先连接AD并延长至点F,然后根据外角的性质,即可判断出∠BDC=∠A+∠B+∠C.(2)①由(1)可得∠ABX+∠ACX+∠A=∠BXC,然后根据∠A=40°,∠BXC=90°,求出∠ABX+∠ACX的值是多少即可.②由(1)可得∠DBE=∠DAE+∠ADB+∠AEB,再根据∠DAE=40°,∠DBE=130°,求出∠ADB+∠AEB的值是多少;然后根据∠DCE=12(∠ADB+∠AEB)+∠DAE,求出∠DCE的度数是多少即可.③根据∠BG1C=110(∠ABD+∠ACD)+∠A,∠BG1C=70°,设∠A为x°,可得∠ABD+∠ACD=133°﹣x°,解方程,求出x的值,即可判断出∠A的度数是多少.【解答】解:(1)如图(1),连接AD并延长至点F,,根据外角的性质,可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD,又∵∠BDC=∠BDF+∠CDF,∠BAC=∠BAD+∠CAD,∴∠BDC=∠A+∠B+∠C;(2)①由(1),可得∠ABX+∠ACX+∠A=∠BXC,∵∠A=40°,∠BXC=90°,∴∠ABX+∠ACX=90°﹣40°=50°,故答案为:50.②由(1),可得∠DBE=∠DAE+∠ADB+∠AEB,∴∠ADB+∠AEB=∠DBE﹣∠DAE=130°﹣40°=90°,∴12(∠ADB+∠AEB)=90°÷2=45°,∴∠DCE=12(∠ADB+∠AEB)+∠DAE=45°+40°=85°;③∠BG1C=110(∠ABD+∠ACD)+∠A,∵∠BG1C=70°,∴设∠A为x°,∵∠ABD+∠ACD=133°﹣x°∴110(133﹣x)+x=70,∴13.3−110x+x=70,解得x=63,即∠A的度数为63°.【知识点5风筝模型】【条件】四边形ABPC,分别延长AB、AC于点D、E,如上左图所示.【结论】∠PBD+∠PCE=∠A+∠P.【证明】如上右图,连接AP,则:∠PBD=∠PAB+∠APB,∠PCE=∠PAC+∠APC,∴∠PBD+∠PCE=∠PAB+∠APB+∠PAC+∠APC=∠BAC+∠BPC,得证.【题型5风筝模型】【例5】(2022春•南通期末)如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),图中∠1+∠2+∠3+∠4+∠5+∠6=360°.【分析】由折叠可知∠1+∠2+∠3+∠4+∠5+∠6等于六边形的内角和减去(∠B'FG+∠B'GF)以及(∠C'HI+∠C'IH)和(∠A'DE+∠A'ED),再利用三角形的内角和定理即可求解.【解答】解:由题意知,∠1+∠2+∠3+∠4+∠5+∠6=720°﹣(∠B'FG+∠B'GF)﹣(∠C'HI+∠C'IH)﹣(∠A'DE+∠A'ED)=720°﹣(180°﹣∠B')﹣(180°﹣C')=(180°﹣A')=180°+(∠B'+∠C'+∠A')又∵∠B=∠B',∠C=∠C',∠A=∠A',∠A+∠B+∠C=180°,∴∠1+∠2+∠3+∠4+∠5+∠6=360°.故答案为:360.【变式5-1】(2022春•铜山区期中)(1)如图1,把△ABC沿DE折叠,使点A落在点A′处,请直接写出∠1+2与∠A的关系:∠1+∠2=2∠A.(2)如图2,把△ABC分别沿DE、FG折叠,使点A落在点A′处,使点B落在点B′处,若∠1+∠2+∠3+∠4=220°,则∠C=70°(3)如图3,在锐角△ABC中,BM⊥AC于点M,CN⊥AB于点N,BM、CN交于点H,把△ABC沿DE折叠使点A和点H重合,则∠BHC与∠1+∠2的关系是A.A.∠BHC=180°−12(∠1+∠2)B.∠BHC=∠1+∠2C.∠BHC=90°+12(∠1+∠2)D.∠BHC=90°+∠1﹣∠2(4)如图4,BH平分∠ABC,CH平分∠ACB,把△ABC沿DE折叠,使点A与点H重合,若∠1+∠2=100°,求∠BHC的度数.【分析】(1)根据翻折变换的性质以及三角形内角和定理以及平角的定义求出即可;(2)根据(1)的结论即可得到结果;(3)根据翻折变换的性质以及垂线的性质得出,∠AMH+∠ANH=90°+90°=180°,进而求出∠A=12(∠1+∠2),即可得出答案;(4)根据三角形角平分线的性质得出∠HBC+∠HCB=90°−12∠A,得出∠BIC的度数即可;【解答】解:(1)∠1+∠2=2∠A;理由如下:由折叠的性质得:∠1+2∠ADE=180°,∠2+2∠AED=180°,∴∠1+2∠ADE+∠2+2∠AED=360°①,又∵∠A+∠ADE+∠AED=180°,∴2(∠A+∠ADE+∠AED)=360°②,由①②得:∠1+∠2=2∠A;故答案为:∠1+∠2=2∠A;(2)由(1)可得,∠A=12(∠1+∠2),∠B=12(∠3+∠4),∴∠A+∠B=12(∠1+∠2+∠3+∠4)=12×220=110,∴∠C=180°﹣∠A﹣∠B=70°,故答案为:70°;(3)理由:∵BM⊥AC,CN⊥AB,∴∠AMH+∠ANH=90°+90°=180°,∠MHN+∠A=180°,∴∠BHC=∠MHN=180°﹣∠A,由(1)知∠1+∠2=2∠A.∴∠A=12(∠1+∠2).∴∠BHC=180°−12(∠1+∠2).故选A;(4)由(1)得:∠1+∠2=2∠A,得2∠A=100°,∴∠A=50°,∵HB平分∠ABC,HC平分∠ACB,∴∠HBC+∠HCB=12(∠ABC+∠ACB)=12(180°﹣∠A)=90°−12∠A,∴∠BHC=180°﹣(∠HBC+∠HCB)=180°﹣(90°−12∠A)=90°+12∠A=90°+12×50°=115°.【变式5-2】(2022春•常州期中)已知△ABC是一张三角形的纸片.(1)如图①,沿DE折叠,使点A落在边AC上点A′的位置,∠DA′E与∠1的之间存在怎样的数量关系?为什么?(2)如图②所示,沿DE折叠,使点A落在四边形BCED的内部点A′的位置,∠A、∠1与∠2之间存在怎样的数量关系?为什么?(3)如图③,沿DE折叠,使点A落在四边形BCED的外部点A′的位置,∠A、∠1与∠2之间存在怎样的数量关系?为什么?【分析】(1)根据翻折的性质可得∠A=∠DA′E,然后根据三角形的一个外角等于与它不相邻的两个内角的和解答即可;(2)根据翻折变换的性质用∠1、∠2表示出∠ADE和∠AED,再根据三角形的内角和定理列式整理即可得解;(3)根据翻折的性质可得∠A=∠DA′E,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式整理即可得解.【解答】解:(1)∵点A沿DE折叠落在点A′的位置,∴∠A=∠DA′E,根据三角形外角性质,∠1=∠A+∠DA′E=2∠DA′E,即∠1=2∠DA′E;(2)∵点A沿DE折叠落在点A′的位置,∴∠ADE=∠A′DE,∠AED=∠A′ED,∴∠ADE=12(180°﹣∠1),∠AED=12(180°﹣∠2),在△ADE中,∠A+∠ADE+∠AED=180°,∴∠A+12(180°﹣∠1)+12(180°﹣∠2)=180°,整理得,2∠A=∠1+∠2;(3)如图③,∵点A沿DE折叠落在点A′的位置,∴∠A=∠A′,根据三角形的外角性质,∠3=∠2+∠A′,∠1=∠A+∠3,∴∠1=∠A+∠2+∠A′=∠2+2∠A,即∠1=∠2+2∠A.【变式5-3】(2022春•姜堰市期中)△ABC,直线DE交AB于D,交AC于E,将△ADE沿DE折叠,使A落在同一平面上的A′处,∠A的两边与BD、CE的夹角分别记为∠1,∠2如图①,当A落在四边形BDEC内部时,探索∠A与∠1+∠2之间的数量关系,并说明理由.如图②,当A′落在BC下方时,请直接写出∠A与∠1+∠2之间的数量关系.如图③,当A′落在AC右侧时,探索∠A与∠1,∠2之间的数量关系,并说明理由.【分析】(1)根据图①中∠A与∠DA′E是相等的,再结合四边形的内角和及互补角的性质可得结论2∠A=∠1+∠2;(2)与(1)的证明过程完全相同;(3)根据图③中由于折叠∠A与∠A′是相等的,再两次运用三角形外角的性质可得结论2∠A=∠1﹣∠2.【解答】解:(1)2∠A=∠1+∠2.理由如下:如图①,∵∠A+∠A′+∠AEA′+∠ADA′=360°,又∵∠1+∠ADA′+∠2+∠AEA′=360°,∴∠A+∠A′=∠1+∠2,又∵∠A=∠A′,∴2∠A=∠1+∠2;(2)2∠A=∠1+∠2.理由:∵∠A+∠A′+∠AEA′+∠ADA′=360°,又∵∠1+∠ADA′+∠2+∠AEA′=360°,∴∠A+∠A′=∠1+∠2,又∵∠A=∠A′,∴2∠A=∠1+∠2;(3)2∠A=∠1﹣∠2.理由如下:如图③,设DA′交AC于点F.∵∠1=∠A+∠DFA,∠DFA=∠A′+∠2,∴∠1=∠A+∠A′+∠2,∴∠A+∠A′=∠1﹣∠2,∵△A′DE是由△ADE沿直线DE折叠而得,∴∠A=∠A′,∴2∠A=∠1﹣∠2.【知识点6两内角角平分线模型】【条件】△ABC 中,BI 、CI 分别是∠ABC 和∠ACB 的角平分线,且相交于点I.【结论】A I ∠+︒=∠2190【证明】∵BI 是∠ABC 平分线,∴ABC ∠=∠212∵CI 是∠ACB 平分线,∴ACB ∠=∠213由A →B →I →C →A 的飞镖模型可知:∠I =∠A +∠2+∠3=∠A +ABC ∠21+ACB ∠21=∠A +)180(21A ∠-︒=A ∠+︒2190.【题型6两内角角平分线模型】【例6】(2022春•靖江市校级月考)如图,△ABC 中,∠BAC =50°,∠ABC 的角平分线与∠ACB 的角平分线交于点O .则∠BOC =115°.【分析】利用三角形内角和定理先求出∠ABC +∠ACB 的度数,再利用角平分线的定义即可求解.【解答】解:∵∠BAC =50°,∴∠ABC +∠ACB =180°﹣50°=130°,∵∠ABC 的角平分线与∠ACB 的角平分线交于点O ,∴∠ABO =∠OBC =12∠ABC ,∠ACO =∠OCB =12∠ACB ,∴∠OBC+∠OCB=12∠ABC+12∠ACB=12(∠ABC+∠ACB)=12×130°=65°,∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣65°=115°,故答案为:115°.【变式6-1】(2022春•昌平区校级期中)如图,BD,CE,AF分别是△ABC的角平分线,且相交于点O,OH⊥BC于H,试问∠1=∠2?请说明理由.【分析】根据角平分线定义得∠ABO=12∠ABC,∠BAO=12∠BAC,∠OCB=12∠ACB,再根据三角形外角性质得∠1=∠ABO+∠BAO,则∠1=12(∠ABC+∠BAC),然后根据三角形内角和定理得∠ABC+∠BAC+∠ACB=180°,所以∠1=12(180°﹣∠ACB)=90°−12∠ACB;再由OH⊥BC得∠OHC=90°,利用三角形内角和定理得∠2=90°﹣∠OCH=90°−12∠ACB,于是可得到∠1=∠2.【解答】解:∠1=∠2.理由如下:∵BD,CE,AF分别是△ABC的角平分线,∴∠ABO=12∠ABC,∠BAO=12∠BAC,∠OCB=12∠ACB,∵∠1=∠ABO+∠BAO,∴∠1=12(∠ABC+∠BAC),∵∠ABC+∠BAC+∠ACB=180°,∴∠1=12(180°﹣∠ACB)=90°−12∠ACB,又∵OH⊥BC,∴∠OHC=90°,∴∠2=90°﹣∠OCH=90°−12∠ACB,∴∠1=∠2.【变式6-2】(2022春•秀英区校级期末)如图,在△ABC中,∠ABC,∠ACB的平分线BD,CE相交于点O.(1)若∠A=60°,求∠BOC的度数;(2)求证:∠BOC=90°+12∠A.【分析】(1)利用角平分线的性质求出∠2+∠4的度数,再由三角形的内角和定理便可求出∠BOC;(2)方法同(1).【解答】(1)解:∵∠ABC和∠ACB的平分线BD、CE相交于点O,∴∠1=∠2,∠3=∠4,∴∠2+∠4=12(180°﹣∠A)=12(180°﹣60°)=60°,故∠BOC=180°﹣(∠2+∠4)=180°﹣60°=120°.(2)证明:∵∠ABC和∠ACB的平分线BD、CE相交于点O,∴∠1=∠2,∠3=∠4,∴∠2+∠4=12(180°﹣∠A)=90°−12∠A,故∠BOC=180°﹣(∠2+∠4)=180°﹣(90°−12∠A)=90°+12∠A.【变式6-3】(2022春•海淀区校级期中)已知AB∥CD,直线EF与AB、CD分别交于点E、F,点G为落在直线AB和直线CD之间的一个动点.(1)如图1,点G恰为∠BEF和∠DFE的角平分线的交点,则∠EGF=90°;(2)若点G恰为∠BEF和∠DFE的三等分线的交点,有如下结论:①∠EGF一定为钝角;②∠EGF可能为60°;③若∠EGF为直角,则EF⊥CD.其中正确结论的序号为②③.(3)进一步探索,若EF⊥CD,且点G不在线段EF上,记∠AEG=α,∠CFG=β,EM为∠AEG最接近EG的n等分线,FN是∠CFG最接近CF的n等分线(其中n≥2).直线EM、FN交于点P n,是否存在某一正整数n,使得∠EP n F=90°?说明理由.【分析】(1)根据平行线的性质定理,两直线平行同旁内角互补,以及三角形内角和定理来完成.(2)根据平行线的性质定理,两直线平行同旁内角互补,以及三角形内角和定理,另外角的等分来判断.(3)按题意添加辅助线,画出相应的EM、FN、点P n,再根据平行线的性质定理,两直线平行同旁内角互补,以及三角形内角和定理、角的n等分,通过分类别讨论推测出n是否存在,存在的值.【解答】解:(1)∵AB∥CD,∴∠BEF+∠DFE=180°,∵点G恰为∠BEF和∠DFE的角平分线的交点,∴∠FEG+∠EFG=12×180°=90°,∴∠EGF=180°﹣90°=90°.故答案为:90°.(2)若点G恰为∠BEF和∠DFE的三等分线的交点,∴∠FEG+∠EFG=13×180°或者∠FEG+∠EFG=23×180°,∠FEG+∠EFG=60°或∠FEG+∠EFG=120°,∴∠EGF=180°﹣60°=120°或∠EGF=180°﹣120°=60°,∴①错误,②正确,当∠EGF为直角,只有13∠BEF+23∠DFE=90°或23∠BEF+13∠DFE=90°,不妨假设13∠BEF+23∠DFE=90°,∴23∠BEF+13∠DFE=90°,∴13(∠BEF﹣∠DFE)+23(∠DFE﹣∠BEF)=0,∴∠BEF=∠DFE,∵∠BEF+∠DFE=180°,∴∠BEF=∠DFE=90°,∴EF⊥CD,故③正确.故答案为:②③.(3)不存在某一整数n,使得∠EP n F=90°,理由如下:∵EM为∠AEG最接近EG的n等分线,FN是∠CFG最接近CF的n等分线(其中n≥2),∴∠AEM=K1α,∠CFM=1β.①当点G在EF的左侧,此时α<90°,β<90°,P n必在EF的左侧,如图2所示,过点P n作P n Q∥AB,∵AB∥CD,∴P n Q∥CD,∴∠EP n F=∠EPnQ+∠FP n Q=∠AEM+∠CFN=K1α+1β<K1×90°+1×90°<90°,②当点G在右侧,此时α>90°,β>90°.若K1α<90°,则P n在EF的左侧,如图3中,同理可得∠EP n F=K1α+1β>90°.若K1α=90°,则P n 与F 重合,不存在∠EP n F ,舍弃.若K1α>90°,则P n 在EF 的右侧,如图4中,过点P n 作P n Q ∥AB ,∵AB ∥CD ,∴P n Q ∥CD ,∴∠EP n F =∠EP n Q ﹣∠FP n Q =∠BEM +∠CFN =(180°−K1α)−1β,∵K1α>90°,1β>0,∴(180°−K1α)−1β<90°,即∠EP n F <90°,综上所述,不存在某一整数n ,使得∠EP n F =90°.【条件】△ABC 中,BI 、CI 分别是△【结论】A O ∠-︒=∠2190.【证明】∵BO 是∠EBC 平分线,∴由△BCO 中内角和定理可【题型7两外角角平分线模型】【例7】(2022•平湖市模拟)如图,在△ABC中,∠B,∠C的外角平分线相交于点O,若∠A=74°,则∠O=53度.【分析】根据三角形的内角和定理,得∠ACB+∠ABC=180°﹣74°=106°;再根据邻补角的定义,得两个角的邻补角的和是360°﹣106°=254°;再根据角平分线的定义,得∠OCB+∠OBC=127°;最后根据三角形的内角和定理,得∠O=53°.【解答】解:∵∠A=74°,∴∠ACB+∠ABC=180°﹣74°=106°,∴∠BOC=180°−12(360°﹣106°)=180°﹣127°=53°.【变式7-1】(2022春•新北区校级期中)(1)如图①,在△ABC中,∠ABC、∠ACB的平分线相交于点O,∠A=40°,求∠BOC的度数;(2)如图②,△A′B′C′的外角平分线相交于点O′,∠A′=40°,求∠B′O′C′的度数;(3)上面(1)、(2)两题中的∠BOC与∠B′O′C′有怎样的数量关系若∠A=∠A′=n°,∠BOC 与∠B′O′C′是否还具有这样的关系?这个结论你是怎样得到的?【分析】(1)(2)根据三角形内角和定理和角平分线定义解答;(3)由前两问提供的思路,进一步推理.【解答】解:(1)在△ABC中,∠ABC、∠ACB的平分线相交于点O,则∠1+∠2=12∠ABC+12∠ACB=12(∠ABC+∠ACB)=12(180°﹣∠A)=12×(180°﹣40°)=70°.故∠BOC=180°﹣70°=110°;(2)因为∠A的外角等于180°﹣40°=140°,△A′B′C′另外的两外角平分线相交于点O′,根据三角形的外角和等于360°,所以∠1+∠2=12×(360°﹣140°)=110°,∠B′O′C′=180°﹣110°=70°;(3)∵(1)(2)中∠BOC+∠B′O′C′=110°+70°=180°,∴∠BOC与∠B′O′C′互补;证明:当∠A=n°时,∠BOC=180°﹣[(180°﹣n°)÷2]=90°+U2,∵∠A′=n°,∠B′O′C′=180°﹣[360°﹣(180°﹣n°)]÷2=90°−U2,∴∠A+∠A′=90°+U2+90°−U2=180°,∠BOC与∠B′O′C′互补,所以当∠A=∠A′=n°,∠BOC与∠B′O′C′还具有互补的关系.【变式7-2】(2022春•江夏区期末)如图,在四边形ABCD中,AD∥BC,∠B=∠D,延长BA至E,连接CE交AD于F,∠EAD和∠ECD的角平分线相交于点P.若∠E=60°,∠APC=70°,则∠D的度数是()A.80°B.75°C.70°D.60°【分析】由角平分线的定义可知,∠1=∠2,∠3=∠4,根据三角形的内角和定理,可得:∠E+∠1=∠P+∠3,进而∴∠1﹣∠3=∠P﹣∠E=70°﹣60°=10°=∠2﹣∠4,同理∴∠2﹣∠4=∠D﹣∠P=10°,从而求出∠D的度数.【解答】解:由题意得:∠1=∠2,∠3=∠4,∠E=60°,∠P=70°,在△AME和△PMC中,由三角形的内角和定理得:∠E+∠1=∠P+∠3,∴∠1﹣∠3=∠P﹣∠E=70°﹣60°=10°=∠2﹣∠4,同理:∠P+∠2=∠D+∠4,∴∠2﹣∠4=∠D﹣∠P=10°,∴∠D=80°.故选:A.【变式7-3】(2022春•丰县月考)如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.(1)如图1,若α+β=105°,求∠MBC+∠NDC的度数;(2)如图1,若BE与DF相交于点G,∠BGD=45°,请直接写出α,β所满足的数量关系式;(3)如图2,若α=β,判断BE,DF的位置关系,并说明理由.【分析】(1)利用四边形的内角和和平角的定义推导即可;(2)利用角平分线的定义,四边形的内角和以及三角形的内角和转化即可;(3)利用角平分线的定义以及平行线的判定与性质即可解答.【解答】解:(1)∵四边形ABCD的内角和为360°,∴α+β=∠A+∠BCD=360°﹣(∠ABC+∠ADC),∵∠MBC和∠NDC是四边形ABCD的外角,∴∠MBC=180°﹣∠ABC,∠NDC=180°﹣∠ADC,∴∠MBC+∠NDC=180°﹣∠ABC+180°﹣∠ADC=360°﹣(∠ABC+∠ADC),=α+β=105°;(2)β﹣α=90°(或α﹣β=﹣90°等均正确).理由:如图1,连接BD,由(1)有,∠MBC+∠NDC=α+β,∵BE、DF分别平分四边形的外角∠MBC和∠NDC,∴∠CBG=12∠MBC,∠CDG=12∠NDC,∴∠CBG+∠CDG=12∠MBC+12∠NDC=12(∠MBC+∠NDC)=12(α+β),在△BCD中,∠BDC+∠CBD=180°﹣∠BCD=180°﹣β,在△BDG中,∠BGD=45°,∠GBD+∠GDB+∠BGD=180°,∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,∴(∠CBG+∠CDG)+(∠BDC+∠CBD)+∠BGD=180°,∴12(α+β)+180°﹣β+45°=180°,∴β﹣α=90°.(3)BE∥DF.理由:如图2,过点C作CP∥BE,则∠EBC =∠BCP ,∴∠DCP =∠BCD ﹣∠BCP =β﹣∠EBC ,由(1)知∠MBC +∠NDC =α+β,∵α=β,∴∠MBC +∠NDC =2β,又∵BE 、DF 分别平分∠MBC 和∠NDC ,∴∠EBC +∠FDC =12(∠MBC +∠NDC )=β,∴∠FDC =β﹣∠EBC ,又∵∠DCP =β﹣∠EBC ,∴∠FDC =∠DCP ,∴CP ∥DF ,又CP ∥BE ,∴BE ∥DF .【条件】△ABC 中,BP 、CP 分别是△【结论】A P ∠=∠21【证明】∵BP 是∠ABC 平分线,∴由△ABC 外角定理可知:∠ACE 【题型8内外角角平分线模型】【例8】(2022春•榕城区期末)如图,∠AOB =60°,点M 、N 分别在OA 、OB 上运动(不与点O 重合),ME 平分∠AMN ,ME 的反向延长线与∠MNO 的平分线交于点F ,在M 、N 的运动过程中,∠F 的度数()A.变大B.变小C.等于45°D.等于30°【分析】由∠AMN是△OMN的外角,∠EMN是△FMN的外角,得到∠AMN=∠O+∠ONM,∠EMN=∠F+∠FNM,再由角平分线,得到∠AMN=2∠EMN,∠ONM=2∠FNM,从而得到∠F=12∠O.【解答】解:∵∠AMN是△OMN的外角,∴∠AMN=∠O+∠ONM,∵∠EMN是△FMN的外角,∴∠EMN=∠F+∠FNM,∵ME平分∠AMN,FN平分∠MNO,∴∠AMN=2∠EMN,∠ONM=2∠FNM,∴∠O=2∠F,∴∠F=30°.故选:D.【变式8-1】(2022春•海陵区校级期末)△ABC中,三个内角的平分线交于点O,过点O作∠ODC=∠AOC,交边BC于点D.(1)如图1,求∠BOD的度数;(2)如图2,作∠ABC外角∠ABE的平分线交CO的延长线于点F.①求证:BF∥OD;②若∠F=50°,求∠BAC的度数;③若∠F=∠ABC=50°,将△BOD绕点O顺时针旋转一定角度α(0°<α<360°)后得△B'O′D′,B′D′所在直线与FC平行,请直接写出所有符合条件的旋转角度α的值.【分析】(1)根据角平分线的定义,结合三角形内角和即可得到答案.(2)①根据角平分线的定义,结合三角形内角和即可得到答案.②结合角平分线的性质,根据三角形外角的性质即可得到答案.③求出∠ODB的度数即可解决【解答】解:(1)∵三个内角的平分线交于点O,∴∠OAC+∠OCA=12(∠BAC+∠BCA)=12(180°﹣∠ABC),∵∠OBC=12∠ABC,∴∠AOC=180°﹣(∠OAC+∠OCA)=90°+12∠ABC=90°+∠OBC,∵∠ODC=∠BOD+∠OBC=∠AOC,∴∠BOD=90°;(2)①∵三个内角的平分线交于点O,∴∠EBF=12∠ABE=12(180°﹣∠ABC)=90°﹣∠DBO,∵∠ODB=90°﹣∠OBD,∴∠FBE=∠ODB,∴BF∥OD;②∵三个内角的平分线交于点O,∴∠EBF=12∠ABE=12(∠BAC+∠ABC),∴∠FCB=12∠ACB,∵∠F=∠FBE﹣∠BCF=12(∠BAC+∠ACB)−12∠ACB=12∠BAC,∵∠F=50°,∴∠BAC=2∠F=100°;③∠F=∠ABC=50°,由②可知,∠BAC=100°,∠BDO=65°,∠ACB=30°,∠OCD=15°,∠COD=50°,易知△BOD绕点O顺时针旋转15°或195°后得△B'O′D′,B′D′所在直线与FC平行.【变式8-2】(2022•平湖市模拟)如图,在△ABC中,∠A=α,∠ABC的平分线与△ABC的外角∠ACD的平分线交于点A1,得∠A1=2;∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2;…;∠A2010BC的平分线与∠A2010CD的平分线交于点A2011,得∠A2011,则∠A2011=22011.【分析】根据角平分线的定义可得∠A1BC=12∠ABC,∠A1CD=12∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,整理即可求出∠A1的度数,同理求出∠A2,可以发现后一个角等于前一个角的12,根据此规律即可得解.【解答】解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,∴∠A1BC=12∠ABC,∠A1CD=12∠ACD,又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,∴12(∠A+∠ABC)=12∠ABC+∠A1,∴∠A1=12∠A,∵∠A=α,∴∠A1=2;同理可得∠A2=12∠A1=12•12α=22,∴∠A n=2,∴∠A2011=22011.故答案为:2,22011.【变式8-3】(2022春•东海县期中)在数学学习过程中,对有些具有特殊结构,且结论又具有一般性的数。
八年级上册数学八字模型

初中中考数学几何模型之8字模型一、8 字模型模型1:角的“8”字模型如图所示,AC、BD 相交于点0,连接AD、BC结论:∠A+∠D=∠B+∠C。
证明:在∠AOD 和∠BOC 中,∠AOD= ∠BOC (对顶角)又∠∠A+∠D+∠AOD=∠B+∠C+∠BOC=180°∠∠A+∠D = ∠B+∠C模型分析8字模型往往在几何综合题目中推导角度时用到模型实例观察下列图形,计算角度:(1)如图∠,∠A+∠B+∠C+∠D+∠E= ;(2)如图∠,∠A+∠B+∠C∠D+∠E+∠F= 。
模型精练1.(1)如图∠,求∠CAD+∠B+∠C+∠D+∠E= 。
(2)如图∠,求∠CAD+∠B+∠ACE+∠D+∠E= 。
2.如图∠,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=。
模型2: 边的“8”字模型如图所示,AC、BD 相交于点0,连接AD、BC结论:AC+BD>AD+BC。
证明:在∠AOD 中,AO+OD > AD在∠BOC中,BO+OC > BC∠AC+BD=(AO+OC)+(BO+OD)>AD+BC∠AC+BD > AD+BC模型实例如图,四边形ABCD 的对角线AC、BD 相交于点O.求证: (1) AB+BC+CD+AD > AC+BD:(2)B+BC+CD+AD < 2AC+2BD模型 3 相似8 字模型(又称X 字型)(1)如图8 型,对顶角的对边平行,则∠ADE ∽∠ABC;(2)如图反8 型,对顶角的对边不平行,且有另一对角相等,则∠ADE∠∠ABC.已知: ∠1=∠2,结论:∠ADE∠∠ABC证明:如图∠1=∠2,又∠DAE=∠BAC (对顶角)∠∠E=∠C(∠D=∠B)∠∠ADE∠∠ABC (AAA)模型分析在相似三角形的判定中,我们常通过作平行线,从而得到8 字形相似(有时得到A 字形相似,后面会讲到),在做题时,我们也常常关注题目中由平行线产生的相似三角形。
2020-2021学年人教版八年级上册常考几何模型汇总

人教版八年级上常考几何模型汇总序号基本图形条件结论解题思路及作用1模型1 角的“8”字模型如图所示,AB、CD相交于点O,连接AD、BC。
结论:∠A+∠D=∠B+∠C8字模型往往在几何综合题目中推导角度时用到。
2模型角的双“8”字模型CP平分∠DCA,BP平分∠ABO,求∠P结论:∠P=12(∠A+∠D)设∠DCO=2α,∠DCO=2β,由8字形得∠P+α=∠D+β,∠P+β=∠A+α则∠P=12(∠A+∠D)3模型角的飞镖模型如图如图所示,有结论:∠D=∠A+∠B+∠C。
飞镖模型往往在几何综合题目中推导角度时用到。
4模型角的双飞镖模型CP平分∠DCA,BP平分∠ABD,求∠P∠P=12(∠A+∠D)设∠ABD=2α,∠ACD=2β由飞镖型得∠P=∠A+α+β∠P+α+β=∠D得∠P=12(∠A+∠D)5模型A字型及其变式如图∠ADE+∠AED=∠ABC+∠C在几何综合题目中推导角度时用到。
6模型4.内角平分线夹角在△ABC中,∠ABC与∠ACB的平分线相交于点D∠D=90°+12∠A思路;利用角平分线的性质及三角形内角和定理即可证明。
7模型5 内角和外角的平分线的夹角在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E∠E=12∠A∠E=∠ECM-∠EBC=12(∠ACM-∠ABC)=12∠A序号基本图形条件结论解题思路及作用8模型6 外角的平分线的夹角点P是△ABC的两个外角∠EBC,∠FCB的平分线的交点∠P=90°-12∠A.∠P=180°-(∠PBC+∠PCB)=180°-(90°+12∠A)=90°-12∠A.9类型7 线段(角)的和差(1)BE=CF(2)∠BAD=∠EAC(1)BC=EF(2)∠BAC=∠EAD1.∵BE=CF∴BE+EC=CF+EC即BC=EF2证法同110模型三垂直全等模型(K型)∠D=∠BCA=∠E=90°,BC=ACRt△BCD≌Rt△CAE图1中DE=BD+AE图2中DE=AD-BE利用互余证∠B=∠ACE,再AAS证全等。
11.4角度的模型总结(讲练)-2022-2023学年八年级数学上册重要考点(人教版)

11.4角度的模型总结模型1:8字模型题型练习:1.如图,五角星的五个角之和,即:∠A+∠B+∠C+∠D+∠E=()A.180°B.90°C.270°D.240°【分析】连接CD,由∠BOE=∠COD得:∠B+∠E=∠OCD+∠ODC,再由三角形的内角和定理,即可得出五角星的五个角之和.【解答】解:连接CD,设BD与CE交于点O,由∠BOE=∠COD得:∠B+∠E=∠OCD+∠ODC,在△ACD中,∠A+∠ACD+∠ADC=180°,即∠A+∠ACE+∠OCD+∠ODC+∠ADB=180°,∴∠A+∠ACE+∠B+∠E+ADB=180°,即五角星的五个内角之和为180°.故选:A.【点评】本题考查的是三角形内角和定理,根据题意作出辅助线,利用三角形的内角和定理进行推理是解答此题的关键.2.如图,∠A+∠B+∠C+∠D+∠E=°.【分析】如图根据三角形的外角的性质,三角形内角和定理可知:∠DNC+∠D+∠C=180°,由三角形外角性质可知:∠AMB=∠A+∠E,∠DNC=∠B+∠AMB,根据三个等式即可求解.【解答】解:如图,设线段BD,BE分别与线段AC交于点N,M.∵∠AMB=∠A+∠E,∠DNC=∠B+∠AMB,∠DNC+∠D+∠C=180°,∴∠A+∠B+∠D+∠E+∠C=180°,故答案为:180.【点评】此题考查了多边形的内角与外角,熟记三角形的外角定理及内角和是解题的关键.3.如图,∠A+∠B+∠C+∠D+∠E=°.【分析】如图根据三角形的外角的性质,三角形内角和定理可知∠1=∠B+∠2,∠2=∠D+∠E,∠A+∠1+∠C=180°,由此不难证明结论.【解答】解:如图,∵∠1=∠B+∠2,∠2=∠D+∠E,∠A+∠1+∠C=180°,∴∠A+∠B+∠D+∠E+∠C=180°,故答案为:180.【点评】本题考查三角形的外角的性质、三角形内角和定理等知识,解题的关键是灵活应用所学知识解决问题,属于基础题,中考常考题型.4.“8字”的性质及应用:(1)如图①,AD、BC相交于点O,得到一个“8字”ABCD,求证:∠A+∠B=∠C+∠D.(2)图②中共有多少个“8字”?(3)如图②,∠ABC和∠ADC的平分线相交于点E,利用(1)中的结论证明∠E=(∠A+∠C).【分析】(1)根据三角形内角和定理和对顶角相等解答即可;(2)根据题中给出的“8字”的概念解答即可;(3)根据角平分线的定义和三角形的外角的性质解答即可.【解答】解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,又∠AOB=∠COD,∴∠A+∠B=∠C+∠D;(2)图②中有:ABCD、BECD、ABED,BFDC、BFDH、ABHD6个“8字”;(3)∵BE平分∠ABC,DE平分∠ADC,∴∠ABE=∠CBE=ABC,∠CDE=∠ADE=∠ADC,∵∠A+∠ABE=∠E+∠ADE,∠C+∠CDE=∠E+∠CBE,∴∠E=(∠A+∠C).【点评】本题考查的是三角形内角和定理、三角形外角的性质和对顶角相等的综合运用,掌握三角形内角和等于180°和三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.5.如图,DE⊥AB,∠A=25°,∠D=45°,求∠ACD的度数.【分析】先根据∠DEB=90°,求得∠B的度数,再根据三角形外角性质,求得∠ACD的度数.【解答】解:∵DE⊥AB,∴∠DEB=90°,∴∠B=90°﹣∠D=90°﹣45°=45°,∵∠ACD是△ABC的外角,∴∠ACD=∠A+∠B=25°+45°=70°.【点评】本题主要考查了三角形外角性质以及三角形内角和定理,解题时注意:三角形的一个外角等于和它不相邻的两个内角的和.模型2:飞镖模型【证明】题型练习:1.如图所示,∠B=20°,∠D=40°,∠BCD=2∠A,求∠A的度数.【分析】连接AC并延长,根据三角形外角的性质可得∠B+∠BAE=∠BCE,∠D+∠DAC=∠DCE,再把两式相加即可得出结论.【解答】解:连接AC并延长,∵∠BCE是△ABC的外角,∠DCE是△ACD的外角,∴∠B+∠BAE=∠BCE①,∠D+∠DAC=∠DCE②,①+②得,∠B+∠C+∠BAD=∠BCD,∵∠B=20°,∠D=40°,∠BCD=2∠A,∴20°+40°=∠A,即∠A=60°.【点评】本题考查是三角形外角的性质,熟知三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键.2.已知:如图,∠BGF=140°,求∠A+∠B+∠C+∠D+∠E+∠F的度数?【分析】根据三角形内角和定理和三角形的性质进行转换即可得出答案.【解答】解:根据三角形中,一个内角的补角等于其余两个内角的和,∴四边形CGED中:∠CGE=∠C+∠E+∠D,四边形ABGF中:∠BGF=∠A+∠B+∠F,∴∠CGE=∠BGF=140°,∴∠A+∠B+∠C+∠D+∠E+∠F=280°【点评】本题主要考查了三角形内角和定理,关键是根据三角形内角和定理解答.3.如图,在四边形ABCD中,AB∥CD,点E为对角线BD上一点,且BE=BC,∠F=∠ABD,EF交BC的延长线于点F.求证:FB=DB.【分析】要证明FB=DB,转化证明△BCD≌△BEF便可.【解答】证明:∵AB∥CD,∴∠ABD=∠CDB,∵∠F=∠ABD,∴∠CDB=∠F,在△BCD和△BEF中,,∴△BCD≌△BEF(AAS),∴FB=DB.【点评】本题主要考查了全等三角形的性质与判定.关键是将线段相等转化为证明三角形全等.4.一个零件的形状如图,按要求∠A=90°,∠B=32°,∠C=21°,检验工人量得∠CDB=148°,就断定这个零件不合格,运用三角形的有关知识说明零件不合格的理由.【分析】延长CD交AB于E,根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠BDC,然后即可判断.【解答】解:如图,延长CD交AB于E,∵∠A=90°,∠C=21°,∴∠1=∠A+∠C=90°+21°=111°,∵∠B=32°,∴∠BDC=∠B+∠1=32°+111°=143°.又∵∠BDC=148°,∴这个零件不合格.【点评】本题考查的是三角形外角的性质,根据题意作出辅助线,构造出三角形,利用三角形外角的性质求解是解答此题的关键.5.探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”,(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;(2)请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=54°,则∠ABX+∠ACX=36°;②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=α,∠DBE=β,请直接写出∠DCE的度数(用含α和β的式子表示);③如图4,∠ABD,∠ACD的12等分线相交于点G1、G2…、G11,若∠BDC=115°,∠BG1C=60°,求∠A的度数.【分析】(1)结论:∠BDC=∠A+∠B+∠C.连接AD并延长到点E,利用三角形的外角的性质求解即可.(2)①利用(1)中结论计算即可.②图3中,设∠ADC=∠CDB=x,∠AEC=∠CEB=y,构建方程组解决问题即可.③设∠ABD=x°,∠ACD=y°,构建方程组解决问题即可.【解答】解:(1)∠BDC=∠A+∠B+∠C.理由:连接AD并延长到点E.∵∠BDE=∠BAD+∠B,∠CDE=∠CAD+∠C,∴∠BDE+∠CDE=∠BAD+∠B+∠CAD+∠C,∴∠BDC=∠BAC+∠B+∠C.(2)①∵∠BXC=∠ABX+∠ACX+∠A=90°,∠A=54°,∴∠ABX+∠ACX=36°.故答案为36.②如图3中,设∠ADC=∠CDB=x,∠AEC=∠CEB=y,则有∠DCE=x+y+α,β=2x+2y+α,∴∠DCE=.故答案为.③设∠ABD=x°,∠ACD=y°.由题意可得,解得∠A=55°.【点评】本题考查三角形的外角的性质,解题的关键是学会利用参数构建方程组解决问题,属于中考常考题型.6.如图:(1)求证:∠BDC=∠A+∠B+∠C;(2)如果点D与点A分别在线段BC的两侧,猜想∠BDC、∠A、∠B、∠C这4个角之间有怎样的关系,并证明你的结论.【分析】根据三角形内角和定理及内角和外角的关系解答.【解答】(1)证明:延长BD交AC于点E,∵∠BEC是△ABE的外角,∴∠BEC=∠A+∠B,∵∠BDC是△CED的外角,∴∠BDC=∠C+∠DEC=∠C+∠A+∠B;(2)猜想:∠BDC+∠C+∠A+∠B=360°.证明:∠BDC+∠C+∠A+∠B=∠3+∠2+∠6+∠5+∠4+∠1=(∠3+∠2+∠1)+(∠6+∠5+∠4)=180°+180°=360°.【点评】根据三角形内角和定理,将四边形转化为两个三角形,可根据三角形内角和定理和推论解答.模型3:A字模型【结论】如图所示,△DAE的两边上各有一点B,C,连接BC,则∠DBC+∠ECB=180°+∠A.题型练习:1.我们容易证明,三角形的一个外角等于它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?Ⅰ.尝试探究:(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?Ⅱ.初步应用:(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2﹣∠C=;(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案.【分析】(1)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠DBC+∠ECB,再利用三角形内角和定理整理即可得解;(2)根据(1)的结论整理计算即可得解;(3)表示出∠DBC+∠ECB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形内角和定理列式整理即可得解;【解答】解:(1)∠DBC+∠ECB=180°﹣∠ABC+180°﹣∠ACB=360°﹣(∠ABC+∠ACB)=360°﹣(180°﹣∠A)=180°+∠A;(2)∵∠1+∠2=∠180°+∠C,∴130°+∠2=180°+∠C,∴∠2﹣∠C=50°;(3)∠DBC+∠ECB=180°+∠A,∵BP、CP分别平分外角∠DBC、∠ECB,∴∠PBC+∠PCB=(∠DBC+∠ECB)=(180°+∠A)在△PBC中,∠P=180°﹣(180°+∠A)=90°﹣∠A;即∠P=90°﹣∠A;故答案为:50°,∠P=90°﹣∠A.【点评】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,角平分线的定义,熟记性质并读懂题目信息是解题的关键.2.如图,已知∠CBE+∠BCD=256°,求∠A的度数.【分析】先根据三角形外角的性质把∠CBE+∠BCD=256°转化为三角形的内角和的形式,再根据三角形的内角和定理即可求出∠A的度数.【解答】解:∵∠CBE是△ABC的外角,∴∠CBE=∠1+∠A,∵∠BCD是△ABC的外角,∴∠BCD=∠2+∠A,∵∠CBE+∠BCD=256°,∴∠1+2∠A+∠2=256°,∵∠1+∠2+∠A=180°,∴∠A+180°=256°,∴∠A=256°﹣180°=76°.【点评】本题考查的是三角形内角和定理与外角的性质,解答此题的关键是熟知以下知识:(1)三角形的内角和为180°;(2)三角形的外角等于不相邻的两个内角的和.3.如图所示,已知∠CBE+∠BCD=236°,求∠A的度数.【分析】先根据三角形外角的性质把∠CBE+∠BCD=236°转化为三角形的内角和的形式,再根据三角形的内角和定理即可求出∠A的度数.【解答】解:∵∠CBE是△ABC的外角,∴∠CBE=∠2+∠A,∵∠BCD是△ABC的外角,∴∠BCD=∠2+∠A,∵∠CBE+∠BCD=236°,∴∠1+2∠A+∠2=236°,∵∠1+∠2+∠A=180°,∴∠A+180°=236°,∴∠A=236°﹣180°=56°.【点评】本题主要考查的是三角形内角和定理与外角的性质,解答此题的关键是熟知以下知识:(1)三角形的内角和为180°;(2)三角形的外角等于不相邻的两个内角的和.4.探索归纳:(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于A.90°B.135°C.270°D.315°(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.【分析】(1)利用了四边形内角和为360°和直角三角形的性质求解;(2)根据三角形的外角等于与它不相邻的两个内角和求解;(3)根据(1)(2)可以直接写出结果;(4)根据折叠的性质,对应角相等,以及邻补角的性质即可求解.【解答】解:(1):∵四边形的内角和为360°,直角三角形中两个锐角和为90°∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.∴∠1+∠2等于270°.故选C;(2)∠1+∠2=180°+40°=220°,故答案是:220°;(3)∠1+∠2与∠A的关系是:∠1+∠2=180°+∠A;(4)∵△EFP是由△EF A折叠得到的,∴∠AFE=∠PFE,∠AEF=∠PEF∴∠1=180°﹣2∠AFE,∠2=180°﹣2∠AEF∴∠1+∠2=360°﹣2(∠AFE+∠AEF)又∵∠AFE+∠AEF=180°﹣∠A,∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A.【点评】主要考查了三角形的内角和外角之间的关系.(1)三角形的外角等于与它不相邻的两个内角和.(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.5..如图1,已知∠ACD是△ABC的一个外角,我们容易证明∠ACD=∠A+∠B,即三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?尝试探究:(1)如图2,∠DBC与∠ECB分别为△ABC的两个外角,则∠DBC+∠ECB∠A+180°(横线上填>、<或=)初步应用:(2)如图3,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=135°,则∠2﹣∠C=.(3)解决问题:如图4,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案.(4)如图5,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,请利用上面的结论探究∠P与∠A、∠D的数量关系.【分析】(1)根据三角形外角的性质得:∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,两式相加可得结论;(2)利用(1)的结论:∵∠2+∠1﹣∠C=180°,将∠1=135°代入可得结论;(3)根据角平分线的定义得:∠CBP=∠DBC,∠BCP=∠ECB,根据三角形内角和可得:∠P的式子,代入(1)中得的结论:∠DBC+∠ECB=180°+∠A,可得:∠P=90°﹣∠A;(4)根据平角的定义得:∠EBC=180°﹣∠1,∠FCB=180°﹣∠2,由角平分线得:∠3=∠EBC =90°﹣∠1,∠4=∠FCB=90°﹣∠2,相加可得:∠3+∠4=180°﹣(∠1+∠2),再由四边形的内角和与三角形的内角和可得结论.【解答】解:(1)∠DBC+∠ECB﹣∠A=180°,理由是:∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,∴∠DBC+∠ECB=2∠A+∠ACB+∠ABC=180°+∠A,∴∠DBC+∠ECB=∠A+180°.故答案为:=.(2)∠2﹣∠C=45°.理由是:∵∠2+∠1﹣∠C=180°,∠1=135°,∴∠2﹣∠C+135°=180°,∴∠2﹣∠C=45°.故答案为:45°;(3)∠P=90°﹣∠A,理由是:∵BP平分∠DBC,CP平分∠ECB,∴∠CBP=∠DBC,∠BCP=∠ECB,∵△BPC中,∠P=180°﹣∠CBP﹣∠BCP=180°﹣(∠DBC+∠ECB),∵∠DBC+∠ECB=180°+∠A,∴∠P=180°﹣(180°+∠A)=90°﹣∠A.故答案为:∠P=90°﹣∠A,(4)∠P=180°﹣(∠A+∠D).理由是:∵∠EBC=180°﹣∠1,∠FCB=180°﹣∠2,∵BP平分∠EBC,CP平分∠FCB,∴∠3=∠EBC=90°﹣∠1,∠4=∠FCB=90°﹣∠2,∴∠3+∠4=180°﹣(∠1+∠2),∵四边形ABCD中,∠1+∠2=360°﹣(∠A+∠D),又∵△PBC中,∠P=180°﹣(∠3+∠4)=(∠1+∠2),∴∠P=×[360°﹣(∠A+∠D)]=180°﹣(∠A+∠D).【点评】本题是四边形和三角形的综合问题,考查了三角形和四边形的内角和定理、三角形外角的性质、角平分线的定义等知识,难度适中,熟练掌握三角形外角的性质是关键.模型4:老鹰抓小鸡模型如图,延长任意一个四边形的邻边后,就构成老鹰抓小鸡模型.结论∶如图所示,∠A+∠BFC=∠DBF+∠FCE.题型练习:1.如图,把△ABC纸片任意折叠,使点A落在纸外,设折痕为DE,∠A、∠1、∠2之间有一种始终保持不变的数量关系,请写出这种数量关系,并说明理由.【分析】延长BE,CD交于点A′,根据三角形的外角等于不相邻的两个外角的和即可求解.【解答】解:2∠A=∠2﹣∠1,理由:延长BE,CD交于点A′.在△A′DF中,根据外角的性质∠2=∠EFD+∠A′,∠EFD=∠1+∠A,∴∠2=∠1+∠A+∠A′=2∠A+∠1,又∵∠A=∠A′∴2∠A=∠2﹣∠1.【点评】本题考查了折叠的性质,三角形的外角等于不相邻两个内角的和,正确的作出辅助线是解题的关键.2.如图1和图2,在三角形纸片ABC中,点D,E分别在边AC,AB上,沿DE折叠,点A落在点A'的位置.(1)如图1,当点A′落在CD边上时,∠DAE与∠1之间的数量关系为(只填序号),并说明理由;①∠DAE=∠1②∠DAE=2∠1③∠1=2∠DAE(2)如图2,当点A落在△ABC内部时,直接写出∠DAE与∠1,∠2之间的数量关系.【分析】(1)根据三角形外角的性质,得∠1=∠EAD+∠EA′D.由题意得:∠DAE=∠DA′E,可推断出∠1=2∠DAE.(2)如图2,连接AA′.由三角形外角的性质,得∠1=∠A′AE+∠AA′E,∠2=∠A′AD+∠AA′D.由题意知:∠EAD=∠EA′D,进而推断出∠1+∠2=2∠EAD.【解答】解:(1)由题意得:∠DAE=∠DA′E.∵∠1=∠EAD+∠EA′D=2∠DAE.故答案为:③.(2)∠1+∠2=2∠DAE,理由如下:如图2,连接AA′.由题意知:∠EAD=∠EA′D.∵∠1=∠A′AE+∠AA′E,∠2=∠A′AD+∠AA′D,∴∠1+∠2=∠EAA′+∠A′AD+∠EA′A+∠AA′D=∠EAD+∠EA′D=2∠EAD.【点评】本题主要三角形外角的性质,熟练掌握三角形外角的性质是解决本题的关键.3.将纸片△ABC沿DE折叠使点A落在A′处的位置.(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是.(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.【分析】(1)根据折叠性质得出∠AED=∠A′ED,∠ADE=∠A′DE,根据三角形内角和定理得出∠AED+∠ADE=180°﹣∠A,代入∠1+∠2=180°+180°﹣2(∠AED+∠ADE)求出即可;(2)根据三角形外角性质得出∠DME=∠A′+∠1,∠2=∠A+∠DME,代入即可求出答案;(3)根据三角形外角性质得出∠DME=∠A′+∠1,∠2=∠A+∠DME,推出∠2=∠A+∠A′+∠1,即可得出答案.【解答】解:(1)图1中,2∠A=∠1+∠2,理由是:∵延DE折叠A和A′重合,∴∠AED=∠A′ED,∠ADE=∠A′DE,∵∠AED+∠ADE=180°﹣∠A,∠1+∠2=180°+180°﹣2(∠AED+∠ADE),∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A;(2)2∠A=∠2,如图∠2=∠A+∠EA′D=2∠A,故答案为:2∠A=∠2;(3)如图2,2∠A=∠2﹣∠1,理由是:∵延DE折叠A和A′重合,∴∠A=∠A′,∵∠DME=∠A′+∠1,∠2=∠A+∠DME,∴∠2=∠A+∠A′+∠1,即2∠A=∠2﹣∠1.【点评】本题考查了折叠的性质,三角形外角性质,三角形内角和定理的应用,主要考查学生运用定理进行推理和计算的能力.4.[探究]如图1,将△ABC沿着DE折叠后,使点A落在∠BAC的内部点A′处.试判断∠1、∠2与A的数量关系.并证明.[应用]如图2,将△ABC沿着DE折叠后,使点A落在∠BAC的内部.(1)若∠B=95°,∠C=25°,则∠1+∠2=;(2)若∠1+∠2=80°,则∠B+∠C=;(3)若AE∥BD,∠B+∠C=130°,则∠2=.[变式]如图3,将△ABC沿着DE折叠后,使点A落在∠BAC的外部点A′处,试判断∠1、∠2与∠A的数量关系,并证明.【分析】[探究]运用折叠原理及四边形的内角和定理即可解决问题;[应用](1)运用折叠原理及四边形的内角和定理即可解决问题;(2)根据[探究]的结论代入数据即可得到结果;(3)根据平行线的性质得到∠1=∠A′,由三角形的内角和得到∠A的度数,然后根据[探究]的结论即可求得结果;[变式]运用三角形的外角性质即可解决问题.【解答】解:[探究]如图1,∠A=∠1+∠2.理由如下:∵∠1+∠A′EA+∠2+∠A′DA=360°,∠A+∠A′+∠A′EA+∠A′DA=360°,∴∠A′+∠A=∠1+∠2,由折叠知识可得∠A=∠A′,∴2∠A=∠1+∠2;[应用](1)如图1,延长BD,CE交于A,∵∠B=95°,∠C=25°,∴∠A=180°﹣∠B﹣∠C=60°由[探究]得,2∠A=∠1+∠2,∴∠1+∠2=2∠A=120°;故答案为:120°;(2)∵∠1+∠2=80°,∴∠A=(∠1+∠2)=40°,∴∠B+∠C=180°﹣∠A=140°;故答案为:140°;(3)∵A′E∥BD,∴∠1=∠A′=∠A,∵∠B+∠C=130°,∴∠A=50°,∠1=50°,∵∠1+∠2=2∠A=100°,∴∠2=50°,故答案为:50°2∠A=∠1﹣∠2.证明:∵∠1=∠EF A+∠A,∠EF A=∠A′+∠2,∴∠1=∠A+∠A′+∠2=2∠A++∠2,∴2∠A=∠1﹣∠2.【点评】本题考查了三角形的内角和定理,平行线的性质,外角性质;解题的关键是结合图形灵活运用有关定理来解题.5.将纸片△ABC沿DE折叠使点A落在A′处的位置.(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.(2)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.【分析】(1)根据折叠性质得出∠AED=∠A′ED,∠ADE=∠A′DE,根据三角形内角和定理得出∠AED+∠ADE=180°﹣∠A,代入∠1+∠2=180°+180°﹣2(∠AED+∠ADE)求出即可;(2)根据三角形外角性质得出∠DME=∠A′+∠1,∠2=∠A+∠DME,推出∠2=∠A+∠A′+∠1,即可得出答案.【解答】解:(1)2∠A′=∠1+∠2,理由沿DE折叠使点A落在A′处的位置,∴∠AED=∠A′ED,∠ADE=∠A′DE,∵∠AED+∠ADE=180°﹣∠A,∠1+∠2=180°+180°﹣2(∠AED+∠ADE),∴∠1+∠2=360°﹣2(180°﹣∠A′)=2∠A′;(2)2∠A′=∠2﹣∠1,理由:∵沿DE折叠使点A落在A′处的位置,∴∠A=∠A′,∵∠DME=∠A′+∠1,∠2=∠A+∠DME,∴∠2=∠A+∠A′+∠1,即2∠A′=∠2﹣∠1.【点评】本题考查了折叠的性质,三角形外角性质,三角形内角和定理的应用,主要考查学生运用定理进行推理和计算的能力.模型5:双角平分线模型题型练习:1.如图,在△ABC中,∠ABC、∠ACB的平分线交于点O.(1)若∠ACB=50°,∠ABC=70°,则∠BOC=°(2)若∠A=40°,则∠BOC=°(3)若∠A=x°,试猜想∠BOC=°,并证明你的猜想的正确性.【分析】(1)根据角平分线的定义,即可得到∠OBC=ABC,∠OCB=∠ACB,再根据三角形内角和定理进行计算,即可得到∠BOC的度数;(2)根据角平分线的定义,即可得到∠OBC=ABC,∠OCB=∠ACB,再根据三角形内角和定理进行计算,即可得到∠BOC的度数;(3)根据角平分线的定义,即可得到∠OBC=ABC,∠OCB=∠ACB,再根据三角形内角和定理进行计算,即可得到∠BOC的表达式.【解答】解:(1)∵∠ABC、∠ACB的平分线交于点O,∴∠OBC=ABC,∠OCB=∠ACB,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(∠ABC+∠ACB)=180°﹣(70°+50°)=120°,故答案为:120;(2)∵∠ABC、∠ACB的平分线交于点O,∴∠OBC=ABC,∠OCB=∠ACB,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=180°﹣(180°﹣40°)=110°,故答案为:110;(3)∵∠ABC、∠ACB的平分线交于点O,∴∠OBC=ABC,∠OCB=∠ACB,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A=90°+x°,故答案为:(90+x).【点评】本题主要考查了三角形内角和定理以及角平分线的定义的运用,解题时注意:三角形内角和等于180°.2.(1)如图①,在△ABC中,∠ABC,∠ACB的平分线相交于点O,且∠A=40°,求∠BOC的度数;(2)如图②,△A′B′C′的两个外角∠C′B′D,∠B′C′E的平分线交于点O′,且∠A′=40°,求∠B′O′C′的度数;(3)由(1)(2)可以发现∠BOC与∠B′O′C′有怎样的数量关系?若∠A=∠A′=n°,则∠BOC 与∠B′O′C′之间是否还具有这样的关系?为什么?【分析】(1)利用三角形的内角和定理以及角平分线的定义求∠BOC与∠A的关系,再把∠A代入即可求∠BOC的度数.(2)先根据外角平分线的性质求出∠B′C′O′、∠O′B′C′与∠A′的关系,再由三角形内角和定理解答即可;(3)根据(1)(2)中所得的∠BOC和∠B′O′C′与∠A和∠A′的关系可得答案.【解答】解:(1)∵BO、CO分别平分∠ABC和∠ACB,∴∠OBC=∠ABC,∠OCB=∠ACB,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(∠ABC+∠ACB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A.当∠A=40°时,∠BOC=90°+∠A=110°.(2)∵B′O′、C′O′是△ABC的两个外角的平分线,∴∠B′C′O′=(∠A′+∠A′B′C′),∠O′B′C′=(∠A′+∠A′C′B′),∵∠B′C′A′+∠A′B′C′=180°﹣∠A′,∴∠B′O′C′=180°﹣∠O′B′C′﹣∠O′C′B′,=180°﹣(∠A′+∠A′B′C′+∠A′+∠A′C′B′),=180°﹣(180°+∠A′),=90°﹣∠A′.∵∠A′=40°,∴∠B′O′C′=90°﹣20°=70°;(3)∠BOC﹣∠B′O′C′=∠A=40°,∠BOC﹣∠B′O′C′=∠A=n°,∵∠BOC=90°+∠A,∠B′O′C′=90°﹣∠A′,∴∠BOC﹣∠B′O′C′=∠A=n°.【点评】本题考查的是三角形内角和定理,以及三角形内角与外角的关系,熟知三角形的内角和等于180°,三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键.3.(1)图①所示,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点O,试探究∠BOC与∠A 的等量关系.(2)图②所示,将∠ABC的一边BC延长至D,∠ABC的平分线与∠ACD的平分线相交于点O,试探究∠BOC与∠A的等量关系.【分析】(1)先根据BO、CO分别是∠ABC、∠ACB的平分线得出∠1+∠2=(180°﹣∠A),再根据∠1+∠2+∠BOC=180°即可得出结论;(2)根据角平分线的定义得∠OBC=∠ABC,∠OCD=∠ACD,再根据三角形外角性质得∠ACD=∠A+∠ABC,∠OCD=∠OBC+∠BOC,所以(∠A+∠ABC)=∠OBC+∠BOC=∠ABC+∠BOC,然后整理可得∠BOC=∠A.【解答】解:(1)∠BOC=90°+∠A.∵BO、CO分别是∠ABC、∠ACB的平分线,∴∠1+∠2=(180°﹣∠A),∴∠BOC=180°﹣(∠1+∠2)=180°﹣(180°﹣∠A)=90°+∠A;(2)∵△ABC的内角平分线BO与外角平分线CO交于O,∴∠OBC=∠ABC,∠OCD=∠ACD,∵∠ACD=∠A+∠ABC,∠OCD=∠OBC+∠BOC,∴(∠A+∠ABC)=∠OBC+∠BOC=∠ABC+∠BOC,∴∠BOC=∠A.【点评】本题考查了三角形内角和定理,即三角形内角和是180°,也考查了三角形外角性质.4.(1)如图1,在△ABC中,∠ABC,∠ACB的平分线交于点O,过点O作EF∥BC分别交AB,AC于点E,F.直接写出线段EF与BE,CF之间的数量关系:.(2)如图2,若△ABC中∠ABC的平分线BO与三角形外角平分线CO交于点O,过O点作OE∥BC 交AB于点E,交AC于点F.则EF与BE,CF之间的数量关系又如何?说明你的理由.【分析】(1)利用角平分线与平行线证明△BEO和△CFO是等腰三角形即可;(2)利用角平分线与平行线证明△BEO和△CFO是等腰三角形即可.【解答】解:(1)∵BO平分∠ABC,CO平分∠ACB,∴∠ABO=∠OBC,∠ACO=∠OCB,∵EF∥BC,∴∠EOB=∠OBC,∠FOC=∠OCB,∴∠EBO=∠EOB,∠FOC=∠FCO,∴EB=EO,FC=FO,∵EF=EO+FO,∴EF=EB+FC,故答案为:EF=EB+FC;(2)EF=BE﹣CF,理由是:∵BO平分∠ABC,∴∠ABO=∠OBC,∵EF∥BC,∴∠EOB=∠OBC,∴∠EBO=∠EOB,∴EB=EO,同理可得:FO=CF,∵EF=EO﹣FO,∴EF=BE﹣CF.【点评】本题考查了等腰三角形的判定与性质,平行线的性质,结合图形找到角与边的关系是解题的关键.5.如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点O,且∠BAC=60°,∠C=70°.求∠DAC和∠BOE的度数.【分析】根据垂直的定义得到∠ADC=90°根据三角形的内角和即可得到结论;根据三角形的内角和和角平分线的定义即可得到结论.【解答】解:∵AD是高,∴∠ADC=90°,∵∠C=70°,∴∠DAC=180°﹣90°﹣70°=20°,∵∠BAC=60°∠C=70°,∴∠ABC=180°﹣60°﹣70°=50°,∵BF平分∠ABC,∴∠ABF=∠ABC=25°,∵AE平分∠BAC,∴∠BAE=∠BAC=30°,∴∠BOE=∠BAE+∠ABF=55°.【点评】本题考查了三角形内角和定理、角平分线定义.关键是利用角平分线的性质解出∠ABF、∠BAE.6.在△ABC中,∠A=40°:(1)如图(1)BO、CO是△ABC的内角角平分线,且相交于点O,求∠BOC;(2)如图(2)BO、CO是△ABC的外角角平分线,且相交于点O,求∠BOC;(3)如图(3)BO、CO分别是△ABC的一内角和一外角角平分线,且相交于点O,求∠BOC;(4)根据上述三问的结果,当∠A=n时,分别可以得出∠BOC与∠A有怎样的数量关系(只需写出结论).【分析】(1)根据三角形内角和定理得到∠BOC=180°﹣∠OBC﹣∠OCB,则2∠BOC=360°﹣2∠OBC﹣2∠OCB,再根据角平分线的定义得∠ABC=2∠OBC,∠ACB=2∠OCB,则2∠BOC=360°﹣∠ABC﹣∠ACB,易得∠BOC=90°+∠A.(2)根据三角形内角和定理和外角性质可得到∠BOC=90°﹣∠A;(3)根据角平分线的定义得∠ACD=2∠OCD,∠ABC=2∠OBC,由三角形外角的性质有∠OCD=∠BOC+∠OBC,∠ACD=∠ABC+∠A,则2∠BOC+2∠OBC=∠ABC+∠A,即可得到∠BOC=∠A;(4)利用以上结论直接得出答案即可.【解答】解:(1)∵∠BOC=180°﹣∠OBC﹣∠OCB,∴2∠BOC=360°﹣2∠OBC﹣2∠OCB,而BO平分∠ABC,CO平分∠ACB,∴∠ABC=2∠OBC,∠ACB=2∠OCB,∴2∠BOC=360°﹣(∠ABC+∠ACB),∵∠ABC+∠ACB=180°﹣∠A,∴2∠BOC=180°+∠A,∴∠BOC=90°+∠A.当∠A=40°,∠BOC=110°;(2)∠OBC=(∠A+∠ACB),∠OCB=(∠A+∠ABC),∠BOC=180°﹣∠0BC﹣∠OCB,=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),=180°﹣∠A﹣(∠A+∠ABC+∠ACB),结论∠BOC=90°﹣∠A.∠BOC=90°﹣∠A.当∠A=40°,∠BOC=70°.(3)∵∠OCD=∠BOC+∠OBC,∠ACD=∠ABC+∠A,而BO平分∠ABC,CO平分∠ACD,∴∠ACD=2∠OCD,∠ABC=2∠OBC,∴2∠BOC+2∠OBC=∠ABC+∠A,∴2∠BOC=∠A,即∠BOC=∠A.当∠A=40°,∠BOC=20°;(4)∠BOC=90°+n;∠BOC=90°﹣n;∠BOC=n.【点评】本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.7.如图,已知∠ABC、∠ACB的平分线相交于点O,EF过点O且EF∥BC.(1)若∠ABC=50°,∠ACB=60°,求∠BOC的度数;(2)若∠BOC=130°,∠1:∠2=3:2,求∠ABC、∠ACB的度数.【分析】(1)由角平分线的定义可求解∠OBC=25°,∠OCB=30°,再利用三角形的内角和定理可求解;(2)由已知条件易求∠1,∠2的度数,根据平行线的性质即可得∠OBC,∠OCB的度数,利用角平分线的定义可求解.【解答】解:(1)∵∠ABC和∠ACB的平分线BO与CO相交于点O,所以∠EBO=∠OBC=,∠FCO=∠OCB=,又∠ABC=50°,∠ACB=60°,∴∠OBC=25°,∠OCB=30°,∴∠BOC=180°﹣∠OBC﹣∠OCB=125°;(2)∵∠BOC=130°,∴∠1+∠2=50°,∵∠1:∠2=3:2,∴,,∵EF∥BC,∴∠OBC=∠1=30°,∠OCB=∠2=20°,∵∠ABC和∠ACB的平分线BO与CO相交于点O,∴∠ABC=60°,∠ACB=40°.【点评】本题主要考查角平分线的定义,三角形的内角和定理,平行线的性质,等腰三角形的性质等知识的综合运用.8.已知△ABC(1)①如图1,若P点是∠ABC和∠ACB的角平分线的交点,探究∠P与∠A之间数量关系,并说明理由;②如图2,若P点是∠ABC和∠ACE的角平分线的交点,∠P与∠A之间数量关系是;③如图3,若P点是∠CBF和∠BCE的角平分线的交点,∠P与∠A之间数量关系是.(2)运用所得到的结论,解决下面的问题:如图4,在△ABC中,∠ABC与∠ACB的平分线相交于点O,连接AO,若∠BOC=130°,则∠BAC =°,∠BAO=°.【分析】(1)根据三角形的外角性质、内角和定理、角平分线的定义探求并证明.(2)求出∠OBC+∠OCB,根据角平分线性质求出∠ABC+∠ACB,根据三角形内角和定理求出∠BAC,即可求出答案.【解答】解:(1)①如图1:∠P=90°+∠A;理由:∵BP平分∠ABC,CP平分∠ACB,∴∠PBC=∠ABC,∠BCP=∠ACB.∵∠P=180°﹣∠PBC﹣∠BCP,∴∠P=180°﹣∠ABC﹣∠ACB=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A.②如图2:∠P=∠A;③如图3:∠P=90°﹣∠A;故答案为:∠P=∠A,∠P=90°﹣∠A;(2)∵BO、CO分别为∠ABC与∠ACB的角平分线,∴OA是∠BAC的角平分线,∴∠BAO=∠BAC,∵∠BOC=130°,∴∠OBC+∠OCB=180°﹣130°=50°,∵BO、CO分别为∠ABC与∠ACB的角平分线,∴∠ABC=2∠OBC,∠ACB=2∠OCB,∴∠ABC+∠ACB=2×50°=100°,∴∠BAC=180°﹣(∠ABC+∠ACB)=80°,∴∠BAO=∠BAC=40°,故答案为:80,40.【点评】本题考查了角平分线性质,三角形内角和定理的应用,此题是一道比较典型的题目,难度适中,注意:角平分线上的点到角的两边的距离相等.9.已知△ABC中,∠A=x°(1)如图1,若∠ABC和∠ACB的角平分线相交于点O,则用含x的代数式表示∠BOC,写出推理过程.(2)如图2,若∠ABC和∠ACB的三等分线相交于点O1、O2,则用含x的代数式表示∠BO1C,写出推理过程.(3)如图3,若∠ABC和∠ACB的n等分线相交于点O1、O2、…、O n﹣1,则用含n,x的代数式表示∠BO1C,不需要推理过程,直接写出结果.【分析】(1)由∠ABC和∠ACB的角平分线相交于点O,易得:2∠OBC=∠ABC,2∠OCB=∠ACB,又由三角形内角和定理,可得:∠A+2∠OBC+2∠OCB=180°,∠BOC+∠OBC+∠OCB=180°,即可求得∠BOC的值;(2)由∠ABC和∠ACB的三等分线相交于点O1、O2,即可得∠O1BC=∠ABC,∠O1CB=∠ACB,又由三角形内角和定理,可得:∠A+∠O1BC+∠O1CB=180°,∠BO1C+∠O1BC+∠O1CB=180°,即可求得∠BO1C的值;(3)观察(1)(2),即可得规律:若∠ABC和∠ACB的n等分线相交于点O1、O2、…、O n﹣1,则∠BO1C=(+x)°【解答】解:(1)∵∠ABC和∠ACB的角平分线相交于点O,∴2∠OBC=∠ABC,2∠OCB=∠ACB,∵∠A+∠ABC+∠ACB=180°,∴∠A+2∠OBC+2∠OCB=180°,∴∠OBC+∠OCB=90°﹣∠A,∵∠BOC=180°﹣(∠OBC+∠OCB)=90°+∠A,∵∠A=x°,∴∠BOC=(90+x)°;(2)∵∠ABC和∠ACB的三等分线相交于点O1、O2,∴∠O1BC=∠ABC,∠O1CB=∠ACB,∴∠O1BC=∠ABC,∠O1CB=∠ACB,∵∠A+∠ABC+∠ACB=180°,∴∠A+∠O1BC+∠O1CB=180°,∴∠O1BC+∠O1CB=(180°﹣∠A),∵∠BOC=180°﹣(∠O1BC+∠O1CB)=60°+∠A,∵∠A=x°,∴∠BOC=(60+x)°;(3)由(1)(2)可得规律为:若∠ABC和∠ACB的n等分线相交于点O1、O2、…、O n﹣1,则用x表示∠BO1C=(+x)°【点评】此题考查了角的等分线的性质以及三角形内角和定理.注意找的规律:若∠ABC和∠ACB的n等分线相交于点O1、O2、…、O n﹣1,则用x表示∠BO1C=(+x)°,是解此题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角度计算中的经典模型【举一反三】【模型1 双垂直模型】【条件】∠B=∠D=∠ACE=90°.【结论】∠BAC=∠DCE,∠ACB=∠CED.【例1】(2019春•润州区校级月考)如图,在△ABC中,∠ACB=90°,F是AC延长线上一点,FD⊥AB,垂足为D,FD与BC相交于点E,∠BED=55°.求∠A的度数.【变式1-1】(2019秋•凉州区校级期中)如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠A的度数.【变式1-2】(2019春•莲湖区期中)如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.(1)求证:∠ACD=∠B;(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.【变式1-3】(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,∠ACD与∠B有什么关系?为什么?(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状是什么?为什么?(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,AB⊥BD,点C,B,E在同一直线上,∠A与∠D有什么关系?为什么?【模型2 A字模型】【结论】∠BDE+∠CED=180°+∠A【例2】(2019春•资中县月考)如图所示,△ABC中,∠C=75°,若沿图中虚线截去∠C,则∠1+∠2等于多少度?【变式2-1】(2019春•长沙县校级期中)如图,已知∠A=40°,求∠1+∠2+∠3+∠4的度数.【变式2-2】(2019春•盱眙县期中)我们容易证明,三角形的一个外角等于它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?Ⅰ.尝试探究:(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?Ⅱ.初步应用:(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2﹣∠C=;(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案.【变式2-3】(2019春•盐都区期中)(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于A.90°B.135°C.270°D.315°(2)如图2,已知△ABC中,∠A=50°,剪去∠A后成四边形,则∠1+∠2=°.(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是.(4)如图3,若∠A没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.【模型3 双内角平分线模型】【条件】BP、CP分别为∠ABC、∠ACB的角平分线.1∠A.【结论】∠P=90°+2【例3】(2018秋•开封期中)如图,△ABC中,(1)若∠B=70°,点P是△ABC的∠BAC和∠ACB的平分线的交点,求∠APC的度数.(2)如果把(1)中∠B=70°这个条件去掉,试探索∠APC和∠B之间有怎样的数量关系.【变式3-1】(2018秋•徐闻县期中)如图,在△ABC 中,∠ABC 与∠ACB 的平分线交于点O . (1)如图1,已知∠ABC =40°,∠ACB =60°,求∠BOC 的度数. (2)如图2,已知∠A =90°,求∠BOC 的度数. (3)如图1,设∠A =m °,求∠BOC 的度数.【变式3-2】(2019春•南岗区期末)已知在△ABC 中,∠A =100°,点D 在△ABC 的内部连接BD ,CD , 且∠ABD =∠CBD ,∠ACD =∠BCD . (1)如图1,求∠BDC 的度数;(2)如图2,延长BD 交AC 于点E ,延长CD 交AB 于点F ,若∠AED ﹣∠AFD =12°,求∠ACF 的度数.【变式3-3】(2019春•东阿县期末)已知任意一个三角形的三个内角的和是180°.如图1,在△ABC 中, ∠ABC 的角平分线BO 与∠ACB 的角平分线CO 的交点为O (1)若∠A =70°,求∠BOC 的度数; (2)若∠A =a ,求∠BOC 的度数;(3)如图2,若BO 、CO 分别是∠ABC 、∠ACB 的三等分线,也就是∠OBC=31∠ABC ,∠OCB=31∠ACB ,∠A =a ,求∠BOC 的度数.【模型4 内外角平分线模型】【条件】BP、CP分别为∠ABC、∠ACD的角平分线.1∠P.【结论】∠A=2【例4】(2018秋•江岸区期中)如图,△ABC中,∠ABC与∠ACB的外角的平分线相交于点E.(1)已知∠A=60°,求∠E的度数;(2)直接写出∠A与∠E的数量关系:.【变式4-1】(2019秋•卫滨区校级期中)如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP 交于点P,若∠BPC=40°,求∠CAB的度数.【变式4-2】(2019秋•莆田校级期中)如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE 的平分线,且与BD交于点D;(1)若∠ABC=60°,∠DCE=70°,则∠D=°;(2)若∠ABC=70°,∠A=80°,则∠D=°;(3)当∠ABC和∠ACB在变化,而∠A始终保持不变,则∠D是否发生变化?为什么?由此你能得出什么结论?(用含∠A的式子表示∠D)【变式4-3】(2018秋•彭水县校级月考)如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE 的外角平分线,CD与BD交于点D.(1)若∠A=50°,则∠D=;(2)若∠A=80°,则∠D=;(3)若∠A=130°,则∠D=;(4)若∠D=36°,则∠A=;(5)综上所述,你会得到什么结论?证明你的结论的准确性.【模型5 双外角平分线模型】【条件】BP 、CP 分别为∠EBC 、∠BCD 的角平分线. 【结论】∠P=90°-21∠A.【例5】(2018秋•鄂伦春自治旗月考)如图,△ABC 中,分别延长△ABC 的边AB 、AC 到D 、E ,∠CBD 与∠BCE 的平分线相交于点P ,爱动脑筋的小明在写作业的时发现如下规律: (1)若∠A =60°,则∠P = °; (2)若∠A =40°,则∠P = °; (3)若∠A =100°,则∠P = °;(4)请你用数学表达式归纳∠A 与∠P 的关系 .【变式5-1】(2019秋•团风县校级月考)BD 、CD 分别是△ABC 的两个外角∠CBE 、∠BCF 的平分线, 求证:∠BDC =90°21∠A .【变式5-2】(2019春•雨城区校级期中)如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,(1)若∠ABC=40°,∠ACB=36°,求∠BIC的大小;(2)若∠A=96°,试求∠BIC;(3)根据前面问题的求解,请归纳∠BIC和∠A的数量关系并进行证明.【变式5-3】如图,在△ABC中,BD,CD是内角平分线,BP,CP是∠ABC,∠ACB的外角平分线,分别交于点D,P.(1)若∠A=30°,求∠BDC,∠BPC的度数.(2)若∠A=m°,求∠BDC,∠BPC的度数(直接写出结果,不必说明理由)(3)想一想,∠A的大小变化,对∠D+∠P的值是否有影响,若有影响,请说明理由,若无影响,直接求出其值.【模型6 8字模型】【结论】∠A+∠B=∠D+∠E.【例6】(2019春•辉县市期末)图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:;(2)仔细观察,在图2中“8字形”的个数:个;(3)图2中,当∠D=50度,∠B=40度时,求∠P的度数.(4)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结果,不必证明).【变式6-1】(2018春•新泰市期中)已知:如图,AM,CM分别平分∠BAD和∠BCD.①若∠B=32°,∠D=38°,求∠M的度数;②探索∠M与∠B、∠D的关系并证明你的结论.【变式6-2】(2018秋•南昌期中)如图1,已知线段AB 、CD 相交于点O ,连接AC 、BD ,则我们把形如这 样的图形称为“8字型”. (1)求证:∠A +∠C =∠B +∠D ;(2)如图2,若∠CAB 和∠BDC 的平分线AP 和DP 相交于点P ,且与CD 、AB 分别相交于点M 、N . ①以线段AC 为边的“8字型”有 个,以点O 为交点的“8字型”有 个; ②若∠B =100°,∠C =120°,求∠P 的度数;③若角平分线中角的关系改为“∠CAP=31∠CAB ,∠CDP=31∠CDB ”,试探究∠P 与∠B 、∠C 之间存在的数量关系,并证明理由.【变式6-3】(2018秋•青岛期末)【问题背景】(1)如图1的图形我们把它称为“8字形”,请说理证明∠A +∠B =∠C +∠D【简单应用】(2)如图2,AP 、CP 分别平分∠BAD 、∠BCD ,若∠ABC =20°,∠ADC =26°,求∠P 的度数(可直接使用问题(1)中的结论) 【问题探究】(3)如图3,直线AP 平分∠BAD 的外角∠F AD ,CP 平分∠BCD 的外角∠BCE ,若∠ABC =36°,∠ADC =16°,猜想∠P 的度数为【拓展延伸】(4)在图4中,若设∠C =x ,∠B =y ,∠CAP=31∠CAB ,∠CDP=31∠CDB ,试问∠P 与∠C 、∠B 之间的数量关系为 (用x 、y 表示∠P )(5)在图5中,AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、∠D 的关系,直接写出结论 . 【模型7 燕尾模型】【结论】∠BPC=∠A+∠B+∠C.【例7】(2019春•冠县期末)(1)探究:如图1,求证:∠BOC =∠A +∠B +∠C .(2)应用:如图2,∠ABC =100°,∠DEF =130°,求∠A +∠C +∠D +∠F 的度数.【变式7-1】(2019秋•平度市期末)材料阅读:如图①所示的图形,像我们常见的学习用品﹣圆规.我 们不妨把这样图形叫做“规形图”. 解决问题:(1)观察“规形图”,试探究∠BDC与∠A,∠B,∠C之间的数量关系,并说明理由;(2)请你直接利用以上结论,解决以下两个问题:Ⅰ.如图②,把一块三角尺DEF放置在△ABC上,使三角尺的两条直角边DE,DF恰好经过点B,C,若∠A=40°,则∠ABD+∠ACD=°.Ⅱ.如图③,BD平分∠ABP,CD平分∠ACP,若∠A=40°,∠BPC=130°,求∠BDC的度数.【变式7-2】(2019秋•阜阳月考)在数学学习中整体思想与转化思想是我们常用到的数学思想.如图(1)中,求∠A+∠B+∠C+∠D+∠E的度数等于多少时,我们可以连接CD,利用三角形的内角和则有∠B+∠E =∠ECD+∠BDC,这样∠A、∠B、∠C、∠D、∠E的和就转化到同一个△ACD中,即∠A+∠B+∠C+∠D+∠E=180°.尝试练习:图(2)中∠A+∠B+∠C+∠D+∠E的度数等于.图(3)中∠A+∠B+∠C+∠D+∠E的度数等于.图(4)中∠A+∠B+∠C+∠D+∠E+∠F的度数等于.【变式7-3】(2019秋•襄城区期中)已知:点D是△ABC所在平面内一点,连接AD、CD.(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;(3)如图3,在(2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.【模型8 筝型】【结论】∠PBD+∠PCD=∠A+∠P【例8】(2019春•邳州市校级月考)如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合.(1)若∠A=75°,则∠1+∠2=.(2)若∠A=n°,则∠1+∠2=.(3)由(1)(2)探索∠A与∠1+∠2之间的数量关系,并说明理由.【变式8-1】(2018春•迁安市期末)动手操作:一个三角形的纸片ABC,沿DE折叠,使点A落在点Aˊ处.观察猜想(1)如图1,若∠A=40°,则∠1+∠2=°;若∠A=55°,则∠1+∠2=°;若∠A=n°,则∠1+∠2=°.探索证明:(2)利用图1,探索∠1、∠2与∠A有怎样的关系?请说明理由.拓展应用:(3)如图2,把△ABC折叠后,BA′平分∠ABC,CA′平分∠ACB,若∠1+∠2=108°,利用(2)中结论求∠BA′C的度数.【变式8-2】(2019春•宿城区校级月考)Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图(1)所示,且∠α=50°,求∠1+∠2的度数;(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由;(3)若点P运动到边AB的延长线上,如图(3)所示,直接写出∠α、∠1、∠2之间关系为:.(不需说明理由).【变式8-3】(2019秋•南漳县校级月考)如图(1),在折纸活动中,小明制作了一张△ABC的纸片,点D、E分别在AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=70°,则∠1+∠2=;如图(2),当点A落在△ABC外部时,那么∠2﹣∠1=.专题02 角度计算中的经典模型【举一反三】【模型1 双垂直模型】【条件】∠B=∠D=∠ACE=90°.【结论】∠BAC=∠DCE,∠ACB=∠CED.【例1】(2019春•润州区校级月考)如图,在△ABC中,∠ACB=90°,F是AC延长线上一点,FD⊥AB,垂足为D,FD与BC相交于点E,∠BED=55°.求∠A的度数.【分析】首先由FD⊥AB于D,根据直角三角形两锐角互余得出∠BED+∠B=90°,同理,由∠ACB=90°,得出∠A+∠B=90°,然后根据同角的余角相等得出∠A=∠BED=55°.【答案】解:∵FD⊥AB于D,∴∠BED+∠B=90°,∵∠ACB=90°,∴∠A+∠B=90°,∴∠A=∠BED=55°.【点睛】本题主要考查了直角三角形的性质以及余角的性质,比较简单.【变式1-1】(2019秋•凉州区校级期中)如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠A的度数.【分析】利用外角性质可求得∠C,在△ABC中利用三角形内角和定理可求得∠A.【答案】解:∵DF⊥BC,∴∠FDC=90°,∵∠AFD=152°,∴∠C=∠AFD﹣∠FDC=152°﹣90°=62°,∵∠B=∠C,∴∠A=180°﹣∠B﹣∠C=180°﹣62°﹣62°=56°.【点睛】本题主要考查三角形内角和定理,掌握三角形三个内角和为180°是解题的关键.【变式1-2】(2019春•莲湖区期中)如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.(1)求证:∠ACD=∠B;(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.【分析】(1)由于∠ACD与∠B都是∠BCD的余角,根据同角的余角相等即可得证;(2)根据直角三角形两锐角互余得出∠CF A=90°﹣∠CAF,∠AED=90°﹣∠DAE,再根据角平分线的定义得出∠CAF=∠DAE,然后由对顶角相等的性质,等量代换即可证明∠CEF=∠CFE.【答案】证明:(1)∵∠ACB=90゜,CD⊥AB于D,∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,∴∠ACD=∠B;(2)在Rt△AFC中,∠CF A=90°﹣∠CAF,同理在Rt△AED中,∠AED=90°﹣∠DAE.又∵AF平分∠CAB,∴∠CAF=∠DAE,∴∠AED=∠CFE,又∵∠CEF=∠AED,∴∠CEF=∠CFE.【点睛】本题考查了直角三角形的性质,三角形角平分线的定义,对顶角的性质,余角的性质,难度适中.【变式1-3】(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,∠ACD与∠B有什么关系?为什么?(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状是什么?为什么?(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,AB⊥BD,点C,B,E在同一直线上,∠A与∠D有什么关系?为什么?【分析】(1)根据直角三角形的性质得出∠ACD+∠A=∠B+∠DCB=90°,再解答即可;(2)根据直角三角形的性质得出∠ADE+∠A=∠A+∠B=90°,再解答即可;(3)根据直角三角形的性质得出∠ABC+∠A=∠ABC+∠DBE=∠DBE+∠D=90°,再解答即可.【答案】解:(1)∠ACD=∠B,理由如下:∵在Rt△ABC中,∠ACB=90°,CD⊥AB,∴∠ACD+∠A=∠B+∠DCB=90°,∴∠ACD=∠B;(2)△ADE是直角三角形.∵在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,∠A为公共角,∴∠AED=∠ACB=90°,∴△ADE是直角三角新;(3)∠A+∠D=90°.∵在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,AB⊥BD,∴∠ABC+∠A=∠ABC+∠DBE=∠DBE+∠D=90°,∴∠A+∠D=90°.【点睛】此题考查直角三角形的性质,关键是根据直角三角形的性质得出两锐角互余.【模型2 A字模型】【结论】∠BDE+∠CED=180°+∠A【例2】(2019春•资中县月考)如图所示,△ABC中,∠C=75°,若沿图中虚线截去∠C,则∠1+∠2等于多少度?【分析】根据三角形内角和定理求出∠A+∠B,根据多边形的内角和公式求出即可.【答案】解:∵∠A+∠B+∠C=180°,∴∠A+∠B=180°﹣∠C,∵∠C=75°,∴∠A+∠B=180°﹣75°=105°,∵∠1+∠2+∠A+∠B=360°,∴∠1+∠2=360°﹣(∠A+∠B),∴∠1+∠2=360°﹣105°=255°.【点睛】本题考查了三角形的内角和定理和多边形的内角和公式,能熟记定理是解此题的关键.【变式2-1】(2019春•长沙县校级期中)如图,已知∠A=40°,求∠1+∠2+∠3+∠4的度数.【分析】根据三角形的内角和定理分别求得∠1+∠2,∠3+∠4,就可求得最后结果.【答案】解:∵∠A=40°,∴∠1+∠2=∠3+∠4=180°﹣∠A=140°.∴∠1+∠2+∠3+∠4=280°.【点睛】此题主要是三角形内角和定理的运用.【变式2-2】(2019春•盱眙县期中)我们容易证明,三角形的一个外角等于它不相邻的两个内角的和,那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?Ⅰ.尝试探究:(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?Ⅱ.初步应用:(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2﹣∠C=;(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案.【分析】(1)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠DBC+∠ECB,再利用三角形内角和定理整理即可得解;(2)根据(1)的结论整理计算即可得解;(3)表示出∠DBC+∠ECB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形内角和定理列式整理即可得解;【答案】解:(1)∠DBC+∠ECB=180°﹣∠ABC+180°﹣∠ACB=360°﹣(∠ABC+∠ACB)=360°﹣(180°﹣∠A)=180°+∠A;(2)∵∠1+∠2=∠180°+∠C,∴130°+∠2=180°+∠C,∴∠2﹣∠C=50°;(3)∠DBC+∠ECB=180°+∠A,∵BP、CP分别平分外角∠DBC、∠ECB,∴∠PBC+∠PCB=(∠DBC+∠ECB)=(180°+∠A)在△PBC中,∠P=180°﹣(180°+∠A)=90°﹣∠A;即∠P=90°﹣∠A;故答案为:50°,∠P=90°﹣∠A.【点睛】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,角平分线的定义,熟记性质并读懂题目信息是解题的关键.【变式2-3】(2019春•盐都区期中)(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于A.90°B.135°C.270°D.315°(2)如图2,已知△ABC中,∠A=50°,剪去∠A后成四边形,则∠1+∠2=°.(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是.(4)如图3,若∠A没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.【分析】(1)利用了四边形内角和为360°和直角三角形的性质求解;(2)根据三角形的外角等于与它不相邻的两个内角和求解;(3)根据(1)(2)可以直接写出结果;(4)根据折叠的性质,对应角相等,以及邻补角的性质即可求解.【答案】解:(1)∵四边形的内角和为360°,直角三角形中两个锐角和为90°∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.∴∠1+∠2等于270°.故选C;(2)∠1+∠2=180°+50°=230°.故答案是:230;(3)∠1+∠2与∠A的关系是:∠1+∠2=180°+∠A;故答案是:∠1+∠2=180°+∠A;(4)∵△EFP是由△EF A折叠得到的,∴∠AFE=∠PFE,∠AEF=∠PEF∴∠1=180°﹣2∠AFE,∠2=180°﹣2∠AEF∴∠1+∠2=360°﹣2(∠AFE+∠AEF)又∵∠AFE+∠AEF=180°﹣∠A,∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A,即∠1+∠2=2∠A.【点睛】主要考查了三角形的内角和外角之间的关系.(1)三角形的外角等于与它不相邻的两个内角和.(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.【模型3 双内角平分线模型】【条件】BP、CP分别为∠ABC、∠ACB的角平分线.1∠A.【结论】∠P=90°+2【例3】(2018秋•开封期中)如图,△ABC中,(1)若∠B=70°,点P是△ABC的∠BAC和∠ACB的平分线的交点,求∠APC的度数.(2)如果把(1)中∠B=70°这个条件去掉,试探索∠APC和∠B之间有怎样的数量关系.【分析】(1)依据点P是△ABC的∠BAC和∠ACB的平分线的交点,即可得到∠P AC=∠BAC,∠PCA =∠BCA,再根据三角形内角和定理,即可得到∠APC的度数.(2)依据点P是△ABC的∠BAC和∠ACB的平分线的交点,即可得到∠P AC=∠BAC,∠PCA=∠BCA,进而得出∠P AC+∠PCA=(∠P AC+∠PCA),再根据∠P=180°﹣(∠P AC+∠PCA)进行计算即可.【答案】解:(1)∵∠B=70°,∴∠BAC+∠BCA=110°,∵点P是△ABC的∠BAC和∠ACB的平分线的交点,∴∠P AC=∠BAC,∠PCA=∠BCA,∴∠P AC+∠PCA=(∠P AC+∠PCA)=×110°=55°,∴∠P=180°﹣55°=125°;(2)∵点P是△ABC的∠BAC和∠ACB的平分线的交点,∴∠P AC=∠BAC,∠PCA=∠BCA,∴∠P AC+∠PCA=(∠P AC+∠PCA),∴∠P=180°﹣(∠P AC+∠PCA)=180°﹣(∠BAC+∠BCA)=180°﹣(180°﹣∠B)=90°+∠B.【点睛】本题主要考查了三角形内角和定理以及角平分线的定义,解决问题的关键是掌握三角形内角和定理:三角形内角和是180°.【变式3-1】(2018秋•徐闻县期中)如图,在△ABC中,∠ABC与∠ACB的平分线交于点O.(1)如图1,已知∠ABC=40°,∠ACB=60°,求∠BOC的度数.(2)如图2,已知∠A=90°,求∠BOC的度数.(3)如图1,设∠A=m°,求∠BOC的度数.【分析】根据三角形内角和定理以及角平分线的定义求解即可;【答案】解:(1)∵BC平分∠ABC,∠ABC=40°,∴∠OBC=∠ABC=20°,∵CO平分∠ACB,∠ACB=60°,∴∠OCB=∠ACB=30°,∴∠BOC=180°﹣20°﹣30°=130°.(2)∵∠A=90°,∴∠ABC+∠ACB=180°﹣90°=90°,又∵∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=45°,∴∠BOC=180°﹣45°=135°.(3)∵∠A=m°∴∠ABC+∠ACB=180°﹣m°,又∵∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=90°﹣m°,∴∠BOC=90°+m°.【点睛】本题考查三角形内角和定理,角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.【变式3-2】(2019春•南岗区期末)已知在△ABC中,∠A=100°,点D在△ABC的内部连接BD,CD,且∠ABD=∠CBD,∠ACD=∠BCD.(1)如图1,求∠BDC的度数;(2)如图2,延长BD交AC于点E,延长CD交AB于点F,若∠AED﹣∠AFD=12°,求∠ACF的度数.【分析】(1)依据三角形内角和定理以及角平分线的定义,即可得到∠BDC的度数;(2)设∠ACF=α,则∠BCD=α,∠CBD=40°﹣α=∠ABD,依据三角形外角性质,即可得到∠AED =∠ACF+∠CDF,∠AFD=∠ABE+∠BDF,再根据∠AED﹣∠AFD=12°,即可得到α的值.【答案】解:(1)∵∠A=100°,∴∠ABC +∠ACB =80°,又∵∠ABD =∠CBD ,∠ACD =∠BCD , ∴∠CBD =∠ABC ,∠BCD =∠ACB , ∴∠CBD +∠BCD =(∠ABC +∠ACB )=40°, ∴∠BDC =180°﹣40°=140°;(2)设∠ACF =α,则∠BCD =α, ∵∠BDC =140°,∴∠CBD =40°﹣α=∠ABD ,∵∠AED 是△DCE 的外角,∠AFD 是△BDF 的外角, ∴∠AED =∠ACF +∠CDF ,∠AFD =∠ABE +∠BDF ,∴∠AED ﹣∠AFD =∠ACF +∠CDF ﹣∠ABE ﹣∠BDE =α﹣(40°﹣α)=12°, 解得α=26°, ∴∠ACF =26°.【点睛】本题主要考查了三角形内角和定理以及三角形外角性质的运用,解题时注意:三角形内角和是180°.【变式3-3】(2019春•东阿县期末)已知任意一个三角形的三个内角的和是180°.如图1,在△ABC 中, ∠ABC 的角平分线BO 与∠ACB 的角平分线CO 的交点为O (1)若∠A =70°,求∠BOC 的度数; (2)若∠A =a ,求∠BOC 的度数;(3)如图2,若BO 、CO 分别是∠ABC 、∠ACB 的三等分线,也就是∠OBC=31∠ABC ,∠OCB=31∠ACB ,∠A =a ,求∠BOC 的度数.【分析】(1)根据三角形的内角和定理求出∠ABC +∠ACB ,根据角平分线的定义求出∠OBC +∠OCB ,根据三角形内角和定理求出即可;(2)根据三角形的内角和定理求出∠ABC+∠ACB,根据角平分线的定义求出∠OBC+∠OCB,根据三角形内角和定理求出即可;(3)根据三角形的内角和定理求出∠ABC+∠ACB,求出∠OBC+∠OCB,根据三角形内角和定理求出即可.【答案】解:(1)∵∠A=70°,∴∠ABC+∠ACB=180°﹣∠A=110°,∵在△ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O,∴∠OBC=∠ABC,∠OCB=ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=55°,∴∠BOC=180°﹣(∠OBC+∠OCB)=125°;(2)∵∠A=α,∴∠ABC+∠ACB=180°﹣∠A=180°﹣α,∵在△ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O,∴∠OBC=∠ABC,∠OCB=ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣α)=90°﹣,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(90°﹣)=90°+;(3)∵∠A=α,∴∠ABC+∠ACB=180°﹣∠A=180°﹣α,∵∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣α)=60°﹣,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(60°﹣)=120°+.【点睛】本题考查了三角形的内角和定理和角平分线的定义,能求出∠OBC+∠OCB是解此题的关键,求解过程类似.【模型4 内外角平分线模型】【条件】BP、CP分别为∠ABC、∠ACD的角平分线.1∠P.【结论】∠A=2【例4】(2018秋•江岸区期中)如图,△ABC中,∠ABC与∠ACB的外角的平分线相交于点E.(1)已知∠A=60°,求∠E的度数;(2)直接写出∠A与∠E的数量关系:.【分析】(1)根据角平分线的定义得到∠ECD=∠ACD,∠EBC=∠ABC,根据三角形的外角的性质计算;(2)仿照(1)的计算过程证明.【答案】解:(1)∵CE、BE分别平分∠ACD、∠ABC,∴∠ECD=∠ACD,∠EBC=∠ABC,∴∠E=∠ECD﹣∠EBD=(∠ACD﹣∠ABC)=∠A=30°;(2)由(1)得,∠E=∠A,∴∠A=2∠E故答案为:∠A=2∠E.【点睛】本题考查的是角平分线的定义,三角形的外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.【变式4-1】(2019秋•卫滨区校级期中)如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB的度数.【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠BAC+∠ABC,∠PCD=∠P+∠PCB,根据角平分线的定义可得∠PCD=∠ACD,∠PBC=∠ABC,然后整理得到∠PCD=40°+∠ABC,再代入数据计算即可得解.【答案】解:在△ABC中,∠ACD=∠BAC+∠ABC,在△PBC中,∠PCD=∠BPC+∠PBC,∵PB、PC分别是∠ABC和∠ACD的平分线,∴∠PCD=∠ACD,∠PBC=∠ABC,∴∠PCD=∠BPC+∠PBC=40°+∠ABC,∴∠ACD=∠ABC+40°,∴∠ACD﹣∠ABC=80°,∴∠BAC=∠ACD﹣∠ABC=80°,即∠CAB=80°.【点睛】本题考查了三角形内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记定理与性质并求出∠PCD=40°+∠ABC是解题的关键.【变式4-2】(2019秋•莆田校级期中)如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE 的平分线,且与BD交于点D;(1)若∠ABC=60°,∠DCE=70°,则∠D=°;(2)若∠ABC=70°,∠A=80°,则∠D=°;(3)当∠ABC和∠ACB在变化,而∠A始终保持不变,则∠D是否发生变化?为什么?由此你能得出什么结论?(用含∠A的式子表示∠D)【分析】(1)根据三角形内角和定理和三角形外角的性质即可求得;(2)根据三角形内角和定理和三角形外角的性质即可求得;(3)根据三角形内角和定理以及角平分线性质,先求出∠D、∠A的等式,推出∠D=∠A,即可求得结论.【答案】解:(1)∵BD为△ABC的角平分线,∠ABC=60°,∴∠DBC=30°,∵∠DCE=70°,∴∠D=∠DCE﹣∠DBC=70°﹣30°=40°;(2)∵∠ABC=70°,∠A=80°,∴∠ACE=150°∵BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,∴∠DBC=∠ABC=35°,∠DCE=∠ACE=75°,∴∠D=∠DCE﹣∠DBC=75°﹣35°=40°;(3)不变化,理由:∵∠DCE=∠DBC+∠D,∴∠D=∠ACE﹣∠ABC=(∠A+∠ABC)﹣∠ABC=∠A.故答案为40;40.【点睛】此题考查三角形内角和定理以及三角形外角的性质的综合运用,解此题的关键是求出∠D=∠A.【变式4-3】(2018秋•彭水县校级月考)如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE 的外角平分线,CD与BD交于点D.(1)若∠A=50°,则∠D=;(2)若∠A=80°,则∠D=;(3)若∠A=130°,则∠D=;(4)若∠D=36°,则∠A=;(5)综上所述,你会得到什么结论?证明你的结论的准确性.【分析】先根据角平分线定义得到∠ACE=2∠2,∠ABC=2∠1,再根据三角形外角性质得∠ACE=∠ABC+∠A,则2∠2=2∠1+∠A,接着再根据三角形外角性质得∠2=∠1+∠D,易得∠A=2∠D,即∠D =∠A,然后利用此结论分别解决(1)、(2)、(3)(4)(5).【答案】解:如图,∵BD是△ABC的角平分线,CD是△ABC的外角∠ACE的平分线,∴∠ACE=2∠2,∠ABC=2∠1,∵∠ACE=∠ABC+∠A,∴2∠2=2∠1+∠A,而∠2=∠1+∠D,∴2∠2=2∠1+2∠D,∴∠A=2∠D,即∠D=∠A,(1)当若∠A=50°,则∠D=25°;(2)若∠A=80°,则∠D=40°;(3)若∠A=130°,则∠D=65°.(4)若∠D=36°,则∠A=72°,故答案为25°,40°,65°,72°;(5)综上所述,∠D=∠A;【点睛】本题考查了三角形内角和定理:三角形内角和是180°.主要用在求三角形中角的度数:①直接根据两已知角求第三个角;②依据三角形中角的关系,用代数方法求三个角;③在直角三角形中,已知一锐角可利用两锐角互余求另一锐角.也考查了三角形外角性质.【模型5 双外角平分线模型】【条件】BP、CP分别为∠EBC、∠BCD的角平分线.1∠A.【结论】∠P=90°-2【例5】(2018秋•鄂伦春自治旗月考)如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD 与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:(1)若∠A=60°,则∠P=°;(2)若∠A=40°,则∠P=°;(3)若∠A=100°,则∠P=°;(4)请你用数学表达式归纳∠A与∠P的关系.【分析】(1)若∠A=60°,则有∠ABC+∠ACB=120°,∠DBC+∠BCE=360°﹣120°=240°,根据角平分线的定义可以求得∠PBC+∠PCB的度数,再利用三角形的内角和定理即可求得∠P的度数.(2)(3)和(1)的解题步骤相似.(4)利用角平分线的性质和三角形的外角性质可求出∠BCP =(∠A +∠ABC ),∠CBP =(∠A +∠ACB );再利用三角形内角和定理便可求出∠A 与∠P 的关系.【答案】解:(1)∵∠A =60°,∴∠ABC +∠ACB =180°﹣60°=120°,∠DBC +∠BCE =360°﹣120°=240°,又∵∠CBD 与∠BCE 的平分线相交于点P ,∴∠PBC =∠DBC ,∠PCB =∠BCE ,∴∠PBC +∠PCB =(∠DBC +∠ECB )=120°,∴∠P =60°.同理得:(2)70°;(3)40°(4)∠P =90°﹣∠A .理由如下:∵BP 平分∠DBC ,CP 平分∠BCE ,∴∠DBC =2∠CBP ,∠BCE =2∠BCP又∵∠DBC =∠A +∠ACB ∠BCE =∠A +∠ABC ,∴2∠CBP =∠A +∠ACB ,2∠BCP =∠A +∠ABC ,∴2∠CBP +2∠BCP =∠A +∠ACB +∠A +∠ABC =180°+∠A ,∴∠CBP +∠BCP =90°+∠A又∵∠CBP +∠BCP +∠P =180°,∴∠P =90°﹣∠A .故答案为:60,70,40,90°﹣∠A .【点睛】本题主要考查三角形的一个外角等于和它不相邻的两个内角的和的性质以及角平分线的定义,熟练掌握性质和定义是解题的关键.【变式5-1】(2019秋•团风县校级月考)BD 、CD 分别是△ABC 的两个外角∠CBE 、∠BCF 的平分线, 求证:∠BDC =90°21∠A .【分析】先根据BD、CD分别是∠CBE、∠BCF的平分线可知∠DBC=∠EBC,∠BCD=∠BCF,再由∠CBE、∠BCF是△ABC的两个外角得出∠CBE+∠BCF=360°﹣(180°﹣∠A)=180°+∠A,故∠DBC+∠BCD=(∠EBC+∠BCF)=(180°+∠A)=90°+∠A,根据在△DBC中∠BDC=180°﹣(∠DBC+∠BCD)即可得出结论.【答案】证明:∵BD、CD分别是∠CBE、∠BCF的平分线∴∠DBC=∠EBC,∠BCD=∠BCF,∵∠CBE、∠BCF是△ABC的两个外角∴∠CBE+∠BCF=360°﹣(180°﹣∠A)=180°+∠A∴∠DBC+∠BCD=(∠EBC+∠BCF)=(180°+∠A)=90°+∠A,在△DBC中,∠BDC=180°﹣(∠DBC+∠BCD)=180°﹣(90°+∠A)=90°﹣∠A.【点睛】本题考查的是三角形内角和定理及三角形外角的性质,熟知三角形的内角和等于180°是解答此题的关键.【变式5-2】(2019春•雨城区校级期中)如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,(1)若∠ABC=40°,∠ACB=36°,求∠BIC的大小;(2)若∠A=96°,试求∠BIC;(3)根据前面问题的求解,请归纳∠BIC和∠A的数量关系并进行证明.【分析】(1)运用三角形的内角和定理及角平分线的定义,求出∠IBC+∠ICB的值,即可解决问题.(2)先根据∠A=96°,得出∠1+∠2=84°,再运用(1)中的方法即可解决问题.(3)证明思路方法即(2)中的方法.【答案】解:(1)如图所示,∵∠ABC=40°,∠ACB=36°,∴∠DBC=140°,∠ECB=144°,又∵BI,CI分别平分△ABC的外角∠DBC和∠ECB,∴∠3=∠DBC=70°,∠4=∠ECB=72°,∴△BCI中,∠I=180°﹣70°﹣72°=38°;(2)∵∠A=96°,∴∠1+∠2=84°,∴∠DBC+∠ECB=276°,又∵BI,CI分别平分△ABC的外角∠DBC和∠ECB,∴∠3+∠4=(∠DBC+∠ECB)=×276°=138°,∴△BCI中,∠I=180°﹣138°=42°;(3)∠BIC=90°﹣∠A.证明:△ABC中,∠1+∠2=180°﹣∠A,∴∠DBC+∠ECB=360°﹣(180°﹣∠A)=180°+∠A,又∵BI,CI分别平分△ABC的外角∠DBC和∠ECB,∴∠3+∠4=(∠DBC+∠ECB)=×(180°+∠A)=90°+∠A,∴△BCI中,∠I=180°﹣(∠3+∠4)=180°﹣(90°+∠A)=90°﹣∠A.【点睛】本题主要考查了三角形的内角和定理及角平分线的定义的运用;解题的关键是灵活运用三角形内角和为180°.【变式5-3】如图,在△ABC中,BD,CD是内角平分线,BP,CP是∠ABC,∠ACB的外角平分线,分别交于点D,P.(1)若∠A=30°,求∠BDC,∠BPC的度数.(2)若∠A=m°,求∠BDC,∠BPC的度数(直接写出结果,不必说明理由)(3)想一想,∠A的大小变化,对∠D+∠P的值是否有影响,若有影响,请说明理由,若无影响,直接求出其值.【分析】(1)通过角的平行线的定义以及三角形的内角和可得出∠CBD+∠BCD=75°,再利用三角形的内角和为180°即可得出∠BDC的度数,同理可求出∠BPC的度数;(2)根据(1)的求角过程将30换成m,即可得出结论;(3)由(2)的结论,将两角相加即可得出结论.【答案】解:(1)∵BD,CD是内角平分线,∴∠CBD+∠BCD=(∠ABC+∠ACB),∵∠A+∠ABC+∠ACB=180°,∠A=30°,∴∠ABC+∠ACB=150°,∴∠CBD+∠BCD=75°.又∵∠BDC+∠CBD+∠BCD=180°,∴∠BDC=105°.∵∠CBE+∠BCF=360°﹣(∠ABC+∠ACB)=210°,BP,CP是∠ABC,∠ACB的外角平分线,∴∠CBP+∠BCP=(∠CBE+∠BCF)=105°,∵∠BPC+∠CBP+∠BCP=180°,∴∠BPC=75°.(2)根据(1)的求角过程可知:∠BDC=90°+°,∠BPC=90°﹣°.(3)∵∠D+∠P=90°+°+90°﹣°=180°为定值,∴∠A的大小变化,对∠D+∠P的值无影响.【点睛】本题考查了三角形外角性质、三角形内角和定义以及角平分线的定义,解题的关键是熟练掌握三角形内角和定理是关键.【模型6 8字模型】【结论】∠A+∠B=∠D+∠E.【例6】(2019春•辉县市期末)图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:;(2)仔细观察,在图2中“8字形”的个数:个;(3)图2中,当∠D=50度,∠B=40度时,求∠P的度数.(4)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结果,不必证明).【分析】(1)根据三角形内角和定理即可得出∠A+∠D=∠C+∠B;(2)根据“8字形”的定义,仔细观察图形即可得出“8字形”共有6个;(3)先根据“8字形”中的角的规律,可得∠DAP+∠D=∠P+∠DCP①,∠PCB+∠B=∠P AB+∠P②,再根据角平分线的定义,得出∠DAP=∠P AB,∠DCP=∠PCB,将①+②,可得2∠P=∠D+∠B,进而求出∠P的度数;(4)同(3),根据“8字形”中的角的规律及角平分线的定义,即可得出2∠P=∠D+∠B.【答案】解:(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,∴∠A+∠D=∠C+∠B;(2)①线段AB、CD相交于点O,形成“8字形”;②线段AN、CM相交于点O,形成“8字形”;③线段AB、CP相交于点N,形成“8字形”;④线段AB、CM相交于点O,形成“8字形”;⑤线段AP、CD相交于点M,形成“8字形”;⑥线段AN、CD相交于点O,形成“8字形”;故“8字形”共有6个;(3)∠DAP+∠D=∠P+∠DCP,①∠PCB+∠B=∠P AB+∠P,②∵∠DAB和∠BCD的平分线AP和CP相交于点P,∴∠DAP=∠P AB,∠DCP=∠PCB,①+②得:∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠P AB+∠P,即2∠P=∠D+∠B,又∵∠D=50度,∠B=40度,∴2∠P=50°+40°,∴∠P=45°;(4)关系:2∠P=∠D+∠B.由∠D+∠1+∠2=∠B+∠3+∠4①由∠ONC=∠B+∠4=∠P+∠2,②①+②得:∠D+2∠B+2∠1+2∠3=∠B+2∠3+2∠P+2∠1,。
