最新八年级上-数学-计算题
完整word版,八年级上学期数学计算题

八年级上学期数学计算题1、观察下列各式:1×3=12+2×1,2×4=22+2×2,3×5=32+2×3,…,请你将猜想到的规律用自然数n(n≥1)表示出来:__________________________.2、通过计算几何图形的面积可表示一些代数恒等式(一定成立的等式),请根据右图写出一个代数恒等式是:________________.3、若(9+x 2)(x+3)·M=81-x 4,则M=______.4、 若整式4x 2+Q +1是完全平方式,请你写一个满足条件的单项式Q 是________________ 5、(1)2(a 5)2·(a 2)2-(a 2)4·(a 2)2·a 2; (2)(b n )3·(b 2)m +3(b 3)n ·b 2·(b m -1)2; (3)(-a 6b 3+a 3b 4-ab 3)÷(-ab 3)(4)4a 2x 2·(-a 4x 3y 3)÷(-a 5xy 2) (5)( 2a+3b)2−2( 2a+3b)(a−2b)+(−a+2b)2(6)(2a -b)(2a+b)-(-3a -b)(-3a+b); (7)6、 化简求值:(x -2)(x -3)+2(x+6)(x -5)-3(x 2-7x+13),其中x =-;7、分解因式(1); (2). (3);(4); (5); (6).3465910355221⋅--÷-++--+)64121()622322(222x x x x x x x x 718)()(22a b b b a a -+-)44(22+--y y x xy y x 4)(2+-)1(4)(2-+-+y x y x 1)3)(1(+--x x 22222222x b y a y b x a -+-()01113=++++-x x a x x x 8、解方程:.9、a 为何值时,分式方程无解?10、大家已经知道,完全平方公式和平方差公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如:2x(x+y)=2x 2+2xy 就可以用图15-3-2(1)的面积表示.(1)请写出图(2)所表示的代数恒等式:__________;(2)请写出图(3)所表示的代数恒__________;(3)试画出一个几何图形,使它的面积能表示(x+y)(x+3y)=x 2+4xy+3y 2.11、已知,A =2x,B 式多项式,在计算B+A 时,某同学把B+A 看成结果得,求B+A.12、已知,的展开式中不含项和项,求的值.13、已知、、满足,,求的值.)2)(13()2(2)1)(1(2+-=++-+x x x x x ⋅++=+-312132x x x ⋅--+=--2163524245m m m m A B ÷x x 212+)3)(8(22q x x px x +-++2x 3x q p +a b c 5=+b a 92-+=b ab c c。
八年级上数学计算题40道

八年级上数学计算题40道一)填空题(每一题每空1分,第二、三、五题每空3分,其余题每空四分,共42分)?(1)由5、6、3三个数字可组成__________个三位数,其中最大数是________,最小数是________。
?答案:6 653 356?分析:法一,用树型结构把它们一一列举出来。
?共有6个三位数,最大数为653,最小数为356。
?法二:利用排列数公式计算:由5、6、3三个数字组成的全排列个数为?的是________。
?答案:?分析:我们任意选出两个连续整数n,n+1,那么它们的倒数为?(3)已知a和b都是自然数,且a÷b=8,那么a与b的最大公约数是_______,最小公倍数是________。
?答案:b a?分析:由a÷b=8可知a=8b,所以8b与b的最大公约数为b,最小公倍数为8b,即为a。
? (4)按规律填空:?答案:5.625?分析:首先找出这四个数的规律,有两种方法。
?方法一:将四个数都化为小数为:1.125,2.25,3.375,4.5,我们发现相邻两个数之间后一个数比前一个多1.125,(或者发现第二个数是第一个数的2倍,第三个数是第一个数的3倍,第四个数是第一个数的四倍),则第5个数是4.5+1.125=5.625(或1.125×5=5.625)。
?方法二:?(5)如图,一个正方体切去一个长方体后(单位:厘米)剩下的图形的体积是___________,表面积是_____________。
?答案:113立方厘米150平方厘米?分析:正方体的体积为5×5×5=125立方厘米,长方体的体积为2×2×3=12立方厘米,则剩下的图形的体积为正方体的体积减去长方体的体积,即:125-12=113立方厘米。
?在切下的长方体中,上、下表面积相等,左、右表面积相等,前、后表面积相等,所以剩下的立体图形的表面积与正方体的表面积相等,即5×5×6=150平方厘米。
八年级数学上册分式加减运算计算题练习(含答案)(最新整理)

八年级数学上册 分式加减运算 计算题练习1、化简:.2、化简:. 2(2222abb a b a b a ++÷--421444122++--+-x x x x x 3、化简:. 4、化简:.a a a a 21222-÷-+a a ---1115、化简:.6、化简:. 2222)2(nm mnm m n mn m --⋅++1224422-+÷--x x x x 7、化简:. 8、化简:.)111(111(2+-÷-+a a 1)12111(2-÷+-+-+x xx x x x 9、化简:. 10、化简:.a a a a a -+-÷--2244)111(14414(2-+-÷---x x x x x x 11、化简:. 12、化简:.962966322--+++⋅+a a a a a a 112222+---x xx x x 13、化简:. 14、化简:.1231621222+-+÷-+-+x x x x x x x 12)121(22+-+÷-+x x xx x 15、化简:. 16、化简:.)111(12+-÷-x x x 44211(22+++÷+-x x xx x 17、化简:. 18、化简:.11221(223+-+--÷--x xx x x x x x x 24)2122(--÷--+x x x x 19、化简:. 20、化简:.1112221222-++++÷--x x x x x x 11131332+-+÷--x x x x x 21、化简:. 22、化简:.9)3132(2-÷-++x x x x 12242(2++÷-+-x x x x x23、化简:. 24、化简:.x x x x x x x x -⋅+----+444122(22344)3392(2--+-÷+-+-x x x x x x 25、化简:. 25、化简:. 121441222+-÷-+-+-a a a a a a 2422(2+÷---m m m m m m 27、化简:. 28、化简:.222a b ab b a a b a b --++-x x x x x x -+⋅+÷++-21)2(1242229、化简:. 30、化简:12412122++-÷+--x x x x x )111(1222+-+÷+-x x x x x 31、化简:. 32、化简:.1221122+-+÷--+a a a a a a ba ba b a b b a b a +-÷--+-2)2(33、化简:. 34、化简:.121)121(2+-+÷-+x x x x 11211222---+--⨯+-x aax a a a a a a 35、化简:. 36、化简:. 41)2212(216822+++-+÷++-x x x x x x x xa x x a 221(-÷-37、化简:. 38、化简:.1)11(22-÷---x xx x x 1)112(2-÷+--a a a a a a 39、化简:421211(2--÷-+x x x参考答案1、原式=.2、原式=.3、原式=a 2+2a.4、原式=.5、原式=m+n.b a ab +2)2(24--x x 122--a a6、原式=.7、原式=.8、原式=.9、原式=. 10、原式=.x x -1a a 1+1-x x 2-a a 22-+x x 11、原式=. 12、原式=. 13、原式=3x-7. 14、原式=. 15、原式=.a 21+x x x x 1-11-x 16、原式=1+. 17、原式=. 18、原式=-x-4. 19、原式=.2x x +-2122-x x20、原式=. 21、原式=. 22、原式=x+1. 24、原式=. x x +21x x 9-2)2(1--x 25、原式=. 26、原式=. 27、原式=. 28、原式=. 2-x x 1-a a 2-m m b a ba -+29、原式=. 30、原式=. 31、原式=. 32、原式=.11+-x 21+x 11-x 21+a 33、原式=. 34、原式=x ﹣1. 35、原式=0. 36、原式=.b a a -2x x 442+37、原式=. 38、原式=. 39、原式=a+3. 40、原式=.a x +1x x 1+12+x。
八年级数学上册实数计算题

八年级数学上册实数计算题一、实数计算题20题。
1. 计算:√(4) + sqrt[3]{-8}- 解析:- 先分别计算各项。
- 因为√(4)=2,sqrt[3]{-8}=-2(因为(-2)^3 = -8)。
- 所以√(4)+sqrt[3]{-8}=2+( - 2)=0。
2. 计算:√(9)-√(16)- 解析:- 先计算根号下的数。
- √(9) = 3,√(16)=4。
- 则√(9)-√(16)=3 - 4=-1。
3. 计算:√(25)+√(36)- 解析:- √(25)=5,√(36)=6。
- 所以√(25)+√(36)=5 + 6=11。
4. 计算:√(1)-√(0)- 解析:- 因为√(1)=1,√(0)=0。
- 所以√(1)-√(0)=1-0 = 1。
5. 计算:√(121)-√(144)- 解析:- √(121)=11,√(144)=12。
- 则√(121)-√(144)=11-12=-1。
6. 计算:√(169)+√(196)- 解析:- √(169)=13,√(196)=14。
- 所以√(169)+√(196)=13 + 14=27。
7. 计算:√(49)-√(64)- 解析:- √(49)=7,√(64)=8。
- 所以√(49)-√(64)=7-8=-1。
8. 计算:√(81)+√(100)- 解析:- √(81)=9,√(100)=10。
- 所以√(81)+√(100)=9 + 10=19。
9. 计算:sqrt[3]{27}+sqrt[3]{-1}- 解析:- 因为sqrt[3]{27}=3(因为3^3 = 27),sqrt[3]{-1}=-1(因为(-1)^3=-1)。
- 所以sqrt[3]{27}+sqrt[3]{-1}=3+( - 1)=2。
10. 计算:sqrt[3]{64}-sqrt[3]{125}- 解析:- sqrt[3]{64}=4(因为4^3 = 64),sqrt[3]{125}=5(因为5^3 = 125)。
八年级上册数学幂的运算计算题

八年级上册数学幂的运算计算题在八年级数学课程中,幂的运算是一个重要的知识点。
幂的运算涉及到指数、底数的运算,也包括了幂的乘法、除法、幂的零次和一次运算等内容。
通过解决一些实际问题和计算题,可以更好地掌握和理解幂的运算方法,从而提高数学运算的水平。
1. 幂的乘法计算题1)计算:\[4^3 \times 4^2\]解析:根据幂的乘法法则,\(a^m \times a^n = a^{m+n}\),所以\[4^3 \times 4^2 = 4^{3+2} = 4^5 = 1024\]2)计算:\[5^4 \times 5^6\]解析:根据幂的乘法法则,\(a^m \times a^n = a^{m+n}\),所以\[5^4 \times 5^6 = 5^{4+6} = 5^{10}\]3)计算:\[(3^2)^3\]解析:根据幂的乘法法则,\((a^m)^n = a^{m \times n}\),所以\[(3^2)^3 = 3^{2 \times 3} = 3^6 = 729\]2. 幂的除法计算题1)计算:\[\frac{3^5}{3^2}\]解析:根据幂的除法法则,\(\frac{a^m}{a^n} = a^{m-n}\),所以\[\frac{3^5}{3^2} = 3^{5-2} = 3^3 = 27\]2)计算:\[\frac{5^7}{5^4}\]解析:根据幂的除法法则,\(\frac{a^m}{a^n} = a^{m-n}\),所以\[\frac{5^7}{5^4} = 5^{7-4} = 5^3 = 125\]3)计算:\[\frac{(2^3)^5}{2^4}\]解析:根据幂的除法法则,\(\frac{(a^m)^n}{a^n} = a^{m \times n - n}\) ,所以\[\frac{(2^3)^5}{2^4} = 2^{3 \times 5 - 4} = 2^{15-4} = 2^{11}\]3. 幂的零次和一次计算题1)计算:\(5^0\)解析:根据幂的零次法则,任何非零数的零次幂都是1,所以\(5^0 = 1\)2)计算:\(2^1\)解析:根据幂的一次法则,任何数的一次幂都是它本身,所以\(2^1 = 2\)3)计算:\((7^2)^0\)解析:根据幂的零次法则,任何非零数的零次幂都是1,所以\((7^2)^0 = 1\)4. 理解幂的运算的重要性幂的运算在数学中有着非常重要的地位,它不仅在简单的计算题中有所体现,更在代数式的简化、方程的求解等更为复杂的数学问题中发挥着重要作用。
最新人教版八年级上册数学《分式》计算题专项练习(含答案)
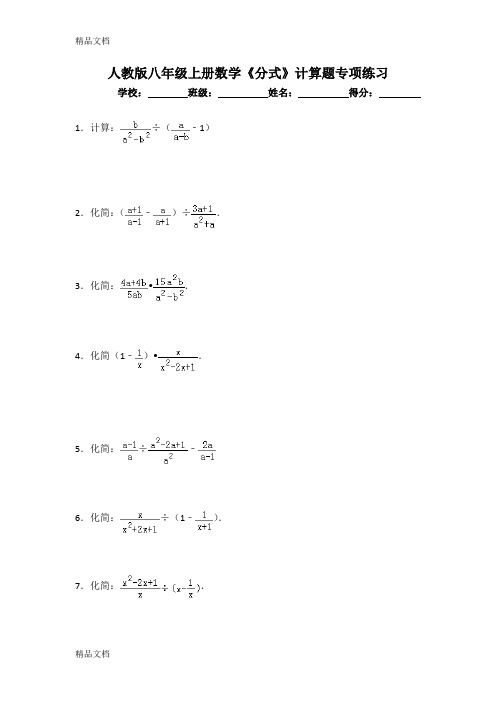
人教版八年级上册数学《分式》计算题专项练习学校:班级:姓名:得分:1.计算:÷(﹣1)2.化简:(﹣)÷.3.化简:•.4.化简(1﹣)•.5.化简:÷﹣6.化简:÷(1﹣).7.化简:.8.计算÷().9.化简:1+÷.10.先化简,再求值:•﹣,其中x=2.11.先化简,再求值•+.(其中x=1,y=2)12.先化简,再求值:,其中x=2.13.先化简,再求值:(+)÷,其中x=﹣.14.先化简,再求值:(x﹣)÷,其中x=.15.先化简,再求值:(1+)÷.其中x=3.16.化简分式(+)÷,并在2,3,4,5这四个数中取一个合适的数作为a的值代入求值.17.先化简,再求值:÷(a﹣1﹣),并从﹣1,0,1,2四个数中,选一个合适的数代入求值.18.先化简,再求值:÷(﹣x﹣2),其中|x|=2.19.先化简,再求值:(+)÷,且x为满足﹣3<x<2的整数.20.先化简(﹣)÷,再从﹣2,﹣1,0,1,2中选一个你认为合适的数作为x的值代入求值.21.先化简,再求值:﹣÷,其中a=﹣1.22.先化简÷(a﹣2+),然后从﹣2,﹣1,1,2四个数中选择一个合适的数作为a的值代入求值.人教版八年级上册数学《分式》计算题专项练习参考答案与试题解析1.【解答】解:原式=÷(﹣)=÷=•=.2.【解答】解:原式=[﹣]÷=÷=•=.3.【解答】解:原式=•=.4.【解答】解:(1﹣)•==.5.【解答】解:原式=•﹣=﹣=6.【解答】解:÷(1﹣)===.7.【解答】解:原式=÷(﹣)=÷=•=.8.【解答】解:原式=÷=•=﹣(a+b)=﹣a﹣b.9.【解答】解:原式=1+•=1+=+=.10.【解答】解:原式=•﹣=﹣=﹣=,当x=2时,原式==.11.【解答】解:当x=1,y=2时,原式=•+=+==﹣312.【解答】解:原式=把x=2代入得:原式=13.【解答】解:原式=•=,当x=﹣时,原式=2.14.【解答】解:(x﹣)÷====x﹣2,当x=时,原式=﹣2=﹣.15.【解答】解:(1+)÷=×=x+2.当x=3时,原式=3+2=5.16.【解答】解:原式=[﹣]÷=(﹣)•=•=a+3,∵a≠﹣3、2、3,∴a=4或a=5,则a=4时,原式=7,a=5时,原式=8.17.【解答】解:原式=÷(﹣)=÷=•=,∵a≠﹣1且a≠0且a≠2,∴a=1,则原式==﹣1.18.【解答】解:÷(﹣x﹣2)====,∵|x|=2,x﹣2≠0,解得,x=﹣2,∴原式=.19.【解答】解:原式=[+]÷=(+)•x=x﹣1+x﹣2=2x﹣3由于x≠0且x≠1且x≠﹣2所以x=﹣1 原式=﹣2﹣3=﹣5 20.【解答】解:原式=[﹣]÷=•=,∵x≠±1且x≠﹣2,∴x只能取0或2,当x=0时,原式=﹣1.21.【解答】解:原式====当a=﹣1时,原式=22.【解答】解:原式=•=当a=2时,原式==3.。
人教版八年级上数学计算题

人教版八年级上数学计算题一、整式乘法与因式分解相关计算(1 - 10题)1. 计算:(2x + 3)(3x - 2)- 解析:- 根据多项式乘法法则,用一个多项式的各项去乘另一个多项式的每一项,再把所得的积相加。
- 原式=2x×3x - 2x×2+3×3x - 3×2- =6x^2-4x + 9x - 6- =6x^2+5x - 62. 计算:(x + 2y)^2- 解析:- 根据完全平方公式(a + b)^2=a^2+2ab + b^2,这里a = x,b = 2y。
- 原式=x^2+2× x×2y+(2y)^2- =x^2+4xy + 4y^23. 分解因式:x^2-9- 解析:- 根据平方差公式a^2-b^2=(a + b)(a - b),这里a = x,b = 3。
- 原式=(x + 3)(x - 3)4. 分解因式:x^3-2x^2+x- 解析:- 先提取公因式x,得到x(x^2-2x + 1)。
- 然后根据完全平方公式,x^2-2x + 1=(x - 1)^2。
- 所以原式=x(x - 1)^25. 计算:(3x^2y)^3·(-2xy^3z)- 解析:- 先根据幂的乘方公式(a^m)^n=a^mn计算(3x^2y)^3=3^3×(x^2)^3×y^3=27x^6y^3。
- 再根据单项式乘法法则计算27x^6y^3·(-2xy^3z)=27×(-2)× x^6 + 1× y^3+3×z=- 54x^7y^6z6. 分解因式:9x^2-12xy + 4y^2- 解析:- 根据完全平方公式a^2-2ab + b^2=(a - b)^2,这里a = 3x,b = 2y。
- 原式=(3x - 2y)^27. 计算:(x - 1)(x^2+x + 1)- 解析:- 根据立方差公式(a - b)(a^2+ab + b^2)=a^3-b^3,这里a = x,b = 1。
八年级上册数学北师版计算题

八年级上册数学北师版计算题一、实数运算类。
1. 计算:√(16) - sqrt[3]{-8} + √(0)- 解析:- 先分别计算各项。
√(16)=4,因为4^2 = 16。
- sqrt[3]{-8}=- 2,因为(-2)^3=-8。
- √(0) = 0。
- 所以原式=4-(-2)+0=4 + 2=6。
2. 计算:(√(3))^2+ - 2√(9)- 解析:- (√(3))^2 = 3。
- 2=2。
- √(9)=3。
- 则原式=3 + 2-3=2。
3. 计算:√(25)+sqrt[3]{64}-√(169)- 解析:- √(25) = 5。
- sqrt[3]{64}=4,因为4^3 = 64。
- √(169)=13。
- 所以原式=5 + 4-13=-4。
二、整式运算类。
4. 计算:(2x^2y)^3·(- 3xy^2)÷6xy- 解析:- 先计算幂的乘方,(2x^2y)^3=2^3×(x^2)^3× y^3 = 8x^6y^3。
- 然后进行乘法运算:8x^6y^3·(-3xy^2)=-24x^7y^5。
- 最后进行除法运算:-24x^7y^5÷6xy=-4x^6y^4。
5. 计算:(3a + 2b)(2a - 3b)- 解析:- 利用多项式乘法法则展开:- 原式=3a×2a-3a×3b+2b×2a - 2b×3b- =6a^2-9ab + 4ab-6b^2- =6a^2-5ab - 6b^2。
6. 计算:(x + 2y)^2-(x - 2y)^2- 解析:- 根据完全平方公式(a + b)^2=a^2+2ab + b^2和(a - b)^2=a^2-2ab + b^2。
- 则(x + 2y)^2=x^2+4xy+4y^2,(x - 2y)^2=x^2-4xy + 4y^2。
- 原式=(x^2 + 4xy+4y^2)-(x^2-4xy + 4y^2)- 去括号得:x^2+4xy + 4y^2-x^2 + 4xy-4y^2 = 8xy。
八年级上册数学计算题专项训练

八年级上册数学计算题专项训练一、整式乘法与因式分解类。
1. 计算:(2x + 3y)(3x 2y)解析:根据多项式乘法法则,用一个多项式的各项去乘另一个多项式的每一项,再把所得的积相加。
原式=2x×3x 2x×2y+3y×3x 3y×2y = 6x^2-4xy + 9xy-6y^2=6x^2+5xy 6y^2。
2. 分解因式:x^2-9解析:这是一个平方差的形式,根据平方差公式a^2-b^2=(a + b)(a b),这里a=x,b = 3。
所以x^2-9=(x + 3)(x 3)。
3. 分解因式:2x^2-8x解析:先提取公因式2x,得到2x(x 4)。
二、分式运算类。
4. 计算:frac{x^2-1}{x^2+2x + 1}÷(x 1)/(x + 1)解析:先将分子分母进行因式分解,x^2-1=(x + 1)(x 1),x^2+2x + 1=(x + 1)^2。
原式=((x + 1)(x 1))/((x + 1)^2)÷(x 1)/(x + 1)=((x + 1)(x 1))/((x + 1)^2)×(x + 1)/(x 1)=1。
5. 计算:(1)/(x 1)-(1)/(x + 1)解析:先通分,通分后分母为(x 1)(x + 1)=x^2-1。
原式=(x + 1-(x 1))/(x^2)-1=(x + 1 x + 1)/(x^2)-1=(2)/(x^2)-1。
6. 化简求值:frac{x^2-4x + 4}{x^2-4},其中x = 3解析:先对分子分母进行因式分解,分子x^2-4x + 4=(x 2)^2,分母x^2-4=(x + 2)(x 2)。
原式=frac{(x 2)^2}{(x + 2)(x 2)}=(x 2)/(x + 2),当x = 3时,(32)/(3+2)=(1)/(5)。
三、二次根式运算类。
7. 计算:√(12)+√(27)-√(48)解析:先将各项化为最简二次根式,√(12) = 2√(3),√(27)=3√(3),√(48)=4√(3)。
八年级上数学计算题道

八年级上数学计算题40道一)填空题(每一题每空1分,第二、三、五题每空3分,其余题每空四分,共42分)(1)由5、6、3三个数字可组成__________个三位数,其中最大数是________,最小数是________。
答案:6 653 356分析:法一,用树型结构把它们一一列举出来。
共有6个三位数,最大数为653,最小数为356。
法二:利用排列数公式计算:由5、6、3三个数字组成的全排列个数为的是________。
答案:分析:我们任意选出两个连续整数n,n+1,那么它们的倒数为(3)已知a和b都是自然数,且a÷b=8,那么a与b的最大公约数是_______,最小公倍数是________。
答案:b a分析:由a÷b=8可知a=8b,所以8b与b的最大公约数为b,最小公倍数为8b,即为a。
(4)按规律填空:答案:5.625分析:首先找出这四个数的规律,有两种方法。
方法一:将四个数都化为小数为:1.125,2.25,3.375,4.5,我们发现相邻两个数之间后一个数比前一个多1.125,(或者发现第二个数是第一个数的2倍,第三个数是第一个数的3倍,第四个数是第一个数的四倍),则第5个数是4.5+1.125=5.625(或1.125×5=5.625)。
方法二:(5)如图,一个正方体切去一个长方体后(单位:厘米)剩下的图形的体积是___________,表面积是_____________。
答案:113立方厘米150平方厘米分析:正方体的体积为5×5×5=125立方厘米,长方体的体积为2×2×3=12立方厘米,则剩下的图形的体积为正方体的体积减去长方体的体积,即:125-12=113立方厘米。
在切下的长方体中,上、下表面积相等,左、右表面积相等,前、后表面积相等,所以剩下的立体图形的表面积与正方体的表面积相等,即5×5×6=150平方厘米。
数学初二上学期计算题精选

2011.1.81 (X-2y)2 (2y-x)3 2. x n.x n-1+x n+1 x n-2+(-x)3 (-x)2n-43. 已知52x+1 =125求(x-2)2001+3x4. 已知2x=3求2x+32011.1.95.(m-n)2 (n-m)3 (n-m)4 6.(y-x)3 (x-y)5+(x-y)6 (y-x)27, (a+b)9 (-a-b)4 +(a+b)6 (a-b)7 8. 已知x3x a x2a+1=x31 求a的值。
2011.1109.已知2m=4 ,2n=16 求2m+n的值10. 3333333333211. 82002⨯0.1252002 12。
(-8)9⨯0.12582011.1.1113. 3(X2)3 X3-(2X3)3+(5X)2 X7 14. –a a5–(a2)3–(-2a3)215. 2(a4)2 (a3)3-(-a)( a8)2+(-3a2)2(-a4)3(-a) 16. (-2a)6-(-3a3)2-[-(2a)2]32011.1217. 已知m=c 3 c c 4 b b n 求m 18 已知44⨯83=2x 求x19 2a ⨯ 27b ⨯ 37c =1998,a, b, c 是自然数求(a-b-c )2002的值 20。
(.9n )2=316求n 值2011.1.1321 如果2 8n 16n =222 求n 值 22 .[(x+y)2]3{(x+y)3}4-2[(x+y)3]623. 比较3555 4444 5 333 三个数大小 24。
若 a=255,b=344c=433 比较 a,b,c.的大小2011.1.14 25. 比较11112222与22221111大小26。
-6a 2b(x-y)331ab 2(y-x)227 (-7x m y m )2(-xy)3-[4x 2m (-x)3y 2m y 3 28. (-2a n+1b n )2(-3a n b)2(-a 2c)2011.1.1529 [(x+2y)3]5[-(x+2y)2]5 30 .3(a+b)2[2(-a-b)3]+[2(a+b)]3(-a-b)2 1322103a b c2011.1.16 33.. ( 132a 2b-331a 3b 2+1) (0.2ab) 34. 12x n y 2[3y n-1-2xy n+1+(-1)888].35. (3a 2b-2ab 2-4b 3)(-4a 2b) 36 . 3x n (x n+1-x n +x n-1-1)2011.1.1737. . 4(x-y+z)-2(x+y-z)-3(-x-y-z) 38. (-5xy)2(-xy)3+(4x 2y-3x)(-x 3y 4)+x 5y 539. 5x-2(x+2)-3[x-2(3-5x)+7] 40.. 2x 2(x 2+3xy-y 2)-xy(6x 2-4y 2)+y 2(2x 2-4xy+y 2)2011.1.18 41 .若 x 2+x-1=365,a+b+c=571, a(x 2+x+1)+b(x 2+x+1)+c((x 2+x+1)的值42. (a-b+c )(-a+b+c) 43. (-7+a+b)(-7-a-b) 44. (-3x+4)(-3x-4)2011.1.1945. 4(x-2)(x+5)-(2x-3)(2x+1)=5 46. (3x-2)(2x-3)≤(6x+5)(x+1)47. 2x(x+1)+(-2x)2+1≥x(3x+4)+3x 2 48 10-4(x 2+x-3)≤2(-2x 2+x-1)51 2001 1999-20002 52。
八年级上数学试卷计算题

一、选择题(每题5分,共25分)1. 下列各数中,绝对值最小的是()A. -3B. 0C. 2D. -22. 已知二次函数y=ax^2+bx+c(a≠0),若a>0,b=0,c<0,则该函数的图像()A. 开口向上,顶点在x轴下方B. 开口向下,顶点在x轴上方C. 开口向上,顶点在x轴上方D. 开口向下,顶点在x轴下方3. 若等差数列{an}的前n项和为Sn,公差为d,首项为a1,则下列等式中正确的是()A. Sn = (a1 + an) × n / 2B. Sn = (a1 + an) × nC. Sn = (a1 + an) × (n - 1) / 2D. Sn = (a1 + an) × (n + 1) / 24. 在直角坐标系中,点A(-2,3),点B(4,-1),则AB线段的中点坐标是()A. (1,1)B. (1,2)C. (2,1)D. (2,2)5. 已知三角形ABC中,AB=AC,角BAC=60°,则三角形ABC的面积是()A. 1/2B. √3/2C. √3D. 2二、填空题(每题5分,共25分)6. 若实数x满足不等式|x-3|≤5,则x的取值范围是______。
7. 已知一元二次方程x^2 - 5x + 6 = 0,则该方程的两个实数根是______。
8. 在等差数列{an}中,若a1=3,公差d=2,则第10项an=______。
9. 在直角坐标系中,点P(-3,2),点Q(5,-1),则PQ线段的长度是______。
10. 在三角形ABC中,AB=AC,角BAC=45°,则三角形ABC的面积是______。
三、解答题(每题10分,共30分)11. 计算下列各式的值:(1)-3x^2 + 5x - 2,当x=2时的值;(2)(x - 1)^2 - (x + 1)^2,当x=0时的值。
12. 已知等差数列{an}的前n项和为Sn,公差为d,首项为a1,求证:Sn = (a1 + an) × n / 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
22.解下列方程组.
(1)(用代入法)
(2)(用加减法)
就算你买手工艺品来送给朋友也是一份意义非凡的绝佳礼品哦。而这一份礼物于在工艺品店买的现成的礼品相比,就有价值意义,虽然它的成本比较低但它毕竟它是你花心血花时间去完成的。就像现在最流行的针织围巾,为何会如此深得人心,更有人称它为温暖牌绝大部分多是因为这个原因哦。而且还可以锻炼你的动手能力,不仅实用还有很大的装饰功用哦。23.解方程组:
25.小亮在解方程组 时,因把a看错而得到 而方程组正确的解是 求a-c-d的值.
一、计算题
2.(1)
(2) + +3 -
(3)( + )( -
3.(1) ;
(2)
4.(1)2 +3 -
(2)
(3)(2 — )
(4) —4 +42
5.(1)
(2)
6.计算: .
7.计算:
(1) ;
(2)
8.计算:
9.计算下列各题
(1)
(2)
(3)
(4)
10.计算: ﹣2 +( ﹣3 )÷ .
11.计算:
(2)解方程:
(3)解方程组:
(4)解方程组
手工艺制品是我国一种传统文化的象征,它品种多样,方式新颖,制作简单,深受广大学生朋友的喜欢。当今大学生的消费行为表现在追求新颖,追求时尚。追求个性,表现自我的消费趋向:购买行为有较强的感情色彩,比起男生热衷于的网络游戏,极限运动,手工艺制品更得女生的喜欢。21.解方程组:(1)
(1)
(2) .
12.计算:13.计Leabharlann :(1) ;(2)
14.计算
15.
16.计算: .
17.计算: -|-2|+(-3)0-( )-1.
18. ﹣(﹣2015)0+( )﹣1+| ﹣1|.
19.计算:( ﹣ )2+2 ×3 .
(六)DIY手工艺品的“创作交流性”20.计算题:
(1)解方程:4(2-x)-3(x+1)=6
就算你买手工艺品来送给朋友也是一份意义非凡的绝佳礼品哦。而这一份礼物于在工艺品店买的现成的礼品相比,就有价值意义,虽然它的成本比较低但它毕竟它是你花心血花时间去完成的。就像现在最流行的针织围巾,为何会如此深得人心,更有人称它为温暖牌绝大部分多是因为这个原因哦。而且还可以锻炼你的动手能力,不仅实用还有很大的装饰功用哦。24.已知方程组 的解满足x+y=6,求k的值.
