1确定平面上物体的位置
人教版-数学-六年级上册-《位置与方向(一)》知识讲解 根据方向和距离在平面图上确定物体位置的方法
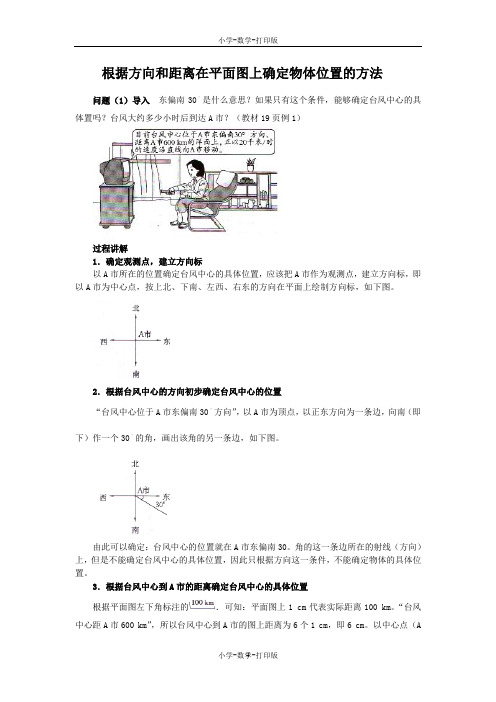
根据方向和距离在平面图上确定物体位置的方法问题(1)导入东偏南30是什么意思?如果只有这个条件,能够确定台风中心的具体置吗?台风大约多少小时后到达A市?(教材19页例1)过程讲解1.确定观测点,建立方向标以A市所在的位置确定台风中心的具体位置,应该把A市作为观测点,建立方向标,即以A市为中心点,按上北、下南、左西、右东的方向在平面上绘制方向标,如下图。
2.根据台风中心的方向初步确定台风中心的位置“台风中心位于A市东偏南30方向”,以A市为顶点,以正东方向为一条边,向南(即下)作一个30的角,画出该角的另一条边,如下图。
由此可以确定:台风中心的位置就在A市东偏南30。
角的这一条边所在的射线(方向)上,但是不能确定台风中心的具体位置,因此只根据方向这一条件,不能确定物体的具体位置。
3.根据台风中心到A市的距离确定台风中心的具体位置根据平面图左下角标注的.可知:平面图上1 cm代表实际距离100 km。
“台风中心距A市600 km”,所以台风中心到A市的图上距离为6个1 cm,即6 cm。
以中心点(A市)为起点,沿着东偏南30方向画6个,并在终点处标上“台风中心”,如下图。
用方向和距离描述台风中心的位置:台风中心在A市东偏南30方向600 km处。
计算台风大约到达A市的时间(1)解题方法:根据“时间一路程÷速度”计算。
(2)列式解题。
600÷20=30(小时)答:台风大约30小时后到达A市。
问题(2)导入台风到达A市后,改变方向,向B市移动。
受台风影响,C市也将有大到暴雨。
(教材20页例2)(I)B市位于A市北偏西30方向、距离A市200 km。
C市在A市正北方,距离A市300km。
请你在例1的图中标出B市、C市的位置。
(2)台风到达A市后,移动速度变为40千米/时,几小时后到达B市?过程讲解1.确定观测点“B市位于A市北偏西30方向,C市在A市正北方”,B市和C市所在的位置都是相对于A市而言的,因此画图时都要以A市为观测点,按上北、下南、左西、右东的方向绘制方向标。
北师大版-数学-八年级上册--例题与讲解-第三章 1 确定位置

【例题与讲解】八年级数学上册第三章 1 确定位置1.行列定位法行列定位法是确定平面内某物体位置的重要方法之一,这种方法是把平面分成若干行、列,然后利用行号和列号表示平面上点的位置;要准确表明某点的位置需要两个互相独立的数据,此方法也是平面直角坐标系内容的一个铺垫.辨误区行列定位法用行列定位法表示平面内某点的位置必须有两个数据,缺一不可.【例1-1】小明站在一个由8行10列组成的队伍中,要想确定小明的位置,需要知道哪些数据?分析:要想确定队伍中某个人的位置,只知道行数不能确定,因为同一行有很多人;只知道列数也不能确定,因为同一列也有很多人,所以,要想确定一个人的位置,必须知道行数和列数.解:需要知道小明所在的行数和列数.【例1-2】你到阳光电影院去看电影,你的票上注明的是9排13号,你准备怎样找到自己的座位?解:路线不唯一,但是总要找到9排,并且找到13号座位.通常先找到排再找到号,也可能先找到号再找到排.2.极坐标定位法这是一种采用方位角和距离的方式来表示物体具体位置的定位方法,运用此方法来确定物体的位置需要两个数据:(1)方位角;(2)距离,两者缺一不可.使用此法首先要找出一个参照点,而其他点的方位角和距离则相对于该参照点而确定下来.【例2】下面为新时代学校的平面示意图,A处是教学楼,B处是实验楼,C处是艺体楼,D处是车棚,E处是办公楼,请你借助刻度尺、量角器,解决下列问题:(1)对教学楼来说,要想确定实验楼的位置,还需要什么数据?(2)对教学楼来说,车棚在什么位置?艺体楼在什么位置?分析:本题可采用极坐标定位法.解:(1)想确定实验楼的位置,还需要知道实验楼在教学楼的哪个方位角上,以及它和教学楼的距离.(2)对教学楼来说,车棚在南偏东35°,图上距离约为0.8 cm;艺体楼在正东方向,图上距离约为1.5 cm.3.经纬定位法经纬定位法就是用经度和纬度来确定物体位置的方法,此法在地理学中有着广泛的应用,使用此法来确定物体的位置必须指明经度和纬度,两者缺一不可.释疑点经纬定位法经纬定位法既适合于在球面上定位,也适合于在平面上定位.【例3-1】“神舟九号”飞船已胜利升空,中国人正在逐渐地向宇宙进军,那么你能猜测出地面上的工作人员是如何来确定飞船的位置的吗?分析:本题为实际应用题目,只要联想到地理上学的经度、纬度,该问题就可以顺利解决.又因为飞船在太空中飞行,所以还需要其与地面的距离才能确定其位置.解:地面上的工作人员一般靠经纬线和飞船所处高度来确定位置.点拨:利用地理学上的经纬度来确定物体的位置的定位方法,应用非常广泛.【例3-2】A地在地球上的位置如图所示,则A地的位置是( ).A.东经130°,北纬50°B.东经130°,北纬60°C.东经140°,北纬50°D.东经140°,北纬60°解析:指明一点的经度和纬度就可以确定物体在地球上的位置.答案:C4.区域定位法它是生活中常用的表示物体位置的方法之一,需要有两个数据才能确定物体的位置,用这种方法确定物体的位置具有简单明了的特点,但有时往往不精确,所以要视情况而定.【例4】如图是某学校平面简图的一部分,其中M1代表仓库,其所在的区域为A2区.M2代表办公楼,M3代表实验楼,试说出办公楼、实验楼所在的区域.分析:要求办公楼、实验楼所在的区域,先竖着找出其所在的字母区域,再横着找出所处的数字区域,两者合在一起便使问题得解.解:办公楼在C3区,实验楼在B4区.析规律区域定位法弄清区域定位法中的字母及数字分别表示的含义,依照已知建筑物的表示方法表示建筑物的位置.5.直角坐标定位法直角坐标定位法是生活中常采用的方法之一,在数学中,它是必须掌握的一种确定位置的方法,是后面学习平面直角坐标系的基础,运用此法确定一个物体的位置也需要有两个数据,一个是横坐标,另一个是纵坐标,两者缺一不可.我们习惯用(a,b)来表示某一个物体的位置,其中a代表横坐标,b代表纵坐标.【例5】如图是中国象棋的一盘残局,如果用(4,0)表示的位置,用(3,9)表示的位置,那么的位置应表示为( ).A.(8,7) B.(7,8)C.(8,9) D.(8,8)答案:A6.在电影院内如何找到电影票上所指的位置在只有一层的电影院内,确定一个座位的位置需要两个数据,一个是排数,一个是号数.要找到自己电影票上所指的位置,先找到排数,再来找号数,此位置即票上所示的位置.如果是多层的电影院,一般还需要另加一个数据——确定位置在几层.点技巧平面上定点平面上确定物体的位置有多种方式,但基本都需要两个数据.【例6】近期某剧院(座位分单、双座)举办某知名歌星个人演唱会,小强与小华买了两张票去观看,座位号分别为10排12号和10排14号.(1)怎样才能既快又准确地找到座位?(2)小强和小华的座位靠在一起吗?分析:要找到自己电影票上所指的位置,先找到排数,再来找号数.解:(1)由于剧院的座位分为单座和双座,因此要既快又准确地找到自己的座位,应先从双座大门进去,找到第10排,再在第10排中找到12号和14号.(2)由于剧院的座位分单座和双座,因此小强和小华的座位靠在一起.7.坐标在生活中的运用人们常说:“找准人生坐标”,意思是很清楚的.事实上,数学中所说的“坐标”在我们日常生活中的应用极为广泛.例如:如图是某公园示意图,请你根据图中比例尺用坐标的方法确定各景点的位置.分析:入口处是我们最先熟悉的地点,因此我们可以选择入口处为坐标原点,西东方向为横轴;南北方向为纵轴建立平面直角坐标系(如图),分别量出各景点到横轴、纵轴的距离,这样便可知道各景点的坐标.例如动物园到纵轴的距离约为4.1 cm,到横轴的距离约为2.8 cm,因此动物园的位置是(4.1,2.8),根据比例尺换算以后,实际是(1 230,840),这表明动物园在入口处的东 1 230 m,北840 m处.其余景点的位置用相同的方法即可确定.【例7】如图,用点A(3,1)表示放置3个胡萝卜、1棵青菜,点B(2,3)表示放置2个胡萝卜、3棵青菜.(1)请你写出其他各点C,D,E,F所表示的意义;(2)若一只兔子从点A到达点B(顺着方格线走),有以下几条路可以选择:①A→C→D→B;②A→F→D→B;③A→F→E→B,问它走哪条路吃到的胡萝卜最多?走哪条路吃的青菜最多?分析:(1)由点A和B的坐标意义即可类比出其他各点所表示的意义;(2)先将所表示的胡萝卜和青菜数计算出来再相加比较即可.解:(1)因为点A(3,1)表示放置3个胡萝卜、1棵青菜,点B(2,3)表示放置2个胡萝卜、3棵青菜,所以可以类比:点C的坐标是(2,1),它表示的意义是放置2个胡萝卜、1棵青菜;点D的坐标是(2,2),它表示的意义是放置2个胡萝卜、2棵青菜;点E的坐标是(3,3),它表示的意义是放置3个胡萝卜、3棵青菜;点F的坐标是(3,2),它表示的意义是放置3个胡萝卜、2棵青菜.(2)若兔子走①A→C→D→B,则可以吃到的胡萝卜数量是3+2+2+2=9个,吃到的青菜数量是1+1+2+3=7棵;走②A→F→D→B,则可以吃到的胡萝卜数量是3+3+2+2=10个,吃到的青菜数量是1+2+2+3=8棵;走③A→F→E→B,则可以吃到的胡萝卜数量是3+3+3+2=11个,吃到的青菜数量是1+2+3+3=9棵;由此可知,走第③条路吃到的萝卜、青菜都最多.。
八年级数学上册第三章位置与坐标1确定位置作业课件新版北师大版

11.(2017·深圳期末)如图,雷达探测器测得六个目标点A,B,C,D,E,F 出现,按照规定的目标表示方法,目标点C,F的位置表示为C(6,120°),F(5, 210°),按照此方法在表示目标点A,B,D,E的位置时,其中表示不正确的 是( ) D
(1)给机器人下一个指令(2,60°),机器人移动到了B,请你画出机器人从 M到B的运动路径;
(2)若机器人从M运动到了C点,则给机器人下了一个什么指令? 解:(1)图略 (2)(3,340°)
1.老师对班上的同学的座位进行调整,下面说法能找到座位的是( D ) A.3排4列 B.从前数第3排4列 C.3排从左数第4列 D.从前数第3排,从左数第4列 2.如果电影票上的“5排2号”记作(5,2),那么(4,3)表示( C) A.3排5号 B.5排3号 C.4排3号 D.3排4号
3.若我军战舰攻打敌军战舰,需要知道(D ) A.我军战舰的位置 B.敌军战舰相对于我军战舰的方向 C.敌军战舰相对于我军战舰的距离 D.敌军战舰相对于我军战舰的方向和距离 4.如图,OP是一条射线,OA,OB,OC是三条线段,其中OA=a,OB= b,OC=c,并且∠BOP=30°,AO⊥BO,OC是∠AOB的角平分线.若点B 可表示为(b,30°),则点A可表示为 (a,120°), 点C可表示为 (c,75°) .
A.A(5,30°) B.B(2,90°) C.D(4,240°) D.E(3,60°)
12.(阿凡题:1071119)(2017·东营模拟)将自然数按以下规律排列:
第一列 第二列 第三列 第四列 第五列 …
第一行
1
4
5
16
八年级数学上册第三章位置与坐标1确定位置教案北师大版

第三章位置与坐标1确定位置1.在现实情境中感受物体定位的多种方法.2.能较灵活地运用不同的方式对物体定位.3.了解在平面上确定物体位置的方法的统一性:都需要两个数据.重点根据行和列确定并描述物体的位置.难点用坐标的思想表示点的位置.一、情境导入课件出示教材第54页“议一议"上面的主题图.(1)在电影院内如何找到电影票上所指的位置?(2)在电影票上,“3排6座”与“6排3座"中的“6"的含义有什么不同?师:如果将“3排6座”记作(3,6),那么“6排3座”如何表示?(5,6)表示什么含义?二、探究新知确定位置.课件出示教材第54页例题.结论:生活中常常用“方位角”和“距离”来确定位置.三、举例分析1.课件出示教材第55页“做一做"第(1)小题.结论:生活中常常用“经度”和“纬度”来确定位置.2.课件出示教材第55页“做一做”第(2)小题.3.课件出示教材第55页“议一议”.结论:在平面内,确定一个物体的位置一般需要2个数据.若设这两个数据分别为a和b,则:a表示:排数、行数、经度、方位……b表示:座数、列数、纬度、距离……拓展:确定平面上的点的位置方法很多,不管采用哪种方法,都需要两个量,特别是用数对表示位置时,应该注意数是有顺序的,顺序不同表示点的位置就不同.四、练习巩固教材第56页“随堂练习”第1~2题.五、小结1.在现实情境中感受了确定物体位置的多种方式,并能灵活运用不同方式确定物体的位置.2.在数轴上,确定一个点的位置一般需要一个数据.在平面内,确定一个物体的位置一般需要两个数据。
若设这两个数据分别为a和b,则:a表示:排数、行数、经度、方位……b表示:座数、列数、纬度、距离……六、课外作业教材第57页习题3。
1第1~3题.本节内容与现实生活联系紧密,学生在生活中经常能遇到相关的知识,因此在教学时尽量让学生参与进来.学生在亲身体验中学习知识,加深印象,并培养认真的学习态度.要让学生学习时有条理地思考和表达,在确定位置的活动中,学生不仅自己要明白物体的位置,而且要能有条理地向别人表述.这种表达可以反映学生的表达水平、有关知识的掌握程度和空间观念.。
鲁教版(五四制)七年级上册数学课件第五章1确定位置(鲁教版七年级上·五四制)

【点拨】在现实生活中,确定位置的方式很多,不管什么定位 方式,平面内确定位置都需要两个数据. 【预习思考】北偏东30°能否确定物体的位置? 提示:不能.在平面内确定一个物体的位置要用两个数据,而 北偏东30°只有一个数据,故不能确定该物体的位置.
灿若寒星
知识点1生活中确定位置的方法 【例1】小明家和学校的位置关系如图所示,已知图上距离: OA=2cm,OB=2.5cm,OP=4cm,且C为OP的中点. (1)图中与小明家距离相等的是哪些地方? (2)从图上看商场、学校、公园、停车场分别在小明家的什么 位置?
【高手支招】 用有序实数对确定点的位置时,先确定两个实数的先后顺序, 同学们在做题时易由于颠倒而出错,应加强注意.
灿若寒星
1.某人站在A点,他不能确定B点位置的情况是( ) (A)B点离A点30m (B)B点离A点30m,且在A点北偏西30°方向上 (C)B点在A点向东30m,再向南20m位置 (D)B点在A点正南方向,且AB=50m 【解析】选A.B点离A点30m只能确定点B在以A为圆心,30m为半 径的圆上,不能确定具体位置.
灿若寒星
【互动探究】从商场向东多少cm,再向南多少cm恰好就是小明
家的位置?
提示:过点B作南北方向线的垂线,垂足为D,则∠BOD=30°,
所以BD=O1B=cm,5 由勾股定理可得OD=cm,则5 向3 东cm, 5
24
4
4
再向南c5m.3
4
灿若寒星
【规律总结】 平面上确定位置常用的三种方法
1.行列定位法:常把平面分成若干行、列,然后利用行号和列 号表示平面上点的位置.注意,同样的两个数据若顺序不同, 表示的位置则不同. 2.方位角距离定位法:该定位法常应用于航海和军事上,运用 此法需要两个数据:方位角和距离. 3.经纬定位法:该法需要两个数据经度和纬度.此方法在地理 学中有着极其广泛的应用灿.若寒星
六年级数学上册第二单元《位置与方向》知识点练习

六年级数学上册第二单元《位置与方向》知识点1、根据方向和距离可以确定物体在平面图上的位置。
2、在平面图上标出物体位置的方法:先用量角器确定方向,再以选定的单位长度为基准用直尺确定图上距离,最后找出物体的具体位置,并标上名称。
3、描述路线图时,要先按行走路线确定每一个参照点,然后以每一个参照点建立方向标,描述到下一个目标所行走的方向和路程,即每一步都要说清是从哪儿走,向什么方向走了多远到哪儿。
4、绘制路线图的方法:(1)确定方向标和单位长度。
(2)确定起点的位置。
(3)根据描述,从起点出发,找好方向和距离,一段一段地画。
除第一段(以起点为参照点)外,其余每一段都要以前一段的终点为参照点。
(4)以谁为参照点,就以谁为中心画出“十”字方向标,然后判断下一地点的方向和距离。
六年级上册数学第二单元同步练习题一、以小丽的家为参照点进行填空。
1、超市在小丽家的()偏()()方向上,距离()。
2、图书馆在小丽家的()偏()()方向上,距离()。
3、公园在小丽家的()偏()()方向上,距离()。
二、根据下面的路线图,说一说小红上学和放学所走的方向和路程。
三.根据下面的路线图,说一说亮亮从动物园入口进入,依次参观海豚馆、熊猫馆、大象馆所走的方向和路程。
四、小山下午放学回家,她从学校出发,先向正南方向走200米,然后向西偏北20度方向走了100米,接着向南偏西45度方向走了300米,最后向正东方向走了200米到家。
请你根据上面的描述画出小山的路线图。
五、周末的一天,笑笑一家去游玩,他们一家从家里出发,先向东偏南40度方向走了400米,然后向南偏西20度方向走了200米,最后向西偏北70度方向走了100米到达目的地。
请你根据上面的描述画出笑笑一家的路线图。
六、一艘轮船从甲港口到丁港口,航行路线如下图。
1、说说这艘轮船的航行路线。
2、这艘轮船一共行驶了多少千米?参考答案一、1、东,北,40度,1750米2、南,西,50度,950米3、西,北,45度,1250米二、答:小红上学所走的方向和路程是小红从家出发,向北偏东45度方向上走800米,到达百货商场,然后向东偏南30度方向上走1000米,到达学校。
2023年人教版小学六年级数学上册第2单元“位置与方向(二)”第1课时《描述物体的位置》优质课教案

2023年人教版小学六年级数学上册优质课教案第2单元位置与方向(二)第1课时描述物体的位置【教学内容】教材第18页例1及相关内容。
【教学目标】1.结合具体情境,用相对于观测点的方向和距离描述平面上物体的位置。
2.在经历不断发现、提出问题,尝试分析、解决问题的过程中,逐步掌握确定准确位置的方法。
3.在实际应用中感受数学与生活的紧密联系。
【重点难点】重点:会用相对于观测点的方向和距离确定平面上物体的位置。
难点:能用较规范的语言准确地描述平面上物体的位置。
【教学过程】一、复习导入将下面的方位图补齐。
二、探究新知1.自学提示:自学教材第18页的内容,回答以下问题。
(1)东偏南30°是什么意思?如果只有这个条件,能够确定台风中心的具体位置吗?(2)台风大约多少小时后到达A市?2.教学例1。
【课件出示教材第18页例1】(1)学生观察情境图,说说可以从图中获得哪些信息。
(2)交流确定台风中心具体位置的方法。
师:东偏南30°是什么意思?预设:东偏南30°表示的是台风中心位置相对于A市所在的方向,也就是台风中心位置与A市的连线和正东方向的夹角是30°,即正东方向往南偏30°。
师:如果只有这个条件,能够确定台风中心的具体位置吗?引导学生得出:要确定台风中心的具体位置必须知道两个条件,即物体所在的方向和物体在这个方向上距离观察点的距离,简单地说就是要用“方向+距离”的方法来确定物体所在的具体位置。
(3)组织计算。
师:现在我们知道台风中心所在的具体位置了,那台风大约多少小时后到达A市呢?(学生独立计算,组织交流。
)预设:600÷20=30(时)3.课堂练习,强化新知。
完成教材第19页做一做。
(1)让学生独立进行测量、计算、填空。
(2)组织交流。
三、巩固运用1.完成教材第22页第1题。
学生先独立测量,然后组织交流。
2.完成教材第22页第2题。
(1)学生独立填空。
北师大版数学五年级下册《确定位置(一)》说课稿1

北师大版数学五年级下册《确定位置(一)》说课稿1一. 教材分析《确定位置(一)》是人教版小学五年级下册数学教材的一个知识点。
这部分内容是在学生掌握了基本的平面几何知识和对称知识的基础上进行学习的。
通过这部分内容的学习,使学生能够理解坐标的概念,学会用坐标表示点的位置,以及通过坐标来确定物体在平面上的位置。
教材通过生活实例引入坐标的概念,让学生感受到数学与生活的紧密联系,培养学生运用数学知识解决实际问题的能力。
二. 学情分析五年级的学生已经具备了一定的几何知识和逻辑思维能力,对于平面图形的认识和操作也已经有一定的基础。
但是,坐标概念的引入对于学生来说是一个新的挑战,需要学生能够从生活的实例中抽象出坐标的概念,理解坐标的意义,并能够运用坐标来解决问题。
三. 说教学目标1.知识与技能目标:学生能够理解坐标的概念,学会用坐标表示点的位置,并能够通过坐标来确定物体在平面上的位置。
2.过程与方法目标:通过生活实例的引入和学生的实践操作,培养学生的抽象思维能力和解决问题的能力。
3.情感态度与价值观目标:让学生感受到数学与生活的紧密联系,培养学生的学习兴趣和合作意识。
四. 说教学重难点1.教学重点:学生能够理解坐标的概念,学会用坐标表示点的位置,并能够通过坐标来确定物体在平面上的位置。
2.教学难点:学生能够从生活的实例中抽象出坐标的概念,理解坐标的意义,并能够运用坐标来解决问题。
五.说教学方法与手段在教学过程中,我将以学生为主体,采用引导发现法、情境教学法、实践操作法等多种教学方法,激发学生的学习兴趣,培养学生的抽象思维能力和解决问题的能力。
同时,我还将运用多媒体教学手段,为学生提供丰富的学习资源,帮助学生更好地理解和掌握坐标的概念。
六.说教学过程1.导入:通过一个生活实例,如在地图上查找某个地点的位置,引出坐标的概念,激发学生的学习兴趣。
2.探究:让学生通过实践操作,如在坐标系中确定物体的位置,引导学生发现坐标的意义和运用坐标解决问题的方法。
人教版六年级数学上册同步教案2-1用方向和距离确定物体在平面图上的位置

人教版六年级数学上册同步教案2.1用方向和距离确定物体在平面图上的位置教学内容:P19-P21 例1、例2教学目标知识与技能1.理解和掌握根据方向和距离确定物体位置的方法。
2.能根据方向和距离准确地说出物体所在的位置。
3.知道如何根据方向和距离在平面图上标出物体的位置。
过程与方法1.经历观察、测量、画图、描述等过程,感受从实践中学习的策略和方法。
2.通过在平面图上标出物体的位置,培养学生的动手操作能力,进一步发展空间观念,培养学生合作探究的意识和能力。
情感、态度与价值观1.在学习的过程中感受数学与日常生活的密切联系,增强数学的应用意识。
2.使学生体会所学知识在生活中的应用,增强学好数学的信心。
3.在探究活动中获得成功的经验,发展学生的空间观念。
重点难点重点:掌握根据方向和距离在平面图上确定物体位置的方法。
难点:能够根据方向和距离在平面图上标出物体的位置。
课前准备教师准备PPT课件任务书彩色卡片学生准备直尺量角器教学过程板块一趣味游戏,导入新课1.小游戏——夺宝奇兵。
(1)游戏说明:教师课前设计好任务书两份,并说明宝物(用彩色卡片代替)所藏地点。
例如:宝物一在第2行第3列,宝物二在第4行第5列……教师先请参赛的两组同学回避,然后将宝物交给任务书上所写位置的同学藏好。
(2)教师宣布游戏任务和游戏规则,请参赛的两组同学按照各自任务书上的提示寻找宝物,先找到宝物的小组获胜。
(3)开始游戏。
请参赛的两组同学讲一讲,你们是怎样找到宝物的?(教师注意引导学生从解决问题的方面谈一谈)复习用数对确定物体位置的方法。
2.在低年级的时候,我们背过一首儿歌,从此,我们学会了辨认方向。
早上起床,面向太阳,谁还会继续背诵下去?(前面是东,后面是西,左边是北,右边是南)知道了这首儿歌,即使在大森林里,也会辨认方向。
那么,平面图上的方向一般是怎么规定的呢?(上北、下南、左西、右东)今天,我们就来尝试通过平面图解决问题吧!操作指导在游戏中教师引导参赛的两组同学读清楚各自任务书上的提示,按照用数对确定物体位置的方法寻找宝物。
冀教版八年级下册数学第19章 平面直角坐标系 确定平面上物体的位置(1)

第十九章 平面直角坐标系
19.1确定平面上物体的位置
提示:点击 进入习题
1B 2D 3 (3,240°) 4D 5A
6A 7 见习题
答案显示
1.【2020·河北唐山丰润区期中】如果用有序数对(3,2)表示教室里第3
列第2排的座位,那么位于第5列第4排的座位应记作( )
A.(4,5)
点A,B的坐标分别表示为(5,0°), (4,300°),则点C的坐标表示为 __________.
(3,240°)
4.【易错:因方位角找错而出错】如图,下列关于点A位置的描述,正确的是
()
A.距O点3km的地方
D
B.在O点北偏东40°方向,距O
点3km的地方ຫໍສະໝຸດ C.在O点东偏北40°的方向上
D.在O点北偏东50°方向,距O点3km的地方
解:点C的位置如图①所示.
(2)若点A用(-3,1)表示,点B用(-2,2)表示,点D用(0,0)表示,请 在图②中标出点D的位置,并说明(1)中的点C应如何表示.
解:点D的位置如图②所示,点C应用(-4,0) 表示.
A.从点P出发向北偏西45°方向走3km到达l B.公路l的走向是南偏西45° C.公路l的走向是北偏东4A5° D.从点P出发向北走3km后,再向西走3km到达l
7.如图,一个正方形被等分成4行4列. (1)若点A用(1,1)表示,点B用(2,2)表示,点C用(0,0)表示,请在图①中
标出点C的位置;
B.(5,4)
C.(3,2)
D.(2,3) B
2.【2021·海南】如图,点A,B,C都在方格纸的格点上,若点A的坐标
为(0,2),点B的坐标为(2,0),则点C的坐标是( )
17.中考数学专题09 平面直角坐标系章末重难点题型(举一反三)(解析版)

专题09 平面直角坐标系章末重难点题型汇编【举一反三】【考点1 确定位置】【方法点拨】在平面内,确定一个物体的位置一般需要两个数据.若设这两个数据分别为a和b,则:a表示:排数、行数、经度、方位……b表示:座数、列数、纬度、距离……【例1】(2019春•颍泉区校级期中)如图,军训时七(1)班的同学按教官的指令站了7排8列,如果第7排第8列的同学的位置在队列的东北角,可以用有序数对(7,8)来表示,那么表示站在西南角同学的位置的有序数对是()A.(7,8)B.(1,1)C.(1,2)D.(2,1)【分析】根据“某同学坐在7排8列,用(7,8)表示,”得出排数写在数对中的第一个数,列数写在数对中的第二个数,由此表示站在西南角同学的位置的有序数对.【答案】解:因为,排数写在数对中的第一个数,列数写在数对中的第二个数,所以,表示站在西南角同学的位置的有序数对是(1,1),故选:B.【点睛】考查了坐标确定位置,解答此题的关键是根据所给出的同学的位置的确定方法,来确定要求同学的位置.【变式1-1】(2019春•江城区期中)以校门所在位置为原点,分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,如果出校门向东走60m,再向北走80m,记作(60,80),那么明明家位置(﹣30,60)的含义是()A.出校门向西走30m,再向南走60mB.出校门向西走30m,再向北走60mC.出校门向东走30m,再向南走60mD.出校门向东走30m,再向北走60m【分析】根据从原点向东为正,向北为正,可得明明家位置(﹣30,60)的含义.【答案】解:由以校门所在位置为原点,分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,得明明家位置(﹣30,60)表示出校门向西走30米,向北走60米,故B符合题意.故选:B.【点睛】本题考查了坐标确定位置,利用坐标表示点的位置的关键是确定原点的位置.【变式1-2】(2018秋•桥东区期中)小明乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km(小圆半径是1km),若小艇C在游船的正南方2km,则下列关于小艇A、B的位置描述,正确的是()A.小艇A在游船的北偏东60°,且距游船3kmB.游船在的小艇A北偏东60°,且距游船3kmC.小艇B在游船的北偏西30°,且距游船2kmD.小艇B在小艇C的北偏西30°,且距游船2km【分析】利用方向角的表示方法对各选项进行判断.【答案】解:小艇A在游船的北偏东30°,且距游船3km;小艇B在游船的北偏西60°,且距游船2km;游船在小艇的南偏西30°,且距游船3km;小艇B在小艇C的北偏西30°,且距游船2km.故选:D.【点睛】本题考查了坐标确定位置:是熟练掌握平面内特殊位置的点的坐标特征.理解方向角的表示方法.【变式1-3】(2018春•孝义市期中)如图呈现的是一局围棋比赛中的几手棋,为记录棋谱方便,横线用字母表示,纵线用英文数字表示,这样,黑棋❶的位置可记为(C,4),则白棋⑥的位置可记为()A.(E,3)B.(F,3)C.(G,5)D.(D,6)【分析】直接利用黑棋❶的位置表示方法,进而得出白棋⑥的位置.【答案】解:∵黑棋❶的位置可记为(C,4),∴白棋⑥的位置可记为:(G,5).故选:C.【点睛】此题主要考查了坐标确定位置,正确理解横纵坐标的意义是解题关键.【考点2 象限内点的特征】【方法点拨】掌握第1~4象限内点的坐标符号特点分别是:(+,+)、(-,+)、(-,-)、(+,-).【例2】(2019春•天门校级期中)已知点P(a,b)在第四象限,则点Q(2a﹣b,2b﹣a)在第()象限.A.一B.二C.三D.四【分析】根据各象限内点的坐标特征解答即可.【答案】解:由题意,得a>0,b<0.由不等式的性质,得2a﹣b>0,2b﹣a<0,点Q(2a﹣b,2b﹣a)在第四象限,故选:D.【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).【变式2-1】(2019春•信丰县期中)如果P(a+b,ab)在第二象限,那么点Q(﹣a,b)在第()象限.A.一B.二C.三D.四【分析】直接利用第二象限内点的坐标特点得出a,b的符号,进而得出答案.【答案】解:∵P(a+b,ab)在第二象限,∴a+b<0,ab>0,∴a<0,b<0,∴﹣a>0,∴点Q(﹣a,b)在第四象限.故选:D.【点睛】此题主要考查了点的坐标,正确得出a,b的符号是解题关键.【变式2-2】(2019春•卫辉市期中)若点A(a+1,b﹣2)在第二象限,则点B(﹣a,b+1)在第()象限.A.四B.三C.二D.一【分析】根据第二象限内点的横坐标是负数,纵坐标是正数列不等式求出a、b的取值范围,然后求解即可.【答案】解:∵点A(a+1,b﹣2)在第二象限,∴a+1<0,b﹣2>0,∴a<﹣1,b>2,∴﹣a>1,b+1>3,∴点B(﹣a,b+1)在第一象限.故选:D.【点睛】本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).【变式2-3】(2019春•汉阳区期末)直角坐标系中点P(a+2,a﹣2)不可能所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限【分析】确定出点P的横坐标比纵坐标大,再根据各象限内点的坐标特征解答.【答案】解:∵(a+2)﹣(a﹣2)=a+2﹣a+2=4,∴点P的横坐标比纵坐标大,∵第二象限内点的横坐标是负数,纵坐标是正数,∴点P不可能在第二象限.故选:B.【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).【考点3 坐标轴上点的特征】【方法点拨】坐标系内点的坐标特点:坐标原点(0,0)、x轴(x,0)、y轴(0,y).注意若点在坐标轴上,则要分成在x轴、y轴上两种情况来讨论.【例3】(2019秋•市北区期中)如果点P(m+3,2m+4)在y轴上,那么点Q(m﹣3,﹣3)的位置在()A.纵轴上B.横轴上C.第三象限D.第四象限【分析】由点P在y轴上可得出关于m的一元一次方程,解之即可得出m的值,将其代入点Q的坐标中可得出点Q在第三象限,此题得解.【答案】解:∵点P(m+3,2m+4)在y轴上,∴m+3=0,∴m=﹣3,∴点Q的坐标为(﹣6,﹣3),∴点Q在第三象限.故选:C.【点睛】本题考查了点的坐标以及解一元一次方程,根据点P在y轴上找出关于m的一元一次方程是解题的关键.【变式3-1】(2019春•邓州市期中)若点A(﹣2,n)在x轴上,则点B(n﹣1,n+1)在第()象限.A.一B.二C.三D.四【分析】由点在x轴的条件是纵坐标为0,得出点A(﹣2,n)的n=0,再代入求出点B的坐标及象限.【答案】解:∵点A(﹣2,n)在x轴上,∴n=0,∴点B的坐标为(﹣1,1).则点B(n﹣1,n+1)在第二象限.故选:B.【点睛】此题主要考查了点的坐标,解决本题的关键是掌握好四个象限的点的坐标的特征:第一象限正正,第二象限负正,第三象限负负,第四象限正负.【变式3-2】(2019春•柳江区期中)若点A(m+2,2m﹣5)在y轴上,则点A的坐标是()A.(0,﹣9)B.(2.5,0)C.(2.5,﹣9)D.(﹣9,0)【分析】直接利用y轴上横坐标为0,进而得出m的值即可得出答案.【答案】解:∵点A(m+2,2m﹣5)在y轴上,∴m+2=0,解得:m=﹣2,故2m﹣5=﹣9,故点A的坐标为:(0,﹣9).故选:A.【点睛】此题主要考查了点的坐标,正确得出m的值是解题关键.【变式3-3】(2018秋•章丘区期末)已知点A(2x﹣4,x+2)在坐标轴上,则x的值等于()A.2或﹣2B.﹣2C.2D.非上述答案【分析】依据坐标轴上的点的坐标特征,即可得到x的值.【答案】解:∵点A(2x﹣4,x+2)在坐标轴上,∴当2x﹣4=0时,x=2,当x+2=0时,x=﹣2,∴x的值为±2,故选:A.【点睛】本题考查了点的坐标:坐标平面内的点与有序实数对是一一对应的关系;解题时注意:x轴上点的纵坐标为0,y轴上点的横坐标为0.【考点4 点到坐标轴的距离】【方法点拨】点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值.【例4】(2019春•兰山区期中)在平面直角坐标系中,点E在x轴上方,y轴的左侧,距离x轴3个单位,距离y轴4个单位,则E点的坐标为()A.(3,﹣4)B.(4,﹣3)C.(﹣4,3)D.(﹣3,4)【分析】先判断出点E在第二象限,再根据点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.【答案】解:∵点E在x轴上方,y轴的左侧,∴点E在第二象限,∵距离x轴3个单位长度,距离y轴4个单位长度,∴点E的横坐标为﹣4,纵坐标为3,∴点E的坐标是(﹣4,3).故选:C.【点睛】本题考查了点的坐标,熟记点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值是解题的关键.【变式4-1】(2019春•郯城县期中)点P(a+3,b+1)在平面直角坐标系的x轴上,并且点P到y轴的距离为2,则a+b的值为()A.﹣1B.﹣2C.﹣1或﹣6D.﹣2或﹣6【分析】根据x轴上点的纵坐标为0以及点到y轴的距离等于横坐标的长度解答.【答案】解:∵点P(a+3,b+1)在平面直角坐标系的x轴上,并且点P到y轴的距离为2,∴b+1=0,|a+3|=2,∴a=﹣1或﹣5,b=﹣1,∴a+b=﹣2或﹣6,故选:D.【点睛】本题考查了点的坐标,熟记点到y轴的距离等于横坐标的长度以及x轴上点的坐标特征是解题的关键.【变式4-2】(2018春•新罗区校级期中)若点P(2x,3x+5)在第二象限,且点P到两坐标轴的距离相等,则点Q(﹣x2,2x2+2)的坐标是()A.(1,﹣4)B.(﹣1,﹣4)C.(﹣1,4)D.(1,4)【分析】根据第二象限角平分线上的点到两坐标轴的距离相等,可得答案.【答案】解:由题意,得2x+3x+5=0,解得x=﹣1.当x=﹣1时,﹣x2=﹣1.2x2+2=4,Q(﹣x2,2x2+2)的坐标是(﹣1,4),故选:C.【点睛】本题考查了点的坐标,利用第二象限角平分线上的点到两坐标轴的距离相等得出2x+3x+5=0是解题关键.【变式4-3】(2019春•栾城区期中)已知直线MN垂直于x轴,若点M的坐标为(﹣5,2),点N距x轴的距离为3个单位,则点N的坐标为()A.(﹣5,3)B.(﹣5,3)或(﹣5,﹣3)C.(3,2)D.(3,2)或(﹣3,2)【分析】根据平行于y轴的直线上点的横坐标相等,点到x轴的距离是纵坐标的绝对值,可得答案.【答案】解:由直线MN垂直于x轴,若点M的坐标为(﹣5,2),点N的横坐标为﹣5,由点N距x轴的距离为3个单位,则点N的纵坐标为3或﹣3,故选:B.【点睛】本题考查了点的坐标,利用平行于y轴的直线上点的横坐标相等得出点的横坐标是解题关键.【考点5 角平分线上点的特征】【方法点拨】象限角平分线上点的坐标特点:第1、3象限中x=y,第二、四象限中x+y=0.【例5】(2019春•武平县校级期中)已知点A(2a+1,5a﹣2)在第一、三象限的角平分线上,点B(2m+7,m﹣1)在二、四象限的角平分线上,则()A.a=1,m=﹣2B.a=1,m=2C.a=﹣1,m=﹣2D.a=﹣1,m=2【分析】已知一、三象限上的点的横纵坐标相等,故按照题目要求,使横纵坐标相等,可列出等式,即可求出a的值;根据第二、第四象限坐标轴夹角平分线上的点,横纵坐标互为相反数,由此就可以得到关于m的方程,解出m的值.【答案】解:由已知条件知,点A位于一、三象限夹角平分线上,所以有2a+4=5a﹣2,解得:a=1;∵点B(2m+7,m﹣1)在第二、四象限的夹角角平分线上,∴(2m+7)+(m﹣1)=0,解得:m=﹣2.故选:A.【点睛】本题考查了点的坐标的知识,注意掌握知识点:第二、四象限的夹角角平分线上的点的横纵坐标互为相反数.【变式5-1】(2019春•德州期末)若点A(a+1,a﹣2)在第二、四象限的角平分线上,则点B(﹣a,1﹣a)在()A.第一象限B.第二象限C.第三象跟D.第四象限【分析】根据第二、四象限点的横坐标与纵坐标互为相反数列出方程求出a的值,再根据各象限内点的坐标特征求解即可.【答案】解:∵点A(a+1,a﹣2)在第二、四象限的角平分线上,∴a+1=﹣(a﹣2),解得a=1 2.∴﹣a=−12,1﹣a=1−12=12,∴点B(﹣a,1﹣a)在第二象限.故选:B.【点睛】本题考查了点的坐标,掌握第二、四象限点的横坐标与纵坐标互为相反数以及各象限内点的坐标特征是解题的关键.【变式5-2】若A(a,﹣b),B(﹣b,a)表示同一个点,那这个点一定在()A.第二、四象限的角平分线上B.第一、三象限的角平分线上C.平行于x轴的直线上D.平行于y轴的直线上【分析】先判断出a=﹣b,则点的横坐标与纵坐标符号相反.【答案】解:∵点A(a,﹣b),B(﹣b,a)表示同一个点,∴a=﹣b,∴这个点一定在第一、三象限的角平分线上.故选:B.【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).【变式5-3】(2019春•福州校级月考)已知点M(a﹣1,﹣a+3)向右平移3个单位,之后又向下移7个单位,得到点N、若点N恰在第三象限的角平分线上,则a的值为()A.2B.0C.3D.﹣3【分析】让点M的横坐标加3,纵坐标减7得到点N的坐标,让点N的横纵坐标相等即可求得a的值.【答案】解:∵点M(a﹣1,﹣a+3)向右平移3个单位,之后又向下移7个单位,得到点N,∴点N的横坐标为a﹣1+3=a+2;纵坐标为﹣a+3﹣7=﹣a﹣4;∵点N恰在第三象限的角平分线上,∴a+2=﹣a﹣4,∴a=﹣3,故选:D.【点睛】本题考查了平移中点的变化规律:左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.注意第三象限上点的横纵坐标相等.【考点6 点的坐标确定位置】【方法点拨】首先由点的坐标确定坐标系,进而可确定所求位置的坐标.【例6】(2019春•郯城县期中)课间操时,小华、小军、小刚的位置如图,小军对小华说,如果我的位置用(0,﹣2)表示,小刚的位置用(2,0)表示,那么你的位置可以表示为()A.(﹣2,﹣3)B.(﹣3,﹣2)C.(﹣3,﹣4)D.(﹣4,﹣3)【分析】根据小军和小刚的坐标建立平面直角坐标系,据此可得答案.【答案】解:由小军和小华的坐标可建立如图所示平面直角坐标系:则小华的位置可表示为(﹣2,﹣3),故选:A.【点睛】本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住直角坐标系中特殊位置点的坐标特征.【变式6-1】(2019春•蒙阴县期中)如图是中国象棋的一盘残局,如果用(2,﹣3)表示“帅”的位置,用(6,4)表示的“炮”位置,那么“将”的位置应表示为()A.(6,4)B.(4,6)C.(1,6)D.(6,1)【分析】以帅的坐标向左两个单位,向上3个单位为坐标原点建立平面直角坐标系,然后写出将的坐标即可.【答案】解:建立平面直角坐标系如图所示,将(1,6).故选C.【点睛】本题考查了坐标确定位置,读懂题目信息,准确确定出坐标原点是解题的关键.【变式6-2】(2018春•越秀区期中)如图所示为某战役潜伏敌人防御工亭坐标地图的碎片,一号墙堡的坐标为(4,2),四号墙堡的坐标为(﹣2,4),由原有情报得知:敌军指挥部的坐标为(0,0),你认为敌军指挥部的位置大概()A.A处B.B处C.C处D.D处【分析】根据一号暗堡的坐标和四号暗堡的横坐标为一正一负分析,于是四点中只有B点可能为坐标原点.【答案】解:∵一号墙堡的坐标为(4,2),四号墙堡的坐标为(﹣2,4),∴一号暗堡的坐标和四号暗堡的横坐标为一正一负,∴B点可能为坐标原点,∴敌军指挥部的位置大约是B处.故选:B.【点睛】本题考查了坐标确定位置:平面直角坐标系中点与有序实数对一一对应;记住各象限内的点的坐标特征和坐标轴上的坐标特征.【变式6-3】(2018春•阳信县期中)如图中的一张脸,小明说:“如果我用(0,2)表示左眼,用(2,2)表示右眼”,那么嘴的位置可以表示成()A.(0,1)B.(2,1)C.(1,0)D.(1,﹣1)【分析】先根据左眼和右眼所在位置点的坐标画出直角坐标系,然后写出嘴的位置所在点的坐标即可.【答案】解:如图,嘴的位置可以表示成(1,0).故选:C.【点睛】本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住直角坐标系中特殊位置点的坐标特征.【考点7 坐标与图形的性质】【方法点拨】与坐标轴平行的直线上点的坐标特点:与x轴平行,纵坐标y相等;与y轴平行,横坐标x 相等.【例7】(2019春•海安县期中)已知直线a平行于x轴,点M(﹣2,﹣3)是直线a上的一个点.若点N 也是直线a上的一个点,MN=5,则点N的坐标为.【分析】根据平行于x轴的直线上点的距离等于横坐标之差的绝对值可列出方程|﹣2﹣x|=5,求出x即可.【答案】解:设M(x,﹣3),|﹣2﹣x|=5,∴x=3或﹣7,∴N(﹣7,﹣3)或(3,﹣3);故答案为(﹣7,﹣3)或(3,﹣3).【点睛】本题考查了坐标与图形性质,正确理解坐标系内点的特征是解题的关键.【变式7-1】(2018春•繁昌县期中)已知A(﹣3,2)与点B(x,y)在同一条平行于y轴的直线上,且点B到x轴的距离等于3,则B点的坐标为.【分析】利用平行于y轴的直线上所有点的横坐标相同得到x=﹣3,再根据B点到x轴的矩离等于3得到|y|=3,然后求出y即可得到B点坐标.【答案】解:∵A(﹣3,2)与点B(x,y)在同一条平行于y轴的直线上,∴x=﹣3,∵点B到x轴的距离等于3,∴|y|=3,∴y=3或y=﹣3,则点B的坐标为(﹣3,3)或(﹣3,﹣3),故答案为:(﹣3,3)或(﹣3,﹣3).【点睛】本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.点到坐标轴的距离与这个点的坐标是有区别的,到x轴的距离与纵坐标有关,到y轴的距离与横坐标有关.【变式7-2】(2018春•邹城市期中)已知点M的坐标为(a﹣2,2a﹣3),点N的坐标为(1,5),直线MN ∥x轴,则点M的横坐标为.【分析】根据平行于x轴的直线上任意两点的纵坐标相同列出方程求出a的值,然后即可得解.【答案】解:∵直线MN∥x轴,点M的坐标为(a﹣2,2a﹣3),点N的坐标为(1,5),∴2a﹣3=5,解得a=4,a﹣2=4﹣2=2,所以,点M的横坐标为2.故答案为2.【点睛】本题考查了坐标与图形性质,掌握平行于x轴的直线的上的点的坐标特征是解题的关键.【变式7-3】(20197秋•汝州市校级期中)已知点A(b﹣4,3+b),B(3b﹣1,2),AB⊥x轴,则点A的坐标是.【分析】根据AB⊥x轴知b﹣4=3b﹣1,解之求得b的值,继而可得坐标.【答案】解:∵AB⊥x轴,∴b﹣4=3b﹣1,解得:b=−3 2,则b ﹣4=−32−4=−112,3+b =3−32=32, 所以点A 的坐标为(−112,32), 故答案为:(−112,32) 【点睛】本题主要考查坐标与图形的性质,解题的关键是根据垂直于x 轴得出横坐标相等.【考点8 图形在坐标系中的平移】【方法点拨】平面直角坐标内点的平移规律,设a >0,b >0(1)一次平移:P (x ,y ) P '(x +a ,y )P (x ,y ) P '(x ,y -b ) (2)二次平移:【例8】(2019春•番禺区期中)△ABC 与△A ′B ′C ′在平面直角坐标系中的位置如图(1)分别写出下列各点的坐标:A ′ ;B ′ ;C ′(2)若点P (m ,n )是△ABC 内部一点,则平移后△A ′B ′C ′内的对应点P ′的坐标为 .(3)求△ABC 的面积.【分析】(1)根据平面直角坐标系的特点直接写出坐标;(2)首先根据A 与A ′的坐标观察变化规律,P 的坐标变换与A 点的变换一样,写出点P ′的坐标;(3)先求出△ABC 所在的矩形的面积,然后减去△ABC 四周的三角形的面积即可.【答案】解:(1)如图所示:A ′(﹣3,﹣4),B ′(0,﹣1)、C ′(2,﹣3);(2)A (1,0)变换到点A ′的坐标是(﹣3,﹣4),向右平移a 个单位 向下平移b 个单位P (x ,y ) P (x - a ,y +b ) 向左平移a 个单位再向上平移b 个单横坐标减4,纵坐标减4,∴点P的对应点P′的坐标是(m﹣4,n﹣4);(3)△ABC的面积为:3×5−12×1×5−12×2×2−12×3×3=6.故答案为:(﹣3,﹣4),(0,﹣1)、(2,﹣3);(m﹣4,n﹣4).【点睛】此题主要考查了平移变换作图,三角形的面积,网格图形中经常利用三角形所在的矩形的面积减去四周三角形的面积的方法求解.【变式8-1】(2019春•兰陵县期中)△ABC与△A′B′C′在平面直角坐标系中的位置如图所示.(1)分别写出下列各点的坐标:A;B;C;(2)△ABC由△A′B′C′经过怎样的平移得到?答:.(3)若点P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为;(4)求△ABC的面积.【分析】(1)根据平面直角坐标系写出各点的坐标即可;(2)根据对应点A、A′的变化写出平移方法即可;(3)根据平移规律逆向写出点P′的坐标;(4)利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.【答案】解:(1)A(1,3);B(2,0);C(3,1);(2)先向右平移4个单位,再向上平移2个单位;或:先向上平移2个单位,再向右平移4个单位;(3)P′(x﹣4,y﹣2);(4)△ABC的面积=2×3−12×1×3−12×1×1−12×2×2=6﹣1.5﹣0.5﹣2=2.故答案为:(1)(1,3);(2,0);(3,1);(2)先向右平移4个单位,再向上平移2个单位;(3)(x ﹣4,y﹣2).【点睛】本题考查了利用平移变换作图,熟练掌握网格结构,根据对应点的坐标确定出平移的方法是解题的关键.【变式8-2】(2019春•金平区校级期中)已知,△ABC在平面直角坐标系中的位置如图所示.(1)写出A、B、C三点的坐标.(2)△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+4,y0﹣3),先将△ABC作同样的平移得到△A1B1C1,并写出B1、C1的坐标.(3)求△ABC的面积.【分析】(1)根据平面坐标系得出A、B、C三点的坐标即可;(2)根据点P(x0,y0)经平移后对应点为P1(x0+4,y0﹣3),得出平移变换的规律即可得出△ABC的三个顶点的对应点;(3)根据各点坐标,利用梯形面积与三角形面积公式求出即可.【答案】解:(1)如图所示:A、B、C三点的坐标分别为:(﹣2,4),(﹣6,2),(﹣9,7);(2)∵△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+4,y0﹣3),∴P点象右平移4个单位,又向下平移3个单位,∴将△ABC作同样的平移得到△A1B1C1,B1、C1的坐标分别为:(﹣2,﹣1),(﹣5,4);(3)△ABC 的面积=S 梯形CDEA ﹣S △CDB ﹣S △ABE =12×(5+2)×7−12×5×3−12×2×4=13 【点睛】此题主要考查了平移的性质以及平移图形的画法和三角形面积求法,根据平移的性质正确平移对应顶点是解题关键.【变式8-3】(2019春•厦门期末)在平面直角坐标系中,O 为坐标原点,将三角形ABC 进行平移,平移后点A 、B 、C 的对应点分别是点D 、E 、F ,点A (0,a ),点B (0,b ),点D (a ,12a ),点E (m ﹣b ,12a +4). (1)若a =1,求m 的值;(2)若点C (﹣a ,14m +3),其中a >0.直线CE 交y 轴于点M ,且三角形BEM 的面积为1,试探究AF 和BF 的数量关系,并说明理由.【分析】(1)当a =1时,得出A 、B 、D 、E 四点的坐标,再根据平移的规律得到{m −b =1b −92=1−12,即可求出m 的值;(2)由平移的规律得出{a =m −b①a −12a =b −(12a +4)②,变形整理得到14m +3=12a +4,那么CE ∥x 轴,根据三角形BEM 的面积=12BM •EM =1,求出a =2,A (0,2),B (0,6),C (﹣2,5).根据点F 与点C是对应点,得出F (0,4),求出AF =BF =2.【答案】解:(1)当a =1时,由三角形ABC 平移得到三角形DEF ,A (0,1),B (0,b )的对应点分别为D (1,12),E (m ﹣b ,92), 可得{m −b =1b −92=1−12,解得{b =5m =6. 故m 的值为6;(2)AF =BF .理由如下:由三角形ABC 平移得到三角形DEF ,点A (0,a ),点B (0,b )的对应点分别为D (a ,12a ),点E (m ﹣b ,12a +4), 可得{a =m −b①a −12a =b −(12a +4)②, 由②得b =a +4③,把③代入①,得m =2a +4,∴14m +3=12a +4, ∴点C 与点E 的纵坐标相等,∴CE ∥x 轴,∴点M (0,12a +4), ∴三角形BEM 的面积=12BM •EM =1,∵a >0,∴BM =a +4﹣(12a +4)=12a ,EM =a , ∴14a 2=1, ∴a =2,∴A (0,2),B (0,6),C (﹣2,5).又∵在平移中,点F 与点C 是对应点,∴F (0,4),∴AF =4﹣2=2,BF =6﹣4=2,∴AF =BF .【点睛】本题考查了坐标与图形变化﹣平移,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.也考查了三角形的面积,有一定难度.【考点9 坐标与图形的变化—对称】【例9】(2018秋•南昌期中)在平面直角坐标系中,有点A (a ,1)、点B (2,b ).(1)当A 、B 两点关于直线y =﹣1对称时,求△AOB 的面积;(2)当线段AB∥x轴,且AB=4时,求a﹣b的值.【分析】(1)利用对称的性质得a=2,b=﹣3,进而得到A(2,1),B(2,﹣3),然后根据三角形面积公式求解;(2)利用AB∥x轴得到A、B的纵坐标相同,则b=1,所以|a﹣2|=4,解得b=﹣2或b=6,然后分别计算对应的a﹣b的值.【答案】解:(1)由题意,得a=2,b=﹣3,则A(2,1),B(2,﹣3).设AB与x轴相交于点D,则OD=2,AB=4.∴S△AOB=AB×OD=×4×2=4.(2)∵AB∥x轴,∴A、B的纵坐标相同,∴b=1.∴B(2,1)∵AB=4,∴|a﹣2|=4.解得a=﹣2或a=6.当a=﹣2,b=1时,a﹣b=﹣3.当a=6,b=1时,a﹣b=5.【点睛】本题考查了坐标与图形变化﹣对称:关于x轴对称,横坐标相等,纵坐标互为相反数;关于y 轴对称,纵坐标相等,横坐标互为相反数.【变式9-1】(2018秋•蔡甸区期中)如图,在平面直角坐标系中有一个轴对称图形,A(3,﹣2),B(3,﹣6)两点在此图形上且互为对称点,若此图形上有一个点C(﹣2,+1).(1)求点C的对称点的坐标.(2)求△ABC的面积.【分析】(1)根据A、B的坐标,求出对称轴方程,即可据此求出C点对称点坐标.(2)根据三角形面积公式可得结论.【答案】解:∵A、B关于某条直线对称,且A、B的横坐标相同,∴对称轴平行于x轴,又∵A的纵坐标为﹣2,B的纵坐标为﹣6,∴故对称轴为y==﹣4,∴y=﹣4.则设C(﹣2,1)关于y=﹣4的对称点为(﹣2,m),于是=﹣4,解得m=﹣9.则C的对称点坐标为(﹣2,﹣9).(2)如图所示,S△ABC=×(﹣2+6)×(3+2)=10.【点睛】此题考查了坐标与图形变化﹣对称,要知道,以关于x轴平行的直线为对称轴的点的横坐标不变,纵坐标之和的平均数为对称轴上点的纵坐标.【变式9-2】(2019秋•抚州期中)如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;(2)如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.【分析】(1)根据关于y轴对称点的坐标特点是横坐标互为相反数,纵坐标相同可以得到△A1B1C1各点坐标,又关于直线l的对称图形点的坐标特点是纵坐标相同,横坐标之和等于3的二倍,由此求出△A2B2C1的三个顶点的坐标;(2)P与P1关于y轴对称,利用关于y轴对称点的特点:纵坐标不变,横坐标变为相反数,求出P1的坐标,再由直线l的方程为直线x=3,利用对称的性质求出P2的坐标,即可得出PP2的长.【答案】解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2);(2)如图1,当0<a<3时,∵P与P1关于y轴对称,P(﹣a,0),∴P1(a,0),又∵P1与P2关于l:直线x=3对称,设P2(x,0),可得:=3,即x=6﹣a,∴P2(6﹣a,0),则PP2=6﹣a﹣(﹣a)=6﹣a+a=6.【点睛】本题考查学生“轴对称”与坐标的相关知识的试题,掌握轴对称的性质是解本题的关键.【变式9-3】(2019•南京校级期中)在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;(2)如果点P的坐标是(﹣a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.【分析】(1)根据关于y轴对称点的坐标特点是横坐标互为相反数,纵坐标相同可以得到△A1B1C1各点坐标,又关于直线l的对称图形点的坐标特点是纵坐标相同,横坐标之和等于3的二倍,由此求出△A2B2C1的三个顶点的坐标;(2)P与P1关于y轴对称,利用关于y轴对称点的特点:纵坐标不变,横坐标变为相反数,求出P1的坐标,再由直线l的方程为直线x=3,利用对称的性质求出P2的坐标,即可PP2的长.【答案】解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2);(2)如图1,当0<a≤3时,∵P与P1关于y轴对称,P(﹣a,0),。
六年级上册数学教案《02在平面上标出物体位置》(人教新课标 )

六年级上册数学教案《02在平面上标出物体位置》(人教新
课标)
一、教学内容
1. 教学目标
•知识目标:掌握在平面上标出物体位置的方法。
•能力目标:培养学生观察、分析和描述物体位置的能力。
•情感目标:培养学生积极参与课堂活动的意识。
2. 教学重点
•掌握标出物体位置的方法。
•培养观察与描述物体位置的能力。
3. 教学难点
•灵活运用不同方法标出物体位置。
二、教学过程
1. 导入
老师通过展示一些简单的平面图案,让学生观察并回答图案中物体的位置,引入标出物体位置的话题。
2. 讲授
1.在平面上标出物体位置的方法:
–使用坐标轴表示位置。
–使用方位词描述位置。
2.案例讲解:
–老师通过案例演示如何使用坐标轴和方位词标出物体位置,让学生理解方法的具体应用。
3. 练习
1.集体练习:
–老师提供几个简单的图案,让学生分组合作,标出各个物体的位置。
2.个人练习:
–学生自行完成练习册上相关练习题,巩固方法和技能。
4. 拓展
老师可以设计一些拓展题目,让学生在实际生活中找到标出物体位置的场景,并分享给同学。
三、教学反思
本节课主要以引导学生认识在平面上标出物体位置的方法为主,通过案例和练习的方式让学生掌握这一技能。
在教学过程中,要注重引导学生养成仔细观察和描述的习惯,培养他们的逻辑思维能力。
同时,要根据学生的实际水平调整教学内容和难度,确保教学效果的最大化。
以上是本节课的教案内容,希望能够帮助学生更好地理解和掌握在平面上标出物体位置的方法。
2022年北师大版八年级上册数学第三章位置与坐标第1节确定位置

第三章位置与坐标1确定位置判一判:1.在平面内确定一个物体的位置至少需要两个数据.( √)2.“北偏西30°”能确定物体的位置.( ×)3.(2,6)与(6,2)表示同一位置.( ×)1.在某个电影院里,如果用(2,5)表示2排5号,那么图框中的座次可以表示为(C)A.(9,9) B.(5,5)C.(5,9) D.(9,5)2.电影院里的座位按“×排×号”编排,小明的座位简记为(12,6),小菲的位置简记为(12,12),则小明与小菲坐的位置为(A)A.同一排B.前后在同一条直线上C.中间隔六个人D.前后隔六排3.以下能准确表示某地地理位置的是(B)A.在广州的西北方B.东经113°,北纬23°C.距离广州40公里处D.东经113°4.如图是一台雷达探测相关目标得到的部分结果,若图中目标A的位置为(2,90°),目标B的位置为(4,210°),则目标C的位置为__(3,150°)__.重点1 利用行列定位法确定位置【典例1】(教材P54引例拓展)如图,是光明小区内的一幢商品房的示意图.若小赵家所在的位置用(4,2)表示.(1)用有序数对表示小李、小张家的位置;(2)(3,5),(5,4)分别表示谁家所在的位置?【解析】(1)小赵家所在的位置用(4,2)表示,结合题图可得:小赵在第4列第2行,小李家在第2列第1行,所以可记为:(2,1),小张家在第1列第3行,所以可记为:(1,3).(2)(3,5)表示第3列第5行,是小王家,(5,4)表示第5列第4行,是小周家.1.用有序数对(2,9)表示某住户住2单元9号房,请问(3,11)表示住户住__3__单元__11__号房.【解析】用有序数对(2,9)表示某住户住2单元9号房,所以(3,11)表示住户住3单元11号房.2.做课间操时,小明、小刚和小红三人的相对位置(如图),如果用(3,4)表示小明的位置,(1,3)表示小刚的位置,则小红的位置可表示为__(0,1)__.【解析】根据题目有序数对表示的小明、小刚的位置,确定小红的位置的有序数对.【加固训练】如图是某个小岛的简图,试用有序数对表示出相关地点的位置.【解析】根据题图可知,码头(4,3),营房(6,2),雷达(9,6),小广场(5,6),哨所1(5,9),哨所2(1,6).【技法点拨】用行列定位法确定位置的三点注意(1)行列定位法确定位置时,一般行在前列在后,用两个数表示;(2)在确定位置时,要事先约定,即有序;(3)用行列定位法确定位置都是用一个有序实数对.重点2 区域定位【典例2】如图是北京市地图简图的一部分,图中“故宫”“颐和园”所在的区域分别是(C)D E F6颐和园奥运村7故宫日坛8天坛A.D7,E6C.E7,D6 D.E6,D7【自主解答】题图中“故宫”“颐和园”所在的区域分别是:E7,D6.1.共享单车提供了便捷、环保的出行方式.小白同学在北京植物园打开某共享单车APP,如图,“”为小白同学的位置,“”为检索到的共享单车停放点.为了到达距离最近的共享单车停放点,下列四个区域中,小白同学应该前往的是(C)A.D5 B.F5 C.F6 D.F7【解析】距E6最近的是F6.2.如图,围棋盘的左下角呈现的是一局围棋比赛中的几手棋,为记录棋谱方便,横线用数字表示,纵线用英文字母表示,这样,黑棋的位置可记为(C,4),白棋的位置可记为(E,3),则黑棋的位置应记为__(D,6)__.【解析】由题意可知:黑棋在纵线对应D,横线对应6的位置,故记作(D,6).【技法点拨】平面上确定位置常用的四种方法1.行列定位法:常把平面分成若干行、列,然后利用行号和列号表示平面上点的位置.注意,同样的两个数据若顺序不同,表示的位置则不同.2.方位角距离定位法:常应用于航海和军事上,运用此法需要两个数据:方位角和距离.3.经纬度定位法:该法需要两个数据,经度、纬度.此方法在地理学中有着极其广泛的应用.4.区域定位法:该法需要两个数据,相对于其他方法而言,此方法较简单,但有时不够准确.如图,是小明制作的他家附近的简单地图,已知OA=2 km,OB=3.5 km,OP=4 km,点C为OP的中点.回答下列问题:(1)图中到小明家距离相同的是哪些地方?(2)由图可知,公园在小明家南偏东60°方向2 km处.请用方向与距离描述学校、商场、停车场相对于小明家的位置.【解析】(1)∵点C为OP的中点,∴OC=12OP=12×4=2(km),∵OA=2 km,∴到小明家距离相同的是学校和公园.(2)学校在小明家北偏东45°的方向上,且到小明家的距离为2 km,商场在小明家北偏西30°的方向上,且到小明家的距离为3.5 km,停车场在小明家南偏东60°的方向上,且到小明家的距离为4 km.。
八年级数学上册期中知识点归纳

八年级数学上册期中知识点归纳1.八年级数学上册期中知识点归纳一、在平面内,确定物体的位置一般需要两个数据。
二、平面直角坐标系及有关概念1、平面直角坐标系在平面内,两条互相垂直且有公共原点的数轴,组成平面直角坐标系。
其中,水平的数轴叫做x轴或横轴,取向右为正方向;铅直的数轴叫做y轴或纵轴,取向上为正方向;x轴和y轴统称坐标轴。
它们的公共原点O称为直角坐标系的原点;建立了直角坐标系的平面,叫做坐标平面。
2、为了便于描述坐标平面内点的位置,把坐标平面被x轴和y轴分割而成的四个部分,分别叫做第一象限、第二象限、第三象限、第四象限。
注意:x轴和y轴上的点(坐标轴上的点),不属于任何一个象限。
3、点的坐标的概念对于平面内任意一点P,过点P分别x轴、y轴向作垂线,垂足在上x轴、y轴对应的数a,b分别叫做点P的横坐标、纵坐标,有序数对(a,b)叫做点P的坐标。
点的坐标用(a,b)表示,其顺序是横坐标在前,纵坐标在后,中间有“,”分开,横、纵坐标的位置不能颠倒。
平面内点的坐标是有序实数对,当时,(a,b)和(b,a)是两个不同点的坐标。
平面内点的与有序实数对是一一对应的。
4、不同位置的点的坐标的特征(1)各象限内点的坐标的特征点P(x,y)在第一象限:x;0,y;0点P(x,y)在第二象限:x;0,y;0点P(x,y)在第三象限:x;0,y;0点P(x,y)在第四象限:x;0,y;0(2)坐标轴上的点的特征点P(x,y)在x轴上,y=0,x为任意实数点P(x,y)在y轴上,x=0,y为任意实数点P(x,y)既在x轴上,又在y轴上,x,y同时为零,即点P坐标为(0,0)即原点(3)两条坐标轴夹角平分线上点的坐标的特征点P(x,y)在第一、三象限夹角平分线(直线y=x)上,x与y相等点P(x,y)在第二、四象限夹角平分线上,x与y互为相反数(4)和坐标轴平行的直线上点的坐标的特征位于平行于x轴的直线上的各点的纵坐标相同。
1 物体位置的确定 (1)

例2.在平面直角坐标系中,下面的点在第一象限的是( A ) A.(1,2) B.(-2,3) C.(0,0) D.(-3-2)
变式1:已知点M(3|a|-9,4-2a)在y轴的负半轴上. (1)求M点的坐标; (2)求(2-a)2015+1的值.
变式2:(2017秋•遂川县期末)如果点P在第二象限内,点P到x轴的距离 是4,到y轴的距离是3,那么点P的坐标为_______.
命题点一:确定物体的位置
例4.图是某校的部分平面示意图,借助刻度尺、量角器,看图填空.
(1)图书馆位于桃李亭的 方向上,
(2)如果用(2,4)表示图上桃李亭的位置,那么
综合楼的位置表示为 ,(6,8)表示的位置 ,
(7,1)表示校园内某个地方,它是
.
命题点二:利用不同的定位方式确定同一位置
例5.一个正方形等分成4行4列. (1) 若点A用(1,1)表示,点B用(2,2)表示,点C用(0,0)表示,请在图中标出点C 的位置;
(2)当m=3时,B(4,4)关于原点的对称点坐标(-4,-4); 当m=1时,B(2,-2)关于原点的对称点坐标(-2,2).
变式2:①已知点A(-3,2a-1)与点B(b,-3)关于原点对称,那么点 P(a,b)关于y轴的对称点P′的坐标为_________. ②当m为何整数值时,点A(4-m,3m+2)到x轴的距离等于它到y轴的距 离的一半.
(2) 若点A用(-3,1)表示,点B用(-2,2)表示,点D用(0,0)表示,请标出点D的 位置,并说明第1问中点C应如何表示.
要点一、平面直角坐标系
平面直角坐标系
平面内两条互相垂直的数轴构成平面直角坐标系,简称为直角坐标系 x 轴或横轴:水平方向的数轴,向右为正方向
【苏科版】数学八年级上册:物体位置的确定1

苏科版数学八年级上册:物体位置的 确定1- 精品课 件ppt( 实用版)
2.下列数据不能确定物体位
置的是( )
5
A. 4楼8号 B. 北偏东30°
4
C. 希望路25号
B
3
D.东经118°,北纬40° 2
A.3.如图,A点为一个观测 1 点,B点为一着火点,请 用两种不同方式描述B点 A 1 2 3 4 5 的位置.
点D的位置是______,
4
点E的位置是_____,
3
2
点F的位置是_____;
1
B
(2)请找出(0,6)、 (3,4)、(2,0)所表
A
123
示的点.
苏科版数学八年级上册:物体位置的 确定1- 精品课 件ppt( 实用版)
E F
4 56
自学指导二: (5 分钟) 苏科版数学八年级上册:物体位置的确定1-精品课件ppt(实用版) 认真阅读课本P148例2和“想一想”,思考回
未如王来图丽大所为学示自校,己园请设的根想平据并面她绘示画制意的了图图,8比例尺1:10000图(书每馆小格为1cm)游
回答下列问题:
7
泳
(1)花坛位于校门的什 6 校门 花坛
馆 电影院
么方向上?到校门的图 5
上距离为多少?实际距 4
离为多少?
3
教学楼
(2)花坛的北偏东45° 2
方向上有什么建筑物? 1
苏科版数学八年级上册:物体位置的 确定1- 精品课 件ppt( 实用版)
苏科版数学八年级上册:物体位置的 确定1- 精品课 件ppt( 实用版)
4.如图,小明从O点出发,先向西走40m,再向南走 30m,到达点M,如果M的位置用(-40,-30)表示, 那么(10,20)表示的位置是_______.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
19.1 确定平面上物体的位置
(-)知识目标
1.通过现实情境感受在平面上确定物体位置的多种方法;
2.能说出平面上确定物体位置需要的两个条件;
3.能根据不同情境选择合适的方法来确定物体的位置;
(二)能力目标
1.通过丰富多彩,形式多样的确定平面上物体位置的方式,使学生感受丰富的确定位置的现实背景.
2.进一步发展形象思维能力和数学应用的能力。
(三)情感目标
1.让学生主动地参与观察、操作与活动.
2.让学生能把思考的结果用语言很好地表达出来,同时要让学生很好地交流和合作.〖教学重点〗
1.在平面上某点的位置可以用唯一一对数来表示。
2.在平面上某点的位置可以用方位角+距离来表示。
〖教学难点〗
比较灵活地运用不同的方式确定平面上物体的位置。
〖教学方法〗
引导发现法、小组讨论
〖教学过程〗
一、创设情境引入:
[师]生活中我们常常需要确定物体的位置.如,确定学校、家庭的位置,确定地图上城市的位置,在棋盘上确定棋子的位置,在海战中确定舰艇的位置……,本节课我们就来研究确定平面上物体位置的一些基本方法.
二、探索新知:
探索确定位置需要两个数据
环节(一)有序数对定位法
展示进入电影院依据电影票找位置的情景和问题。
问题:在电影院内如何找到电影票上所指的位置?
具体问题
如果A、B两人各拿到一张只有6排和只有6号的电影票,
1、A、B两人能否找到属于自己的位置?
2、假如A要找到属于他的位置,还需加什么条件? B呢?
3、假如换两张电影票A的为6排3号,B的为3排6号,那么A、B能否找到自己的位置?请同学们在平面图中找出“6排3号”与“3排6号”的位置?
4、如果将“6排3号”简记作(6,3),
那么“3排6号”如何表示?
(5,6)表示什么含义?(6,5)呢?
从刚才的讨论中,你知道在电影院内,确定一个座位一般需要几个数据?
学生活动:根据教师的层层设问积极主动的思考并回答,从中学习新的表示方法,同时感知确定平面上物体的位置需要两个数据,并且这两个数据是有顺序的。
思考:每个座位都能用唯一一对数表示吗?
学生活动:小组讨论
做接龙游戏
约定教室里的学生从左边数为第一列、第二列……从前到后为第一排、第二排……
教师先说一对列数在前排数在后的数对如(1,2),与此对应的学生站起来再说一对数如(5,3),与此对应的学生站起来再说一对数, ……依次接龙下去。
由此得到平面上物体的位置可以用唯一一对数来表示。
随堂练习
说出在棋盘中棋子的位置
设计意图:巩固新知
环节(二)方位角+距离定位法
展示一个与电影票这一情境不同的实例
在解决问题中思考:这个实例中确定平面上物体位置用到了哪些量,分别是什么?
具体问题
下图是某次海战中敌我双方舰艇对峙示意图,对我方潜艇来说:
(1)北偏东40°的方向上有哪些目标?
(2)距我方潜艇图上距离1 cm处的敌舰有哪几艘?
(3)要确定每艘敌舰的位置,各需要几个数据?
解:(1)对我方潜艇来说,北偏东40°的方向上有两个目标:敌舰B和小岛.(2)距我方潜艇图上距离1 cm处的敌舰有两艘:敌舰A和敌舰C.
(3)要确定每艘敌舰的位置,各需要两个数据:距离和方位角.如,对我方潜艇来说,敌舰A在正南方向,图上距离为1 cm处;敌舰B在北偏东40°,图上距离为1.4 cm处;敌舰C在正东方向,图上距离为1 cm.
教师活动:组织学生完成,引导学生探索。
学生活动:观察分析,回答问题,相互交流,总结出确定每艘敌舰的位置还是需要2个数据——方位角和距离。
练习:如下图,8月30日江苏省4艘渔船在回港途中,突遭9级强风,船上共35名船员遇险,岛上边防战士接到命令后立即出发,进行拉网式搜救。
以小岛为观测点,你能告诉边防战士渔船A、B、C、D位置吗?小岛南偏西60°方向的15km 处是什么?…
学生活动:独立思考并回答为题,学生互评。
环节(三)经纬度定位法
如下图,今年第5号台风“海棠”,7月17日晚上8时中心位置在台湾省台北市东南方向大约795公里的洋面上,即北纬20.7度,东经127.7度,中心气压910百帕,近中心最大风力12级以上(65米/秒)。
而后台风中心向西北方向移动,并于18日夜间到19日中午在福建到浙江南部一带沿海登陆。
请用数对的形式表示台风中心位置,并在图上标出台风中心。
(130,30)(120,25)是否位于台风移动的主要路径上?
学生活动:用数对的形式书写台风中心位置,学生互评。
学生分别指出(130,30)、(120,25)的位置并进行解释,学生评价。
三、归纳小结,梳理知识
提问:今天你学会了什么?用几个数据可以确定平面内物体位置的位置?表示时注意什么?
教师活动:教师提问,引导学生回答,注意学生回答时数学语言的准确性。
学生活动:小结由学生来完成,同时其他学生进行补充。
四、实际应用,拓展提升
设置利用方位角+距离确定位置的练习。
设置利用有序数对表示棋盘上棋子位置、依据数对找棋子位置的练习以及一些生活实际问题和趣味性练习。
教师活动:提出问题,让学生相互交流,相互探讨。
学生活动:相互交流探讨,积极思考。
五、知识拓展
生活中还有其他一些确定位置方法
(1)全班同学站成一列做早操,现在教师想找某个同学,只需要用1个数据。
(2)多层电影院确定座位位置用两个数据是不够的。
必须有三个数据(a,b,c),其中a表示层数,b表示排号,c表示座号,即“a层b排c号”。
(3)确定小区中住户的位置必须有四个数据,分别为楼号a,单元号b,层数c和住户号d,即“a楼b单元c层d号。
”
六、课堂小结:
这节课你有什么收获和体会?
七、板书设计
确定平面上物体的位置
1.有序数对定位法(行列定位法)
方法 2. 方位角+距离定位法
3. 经纬度定位法
教学反思:。
