节约里程法典型实例

合集下载

6.节约里程法用

节约里程表
ABCDEFGHI
A
16 10 3 0 0 0 6 12
B
14 7 2 0 0 0 6
C
11 6 0 0 0 0
D
71 00 0
E
8 00 0
F
60 0
G
60
H
8
I
根据节约里程表中节约里程多少的顺序，由大到小排列，编制节约里程顺序表，以便尽量使节约里程最多的点组合装车配送。
顺位里程节约里顺位里程节约里顺位里程节约里
总共节约里程为：362－170=192 或（33+34+16）+（28+21）+（22+18+18）+2=192
例：由配送中心P向A—I等9个用户配送货物。图中连线上的数字表示公路里程（km）。靠近各用户括号内的数字，表示各用户对货物的需求量（t）。配送中心备有2t和4t载重量的汽车，且汽车一次巡回走行里程不能超过35km，设送到时间均符合用户要求，求该配送中心的最优送货方案。
根据节约里程排序表和配车（车辆的载重和容积因素）、车辆行驶里程等约束条件，渐进绘出配送路径：
(0.9)
C
5
(1.2)
4
D
6
B (0.5)
5
(1.6)
E
6
路径A A (1.7)
(1.1)
9 路径B
P
10
F
10
路径C
G
(0.9)
12
7
8
H
6
I (0.6)
(0.9)
• 路径A：4t车，走行32km，载重量3.7t； • 路径B：4t车，走行31km，载重量3.9t； • 路径C：2t车，走行30km，载重量1.8t。

物流工程——节约里程法

8
P2P5
9
P3P5
10
P1P4
节约里程 10 8 6 5 4 2 1 0 0 0
节约里程法
第4步：根据载重量约束与节约里程大小，顺序连接各客户
结点,形成二个配送路线 .
（0.9）
P3
4
优先考虑节约里程最大的路线，以此类推，如果前面涉及了某些路线，往后就考虑未涉及的路线 P2P3----P3P4-----P1P5
D E
F
C B A
P
G H
图1 配送网络图
J I
表1 各连锁分店需求量重量单位：吨
分店 A B C D E F G H I J 合计
数量
41
重量
节约里程法
第二步:计算连接城市到同一线路上的距离节约值
节约里程法
第三步:确定初始方案的运输线路及运输费用,现安排4辆2吨、4辆5吨的车给每个客户送货。运输线路及运输费用见下表所示。
节约里程法
第四步:进行线路第一次优化。
节约里程法
第一次修改后的车辆调度结果：
节约里程法
第五步:继续进行线路优化。
节约里程法节约里程法从表中可以看出广州惠州揭阳汕头漳州路线上的总货运量达到79吨再连接任何一个城市都将使货运量超过最高限制8吨则不能继续配载所以可以首先确定的是这一条线路
物流配送——节约里程法(Saving Algorithm)
• 车辆调度程序法(Vehicle Scheduling Program:VSP)
节约里程法
第二次修改后的车辆调度结果：
节约里程法
节约里程法
• 从表中可以看出,广州-惠州-揭阳-汕头-漳州路线上的总货运量达到7.9吨,再连接任何一个城市都将使货运量超过最高限制(8吨),则不能继续配载,所以可以首先确定的是这一条线路。然后在剩下的东莞、江门、阳江和汕尾重复以上的优化步骤。得到最终配送计划。

劳动部物流师2级节约里程法

图3-17 配送中心网络图分送式运输是指由一个供应点对多个客户的共同送货。

其基本条件是所有客户的需求量总和不大于一辆车的额定载重量。

送货时，由这一辆车装着所有客户的货物，沿着一条精心选择的最佳线路一次将货物送到各个客户手中，这样既保证按时按量将用户需要的货物及时送到，又节约了车辆，节省了费用，缓解了交通紧张的压力，并减少了运输对环境造成的污染。

例：图3-17所示为某配送中心的配送网络，图中P0点为配送中心，P1、P2、P3、P4、P5、P6、P7、P8、P9、P10为配送客户，共10位客户，括号内为配送货物吨数，线路上的数值为道路距离，单位为km。

现配送中心有额定载重量分别为2吨和4吨两种厢式货车可供送货使用，试用节约法设计最佳送货路线。

第一步计算最短距离首先计算网络结点之间的最短距离（可采用最短路求解法）。

计算结果如表3-16所示。

表3-16 最短距离表第二步计算节约里程根据最短距离结果，计算出各客户之间的节约行程，结果见表3-17所示。

表3-17 节约里程表第三步将节约里程进行分类对节约行程按从大到小的顺序排列，如表3-18所示。

表3-18 节约里程排序第四步确定配送线路按节约里程大小顺序，组成线路图。

1、初始方案：如图3-18所示，从配送中心P0分别向各个客户进行配送，对每一客户分别单独派车送货，共有10条配送线路，总行程为148公里，需2吨货车10辆。

2、修正方案1：图3-18 图3-19按照节约行程的由大到小的顺序，连接P1和P2，P1和P10，P2和P3，P3和P4，形成巡回路线P0-P10-P1-P2-P3-P4-P0的配送线路，如图所示，装载货物4吨，这时配送路线总运行距离为109公里，配送线路6条，需4吨货车1辆，需2吨货车5辆，如图3-19所示。

3、修正方案2：按节约里程由大到小的顺序，连接P5和P6，P6和P7，形成巡回路线P0-P5-P6-P7-P0的配送线路，如图所示，装载货物3.5吨，这时配送路线总运行距离为85公里，配送线路4条，需4吨货车2辆，图3-20 需2吨货车2辆，如图3-20所示。

计算题节约里程法

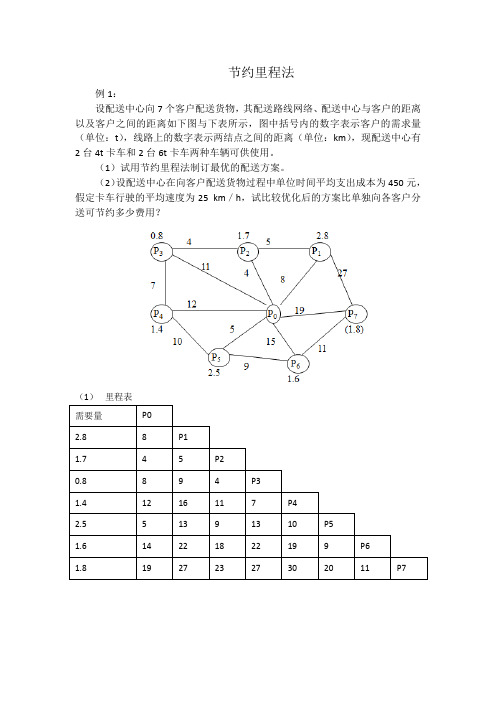
节约里程法例1：设配送中心向7个客户配送货物，其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示，图中括号内的数字表示客户的需求量（单位：t），线路上的数字表示两结点之间的距离（单位：km），现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。

（1）试用节约里程法制订最优的配送方案。

（2）设配送中心在向客户配送货物过程中单位时间平均支出成本为450元，假定卡车行驶的平均速度为25 km／h，试比较优化后的方案比单独向各客户分送可节约多少费用？（1）里程表需要量P02.8 8 P11.7 4 5 P20.8 8 9 4 P31.4 12 16 11 7 P42.5 5 13 9 13 10 P51.6 14 22 18 22 19 9 P61.8 19 27 23 27 30 20 11 P7（2）节约里程表需要量P02.8 8 P11.7 4 5（7）P20.8 8 9（7）4（8）P31.4 12 16（4）11（5）7（13）P42.5 5 13（0）9（0）13（0）10（7）P51.6 14 22（0）18（0）22（0）19（7）9（10）P61.8 19 27（0）23（0）27（0）30（1）20（4）11（22）P7（3）节约里程数排序序号路线节约里程序号路线节约里程1 P6P722 7 P4P572 P3P413 8 P1P273 P5P610 9 P2P4 54 P2P38 10 P1P4 45 P1P37 11 P5P7 46 P4P67 12 P4P7 1（4）配送路线选择节省的配送时间为节省的费用为：例2：设配送中心向5个客户配送货物，其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示，图中括号内的数字表示客户的需求量（单位：t），线路上的数字表示两结点之间的距离（单位：km），现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。

节约里程法应用案例

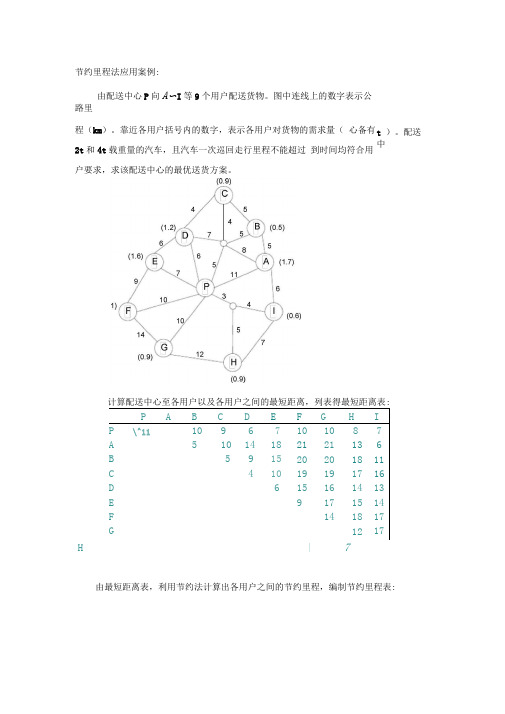
节约里程法应用案例:
由配送中心P向A〜I等9个用户配送货物。

图中连线上的数字表示公
路里
程（km）。

靠近各用户括号内的数字，表示各用户对货物的需求量（心备有
2t和4t载重量的汽车，且汽车一次巡回走行里程不能超过到时间均符合用
户要求，求该配送中心的最优送货方案。

计算配送中心至各用户以及各用户之间的最短距离，列表得最短距离表:
P A B C D E F G H I P \^1110 9 6 710 10 8 7
A 5 10 14 18 2121 136
B 5 9 1520 20 1811
C 4 1019 19 17 16
D 6 15 16 14 13
E 9 17 15 14
F 14 18 17
G 12 17
H \ 7
由最短距离表，利用节约法计算出各用户之间的节约里程，编制节约里程表:
t ）。

配送
中
A B c D E F G H I
A 16 10 3 0 0 0 6 12
B14 7 2 0 0 0 6
C 11 6 0 0 0 0
D 7 10 0 0
E -8 0 00
F 6 00
G 6 0
H8
1
根据节约里程表中节约里程多少的顺序，由大到小排列，编制节约里程顺序表，以便尽量使节约里程最多的点组合装车配送。

束条件，渐进绘出配送路径:
6
A
B
6
D
o
- 1
E
6
6
c
9
A
径 B
径 c
径
1 1
9) a。

物流方案设计(最优运输路线决策-节约里程法)典型实例

物流方案设计（最优运输路线决策－节约里程法）典型实例：已知配送中心P O向 5 个用户 P j配送货物，其配送路线网络、配送中心与用户的距离以及用户之间的距离如下图与表所示：图中括号内的数字表示客户的需求量（单位：吨），线路上的数字表示两结点之间的距离，配送中心有 3 台 2t 卡车和 2 台 4t 两种车辆可供使用，1、试利用节约里程法制定最优的配送方案？2、设卡车行驶的速度平均为40 公里 / 小时，试比较优化后的方案比单独向各用户分送可节约多少时间？（ 0.9）P3 4（ 1.7）5P2 6128（ 1.4）12 P4 7 P0 1312 10 8P5 16P1 （ 1.5）需要量P0（ 2.4）1.5 8 P11.7 8 12 P20.9 6 13 4 P31.4 7 15 9 5 P42.4 10 16 18 16 12 P5第（ 1）步：作运输里程表，列出配送中心到用户及用户间的最短距离。

需要量0 P1.5 8 P11.7 8 （ 4）P12 20.9 6 （1）（ 10）P3 13 41.4 7 （0）（6）（8）4 15 9 5 P2.4 10（2）（0）（0）（5）16 18 16 P512第（ 2）步：由运输里程表、按节约里程公式，求得相应的节约里程数，如上表（）内。

第（ 3）步：将节约里程sij 进行分类，按从大到小顺序排列序号路线节约里程序号路线节约里程1 P2P3 10 6 P1 P5 22 P P 8 7 P P 13 4 1 33 P P 6 8 P P 02 4 2 54 P4P5 5 9 P3 P5 05 P1P2 4 10 P1 P4 0第（ 4）步：确定单独送货的配送线路（0.9）P3 （ 1.7 ）P268（ 1.4）P4 7P0108P5P1（1.5）（2.4 ）得初始方案配送距离 =39× 2=78KM第（ 5）步：根据载重量约束与节约里程大小，将各客户结点连接起来，形成二个配送路线。

节约里程法应用案例

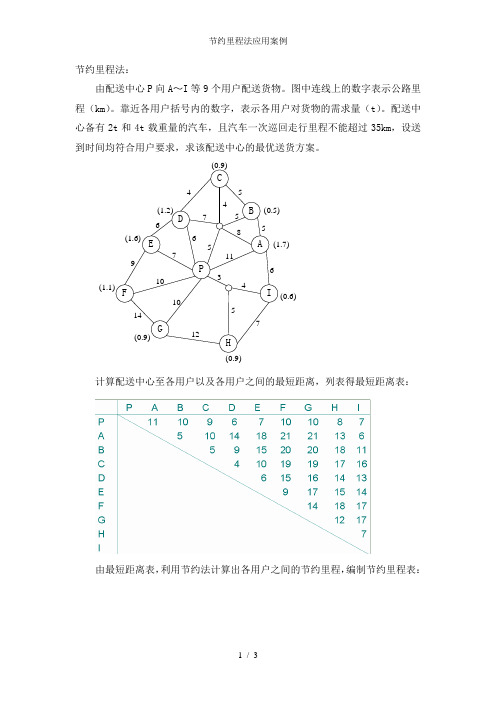
节约里程法：
由配送中心P 向A ～I 等9个用户配送货物。

图中连线上的数字表示公路里程（km ）。

靠近各用户括号内的数字，表示各用户对货物的需求量（t ）。

配送中心备有2t 和4t 载重量的汽车，且汽车一次巡回走行里程不能超过35km ，设送到时间均符合用户要求，求该配送中心的最优送货方案。

计算配送中心至各用户以及各用户之间的最短距离，列表得最短距离表：
由最短距离表，利用节约法计算出各用户之间的节约里程，编制节约里程表：
A
B C
D
E
F
G
H
I P
(0.9)
(1.2)(1.6)(0.9)
(0.9)
(0.6)
(1.7)(0.5)4
44
5
555
5
66
6
3
77
7
8
9
1010
1112
14
根据节约里程表中节约里程多少的顺序，由大到小排列，编制节约里程顺序表，以便尽量使节约里程最多的点组合装车配送。

根据节约里程排序表和配车（车辆的载重和容积因素）、车辆行驶里程等约束条件，渐进绘出配送路径：
(0.9)。

节约里程法应用案例

节约里程法应用案例在当今竞争激烈的商业环境中，物流成本的有效控制对于企业的生存和发展至关重要。

节约里程法作为一种优化配送路线的有效方法，能够显著降低运输成本，提高物流效率。

接下来，让我们通过一个具体的案例来深入了解节约里程法的实际应用。

假设我们有一家位于城市中心的配送中心，需要向位于城市不同区域的五个客户（A、B、C、D、E）配送货物。

每个客户的需求量以及他们之间的距离如下表所示：｜客户|需求量（吨）｜与配送中心距离（公里）｜｜｜｜｜｜A|5|10|｜B|8|12|｜C|3|8|｜D|6|15|｜E|4|11|｜客户|A|B|C|D|E|｜｜｜｜｜｜｜｜A| ｜ 18 ｜ 22 ｜ 25 ｜ 16 ｜｜B| 18 ｜｜ 10 ｜ 18 ｜ 12 ｜｜C| 22 ｜ 10 ｜｜ 14 ｜ 9 ｜｜D| 25 ｜ 18 ｜ 14 ｜｜ 20 ｜｜E| 16 ｜ 12 ｜ 9 ｜ 20 ｜｜首先，我们按照传统的方法，即每个客户单独配送，计算出总运输里程。

配送中心到客户 A 的往返里程为 2×10 ＝ 20 公里。

配送中心到客户 B 的往返里程为 2×12 ＝ 24 公里。

配送中心到客户 C 的往返里程为 2×8 ＝ 16 公里。

配送中心到客户 D 的往返里程为 2×15 ＝ 30 公里。

配送中心到客户 E 的往返里程为 2×11 ＝ 22 公里。

总运输里程为 20 ＋ 24 ＋ 16 ＋ 30 ＋ 22 ＝ 112 公里。

接下来，我们应用节约里程法来优化配送路线。

第一步，计算两两客户之间的节约里程数。

例如，客户 A 和客户 B 之间的节约里程数为：（配送中心到 A 的距离＋配送中心到 B 的距离 A 到 B 的距离）× 2 ＝（10 ＋ 12 18）× 2 ＝ 8 公里。

按照同样的方法，计算出所有两两客户之间的节约里程数，如下表所示：｜客户|A|B|C|D|E|｜｜｜｜｜｜｜｜A| ｜ 8 ｜ 6 ｜ 5 ｜ 2 ｜｜B| 8 ｜｜ 4 ｜ 3 ｜ 4 ｜｜C| 6 ｜ 4 ｜｜ 2 ｜ 3 ｜｜D| 5 ｜ 3 ｜ 2 ｜｜ 5 ｜｜E| 2 ｜ 4 ｜ 3 ｜ 5 ｜｜第二步，根据节约里程数的大小对路线进行合并和优化。

节约里程法例题

节约里程法例题
问题描述
某公司为了降低员工的交通成本，制定了节约里程法，规定员工在每周的通勤过程中，只能行驶一定的里程数。

具体规定如下：
•每位员工每周最多行驶300公里的里程数；
•员工每行驶一公里，公司会额外支付0.5元。

现在需要使用节约里程法计算员工每周的交通费用。

算法设计
节约里程法的核心思想是根据员工的行驶距离来计算交通费用。

算法的基本步骤如下：
1.设置变量total_mileage为员工总行驶里程数，初始值为0；
2.设置变量total_cost为员工总交通费用，初始值为0；
3.循环执行以下步骤：
–输入本次行驶的里程数mileage；
–如果mileage + total_mileage大于300，则将total_cost 增加300 - total_mileage * 0.5，并将total_mileage更新为300；
–否则，将total_cost增加mileage * 0.5，并将
total_mileage增加mileage；
–如果total_mileage等于300，则退出循环。

4.输出员工总交通费用total_cost。

算法实现
以下是使用Python语言实现节约里程法的代码示例：
```python def calculate_transport_cost(): total_mileage = 0 total_cost = 0
while total_mileage < 300:
mileage = float(input(\。

物流工程节约里程法教学课件讲议

节约里程法
第六步:最终方案的确定。
节约里程法
• 最终修改后的车辆调度结果:
节约里程法
• 通过对比初始方案与最终方案可知,通过优化可节约里程 (1768-1047)=721(公里),节约成本(4476.33384.55)=1091.75(元),仅8家客户的一次配送就节约了物流配送成本1091.75。
节约里程法
（0.9）
P3
6
（1.4）
P4
7
P0
10
（1.7）
P2
8
8
P5
（2.4）
初始方案: 配送线路5条，需要车5辆配送距离=39×2=78KM
P1 (1.5)
节约里程法
• 初始方案: • 配送线路5条，需要车5辆 • 配送距离: 39×2=78KM
• 优化后的方案: • 2条配送线路，2辆4t车 • 配送距离: 24＋34＝58km
10
16
18
16
12
P5
节约里程法
第2步: 按节约里程公式求得相应的节约里程数
需求量
P0
1.5
8
P1
12
1.7
8
4
13
0.9
6
1
15
1.4
7
0
16
2.4
10
2
如: P0 P1+ P0P2 -
P2
P1P2 =8+8 -12
4
=4
10
P3
9
5
6
8
P4
18
16
12
0
0
5
P5
节约里程法
第 3 步: 将节约里程按从大到小顺序排列

[管理学]第九讲节约里程法案例详解

某配送中心配送网络图
(0.9)
C
4
5
(1.2)
D
4
B (0.5)
7
5
6
(1.6) E
6 5
8
5
A (1.7)
7
11
9
P
6
(1.1) F
10 10
3
4
I (0.6)
14
5
G
(0.9)
7 12
H
(0.9)
计算配送中心至各用户以及各用户之间的最短距离，列表得最短距离表：
PABCDEFGHI
P
11 10 9 6 7 10 10 8 7
A
5 10 14 18 21 21 13 6
B
5 9 15 20 20 18 11
C
4 10 19 19 17 16
D
6 15 16 14 13
E
9 17 15 14
F
14 18 17
G
12 17
H
7
I
由最短距离矩阵，利用节约法计算出各用户之间的节约里程，编制节约里程表：
ABCDEFGHI
A
16 10 3 0 0 0 6 12
2.分拣费用
（1）分拣人工费用。这是指从事分拣工作的作业人员及有关人员工资、奖金、补贴等费用的总和。
（2）分拣设备费用。这是指分拣机械设备的折旧费用及修理费用。
3.配装费用
（1）配装材料费用。常见的配装材料有木材、纸、自然纤维和合成纤维、塑料等。这些包装材料功能不同，成本相差很大。
（2）配装辅助费用。除上述费用外，还有一些辅助性费用，如包装标记、标志的印刷，拴挂物费用等的支出。

物流管理《8节约里程法及举例(郑克俊2019.11.30修订)》

节约里程法及举例1当由一个配送中心向多个客户进行共同送货，在一条线路上的所有客户的需求量总和不大于一辆车的额定载重量时，由这一辆车配装着所有客户需求的货物，按照一条预先设计好的最正确路线依次将货物送到每一客户手中，这样既可保证按需将货物及时送交，同时又能节约行驶里程，缩短整个送货时间，节约费用。

节约里程法正是用来解决这类问题的较成熟的方法。

用节约里程法确定配送路线的主要思路是，根据配送中心的运输能力及其到各客户之间的距离和各客户之间的相对距离，来制定使总的配送车辆吨公里数到达或接近最小的配送方案。

节约里程法的根本思路如下图，P 为配送中心所在地，A 和B 为客户所在地，相互之间道路距离分别为a 、b 、c 。

最简单的配送方法是利用两辆车分别为A 、B 客户配送，此时，如图〔b 〕所示，车辆运行距离为2a 2b 。

然而，如果按图〔c 〕所示改用一辆车巡回配送，运行距离为abc 。

如果道路没有什么特殊情况，可以节省的车辆运行距离为2a 2b –abc =ab –c >0，这个节约量“ab –c 〞被称为“节约里程〞。

AAABPPPB（a ）物流网络（c ）用一辆车配送ac ba cb ab c图配送中心配送路线的选择1郑克俊仓储与配送管理〔第四版〕科学出版社修订。

步骤：实际上如果给数十家、数百家客户配送，〔1〕应首先计算包括配送中心在内的相互之间的最短距离，〔2〕然后计算各客户之间的可节约的运行距离，〔3〕按照节约运行距离的大小顺序连结各配送地并设计出配送路线。

下面举例说明节约里程法的求解过程。

例节约里程法举例图为某配送网络，P为配送中心所在地，A～J为客户所在地，共10个客户，括号内的数字为配送量〔单位：吨〕，路线上的数字为道路距离〔单位：千米〕。

现有可以利用的车辆是最大装载量为2吨和4吨的两种厢式货车，并限制车辆一次运行距离在30千米以内。

为了尽量缩短车辆运行距离，试用节约里程法设计出最正确配送路线。

物流——节约里程法讲解学习

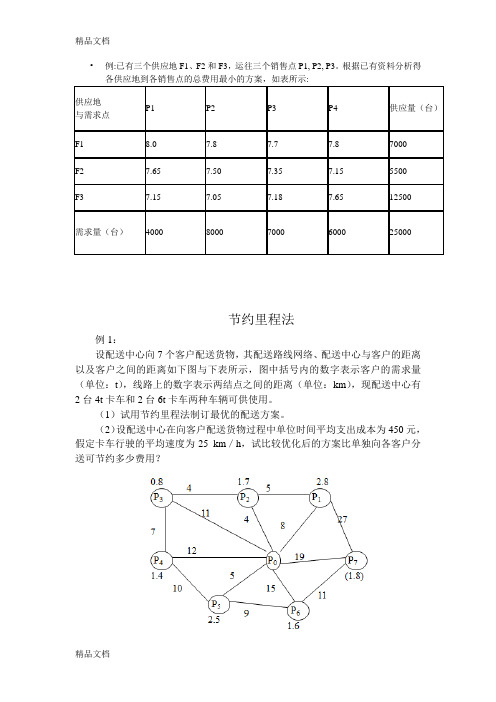
•例:已有三个供应地F1、F2和F3，运往三个销售点P1, P2, P3。

根据已有资料分析得供应地P1 P2 P3 P4 供应量（台）与需求点F1 8.0 7.8 7.7 7.8 7000F2 7.65 7.50 7.35 7.15 5500F3 7.15 7.05 7.18 7.65 12500需求量（台）4000 8000 7000 6000 25000节约里程法例1：设配送中心向7个客户配送货物，其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示，图中括号内的数字表示客户的需求量（单位：t），线路上的数字表示两结点之间的距离（单位：km），现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。

（1）试用节约里程法制订最优的配送方案。

（2）设配送中心在向客户配送货物过程中单位时间平均支出成本为450元，假定卡车行驶的平均速度为25 km／h，试比较优化后的方案比单独向各客户分送可节约多少费用？（1）里程表（2）节约里程表（3）节约里程数排序5 P1P37 11 P5P7 46 P4P67 12 P4P7 1（4）配送路线选择节省的配送时间为节省的费用为：例2：设配送中心向5个客户配送货物，其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示，图中括号内的数字表示客户的需求量（单位：t），线路上的数字表示两结点之间的距离（单位：km），现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。

（1）试用节约里程法制订最优的配送方案。

（2）假定卡车行驶的平均速度为40 km／h，试比较优化后的方案比单独向各客户分送可节约多少时间？里程表节约里程表节约里程排序P2P3 P2P4 6 85P3P0 4 P4P5 5 95P1P0 5 P1P2 4 104路线选择节约的总里程：节省的配送时间为G=6500X 7. 70+500X 7. 80+5500X 7. 15+ 4000X 7. 15+8000X 7. 05+ 500X 7. 18 = 181865(万元)。

节约里程法

A2、A3、A4共同配送需求总量：1.5+2.2+1.0=4.7（t）选一辆载重5吨的汽车 A1、A5共同配送需求总量：0.8+2.1=2.9（t）选一辆载重3吨的汽车
共节约的里程数为4+3+2=9（公里）
配送路径如下
A1
0.8
2.1
A5
5
4 3
A0
3
A2
1.5
2
4
1.0
A4
4A3Biblioteka 2.2• 案例：某货物配送中心A0
每两地之间的最短路径
A0 3 3 5 2 4 A1 4 8 5 5 A2 4 5 7 A3 4 8 A4 4 A5
L12=3+3-4=2 L13=0 L14=0 L15=7-5=2 L23=8-4=4 L24=0 L25=0
L34=3 L35=1 L45=2
按节约里程数排序
节约里程法
目录
基本原理案例分析优缺点分析改进建议
2
A
B
1 P
1
如果P（配送中心）分别向A、B客户送货，有两种送货方案第一种：P—A—P—B—P 总距离为：L1=2（PA+PB）第二种：P—A—B—P 总距离为：L2=PA+AB+PB
• • • •
PAB可以看作三角形，PA+PB>=AB L1 >=L2 可以看出方案二优于方案一二都比较方案二比方案一节约了里程 L=PA+PB-AB
宝洁案例
110
• 还可以用两个8T、一个5T的车，但费用就要高一点
缺点：第一：利用节约法选择配送路线过于强调节约路程，而没有考虑行程中的时间因素。第二：利用节约法选择配送路线不能对客户的需求的需求进行灵活多变的处理。节约法更适合需求稳定或需求的时间不紧迫，这显然不满足现代多变的市场环境。

两个例子-节约里程法

ቤተ መጻሕፍቲ ባይዱ原理
该方法基于节约思想，即在一辆运输车辆上装载多个客户的货物，通过合理规划运输路线，使得车辆可以依次经过这些客户的所在地，并在满足车辆载重和容量限制的前提下，实现运输里程的最小化。
发展历程及应用领域
发展历程
节约里程法最初由国外学者提出，后来经过不断改进和完善，逐渐形成了较为成熟的理论体系。目前，该方法已经在国内外得到了广泛应用。
空间。
挑战
新技术的发展和应用需要大量的投入和研发，同时也需要面对技术更新换代快、数据安全等问题。此外，新技术在节约里程法中的应用还需要与实际业务场景相结合，需要进
行不断的实践和调整。
行业应用拓展方向预测
物流行业
节约里程法在物流行业的应用已经比较成熟，未来可以进一步拓展到智能物流、绿色物流等领域，实现更加高效、环保的物流运输。
局限性
虽然节约里程法在优化运输路径方面具有一定的优势，但也存在一些局限性。例如，该方法只考虑了运输里程的节约，而忽略了其他因素（如时间、服务质量等）对运输成本的影响。此外，在实际应用中，还需要考虑车辆的载重和容量限制、道路状况、客户需求等多种因素，这也会增加该方法的复杂性和难度。
02 节约里程法实例一：物流配送优化
01
节约里程法的时间复杂度主要取决于需求点的数量和合并运输的次数。
02
在需求点数量较多的情况下，算法可能需要较长的时间来寻找最优解。
03
为了优化算法，可以考虑采用启发式搜索策略，如贪婪算法、遗传算法等，来加快搜索速度并提高解的质量。
04
此外，还可以考虑对需求点进行聚类处理，以减少合并运输的次数和降低算法复杂度。
节约里程法在路线规划中应用
景点间距离与交通方式选择