第 3 讲 直角三角形
第三讲 直角三角形的边角关系讲义
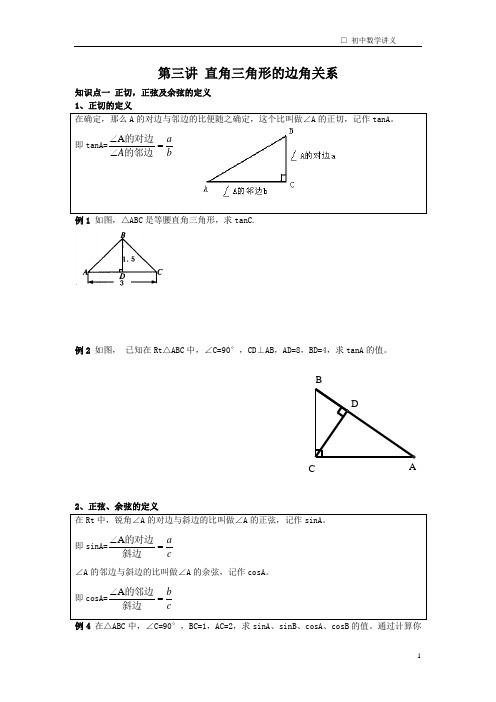
第三讲 直角三角形的边角关系知识点一 正切,正弦及余弦的定义1、正切的定义的对边与邻边的比便随之确定,这个比叫做∠A 的正切,记作例1 如图,△ABC 是等腰直角三角形,求tanC.例2 如图, 已知在Rt △ABC 中,∠C=90°,CD ⊥AB ,AD=8,BD=4,求tanA 的值。
C B A有什么发现?请加以证明。
3、三角函数的定义(重点)能判断谁的木棒更陡吗?说明理由。
同步练习:1、∠C=90°,点D 在BC 上,BD=6,AD=BC ,cos ∠ADC=53,求CD 的长。
2、P 是a 的边OA 上一点,且P 点的坐标为(3,4),求sina 、tana 的值。
3、在△ABC 中,D 是AB 的中点,DC ⊥AC ,且tan ∠BCD=31,求tanA 的值。
4、在Rt △ABC 中,∠C=90°,tanA=125,周长为30,求△ABC 的面积。
5、(2008·浙江中考)在Rt △ABC 中,CD 是斜边AB 上的中线,已知CD=2,AC=3,则sinB 的值是多少?知识点二 30°,45°,60°角的三角函数值例 求下列各式的值。
(1)︒︒-︒60tan 30sin 60sin ;(2)︒-+︒-︒45sin 22460tan 460tan 2。
同步练习:1、 求下列各式的值。
(1)︒+︒+︒45tan 30tan 330sin 2; (2)︒⋅︒+︒30cos 60tan 45cos 2。
(3) 6tan 2 30°-3sin 60°+2tan45°(4)022)30tan 45(sin )60cos (160sin 260sin 60tan 245tan o o o o o oo-+-++----2、 已知a 为锐角,且tana=5,求aa aa sin cos 2cos 3sin +-的值。
解直角三角形方位角、坡度角讲课教案

解直角三角形方位角、坡度角讲课教案一、教学内容本节课的内容选自《初中数学》八年级下册第九章“勾股定理及其应用”的第三节“解直角三角形”。
具体包括:直角三角形的定义及性质,解直角三角形的概念,利用三角函数解直角三角形,以及方位角和坡度角的实际应用。
二、教学目标1. 知识目标:学生能够理解并掌握解直角三角形的基本概念,熟练运用三角函数求解直角三角形的未知边和角。
2. 技能目标:培养学生运用数学知识解决实际问题的能力,提高学生的空间想象力和逻辑思维能力。
3. 情感目标:激发学生学习数学的兴趣,培养学生合作交流、积极参与的学习态度。
三、教学难点与重点教学难点:解直角三角形的实际应用,特别是方位角和坡度角的计算。
教学重点:熟练运用三角函数解直角三角形,以及在实际问题中求解方位角和坡度角。
四、教具与学具准备教具:三角板、直尺、量角器、多媒体课件。
学具:直角三角形模型、计算器、练习本。
五、教学过程1. 导入:通过实际情景引入,如建筑工地上的方位角和坡度角问题,让学生了解解直角三角形在实际生活中的应用。
2. 新课导入:讲解直角三角形的定义及性质,引导学生回顾勾股定理,为解直角三角形打下基础。
3. 新知讲解:(1)介绍解直角三角形的定义及方法,如正弦、余弦、正切函数的定义和应用。
(2)通过例题讲解,让学生掌握解直角三角形的方法。
(3)讲解方位角和坡度角的概念,以及在实际问题中的应用。
4. 随堂练习:布置相关练习题,让学生独立完成,巩固所学知识。
5. 小组讨论:针对练习题中的问题,组织学生进行小组讨论,互相交流解题思路。
六、板书设计1. 直角三角形的定义及性质2. 解直角三角形的方法:(1)正弦函数:sin A = 对边/斜边(2)余弦函数:cos A = 邻边/斜边(3)正切函数:tan A = 对边/邻边3. 方位角和坡度角的计算方法七、作业设计1. 作业题目:(1)已知直角三角形的两个角和一条边,求其他未知边和角。
解直角三角形 第3课时 复习 (湘教版九年级全)课件

sin B
PC PB
B
PB
PC PC 72.505 129.7 sin B sin 34 0.559
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约129.7海里.
当堂反馈
1.如图1,从地面上的C,D两点测得树顶A仰角分别是 45°和30°,已知CD=200m,点C在BD上,则树高 AB等于 100( 3 1)m(保留根号).
A 仰角 水平线
B
α β D
Rt△ABC中,a =30°,AD=120,
所以利用解直角三角形的知识求出
俯角 C
BD;类似地可以求出CD,进而求出BC.
解:如图,a = 30°,β= 60°, AD=120.
BD CD tan a , tan AD AD
BD AD tana 120 tan30
B α A β D
3 120 40 3 3
CD AD tan 120 tan60
120 3 120 3
BC BD CD 40 3 120 3
160 3 277.1
答:这栋楼高约为277.1m
C
教材:P89 例5 例5 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里 的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东 34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确 到0.1海里)? A 解:如图 ,在Rt△APC中, 65° PC=PA· cos(90°-65°) P =80×cos25° C ≈72.505 在Rt△BPC中,∠B=34° 34°
D
图1
图2
2.如图2,将宽为1cm的纸条沿BC折叠,使∠CAB=45° 2 2 则折叠后重叠部分的面积为 cm (根号保留).
三角形边角关系-第3讲的角与边学

第三讲三角形的角与边一、基础知识本讲重点介绍三角形的边、角不等关系,包括同一个三角形中的边、角不等关系以及不同三角形中的边、角不等关系.1.边与边的关系(1)在同一个三角形中两边之和大于第三边,两边之差小于第三边(三边满足什么条件时,三角形必然存在?);(2)勾股定理:即在直角三角形中两条直角边的平方和等于斜边的平方.2.角与角的关系(1)三角形的内角和为180︒;(2)直角三角形中两锐角互余;(3)三角形的一个外角大于任何一个与它不相邻的内角;(4)三角形的一个外角等于与它不相邻的两内角之和.3.边和角的关系(1)在同一个三角形中,大边对大角,大角对大边;(2)在两个三角形中,如果有两条边对应相等,那么夹角大的所对的边也大;反之也成立,即在两个三角形中,如果有两条边对应相等,那么第三边大,则所对的角也大.4.不等式变形时常用的性质(1)若a>b,c>d,则a+c>b+d;(2)若a>b,c>d,则a-d>b-c;(3)若a>b,c>0,则ac>bc;若a>b,c<0,则ac<bc;(4)若a>b>0,则11 a b <;(5)总量大于任何一个部分量.5.三角形中的不等关系根源:(1)两点之间线段最短;(2)垂线段最短.二、例题第一部分边的问题例1. (★★希望杯训练题)将三边长为a,b,c的三角形记作(a,b,c).写出周长为20,各边长为正整数的所有不同的三角形.例2. (★★★ 2000年希望杯竞赛题)一个三角形的三条边的长分别是a,b,c(a,b,c都是质数),且a+b+c=16,则这个三角形是()A.直角三角形B.等腰三角形C.等边三角形D.直角三角形或等腰三角形例3. (★★★1998年江苏省竞赛题)在不等边三角形中,如果有一条边长等于另两条边长的平均值,那么最大边上的高与最小边上的高的比值的取值范围是( )A.31 4k<<B.113k<<C.12k<< D.112k<<例4. (★★★1997年北京市竞赛题)等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm 两部分,则这个等腰三角形的底边的长为( )A.17cmB.5cmC.17cm或5cmD.无法确定例5. (★★★)如图3-1,已知P为三角形ABC内一点,求证:1()2AB AC BC PA PB PC AB AC BC++<++<++.例6. (★★★第三十二届美国邀请赛试题)不等边三角形ABC的两条高长度为4和12,若第三条高的长也是整数,试求它的长.例7. (★★★)若三角形ABC 的三边长是a,b,c,且满足:444224442244422,,a b c b c b c a a c c a b a b =+-=+-=+-,则ABC ∆是( )A.钝角三角形B.直角三角形C.等腰直角三角形D.等边三角形第二部分 角的问题例8. (★★)如图3-4,在三角形ABC 中,042A ∠= ,ABC ∠和ACB ∠的三等分线分别交于D,E,求BDC ∠的度数.例9. (★★★1999年重庆市竞赛题)三角形的三个内角分别为,,αβγ,且αβγ≥≥,2αγ=.则β的取值范围是( )A.003645β≤≤B.004560β≤≤C.006090β≤≤D.004572β≤≤例10. (★★★)如图3-7,延长四边形ABCD 对边AD,BC 交于F ;DC,AB 交于E,若AED ∠,AFB ∠平分线交于O,求证:1()2EOF EAF BCD ∠=∠+∠第三部分边角综合24,例11. (★★★ 2000年江苏省竞赛题)在锐角三角形ABC中,AB>BC>AC,且最大内角比最小内角大0 的取值范围是( ).则A例12. (★★★★)如图3-2,在三角形ABC中,AB>AC>BC,P为三角形内任意一点,连结AP并延长交BC于点D.求证:(1)AB+AC>AD+BC;(2)AB+AC>AP+BP+CP.例13. (★★★★)如图,在三角形ABC中,角A=90度,AD垂直于BC,求证:AB+AC<AD+BC例14.(★★★★)如图,在三角形ABC中,AC>AB,在CA上截取CD=AB,E,F分别是BC,AD的中点,连接EF 并延长交BA的延长线于G,求证:AF=AG例15. (★★★★★)设三角形的三个内角度数分别为A,B,C,相应的对边长分别为a,b,c,求证:60 aA bB cCa b c︒++≥++三、练习题1. (★★)设m,n,p均为自然数,满足m n p≤≤,且m+n+p=15,试问以m,n,p为边长的三角形有多少个?2.(★★ 1998年山东省竞赛题) 已知三角形三边的长均为整数,其中某两条边长之差为5,若此三角形周长为奇数,则第三边长的最小值为( )** B.7 C.6 D.43.(★★★)一个三角形的周长为偶数,其中的两条边长分别为4和2003,则满足上述条件的三角形的个数为( )A.1个B.3个C.5个D.7个4.(★ 2002,云南省中考题)两根木棒的长分别是7cm和10cm,要选择第三根木棒,将它们钉成一个三角形,若第三根木棒的长是acm,则a的取值范围是( ).5. (★)ABC 的一个内角的大小是040,且A B ∠=∠,那么C ∠的外角的大小是( )A.140︒B.80︒或100︒C.100︒或140︒D.80︒或140︒6. (★★★)如图3-5,在ABC ∆中,90ACB ︒∠=,D,E 为AB 上的两点,若AE=AC,45DCE ︒∠=则图中与BC 等长的线段是( ) A.CD B.BD C.CE D.AE-BE7. (★★★)如图3-6,在ABC ∆中,B ∠的平分线与C ∠的外角平分线相交于D,40D ︒∠=.则A ∠等于( )A.50︒B. 60︒C. 70︒D.80︒8. (★★ 第12届希望杯竞赛题)如图3-9,127.5︒∠=,295︒∠=,338.5︒∠=求4∠的大小.9. (★★★第5届希望杯竞赛题)如图3-8,BE 是ABD ∠的平分线,CF 是ACD ∠的平分线,BE 与CF 交于G,若140BDC ︒∠=,110BGC ︒∠=,求A ∠的度数.10. (★★★★)如图,三角形ABC 中,AB=BC=CA,AE=CD,AD,BE 相交于P,BQ 垂直于AD 于Q ,求证:BP=2PQ课外小故事五枚金币有个叫阿巴格的人生活在内蒙古草原上.有一次,年少的阿巴格和他爸爸在草原上迷了路,阿巴格又累又怕,到最后快走不动了.爸爸就从兜里掏出5枚硬币,把一枚硬币埋在草地里,把其余4枚放在阿巴格的手上,说:“人生有5枚金币,童年、少年、青年、中年、老年各有一枚,你现在才用了一枚,就是埋在草地里的那一枚,你不能把5枚都扔在草原里,你要一点点地用,每一次都用出不同来,这样才不枉人生一世.今天我们一定要走出草原,你将来也一定要走出草原.世界很大,人活着,就要多走些地方,多看看,不要让你的金币没有用就扔掉.”在父亲的鼓励下,那天阿巴格走出了草原.长大后,阿巴格离开了家乡,成了一名优秀的船长.珍惜生命,就能走出挫折的沼泽.。
第3讲等腰(直角)三角形存在性处理策略

第三讲等腰(直角)三角形的存在性问题处理策略一、两圆一线与两线一圆二、代数解法(SSS法)前提:三边的平方是常数或者是关于某个参数的二次式,根据边或直角分类三、几何解法(SAS法)1等腰三角形的存在性问题前提:三角形有一个不变的内角θ步骤:①用同一个参数表示该不变角相邻的两条边;②以腰为标准分三类列方程。
具体如下:情形一、当定角θ为顶角时,如图3-2-6,有a=b;情形二1等腰三角形的存在性问题、当定角θ为底角且b为腰时,如图3-2-7,有cosθ=a/2b;情形三、当定角θ为底角且a为腰时,如图3-2-8,有cosθ=b/2a.2直角三角形存在性问题法1:若直角三角形有一个不变的锐角θ,可狠抓不变角θ,利用其三角函数列式计法2:依托直角三角形,作“横平竖直”辅助线,造“一线三直角”,利用相似求解3等腰直角三角形存在性问题方法:一般构造“一线三直角”全等,即“K 字型”全等值得一提的是,以上问题,有时还可以结合导角、相似等转化手段进行求解例1、在菱形ABCD中,∠ABC=60°,AB=12,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(两点不重合)两点间的最短距离是_________。
变式1、在菱形ABCD中,∠ABC=120°,AB=12,点P是这个菱形外部的一点,若以点P、B、D为顶点的三角形是Z直角三角形,则P、C(两点不重合)两点间的最短距离是_________。
例2、已知点A(3,0),B(0,4),在坐标轴上找一点C,使△ABC为等腰三角形,求所有点C的坐标..变式1、已知点A(3,0),B(0,4),在坐标轴上找一点C,使△ABC为直角三角形,求所有点C的坐标..例3、如图,二次函数y=a(x2﹣2mx﹣3m2)(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,﹣3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.(1)用含m的代数式表示a;(2)求证:为定值;(3)设该二次函数图象的顶点为F,探索:在x轴的负半轴上是否存在点G,连接GF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.以下是几何解法(一、)显性的不变角(二、例4已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8),抛物线y=ax2+bx+c过A、C两点.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E.①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值.例5在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B,若AB=10,BC=16,当△APD为直角三角形时,求BP的长变式:在△ABC中,AB=AC,点P、D分别是BC、AC边上的点(点P不与B、C重合),且∠ABD=∠B,若AB=10,BC=16,当△APD为等腰三角形时,求BP的长(二)隐形的不变角(三)例6、如图,已知Rt△ABC中,∠C=90°,AC=8,BC=6,点P以每秒1个单位的速度从A向C运动,同时点Q以每秒2个单位的速度从A→B→C方向运动,它们到C点后都停止运动,设点P,Q运动的时间为t秒.(1)在运动过程中,求P,Q两点间距离的最大值;(2)经过t秒的运动,求△ABC被直线PQ扫过的面积S与时间t的函数关系式;(3)P ,Q 两点在运动过程中,是否存在时间t ,使得△PQC 为等腰三角形?若存在,求出此时的t 值;若不存在,请说明理由例7在平面直角坐标系中,已知点A(1,0)与直线l :y=x 34,点B 在x 轴正半上,且位于点A 的右侧,过点B 作x 轴的垂线,交直线l 于点C,再过点C 作直线l 的垂线,交x 轴于点D 在BC 上取点E ,使BE=BA,连接OE,并延长,交CD 于点F,当△CEF 为等腰三角形时,求点C 的坐标..练习1、直线y=-x+4与x 轴交于点B,点C 在直线AB 上,在平面直角坐标系中求一点,使得以O 、A 、C 、D 为顶点的四边形是菱形。
教学设计_解直角三角形(第3课时)_2

28.2解直角三角形(3)教学目标:1.巩固用三角函数有关知识解决问题,学会解决坡度问题。
2.掌握坡度与坡角的关系,能利用解直角三角形的知识,解决与坡度有关的实际问题。
3.培养学生用数学的意识,渗透数形结合的思想和方法。
教学重点:理解坡度和坡角的概念。
教学难点:利用坡度和坡角解决有关实际问题。
教学过程:一、新知引入你觉得哪幅图的坡更好爬?为什么?(教师展示ppt )我们知道坡越陡,倾斜的角度越大,那与我们直角三角形有什么联系呢?我们一起来探索吧!二、新知讲解知识1:基本概念:坡角:坡面与水平面的夹角叫做坡角,用字母α表示。
坡度(坡比):坡面的铅直高度h 和水平距离l 的比叫做坡度,用字母i 表示,则i=l h = tan 如图,坡度通常写成i=h:l 的形式。
※注意:①(坡度等于坡角的正切值)坡度越大,坡角a 就越大,坡面就越陡.②坡度的结果不是一个度数,而是一个比值,不要与坡角相混淆.巩固练习:试一试,你最棒!1、斜坡的坡度是1:3,则坡角α=______度。
(答案:30)2、斜坡的坡角是450,则坡比是_______。
(答案:1:1)3、斜坡长是12米,坡高6米,则坡比是_______。
(答案:1:3)知识2:如何解决实际生活中的坡度、坡角问题?解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,如,我们要测量如图所示大坝的高度h 时,只要测出仰角a 和大坝的坡面长度l ,就能算出h=lsina ,但是,当我们要测量如图所示的山高h 时,问题就不那么简单了,这是由于不能很方便地得到仰角a 和山坡长度l与测坝高相比,测山高的困难在于;坝坡是“直”的,而山坡是“曲”的,怎样解决这样的问题呢?我们设法“化曲为直,以直代曲”. 把山坡“化整为零”地划分为一些小段,图表示其中部分小段,划分小段时,注意使每一小段上的山坡近似是“直”的,可以量出这段坡长l 1,测出相应的仰角a 1,就可以算出这段山坡的高度h 1=l 1sina 1.在每小段上,都构造直角三角形,利用上面的方法算出各段山坡的高度h 1,h 2,…,h n ,然后我们再“积零为整”,把h 1,h 2,…,h n 相加,于是得到山高h.以上解决问题中所用的“化整为零,积零为整”“化曲为直,以直代曲”的做法,它在数学中有重要地位。
2022秋八年级数学上册 第14章 勾股定理14.1 勾股定理 3直角三角形的判定授课课件华东师大版

知1-讲
例5 如图,E、F分别是正方形ABCD中BC和CD边
上的点,且AB=4,CE=
1 4
BC,F为CD的中
点,连结AF,AE,EF,问:△AEF是什么三
角形?请说明理由.
知1-讲
导引:直接判断EF2+AF2与AE2的关系不太容易, 1
但由于“AB=4,CE= 4 BC,F为CD的中 点”,因此可以很容易求出AF,EF,AE的 长,然后判断EF2+AF2与AE2的关系,从而 得到三角形的形状.
知1-讲
解: (1)在△ABC中,∵∠A+∠B+∠C=180°, ∴∠B=180°-25°-65°=90°, ∴△ABC是直角三角形.
(2)在△ABC中,∵AC2+BC2=122+162=202 =AB2, ∴△ABC是直角三角形,且∠C为直角.
(3)∵三角形的三边长满足b2-a2=c2, 即b2=a2+c2, ∴此三角形是直角三角形,且b是斜边长.
知2-讲
解: ∵AB2 + BC2 = (n2 -1)2 + (2n)2 =n4 - 2n2 + 1 + 4n2 =n4 + 2n2 + 1 =(n2 + 1) 2
想一想,为什么 选择AB2 + BC2 ? AB、BC、CA的 大小关系是怎样 的?
=AC 2
∴△ABC是直角三角形,边AC所对的角是直角.
导引:先将等式两边同时分解因式,然后通过对分 解后的式子的讨论,得出△ABC的形状.
解:
∵a2c2-b2c2=a4-b4,
知1-讲
∴c2(a2-b2)=(a2-b2)(a2+b2).
即(a2-b2)(a2+b2-c2)=0.
(1)当a2-b2≠0时,则有c2=a2+b2.
初中数学 三角形模块5-3 直角三角形讲义(含答案解析)

第三部分直角三角形一、知识梳理:1.直角三角形的性质:(1)直角三角形两个锐角互余;(2)直角三角形斜边上的中线等于斜边的一半;(3)直角三角形中,30°角所对的直角边等于斜边的一半;(4)勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方,即如果设直角三角形的两条直角边长度分别是a和b,斜边长度是c,那么可以用数学语言表达:222+=a b c (5)勾股数:勾股数就是可以构成一个直角三角形三边的一组正整数.2.直角三角形的判定:(1)有一个角是90°的三角形是直角三角形;(2)有两个角的三角形是直角三角形;(3)如果三角形一边的中线等于这边的一半,那么这个三角形是直角三角形;(4)勾股定理逆定理:如果三角形的三条边长a,b,c满足关系式:222+=a b c,那么这个三角形是直角三角形.二、题型练题型一直角三角形的两锐角互余例1.若直角三角形的一个锐角为15︒,则另一个锐角等于________.75°【分析】根据三角形内角和定理计算即可.【详解】解:∵另一个锐角为15°,∴另一个锐角为180°-90°-15°=75°,故答案为:75°.【点睛】本题考查了直角三角形的性质,解题的关键是掌握直角三角形两锐角互余.变式11.如图,直线a ∥b ,直线l 与a 、b 分别相交于A 、B 两点,过点A 作直线l 的垂线交直线b 于点C ,若∠1=60°,则∠2的度数为()A.30°B.35°C.40°D.60°【答案】A【解析】【分析】由AC l ⊥及160∠=︒,可求得ACB ∠的度数,再由//a b 即可求出2∠的度数.【详解】∵AC l ⊥,160∠=︒∴90130ACB ∠=︒-∠=︒∵//a b∴230ACB ∠=∠=︒故选:A【点睛】本题主要考查了平行线的性质及直角三角形的性质.题型二直角三角形斜边上的中线例2.如图在ABC ∆中,CF AB ⊥于F ,BE AC ⊥于E ,M 为BC 的中点,5EF =,EFM ∆的周长为13,则BC 的长是()A .6B .8C .10D .12B 【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半,求出BC =2MF =2EM ,所以MF =EM ,然后列式整理得到△EFM的周长=BC+EF,代入数据进行计算即可.【详解】解:∵在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,∴BC=2MF,BC=2EM.∴MF=EM.∴△EFM的周长=MF+EM+EF=BC+EF.∵EF=5,△EFM的周长为13,∴BC=13-5=8故选:B.【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,熟练掌握性质是解题的关键.变式22.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是()A.2B.3C.4D.5【答案】B【解析】【分析】根据直角三角形的性质得到DF=4,根据BC=14,由三角形中位线定理得到DE=7,解答即可.【详解】解:∵∠AFB=90°,点D是AB的中点,∴DF=12AB=4,∵BC=14,D、E分别是AB,AC的中点,∴DE=12BC=7,∴EF=DE-DF=3,故选:B【点睛】本题考查了直角三角形的性质和中位线性质,掌握定理是解题的关键.题型三直接考查勾股定理例3.已知直角三角形的两边长分别为3和4,则斜边长为()A.4B.5C.4或5D.5C【分析】由于此题中直角三角形的斜边不能确定,故应分4是直角三角形的斜边长和直角边长两种情况讨论.【详解】解: 直角三角形的两边长分别为3和4,∴①4是此直角三角形的斜边长;②当45=.综上所述,斜边长为4或5故选:C.【点睛】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.变式33.如图,在三角形ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心,AC长为半径画弧,交AB于点D,则BD=()A. 2.5B.3C.2D.3.5【答案】C【解析】【分析】首先利用勾股定理可以算出AB的长,再根据题意可得到AD=AC,根据BD=AB-AD即可算出答案.【详解】解:∵AC =3,BC =4,∴AB =5,∵以点A 为圆心,AC 长为半径画弧,交AB 于点D ,∴AD =AC ,∴AD =3,∴BD =AB -AD =5-3=2.故选C .【点睛】此题主要考查了勾股定理,关键是熟练掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.题型四勾股数例4.下列数组是勾股数的是()A .2、3、4B .0.3、0.4、0.5C .6、8、10D .7、12、15C【分析】根据勾股数的定义:满足222+=a b c 的三个正整数,称为勾股数逐一判断即可.【详解】A .22223134+=≠,此数组不是勾股数;B .0.3、0.4、0.5不是整数,此数组不是勾股数;C .222 6810+=,此数组是勾股数;D .222 71219315+=≠,此数组不是勾股数;故选:C .【点睛】本题考查了勾股数的知识,解答此题要用到勾股数的定义,及勾股定理的逆定理:已知△ABC 的三边满足222+=a b c ,则△ABC 是直角三角形.变式44.如图,这是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A 、B 、C 、D 的边长是3、5、2、3,则最大正方形E 的边长是()A.13B.C.47D.【答案】B【解析】【分析】设中间两个正方形的边长分别为x 、y ,最大正方形E 的边长为z ,根据勾股定理进行求解.【详解】设中间两个正方形的边长分别为x 、y ,最大正方形E 的边长为z ,由勾股定理得:x 2=32+52=34,y 2=22+32=13,z 2=x 2+y 2=47,即最大正方形E 的面积为:z 2=47,边长为z 故选B .【点睛】本题考查勾股定理,掌握以直角三角形斜边为边长的正方形的面积等于两个以直角边为边长的正方形面积之和是解题的关键.题型五勾股定理的证明例5.勾股定理是人类最伟大的十个科学发现之一,在《周髀算经》中就有“若勾三,股四,则弦五”的记载,汉代数学家赵爽为证明勾股定理创制的“赵爽弦图”也流传至今.迄今为止己有400多种证明勾股定理的方法.下面是数学课上创新小组验证过程的一部分.请认真阅读并根据他们的思路将后续的过程补充完整:将两张全等的直角三角形纸片按图所示摆放,其中b a >,点E 在线段AC 上,点B D 、在边AC 两侧,试证明:222+=a b c .见解析.【分析】首先连结BD ,作DF BC ⊥延长线于F ,则AE b a =-,根据Rt ABC Rt DAE D @D ,易证90DAB ︒∠=,再根据ADE ABC ADFB DFCE S S S S D D =++四边形四边形,ADB DFB ADFB S S S ∆∆=+四边形,两者相等,整理即可得证.【详解】证明:连结BD ,作DF BC ⊥延长线于F ,则AE b a=-ADE ABC ADFB DFCES S S S D D =++四边形四边形()1122ab ab b a b =++-⋅2ab b ab=+-2b =Rt ABC Rt DAE∆≅∆ AB AD c\==ADE BAC∴∠=∠90ADEDAE °??Q 90BAC DAE °\??即90DAB ︒∠=,∴AD AB⊥∴ADB DFBADFB S S S ∆∆=+四边形()()21122c a b b a =++⋅-222111222c b a =+-即有:2222111222b c b a =+-∴222+=a b c 【点睛】本题考查了勾股定理的证明,用两种方法表示出四边形ADFB 的面积是解本题的关键.变式55.勾股定理现约有500种证明方法,是用代数思想解决几何问题的最重要的工具之一.中国古代最早对勾股定理进行证明的是三国时期吴国的数学家赵爽,赵爽创制了如图1所示的“勾股圆方图”,在该图中,以弦c 为边长所得到的正方形ABCD 是由4个全等的直角三角形再加上中间的小正方形EFGH 组成的,其中BF a =,AF b =.(1)请利用面积相等证明勾股定理;(2)在图1中,若大正方形ABCD 的面积是13,2BF =,求小正方形EFGH 的面积;(3)图2是由“勾股圆方图”变化得到的,正方形MNKT 由八个全等的直角三角形和正方形EFGH 拼接而成,记图中正方形MNKT ,正方形ABCD ,正方形EFGH 的面积分别为1S ,2S ,3S .若12348S S S ++=,求边AB 的长度.【答案】(1)证明见解析;(2)1;(3)4【解析】【分析】(1)根据大正方形的面积=4个全等直角三角形的面积+小正方形的面积证明可得结论;(2)由勾股定理可得AF 的长,从而可得小正方形的边长,进一步可求出小正方形的面积;(3)分别求出正方形MNKT ,正方形ABCD ,正方形EFGH 的边长,求出其面积,代入12348S S S ++=,进一步整理可得解.【详解】解:(1)∵Rt ABF Rt DAE Rt CDH Rt BCG∆≅∆≅∆≅∆∴BF AF DH CG a ====,AF DE CH BG b====∴小正方形EFGH 的边长=b a-又大正方形的边长为c∴正方形ABCD 的面积为2c ,4个全等直角三角形的面积和为2ab ,正方形EFGH 的面积为()2b a -,由“大正方形的面积=4个全等直角三角形的面积+小正方形的面积”得;2214()2c ab b a =⨯+-∴()222c ab b a =+-经过整理可得222c a b =+(2)∵大正方形ABCD 的面积是13,∴213c =∵2BF =,且222BF AF AB +=∴2221349AF AB BE =-=-=∴3AF =(负值舍去)∴321EF =-=∴小正方形EFGH 的面积为1;(3)∵正方形MNKT 由八个全等的直角三角形和正方形EFGH 拼接而成,∴AM AF b ==,MB BF a ==,∴正方形MNKT 的边长为a b +,∴正方形MNKT 的面积为()2a b +.而正方形ABCD 的边长为c ,正方形EFGH 的边长为()b a -,∴正方形ABCD 的面积为2c ,正方形EFGH 的面积为()2b a -,∴()()22248a b c b a +++-=,整理得,2348c =,∴4c =(负值舍去)【点睛】此题考查的是勾股定理的证明和应用,能够准确识图是解答本题的关键.题型六勾股定理的实际应用例6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底墙到左墙角的距离为1.5m ,顶端距离地面2m ,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面0.7m ,那么小巷的宽度为()A .3.2mB .3.5mC .3.9mD .4mC【分析】如图,在Rt △ACB 中,先根据勾股定理求出AB ,然后在Rt △A ′BD 中根据勾股定理求出BD ,进而可得答案.【详解】解:如图,在Rt △ACB 中,∵∠ACB =90°,BC =1.5米,AC =2米,∴AB 2=1.52+22=6.25,∴AB =2.5米,在Rt △A ′BD 中,∵∠A ′DB =90°,A ′D =0.7米,BD 2+A ′D 2=A ′B 2,∴BD 2+0.72=6.25,∴BD 2=5.76,∵BD>0,∴BD=2.4米,∴CD=BC+BD=1.5+2.4=3.9米.故选:C.【点睛】本题考查了勾股定理的应用,正确理解题意、熟练掌握勾股定理是解题的关键.变式66.小明想知道学校旗杆多高,他发现旗杆上的绳子垂到地面还多2m,当他把绳子的下端拉开10m后,发现下端刚好接触地面,则旗杆的高为()A.16mB.20mC.24mD.28m【答案】C【解析】【分析】根据题意设旗杆的高AB为x米,则绳子AC的长为(x+2)米,再利用勾股定理即可求得AB的长,即旗杆的高.【详解】解:如图:设旗杆的高AB为x米,则绳子AC的长为(x+2)米,在Rt△ABC中,BC=10米,由勾股定理得:AB2+BC2=AC2,∴x2+102=(x+2)2,解得:x=24,∴AB=24.∴旗杆的高24米,故选:C .【点睛】本题考查学生利用勾股定理解决实际问题的能力,解题关键是构造直角三角形利用勾股定理列出方程.题型七勾股定理的逆定理例7.下列四组数中不能构成直角三角形的一组是()A .4,5,6B .7,24,25C .5,12,13D .1,2A【分析】分别把选项中的三边平方后,根据勾股定理逆定理即可判断能否构成直角三角形.【详解】解:A 、∵222456+≠,∴三条线段不能组成直角三角形,故A 选项符合题意;B 、∵22272425+=,∴三条线段能组成直角三角形,故B 选项不符合题意;C 、∵22251213+=,∴三条线段能组成直角三角形,故C 选项不符合题意;D 、∵22212+=,∴三条线段能组成直角三角形,故D 选项不符合题意;故选:A .【点睛】本题考查了勾股定理逆定理,熟悉定理是关键.变式77.在如图的网格中,每个小正方形的边长为1,A 、B 、C 三点均在正方形格点上,若AD 是ABC 的高,则AD 的长为()A. B. C. D.2【答案】D【解析】【分析】结合格点的特点利用勾股定理求得AB 2,AC 2,BC 2,然后利用勾股定理逆定理判定△ABC 的形状,从而利用三角形面积求解.【详解】解:由题意可得:2222420AB =+=222215AC =+=2223425BC =+=∵222+AB AC BC =∴△ABC 是直角三角形又∵AD 是ABC 的高∴1122AC AB BC AD ⋅=⋅,11522AD ⨯,解得:=2AD 故选:D .【点睛】本题考查勾股定理及其逆定理,掌握勾股定理,利用网格特点,准确计算是解题关键.题型八勾股定理的逆定理的应用例8.如图所示的网格是正方形网格,ABC ∆是()三角形.A .锐角B .直角C .钝角D .等腰A【分析】根据勾股定理求出三边的长,再利用勾股定理逆定理可作判断.【详解】解:根据网格图可得:2224117AC =+=,2223110AB =+=,2224325CB =+=,222171025AC AB CB +=+>= ,ABC ∆∴是锐角三角形,故选:A .【点睛】本题考查了三边的关系,会利用三边关系确定三角形的形状:若三角形的三边分别为a 、b 、c ,①当a 2+b 2>c 2时,△ABC 为锐角三角形;②当a 2+b 2<c 2时,△ABC 为钝角三角形;③当a 2+b 2=c 2时,△ABC 为直角三角形.变式88.甲、乙两艘轮船同时从港口出发,甲以16海里/时的速度向北偏东75︒的方向航行,它们出发1.5小时后,两船相距30海里,若乙以12海里/时的速度航行,则它的航行方向为()A.北偏西15︒B.南偏西75°C.南偏东15︒或北偏西15︒D.南偏西15︒或北偏东15︒【答案】C【解析】【分析】先求出出发1.5小时后,甲乙两船航行的路程,进而可根据勾股定理的逆定理得出乙船的航行方向与甲船的航行方向垂直,进一步即可得出答案.【详解】解:出发1.5小时后,甲船航行的路程是16×1.5=24海里,乙船航行的路程是12×1.5=18海里;∵222241857632490030+=+==,∴乙船的航行方向与甲船的航行方向垂直,∵甲船的航行方向是北偏东75°,∴乙船的航行方向是南偏东15°或北偏西15°.故选:C .【点睛】本题考查了勾股定理的逆定理和方位角,属于常考题型,正确理解题意、熟练掌握勾股定理的逆定理是解题的关键.题型九勾股定理与折叠问题例9.如图,矩形纸片ABCD 中,AB =CD =4,AD =BC =8,∠BAD =∠B =∠C =∠D =90°,将纸片沿EF 折叠,使点C 与点A 重合,使点G 与点D 重合.(1)求证:AE =AF ;(2)求GF 的长.(1)详见解析;(2)3【分析】(1)根据翻折的性质可得AEF CEF ∠=∠,根据两直线平行,内错角相等可得∠=∠AFE CEF ,然后求出AEF AFE ∠=∠,根据等角对等边可得AE AF =;(2)根据翻折的性质可得AE CE =,设AE CE x ==,则8BE x =-,再根据勾股定理有:2224(8)x x =+-,于是有5AE AF ==,进而得到3GF FD ==.【详解】解:(1)由翻折的性质得,AEF CEF ∠=∠,矩形ABCD 的对边//AD BC ,AFE CEF ∴∠=∠,AEF AFE ∴∠=∠,AE AF ∴=;(2)由翻折的性质得,AE CE =,设AE CE x ==,则8BE x =-,在Rt ABE ∆中,222AE AB BE =+,2224(8)x x ∴=+-,解得:5x =,5AE ∴=,又由(1)可知,5AF =,853FD AD AF ∴=-=-=,由翻折的性质得,3GF FD ==.【点睛】本题考查了翻折变换的性质,矩形的性质,勾股定理,熟记各性质并作利用勾股定理列方程求出AE 的长度是解题的关键.变式99.如图,在Rt ABC 中,90,5,8ACB AC BC ∠=︒==,点D 是边BC 的中点,点E是边AB 上的任意一点(点E 不与点B 重合),沿DE 翻折DBE 使点B 落在点F 处,连接AF ,则线段AF 长的最小值是()A.2B.4-C.3D.4-【答案】B【解析】【分析】连接AD ,以D 为圆心,以CD 为半径画圆,交AD 于G ,根据题意可知点F 在D 上,当G 和F 重合时AF 有最小值,然后利用勾股定理计算长度即可.【详解】解:连接AD ,以D 为圆心,以CD 为半径画圆,交AD 于G ,根据题意可知点F 在D 上,当G 和F 重合时AF 有最小值,∵点D 是边BC 的中点,∴142CD GD BC ===,在Rt △ACD 中AD =∴4AG AD GD =-=.故选:B【点睛】本题主要考查圆的性质和勾股定理,能够找到点F 的运动轨迹是解题的关键.题型十最短距离问题例10.如图,台阶A 处的蚂蚁要爬到B 处搬运食物,它爬的最短距离是_____.25【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.【详解】解:如图所示:台阶平面展开图为长方形,根据题意得:20AC =,55515BC =++=,则蚂蚁沿台阶面爬行到B 点最短路程是此长方形的对角线长.由勾股定理得:222AB AC BC =+,即2222015AB =+,∴25AB =,故答案为:25【点睛】本题主要考查了平面展开图—最短路径问题,用到台阶的平面展开图,只要根据题意判断出长方形的长和宽即可解答.变式1010.如图,正方形ABCD ,AB 边上有一点E ,3AE =,1EB =,在AC 上有一点P ,使为EP BP +最短.则最短距离EP BP +为_________.【答案】5【解析】【分析】连接DE ,交直线AC 于点P ,根据四边形ABCD 是正方形可知B 、D 关于直线AC 对称,所以DE 的长即为EP+BP 的最短距离,再根据勾股定理即可得出结论.【详解】连接DE,交直线AC于点P,∵四边形ABCD是正方形,∴B、D关于直线AC对称,∴DE的长即为EP+BP的最短距离,∵AE=3,EB=1,∴AD=AB=AE+BE=4,∴5==.故答案为:5.【点睛】本题考查了轴对称-最短路线问题、正方形的性质以及勾股定理的运用,熟知两点之间线段最短是解答此题的关键.实战练11.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M、C两点间的距离为()A0.5km A.0.6km B.0.9km C.1.2km【答案】D【解析】【详解】根据直角三角形斜边上的中线等于斜边的一半即可求得距离为1.2km.故选D视频12.如图,在Rt △ABC 中,∠C =90︒,AC =4,BC =3,把Rt △ABC 绕着点A 逆时针旋转,使点C 落在AB 边的C ′上,C'B 的长度是()A.1B.32C.2D.52【答案】A【解析】【分析】首先由勾股定理求出AB =5,再由旋转的性质得出4AC AC '==,从而可求出BC '的长.【详解】解:在Rt △ABC 中,∠C =90︒,AC =4,BC =3,∴222AB AC BC =+∴5AB ===由旋转的性质得,4AC AC '==∴541C B AB AC ''=-=-=故选:A .【点睛】此题主要考查了旋转的性质和勾股定理的运用,运用勾股定理求出AB =5是解答此题的关键.13.下列各组数中不是勾股数的是()A.3,4.5B.6.8.10C.5,12.13D.4,5,6【答案】D【解析】【分析】欲判断是否为勾股数,必须根据勾股数是正整数,同时还需满足两小边的平方和等于最长边的平方.【详解】解:A 、32+42=25=52,是勾股数,此选项不符合题意;B 、62+82=100=102,是勾股数,此选项不符合题意;C 、52+122=169=132,是勾股数,此选项不符合题意;D 、42+52=41≠62,不是勾股数,此选项符合题意.故选:D .【点睛】此题主要考查了勾股数:满足a 2+b 2=c 2的三个正整数,称为勾股数.注意:①三个数必须是正整数,例如:2.5、6、6.5满足a 2+b 2=c 2,但是它们不是正整数,所以它们不是勾股数.②一组勾股数扩大相同的整数倍得到三个数仍是一组勾股数.③记住常用的勾股数再做题可以提高速度.如:3,4,5;6,8,10;5,12,13;…14.满足下列条件的三角形:①三边长之比为3:4:5;②三内角之比为3:4:5;③n 2﹣1,2n ,n 2+1;1+1-,6.其中能组成直角三角形的是()A.①③B.②④C.①②D.③④【答案】A【解析】【分析】欲求证是否为直角三角形,若已知三边长,只要验证两小边的平方和是否等于最长边的平方;若已知三个角的度数,只要验证是否存在直角即可.【详解】①三边长之比为3:4:5;则有222(3)(4)(5)x x x +=,为直角三角形;②三个内角度数之比为3:4:5,则各角度数分别为31804512︒⨯=︒,41806012︒⨯=︒,51807512︒⨯=︒,不是直角三角形;③22222(1)(2)(1)n n n -+=+ ,∴是直角三角形;④116++=<,∴构不成三角形.故选:A .【点睛】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.15.《九章算术》是我国古代的数学名著,书中有“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺.问折者高几何?意思是:一根竹子,原高一丈(一丈10=尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部3尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x 尺,则可列方程为()A.2223(1)x x -=- B.2223(10)x x -=-C.2223(1)x x +=- D.2223(10x)x +=-【答案】D【解析】【分析】根据勾股定理列方程解答.【详解】解:设折断处离地面的高度为x 尺,则斜边为(10-x )尺,根据勾股定理得:2223(10x)x +=-,故选:D .【点睛】此题考查勾股定理的实际应用,正确理解题意得到直角三角形确定三边的关系式是解题的关键.16.如图所示,将一根长为24cm 的筷子,置于底面直径为5cm ,高为12cm 的圆柱形水杯中,设筷子露在外面的长为hcm ,则h 的取值范围是()A.0<h ≤11B.11≤h ≤12C.h ≥12D.0<h ≤12【答案】B【解析】【分析】根据题意画出图形,先找出h的值为最大和最小时筷子的位置,再根据勾股定理解答即可.【详解】解:当筷子与杯底垂直时h最大,h最大=24﹣12=12cm.当筷子与杯底及杯高构成直角三角形时h最小,如图所示:此时,AB=13cm,∴h=24﹣13=11cm.∴h的取值范围是11cm≤h≤12cm.故选:B.【点睛】本题考查了勾股定理的实际应用问题,解答此题的关键是根据题意画出图形找出何时h有最大及最小值,同时注意勾股定理的灵活运用,有一定难度.17.某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q、R处,且相距30海里.如果知道“远航”号沿东北方向航行,则“海天”号沿()方向航行.A.西南B.东北C.西北D.东南【答案】C【解析】【分析】根据路程=速度×时间分别求得PQ、PR的长,再进一步根据勾股定理的逆定理可以证明三角形PQR是直角三角形,从而进行分析求解.【详解】解:根据题意得PQ=16×1.5=24(海里),PR=12×1.5=18(海里),QR=30(海里).∵242+182=302,即PQ2+PR2=QR2,∴∠QPR=90°.由“远航号”沿东北方向航行可知,∠1=45°,则∠2=45°,即“海天”号沿西北方向航行.故选:C.【点睛】本题考查勾股定理的应用,解题的关键是能够根据勾股定理的逆定理发现直角三角形进行解答.18.如图,在 ABC中,AB=8,BC=6,AC=10,D为边AC上一动点,DE⊥AB于点E,DF⊥BC于点F,则EF的最小值为()A.5B. 4.8C.3D.2.4【答案】B【解析】【分析】根据三个角都是直角的四边形是矩形,得四边形EDFB是矩形,根据矩形的对角线相等,得EF=BD,则EF的最小值即为BD的最小值,根据垂线段最短,知:BD的最小值即等于直角三角形ABC斜边上的高.【详解】如图,连接BD.∵在△ABC中,AB=8,BC=6,AC=10,∴AB 2+BC 2=AC 2,即∠ABC =90°.又∵DE ⊥AB 于点E ,DF ⊥BC 于点F ,∴四边形EDFB 是矩形,∴EF =BD .∵BD 的最小值即为直角三角形ABC 斜边上的高,即4.8,∴EF 的最小值为4.8,故选:B .【点睛】此题综合运用了勾股定理的逆定理、矩形的判定及性质、直角三角形的性质,要能够把要求的线段的最小值转换为便于分析其最小值的线段.19.如图,在四边形ABCD 中,1AB BC ==,CD =,AD =,AB BC ⊥,则四边形ABCD 的面积是()A. 2.5B.3C. 3.5D.4【答案】A【解析】【分析】如下图,连接AC ,在Rt △ABC 中先求得AC 的长,从而可判断△ACD 是直角三角形,从而求得△ABC 和△ACD 的面积,进而得出四边形的面积.【详解】如下图,连接AC∵AB=BC=1,AB ⊥BC∴在Rt △ABC 中,,111122ABC S =⨯⨯=∵,又∵(222+=∴三角形ADC 是直角三角形∴122ADC S == ∴四边形ABCD 的面积=12+2=52故选:A .【点睛】本题考查勾股定理的逆定理,遇到此类题型我们需要敏感一些,首先就猜测△ADC 是直角三角形,然后用勾股定理逆定理验证即可.20.某高速公路的同一侧有A ,B 两个城镇,如图所示,它们到高速公路所在直线MN 的距离分别为2km AE =,3km BF =,12km EF =,要在高速公路上E 、F 之间建一个出口Q ,使A 、B 两城镇到Q 的距离之和最短,在图中画出点Q 所在位置,并求出这个最短距离.【答案】见解析,13km【解析】【分析】作点B 关于MN 的对称点C ,连接AC 交MN 于点Q ,连接QB ,此时QA+QB 的值最小.作AD ⊥BC 于D ,在Rt △ACD 中,利用勾股定理求出AC 即可;【详解】解:作点B 关于MN 的对称点C ,连接AC 交MN 于点Q ,则点Q 为所建的出口;此时A 、B 两城镇到出口Q 的距离之和最短,最短距离为AC 的长.作AD BC ⊥于D ,则90ADC ∠=︒,AE ⊥MN ,BF ⊥MN∴四边形AEFD 为矩形∴12AD EF ==,2DF AE ==在t R ADC 中,12AD =,5DC DF CF =+=,∴由勾股定理得:13AC ===∴这个最短距离为13km .【点睛】本题考查作图-应用与设计,轴对称-最短问题、勾股定理等知识,解题的关键是学会利用轴对称解决最短问题,学会添加常用辅助线,构造直角三角形解决问题.培优练21.台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB 由点A 行驶向点B ,已知点C 为一海港,且点C 与直线AB 上两点A ,B 的距离分别为300km 和400km ,又AB=500km ,以台风中心为圆心周围250km 以内为受影响区域.(1)海港C 受台风影响吗?为什么?(2)若台风的速度为20km/h,台风影响该海港持续的时间有小时.【答案】(1)海港C受台风影响,理由见解析;(2)7.【解析】【分析】(1)根据勾股定理的逆定理得出△ABC是直角三角形,利用等面积法得出CD的长,从而可得海港C是否受台风影响;(2)根据勾股定理得出ED以及EF的长,进而得出台风影响该海港持续的时间.【详解】解:(1)海港C受台风影响.理由:如图,过点C作CD⊥AB于D,∵AC=300km,BC=400km,AB=500km,∴AC2+BC2=AB2.∴△ABC是直角三角形.∴AC•BC=CD•AB∴CD=240(km)∵以台风中心为圆心周围250km以内为受影响区域,∴海港C受到台风影响.(2)当EC=250km,FC=250km时,正好影响C港口,∵ED=70(km)∴EF=140km∵台风的速度为20km/h,∴140÷20=7(小时)即台风影响该海港持续的时间为7小时.故答案为:7.【点睛】本题考查了勾股定理及逆定理的应用,解答此类题目的关键掌握勾股定理及其逆定理并构造直角三角形,利用勾股定理解决问题.。
新苏科版八年级上册初中数学 2-5 课时3 直角三角形斜边上的中线等于斜边长的一半 教学课件

所以△EFM 的周长=5+4+4=13.
拓展与延伸
如图,已知 Rt△CDE ≌ Rt△ACF,则∠DCE + ∠ACF =___9_0_°__,即 ∠ACB=__9_0_°___. ① 设小方格的边长为 1 ,则 AB=___1_0__; ② 取 AB 的中点 M ,连接 CM,则 CM=___5____, 理由是 直角三角形斜边上的中线等于斜边的一半 .
2
等于斜边的一半).
新课讲解
练一练
在 Rt△ABC 中,如果斜边 AB 为 4 cm,那 么斜边上的中线 CD =___2___cm.
课堂小结
定理 直角三角形斜边上的中线等于斜边的一半.
当堂小练
如图,在 Rt△ABC 中,∠ACB = 90°,CA=CB,如果 斜边 AB= 5cm,那么斜边上的高CD=____2_.5____cm.
新课导入
你能用折纸的方法将一个直角三角形分成两个等腰三角形吗?
新课导入
1.任意剪出一张直角三角形纸片(如图1).
你还有其 他发现吗?
图1
图2
图3
2.剪得的纸片是否能折成图2的形状?
3.△ACD 与 △BCD 为什么是等腰三角形?请说明理由.
新课讲解
知识点1 直角三角形斜边上的中线等于斜边长的一半
在直角三角形中,30°的内角所对的直角边等于 斜边的一半.
新课讲解
证明:如图,作斜边上的中线 CD.
∵∠ACB = 90°,∠A=30°,
∴∠B=60°.
∵∠ACB = 90°,CD是斜边上的中线,
∴CD
=
1 2
AB
=BD.
∴△BCD 是等边三角形(有一个角是60°的
小学数学四年级 第三讲 三角形

小学数学四年级第三讲三角形(1).三角形的定义:由三条线段围成的图形(每相邻两条线段的端点相连)叫做三角形(2).三角形有三个顶点,三条边和三个角。
从三角形的一个顶点到它的对边做一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。
为了表达方便,用字母A,B,C分别表示三角形的三个顶点,这个三角形可以表示成三角形ABC。
(3).三角形具有稳定的特性,这一特性在生活中有着广泛的应用(4).三角形边的关系:三角形任意两边的和大于第三边,如果用a,b,c表示三角形三条边的长度,则有:a+b>c;a+c>b;b+c>a。
(5).认识几种三角形锐角三角形:三个角都是锐角的三角形直角三角形:有一个角是直角的三角形钝角三角形:有一个角是钝角的三角形(6).三角形的分类:(1)按角分有:锐角三角形,直角三角形和钝角三角形。
(2)按边分有:不等边三角形和等腰三角形,其中等腰三角形中还包括三条边都相等的等边三角形。
(7).等腰三角形各部分的名称;在等腰三角形里,相等的两条边叫做腰;另一条边叫做底;两腰的夹角叫做顶角;底边上的两个角叫做底角。
等腰三角形的两个底角相等。
(8).三角形的内角和:任何三角形三个内角的和都是180度。
一个三角形,已知两个角的度数,可以根据“三角形的内角和是180度”求出第三个角的度数。
(9).用三角形拼四边形两个完全相同的三角形可以拼成一个平行四边形;两个完全相同的直角三角形可以拼成一个长方形;两个完全相同的等腰直角三角形可以拼成一个正方形;三个完全相同的三角形可以拼成一个梯形。
一:三角形内角和定理的应用。
二:三角形三边关系的应用,及画钝角三角形高。
1.两个椭圆圈重合的部分应是什么三角形?答案:等腰直角三角形2.在能组成的三角形的三个角后面画“√”。
1.900500400()√2.500500500()3.1200300300()√4.1000320190()5.600600600()√3.在能组成三角形的三条线段后面画“√”。
第3讲直角三角形的性质应用(2012)

第3讲 直角三角形与勾股定理一、内容提要1、理解直角三角形的有关概念;2、掌握直角三角形中两锐角互余的性质,会根据一个角、两个角的大小关系来判定直角三角形;3、掌握直角三角形斜边上的中线等于斜边的一半的性质和直角三角形全等的HL 判定定理的应用;其它性质:(1)在直角三角形中,如果一个锐角等于30°,则它所对的直角边等于斜边的一半;(2)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角为30°. 4、掌握勾股定理及逆定理的应用二、热身练习 【A 】组题1. 1. 下列说法错误的是(下列说法错误的是(下列说法错误的是( ))A.A.有一个外角是锐角的三角形是钝角三角形有一个外角是锐角的三角形是钝角三角形有一个外角是锐角的三角形是钝角三角形B. B. B.有两个角互余的三角形是直角三角形有两个角互余的三角形是直角三角形有两个角互余的三角形是直角三角形C.C.直角三角形只有一条高直角三角形只有一条高直角三角形只有一条高D. D. D.任何一个三角形中,最大角不小于任何一个三角形中,最大角不小于60度 2.如图3,在△ABC 中,∠C=90°,BC=6,D,E 分别在AB,AC 上,将△ABC 沿DE 折叠,使点A 落在点A ′处,若A ′为CE 的中点,则折痕DE 的长为(为( ) A .21B .2 C .3 D .4 3.如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6m 和8m.按照输油中心O 到三条支路的距离相等来连接管道,则O 到三条支路的管道总长(计算时视管道为线,中心O 为点)是(为点)是( )A2m B.3m C.6m D.9m 4.若△.若△ABC ABC 三边长a,b,c 满足满足|a+b |a+b |a+b--7|+|a 7|+|a--b -1|+1|+((c -5)2=0=0,,则△则△ABC ABC 是(是( )) A .等腰三角形.等腰三角形 B B B.等边三角形.等边三角形.等边三角形 C C C.直角三角形.直角三角形.直角三角形 D D D.等腰直角三角形.等腰直角三角形.等腰直角三角形 5、如图,△、如图,△ABC ABC 中,∠中,∠C=90C=90C=90°,°,°,AB AB 的中垂线DE 交AB 于E ,交BC 于D ,若AB=10AB=10,,AC=6AC=6,则△,则△ACD 的周长为(的周长为( )) A 、16 B 16 B、、14 C 14 C、、20 D 20 D、、186、已知直角三角形的两边长为3cm 和4cm 4cm,则斜边上的中线长是,则斜边上的中线长是,则斜边上的中线长是 cm cm cm,斜边上的高为,斜边上的高为,斜边上的高为7、有一块田地的形状和尺寸如图所示,则它的面积为、有一块田地的形状和尺寸如图所示,则它的面积为O (第3题图)题图)的值是三、例题分析:例1、如图,用硬纸板做成四个全等的直角三角形,两直角边长分别是6 EFF BD CEAcC D A C E 第5题 13 3 4 第8题★★例4、某数学兴趣小组开展了一次活动,过程如下:、某数学兴趣小组开展了一次活动,过程如下:设∠BAC=q (0°<q<90°).现把小棒依次摆放在两射线AB,AC之间,并使小棒两端分别落在两射线上. 活动一:活动一:如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在两端点处互相垂直,A1A2为第1根小棒. 数学思考:数学思考:(1)小棒能无限摆下去吗?答:)小棒能无限摆下去吗?答: .(填“能”或“不能”)(2)设AA1=A1A2=A2A3=1. ①q= 度;度;②若记小棒A2n-1A2n的长度为a n(n为正整数,如A1A2=a1,A3A4=a2,),求此时a2,a3的值,并直接写出a n(用含n的式子表示). 图甲图甲活动二:活动二:如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2= AA1. 数学思考:数学思考:(3)若已经向右摆放了3根小棒,则1q= ,2q= ,3q= ;(用含q的式子表示)式子表示)(4)若只能..摆放4根小棒,求q的范围. AEFBCDMN 第3题图乙图乙四、思维提升 【B 】组题1、如图,△ABC 是一个边长为2的等边三角形,AD 0⊥BC ,垂足为点D 0.过点D 0作D 0D 1⊥AB ,垂足为点D 1;再过点D 1作D 1D 2⊥AD 0,垂足为点D 2;又过点D 2作D 2D 3⊥AB ,垂足为点D 3;……;这样一直作下去,得到一组线段:D 0D 1,D 1D 2,D 2D 3,……,则线段D n-1D n 的长为_ _ (n 为正整数).2、在Rt ABC △中,90A Ð=°,BD 平分ABC Ð,交AC 于点D ,且4,5AB BD ==,则点D 到BC 的距离是:的距离是:A.3 B.4 C.5 D.6 3、如图所示,90E F Ð=Ð=,B C Ð=Ð,AE AF =,结论:①EM FN =;②C D D N =;③FAN EAM Ð=Ð;④ACN ABM △≌△.其中正确的有.其中正确的有 A .1个 B .2个 C .3个 D .4个4.将一副直角三角板如图放置,使含30°角的三角板的段直角边和含45°角的三角板的一条直角边重合,则∠1的度数为______________.5、如图,以Rt Rt△△ABC 的三边a 、b 、c 为边向外作三个正方形,面积分别是S 1 ,S 2 , S 3,根据勾股定理可得,勾股定理可得,S S 1 +S 2=S 3DA C 第2题B BA第1题D 1 D 5 D 2D 3 D 4D 0C1第4题C A S 2 S3 S 1 B BC于E,,请说明AG=AB。
《直角三角形的性质和判定(Ⅱ)》第3课时参考课件

练习
1.判断由线段a、b、c组成的三角形是不是直角三角形?
(1)a=8 b=15 c=17;√ (2)a=10 b=24 c=25;× (3)a=4 b=5 c= 41 .√
由 a2 b2 c2 可知c>a,且c>b.
方法:只需看两条较小边长的平方和是
否等于最大边长的平方.
2.如图,在边长为4的正方形ABCD中,F为CD的中点,
分析: 作一个Rt△A´B´C´,使∠C´=90°,B´C´=a,A´C´=b,
A
证明:在Rt△A´B´C´ 中,
A'B'2 a2 b2
c
b
又∵a2 b2 c2
Ba
C
A´
c
b
B´ a
C´
A'B'2 c2 A'B' c
在△ABC和△A´B´C´中,
AC b A'B' BC a B'C'
如果三角形的三边长是a、b、c,满足 a2 b2 c2 ,
那么这个三角形是__直__角__三__角__形___.
A
探究
如图,在△ABC中,AB=c,BC=a,AC=b,
c
b
且a2 +b2 =c2,那么△ABC是直角三角形吗?
B
a
C
如果我们能够构造一个直角三角形,然 后证明△ABC与所构造的直角三角形全 等,即可得△ABC是直角三角形。
分析:根据勾股定理的逆定理,判断一个三角形是直角 形,只要看两条较短边的平方和是否等于最长边的平三角形。
(1)a=6,b=8,c=10; (2)a=12,b=15,c=20;
(3)a=13,b=5,c=12; 解 (1)∵62+82=100;102=100
第3讲 直角三角形全等的性质与判定(培优)

1.如图1,CD AB ⊥于D ,BE AC ⊥于E ,BE 与CD 交于O ,OB OC =,则图中全等的直角三角形共有()A .2对B .3对C .4对D .5对2.如图2,在Rt ABC ∆中,90ACB ∠=︒,30A ∠=︒,点D 是AC 上一点,将ABD ∆沿线段BD 翻折,使得点A 落在A '处,若28A BC '∠=︒,则(CBD ∠=)A .15︒B .16︒C .18︒D .20︒3.已知如图3,//AD BC ,AB BC ⊥,CD DE ⊥,CD ED =,2AD =,3BC =,则ADE ∆的面积为()A .1B .2C .5D .无法确定4.把两个同样大小的含45°角的三角尺按如图4所示的方式放置,其中一个锐角顶点与另一个的直角顶点重合于点A ,且另外三个锐角顶点B ,C ,D 在同一条直线上,若AB =,则CD 的长为()A .﹣1B .C .﹣1D .5.如图5,ABC ∆的角平分线CD 、BE 相交于F ,90A ∠=︒,//EG BC ,且CG EG ⊥于G ,下列结论:①2CEG DCB ∠=∠;②12DFB CGE ∠=∠;③ADC GCD ∠=∠;④CA 平分BCG ∠.其中正确的结论是()A .③④B .①②④C .①②③D .①②③④6.如图6,ABC ∆中,10AB AC ==,210BC =,点D 是AB 上一点,连接CD ,将BCD ∆沿CD 翻折得到△B CD ',若B D AC '⊥于点E ,则E 到CD 的距离为()A .6B .8C .455D .6557.如图7,在Rt ABC ∆中,90C ∠=︒,62B ∠=︒,D 、E 分别在AB 、AC 上,将ADE ∆沿DE 折叠得FDE ∆,且满足//EF AB ,则1∠=.8.如图8,已知∠AOB =45°,点P 在OA 边上,OP =8cm ,点M 、N 在边OB 上,PM =PN ,若MN =2cm ,则ON 的长为.9.如图9,△ACB 和△ECD 都是等腰直角三角形,CA =CB =6,CE =CD ,△ACB 的顶点A 在△ECD 的斜边DE 上,若AE :AD =1:2,则两个三角形重叠部分的面积为.10.如图10,在ABC ∆中,90BAC ∠=︒,AB AC =,D 为ABC ∆外一点,连接AD ,BD ,CD ,发现4AD =,2CD =且45ADC ∠=︒,则BD =.11.如图11,在等腰三角形ABC 中,4AC BC ==,30A ∠=︒,点D 为AC 的中点,点E 为边AB 上一个动点,连接DE ,将ADE ∆沿直线DE 折叠,点A 落在点F 处.当直线EF 与直线AC 垂直时,则AE 的长为.12.如图12,ABC ∆中60CAB ∠=︒,AD 平分CAB ∠交BC 于点D ,6AC AB +=,当ABD ∆为直角三角形时,线段AD 的值为.13.小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板按如图所示的位置摆放,A 、B 、D 三点在同一直线上,//EF AD ,90CAB EDF ∠=∠=︒,45C ∠=︒,60E ∠=︒,量得8DE =.(1)试求点F 到AD 的距离.(2)试求BD 的长.14.如图,在ABC ∆中,AC AB >,以点A 为圆心、AB 长为半径的弧交BC 于点D ,连接AD ,过点B 作BE AD ⊥,垂足为点E .(1)若10AB =,2DE =,求ABD ∆的面积;(2)若125AC =,20AD =,410CD =,求ABC ∆的面积.15.如图1,点A 、D 在y 轴正半轴上,点B 、C 分别在x 轴上,CD 平分ACB ∠与y 轴交于D 点,90CAO BDO ∠=︒-∠.(1)求证:AC BC =;(2)如图2,点C 的坐标为(4,0),点E 为AC 上一点,且DEA DBO ∠=∠,求BC EC +的长.16.在ABC ∆中,90BAC ∠=︒,AB AC =,AD BC ⊥于点D .(1)如图1,点M ,N 分别在AD ,AB 上,且90BMN ∠=︒,当30AMN ∠=︒,2AB =时,求线段AM 的长;(2)如图2,点E ,F 分别在AB ,AC 上,且90EDF ∠=︒,求证:BE AF =;(3)如图3,点M 在AD 的延长线上,点N 在AC 上,且90BMN ∠=︒,求证:2AB AN AM +=.17.在Rt ABC ∆中,90C ∠=︒,30B ∠=︒,10AB =,点D 是射线CB 上的一个动点,ADE ∆是等边三角形,点F 是AB 的中点,连接EF .(1)如图,当点D 在线段CB 上时,①求证:AEF ADC ∆≅∆;②连接BE ,设线段CD x =,线段BE y =,求y 关于x 的函数解析式及取值范围;(2)当15DAB ∠=︒时,求ADE ∆的面积.。
第3讲等腰(直角)三角形存在性处理策略

B第三讲等腰(直角)三角形存在性处理策略知识必备一、平面直角坐标系与两点间距离公式如图3-1-1,已知P 1(x 1,y 1),P 2(x 2,y 2),则P 1P 2=√(x 2−x 1)2+(y 2−y 1)2.证明:如图3-1-2,作系列“水平/竖直辅助线”,易知P 1G =MN =︱x 2− x 1︱,P 2G =P 1N −GN =︱y 2− y 1︱,故P 1P 2=√(x 2−x 1)2+(y 2−y 1)2.注1:为考虑全面,这里实施绝对值策略,即便两点位置发生变化,上述过程均成立. 注2:此结论用文字语言叙述为“平面直角坐标系中,任意两点之间的距离等于其横坐标之差与纵坐标之差的平方和的算术平方根” . 二、“三线合一”定理与勾股定理1.如图3-1-3,在等腰三角形ABC 中,若AB =AC ,则有AD 平分∠BAC ⇔AD ⊥BC ⇔ BD =CD ,即等腰三角形顶角的角平分线、底边上的高线以及底边上的中线重合,简称“三线合一”定理,其逆命题依旧成立.2.在RtΔABD 中,若∠ADB =90°,则有BD 2+AD 2=AB 2,即直角三角形两直角边的平方和等于斜边的平方,称为勾股定理,其逆命题依旧成立.3.值得一提的是,常利用“三线合一”定理,将等腰三角形转化为直角三角形解决问题,如图3-1-3,有cos ∠B =BD AB=BC 2AB,此结论常用于解决与等腰三角形相关的存在性问题.三、全等判定方法与确定性分析1.三边分别相等的两个三角形全等,简称“边边边”,记为“SSS ” .2.两边及其夹角分别相等的两个三角形全等,简称“边角边”,记为“SAS ” .图3-1-1 图3-1-2图3-1-33.全等是两个三角形之间的关系,若一个三角形具备“SSS ” 或“SAS ”等全等特征,则这个三角形是确定的,必可解.方法提炼一、“两圆一线法”与“两线一圆法”问题1:如图3-2-1,请借助尺规作图,在平面内找出所有的点C ,使△ABC 为等腰三 角形.问题2:如图3-2-2,请在平面内找出所有的点C ,使△ABC 为直角三角形.问题3:如图3-2-3,请在平面内找出所有的点C ,使△ABC 为等腰直角三角形. 二、代数解法(“SSS ”法)1.等腰三角形存在性问题前提:该三角形三边的平方为常数或者是关于某个参数的二次式. 步骤:①写出或设出三角形三个顶点的坐标; ②利用两点间距离公式,计算三角形三条边长的平方;③由等腰三角形的三边长(的平方)可以两两相等,需分三类,列方程求解; ④检验求出的点是否符合题意,即能否构成三角形.注:这里指平面直角坐标系中的存在性问题,若无坐标系,可利用勾股定理直接表述出三边(的平方),下同. 2.直角三角形存在性问题只有第③步分类标准不同,即以斜边为标准分三类,列方程求解,其他步骤同上.二、几何解法(“SAS ”法)1. 等腰三角形存在性问题前提:该三角形有一个不变的内角θ.图3-2-1图3-2-2图3-2-3步骤:①用同一个参数表示出该不变角相邻的两条边,如图3-2-5; ②以腰为标准分三类,列方程求解,具体如下:情形一:当定角θ为顶角时,如图3-2-6,有a =b ; 情形二:当定角θ为底角且b 为腰时,如图3-2-7,有cosθ=a 2b ; 情形三:当定角θ为底角且a 为腰时,如图3-2-8,有cosθ=b 2a. 2.直角三角形存在性问题法1:若直角三角形有一个不变的锐角θ,可狠抓不变角θ,利用其三角函数列式计算.法2:依托直角三角形,作“横平竖直”辅助线,造“一线三直角”,利用相似求解. 3.等腰直角三角形存在性问题方法:一般构造“一线三直角”全等,即“K 字型”全等.值得一提的是,以上问题,有时还可以结合导角、相似等转化手段进行求解.实战分析例1 (2016年陕西中考)如图3-3-1,在菱形ABCD 中,∠ABC =60°,AB =2,点P 是这个菱形内部或边上一点,若以点P 、B 、C 为顶点的三角形是等腰三角形,则P 、D (P 、D 两点不重合)两点间的最短距离为____________.B图3-2-5图3-2-6图3-2-7图3-2-8图3-3-1反思:“两圆一线法”可精准定位“两定一动”型等腰三角形存在性问题中动点的路径,若是直角三角形存在性问题,可借助“两线一圆法”精准作图,请看下面的变式.变式:如图3-3-3,在菱形ABCD中,∠ABC=120°,AB=2,点P是这个菱形外部的一点,若以点P、B、D为顶点的三角形是直角三角形,则P、C两点间的最短距离为__________.图3-3-4例2 如图3-3-5,已知点A(3,0),B(0,4),在坐标轴上找一点C,使△ABC为等腰三角形,求所有点C的坐标.图3-3-5反思:代数解法的最大优势是实现盲解盲算,若精准作图,利用“两圆一线法”找到C点所有位置,如图3-3-6,可直接口算出“两圆”与坐标轴的六个交点,而“一线”与坐标轴的两个交点可利用勾股定理求解.代数解法盲解盲算,“两圆一线”精准定位,两者各具优势,结合使用亦可,以数解形,以形助数,数形结合,百般为好.例3 (2014年苏州中考)如图3-3-8,二次函数y =a (x 2−2mx −3m 2)(其中a ,m 是常数,且a >0,m >0)的图像与x 轴分别交于点A 、B (点A 位于点B 的左侧),与y 轴交于点C (0,-3),点D 在二次函数的图像上,CD //AB ,连接AD .过点A 射线AE 交二次函数的图像于点E ,AB 平分∠DAE .(1) 用含m 的代数式表示a ; (2) 求证:ADAE为定值;(3) 设该二次函数图像的顶点为F ,探索:在x 轴的负半轴上是否存在点G ,连接GF ,以线段GF ,AD ,AE 的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G 即可,并用含m 的代数式表示该点的横坐标;如果不存在,请说明理由.反思:此类含参型二次函数问题属中考的热点压轴题型,需要学生具备一定的代数运算技能,以算代证,应引起重视.中考压轴题的问题设计,往往采用层层递进式的命题方式,解题需要不时“回头看” “没有代数解法是万万不能的,但代数解法也并不是万能的”,这也是部分学生经常做的傻事,遇到等腰(直角)三角形存在性问题,管他三七二十一,上来就是硬算、狂算,到头来一场空,算不下去也有可能,请谨记:“世界上没有绝对的通法.”图3-3-8下面请欣赏所谓的“几何解法” (一)显性的“不变角”例4 如图3-3-11,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8),抛物线y =ax 2+bx 过A 、C 两点.(1)求出抛物线的解析式;(2)动点P 从点A 出发沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD 向终点D 运动,速度均为每秒1个单位长度,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ,过点E 作EF ⊥AD 于点F ,交抛物线于点G ,连接EQ . ①求EG 的最大值;②在点P 、Q 运动过程中,判断有几个时刻使△CEQ 是等腰三角形?请求出相应的t 值.反思:所谓“几何解法”,就是“抓不变角”,再结合“三线合一”定理等,导比导边,需“眼中有角,心中有比”,即不变的角就是不变的比.图3-3-11例5 如图3-3-15,在△ABC 中,AB =AC ,点P ,D 分别是BC ,AC 边上的点,且∠APD =∠B .若AB =10,BC =16,当△APD 为直角三角形时,求BP 的长.反思:看似两种情形,实则算理一致,只需狠抓不变角,易于掌握,便于实施. 情形二,若不能着急计算,导角得出∠APC =90°,由“三线合一”定理可立秒.变式:如图3-3-18,△ABC 中,AB =AC ,点P ,D 分别为BC ,AC 边上的点(点P 不与B 、C 重合),且∠APD =∠B .若AB =10,BC =16,当△APD 为等腰三角形时,求BP 的长.反思:“眼中有角,心中有比”,利用三角比结合相似比,转化比例,列式计算.情形三,若能不着急计算,导角可得:∠APD =∠ADP >∠C ,引出矛盾,可直接舍去.(二)隐性的“不变角”例6 (2015年湖南怀化中考压轴题)如图3-3-22,已知Rt △ABC 中,∠C =90°,AC =8,BC =6,点P 以每秒1个单位的速度从A 向C 运动,同时点Q 以每秒2个单位的速度从A →B →C 方向运动,它们到C 点后都停止运动,设点P ,Q 运动的时间为t 秒. (1) 在运动过程中,求P ,Q 两点间距离的最大值;BB图3-3-15图3-3-18(2) 经过t 秒的运动,求△ABC 被直线PQ 扫过的面积S 与时间t 的函数关系式; (3) P 、Q 两点在运动过程中,是否存在时间t ,使得△PQC 为等腰三角形?若存在,求出此时的t 值;若不存在,请说明理由.反思:本题若采取“代数解法”也并非不可,但计算量颇大,很可能面临无功而返之窘境,并非方法不通,而是运算能力不到位.然“几何解法”需具备敏锐的洞察力,以算代证,发现不变角∠CPQ ,但比较隐藏,难以察觉,事实上,在第二大类中,依然有tan ∠CPQ =CQ CP=2不变.两种解法,各有裨益,孰轻孰重,不好权衡,建议皆会,合理使用,方可自如.例7(自编题)如图3-3-28,在平面直角坐标系中,已知点A (1,0)与直线l :y =43x ,点B 在x 轴正半轴上,且位于点A 的右侧,过点B 作x 轴的垂线,交直线l 于点C ,再过点C 作直线l 的垂线,交x 轴于点D ,在BC 上取点E ,使BE =BA ,连接OE 并延长,交CD 于点F .当△CEF 为等腰三角形时,求点C 的坐标.A图3-3-22图3-3-28反思:本题表面看上去是一个等腰三角形存在性问题,但通过导角转移,情形一变为“角处理”问题,情形二变为角平分线的处理问题,情形三转化为等腰三角形OCE的存在性问题,真可谓“问山不是山,转化妙无穷” .解题启示:先定性分析,后定量计算.即解题时,莫要着急求边长,可以先考虑导角分析,看看能不能转化成其他常规问题.这里等腰三角形存在性问题的特殊解法,可以与下一讲相似三角形存在性问题中所谓“AA”解法,类比巩固,将更加有趣.总结等腰(直角)三角形存在性问题常见的处理策略有:1.代数法→实现盲解盲算2.几何法→狠抓不变角,“眼中有角,心中有比”3.垂直处理→构造“一线三直角”,即“K字型”4.混和解法→综合以上各种解法,灵活使用.类题巩固1.如图3-4-1,在平面直角坐标系中,直线y=−x+4与x轴交于点A,与y轴交于点B,点C在直线AB上,在平面直角坐标系中求一点D,使得以O、A、C、D为顶点的四边形是菱形.图3-4-12.如图3-4-2,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,将△DEF绕点D旋转,点D与AB的中点重合,DE、DF分别交AC于点M、N.若△DMN为等腰三角形,求此时重叠部分(△DMN)的面积.图3-4-23.(2017年新疆乌鲁木齐市压轴题)如图3-4-3,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(-1,0),B(4,m)两点,且抛物线经过点C(5,0).(1)求该抛物线的解析式;(2)点P事抛物线上的一个动点(不与点A、点B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E.①PE=2ED时,求P点的坐标;②是否存在点P,使△BEC为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.图3-4-34.(2016年镇江中考)如图3-4-4,在菱形ABCD中,AB=6√5,tan∠ABC=2,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.(1)求证:BE=DF;(2)当t=________秒时,DF的长度有最小值,最小值等于________;(3)如图3-4-5,连接BD、EF,BD交EC、EF于点P、Q,当t为何值时,△EPQ 是直角三角形?图3-4-4图3-4-5。
第三节等腰三角形与直角三角形

第三节等腰三角形与直角三角形,河北8年中考命题规律)等边三角形的相关计算(2次)1.(2013河北13题3分)一个正方形和两个等边三角形的位置如图所示,若∠3=∠50°,则∠1+∠2=( ) A .90° B .100° C .130° D .180°(第1题图)(第2题图)2.(2009河北17题3分)如图,等边△ABC 的边长为1cm ,D 、E 分别是AB 、AC 上的点,将△ABC 沿直线DE 折叠,点A 落在点A′处,且点A′在△ABC 外部,则阴影部分图形的周长为________cm .直角三角形的相关计算(3次)3.(2011河北9题3分)如图,在△ABC 中,∠C =90°,BC =6,D 、E 分别在AB 、AC 上,将△ABC 沿DE 折叠,使点A 落在点A′处,若A′为CE 的中点,则折痕DE 的长为( )A .12B .2C .3D .4 (第3题图)(第4题图)4.(2012河北14题3分)如图,AB 、CD 相交于点O ,AC ⊥CD 于点C ,若∠BOD =38°,∠A 等于______. 5.(2008河北18题3分)如图(1)是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC =6,BC =5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图(2)所示的“数学风车”,则这个风车的外围周长是________.(第5题图)(第6题图)6.(2015唐山丰润区二模)如图,已知△ABC 为等边三角形,BD 为中线,延长BC 至E ,使CE =CD =1,连接DE ,则DE 等于( )A .32B . 3C .2 3D .127.(2015秦皇岛模拟)已知:一等腰三角形的两边长x ,y 满足方程组⎩⎪⎨⎪⎧2x -y =3,3x +2y =8,则此等腰三角形的周长为________.8.(2015唐山滦县一模)等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为______. 9.(2015唐山路北区二模)如图,在等边三角形ABC 中,点D 、E 分别在边BC 、AC 上,且DE ∥AB ,过点E 作EF ⊥DE ,交BC 的延长线于点F.(1)求∠F 的度数;(2)若CD =2,求DF 的长.,中考考点清单)等腰三角形的性质与判定1有两边相等的三角形是等腰三角形,相等的两边叫腰,第三边为底(1)等腰三角形两腰相等(即AB =AC);(2)等腰三角形的两底角________(即∠B =________);(3)等腰三角形是轴对称图形,有一条对称轴;(4)等腰三角形顶角的平分线、底边上的高和底边的中线互相重合;三边相等的三角形是等边三角形(1)等边三角形三边相等(即AB =BC =AC);(2)等边三角形三角相等,且每一个角都等于________(即∠A =∠B =∠C =________);(3)等边三角形内、外心重合;(4)等边三角形是轴对称图形,有三条对称轴;(5)面积:S △ABC =12BC ·AD(1)三边都相等的三角形是等边三角形;直角三角形的性质与判定(高频考点)直角三角形的性质与判定近8年考查3次,题型均为填空题,设问方式为:1.求角度;2.求线段长度;3.求周长.结合的背景有:1.与三角形折叠结合;2.以赵爽弦图为背景;3.利用三角形余角的性质求角度.3 有一个角等于90°的三角形叫做直角三角形(1)直角三角形的两个锐角之和等于______;(2)直角三角形斜边上的____等于斜边的一半(即BD =12AC);(3)直角三角形中________角所对应的直角边等于斜边的一半(即AB =12AC);(4)勾股定理:如果直角三角形两直角边分别为a ,b ,斜边为c ,那么a 2+b 2=c 2; (5)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°4.等腰三角形的相关计算【例1】如图,等腰△ABC 中,AB =AC ,AB 的垂直平分线MN 交AC 于点D ,且∠DBC =15°,则∠A =________.【解析】由线段垂直平分线定理知AD=BD,∴∠A=∠ABD,又∵AB=AC,∴∠ABC=∠ACB,设∠A=x,则2(x+15°)+x=180°,∴∠A=x=50°.【学生解答】1.(2014扬州中考)如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=()A.3B.4C.5D.6,(第1题图)),(第2题图)) 2.(2015舟山中考)如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,已知∠ADE=40°,则∠DBC =________.直角三角形的相关计算【例2】(2015宿迁中考)如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=4,CD=2,则AB的长是________.,(例2题图)),(例2题解图)) 【解析】如解图,过D作DE⊥AB,∵∠ACB=90°,AD平分∠BAC,∴DE=CD=2,在Rt△BDE中,DE=2,BD=4,∴∠B=30°,在Rt△ABC中,BC=CD+BD=6,∴AC=63=23,∴AB=23·2=4 3.【学生解答】3.(2015吉林中考)如图,△ABC中,∠C=45°,点D在AB上,点E在BC上.若AD=DB=DE,AE=1,则AC的长为()A. 5 B.2 C. 3 D. 24.如图,在△ABC 中,∠B =30°,BC 的垂直平分线交AB 于点E ,垂足为D ,CE 平分∠ACB ,若BC =2,则AC 的长为( )A . 3B .1C . 2D .2,中考备考方略)1.(2015秦皇岛二模)若实数x ,y 满足|x -4|+y -8=0,则以x ,y 的值为两边长的等腰三角形的周长是( ) A .12 B .16 C .16或20 D .202.(2014滨州中考)下列四组线段中,可以构成直角三角形的是( ) A .4,5,6 B .1.5,2,2.5 C .2,3,4 D .1,2,3 3.(2015秦皇岛11中模拟)如图,在△ABC 中,∠C =90°,∠B =30°,AD 是△BAC 的角平分线,DE ⊥AB ,垂足为E ,DE =1,则BC =( )A .3B .2C .3D .3+2(第3题图)(第4题图)4.(2015沧州中考)如图,在锐角三角形ABC 中,AD 、CE 分别是边BC 、AB 上的高,垂足分别是D 、E ,AD 、CE 相交于点O ,若∠B =60°,则∠AOE 的度数是( )A .60°B .50°C .70°D .80°5.(2015保定中考)在△ABC 中,若AC =15,BC =13,AB 边上的高CD =12,则△ABC 的周长为( ) A .32 B .42C .40或42D .32或426.(2015枣庄中考)如图,△ABC 中,AB =4,AC =3,AD 、AE 分别是其角平分线和中线,过点C 作CG ⊥AD 于F ,交AB 于G ,连接EF ,则线段EF 的长为( )A .12B .1C .72D .7 (第6题图)(第7题图)7.(2015吉林中考)如图,△ABC 中,∠C =45°,点D 在AB 上,点E 在BC 上,若AD =DB =DE ,AE =1,则AC 的长为( )A . 5B .2C . 3D . 28.(2015聊城中考)如图,在△ABC 中,∠C =90°,∠A =30°,BD 是∠ABC 的平分线,若AB =6,则点D到AB 的距离是________.(第8题图)(第9题图)9.(2015陕西中考)如图,在△ABC 中,∠A =36°,AB =AC ,BD 是△ABC 的角平分线,若在边AB 上截取BE =BC ,连接DE ,则图中等腰三角形共有( )A .2个B .3个C .4个D .5个10.(2014德阳中考)如图,△ABC 中,∠A =60°,将△ABC 沿DE 翻折后,点A 落在BC 边上的点A′处,如果∠A′EC =70°,那么∠A′DE 的度数为________.11.(2015资阳中考)如图,在△ABC 中,∠ACB =90°,AC =BC =1,E 、F 为线段AB 上两动点,且∠ECF =45°,过点E 、F 分别作BC 、AC 的垂线相交于点M ,垂足分别为H 、G.现有以下结论:①AB =2;②当点E与点B 重合时,MH =12;③AF +BE =EF ;④MG·MH =12.其中正确结论为( )A .①②③B .①③④C .①②④D .①②③④(第11题图)(第12题图)12.(2015苏州中考)如图,在△ABC 中,CD 是高,CE 是中线,CE =CB ,点A 、D 关于点F 对称,过点F 作FG ∥CD ,交AC 边于点G ,连接GE.若AC =18,BC =12,则△CEG 的周长为________.13.(2015北京中考)如图,在△ABC 中,AB =AC ,AD 是BC 边上的中线,BE ⊥AC 于点E.求证:∠CBE =∠BAD.14.(2014承德2中模拟)如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.(1)求sin B的值;(2)如果CD=5,求BE的长.15.(2015菏泽中考)如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.(1)如下图,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;(2)如下图,E是直线BC上的一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数,若不是,请说明理由.。
《解直角三角形》第3课时教案

《解直角三角形》第3课时教案教学目标:1、进一步掌握解直角三角形的方法;2、比较熟练的应用解直角三角形的知识解决与仰角、俯角有关的实际问题;3、培养学生把实际问题转化为数学问题的能力。
教学重点:解直角三角形在测量方面的应用;教学难点:选用恰当的直角三角形,解题思路分析。
教学过程一、给出仰角、俯角的定义在本章的开头,我们曾经用自制的测角仪测出视线(眼睛与旗杆顶端的连线)与水平线的夹角,那么把这个角称为什么角呢?如右图,从下往上看,视线与水平线的夹角叫仰角,从上往下看,视线与水平线的夹角叫做俯角。
右图中的∠1就是仰角,∠2就是俯角。
二、例题讲解例1.如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高度。
分析:因为AB=AE+BE,AE=CD=1.20米,所以只要求出BE的长度,问题就得到解决,在△BDE 中,已知DE=CA=22.7米,∠BDE=22°,那么用哪个三角函数可解决这个问题呢?显然正切或余切都能解决这个问题。
例2.如图,A、B是两幢地平高度相等、隔岸相望的建筑物,B楼不能到达,由于建筑物密集,在A楼的周围没有开阔地带,为测量B楼的高度,只能充分利用A楼的空间,A楼的各层都可到达且能看见B楼,现仅有测量工具为皮尺和测角器(皮尺可用于测量长度,测角器可以测量仰角、俯角或两视线的夹角)。
(1)你设计一个测量B楼高度的方法,要求写出测量步骤和必需的测量数据 (用字母表示),并画出测量图形。
(2)用你测量的数据(用字母表示)写出计算B楼高度的表达式。
分析:如右图,由于楼的各层都能到达,所以A楼的高度可以测量,我们不妨站在A楼的顶层测B楼的顶端的仰角,再测B楼的底端的俯角,这样在Rt△ABD中就可以求出BD的长度,因为AE=BD,而后Rt△ACE中求得CE的长度,这样CD的长度就可以求出.请同学们想一想,是否还能用其他的方法测量出B楼的高度。
北师大版七年级下册第三章三角形讲义

三角形 1.认识三角形1、它的三个顶点分别是 ,三条边分别是 ,三个内角分别是 。
2、分别量出这三角形三边的长度,并计算任意两边之和以及任意两边之差。
你发现了什么?结论:三角形任意两边之和大于第三边三角形任意两边之差小于第三边例:有两根长度分别为5cm 和8cm 的木棒,用长度为2cm 的木棒与它们能摆成三角形吗?为什么?长度为13cm 的木棒呢?长度为7cm 的木棒呢? 二、稳固练习:1、以下每组数分别是三根小木棒的长度,用它们能摆成三角形吗?为什么?〔单位:cm 〕 〔1〕 1, 3, 3 〔2〕 3, 4, 7 〔3〕 5, 9, 13 〔4〕 11, 12, 22 〔5〕 14, 15, 302、已知一个三角形的两边长分别是3cm 和4cm ,则第三边长X 的取值范围是 。
假设X 是奇数,则X 的值是 。
这样的三角形有 个;假设X 是偶数,则X 的值是 , 这样的三角形又有 个3、一个等腰三角形的一边是2cm ,另一边是9cm ,则这个三角形的周长是 cm夯实基础1、填空:〔1〕当0°<α<90°时,α是 角; 〔2〕当α= °时,α是直角;〔3〕当90°<α<180°时,α是 角; 〔4〕当α= °时,α是平角。
2、如右图,∵AB ∥CE ,〔已知〕 ∴∠A = ,〔 〕∴∠B = ,〔 〕 〔第2题〕 二、探索练习:根据知道三角形的三个内角和等于180°,那么是否对其他的三角形也有这样的一个结论呢?〔提出问题,激发学生的兴趣〕结论:三角形三个内角和等于180°〔几何表示〕 练习1: 1、判断:〔1〕一个三角形的三个内角可以都小于60°; 〔 〕 〔2〕一个三角形最多只能有一个内角是钝角或直角; 〔 〕 2、在△ABC 中,A BC a bcABCDE123〔1〕∠C=70°,∠A=50°,则∠B= 度; 〔2〕∠B=100°,∠A=∠C ,则∠C= 度; 〔3〕2∠A=∠B+∠C ,则∠A= 度。
奥数讲义-第3讲三角形-希望杯学生版

09预测考点:1. 全等三角形2. 勾股定理3. 轴对称、中心对称、平移旋转4. 等边三角形的性质5. 多边形及其内角和6. 正方形、矩形、平行四边形、菱形、梯形需掌握的基本知识点1. 三角形的三边关系定理、大边对大角、小边对小角;2. 求线段和、线段差的最小值、最大值问题;3. 勾股定理;4. 特殊直角三角形(其中一个锐角是30︒、45︒)的性质;5. 等腰三角形的性质;6. 等边三角形的性质;7. 全等三角形的判定与性质;8. 角平分线的性质就以及利用角平分线构造全等三角形; 9. 倍长中线的技巧;10. 特殊三角形(等边、等腰直角)中的旋转问题.一、三角形的三边关系【例1】 ⑴(2007年“希望杯“试题)若三角形三边的长均能使代数式2918x x -+的值为零,则此三角第3讲希望杯专题——三角形|初二 第三讲 希望杯初赛特训班|2形的周长是( ).(A )9或18. (B )12或15 .(C )9或15或18. (D )9或12或15或18.⑵(第14届“希望杯”初试)如图,两点A 、B 在直线MN 外的同侧,A 到MN 的距离8AC =,B 到MN 的距离5BD =,4CD =,P 在直线MN 上运动,则PA PB -的最大值等于 .【例2】 ⑴(第20届希望杯培训题)设ABC ∆的三条边的长分别为a ,b ,c ,且代数式||a b c -+与2()a b c +-的值相等,则ABC ∆的形状是( )A .直角三角形B .等腰三角形C .等边三角形D .等腰直角三角形⑵(第19届希望杯)已知ABC ∆的三边长分别为a b c ,,,且a a b cb c b c a++=+-,则ABC ∆一定是( )A .等边三角形B .腰长为a 的等腰三角形C .底边长为a 的等腰三角形D .等腰直角三角形【例3】 100条线段的长度分别为1,2,3,…,99,100,从中取出一些线段,要使取出的线段中的任意三条都能构成一个三角形,问最多能取出多少条线段?二、三角形的内角和【例4】 (第20届希望杯培训题)若三角形的三个内角A ∠、B ∠、C ∠满足2A B ∠<∠和2C B ∠>∠,那么这个三角形是( ) A .钝角三角形 B .直角三角形 C .等腰三角形 D .锐角三角形【例5】 (第19届希望杯)如图,I 是ABC ∆的内心,且CA AI BC +=.若80BAC ∠=︒,则ABC ∠的大小为_______,AIB ∠的大小为________.ICBA三、全等三角形及图形的变换PCDB A MN【例6】 (第20届希望杯培训题)如图7,将ABC ∆沿DE 折叠,使点A 与BC 边的中点F 重合,有下面四个结论:①EF AB ∥且12EF AB =②AF 平分DFE ∠③12ADFE S AF DE =⋅四边形 ④2BDF FEC BAC ∠+∠=∠其中,一定成立的结论有( ) A .1个 B .2个 C .3个 D .4个【例7】 (第20届希望杯培训题)如图6,在ABC ∆中,90BAC ∠=︒,点O 是正方形BCDE 对角线的交点,则BAO ∠和CAO ∠的大小关系是( ) A .BAO CAO ∠>∠ B .BAO CAO ∠=∠C .BAO CAO ∠<∠D .无法确定的【例8】 (第16届“希望杯”2试)如图,正ABC ∆的边长为a ,D 是BC 的中点,P 是AC 边上的动点,连结PB 和PD 得到PBD ∆.求:⑴ 当点P 运动到AC 的中点时,PBD ∆的周长; ⑵ PBD ∆的周长的最小值.PC D BAPCDBA【例9】 (第20届希望杯培训题)In ABC ∆,12cm BC =, the area of the triangle is 227cm . Then theminimum of the perimeter of the triangle is ( ) A .35cm B .27cm C .(1245)cm + D .25cm(英汉词典:minimum 最小值;perimeter 周长)四、等腰三角形及直角三角形【例10】 (第20届希望杯培训题)如图9,ABC ∆是等腰三角形,且AB AC =,图 6O B C D EA 图 9ABCDE 图 7F A BDCOE|初二 第三讲 希望杯初赛特训班|2BCD ∆是等腰直角三角形,90BDC ∠=︒,AE BD ⊥交BD 的延长线于E ,则AE _______DE (填“>”、“<”或“=”).【例11】 (第14届“希望杯”初试)如图,ABC ∆中,5AC BC ==,80ACB ∠=︒,O 为ABC ∆中一点,10OAB ∠=︒,30OBA ∠=︒,则线段AO 的长是 .OCBA【例12】 ⑴ (2007年培训题)直角三角形三边长均为整数,其中一条直角边长为35,则它的周长的最大值是 ,最小值是 .⑵ (2007年“希望杯”试题)直角三角形有一条边长为11,另外两边的长是自然数,那么它的周长等于( ).(A )132. (B )121. (C )120. (D )111.【例13】 (第14届“希望杯”初试)如图,在四边形ABCD 中,90ABC ADC ∠=∠=︒,点E 、F 分别是对角线AC 、BD 的中点,则( )(A )EF BD ⊥ (B )AEF ABD ∠=∠ (C )1()2EF AB CD =+ (D )1()2EF AB CD =-【例14】 (第16届“希望杯”初试)如图,点D 是ABC ∆的边BC 上一点,如果2AB AD ==,4AC =, 且:2:3BD DC =,则ABC ∆是( )(A )锐角三角形 (B )直角三角形(C )钝角三角形 (D )锐角三角形或直角三角形【例15】 (第20届希望杯培训题)如图24,在Rt ABC ∆中,90BAC ∠=︒,M 、N 是BC 边的三等分点,已知4AM =,3AN =,则BC =____________.C D B A F E C D B ANM CBA习题1. 如图,ABC ∆中,90C ∠=︒,13EC AC =,13CD BC =,8BE =,6AD EC CD =+=,则ECDS ∆=_____习题2. a ,b ,c 是三角形的三边,它们满足223ac b c b abc +-=,若三角形的一个内角是120︒,那么::a b c = .习题3. 如图,ABC ∆的边AB 长为2,AB 边上的中线CD 长为1,AC 、BC 两边之和为31+,则ABC ∆的面积为 .习题4. (第20届希望杯培训题)一枚空对地导弹沿直线向地平面上的一个目标匀速飞去,运行方向与水平方向的夹角为30︒.地平面上离目标3km 远处有一拦截导弹,当空对地导弹飞行至拦截导弹的正上空时,拦截导弹开始出发,并成功拦截了空对地导弹.若两枚导弹的速度相等,拦截导弹也是沿直线飞行,那么两枚导弹撞击处离地面的高度等于___________km .习题5. (第20届希望杯培训题)如图11,在ABC ∆中,10AB =,AD 是BAC∠的角平分线,作CM AD ⊥于M ,且N 是BC 的中点,连接MN ,MN 的长是2,则AC 的长是__________.习题6. 如图,等腰Rt ABC ∆的直角边长为32,从直角顶点A 作斜边BC 的垂线交BC 于D ,再从1D 作12D D AC ⊥交AC 于2D ,再从2D 作23D D BC ⊥交BC 于3D ,…,则123456789______AD D D D D D D D D ++++=,12345678910____D D D D D D D D D D ++++=习题7. (第19届希望杯)如图,ABC ∆的面积为24,点D 是边BC 中点,点E是边AB 上的一个三等分点,CE 交AD 于点F ,则AEF ∆的面积为_________.E CDBACDB A 图 1121MN AB C D D 5D 4D 3D 2D 1C BA|初二 第三讲 希望杯初赛特训班|2FEDCBA习题8. (第20届希望杯培训题)在直角坐标系中,以点(11)A ,、(41)B ,、(15)C ,为顶点的三角形ABC的AC 、BC 边上各有一点P 、Q ,线段PQ 将ABC 的面积分为相等的两部分,则线段PQ 的长度最大可达到_________.图 371234OP 0P Q M C BAyx54321。
数学人教版八年级上册《第三节 直角三角形的性质》

数学人教版八年级上册《第三节直角三角形的性质》直角三角形是初中数学中比较重要的概念之一,它具有一些独特的性质。
本文将介绍《数学人教版八年级上册》第三节《直角三角形的性质》,包括直角三角形的定义、勾股定理、特殊的直角三角形以及与直角三角形相关的一些例题和应用。
通过学习本节内容,读者将能够更好地理解和运用直角三角形的性质。
直角三角形是指一个角为90度的三角形。
在直角三角形中,有一个特殊的定理,被称为勾股定理。
勾股定理表明,在直角三角形中,直角边的平方等于其他两条边平方的和。
例如,在一个直角三角形中,较短的直角边为3,较长的直角边为4,那么斜边的长度可以通过勾股定理计算得出,即斜边的长度为5。
勾股定理是直角三角形的重要性质,我们可以通过它解决一些实际问题,比如测量不可直接测量的距离或确定物体之间的距离和角度关系。
除了勾股定理,直角三角形还有一些特殊的性质。
我们先来看一下等腰直角三角形。
等腰直角三角形是指两条直角边长度相等的直角三角形。
在等腰直角三角形中,斜边的长度可以通过直角边的长度计算得出,即斜边长度为直角边长度的平方根乘以2。
比如,如果等腰直角三角形的直角边长为3,那么斜边的长度可以通过计算√3^2+3^2得出,即斜边的长度为3√2。
另一个特殊的直角三角形是45度角三角形。
45度角三角形是指一个角为45度的直角三角形。
在45度角三角形中,两条直角边长度相等,即两条直角边的长度均为斜边长度的平方根。
比如,如果45度角三角形的斜边长度为2,那么两条直角边的长度也为2的平方根。
45度角三角形经常在实际问题中出现,比如在建筑和几何图形设计中的应用。
了解了直角三角形的基本性质和特殊情况后,我们来看一些与直角三角形相关的例题和应用。
通过解答这些问题,我们可以更深入地理解直角三角形的性质。
例如,题目如下:已知一个直角三角形的直角边为3,斜边为5,求另一直角边的长度。
解答:根据勾股定理,直角边的长度可以通过计算√5^2-3^2得出,即直角边的长度为4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3讲 直角三角形【知识体系】直角三角形是一种特殊的三角形,它有许多重要的性质,如两个锐角互余,30°的角所对的直角边等于斜边的一半等. 另外, 如勾股定理与其逆定理,包括它们的发现、证明和应用,揭示了直角三角形三条边之间的数量关系,它可以解决许多直角三角形中的计算问题,是解直角三角形的主要依据之一,在生产生活实际中用途很大. 它不仅在数学中,而且在其他自然科学中也被广泛地应用.【热身训练】1. 如图,在△ABC 中,∠ACB=90°,∠ABC=25°,CD ⊥AB 于D ,则∠ACD =度.2. 如图,正方形ODBC 中,OC=1,OA=OB ,则数轴上点A 表示的数是 .3. 将一个有45°角的三角板的直角顶点放在一张宽为3cm 的纸带边沿上. 另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为 ( )A .3cmB .6cmC .cmD .4. 如图,在四个均由16 个小正方形组成的网格正方形中,各有一个格点三角形,那么这四个三角形中,与众不同的是 ,不同之处是 .5. 若,,a b c 分别是△ABC 的三条边长,且222610850a a b c c b -+-+=-,则这个三角形的形状是 .6. 如图,在△ABC 中,AB =3,AC =2,∠A =300,则△ABC 的面积等于 ( )A.B. 32C.D.DB CA230°第1题图 第2题图 第3题图DC B A BCA 第4题图 第6题图8.如图,将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm和的长方体无盖盒子中,则细木棒露在盒外面的最短长度是cm.9.如图,由7个形状、大小完全相同的正六边形组成网格,正六边形的顶点称为格点. 已知每个正六边形的边长为1,△ABC的顶点都在格点上,则ABCS∆=.【典型例题】例1如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:ADEBEλ=.特别地,当点D、E重合时,规定:0Aλ=.另外,对,B Cλλ 作类似的规定.(1)如图2,在△ABC中,∠C=90º,∠A=30º,求,A Cλλ ;(2)在每个小正方形边长均为1的4×4的方格纸(图3)上,画一个△ABC,使其顶点在格点(格点即每个小正方形的顶点)上,且2Aλ=,面积也为2;(3)若△ABC为锐角三角形, 则应该有:①△ABC中1Aλ<; ②△ABC中1Aλ=; ③△ABC中1Aλ>.CCDEBA图3图2图1简答:(1)作BC边上的中线AD,λA=CDBD=1 ; 过点C分别作AB边上的高CE和中线CF,λC=EFAF=12; (2)请同学自行完成;(3)③ .第7题图第8题图第9题图例2 如图,在由24个边长都为1的小正三角形的网格中, 点P 是正六边形的一个顶点,以点P 为直角顶点作格点直角 三角形(即顶点均在格点上的三角形),请你写出所有可能的 直角三角形斜边的长为多少?提示:通过作图,知以点P 为直角的三角形有四种情况: 如图,△PCB 、△PCA 、△PDB 、△PDA ,均是以点P 为直角的直角三角形. ∴所有可能的直角三角形斜边的长为4,2例3 在三角形ABC 中, ∠BAC = 75︒,∠B = 45︒,AB,求ABC 的面积.提示:作AD ⊥BC 于D , 则在等腰Rt ∆ABD 中, 可得AD =3,又∠CAD = 30︒, 在Rt ∆ADC 中,可得DC = 1, 则BC = 1 +3, ()2232321cm AD BC S ABC +==∆·.例4 已知,等腰三角形一边上的高是另一边的一半,求顶角的度数. 提示:本题有四种情况:(1)如图a 中底边上的高是腰长的一半,∵CD AC =12,∴∠A = 30︒,∠ACB = 120︒; (2)如图b 中一腰上的高是底边的一半,∵BD AB =12,∴∠A = 30︒,∠ACB = 120︒; (3)如图c 中一腰上的高是另一腰的一半,且高在∆ABC 外时,∵DB BC =12,∴∠BCD = 30︒,∠ACB = 150︒;(4)如图d 中,一腰上的高是另一腰的一半且高在∆ABC 内时,∵ DB BC =12,∴∠C = 30︒. 所以顶角的度数可能是30︒, 120︒或150︒.例5 据气象台预报,一强台风的中心位于宁波(指城区,下同)东南方向( 千米的海面上,目前台风中心正以20千米/时的速度向北偏西60°的方向移动,距台风中心50千米的圆形区域均会受到强袭击.已知宁海位于宁波正南方向72千米处,象山位于宁海北偏东60°方向56千米处.请问:宁波、宁海、象山是否会受这次台风的强袭击?如果会,请求出受强袭击的时间;如果不会,请说明理由.(为解决问题,须画出示意图,现已画出其中一部分,请根据需要,把图形画完整)(台风中心)(宁波)(宁海)PBA北仑镇海余姚慈溪奉化宁波宁海象山舟山解析:如图过P 作东西方向(水平)直线与AB (南北)延长线交于O ,延长台风中 心移动射线PQ 与AO 相交于M .由题易得108OA OP ==,36BO = ∵ ∠OPM=30°,∴ MO=OP tan30°=36+. ∴MO=OB . ∴M 与B 重合. ∴ 台风中心必经过宁海, 经过宁海的时间为502520⨯= (时). 如图C 为象山,过C 作CN ⊥PQ 于N ,由题意可得∠CBP=60°,CM=56,CN=56 sin60°=50<,∴ 象山会受到此次台风强袭击.求受袭击时间可先求以C 为圆心,50km 为半径的圆与 PQ相交的弦长等于205=(时) .过A 作AD ⊥PQ 于D ,sin 60AD AB =⋅50=>, ∴ 宁波不会遭受此次台风的强袭击.综上所述,宁波不会遭受此次台风的强袭击;宁海和象山会遭受此次台风的强袭击,受袭击时间分别为5小时和5小时 (约1小时13分).【独立尝试】1. 如图,在△ABC 中,三边,,a b c 的大小关系是 ( )A .a b c <<B .c a b <<C .c b a <<D .b a c <<BA第1题图 第5题图2. 如果直角三角形的三条边为2,4,a ,那么a 的取值可以有 ( )A. 0个B. 1个C. 2个D. 3个 3. 在Rt △ABC 中,∠C =90°,AC =9,BC =12,则点C 到AB 的距离是 ( )A .365 B .1225 C .94 D4. 等腰直角三角形的斜边长是有理数,则面积S 和周长C 分别是 ( )A. 都是有理数B. 都是无理数C. 有理数和无理数D. 无理数和有理数 5. 如图是一个三级台阶,它的每一级的长、宽、高分别为55寸、10寸和6寸,A 和B 是这个台阶的两个相对端点,A 点上有一只蚂蚁想到B 点去吃可口的食物,则它所走的最短路线长度是 ( )A .71寸B .73寸C .100寸D .103寸6. 如图,在△ABC 中,∠CAB =120°,AB =4,AC =2,AD ⊥BC ,D 是垂足. 则AD= ______ .7. 如图,已知在Rt △ABC 中,∠ACB =90°,AB =4,分别以AC 、BC 为直径作半圆,面积分别记为12,S S ,则12S S +等于 .8. 如图,已知图中每个小方格的边长为1,则点C 到AB 所在直线的距离等于 .9. 在等腰Rt △ABC 中,∠C =90°,AC =1,过点C 作直线l ∥AB ,F 是l 上的一点,且AB =AF ,则点F 到直线BC 的距离为 .10. 一个长方体箱沿斜面下滑,当木箱滑至如图位置时,AB =3m ,已知木箱高BE ,斜面坡角为300,求木箱端点E 距地面AC 的高度.第10题图第11题图11. 如图,在△ABC 中,AB=AC .M 、N 分别是AB 、AC 的中点,D ,E 为BC 上的点,连接DN ,EM .若AB=13cm ,BC =10cm ,DE =5cm ,求图中阴影部分的面积.第6题图 第7题图 第8题图12. 台风中心位于图中点P ,并沿东北方向PQ 移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米, B 市位于点P 的北偏东75°方向上,距离点P 320千米. (1)说明本次台风会影响B 市; (2)求这次台风影响B 市的时间. 【拓展提升】1. 设直角三角形的边长均是正整数,且周长和面积数值相等,则其三条边长可以是 ________ .2. 边长为整数的等腰三角形一腰上的中线将其周长分为1∶2的两部分,那么所有这些等腰三角形中,面积最小的三角形的面积是 .3. 勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC =90°,AB =3,AC =4,点D ,E ,F ,G ,H ,I 都在矩形KLMJ 的边上,则矩形KLMJ 的面积为 ( ) A .90 B .100 C .110 D .121图1图2CBAD E KFLG MHIJ4. 满足两条直角边长均为整数,且周长恰好等于面积的整数倍的直角三角形的个数有( )A. 1个B. 2个C. 3个D. 无穷多个5. 如图,长方体的底面边长分别为1cm 和3cm ,高为6cm .如果用一根细线从点A 开始经过4个侧面缠绕一圈到达点B ,那么所用细线最短需要 cm ;如果从点A 开始经过4个侧面缠绕n 圈到达点B ,那么所用细线最短需要 cm .di第5题图 第6题图6. 如图,在Rt △ABC 中,M 为斜边AB 上的中点,D ,E 分别在AC ,BC 边上,∠DME=90°. 求证:2222CD CE AD BE +=+.北QBP7. 如图,已知三角形ABC 是等腰直角三角形,AB=AC ,D 是斜边BC 的中点,E ,F 分别是AB ,AC 边上的点, 且DE DF ⊥,若BE=12,CF=5,求DEF ∆的面积.【挑战探索】【热身训练】【独立尝试】1—5. DCACB 6.7,提示:过C 作BA 延长线的垂线并利用等面积方法可求.7. 2π 8.9.10. 提示:连接AE ,在Rt △ABE 中,已知AB=3m ,,∴=.又∵tan ∠EAB=BE AB =3,∴∠EAB=30°. 在Rt △AEF 中,∠EAF=∠EAB+∠BAC=60°,∴EF=AE •sin ∠EAF===3m. 11. 提示:连接MN ,则MN 是△ABC 的中位线,∵BC=10cm ,∴MN=12BC=5cm. 过点A 作AF ⊥BC 于F ,则∵AB=AC=13cm ,BC=10cm ,∴BF=CF=5cm. ∴AF=12cm.图中阴影部分的三个三角形的底(MN ,MN ,DE )长都是5cm ,且高的和为12cm ,∴S 阴影=12×5×12=30cm 2. 12. 提示:(1)作BH ⊥PQ 于点H ,在Rt △BHP 中,由条件知, PB = 320, ∠BPQ = 30°, 得 BH = 320sin30° = 160 < 200. ∴本次台风会影响B 市.(2)如图, 若台风中心移动到P 1时, 台风开始影响B 市, 台风中心移动到P 2时, 台风影响结束. 由(1)得BH = 160,由条件得BP 1=BP 2 = 200,∴P 1P 2 =240. ∴台风影响的时间t = 24030= 8(小时). 【拓展提升】⎪⎪⎩⎪⎪⎨⎧=+=+n y x n x x 222 或⎪⎪⎩⎪⎪⎨⎧=+=+n y x n x x 222 ,解得⎪⎪⎩⎪⎪⎨⎧==3532n y n x 或⎪⎪⎩⎪⎪⎨⎧==334n y n x . ∵ 35322n n <⨯(舍去), ∴ 取⎪⎪⎩⎪⎪⎨⎧==334n y n x 其中n 是3的倍数.其面积2223663634321n n n n S =⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⨯⨯=∆.对于23663n S =∆,当0≥n 时,∆S 随着n 的增大而增大,故当3=n 时,463=∆S 取最小.3. C 提示:延长AB 交KF 于点O ,延长AC 交GM 于点P ,所以,四边形AOLP 是正方形,边长AO=AB+AC=7. 所以KL=10,LM=11,因此,矩形KLMJ 的面积为10×11=110.4. 提示:设直角三角形的两条直角边长为,a b (a b ≤),则12a b k ab +=⋅(a ,b ,k 均为正整数),化简,得(4)(4)8ka kb --=,所以4148ka kb -=⎧⎨-=⎩或4244ka kb -=⎧⎨-=⎩.解得1512k a b =⎧⎪=⎨⎪=⎩或234k a b =⎧⎪=⎨⎪=⎩或⎪⎩⎪⎨⎧===.8,6,1b a k 即有3组解.5. 10,6. 提示:延长DM 到N ,使MN=DM ,连结BN ∵AM=BM ,∠AMD=∠BMN ,∴△ADM ≌△BNM∴AD=BN ,∠A=∠ABN ,∴AC ∥BN ,∵∠C=90°,∴∠CBN=90°再连结EN ,则△EBN 为直角三角形. 由勾股定理得222BN BE EN +=,即222AD BE EN +=,在Rt △ECD 中,由勾股定理得222CD CE ED +=∵EM ⊥DN ,DM=MN ,EM=EM ,∴△EDM ≌△ENM ∴ED=EN ,故2222CD CE AD BE +=+.7. 提示:过D 点作DH AB ⊥于H 并连接AD ,显然17CF E B A D D A ≅∆→=∆;在Rt H AD ∆和Rt H ED ∆中利用勾股定理求出DE =2116924DEF S DE ∆∴==.【挑战探索】1. 提示:在AP 上取点D ,让AD BD =,容易证明BPD ∆是等腰三角形,即。
