关于镜像法与电轴法静电场课件
电磁场课件 Part8--镜像法(1)

Topic # 8—镜像法(method ofimages)Part1n镜像法n点电荷~无限大的接地导板系统n电轴~无限大接地导电平面系统的电场n电轴法 (广义镜像法)1n镜像法n定义The method of images is an analytical technique that involves replacing constantpotential surfaces with equivalent sources called image sources that generate the same fields.镜像法——用场域闭合边界外虚设的较简单的电荷分布来等效替代该边界上未知的较为复杂的电荷分布以简化原问题的分析和计算。
场域闭合边界—一般为导体组成等位面2n镜像法n适用场合The conducting boundaries that can be modeled inthis way include infinite planes, spheres, infinitecylinders, and wedges.34n 点电荷~无限大的接地导板系统 n Background对于大地上方输电线、雷电形成的电场,可以典型化为最 基本的问题:无限大接地导体上方点电荷激发的电场问题+q2s DP (x,y,z )1s he 导板¥r 2 0j Ñ=5n 点电荷~无限大的接地导板系统 n 分析—直接求解是否可能1. ? 不行,2. 已知场源分布,求3. 高斯定理?0 4 P qrj e = p E vd SE S · ò vv Ñ0 E S × 或 非单一媒质需要探索新的求解方法不通6n 点电荷~无限大的接地导板系统n 换一个角度考虑:考虑其边值问题20 in Dj Ñ= 1||0S j j == 导板表面 |0t E = 导板表面 211221 10 00 d d s C s s S S q n j j s e = ®® ¶ ====-= ¶ òò ÑÑ7n 点电荷~无限大的接地导板系统 n 能否找到较简单的等效模型?一对相距2h 位于e 0 单一媒质的上半空间的电场—仅考虑上半空间 q+ 2s 1s h0 e ¥e hq- 2 2 0j Ñ= xy o Er边值问题22 0 ()j Ñ= 在上半空间 12 |0S j = 0 | y n n E E e= = r r8n 点电荷~无限大的接地导板系统 n 能否找到较简单的等效模型?一对相距2h 位于e 0 单一媒质的上半空间的电场—仅考虑上半空间 边值问题22 0 ()j Ñ= 在上半空间 1 2 |0 S j = 0 | y n nE E e = = r r y =0的平面为等位面,且其电位为零9n 点电荷~无限大的接地导板系统 n 能否找到较简单的等效模型?一对相距2h 位于e 0 单一媒质的上半空间的电场—仅考虑上半空间 22122210 00 d d s C s s S S q n j j s e = ®® ¶ ====-= ¶ òò ÑÑ 在正点电荷处取同样“大小”的面元S 2,可近似认为该 面元为等位面,于是:q+ 2s 1s h0 e ¥e hq- 2 2 0j Ñ= xy o Er10n 点电荷~无限大的接地导板系统 n 比较边值问题一对相距2h 位于e 0 单一媒质的上半空间的电场原问题22 0 () j Ñ= 在上半空间 1 220 ||=0S y j j = =0 |0t y E = = 22122 210 00 d d s C s s S S q n j j s e = ®®¶ ====-= ¶ òò ÑÑ 20 in Dj Ñ= 1||0S j j == 导板表面 |0t E = 导板表面 21122110 00 d d s C s s S S q n j j s e = ®® ¶ ====-= ¶ òò ÑÑ 二者完全一样(y =0平面对应导板表面)11n 点电荷~无限大的接地导板系统 n 结论由唯一性定理可知,两者的解答 j =j 2注意适用区域:仅上半平面?为什么?计算导板上方的电场时,可以把导板上的感应电荷的影响 用一置于对称位置上的集中电荷等效由于引入的电荷位于原电荷对导板的镜像处—镜像法n点电荷~无限大的接地导板系统 n计算模型—原问题De导体j = x1ryo(,,0)P x yq+h1213n 点电荷~无限大的接地导板系统 n 计算模型—镜像法模型场中电场分布,等效于引入镜 像电荷q ,撤去 导板,整个空 间充满同一种 电介质的电场。
镜像法和电轴法课件

建立更加完善的理论体系,为镜像法和电轴法的进一步发展提供坚实的理论基础。
技术手段的创新与升级
探索新的技术手段和方法,提高 镜像法和电轴法的测量精度和稳
定性。
结合人工智能、机器学习等先进 技术,实现自动化、智能化的数
据处理和分析。
它可用于改善信号质量,提高接收机的灵敏度和抗干扰能力 ,从而提高通信系统的可靠性和稳定性。
02 电轴法介绍
电轴法的定义
电轴法是一种测量和分析电子元件中电场分布的方法,通过测量电场在某一方向 上的分量,可以推断出电场在该方向上的分布情况。
电轴法通过将电场分解为相互垂直的分量,分别测量每个分量的大小和方向,从 而全面了解电场分布。
镜像法的原理
镜像法基于镜像反转的原理,将输入 信号复制并反转,然后将反转后的信 号与原始信号混合,以消除噪声和其 他干扰。
通过调整反转信号的幅度和相位,可 以精确地抵消原始信号中的干扰成分 ,从而获得更加纯净的输出信号。
镜像法的应用场景
镜像法在通信系统雷达、声呐、无线电导航等领域有广泛 应用。
根据分析结果,判断待测 物体的质量、性能等,并 应用于实际生产中。
05 镜像法和电轴法的实际应 用案例
镜像法在物理学中的应用案例
光学镜像
通过使用透镜或反射镜, 将光线进行反射或折射, 形成光线的镜像。
电磁波传播
在电磁波传播过程中,通 过使用介质或反射面,使 得电磁波发生反射或折射, 形成电磁波的镜像。
镜像法和电轴法课件
目录
CONTENTS
• 镜像法介绍 • 电轴法介绍 • 镜像法和电轴法的比较 • 镜像法和电轴法的实验操作 • 镜像法和电轴法的实际应用案例 • 镜像法和电轴法的未来发展与展望
电动力学镜像法课件

03
理论框架完善
未来研究将进一步完善镜像法的理论框架,建立更严谨的数学和物理基
础,为解决复杂问题提供更有力的工具。
镜像法在其他领域的应用前景
光学领域
镜像法在光学领域有广泛的应用前景,如光子晶体、光子器件的 设计与模拟等。
生物医学工程
镜像法可用于模拟生物组织的电磁特性,为医学成像和诊断提供技 术支持。
镜像法在静电场中主要用于解决导体表面的电荷分布和电场分布问题。
详细描述
当一个带电体放置在导体附近时,导体表面的电荷分布会受到带电体的影响。通 过应用镜像法,可以计算出导体表面的电荷分布和电场分布,从而进一步分析带 电体与导体之间的相互作用。
镜像法在静磁场中的应用
总结词
镜像法在静磁场中主要用于解决磁力线和磁感应强度分布问题。
详细描述
电动力学在许多领域都有重要的应用。例如,无线通信依赖于电磁波在空间的传播,雷达通过发射电磁波并检测 其反射来探测目标,电子显微镜利用电磁场来控制电子束的传播和成像。此外,电动力学还在电力传输、电磁兼 容性、粒子加速器等领域有广泛应用。
03 镜像法在电动力学中的应用
镜像法在静电场中的应用
总结词
镜像法的计算步骤
确定原问题和镜像模型
根据实际问题,确定需要求解的原问 题和对应的镜像模型。
建立等效关系
根据镜像法的数学模型,建立镜像电 荷或镜像边界与原电荷或原边界之间 的等效关系。
求解等效问题
利用等效关系,求解等效的静电场或 静磁场问题。
计算结果分析
对计算结果进行分析,得出原问题的 解。
镜像法的计算实例
电动力学镜像法课件
目录
Contents
• 镜像法简介 • 电动力学基础 • 镜像法在电动力学中的应用 • 镜像法的计算方法 • 镜像法的优缺点分析 • 镜像法的发展前景
电磁场课件6镜像法、电轴法、电容

电磁场问题求解
• 电磁场问题可以分为电磁场分析(正问题)、逆问题 (含优化设计问题)和电磁场工程三个部分。
➢求解电磁场问题的方法,归纳起来可分为三大类,分别 是解析法、数值法和半解析数值法。
解析法包括积分法、分量变量法、镜像法、电轴法等 ; 数值计算方法包括有限元法(FEM)、时域有限差分法 (FDTD)、矩量法(MOM)和边界元法等 ; 半解析数值法是解析法和数值法的综合。
联立求解
q2 (b2 R2 ) q'2 (d 2 R2 ) 0 q'2 d q2b 0
得到
b R2 d
镜像电荷位置
q' b q R q 镜像电荷大小 dd
图1.7.4 球外的电场计算
球外任一点 P 的电位与电场为
p
q
4π 0r1
q'
4π 0r2
q
qR
EP 4π 0r12 er1 4π 0dr22 er2
1.7 镜像法与电轴法
1.7.1 镜像法
1.接地无限大导体平面上方点电荷的电场
2 0 0
s D dS q
(除 q 所在点外的区域) (导板及无穷远处)
(S 为包围 q 的闭合面)
2.正负点电荷在上半空间产生的电场
2 0
除 q 所在点外的区域
q q 0 4 0r 4 0r
中间对称面处
s D dS q
设镜像电荷 q'如图,球面电位
p
q
4π 0r1
q'
4π 0r2
0
图1.7.3 点电荷对接地导体球的镜像
r12 d 2 R2 2Rd cos r22 b2 R2 2Rb cos
将 r1, r2 代入方程 qr2 q 'r1 0,得
高中物理竞赛难点专题之电像法(共49张PPT)

q
q1 R
R
E 4 0 ( r 2 er dr12 er1 dr22 er2 )
不接地导体球面上的正负感应电荷的绝对值等于镜像电荷 q 吗? 为什么?
镜像法小结
镜像法的理论基础是静电场唯一性定理; 镜像法的实质是用虚设的镜像电荷替代未知电荷的分布,使 计算场域为无限大均匀介质; 镜像法的关键是确定镜像电荷的个数,大小及位置; 应用镜像法解题时,注意:镜像电荷只能放在待求场域以外 的区域。叠加时,要注意场的适用区域。
dq
dq
Ox
L
解:
dq dx
2L x 3L x
dq dx
dF
dxdx 40 (x x)2
F
3L
dx
2L
L 0
2dx 40 (x
x)2
2 4 0
ln
4 3
例题4. 球形金属空腔内外半径 a < b,带电 Q,腔内点电荷q,距球 心 r < a。求球心 O 点电位。
镜像法
几个实例:
求解位于接地导体板附近的点电荷产生的电位
非均匀感应电荷 q
等效电荷
q′
非均匀感应电荷产生的 电位很难求解,可以用 等效电荷的电位替代
接地导体球附近有一个点电荷,如图。
等效电荷
q
非均匀感应电荷产生的
q′
电位很难求解,可以用
等效电荷的电位替代
非均匀感应电荷
1.平面导体的镜像
镜像法最简单的例子:接地无限 大导体平面上方一个点电荷,根 据唯一性定理,导体平面上半空 间的电为分布应满足:
[q2 (b2 R2 ) q'2 (d 2 R2 )]
电动力学镜像法ppt课件

性,电势也应具有球对称性。当考虑较
r
远处场时,导体球可 视为点电荷。
2 0 (r a)
r 0
r3
(r 0) r , 0
B0 A
r
A
n r r 2
Q
0
r
dS
ra
0
A dS 0 A4 a 2
a2
a2
A Q
4 0
Q 4 0r
E
Q
(r a)
r Qr
2、导体内部电场为零;
3、导体表面上电场必沿法线方向,因此导体表面为 等势面,整个导体的电势相等。
设导体表面所带电荷面密度为σ,设它外面的介质电容率
为ε,导体表面的边界条件为
|s 常数
n s
Q dS dS
S
S n
En
三.静电场的能量
仅讨论均匀介质
1. 一般方程: 能量密度
本节主要内容
一、静电场的标势 二、静电势的微分方程和边值关系 三.静电场的能量
一、静电场的标势
在静止情况下,电场与磁场无关,
麦氏方程组的电场ห้องสมุดไป่ตู้分为
E 0
E
D 静电场的无旋性是它的一个重要特
性,由于无旋性,我们可以引入一
这两方程连同介质 的电磁 性质方程 D 是E 解决静
个标势来描述静电场,和力学中用 势函数描述保守力场的方法一样。
把单位正电荷由P1点移至 P2点,电场E对它所作的
功为
P2 E dl P1
这功定义为P1点和P2点的
电势差。若电场对
电荷做了正功,则电势
下降。由此
(P2 )
(P1 )
P2 P1
E
dl
第8讲 镜像法 ppt课件

(r a)
S
r
ra
4πa(a2
q(d 2 a2)
d 2 2ad cos )3
2
➢ 导体球面上的总感应电荷为
qin
S
S dS
q(d 2 a2 4πa
)
2π 0
π
0 (a2
a2 sindd d 2 2ad cos )3 2
a d
q
导体球面上的总感应电荷也与所设置的镜像电荷电量相等。
1 ( q q ) 4π R R
问题: d ? q ?
P
r
R
a
q
d
P
r
R
a
R' q
q'
d' d
第八讲 镜像法
三、导体球面的镜像
1、点电荷位于接地导体球面外
P
镜像电荷的确定
由镜像法原理:镜像电荷位于球内区域, a
且镜像电荷与原电荷共同作用使得在球
r
R
R' q
q'
面上电位为0,即:
d' d
1 [q q'] 0 ra 4 R R ' ra
特点:
• 在介质分界面上存在极化电荷分布 • 空间中任一点的电场由点电荷与极化电
荷共同产生。
z
q
1 h x
2
图1 点电荷与电介质 分界平面
问题:如何确定镜像电荷?
第八讲 镜像法
五、无限大介质分界平面的镜像
1、点电荷与无限大电介质分界平面的镜像
第八讲 镜像法
三、导体球面的镜像
2、点电荷位于接地导体球壳内
镜像电荷的确定
如图所示接地空心导体球壳的内半径 为a 、外半径为b,点电荷q 位于球壳内, 与球心相距为d ( d < a )。
电磁场 镜像法与电轴法(完美解析)

r
球面
0
设镜像电荷 q '如图,球面电位
q q' p 0 4 π 0 r1 4 π 0 r2
r1 d 2 R 2 2 Rd cos
2
图1.7.3 点电荷对接地导体球的镜像
r2 b 2 R 2 2 Rb cos
2
返 回
上 页
下 页
第 一 章
qh p=Dn 0 E 2 π(h 2 x 2 ) 3 / 2
地面上感应电荷的总量为 qh S p dS 0 2π(h2 x 2 )3/ 2 2πxdx
q
图1.7.2 地面电荷分布
返 回 上 页 下 页
第 一 章
静 电 场
2. 球面导体的镜像 点电荷位于接地导体球外的边值问题 (除q点外的空间) 2 0
q q' q' ' sin sin sin 2 2 2 4πr 4πr 4πr
2 2 1 2 q 解得 q ' q 和 q' ' 1 2 返 回 1 2
上 页
下 页
第 一 章
静 电 场
思考
1 中的电场由 q 与 q’ 共同产生,q’
等效替代极化电荷的影响。
球面电位
q = 4 π 0 d
图1.7.7 点电荷位于不接地导体 球附近的场图
返 回
上 页
下 页
第 一 章
静 电 场
3. 不同介质分界面的镜像
图1.7.9 点电荷对无限大介质分界面的镜像
根据惟一性定理
E1t E2 t
D1n D2n
q q' q' ' cos cos cos 2 2 2 4π1r 4π1r 4π 2 r
镜像法电轴法电容部分电容静电能量与力副本.pptx
上页 下页
P
1
2
20
ln
2 1
C
以 y 轴为参考电位
P
20
ln
2 1
20
ln
( x b)2 y2 ( x b)2 y2
令:P 常 数,等位线方程
( x b)2 y2 K 2 ( x b)2 y2
( x K 2 1b)2 y2 ( 2bK )2
K2 1
K2 1
第26页/共83页
2 0
思路
边值问题
S U0
导体球外(除q点)空间:
S
D dS
Q
D dS q
S
S U0
+Q
Q
4R
Q 4πεRU0 Q q
第13页/共83页
上页 下页
讨论 4.点电荷q 在不带电的金属球壳内的镜像。
思路
边值问题
导体球内(除q点)空间:
2 0
C
S
S D dS q
q
-q
q S 4R
3. 部分(分布)电容(Distributed Capacitance)
对于多导体系统,每两个导体上的电压受到所有导体上 电荷的影响,这时系统中导体电荷与导体电压的关系不能 仅用一个电容来表示而需引入部分电容的概念。
三导体静电独立系统
第42页/共83页
上页 下页
讨论前提
多导体系统
电位系数
静电独立系统 线性系统
q
41r 2
cos
q'
41r 2
cosBiblioteka q''42r 2
cos
q
4r 2
sin
q'
镜像法与电轴法

电工基础教研室金钊
21
二、电轴法
2. 电轴法 例4. 自由空间,相同半径的平行导体圆柱的情况。
导体圆柱外部
y
0
2
导体圆柱表面
R0
o
R0
0 l n dl
x
圆柱面 C
2016/10/29 电工基础教研室金钊
d
d
22
二、电轴法
2. 电轴法 例4. 自由空间,相同半径的平行导体圆柱的情况。
a b h
2 2
2
y
R0
b
d
R0
b
o
b
d
R0
x
R b d
2 0 2
2016/10/29
2
d
电工基础教研室金钊
23
二、电轴法
2. 电轴法 例5. 自由空间,不同半径的平行导体圆柱的情况。
a b h
2 2
2
y
R b h
2 1 2 2 2 2
2 1 2 2
P( x, y, z)
I 0 除点 (0,0, d ) 外 I r a 0
2
I r 0
球内(r <a):
a o
q
(0,0, d )
z
II 0
2
II r a 0
II r 0
2016/10/29 电工基础教研室金钊 6
一、镜像法
例2. 自由空间,接地导体球与点电荷。
r1 x 2 y 2 ( z d )2 r2 x y ( z d )
2 2 2
P( x, y, z)
1 12
静电场4-静电场的解(镜像法+场图)(1)

v∫⎪⎪ϕ
⎪⎪ ⎨
SA SA
= con D ⋅dS
st1
=τ
l
⎪⎪ϕ SB = const 2
v∫⎪
⎪⎩ SB
D
⋅ dS
=
−τ l
两导电圆柱形传输线
圆柱的镜像—电轴法
镜像法的思路:假定导体圆柱能够用线电荷等效,设 法依据“三不变”原则确定它的位置和大小。
预问题1:单根电轴的电场与电位。
E = τ eρ
电荷与镜像关于球 面反演。
球内是两个电荷作 用的叠加;球外电 位与电场都为0。
点电荷对球面导体的镜像
d.在问题c中,球壳不接地,求球壳内外的电位及电 场分布。
球内电场分布不变,但电位被抬高;球外的场相 当于电荷位于球心的作用。
镜像法
(4) 导电圆柱之间的镜像——电轴法
边值问题:
⎧∇ 2ϕ = 0 (导线以外空间)
• 镜像法只能解决一些特殊的边值问题。更一般的边值 问题的求解方法,包括解析法和数值法,下节讨论。
作业:
3.18, 3.24, 3.27
选做有奖题:能否用镜像法分析
两个带电导体球之间的电场?给出 详细分析论证。(满分2分)
一些典型的场图
方芯圆壳偏心电缆电 位分布与电力线分布
静电场场图
• 导体表面是等位面; • 两导体之间,等位面
ρ22 = a12 + (h1 + b)2 − 2a1(h1 + b) cosθ
ϕP
=
τ 2πε 0
ln
ρ2 ρ1
=const
⇒
ρ
2 2
=
k 2 ρ12
电轴法
⇒ a12 + (h1 + b)2 − 2a1(h1 + b) cosθ
电磁场课件 Part9--镜像法(2)

Topic # 9—镜像法(method ofimages)Part2n电轴法 (广义镜像法)n点电荷~ 无限大介质平面系统的电场n点电荷 ~ 导体球 (球面镜像法)1n计算n等位线在xoy平面内,等位线轨迹是一族偏心圆就每个等位圆轨迹而言,半径a,圆心至原点的距离h,线 电荷至原点的距离b,三者间的关系式为:h 2 = a 2 + b 2∴ a 2 = h 2 - b 2 =( h + b )( h - b)即 (±t) 电轴位置对每个等位圆的圆心来说,互为反演点。
23n 计算n 等位线图示1K oyxt+ t- b1 h 2h 3h b2 K 3K 31 K2 1 K 1 1 K1 a 2a 3an计算n启示n如果一静电场的等位线为一族偏心圆,其电场的计算问题,可考虑等效为一对正负电轴产生的电场n电轴的位置则由上面的a,b,h关系式确定n由于共有a,b,h三个参数,因此至少给出2个等位圆,才能确定电轴的位置。
n按已知2个等位圆的不同,可得不同的等效计算模型。
45n 同半径的两线输电线电场 n 问题半径为a 的两输电线分别带有等量异号的线电荷 (±t ),计算其产生的电场oyt+ t- aa1o 2o dxn同半径的两线输电线电场n分析输电线是导体,导体为等位体、导体表面为等位面 在xoy平面,两导体的圆表面迹线为等位线等位线为同半径的两个偏心圆可用一对电轴模型计算原场的分布67n 同半径的两线输电线电场 n 电轴法模型参数b,h 必须满足相距为d 半径分别为a 的两个圆为等位 圆,即已知等位圆半径a , 等位圆圆心之间的距离d ,确 定线电荷(电轴)至原点的距离b 和y 轴的位置变量h2d h =o a a 1o 2o dxhhbb22222 d b h a aæö =-=- ç÷ èø8n 同半径的两线输电线电场 n 镜像法模型oy t+ t- b hbdxh 1r 2r (,)P x y a电轴 ±t 的位置 22222 d b h a aæö =-=- ç÷ èø9n 同半径的两线输电线电场 n 镜像法模型oyt+ t- b hbdxh 1r 2r (,)P x y a适用区域那个区域没有引入电荷==适用于那个区域不包含同半径两 导体的所有区域 任意点电位2 01ln2 P r tj e r = p10n 两个不同半径的两线输电线电场 n 问题t+ t- d1a 2o 1o 2a11n 两个不同半径的两线输电线电场 n 已知条件n 待求量oy t+ t- bb dx1r 2r (,)P x y 1 a b 1h 2h b2o 1o 2a 两等位圆半径 a 1 、a 2,及其圆心间的距离 d 两圆心与原点的距离h 1 、h 2、线电荷与原点的距离 b12n 两个不同半径的两线输电线电场 n 已知与待求量的关系h 2 = a 2 + b2 22211 b h a=- 12d h h =+ 222 22b h a =- oy t+ t- b b dx1r 2r (,)P x y 1 a b 1h 2h b2o 1o 2a13n 两个不同半径的两线输电线电场 n 已知与待求量的关系222 121 222 212 2 2 d a a h d d a a h d +- =+- =2222 1122b h a h a=-=- oyt+ t- b b dx1r 2r (,)P x y 1 a b 1h 2h b2o 1o 2a 适用区域 不包含不同半径两导体内区域14n 偏心电缆的电场 n 问题d1 a 1o 2o 2a t+ t-15n 偏心电缆的电场 n 分析仍可应用电轴法。
镜像法电轴法电容部分电容静电能量与力副本
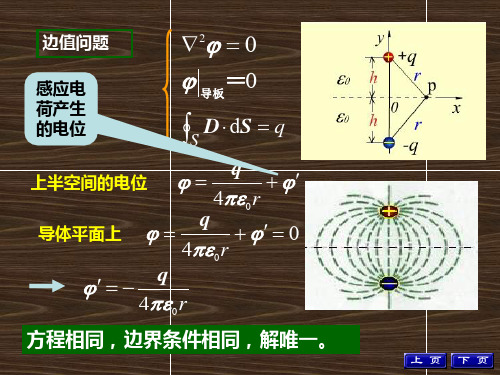
P
1
2
20
ln
2 1
C
以 y 轴为参考电位
P
20
ln
2 1
20
ln
( x b)2 y2 ( x b)2 y2
令:P 常 数,等位线方程
( x b)2 y2 K 2 ( x b)2 y2
( x K 2 1b)2 y2 ( 2bK )2
S
S U0
+Q
Q
4R
Q 4πεRU0 Q q
上页 下页
讨论 4.点电荷q 在不带电的金属球壳内的镜像。
思路 边值问题
导体球内(除q点)空间:
2SC0
S D dS q
q
-q
q S 4R
b d
b
R2 d
q
R d
q
上页 下页
讨论 5.求图示问题的镜q 像电荷的位置和大小。
思路 边值问题
球外任一点P 的电位与电场为
球外的电场计算
p
q
4
球外的电场分布
EP
q
40r12
er1
qR
40dr22
er2
上页 下页
讨论 1.点电荷q 对不接地金属球的镜像。
思路 边值问题
导体球外(除q点)空间:
2 0
S C
D dS 0
球S
D dS q
S
上页 下页
导体球零电位
E E E
垂直地面的电场分量
E
2
q cos 40r 2
qh
20 (h2
x2 )3/2
地面电荷分布
p=Dn
0 E
2
qh (h2 x2 )3/2
第7讲-镜像法与电轴法
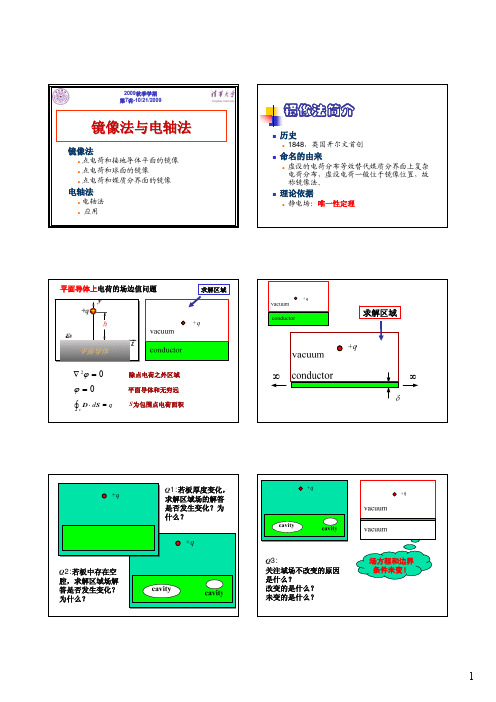
U0 =
⎧b 2 = h 2 − a 2 d ⇒ b = ( )2 − a 2 ⎨ 2 ⎩ d = 2h
镜像法(电轴法)小结
镜像法(电轴法)的理论基础是静电场唯一 性定理; 镜像法(电轴法)的实质是用虚设的镜像电 荷(电轴)替代未知电荷的分布,使计算场域为 无限大均匀介质; 镜像法(电轴法)的关键是确定镜像电荷 (电轴)的个数(根数),大小及位置; 镜像电荷(电轴)只能放在待求场域以外的 区域。叠加时,要注意场的适用区域。
−
2
q' 4 π ε 0 r2
=0
点电荷对接地球的镜像
r1 = d + R − 2Rdcosθ r2 = b2 + R2 − 2Rbcosθ
p r2 r r1 b -q' d q
∫
[q 2 (b2 + R 2 ) − q'2 (d 2 + R 2 )] + 2R(q'2 d − q 2b) cosθ = 0
2
+q' R
o
点电荷对不接地金属球的镜像
2
p r2 +q' R
o
r r1 q
任一点电位及电场强度为:
接地球壳,点电荷在球壳 内部,如何布置镜像电荷
b -q' d
ϕ=
=
1 q q′ q′ ( − + ) 4πε 0 r r1 r2 q 1 R R + ( − ) dr2 4πε 0 r dr 1
E=
τ
2 πε 0
ln
b + (h − a ) τ b − (h − a ) − ln b − (h − a ) 2 πε 0 b + (h − a )
镜像法(课堂PPT)
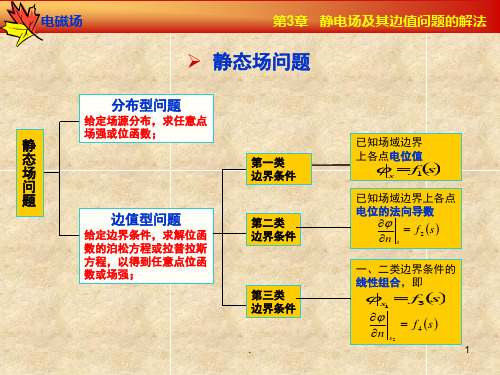
第3章 静电场及其边值问题的解法
1
d1
q d2
2
电位函数
q (1111) 4π R R1 R2 R3
q1
d1
d2 R1
d1 q R d2
d2 R3 q3 d1
R2 d2
d1
q2
镜像电荷q1=-q,位于(-d1, d2 )
镜像电荷q2=-q,位于( d1, -d2 ) 镜像电荷q3 = q , 位于(-d1, -d2 )
q q 0 4 R0
得 q q
于 是 4 q R 1 , R 1 4 q x 2 y 2 1 ( z h ) 2x 2 y 2 1 ( z h ) 2
可见,引入镜像电荷 q q 后保证了边界条件不变;镜像点电荷位于z<0的空间,未改变所 求空间的电荷分布,因而在z>0的空间,电位仍然满足原有的方程。由惟一性定理知结果正确。
5. 确定镜像电荷的两条原则 镜像电荷必须位于所求解的场区域以外的空间中;
镜像电荷的个数、位置及电荷量的大小以满足所求解的场 区域 的边界条件来确定;
.
13
电磁场
第3章 静电场及其边值问题的解法
二、 接地导体平面的镜像
1. 点电荷对无限大接地导体平面的镜像 2. 线电荷对无限大接地导体平面的镜像 3. 点电荷对半无限大接地导体角域 (导体劈) 的镜像
域边界以外虚设的较简单的等效电荷来等效替代场域边界上
未知的较为复杂的电荷分布的作用,且保持原有边界上边界 条件不变,则根据惟一性定理,待求场域空间电场可由原来
的电荷和所有等效电荷产生的电场叠加得到。
从而将原含该边界的非均匀媒质空间变换成无限大单一均匀 媒质的空间,使分析计算过程得以明显简化;
高中物理课件-镜像法

机动 目录 上页 下页 返回 结束
Q dS Qa 2rdr Q Q
2 0 (r 2 a 2 )3/ 2
(b)电荷Q 产生的电场的电力线全部终止在导体面上 它与无导体时,两个等量异号电荷产生的电场在 右半空间完全相同。
(c)Q与 Q 位置对于导体板镜象对称,故这种方法称
为镜象法(又称电象法)
右半空间,Q在(0,0,a)点, Q/
P
r
Qr
a
z
电势满足泊松方程。
边界上 0 z0
从物理问题的对称性和边界条件考虑,假想电荷应在左
半空间 z 轴上。
设电量为 Q,位置为(0,0,a )
1 [
Q
Q
]
40 x2 y2 (z a)2 x2 y2 (z a)2
机动 目录 上页 下页 返回 结束
y
-Q(-a, b, 0)
O
Q(-a, -b, 0)
Q(a, b, 0)
x
-Q(a, -b, 0)
机动 目录 上页 下页 返回 结束
(2)电势分布
Q [
1
1
40 (x a)2 ( y b)2 z2 (x a)2 ( y b)2 z2
1
(x a)2 ( y b)2 z2
1
]
8 –7 电势
第八章静电场
8 –7 电势
第八章静电场
四.等势面: 电场中电势相同的各点构成的面
等量同号点电荷的电场 正点电荷的电场
等量异号点电荷的电场
孤立带电体的电场
匀强电场
等差等势面: 两个相邻的 等势面间的 电势之差是 相等的
说明:
1.电场线与等势面垂直 2.电场线由高等势面指向低等势面,等势面不相交 3.在同一等势面上移动电荷电场力不做功 4.相邻两个等势面间的电势差相等,场强大的地方
电磁场 镜像法及电轴法

思考:导体表面的电荷分布 密度 ? I I 0 0
n
z 0
z P( x, y, z )
(0,0, d ) q
z
z 0
qd 2 2 2 3/2 2( x y d )
2018/11/12 电工基础教研室金钊 5
一、镜像法
例2. 自由空间,接地导体球与点电荷。 球外(r >a):
P( x, y, z )
I 0 除点 (0,0, d ) 外 I r a 0
2
I r 0
球内(r <a):
a o
q
(0,0, d )
z
II 0
2
II r a 0
II r 0
2018/11/12 电工基础教研室金钊 6
一、镜像法
例2. 自由空间,接地导体球与点电荷。
z
I r a 0
2018/11/12
b a2 / d q ( a / d ) q
电工基础教研室金钊 7
一、镜像法
例3. 点电荷对无限大介质分界面。 区域I ( z 0) :
1 2
o
q (0,0, d )
1 0 除点 (0,0, d ) 外
2
1 r 0
电工基础教研室金钊
1 2 q q 1 2 2 2 q q 1 2
11
二、电轴法
2018/11/12
电工基础教研室金钊
12
二、电轴法
1. 两传输线的电场
y
P( x, y, z )
2
(b, 0, 0)
1
o
(b, 0, 0)
第7次课-镜像法与电轴法

图1.7.16 平行传输线电场的计算
1 1 EP ( e e ) 2π 0 1 2 2 p ln 2π 0 1 ( 以 y 轴为参考电位)
1 2
第 一 章
静 电 场
例1.7.4 试决定图示不同半径平行长直导线的电轴位置。
图1.7.17 不同半径传输线的电轴位置
[q 2 (b 2 R 2 ) q'2 (d 2 R 2 )] 2R(q'2 d q 2b) cos 0
联立求解
q (b R ) q' (d R ) 0
2 2 2 2 2 2
q '2 d q 2b 0
R2 b 镜像电荷位置 d b R q' q q 镜像电荷大小 d d
D1n D2n
q q' q' ' cos cos cos 2 2 2 4π1r 4π1r 4π 2 r
q q' q' ' sin sin sin 2 2 2 4πr 4πr 4πr
2 2 1 2 q 解得 q ' q 和 q' ' 1 2 1 2
确定镜像电荷的个数、大小及位置; 应用镜像法解题时,注意:
镜像电荷(电轴)只能放在待求场域以外的区
域。叠加时,要注意场的适用区域。
第 一 章
静 电 场
2. 点电荷对球面导体的镜像 点电荷位于接地导体球外的边值问题
(除q点外的空间) 2 0
r
球面
0
设镜像电荷 q '如图,球面电位
2 K 1 2 bK 2 2 2 K 1 整理后,等位线方程 ( x b ) y ( ) h 2 b K 2 1 2 K 1 K 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b
R2 d
q
'
bq Rq dd
计算不接地金属球附近放置点电荷时的电场分布
2 0
r
0
除 q 点外 球外空间
球面s
常数
0
p
r2
r
+q'
r1
q
R
o b-q'
d
点电荷对不接地金属球的镜像
感应电荷分布及球对称性, 在球内有两个等效电荷。
正负镜像电荷绝对值相等; 正镜像电荷只能位于球心。
p
ห้องสมุดไป่ตู้
E2t D2
n
4q1r2cos4q1'r2cos 4q2''r2cos 4qr2sin4qr'2sin 4qr''2sin
q q
' '
'
1 1
2
2
2 2
q q
1 2
1中的电场是由q与q’共同产生,其有效区在上
半空间,q’是等效替代极化电荷的影响。
2中的电场是q”由决定,其有效区在下半空间,
qh(h2
1
x2)1/20
q
设有一点电荷q置于相互直角的两个接地的半无限大 导电平板附近,试求解这一电场。
夹角为α=π/3的两相联无限大导电平面的镜象
导体球面镜像:设在点电荷附近有一接地导体球, 求导体球外空间的电位及电场分布。
2
r
0
球外空间(除q点外)
0
导球面 0
设置-q’放置在球内(无效区),使 其等效球壳上的感应电荷,对照两 种情况下的边值问题,关键问题是 确定等效电荷的量值大小和位置。
两根输电线表面的电位为:
当h>>a,b ≈h时:1220lnb b ((h h a a))
1
20
ln
2h a
201
ln2h
,p
1 ln2 ln2h 1
a
a
已知两根不同半径,相互平行,轴线距离为d 的带 电长直圆柱导体,试决定电轴位置。
b2
b
2
h
2 1
h
2 2
a
2 1
a
2 2
d
h1
h2
置于电轴上的等效线电荷,来代替圆柱 导体面上分布电荷,从而求得电场的方法, 称为电轴法。
两根平行的带等值异号电荷的等半径输电线的电场
解:采用电轴法
建立坐标系,确定电轴位置
b h2 a2
圆柱导线间电场和电位
EP
2π0
(1
1
e1
1
2
e2
)
p
2π0
ln
2 1
两根平行的带等值异号电荷的等半径输电线的电场
d
2
)2
a
2 1
已知一对半径为a,相距为d的长直圆柱导体传输线 之间电压为U0,试求圆柱导体间电位的分布。
a)确定电轴的位置
b2h2a2
b
d2h
(d)2a2 2
b) 场中任一点电位为
ln 2 2π0 1
为集中到几何轴线上的线电荷,镜像电荷为:
22 160 12 81
E
22r
er
22r
(
x r
ex
y
r
h
ey
)
160 162 800
x (r2
ex
y r2
h
ey
)
810
(
x2
x (y
h)2
ex
x2
y (y
h
h)2
ey
)
电轴法工程背景
两根等量异号线电荷的电场
以原点o1为参b 1考2点0 ,d 则2π 0(lnbln1)
h1
d2
a
2 1
2d
a
2 2
h2
d2
a
2 2
2d
a
2 1
b
(
d
2
a
2 1
2d
a
2 2
)2
a
2 1
试确定图示偏心电缆的电轴位置
h12
h
2 2
a
2 1
a
2 2
b2 b2
h
2
h1
d
h1
a
2 2
a
2 1
2d
d2
h2
a
2 2
a
2 1
2d
d2
b
(
a
2 2
a
2 1
2d
点电荷之外区域 平面导体和无穷远
接地导体平面上电荷的场
上半区域场边值问题
点电荷的镜像
2 0
点电荷之外区域
q
4 0 r
q
4 0 r
0
导体平面 和无穷远
注意: 1、有效区域:用镜像求得的解答只对上半空 间才是正确的,因为它符合唯一性定理的要求。 2、镜像法特点:将计算场域不均匀空间转化 为均匀空间,降低了问题求解难度。
K2 1
圆半径 a
2bK K 2 1
a、h、b三者之间的关系满足
a2b2(2bK )2b2(K21b)2h2
K21
K21
=0
负电位区域
正电位区域
等位线与电力线分布图
电轴法基本思路
若在任一等位面上放一无厚度的金属圆柱壳, 是否会影响电场分布?感应电荷是否均匀分布?若 在金属圆柱管内填充金属,重答上问。
关于镜像法与电轴法静电场
镜像法基本思路
首先把原来具有边界的场域空间 看成是一个无限大的均匀空间,然后 用虚设的电荷分布等效替代媒质分界 面上复杂电荷分布,虚设电荷的个数、 大小与位置使场的解答满足唯一性定 理。虚设电荷一般位于镜像位置,故 称镜像法。
接地导体平面上电荷的场边值问题
2 0
0
q”是等效替代自由电荷与极化电荷的作用。
q''qq'q1 2 2 1q2221q
求图示1与2
区域的电场强 度,确定镜像 电荷的个数、 大小与位置。
例3-1 离河面高度为h处,有一输电线经过,导 线单位长度的电荷量为τ,且导线半径远小于h。 设河水的介电常数为80ε0,求水中的电场强度。
解:由于导线半径远小于h,所以可将导线表面电荷视
求空气中点电荷q在地面引起的感应电荷分布情况
解: 设点电荷q离地面高度为h,则
EEE (方向指向地面)
E 24 πq 0r2co sey2 π0(h q 2h x2)3/2ey
pD0Ey2π(h2q hx2)3/2
整个地面上感应电荷的总量为
地面引起的感应电荷的分布
SpdS02π(h2 qx2 h)3/22πxdx
p 0
点电荷对接地球的镜像
p4πq0r14πq0 'r2 0
r1 d2 R2 2Rdcos r2 b2 R2 2Rbcos
[ q 2 ( b 2 R 2 ) q '2 ( d 2 R 2 ) 2 ]R ( q '2 d q 2 b )co 0 s
q2(b2R2)q'2(d2R2)0 q'2dq2b0
r2
r
+q'
r1
q
R
o b-q'
d
任一点电位及电场强度为:
1 (q q q) 4π0 r r1 r2
q (1 R R )
4π0 r dr1 dr2
q1 R R
E4π0(r2erd12rer1d22 rer2)
点电荷位于不接地 导体球附近的场图
介质分界面的镜像
21 0 22 0
E1t D1n
2b22 0d2 π0(lnbln2)
P122π 0ln 1 22π 0ln((x x b b))2 2 y y2 2
若p2 0ln ( 1 2)2 0ln (K )常 数 则
(x (x
b)2 b)2
y2 y2
K2
等位线方程为:
(xK21b)2y2( 2b K)2
K21
K21
圆心坐标(h,0) h K2 1b
