圆柱和圆锥精选拓展提高专项训练附答案
六年级下册数学《圆柱与圆锥》专项练习题50道及答案【全优】

六年级下册数学《圆柱与圆锥》专项练习题50道一.选择题(共10题,共20分)1.圆柱的底面半径扩大到原来的3倍,高不变,圆柱的侧面积扩大到原来的()倍。
A.3B.9C.62.用一块长25.12厘米,宽18.84厘米的长方形铁皮,配上下面()圆形铁片正好可以做成圆柱形容器。
(单位;厘米)A.r=1B.d=3C.r=4 D.d=53.圆锥的高有()条。
A.无数B.3C.14.一个圆锥的体积是720立方厘米,底面积是80平方厘米,它的高是()厘米。
A.3B.27C.95.如果圆柱的侧面展开后是一个正方形,那么这个圆柱的()一定和高相等。
A.直径B.半径C.底面周长6.把一个圆柱的侧面展开,不可能得到下面的图形是()。
A. B. C. D.7.如图所示,圆锥的高是圆柱高的,底面积相等,圆柱的体积是圆锥体积的()。
A.20倍B.C.8倍D.27倍8.一个圆柱和一个圆锥的底面积相等,体积也相等。
已知圆柱高为9cm,圆锥高为()厘米。
A.9B.27C.3D.189.圆柱的底面半径是5厘米,高3厘米,它的表面积是()。
A.94.2cm2B.251.2cm2C.157cm210.一个高12厘米的圆锥形容器,盛满水后倒入和它等底、高是8厘米的圆柱形容器里,该圆柱水面的高是()厘米。
A.3B.12C.4二.判断题(共10题,共20分)1.一个圆锥体的底面半径扩大到原来的2倍,高不变,它的体积就扩大到原来的4倍。
()2.圆锥的体积等于圆柱体积的。
()3.一个圆柱的直径和高相等,则圆柱体的侧面展开图是正方形。
()4.正方体、长方体和圆柱体的侧面积都可以用底面周长乘高来计算。
()5.等底等高的圆柱和长方体的体积相等。
()6.圆柱的底面直径可以和高相等。
()7.圆锥的体积比圆柱的体积小。
()8.如果圆锥的底面积是圆柱底面积的3倍,则圆锥和圆柱的体积相等。
()9.圆柱两个底面之间的距离,叫做圆柱的高。
()10.圆锥的底面半径扩大到原来的3倍,高不变,体积也扩大到原来的3倍。
【精品】圆柱与圆锥能力提升题

【精品】圆柱与圆锥能力提升题一、圆柱与圆锥1.一个圆锥形沙堆,底面周长是31.4米,高是1.2米.每立方米黄沙重2吨,这堆黄沙重多少吨?【答案】解:底面半径:31.4÷(2×3.14)=31.4÷6.28=5(米)这堆沙子的总重量: ×3.14×52×1.2×2=3.14×25×0.4×2=78.5×0.4×2=31.4×2=62.8(吨)答:这堆黄沙重62.8吨。
【解析】【分析】用底面周长除以圆周率的2倍即可求出底面半径。
根据圆锥的体积公式计算出沙子的体积,再乘每立方米沙子的重量即可求出总重量。
2.计算下面圆柱的表面积和体积,圆锥的体积。
(1)(2)【答案】(1)解:表面积:3.14×52×2+3.14×5×2×13=157+408.2=565.2(cm2)体积:3.14×52×13=1020.5(dm3)(2) ×3.14×82×15= ×3.14×64×15=1004.8(cm3)【解析】【分析】(1)圆柱的表面积=底面积×2+侧面积,侧面积=底面周长×高,圆柱的体积=底面积×高,根据公式计算即可;(2)圆锥的体积=底面积×高×,根据公式计算体积即可。
3.一个圆柱形钢管,内直径是20cm,水在钢管内的流速是每秒40cm,每秒流过的水是多少cm3?【答案】解:3.14×(20÷2)2×40=314×40=12560(cm3)答:每秒流过的水是12560cm3。
【解析】【分析】钢管是圆柱形,流出的水也是圆柱形。
用钢管的横截面面积乘每秒流出水的长度即可求出流过水的体积。
人教版数学六年级下册第三单元《圆柱与圆锥》提升测评卷含答案

人教版数学六年级下册第三单元《圆柱与圆锥》提升测评卷一、选择题1.圆柱体的底面半径扩大3倍,那么它的体积扩大的倍数是()A.3B.6C.9D.272.一个圆柱体和一个圆锥体的底面积和体积都分别相等,圆柱的高是3分米,圆锥体的高是()A.分米B.1分米C.6分米D.9分米3.一个圆锥与一个圆柱体积相等,高也相等。
已知圆柱的底面积是13dm2,则圆锥的底面积是()dm2。
A.13B.19C.1D.164.李师傅准备用下图左面的长方形铁皮卷成一个圆柱形水桶的侧面,再从下图右面的铁皮中选一个作底面,可直接选用的底面有()。
(接缝处忽略不计,无盖)(单位:cm)A.③③B.③③C.③③D.③③5.圆锥的体积不变,当底面半径扩大3倍时,则高应()。
A.扩大3倍B.缩小3倍C.缩小9倍6.圆锥的体积是8立方分米,与它等底等高的圆柱的体积是()A.3立方分米B.2立方分米C.24立方分米7.把一个底面直径是6厘米,高是5厘米的圆柱体沿底面直径切开成两个半圆柱后,表面积增加了()平方厘米.A.60B.788.圆柱内的沙子占圆柱体积的,倒入()号圆锥内正好倒满.A.B.C.9.一个矿泉水瓶的容积约为500()。
A.L B.mL C.3m D.千克10.压路机滚筒滚一周,求压路的面积是多少,就是求()。
A.底面积B.—个底面积与侧面积的和C.两个底面积与侧面积的和D.侧面积11.由一个正方体木块加工成的最大圆锥,它的底面半径是5厘米,这个正方体的体积是()立方厘米。
A.125B.6000C.1000D.250二、图形计算12.求圆锥的体积.(单位:厘米)三、填空题13.有一个长是8分米、宽是6分米、高是7分米的长方体木块,它的体积是( )3dm。
如果把两个这样的长方体拼成一个长方体,它的表面积最小是( )2dm。
如果把其中的一个长方体削成一个体积最大的圆柱,这个圆柱的体积是( )3dm。
14.一个圆柱的底面半径是2 cm,高是5 cm,它的侧面积是( ),表面积是( ),体积是( ).15.如果圆锥的体积为628立方厘米,高为6厘米,那么它的底面半径是厘米.16.一个圆柱的底面直径和高都是8厘米,它的侧面积是,表面积是,体积是.17.圆柱的上、下两个底面都是____形,而且大小____,圆柱的侧面沿高展开是____形或____形,它的一边是圆柱的____,相邻的另一边是圆柱的____。
六年级数学拓展题之《16圆柱和圆锥(含答案)》

16.圆柱和圆锥一、填空1.一个圆柱和一个圆锥的底面周长比是2:3,体积比是5:6,圆锥与圆柱高的最简整数比是()。
2.把一个底面直径4厘米,高6厘米的圆柱形钢材截成两段小圆柱,表面积增加()平方厘米。
二、应用3.求长方形绕长边旋转一周后形成图形的表面积。
4.一台压路机的前轮宽1.5米,直径是0.8米。
这台压路机行驶一段距离后,前轮压过的路面有12π平方米。
这台压路机的前轮滚动了几周?5.一个圆柱被截取5厘米,圆柱的表面积减少了31.4平方厘米。
原来圆柱的底面积是多少平方厘米?练习题:一个圆柱,若高增加2分米,则表面积增加25.12平方分米,体积增加20%。
原来圆柱的体积是多少立方分米?原来圆柱的表面积是多少平方分米?6.一根底面周长为62.8厘米的圆柱形木材,沿着它的直径竖着切成两半,表面积增加了400平方厘米。
这根圆柱形木材的体积是多少立方厘米?7.把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体,如图,求圆柱的体积。
8.小华想测量一个小铅球的体积,它把铅球完全浸没在有一定量水的圆柱形容器中。
测得水面上升了3cm。
如果再往这个容器内倒入1256cm³的水(水没有溢出),水面会再上升多少厘米?9.有甲、乙两个圆柱形容器,从里面量得他们的底面半径分别是10厘米和5厘米,两个容器内分别盛有深10厘米和15厘米的水,现将乙容器中的一部分水倒入甲容器内,使得两个容器里的水面相平,这时水深为多少厘米?10.把一个长6厘米,宽和高都是4厘米的长方体橡皮削成一个体积最大的圆锥,这个圆锥的体积是多少方厘米?11.一个圆锥的底面半径和高都等于一个正方体的棱长。
正方体的体积是24立方厘米。
则这个圆锥的体积是多少立方厘米?12.一个圆锥形容器中有1升水,水面高度正好是圆锥高度的一半。
这个容器还能装()升水。
13.烧锅炉的师傅为了节约空间,把底面直径1m、高0.6m的圆锥形煤堆靠锅炉房墙角堆放,高度仍堆成0.6m。
六下 第三单元圆柱与圆锥提高题和奥数题(附答案)
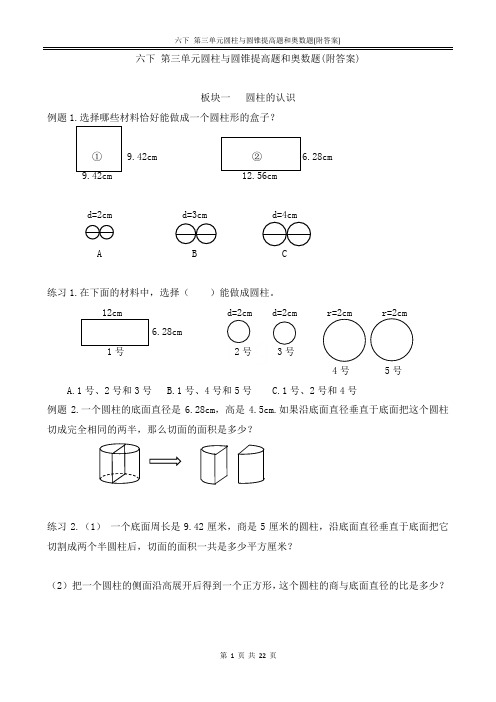
六下第三单元圆柱与圆锥提高题和奥数题(附答案)板块一圆柱的认识例题1.选择哪些材料恰好能做成一个圆柱形的盒子?d=2cm d=3cm d=4cmA B C练习1.在下面的材料中,选择()能做成圆柱。
3号4号 5号A.1号、2号和3号B.1号、4号和5号C.1号、2号和4号例题2.一个圆柱的底面直径是6.28cm,高是4.5cm.如果沿底面直径垂直于底面把这个圆柱切成完全相同的两半,那么切面的面积是多少?练习2.(1)一个底面周长是9.42厘米,商是5厘米的圆柱,沿底面直径垂直于底面把它切割成两个半圆柱后,切面的面积一共是多少平方厘米?(2)把一个圆柱的侧面沿高展开后得到一个正方形,这个圆柱的商与底面直径的比是多少?例题3.一个圆柱形蛋糕盒的底面直径是20厘米,高是15厘米,用彩绳将它捆扎(如右图),打结处在圆心,打结部分长30厘米。
求所用彩绳的全长是多少厘米?练习3.一个圆柱形蛋糕用彩绳捆扎,如果打结部分用了35厘米,打结处在圆心,一共用了多长彩绳?板块二圆柱的表面积例题1.一块长方形的钢板,利用图中阴影部分刚好能做成一个圆柱形的带盖水桶(接头处忽略不计),求这个水桶的表面积。
练习 1.(1)如下图,有一张长方形铁皮,剪下两个圆及一个长方形,正好可以做成一个圆柱,这个圆柱的底面半径为10厘米,原来这张长方形铁皮的面积是多少平方厘米?(2)有一张长方形铁皮(尺寸如图所示),剪下阴影部分正好能围成一个圆柱,求圆柱的表面积是多少。
例题2.工人师傅要在一个零件(如右图)的表面涂一层防锈材料。
这个零件是由两个圆柱构成的,小圆柱的直径是4厘米,高是2厘米;大圆柱的直径是6厘米,高是5厘米。
这个零件涂防锈材料的面积是多少?练习2.用3个高都是2分米,底面半径分别为2分米、1分米和0.5分米的圆柱组成一个物体(如图),求该物体的表面积。
例题3.如图,是长为8,宽为4的长方形,以长方形的长为轴旋转一周。
求所形成的立体图形的表面积。
【数学】圆柱与圆锥能力提升题

【数学】圆柱与圆锥能力提升题一、圆柱与圆锥1.图“蒙古包”是由一个近似的圆柱形和一个近似的圆锥形组成,这个蒙古包的空间大约是多少立方米?【答案】解:3.14×(8÷2)2×2+3.14×(8÷2)2×1×=3.14×16×2+3.14×16×1×≈100.48+16.75=117.23(立方米)答:这个蒙古包所占的空间大约是117.23立方米。
【解析】【分析】这个蒙古包是由圆锥和圆柱组成,所以这个蒙古包的空间是圆锥的体积和圆柱的体积,圆柱的底面半径=底面直径÷2,圆柱的底面积=圆锥的底面积,所以圆柱的体积=πr2h,那么圆锥的体积=πr2h。
2.一个圆锥形沙堆,底面积是45.9m2,高1.2m.用这堆沙在12m宽的路面上铺3cm厚的路基,能铺多少米?【答案】解:3厘米=0.03米×45.9×1.2÷(12×0.03)=18.36÷0.36=51(米)答:能铺51米。
【解析】【分析】现根据圆锥的体积=×底面积×高求出圆锥形沙堆的体积,然后根据长方体的体积=长×宽×高,求出铺路的长度即可。
3.一堆圆锥形黄沙,底面周长是25.12米,高1.5米,每立方米的黄沙重2吨,这堆沙重多少吨?【答案】解:底面半径:25.12÷3.14÷2=8÷2=4(米)×3.14×42×1.5=×3.14×16×1.5=3.14×16×0.5=50.24×0.5=25.12(立方米)25.12×2=50.24(吨)答:这堆沙重50.24吨.【解析】【分析】已知圆锥的底面周长,求底面半径,用C÷π÷2=r,然后求出圆锥的体积,用公式:S=πr2h,据此列式计算,最后用黄沙的体积×每立方米黄沙的质量=这堆黄沙的总质量,据此列式解答.4.把两根底面积相等高为 2.5m的圆柱形钢材拼成一根圆柱形钢材,表面积减少了16dm2,如果每立方分米的钢材的质量为7.9kg,拼成的这根钢材的质量为多少千克? 【答案】解:2.5m=25dm16÷2×(25+25)×7.9=8×50×7.9=400×7.9=3160(千克)答:拼成的这根钢材的质量为3160千克。
六年级下册数学《圆柱与圆锥》专项练习题50道附答案【巩固】

六年级下册数学《圆柱与圆锥》专项练习题50道一.选择题(共10题, 共22分)1.一个圆柱体和一个圆锥体, 底面周长的比是2:3, 它们的体积比是5:6, 圆柱和圆锥高的最简单的整数比是()。
A.5:8B.8:5C.15:8D.8:152.圆柱的表面有个()面, 圆锥的表面有()个面。
A.2B.3C.4D.63.圆锥的体积一定, 它的底面积和高()。
A.不成比例B.成正比例C.成反比例4.小明做了一个圆柱形状的容器和三个圆锥形状的容器(如下图), 将圆柱形状容器中的水倒入第()个圆锥形状的容器, 正好可以倒满。
A. B. C.5.把一根长1米, 底面积为3.14平方米的圆柱锯成两个小圆柱, 它的表面积()。
A.增加3.14平方米B.减少3.14平方米C.增加6.28平方米 D.减少6.28平方米6.一个圆柱的侧面展开图如图, 那么这个圆柱可能是下列图中的()。
A. B. C.7.把一个棱长是6分米的正方体木料用车床切削成一个最大的圆锥体零件, 这个零件的体积是()。
A.56.52cm3B.169.5cm3C.678.24cm38.一个圆柱的侧面积是125.6平方米, 高是10分米, 它的体积是()立方分米。
A.125.6B.1256C.12560D.12560009.一个圆锥的体积是36立方厘米, 底面积是12平方厘米, 高是()厘米。
A.9B.6C.310.圆柱的底面半径是r, 高是h, 它的表面积可以用式子()来表示。
A.2πr2+2πrhB.2πr2+πrhC.πr2+2πrh二.判断题(共10题, 共20分)1.如果圆柱和圆锥的体积和高都相等, 那么圆锥底面积与圆柱底面积的比3:1。
()2.圆锥的体积等于圆柱体积的三分之一。
()3.两个等高圆柱半径比是2:3, 则它们体积的比是4:9。
()4.一个圆锥的高不变, 底面半径扩大到原来的3倍, 这个圆锥的体积也扩大到原来的3倍。
()5.底面积相等的两个圆柱体积相等。
2021-2022学年数学六年级下册圆柱和圆锥专项练习附答案【能力提升】

2021-2022学年数学六年级下册圆柱和圆锥专项练习一.填空题(共20题,共30分)1.一个圆柱的底面直径是15 cm,高是8 cm,这个圆柱的侧面积是()cm2。
2.一个圆柱的体积是314dm3,它的底面面积是6.28dm2,它的高是()分米。
3.如图,甲圆柱形容器是空的,乙长方体容器水深6.28厘米,若将容器乙中的水全部倒入甲容器,这时水深()厘米。
4.计算圆锥体积的字母公式是()。
5.长方体、正方体、圆柱的体积计算公式都可以写成()。
6.一个圆锥的体积是7.2立方米,与它等底等高的圆柱的体积是()立方米。
7.如图把这个圆柱的侧面展开可以得到一个长方形,这个长方形的面积是()。
8.把一个圆锥沿底面直径纵切开,切面是一个()形。
9.把一个底面直径和高都是2分米的圆柱体切开拼成一个近似的(),这个长方体底面的长约是(),宽约是(),底面面积约是(),体积约是()。
10.把一根圆柱形木料截成3段,表面积增加了45.12平方厘米,这根木料的底面积是()平方厘米。
11.一个圆柱的体积是100.48dm3,它的底面半径是2dm,高是()dm。
12.已知一个圆锥的底面直径是4厘米,高是6厘米,这个圆锥的体积是()立方厘米。
13.圆锥的侧面展开图是一个()。
14.一个圆柱的底面周长是12.56厘米,高是6厘米,那么底面积是()平方厘米,体积是()立方厘米。
15.把一个圆柱形纸盒沿高线剪开,侧面展开图是一个(),它的一条边就等于圆柱的(),另一条边就等于圆柱的()。
16.把一根长5米的圆柱形木料截成相等的三段,表面积增加了10平方分米,这根木料原来的体积是()立方分米。
17.圆锥的底面是个()形,从圆锥的顶点到底面圆心的距离叫做圆锥的()。
18.一个圆柱的底面半径为4厘米,侧面展开后正好是一个正方形,这个圆柱的体积是()立方厘米。
19.有五根小棒,分别长1厘米、3厘米、4厘米、5厘米、9厘米,从中选三根小棒围成一个直角三角形,这个直角三角形的面积是()cm2;如果以其中的一条直角边为轴旋转一周,形成立体图形的体积最小是()cm3。
人教新课标六年级下册数学圆柱和圆锥同步拓展习题 (含答案)

六下圆柱和圆锥同步拓展习题一填空:1,用边长是62.8dm的正方形围成一个最大的圆柱形纸筒,这个纸筒的高是()dm2,一个圆柱的侧面展开得到一个长方形,这个长方形等于圆柱的(),宽等于圆柱的()。
3,一根圆木底面的直径和高都是4分米,它的侧面积是()平方分米,体积是()立方分米4,如下图,将长方形绕直线L旋转,能形成一个圆柱,那么圆柱的体积是()立方厘米5,一个圆柱的底面周长是12.5dm,它的高是2cm。
它的体积是()立方厘米6,从一个圆柱上截下一段高为10cm的小圆柱后,表面积比原来减少了62.8平方厘米,截下的这段圆柱的体积是()立方厘米7,圆柱的底面半径扩大2倍,侧面积就扩大()倍,体积就扩大()倍8,圆柱的高扩大2倍,侧面积就扩大()倍,体积就扩大()倍9,圆柱的侧面展开图不可能是()A.平行四边形 B.长方形 C.梯形 D.正方形10,圆柱,正方体和长方体的底面周长相等,高也相等,则()的体积最大A.圆柱 B.正方体 C.长方体11,用一块长28.26cm,宽15.7cm的长方形铁皮,应该配上直径()cm的圆形铁皮就可以做成一个容积最大的容器12,一个圆柱和一个圆锥的底面半径的比是3:4,高的比是2:3,圆柱与圆锥的体积比是()13,等底等高的圆柱和圆锥的体积一共是48 m³,则圆柱的体积是()m³14,两个等高的圆柱,底面直径的比是1:2,则它们的体积比是()15,一个体积是60立方厘米的圆柱,削成一个最大的圆锥,这个圆锥的体积是()立方厘米二判断:1,一个圆锥和一个正方体底面积相等,高也相等,这个正方体体积是圆锥的3倍()2,圆锥的侧面展开图是一个三角形()3,一个圆柱和圆锥的底面积和体积都相等,圆锥的高是18cm,即圆柱的高是6cm()4,一个圆柱,截去一半后表面积缩小为原来的一半,体积也缩小为原来的一半()5,圆柱的底面半径和高都扩大2倍,它的体积就扩大4倍()6,一个正方体和一个圆锥的底面积和高都相等,这个正方体的体积是圆锥体积的3倍()三:解决问题1,博士帽用黑色卡纸做成的,上面是底面边长为30厘米的正方形。
苏教版数学六年级下册第二单元《 圆柱和圆锥》学习力提升练习卷(含答案)

苏教版版数学六年级下册单元学习力提升练习卷第二单元《圆柱和圆锥》哈喽,孩子们好!美好的一天开始啦!提高学习力才能达到真正意义上的减负!学习力分为三个阶段,从知识层面的接受,到技能层面的模仿,再到知识层面的内化。
“磨刀不误砍柴工”,只有打好能力基础,才能高效学习。
让我们以解决问题为目的,以学习力为帆,以内驱力为桨,展开新的征程。
提升学习力,我能行!名师指导:例1.13.圆柱体的底面半径和高都扩大3倍,它的底面积扩大到原来的________倍;它的侧面积扩大到原来的________倍;它的体积扩大到原来的________倍。
例2:小明用彩纸做了一个圆柱体的灯笼.他在灯笼的上、下底面的中间,分别留下一个直径是18.84厘米的圆形口(如右图)。
小明做这个灯笼至少要用________平方厘米的彩纸?(图中单位:厘米,得数保留整数)例3:有一根半径是2厘米,高6厘米的圆柱形钢材,加工成与它等底等高的圆锥,要切去( )立方厘米钢材。
【考点】圆柱体的表面积。
【分析】根据题意,要求这个灯笼需要多少平方厘米的纸,就是求灯笼的表面积,用侧面积+底面积×2=表面积,侧面积公式:S=πdh ,底面是两个圆环,依据圆环的面积公式:S=π(R 2-r 2),据此求出一个底面积,然后乘2,最后相加即可求出表面积,据此解答。
解:37.68÷2=18.84(厘米) 18.84÷2=9.42(厘米) 3.14×37.68×30+3.14×(18.842-9.422)×2 =118.3152×30+3.14×(354.9456-88.7364)×2=3549.375+3.14×266.2092×2=3549.375+835.896888×2=3549.375+1671.793776=5221.168776(平方厘米)≈5221(平方厘米)故答案为:5221. 【考点】圆柱圆锥的容积。
2021-2022学年数学六年级下册圆柱和圆锥专项练习附参考答案(综合卷)

2021-2022学年数学六年级下册圆柱和圆锥专项练习一.解答题(共20题,共111分)1.一个圆柱体的蓄水池,从里面量底面周长31.4米,深2米,在它的内壁与底面抹上水泥。
(1)抹水泥的面积是多少平方米?(2)蓄水池能蓄多少吨水?(每立方米水约重1.1吨)2.一个圆锥体的体积是15.7立方分米,底面积是3.14平方分米,它的高有多少分米。
3.一个圆锥形的煤堆,底面直径是8米,高1.4米,如果每立方米煤重2500千克,这堆煤共有多少千克?4.一个圆柱形的粮仓,从里面量得底面直径是3米,装有2.5米高的小麦.如果每立方米小麦重0.7吨,这个粮仓装有多少吨的小麦?5.在一个底面半径为10厘米的圆柱形杯里装满水,水里放了一个底面半径为5厘米的圆锥形铅锤,当铅锤从水中完全取出后,杯里的水面下降了0.5厘米,这个铅锤的体积是多少?6.把一个底面半径是4厘米,高是6分米的铁制圆锥体放入盛满水的桶里,将有多少立方厘米的水溢出?7.一个圆柱和一个圆锥底面积比为2:3,体积比为5:6,求高的比。
8.一个压路机的滚筒横截面的直径是1米,长是1.8米,转一周能压路多少平方米?如果每分钟转8周,半小时能压路多少平方米?9.一个圆锥体钢制零件,底面半径是3cm,高是2m,这个零件的体积是多少立方厘米?10.一个圆柱形铁皮水桶(无盖),高10dm,底面直径是6dm,做这个水桶大约要用多少铁皮?11.一堆圆锥形黄沙,底面周长是25.12米,高1.5米,每立方米的黄沙重2吨,这堆沙重多少吨?12.一个底面直径为20厘米的圆柱形容器里,盛有一些水。
把一个底面半径为3厘米的圆锥形铅锤完全浸没在水中,水面上升0.3厘米,这个铅锤的高是多少厘米?13.李大爷家去年夏季收获的小麦堆成了圆锥形,高1.5m,底面周长是18.84m,这堆小麦的体积是多少?14.做一个圆柱形的笔筒,底面半径是4厘米,高是10厘米,做这个笔筒至少需要多少平方厘米的铁皮?(保留整数)15.一个无盖圆柱形油桶,底面半径2分米,高8分米,里面装满汽油,1升汽油重0.8千克。
2024年人教版六年级下册数学暑假专项提升训练:圆柱与圆锥(含答案)

2024年人教版六年级下册数学暑假专项提升训练:圆柱与圆锥一、单选题1.一个圆柱和一个圆锥的底面积之比是1 ∶ 3,高之比是2 ∶ 3,体积之比是( )。
A.1 ∶ 3B.2 ∶ 3C.2 ∶ 9D.4 ∶ 92.如图,长方形的长是4 cm,宽是2 cm,分别以长边和宽边所在的直线为轴,旋转一周可以得到两个不同的圆柱。
这两个圆柱的体积相比较,( )。
A.甲大B.乙大C.同样大D.无法判断3.若圆柱的底面半径和高都扩大到原来的3 倍,则它的体积扩大到原来的( )倍。
A.3B.6C.27D.364.若一个圆柱的高缩小到原来的1,底面半径扩大到原来的3倍,则体积( )。
3A.扩大到原来的3倍B.扩大到原来的9倍C.缩小到原来的1D.不变35.一个圆柱形零件,把它浸入一个装水的容器中,两种摆法都恰好有一半浸没在水中(如甲、乙两图所示)。
下面说法正确的是( )。
A.浸没在水中的体积相等,表面积不相等B.浸没在水中的体积相等,表面积也相等C.浸没在水中的表面积相等,体积不相等D.浸没在水中的体积和表面积都不相等二、填空题6.一个圆柱形状的饼干盒,底面直径是20厘米,高10厘米,要在它的侧面贴上的商标纸,商标纸的面积至少是 平方厘米。
7.一圆锥形沙堆,底面积是5平方米,高2.1米,这堆沙 立方米。
8.一个圆柱形的饮料瓶,从里面量半径是3厘米,高1分米,这个饮料瓶最多能装 毫升的饮料。
9.一个圆柱的底面周长是12.56分米,高是6分米,它的侧面积是 平方分米,表面积是 平方分米,体积是 立方分米。
10.甲、乙两个圆柱高的比是3:2,底面直径的比是2:3,则甲、乙体积比为 ,如果乙圆柱的体积是54立方厘米。
则甲圆柱的体积是 。
11.自来水管的内直径是2cm,水管内水的流速是每秒8cm,一位同学去洗手,走时忘记关水龙头,5分钟后另一位同学发现并关掉了水龙头,共浪费了 升水。
12.一个棱长为6分米的正方体木块的表面积是 平方分米,把它削成一个最大的圆锥,这个圆锥的体积是 立方分米。
圆柱与圆锥(能力提升题)

圆柱与圆锥(能力提升题)专项一:圆柱、圆锥切割问题例1:把一个圆柱沿底面直径竖直切成2块,表面积增加了24cm²。
若平行于底面切成三块,表面积增加了50.24cm²。
若削成一个最大的圆锥,则体积减少多少立方厘米?分析:这类问题要弄清楚增加或减少的表面积或体积是哪一部分,与原图形的什么量有关系。
由平行于底面切割的条件,可以求出底面积,进而求出底面半径;根据沿底面直径切割的条件,可以求出底面直径乘高的结果,再根据前面求出的半径,可以求出圆柱的高,进而求得圆柱的体积,也就可以求出体积减少多少了。
解答圆柱的底面积:50.24÷4=12.56(cm)r²:12.56÷3.14=4(cm²)r=2cm圆柱的高:24÷2÷(2×2)=3(cm圆柱的体积:3.14×2²×3=37.68(cm³)减少的体积:37.68×(1-)=25.12(cm³)反馈练习把一个圆柱沿两条垂直的底面直径竖直切成4块,表面积增加了192cm²;平行于底面切成两块,表面积增加了56.52cm²,原来圆柱的体积是多少立方厘米?2.若把一个圆柱平行于底面切去2cm厚,则表面积减少50.24cm²,体积变成原来的。
如果将这个圆柱切成一个最大的圆锥,那么圆锥的体积是多少立方厘米?专项二:利用比的知识解决圆柱、圆锥问题例2:一个圆柱和一个圆锥底面半径的比是2∶1,高的比是1∶3,它们的体积和是31.4cm³。
圆柱和圆锥的体积各是多少立方厘米?分析:解决此类实际问题,通常需要根据题目中给出的已知量的比,求出未知量的比或未知量与已知量的比,然后再结合已知量求出未知量。
根据“圆柱和圆锥底面半径的比是2∶1”可知,圆柱和圆锥底面积的比是2²∶1²=4∶1。
圆柱和圆锥精选拓展提高专项训练(一)附答案

圆柱与圆锥精选拓展提高专项训练(一)2017年2月一.解答题(共30小题)1、(2011•龙湖区)一个高为20厘米得圆柱体,如果它得高增加3厘米,则它得表面积增加150、72平方厘米,求原来圆柱体得体积就是多少立方厘米?2、(2008•高邮市)如图中就是一块长方形铁皮(每个方格得边长表示1平方分米),剪下图中得涂色部分可以围成一个圆柱.这个圆柱得侧面积就是多少平方分米?体积就是多少立方分米?3.如图就是一个油桶,里面装了一些油(图中阴影部分),求油有多少升?4。
求表面积(单位:厘米)5。
只列式,不计算、(1)做30根圆柱形铁皮通风管,每根底面直径为26厘米,长85厘米,至少需要多少铁皮?(2)明珠灯泡厂原计划30天生产4。
2万只,实际提前4天完成任务,实际每天生产多少只?6、A与B都就是高度为12厘米得圆柱形容器,底面半径分别就是1厘米与2厘米,一水龙头单独向A注水,一分钟可注满.现将两容器在它们得高度得一半出用一根细管连通(连通管得容积忽略不计),仍用该水龙头向A注水,求(1)2分钟容器A中得水有多高?(2)3分钟时容器A中得水有多高。
7、(2013•陆良县模拟)一个圆柱体得底面半径与一个圆锥体得底面半径之比为4:1,该圆锥体得底面积为12、56平方米,已知圆柱体得高为3厘米,试求圆柱体得体积就是多少?8、(2005•华亭县模拟)瞧图计算:右边就是一个圆柱体得表面展开图,根据所给得数据,求原来圆柱体得体积。
9。
在方格纸上画出右边圆柱得展开图(每个方格边长1cm)、算出制作这个圆柱所用材料得面积、10、选择下面合适得图形围成最大得圆柱.(单位:厘米)(1)您会选择_________ 图形(填编号)(2)计算它得表面积与体积.11、一个圆柱形玻璃缸,底面直径20厘米,把一个钢球放入水中,缸内水面上升了2厘米,求这个钢球得体积。
(π取3、1)12、一个圆柱侧面展开就是一个正方形,这个圆柱得底面直径就是4厘米,高就是多少?13.将下面得长方形(图1)绕着它得一条边旋转一周,得到一个圆柱体(图2),求旋转所形成得圆柱体得体积.(单位:厘米)14。
2021-2022学年六年级数学下册第三单元圆柱与圆锥检测卷(拓展卷)(含答案)人教版

需要今年的学习资料请关注微信公众号“学海无涯甜作舟”秒到,也可以打开入微信群秒进,也可以加老师微信shen88168007秒发,只需要10秒即可获得你需要的资料!绝密★启用前2021-2022学年六年级数学下册第三单元圆柱与圆锥检测卷(拓展卷)考试时间:90分钟;满分:102分班级:姓名:成绩:注意事项:1.答题前填写好自己的班级、姓名等信息。
2.请将答案正确填写在答题区域,注意书写工整。
卷面(2分)。
我能做到书写端正,格式正确,卷面整洁。
一、认真填一填。
(每空2分,共28分)1.一个圆柱的底面半径为5厘米,侧面展开后正好是一个正方形,圆柱的体积是( )立方厘米。
2.把一个高为5厘米的圆柱沿着底面直径往下切,表面积增加40平方厘米,这个圆柱的表面积是( )平方厘米。
3.如图所示,将底面直径是8cm的圆柱若干等分,拼成一个近似的长方体,表面积增加了280cm,拼成的长方体的体积是( )3cm。
4.一根圆柱形木料底面直径20厘米,长1.8米。
把它截成3段,使每一段都是圆柱形,截开后表面积增加了( )平方厘米。
5.爷爷有一只玻璃茶杯(如图),为了防止烫手,妈妈制作了这个杯子的布套,布套的高是茶杯的1 2,做这个布套至少要用布( )平方厘米。
(结果保留整数)6.一个长方体水池,长15米,宽8米,深1.57米,池底有根内径为2分米的出水管.放水时,水流速度平均每秒2米.放完池中的水需要()分钟。
7.把长2.4米的圆柱形钢材按1∶2∶3截成三段,表面积比原来增加56平方厘米,这三段圆钢材中最长的一段比最短的一段体积多( )立方厘米。
8.一个圆柱形状的容器装满水(如图)。
将一个底面半径为0.5dm,高为2.4dm的圆柱形状的石柱竖直放入容器中(石柱的底面与容器完全接触),容器中的水溢出( )3dm。
9.一个药瓶,它的瓶身呈圆柱形(不包括瓶颈),如下图所示,瓶内药水的体积为25.2cm3。
瓶子正放时,瓶内药水液面高7cm,瓶子倒放时,空余部分高2cm。
2023-2024学年六年级数学下册 第3单元 圆柱与圆锥 能力提升训练 人教版

2023-2024学年六年级数学下册第3单元圆柱与圆锥能力提升训练人教版一、选择题(共9题;共18分)1.(2分)一个圆柱和一个圆锥,底面积的比是2∶3,它们的体积相等。
圆柱和圆锥的高的最简整数比是()。
A.1∶2B.5∶12C.8∶5D.2∶12.(2分)把棱长r厘米的正方体木料削成一个最大的圆锥,圆锥的体积占正方体体积的()。
A.π4B.π12C.12π3.(2分)下面的说法中,错误的是()。
A.一个长方体和一个圆锥等底等高,这个长方体的体积是圆锥的3倍B.圆柱有无数条高,圆锥只有1条高C.两个圆柱的侧面积相等,这两个圆柱的体积也一定相等D.圆柱的底面周长和高相等,它的侧面沿高剪开后一定是一个正方形4.(2分)将一个高为5厘米的圆柱分成若干等份后,拼成一个近似长方体,表面积比圆柱多30平方厘米。
圆柱的体积是()A.45πB.90πC.1505.(2分)一张长方形纸分别沿长和宽可以围成两个不同的圆柱,即甲圆柱和乙圆柱(如图),比较这两个圆柱的侧面积的大小,下面说法正确的是().A.甲圆柱侧面积大B.乙圆柱侧面积大C.侧面积相等D.不能确定6.(2分)把底面直径3cm,高6cm的圆柱,沿底面直径切割成两个半圆柱后,表面积共增加了()cm2。
A.54B.36C.18D.97.(2分)一个圆锥的体积是12.56cm³,比与它等底等高的圆柱的体积少()cm³。
A.12.56B.25.12C.3.14D.6.288.(2分)典典、聪聪两人分别将一张长6.28cm,宽3.14cm的长方形纸以不同的方法围成一圆柱(接头处不重叠),那么围成的两个圆柱的()。
A.高一定相等B.侧面积一定相等C.底面积一定相等D.体积一定相等9.(2分)下面测量圆锥的高的方法正确的是()。
A.B.C.D.二、判断题(共6题;共12分)10.(2分)一个圆柱的底面周长和高相等,那么它的侧面沿高展开一定是正方形。
2021-2022学年六年级数学下册第三单元圆柱与圆锥检测卷(拓展卷)(含答案)人教版

需要今年的学习资料请关注微信公众号“学海无涯甜作舟”秒到,也可以打开入微信群秒进,也可以加老师微信shen88168007秒发,只需要10秒即可获得你需要的资料!绝密★启用前2021-2022学年六年级数学下册第三单元圆柱与圆锥检测卷(拓展卷)考试时间:90分钟;满分:102分班级:姓名:成绩:注意事项:1.答题前填写好自己的班级、姓名等信息。
2.请将答案正确填写在答题区域,注意书写工整。
卷面(2分)。
我能做到书写端正,格式正确,卷面整洁。
一、认真填一填。
(每空2分,共28分)1.一个圆柱的底面半径为5厘米,侧面展开后正好是一个正方形,圆柱的体积是( )立方厘米。
2.把一个高为5厘米的圆柱沿着底面直径往下切,表面积增加40平方厘米,这个圆柱的表面积是( )平方厘米。
3.如图所示,将底面直径是8cm的圆柱若干等分,拼成一个近似的长方体,表面积增加了280cm,拼成的长方体的体积是( )3cm。
4.一根圆柱形木料底面直径20厘米,长1.8米。
把它截成3段,使每一段都是圆柱形,截开后表面积增加了( )平方厘米。
5.爷爷有一只玻璃茶杯(如图),为了防止烫手,妈妈制作了这个杯子的布套,布套的高是茶杯的1 2,做这个布套至少要用布( )平方厘米。
(结果保留整数)6.一个长方体水池,长15米,宽8米,深1.57米,池底有根内径为2分米的出水管.放水时,水流速度平均每秒2米.放完池中的水需要()分钟。
7.把长2.4米的圆柱形钢材按1∶2∶3截成三段,表面积比原来增加56平方厘米,这三段圆钢材中最长的一段比最短的一段体积多( )立方厘米。
8.一个圆柱形状的容器装满水(如图)。
将一个底面半径为0.5dm,高为2.4dm的圆柱形状的石柱竖直放入容器中(石柱的底面与容器完全接触),容器中的水溢出( )3dm。
9.一个药瓶,它的瓶身呈圆柱形(不包括瓶颈),如下图所示,瓶内药水的体积为25.2cm3。
瓶子正放时,瓶内药水液面高7cm,瓶子倒放时,空余部分高2cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱和圆锥精选拓展提高专项训练(一)2017年2月一.解答题(共30小题)1.(2011•龙湖区)一个高为20厘米的圆柱体,如果它的高增加3厘米,则它的表面积增加平方厘米,求原来圆柱体的体积是多少立方厘米2.(2008•高邮市)如图中是一块长方形铁皮(每个方格的边长表示1平方分米),剪下图中的涂色部分可以围成一个圆柱.这个圆柱的侧面积是多少平方分米体积是多少立方分米3.如图是一个油桶,里面装了一些油(图中阴影部分),求油有多少升4.求表面积(单位:厘米)5.只列式,不计算.(1)做30根圆柱形铁皮通风管,每根底面直径为26厘米,长85厘米,至少需要多少铁皮(2)明珠灯泡厂原计划30天生产万只,实际提前4天完成任务,实际每天生产多少只6.A和B都是高度为12厘米的圆柱形容器,底面半径分别是1厘米和2厘米,一水龙头单独向A注水,一分钟可注满.现将两容器在它们的高度的一半出用一根细管连通(连通管的容积忽略不计),仍用该水龙头向A注水,求(1)2分钟容器A中的水有多高(2)3分钟时容器A中的水有多高.7.(2013•陆良县模拟)一个圆柱体的底面半径与一个圆锥体的底面半径之比为4:1,该圆锥体的底面积为平方米,已知圆柱体的高为3厘米,试求圆柱体的体积是多少8.(2005•华亭县模拟)看图计算:右边是一个圆柱体的表面展开图,根据所给的数据,求原来圆柱体的体积.9.在方格纸上画出右边圆柱的展开图(每个方格边长1cm).算出制作这个圆柱所用材料的面积.10.选择下面合适的图形围成最大的圆柱.(单位:厘米)(1)你会选择_________ 图形(填编号)(2)计算它的表面积和体积.11.一个圆柱形玻璃缸,底面直径20厘米,把一个钢球放入水中,缸内水面上升了2厘米,求这个钢球的体积.(π取)12.一个圆柱侧面展开是一个正方形,这个圆柱的底面直径是4厘米,高是多少13.将下面的长方形(图1)绕着它的一条边旋转一周,得到一个圆柱体(图2),求旋转所形成的圆柱体的体积.(单位:厘米)14.计算下面图形的表面积.(单位:分米)15.制作一个底面直径是4厘米,高也是4厘米的圆柱.(1)模型是否已经制作_________(2)画出侧面展开图的草图,并标上有关数据:(3)画出该圆柱沿直径劈成相等的两半,所得到的截面的草图,并标出相关数据:(4)求出这个圆柱的表面积(写出每一步的计算公式).(5)求出圆柱的体积(写出每一步的计算公式).(6)如果把这圆柱看作是一块圆柱形木料,沿横截面切成两段,表面积多出多少(7)如果把这圆柱看作是一块圆柱形木料,沿直径劈成相等的两半,表面积多出多少16.一根圆柱形钢材长2米,如果把它锯成两段,表面积比原来增加平方分米,求这根2米长钢材的质量.(每立方分米钢重千克)17.在一个底面直径为20厘米的圆柱形容器中装有水,将一个底面直径为10厘米的圆柱铁锤放入水中,当铁锤从圆柱形容器中取出后,水面下降1厘米,求铁锤的高.18.一个圆柱形玻璃容器的底面直径是10厘米.把一块铁块从这个容器的水中取出后,水面下降2厘米,这块铁块的体积是多少19.把一个高3分米的圆柱体的底面分成许多相等的扇形,然后把圆柱体切开,拼成一个与它等底等高的近似长方体,它的表面积比圆柱体的表面积增加了36平方分米,求这个圆柱体的体积.20.求表面积.(单位:厘米)21.一个圆柱形量筒,底面半径是5厘米,把一块铁块从这个量筒里取出后,水面下降3厘米,这块铁块的体积是多少(π取)22.用铁皮做20节同样大小的圆柱形烟囱,每节长8分米,底面直径是10厘米,至少需要铁皮多少平方分米23.两个底面积相等的圆柱,高的比是5:8,第一个圆柱的体积是90立方厘米,第二个圆柱的体积是多少立方厘米24.一个圆柱体的直径是8厘米,沿这个圆柱体的直径竖直分成相同的两块,表面积增加了112平方厘米.求这个圆柱体的体积25.一个圆柱形水槽,底面半径是8厘米,水槽中完全浸没着一块铁件,当铁件取出时,水面下降了5厘米.这块铁件的体积是多少立方厘米26.一个圆柱体木块的高是8厘米,沿直径竖直从中间切开,表面积增加了96平方厘米,这个圆柱体的表面积是多少平方厘米27.一个长方形长5厘米,宽2厘米,若以长为轴旋转一周,得到的几何体的体积是多少立方厘米若以宽为轴旋转一周,得到的几何体的体积是多少立方厘米28.一个长为8厘米,宽为2厘米的长方形,以长为旋转轴旋转一周得到的立方体是一个_________ .(1)它的高是_________ 厘米,底面圆的半径是_________ 厘米;(2)它的底面积是多少(3)它的侧面积为多少(4)这个立方体的表面积是多少平方厘米29.一个长方形的长是5厘米,宽是2厘米,以其中的一条边为轴旋转一周,可以得到一个圆柱,圆柱体积最大是多少立方厘米30.一个长方形的长是8厘米,宽是4厘米,以长为轴旋转一周,形成的圆柱体的体积是多少立方厘米2014年3月yang_194911的小学数学组卷参考答案与试题解析一.解答题(共30小题)1.(2011•龙湖区)一个高为20厘米的圆柱体,如果它的高增加3厘米,则它的表面积增加平方厘米,求原来圆柱体的体积是多少立方厘米考点:圆柱的侧面积、表面积和体积.专题:压轴题;立体图形的认识与计算.分析:增加的表面积就是增加的圆柱的侧面积,可用增加的侧面积除以3得到这个圆柱的底面周长,然后再利用圆的周长公式C=2πr和圆的面积公式S=r2π计算出圆柱的底面积,最后再根据圆柱的体积公式底面积×高进行计算即可得到答案.解答:解:圆柱的底面周长为:÷3=(厘米),圆柱的底面半径为:÷÷2=8(厘米),原来圆柱的体积为:×82×20=×20,=(立方厘米),答:原来圆柱体的体积是立方厘米.点评:解答此题的关键是确定计算出圆柱的底面周长进而计算出圆柱的底面半径,然后再按照圆柱体的体积公式进行计算即可.2.(2008•高邮市)如图中是一块长方形铁皮(每个方格的边长表示1平方分米),剪下图中的涂色部分可以围成一个圆柱.这个圆柱的侧面积是多少平方分米体积是多少立方分米考点:圆柱的侧面积、表面积和体积;圆柱的展开图.分析:圆柱的侧面积就是这个长方形铁皮的面积,长方形的宽等于圆柱的高即2分米;长即分米等于圆形底面的周长,所以可以求出底面半径列式为:÷÷2=1(分米),然后利用圆柱的体积公式V=Sh和长方形的面积公式S=ab即可解答.解答:解:侧面积:×2=(平方分米);体积:÷÷2=1(分米),12×=(立方分米);答:这个圆柱的侧面积是平方分米;体积是立方分米.点评:本题考查了圆柱的体积公式V=Sh和长方形的面积公式S=ab的灵活应用,知道求圆柱的侧面积就是求这个长方形铁皮的面积是本题解答的关键.3.如图是一个油桶,里面装了一些油(图中阴影部分),求油有多少升考点:圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:根据圆柱的体积公式V=sh=π(d÷2)2h,把直径10厘米,高18﹣12厘米代入公式,解答即可.解答:解:×(10÷2)2×(18﹣12),=×25×6,=×150,=471(立方分米),471立方分米=471升;答:油有471升.点评:本题主要是利用圆柱的体积公式V=sh=π(d÷2)2h解决生活中的实际问题.4.求表面积(单位:厘米)考点:圆柱的侧面积、表面积和体积.分析:此图形是由两个圆柱组成的,要求此图形的表面积,只要求出大圆柱的表面积与小圆柱的侧面积即可,用大圆柱的表面积加小圆柱的侧面积就是此题图形的表面积.解答:解:大圆柱的侧面积为:×8×5,=×40,=(平方厘米);大圆柱的底面积是:×(8÷2)2,=×16,=(平方厘米);大圆柱的表面积:+=(平方分米);小圆柱的侧面积是:×6×3,=×18,=(平方厘米),表面积:+=(平方厘米),答:该图形的表面积是平方厘米.点评:解答此题的关键是,观察该图形的表面都是由哪些面组成的,再根据相应的公式解决问题.5.只列式,不计算.(1)做30根圆柱形铁皮通风管,每根底面直径为26厘米,长85厘米,至少需要多少铁皮(2)明珠灯泡厂原计划30天生产万只,实际提前4天完成任务,实际每天生产多少只考点:圆柱的侧面积、表面积和体积;整数、小数复合应用题.分析:(1)要求做圆柱形铁皮通风管需要的铁皮,实际是求圆柱形铁皮通风管的侧面积,根据圆柱的侧面积公式,S=ch,求出做一根圆柱形铁皮通风管需要的铁皮,进而求出做30根圆柱形铁皮通风管需要的铁皮;(2)要求实际每天生产灯泡的只数,必须知道生产灯泡的总只数与实际生产的天数,用30﹣4就是实际生产的天数,由此列式解决问题.解答:解:(1)×26×85×30;(2)万只=42000只,42000÷(30﹣4).点评:解答此题的关键是根据两个题目的特点,知道做铁皮通风管需要的铁皮实际是求圆柱形铁皮通风管的侧面积;在解答有关计划与实际的问题时,找出各个量之间的关系,由问题到条件,一步一步的确定列式方法.6.A和B都是高度为12厘米的圆柱形容器,底面半径分别是1厘米和2厘米,一水龙头单独向A注水,一分钟可注满.现将两容器在它们的高度的一半出用一根细管连通(连通管的容积忽略不计),仍用该水龙头向A注水,求(1)2分钟容器A中的水有多高(2)3分钟时容器A中的水有多高.考点:等积变形(位移、割补);圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:已知B容器的底面半径是A容器的2倍,高相等,B容器的容积就是A容器的4倍;因此,单独注满B 容器需要4分钟,要把两个容器都注满一共需要1+4=5(分钟),已知现在两个容器在它们高度一半处用一个细管连通,2分钟后A中的水位是容器高的一半,即12÷2=6(厘米)(其余的水流到B容器了);由此可知,用分钟的时间两个容器中的水的高度相等,都是6厘米;以后的时间两个容器中的水位同时上升,用3﹣=(分钟)分钟注入两个容器的高度加上6厘米即是3分钟后的高度.解答:解:(1)A容器的容积是:×12=×1=(立方厘米),B容器的容积是:×22=×4=(立方厘米),÷=4,即B容器的容积是A容器容积的4倍,因为一水龙头单独向A注水,一分钟可注满,所以要注满B容器需要4分钟,因此注满A、B两个容器需要1+4=5(分钟),已知现在两个容器在它们高度一半处用一个细管连通,2分钟后A中的水位是容器高的一半,即12÷2=6(厘米);(2)因为注满A、B两个容器需要1+4=5(分钟),所以5÷2=(分钟)时,A、B容器中的水位都是容器高的一半,即6厘米,分钟后两容器中的水位是同时上升的,3分钟后,实际上3﹣=(分钟)水位是同时上升的,÷5=,12×=(厘米),6+=(厘米);答:2分钟时,容器A中的高度是6厘米,3分钟时,容器A中水的高度是7.2厘米.点评:此题主要考查圆柱的体积(容积)的计算,解答关键是理解现在两个容器在它们高度一半处用一个细管连通,当A中的水高是容器高的一半时,其余的水流到B容器了;以后的时间两个容器中的水位同时上升,即注满两容器时间的乘容器高就是分钟上升的水的高度.7.(2013•陆良县模拟)一个圆柱体的底面半径与一个圆锥体的底面半径之比为4:1,该圆锥体的底面积为平方米,已知圆柱体的高为3厘米,试求圆柱体的体积是多少考点:圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:先根据圆的面积公式求出这个圆锥的底面半径,再利用圆柱体的底面半径与一个圆锥体的底面半径之比,求出圆柱的底面半径,圆柱的高已知,据此利用圆柱的体积公式即可解答问题.解答:解:÷=4,因为4=2×2,所以圆锥的底面半径是2米,则圆柱的底面半径就是2×4=8(米),3厘米=0.03米,所以圆柱的体积是:×82×,=×64×,=(立方米),答:这个圆柱的体积是6.0288立方米.点评:此题主要考查圆柱的体积公式的计算应用,关键是求得圆锥的底面半径,从而得出圆柱的底面半径,要注意单位名称的统一.8.(2005•华亭县模拟)看图计算:右边是一个圆柱体的表面展开图,根据所给的数据,求原来圆柱体的体积.考点:圆柱的展开图;圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:观察图形可知,圆柱的底面周长是25.12厘米,高是5厘米,先利用圆柱的底面周长求出这个圆柱的底面半径:÷÷2=4厘米,再利用圆柱的体积公式V=sh=πr2即可解答.解答:解:底面半径是:÷÷2=4(厘米),体积是:×42×5,=×80,=(立方厘米),答:原来圆柱的体积是立方厘米.点评:此题考查圆柱的底面周长和体积公式的综合应用,熟记公式即可解答.9.在方格纸上画出右边圆柱的展开图(每个方格边长1cm).算出制作这个圆柱所用材料的面积.考点:圆柱的展开图;画指定周长的长方形、正方形;画圆;圆柱的侧面积、表面积和体积.分析:(1)应明确圆柱由三部分组成:圆柱的侧面、圆柱的上、下两个底面;由题意可知:该圆柱的底面直径是2厘米,高为3厘米,根据“圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高”可知:先根据圆的周长=πd求出圆柱侧面展开后的长,宽为圆柱的高;圆柱的上下两个底面为直径为2厘米的圆,画出即可;(2)根据“圆柱的表面积=侧面积+2个底面积=πdh+π(d÷2)2×2”代入数值解答即可.解答:解:(1)长方形的长:×2=(厘米),宽为3厘米;两个直径为2厘米的圆;画图如下:(2)×2×3+×(2÷2)2×2,=+,=(平方厘米);答:这个圆柱所用材料的面积为平方厘米.点评:此题主要考查了圆柱的特征以及圆柱的表面积的计算方法.10.选择下面合适的图形围成最大的圆柱.(单位:厘米)(1)你会选择③⑥⑨图形(填编号)(2)计算它的表面积和体积.考点:圆柱的侧面积、表面积和体积;圆柱的展开图.分析:圆柱侧面展开图是个长方形,长方形的长等于圆柱底面周长,宽等于圆柱的高,可选出3组图形围成圆柱,其中底面积最大的圆柱,它的体积为最大,再根据表面积和体积公式,即可列式解答.解答:解:(1)×2×2=(厘米),×2×3=(厘米),×2×4=(厘米),所以②④⑦、①⑤⑧、③⑥⑨每三个图形能围成圆柱,其中底面积最大的是⑥⑨,因此③⑥⑨能围成最大的圆柱;故答案为:③⑥⑨.(2)侧面积:×5+×42×2,=+,=(平方厘米),体积:×42×5,=×80,=(立方厘米);答:它的表面积是平方厘米,体积是立方厘米.点评:此题主要考查圆柱的侧面展开图(长方形)与圆柱之间的关系及圆柱的侧面积、体积公式及其计算.11.一个圆柱形玻璃缸,底面直径20厘米,把一个钢球放入水中,缸内水面上升了2厘米,求这个钢球的体积.(π取)考点:探索某些实物体积的测量方法;圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:根据题意知道,圆柱形玻璃缸的水面上升的2厘米的水的体积就是钢球的体积,由此根据圆柱的体积公式,V=sh=πr2h,代入数据,列式解答即可.解答:解:×(20÷2)2×2,=×100×2,=620(立方厘米);答:这个钢球的体积是620立方厘米.点评:把钢球完全放入水中,水上升的部分的体积就是钢球的体积,由此利用圆柱的体积公式,列式解答即可.12.一个圆柱侧面展开是一个正方形,这个圆柱的底面直径是4厘米,高是多少考点:圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:由题意知,圆柱的侧面展开正好是一个正方形,也就是说,它的底面周长和高是相等的,要求圆柱的高,只要求出圆柱的底面周长是多少即可.解答:解:×4=(厘米);答:高是12.56厘米.点评:此题是有关圆柱侧面的问题,圆柱的侧面展开图的长和宽分别是圆柱的底面周长和高.13.将下面的长方形(图1)绕着它的一条边旋转一周,得到一个圆柱体(图2),求旋转所形成的圆柱体的体积.(单位:厘米)考点:圆柱的侧面积、表面积和体积.分根据题意可知,圆柱的底面半径是2厘米,高是4厘米,圆柱的体积公式是:v=sh,代入数据计算即析:可.解答:解:×22×4=×4×4=×4=(立方厘米);答:这个圆柱体的体积是立方厘米.点评:此题主要考查圆柱体的体积计算,关键是理解圆柱是由一个矩形(长方形),以一条边为轴旋转得到的立体图形,作为轴的一边就是圆柱的高,它的邻边就是圆柱的底面半径;根据圆柱的体积公式v=sh,列式解答即可.14.计算下面图形的表面积.(单位:分米)考点:圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:根据图示可知,图示的表面积为底面直径为8分米,高为12分米的圆柱体表面积的一半再加长为12分米,宽为8分米的长方形的面积,根据圆柱体的表面积公式和长方形的面积公式进行解答即可.解答:解:[×8×12+2××()2]÷2+8×12,=[+]÷2+96,=÷2+96,=+96,=(平方分米);答:图形的表面积是平方分米.点评:此题主要考查的是圆柱体表面积计算公式的灵活应用.15.制作一个底面直径是4厘米,高也是4厘米的圆柱.(1)模型是否已经制作已制作(2)画出侧面展开图的草图,并标上有关数据:(3)画出该圆柱沿直径劈成相等的两半,所得到的截面的草图,并标出相关数据:(4)求出这个圆柱的表面积(写出每一步的计算公式).(5)求出圆柱的体积(写出每一步的计算公式).(6)如果把这圆柱看作是一块圆柱形木料,沿横截面切成两段,表面积多出多少(7)如果把这圆柱看作是一块圆柱形木料,沿直径劈成相等的两半,表面积多出多少考点:简单的立方体切拼问题;圆柱的特征;圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:(1)模型已制作;(2)根据圆柱的特征展开,然后标上数据即可;(3)把圆柱沿直径劈成相等的两半,然后截面的草图,并标上数据即可;(4)根据圆柱的表面积公式计算即可;(5)根据圆柱的体积公式计算即可;(6)沿横截面切成两段后实际上多出了2个底面的面积;(7)沿直径劈成相等的两半后实际多出的两个正方形的面积,正方形的边长为圆柱的直径(或者高)是4厘米.解答:解:(1)模型已制作;(2)根据圆柱的特征展开,然后标上数如下:(3)把圆柱沿直径劈成相等的两半,并标上数据如下:(4)圆柱的表面积:S=π×2+2πrh,=××2+2×××4,=×4×2+2××2×4,=+,=(平方厘米);(5)圆柱的体积:V=πh,=××4,=×4×4,=(立方厘米);(6)S=π×2,=××2,=×4×2,=(平方厘米);答:表面积多出平方厘米.(7)S=d2×2,=42×2,=16×2,=32(平方厘米);答:表面积多出32平方厘米.点评:此题考查了圆柱的特征,及圆柱的展开图和圆柱的体积,然后代入表面积和体积公式进行计算即可;对于横截面只要区分开是沿那个方向切开即可.16.一根圆柱形钢材长2米,如果把它锯成两段,表面积比原来增加平方分米,求这根2米长钢材的质量.(每立方分米钢重千克)考点:简单的立方体切拼问题;圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:平方分米是圆柱形钢材的两个底面的面积,由此根据圆柱的体积公式,V=sh,求出圆柱形钢材的体积,再用体积乘千克就是钢材的重量.解答:解:2米=20分米,(÷2)×20×,=×20×,=×,=(千克);答:这根钢材重489.84千克.点评:关键是知道平方分米是哪部分的面积,再利用相应的公式解决问题.17.在一个底面直径为20厘米的圆柱形容器中装有水,将一个底面直径为10厘米的圆柱铁锤放入水中,当铁锤从圆柱形容器中取出后,水面下降1厘米,求铁锤的高.考点:探索某些实物体积的测量方法;圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:此题中下降水的体积就是圆柱铁锤的体积,再用下降水的体积除以圆柱铁锤的底面积,即可解决问题.解答:解:[×(20÷2)2×1]÷[×(10÷2)2],=×100÷[×25],=4(厘米);答:容器的水面下降了4厘米.点评:此题主要考查圆柱的体积公式及其应用,关键要理解下降水的体积即从水中取出物体的体积.18.一个圆柱形玻璃容器的底面直径是10厘米.把一块铁块从这个容器的水中取出后,水面下降2厘米,这块铁块的体积是多少考点:探索某些实物体积的测量方法;圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:只要求出下降水的体积就是这个铁球的体积,由题可知道圆柱的底面直径是10厘米,下降的水深是2厘米,运用圆柱的体积公式v=πr2h解答出来即可.解答:解:×(10÷2)2×2,=×25×2,=157(立方厘米);答:这块铁块的体积是157立方厘米.点评:本题考查了圆柱的体积公式的运用,同时考查了学生的转化思想,即把铁块的体积转化成下降水的体积.19.把一个高3分米的圆柱体的底面分成许多相等的扇形,然后把圆柱体切开,拼成一个与它等底等高的近似长方体,它的表面积比圆柱体的表面积增加了36平方分米,求这个圆柱体的体积.考点:简单的立方体切拼问题;圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:圆柱体底面平均分成若干扇形,切开后拼成一个与它等底等高的近似长方体,则比原来圆柱的表面积增加了2个以底面半径和高为边长的长方形的面的面积,因为圆柱的高是3分米,由此可以求出圆柱的底面半径是36÷2÷3=6分米,再利用圆柱的体积公式即可计算解答.解答:解:圆柱的底面半径是:36÷2÷3=6(分米),圆柱的体积是:×62×3,=×36×3,=(立方分米);答:这个圆柱的体积是立方分米.点评:解决此类问题的关键是:根据圆柱切割拼组长方体的方法,得出增加了的表面积是以底面半径和高为边长的两个长方形的面的面积.20.求表面积.(单位:厘米)考点:圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:圆柱的体积=πr2h,据此代入数据即可解答.解答:解:10÷2=5(厘米),×(10÷2)2×15,=×25×15,=(立方厘米),答:圆柱体的体积是立方厘米.点评:此题主要考查圆柱的体积公式的计算应用.21.一个圆柱形量筒,底面半径是5厘米,把一块铁块从这个量筒里取出后,水面下降3厘米,这块铁块的体积是多少(π取)考点:探索某些实物体积的测量方法;圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:分析条件后可得出“铁块的体积=水面下降后减少的水那一部分的体积”,则求这块铁块的体积是多少,也就是求半径是5厘米,高是3厘米的圆柱形容器里水的体积.解答:解:V=sh,=×52×3,=×75,=(立方厘米);答:这块铁块的体积是立方厘米.点评:本题主要考查不规则物体体积的求法,明确这块铁块的体积,也就是求半径是5厘米,高是3厘米的圆柱形容器里水的体积.22.用铁皮做20节同样大小的圆柱形烟囱,每节长8分米,底面直径是10厘米,至少需要铁皮多少平方分米考点:圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:烟囱要用多少铁皮,求的是圆柱的侧面积,已知底面直径可求底面周长,进而乘圆柱的高可得一节烟囱要用多少铁皮,然后乘20节即可得20节烟囱要用多少铁皮.解答:解:10厘米=1分米,一节烟囱要用铁皮面积:×1×8=(平方分米);20节烟囱要用铁皮的面积:×20=(平方分米);答:至少需要铁片平方分米.点评:此题考查圆柱的侧面积,按公式计算即可,计算时注意别漏了乘20.23.两个底面积相等的圆柱,高的比是5:8,第一个圆柱的体积是90立方厘米,第二个圆柱的体积是多少立方厘米考点:圆柱的侧面积、表面积和体积.专题:立体图形的认识与计算.分析:根据题意,圆柱的体积=底面积×高,可知底面积相等的两个圆柱体高的比等于体积的比,所以可设第二个圆柱的体积为x立方厘米,然后列出比例式,解答即可.解答:解:设第二个圆柱的体积是x立方厘米,5:8=90:x,5x=90×8,5x=720,x=144;答:第二个圆柱的体积是144立方厘米.点评:解答此题的关键是确定底面积相等的两个圆柱体,高的比=体积的比,进行计算即可.24.一个圆柱体的直径是8厘米,沿这个圆柱体的直径竖直分成相同的两块,表面积增加了112平方厘米.求这个圆柱体的体积。
