讲梁的挠曲线方程与积分解法
梁的挠曲线近似微分方程及其积分.

二、结构形式叠加(逐段刚化法):
A a
P q
C a
P
a
a
q
a
a
+
=
例6-4-1 按叠加原理求A点转角 和C点挠度.
解、载荷分解如图
、由梁的简单载荷变形表,
查简单载荷引起的变形。
PA
Pa 2 4 EI
f ( x) M ( x) I0 M ( x)
EI ( x) I0
EI 0
EI 0 f ( x) M ( x)
M(x) M(x) I0
I(x)
:几何形状:长度不变,惯性矩变为I0 。
:实梁对应方程: EI0 f ( x) M ( x)
虚梁对应方程:
M (x) q(x)
:令:q(x) M ( x ) 依此建立虚梁上的分布载荷。
8
2
- q a2
a2
C
a
求虚梁B点的剪力和弯矩
x
13qa 3 RA 72
QB
13qa3 72
1 2
qa2 2
a
5 72
qa3
MB
13qa3 72
a
1 2
qa2 2
a
a 3
7 72
qa4
D
B
5qa 3 72EI
7qa4 f B 72EI
C点左右位移怎样?
四、变截面直梁的共轭梁法: :将截面的变化折算到弯矩之中去。
梁的挠曲线微分:方E程 If ( x) M ( x) 梁的外载与内力的为关 : M系(x) q(x)
上二式形式相同,用类比法,将微分方程从形式上转化为 外载与内力的关系方程。从而把求挠度与转角的问题转化为求 弯矩与剪力的问题。
工程力学第2节 确定梁位移的积分法

例10-3 如图图示简支梁, l 4m ,弯曲刚度EI 1640N m2。在无限接近右支座 B 处受到矩为的集中 力偶 M e 120 N m 作用,试求 (1)转角方程和位移方 程;(2)梁的最大挠度。
解:(1)转角方程和 位移方程 x
Me FA FB l
梁的弯矩方程为
5
3
4
令 x 0,得B截面的挠度为
ql yB ( ) 30 EI
Me 2 x C (1) 将上式一次积分得转角 y' 2EIl
Me M ( x) x l
转角方程
Me 2 y' x C 2EIl
(1)
再次积分,可得挠度方程:
Me 3 y x Cx D (2) 6EIl 边界条件: x 0 时,y0 0 ; x l 时,yl 0 M el D0 C 6EI M e 2 M el 2 0 . 00915 x 0.0488 x 2EIl 6EI M e 3 M el 3 x 0.0488x y x x 0.00305 6EIl 6EI
再次积分,可得挠度方程:
1 1 1 3 4 y ( qlx qx ) Cx D EI 12 24
1 1 1 3 2 ( qlx qx ) C EI 4 6 1 1 1 3 4 y ( qlx qx ) Cx D EI 12 24 边界条件: x 0 时,y0 0 ; x l 时,yl 0
补充例 悬臂梁AB在三角形分布载荷作用下,跨 度为l,抗弯刚度为EI,如图所示。试求B截面的挠度。 解:与B截面距离为 x 的任一截面的载荷集度为
x q( x) q l
(0 x l )
概述梁的挠曲线近似微分方程及其积分用积分

x 0 时, , wA 0 A w A 0
当
求得:
C 0; D 0
y
L
P
B
B
wB
x
写出挠曲线方程并画出挠曲线的大致形状
Px 2 w( x) ( x 3L) 6EI
最大转角及最大挠度(绝对值最大)
max
PL2 B ( ) 2 EI
wmax
PL3 wB ( ) 3EI
C
x1
x2
AB段 (0 x1 a)
a
a
M1 Px1
BC段 (0 x2 a)
M 2 P(a x2 )
写出挠曲线微分方程并积分 AB段
M1 Px1 EIw1
P 2 EI1 x1 C1 EIw1 2 P 3 EIw x1 C1 x1 D1 6
1
y
M<0
d2w 0 2 dx
d2w M ( x) 2 EI dx
o
x
d 2 w M ( x) (2) 2 EI dx
式(2)就是挠曲线近似微分方程。
对于等截面直梁,挠曲线近似微分方程可写成如下形式:
d w M ( x) 2 EI dx
二、求转角方程、挠曲线方程 1.微分方程的积分
最大挠度及最大转角
dw( x 2 ) Pa 2 ( x2 ) dx 2 2 EI
2
y
a
P
C
C
max C CB
wmax
Pa 2 2EI
L
B
x
wB
Pa 2 wB (3L a) 6EI
例2 求图示梁自由端的转角和挠度。
用积分法求挠度和转角

确定。例如,在固定端处的挠度w=0,转角=0。在铰支座处的挠
度w=0。这种条件称为边界条件。
当梁的弯矩方程必须分段建立时,挠曲线微分方程也应该分段
建立。在这种情况下,经过积分后,积分常数增多,除利用边界条
件确定积分常数外,还应根据挠曲线为连续光滑这一特征,利用分
段处有相同挠度和相同转角的条件来确定积分常数。这种条件称为
1 M (x) ρ(x) EI
由高等数学可知,平面曲线w = w(x)上任一点的曲率为
目录
弯曲变形\用积分法求挠度和转角
d2w
1 dx 2
(x)
[1
(
dw
)
2
]
3 2
dx
在小变形条件下,转角是一个很小的量,故 (dw)2 << 1,于是
上式可简化为
dx
1 ρ(x)
d2w dx2
d2w dx2
最大挠度发生的位置。在本例中梁的挠曲线应为一上凸曲线,并在
固定端处与梁变形前的轴线相切。由此可知,梁的最大转角和最大
挠度都发生在自由端B处。
目录
弯曲变形\用积分法求挠度和转角
将x=l代入方程,得
max
B
ql3 6EI
wmax
wB
ql4 8EI
() (↓)
所得B为正值,说明横截面B顺时针方向转动;所得wB为正值,
梁的挠曲线近似微分方程也分段建立,分别为
AC段:
d 2 w1 dx 2
Fb EIl
x
CB段:
d2w2 Fb x F (x a) dx2 EIl EI
目录
弯曲变形\用积分法求挠度和转角
2) 对微分方程进行积分并确定积分常数。对两段的挠曲线近似 微分方程分别积分两次后得
§6-2梁的挠曲线近似微分方程及其积分(精)
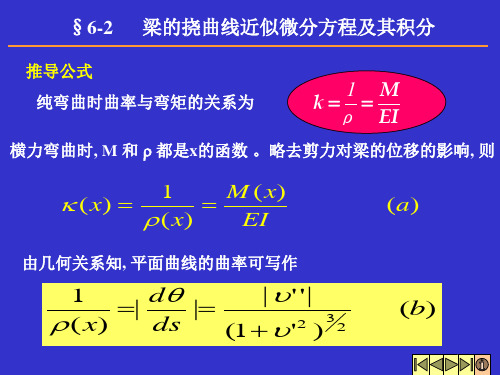
大挠度fmax和最大转角max。
解: 由对称性可知梁的两个支反力为
RA
q
RB
ql RA RB 2
A
B
x
y
l
例题 6 -2 图
此梁的弯矩方程及挠曲线微分方程分别为
ql 1 2 q M ( x) x qx (lx x 2 ) 2 2 2 q 2 EI ' ' M ( x) (lx x ) 2
EI ' ' M ( x) Pl Px (2)
例题 6-1 图
对挠曲线近似微分方程进行积分, 得
Px 2 EI ' Plx C1 (3) 2 Plx 2 Px 3 EI C1 x C 2 (4) 2 6
边界条件为 :
x
A
l x
B x
x 0, 0 x 0, ' 0
EIυ [ M ( x )dx ]dx C1x C2
得
C1 EI '| x 0 EI 0 C2 EI 0
式中,θ 0 和 v0 分别代表坐标原点处截面的转角和挠度。
例题6-3 图示一抗弯刚度为EI的简支梁, 在D点处受一集中 力P的作用。试求此梁的挠曲线方程和转角方程,并求其最大 挠度和最大转角。
两段梁的挠曲线方程分别为
1 挠曲线方程 转角方程 挠度方程
( 0 «x «a)
2
( a«x « l )
b " P x EIv1 M1 l
b EIv2 " M 2 P x P( x a) l
3 θA ql θ max θB 24 EI
x
q
用积分法求梁的挠和转角

d2y dx 2
M (x) EI
EI
d2y dx2
M
(x)
积分一次得转角方程为:
EIy M (x)
dy dx
M (x) EI
dx
C
再积分一次得挠度方程为:
y
M (x) EI
dx
dx
Cx
D
§8-3 用积分法求梁的挠度和转角
梁截面的已知位移条件或位移约束条件,称为梁位移的边界条件。 积分常数C、D 由梁的位移边界条件和光滑连续条件确定。
5ql 4
ymax
y
x l 2
384EI
max
A
B
ql3 24 EI
§8-3 用积分法求梁的挠度和转角 外伸梁,承受集中载荷作用,试绘制挠曲线的大致形状图。
设弯矩刚度EI为常数。
§8-3 用积分法求梁的挠度和转角
解:1、绘制挠曲线的基本依据
1 y M (x)
(x)
EI z
根据弯矩的正、负、零值点或零值区,确定挠曲线的凹、
凸、拐点或直线区。
在梁的被约束处,应满足位移边界条件;在分段处,则 应满足位移连续条件。
§8-3 用积分法求梁的挠度和转角
三、使用视频 1.可使用的视频文件类型 常用格式为AVI,另一种为RealAudio。 2.加入视频 1)定位光标 2)选择“插入/图片/视频”菜单命令,弹出
“视频”对话框 3)选择视频文件 3.修改视频属性 1)选定视频位置上出现的图片 2)单击右键选择“图片属性” 3)在“图片属性”对话框中设置视频的属性
C ql3 24
EIy ql x3 q x4 Cx D 12 24
材料力学 积分法求梁的变形

M ( x ) = r EI Z 1
1 = ± r d 2 w dx 2 d w é 2 ù 1 + ( ) ê ú dx ë û
3
±
d 2 w dx 2 d w 2 ù é 1 + ( ) ú ê dx û ë
3
M ( x ) = EI Z
边界条件、连续条件应用举例
弯矩图分三段,共6 个积分常数需6个边界条 件和连续条件 A B
P C D
w
铰连接
ω A点: A = 0, q A = 0
B 点 : w B 左 = w B 右
C点 : w C左 = w C右
D点:w D = 0
q C 左 = q C 右
边界条件、连续条件应用举例
y
边界条件
3 qL C1 = 6 EI z
EI zw =
1 (L - x )4 + C q 1 x + C 2 24
x = 0 x = 0 x = L
q = 0 w = 0
qL3 q B = 6 EI z
q =-
3 qL C2 =24 EI z
挠曲线方程应分两段AB,BC.
F A
a
q
B
EI z
L
共有四个积分常数
C
x
边界条件
x = a x = a + L
连续条件
w B = 0 wC = 0
y
x = a
w B1 = w B 2 q B1 = q B 2
例题 5.4 &
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
梁的挠曲线近似微分方程

由边界条件:
x 0,yA 0 ; D 0
xl,
yB 0 ;
C ql3 24
q
A
x θA
θB
y
l
B
x
EIy ql x3 q x4 Cx D 12 24
EIy ql x2 q x3 ql3 4 6 24
q (l3 6lx2 4x3)
ql x3 q x4 ql3 x 12 24 24
24EI
最大转角和最大挠度分别为:
y qx (l3 2lx2 x3) 24EI
ymax
y
x l 2
5ql 4 384EI
max
A
B
ql3 24 EI
外伸梁,承受集中载荷作用,试绘制挠曲线的大致形状图。 设弯矩刚度EI为常数。
§6-3 用积分法求梁的变形
解:1、绘制挠曲线的基本依据
1 y M (x)
(x)
EI z
根据弯矩的正、负、零值点或零值区,确定挠曲线的凹、
凸、拐点或直线区。
在梁的被约束处,应满足位移边界条件;在分段处,则 应满足位移连续条件。
载荷作用。试求此梁的转角方程和挠度方程,并确定最大转角
和最大挠度。
y
q
解:
FRA
FRB
ql 2
A
B
x
M(x) ql x q x2 22
x
l
EIy ql x q x2 22
EIy ql x2 q x3 C 46
EIy ql x3 q x4 Cx D 12 24
§6-3 用积分法求梁的变形
§6-3 用积分法求梁的变形
梁的挠曲线近似微分方程:
d 2 y M (x) dx2 EI
里兹法积分法求塔式简支梁挠曲线方程

6、塔式简支梁的弯曲。
如图所示两端简支的梁,梁的抗弯刚度不均匀,梁的中间有一段刚度为2EI ,其为梁长2l 的一半,梁两端各有一段刚度为EI ,其长为2/l ,如果梁的中间受均布荷载q ,用里兹法求梁中点最大挠度和近似挠度曲线。
里兹法:解:设OB 段的挠曲线为321123()()2l w a x l a x l a x ⎛⎫=-+-+- ⎪⎝⎭BC 段的挠曲线为2212()()w a x l a x l =-+-从中可以看出,这两个函数满足2()0w l =;1222l l w w ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭;''1222l l w w ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭又由'1(0)0w =得2123324a a l a l =-所以3221232332()()42l w a l a l x l a x l a x ⎛⎫⎛⎫=--+-+- ⎪ ⎪⎝⎭⎝⎭22223232()()4w a l a l x l a x l ⎛⎫=--+- ⎪⎝⎭由对称性可得''2''22222122233022()()3(22)lll U EI w dx EI w dx EIl a a a l a l =+=-+⎰⎰321230111721232lq E qw dx ql a a l ⎛⎫=-=- ⎪⎝⎭⎰故总势能222322332311173(22)1232=+q U E EIl a a a l a l ql a a l ∏⎛⎫+=-+-⎪⎝⎭由势能驻值条件20a ∏∂=∂;30a ∏∂=∂得 3232432116(2)012176()032EIl a a l ql EIl a l a ql -+=--=联立得2237576ql a EI=-;37288ql a EI =则33221169377()()11525762882ql ql ql l w x l x l x EI EI EI ⎛⎫=----+- ⎪⎝⎭322216937()()1152576ql ql w x l x l EI EI=----DO 段近似挠曲线可相应由对称性得到,且跨中挠度4161(0)768ql w EI=.积分法求解挠曲线及跨中挠度: OB 段的挠曲线微分方程为2''221111132()()22228l EIw M x q x ql l x qx ql ⎛⎫=-=---=- ⎪⎝⎭则'321113268EIw qx ql x A =-+ 4221121322416EIw qx ql x A x A =-++OB 段的挠曲线微分方程为''222111()()222EIw M x ql l x qlx ql =-=--=-则'22211142EIw qlx ql x B =-+ 32221211124EIw qlx ql x B x B =-++由边界条件及连续性条件'1(0)0w =;12(2)(2)//w l w l =;''12(2)(2)//w l w l =;2()0=w l得10A =;4265384=A ql ;31548B ql =;42116B ql = 所以4224113654832768w qx ql x ql EI EI EI =-+ 32234211511244816w qlx ql x ql x ql EI EI =-++跨中挠度4165(0)768ql w EI=.里兹法相对于积分法跨中挠度相对误差为444616565 6.15%768768768=ql ql ql EI EI EI-。
梁的挠曲线近似微分方程及其积分
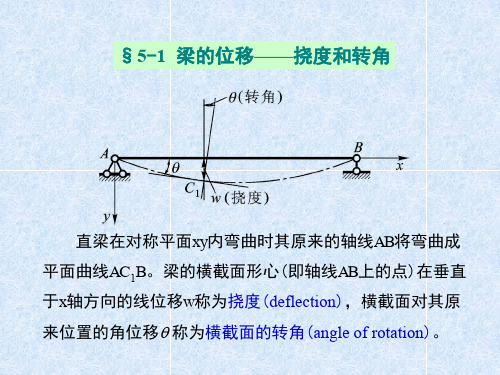
qmax和最大挠度wmax为
qmax qA qB
Fl 2 16 EI
wm a x
wC
Fl 3 48 EI
思考: 试绘出图示两根简支梁的弯矩图,并描出它们的挠 曲线。并指出:(1) 跨中挠度是否最大?(2)跨中挠度的值 是否接近最大挠度值?
l/2
l/4
§5-3 按叠加原理计算梁的挠度和转角
22
2
挠曲线近似微分方程为
EIw M x q lx x2 2 以x为自变量进行积分得:
EIw
q 2
lx2 2
x3 3
C1
EIw
q 2
lx3 6
x4 12
C1x
C2
该梁的边界条件为 在 x=0 处 w=0, 在 x=l 处 w=0
D2 0
由另一支座约束条件 w2|x=l=0 有
b l3 F l a3
EIw2 |xl F l b 6 C2l 0
即
C2
Fb 6l
l2
b2
从而也有
C1
Fb 6l
l2 b2
从而得两段梁的转角方程和挠曲线方程如下:
左段梁 (0 x a)
等,且均为最大值,故
qmax q A qB
ql3
24 EI
最大挠度在跨中,其值为
wmax
w
|xl
2
ql 2
24 EI
l 3
2l
l 2
2
l 2
概述梁的挠曲线近似微分方程及其积分用积分

y
a
P
A x1
C
x2
L
x B
EIw
0
P(a
x1)
(0 x1 a) (a x2 L)
EIw
P 2
x12
Pax1
C1
C2
EIw
P
6
x13
Pa 2
x12
C1x1
D1
C2 x2 D2
确定积分常数 边界条件
EI 0 x1 0
EI w 0 x1 0
C1 0 D1 0
连续性条件
当 x1 x2 a 时,
讨论题:指出下列梁的边界条件。
q
q
A
A
B
a
l
a
B L
连续性条件: 挠曲线上任意点有唯一确定的挠度和转角。 若连续性条件不满足,则挠曲线就不连续(图a)和不光滑(图b)。
A
C
B
A
C
B
(图a)
(图b)
对上述梁:
边界条件: wA 0, wB 0
连续性条件: wC左 wC右 , C 左 C 右
挠曲线近似微分方程
(x2 )
dw(x2 ) dx2
Pa 2 2EI
y
a
P
C
Bx
C wB
L
例2 求图示梁自由端的转角和挠度。
P
EI
2EI
解: 建立坐标系并写出弯矩方程
A x1
B x2 C
a
a
AB段 (0 x1 a)
M 1 Px1
BC段 (0 x2 a)
M 2 P(a x2 )
写出挠曲线微分方程并积分
AB段 EIw1 M1 Px1
3 2EI
《材料力学》课件5-2梁的挠曲线近似微分方程及积分
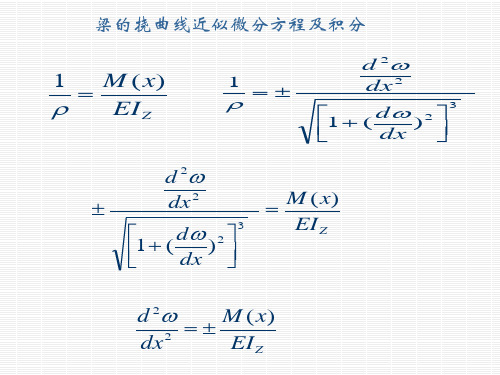
例题 5.3 求图示简支梁在集中荷载F的作用下(F力在右半跨)的最大挠度。
a A
F b
B
M1x x
Fb L
x
0 xa
C
Fb
l
L
x
y
x
Fa
M 2x
Fb L
x
F x
a
axL
L
AC段
EEIIzz11M2F1Lbxx 2
CF1b L
x
CB段
EI
C
q
EA
L1
x
B EI Z
L
全梁仅一个挠曲线方程
共有两个积分常数
边界条件
x0
A 0
xL
B
LBC
qLL1 2EA
例题 5.5
用积分法求图示各梁挠曲线方程时,试问在列各梁 的挠曲线近似微分方程时应分几段;将分别出现几个 积分常数,并写出其确定积分常数的边界条件
挠曲线方程应分两段AB,BC.
A
EI z
zz222FMLb2xx2
1FFbx
2L
x
aF2 xC2
a
EI z1
Fb 6L
x3
C1x
D1
x 0D1 00 0 x L L 0
EI z2
Fb 6L
x3
1 6
Fx
a3
C2 x
D2
x a 1Da1 D22a 1aC1C22a
6FEELbI2FIzaZLb32Ca1L3C1aCC2F1Lb2 D6FxL1b26FL2FLb3L12b6FLFa16Lb22Fax3bL122aF162aFa3aFaCba22L6L23LC0bC2 22a D2
梁的变形,挠曲线微分方程及其积分

w
M (x)dx EI
C
w
M (x) EI
dxdx
Cx
D
3.积分常数C、D的确定
边界条件
θ
连续性条件 w1 w2
1 2
(c)
4.挠曲线的大致形状
正的弯矩,挠曲线向上凹 负的弯矩,挠曲线线上凸
积分法求梁的弯曲变形 ---例题
例 如图示的悬臂梁,抗弯刚度为EI,集中载荷F,求 w(x)、θ(x)及wmax、θmax。
将边界条件代入(1)(2)两式
22
挠曲线近似微分方程:
D=0 C ql3 24
EIw M (x) ql x 1 qx2 22
积分得
EIw ql x2 q x3 C — (1)
EIw EI
EIw
ql 12
x3
ql x2 q x3 46 q x4 ql3 24 24
x
ql 3 24
46
EIw ql x3 q x4 Cx D — (2) 12 24
边界条件为
x 0, wA 0 x l, wB 0
max
A
B
ql 3 24EI
wmax
w x l 2
5ql 4 384EI
例 如图示的简支梁,抗弯刚度为EI,集中载荷F,求 w(x)、θ(x)及wmax、θmax。
对各段梁,都是由坐标原点到所研究截面之间的 梁段上的外力来写弯矩方程的。所以后一段梁的 弯矩方程包含前一段梁的弯矩方程。只增加了 (x-a)的项。
对(x-a)的项作积分时,应该将(x-a)项作为 积分变量,从而简化了确定积分常数的工作。
梁的变形,挠度和转角 挠曲线近似微分方程
一、梁的弯曲变形 挠度w 挠曲线方程
第13讲 Chapter5-1梁弯曲时的位移(挠曲线方程及其积分)

q q (6lx24x3l3)
q
2E 4 I
A
B
w qx(2lx2x3l3)
x
x
2E 4 I
y
l
最大转角和最大挠度分别为:
qmaxqA
qB
ql3 24EI
wmaxwxl 2
5ql4 384EI
转角qA为正:说明A端的横
截面沿顺时针方向转动;
wmax为正:说明梁的中点向 下移动。
25
例:已知梁的抗弯刚度为EI。试求图示悬臂梁在集中力
弯矩与二阶导数的符号总是相反
故 EIw''M式中应取负号
20
梁的挠曲线近似微分方程
EI'' w M (x) 理解近似的含义:
1. 略去了剪力的影响;
(利用了纯弯曲变形公式)
EIdd2xw2 M(x)
2. 略去了w’的影响; (利用了挠曲线的平坦特性)
21
二、用积分法求梁的变形
EI'' wM(x)
一、梁的挠曲线近似微分方程式
曲线 w w(x) 的曲率为
k1
ds dq
1 dq ds
dq
w w(x) ds
16
曲率公式的推导
ds (dx)2(dw)2 dx 1(ddwx )2 dx 1(w')2
tanq
dw dx
d dx
(tanq)w''
q q d d x(tan)d d q(tan)d d q x
因此,通常用梁的这两个位移量(w,q)来反映梁的变
形情况。
12
几个概念(一)
q
P
C
x
w
y
§8-3 用积分法求梁的挠度和转角

§8-3 用积分法求梁的挠度和转角梁是一种常见的结构,在结构设计和分析中经常需要求解梁的挠度和转角。
挠度和转角是评价梁在受载过程中变形情况的重要指标,对于保证梁的安全性和使用寿命有着重要作用。
本文将介绍用积分法求解梁的挠度和转角的方法。
首先,需要明确梁的基本假设及其约束条件。
梁的基本假设包括:梁轴线是直线、截面内部应力分布均匀、横截面形状及尺寸在受力过程中不变、截面在平面内转动的角度很小、且不影响梁内部的应力分布等。
约束条件一般有:端部固定或支承等。
接着,需要根据约束条件和配重条件列出梁的弯曲方程和边界条件。
假设梁长度为L,x轴方向为梁轴线方向,则弯曲方程为:d^2y/dx^2+M/(EI)=0其中,y是梁的挠度,M是弯矩,E是杨氏模量,I是梁的截面惯性矩,上述方程即为梁的弯曲方程。
根据约束条件和配重条件,可以列出边界条件。
对于悬臂梁,端点处有一个支承,因此边界条件为y(0)=0,d^2y/dx^2(0)=0;对于双端支承梁,两端都有支承,因此边界条件为y(0)=y(L)=0,d^2y/dx^2(0)=d^2y/dx^2(L)=0。
根据弯曲方程和边界条件可以解出梁的挠度和转角。
但是,弯曲方程中的弯矩是未知的,需要通过力学分析求解。
通常的做法是,将梁截面分成若干小段,每段长度为dx,考虑该段上下两点的受力平衡条件,可以得到该段的弯矩M。
然后将弯矩代入弯曲方程求解,就可以得到该段的挠度和转角。
最后将所有小段的挠度和转角相加即可得到整个梁的挠度和转角。
具体的计算过程可以用数值方法进行,也可以用解析方法求解。
下面介绍解析方法的两种常用技巧:超定积分法和欧拉-伯努利积分法。
超定积分法是一种较为简单和常用的求解梁挠度和转角的方法。
它的基本思想是将弯曲方程两端同时积分两次,得到整个梁的挠度函数和转角函数,然后根据边界条件解出各个常数。
以悬臂梁为例,弯曲方程为:将上式积分两次,得到:其中,b1和b2是积分常数,需要根据边界条件求解。
10.2 梁的挠曲线近似微分方程及其积分

10.2 梁的挠曲线近似微分方程及其积分纯弯曲 EIM =ρ1挠曲线曲率()322"1w w κ=⎡⎤'+⎣⎦EIM ±=d θFFxd xyxρ O正负号的确定xyOxyOM > 0w ″< 0M < 0w ″>0M 与 w ″异号()322"1w w κ=⎡⎤'+⎣⎦EIM ±=()3221w M EIw ''=-⎡⎤'+⎣⎦小变形:转角 w ′ ≈ 0 适用条件: 1. 坐标系,正负号;2. 忽略剪力 F S 对变形的影响;3. 线弹性,小变形,w′ ≈ 0。
M w EI''=-EI ——梁的抗弯刚度, 若为等直梁,EI =C ,则 EIw M''=-挠曲线近似微分方程1'd Mw x C EIθ==-+⎰12d d M w x x C x C EI ⎛⎫=-++ ⎪⎝⎭⎰⎰一次积分:二次积分:积分法计算梁的变形BAlw A = 0 w B = 0BAlw A = 0 θA =0EIw M''=-挠曲线近似微分方程 由边界条件,确定积分常数光滑连续条件——相邻挠曲线必须光滑连续。
挠曲线近似微分方程及其积分w C2= w C3θC2=θC2w B1= w B2θB1=θB2挠曲线近似微分方程及其积分——例题[例题1] 已知悬臂梁的抗弯刚度为EI,求在荷载P 作用下梁的挠曲线方程,并确定梁上的最大挠度和转角。
BAxL P有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)[解] (1)建立弯矩方程 ()()M x P L x =-()()E Iw M x P L x ''=-=--21()2xEIw P Lx C '=--+2312()26Lx x EIw P C x C =--++(3)确定积分常数 0,0x w ==0,0x w '==20C=10C=挠曲线近似微分方程及其积分——例题BALxPx(2)代入挠曲线方程并积分挠曲线近似微分方程222PLx Pxw EIθ-'==-23(3)6P Lx x w EI-=-最大挠度和转角3max()3PL f EI=↑2max2PL EIθ=挠曲线近似微分方程及其积分——例题B ALxPxmaxθmaxw挠曲线近似微分方程及其积分——例题[例题2] 已知:EI = 常数,求:1. 挠度、转角方程; 2. |θmax |, |w max |。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
②积分常数的确定——边界条件和连续条件:
边界条件:梁在其支承处的挠度或转角是已知的, 这样的已知条件称为边界条件。 连续条件:梁的挠曲线是一条连续、光滑、平坦 的曲线。因此,在梁的同一截面上不可能有两个 不同的挠度值或转角值,这样的已知条件称为连 续条件。
边界条件
积分常数2n个=2n个
连续条件
列出图示结构的边界条件和连续条件。
8
代入(1)(2)得:
1 ( 1 qx3 1 qL3)
EI 6 6
1 ( 1 qx4 qL3 x qL4 )
EI 24
68
将 x 0 代入得:
A
qL3 6EI
(与C比较知E:I A C)
A
qL4 8EI
(与D比较知E:IA )D
因此
常数C表示起始截面的转角×刚度(EI)
常数D表示起始截面的挠度×刚度(EI)
x L
2
2、
d 2
dx 2
M (x) EI z
EI" 1 qx2
2
积分一次: EI' EI 1 qx3 C (1)
积分二次:
6
EI 1 qx4 Cx D (2)
24
B X``
3、确定常数C、D.
由边界条件: x L, 0 代入(1)得: C 1 qL3
6
x L, y 0 代入(2)得: D 1 qL4
支座反力,分段列弯矩方程; 分段的原则:
①凡载荷有突变处(包括中间支座),应作为分段点;
②凡截面有变化处,或材料有变化处,应作为分段点;
③中间铰视为两个梁段间的联系,此种联系体现为两部分之间 的相互作用力,故应作为分段点;
(2)分段列出梁的挠曲线近似微分方程,并对其积分 两次
对挠曲线近似微分方程积分一次,得转角方程:
b2
)x],
BC段 (a x L)
2 ( x)
Fb 6LEI
dx 2
d2
dx2
=
M(x) EI
近似解释: (1)忽略了剪力的影响; (2)由于小变形,略去 了曲线方程中的高次项。
(3)选用不同坐标系下的挠曲线近似微分方程
2 2
d2 dx2
=
M(x) EI
d2 dx2
=
M(x) EI
二 计算弯曲变形的两种方法
1、积分法——基本方法
利用积分法求梁变形的一般步骤: (1)建立坐标系(一般:坐标原点设在左 B右
B左 B右
列出图示结构的边界条件和连续条件。
A 0
解:边界条件: A 0
C 0
D左 D右
连续条件: D左 D右
B左 B右
积分常数的物理意义和几何意义
物理意义:将x=0代入转角方程和挠曲线方程,得
C 即EI坐o标原点处梁的转角,它的EI倍就是积分常数C;
(x) d 1 ( M (x)dx c)
dx EI
再积分一次,得挠曲线方程:
(x) 1 ( M (x)dx) cx D EI
(3)利用边界条件、连续条件确定积分常数
①积分常数的数目——取决于的分段数
M (x) —— n 段 积分常数——2n个
举例:
M (x) 分2段,则积分常数2x2=4个
由光滑连续条件: x a时,1 2
x a时,1 2
可解得:
C1
Fb 6L
(L2
b2 )
C2 ,
x L,B 0
(3) (4)
D1 D2 0
(2)
则简支梁的转角方程和挠度方程为
AC段 (0 x a)
1(x)
Fb 6LEI
[3x2
(L2
b2
)],
1 ( x)
Fb 6LEI
[x3
(L2
c
c
w
x
x
W(-) θ(-)
(1)坐标系的建立: 坐标原点一般设在梁的左端,并规 定:以变形前的梁轴线为x轴,向右为正;以y轴代表曲线 的纵坐标(挠度),向上为正。
(2)挠度的符号规定:向上为正,向下为负。
(3)转角的符号规定:逆时针转向的转角为正; 顺时针转向的转角为负。
1、挠曲线:
在平面弯曲的情况下,梁变形后的轴线在弯曲 平面内成为一条曲线,这条曲线称为挠曲线。
EI2 "
Fb L
x
F(x
a),
AC段 (0 x a)
EI1'
EI1
Fb 2L
x2
C1,
EI1
Fb 6L
x3
C1x
D1,
3、确定常数
BC段 (a x L)
EI2 '
EI2
Fb 2L
x2
F 2
(x
a)2
C2
EI2
Fb 6L
x3
F 6
(x
a)3
C2 x
D2 ,
由边界条件: x 0,A 0 (1)
例题2: 一简支梁受力如图所示。试求 (x),(x) 和 A,max 。
解: 1、求支座反力
FAy
Fb L
,
FBy
Fa L
2、分段列出梁的弯矩方程
y
x
F
x A
a
C
B
b
x
L
FBy
FAy
AC段 (0 x a)
BC段 (a x L)
Fb M1(x) FAx L x,
EI1"
Fb L
x,
Fb M 2 (x) L x F (x a),
F
q
M
轴线
弯曲后梁的轴线 (挠曲线)
纵向对称面
2、挠曲线的近似微分方程
(1)曲率与弯矩、抗弯刚度的关系
纯弯曲
1
=
M EI
力学公式
横力弯曲 ( l/h>5)
1
M(x)
=
(x) EI
数学公式
d2w (1x)=+ -[1+(ddxw2 )2]3/2
dx
小挠度情形下
max=(0.01-0.001)l ;
D E即I坐o标原点处梁的挠度的EI倍就是积分常数D。
几何意义:C——转角 D——挠度
(4)建立转角方程和挠曲线方程;
(5)计算指定截面的转角和挠度值,特别注意 和
所在截 面。
max
max
及其
例题1: 悬臂梁受力如图所示。求 A和 A 。
解: 取参考坐标系Axy。
y
q
1、列出梁的弯矩方程
A
M (x) 1 qx2 (0 x L)
一 弯曲变形的量度及符号规定
梁的挠度和转角
y
p
c
c
w
x
x
1、度量弯曲变形的两个量:
(1)挠度:梁轴线上的点在垂直于梁轴线方向的所发生的线 位移ω称为挠度。(工程上的一般忽略水平线位移)
(2)转角:梁变形后的横截面相对于原来横截面绕中性轴所 转过的角位移θ称为转角。
梁的挠度和转角 2、符号规定:
y
p
max 10 or 0.0175 rad.
横力弯曲
d2 (1x)=+-[1+(ddx2 )2]3/2
dx
( d )2 << 0
dx
1
M(x)
=
(x)
EI
+ -
d2 dx2
=
M(x) EI
此即弹性曲线的小挠度微分方程
(2)挠曲线近似微分方程符号及近似解释
w
dw2 dx 2
0
2
M 0
M
M
o
x
选取如图坐标系,则 弯矩M与 d 2 恒为同号
