管理运筹学 排队论
运筹学第五章排队论

§2 排队论基本理论总廓
§2.1 排队论研究的基本问题
1.排队系统的统计推断:即通过对排队系统主 要参数的统计推断和对排队系统的结构分析,判 断一个给定的排队系统符合于哪种模型,以便根 据排队理论进行研究。
3. 服务机构
1)服务机构可以是单服务员和多服务员服务, 这种服务形式与队列规则联合后形成了多种不同队 列,不同形式的排队服务机构,如:
1 单队单服务台
1
2
..
..
nLeabharlann 多队多服务台(并列)1
2 。。。
n
单队多服务台(并列)
1
2
... n
单队多服务台(串列)
1
1
2
3
2
混合形式
2)服务方式分为单个顾客服务和成批顾客服务。 3)服务时间分为确定型和随机型。 4)服务时间的分布在这里我们假定是平稳的。
值得注意的是求稳态概
率Pn并不一定求t→∞的 极限,而只需求
P ’(t)=0 即可。
过渡状态
稳定状态
t
图3 排队系统状态变化示意图
3.根据排队系统对应的理论模型求出用以判断系统 运行优劣的基本数量指标的概率分布或特征数。 数量指标主要包括:
(1)平均队长(Ls):系统中的顾客数。 平均队列长(Lq):系统中排队等待服务的顾客数。 系统中顾客数Ls =系统中排队等待服务的顾客数Lq +正被
含优化设计与优化运营。
问题1 系统中顾客数=平均队列长(Lq)+1?
§2.3 排队论主要知识点
运筹学课件第十章排队论

第一节 引言
一、排队系统的特征及排队论 排队论研究排队系统的数学理论和方法, 是运筹学的一个重要分支。 排队问题表现:
到达的顾客 1、不能运转机器 2、病人 3、打电话 4、等待降落飞机 5、河水进入水库
要求的服务 修理 就诊 通话 降落 放水,调整水 位
服务机构 修理工人 医生 交换台 跑道指挥机构 水闸管理员
四、排队系统的主要数量指标和记号 描述一个排队系统运行状况的主要指标: 1、队长、排队长 队长:系统中的顾客数量(排队顾客+接受服务顾客)。
排队长:系统中的正在排队等待服务的顾客数量。
2、等待时间和逗留时间 等待时间:从顾客到达时刻起到他开始接受服务止这段时间 为等待时间。 逗留时间:从顾客到达时刻起到他接受服务完成这段时间为 逗留时间。
(i)队长有限:系统等待空间有限。 有限系统的空间为K, 顾客到达时的队长为L。若 L<K,则顾客进入队列等待服务,若L=K,则 顾客离去。 (ii) 等待时间有限: 顾客对等待时间具有不耐烦 性的系统。设最长等待时间是T0,某个顾客从 进入队列后的等待时间为 T。若T<T0,顾客继 续等待;若T=T0,则顾客脱离队列而离去。 (iii)逗留时间有限:等待时间与服务时间之和。
排队可以是人,也可以是物。 为了一致:将要求得到服务的对象统称为“顾客”,将提 供服务的服务者称为“服务员”或“服务机构”。
排队系统的一般描述; 顾客为了得到服务而到达系统,如果不能 立刻得到服务而又允许排队等待,则加入 等待队伍,待获得服务后离开系统。
顾客到达 队列 服务台 单服务台服务系统 服务完后离开
n 0
n ,n C 1 , 2 , 3 ,...... n u n p p , n 1 , 2 , 3 ,...... n 0
运筹学-排队论

(接受服务)
5
二、排队系统的组成和特征
1、输入过程
输入即指顾客到达排队系统,可能有以下不同情况。
(1)顾客源的组成
有限的 无限的
(2)顾客到来的方式
一个一个的 成批的
(3)顾客相继到达的间隔时间
确定型的 随机型的
(4)顾客的到来
相互独立的 关联的
(5)输入过程
平稳的,或称对时间是齐次的 非平稳的
6
14
9、其他常用数量指标
s —— 系统中并联服务台的数目;
—— 平均到达率;
1/
—— 平均到达间隔。
—— 平均服务率;
1/ —— 平均服务时间。
—— 服务强度,
每个服务台单位时间内的平均服务时间;
一般有 s ;当s=1时:
15
对于损失制和混合制的排队系统,顾客在到达服务系统时, 若系统容量已满,则自行消失。这就是说,到达的顾客不 一定全部进入系统,为此引入:
例如:某排队问题为
M / M / s / ∞ / ∞ /FCFS
则表示顾客到达间隔时间为负指数分布(泊松流);服务时 间为负指数分布;有s(s>1)个服务台;系统等待空间容量无 限(等待制);顾客源无限,采用先到先服务规则。 可简记为: M / M / s
12
四、排队系统的参数(分析结果)
1、队长(Ls) 指在系统中的顾客数,期望值 2、排队长(Lq) 指系统中排队等候服务的顾客数
13
5、忙期 指从顾客到达空闲服务机构起到服务机构再次空 闲止 这段时间长度,即服务机构连续繁忙的时间长度。 6、系统的状态n:指系统中的顾客数。 7、系统状态的概率Pn(t):指时刻t、系统状态为n的概率。 一般为关于t的微分方程、关于n的差分方程。 8、稳定状态:t→时,t=0时的系统不稳定状态将消失, 系统的状态概率分布不再随时间变化,即 limPn(t)→Pn。
运筹学排队论2

换为 t ,得到
pn
(t)
(t)n
n!
et
,
t
0,
n
0,1,2,.
表示长为t的时间区间内到达n个顾客的概率为 pn (t) ,且服从泊松分布.这称为泊松流或泊松过 程或简单流. 设t时间内到达的顾客数为随机变量N(t),则有
E[N(t)] t, D[N(t)] t.
服务台
2.C个服务台,一个公共队伍
服务台1 服务台2 服务台C
3.C个服务台,C个队伍
服务台1 服务台2 服务台C
二.排队系统的三个组成部分
1.输入过程:指顾客按怎样的规律到达. ⑴顾客的总体数或顾客源:指可能到达服务机
构的顾客总数.顾客总体数可以是有限的,也可 以是无限的; ⑵顾客到达的类型:顾客是单个到达还是成批 到达; ⑶顾客相继到达时间间隔的分布,如按泊松 分布,定长分布还是负指数分布.
排队论的创始人是丹麦哥本哈根市电话局的 工程师爱尔朗(A.K.Erlang),他早期研究电话 理论,特别是电话的占线问题,就是早期排队 论的内容.
§2 排队论的基本概念
一.排队现象的共同特征:为了获得某种服务而 到达的顾客,如不能立即得到服务而又允许排 队等候,则加入等待的队伍,获得服务后离开.我 们把包含这些特征的系统称为排队系统. 排队系统的几种情况: 1.单服务台排队系统
例9.1 某仓库全天都可以进行发料业务,假设 顾客到达的时间间隔服从均值为1的负指数分 布现在有一位顾客正好中午12:00到达领料, 试求:
(1)下一个顾客将在下午1:00前到达的概率; (2)在下午1:00与2:00之间到达的概率: (3)在下午2:00以后到达的概率。
管理运筹学课件第11章 排队论

11.1.2 排队系统的三个特征
3.服务机构 从机构形式和工作情况来看有以下几种: (1)服务机构可以没有服务员,也可以有一个或多个服务员 (服务台、窗口)。如超市的货架可以没有服务员,但交款时可 能有多个服务员。 (2)多个服务台的情况中,可以是平行排列的(并联),也可 以是前后排列的(串联),也可以是混合的。 (3)服务方式可以对单个顾客进行,也可成批进行。我们只讨 S1 S1 论单个服务情况。 S S2 S2 (4)服务时间可分为确定型的和随机型的。如旅客列车对乘客 S3 S3 的服务是按列车时刻表进行位移服务的,是确定型的;因患者病 (a)单台单队 (b)多队多台并联 (c)单队多台并联 情不同,医生诊断的时间不是确定的,是随机型的。 S1 S4 (5)服务时间的分布总假定是平稳的,即分布的期望值、方差 S1 S2 S2 等参数不受时间的影响。
第11章 排队论
教学目标与要求
【教学目标】 1.理解下列基本概念:排队系统构成、特征、分类、主要性能指标及相互关系 2.掌握以下三种排队系统主要性能指标的计算:M/M/C/∞/∞;M/M/C/N/∞; M/M/C/∞/m。 3.了解M/G/1、M/D/1的主要指标计算公式 【知识结构】
基本概念 系统、特征、分类、指标、输入输出
2013-8-9
Ls Ws , 或Ws Ls
Lq Wq ,
Ws Wq 1
Ls Lq
Ls nPn
n 0
管理运筹学课件 n s 1
Lq
(n s ) P
n
12
11.1.5 排队系统的输入和输出
2013-8-9
模型的优化(目的) 管理运筹学课件
运筹学排队论

降低平均服务时间
降低服务时间旳可变性
增长服务人员
降低平均到达人数
经过顾客预约等方法来降低到达旳可变性
集中使用服务资源
更加好地计划和调度
23
处理排队问题旳措施
2.其他措施
服务场合提供娱乐设施
医生等待室放报纸杂志
自动维修间用收音机或电视
航空企业提供空中电影
等待电梯处放镜子
超级市场把冲动性商品摆放在收款台附
排队论
1
2
•
排队论,又称随机服务系统理论(,是一
门研究拥挤现象(排队、等待)旳科学。详细
地说,它是在研究多种排队系统概率规律性
旳基础上,处理相应排队系统旳最优设计和
最优控制问题。
•排队论是1923年由丹麦工程师爱尔朗
(A.K.Erlang)在研究电活系统时创建旳.
3
案例-1 银行排队系统
4
案例-2 医院排队系统
用更快旳服务人员、机器或采用不同旳设施布局和政
策来影响顾客旳到达时间和服务时间。
9
1 排队论旳基本问题
1.1 排队论旳主要研究内容
• 数量指标
– 研究主要数量指标在瞬时或平稳状态下旳
概率分布及其数字特征,了解系统旳基本
运营特征。
• 统计推断
– 检验系统是否到达平稳状态;检验顾客到
达间隔旳独立性;拟定服务时间分布及参
数。
• 系统优化
– 系统旳最优设计和最优运营问题。
10
1.2排队论旳经济含义
• 排队问题旳关键问题实际上就是对不同
原因做权衡决策。管理者必须衡量为提
供更快捷旳服务(如更多旳车道、额外
旳降落跑道、更多旳收银台)而增长旳
运筹学——排队论
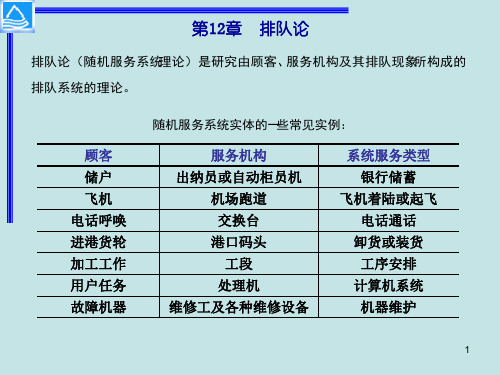
1 对于泊松流, λ表示单位时间内平均到 达的顾客数,因此, 就表示
λ
相继顾客到达的平均间 隔时间,这与 E[T ] =
1
λ
的意义正好相符。
18
服务时间v的分布 对一顾客的服务时间(也即在忙期相继离开系统的两顾客的间隔时间) 有时也服从负指数分布。这时设它的分布函数和密度函数分别为 Fv (t ) = 1 − e − µt , v的期望值 E (v) = 1 f v (t ) = µe − µt
期望值和方差相等,是泊松分布的一个重要特征,可以由此对一个 经验分布是否是泊松分布进行初步的识别。
16
3、负指数分布(negtive exponential distribution)
随机变量T的概率密度若是 λe −λt , t ≥ 0 fT (t ) = 0, t < 0 则称T服从负指数分布。T 分布函数是 1 − e −λt , t ≥ 0 FT (t ) = 0, t < 0 E[T ] = 1
∞
∑ P (t , t + ∆t ) = o( ∆t )
n=2 n
15
通过建立Pn (t )与Pn (t + ∆t )之间的关系方程并求解,得到
( λ t ) n − λt Pn (t ) = e n! t > 0, n = 0,1,2,L
Pn (t ) = Pn (0, t )表示长为t的时间区间内到达n个顾客的概率,并称随机变量 N (t )服从泊松分布,其数学期望和方差分别为 E[ N (t )] = λt Var[ N (t )] = λt
第12章 12章
排队论
排队论(随机服务系统理论)是研究由顾客、服务机构及其排队现象所构成的 排队系统的理论。
运筹学 排队论(1)

运筹学排队论1. 简介排队论是运筹学中重要的一个分支,它研究了在人员、物品或信息流动过程中产生的排队现象,并通过建立数学模型和分析这些模型来探讨和优化系统中的排队行为。
排队论在各个领域都有广泛的应用,如交通运输、电信网络、生产制造等。
2. 排队模型排队论中常用的模型包括M/M/1模型、M/M/s模型、M/G/1模型等。
其中,M表示到达过程的分布,而G表示服务时间的分布。
而数字1或s则表示系统中的服务通道数。
2.1 M/M/1模型M/M/1模型是排队论中最简单的一个模型,它假设到达过程和服务时间都服从指数分布。
该模型中只有一个服务通道。
2.2 M/M/s模型M/M/s模型是M/M/1模型的扩展,它假设到达过程和服务时间仍然服从指数分布,但有s个服务通道。
M/M/s模型适用于有多个并行服务通道的排队系统。
2.3 M/G/1模型M/G/1模型假设到达过程服从泊松分布,而服务时间服从一般分布。
该模型在实际应用中更为常见,因为服务时间往往不服从指数分布。
3. 排队论的性能度量排队论的性能度量是对排队模型进行定量分析和评估的重要手段,常见的性能度量指标包括平均等待时间、平均逗留时间、系统繁忙率等。
3.1 平均等待时间平均等待时间是指在排队系统中,每个顾客平均等待的时间长度。
通过对排队模型的分析和计算,可以得到平均等待时间的具体数值。
3.2 平均逗留时间平均逗留时间是指每个顾客在排队系统中逗留的平均时间长度。
它等于平均等待时间加上服务时间。
3.3 系统繁忙率系统繁忙率是指服务通道在单位时间内处于工作状态的比例。
它可以用来评估系统是否能够满足顾客的需求。
4. 排队论的应用4.1 交通运输排队论在交通运输领域的应用非常广泛。
例如,交通信号灯的控制就可以通过排队论进行优化,以减少车辆的等待时间和交通拥堵。
4.2 电信网络在电信网络中,排队论被用于研究数据包的传输和路由机制。
通过对排队论模型的分析,可以提高网络的传输效率和质量。
运筹学 100排队论

第10章排队论第一节排队服务系统的基本概念一、排队系统的特性排队问题的实例:超市付款,自动取款机取款,医院门诊,乘公交车,设备修理。
排队服务系统的要素:顾客源,等待队列,服务机构。
要素的特性:1. 顾客源顾客到达的间隔时间:确定、随机(分布类型);一次到达人数:单个到达,成批到达;顾客源:数量无限,数量有限。
2. 等待队列等待规则:损失制,等待制,混合制;接受服务顺序:先到先服务,后到先服务,按优先权服务,随机服务。
3. 服务机构服务台数量:单个,多个;排列方式:串联、并联、混合排列。
服务时间:固定,随机(分布类型);一次服务人数:单人,成批。
三、排队服务系统的分类按上面所讨论的排队系统各项的特性,可对排队系统作出分类。
通常按如下6方面的特性对排队系统进行分类:(a/b/c) : (d/e/f)每个字母代表一个特征,它们分别是:a:顾客到达间隔的分布,有:M──负指数分布;D──确定型;E k ──k 阶爱尔郎分布; GI ──一般相互独立的分布。
b :服务时间的分布有:M 、D 、E k 、Gc :系统中并联的服务台数,记为Sd :系统中最多可容纳的顾客数,∞~1e :顾客源总数,为∞~1f :排队服务规则 FCFS ──先到先服务 LCFS ──后到先服务 用这6个参数我们可以表示出某种类型的排队系统,如:M /M /1/10/∞/FCFS其中后三项可以省略,这时表示的是:a /b /c /∞/∞/FCFS三、排队系统的状态及参数系统状态N (t )——排队系统中的顾客数,包括等待的和正在被服务的。
其与系统运行的时刻t 相关,且是一个随机变量。
稳定状态——当系统状态与时刻t 无关时,称系统处于稳定状态。
在系统开始运行的一段时间内,系统状态随时间而变化,在运行一段时间之后,系统的状态将不随时间变化,此时系统即进入稳定状态。
排队论主要研究系统处于稳定状态的工作情况,以下参数也都针对于稳定状态进行定义。
管理运筹学讲义 第12 章 排队理论

10
OR:SM
第三节 标准M/M/1模型
一、模型特征
输入过程
顾客源无限; 顾客到达方式是单个到达,且相互独立; 输入过程服从参数为 的泊松分布,到达过程平稳。 队列为单队; 队长无限,即系统容量无限; 系统按先到先服务的等待制规则进行服务 只有一个服务台; 服务方式为单个服务,服务时间相互独立; 服务时间服从相同参数 的负指数分布。
第12 章 排队理论
学习要点 Sub title
正确理解排队系统中排队规则和服务规则 顾客输入过程和服务过程的时间分布函数 排队问题的求解步骤及运行指标间的关系 标准M/M/1模型的状态方程及其运行指标 标准M/M/c模型与c个M/M/1模型的差别 典型排队系统的结构优化和运行优化问题
求运行指标:
• 顾客数 • 排队时间 • 忙期
8 OR:SM
第二节 排队问题求解
二、分布函数
• 泊松分布
条件:
输入流的平稳性 输入流无后效性 输入流的普通性 输入流的有限性
n! 期望E (t ) t 方差 2 t
v0 v0
Pn (t )
性质: ( t ) n
平均等待时间 Wq Ws [服务时间]
忙期概率
P 0 忙 1 P
Ws Wq 1
Ws
1
Ws
Ls Ws
Lq Wq
16
Ls Lq Lq
OR:SM
第三节 标准M/M/1模型
例题
为了评价某单人理发馆随机服务系统,记录了100个工作小时, 每小时来理发的顾客数的统计情况。又记录了100次理发所用的时 间,如表所示。
管理运筹学-排队论
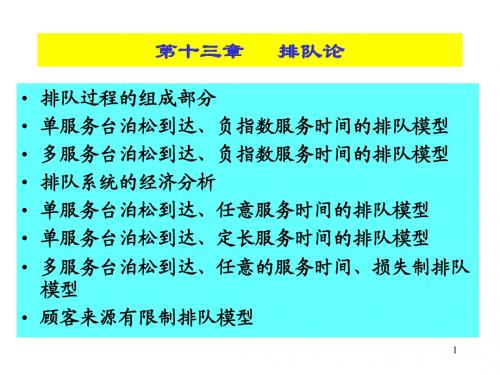
排队系统
顾客到达
排队Biblioteka 服务机构服务顾客离去
2
§1 排队过程的组成部分(2)
• 考虑要点: 1、服务台个数:单服务台、多服务台 2、顾客到达过程:本教材主要考虑顾客泊松到达情况。 满足以下四个条件的输入流称为泊松流(泊松过程) *平稳性:在时间区间[t, t+t)内到达k个顾客的概率与t无关,只与t有关。记为pk(t)。 *无后效性:不相交的时间区间内到达的顾客数互相独立。 *普通性:在足够短的时间内到达多于一个顾客的概率可以忽略;
第十三章
• • • • • • •
排队论
排队过程的组成部分 单服务台泊松到达、负指数服务时间的排队模型 多服务台泊松到达、负指数服务时间的排队模型 排队系统的经济分析 单服务台泊松到达、任意服务时间的排队模型 单服务台泊松到达、定长服务时间的排队模型 多服务台泊松到达、任意的服务时间、损失制排队 模型 • 顾客来源有限制排队模型
3
§2 单服务台泊松到达、负指数 服务时间的排队模型
• 记号: M / M / 1 / ∞ / ∞ • 条件:单位时间顾客平均到达数
单位平均服务顾客数 P0 Lq Ls Wq Ws Pw Pn
4
• 关心的项目:
1、系统中无顾客的概率 2、系统中平均排队的顾客数 3、系统中的平均顾客数 4、系统中顾客平均的排队等待时间 5、系统中顾客的平均逗留时间 6、系统中顾客必须排队等待的概率 7、系统中恰好有 n 个顾客的概率
§3 多服务台泊松到达、负指数 服务时间的排队模型
• 记号: M / M / C / ∞ / ∞ • 条件:单位时间顾客平均到达数
单位平均服务顾客数 P0 Lq Ls Wq Ws Pw Pn
运筹学第十章 排队论

一类非常重要其广泛存在的排队系统是生灭过程排队系统。 生灭过程是一类特殊的随机过程,在生物学、物理学、运筹学 中有广泛的应用。
定义1 设{N(t),t≥0 }为一个随机过程。 如N(t)的概率分布具有以下性质:
(1)假设N(t)= n,则从时刻 t 起到下一个顾客到达时刻止的 时 间服从参数为λn 的负指数分布,n=0,1,2,…。
排队是我们在日常生活和生产中经常遇到的现象。例如, 上、下班搭乘公共汽车;顾客到商店购买物品;病员到医 院看病;旅客到售票处购买车票;学生去食堂就餐等就常 常出现排队和等待现象。
除了上述有形的排队之外,还有大量的所谓“无形”排队现 象,如几个顾客打电话到出租汽车站要求派车,如果出租汽 车站无足够车辆、则部分顾客只得在各自的要车处等待,他 们分散在不同地方,却形成了一个无形队列在等待派车。
到 (7)无限长,顾客到达系统后均可进入系统排队或接受服务, (8)这类系统又称为等待制排队系统。
有限排队系统
损失制排队系统(排队空间为0的系统) (允许排队,但又不
混合制排队系统 允许队列无限长)
损失制排队系统 (排队空间为0的系统)
这是指如果顾客到达排队系统时,所有服务台都已被先来的顾 客占用,那么他们就自动离开系统永不再来。典型例子是,如 电话拔号后出现忙音,顾客不愿等待而自动挂断电话,如要再 打,就需重新拔号,这种服务规则即为损失制。
二、排队系统的描述
实际中的排队系统各有不同,但概括起来都由三个基本部 分组成:
1 输入过程; 2 排队及排队规则 3 服务机制
1.输入过程. 这是指要求服务的顾客是按怎样的规律到达排队系统的 过程,有时也把它称为顾客流. 一般可以从3个方面来描述一个输入过程。
上海交通大学管理科学-运筹学课件第六章排队论

第6章 排队论在日常生活和工作中,人们常常会为了得到某种服务而排队等候。
比如顾客到商店购买东西,病人到医院看病,汽车进加油站加油,轮船进港停靠码头等,都会因为拥挤而发生排队等候的现象。
这时,商店的售货员和顾客,医院的医生和病人,加油站的加油泵和待加油的汽车,码头的泊位和停泊的轮船等,形成了各自的排队服务系统,简称排队系统。
在一个排队系统中,通常包括一个或多个“服务设施”,服务设施可以指人,如售货员,医院大夫等。
也可以是物,如加油泵、码头泊位等。
同时还包括许多进入排队系统要求得到服务的“顾客”。
这里的顾客是指请求服务的人或物。
如到医院看病的病人,或等待加油的汽车等。
作为顾客总希望一到系统马上就能得到服务,但客观情况并非如此。
由于顾客的到达和服务机构对每个顾客的服务时间具有随机性,因此出现排队现象几乎是不可避免的。
当然,为了方便顾客减少排队时间,排队系统可以多开设服务设施。
但那将增加系统的投资和运营成本,还可能发生空闲浪费。
排队论(Queueing Theory )是为解决上述问题而发展起来的一门学科。
排队论起源于上世纪初,当时的美国贝尔(Bell )电话公司发明了自动电话后,满足了日益增长的电话通讯的需要。
但另一方面,也带来了新的问题,即如何合理配置电话线路的数量,以尽可能减少用户的呼叫次数。
如今,通讯系统仍然是排队论应用的主要领域。
同时在运输、港口泊位设计、机器维修、库存控制等领域也获得了广泛的应用。
6. 1 排队系统的基本概念6. 1. 1排队系统的一般表示一个排队系统可以抽象描述为:为了获得服务的顾客到达服务设施前排队,等候接受服务。
服务完毕后就自行离开。
其中把要求得到服务的对象称为顾客,而把服务者统称为服务设施或服务台。
在排队论中,把顾客的到达和离开称为排队系统的输入和输出。
而潜在的顾客总体又称为顾客源或输入源。
因此任何一个排队系统是一种输入-输出系统,其基本结构如图6-1所示。
排队系统图6-16. 1. 2排队系统的特征由排队系统的基本结构可知,任何一个排队系统的特征可以从以下三个方面加以描述。
运筹学中的排队论分析与应用

运筹学中的排队论分析与应用运筹学是一门研究如何最优化决策的学科。
在现代社会中,许多场景下都存在排队现象,例如银行、超市、机场等场所。
排队论作为运筹学的一个重要分支,专门研究如何通过合理的排队策略来优化服务效率与用户体验。
本文将介绍排队论的基本原理、应用场景以及如何利用排队论进行实际问题的分析与解决。
一、排队论的基本原理排队论是研究排队系统的理论与方法,其基本原理包括排队模型、排队规则以及排队指标。
1. 排队模型排队模型是对排队系统进行抽象和建模的过程,常用的排队模型有M/M/1、M/M/c、M/G/1等。
其中,M表示顾客到达过程符合泊松分布,而服务过程符合指数分布;1表示一个服务台,c表示多个服务台;G表示总体服从一般分布。
2. 排队规则排队规则是指在排队系统中,顾客到达和离开的规则。
常用的排队规则有先到先服务(First-Come-First-Serve,简称FCFS)、最短作业优先(Shortest Job First,简称SJF)、优先级法则等。
3. 排队指标排队指标是对排队系统性能的度量,常用的排队指标包括平均等待时间、平均逗留时间、系统繁忙度等。
这些指标可以帮助我们评估排队系统的效率,并进行比较和优化。
二、排队论的应用场景排队论的应用场景非常广泛,几乎可以涵盖各个行业。
下面以几个典型的应用场景为例,介绍排队论在其中的分析与应用。
1. 银行排队银行是排队论的典型应用场景之一。
通过排队论的分析,银行可以确定合理的柜台数量和工作人员配置,以减少客户的等待时间和提高服务效率。
此外,银行还可以考虑引入预约系统、自助服务等方式,进一步优化排队系统。
2. 售票窗口排队售票窗口也是一个常见的排队场景,如电影院、火车站等。
利用排队论,可以根据顾客到达的速率和服务时间的分布,预测等待时间,并提前安排足够的窗口进行服务,以提高售票效率和用户体验。
3. 交通信号灯优化交通信号灯的优化也可以借助排队论的方法。
通过对道路上车辆到达和通过的流量进行统计和分析,可以调整信号灯的信号周期和配时方案,以减少交通拥堵和减少等待时间。
运筹学 排队论

运筹学排队论引言排队论是运筹学中的一个重要分支,它研究的是如何优化排队系统的设计和管理。
排队论广泛应用于各个领域,如交通流量控制、银行业务流程优化、生产线调度等,对于提高效率和降低成本具有重要意义。
本文将介绍排队论的基本概念、排队模型以及应用案例,帮助读者了解运筹学中排队论的基本原理和应用方法。
什么是排队论排队论是一门研究排队现象的数学理论,它通过定义排队系统的各个要素,如顾客到达率、服务率、队列容量等,建立数学模型分析和优化排队系统的性能指标。
排队论主要研究以下几个方面:•排队系统的模型:包括单服务器排队系统、多服务器排队系统、顾客数量有限的排队系统等。
•排队系统的性能指标:包括平均等待时间、系统繁忙率、系统容量利用率等。
•排队系统的优化方法:包括服务策略优化、系统容量规划等。
排队论的基本概念到达过程排队论中的到达过程是指顾客到达排队系统的时间间隔的随机过程。
常用的到达过程有泊松过程、指数分布等。
到达过程的特征决定了顾客到达的规律。
服务过程排队论中的服务过程是指服务器对顾客进行服务的时间间隔的随机过程。
常用的服务过程有指数分布、正态分布等。
服务过程的特征决定了服务的速度和效率。
排队模型排队模型是排队论中的数学模型,用于描述排队系统的性能和行为。
常用的排队模型有M/M/1模型、M/M/s模型等。
这些模型分别表示单服务器排队系统和多服务器排队系统。
性能指标排队系统的性能指标用于评估系统的性能,常见的性能指标有平均等待时间、系统繁忙率、系统容量利用率等。
这些指标可以帮助决策者优化排队系统的设计和管理。
排队模型与分析M/M/1模型M/M/1模型是排队理论中最简单的排队系统模型,它是一个单服务器、顾客到达过程和服务过程均为指数分布的排队系统。
M/M/1模型的性能指标可以通过排队论的公式计算得出。
M/M/s模型M/M/s模型是排队理论中的多服务器排队模型,它是一个多个服务器、顾客到达过程和服务过程均为指数分布的排队系统。
运筹学第8章排队论

第八章 排队论排队是日常生活和经济管理经常遇到的问题,如医院等待看病的病人、加油站等待加油的汽车、工厂等待维修的机器、港口等待停泊的船只等。
在排队论中把服务系统中这些服务的客体称为顾客。
由于系统中顾客的到来以及顾客在系统中接受服务的时间等均是随机的,因此排队现象是不可避免的。
对于随机服务系统,若扩大系统设备,会提高服务质量,但会增加系统费用。
若减少系统设备,能节约系统费用,但可能使顾客在系统中等待的时间加长,从而降低了服务质量,甚至会失去顾客而增加机会成本。
因此,对于管理人员来说,解决排队系统中的问题是:在服务质量的提高和成本的降低之间取得平衡,找到最适当的解。
排队论是优化理论的重要分支。
排队论是1909年由丹麦工程师爱尔郎(A.K.Erlang )在研究电话系统时首先提出,之后被广泛应用于各种随机服务系统。
第一节 排队论的基本概念及所研究的问题一、基本概念(一)排队系统的组成一般的排队系统有三个基本组成部分:顾客的到达(输入过程)、排队规则和服务机构,如图8—1所示。
1.输入过程输入过程指顾客按什么样的规律到达。
包括如下三个方面的内容:(1)顾客总体(顾客源) 指可能到达服务机构的顾客总数。
顾客总体数可能是有限的,也可能是无限。
如工厂内出现故障而等待修理的机器数是有限的,而到达某储蓄所的顾客源相当多,可近似看成是无限的。
(2)顾客到达的类型 指顾客的到达是单个的还是成批的;(3)顾客相继到达的时间间隔分布 即该时间间隔分布是确定的(定期运行的班车、航班等)还是随机的,若是随机的,顾客相继到达的时间间隔服从什么分布(一般为负指数分布);2.排队规则排队规则指顾客接受服务的规则(先后次序),有以下几种情况。
(1)即时制(损失制) 当顾客来到时,服务台全被占用,顾客随即离去,不排队等候。
这种排队规则会损失许多顾客,因此又称为损失制。
(2)等待制 当顾客来到时,若服务台全被占用,则顾客排队等候服务。
在等待制中,又可按顾客顾客达到排队系统 图8—1服务的先后次序的规则分为:先到先服务(FCFS,如自由卖票窗口等待卖票的顾客)、先到后服务(FCLS,如仓库存放物品)、随机服务(SIRO,电话交换台服务对话务的接通处理)和优先权服务(PR,如加急信件的处理)。
运筹学第14章排队论

(1)单服务台单队
进入队列 服务台
顾客到达
…
…
顾客离去
接受服务
图9-2单服务台单队系统
(2)多服务台单队
服务台
顾客到达
…
服务台
…
顾客离去
服务台
图9-3 多服务台单队系统
(3)多队多服务台 …
顾客到达
…
服务台 服务台
…
顾客离去
…
服务台
图9-4 多服务台多队系统
(4)多服务台串联服务
顾客到达
… 服务台 … 服务台 …
P0
n1 0 n 1
P0
1
即有
P0
1
n1
n1 0 n 0
1
2、生灭过程及生灭过程排队系统
即当
n1 0
n1 n 0
时,此生灭过程存在平稳状态分布:
P0
1
n1
n1 0 n 0
1
Pn
n1 n2 0 nn1 1
P0 , n
1, 2,
• 3)在足够小的时间区间内只能有一个顾客到达,不可能有 两个以上顾客同时到达。单位时间里有x个顾客到达的概率 为:
P(x) xe ( 0, x 0,1, 2, )
x!
• 其中,λ为单位时间平均到达的顾客数,此时顾客相继到达 的时间间隔是独立的,服从参数为λ的负指数分布。
• 2、排队规则
• (1)排队系统
第十四章 排队论 1、排队的组成及基本概念 2、生灭过程 3、六个排队模型
第十四章 排队论
• 排队是日常生活中经常遇到的现象,如顾客 到商店去买东西,病人到医院去看病,当售 货员、医生的数量满足不了顾客或病人及时 服务的需要时,就出现了排队的现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 客可泛指机器、病人、飞机、轮船等,
• 服务员可泛指机修工、医生、码头等。
精选课件
3
•.
服 务 系 统
第十章
排队论
顾客:机器、飞机、轮船、病人……
顾客到达——等待服务——接受服务——顾客离去
服务员:机修工、码头设备、医生……
到达时间>服务时间
系统空闲
到达时间=服务时间 充分利用,无排队
到达时间<服务时间
3、系统中平均逗留时间
——从长远看,
入任系一统进货轮用于等待服务W加上接受服务的期望时间;
4、任在一队进中平均等待时间W q
——从长远看,
入系统货轮用于等待服务的期望时间。
精选课件
8
第十章
排队论
• 一、服务系统的结构
• 假如将要求服务的对象统称为“顾客”,
• 进行服务的统称为“服务机构”或“服务员”, 一
如果s<a,则服务员的空闲时间为总时间的 a s倍; 如果s=a,则服务员得到充分利用,且无货轮等a待;
如果s>a,则形成等待卸货队伍,且队长不断增加。
精选课件
6
第十章
排队论
.如果货轮到达时间间隔是随机变量,码头卸货时间也为随
机变量,则构成一个随机服务系统。即便货轮到达时间间
隔的平均时间还为6小时,但每一个间隔时间Xi(i=1、
• 1/ :相继顾客到达的平均间隔时间; • 1/ :一个顾客的平均服务时间;
• =(1/ :1/ )= / 称为服务强度, 指相同时
• 间区间内顾客到达的平均数与能被服务完的平均 顾
• 客数之比;
精选课件
16
第十章
排队论
• 四、系统的稳态性态
• 1、 j——稳态概率
• j定义为稳态系统中有j个顾客(包括正在服 务的)
• 都与时间无关,否则称为非平稳的;
• 6)具有不耐烦顾客的输入 • a)弃长队而去 • b)排队太久而去 • c)转队
精选课件
11
第十章
排队论
• 2、排队规则(到达的顾客按什么样的规则接受服务)
• 1)损失制 即服务台一旦占用,顾客随即离去;
• 2)等待制 顾客到达后须等待服务,服务次序为:
• a)先到先服务
2……)并不都是6小时,只是指:
n
x / n 6小时 同理,平均服务时间为4小时,从而会产生排队或服务空
闲时间。但事先无法确定。 i
i1
精选课件
7
第十章
Hale Waihona Puke 排队论对于随机服务系统希望知道:
1、在系统中平均队长L——从长远来看,平均等待 服务加上正接受服务的货轮期望数;
2、服在务队的中货平轮均期队望长数L;q——从长远来看,平均等待
运筹学
上海应用技术学院经管学院
精选课件
1
第十章 排队论
精选课件
2
第十章
• §10.1概述
排队论
• 排队论(Queing Theory)也称随机服务
• 系统。任何一个服务系统均由客体和主
• 体组成。前者是要求服务的对象,我们
• 一律称之为“顾客”;后者是提供服务的
• 机构或人员,一律称之为“服务员”。顾
• b)后到先服务
• c)随机服务
• d)有优先权的服务
• 3)混合制(损失制与等待制的混合)
• a)队长有限制的情形
• 队长<k,排队;队长>k,离去
精选课件
12
第十章
排队论
• b)等待(或逗留)时间有限制的情形
• 排队时间>t0,离去;反之排下去
• 4)从队伍的数目看,可以是单列,也可以是多列
• i:到达过程的分布;j:服务过程分布;c:服务员 数
(到达分布/服务分布/服务员数/系统容量/顾客源/排队规则)
• 到了1971年进一步定为:
(M/M/1/∞/∞/FCFS)
常规表示法为(M/M/1)
精选课件
15
第十章
排队论
• 三、排队模型中常用参数
• :到达速度(单位时间到达顾客数);
• :服务速度(单位时间服务完成数);
• 个排队系统就能抽象地描述为: • 为了获得某种服务而到达的顾客,若不能立即 • 获得服务,而又允许排队等待,则加入等待队 • 伍,获得服务之后离开系统。 • 作为服务系统基本上由三个部分组成:
精选课件
9
第十章
排队论
• 1、输入过程
刻划顾客按怎样的规律
到达服务系统,主要有以下几方面:
• 1)顾客总体(顾客源)数可能是有限的(例 厂内故障设备数)也可能是无限的(到达售票
• a)顾客可转移;
• b)顾客不可转移;
精选课件
13
第十章
排队论
• 3、服务机构 • 1)服务员的数目 • 串列、并列、串并混合 • 2)服务方式 • 对单个顾客服务或对成批顾客服务 • 3)服务时间 • 分确定型和随机型服务时间
精选课件
14
第十章
排队论
• 二、表示排队模型的符号
• D.G.Kendall 于1953 年提出排队符号: (i/j/c)
•
的概率。
j
j0
j0
0=1- ——称为系统空闲的概率
精选课件
17
第十章
排队论
• 2、
L
j0
jj
(系统人数) 1
•
3、 Lq (j1)j
j1
2(排队人数) 1
•
4、
W
(11)
1 (逗留时间
•
5、
Wq
(等待时
(1 ) 精选课件
18
第十章
排队论
进入系统的顾客逗留时间超过t的概率。
• 6、 •{w st} e( 1) t
进入系统的顾客等待时间超过t的概率。
• 7、 •P { q w t} e( 1) t
精选课件
19
第十章
排队论
• 五、稳态性态中各量值的分析
• 1、 =/ 的意义
• 1)平均到达速度与平均服务速度之比;
• 2)服务员利用率
• =1- 0 • 3)一个平均服务时间内到达的顾客平均数
排队越来越长
精选课件
4
第十章
问题是:
排队论
到达间隔、服务时间均
为随机变量,这也是随机服务 系统的基本特征。所以难以确 定系统状态,只能求期望值。 我们希望借助随机服务系统理 论来揭示这些规律。
精选课件
5
第十章
排队论
例:某港口装卸台负责货轮装卸工作,货轮即顾客以 某固定周期间隔到达港口,比如每隔a=6小时到达一艘, 而装卸台卸货需要一段时间,假定它对每艘货轮的服 务时间也是定长的,比如每艘需卸时间为s=4小时。这 一服务系统的特征是到达和服务时间均是确定不变的 定长。 结论:
窗口前的顾客总体);
• 2)顾客可能是单个到达,也可能是成批到达;
• 3)顾客相继到达的间隔时间分布可以是确定 型,也可以是随机型;
• 4)顾客的到达可以是相互独立的,即以前的 到达情况对以后顾客的到来没有影响;
精选课件
10
第十章
排队论
• 5)输入过程可以是平稳的(指描述相继到达的
• 间隔时间分布和所含参数(如 x和 2等)
