刚体、转动动能、转动惯量

合集下载

大学物理.第三章.刚体的转动

动 .试计算细杆转动到与竖直线成角时的角加速度
和角速度 .
解细杆受重力和
铰链对细杆的约束力
FN
作用 3g sin
2l
3g (1 cos )
l
§3-4 力矩的功定轴转动的动能定理
一、力矩的功
z

O
d r
速度ω 绕端点转动，摩擦系数为μ 求M摩擦力。
ω
解: 质量线密度:
m L
dm
r dr
质量元:
r dm dr
所受摩擦力为:
dF gdm gdr
例3-5 现有一圆盘在平面内以角速度ω 转动，求摩擦力产生的力矩（μ 、m、R）。
dr
ωr
解:
dm ds rdrd dF gdm grdrd dM1 rdF r2gdrd
I mi ri2 －质量不连续分布
i
r 2dm －质量连续分布
d －线分布λ＝m/ι 质量元: dm ds －面分布σ＝m/S
dV －体分布ρ＝m/V
二、决定转动惯量的三因素
1）刚体的质量； 2）刚体的质量分布；（如圆环与圆盘的不同）；
3）刚体转轴的位置。（如细棒绕中心、绕一端）
运动。一、何谓刚体
在任何情况下形状和大小都不发生变化的
物体。即每个质元之间的距离无论运动或
受外力时都保持不变。
理想模型
ri j c mj
二、刚体运动的两种基本形式 mi
平动----刚体运动时，刚体内任一直线恒保持平行的运动(即该直线方向保持不变)
刚体的平动过程
c a b
刚体的平动过程
能运用以上规律分析和解决包括质点和刚体的简单系统的力学问题.

刚体的角动量_转动动能_转动惯量

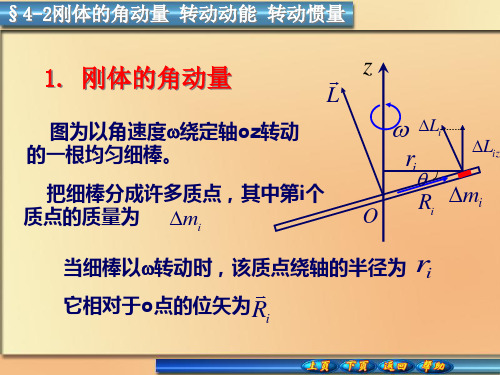
§4-2刚体的角动量转动动能转动惯量
1. 刚体的角动量
L
图为以角速度绕定轴oz转动的一根均匀细棒。
把细棒分成许多质点，其中第i个
质点的质量为 mi
z
Li
ri
Liz
O
Ri mi
当细棒以转动时，该质点绕轴的半径为
ri
它相对于o点的位矢为Ri
刚体的角动量
则 m对i o点的角动量为：
Li
Ri
mivi
就转动规律而言，刚体的质量等价于集中在离轴距离为rG的圆环上。
解设圆盘的质量面密度为，在圆盘上取一半径为r、
宽度为dr的圆环（如图），环的面积为2rdr，环的
质量dm= 2rdr 。可得
J
r2dm
R
0
2r
3dr
R4
2
1 mR2 2
转动惯量的计算
回转半径考虑到刚体的转动惯量与总质量有关，可写为
J miri2 mrG2
i
rG 称为刚体对该定轴的回转半径。
刚体的转动动能应该是组成刚体的各个质点
的动能之设和刚。体中第i个质点的质量
速度m为i
vi 则该质点的动能为：
刚体做定轴转动时12，各mi质vi2点的角速度相同。
设质点 mi 离轴的垂直距离为 ri ，则它的线速度 vi ri
因此整个刚体的动能
EK
1 2mi
vi2
1 2
miri2 2
刚体的转动动能
式中是m刚iri体2 对转轴的转动惯量
式写为
EK
1 2
J 2
，所J 以上
上式中的动能是刚体因转动而具有的动能，因
此叫刚体的转动动能。
转动惯量的计算

刚体旋转知识点归纳总结

刚体旋转知识点归纳总结1. 刚体旋转的基本概念刚体是指在一定时间内，其内部各点的相对位置不改变的物体。

刚体旋转是指刚体围绕固定点或固定轴发生的旋转运动。

在刚体旋转中，需要引入一些基本概念：1.1 刚体的转动刚体的旋转可以是定点转动，也可以是定轴转动。

在定点转动中，刚体绕固定点旋转，而在定轴转动中，刚体绕固定轴旋转。

定点转动和定轴转动都是刚体旋转运动的两种基本形式。

1.2 刚体的转动角度和角速度刚体的转动角度是刚体在单位时间内所转过的角度，通常用θ表示。

刚体的角速度是指刚体单位时间内转过的角度，通常用ω表示。

在刚体定点转动中，角速度是刚体绕定点旋转的角度速度；在刚体定轴转动中，角速度是刚体绕定轴旋转的角度速度。

1.3 刚体的转动惯量刚体的转动惯量是衡量刚体抵抗旋转的惯性大小，通常用I表示。

刚体转动惯量的大小取决于刚体形状、质量分布以及旋转轴的位置。

对于质点组成的刚体，其转动惯量可以通过对质点的质量进行积分得到。

1.4 刚体的角动量刚体的角动量是刚体旋转运动的物理量，通常用L表示。

角动量的大小和方向分别由角速度和转动惯量决定。

在定点转动中，如果刚体的角速度和转动惯量都不变，那么刚体的角动量也保持不变；在定轴转动中，如果刚体绕固定轴旋转，那么刚体的角动量也保持不变。

2. 刚体的转动力学刚体的转动力学研究刚体在旋转运动中所受的力和力矩，包括转动定律、角动量定理、动能定理等内容。

2.1 刚体的平衡刚体旋转平衡需要满足一定的条件，包括力矩平衡条件和动量平衡条件。

刚体力矩平衡条件是指刚体所受的合外力矩为零；刚体动量平衡条件是指刚体所受的合外力矩关于某一点的力矩为零。

2.2 刚体的角动量定理刚体的角动量定理描述了刚体在受到外力矩作用下，其角动量的变化规律。

根据角动量定理，刚体所受外力矩产生的角动量变化率等于刚体所受外力矩的矢量和。

2.3 刚体的动能定理刚体的动能定理描述了刚体在旋转运动中，其动能的变化规律。

根据动能定理，刚体所受外力矩产生的功率等于刚体动能的变化率。

刚体转动的动能定理

一、力矩的功 1 力矩的定义若作用的质点上的力为F ,则将r ×F 定义为力F 对O 点的力矩，记为M 。

M r F =⨯M 、F 、r 三者的方向构成右手螺旋关系。

M大小：方向：右手法则2 力矩的功设：；转盘上的微小质量元Δm 在力F 作用下以R 为半径绕O 轴转动，在dt 时间内转过角度d ，对应位移d r,路程ds,此时F 所做的元功为则总功为二、转动惯量设初速为零，质量元Δm 的动能为转盘的总动能1 定义：为物体的转动惯量。

意义：由质量和质量对于转轴的分布情况决定。

描述转动的惯性。

o z FtF nF tF ord rd θt t d d d d A F r F s F r θ=⋅==d d A M θ=21d A M θθθ=⎰αrsin t M Fr F rα==d θFtF ord r12ki i iE m v =212k ki i i i i E E m ==∆∑∑v 221()2i i i m r ω=∆∑2i i iI m r =∆∑单位：SI 制 kg m 22 定轴转动物体转动惯量的计算质量不连续分布的质点系：转动惯量定义为各个质点对该定轴的转动惯量之和2i i iI m r =∑质量连续分布的刚体：转动惯量定义为各个质点对该定轴的转动惯量的积分。

2mI r dm =⎰转动惯量的大小不仅取决于物体的质量，还与质量的分布和轴线的位置有关。

例1 求小球m 的转动惯量。

解：m 看作质点 I = m R 2例2 质量为m 的细圆环，求I 。

解：把环分成无限多个质量为dm 的小段，对每个d m 有d J = R 2对整个环有I = R 2d m = mR 2例3质量m ，半径 R 的薄圆盘，求I 。

解：把盘分成无限多个环。

取其中的一个环(半径r ，宽d r ，质量 d m )，其转动惯量 d I = r 2d m22mdm rdr Rππ=整个盘的转动惯量d rd md SrRd mRRm22322200002122R R R Rm m I dI r dm r rdr r dr mR R R ππ=====⎰⎰⎰⎰例4 长为L 、质量为m 的细长直杆，转轴垂直于细杆且通过杆中心解：杆长为L,质量为m, 则密度为＝m / L 。

3-1刚体的转动动能_转动惯量

r dr
轴
J
L
2 L
2
r
2
m L
dr
1 12
mL2
结论：同一刚体对不同的转轴有不同的转动惯量。
例2 分别求质量为m，半径为R的均匀圆环和圆盘的转动惯量（轴与圆环或圆盘平面垂直，并通过其圆心）。
mR
dm 轴
R r dr m
轴
解（1）圆环 J R2dm R2 dm mR2
（2）圆盘
dJ
r2 dm
r2 m R 2
2rdr
2m r 3dr R2
2m
J R2
R r3dr 1 mR 2
0
2
越远，转动惯量越大。
四平行轴定理
质量为m 的刚体，
如果对其质心轴的转动惯量为 JC ，则对任一与
该轴平行，相距为 d 的
转轴的转动惯量
JO JC md 2
d
C mO
J Jc md 2
圆盘对P 轴的转动惯量 P R O m
JP
1 2
mR2
mR2
质量为m，长为L的细棒绕其一端的J
Jc
1 12
mL2
O1
O1’
J
Jc
m( L)2 2
1 3
mL2
d=L/2
O2
O2’
3-1 刚体定轴转动的转动动能
Ek
i
(
1 2
mi
vi2
)
1 (
2
i
miri2 ) 2
1 J 2
2
Ek
1 2
J 2
z
vi
O
ri
mi
二转动惯量
J mjrj2 J r2dm j

第三章刚体的定轴转动

令
m r
i 1
n
2
i i
=J
1 2 Ek Jω 2
转动动能
ω 对应 v
J 对应 m
1 2 Ek mv 2
质点的动能
二转动惯量 ( moment of inertia ) 质量质点惯性大小的量度
J 与 m 对应
转动惯量刚体转动惯性大小的量度
n
J mi ri
i 1
2
体分布
dm =ρdV dm =σdS dm =λdl
面分布线分布
J r dm
2 m
单位:
kg · 2 m
说明： J r 2dm
m
1. J 与刚体的质量有关； 2. 质量一定，与质量的分布有关；
3. 与轴的位置有关。因此叫作绕轴的
转动惯量。
转动惯量的计算
例1 质量为m，半径为 r 的均匀细圆环，对通过其中心并垂直环面的转轴的转动惯量。解：根据转动惯量的定义求解。
3. 题 3－2，3－8，3－9。
§3-1
刚体的定轴转动
刚体 ( rigid body ) ：在任何情况下，其形状和大小都不发生任何变化的物体刚体是一种理想模型
一刚体的运动刚体的运动
｛转动
平动
平动 ( translation ) 刚体运动时，其上任意两点的连线，在运动过程中始终保持其方向不变。刚体的平动遵从质点运动的规律
ω ω0 αt
1 2 θ θ0 ω0t αt 2 2 2 ω ω0 2α(θ θ0 )
切向加速度 ( tangential acceleration )
dv at dt d (rω) dt dω r dt

-,-,-,-刚体的定轴转动转动定律转动惯量角动量角动量守恒定律动能定理(forC)

其中 Fz对转轴的
力矩为零，故 F 对转
轴的力矩 M zk

r

F
z

F
k
O rFz
F

M z rF sin
2019/10/24
shenyuhm44@
16
（2）合力矩等于各分力矩的矢量和 M M1 M2 M3
（3）刚体内作用力和反作用力的力矩互相抵消．
杆将在重力作用下由静止开始绕铰链O 转
动．试计算细杆转动到与竖直线成角时
的角加速度和角速度．
2019/10/24
shenyuhm44@
32
解细杆受重力和铰链对细杆的约束力FN
作用，由转动定律得
1 mgl sin J
2

m,l FN
θ mg
O
式中 J 1 ml2 3
盘, 可绕通过盘心 O 垂直盘面的水平轴转动. 转轴与
圆盘之间的摩擦略去不计. 圆盘上绕有轻而细的绳索,
绳的一端固定在圆盘上, 另一端系质量为 m 的物体.
试求物体下落时的加速度、绳中的张力和圆盘的角加速
度.
m
Ro
m

T
m
oR m
T'
Py
解：1）分析受力 2）选取坐标
注意：转动和平动的坐标取向要一致.
转轴旋转．开始起动时，角速度为零．起动
后其转速随时间变化关系为： m (1 et / )
式中 m 540 r s1， 2.0 s ．求： (1)t=6 s时电动机的转速．(2)起动后，电动机在 t=6 s时间内转过的圈数．(3)角加速度随时间变化的规律．

大学物理4-2刚体的角动量转动动能转动惯量

J ri2mi r2dm
刚体绕定轴的角动量表达式：
Lz J
刚体的转动动能
2. 刚体的转动动能
刚体的转动动能应该是组成刚体的各个质点
的动能之设和刚。体中第i个质点的质量为， mi
速度为 v,i 则该质点的动能为：
1 2
mivi2
刚体做定轴转动时，各质点的角速度相同。
设质点
mi
离轴的垂直距离为
vi ri
ri ，则它的线速度
因此整个刚体的动能
EK
12mivi2
1 2
ri2mi 2
刚体的转动动能
式中式写为
是m刚iri体2 对转轴的转动惯量
EK
1 2
J 2
，所J以上
上式中的动能是刚体因转动而具有的动能，因此叫刚体的转动动能。
转动惯量的计算
3. 转动惯量的计算
按转动惯量的定义： J ri2mi
刚体的质量可认为是连续分布的，所以上式可写成积分形式
J r2dm 要求: 细棒、薄圆盘、圆环
dl 其中质元dm可表示为 dm ds
dv
r —为质元到转轴的距离
转动惯量的计算
刚体运动：
平动：平动动能 1 mv2 线动量 mv
2
定轴转动：转动动能 1 J 2 角动量 J
2
质量是刚体平动时惯性大小的量度。转动惯量是刚体转动时惯性大小的量度。补：平行轴定理、垂直轴定理（适用于薄平面刚体）。
Li Ri pi Ri mivi
因 vi Ri ，所以 L的i 大小为
Li mi Rivi
方向如图所示。
z
L
Li Liz
ri
O Ri mi
刚体的角动量

3-(1-2)刚体、转动动能、转动惯量

O
R
Y
r
2
R Z
2
2
X
其体积：
2 2
dV r dZ ( R Z )dZ
其质量： dm dV ( R Z )dZ
2 2
其转动惯量： dI
1 2
r dm
2
1 2
( R Z ) dZ
2 2 2
15 – 8 1 多普勒效应 2
dI

r dm
2 n 2
第十五章机械波

2 i 1 质量连续分布 mi 0
n
ri M
vim
i
Ek lim

mi 0 i 1 n
2m r
2 i i
2
1
2
令I
r dm
2 n 2
1 2 1
2
( r dm )
2
或I= mi ri
i 1
I
2
Ek
1 2
对（1）式求导：
rj
mj
rij
O
rj ri rij (1) v j vi a j ai
选取参考点O，则：
mi ri
rij c
第十五章机械波 15 – 8 多普勒效应结论：刚体平动时，其上各点具有相同的速度、加速
I
2
15 – 8
多普勒效应
1 2
2
第十五章机械波
Ek
I
2
Ek
1 2
mv
2
I－转动惯量
I mi ri －质量不连续分布
i
I r dm

刚体力学

讨论：ｉ）当ｍ2R2 <ｍ1R1时，α <0，则表明圆柱体实际转动方向与所设方向相反，即ｍ2上升，而ｍ1下降。ｉｉ）当ｍ2R2 ＝ｍ1R1时，α ＝0，此时圆柱体不转动或匀速转动，ｍ2、ｍ1不运动或匀速直线运动。
25
4.定轴转动的动能定理和机械能守恒定律一. 力矩的功
ｄ A ＝ F ｄ r ＝ FC ｏｓｄｓ＝ FS ｉｎｒｄ＝ M Zｄ
刚体力学
主要内容： 1.刚体定轴转动的描述 2.力矩、刚体定轴转动定律、转动惯量
3.刚体定轴转动的动能定理和机械能守恒定律
*4.刚体定轴转动的角动量定理、角动量守恒定律
1
1. 刚体的平动、转动和定轴转动一.刚体
1.定义：在任何条件下大小和形状都不发生变化的物体称为刚体。 2.说明：刚体与质点、理想气体、点电荷等一样是
m
J
2
2
m 2 R d mR 2
2
15
例2.3 试计算质量均匀分布的薄圆盘的垂直于盘面
的中心轴的转动惯量。设圆盘质量为ｍ，半径为R。
解：
J ＝∫ ｒｄｍ
２
ｄｍ＝ •2ｒｄｒ
J＝ ∫
R 0
2 ｒｄｒ
３ 4
R 1 2 ＝＝ｍR 2 2
16
例2.4
在质量为 M ，半径为 R 的匀质
例3.3 在倾角为θ 的斜面顶端固定一滑轮，用一根绳子缠绕数圈后引出与M连接，M与斜面摩擦系数为μ （如图），设滑轮质量为ｍ，半径为R，轴处无摩擦。试分析M作加速运动的条件。Ｎ‘
解: 由牛顿第二定律
Ｏｍｇｆ
Ｔ
Ｎ
M ｇ s in θ － T － μ N ＝ M a

6.1 刚体运动学(大学物理)

1、转动惯量

刚体转动时，刚体内的各质点作圆周运动，刚体的动能等于各质点动能之和。
mn
m1
rn
r1
r2 m2
1 1 1 2 2 2 Ek m1v1 m2v2 mnvn 2 2 2 n n 1 1 2 2 mivi mi (ri ) i 1 2 i 1 2 1 n 2 2 ( miri ) 2 i 1
1 l 1 2 2 J ml m ml 结果与前相同。 3 12 2
t
0
1 2 0 0 t t 2
v v 2a( x x0 )
2 2 0
2 ( )
2 2 0 0
匀变速转动
六角量与线量之间的关系
1、位移与角位移之间的关系刚体转过刚体上的一点位移 s
o
r
s
x
s r
第六章刚体力学
本章主要内容：
6－1 刚体的运动 6－2 刚体的角动量、转动动能、转动惯量
6－3 力矩
刚体定轴转动定律
6－4 定轴转动的动能定理 6－5 刚体对定轴的角动量守恒定律
6－6 进动*
本章学习要求
2.理解转动惯量、力矩的概念，掌握转动定律。 3.掌握刚体转动的动能定理、角动量定理。
1.掌握刚体定轴转动的特点，理解角坐标、角位移角速度、角加速度的概念。
1 n 刚体的转动动能 Ek ( miri2 ) 2 2 i 1 1 2 与平动动能比较 Ek mv 2 n 2 miri ：相对于转轴的特征的物理量
i 1
转动惯量的定义：
单位：kg ·m2
J m r
i 1

第十三讲刚体的运动和动力学问题 (1)

第十三讲刚体的运动学与动力学问题一竞赛内容提要 1、刚体；2、刚体的平动和转动；3、刚体的角速度和角加速度；4、刚体的转动惯量和转动动能；5、质点、质点系和刚体的角动量；6、转动定理和角动量定理；7、角动量守恒定律。

二竞赛扩充的内容1、刚体：在外力的作用下不计形变的物体叫刚体。

刚体的基本运动包括刚体的平动和刚体绕定轴的转动，刚体的任何复杂运动均可由这两种基本运动组合而成。

2、刚体的平动；刚体的平动指刚体内任一直线在运动中始终保持平行，刚体上任意两点运动的位移、速度和加速度始终相同。

3、刚体绕定轴的转动；刚体绕定轴的转动指刚体绕某一固定轴的转动，刚体上各点都在与转轴垂直的平面内做圆周运动，各点做圆周运动的角位移Φ、角速度ω和角加速度β相同（可与运动学的s 、v 、a 进行类比）。

且有：ω=t t ∆∆Φ→∆lim 0；β=t t ∆∆→∆ωlim0。

当β为常量时，刚体做匀加速转动，类似于匀加速运动，此时有：ω=ω0+βt ； Φ=Φ0+ω0t+βt 2/2；ω2－ω02=2β（Φ－Φ0）。

式中，Φ0、ω0分别是初始时刻的角位移和角速度。

对于绕定轴运动的刚体上某点的运动情况，有：v=ωR ， a τ=βR ， a n =ω2R=v 2/R, 式中，R 是该点到轴的距离，a τ、a n 分别是切向加速度和法向加速度。

例1 有一车轮绕轮心以角速度ω匀速转动，轮上有一小虫自轮心沿一根辐条向外以初速度v 0、加速度a 作匀加速爬行，求小虫运动的轨迹方程。

例2 一飞轮作定轴转动，其转过的角度θ和时间t 的关系式为：θ=at+bt 2－ct 3，式中，a 、b 、c 都是恒量，试求飞轮角加速度的表示式及距转轴r 处的切向加速度和法向加速度。

例3 如图所示，顶杆AB 可在竖直槽K 内滑动，其下端由凸轮K 推动，凸轮绕O 轴以匀角速度ω转动，在图示瞬间，OA=r ，凸轮轮缘与A 接触处，法线n 与OA 之间的夹角为α，试求此瞬时顶杆OA 的速度。

5-2转动惯量、功、能、角动量

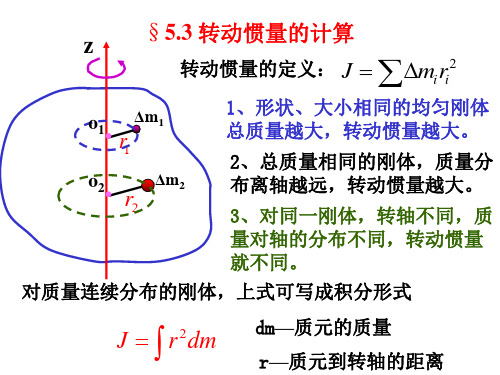
J r dm
2
dm—质元的质量
r—质元到转轴的距离
例5.2求质量为m，半径为R的均匀薄圆环的转动惯量。轴与圆环平面垂直并通过其圆心。
解： m
●
取小质元dm如图
dm
o R
环上各质元到轴的垂直距离都等于R
J r dm R dm
2 2
mR
对同一转轴转动惯量J具有可叠加性
2
dA Md
A Md
1
d d J d Jd Jd dt dt
合外力矩对刚体所作的总功为：
2
1 2 猜一猜 J 的物理属性是什么？ 2
设刚体中第i个质点的质量为Δ mi,速度为vi 则该质点的动能为：

2
1
1 1 2 2 Jd J 2 J1 2 2
Mdt d ( J )
两边积分得：
M d t J J
t0
t
0Байду номын сангаас
——定轴的角动量定理的积分形式

t
t0
M d t 表示力矩对时间的积累。
称为力矩 M 的角冲量。
定轴转动物体所受外力矩的角冲量，等于物体对轴的角动量的增量。
由几个物体组成的系统，每个物体对转轴的角动量
Li J ii
1、定轴转动刚体的角动量定理
d d J dL M J dt dt dt
——刚体定轴转动角动量定理微分形式
刚体对定轴的角动量为
L J
刚体在外力矩作用下，经 Δt=t-t0 的时间间隔角动量由 L0 J 0
L J
得
d dL J 由 M dt dt
L2

4第四章刚体的定轴转动

七、能综合应用转动定律和牛顿运动定律及质点、刚体定轴转动的运动学公式计算质点刚体系统的简单动力学问题. 八、能综合应用守恒定律求解质点刚体系统的简单动力学问题. 明确选择分析解决质点刚体系统力学问题规律时的优先考虑顺序.
第 1 讲刚体的定轴转动
预习要点 1. 理解刚体的运动； 2. 掌握描述刚体定轴转动的运动学方法； 3. 理解力矩的概念及力矩的功；
式中 mi ri2 表示第i个质点对转轴的转动惯量；
对质量连续分布的刚体，任取质量元 dm ，其到轴的
距离为 r ，则转动惯量：
J r2dm 单位：kg ·m2
若系统由多个刚体组成，则系统对转轴的总转动惯量，等于各部分对同一转轴的转动惯量之和
一个长为4L的轻杆，连有两个质量都是m的小球（大小可忽略），此系统可绕垂直于杆的轴转动，求下列转动惯量；
在转动平面内，O为转动平面与转轴的焦点，r 为从O 点指向
M 力的作用点 A 的位矢，两矢量的夹角为；
力 F 对定轴 OZ 的力矩：
（力臂：力的作用线到转轴的距离）
z
M Z Fd Fr sin
通常，从OZ轴正向俯视，有逆时针转动（趋势）力矩为正，反之为负；
单位：牛·米（N ·m）
F
Or
例:一轻绳跨过一轴承光滑的定滑轮，绳的两端分别悬
有质量为m1和m2的物体，滑轮可视为均质圆盘，质量为m，半径为r，绳子不可伸长而且与滑轮之间无相对滑动.求物体加速度、滑轮转动的角加速度和绳子的张
力. 设 m2 m1
解: 受力分析如图：
FT1 m1g m1a m2g FT2 m2a
FT2R FT1R J a r
m2
)
gl
sin
α

刚体绕定轴转动的转动定律和转动惯量

0 R2
1 mR2 2
Z
m R2
R1
薄圆环
dm
ds
m (R22
R12
)
ds
ds 2 rdr
dJ r2dm
J R2 r 2
m
2 rdr
R1
(R22 R12 )
1 2
m(R22
R12 )
R
m
H
空心圆柱面
dm ds m ds 2 RH
ds 2 Rdh
dJ r2dm
J H R2 m 2 Rdh
0 2 RH
mR3
r
R
H m
实心圆柱
dm
dV
m
R2H
dV
dV 2 rHdr
dJ r2dm
J R r2 m 2 rHdr
0 R2H
R2 R1
H m
同轴空心圆柱
dm
dV
mg
H (R22
R12 )
dV
dV 2 rHdr
dJ r2dm
J R2 r2
mg
2 rHdr
R1 H (R22 R12 )
R
+
T1
+
T2
N
m
4m
2m ＋ o
P1
P2
mg
4m
T1
T2
2m
分别对人、物、滑轮建立方程：
4mg-T1 4ma人地
（1 ）
T2-2mg 2ma物地 2ma绳地（2） R
T1R -T2 R
J
1 2
mR2
（3） m
人相对绳匀加速a0上爬，则
a人地 a人绳 a绳地
4m

用三线摆测物体的转动惯量.

是以a和b为边长的等边三角形外接圆的半径）。 5．计算出两圆盘之间的垂直距离H，圆环的内直径和外直径为2R1、2R2． 6．称出悬盘m和圆环质量M。 7．计算测量误差。 [数据记录与处理] 3 3 R b = r a = 3 3 两圆盘之间垂直距离 H l ( R r ) = 悬盘质量m= 圆环质量M=
2 2
悬盘摆动50次所需时间t（s） 1 2 3 平均周期 T0= （S） 1 2 3 平均 T1=
悬盘加圆环
（S）
项目次数
上圆盘悬孔间距离a （cm） 1 2 3
悬盘悬孔间距离b （cm）
待测圆环外直径2R1（cm）内直径2R2(cm)
平均
a=
b=
R1=
R2=
[思考题]： 1．用三线扭摆测定物体的转动惯量时，为什么要求悬盘水平，且摆角要小？ 2．测圆环的转动惯量时，把圆环放在是盘的同心位置上。若转轴放偏了，测出的结果是偏大还是偏小？为什么？
对称地连接在置于上部的一个水平小圆盘的下面，小圆盘可以绕自身的垂直轴转动。当均匀圆盘（以下简称悬盘）水平，三线等长时，轻轻转动上部小圆盘，由于悬线的张力作用，悬盘即绕上下圆盘的中心连线轴00‘周期地反复扭转运动。当悬盘离开平衡位置向某一方向转动到最大角位移时，整个悬盘的位置也随着升高h。若取平衡位置的位能为零，则悬盘升高h时的动能等于零，而位能为： E 1 mgh 式中m是悬盘的质量，g是重力加速度。转动的悬盘在达到最大角位移后将向相反的方向转动，当它通过平衡位置时， 1 其位能和平衡动能为零，而转动动能为：E 2 I 式中I。为悬盘的转动惯量，ω0为悬盘通过平衡位置时的角速度。如果略去摩擦力的影响，根据机械能守衡定律， 1 E1＝E2，即 mgh I 2 若悬盘转动角度很小，可以证明悬盘的角位移与时间的 2 关系可写成： sin( )t T 式中θ是悬盘在时刻t的位移，θ0是悬盘的最大角位移

转动定理的积分形式力矩对时间和空间的累积效应

刚体绕定轴转动的动能定理：合外力矩对绕定
0
轴转动的刚体所作的功
W＝
1 2
J
2－
1 2
J
2 0
等于刚体的转动动能的增量。
例题：如图所示，一质量为M、半径为R的圆盘，可绕一无摩擦的水平轴转动。圆盘上绕有轻绳，一端悬挂质量为m的物体。问物体由静止下落高度h时，其速度的大小为多
少？设绳的质量忽略不计。
dW
Fvgdrv
F
drv
cos
2
Frd
sin
dW Md
W Md
说明：力矩作功的实质仍然是力作功。只是
对于刚体转动的情况，这个功不是用力的位移来表示，而是用力矩的角位移来表示。
0
2、力矩的功率
（1）定义：
单位时间内力矩对刚体所作的功。
（2）公式
P dW ＝M d M
dt
dt
功率一定时，转速越大，力矩越小；转速越小，力矩越大。
一、刚体定轴转动的角动量定理
v
定轴转动定理
v M
v dL
同牛顿第二定律
v F
dpv
dt
dt
类似，以微分形式反映了力或力矩对刚体质点或质点系的瞬时作用规律。如果我们要考虑一段时间内外力矩对刚体的作用效果，则可对转动定理
表式对时间积分可得积分形式——刚体定轴转动的角动量定理
由
M
dL
dt
得
Mdt dL
（3）意义
表示力矩对刚体作功的快慢
3、刚体的转动动能
刚体以角速度ω作定轴转动，取一质元Δmi，距转轴 ri，则此质元的速度为vi=riω，
动能为ห้องสมุดไป่ตู้

转动惯量

§3.5转动惯量教学目的能够熟练掌握推导动量矩的表达式，能够求导出刚体对定点的转动动能，理解和掌握刚体的转动惯量的定义及定义式，牢记并能熟练运用平行轴定理，了解刚体的惯量张量及惯量椭球，能够运用惯量椭球消去惯量积。

重点刚体的动量矩，刚体的转动动能，转动惯量，惯量张量和惯量椭球，惯量主轴极其求法。

教学过程一、刚体的动量矩在质点动力学和质点组动力学重，我们都曾遇到动量矩定理，并把它作为三大基本定理之一。

在刚体动力学重，大量篇幅是研究刚体的转动问题。

因此，就经常要用到动量矩定理。

在还没有研究动量矩定理在刚体动力学中的作用以前，让我们先来研究一下，在转动问题中，动量矩的表达式是怎样的？图3.5.1假设刚体在某一时刻以角速度ω作定点转动。

在它里面，取任一质点P，它i的质量是m，速度为i v（未画出）。

如i P对定点O的位矢是i r（图3.5.1），则此i质点对定点O的动量矩为i i i v r m ⨯而整个刚体对O 的动量矩为刚体中各质点对同一点的动量矩的矢量和：∑=⨯=ni i i i v r J 1)(m （3.5.1）因为i i r ωv ⨯=故])([1∑=⨯⨯=ni i i i r ωr J m即])([12∑=⋅-=ni i i i i r ωr r ωJ m （3.5.2）式（3.5.2）告诉我们，动量矩J 一般并不与角速度ω共线。

在平动中，动量p 与线速度v 总是共线的。

在定点转动中，只在惯量主轴上，J才与ω共线[参看本节中的（4）及（5）]。

现在来求在一般情况下动量矩J 的分量表达式。

把动量矩矢量J 和角速度矢量ω都分为沿三正交坐标轴x ，y ，z （原点在O ）上的分量，则因k j i r i i i i z y x ++=k j i ωz y x ωωω++=故得J 在x 方向上的分量x J 为ii ni i z i i n i i y i i n i i x i z i y i x i i i i x ni i x z x m y x m z y m z y x x z y x m J ∑∑∑∑====--+=++-++=112212221)()]()([ωωωωωωω（3.5.3）同理⎪⎪⎭⎪⎪⎬⎫++--=-++-=∑∑∑∑∑∑======)()(2211112211i i ni i z i i n i i y i i n i i x z i i ni i z iini i y i i ni i x y y z m y z m x z m J z y m x z m x y m J ωωωωωω（3.5.4）)()()(221221221i i n i i i i ni i i i ni i y x m I x z m I z y m I +=+=+=∑∑∑===zz yy xx （3.5.5）及ii n i i yx xy i i n i i xz zx ii ni i zy yz y x m I I x z m I I z y m I I ∑∑∑=========111 （3.5.6）关于xx I ，yy I 和zz I 以及yz I 、zx I 和xy I 的物理意义，我们下面还要作进一步的讨论。

第3章刚体转动动能和角动量

2 Mdθ = Jω 2 / 2 − J 0ω 0 / 2 ∫
17
牛顿力学的知识结构
外力牛顿第二定律
F = dP dt M = dL dt
力对时间累积
动量守恒作功机械能守恒外力矩为零角动量守恒
18
力对时间累积
为牛顿第三定律
12 21
df = µ gdm m σ= 2 dm = σ 2π rdr πR 2 R 2 M = − ∫ µσ 2π gr dr = − mg µ R 0 3 2π 4π A = ∫ Mdθ = − mg µ R 0 3 dM = −rdf
Байду номын сангаас
r
6
光滑，例2：已知：均匀直杆质量为，长为，轴o光滑，：已知：均匀直杆质量为m，长为l，初始静止在水平位置。 AO = l / 4 初始静止在水平位置。
ω0 例1：在摩擦系数为µ桌面上有细杆，细杆，质量为 m、长度为 l，、， m, l o 以初始角速度 ω0 绕垂直于杆的质心轴转动，的质心轴转动，问细杆经过多 µ 长时间停止转动。长时间停止转动。以细杆为研究对象，受力分析，解：以细杆为研究对象，受力分析，重力及桌面的支持力不产生力矩，只有摩擦力产生力矩。支持力不产生力矩，只有摩擦力产生力矩。
刚体定轴转动动能角动量
1
转动中的功和能
一、力矩的功
设刚体上P点受到外力的作用，设刚体上点受到外力 F 的作用，点受到位移为 d r , 功为 d A ,
z
0′
F ∥
r
F
F⊥
0′
dθ
dr
P
r
P