求出下图的最小生成树
最小生成树及算法
|S|=n-1, 说明是树 最后S={a1, a2, a3,… ,an-1}
B. 破圈法
算法2 步骤如下: (1) 从图G中任选一棵树T1. (2) 加上一条弦e1,T1+e1中 生成一个圈. 去掉此圈中最大权边,得到新树T2, 以T2代T1,重复(2)再检查剩余的弦,直到全部弦 检查完毕为止.
例 n个城市,各城市之间的距离如下表(距离为 ∞,表示两个城市之间没有直接到达的线路)。 从一个城市出发走遍各个城市,如何选择最优的 旅行路线.
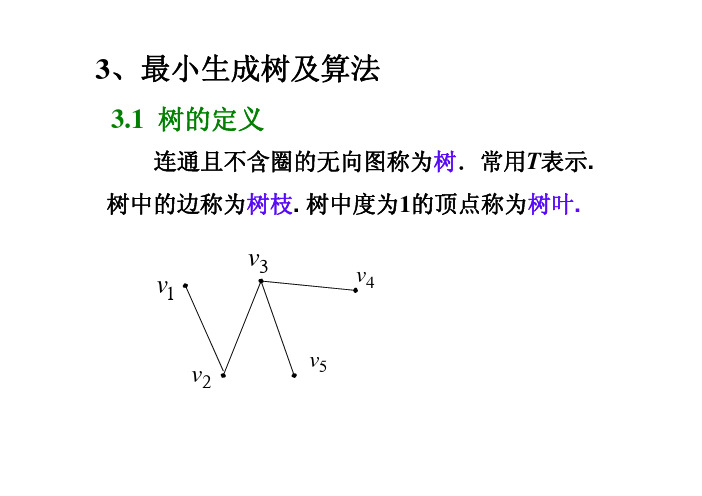
性质 任何一棵树至少有两片树叶。 证明 设树T=(V,E),结点数为v,因T是连通的,因 此,树中每个结点vi,有deg(vi)1,且 deg(vi)=2(v-1)=2v-2. 若T中结点度数都大于2,则 deg(vi) 2v,矛盾。 若T中只有一个结点度数为1,则 deg(vi) 2(v-1)+1=2v-1 矛盾。
4 3
v5 3 v6
3.5 生成树的计数
1、一些概念 • • ① 设 G 是一个连通图。 T , T 分别是 G 的两个生成树,如果 E (T ) E (T ) ,则认为 T , T 是 G 的两个不同的生成树。 G 的 不同的生成树个数用 (G) 表示。 如:
v1 v3 v2 v3 v1 v2 v3 v1 v2 v3 v1 v2
证明:⑴⑵ 当 n=2时, e=1, 显然 e=n-1. 假设n=k-1时命题成立,当n=k时,因G无圈、连 通,则至少有一条边(u,v),deg(u)=1,删去u,得到 连通无圈的图G1, G1的边数e1,结点数n1满足: e1=n1-1= k-2 将u,边(u,v)加到 G1中,得到T,且 e=n-1.
( K3 ) 3。 则:
② G-e: 从G中去掉边e后所得的图。
求出下图的最小生成树

求出下图的最小生成树解:MATLAB程序:% 求图的最小生成树的prim算法。
% result的第一、二、三行分别表示生成树边的起点、终点、权集合% p——记录生成树的的顶点,tb=V\pclc;clear;% a(1,2)=50; a(1,3)=60;% a(2,4)=65; a(2,5)=40;% a(3,4)=52;a(3,7)=45;% a(4,5)=50; a(4,6)=30;a(4,7)=42;% a(5,6)=70;% a=[a;zeros(2,7)];e=[1 2 20;1 4 7;2 3 18;2 13 8;3 5 14;3 14 14;4 7 10;5 6 30;5 9 25;5 10 9;6 10 30;6 11 30;7 8 2;7 13 5;8 9 4;8 14 2;9 10 6;9 14 3;10 11 11;11 12 30];n=max([e(:,1);e(:,2)]); % 顶点数m=size(e,1); % 边数M=sum(e(:,3)); % 代表无穷大a=zeros(n,n);for k=1:ma(e(k,1),e(k,2))=e(k,3);enda=a+a';a(find(a==0))=M; % 形成图的邻接矩阵result=[];p=1; % 设置生成树的起始顶点tb=2:length(a); % 设置生成树以外顶点while length(result)~=length(a)-1 % 边数不足顶点数-1temp=a(p,tb);temp=temp(:); % 取出与p关联的所有边d=min(temp); % 取上述边中的最小边[jb,kb]=find(a(p,tb)==d); % 寻找最小边的两个端点(可能不止一个)j=p(jb(1));k=tb(kb(1)); % 确定最小边的两个端点result=[result,[j;k;d]]; % 记录最小生成树的新边p=[p,k]; % 扩展生成树的顶点tb(find(tb==k))=[]; % 缩减生成树以外顶点endresult % 显示生成树(点、点、边长)weight=sum(result(3,:)) % 计算生成树的权程序结果:result =1 4 7 8 14 7 9 13 10 10 14 10 11 4 7 8 14 9 13 102 5 113 6 12 7 10 2 2 3 5 6 8 9 11 14 30 30 weight =137附图最小生成树的权是137。
最小生成树的算法

最小生成树的算法王洁引言:求连通图的最小生成树是数据结构中讨论的一个重要问题.在现实生活中,经常遇到如何得到连通图的最小生成树,求最小生成树不仅是图论的基本问题之一 ,在实际工作中也有很重要的意义,,人们总想寻找最经济的方法将一个终端集合通过某种方式将其连接起来 ,比如将多个城市连为公路网络 ,要设计最短的公路路线;为了解决若干居民点供水问题 ,要设计最短的自来水管路线等.而避开这些问题的实际意义 ,抓住它们的数学本质 ,就表现为最小生成树的构造。
下面将介绍几种最小生成树的算法。
一,用“破圈法”求全部最小生成树的算法1 理论根据1.1 约化原则给定一无向连通图 G =(V ,E )( V 表示顶点,E 表示边),其中 V={ 1v , 2v ,3v …… n v },E= { 1e , 2e , 3e …… n e }对于 G 中的每条边 e ∈ E 都赋予权ω(i e )>0,求生成树 T = (V ,H ),H ⊆ E ,使生成树所有边权最小,此生成树称为最小生成树.(1) 基本回路将属于生成树 T 中的边称为树枝,树枝数为n -1,不属于生成树的边称为连枝.将任一连枝加到生成树上后都会形成一条回路.把这种回路称为基本回路,记为()cf e 。
基本回路是由 T 中的树枝和一条连枝构成的回路.(2) 基本割集设无向图 G 的割集 S (割集是把连通图分成两个分离部分的最少支路集合) ,若 S 中仅包含有T 中的一条树枝,则称此割集为基本割集,记为()S e 。
基本割集是集合中的元素只有一条是树枝,其他的为连枝.(3) 等长变换设T=(V,H),为一棵生成树,e ∈ H, 'e ∈ E, 'e ∉ H,当且仅当'e ∈()cf e ,也就是说e ∈()S e ,则'T =T ⊕{e, 'e }也是一棵生成树。
当()e ω='()e ω时,这棵生成树叫做等长变换。
最小生成树求解

最小生成树求解最小生成树(Minimum Spanning Tree, MST)是图论中的一个重要概念,用于解决有权无向连通图中的最小连接问题。
最小生成树是指在一个连通图中,选取一些边,使得这些边构成的子图是一棵树,并且这棵树的所有边权之和最小。
最小生成树的求解方法有多种,其中最经典且常用的方法是普利姆(Prim)算法和克鲁斯卡尔(Kruskal)算法。
一、普利姆算法普利姆算法是一种基于贪心策略的算法,用于解决最小生成树问题。
其基本思想是从连通图中任选一个顶点开始,然后逐步选择与已选顶点集合相连的权值最小的边,直到选取了所有顶点为止。
具体步骤如下:1. 初始化:选择其中一个顶点作为起始顶点,并将其标记为已访问。
2. 迭代过程:从已访问的顶点集合中,选择一条边的权值最小且与未访问的顶点相连的边,将该边加入最小生成树的边集合,并将访问顶点集合扩展至新连接的顶点。
3. 重复步骤2,直到所有顶点都被访问。
普利姆算法的优势在于适合处理稠密图,时间复杂度为O(V^2),其中V为顶点数。
二、克鲁斯卡尔算法克鲁斯卡尔算法也是一种常用的最小生成树求解算法,它基于并查集(Disjoint Set)实现。
与普利姆算法不同的是,克鲁斯卡尔算法是通过选择权值最小的边,判断该边的两个顶点是否已经在同一个连通分量中,若不在同一分量,则选择该边,直到最小生成树中的边数为V-1为止。
具体步骤如下:1. 初始化:将图中所有边按照权值从小到大进行排序。
2. 重复选择:依次选择排序后的边,若该边的两个顶点不在同一连通分量中,则将该边加入最小生成树的边集合。
3. 结束条件:当最小生成树的边数达到V-1时,停止选择。
克鲁斯卡尔算法的优势在于适合处理稀疏图,时间复杂度为O(ElogE),其中E为边数。
三、算法选择普利姆算法和克鲁斯卡尔算法的选择应根据具体问题而定。
如果图较为稠密,则普利姆算法更为高效;如果图较为稀疏,则克鲁斯卡尔算法更为高效。
图的常用算法——最小生成树

TE= {(V1,V4)5,(V4,V2)3 ,(V4,V6)7,
(V6,V3)2 ,(V3,V5)6 } LW= {(V4,V7)15
9
第六次 U={ V1,V4,V2 ,V6,V3 ,V5,V7 } TE= {(V1,V4)5,(V4,V2)3 ,(V4,V6)7, (V6,V3)2 ,(V3,V5)6},(V4,V7)15 } LW= { }
3
5
7
20
所以最小生成树由GE数组中的1,2,3,5,7 边组成。 2012-1-10
2012-1-10
10
2012-1-10
11
(4)算法如下: Procedure Prim(GA,CT); begin for I:=1 to n-1 do { 给CT赋初值,对应第0次的LW值 } [ CT[I].from :=1 ; ct[I].end: =I+1 ; ct[I].w:=GA[1, i+1 ]; for k:=1 to n-1 do { 进行n-1次循环,求出最小生成树的第K条边 } ①[ min:=maxint ; m:=k ; for j:=k to n-1 do if ct[j].w < min then min:=ct[j].w ; m:=j; ] ② if m<> k then ct[k] 与ct[m] 的交换 { 将最短边调到第K单元 }
1. 从图“G”的选取一个顶点放到“G’” 中,因只有一个顶点,因此该图是连通 的; 2. 以后每加入一个顶点,都要加入以该点 为顶点与已连通的顶点之中的一个顶点 为端点的一条边,使其既连通而不产生 回路,进行n-1次后,就产生G’,在G’ 中有n个顶点,n-1条边且不产生回路。
二、图的最小生成树
最小生成树的模型数学公式

最小生成树的模型数学公式
最小生成树的模型数学公式是:
给定无向连通图G(V,E),其中V为图的顶点集合,E为图的边集合。
每条边e∈E都带有一个非负权重w(e)。
找到一个包含图中所有顶点的子图T(V,E'),使得E' ⊆ E,并且E'构成一颗树(即连通且无环),使得所有的边的权重之和最小。
拓展:
最小生成树的应用十分广泛,可以用于解决多种问题。
以下是最小生成树的一些常见拓展场景:
1.带有约束条件的最小生成树:
在某些情况下,除了最小化权重之和外,还需要满足一些特定的约束条件。
例如,可以要求最小生成树的边数限制在特定的范围内,或者要求选择特定类型的边。
这时可以在最小生成树的模型中引入额外的约束条件,从而得到满足要求的最小生成树。
2.多目标最小生成树:
有时候,最小生成树问题不仅需要最小化权重之和,还需要考虑其他目标。
例如,可以同时考虑最小化权重之和和最大化生成树中的最长边权重。
这样的问题可以转化为多目标优化问题,并通过权衡不同目标之间的关系来求解。
3.带有边权重动态变化的最小生成树:
在某些场景中,图的边权重可能会根据一些规则进行动态变化。
例如,网络中的通信链路可能会根据网络拓扑和负载情况进行变化。
这时可以通过动态更新最小生成树来快速适应环境变化,从而保持最小生成树的有效性。
总之,最小生成树的模型可以通过引入不同的约束条件和目标函数进行拓展,以适应不同的应用场景。
最小生成树问题(共7张PPT)

个,所以支撑树是有不唯一]。
C n1 m
求最小树的Kruskal算法
赋权的连通图G=(V,E)中m=|E|,n=|V|,
S1:对E中各边的权排序,设 w1≤w2≤…≤wm,wi=w(ei)
S2:初始化: w←0,T←φ,k←1,t←0
S3:若t=n-1则转S6,否则转S4
Y
N
T’←T∪{ek}
T’成圈? N END
Y
T←T+ {ek},
k←k+1 w←w+wk,
t←t+1,k←k+1
用Kruskal算法求最小树
用Kruskal算法(避圈法)求赋权连通图G的最小树
V2
5
V6
Kruskal法盯住边,而Prim法更注意顶点:
T为最小树,w为T的权。
4
T={v1,v2,v3,v5}
Prim法求最小支撑树 E的权排序w1≤w2≤…≤wm w←0,T←φ,k←1,t←0
对要m让条程边序的读边懂长“图排”,序S程3,:序m如个何元判素断排是序否较成好“的圈算”?法谈是何基容于易分,治时策间略、的空快间速复排杂序性(Q绝u不ick应S小or看ting),其时间复杂性是O(m㏒m)。
min S2:初始化:w←0,T←φ,k←1,t←0 设: {w(vv )}w(vv ) 简对称m条最边小的树边或长最排短序树,[管vvm线ij个 铺ST 元设素]。排序较好的i算法j是基于分治策略的快l速排k序(Quick Sorting),其时间复杂性是O(m㏒m)。
S4:若T∪{ek}有圈则k←k+1转S4,否则 转S5
S5: T←T∪{ek},w←w+wk, t←t+1, k←k+1,转S3
最小生成树寻找算法

最小生成树寻找算法一、什么是最小生成树?最小生成树(Minimum Spanning Tree,简称MST)是一种用于连接无向图中所有顶点的树,且其边的权值之和最小。
在实际应用中,最小生成树常常被用来解决网络优化问题和建立通信网络等问题。
二、最小生成树的寻找算法目前,常见的最小生成树寻找算法主要包括Prim算法和Kruskal算法两种。
1. Prim算法Prim算法是一种贪心算法,其基本思想是从一个点开始,每次选择与当前已经构造好的部分形成最短路径的边加入到MST中。
具体实现过程如下:(1)设图G=(V,E)为无向连通图,V为顶点集合,E为边集合。
(2)任选一个起始顶点v0∈V,并将v0加入到集合U中。
(3)从集合U中所有顶点出发寻找权值最小的边,并将该边所连接的顶点加入到集合U中。
(4)重复执行步骤3直至集合U包含了所有顶点。
Prim算法可以使用堆优化来提高时间效率,在稠密图上表现良好。
时间复杂度为O(n^2)或O(nlogn),其中n为顶点数。
2. Kruskal算法Kruskal算法也是一种贪心算法,其基本思想是将边按照权值从小到大排序,然后依次加入到MST中,如果加入该边会形成环,则不加入该边。
具体实现过程如下:(1)设图G=(V,E)为无向连通图,V为顶点集合,E为边集合。
(2)将所有边按照权值从小到大排序。
(3)依次选择每条边,如果该边所连接的两个顶点在同一个连通块中,则不加入该边;否则将该边加入MST中,并将两个连通块合并成一个。
(4)重复执行步骤3直至MST包含了所有顶点。
Kruskal算法适用于稀疏图,在时间效率上比Prim算法更优秀。
时间复杂度为O(elog e),其中e为边数。
三、应用场景最小生成树常被应用于网络设计、通信网络建立、物流配送等领域。
例如,在城市规划中,可以使用最小生成树来确定道路建设的优先级和路线。
在电信网络建设中,可以使用最小生成树来确定光缆的铺设方案和传输路线。
最小生成树的模型数学公式

最小生成树的模型数学公式【原创实用版】目录1.最小生成树的概念2.最小生成树的数学公式3.举例说明最小生成树的计算过程正文1.最小生成树的概念最小生成树(Minimum Spanning Tree,简称 MST)是一种图论中的算法,用于在一个加权连通图中找到一棵包含所有顶点且边权值之和最小的生成树。
这里的生成树是指一个连通图的生成树,即保留图中所有的节点,但只保留足以保持这些节点连通的边的集合。
2.最小生成树的数学公式假设有一个加权连通图 G(V, E),其中 V 是顶点集合,E 是边集合,每条边的权值为 w_ij,表示顶点 v_i 和 v_j 之间的边的权值。
设 T 为G 的最小生成树,|T| 表示 T 中边的数量,那么最小生成树的数学公式可以表示为:|T| = ∑(w_ij)其中,∑(w_ij) 表示 T 中所有边的权值之和。
3.举例说明最小生成树的计算过程假设有一个图 G(V, E),其中 V = {1, 2, 3, 4, 5},E = {(1, 2), (1, 3), (2, 3), (3, 4), (3, 5), (4, 5)},权值分别为 1, 2, 3, 4, 5, 6。
首先,我们需要计算图中每条边的权值之和,结果如下:- (1, 2):1- (1, 3):2- (2, 3):3- (3, 4):4- (3, 5):5- (4, 5):6接下来,将这些权值相加,得到:∑(w_ij) = 1 + 2 + 3 + 4 + 5 + 6 = 21因此,最小生成树的边数为 21 / 2 = 10.5,但由于边数必须为整数,所以最小生成树的边数为 11。
计算生成树时,可以从任意一个顶点开始,这里我们以顶点 1 为例,计算生成树的过程如下:- 1 -> 2,权值为 1- 2 -> 3,权值为 3- 3 -> 4,权值为 4- 3 -> 5,权值为 5将这些边按照权值从小到大排序,得到:1 ->2 (权值:1)3 ->4 (权值:4)3 -> 5 (权值:5)接下来,我们依次将这些边加入生成树,同时删除原图中的对应边,得到最小生成树:1 ->2 ->3 -> 4//3 5最后,我们可以验证一下最小生成树的权值之和是否等于 11:1 + 2 + 4 + 5 = 12由于计算过程中出现了误差,我们需要重新计算最小生成树。
最小生成树(最小支撑树)

(a)
图11-12
(b)
(c)
§3 最小生成树问题
一、求解最小生成树的破圈算法 算法的步骤:
1、在给定的赋权的连通图上任找一个圈。
2、在所找的圈中去掉一个权数最大的边(如果有两条或两条 以上的边都是权数最大的边,则任意去掉其中一条)。
3、如果所余下的图已不包含圈,则计算结束,所余下的图即最小生成树问题
给了一个无向图G=(V,E),我们保留G的所有点,而删掉部分G的边或 者说保留一部分G的边,所获得的图G,称之为G的生成子图。在图11-12中, (b)和(c)都是(a)的生成子图。 如果图G的一个生成子图还是一个树,则称这个生成子图为生成树, 在图11-12中,(c)就是(a)的生成树。 最小生成树问题就是指在一个赋权的连通的无向图G中找出一个生成 树,并使得这个生成树的所有边的权数之和为最小。
个网络能联通7个学院办公室,并使总的线路长度为最短。
v2 3 1 4 v7 3 v6 5 2 8 v5 v3
7
v4
图11-14
v1 10
3
4
解:此问题实际上是求图11-14的最小生成树,这在例4中已经求得, 也即按照图11-13的(f)设计,可使此网络的总的线路长度为最短,为19 百米。 “管理运筹学软件”有专门的子程序可以解决最小生成树问题。
§3 最小生成树问题
例4 用破圈算法求图(a)中的一个最小生成树
v2 3 3 1 v3 v2 3 3 v6 v2 v4 v1 3 3 v6 v2 1 v3 v4
v1
10
7 3 4 v7 2 4 5 v5 v3 8
v4
v1
7 3 4 v7 2
4 5 v5 v3 7 8
v6
v2 v1 3 3 v6 v2 v1 3 3 v6
最小生成树(Kruskal和Prim算法)

最⼩⽣成树(Kruskal和Prim算法)关于图的⼏个概念定义:关于图的⼏个概念定义:连通图:在⽆向图中,若任意两个顶点vi与vj都有路径相通,则称该⽆向图为连通图。
强连通图:在有向图中,若任意两个顶点vi与vj都有路径相通,则称该有向图为强连通图。
连通⽹:在连通图中,若图的边具有⼀定的意义,每⼀条边都对应着⼀个数,称为权;权代表着连接连个顶点的代价,称这种连通图叫做连通⽹。
⽣成树:⼀个连通图的⽣成树是指⼀个连通⼦图,它含有图中全部n个顶点,但只有⾜以构成⼀棵树的n-1条边。
⼀颗有n个顶点的⽣成树有且仅有n-1条边,如果⽣成树中再添加⼀条边,则必定成环。
最⼩⽣成树:在连通⽹的所有⽣成树中,所有边的代价和最⼩的⽣成树,称为最⼩⽣成树。
构造最⼩⽣成树的准则有3条:(1)必须只使⽤该⽹络中的边来构造最⼩⽣成树。
(2)必须使⽤且仅使⽤n-1条边来连接⽹络中的n个顶点。
(3)不能使⽤产⽣回路的边。
下⾯介绍两种求最⼩⽣成树算法1 Prim(普利姆算法)算法--加点法此算法可以称为“加点法”,每次迭代选择代价最⼩的边对应的点,加⼊到最⼩⽣成树中。
算法从某⼀个顶点s开始,逐渐长⼤覆盖整个连通⽹的所有顶点。
Prim算法从任意⼀个顶点开始,每次选择⼀个与当前顶点集最近的⼀个顶点,并将两顶点之间的边加⼊到树中。
Prim算法在找当前最近顶点时使⽤到了贪婪算法。
实现过程:5int logo[1010];///⽤0和1来表⽰是否被选择过6int map1[1010][1010];7int dis[1010];///记录任意⼀点到这⼀点的最近的距离8int n,m;9int prim()10 {11int i,j,now;12int sum=0;13for(i=1;i<=n;i++)///初始化14 {15 dis[i]=MAX;16 logo[i]=0;17 }18for(i=1;i<=n;i++)19 {20 dis[i]=map1[1][i];21 }22 dis[1]=0;23 logo[1]=1;24for(i=1;i<n;i++)///循环查找25 {26 now=MAX;27int min1=MAX;28for(j=1;j<=n;j++)29 {30if(logo[j]==0&&dis[j]<min1)31 {32 now=j;33 min1=dis[j];34 }35 }36if(now==MAX)///防⽌不成图37 {38break;39 }40 logo[now]=1;41 sum=sum+min1;42for(j=1;j<=n;j++)///填⼊新点后更新最⼩距离,到顶点集的距离43 {44if(logo[j]==0&&dis[j]>map1[now][j])45 {46 dis[j]=map1[now][j];47 }48 }49 }50if(i<n)51 {52 printf("?\n");53 }54else55 {56 printf("%d\n",sum);57 }58 }59int main()60 {61while(scanf("%d%d",&m,&n)!=EOF)///n是点数62 {63if(m==0)64 {65break;66 }67 memset(map1,0x3f3f3f3f,sizeof(map1));///map是邻接矩阵储存图的信息68for(int i=0;i<m;i++)69 {70int a,b,c;71 scanf("%d%d%d",&a,&b,&c);72if(c<map1[a][b])///防⽌出现重边73 {74 map1[a][b]=map1[b][a]=c;75 }76 }77 prim();78 }79return0;80 }邻接表实现:1 #include<stdio.h>2 #include<string.h>3 #include<vector>4 #include<algorithm>5#define INF 0x3f3f3f3f6using namespace std;7struct node8 {9int end;///终点10int power;///权值11 } t;12int n;///n为点数13 vector<node>q[500001];///邻接表储存图的信息14int dis[500001];///距离15int vis[500001];///标记数组16void prime()17 {18int i,len,j,pos,sum,start;19 memset(vis,0,sizeof(vis));20 sum=0;21 start=1;///任意取起点22for(i=0; i<=n; i++)23 {24 dis[i]=INF;25 }26 len=q[start].size();27for(i=0; i<len; i++)///从任意起点开始的dis数组更新28 {29if(q[start][i].power<dis[q[start][i].end])30 {31 dis[q[start][i].end]=q[start][i].power;32 }33 }34 vis[start]=1;35for(j=0; j<n-1; j++)36 {37int pos,min=INF;38for(i=1; i<=n; i++)39 {40if(vis[i]!=0&&dis[i]<min)41 {42 min=dis[i];43 pos=i;///找到未访问节点中权值最⼩的44 }45 }46if(pos==INF)///防⽌不成图47 {48break;49 }50 vis[pos]=1;51 sum=sum+min;52 len=q[pos].size();///再次更新dis数组53for(j=0; j<len; j++)54 {55if(vis[q[pos][j].end]==0&&dis[q[pos][j].end]>q[pos][j].power)56 {57 dis[q[pos][j].end] = q[pos][j].power;58 }59 }60 }61if(j<n)62 {63 printf("?\n");64 }65else66 {67 printf("%d\n",sum);68 }69 }70int main()71 {72int m,i;73int begin,end,power;74int a,b;75while(scanf("%d%d",&n,&m)!=EOF)76 {77for(i=0; i<=n; i++)78 {79 q[i].clear();///将victor数组清空80 }81for(i=0; i<m; i++)82 {83 scanf("%d%d%d",&begin,&end,&power);///输⼊84 t.end=end;85 t.power=power;86 q[begin].push_back(t);87 t.end=begin;///⽆向图88 t.power=power;89 q[end].push_back(t);90 }91 prime();92 }93return0;94 }这⾥再给出⼀个没有使⽤标记数组的代码:int prim(int s){int i,j,sum=0;int now;for(i=1;i<=n;i++){closest[i]=INT_MAX;}for(i=1;i<=n;i++){closest[i]=map[s][i];}closest[s]=0;for(i=1;i<n;i++)//这⾥的i代表的是边数,有n个点就会有n-1条边{int min=INT_MAX;for(j=1;j<=n;j++){if(closest[j]&&closest[j]<min){min=closest[j];now=j;//找到所需的最⼩边}}sum+=min;closest[now]=0;//将找到的边加⼊到最⼩⽣成树之中for(j=1;j<=n;j++)//找到新的点加⼊已选点集合之后,更新该点到未选点集合的距离{if(map[now][j]&&map[now][j]<closest[j]){closest[j]=map[now][j];}}}return sum;}2 Kruskal(克鲁斯卡尔)算法--加边法1.概览 Kruskal算法是⼀种⽤来寻找最⼩⽣成树的算法,在剩下的所有未选取的边中,找最⼩边,如果和已选取的边构成回路,则放弃,选取次⼩边。
图的最小生成树(java实现)

图的最⼩⽣成树(java实现)1.图的最⼩⽣成树(贪⼼算法)我两个算法的输出都是数组表⽰的,当前的索引值和当前索引对应的数据就是通路,⽐如parent[2] = 5;即2和5之间有⼀个通路,第⼆个可能⽐较好理解,第⼀个有点混乱是什么?将⼀个有权图中的所有顶点都连接起来,并保证连接的边的总权重最⼩,即最⼩⽣成树,最⼩⽣成树不唯⼀为什么?传⼊邻接矩阵,返回可以⽣成最⼩⽣成树的数据我们有两种⽅式⽣成图的最⼩⽣成树1.普⾥姆(Prim)算法2.克鲁斯卡尔(Kruskal)算法怎样做?图⽚参考博客:下⾯是普⾥姆算法的最⼩⽣成树下⾯是克鲁斯卡尔算法的最⼩⽣成树:图的邻接矩阵表⽰法(⽆向图,上三⾓矩阵)int[][] arr = new int[][]{{-1, 4, 0, 0, 0, 0, 0, 8, 0},{0, -1, 8, 0, 0, 0, 0, 11, 0},{0, 0, -1, 7, 0, 4, 0, 0, 2},{0, 0, 0, -1, 9, 14, 0, 0, 0},{0, 0, 0, 0, -1, 10, 0, 0, 0},{0, 0, 0, 0, 0, -1, 2, 0, 0},{0, 0, 0, 0, 0, 0, -1, 1, 6},{0, 0, 0, 0, 0, 0, 0, -1, 7},{0, 0, 0, 0, 0, 0, 0, 0, -1}};1.普⾥姆算法(加点法)需求:求出最⼩⽣成树的权值输⼊参数:⼆维数组arr(邻接矩阵),列表list(存放已经被加⼊的点),整型sum(存放权值)输出参数:整型数组parent1)先找⼀个起点,这个起点为任意⼀点,放⼊list中2)如果list中不包含全部节点,进⼊循环 1>遍历list中节点,查找不存在list中的邻接节点的最⼩值,记录下begin和end 2>将begin和end放⼊数组中,较⼩值节点赋值给较⼤值所在数组位置3)返回parent实现:import java.util.ArrayList;import java.util.Arrays;import java.util.List;/*** 普⾥姆(Prim)算法** @author Xiong YuSong* 2019/3/22 16:02*/public class Prim {public static void main(String[] args) {int[][] arr = new int[][]{{-1, 4, 0, 0, 0, 0, 0, 8, 0},{0, -1, 8, 0, 0, 0, 0, 11, 0},{0, 0, -1, 7, 0, 4, 0, 0, 2},{0, 0, 0, -1, 9, 14, 0, 0, 0},{0, 0, 0, 0, -1, 10, 0, 0, 0},{0, 0, 0, 0, 0, -1, 2, 0, 0},{0, 0, 0, 0, 0, 0, -1, 1, 6},{0, 0, 0, 0, 0, 0, 0, -1, 7},{0, 0, 0, 0, 0, 0, 0, 0, -1}};List<Integer> list = new ArrayList<>();//先将0放置在list中list.add(0);int begin = 0, end = 0, weight;int[] parent = new int[arr.length];for (int i = 0; i < arr.length; i++) {parent[i] = -1;}while (list.size() < arr.length) {weight = Integer.MAX_VALUE;for (Integer row : list) {for (int i = 0; i < arr.length; i++) {if (!list.contains(i)) {if (i >= row + 1) {if (arr[row][i] > 0 && arr[row][i] < weight) {begin = row;end = i;weight = arr[row][i];}} else if (i <= row - 1) {//我这⾥只⽤了上三⾓矩阵,所以这⾥需要画蛇添⾜写这⼀部分if (arr[i][row] > 0 && arr[i][row] < weight) {begin = row;end = i;weight = arr[i][row];}}}}}list.add(end);parent[end] = begin;}System.out.println(Arrays.toString(parent));}}2.克鲁斯卡尔算法(加边法)需求:求出最⼩⽣成树的权值构建类:Edge<begin,end,weight>三元组,根据weight(权值)排序输⼊参数:存放有Edge的列表list,并查集parent输出参数:并查集parent(最⼩⽣成树的数组表现形式)原理:贪⼼算法的实现,程序中使⽤了并查集(判断两个集合中是否存在相同的数据)这种特殊的数据结构,使⽤数组实现1)创建⼀个三元组<起始点,终⽌点,权值>,将邻接矩阵中数据放⼊三元组中,再放⼊list中,根据权值进⾏排序2)创建变量count=0,整型数组parent3)如果list中还存在值,则进⾏循环 1>判断begin和end是否存在于不同的集合中(判断是否在同⼀棵树中,即判断当前节点在并查集parent中的根节点是否为同⼀个) 2>如果存在不同的集合中,则将较⼩值节点赋值给较⼤值所在数组位置,较⼩值节点为较⼤值节点的⽗节点4)返回parent实现:import java.util.ArrayList;import java.util.Arrays;import java.util.Collections;import java.util.List;/*** @author Xiong YuSong* 2019/3/22 17:04*/class Edge implements Comparable<Edge> {//起始点private int begin;//终⽌点private int end;//权值private int weight;public Edge(int begin, int end, int weight) {this.begin = begin;this.end = end;this.weight = weight;}public int getBegin() {return begin;}public void setBegin(int begin) {this.begin = begin;}public int getEnd() {return end;}public void setEnd(int end) {this.end = end;}public int getWeight() {return weight;}public void setWeight(int weight) {this.weight = weight;}@Overridepublic int compareTo(Edge o) {if (o.weight > this.weight) {return -1;} else {return 1;}}}public class Kruskal {public static void main(String[] args) {//默认以a为根节点的最⼩⽣成树List<Edge> list = new ArrayList<>();int[][] arr = new int[][]{{-1, 4, 0, 0, 0, 0, 0, 8, 0},{0, -1, 8, 0, 0, 0, 0, 11, 0},{0, 0, -1, 7, 0, 4, 0, 0, 2},{0, 0, 0, -1, 9, 14, 0, 0, 0},{0, 0, 0, 0, -1, 10, 0, 0, 0},{0, 0, 0, 0, 0, -1, 2, 0, 0},{0, 0, 0, 0, 0, 0, -1, 1, 6},{0, 0, 0, 0, 0, 0, 0, -1, 7},{0, 0, 0, 0, 0, 0, 0, 0, -1}};for (int i = 0; i < arr.length; i++) {for (int j = i + 1; j < arr.length; j++) {if (arr[i][j] > 0) {list.add(new Edge(i, j, arr[i][j]));}}}Collections.sort(list);//数组中每⼀个节点都只知道他的⽗节点是什么,-1表⽰不存在⽗节点,0位置是根节点int[] parent = new int[arr.length];for (int i = 1; i < arr.length; i++) {parent[i] = -1;}int m = 0, n = 0;for (Edge edge : list) {//寻找这两个点有没有相同的⽗节点m = find(parent, edge.getBegin());n = find(parent, edge.getEnd());if (m != n && parent[edge.getEnd()]>0) {parent[edge.getEnd()] = edge.getBegin();}}System.out.println(Arrays.toString(parent));}private static int find(int[] parent, int ch) {while (parent[ch] > 0) {ch = parent[ch];}return ch;}}。
图的最小生成树prim算法2

7 .刮土移土 被刮下的土壤,可以有两种移运方式,它们分别是:
( l )刮土直移 将刮刀回转角置于0°(刮刀轴线垂 直于行驶方向),此时切削宽度最大, 但只能以较小的人土深度作业,主要用于 辅平作业 。
第四章 土方机械施工运用 25
2 15 6 9
5
6 17 10
4
33 4
1
12 9 9
2 15 6 9
5
6 17 10
4
33 4
1
12 9 9
2 15 6 9
5
6 17 10
4
33 4
1
1
12 9 9
12 9 9
2 15 6 9 6 17 10
52 46
15 6
9
17 10
5 4
33 4
33 4
1
12 9 9
2 15 6 9
5
6 17 10
二、循环作业过程分析 铲运机也是一种循环作业的土方机械,其作业循环由铲装、运输、
卸土和空驶四个过程组成。由于铲运机的运输距离长,功率消耗大 ,所以欲提高铲运机的作业效率,同样应尽力做到以在最短的距离 和时间内装满铲斗,而运输中注意安全的前提下应尽量提高运输速 度,提高卸土的质量和速度以缩短整个循环时间。 1 .关于推土机助铲
3 .前轮倾斜的运用 作业时,由于刮刀有一定回转角,或由于刮刀在机外刮侧坡,使
机器受到一个侧向力的作用,常会迫使机器前轮发生侧移以致偏离 行驶方向,加剧轮胎磨损,并对前轮的转向销轴产生很大力矩,使 偏摆前轮阻力增大。这时可以采用倾斜车轮的方法来避免这种状况 ,原则是:前回转角的运用轮的倾斜总是与外力呈相抵消状态。
第四章 土方机械施工运用 7
最小生成树两种算法详解

最⼩⽣成树两种算法详解最⼩⽣成树众所周知, 树是⼀种特殊的图, 是由n-1条边连通n个节点的图.如果在⼀个有n个节点的⽆向图中, 选择n-1条边, 将n个点连成⼀棵树, 那么这棵树就是这个图的⼀个⽣成树.如果保证树的边权和最⼩, 那么这棵树就是图的最⼩⽣成树.为了求⼀棵树的最⼩⽣成树, 有两种算法, ⼀种是选择点加⼊树的Prim算法, 另⼀种是选择边加⼊树的Kruskal算法.Prim算法这个算法的过程和Dijkstra类似, 但有所不同.⾸先选择任意⼀点作为树的第⼀个节点0, 枚举与它相连的所有点i, 将两点之间的边权记为这个点到⽣成树的距离b[i], 选择距离最近的点加⼊⽣成树, 然后枚举与之相邻的节点j, ⽤边权a[i,j]更新b[j], 使其等于min(b[j],a[i,j]), 这样再继续加⼊当前离⽣成树最近的点, 在更新它相邻的点, 以此类推, 直到所有点全部加⼊⽣成树. 这样, 便求出了最⼩⽣成树.关于正确性我⾃⼰的思路是这样的: 如果⽤Prim算法求出了⼀棵最⼩⽣成树, 将⼀条边u换成另⼀条更⼩的v, 就得到⼀棵边权和更⼩的⽣成树. ⾸先保证树连通, 所以去掉u和v, ⽣成树被分成两个连通块是⼀模⼀样的. 在当时连接u的时候, 已经决策完的⽣成树⼀定也和v相连, 这时v连接的节点⼀定会⽐u连接的节点更早加⼊, 所以⼀开始的假设不成⽴, 算法正确.具体代码实现#include<iostream>#include<cstring>#include<cstdio>using namespace std;int n,m,l,r,x,a[5005][5005]/*邻接矩阵*/,b[5005]/*点到⽣成树的最短边权*/,now/*当前加⼊的点*/,k=1/*⽣成树节点数*/,ans=0/*⽣成树总边权和*/;bool vsd[5005]={0};void update(int at){//⽤节点at更新其他点的b[]值for(int i=1;i<=n;i++) {b[i]=min(a[at][i],b[i]);}vsd[at]=true;return;}int find(){//寻找当前离⽣成树最近的点int ft=0;for(int i=1;i<=n;i++){if(!vsd[i]){//不在树中if(b[i]<=b[ft]){ft=i;}}}return ft;}int main(){cin>>n>>m;memset(a,0x3f,sizeof(a));for(int i=1;i<=n;i++){a[i][i]=0;}for(int i=1;i<=m;i++){cin>>l>>r>>x;a[l][r]=min(a[l][r],x);//防⽌有两个点之间出现边权不同的⼏条边a[r][l]=min(a[r][l],x);}memset(b,0x3f,sizeof(b));update(1);while(k<n){//加⼊n-1个点后返回(第⼀个点本来就在树中, ⽆需加⼊)now=find();//加⼊最近的点nowans+=b[now];//统计答案update(now);//更新其他点k++;//统计点数}cout<<ans<<endl;return 0;}Kruskal算法这个算法和Prim相反, 它是将边记为树上的边, 最终得到⼀棵最⼩⽣成树.将所有边按边权排序, 然后将它们从⼩到⼤讨论是否加⼊⽣成树. 如果该边的两个端点属于同⼀个连通块, 这时加⼊该边就会形成环, 不符合树的定义, 所以舍弃. 如果该边两个端点不属于同⼀个连通块, 那么连接该边, 将两个端点所在连通块连成⼀个.当共加⼊n-1条边的时候, 就得到了⼀棵最⼩⽣成树.对于查找两点是否在同⼀个连通块中的⽅法, 我们可以使⽤并查集来维护点之间的连通关系.正确性简易说明Kruskal相对来说更好理解, 因为从⼩到⼤排序后, 使⽤被舍弃的边连成环是⾮法的, 使⽤排在后⾯的合法的边替换已经选择的边, 得到的答案不是最优的. 所以Kruskal算法正确.代码实现#include<cstdio>#include<cstring>#include<iostream>#include<algorithm>using namespace std;int n,m,fa[10005],s,e,l,k=0,ans=0;struct side{int le,ri,len;//起点, 终点, 边权}a[200005];bool cmp(side x,side y){//结构体sort规则return(x.len<y.len);}int find(int x){//并查集寻找最⽼祖先if(fa[x]==x){//⾃⼰就是当前连通块最⽼祖先return x;}fa[x]=find(fa[x]);//⾃⼰祖先的最⽼祖先return fa[x];}int main(){cin>>n>>m;memset(a,0x3f,sizeof(a));for(int i=1;i<=m;i++){cin>>s>>e>>l;a[i].le=s;//结构体存储边a[i].ri=e;a[i].len=l;}sort(a+1,a+m+1,cmp);//按边权升序排列for(int i=1;i<=n;i++){fa[i]=i;//初始化并查集}int i=0;while((k<n-1/*加⼊了n-1个点跳出*/)&&(i<=m/*枚举完了所有的边跳出*/)){i++;int fa1=find(a[i].le),fa2=find(a[i].ri);//两个端点的最⽼祖先if(fa1!=fa2){//不在同⼀连通块ans+=a[i].len;//记录答案fa[fa1]=fa2;//连接连通块k++;//记录边数}}cout<<ans<<endl;return 0;}之前发的是笔记, 现在发的是实战总结。
最小生成树算法详解

closedge[6].adjvex=3 .lowcost=4
adjvex lowcost
v1 6
v1 1
v1 5
{v1}
{v2,v3,v4,v5,v6}
V4
V1
V3
V2
V6
V5
V4
V1
V3
1
{V1 }
{ V2 ,V3 ,V4 , V5 ,V6 }
步骤
(0)
{V1 ,V3 }
{ V2 ,V4 , V5 ,V6 }
(1)
V2
V6
V5
{V1 ,V3 ,V6 }
{ V2 ,V4 , V5 }
(2)
4
{V1 ,V3 ,V6 ,V4 }
{ V2, V5 }
adjvex lowcost
v1 6
v1 1
v1 5
{v1}
{v2,v3,v4,v5,v6}
3
adjvex lowcost
v3 5
0
v1 5
v3 6
v3 4
{v1,v3}
{v2,v4,v5,v6}
6
adjvex lowcost
v3 5
0
v6 2
v3 6
0
{v1,v3,v6}
{v2,v4,v5 }
(3)
2
{V1 ,V3 ,V6 ,V4 ,V2 }
{ V5 }
(4)
5
{V1 ,V3 ,V6 ,V4 ,V2 ,V5 }
{ }
(5)
3
V-U
普里姆(Prim)算法
生成树中只放置一个顶点
图的最小生成树算法

图的最小生成树算法图的最小生成树算法是指找到一个图中的一棵生成树,使得该生成树的所有边的权值之和最小。
最小生成树算法在网络设计、电力传输、交通规划等领域有着广泛的应用。
本篇文章将详细介绍两种常用的最小生成树算法:Prim算法和Kruskal算法。
一、Prim算法Prim算法是一种贪心算法,它从一个顶点开始,逐步扩展生成树,直到包含所有顶点为止。
算法具体步骤如下:1. 初始化生成树为空集,选择任意一个顶点作为起始顶点。
2. 从与生成树中的顶点相连的所有边中选择一条权值最小的边,并将该边的另一个顶点加入生成树。
3. 重复步骤2,直到生成树包含所有顶点为止。
Prim算法的时间复杂度为O(V^2),其中V是图的顶点数。
算法的优化版本可以使用优先队列来选择最小权值的边,时间复杂度可以优化到O(ElogV),其中E是图的边数。
二、Kruskal算法Kruskal算法是一种基于并查集的贪心算法,它将图中的所有边按照权值从小到大进行排序,然后依次选取权值最小的边,如果该边的两个顶点不在同一个连通分量中,则将该边加入生成树中。
算法具体步骤如下:1. 初始化生成树为空集,将图中的所有边按照权值从小到大进行排序。
2. 依次选取权值最小的边,如果该边的两个顶点不在同一个连通分量中,则将该边加入生成树。
3. 重复步骤2,直到生成树的边数等于顶点数减一为止。
Kruskal算法的时间复杂度为O(ElogE),其中E是图的边数。
并查集的操作时间复杂度为O(logV),所以整体的时间复杂度为O(ElogE)。
三、比较与应用Prim算法适用于稠密图,即边的数量接近于顶点数量的平方。
而Kruskal算法适用于稀疏图,即边的数量相对较少。
另外,Prim算法的实现相对简单,而Kruskal算法需要使用并查集来判断两个顶点是否在同一个连通分量中。
最小生成树算法在实际应用中有着广泛的作用。
例如,在网络设计中,最小生成树算法可以用来确定网络中的主干链路,以最小的代价满足网络的连通要求;在电力传输中,最小生成树算法可以用来确定输电线路的布置,以保证电力传输的稳定性和可靠性。
图的最小生成树_prim算法

4 最小生成树
①初始化候选边数组edges[]; ② U={v0}; ③for (i=1; i<=n-1; i++) { k=最小候选边的未选的一端; U=U+{k}; 以k修改edges[]; } 注:edges的元素可以设置为{v} 思考:权值最小的边一定在最小生成树中么? 分析 : prim算法的时间复杂度?
1
12 15
9
9 5 4
2
17
6 9 10 3 4
(1,2)/12 (1,3)/∞
3
{1,6} {1,6,5}
(1,2)/12 (6,3)/17 (6,4)/20 (6,2)/15 (6,4)/20 (1,2)/12 (6,3)/17 (5,4)/4 (6,2)/15 (1,2)/12 (6,3)/17 (6,2)/15 (4,3)/3
2
6 15 17 3 3 6 9 10 4
7
5 4
4 最小生成树
1 12 2 6 15 17 3 3 9 6 9 10 4 9 5 4 2 6 12 15 17 3
1 9
6 9 12 5 4 4 2 6 15 17 3
1 9
6 9
9
10
9
10
5 4 4
3
1
3
1
1 12 9 15 17 3 3 6 9 10 4 9 5 4 2 6
6
4 最小生成树
问题:修建一个连接各个小区与供应站点之间的管道使得造价成本最 低,即构造一颗最小生成树。但是如何求解? 4.1 prim算法 1. 基本思想 在满足如下条件的过程中选出一条最小的边: 一端已选,另一端未选。 因此,该算法需要给出起点,以作为已选顶点。 2. 实例 1 对右图所示图, 12 9 9 用Prim算法求最小生成树。
图论算法--最小生成树
生成树的权值之和为 39。
A, D, F, 无 B, E, C,
G
算法时间复杂度:O (N2)。 【例 02】最优布线问题(wire) 【问题描述】
学校有 n 台计算机,为了方便数据传输,现要将它们用数据线连接起来。两台计算机被 连接是指它们间有数据线连接。由于计算机所处的位置不同,因此不同的两台计算机的连接 费用往往是不同的。
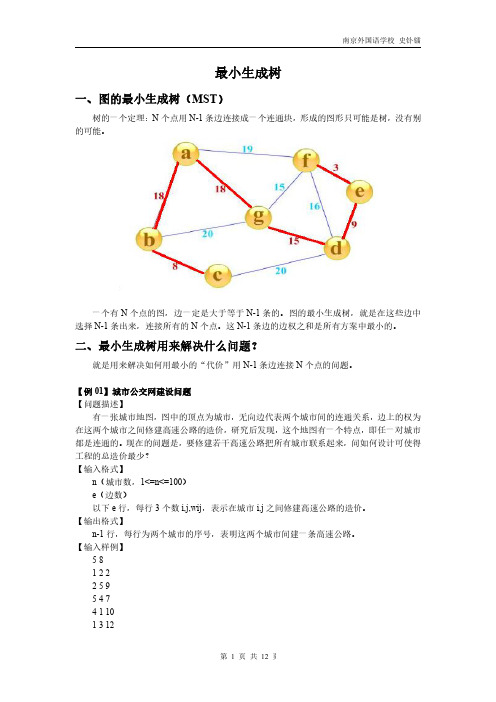
率先选择了边 AD。这样我们的图就变成了左图
第 6 页 共 12 页
南京外国语学校 史钋镭
在剩下的变中寻找。我们找到了 CE。这里边的权重也 是5
依次类推我们找到了 6,7,7,即 DF,AB,BE。
下面继续选择,BC 或者 EF 尽管现在长度为 8 的边是 最小的未选择的边。但是现在他们已经连通了(对于 BC 可以通过 CE,EB 来连接,类似的 EF 可以通过 EB,BA,AD,DF 来接连)。所以不需要选择他们。类似 的 BD 也已经连通了(这里上图的连通线用红色表示 了)。最后就剩下 EG 和 FG 了。当然我们选择了 EG。
二、最小生成树用来解决什么问题?
就是用来解决如何用最小的“代价”用 N-1 条边连接 N 个点的问题。
【例 01】城市公交网建设问题 【问题描述】
有一张城市地图,图中的顶点为城市,无向边代表两个城市间的连通关系,边上的权为 在这两个城市之间修建高速公路的造价,研究后发现,这个地图有一个特点,即任一对城市 都是连通的。现在的问题是,要修建若干高速公路把所有城市联系起来,问如何设计可使得 工程的总造价最少? 【输入格式】
}
int cmp(const point &a,const point &b){
//sort()自定义的比较函数
分别用破圈法和避圈法求下图所示网络的最小生成树

1.分别用破圈法和避圈法求下图所示网络的最小生成树。
2. 设天然气公司计划在下图所示的网络中
铺设天然气管道向五个居民小区V\ ,
V" “V供气,网络中各边的8 权代表相应
小区之间所铺天然气管道的实际长度
(公里)。
试问:应如
何铺设管道,既能保证五个居民小区都能供应天然气,又能使管道的总长度最短从而使用权费用最省?
3. 八口海上油井,相互间的距离如下表所示。
1号井离海岸最
近, 为5海里。
问:从海岸经1号井铺设输油管把各油井连接起来,应如何铺设才能使输油管总长度最短?
] 3 4 5 67
1 13 210.9 U7 18 20 15
r A0.9 1.8 12 16 13 LI
3 1.7 15 1.9 10
4 D7 16 1
5 ns
5 0 9 H 0.8
606 10
7 05
4. 对于所给图,求其最小生树及相应的长度
5. 一个乡有九个自然村,其间道路及各道路长度如下图3.1-10所示, 各边旁的数字表示相应自然村之间的道路的长度。
今欲在该乡的各自然村之间建立电话线路。
问:如何拉线,才能使所用屯话线最短?
6.已知世界上六个最大城市:伦敦(L)、墨西哥城(Me)、纽约(Ny)、巴黎(Pa)、北京(Pe)和东京⑴之间的航线距离(以英里为单位)如表所示:
试求以该六城市为顶点集,以连接两个城市之间的航线为边,以航线距离为边的权的网络的最小生成树及其总距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求出下图的最小生成树
解:MATLAB程序:
% 求图的最小生成树的prim算法。
% result的第一、二、三行分别表示生成树边的起点、终点、权集合
% p——记录生成树的的顶点,tb=V\p
clc;clear;
% a(1,2)=50; a(1,3)=60;
% a(2,4)=65; a(2,5)=40;
% a(3,4)=52;a(3,7)=45;
% a(4,5)=50; a(4,6)=30;a(4,7)=42;
% a(5,6)=70;
% a=[a;zeros(2,7)];
e=[1 2 20;1 4 7;2 3 18;2 13 8;3 5 14;3 14 14;4 7 10;5 6 30;5 9 25;5 10 9;6 10 30;6 11 30;7 8 2;7 13 5;8 9 4;8 14 2;9 10 6;9 14 3;10 11 11;11 12 30];
n=max([e(:,1);e(:,2)]); % 顶点数
m=size(e,1); % 边数
M=sum(e(:,3)); % 代表无穷大
a=zeros(n,n);
for k=1:m
a(e(k,1),e(k,2))=e(k,3);
end
a=a+a';
a(find(a==0))=M; % 形成图的邻接矩阵
result=[];p=1; % 设置生成树的起始顶点
tb=2:length(a); % 设置生成树以外顶点
while length(result)~=length(a)-1 % 边数不足顶点数-1
temp=a(p,tb);temp=temp(:); % 取出与p关联的所有边
d=min(temp); % 取上述边中的最小边
[jb,kb]=find(a(p,tb)==d); % 寻找最小边的两个端点(可能不止一个)
j=p(jb(1));k=tb(kb(1)); % 确定最小边的两个端点
result=[result,[j;k;d]]; % 记录最小生成树的新边
p=[p,k]; % 扩展生成树的顶点
tb(find(tb==k))=[]; % 缩减生成树以外顶点
end
result % 显示生成树(点、点、边长)
weight=sum(result(3,:)) % 计算生成树的权
程序结果:
result =
1 4 7 8 14 7 9 13 10 10 14 10 11 4 7 8 14 9 13 10
2 5 11
3 6 12 7 10 2 2 3 5 6 8 9 11 1
4 30 30 weight =
137
附图
最小生成树的权是137。
