格林公式例题与习题
格林公式及其应用

其中L是 D的取正向的边界曲线.
格林公式的实质: 沟通了沿闭曲线的积分与二重
积分之间的联系.
3. 简单应用
(1) 计算平面面积
格林公式
D
Q x
P y
dxdy
L
Pdx
Qdy
取 P y, Q x,
得
2 dxdy L xdy ydx
D
闭区域D的面积
A 1 xdy ydx 2L
例1 求椭圆 x a cos t, y bsint,0 t 2
解 由格林公式
(e x sin y my )dx (e x cos y m)Ody AO OA
A(a,0)x
mdxdy
1 8
ma 2
OA的方程为y 0, 0 x a
D
故
(e x sin y my )dx (e x cos y m)dy
a
0dx 0
OA
0
所以, I 1 ma2 0 1 ma2.
AO OA OA 8
8
(3) 简化二重积分
D
(Q x
P y
)dxdy
L
Pdx
Qdy
例5 计算 e y2dxdy, 其中D是
D
y 1B
A
以O(0,0), A(1,1), B(0,1)
D
为顶点的三角形闭区域.
解 令 P 0, Q xe y2
O
1x
则 Q P e y2 格林公式
x y
e y2dxdy
规定 边界曲线L的正向 当观察者沿边界行走时,区域D总在他的左边.
y L
D
L
D
l
O
x
L+l 称为复合闭曲线
第四节格林公式

EAC c
⌒
证明(2) 若区域D由按段光滑的 闭曲线围成.如图, 将D分成三个既是 x 型又是 y 型的 区域D1, D2, D3.
L3 D3
D2
L2
L1
D1
D
L
Q P Q P ( x y )dxdy ( x y )dxdy D D1 D2 D3
(
D1 D2 D3
Q P )( )dxdy x y
(
D1
D2
D3
) Pdx Qdy
D
Pdx Qdy.
证明(3) 若D是复连通区域 ,添加直线段
AB,CE. 则D由AB, BA,AFC,CE, EC 及CGA构成. 由(2)知 ( Q P )dxdy D y D x
y2
1
x
e
D
y2
dxdy
x2
OA AB BO
xe
dy
OA
xe
y2
dy
0 xe
1
1 1 x2 1 dx [ e ] 0 (1 e 1 ). 2 2
3) 利用第二类曲线积分可求闭曲线所围区域的面积.
Q P )dxdy Pdx Qdy 格林公式: ( y D x D
y
解 记 L 所围闭区域为 D ,
则原积分
( y
D
2
x )dxdy
2
O
2 x
d 0
2 2
2 cos
d 8
3
2 0
3 cos d . 2
格林公式习题解析

“ u(x, y) (x,y) 2x ydx x2 d y ”. ( x0 , y0 )
图1
又由于积分 u(x, y) (x,y) 2X Y d X X 2 dY 与路径无关, ( x0 , y0 )
也就意味着,我们可以选取使计算简便的路径,通常我们选择 折线路径,如图 1 和图 2 所示.
y
x
y x
符合定理 9.3.2 中的充要条件,因此,积分与路径无关.
再来计算积分值——
本题中并没有指定积分弧段,只取定了起点 (1,1) 和终点 (2,3) . 由于积分与路径无关,
因此,无论沿哪条积分弧段计算曲线积分,积分值都是相同的, 我们可以选择较简便的折线路径(如图 3 所示)进行计算,记
因此,无论沿哪条积分弧段计算曲线积分,积分值都是相同的, 我们可以选择较简便的折线路径(如图 4 所示)进行计算,记
x x
LAB
:
y
2
(x
:1
3)
,
LBC
:
x y
3 y
( y : 2 4) ,则有
图4
(3,4) (6 x y2 y3)dx (6 x2 y 3 x y2 )d y (1,2)
的正向边界;
答案: 1 (e 1) 5
解析: 本题考查课本第 137~138 页知识点——
可简单地理解为曲线上无“尖点”(导数或偏导数不存在的点), 即曲线上处处有切线,且切线随切点的移动而连续转动.
简单地讲,格林公式就是把闭区域内的二重积分和该闭区域边界上的曲线积分联系了起 来,这两种积分可以根据我们的需要相互转化,从而简化计算.
u(x, y) y0 (x2 x02 ) x2 ( y y0) 的全微分,随着 (x0, y0 ) 的不同, u(x, y) 也不同.
数学分析21.3格林公式、曲线积分与路线的无关性(含习题及参考答案)

第二十一章 重积分3格林公式、曲线积分与路线的无关性一、格林公式概念:当区域D 的边界L 由一条或几条光滑曲线所组成时,规定边界曲线的正方向为:当人沿边界行走时,区域D 总在他的左边. 与正方向相反的方向称为负方向,记为-L.定理21.11:若函数P(x,y), Q(x,y)在闭区域D 上连续,且有连续的一阶偏导数,则有格林公式:⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎰+L Qdy Pdx . L 为区域D 的边界曲线,并取正方向.证:根据区域D 的不同形状,可分三种情形来证明: (1)若区域D 既是x 型区域,又是y 型区域(如图1),即 平行于坐标轴的直线和L 至多交于两点,该区域D 可表示为: φ1(x)≤y ≤φ2(x), a ≤x ≤b 或ψ1(x)≤x ≤ψ2(x), c ≤y ≤d.这里y=φ1(x)和y=φ2(x)分别为曲线⌒ACB 和⌒AEB 的方程, x=ψ1(x)和x=ψ2(x) 分别为曲线⌒CAE 和⌒CBE的方程, ∴⎰⎰∂∂Dd x Qσ=⎰⎰∂∂)()(21y y d c dx x Q dy ψψ=⎰d c dy y y Q )),((2ψ-⎰d c dyy y Q )),((1ψ=⎰⋂CBE dy y x Q ),(-⎰⋂CAE dy y x Q ),(=⎰⋂CBE dy y x Q ),(+⎰⋂EAC dy y x Q ),(=⎰L dy y x Q ),(.同理可证:-⎰⎰∂∂Dd y Pσ=⎰L dx y x P ),(. 即有⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎰+L Qdy Pdx . (2)若区域D 是一条按段光滑的闭曲线围成(如图2),则先用几段光滑曲线将D 分成有限个既是x 型又是y 型的子区域,然后逐块按(1)得到它们的格林公式,相加即可.图2中区域D 可分成三个既是x 型又是y 型的区域D 1,D 2,D 3,则有⎰⎰⎪⎪⎭⎫⎝⎛∂∂-∂∂D d y P x Q σ=⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂1D d y P x Q σ+⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂2D d y P x Q σ+⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂3D d y P x Q σ =⎰+1L Qdy Pdx +⎰+2L Qdy Pdx +⎰+3L Qdy Pdx =⎰+L Qdy Pdx.(3)若区域D 由几条闭曲线所围成(如图3), 可适当添加直线AB, CE,把区域转化为(2)的情况处理.图D 的边界线由AB,L 2,BA,⌒AFC ,CE,L 3,EC 及⌒CGA构成. 由(2)知 ⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎪⎭⎫ ⎝⎛+++++++⎰⎰⎰⎰⎰⎰⎰⎰⋂⋂CGA EC l CE AFCBA l AB32(Pdx+Qdy)=()⎰⎰⎰++132L L L (Pdx+Qdy)=⎰+L Qdy Pdx .注:格林公式可写为:⎰⎰∂∂∂∂Dd QP y x σ=⎰+L Qdy Pdx .例1:计算⎰AB xdy ,其中曲线AB 为半径为r 的圆在第一象限部分. 解:如图,对半径为r 的四分之一圆域D 应用格林公式有⎰⎰-D d σ=⎰-L xdy =⎰OA xdy +⎰AB xdy +⎰BO xdy =⎰AB xdy . ∴⎰AB xdy =⎰⎰-Dd σ=-41πr 2.例2:计算I=⎰+-Ly x ydxxdy 22, 其中L 为任一不包含原点的闭区域的边界线.解:⎪⎪⎭⎫ ⎝⎛+∂∂22y x x x =22222)(y x x y +-, ⎪⎪⎭⎫ ⎝⎛+-∂∂22y x y y =22222)(y x x y +- 在上述区域D 上连续且有界,∴⎰⎰⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-∂∂-⎪⎪⎭⎫ ⎝⎛+∂∂Dd yx yx y x x x σ2222=0. 由格林公式可得I=0.注:在格林公式中,令P=-y, Q=x ,则得到一个计算平面区域D 的面积S D 的公式:S D =⎰⎰Dd σ=⎰-L ydx xdy 21.例3:如图,计算抛物线(x+y)2=ax (a>0)与x 轴所围的面积.解:曲线⌒AMO由函数y=x ax -, x ∈[0,a], 直线OA 为直线y=0, ∴S D =⎰-ydx xdy 21=⎰-OA ydx xdy 21+⎰⋂-AMO ydx xdy 21=⎰⋂-AMO ydx xdy 21=dx x ax ax ax a ⎰⎥⎦⎤⎢⎣⎡--⎪⎪⎭⎫ ⎝⎛-0)(1221=dx ax a ⎰-02121=dx x a a⎰4=62a .二、曲线积分与路线的无关性概念:若对于平面区域D 上任一封闭曲线,皆可不经过D 以外的点而连续收缩于属于D 的某一点,则称此平面区域为单连通区域,否则称为复连通区域。
利用格林公式计算面积的一般表达式

J( no一a OO a a bsms)= h O b c0 i d霄 + n
= -
i) c 3时 , i当 = i 有
2 c
,
O P
一
,
故 : { Ⅱ l
( 4 ) ( 5 )
导 出公 式
dd ÷ £d— x x = } yy y d x
1利 用 格 林公 式 计 算 面 积 的 一 般 表 达 式 .
野 , 行研究性学 习具有一定 的借鉴意义 。 进
参 考 文献
A}y。bsO a =x= a = :h d J cO 盯 od
( C 一 ,= b 2 1 lO ) = e
[] 1 同济大学应 用数 学系主编. 高等数学( 第五版) 下册 北京: 高等教
育 出版 社 ,0 2 1 2 1 5 2 0 ,4 - 4
科技信息
高校 理科 研 究
利 用 格 赫 公 式 计算 面 积 髓 一般 表达 式
长 江大 学电子信 息学 院 1 8 1 0 0 班 陈 聪
[a 要 ] g 本文给出利 用格林公式计算面积 的一般表达 式, 明其 正确性 , 证 与教科 书中的计算 实例进行 比较 , 结果表明该表达式是有
效的。
[ 关键词 ] 格林公式 面积计算 应用
格林公式 建立 了闭区域 D上 二重积分 与 D的边 界曲线 L上第二 类曲线 积分之间的联系, 即若 Px ) ( y (y Q x ) ,, , 在闭区域 D上连续, 且有连续
A -i+)c0( sn(n = o b O do)cO)s ) J(s m(s a +d i n a +。 bO
() 1
Jd} (n+—x y f +y y d = 2 )() x xdm d
13格林公式及其应用

§10.3 格林公式及其应用一、格林公式一元微积分学中最基本的公式 — 牛顿、莱布尼兹公式'=-⎰F x dx F b F a ab ()()()表明:函数'F x ()在区间[,]a b 上的定积分可通过原函数F x ()在这个区间的两个端点处的值来表示。
无独有偶,在平面区域D 上的二重积分也可以通过沿区域D 的边界曲线L 上的曲线积分来表示,这便是我们要介绍的格林公式。
1、单连通区域的概念设D 为平面区域,如果D 内任一闭曲线所围的部分区域都属于D ,则称D 为平面单连通区域;否则称为复连通区域。
通俗地讲,单连通区域是不含“洞”(包括“点洞”)与“裂缝”的区域。
2、区域的边界曲线的正向规定设L 是平面区域D 的边界曲线,规定L 的正向为:当观察者沿L 的这个方向行走时,D 内位于他附近的那一部分总在他的左边。
简言之:区域的边界曲线之正向应适合条件,人沿曲线走,区域在左手。
3、格林公式【定理】设闭区域D 由分段光滑的曲线L 围成,函数P x y (,)及Q x y (,)在D 上具有一阶连续偏导数,则有()∂∂∂∂Q x Py dxdy Pdx Qdy DL -=+⎰⎰⎰ (1)其中L 是D 的取正向的边界曲线。
公式(1)叫做格林(green)公式。
【证明】先证 -=⎰⎰⎰∂∂Py dxdy Pdx D L假定区域D 的形状如下(用平行于y 轴的直线穿过区域,与区域边界曲线的交点至多两点)易见,图二所表示的区域是图一所表示的区域的一种特殊情况,我们仅对图一所表示的区域D 给予证明即可。
D a x b x y x :,()()≤≤≤≤ϕϕ12[]-=-=-⎰⎰⎰⎰⎰∂∂∂∂ϕϕϕϕP y dxdy dx P y dy P x y dx D a b x x abx x 1212()()()()(,)=--⎰{[,()][,()]}P x x P x x dxabϕϕ21另一方面,据对坐标的曲线积分性质与计算法有Pdx Pdx Pdx Pdx PdxLABBCCEEA⎰⎰⎰⎰⎰=+++弧弧=+++⎰⎰P x x dx P x x dx ab ba[,()][,()]ϕϕ1200=--⎰{[,()][,()]}P x x P x x dxabϕϕ21因此 -=⎰⎰⎰∂∂Py dxdy Pdx D L再假定穿过区域D 内部且平行于x 轴的直线与的D 的边界曲线的交点至多是两点,用类似的方法可证∂∂Qx dxdy Qdx D L ⎰⎰⎰=综合有当区域D 的边界曲线与穿过D 内部且平行于坐标轴( x 轴或y 轴 )的任何直线的交点至多是两点时,我们有-=⎰⎰⎰∂∂P y dxdy Pdx D L , ∂∂Q x dxdy Qdx D L ⎰⎰⎰=同时成立。
高等数学:格林公式

D
由于 xdy 0,
xdy 0, xdy dxdy 1 r2.
OA
BO
AB D
4
2. 简化二重积分
y
例 2 计算
e y2 dxdy ,其中D 是
B 1
D
D
以O(0,0), A(1,1), B(0,1)为顶点
的三角形闭区域.
o
解 令P 0, Q xe y2 ,
A
1
x
则 Q P e y2 , x y
c
1 ( y) x
d
c
Q(
2
(
y),
y)dy
d
c
Q(
1(
y),
y)dy
ห้องสมุดไป่ตู้
y
Q( x, y)dy Q( x, y)dy
CBE
CAE
d
x 1( y)
Q( x, y)dy Q( x, y)dy
CBE
EAC
A
c
LQ( x, y)dy
o
E D B
C
x 2( y)
x
同理可证
D
P y
dxdy
L
P(
A
1 2
L
xdy
ydx
1
2 ONA
xdy
ydx
1
2 AMO
xdy
ydx
1
2 AMO
xdy
ydx
M
N
A(a,0)
1 2
0
a
x(
2
a ax
1)dx
(
ax x)dx
a a
40
xdx 1 a2 . 6
例3. 计算
格林公式及其应用

易于计算时,可应用格林公式计算
O
L2 L L1 L3
x
(2)L不封闭时,采取“补线”的方法:
L L l lD ( Q x P y)dx d l y
要求右端的二重积分及曲线l积分易于计算。l 选用直线段、折线、圆、半圆、椭圆、抛物线等。
(3)如在D上P、Q一阶偏导连续,且处处有
(1) 沿D中任意光滑闭曲线 L,有 LPdxQdy0。
(2) 对 D中任一分段光滑曲线 L, 曲线积分
PdxQdy与路径无关, 只与起止点有关.
L
(3)PdxQdy在 D内是某一函数 u(x, y)的全微分, 即 d u ( x ,y ) P d x Q d y
(4) 在 D内每一点都有 P Q 。 y x
注意本题只在不含原点的单连通区域内积分与路径无关内有设pq在单连通域d内具有一阶连续偏导数则有思考与练习且都取正向问下列计算是否正确的半圆计算质点m沿着以ab为直径的半圆从a12运动到故所求功为ab锐角其方向垂直于om且与y轴正向夹角为对质点m所作的功
8.2 格林公式及其应用
8.2.1 格林公式 8.2.2 平面上曲线积分与路径无关的条件
a a xdx1a2
40
6
8.2.2 平面上曲线积分与路径无关的条件
如果在区域G内有
y
PdxQdy L1
PdxQdy L2
B G
L1
A
L2
o
x
则称曲线积分L Pdx Qdy在G 内与路径无关,
否则与路径有关。
平面上曲线积分与路径无关的等价条件 定理8.2.2 设 D是单连通域,函数P (x ,y)Q ,(x ,y)在D内 具有一阶连续偏导数, 则以下四个条件等价:
第十一章 曲线积分与曲面积分经典例题

第十一章 曲线积分与曲面积分内容要点一、引例 设有一曲线形构件所占的位置是xOy 面内的一段曲线L (图10-1-1),它的质量分布不均匀,其线密度为),(y x ρ,试求该构件的质量. 二、第一类曲线积分的定义与性质性质1 设α,β为常数,则⎰⎰⎰+=+L L L ds y x g ds y x f ds y x g y x f ),(),()],(),([βαβα;性质2设L 由1L 和2L 两段光滑曲线组成(记为=L 21L L +),则.),(),(),(2121⎰⎰⎰+=+L L LL ds y x f ds y x f ds y x f注: 若曲线L 可分成有限段,而且每一段都是光滑的,我们就称L 是分段光滑的,在以后的讨论中总假定L 是光滑的或分段光滑的.性质3 设在L 有),(),(y x g y x f ≤,则ds y x g ds y x f LL⎰⎰≤),(),(性质4(中值定理)设函数),(y x f 在光滑曲线L 上连续,则在L 上必存在一点),(ηξ,使s f ds y x f L⋅=⎰),(),(ηξ其中s 是曲线L 的长度.三、第一类曲线积分的计算:)(),(),(βα≤≤⎩⎨⎧==t t y y t x xdt t y t x t y t x f ds y x f L)()(])(),([),(22'+'=⎰⎰βα(1.10)如果曲线L 的方程为 b x a x y y ≤≤=),(,则dx x y x y x f ds y x f ba L )(1])(,[),(2'+=⎰⎰ (1.11)如果曲线L 的方程为 d y c y x x ≤≤=),(,则dy y x y y x f ds y x f dcL )(1]),([),(2'+=⎰⎰ (1.12)如果曲线L 的方程为 βθαθ≤≤=),(r r ,则θθθθθβαd r r r r f ds y x f L)()()sin ,cos (),(22'+=⎰⎰例5(E03)计算,||⎰Lds y 其中L 为双纽线(图10-1-4))()(222222y x a y x -=+的弧.解 双纽线的极坐标方程为 .2cos 22θa r =用隐函数求导得 ,2sin ,2sin 22ra r a r r θθ-='-='.2sin 2224222θθθθd r a d ra r d r r ds =+='+= 所以 .)22(2sin 4sin 4||2402402a d a d ra r ds y L -==⋅=⎰⎰⎰ππθθθθ 内容要点一、引例:设有一质点在xOy 面内从点A 沿光滑曲线弧L 移动到点B ,在移动过程中,这质点受到力j y x Q i y x P y x F ρρρ),(),(),(+= (2.1)的作用,其中),(y x P ,),(y x Q 在L 上连续. 试计算在上述移动过程中变力),(y x F ρ所作的功. 二、 第二类曲线积分的定义与性质:j y x Q i y x P y x A ρρϖ),(),(),(+=⎰⎰+=⋅LLds Q P ds t A )cos cos (βαϖϖ平面上的第二类曲线积分在实际应用中常出现的形式是⎰+L dy y x Q dx y x P ),(),(⎰⎰+=L L dy y x Q dx y x P ),(),(性质1 设L 是有向曲线弧, L -是与L 方向相反的有向曲线弧,则⎰⎰+-=+-L L dy y x Q dx y x P dy y x Q dx y x P ),(),(),(),(;即第二类曲线积分与积分弧段的方向有关.性质2 如设L 由1L 和2L 两段光滑曲线组成,则⎰⎰⎰+++=+21L L L Qdy Pdx Qdy Pdx Qdy Pdx .三、第二类曲线积分的计算:),(t x x = ),(t y y =⎰+L dy y x Q dx y x P ),(),(⎰'+'=βαdt t y t y t x Q t x t y t x P )}()](),([)()](),([{. (2.9)如果曲线L 的方程为 ),(x y y =起点为a , 终点为b ,则.)}()](,[)](,[{⎰⎰'+=+ba L dx x y x y x Q x y x P Qdy Pdx如果曲线L 的方程为),(y x x = 起点为c , 终点为d ,则.]}),([)(]),([{⎰⎰+'=+dcLdy y y x Q y x y y x P Qdy Pdx内容要点一、格林公式定理1 设闭区域D 由分段光滑的曲线L 围成,函数),(y x P 及),(y x Q 在D 上具有一阶连续偏导数,则有⎰⎰⎰+=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂L D Qdy Pdx dxdy y P x Q (3.1)其中L 是D 的取正向的边界曲线.若在格林公式(3.1)中,令,,x Q y P =-= 得⎰⎰⎰-=LDydx xdy dxdy 2,上式左端是闭区域D 的面积A 的两倍,因此有 .21⎰-=Lydx xdy A 二、平面曲线积分与路径无关的定义与条件定理2 设开区域D 是一个单连通域,函数),(y x P 及),(y x Q 在D 内具有一阶连续偏导数,则下列命题等价:(1) 曲线积分⎰+LQdy Pdx 在D 内与路径无关;(2)表达式Qdy Pdx +为某二元函数),(y x u 的全微分; (3)xQy P ∂∂=∂∂在D 内恒成立; (4)对D 内任一闭曲线L ,0=+⎰LQdy Pdx .由定理的证明过程可见,若函数),(y x P ,),(y x Q 满足定理的条件,则二元函数⎰+=),(),(00),(),(),(y x y x dy y x Q dx y x P y x u (3.3)满足 dy y x Q dx y x P y x du ),(),(),(+=, 我们称),(y x u 为表达式dy y x Q dx y x P ),(),(+的原函数.C dy y x P dx y x P y x u yy xx ++=⎰⎰00),(),(),(0或 C dy y x P dx y x P y x u yy xx ++=⎰⎰0),(),(),(0例4 计算,2dxdy e Dy ⎰⎰- 其中D 是以)1,0(),1,1(),0,0(B A O 为顶点的三角形闭区域.解 令,0=P ,2y xe Q -=则 yPx Q ∂∂-∂∂.2y e -= 应用格林公式,得dxdy e Dy ⎰⎰-2⎰++-=BOAB OA y dy xe 2⎰-=OAdy xe y 2⎰-=102dx xe x ).1(211--=e 例5(E03)计算,22⎰+-L y x ydx xdy 其中L 为一条无重点)1(, 分段光滑且不经过原点的连续闭曲线, L 的方向为逆时针方向.解 记L 所围成的闭区域为,D 令,22y x y P +-=,22yx xQ += 则当022≠+y x 时,有 x Q∂∂22222)(y x x y +-=.y P ∂∂=(1) 当D ∉)0,0(时,由格林公式知;022=+-⎰L y x ydxxdy(2) 当D ∈)0,0(时,作位于D 内圆周,:222r y x l =+记1D 由L 和l 所围成,应用格林公式,得⎰⎰=+--+-L l y x ydxxdy y x ydx xdy .02222故⎰+-L y x ydx xdy 22⎰+-=l y x ydxxdy 22⎰+=πθθθ2022222sin cos d rr r ⎰=πθ20d .2π=例6(E04)求椭圆θcos a x =,θsin b y =所围成图形的面积A . 解 所求面积A ⎰-=L ydx xdy 21⎰+=πθθθ2022)sin cos (21d ab ab ⎰=πθ2021d ab.ab π=例7 计算抛物线)0()(2>=+a ax y x 与x 轴所围成的面积. 解 ONA 为直线.0=y 曲线AMO 为 ,x ax y -=].,0[a x ∈ ∴A ⎰-=AMOydx xdy 21⎰⎰-+-=AMOONAydx xdy ydx xdy 2121⎰-=AMOydx xdy 21⎰--⎪⎪⎭⎫⎝⎛-=)(1221a dx x ax dx ax a x ⎰=adx x a4.612a =例10(E06)计算,)8,6()0,1(22⎰++yx ydy xdx 积分沿不通过坐标原点的路径.解 显然,当)0,0(),(≠y x 时, 22y x ydy xdx ++,22y x d +=于是⎰++)8,6()0,1(22yx ydy xdx ⎰+=)8,6()0,1(22y x d )8,6()0,1(22y x +=.9=例 12 验证: 在整个xOy 面内, ydy x dx xy 22+是某个函数的全微分, 并求出一个这样 的函数.证2 利用原函数法求全微分函数).,(y x u 由2xy y u =∂∂ ),(2222y y x dx xy u ϕ+==⎰其中)(y ϕ是y 的待定函数.由此得).(2y y x yuϕ'+=∂∂ 又u 必须满足 y x yu2=∂∂ y x y y x 22)('=+ϕ 0)('=y ϕ ,)(C y =ϕ 所求函数为.2/22C y x u +=例13(E07)设函数),(y x Q 在xoy 平面上具有一阶连续偏导数, 曲线积分与路径无关, 并且对任意t , 总有,),(2),(2),1()0,0()1,()0,0(⎰⎰+=+t t dy y x Q xydx dy y x Q xydx求).,(y x Q解 由曲线积分与路径无关的条件知,2x xQ=∂∂ 于是),(),(2y C x y x Q +=其中)(y C 为待定函数.dy y x Q xydx t ),(2)1,()0,0(+⎰⎰+=102))((dy y C t ,)(102⎰+=dy y C tdy y x Q xydx t ),(2),1()0,0(+⎰⎰+=tdy y C 0))(1(,)(0⎰+=t dy y C t由题意可知⎰+12)(dy y C t .)(0⎰+=tdy y C t两边对t 求导,得)(12t C t +=或.12)(-=t t C 所以.12),(2-+=y x y x Q例14(E08)设曲线积分⎰+Ldy x y dx xy )(2ϕ与路径无关, 其中ϕ具有连续的导数, 且,0)0(=ϕ计算.)()1,1()0,0(2⎰+dy x y dx xy ϕ解 ),(y x P ,2xy =),(y x Q ),(x y ϕ= y P ∂∂)(2xy y ∂∂=,2xy =x Q ∂∂)]([x y xϕ∂∂=).('x y ϕ= 因积分与路径无关散,xQy P ∂∂=∂∂ 由xy x y 2)('=ϕ .)(2C x x +=ϕ 由,0)0(=ϕ知0=C .)(2x x =ϕ 故⎰+)1,1()0,0(2)(dy x y dx xy ϕ⎰⎰+=1010ydy dx .21= 例15 选取b a ,使表达式dy e y x be dx ae e y x yxyy])1([])1[(++-++++为某一函数的全微分, 并求出这个函数.解 y P ∂∂])1[(y y ae e y x y +++∂∂=,y y ae e +=x Q ∂∂])1([y x e y x be x ++-∂∂=,y x e be -=若表达式全微分式,则,xQy P ∂∂=∂∂即 .y x y x e be ae e -=+得,1-=a .1=b ),(y x u +-+++=⎰xx dx e e x 00])1()10[(⎰+++-yy x C dy e y x e 0])1([C dy e y x e dx e x yy y xx +++-+-+=⎰⎰])1([]1)1[(C ye xe y e x xe yy y x x x +--+-=00][][.))((C e e y x y x +-+=例16(E09)求方程0)3()3(2323=-+-dy y x y dx xy x 的通解. 解 ,6xQxy y P ∂∂=-=∂∂原方程是全微分方程, ⎰⎰+-=yxdy y dx xy x y x u 0323)3(),(,42344224y y x x +-=原方程的通解为.42344224C y y x x =+- 例19求微分方程0)1(222=---+dy y x dx y x x 的通解.解 将题设方程改写为,02222=---+dy y x dx y x x xdx 即,0)()(2222=---+dy y x x d y x x d 将方程左端重新组合,有,0)()(222=--+y x d y x x d故题设方程的通解为 .)(322/322C y x x =-+内容要点一、 第一类曲面积分的概念与性质定义1 设曲面∑是光滑的, 函数),,(z y x f 在∑上有界, 把∑任意分成n 小块i S ∆(i S ∆同时也表示第i 小块曲面的面积),在i S ∆上任取一点),,,(i i i ζηξ作乘积),,2,1(),,(n i S f i i i i Λ=∆⋅ζηξ并作和,),,(1∑=∆⋅ni i i i i S f ζηξ 如果当各小块曲面的直径的最大值0→λ时, 这和式的极限存在,则称此极限值为),,(z y x f 在∑上第一类曲面积分或对面积的曲面积分,记为∑⎰⎰=→∑∆=ni i i i i S f dS z y x f 1),,(lim ),,(ζηξλ 其中),,(z y x f 称为被积函数,∑称为积分曲面. 二、对面积的曲面积分的计算法.),(),(1)],(,,[),,(22⎰⎰⎰⎰++=∑xyD y x dxdy y x z y x z y x z y x f dS z y x f例4计算,dS xyz ⎰⎰∑其中∑为抛物面).10(22≤≤+=z y x z解 根据抛物面22y x z +=对称性,及函数||xyz 关于yOz xOz 、坐标面对称,有dxdy y x y x xy xyzdS dS xyz xy D ⎰⎰⎰⎰⎰⎰'+++=∑=∑2222)2()2(1)(441⎰⎰⎰⎰+=+⋅=20125122220412sin 241sin cos 4ππdr r r tdt rdr r rt t r dt.420151254141512-=⎪⎭⎫ ⎝⎛-=⎰du u u 例 5 计算,⎰⎰∑xdS 其中∑是圆柱面,122=+y x 平面2+=x z 及0=z 所围成的空间立体的表面.解,=⎰⎰⎰⎰⎰⎰⎰⎰∑+∑+∑∑321∑∑12,在xOy 面上得投影域.1:22≤+y x D xy于是⎰⎰⎰⎰∑==1,0xyD xdxdy xdS ⎰⎰⎰⎰∑=+=2,011xyD dxdy xxdS将)1:,(313223∑∑∑-±=x y 投影到zOx 面上,得投影域 .10,11:+≤≤≤≤-x y x D xydxdz y y x xdS xdS xdS zx D z x ⎰⎰⎰⎰⎰⎰⎰⎰++=∑+∑=∑221232313,12112211222π=-=-+=⎰⎰⎰⎰+-x D dz x xdxdz x x x xz所以.00ππ=++=∑⎰⎰xdS例8 设有一颗地球同步轨道卫星, 距地面的高度为36000=h km ,运行的角速度与地球自转的角速度相同. 试计算该通讯卫星的覆盖面积与地球表面积的比值(地球半径6400=R km).解 取地心为坐标原点,地心到通讯卫星重心的连线为z 轴,建立如图坐标系.卫星覆盖的曲面∑是上半球面倍半顶角为α的圆锥面所截得的部分.∑的方程为,222y x R z --=它在xOy 面上的投影区域.sin :2222αR y x D xy ≤+于是通讯卫星的覆盖面积为).cos 1(22απ-=R A将h R R +=αcos 代入上式得 .21222h R h R h R R R A +⋅=⎪⎭⎫ ⎝⎛+-=ππ 由此得这颗通讯卫星的覆盖面积与地球表面积之比为%.5.4242≈RAπ 由以上结果可知,卫星覆盖了全球三分之一以上的面积,故使用三颗相隔32π角度的通讯卫星就可以覆盖几乎地球全部表面.内容要点二、第二类曲面积分的概念与性质定义1 设∑为光滑的有向曲面, 其上任一点),,(z y x 处的单位法向量,cos cos cos k j i n ρρρργβα++= 又设k z y x R j z y x Q i z y x P z y x A ρρρϖ),,(),,(),,(),,(++=其中函数R Q P ,,在∑上有界, 则函数γβαcos cos cos R Q P n v ++=⋅ϖϖ 则∑上的第一类曲面积分⎰⎰∑⋅dS n v ϖϖ.)cos cos cos (⎰⎰∑++=dS R Q P γβα (5.5)称为函数),,(z y x A ϖ在有向曲面∑上的第二类曲面积分.三、第二类曲面积分的计算法设光滑曲面∑:),(y x z z =,与平行于z 轴的直线至多交于一点,它在xOy 面上的投影区域为xy D , 则.⎰⎰⎰⎰±=∑yzD dxdy y x z y x R dxdy z y x R )],(,,[),,(. (5.9)上式右端取“+”号或“-”号要根据γ是锐角还是钝角而定.内容要点一、高斯公式定理1设空间闭区域Ω由分片光滑的闭曲面∑围成,函数),,(z y x P 、),,(z y x Q 、),,(z y x R 在Ω上具有一阶连续偏导数,则有公式⎰⎰⎰⎰⎰∑Ω++=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂Rdxdy Qdzdx Pdydz dv z R y Q x P (6.1)这里∑是Ω的整个边界曲面的外侧, γβαcos ,cos ,cos 是∑上点),,(z y x 处的法向量的方向余弦. (6.1)式称为高斯公式.若曲面∑与平行于坐标轴的直线的交点多余两个,可用光滑曲面将有界闭区域Ω分割成若干个小区域,使得围成每个小区域的闭曲面满足定理的条件,从而高斯公式仍是成立的.此外,根据两类曲面积分之间的关系,高斯公式也可表为.)cos cos cos (⎰⎰⎰⎰⎰∑Ω++=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂dS R Q P dv z R y Q x P γβα二、通量与散度一般地,设有向量场k z y x R j z y x Q i z y x P z y x A ρρρρ),,(),,(),,(),,(++=,其中函数P 、Q 、R 有一阶连续偏导数,∑是场内的一片有向曲面,ορn 是曲面∑的单位法向量. 则沿曲面∑的第二类曲面积分⎰⎰⎰⎰⎰⎰∑∑∑++=⋅=⋅=ΦRdxdy Qdzdx Pdydz S d n A S d A ρρρρρο称为向量场A ρ通过曲面∑流向指定侧的通量. 而zRy Q x P ∂∂+∂∂+∂∂ 称为向量场A ρ的散度,记为A div ϖ,即zRy Q x P A div ∂∂+∂∂+∂∂=ϖ. (6.5)例4(E04)证明: 若∑为包围有界域Ω的光滑曲面, 则⎰⎰⎰⎰⎰⎰⎰⎰Ω∑Ω⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂+∂∂∂∂-∂∂=∆dV z v z u y v y u x v x u dS n uvudV v其中nu∂∂为函数u 沿曲面∑的外法线方向的方向导数,u ,v 在Ω上具有一阶和二阶连续偏导数,符号222222zy x ∂∂+∂∂+∂∂=∆称为拉普拉斯算子. 这个公式称为格林第一公式.证 因为=∂∂n u γβαcos cos cos z u y u xu∂∂+∂∂+∂∂n u ρ⋅∇=,其中}cos ,cos ,{cos γβα=n ρ是∑在点),,(z y x 处 的外法线的方向余弦,于是⎰⎰⎰⎰⎰⎰∑∑∑⋅∇=⋅∇=∂∂dS n u v dS n u v dS nu v)[()(ρρdS z u v y u v x u v ⎰⎰∑⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=γβαcos cos cos dv z u v z y u v y x u v x ⎰⎰⎰Ω⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂=.dv z v z u y v y u x v x u udv v ⎰⎰⎰⎰⎰⎰ΩΩ⎝⎛⎪⎭⎫∂∂∂∂+∂∂∂∂+∂∂∂∂+∆=将上式右端移至左端即得所要证明的等式.例5(E05)求向量场k z j y i x r ρρρρ++=的流量(1) 穿过圆锥)0(222h z z y x ≤≤≤+的底(向上); (2) 穿过此圆锥的侧表面(向外).解 设21,S S 及S 分别为此圆锥的面,侧面及全表面,则穿过全表面向外的流量 Q ⎰⎰+⋅=S S d r ρρ⎰⎰⎰=Vdv r div ρ⎰⎰⎰=Vdv 3.3h π=(1)穿过底面向上的流量 1Q ⎰⎰+⋅=S S d r ρρ⎰⎰=≤+=hz z y x zdxdy 222⎰⎰≤+=222z y x hdxdy .3h π=(2)穿过侧表面向外的流量2Q 1Q Q -=.0=内容要点一、斯托克斯公式定理1 设Γ为分段光滑的空间有向闭曲线,∑是以Γ为边界的分片光滑的有向曲面,Γ的正向与∑的侧符合右手规则,函数),,(),,,(),,,(z y x R z y x Q z y x P 在包含曲面∑在内的一个空间区域内具有一阶连续偏导数, 则有公式dxdy y P x Q dzdx x R z P dydz z Q y R ⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂⎰⎰∑.⎰++=LRdz Qdy Pdx (7.1)公式(7.1)称为斯托克斯公式.为了便于记忆,斯托克斯公式常写成如下形式:⎰⎰⎰Γ∑++=∂∂∂∂∂∂Rdz Qdy Pdx RQ P zy x dxdy dzdx dydz 利用两类曲面积分之间的关系,斯托克斯公式也可写成.cos cos cos ⎰⎰⎰Γ∑++=∂∂∂∂∂∂Rdz Qdy Pdx dS RQPzy x γβα二、空间曲线积分与路径无关的条件三、环流量与旋度 设向量场,),,(),,(),,(),,(k z y x R j z y x Q i z y x P z y x A ρρρρ++= 则沿场A ρ中某一封闭的有向曲线C 上的曲线积分⎰++=ΓCRdz Qdy Pdx称为向量场A ρ沿曲线C 按所取方向的环流量. 而向量函数⎭⎬⎫⎩⎨⎧∂∂-∂∂∂∂-∂∂∂∂-∂∂y P x Q x R z P z Q y R ,,称为向量场A ρ的旋度,记为A rot ρ,即.k y P x Q j x R z P i z Q y R A rot ρρρρ⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=旋度也可以写成如下便于记忆的形式:RQ Pz y x k j i A rot ∂∂∂∂∂∂=ρρρρ.四、向量微分算子:,k zj y i x ρρρ∂∂+∂∂+∂∂=∇ 例 2 计算曲线积分,)()()(222222dz y x dy x z dx z y -+-+-⎰Γ其中Γ是平面2/3=++z y x 截立方体:,10≤≤x ,10≤≤y 10≤≤z 的表面所得的接痕,从x 轴的正向看法,取逆时针方向.解 取∑为题设平面的上侧被Γ所围成部分,则该平面的法向量,3}3,1,1{=n ρ即,31cos cos cos ===λβα原式dS y x x y z y z y x z⎰⎰∑---∂∂∂∂∂∂=222222313131⎰⎰∑++-=dS z y x )(34.293322334-=-=∑⋅-=⎰⎰⎰⎰xyD dxdy dS 例3(E02)计算,)()()(222222⎰Γ+++++dz y x dy z x dx z y 式中Γ是).0,0(2,222222><<=+=++z R r rx y x Rx z y x此曲线是顺着如下方向前进的: 由它所包围在球面Rx z y x 2222=++上的最小区域保持在左方.解 由斯托克斯公式,有 原式⎰⎰∑-+-+-=dS y x x z z y ]cos )(cos )(cos )[(2γβαdS R z y x R y x z R x z y ⎰⎰∑⎥⎦⎤⎢⎣⎡-+-+⎪⎭⎫ ⎝⎛--=)()(1)( ⎰⎰∑-=dS y z )(2(利用对称性)⎰⎰⎰⎰∑=∑=dS R zdS γcos ..2222R r d R Rdxdy rx y x πσ==∑=⎰⎰⎰⎰≤+ 例5(E03)设,32222yz xy y x u -+= 求grad u ; div(grad u );rot(grad u ). 解 gradu ⎭⎬⎫⎩⎨⎧∂∂∂∂∂∂=z u y u x u ,,}.6,4,2{yz xy xy -=div(gradu)⎭⎬⎫⎩⎨⎧∂-∂+∂∂+∂∂=z yz y xy x xy )6()4()2(y x y 642-+=).(4y x -=rot(gradu).,,222222⎭⎬⎫⎩⎨⎧∂∂∂-∂∂∂∂∂∂-∂∂∂∂∂∂-∂∂∂=x y u y x u z x u x z u y z u z y u 因为22232yz xy y x u -+=有二阶连续导数,故二阶混合偏导数与求导次序无关,故rot(gradu).0=注:一般地,如果u 是一单值函数,我们称向量场A ϖ=grad u 为势量场或保守场,而u 称为场A ϖ的势函数.例6(E04)设一刚体以等角速度k j i z y x ϖϖϖϖωωωω++=绕定轴L 旋转,求刚体内任意一点M 的线速度v ϖ的旋度.解 取定轴l 为z 轴,点M 的内径r ρOM =,k z j y i x ρρρ++=则点M 的线速度v ρr ρρ⨯=ωzyx kji z yx ωωωρρρ=,)()()(k x y j z x i y z y x x z z y ρρρωωωωωω-+-+-=于是v ρrot x y z x y z z y x kj i y x x z z y ωωωωωω---∂∂∂∂∂∂=ρρρ)(2k j i z y x ρρρωωω++=.2ωρ=即速度场v ρ的旋等于角速度ωρ的 2 倍.内容要点点函数积分的概念 点函数积分的性质点函数积分的分类及其关系一、点函数积分的概念定义1 设Ω为有界闭区域, 函数))((Ω∈=P P f u 为Ω上的有界点函数. 将形体Ω任意分成n 个子闭区域,,,,21n ∆Ω∆Ω∆ΩΛ其中i ∆Ω表示第i 个子闭区域, 也表示它的度量, 在i ∆Ω上任取一点i P , 作乘积),,2,1()(n i P f i i Λ=∆Ω并作和∑=∆Ωni iiP f 1)(如果当各子闭区域i ∆Ω的直径中的最大值λ趋近于零时, 这和式的极限存在, 则称此极限为点函数)(P f 在Ω上的积分, 记为⎰ΩΩd P f )(, 即.)(lim )(1∑⎰=→Ω∆Ω=Ωni iiP f d P f λ其中Ω称为积分区域, )(P f 称为被积函数, P 称为积分变量, Ωd P f )(称为被积表达式,Ωd 称为Ω的度量微元.点函数积分具有如下物理意义: 设一物体占有有界闭区域Ω, 其密度为),)((Ω∈=P P f ρ则该物体的质量)0)((,)(≥Ω=⎰ΩP f d P f M特别地, 当1)(≡P f 时, 有).(lim 1度量Ω=∆Ω=Ω∑⎰=→Ωni id λ如果点函数)(P f 在有界闭区域Ω上连续, 则)(P f 在Ω上可积.二、点函数积分的性质设)(),(P g P f 在有界闭区域Ω上都可积, 则有 性质1 .)()()]()([⎰⎰⎰ΩΩΩΩ±Ω=Ω±d P g d P f d P g P f性质2 )()()(为常数k d P f k d P kf ⎰⎰ΩΩΩ=Ω性质3,)()()(21⎰⎰⎰ΩΩΩΩ+Ω=Ωd P f d P f d P f其中,21Ω=ΩΩY 且1Ω与2Ω无公共内点. 性质4 若,,0)(Ω∈≥P P f 则.0)(≥Ω⎰Ωd P f性质5 若,),()(Ω∈≤P P g P f 则.)()(⎰⎰ΩΩΩ≤Ωd P g d P f特别地, 有.|)(|)(⎰⎰ΩΩΩ≤Ωd P f d P f性质6 若)(P f 在积分区域Ω上的最大值为M , 最小值为m , 则.)(Ω≤Ω≤Ω⎰ΩM d P f m性质7 (中值定理)若)(P f 在有界闭区域Ω上连续, 则至少有一点,*Ω∈P 使得.)()(*Ω=Ω⎰ΩP f d P f其中ΩΩ=⎰Ωd P f P f )()(*称为函数)(P f 在Ω上的平均值.三、点函数积分的分类及其关系1.若,],[R b a ⊂=Ω这时],,[),()(b a x x f P f ∈=则.)()(⎰⎰=ΩΩbadx x f d P f (1)这是一元函数)(x f 在区间],[b a 上的定积分. 当1)(=x f 时,a b dx ba-=⎰是区间长.2.右,2R L ⊂=Ω且L 是一平面曲线, 这时,),(),,()(L y x y x f P f ∈=于是⎰⎰=ΩΩLds y x f d P f ),()( (2)当1)(≡P f 时,s ds L =⎰是曲线的弧长. (2)式称为第一类平面曲线积分.3.若,3R ⊂Γ=Ω且Γ是空间曲线, 这时,),,(),,,()(Γ∈=z y x z y x f P f 则.),,()(⎰⎰ΓΩ=Ωds z y x f d P f (3)当1)(≡P f 时,s ds =⎰Γ是曲线的弧长. (3)式称为第一类空间曲线积分.2、3的特殊情形是曲线为直线段, 而直线段上的点函数积分本质上是一元函数的定积分,这说明⎰⎰Γds z y x f ds y x f L),,(,),(可用一次定积分计算, 因此用了一次积分号.4.若,2R D ⊂=Ω且D 是平面区域, 这时,),(),,()(D y x y x f P f ∈= 则⎰⎰⎰=ΩΩDd y x f d P f σ),()( (4)(4)式称为二重积分. 当1),(=y x f 时,σσ=⎰⎰Dd 是平面区域D 的面积.5.若,3R ⊂∑=Ω且∑是空间曲面, 这时,),,(),,,()(∑∈=z y x z y x f P f 则⎰⎰⎰∑Ω=ΩdS z y x f d P f ),,()( (5)(5)式称为第一类曲面积分. 当1)(≡P f 时,S dS =⎰⎰∑是空间曲面∑的面积.由于(5)的特殊情形是平面区域上的二得积分, 说明该积分可化为两次定积分的计算, 因此用二重积分号.6.若3R ⊂Ω为空间立体, 这时,),,(),,,()(Ω∈=z y x z y x f P f 则.),,()(⎰⎰⎰⎰ΩΩ=Ωdv z y x f d P f (5)(6)式称为三重积分. 当1)(≡P f , 则V dv =⎰⎰⎰Ω是空间立体Ω的体积.更进一步, 我们还可以利用点函数积分的概念统一来表述占有界闭区域Ω的物体的重心、转动惯量、引力等物理概念, 此处不再表述.。
数学物理方程第5章习题及答案

11.设 {(x, y) | x2 y2 R2, y 0}, 考虑半圆域狄利克雷问题
u 0, x
u(x, y) (x, y),(x, y)
应用对称法求区域 上的格林函数。
解:该问题所求格林函数应满足
G (P, P0 ), P
G(P, P0 ) 0, P B(圆周) G(P, P0 ) 0, P L(x轴上的边界)
C1
1
4
解为 u 1
4 r
方法二: 本题中u只与r有关,则
所以
uxx
u yy
+uzz
=
1 r
(2ur
rurr )
2ur rurr 0 2rur r 2urr 0 (r 2ur )r 0 r 2ur C
ur
C r2
u
C1
1 r
C2
随后求解过程与方法一相同。
注:在球面坐标系中
uxx
记 G \ B ,则 G B ,在格林第二公式
(uv vu)d
(u
v n
v
u )ds n
中,令 v (P, P0 ),注意到 0 ,则有
ud
G
(u
G
n
u )ds n
或
ud (u u )ds (u u )ds
G
n n
B n n
在圆周B 上有
( 1
随后求解过程与方法一相同。
(3)uxx uyy +uzz =0,r 0
解:方法一: 三维拉普拉斯方程的基本解表示通解
1 u C1 r C2
lim u(r)=0
r
C2
0
u n |B(0, )
u n
B(0, )
高等数学 曲线积分和曲面积分 (10.3.2)--格林公式及其应用

0,
其中 C
为平面区域
x
内的
任一封闭曲线.
6. 设函数 Q(x, y) 在 xOy 平面上具有一阶连续偏导数,曲线积分 2xydx Q(x, y)dy 与 C 路径无关,并且对任意 t 恒有
(2xydx Q(x, y)dy 2xydx Q(x, y)dy ,
(0, 0)
(0, 0)
求 Q(x, y) .
7. 确定常数 p , 使得在任何不含 y 的点的区域上, 曲线积分
C
x y2
(x2
y2)p
ydx
xdy
与路径无关,并求当 C 从点 (1, 1) 到点 (0, 2) 时的积分值.
8. 求下列微分方程的通解:
(1) [ y ln(1 x)]dx (x 1 ey )dy 0 ;
C
a b
(3)
C
(x2
y
2 y)dx
x3 3
x
dy
,其中 C
是直线
x
1,
y
x,
y
2x
所围三角形区
域的正向边界.
(4) (ex sin y my)dx (ex cos y m)dy ,其中 C 为由点 A(a,) 到点 O(,) 的上 C 半圆周 x y ax ;
t
2π
)与
x
轴.
2. 利用 Green 公式, 计算下列第二类曲线积分:
(1) (2x sin y 4y)dx (x2 cos y x)dy ,其中 C 为圆周 x2 y2 3 , 并取逆时针 C 方向;
习题二十一格林公式及其应用(续)
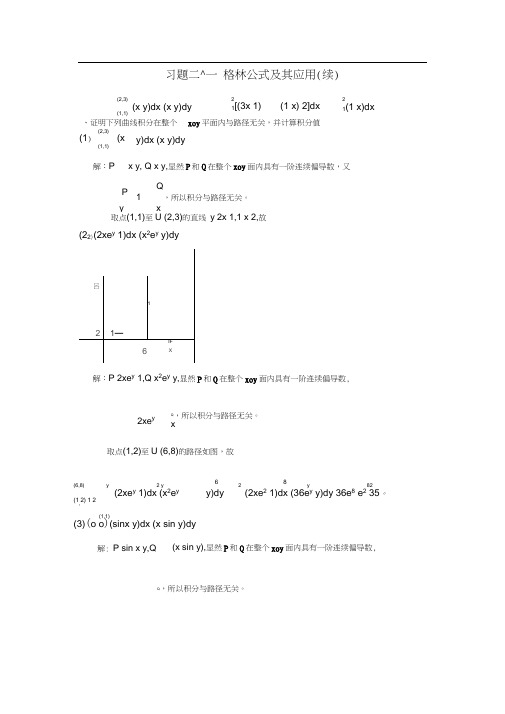
习题二^一 格林公式及其应用(续)、证明下列曲线积分在整个 xoy 平面内与路径无关,并计算积分值 (2,3)(1) (x (1,1) y)dx (x y)dy解:P x y, Q x y,显然P 和Q 在整个xoy 面内具有一阶连续偏导数,又PQ 1 ,所以积分与路径无关。
y x取点(1,1)至U (2,3)的直线 y 2x 1,1 x 2,故(22)(2xe y 1)dx (x 2e y y)dy解:P 2xe y 1,Q x 2e y y,显然P 和Q 在整个xoy 面内具有一阶连续偏导数,取点(1,2)至U (6,8)的路径如图,故(6,8) y2 y 6 2 8y 82 (2xe y 1)dx (x 2e y y)dy (2xe 2 1)dx (36e y y)dy 36e 8 e 2 35。
(1,2) 1 2(1,1) (3)(o o )(sinx y)dx (x sin y)dy(x sin y),显然P 和Q 在整个xoy 面内具有一阶连续偏导数,Q ,所以积分与路径无关。
(2,3) (1,1)(x y)dx (x y)dy 21[(3x 1) (1 x) 2]dx 2 1(1 x)dx 2xe yQ ,所以积分与路径无关。
x 解: P sin x y,Q取点(0,0)至U (1,1)的直线 y x,0 x 1,故(1,1) i(0,0)(sinx y)dx (x siny)dy °[(sinx 2x 上从点(0,0)到点(4,8)。
( )e sin ydx e cos ydy L 1 L 248 4 0 dx e cos ydy 0 04 e sin 8三、设IJe x 2f (x)] ydx f (x)dy 与积分路径L 无关,且f(1) 1 ,求(1,1) I (0,0)[e 2f(x)]ydx f (x)dy 之值。
1x) (x sin x)]dx o 2xdx 1。
高数-格林公式

2(
y),
y]d
y
d c
{Q[
2
(
y),
y]
Q[ 1
(
y),
y]}d
y
D
Q x
dxdy
则有
Q P
(
D
x
y
)dxdy
L
Pdx
Qdy
(1)
证明:(1)设 D 既是 X 型,又是 Y 型区域。
X 型: a x b, 1( x) y 2( x),
L Pdx
D
P y
dxdy
y d
L2 : x 2( y)
D L2
L3
L1
(2)格林公式建立了平面上的曲线积分与二重积分 的关系,它是牛顿莱布尼茨公式在平面上的推广。
主要用途:实现曲线积分与二重积分之间的转换,而 经常用来将复杂的曲线积分转化为二重积分。
D
(
Q x
P y
)dxdy
L
Pdx
Qdy
(1)
(3)便于记忆的形式
若记
Q P x y
x P
y Q
则格林公式可表示为
(
D
x
y
)dxdy
L
Pdx
Qdy
(1)
证明:(1)设 D 既是 X 型,又是 Y 型区域。
X 型: a x b, 1( x) y 2( x),
y L2 : y 2( x)
P
D
y
dxdy
b
a
dx
2 (x) 1 ( x)
P y
dy
ab{
P[
ab
x,2(
2 (x)
P(x, y) | 1 (x)
应用格林公式计算下列曲线积分;

1. 应用格林公式计算下列曲线积分; (1)dy y x dx y x L)()(222+-+⎰,其中L 是以)5,2(),2,3(),1,1(C B A 为顶点的三角形,方向取正向; (2)⎰-+-ABx x dy m y e dx my y e )cos ()sin (,其中m 为常数,AB 为由)0,(a 到)0,0(经过圆ax y x =+22上半部的路线.分析:(1)首先应画出曲线L 的图形,并求出AB ,BC ,CA 的方程;(2)应用格林公式时,首先应是封闭曲线,因此(2)题应补上直线段OA 解:(1) AB 的方程为:)31)(1(21≤≤+=x x y , BC 的方程为: )32(113≤≤+-=x x y CA 的方程为: )21(34≤≤-=x x y , 设)(,)(222y x Q y x P +-=+=,则.24)(22y x y x x yPx Q --=+--=∂∂-∂∂ 把三角形域分成两部分1S 和2S ,于是 原式=⎰⎰⎰⎰⎰⎰--+=--SS S d y x d y x 12)24)(()24(σσ=⎰⎰⎰⎰+-+-+--+--32113)1(212134)1(21)24()24(x x x x dy y x dx dy y x dx=.3246)4483249421()2352774119(232221-=-++-+-⎰⎰dx x x dx x x (2)在Ox 轴上连接点)0,0(O 与点)0,(a A 这样就构成封闭的半圆形A AO,且在线段OA上,0,0==dy y 于是.0)cos ()sin (=-+-⎰dy m y e dx my y e OAx x而⎰⎰⎰⎰=+=OA AAO OA AO .由格林公式得:8)2(21)cos ()sin (22:22a m a m mdxdy dy m y e dx my y e axy x D xA AO xππ=⋅==-+-⎰⎰⎰≤+因此,原式=28a m π. 2. 应用格林公式计算下列曲线所围的平面面积:(1) 星形线:;sin ,cos 33t a y t a x == (2) 双纽线:).()(222222y x a y x -=+分析:封闭曲线L : (),()x x t y y t ==所围的面积公式是:⎰⎰⎰-==LS D ydx xdy d S D21σ 解: (1)⎰⎰⎰-==L S D ydx xdy d S D21σ =dt t t a t a t t a t a )sin cos 3sin cos sin 3cos (21220323⋅+⋅⎰π=dt t t t t a )cos sin sin (cos 232204242⎰+π=tdt t a 22022cos sin 23⎰π=tdt a ⎰π20222sin 83 =dt ta ⎰-π20224cos 183 =ππ83|)4sin 8121(832202a t t a =-. (2) 化双纽线的极坐标方程为参数方程,2cos cos cos )(θθθθa r x == ,2cos sin θθa y =应用面积公式并利用图形的对称性可得.2cos 2142402a d a ydx xdy S L==-⋅=⎰⎰θθπ3. 证明:若L 为平面上封闭曲线,l 为任意方向向量,则⎰=Lds n l ,0),cos(其中n 为曲线L 的外法线方向.分析:设l 与n 的方向余弦分别为βαcos ,cos 与),,cos(),,cos(y n x n 则cos(,)cos cos(,)cos cos(,)l n n x n y αβ=+,又cos(,),cos(,)n y ds dx n x ds dy =-=证: 设l 与n 的方向余弦分别为βαcos ,cos 与),,cos(),,cos(y n x n 则⎰⎰+=ds y n x n ds n l L L)],cos(cos ),cos([cos ),cos(βα由第一、二型曲线积分的关系,有上式=cos cos Ldx dy βα-+⎰由βαcos ,cos 均为常数,故0cos cos =∂∂=∂∂xy αβ 从而由格林公式知⎰=.0),cos(ds n l L4. 求积分值⎰+=,)],cos(),cos([ds y n y x n x I 其中L 为包围有界区域的封闭曲线,n 为L的外法线方向。
深圳大学-高等数学专题-例题线面积分

所以
I
c a
1 b
1
b2
f
(bx)
dx
d b
c y2
1
y2
fБайду номын сангаас
(cy)dy
c a
c
bf (bx)dx
d cf (cy)dy c c c a
bc
f (t)dt
cd
f (t)dt
ba
b
d b d b ab
bc
c a cd
f (t)dt
d b ab
当 ab
cd
cd
L 是上半平面( y 0)内的有向分段光滑曲线,其起点
为 (a,b),终点为(c, d ) ,记
I 1[1 y 2 f (xy)]dx x [ y2 f (xy) 1]dy
Ly
y2
(1) 证明曲线积分 I 与路径无关;
(2) 当ab cd 时,求 I 的值.
【分析】本题主要考查第二类曲线积分与路径无关
2x2
y2
2
2
d
y2
C(x)
解得 从而
(y)
2x2 y4
y2 2x2
y4
C(x)
P(x, y)
( y)
2x2 y4
y2 2x2
y4
C(x)
又
P(x, 0)
(0)
2x2
故
C(x)
(0)
2x2
P(x,
y)
y2 2x2
y4
(0)
2x2
又由
P(x,
y)
( y)
2x2 y4
段 L1,
原式 ex sin y b x y dx ex cos y ax dy
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y dy 0 x2 y2
目录 上页 下页 返回 结束
或
y dy 0 1 y2
π arctan x
2
y
y (1, y) (x, y) O (1,0) ( x,0) x
目录 上页 下页 返回 结束
例7. 设质点在力场
作用下沿曲线 L :
由 A( 0, π ) 移动到 2
求力场所作的功W
y
A
解:
W
Fds
L
L
k r2
( ydx
x d y)
L
令
则有
O Bx
P y
k(x2 y2) r4
Q x
( x2 y2 0)
可见, 在不含原点的单连通区域内积分与路径无关.
目录 上页 下页 返回 结束
取圆弧 AB : x π cos , y π sin ( : π 0)
2
2
2
W
AB
k r2
(y
一、 格林公式
区域 D 分类
单连通区域 ( 无“洞”区 域 多连) 通区域 ( 有“洞”区
L D
规定:域 D 边域界L) 的正向: 域的内部靠左
定理1. 设区域 D 是由分段光滑正向曲线 L 围成, 函数 在 D 上具有连续一阶偏导数, 则有
Q P dxdy Pdx Qdy
D x y
0
1 (1 e1) 2
目录 上页 下页 返回 结束
二、平面上曲线积分与路径无关的等价条件
定理2. 设D 是单连通域 , 函数
在D 内
具有一阶连续偏导数, 则以下四个条件等价:
(1) 沿D 中任意光滑闭曲线 L , 有 L Pdx Qdy 0.
(2) 对D 中任一分段光滑曲线 L, 曲线积分 Pdx Qdy L
0
0
目录 上页 下页 返回 结束
例6.
验证
x
d x
y
2
y y
d
2
x
在右半平面
(
x
>
0
)
内存在原函
数 , 并求出它.
y
(x, y)
证: 令
P
y x2 y2
,
Q
x2
x
y2
则
P x
y2 x2 (x2 y2)2
Q y
( x 0 ) O (1,0)
( x,0) x
由定理 2 可知存在原函数
0 x
1 2π
2 0
(abcos2
absin2 ) d
π ab
定理1 目录 上页 下页 返回 结束
例1. 设 L 是一条分段光滑的闭曲线, 证明
2xy dx x2 dy 0 L
证: 令 P 2xy, Q x2, 则
利用格林公式 , 得
L 2xy dx x2 dy 0dx dy 0 D
L
( 格林公式 )
或
x y dxdy Pdx Qdy
DP Q
L
目录 上页 下页 返回 结束
格林公式
D
Q x
P y
dxd
y
L
Pd
x
Qd
y
推论: 正向闭曲线 L 所围区域 D 的面积
A
1 2
蜒 L xd y
ydx
L
xd y
? L
ydx
例如,
椭圆
L
:
x
y
a cos b sin
(0 2π) 所围面积
yy
( x0 , y0 )
x
y
x0 P(x, y0 )dx
Q(x, y)dy
y0
y0
或
u (x, y)
y
y0 Q(x0 , y)dy
x
P(x, y)dx
x0
O x0
xx
定理2 目录 上页 下页 返回 结束
3) 若已知 d u = P dx + Q dy ,则对D内任一分段光滑曲
线 AB ,有
D x y
设 P, Q 在 D 内具有一阶连续偏导数, 则有
P d x Q d y 在 D 内与路径无关. L
对 D 内任意闭曲线 L 有 P d x Q d y 0 L
在 D 内有 Q P x y
在 D 内有 d u P dx Q dy
P dx Qdy 0 为全微分方程
目录 上页 下页 返回 结束
与路径无关, 只与起止点有关.
(3)
在 D 内是某一函数
的全微分,
即 d u(x, y) P dx Q dy (4) 在 D 内每一点都有 P Q .
y x
目录 上页 下页 返回 结束
说明: 根据定理2 , 若在某区域D内 P Q , 则 y x
1) 计算曲线积分时, 可选择方便的积分路径;
解: 为了使用格林公式, 添加辅助线段 AO,它与L 所围
区域为D , 则
原式
(x2 3y) dx (y2 x) dy
L AO
( x2 3 y)dx ( y2 x) d y AO
(4)dxd y ( x2 3 y)dx
D
OAyBiblioteka 4 dxd y 4 x2 dx
D
0
L D
AB P(x, y)dx Q(x, y)dy
B
A P(x, y)d x Q(x, y)dy
D B
A
B
B
d u u u(B) u(A)
A
A
注: 此式称为曲线积分的基本公式(P213定理4).
它类似于微积分基本公式:
定理2 目录 上页 下页 返回 结束
例4. 计算
其中L 为上半
圆周
从 O (0, 0) 到 A (4, 0).
目录 上页 下页 返回 结束
例2. 计算
其中D 是以 O(0,0) , A(1,1) ,
B(0,1) 为顶点的三角形闭域 .
解: 令P 0, Q xe y2, 则
y
B(0,1)
A(1,1)
D yx
利用格林公式 , 有
O
x
x e y2 dy D
x e y2 dy 1 ye y2 dy
OA
8 π 64 3
O
Ax
目录 上页 下页 返回 结束
例5. 验证
是某个函数的全微分, 并求
出这个函数及
证: 设 P xy2, Q x2 y,则 P 2xy Q
y
x
由定理2 可知, 存在函数 u (x , y) 使
(x, y)
du xy2 dx x2 ydy
(0,0)
( x,0)
0 y x2 y dy y x2 y dy
dx
x d y)
y
A
L
πk
O Bx
2
思考: 积分路径是否可以取 AO OB ? 为什么?
注意, 本题只在不含原点的单连通区域内积分与路径
无关 ! 转内容小结
内容小结 目录 上页 下页 返回 结束
内容小结
1. 格林公式 P d x Q d y Q P d x d y
L
2. 等价条件
2. 设
注: 求曲线积分时,若积分路径不是闭曲线,且难计 算,则可添加辅助线后,利用格林公式简化计算。
2) 可用积分法求d u = P dx + Q dy在域 D 内的原函数:
取定点( x0, y0 ) D及动点 ( x , y ) D , 则原函数为
(x,y)
u ( x, y)
P(x, y)dx Q(x, y)dy
