传感器原理课后答案
传感器原理课后答案

第一章传感与检测技术的理论基础1.什么是测量值的绝对误差、相对误差、引用误差?答:某量值的测得值和真值之差称为绝对误差。
相对误差有实际相对误差和标称相对误差两种表示方法。
实际相对误差是绝对误差与被测量的真值之比;标称相对误差是绝对误差与测得值之比。
引用误差是仪表中通用的一种误差表示方法,也用相对误差表示,它是相对于仪表满量程的一种误差。
引用误差是绝对误差(在仪表中指的是某一刻度点的示值误差)与仪表的量程之比。
2.什么是测量误差?测量误差有几种表示方法?它们通常应用在什么场合?答:测量误差是测得值与被测量的真值之差。
测量误差可用绝对误差和相对误差表示,引用误差也是相对误差的一种表示方法。
在实际测量中,有时要用到修正值,而修正值是与绝对误差大小相等符号相反的值。
在计算相对误差时也必须知道绝对误差的大小才能计算。
采用绝对误差难以评定测量精度的高低,而采用相对误差比较客观地反映测量精度。
引用误差是仪表中应用的一种相对误差,仪表的精度是用引用误差表示的。
3.用测量范围为-50~+150kPa的压力传感器测量140kPa压力时,传感器测得示值为142kPa,求该示值的绝对误差、实际相对误差、标称相对误差和引用误差。
解:绝对误差2140142=-=∆kPa实际相对误差%43.1%100140140142=⨯-=δ标称相对误差%41.1%100142140142=⨯-=δ引用误差%1%10050150140142=⨯---=)(γ4.什么是随机误差?随机误差产生的原因是什么?如何减小随机误差对测量结果的影响?答:在同一测量条件下,多次测量同一被测量时,其绝对值和符号以不可预定方式变化着的误差称为随机误差。
随机误差是由很多不便掌握或暂时未能掌握的微小因素(测量装置方面的因素、环境方面的因素、人员方面的因素),如电磁场的微变,零件的摩擦、间隙,热起伏,空气扰动,气压及湿度的变化,测量人员感觉器官的生理变化等,对测量值的综合影响所造成的。
传感器原理与应用第二版课后答案

传感器原理与应用第二版课后答案1. 传感器原理与应用概述。
传感器是一种能够感知、检测并转换物理量或化学量等非电信号到电信号的装置,它是现代自动化领域中不可或缺的重要组成部分。
传感器的原理与应用涉及到物理学、化学、电子学等多个学科领域,对于各种自动化系统的测量、控制和监测起着至关重要的作用。
2. 传感器的分类及工作原理。
传感器根据其测量原理和测量对象的不同可以分为多种类型,比如光电传感器、温度传感器、压力传感器、湿度传感器等。
不同类型的传感器有着各自独特的工作原理,比如光电传感器是利用光电效应实现光信号到电信号的转换,而温度传感器则是通过测量物体的热量来获取温度信息。
3. 传感器在工业控制中的应用。
传感器在工业控制中有着广泛的应用,比如在自动化生产线上,各种传感器可以用来检测产品的尺寸、形状、颜色等信息,从而实现自动化的生产控制。
此外,传感器还可以用于监测工业设备的运行状态,实现设备的远程监控和故障诊断。
4. 传感器在智能家居中的应用。
随着智能家居的发展,各种传感器也开始在家居领域得到广泛应用。
比如温湿度传感器可以用来监测室内的温度和湿度,光敏传感器可以用来实现智能照明控制,人体红外传感器可以用来实现智能安防监控等。
5. 传感器的未来发展趋势。
随着物联网、人工智能等新技术的发展,传感器也将迎来新的发展机遇。
未来的传感器将更加智能化、多功能化,能够实现更加精准的测量和控制,同时还将更加节能环保,更加适应多样化的应用场景。
6. 结语。
传感器作为现代自动化系统中的重要组成部分,其原理与应用对于各种领域的发展都具有重要意义。
我们需要不断学习和掌握传感器的相关知识,不断创新和完善传感器技术,以推动传感器行业的发展,为人类社会的进步做出贡献。
传感器原理及工程应用第5版答案

实用文档
传感器原理及工程应用第5版答案
第1章传感与检测技术的理论基础(P26)
1-1:测量的定义?
答:测量是以确定被测量的值或获取测量结果为目的的一系列操作。
所以,测量也就是将被测量与同种性质的标准量进行比较,确定被测量对标准量的倍数。
1-2:什么是测量值的绝对误差、相对误差、引用误差?
答:绝对误差是测量结果与真值之差
即:绝对误差=测量值一真值
相对误差是绝对误差与被测量真值之比,常用绝对误差与测量值之比,以百分数表示,即:相对误差=绝对误差/测量值×100%
引用误差是绝对误差与量程之比,以百分数表示,即:引用误差=绝对误差/量程×100%
1-3用测量范围为一50~150kPa的压力传感器测量140kPa的压力时,传感器测得示值为142kPa,求该示值的绝对误差、实际相对误差、标称相对误差和引用误差。
已知:真值L=140kPa测量值x=142kPa测量上限=150kPa测量下限=—50kPa
.绝对误差A=x-L=142-140=2(kPa)
实际相对误差6=2=21.43%
Z140标称相对误差6=A2~1.41%
T142。
传感器原理及工程应用完整版习题参考答案

《传感器原理及工程应用》完整版习题答案第1章传感与检测技术的理论基础(P26)1—1:测量的定义?答:测量是以确定被测量的值或获取测量结果为目的的一系列操作。
所以,测量也就是将被测量与同种性质的标准量进行比较,确定被测量对标准量的倍数。
1 —2 :什么是测量值的绝对误差、相对误差、引用误差?答:绝对误差是测量结果与真值之差,即:绝对误差=测量值一真值相对误差是绝对误差与被测量真值之比,常用绝对误差与测量值之比,以百分数表示,即:相对误差=绝对误差/测量值X100%引用误差是绝对误差与量程之比,以百分数表示,即:引用误差=绝对误差/量程100%示值为142kPa,求该示值的绝对误差、实际相对误差、标称相对误差和引用误差。
解: 已知:真值L = 140kPa测量值x= 142kPa测量上限=150kPa测量下限=—50kPa绝对误差△ = x-L=142-140=2(kPa)实际相对误差=—=2「43%L 140标称相对误差—— 1.41% x 142引用误差2 =测量上限—测量下限'150 —1 —10 对某节流元件(孔板)开孔直径d20的尺寸进行了15次测量,测量数据如下(单位: mm):120.42120.43 120.40 120.42 120.43 120.39 120.30 120.40120.43120.41 120.43 120.42 120.39 120.39 120.40用测量范围为—50〜150kPa的压力传感器测量140kPa的压力时,传感器测得试用格拉布斯准则判断上述数据是否含有粗大误差,并写出其测量结果。
解:序 号测量值 d 2o (mm)残余误差V i (d 20i d 2o )(mm)残余误差V (d 20i d 20 (i7))(mm)1 120.42 0.016 0.009 2 120.43 0.026 0.0193 120.40 —0.004 —0.0114 120.42 0.016 0.0095 120.43 0.0260.0196 120.39 —0.014—0.0217 120.30 —0.1048 120.40 —0.004—0.0119 120.43 0.026 0.01910 120.41 0.006 —0.00111 120.43 0.026 0.019 12 120.42 0.016 0.00913 120.39 —0.014—0.021 14 120.39 —0.014 —0.021 15120.40—0.004—0.011d20120.404mm1 i 10.0327mmJ i 7 0.0161mmd 20(i 7) 120.411mmd201(15 1d20 114 1G d 200.0788( mm) G d 200.0382(mm)当= 时,若取置信概率 = ,查表可得格拉布斯系数 = 。
传感器原理及应用习题答案(完整版)

传感器原理及应用习题答案习题1 (2)习题2 (4)习题3 (8)习题4 (10)习题5 (12)习题6 (14)习题7 (17)习题8 (20)习题9 (23)习题10 (25)习题11 (26)习题12 (28)习题13 (32)习题11-1 什么叫传感器?它由哪几部分组成?并说出各部分的作用及其相互间的关系。
答:传感器是能感受规定的被测量并按照一定的规律将其转换成可用输出信号的器件或装置。
通常传感器由敏感元件和转换元件组成。
敏感元件是指传感器中能直接感受或响应被测量的部分,转换元件是指传感器中将敏感元件感受或响应的被测量转换成适于传输或测量的电信号部分。
由于传感器的输出信号一般都很微弱, 因此需要有信号调节与转换电路对其进行放大、运算调制等。
随着半导体器件与集成技术在传感器中的应用,传感器的信号调节与转换电路可能安装在传感器的壳体里或与敏感元件一起集成在同一芯片上。
此外,信号调节转换电路以及传感器工作必须有辅助的电源,因此信号调节转换电路以及所需的电源都应作为传感器组成的一部分。
1-2 简述传感器的作用和地位及其传感器技术的发展方向。
答:传感器位于信息采集系统之首,属于感知、获取及检测信息的窗口,并提供给系统赖以进行处理和决策所必须的原始信息。
没有传感技术,整个信息技术的发展就成了一句空话。
科学技术越发达,自动化程度越高,信息控制技术对传感器的依赖性就越大。
发展方向:开发新材料,采用微细加工技术,多功能集成传感器的研究,智能传感器研究,航天传感器的研究,仿生传感器的研究等。
1-3 传感器的静态特性指什么?衡量它的性能指标主要有哪些?答:传感器的静态特性是指被测量的值处于稳定状态时的输出—输入关系。
与时间无关。
主要性能指标有:线性度、灵敏度、迟滞和重复性等。
1-4 传感器的动态特性指什么?常用的分析方法有哪几种?答:传感器的动态特性是指其输出与随时间变化的输入量之间的响应特性。
常用的分析方法有时域分析和频域分析。
传感器原理及应用第三版课后答案

传感器原理及应用第三版课后答案1. 答案:传感器是一种能够感知环境变化并将其转化为可识别的信号的装置。
它通过使用特定的物理效应或工作原理来感知和测量环境中的物理量或特定的参数。
2. 答案:传感器的应用非常广泛,涵盖了许多不同的领域。
以下是几个常见的传感器应用示例:- 温度传感器:用于监控和控制温度,例如室内温度控制、工业加热系统等。
- 压力传感器:用于测量液体或气体的压力,例如汽车轮胎压力监测、压力容器监控等。
- 光学传感器:用于检测光照强度和颜色,例如光电开关、自动亮度调节系统等。
- 气体传感器:用于检测和测量空气中的气体成分,例如二氧化碳传感器、氧气传感器等。
- 加速度传感器:用于测量物体的加速度和震动,例如运动传感器、汽车碰撞传感器等。
- 湿度传感器:用于测量空气中的湿度水份,例如室内湿度控制、大气湿度监测等。
3. 答案:传感器的工作原理有很多种,常见的包括:- 电阻效应传感器:基于电阻值的变化来感知和测量物理量,例如温度传感器和应变传感器。
- 电容效应传感器:基于电容值的变化来感知和测量物理量,例如湿度传感器和接近传感器。
- 电感效应传感器:基于电感值的变化来感知和测量物理量,例如金属检测传感器和霍尔效应传感器。
- 光学效应传感器:基于光学特性的变化来感知和测量物理量,例如光电传感器和光纤传感器。
- 声波效应传感器:基于声波信号的变化来感知和测量物理量,例如声波距离传感器和声速传感器。
4. 答案:传感器的选择取决于具体的应用需求和要测量的物理量。
需要考虑以下几个方面:- 测量范围:传感器是否能够覆盖所需的测量范围,以及是否有足够的灵敏度和精度。
- 工作环境:传感器是否适用于所需的工作环境,例如温度、湿度、压力等。
- 响应时间:传感器的反应速度是否满足实际要求,是否能够快速响应变化的物理量。
- 成本和可靠性:传感器的价格是否适宜,并且能够稳定可靠地工作。
- 安装和维护:传感器的安装和维护是否方便,是否需要额外的设备或配件。
《传感器原理及应用》课后答案

第1章传感器基础理论思考题与习题答案1.1什么是传感器?(传感器定义)解:能够感受规定的被测量并按照一定规律转换成可用输出信号的器件或装置,通常由敏感元件、转换元件和调节转换电路组成。
1.2传感器特性在检测系统中起到什么作用?解:传感器的特性是指传感器的输入量和输出量之间的对应关系,所以它在检测系统中的作用非常重要。
通常把传感器的特性分为两种:静态特性和动态特性。
静态特性是指输入不随时间而变化的特性,它表示传感器在被测量各个值处于稳定状态下输入输出的关系。
动态特性是指输入随时间而变化的特性,它表示传感器对随时间变化的输入量的响应特性。
1.3传感器由哪几部分组成?说明各部分的作用。
解:传感器通常由敏感元件、转换元件和调节转换电路三部分组成。
其中,敏感元件是指传感器中能直接感受或响应被测量的部分,转换元件是指传感器中能将敏感元件感受或响应的被测量转换成电信号的部分,调节转换电路是指将非适合电量进一步转换成适合电量的部分,如书中图1.1所示。
1.4传感器的性能参数反映了传感器的什么关系?静态参数有哪些?各种参数代表什么意义?动态参数有那些?应如何选择?解:在生产过程和科学实验中,要对各种各样的参数进行检测和控制,就要求传感器能感受被测非电量的变化并将其不失真地变换成相应的电量,这取决于传感器的基本特性,即输出—输入特性。
衡量静态特性的重要指标是线性度、灵敏度,迟滞和重复性等。
意义略(见书中)。
动态参数有最大超调量、延迟时间、上升时间、响应时间等,应根据被测非电量的测量要求进行选择。
1.5某位移传感器,在输入量变化5mm时,输出电压变化为300mV,求其灵敏度。
解:其灵敏度333001060510UkX--∆⨯===∆⨯1.6某测量系统由传感器、放大器和记录仪组成,各环节的灵敏度为:S1=0.2mV/℃、S2=2.0V/mV、S3=5.0mm/V,求系统的总的灵敏度。
1.7某线性位移测量仪,当被测位移由4.5mm变到5.0mm时,位移测量仪的输出电压由3.5V减至2.5V,求该仪器的灵敏度。
(完整版)传感器课后题答案

第一章1.何为准确度、精密度、精确度?并阐述其与系统误差和随机误差的关系。
答:准确度:反映测量结果中系统误差的影响程度。
精密度:反映测量结果中随机误差的影响程度。
精确度:反映测量结果中系统误差和随机误差综合的的影响程度,其定量特征可用测量的不确定度表示。
4.为什么在使用各种指针式仪表时,总希望指针偏转在全量程的2/3以上范围内使用?答:选用仪表时要考虑被测量的大小越接近仪表上限越好,为了充分利用仪表的准确度,选用仪表前要对被测量有所了解,其被测量的值应大于其测量上限的2/3。
14.何为传感器的静态标定和动态标定?试述传感器的静态标定过程。
答:静态标定:确定传感器的静态特性指标,如线性度、灵敏度、滞后和重复性等。
动态标定:确定传感器的动态特性参数,如频率响应、时间常数、固有频率和阻尼比等。
静态标定过程:①将传感器全量程分成如干等间距点。
②根据传感器量程分点情况,由小到大一点一点地输入标准量值,并记录与各输入值相应的输出值。
③将输入值由大到小一点一点减小,同时记录与各输入值相对应的输出值。
④按②、③所述过程,对传感器进行正反行程往复循环多次测试,将得到的输出-输入测试数据用表格列出或作出曲线。
⑤对测试数据进行必要的处理,根据处理结果就可以确定传感器的线性度、灵敏度、迟滞和重复性等静态特性指标。
第二章1.什么叫应变效应?利用应变效应解释金属电阻应变片的工作原理。
答:应变效应:金属丝的电阻随着它所受的机械形变的大小而发生相应的变化的现象称为金属应变效应。
工作原理:在电阻丝拉伸极限内,电阻的相对变化与应变成正比,即:∆R=K0ε(K0:电阻丝的灵敏系数、ε:导体的纵向应变)R2.金属电阻应变片与的工作原理有何区别?各有何优缺点?答:区别:金属电阻变化主要是由机械形变引起的;半导体的阻值主要由电阻率变化引起的。
优缺点:金属电阻应变片的主要缺点是应变灵敏系数较小,半导体应变片的灵敏度是金属电阻应变片50倍左右。
传感器原理及检测技术部分课后作业答案

部分课后作业答案2-8. 标称电阻为100Ω的应变计贴在弹性试件上。
设试件的截面积 S=1×10-5m 2,弹性模量E=2×1011 N /m 2,若由1.0×104N 的拉力作用,使应变计的电阻相对变化为1%,试求此应变计的灵敏度系数。
解:∵灵敏度系数εRR K /∆=,又已知%1=∆RR,F=1.0×104 N ,S=1×10-5m 2,∴ )/(101101100.129254m N mN S F ⨯=⨯⨯==-σ 由εσ⋅=E ,可得321129105)/(102)/(101-⨯=⨯⨯==m N m N E σε 所以,灵敏度系数2105%1/3=⨯=∆=-εRR K2-9. 将4片相同的金属丝应变片贴在实心圆柱形测力弹性元件上,如题2.9图所示。
设应变片的灵敏度系数K=2,作用力F=1 000kg 。
圆柱形横截面半径r=1cm ,弹性元件的杨氏模量E=2×107N /cm 2,泊松比μ=0.285。
求:(1)画出应变片贴在圆柱上的位置图及相应测量电桥的原理图; (2)各应变片的应变ε;(3)若测量电路采用电桥电路,设供电桥电压E =6V ,桥路输出电压U o 为多少?(4)这种测量方法对环境温度的变化能否具有补偿作用?试说明原因。
解:⑴将R 1~R 4四片应变片按图2-9(a )所示粘贴,其中R 1、R 3沿轴向粘贴,测量轴向应变,R 2、R 4沿径向粘贴,测量径向应变。
测量电桥为全桥测量电路, R 1与R 3置于电桥的一对角线上,R 2与R 4置于电桥的另一对角线上,如右图2-9(b )所示。
题2.9 图⑵∵)(1500105.1)/(102)01.0(14.3/8.9100032722μεπσε=⨯=⨯⨯⨯====-cm N m N Er FE A FE∴εK R R R R =∆=∆3311, R 1与R 3的纵向应变(轴向应变)ε为1500με;μεεK K R R R R r -==∆=∆4422 ,式中μ为泊松比,μ=0.285。
传感器原理及工程应用(第三版)课后题答案
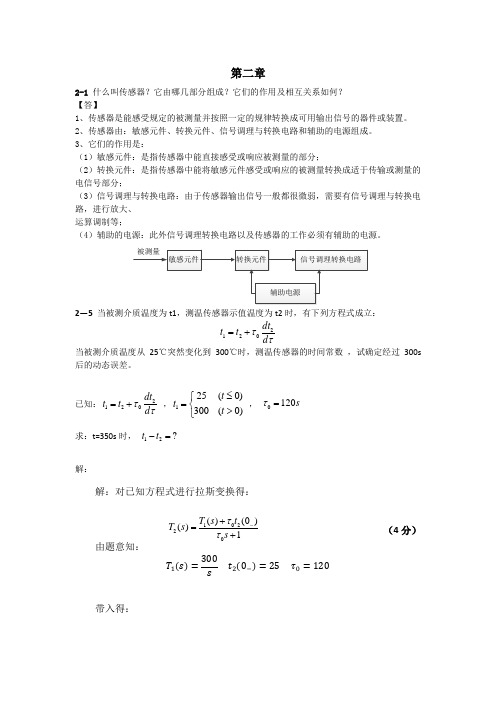
,是单臂工作时的两倍。
(b)如果采用全桥差动电路,需要在等强度梁的上下四个位置安装四个工作应变片,两个受拉应变,两个受压应变,将两个应变符号相同的接入相对桥臂上,构成全桥差动电路。此时电桥的输出电压为
解:
一阶传感器的幅频特性为:
因为幅值误差限制在±5%以内,即
当 时,有 。
若用此传感器测量 的信号,其幅值误差为:
相位误差为:
第三章
3-5题3-5图为一直流电桥,图中E=4V,R1= R2= R3= R4=120Ω,试求:
(1)R1为金属应变片,其余为外接电阻,当R1的增量为ΔR1=1.2Ω时,电桥输出的电压U0=?
当R1受压应变,R2受拉应变时,电桥输出电压为:
3-6题3-6图为等强度梁测力系统,R1 为电阻应变片,应变片灵敏度系数K=2.05,未受应变时,R1=120Ω。当试件受力F 时,应变片承受平均应变ε=800μm/m,试求:
(1)应变片电阻变化量ΔR1 和电阻相对变化量ΔR1/R1。
(2)将电阻应变片R1置于单臂测量电桥,电桥电源电压为直流3V,求电桥输出电压及电桥非线性误差。
第二章
2-1什么叫传感器?它由哪几部分组成?它们的作用及相互关系如何?
【答】
1、传感器是能感受规定的被测量并按照一定的规律转换成可用输出信号的器件或装置。
2、传感器由:敏感元件、转换元件、信号调理与转换电路和辅助的电源组成。
3、它们的作用是:
(1)敏感元件:是指传感器中能直接受或响应被测量的部分;(2)计算传感器在满量程时,各应变片的电阻值;
传感器原理及应用习题答案完整版

传感器原理及应用习题答案习题1 (3)习题2 (5)习题3 (9)习题4 (11)习题5 (13)习题6 (15)习题7 (18)习题8 (21)习题9 (24)习题10 (26)习题11 (27)习题12 (29)习题13 (33)习题11-1 什么叫传感器?它由哪几部分组成?并说出各部分的作用及其相互间的关系。
答:传感器是能感受规定的被测量并按照一定的规律将其转换成可用输出信号的器件或装置。
通常传感器由敏感元件和转换元件组成。
敏感元件是指传感器中能直接感受或响应被测量的部分,转换元件是指传感器中将敏感元件感受或响应的被测量转换成适于传输或测量的电信号部分。
由于传感器的输出信号一般都很微弱, 因此需要有信号调节与转换电路对其进行放大、运算调制等。
随着半导体器件与集成技术在传感器中的应用,传感器的信号调节与转换电路可能安装在传感器的壳体里或与敏感元件一起集成在同一芯片上。
此外,信号调节转换电路以及传感器工作必须有辅助的电源,因此信号调节转换电路以及所需的电源都应作为传感器组成的一部分。
1-2 简述传感器的作用和地位及其传感器技术的发展方向。
答:传感器位于信息采集系统之首,属于感知、获取及检测信息的窗口,并提供给系统赖以进行处理和决策所必须的原始信息。
没有传感技术,整个信息技术的发展就成了一句空话。
科学技术越发达,自动化程度越高,信息控制技术对传感器的依赖性就越大。
发展方向:开发新材料,采用微细加工技术,多功能集成传感器的研究,智能传感器研究,航天传感器的研究,仿生传感器的研究等。
1-3 传感器的静态特性指什么?衡量它的性能指标主要有哪些?答:传感器的静态特性是指被测量的值处于稳定状态时的输出—输入关系。
与时间无关。
主要性能指标有:线性度、灵敏度、迟滞和重复性等。
1-4 传感器的动态特性指什么?常用的分析方法有哪几种?答:传感器的动态特性是指其输出与随时间变化的输入量之间的响应特性。
常用的分析方法有时域分析和频域分析。
(完整版)传感器课后答案解析

第1章概述1.什么是传感器?传感器定义为能够感受规定的被测量并按照一定规律转换成可用输出信号的器件和装置,通常由敏感元件和转换元件组成。
1.2传感器的共性是什么?传感器的共性就是利用物理规律或物质的物理、化学、生物特性,将非电量(如位移、速度、加速度、力等)输入转换成电量(电压、电流、电容、电阻等)输出。
1.3传感器由哪几部分组成的?由敏感元件和转换元件组成基本组成部分,另外还有信号调理电路和辅助电源电路。
1.4传感器如何进行分类?(1)按传感器的输入量分类,分为位移传感器、速度传感器、温度传感器、湿度传感器、压力传感器等。
(2)按传感器的输出量进行分类,分为模拟式和数字式传感器两类。
(3)按传感器工作原理分类,可以分为电阻式传感器、电容式传感器、电感式传感器、压电式传感器、磁敏式传感器、热电式传感器、光电式传感器等。
(4)按传感器的基本效应分类,可分为物理传感器、化学传感器、生物传感器。
(5)按传感器的能量关系进行分类,分为能量变换型和能量控制型传感器。
(6)按传感器所蕴含的技术特征进行分类,可分为普通型和新型传感器。
1.5传感器技术的发展趋势有哪些?(1)开展基础理论研究(2)传感器的集成化(3)传感器的智能化(4)传感器的网络化(5)传感器的微型化1.6改善传感器性能的技术途径有哪些?(1)差动技术(2)平均技术(3)补偿与修正技术(4)屏蔽、隔离与干扰抑制 (5)稳定性处理第2章传感器的基本特性2.1什么是传感器的静态特性?描述传感器静态特性的主要指标有哪些?答:传感器的静态特性是指在被测量的各个值处于稳定状态时,输出量和输入量之间的关系。
主要的性能指标主要有线性度、灵敏度、迟滞、重复性、精度、分辨率、零点漂移、温度漂移。
2.2传感器输入-输出特性的线性化有什么意义?如何实现其线性化?答:传感器的线性化有助于简化传感器的理论分析、数据处理、制作标定和测试。
常用的线性化方法是:切线或割线拟合,过零旋转拟合,端点平移来近似,多数情况下用最小二乘法来求出拟合直线。
传感器课后题答案

传感器课后题答案第⼀章:1、何为准确度、精密度、精确度?并阐述其与系统误差和随机误差的关系.准确度:反应测量结果中系统误差的影响程度;精密度:反应测量结果中随机误差的影响程度;精确度:反应测量结果中系统误差和随机误差综合的影响程度,其定量特性可⽤测量的不确定度(或极限误差)表⽰。
关系:具体的测量,精密度⾼的准确度不⼀定⾼,准确度⾼的精密度不⼀定⾼,但精确度⾼的精密度和准确度都⾼。
4、为什么在使⽤各种指针式仪表时,总希望指针偏转在全量程的2/3⼀上范围内使⽤?答:为了使仪表测出来的数据误差更⼩、更精确。
14、何谓传感器的静态标定和动态标定?试述传感器的静态标定过程。
传感器静态特性标定:传感器静态标定⽬的是确定传感器的静态特性指标,如线性度、灵敏度、精度、迟滞性和重复性等。
传感器动态特性标定:传感器动态特性标定的⽬的确定传感器的动态特性参数,如时间常数、上升时间或⼯作频率、通频带等。
标定步骤:(1)将传感器全量程分成若⼲等间距点;(2)根据传感器量程分点情况,由⼩到⼤⼀点⼀点地输⼊标准量值,并记录与个输⼊值相对应的输出值;(3)将输⼊值由⼤到⼩⼀点⼀点减⼩,同时记录与各输⼊值相对应的输出值;(4)按(2)(3)所述过程,对传感器进⾏正、反⾏程王府循环多次测试,将得到的输出-输⼊测试数据⽤表格列出或作出曲线;(5)对测试数据进⾏必要的处理,根据处理结果就可以确定传感器的线性度、灵敏度、迟滞和重复性等静态特性指标。
第⼆章:1、什么是应变效应?利⽤应变效应解释⾦属电阻应变⽚的⼯作原理。
应变效应:导体或半导体电阻随其机械变形⽽变化的物理现象。
⾦属导体的电阻值随着它受⼒所产⽣机械变形(拉伸或压缩)的⼤⼩⽽发⽣变化的现象称之为⾦属的电阻应变效应。
2、⾦属电阻应变⽚与半导体应变⽚的⼯作原理有何区别?各有何优缺点?⾦属应变⽚是通过电阻的形变导致电阻的变化从⽽被检测的。
半导体是通过PN的应⼒⽽改变的。
机理不同。
半导体应变⽚的特点:在较⼩功耗下具有较⾼的灵敏度和较⼤的电阻变化。
传感器原理及应用第三版课后答案

②当电容式传感器用于变间隙原理进行测量时具有非线性输出特性。
3-2分布和寄生电容的存在对电容传感器有什么影响?一般采取哪些措施可以减小其影响。
1-7:解:YFS=200-0=200
由A=ΔA/YFS*100%有
A=4/200*100%=2%。
精度特级为2.5级。
1-8:解:根据精度定义表达式:A=ΔA/AyFS*100%,由题意可知:A=1.5%,YFS=100
所以ΔA=A YFS=1.5
因为1.4<1.5
所以合格。
1-9:解:Δhmax=103-98=5
2-3:答:金属应变片单位应变引起的应变片电阻的相对变化叫金属应变片的灵敏度系数;它与金属丝应变灵敏度函数不同,应变片由于由金属丝弯折而成,具有横向效应,使其灵敏度小于金属丝的灵敏度。
2-4:答:因为(1)金属的电阻本身具有热效应,从而使其产生附加的热应变;
(2)基底材料、应变片、粘接剂、盖板等都存在随温度增加而长度应变的线膨胀效应,若它们各自的线膨胀系数不同,就会引起附加的由线膨胀引起的应变;常用的温度补偿法有单丝自补偿,双丝组合式自补偿和电路补偿法。
εr=-με=-3*10-4
(2) :F=εES=0.001*2*1011*0.00196=3.92*105N
1-10:解:(1)贴片习题中图2-7所示,R3、R2靠近中心处,且沿切向方向,R1、R4靠近圆片边缘处且沿径向贴。位置在使-εr=εt即
(2)
R1R2
USC
R3R4
E
(3)
εr2、3=
传感器原理与应用第二版课后答案

传感器原理与应用第二版课后答案1. 传感器的基本原理。
传感器是一种能够感知并转换物理量或化学量等非电信号为电信号的装置。
传感器的基本原理是利用特定的物理效应,如电磁感应、压阻效应、光电效应等,将被测量的物理量转换为电信号输出,从而实现对被测量物理量的监测和测量。
2. 传感器的分类及应用。
根据测量的物理量不同,传感器可以分为温度传感器、压力传感器、光电传感器、湿度传感器等多种类型。
每种传感器都有其特定的应用领域,如温度传感器广泛应用于工业生产中的温度监测和控制,压力传感器则常用于汽车制造和航空航天领域的压力监测等。
3. 传感器的工作原理。
传感器的工作原理是将被测量的物理量转换为电信号输出。
以温度传感器为例,当温度发生变化时,传感器内部的电阻值也会发生变化,通过测量电阻值的变化即可得知温度的变化情况。
而光电传感器则是利用光电效应将光信号转换为电信号输出。
4. 传感器的应用案例分析。
在工业自动化领域,传感器被广泛应用于各种生产设备的监测与控制中。
例如,利用压力传感器可以实现对液体管道内部压力的实时监测,以确保生产过程的安全性和稳定性。
另外,在智能家居领域,温度传感器和湿度传感器可以实现对室内环境的实时监测,从而实现空调和加湿器的智能控制。
5. 传感器的发展趋势。
随着科技的不断进步,传感器技术也在不断发展。
未来,传感器将更加智能化、微型化和多功能化,能够实现更精准的监测和更便捷的数据传输。
同时,新型材料和制造工艺的应用也将为传感器的发展提供更广阔的空间。
总结,传感器作为现代化社会不可或缺的一部分,其在工业生产、智能家居、医疗健康等领域都发挥着重要作用。
通过对传感器的基本原理、分类及应用、工作原理、应用案例分析和发展趋势的了解,我们可以更好地认识传感器,并为其未来的发展提供更多的可能性。
2023大学_传感器原理及应用(王化祥著)课后答案下载

2023传感器原理及应用(王化祥著)课后答案下载2023传感器原理及应用(王化祥著)课后答案下载前言绪论第一章传感器及其基本特性第一节传感器的定义、组成及分类第二节传感器的基本特性__小结习题与思考题第二章电阻应变式传感器第一节应变式传感器第二节应变式传感器的测量电路第三节压阻式传感器第四节应变式传感器的应用__小结习题与思考题第三章电容式传感器第一节电容式传感器的'工作原理与类型第二节电容式传感器的测量电路第三节电容式传感器的误差分析及补偿第四节电容式传感器的应用__小结习题与思考题第四章电感式传感器第一节自感式传感器第二节差动变压器式传感器第三节电涡流式传感器__小结习题与思考题第五章压电式传感器第一节压电效应与压电材料第二节压电传感器的等效电路和测量电路第三节引起/玉,E9式传感器测量误差的因素第四节压电传感器的应用__小结习题与思考题第一节磁电感应式传感器第二节霍尔传感器第三节磁敏电阻器第四节磁敏二极管和磁敏三极管第五节磁电传感器的应用__小结习题与思考题第七章热电式传感器第一节热电偶传感器第二节热电阻式传感器第三节半导体式热敏电阻第四节热电式传感器的应用__小结习题与思考题第八章光电传感器第一节光电效应第二节光电器件及其特性第三节红外传感器__小结习题与思考题第九章常用其他新型传感器第一节气体传感器第二节湿敏传感器第三节超声传感器第四节超导传感器第五节仿生传感器__小结习题与思考题第十章智能传感器第一节智能传感器概述第二节智能传感器的实现方式第三节智能传感器的应用第四节智能传感器的发展方向本?小结习题与思考题……第十一章传感器的标定与选用传感器原理及应用(王化祥著):基本信息点击此处下载传感器原理及应用(王化祥著)课后答案传感器原理及应用(王化祥著):目录作者:王桂荣,李宪芝主编出版社:中国电力出版社版次:1字数:500000印刷时间:-5-1ISBN:9787512304109。
传感器原理及其应用(第二版)部分习题答案
24.875
精品
第1章 传感器的一般特性
4、何为传感器的静态特性?静态特性的主要技术指标有 哪些? 答:传感器的静态特性是在稳态信号作用下的输入输出 特性。 衡量静态特性的重要指标有灵敏度、线性度、迟滞、重 复性、稳定性等。
精品
第1章 传感器的一般特性
5、何为传感器的动态特性?动态特性的主要技术指标有 哪些? 答:传感器的动态特性是传感器在被测量随时间变化的 条件下输入输出关系。动态特性有分为瞬态响应和频率 响应。
答:金属应变片在外力的作用下,应变片的几何尺寸(长度和截面积 )发生变化(机械形变)而引起应变片的电阻改变,运用它们的对应 关系实现测量目的;其灵敏系数(k≈1+2μ)主要是材料几何尺寸变化 引起的。半导体应变片受到作用力后,应变片的电阻率ρ发生变化,而 引起应变片的电阻值改变。其灵敏系数(k=△ρ/ρε)主要是半导体材 料的电阻率随应变变化引起的。 当金属丝在外力作用下发生机械变形时,其电阻值将发生变化,这种 现象称为金属的电阻应变效应。 应变片是利用金属的电阻应变效应,将金属丝绕成栅形,称为敏感栅 。并将其粘贴在绝缘基片上制成。精品
精品
第2章 电阻应变式传感器及其应用
解:(1)如图a,当重力F作用梁短部后,梁上表面R1和R3产生正
应变电阻变化而下表面R2和R4则产生负应变电阻变化,其应变的
绝对值应相等,即:
1 = 3 = 2 4 b 6 h F 2 L E 6 b m h 2 g E L
电阻相对变化量为:
R1R3R2 R4 Rk
R1 R3
R2
R4 R
现将四个电阻应变片按照图b所示接入等臂全桥电路,其输出电
桥电路电压为:
U0
R R
U
传感器原理及应用课后习题答案)

习题集及答案第1章概述1.1 什么是传感器?按照国标定义,“传感器”应该如何说明含义?1.2 传感器由哪几部分组成?试述它们的作用及相互关系。
1.3 简述传感器主要发展趋势,并说明现代检测系统的特征。
1.4 传感器如何分类?按传感器检测的范畴可分为哪几种?1.5 传感器的图形符号如何表示?它们各部分代表什么含义?应注意哪些问题?1.6 用图形符号表示一电阻式温度传感器。
1.7 请例举出两个你用到或看到的传感器,并说明其作用。
如果没有传感器,应该出现哪种状况。
1.8 空调和电冰箱中采用了哪些传感器?它们分别起到什么作用?答案:1.1答:从广义的角度来说,感知信号检出器件和信号处理部分总称为传感器。
我们对传感器定义是:一种能把特定的信息(物理、化学、生物)按一定规律转换成某种可用信号输出的器件和装置。
从狭义角度对传感器定义是:能把外界非电信息转换成电信号输出的器件。
我国国家标准(GB7665—87)对传感器(Sensor/transducer)的定义是:“能够感受规定的被测量并按照一定规律转换成可用输出信号的器件和装置”。
定义表明传感器有这样三层含义:它是由敏感元件和转换元件构成的一种检测装置;能按一定规律将被测量转换成电信号输出;传感器的输出与输入之间存在确定的关系。
按使用的场合不同传感器又称为变换器、换能器、探测器。
1.2答:组成——由敏感元件、转换元件、基本电路组成;关系,作用——传感器处于研究对象与测试系统的接口位置,即检测与控制之首。
传感器是感知、获取与检测信息的窗口,一切科学研究与自动化生产过程要获取的信息都要通过传感器获取并通过它转换成容易传输与处理的电信号,其作用与地位特别重要。
1.3答:(略)答:按照我国制定的传感器分类体系表,传感器分为物理量传感器、化学量传感器以及生物量传感器三大类,含12个小类。
按传感器的检测对象可分为:力学量、热学量、流体量、光学量、电量、磁学量、声学量、化学量、生物量、机器人等等。
传感器原理与应用第二版课后答案

传感器原理与应用第二版课后答案1. 什么是传感器?传感器的作用是什么?传感器是一种能够感知、检测和接收外部信息并将其转化为可用信号的装置。
其作用在于将各种物理量、化学量、生物量等转换为电信号或其他所需形式的信号,以便进行测量、控制、记录、显示等。
2. 传感器的分类及其原理。
传感器根据测量的物理量不同可分为光学传感器、压力传感器、温度传感器、湿度传感器、位移传感器、力传感器等。
光学传感器是利用光的传播、反射、折射、吸收等现象进行探测的传感器。
压力传感器是利用介质受力变形的原理进行测量的传感器。
温度传感器是利用物体温度与某种物理特性(如电阻、电压、电流等)的关系进行测量的传感器。
湿度传感器是利用介质的吸湿性质进行测量的传感器。
位移传感器是利用物体位移与某种物理特性(如电容、电感、电阻等)的关系进行测量的传感器。
力传感器是利用受力物体的弹性变形与某种物理特性(如电阻、电容、电感等)的关系进行测量的传感器。
3. 传感器的应用领域。
传感器广泛应用于工业自动化、环境监测、医疗仪器、消费电子、智能家居、汽车电子、航空航天等领域。
在工业自动化领域,传感器用于测量和控制生产过程中的各种物理量,如温度、压力、流量、液位等,以实现自动化生产。
在环境监测领域,传感器用于监测大气、水质、土壤等环境参数,以实现环境保护和资源管理。
在医疗仪器领域,传感器用于监测患者的生理参数,如心率、血压、血氧饱和度等,以帮助医生进行诊断和治疗。
在消费电子领域,传感器用于手机、平板电脑、智能手表等设备中,实现智能化功能。
在智能家居领域,传感器用于监测室内环境,实现智能控制。
在汽车电子领域,传感器用于监测车辆的各种参数,保障行车安全。
在航空航天领域,传感器用于监测飞行器的各种参数,保障飞行安全。
4. 传感器的发展趋势。
随着科技的不断进步,传感器的发展呈现出以下几个趋势,小型化、智能化、多功能化、网络化、无线化。
传感器的小型化使其在各种设备中的应用更加方便灵活;智能化使传感器具有自主判断和处理能力,能够实现更复杂的功能;多功能化使传感器能够同时实现多种测量和控制功能;网络化使传感器能够实现远程监测和控制;无线化使传感器能够摆脱传统的有线连接,实现更灵活的布局和应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章传感与检测技术的理论基础1.什么是测量值的绝对误差、相对误差、引用误差?答:某量值的测得值和真值之差称为绝对误差。
相对误差有实际相对误差和标称相对误差两种表示方法。
实际相对误差是绝对误差与被测量的真值之比;标称相对误差是绝对误差与测得值之比。
引用误差是仪表中通用的一种误差表示方法,也用相对误差表示,它是相对于仪表满量程的一种误差。
引用误差是绝对误差(在仪表中指的是某一刻度点的示值误差)与仪表的量程之比。
2.什么是测量误差?测量误差有几种表示方法?它们通常应用在什么场合?答:测量误差是测得值与被测量的真值之差。
测量误差可用绝对误差和相对误差表示,引用误差也是相对误差的一种表示方法。
在实际测量中,有时要用到修正值,而修正值是与绝对误差大小相等符号相反的值。
在计算相对误差时也必须知道绝对误差的大小才能计算。
采用绝对误差难以评定测量精度的高低,而采用相对误差比较客观地反映测量精度。
引用误差是仪表中应用的一种相对误差,仪表的精度是用引用误差表示的。
3.用测量范围为-50~+150kPa的压力传感器测量140kPa压力时,传感器测得示值为142kPa,求该示值的绝对误差、实际相对误差、标称相对误差和引用误差。
解:绝对误差2140142=-=∆kPa实际相对误差%43.1%100140140142=⨯-=δ标称相对误差%41.1%100142140142=⨯-=δ引用误差%1%10050150140142=⨯---=)(γ4.什么是随机误差?随机误差产生的原因是什么?如何减小随机误差对测量结果的影响?答:在同一测量条件下,多次测量同一被测量时,其绝对值和符号以不可预定方式变化着的误差称为随机误差。
随机误差是由很多不便掌握或暂时未能掌握的微小因素(测量装置方面的因素、环境方面的因素、人员方面的因素),如电磁场的微变,零件的摩擦、间隙,热起伏,空气扰动,气压及湿度的变化,测量人员感觉器官的生理变化等,对测量值的综合影响所造成的。
对于测量列中的某一个测得值来说,随机误差的出现具有随机性,即误差的大小和符号是不能预知的,但当测量次数增大,随机误差又具有统计的规律性,测量次数越多,这种规律性表现得越明显。
所以一般可以通过增加测量次数估计随机误差可能出现的大小,从而减少随机误差对测量结果的影响。
5.什么是系统误差?系统误差可分哪几类?系统误差有哪些检验方法?如何减小和消除系统误差?答:在同一测量条件下,多次测量同一量值时,绝对值和符号保持不变,或在条件改变时,按一定规律变化的误差称为系统误差。
系统误差可分为恒值(定值)系统误差和变值系统误差。
误差的绝对值和符号已确定的系统误差称为恒值(定值)系统误差;绝对值和符号变化的系统误差称为变值系统误差,变值系统误差又可分为线性系统误差、周期性系统误差和复杂规律系统误差等。
在测量过程中形成系统误差的因素是复杂的,通常人们难于查明所有的系统误差,发现系统误差必须根据具体测量过程和测量仪器进行全面的仔细的分析,这是一件困难而又复杂的工作,目前还没有能够适用于发现各种系统误差的普遍方法,只是介绍一些发现系统误差的一般方法。
如实验对比法、残余误差观察法,还有准则检查法如马利科夫判据和阿贝检验法等。
由于系统误差的复杂性,所以必须进行分析比较,尽可能的找出产生系统误差的因素,从而减小和消除系统误差。
1. 从产生误差根源上消除系统误差;2.用修正方法消除系统误差的影响;3. 在测量系统中采用补偿措施;4.可用实时反馈修正的办法,来消除复杂的变化系统误差。
6. 什么是粗大误差?如何判断测量数据中存在粗大误差?答:超出在规定条件下预期的误差称为粗大误差,粗大误差又称疏忽误差。
此误差值较大,明显歪曲测量结果。
在判别某个测得值是否含有粗大误差时,要特别慎重,应作充分的分析和研究,并根据判别准则予以确定。
通常用来判断粗大误差的准则有:3σ准则(莱以特准则);肖维勒准则;格拉布斯准则。
7. 什么是直接测量、间接测量和组合测量?答:在使用仪表或传感器进行测量时,测得值直接与标准量进行比较,不需要经过任何运算,直接得到被测量,这种测量方法称为直接测量。
在使用仪表或传感器进行测量时,首先对与测量有确定函数关系的几个量进行直接测量,将直接测得值代入函数关系式,经过计算得到所需要的结果,这种测量称为间接测量。
若被测量必须经过求解联立方程组求得,如:有若干个被测量y 1,y 2,,…,y m ,直接测得值为,x ,,x ,x n 21 把被测量与测得值之间的函数关系列成方程组,即⎪⎪⎭⎪⎪⎬⎫===)y ,,y ,y (f x )y ,,y ,y (f x )y ,,y ,y (f x m 21n n m 2122m 2111 (1-6)方程组中方程的个数n 要大于被测量y 的个数m ,用最小二乘法求出被测量的数值,这种测量方法称为组合测量。
8. 标准差有几种表示形式?如何计算?分别说明它们的含义。
答:标准偏差简称标准差,有标准差σ、标准差的估计值s σ及算术平均值的标准差x σ。
标准差σ的计算公式 =σn n 22221δδδ+++ n n i i ∑==12δ (∞→n ) 式中i δ为测得值与被测量的真值之差。
标准差的估计值s σ的计算公式 112-=∑=n v ni is σ 式中i v 为残余误差,是测得值与算术平均值之差,该式又称为贝塞尔公式。
算术平均值的标准差x σ的计算公式 n sx σσ=由于随机误差的存在,等精度测量列中各个测得值一般皆不相同,它们围绕着该测量列的算术平均值有一定的分散,此分散度说明了测量列中单次测得值的不可靠性,标准差σ是表征同一被测量的n 次测量的测得值分散性的参数,可作为测量列中单次测量不可靠性的评定标准。
而被测量的真值为未知,故不能求得标准差σ,在有限次测量情况下,可用残余误差代替真误差,从而得到标准差的估计值s σ,标准差的估计值s σ含义同标准差σ,也是作为测量列中单次测量不可靠性的评定标准。
若在相同条件下对被测量进行m 组的“多次重复测量”,每一组测量都有一个算术平均值,由于随机误差的存在,各组所得的算术平均值也不相同,它们围绕着被测量的真值有一定分散,此分散说明了算术平均值的不可靠性,算术平均值的标准差x σ则是表征同一被测量的各个独立测量列算术平均值分散性的参数,可作为算术平均值不可靠性的评定标准。
9.什么是测量不确定度?有哪几种评定方法?答:测量不确定度定义为表征合理赋予被测量之值的分散性,与测量结果相联系的参数。
测量不确定度意味着对测量结果的可靠性和有效性的怀疑程度或不能肯定的程度。
测量不确定度按其评定方法可分为A 类评定和B 类评定。
第二章传感器概述2-1 什么叫传感器?它由哪几部分组成?它们的作用及相互关系如何?答:传感器是能感受规定的被测量并按照一定的规律转换成可用输出信号的器件或装置。
通常传感器有敏感元件和转换元件组成。
其中,敏感元件是指传感器中能直接感受或响应被测量的部份;转换元件是指传感器中能将敏感元件感受或响应的被测量转换成适于传输或测量的电信号部份。
由于传感器输出信号一般都很微弱,需要有信号调理与转换电路,进行放大、运算调制等,此外信号调理转换电路以及传感器的工作必须要有辅助的电源,因此信号调理转换电路以及所需的电源都应作为传感器组成的一部份。
2-2 什么是传感器的静态特性?它有哪些性能指标?分别说明这些性能指标的含义。
答:传感器的静态特性是指被测量的值处于稳定状态(被测量是一个不随时间变化,或随时间变化缓慢的量)时的输出输入关系。
传感器的静态特性可以用一组性能指标来描述,有灵敏度、迟滞、线性度、重复性和漂移等。
①灵敏度是指传感器输出量增量△y 与引起输出量增量△y 的相应输入量增量△x 的之比。
用S 表示灵敏度,即S=△y/△x②传感器的线性度是指在全量程范围内实际特性曲线与拟合直线之间的最大偏差值m ax L ∆满量程输出值FS Y 之比。
线性度也称为非线性误差,用L r 表示,即 %100max ⨯∆±=FS L L Y r 。
③迟滞是指传感器在输入量由小到大(正行程)及输入量由大到小(反行程)变化期间其输入输出特性曲线不重合的现象。
即传感器在全量程范围内最大的迟滞差值ΔH max 与满量程输出值FS Y 之比称为迟滞误差,用L r 表示,即:%100max ⨯∆=FS H H Y r④重复性是指传感器在输入量按同一方向作全量程连续多次变化时,所得特性曲线不一致的程度。
重复性误差属于随机误差,常用均方根误差计算,也可用正反行程中最大重复差值m ax R ∆计算,即:%100)3~2(⨯±=FS R Y σγ 2-3 什么是传感器的动态特性?有哪几种分析方法?它们各有哪些性能指标?答:传感器的动态特性是指输入量随时间变化时传感器的响应特性。
主要的分析方法有:瞬态响应法(又称时域分析法),相应的性能指标有时间常数τ、延迟时间t d 、上升时间t r 、超调量σ和衰减比d 等;频率响应法,相应的性能指标有通频带ω0.707、工作频带ω0。
95、时间常数τ、固有频率ωn 、跟随角φ0。
70等。
第三章 应变式传感器1. 什么叫应变效应?利用应变效应解释金属电阻应变片的工作原理。
答:在外力作用下,导体或半导体材料产生机械变形,从而引起材料电阻值发生相应变化的现象,称为应变效应。
其表达式为ε⋅=K R dR ,式中K 为材料的应变灵敏系数,当应变材料为金属或合金时,在弹性极限内K 为常数。
金属电阻应变片的电阻相对变化量R dR与金属材料的轴向应变ε成正比,因此,利用电阻应变片,可以将被测物体的应变ε转换成与之成正比关系的电阻相对变化量,这就是金属电阻应变片的工作原理。
2. 试述应变片温度误差的概念,产生原因和补偿办法。
答:由于测量现场环境温度偏离应变片标定温度而给测量带来的附加误差,称为应变片温度误差。
产生应变片温度误差的主要原因有:⑴由于电阻丝温度系数的存在,当温度改变时,应变片的标称电阻值发生变化。
⑵当试件与与电阻丝材料的线膨胀系数不同时,由于温度的变化而引起的附加变形,使应变片产生附加电阻。
电阻应变片的温度补偿方法有线路补偿法和应变片自补偿法两大类。
电桥补偿法是最常用且效果较好的线路补偿法,应变片自补偿法是采用温度自补偿应变片或双金属线栅应变片来代替一般应变片,使之兼顾温度补偿作用。
3. 什么是直流电桥?若按桥臂工作方式不同,可分为哪几种?各自的输出电压如何计算?答:如题图3-3所示电路为电桥电路。
若电桥电路的工作电源E 为直流电源,则该电桥称为直流电桥。
按应变所在电桥不同的工作桥臂,电桥可分为:⑴单臂电桥,R 1为电阻应变片,R 2、R 3、R 4为电桥固定电阻。
