新版弹性地基梁计算实际及算例教材
弹性地基梁

5、左端固定右端自由,计自重********************************************************************** 弹性地基梁计算书计算方法:文克尔有限元法计算时间:2006-11-07 10:10:52 星期二********************************************************************** ---------------------------------------------------------------------- [ 计算简图、位移图、剪力图、弯矩图 ]-------------------------------------------------------------------------------------------------------------------------------------------- [ 计算条件 ]---------------------------------------------------------------------- [[[各跨信息]No. L Ix B H A γ u K E Ri Rj1 10.000 427.083 4.100 0.500 2.050 25.00 0.20 1500.020000.0 固定自由注:L ----跨长,单位:mIx ----截面惯性矩,单位:m4/10000B ----截面底部宽度,单位:mH ----截面高度,单位:mA ----截面面积,单位:m2γ ----材料容重,单位:kN/m3u ----材料泊松比K ----基床系数,单位:kN/m3E ----弹性模量,单位:MPaRi ----梁左端约束Rj ----梁右端约束[第注:P1、P2 ----对集中力单位:kN----对分布荷载单位:kN/m----------------------------------------------------------------------[ 各单元计算结果 ]----------------------------------------------------------------------单元号 Xi Xj Qi Qj Mi Mj Di Dj1 0.00 1.00 597.09 458.90 -1430.24 -902.92 0.0 -0.72 1.00 2.00 458.89 332.23 -902.91 -508.58 -0.7 -2.53 2.00 3.00 332.23 222.19 -508.57 -232.90 -2.5 -4.94 3.00 4.00 222.18 131.44 -232.89 -57.76 -4.9 -7.65 4.00 5.00 131.43 61.02 -57.76 36.76 -7.6 -10.46 5.00 6.00 61.02 11.02 36.76 71.10 -10.4 -13.17 6.00 7.00 11.02 -18.95 71.10 65.49 -13.1 -15.88 7.00 8.00 -18.95 -29.39 65.49 39.71 -15.8 -18.39 8.00 9.00 -29.39 -22.43 39.71 12.50 -18.3 -20.810 9.00 10.00 -22.43 -0.00 12.50 0.00 -20.8 -23.4 注:1.Xi----单元i端坐标(m)2.Xj----单元j端坐标(m)3.Qi----单元i端剪力(kN)4.Qj----单元j端剪力(kN)5.Mi----单元i端弯矩(kN-m)6.Mj----单元j端弯矩(kN-m)7.Di----单元i端位移(mm)8.Dj----单元j端位移(mm)----------------------------------------------------------------------[ 各跨计算结果 ]----------------------------------------------------------------------注:下面的“中”是指梁的几何中点,不一定是弯矩最大点跨号: 1 左中右弯矩(kN-m):-1430.24 36.76 0.00剪力(kN): 597.09 61.02 -0.00位移(mm): 0.00 -10.38 -23.36上部纵筋(mm2): 12226.7 4100.0 4100.0下部纵筋(mm2): 4100.0 4100.0 4100.0箍筋(mm2): 595.1 595.1 595.1截面验算:满足满足满足注:1. 输出的内力值不包括“结构重要性系数γ0”。
弹性地基梁计算书

最小弯矩(kN.m) 87.06 -398.71 -768.65 -976.57 -1033.04
内力组合号 ( 6) ( 2) ( 2) ( 2) ( 2)
配筋面积(mm2) 0 0 750 923 750
梁号= 2 梁肋宽=500 梁高=750
翼缘宽=1500 翼缘根部高=500 翼缘端部高=250 翼缘在梁底
翼缘冲切验算:
Fl=pj*Al=161.9*0.040=6.48kN
am=(at+ab)/2=(1.000+1.000)/2=1.000m
0.7*βhp*ft*am*Ho=0.7*1.00*1430.00*1.000*0.46=460.46≥Fl=6.48kN
翼缘剪切验算:
0.7*βh*ft*bo*Ho=0.7*1.00*1430.00*1.000*0.46=460.46≥V=80.96kN
-1- -2- -3- -4- -5-
最小弯矩(kN.m) -1069.55 -738.41 -337.23 104.90 522.36
配筋面积(mm2) 0 1701 3282 4338 4591
配筋率(%) 0.00 0.23 0.44 0.58 0.61
最大弯矩(kN.m) 161.13 -240.61 -493.12 -630.67 -663.78
am=(at+ab)/2=(1.000+1.000)/2=1.000m
0.7*βhp*ft*am*Ho=0.7*1.00*1430.00*1.000*0.46=460.46≥Fl=8.22kN
翼缘剪切验算:
0.7*βh*ft*bo*Ho=0.7*1.00*1430.00*1.000*0.46=460.46≥V=102.70kN
弹性地基梁理论课件
假设梁为连续的一维 弹性体,且忽略梁的 轴向变形。
弹性地基梁的研究目的和意义
研究目的
通过分析弹性地基梁的振动特性,为工程实践提供理论根据和设计指点,以提高结构的稳定性和安全 性。
研究意义
弹性地基梁理论有助于揭示地基与梁之间的相互作用机制,预测结构的振动响应,从而优化结构设计 ,减少地震等自然灾害的影响。此外,该理论还为研究其他复杂结构(如高层建筑、大跨度桥梁等) 的地基基础问题提供了基础和借鉴。
2023-2026
ONE
KEEP VIEW
弹性地基梁理论课件
REPORTING
CATALOGUE
目 录
• 弹性地基梁理论概述 • 弹性地基梁的力学模型 • 弹性地基梁的数值模拟 • 弹性地基梁的实验研究 • 弹性地基梁的应用案例 • 弹性地基梁的未来研究方向 • 参考文献
PART 01
弹性地基梁理论概述
利用边界积分方程求解弹 性问题,适用于处理无界 问题等。
PART 04
弹性地基梁的实验研究
实验设备和方法
实验设备
包括弹性地基梁、加载装置、位移计 、应变计等。
实验方法
在实验室中,将弹性地基梁放置在加 载装置上,通过位移计和应变计测量 梁的位移和应变,从而得到梁的力学 性能。
实验结果和分析
实验结果
边界条件
束缚梁的位移、转角等物理量, 如在支撑处的位移束缚、固定束 缚等。
初始条件
指定梁的初始状态,如初始应力 、初始位移等。
弹性地基梁的求解方法
解析法
利用数学解析方法求解方程,适 用于简单边界条件和初始条件的
情况。
数值法
采用数值计算方法求解方程,如有 限元法、有限差分法等,适用于复 杂边界条件和初始条件的情况。
弹性计算
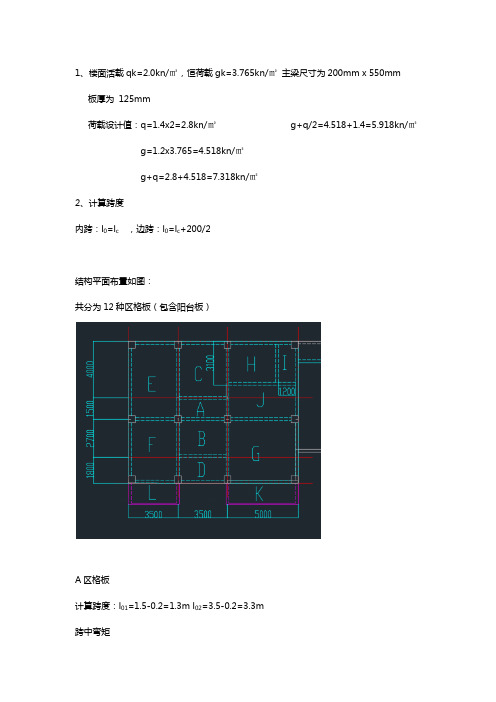
1、楼面活载qk=2.0kn/㎡,恒荷载gk=3.765kn/㎡主梁尺寸为200mm x 550mm板厚为125mm荷载设计值:q=1.4x2=2.8kn/㎡g+q/2=4.518+1.4=5.918kn/㎡g=1.2x3.765=4.518kn/㎡g+q=2.8+4.518=7.318kn/㎡2、计算跨度内跨:l0=l c,边跨:l0=l c+200/2结构平面布置如图:共分为12种区格板(包含阳台板)A区格板计算跨度:l01=1.5-0.2=1.3m l02=3.5-0.2=3.3m跨中弯矩m=(g+q)l201/24=7.318x1.3x1.3/24=0.515kn·m支座弯矩M1=-(g+q)l201/12=-7.318x1.3x1.3/12=-1.03kn·mM2=-(g+q)l201/12=-7.318x1.3x1.3/12=-1.03kn·m环境类别一级,C30混凝土,板的最小保护层厚度C=15mm,假定纵向钢筋直径为6mm,板厚125mm,则截面有效高度h0=125-15-6/2=107mm,板宽b=1000mm。
α1=1.0,f c=14.3kn/m㎡;f y=360 kn/m㎡。
跨中正弯矩配筋计算:αs=M/(α1f c bh2)=0.515/(1x14.3x1x0.1072)=0.031§=1-1−2α=0.0315As= §bh0α1f c/f y=0.0315x1000x107x14.3/360=133.9mm2I区格板计算跨度:l01=1.2-0.1=0.9m l02=3.1-0.1=3.0m跨中弯矩m=(g+q)l201/24=8.018x0.92/24=0.27kn·m支座弯矩M1=-(g+q)l201/12=-8.018x0.92/12=-0.54kn·mM2=-(g+q)l201/12=-8.018x0.92/12=-0.54kn·m跨中正弯矩配筋计算:αs=M/(α1f c bh2)=0.27/(1x14.3x1x0.1072)=0.016§=1-1−2α=0.016As= §bh0α1f c/f y=0.016x1000x107x14.3/360=68.0mm2K区格板计算跨度:l01=1.5-0.1=1.4m l02=5-0.1=4.9m跨中弯矩m=(g+q)l201/24=7.318x1.4x1.4/24=0.6kn·m支座弯矩M1=-(g+q)l201/12=-7.318x1.4x1.4/12=-1.20kn·mM2=-(g+q)l201/12=-7.318x1.4x1.4/12=-1.20kn·m跨中正弯矩配筋计算:αs=M/(α1f c bh2)=0.6/(1x14.3x1x0.1072)=0.037§=1-1−2α=0.038As= §bh0α1f c/f y=0.038x1000x107x14.3/360=161.51mm2L区格板计算跨度:l01=1.5-0.1=1.4m l02=3.5-0.1=3.4m跨中弯矩m=(g+q)l201/24=7.318x1.4x1.4/24=0.6kn·m支座弯矩M1=-(g+q)l201/12=-7.318x1.4x1.4/12=-1.20kn·mM2=-(g+q)l201/12=-7.318x1.4x1.4/12=-1.20kn·m跨中正弯矩配筋计算:αs=M/(α1f c bh2)=0.6/(1x14.3x1x0.1072)=0.037§=1-1−2α=0.038As= §bh0α1f c/f y=0.038x1000x107x14.3/360=161.51mm2G区格板计算跨度:l01=4.6m l02=5.1m跨中弯矩M1=(0.0291+0.2x0.0224)x(g+q/2)l201+(0.0456+0.2x0.0358)ql201/2=8.05kn•mM2=(0.0224+0.2x0.0291)x(g+q/2)l201+(0.0358+0.2x0.0456)ql201/2=6.81kn•m支座弯矩M1`=M1``=-0.0776(g+q)l201=-12.02kn•mM2``=M2``=-0.0716(g+q)l201=-11.08kn•m配筋计算截面有效高度:由于是双向配筋,两个方向的截面有效高度不同。
第三章 弹性地基梁理论new

地基模型
• • • • • • • • 地基反力直线分布模型 文克尔地基模型 半空间弹性地基模型 有限深度可压缩性地基模型 层状地基模型 双参数、三参数弹性地基模型 非线弹性及弹塑性模型 Duncan and Chang、剑桥模型及修正、 沈珠江模型、 Drucker and Prager
1 地基反力直线分布模型
浅基础设计方法
常规设计法
上部结构 基础
上部结构
地基
满足了静力平衡条件,忽略了地基、基础和上部 结构三者之间受荷前后的变形连续性。 地基越软弱,与实际情况差别越大。
常规设计法: 满足下列条件时可以采用:
• (1)沉降较小或较均匀 • (2)基础刚度大
§3.1 弹性地基梁的选择、布置与构造 柱下条形基础 • 连续基础 交叉条形基础 筏板基础 • 特点 底面积大 整体刚度大 补偿作用 箱形基础 地基承载力 减小不均匀沉降 箱形基础, 设置地下室的筏形基础
(3 − 18)
式中 b、l—基础的宽度和长度。 由式(3-18)可得到:条形基础的 k0(或修正 值)是与条形基础同宽的方形基础 k0值的2/3。
(4)考虑基础埋置深度的修正 太沙基1955年建议的公式是
d ' k 0 = k 0 (1 + 2 ) b (3 − 19)
前苏联卡里诺维奇建议的公式是
• 有限压缩层地基模型来源于地基计算的分层总 和法,土中位移采用了布辛奈斯克弹性理论解的 积分形式,而在变形计算中考虑了土的成层特 性。
δ ij = ∑
t =1
nc
σ tij hti
Esti
4 分析方法
• 静力平衡条件 ⎧∑ F = 0 ⎪ ⎨ ⎪∑ M = 0 ⎩ • 变形协调条件
弹性地基梁法计算断面内力

弹性地基梁法计算断面内力一、 基本资料该计算简图仍按上述倒置梁法基本体系:两侧墙高13.6m ,厚1.0m ,其底部固结于泵房地板两端,底板为五等跨(每跨5.5m)连续梁,板总长28.5m ,厚1.0m ,墙底板均C25钢筋混凝土,62=2.510/E T cm ⨯岩。
(一) 地基为重粉质壤土,2=50/E T m 土(二) 所受荷载,侧墙有水压力,构建自重,具体数据仍用“倒置梁法”,成果见下图,边荷载另述。
荷载简图(一)底板向下均布为根据上述“P3不平衡剪力重分配”, =11.1Q T∆↓底11.10/13.750.8/=2.5/=0.80+2.5=3.3/q T m q T mqT m∆==↓↓↓∑底自重底二、 求断面内M Q P (一)求底板柔性指数33550013750101052.510100E L E n τ⎛⎫⎛⎫=⨯⨯=⨯⨯= ⎪ ⎪⨯⎝⎭⎝⎭土岩 均布荷载50τ<,集中荷载10τ<,均属短梁(二) 求q P M 作用弯矩M它有q 均匀、P 集中、弯矩M 三种荷载1. 3.3/,13.75,M q P q T m L m ==均布荷载只求,暂不求220.010.01 3.313.75 6.24q M MqL M M T m ==⨯⨯=⋅,M 查表2. 集中荷载11171.2, 2.75/13.750.2,0.010.0171.213.759.8P Ta M MPL M M T m =====⨯⨯=⋅22271.2,8.25/13.750.6,7.8P P Ta M M Tm ====3367.1,13.75/13.751,0.010.0167.113.759.23P Ta M MPL M M T m =====⨯⨯=⋅3. 98.3,13.75/13.75 1.0,0.010.01M m M T m a M MM M T m =-⋅====-⋅弯矩4. 弯矩M 叠加5. 绘M 图(二)弯矩图(二)(三) 边荷载影响泵房两侧自排涵不同:东侧涵总宽8.2m ,顶底高程差16.578.97.67m ∇-=,填土涵上高程22.00m ∇,其为安装间顶高程38.00m ∇,安装重24/T m 。
弹性地基梁

ik ik bik ip ip bip
底板按弹性地基梁在外荷载 q 作用下,切口处 X i 方向的位移。
框架基本结构在外荷载作用下, X i 方向产生的位移(不包括底板)
求矩形框架 的内力
上部结构
N M M N
根据冗余力可X1、X2和X3计算出上 部框架的内力; (叠加法) 底板的内力根据弹性地基梁方法求出。
13 11 A A 10 9
2 u1 bK
2
13 11 A A 10 9
单位水平力时,墙顶转角及水平位移
2 2 2 u1 bK
2 10 13 A u2 bK 9 10 A
M i M 1i X 1 M 2i X 2 M ip Ni N1i X 1 N 2i X 2 N ip
底板的内力计算
按弹性半无限体计算地基梁的内力,在梁上受集
中力和受力矩荷载进行叠加。
主动侧压力e=1时,墙顶的转角及水平位移
4 3 A e A bK 9 10
1 ue bK
14 15 A A 10 9
式中 A,n及φ1~φ4,φ9~φ15见教材310~ 312
AM 在单位力X1=1作用下,A点产生弯矩:
MA=1kN· m(顺时针)
=表中系数
Ml EI
根据 MA=1 kN· m,按照弹性地基梁计 算,在α=1,ξ=1处,产生的转角
A1 0.952
(1) 2.0 1.904 EI EI
A2
(3) 2.0 5.712 0.952 EI EI
《弹性地基梁理论》PPT课件

3. 初参数解
(一)初参数法
由式(3.11),再据式(3.5)有
y B1chx cosx B2chx sinx B3shx cosx B4shx sinx
2 B1chxsinx shx cosx B2 chx cosx shxsinx
B3 shxsinx chx cosx B4 shx cosx chxsinx
地下建筑结构弹性地基梁可以是平放的,也可以是竖放的,地基介质可以 是岩石、粘土等固体材料,也可以是水、油之类的液体介质。弹性地基梁 是超静定梁,其计算有专门的一套计算理论。
1. 荷载种类和组合
弹性地基梁与普通梁的区别:
普通梁只在有限个支座处与基础相连,梁所受的支座反力是有 限个未知力,因此,普通梁是静定的或有限次超静定的结构。 弹性地基梁与地基连续接触,梁所受的反力是连续分布的,弹 性地基梁具有无穷多个支点和无穷多个未知反力。
M 2EI 2 B1shx sinx B2shx cosx B3chx sinx B4chx cosx
Q 2EI 3B1chxsinx shx cosx B2 chx cosx shxsinx
B3 chx cosx shxsinx B4 chxsinx shx cosx
(3.12)
地基的变形是考虑还是略去,这是它们的另一个主要区别。
2. 弹性地基梁的计算模型
由于地基梁搁置在地基上,梁上作用有荷载,地基梁在荷 载作用下与地基一起产生沉陷,因而梁底与地基表面存在相互作用 反力 ,的大小与地基沉降y 有密切关系,很显然,沉降越大,反 力 也越大,因此在弹性地基梁的计算理论中关键问题是如何确定 地基反力与地基沉降之间的关系,或者说如何选取弹性地基的计算
弹性地基梁理论
本讲内容—弹性地基梁理论
弹性地基梁的计算

第3章 弹性地基梁的计算计算基础梁常用的三种假设: (1)地基反力按直线分布的假定; (2)文克尔假定;(3)地基为弹性半无限体(或弹性半无限平面)的假定。
3.1按文克尔假定计算基础梁的基本方程1. 弹性地基梁的挠度曲线微分方程根据文克尔假定,地基反力用下式表达。
Ky =σ (3-1) 式中,σ-任一点的地基反力(kN/m 2)y -相应点的地基沉陷量(m )K -弹性压缩系数(kN/m 3)梁的角变,位移、弯矩、剪力及荷载的正方向均如图中所示。
推导出基础梁的挠度曲线微分方程。
图3-1从弹性地基梁中取出微段,根据平衡条件∑y =0,得 (dQ Q +)-Q +dx x q )(-dx σ=0 化简后变为)(x q dx dQ-=σ (3-2) 再根据∑M =0,得M -(M +dM )+(dQ Q +)dx +2)(2)()(22dx dx x q σ-=0 整理并略去二阶微量,则得dx dM Q =(3-3) 由式(3-2)和式(3-3),知)(22x q dx Md dx dQ -==σ (3-4)若不计剪力对梁挠度的影响,则由材料力学中得dx dy =θdx d EJM θ-== 22dx y d EJ - (3-5)33dx y d EJ dx dM Q -== 将式(3-5)代人式(3-4),并应用式(3-1),则得)(44x q Ky dx yd EJ +-= (3-6) 令 α=44EJ K(3-7) 代入式(3-6),得)(444444x q K y dx y d αα=+ (3-8)式中α叫做梁的弹性标值。
式(3-8)就是弹性地基梁的挠度曲线微分方程。
为了便于计算,在上式中用变数x α代替变数x ,二者有如下的关系:)()()(x d dy dxx d x d dy dx dy αααα== (3-9) 将上式代入式(3-9),则得)(44)(44x q K y x d y d αα=+ (3-10)2. 挠度曲线微分方程的齐次解解的一般形式为:x x sh C x x sh C x x ch C x x ch C y ααααααααsin cos sin cos 4321+++= (3-11) 在上式中引用了2x x e e x sh ααα--=, 2xx e e x ch ααα-+=3.2按文克尔假定计算短梁1. 初参数和双曲线三角函数的引用图示一等截面基础梁,设左端有位移0y ,角变0θ、弯矩0M 和剪力0Q ,它们的正方向如图中所示。
