零状态响应与零输入响应
rl零状态响应和零输入响应

rl零状态响应和零输入响应RL零状态响应和零输入响应是控制系统中两个重要的概念,它们分别描述了系统在不同输入条件下的响应特性。
在介绍这两个概念之前,我们先来了解一下什么是零状态和零输入。
零状态指的是系统起始时刻的状态,也就是系统还没有受到任何输入时的状态。
零输入则是指系统在没有外部输入的情况下自身产生的响应。
零状态响应是指系统在初始时刻没有输入而产生的响应。
换句话说,系统的初始状态会对零状态响应产生影响。
在实际应用中,我们通常通过给系统一个初始条件来观察其零状态响应。
例如,一个电路系统,我们可以将它充电到一个初始电压,然后切断外部输入,观察电路在没有输入的情况下的响应。
系统的零状态响应与其初始状态和系统自身的特性有关。
通常来说,一个稳态系统的初始状态对其零状态响应影响较小,而非稳态系统的初始状态可能会产生较大的影响。
系统的初始状态对零状态响应的影响也与系统的稳定性和数字信号的特性有关。
零输入响应则是指系统在没有外部输入的情况下自身产生的响应。
这个响应是由系统自身的特性决定的,与初始状态无关。
通过观察系统的零输入响应,我们可以了解到系统自身的特性,比如它的自然频率、阻尼比等。
零输入响应在实际应用中广泛应用于信号处理、滤波器和控制系统中。
在语音信号的处理中,我们可以通过对一段没有语音的信号进行处理,得到系统的零输入响应,从而了解系统的特性,比如它的频率响应。
在控制系统中,我们经常遇到在没有外部控制信号的情况下,系统会产生一些自身变化的情况,这就是系统的零输入响应。
总结起来,RL零状态响应和零输入响应是控制系统中的两个重要概念。
零状态响应是指系统在初始时刻没有输入而产生的响应,它与系统的初始状态和稳定性有关;零输入响应是指系统在没有外部输入的情况下自身产生的响应,它与系统的特性有关,与初始状态无关。
了解这两个概念可以帮助我们更好地理解和设计控制系统。
§2.4 零输入响应和零状态响应

各种响应用初始值确定待定系数的区别: (2)各种响应用初始值确定待定系数的区别:
在经典法求全响应的待定系数时, 在经典法求全响应的待定系数时,用的是 状初始值。 0+状初始值。 在求系统零输入响应时,用的是0-状态初始值。 在求系统零输入响应时,用的是0 状态初始值。 在求系统零状态响应时, 状态初始值, 在求系统零状态响应时,用的是 0+ 状态初始值, 这时的零状态是指0 状态为零。 这时的零状态是指0-状态为零。
(4)0+状态的确定
已知0 状态求0 状态的值, 已知0-状态求0+状态的值,可用冲激函数匹 配法。见有关参考资料。 配法。见有关参考资料。 状态的值还可以用拉普拉斯变换中的初值 求0+状态的值还可以用拉普拉斯变换中的初值 定理求出 求出。 定理求出。
三.对系统线性的进一步认识
由常系数微分方程描述的系统在下述意义上是线性的, 由常系数微分方程描述的系统在下述意义上是线性的, 响应可分解为:零输入响应+零状态响应。 (1)响应可分解为:零输入响应+零状态响应。 零状态线性: 当起始状态为零时, (2) 零状态线性 : 当起始状态为零时 , 系统的零状态响 应对于各激励信号呈线性。 应对于各激励信号呈线性。 (3)零输入线性 当激励为零时, 零输入线性: (3)零输入线性:当激励为零时,系统的零输入响应对 于各起始状态呈线性
信号与系统
Signals and Systems
§时域分析双零法——
零输入响应+ 零输入响应+零状态响应
一.起始状态与激励源的等效转换
在一定条件下,激励源与起始状态之间可以等效转换。 在一定条件下,激励源与起始状态之间可以等效转换。 即可以将原始储能看作是激励源。 即可以将原始储能看作是激励源。
外加激励源 系统的完全响应 共同作用的结果 可以看作 起始状态等效激励源 零状态响应” 系统的完全响应 = 零输入响应 + “零状态响应 零状态响应 线性系统具有叠加性) (线性系统具有叠加性)
信号与系统实验-实验一 零状态输入零状态响应
三、实验原理
1、零输入响应与零状态响应: 零输入响应: 没有外加激励的作用, 只有起始状态 (起始时刻系统储能) 所产生的响应。 零状态响应:不考虑起始时刻系统储能的作用(起始状态等于零) 。 2、典型电路分析: 电路的响应一般可分解为零输入响应和零状态响应。首先考察一个实例:在下图中由 RC 组成一电路,电容两端有起始电压 Vc(0-),激励源为 e(t)。
四实验结果高频r900高频r902中频r900中频r902低频r900低频r902五思考题图211所示电路中根据实验提供的实验元件计算系统的零状态和零输入过程
实验一 零状态输入零状态响应
一、实验内容
1、观察零输入响应的过程。 2、观察零状态响应的过程。
二、实验器材
1、信号与系统实验箱一台(主板) 。2、系统时域与频域分析模块一块。 3、20MHz 示波器一台。
压值开始,以指数规律进行衰减。 第二项与起始储能无关, 只与输入激励有关, 被称为零状态响应。 在不同的输入信号下, 电路会表征出不同的响应。
四、实验结果
高频 r900 高频 r902
中频 r900
中频 r902
低频 r900
低频 r902
五、思考题 图 2-1-1 所示电路中,根据实验提供的实验元件,计算系统的零状态和零输入过程。 解答:
R + e (t) C _ + Vc(0-) Vc(t)
图 2-1-1 则系统响应-电容两端电压:
t
RC 电路
1 ( t ) 1 RC e e()de RC Vc (0)
上式中第一项称之为零输入响应, 与输入激励无关, 零输入响应 e
Vc (0) 是以初始电
零输入响应和零状态响应

计算方法
利用系统的传递函数和初始条 件进行计算。
通过求解常微分方程或差分方 程ห้องสมุดไป่ตู้找到系统的零输入响应。
在MATLAB/Simulink等仿真软 件中,可以通过设置系统的初 始状态来模拟零输入响应。
02 零状态响应
定义
零状态响应:是指在系统无输入 信号的情况下,系统对初始状态
产生的响应。
描述了系统在没有输入信号作用 时,其内部状态的变化情况。
零状态响应完全取决于系统本身 的特性,与输入信号无关。
产生原因
系统内部存在储能元件(如电容、电 感),当输入信号为零时,储能元件 的能量不会立即消失,而是会以某种 形式继续存在并产生响应。
系统参数(如电阻、电感、电容等) 发生变化,导致系统内部状态发生变 化,从而产生零状态响应。
计算方法
根据系统的传递函数 和初始状态进行计算。
针对复杂系统和多尺度问题,发展基于零输入响应和零状态响应的跨学科 解决方案,促进各领域之间的交流与合作。
探索零输入响应和零状态响应在可持续发展、环境保护、公共安全等领域 的潜在应用价值,为社会发展和人类福祉做出贡献。
技术创新
开发高效、稳定的零输入响应和零状态响应算 法,提高计算效率和精度,降低计算成本。
零状态响应
零状态响应描述的是系统在外部输入作用下的输出变化。通过研究零状态响应, 可以了解系统对不同类型输入的响应特性,进而设计出更好的控制系统。
系统建模与仿真
零输入响应
在系统建模与仿真中,零输入响应用 于描述系统的内部动态特性。通过分 析零输入响应,可以深入了解系统的 内部工作原理和稳定性。
零状态响应
零状态响应用于描述系统对外部输入 的响应特性。通过研究零状态响应, 可以预测系统在不同输入条件下的行 为表现,有助于优化系统的设计和控 制。
零输入响应和零状态响应

齐次解
X
第 14
页
两种分解方式的区别:
1、 自由响应与零输入响应的系数各不相同
c c 与 i
xi 不相同
c i 由初始状态和激励共同确定
c xi 由初始状态确定
2、 自由响应包含了零输入响应和零状态响应中的齐次解
对于系统响应还有一种分解方式,即瞬态响应和稳态响应。所谓瞬态响应指
t 时,响应趋于零的那部分响应分量;而稳态响应指 t
(Cte-t
)
3
d dt
(Cte-t
)
2(Cte-t
)
e-t
特解 yp (t) t et
零状态响应: yzs (t) C1et C2e2t t et
由起始状态导出初始条件
y(0 ) 0 y '(0 ) 0
y(0 ) 0 y '(0 ) 0
y(0 ) C1 y '(0 ) C1
r1(t) rzi (t) rzs (t) 2e3t sin(2t) u(t)
r2 (t) rzi (t) 2rzs (t) [e3t 2sin(2t)]u(t)
X
四.对系统线性的进一步认识
第 17
页
解得 rzi (t) 3e3tu(t) rzs (t) [e3t sin(2t)]u(t)
零输入响应: 没有外加激励信号的作用,只由起始状态(起始时刻系 统储能)所产生的响应。
零状态响应: 不考虑原始时刻系统储能的作用(起始状态等于 零),由系统的外加激励信号产生的响应。
X
二.起始状态与激励源的等效转换
第 4
页
在一定条件下,激励源与起始状态之间可以等效转换。 即可以将原始储能看作是激励源。
拉氏变换求零输入响应和零状态响应

拉氏变换求零输入响应和零状态响应拉氏变换可以将微分方程转化为代数方程,从而求得系统的零输入响应和零状态响应。
1. 零输入响应当外部输入为零时,系统的响应完全由初始条件所决定,这种响应称为零输入响应。
设系统的微分方程为:y^{(n)}(t)+a_{n-1}y^{(n-1)}(t)+\cdots+a_1y'(t)+a_0y(t)=0初始条件为:y(0)=y_0,y'(0)=y_1,\cdots,y^{(n-1)}(0)=y_{n-1}对系统的微分方程两边进行拉氏变换,得到:Y(s)[s^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0]=y^{(n-1)}(0)s^{n-1}+\cdots +y_1s+y_0由于外部输入为零,拉氏变换得到的Y(s) 就是系统的零输入响应Y_i(s),即:Y_i(s)=\frac{y^{(n-1)}(0)s^{n-1}+\cdots+y_1s+y_0}{s^n+a_{n-1}s^{n-1}+ \cdots+a_1s+a_0}将Y_i(s) 进行部分分式分解,并利用拉氏反变换求出系统的时域响应y_i(t),即为系统的零输入响应。
2. 零状态响应当初始条件为零,外部输入不为零时,系统的响应称为零状态响应。
设系统的微分方程为:y^{(n)}(t)+a_{n-1}y^{(n-1)}(t)+\cdots+a_1y'(t)+a_0y(t)=b_mu^{(m)}(t)+\cdots+b_1u'(t)+b_0u(t)其中,u(t) 是外部输入,m 是n 的最大值。
对系统的微分方程两边进行拉氏变换,得到:Y(s)[s^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0]=U(s)[b_ms^m+\cdots+b_1s +b_0]由于初始条件为零,拉氏变换得到的Y(s) 就是系统的零状态响应Y_s(s),即:Y_s(s)=\frac{U(s)[b_ms^m+\cdots+b_1s+b_0]}{s^n+a_{n-1}s^{n-1}+\cd ots+a_1s+a_0}将Y_s(s) 进行部分分式分解,并利用拉氏反变换求出系统的时域响应y_s(t),即为系统的零状态响应。
零输入响应与零状态响应

零输入响应与零状态响应一、零输入响应1定义在没有外加激励时,仅有t = 0时刻的非零初始状态引起的响应。
取决于初始状态和电路特性,这种响应随时间按指数规律衰减。
2简介系统的零输入响应完全由系统本身的特性所决定,与系统的激励无关。
当系统是线性的,它的特性可以用线性微分方程表示时,零输入响应的形式是若干个指数函数之和。
指数函数的个数等于微分方程的阶数,也就是系统内部所含"独立"储能元件的个数。
假定系统的内部不含有电源,那么这种系统就被称为"无源系统"。
实际存在的无源系统的零输入响应随着时间的推移而逐渐地衰减为零。
零输入响应是系统微分方程齐次解的一部分。
3起始状态所谓的起始状态,是反映一个系统在初始观察时刻的储能状态。
以电系统为例,我们做如下约定:在研究t=0以后的响应时,把t=0(-)时的值uc(0-)和il(0-)等称为起始状态,而把t=0+时的值uc(0+)和il(0+)以及它们的各阶导数称为初始值或初始条件。
二、零状态响应1定义在动态电路中,动态元件的初始储能为零(即零初始状态)下,仅有电路的输入(激励)所引起的响应。
三、两种响应的区别零状态响应:0时刻以前响应为0(即初始状态为0),系统响应取决于从0时刻开始加入的信号f(t);零输入响应:从0时刻开始就没有信号输入(或说输入信号为0),响应取决于0时刻以前的初始储能。
四、两种响应的判断方法如果有电源激励就是,而元件本身没有电压或电流就是零状态,相反没有电源激励只有元件本身初始值电压电流,就是零输入响应。
五、两种响应的求解方法1零输入响应:就是没有外加激励,由初始储能产生的响应,它是齐次解的一部分;2零状态响应:就是初始状态为零,外加激励产生的响应。
它可以通过卷积积分来求解。
零状态响应等于单位样值相应和激励的卷积。
其中,单位样值相应就是系统函数的反拉式变换或z变换。
六、两种响应之间的联系引起电路响应的因素有两个方面,一是电路的激励,而是动态元件储存的初始能量。
零输入响应与零状态响应

零输⼊响应与零状态响应1.零输⼊响应与零状态响应在Matlab中,lsim函数还可以对带有⾮零起始状态的LTI系统进⾏仿真,使⽤⽅法为y=lsim(sys,u,t,x0),其中sys表⽰LTI系统,⽮量u和t分别表⽰激励信号的抽样值和抽样时间,⽮量x0表⽰该系统的初始状态,返回值y是系统响应值。
如果只有起始状态⽽没有激励信号,或者令激励信号为0,则得到零输⼊响应。
如果既有初始状态也有激励信号,则得到完全响应。
请注意lsim函数只能对⽤状态⽅程描述的LTI系统仿真⾮零起始状态响应,函数ss(对传递函数描述的LTI系统将失效,函数tf)。
例2.5 给定如图所⽰电路,t<0时S处于1的位置⽽且已经达到稳态,将其看做起始状态,当t=0时,S由1转向2.分别求t>0时i(t)的零状态响应和零输⼊响应。
图2.1 例2.4 电路图解:由所⽰电路写出回路⽅程和结点⽅程分别得到状态⽅程和输出⽅程:下⾯将⽤两种⽅法计算完全响应。
第⼀种⽅法:⾸先仿真2V电压e作⽤⾜够长时间(10s)后系统进⼊稳态,从⽽得到稳态值x0,再以该值作为初始值仿真4V电压e作⽤下的输出rf,即是系统的完全响应,为充分掌握lsim函数的使⽤⽅法,还仿真了系统的零状态响应rzs和零输⼊响应rzi。
第⼆种⽅法:构造⼀个激励信号,先保持2V⾜够长时间再跳变为4V,然后即可以零初始状态⼀次仿真得到系统的完全响应r1。
对应程序如下:C=1;L=1/4;R1=1;R2=3/2;A=[-1/R1/C,-1/C;1/L,-R2/L];B=[1/R1/C;0];C=[-1/R1,0];D=[1/R1];sys=ss(A,B,C,D); %建⽴LTI 系统systn=[-10:0.01:-0.01]'; %⽣成-10s 到-0.01s 的抽样时间,间隔为0.01sen=2*(tn<0); %⽣成机理信号的抽样值e(t)=2[rn tn xn]=lsim(sys,en,tn); %仿真t<0时的输出信号x0=xn(length(en),:); %x0记录了初始状态的值t=[0:0.01:10]';e=4*(t>=0); %⽣成激励信号的抽样值e(t)=4ezi=0*(t>=0); %⽣成零输⼊信号的抽样值e(t)=0rzs=lsim(sys,e,t); %仿真零状态响应rzi=lsim(sys,ezi,t,x0); %仿真零输⼊响应rf=lsim(sys,e,t,x0); %仿真完全响应r1=lsim(sys,[en;e],[tn;t]); %⽤另⼀种⽅法仿真完全响应2. 冲激响应与阶跃响应如果分别⽤冲激信号和阶跃信号作激励,lsim 函数可仿真出冲激响应和阶跃响应。
零状态响应与零输入响应

零状态响应的求解-卷积法
系统的零状态响应为 yzs(t) f (t) fT (t)
LTI系统的零状态响应是系统的特征函数和强迫函数的卷积
f (t) b f (m) (t) b f (m1) (t) L b f '(t) b f (t)
m
m1
1
0
f (t) e1t (t) e2t(t) L ent(t) T
zi
1
2
y '(t) [(c c ) cost (c c )sin t]et
zi
21
21
根据起始条件: y(0 ) 1, y(0 ) 2
解得:
c1 1 c2 3
最后得到:
t
yzi (t) e (cost 3sin t),t 0
例3 已知系统微分方程相应的齐次方程为:y''(t) 2y'(t) y(t) 0
m
m1
1
0
强迫函数是方程右端输入信号及其各阶导数的组合
零状态响应的求解-卷积法
回顾一阶系统的微分方程
yzs(t) ayzs (t) f(t)
y (t)eat ay (t)eat eat f (t)
zs
zs
d dt
[
yzs
(t)eat
]
eat
f (t)
yzs(t)eat
t 0
t 0
ea
f (
r (3) 若这些特征根中含有 重根,设 1 2 L r
yzi (t) [(c1 c2t L
crt r1)e1t
c ert1 r 1
L
cnent ],t 0
例1 已知系统微分方程应的齐次方程为 y''(t) 4y'(t) 3y(t) 0 :
零状态响应和零输入响应公式

零状态响应和零输入响应公式
零状态响应和零输入响应是线性时不变系统中重要的概念。
零状态响应是指系统在没有输入信号时的响应,也可以称为自由响应。
零输入响应是指系统在有输入信号时,当输入信号为零时的响应,也可以称为强制响应。
这两种响应都可以用公式来表示。
下面介绍它们的具体公式。
零状态响应公式:
设系统的初始状态为x(0),系统的零状态响应为y_z(t),系统的传递函数为H(s),则系统的零状态响应可以用下面的公式表示: y_z(t) = L^{-1}[H(s)X(s)] + x(0)
其中,L^{-1}表示拉普拉斯变换的反变换,X(s)表示输入信号的拉普拉斯变换。
零输入响应公式:
设系统的输入信号为x(t),系统的零输入响应为y_h(t),系统的冲击响应为h(t),则系统的零输入响应可以用下面的公式表示: y_h(t) = h(t) * x(t)
其中,*表示卷积运算。
总响应公式:
系统的总响应可以表示为零状态响应与零输入响应之和:
y(t) = y_z(t) + y_h(t)
这里需要注意的是,当系统的输入信号为零时,总响应就等于零状态响应。
当系统的初始状态为零时,总响应就等于零输入响应。
因
此,知道了零状态响应和零输入响应公式,就能够求出系统的总响应。
零输入响应和零状态响应PPT课件

第 9 页
iL (0 ) 为零决定的初始值求出待定系数。
n d k y zs (t ) m d k x (t ) ak bk k k dt dt k 0 k 0 系统方程: k d 起始条件: y zx (0 ) 0, k 0,1,2, , n dt k
X
电容器的等效电路
iC ( t ) C
第 5 页
v C (t )
v C ( 0 ) 0, t 0
电路等效为起始状态为零的电容与电压源 vC (0 )ut 的 串联 vC(0 )
iC ( t ) C
vC ( t )
等效电路中的 电容器的起始 状态为零
X
电感的等效电路
零输入响应: 始时刻系
统储能)所产生的响应。 零状态响应: 不考虑原始时刻系统储能的作用(起始状态等于 零),由系统的外加激励信号产生的响应。
X
二.起始状态与激励源的等效转换
第 4 页
在一定条件下,激励源与起始状态之间可以等效转换。 即可以将原始储能看作是激励源。
电容的等效电路 电感的等效电路
外加激励源 系统的完全响应 可以看作 系统的完全响应 = 共同作用的结果 起始状态等效激励源 零输入响应 + 零状态响应 ( 线性系统具有叠加性)
所以:
yzs (t ) et e2t t et
X
三.求解
求解非齐次微分方程是比较烦琐的工作,所以引出卷积积分法。
第 13 页
(t )
e(t )
线性时不变系统
h(t )
h(t )
r (t )
系统的零状态响应=激励与系统冲激响应的卷积,即
零输入响应与零状态响应

零输入响应与零状态响应一、零输入响应1定义在没有外加激励时,仅有t = 0时刻的非零初始状态引起的响应。
取决于初始状态和电路特性,这种响应随时间按指数规律衰减。
2简介系统的零输入响应完全由系统本身的特性所决定,与系统的激励无关。
当系统是线性的,它的特性可以用线性微分方程表示时,零输入响应的形式是若干个指数函数之和。
指数函数的个数等于微分方程的阶数,也就是系统内部所含"独立"储能元件的个数。
假定系统的内部不含有电源,那么这种系统就被称为"无源系统"。
实际存在的无源系统的零输入响应随着时间的推移而逐渐地衰减为零。
零输入响应是系统微分方程齐次解的一部分。
3起始状态所谓的起始状态,是反映一个系统在初始观察时刻的储能状态。
以电系统为例,我们做如下约定:在研究t=0以后的响应时,把t=0(-)时的值uc(0-)和il(0-)等称为起始状态,而把t=0+时的值uc(0+)和il(0+)以及它们的各阶导数称为初始值或初始条件。
二、零状态响应1定义在动态电路中,动态元件的初始储能为零(即零初始状态)下,仅有电路的输入(激励)所引起的响应。
三、两种响应的区别零状态响应:0时刻以前响应为0(即初始状态为0),系统响应取决于从0时刻开始加入的信号f(t);零输入响应:从0时刻开始就没有信号输入(或说输入信号为0),响应取决于0时刻以前的初始储能。
四、两种响应的判断方法如果有电源激励就是,而元件本身没有电压或电流就是零状态,相反没有电源激励只有元件本身初始值电压电流,就是零输入响应。
五、两种响应的求解方法1零输入响应:就是没有外加激励,由初始储能产生的响应,它是齐次解的一部分;2零状态响应:就是初始状态为零,外加激励产生的响应。
它可以通过卷积积分来求解。
零状态响应等于单位样值相应和激励的卷积。
其中,单位样值相应就是系统函数的反拉式变换或z变换。
六、两种响应之间的联系引起电路响应的因素有两个方面,一是电路的激励,而是动态元件储存的初始能量。
《信号与系统教学课件》§2.3零输入响应与零状态响应

下章预告
THANKS
感谢您的观看。
《信号与系统教学课件》
目录
引言 零输入响应 零状态响应 零输入响应与零状态响应的比较 总结
01
CHAPTER
引言
01
02
课程背景
随着信息技术的发展,信号与系统在现实生活和工程应用中的重要性日益凸显。
信号与系统是通信、电子、控制等领域的重要基础课程,为后续专业课程提供必要的知识储备。
零输入响应与零状态响应的定义
信号的运算与变换
信号的运算包括加减、乘除、翻转等基本运算,信号的变换包括傅里叶变换、拉普拉斯变换和Z变换等。这些运算和变换对于信号的分析和处理具有重要意义。
系统的稳定性分析
系统的稳定性是系统的重要特性之一,对于系统的分析和设计具有重要意义。稳定性分析的方法包括代数方法和几何方法,其中几何方法又包括极坐标和波德图等。
零输入响应
体现输入信号对系统的作用效果,是系统对输入信号的响应。
零状态响应
在系统中的作用
用于分析系统内部储能元件的动态特性,如电路中的电感、电容等。
用于分析系统对特定输入信号的响应,如控制系统中的输入信号对输出信号的影响等。
在实际应用中的选择
零状态响应
零输入响应
05
CHAPTER
总结
信号与系统的基本概念
线性时不变系统是信号与系统中最为常见的一类系统,其分析方法包括时域分析和频域分析。时域分析主要通过差分方程和卷积运算进行,频域分析主要通过傅里叶变换进行。
信号的分类与表示方法
信号可以根据不同的特性进行分类,如连续信号和离散信号、确定性信号和随机信号等。信号的表示方法包括时域表示法和频域表示法。
本章重点回顾
零输入响应与零状态响应的比较
零输入响应和零状态响应公式

零输入响应和零状态响应公式在我们学习电路知识的过程中,零输入响应和零状态响应公式可是相当重要的一部分呢。
先来说说零输入响应,它就像是一个独自表演的“演员”,在没有外部激励的情况下,依靠自身的“内力”来展现变化。
比如说一个电容在充电完成后,断开电源,这时候电容开始放电的过程就是零输入响应。
它的公式就像是一个魔法咒语,能帮助我们准确地算出这个过程中的电压或电流变化。
零状态响应呢,则像是一个受到外界刺激后做出反应的“小伙伴”。
当电路在初始状态为零的情况下,加上外部激励,然后产生的响应就是零状态响应。
就好比一个空荡荡的水桶,开始往里注水,这个注水的过程和水量的变化就可以用零状态响应公式来描述。
我记得之前给学生们讲这部分内容的时候,有个学生特别可爱。
他总是把零输入响应和零状态响应搞混,每次做题都是错得五花八门。
有一次,我给他举了个特别有趣的例子。
我跟他说:“你想象一下,零输入响应就像是你兜里原本就有的零花钱,没有爸妈再给你新的,你就靠这点钱花,它会越来越少。
而零状态响应呢,就像是爸妈突然给了你一大笔零花钱,这是新给的,然后你拿着这笔钱去买东西,这就是从零开始的变化。
”这孩子听完,眼睛一下子亮了起来,后来再做相关的题目,错误明显少了很多。
在实际的电路分析中,理解和运用这两个响应公式能让我们轻松解决很多问题。
比如说,在设计一个电源滤波电路的时候,我们要考虑电容的放电过程,这时候零输入响应公式就能派上用场,帮助我们算出电容电压下降的速度,从而选择合适的电容值来保证滤波效果。
再比如,当我们设计一个放大器电路时,要知道输入信号作用下的输出响应,这时候零状态响应公式就能帮助我们计算出输出信号的大小和变化规律,确保放大器能够正常工作,达到我们想要的效果。
总之,零输入响应和零状态响应公式虽然看起来有点复杂,但只要我们用心去理解,多结合实际的例子去思考,就一定能掌握它们的奥秘,让电路知识变得不再那么可怕,反而充满乐趣。
相信大家在学习的过程中,也能像那个可爱的学生一样,一旦找到窍门,就能轻松应对啦!。
信号与系统 零输入响应和零状态响应

中的各项系数 Ci
而作为工程技术问题,一般激励都是从时刻 t 0 加入,系统的响应时
间范围是 0 t ,则系统的初始条件要根据系统的原始内部储能和激
励接入瞬时的情况来确定。
如具体电路系统,根据如下条件从 起始条件求初始条件
uC (0 ) uC (0 ) iL (0 ) iL (0 )
根据微分方程经典解法易求得零状态响应中的特解为常数6
uzs (t) uzs_h (t) uzs_ p (t) Czs1et Czs2tet 6 (t 0)
信号与系统
零状态响应
零状态响应 uzs (t) Czs1et Czs2tet 6 (t 0)
其中,待定系数
C zs1
C 和
得根据初始条件
3e3tu(t) [e3(tt0 ) sin(2t 2t0 )]u(t t0 ) r4 (t) 2rzi (t) 0.5rzs (t)
2 3e3tu(t) 0.5 e3t sin(2t) u(t) 5.5e3t 0.5sin(2t) u(t)
信号与系统
作业(13-4-02)
1H uC (t) 2
u(t)
uC (0 ) uC (0 ) 10V
iL (0 ) iL (0 ) 5A
信号与系统
零输入响应
S1 2 2
iL (t)
3A
1
1 S2 1F 10V
1H uC (t) 2
u(t)
t 0 零输入等效电路
列写电路的微分方程为:
d2 dt
uzi
(t)
uzs (t) Czs1et Czs2tet 6 (t 0)
解得: u(t) uzi (t) uzs (t) (4et 4tet 6)u(t)
零输入响应和零状态响应

零输入响应和零状态响应
线性非时变系统的完全响应也可分解为零输 入响应和零状态响应。在激励信号加入系统之 前,系统原有的储能(如电容上的初始电压, 电感上的初始电流等)构成了系统的初始状态。
1.1 零输入响应的求取
1.2 零状态响应的求取
其中零状态响应的完全解的系数应在零状 态响应的全解中由初始条件
即
。因此,零状态响应的特解、齐次
解和完全解分别为
将零状态响应的初始条件 解得
代入上式
因此,此系统的零状态响应为 (3)求系统的完全响应。
其中,
信号与系统
确定。
1.3 系统的完全响应
系统的完全响应按性质可分为自由响应和 强迫响应,按来源可分为零输入响应和零状态 响应,它们的关系为
式中,
。
例1.1 已知某系统的微分方程模型为
初始条件
,输入
系统的零输入响应 ,零状态响应
全响应 。
解:(1)求零输入响应 。
由特征方程
,求 以及完
得单根
,因此零输入响应为
实验一 零输入响应零状态响应
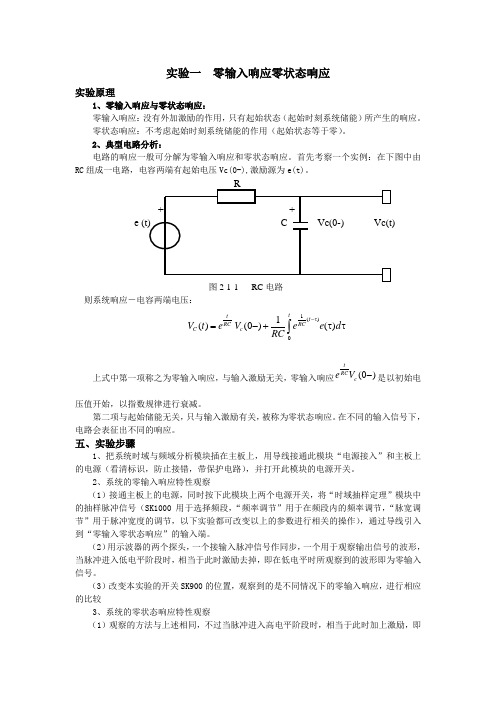
实验一 零输入响应零状态响应实验原理1、零输入响应与零状态响应: 零输入响应:没有外加激励的作用,只有起始状态(起始时刻系统储能)所产生的响应。
零状态响应:不考虑起始时刻系统储能的作用(起始状态等于零)。
2、典型电路分析:电路的响应一般可分解为零输入响应和零状态响应。
首先考察一个实例:在下图中由RC 组成一电路,电容两端有起始电压Vc(0-),激励源为e(t)。
图2-1-1 RC 电路则系统响应-电容两端电压:1()01()(0)()ttt RCRCC c V t eV e e d RC -τ=-+ττ⎰ 上式中第一项称之为零输入响应,与输入激励无关,零输入响应(0)t RCc e V -是以初始电压值开始,以指数规律进行衰减。
第二项与起始储能无关,只与输入激励有关,被称为零状态响应。
在不同的输入信号下,电路会表征出不同的响应。
五、实验步骤1、把系统时域与频域分析模块插在主板上,用导线接通此模块“电源接入”和主板上的电源(看清标识,防止接错,带保护电路),并打开此模块的电源开关。
2、系统的零输入响应特性观察(1)接通主板上的电源,同时按下此模块上两个电源开关,将“时域抽样定理”模块中的抽样脉冲信号(SK1000用于选择频段,“频率调节”用于在频段内的频率调节,“脉宽调节”用于脉冲宽度的调节,以下实验都可改变以上的参数进行相关的操作),通过导线引入到“零输入零状态响应”的输入端。
(2)用示波器的两个探头,一个接输入脉冲信号作同步,一个用于观察输出信号的波形,当脉冲进入低电平阶段时,相当于此时激励去掉,即在低电平时所观察到的波形即为零输入信号。
(3)改变本实验的开关SK900的位置,观察到的是不同情况下的零输入响应,进行相应的比较3、系统的零状态响应特性观察(1)观察的方法与上述相同,不过当脉冲进入高电平阶段时,相当于此时加上激励,即此时零状态响应应在脉冲的高电平进行。
(2)改变本实验的开关SK900的位置,观察到的是不同系统下的零输入响应,进行相应的比较。
《信号与系统教学课件》§2.3零输入响应与零状态响应

卷积法
利用输入信号和系统的冲击响 应求得它的零状态响应。
设置初态与给予输入 如何计算完整响应
设置初态
将系统的初始状态先设置,再给予 一个输入信号,求出此条件下的输 出结果。
给予输入
将一部分的初始状态和输入信号叠 加在一起,求出此条件下的输出结 果。
其他相关概念和扩展阅读
拉普拉斯变换
拉普拉斯变换是一种非常重要的 数学工具,它可以将时域函数转 化为复平面上的解析函数,从而 方便地分析系统的稳定性、因果 性、纵向稳定性等问题。
傅里叶变换
傅里叶变换是一种重要的信号处 理工具,它将连续时间域的信号 转换为连续频率域信号,方便对 信号特性的分析。
差分方程
差分方程是离散时间系统中的一 种描写方式,用于求解从各种输 入得到的输出响应,是离散信号 处理领域的基本工具之一。
总结和要点
1 理解零状态响应和零输入响应的区别 3 了解如何计算系统的完整响应
2 掌握零状态响应和零输入响应的计算方
法
4 了解实际问题中零状态响应和零输入响
应的应用
零输入响应的计算方法
1
寻找系统的零输入响应
将系统输入为0,求出此条件下的输出。
2
插值法
由于信号的初始状态对零输入响应有影响,需要对初始状态进行插值,再求出相 应的零输入响应结果。
3
卷积法
利用被激励系统的冲击响应求得它的零输入响应。
零状态响应的计算方法
寻找系统的零状态响应
将系统初始状态设定为0,求出 对于任意输入条件下的输出。
深入探究《信号与系统教 学课件》§2.3
了解零输入响应与零状态响应的定义、区别以及应用场景。
零输入响应与零状态响应的区别
零输入响应和零状态响应分析

c xi e
i 1
i t
c fi e
i 1
n
i t
自由响应
零输入响应
零状态响应的 齐次解
X
第 14 页
两种分解方式的区别: 1、 自由响应与零输入响应的系数各不相同
X
各种系统响应定义
自由响应: 强迫响应: 暂态响应: 也称固有响应,由系统本身特性决定,与外加激励形 式无关。对应于齐次解。 形式取决于外加激励。对应于特解。 是指激励信号接入一段时间内,完全响应中暂时出现的 有关成分,随着时间t 增加,它将消失。
第 3 页
稳态响应: 由完全响应中减去暂态响应分量即得稳态响应分量。 零输入响应: 没有外加激励信号的作用,只由起始状态(起始时刻系 统储能)所产生的响应。 零状态响应: 不考虑原始时刻系统储能的作用(起始状态等于 零),由系统的外加激励信号产生的响应。
系统方程:
n d k y zi (t ) ak 0 k dt k 0 k d 起始条件: y zi (0 ) c , k 0,1,2, , n k dt k
解的形式:
yzi (t ) Ci ei t
i 1
n
由起始条件求待定系数。 X
三.求解
n d k y zs (t ) m d k x (t ) ak bk k k dt dt 系统方程: k 0 k 0 k d 起始条件: y zx (0 ) 0, k 0,1,2, , n dt k
解的形式:齐次解+特解
y (t ) Ci ei t y p (t )
i 1
n
由初始条件求待定系数。
X
三.求解
例2: 求系统的零状态响应
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统
第8讲
零输入响应和零状态响应
零输入响应和零状态响应的定义 ⏹
从引起系统响应的根源出发,将系统全响应分为零输入响应和零状态响应,即 ⏹
零输入响应是指没有外加激励信号(零输入),仅由系统内部初始储能(电容储有电场能、电感储有磁场能)引起的响应; ⏹零状态响应是指系统内部储能为零(零状态),仅由系统的外部的激励引起的响应。
)()()(t y t y t y zs zi +=
零输入响应的求解
设n 个特征根为 ()(1)(2)1210()()()'()()0n n n n n y t a y t a y t a y t a y t ----+++++=L 00111=++++--a a a n n n λλλΛ其特征方程为 12.n
λλλL 零输入下,系统的微分方程为 系统的零输入响应与微分方程的齐次解相同 以下分三种情况讨论
零输入响应的求解
(2)若存在共轭复根,如 1,2j λαβ=±3123()(cos sin ),0n t t t zi n y t c t c t e c e c e t λλαββ=++++≥L (3) 若这些特征根中含有
重根,设 r 12r λλλ===L 111121()[()],0
n r t t t r zi r r n y t c c t c t e c e c e t λλλ+-+=++++++≥L L 1212(),0
n t t t zi n y t c e c e c e t λλλ=+++≥L (1)若这些特征根都是单根,则
由起始状态值确定待定系数
【解】 特征方程为 其特征根为 λ1 = -1, λ 2= -3
零输入响应为: (0)1,(0)2
y y --'==得到:
最后得到: 根据起始条件: 例1 已知系统微分方程应的齐次方程为: (0)1,(0)2y y --'==,求系统零输入响应。
)(3)('4)(''=++t y t y t y 0
342=++λλ312()t t
zi y t c e c e --=+312'()3t t
zi y t c e c e --=--121=+c c 2321=--c c 251=c 2
32-=c 353()(),022t t zi y t e e t --=-≥
例2 已知系统微分方程相应的齐次方程为:
(0)1,(0)2y y --'==,求系统零输入响应。
【解】
特征方程为 零输入响应为:
(0)1,(0)2
y y --'==解得:
最后得到: 根据起始条件: 0)(2)('2)(''=++t y t y t y 0222=++λλj ±-=12,1λ12()(cos sin )t zi y t e c t c t -=+2121'()[()cos ()sin ]t
zi y t c c t c c t e -=--+其特征根为 11=c 32=c ()(cos 3sin ),0
t zi y t e t t t -=+≥
例3 已知系统微分方程相应的齐次方程为:
(0)1,(0)2y y --'==,求系统零输入响应。
【解】 特征方程为
其特征根为
零输入响应为:
(0)1,(0)2y y --'==得到: 最后得到: 根据起始条件:
0)()('2)(''=++t y t y t y 0122=++λλ121λλ==-12()(+)t zi y t c c t e -=212'()()t zi y t c c c t e -=--11=c 32=c ()(13),0
t zi y t t e t -=+≥
零状态响应的求解-卷积法 零状态情况下,系统的微分方程的形式为 强迫函数:
()(1)(2)12
10()()()'()()()n n n n n y t a y t a y t a y t a y t f t ----∑+++++=L ()(1)110()()()'()()m m m m f t b f t b f t b f t b f t -∑-=++++L 强迫函数是方程右端输入信号及其各阶导数的组合
回顾一阶系统的微分方程
()()()
zs zs y t ay t f t ∑'+=()()()
at at at zs zs y t e ay t e e f t ∑'+=d [()]()d at at zs y t e e f t t
∑=0()()0t at
a zs t y t e e f d τττ-∑-=⎰零状态响应的求解-卷积法
()()()zs T y t f t f t ∑=*0()(0)()t
at
a zs zs y t e y e f d τττ--∑-=⎰(0)0
y -=零状态响应的求解-卷积法
()0()()()*()t
a t at zs y t e f d e t f τττετ----∑∑==⎰()()
at T f t e t ε-=一阶系统的特征函数
类似地,对于二阶系统,由其特征根可以导出二阶系统的特征函数
12121212121.21()() ()()()() 1sin () =t t t t t T t e e t f t e t e t te t e t t j λλλλλαελλλλεεελλλ
βελαββ⎧-≠⎪-⎪⎪=*===⎨⎪⎪±⎪⎩推而广之,设特征根为
,1,i i n λ=L 12()()()()
n t t t T f t e t e t e t λλλεεε=***L
零状态响应的求解-卷积法 n 阶LTI 系统的特征函数为
零状态响应的求解-卷积法 系统的零状态响应为
()()()
zs T y t f t f t ∑=*()(1)110()()()'()()
m m m m f t b f t b f t b f t b f t -∑-=++++L 12()()()()
n t t t T f t e t e t e t λλλεεε=***L LTI 系统的零状态响应是系统的特征函数和强迫函数的卷积
例4 某连续LTI 系统的系统方程为 )
(3)(')(2)('3)(''t f t f t y t y t y +=++求下面两种情况下的零状态响应:
(1)()()f t t ε=3(2)()()t f t e t ε-=解:系统的特征根为 11-=λ2
2-=λ 系统的特征函数为 22()()()()()
t t t t T f t e t e t e e t εεε----=*=-(1)系统的强迫函数为 )
(3)()(t t t f εδ+=∑零状态响应为 ()()()zs T y t f t f t ∑=*)]
(3)([)()(2t t t e e t t εδε+*-=--)()2
1223(2t e e t t ε--+-=零状态响应的求解-卷积法
例4 某连续LTI 系统的系统方程为 )
(3)(')(2)('3)(''t f t f t y t y t y +=++求下面两种情况下的零状态响应:
(1)()()f t t ε=3(2)()()t f t e t ε-=解:系统的特征根为 11-=λ2
2-=λ 系统的特征函数为 22()()()()()
t t t t T f t e t e t e e t εεε----=*=-(2)系统的强迫函数为 零状态响应为 ()()()
zs T y t f t f t ∑=*33()()3()3()()
t t f t t e t e t t δεεδ--∑
=-+=22()()()()()()
t t t t zs y t e e t t e e t εδε----=-*=-零状态响应的求解-卷积法
将LTI系统的响应分解为零输入响应和零状态响应,则可以对LTI系统的线性性质进一步有如下理解:
(1)响应的可分解性:系统的完全响应可分解为零输入响应和零状态响应;
(2)零输入线性:当外加激励信号为零时,系统的零输入响应对于各起始状态呈线性关系,称为零输入线性;
(3)零状态线性:当起始状态为零时,系统的零状态响应对于各个外加激励信号呈线性关系,称为零状态线性。
)(1t f ),()cos ()(1t t e t y t επ+=-)(1t f ),(cos 2)(2t t t y επ=)(1t f 3()y t 例5 .某LTI 系统起始状态不变,当激励为
时,响应为 当激励为2 时,响应为 求当激励为3 时的全响应 解:根据题意可得: ()()(cos )()()2()2cos ()
t zi zs zi zs y t y t e t t y t y t t t πεπε-⎧+=+⎨+=⎩解得: ()(cos )()
t zs y t t e t πε-=-()2()t zi y t e t ε-=根据零输入线性和零状态线性的性质,则
3()()3()(3cos )()
t zi zs y t y t y t t e t πε-=+=-
思考与练习 ⏹
1、何谓零输入响应,何谓零状态相应? ⏹
2、求系统的零输入响应与求解齐次微分方程有什么差别? ()2()2()dy t y t f t dt
+=()()f t t ε=21()1,03
t y t e t -=+≥(0)y -3、已知系统微分方程为 若 解得完全响应 则系统的起始状态 应该为( )。
