材料力学 杆件的变形计算
材料力学例题
0.75m 1m
A
D 1.5m
B
F
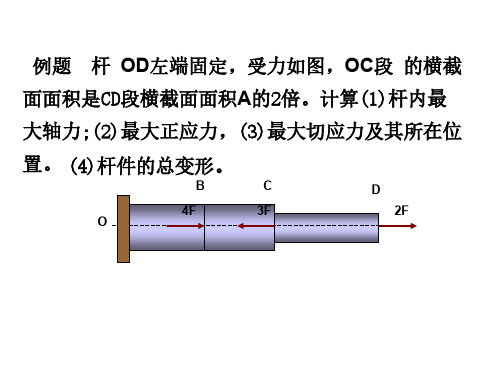
横梁BC为刚杆,自重Q=2KN,力P=10KN可在横 梁BC上自由移动。AB杆的许用应力为[σ]=100MP a,设计AB杆的横截面面积。如果AB杆采用直径 为10毫米的细丝,需要几根?
P C
30°
B
• [例] 长为 L=2m 的圆杆受均布力偶 m=20Nm/m 的作用,如图,若杆的内外径之比为 =0.8 ,
例题 空心圆杆AB和CD杆焊接成整体结构,受力如图.AB杆的外径 D=140mm,内外 径之比α= d/D=0.8,材料的许用应力[] = 160MPa。试用第三强度理论校核AB杆的 强度。 解:(1)外力分析 将力向AB杆的B截面形心简化得
10kN
0.8m A
B D
F 25kN
M e 15 1 . 4 10 0 . 6 15 kN m
G=80GPa ,许用剪应力 []=30MPa,试设计杆
的外径;若[]=2º /m ,试校核此杆的刚度,并
求右端面转角。
[例题] 某传动轴设计要求转速n = 500 r / min,输入功率P1 = 500 马力, 输出功率分别 P2 = 200马力及 P3 = 300马力,已 知:G=80GPa ,[ ]=70M Pa,[ ]=1º /m ,试确定: ①AB 段直径 d1和 BC 段直径 d2 ? ②若全轴选同一直径,应为多少? ③主动轮与从动轮如何安排,轴的受力合理? P2 A 500 B 400 P3 C
y Me A x B l/2 F1
F2
D F2 D M e C ( F1 F 2 ) 2 2 20 F2 kN 3 F 20kN
轴产生扭转和垂直纵向对称面内的平 面弯曲
材料力学-第三章扭转
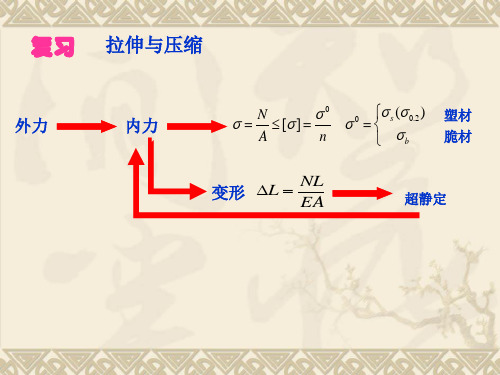
3、物理方程 mA a mA a AC 2GI p GI p
BC
2 mB a GI p
4 解得: m A 7 T 3 mB T 7
AB AC BC 0
例:由实心杆 1 和空心杆 2 组成的组合轴,受扭矩 T, 两者之间无相对滑动,求各点切应力。 T 解: 设实心杆和空心杆承担的扭矩分别为 G 2 Ip 2 M n 1 、 M n2 。 R2
二 刚度条件
M 180 刚度 n 0.50~1.0 / m 一般轴 l G Ip 条件
0.25~0.5 / m 精密轴
1.0 ~3.0 / m 粗糙轴
例 传动主轴设计,已知:n = 300r/m,P1 = 500kW,P2=200kW P3=300kW,G=80GPa [ ] 40MPa , [] 0.3 求:轴的直径d 解:1、外力分析
圆轴扭转的强度条件
max
Mn D Mn I p 2 Wp
Wp
2I p D
Mn
D 3 D 3 Wp 1 4 抗扭截面系数Wp : W p 16 16
强度条件:
Mn max Wp
例 已知汽车传动主轴D = 90 mm, d = 85 mm [ ] 60MPa, T = 1.5 kNm
Mn d
3
圆形优于矩形
Aa
= 0.208
3
a
3
4
3
d 0.886 d
2
Mn
a
2
Mn 0.208 0.886 d
b
6.913
工程材料力学第四章轴向拉压杆的变形

拉(压)杆的纵向变形 (轴向变形) 基本情况下(等直杆,两端受轴向力):
纵向总变形Δl = l1-l (反映绝对变形量)
l 纵向线应变 (反映变形程度) l
1
fl
f ( x x)
x
f
l
x
x
沿杆长均匀分布 的荷载集度为 f 轴力图
fx
微段的分离体
y
pbd 2b 0
pd 2
13
所以
pd (2 10 Pa)(0.2m) -3 2 2(510 m)
6
4010 Pa 40 MPa
6
14
2.
如果在计算变形时忽略内压力的影响,则可认为
薄壁圆环沿圆环切向的线应变e(周向应变)与径向截面上
的正应力s 的关系符合单轴应力状态下的胡克定律,即
ν
亦即
- n
低碳钢(Q235):n = 0.24~0.28。
7
思考:等直杆受力如图,已知杆的横截面面积A和材料的 弹性模量E。
1.列出各段杆的纵向总变形ΔlAB,ΔlBC,ΔlCD以及整个 杆纵向变形的表达式。
2.横截面B, C及端面D的纵向位移与各段杆的纵向总变
形是什么关系?
uB L1
22
作业:4-7,4-91 Pa ~ 2.101011 Pa 200GPa ~ 210GPa
l 1 FN 胡克定律的另一表达形式: l E A
E
←单轴应力状态下的胡克定律
6
横向变形因数(泊松比)(Poisson’s ratio)
单轴应力状态下,当应力不超过材料的比例极限时,
材料力学常用基本公式

面积A,拉应力为正)d,拉伸后试样直径 d1)纵向线应变和横向线应变外力偶P 功率, n 转速)弯矩、剪力和荷载集度之间的关系式轴向拉压杆横截面上正应力的计算公式杆件横截面轴力F N,横截面1.2.3.4.5.6.7.8.9.10.11.12.泊松比胡克定律受多个力作用的杆件纵向变形计算公式轴向拉压杆斜截面上的正应力与切应力计算公式夹角a 从x 轴正方向逆时针转至外法线的方位角为正)纵向变形和横向变形(拉伸前试样标距l ,拉伸后试样标距 l1 ;拉伸前试样直径承受轴向分布力或变截面的杆件,纵向变形计算公式轴向拉压杆的强度计算公式许用应力,脆性材料延伸率截面收缩率剪切胡克定律拉压弹性模量,塑性材料切变模量G,切应变gE、泊松比和切变模量圆截面对圆心的极惯性矩( a)实心圆b)空心圆)G之间关系式圆轴扭转时横截面上任一点切应力计算公式圆截面周边各点处最大切应力计算公式扭转截面系数,( a)实心圆扭矩T,所求点到圆心距离r )13.14.15.16.17.18.19.20.21.22.23.24.薄壁圆管(壁厚 δ≤ R 0 /10 ,R 0 为圆管的平均半径)扭转切应力计算公式圆轴扭转角 与扭矩 T 、杆长 l 、 扭转刚度 GH p 的关系式 同一材料制成的圆轴各段内的扭矩不同或各段的直径不同(如阶梯轴)时等直圆轴强度条件受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式平面应力状态下斜截面应力的一般公式b )空心圆25.26. 27. 28. 29. 30.31.32.33.或 塑性材料或 扭转圆轴的刚度条件 ? ;脆性材料平面应力状态的三个主应力 主平面方位的计算公式 ,面内最大切应力 三向应力状态最大切应力 广义胡克定律 四种强度理论的相当应力34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44.任意截面图形对一点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之 和的关系式平行移轴公式(形心轴 z c 与平行轴 z 1的距离为 a ,图形面积为 A )纯弯曲梁的正应力计算公式45. 46.47.48.49. 50.51.52.53.54., 组合图形的形心坐标计算公式 截面图形对轴 z 和轴y 的惯性半径 ?矩形、圆形、空心圆形的弯曲截面系数几种常见截面的最大弯曲切应力计算公式( 轴 z 的静矩, b 为横截面在中性轴处的宽度)为中性轴一侧的横截面对中性横力弯曲最大正应力计算公式工字形截面梁腹板上的弯曲切应力近似公式轧制工字钢梁最大弯曲切应力计算公式 圆形截面梁最大弯曲切应力发生在中性轴处弯曲正应力强度条件弯曲梁危险点上既有正应力 σ 又有切应力 τ 作用时的强度条件 或,梁的挠曲线近似微分方程 轴向荷载与横向均布荷载联合作用时杆件截面底部边缘和顶部边缘处的正应力计弯扭组合变形时圆截面杆按第三和第四强度理论建立的强度条件表达式55.56.57.58.59. 60.61.62.63.64.65. 66.算公式偏心拉伸(压缩) 圆环形薄壁截面梁最大弯曲切应力发生在中性轴处 几种常见截面梁的弯曲切应力强度条件梁的转角方程梁的挠曲线方程圆截面杆横截面上有两个弯矩 和 同时作用时,合成弯矩为圆截面杆横截面上有两个弯矩和同时作用时强度计算公式弯拉扭或弯压扭组合作用时强度计算公式剪切实用计算的强度条件挤压实用计算的强度条件 等截面细长压杆在四种杆端约束情况下的临界力计算公式 压杆的约束条件:( a )两端铰支 μ =l( b )一端固定、一端自由 μ =2( c )一端固定、一端铰支d )两端固定 μ =0.567.68.69.70.71.72.73. 74. 75. 76. 77.μ=0.778.压杆的长细比或柔度计算公式79.细长压杆临界应力的欧拉公式80.欧拉公式的适用范围81.压杆稳定性计算的安全系数法82.压杆稳定性计算的折减系数法83. 关系需查表求得3截面的几何参数4应力和应变5应力状态分析6内力和内力图7强度计算刚度校核9 压杆稳定性校核10 动荷载11 能量法和简单超静定问题材料力学公式汇总、应力与强度条件1、拉压maxmax2、剪切max3、4、挤压挤压圆轴扭转P挤压A挤压TWtmax平面弯曲①maxM maxy t maxI z*③ Q max S z max②t max5、斜弯曲max M z M yW z W yW z maxtmaxt maxmax注意:“5”与“ 6”两式仅供参考 ②第四强度理论r4w 2 3 n 2M w 20.75M n 2r4 w 3 n WWz二、变形及刚度条件1拉压LNLNLN i L iN ( x) dxEA EA LEA2扭转TLT i L i T x dx T 180 0( /GI pGI pGI pL GI p3弯曲(1) 积分法 : EIy ''( x) M(x) E Iy '(x) EI (x) M(x)dx CEIy ( x) [ M (x)dx]dx Cx D(2)叠加法 : f P 1,P 2 ⋯= f P 1 f P 2 +⋯, P 1, P 2 = P 1 P 2 ⋯M 2L =M i 2L i =M 2xdx2EI 2EI i 2EI(5)卡氏第二定理 ( 注:只给出线性弹性弯曲梁的公式 ) 三、应力状态与强度理论 1、 二向应力状态斜截面应力2、 二向应力状态极值正应力及所在截面方位角 3、 二向应力状态的极值剪应力注:极值正应力所在截面与极值剪应力所在截面夹角为 4504、 三向应力状态的主应力: 1 2 36、拉(压)弯组合 maxNM7、圆轴弯扭组合:①第三强度理论M w 2 M n2Wz(3)基本变形表 ( 注意:以下各公式均指绝对值,使用时要根据具体情 况赋予正负号 )ML3EI, A MLA6EIBA PL 216EI qL3 24EI (4)弹性变形能 ( 注:以下只给出弯曲构件的变形能 响, 其他变形与此相似 ,不予写出 ) 并忽略剪力影 B最大剪应力 : max1 325、二向应力状态的广义胡克定律(1)、表达形式之一(用应力表示应变) (2)、表达形式之二(用应变表示应力) 6、三向应力状态的广义胡克定律 强度理论 1) r1 1 1 bnb2)r 3 1 3五、动载荷(只给出冲击问题的有关公式)能量方程TVU7、 sn s8、平面应力状态下的应变分析sin 2x y x y1)2 2xys i n222tg2 0 xyxy四、压杆稳定1、临界压力与临界应力公式(若把直杆分为三类) ① 细长受压杆 p ② 中长受压杆 p ③ 短粗受压杆s2EI minPcr 2PcrL2cr a b“ cr ”2Ecr22、关于柔度的几个公式 或 b2Epasb3、惯性半径公式 i I Az短边长度 ))圆截面 i d4,矩形截面 i min b12(b 为2cos 2xyc o 2s2冲击系数 K d 1 1 2hst (自由落体冲击)K dgv0st(水平冲击)六、截面几何性质1、 惯性矩(以下只给出公式,不注明截面的形状) 442 d D 4 d132 DI P 2dA =2、惯性矩平移轴公式32。
杆件的轴向拉压变形及具体强度计算

根据强度条件,可以解决三类强度计算问题
1、强度校核:
max
FN A
2、设计截面:
A
FN
3、确定许可载荷: FN A
目录
拉压杆的强度条件
例题3-3
F
F=1000kN,b=25mm,h=90mm,α=200 。
〔σ〕=120MPa。试校核斜杆的强度。
解:1、研究节点A的平衡,计算轴力。
目录
——横截面上的应力
目录
FN
A
——横截面上的应力
该式为横截面上的正应力σ计 算公式。正应力σ和轴力FN同号。 即拉应力为正,压应力为负。
根据杆件变形的平面假设和材料均匀连续性假设 可推断:轴力在横截面上的分布是均匀的,且方向垂 直于横截面。所以,横截面的正应力σ计算公式为:
目录
• 拉(压)杆横截面上的应力
FN 2 45° B
F
FN1 28.3kN FN 2 20kN
2、计算各杆件的应力。
B
1
FN1 A1
28.3103 202 106
4
F
90106 Pa 90MPa
x
2
FN 2 A2
20103 152 106
89106 Pa 89MPa
目录
三、材料在拉伸和压缩时的力学性质
教学目标:1.拉伸、压缩试验简介; 2.应力-应变曲线分析; 3.低碳钢与铸铁的拉、压的力学性质; 4.试件的伸长率、断面收缩率计算。
教学重点:1.应力-应变曲线分析; 2.材料拉、压时的力学性质。
教学难点:应力-应变曲线分析。 小 结: 塑性材料与脆性材料拉伸时的应力-应变曲线分析。 作 业: 复习教材相关内容。
工程力学(材料力学)6拉压杆件的强度与变形问题

机械制造中的拉压杆件
机械制造中的拉压杆件主要用于 实现运动传递、力的传递和变形 等,如连杆、活塞杆、传动轴等。
这些杆件需要在高速、高温、重 载等极端条件下工作,因此需要 具备优异的力学性能和耐久性。
在机械制造中,拉压杆件的设计 和制造需要精确控制尺寸、形状 和材料,以确保其工作性能和可
靠பைடு நூலகம்。
其他工程领域中的拉压杆件
总结词
新型材料如碳纤维复合材料、钛合金等具有高强度、轻质等优点,在拉压杆件中得到广 泛应用。
详细描述
随着科技的不断发展,新型材料如碳纤维复合材料、钛合金等逐渐应用于拉压杆件的制 作。这些新型材料具有高强度、轻质、耐腐蚀等优点,能够提高杆件的力学性能和使用
寿命。
高性能的拉压杆件设计
总结词
通过优化设计,可以显著提高拉压杆件的性能。
刚度分析
对杆件的刚度进行分析, 可以确定其变形程度和承 载能力,为结构设计提供 依据。
拉压杆件的稳定性问题
稳定性定义
01
稳定性是指杆件在受到载荷作用时,保持其平衡状态的能力。
稳定性分析
02
通过稳定性分析,可以确定杆件在受到载荷作用时是否会发生
失稳现象,以及失稳的临界载荷。
稳定性要求
03
在工程应用中,杆件的稳定性需要满足一定的要求,以保证结
强度失效准则
当拉压杆件内部的应力达到或超过材料的屈服极限时,杆件会发生屈服失效, 丧失承载能力。
拉压杆件的强度计算
静力分析
根据外力的大小和方向,以及杆件的几何尺寸和材料属性,计算杆件内部的应力 分布。
动力分析
考虑动载荷的影响,分析杆件在振动、冲击等动态过程中的应力变化。
拉压杆件的强度校核
工程力学-第7章-轴向拉压杆件的强度与变形计算

7
Guang Zhou Auto College
工程力学
第7章 轴向拉压杆件的强度与变形计算
广 州 汽
斜拉桥承受拉力的钢缆 车 学 院
8
Guang Zhou Auto College
工程力学
第7章 轴向拉压杆件的强度与变形计算
广 州 汽 车 学 院9来自 7-1轴向拉压杆横截面上的应力
胡克定律
车
学
院
工程力学
17
轴向拉压的变形分析
P
P
A 细长杆受拉会变长变细,
P
B 受压会变短变粗
C 长短的变化,沿轴线方向, 称为纵向变形
l+Dl l
d-Dd d
D 粗细的变化,与轴线垂直,
称为横向变形
P
P
P
7-3轴向拉压杆的变形计算 胡克定律
工程力学
Guang Zhou Auto College
变形量的代数和:
汽
车
Δ
l
=
FNi li FNi ADlEADA+i
=Dl AD DlDE DlEB Dl
FNDElDE + FNEBlEB + FNBClBC
BC
学
Ec AAD
Ec ADE
Es AEB
Es ABC
=1.2106 m 0.6106 m 0.285106 m 0.428106 m
广
承受轴向载荷的拉(压)杆在工程中的
州
应用非常广泛。
汽
由汽缸、活塞、连
杆所组成的机构中,不
车
仅连接汽缸缸体和汽缸
盖的螺栓承受轴向拉力,
学
带动活塞运动的连杆由
第四章 杆件的变形计算

3)分别作AC1和BC2的垂线交于C0
A F B 30oC2 C
Cx CC2 0.277mm C y CC1 / sin30 CC 2 cot30
C1
1.44mm
C点总位移:
Cy
C C y C x 1.47mm
(此问题若用圆弧精确求解)
2
2
Cx
C0
T3 C
1)根据题意,首先画出扭矩图
T1 d1 A Mx N· m B T2 d2 C T3
2)AB 段单位长度扭转角:
1400
800
AB
M xAB GI pAB
+
x
1400 4 π 0.06 80 10 9 32 0.01375rad / m
3)BC 段单位长度扭转角: M xBC BC
M xi li j i 1 GI pi
n
请注意单位长度扭转角和相对扭转角的区别
例4-3 一受扭圆轴如图所示,已知:T1=1400N· m, T2=600N· m, T3=800N· m, d1=60mm,d2=40mm,剪切弹性模量G=80GPa,计 算最大单位长度扭转角。
T1 d1 A
T2 d2 B
第四章
• • • • •
杆件的变形计算
本部分主要内容:
拉压杆的轴向变形 圆轴的扭转变形与相对扭转角 梁的弯曲变形、挠曲线近似微分方程 用积分法求梁的弯曲变形 用叠加法求梁的弯曲变形
第一节 拉压杆的轴向变形
直杆在其轴线的外力作用下,纵向发生伸长或缩短变形, 而其横向变形相应变细或变粗 杆件在轴线方向的伸长
泊松比ν 、弹性模量 E 、切变模量G 都是材料的弹性常数, 可以通过实验测得。对于各向同性材料,可以证明三者之间存 在着下面的关系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题4-2: 已知:l = 54 mm ,di = 15.3 mm,E=200 GPa, ν = 0.3,拧紧后,△l =0.04 mm。 试求:(a) 螺栓横截面上的正应力 σ (b) 螺栓的横向变形△d
解:1) 求横截面正应力 :
ε=
∆l 0.04 = = 7.41×10-4 l 54
l = 54 mm ,di = 15.3 mm, E=200 GPa, ν = 0.3, △l =0.04 mm
∆ac = a ′c′ − ac
∆ac ε′ = ac
二、拉压杆的弹性定律 1、等内力拉压杆的弹性定律 P P
PL NL dL = = EA EA
PL dL ∝ A
2、变内力拉压杆的弹性定律
N(x) N(x)
x dx dx 内力在n段中分别为常量时 内力在 段中分别为常量时
※“EA”称为杆的抗拉压刚度。 ※“ ”称为杆的抗拉压刚度。
C1
C点总位移: 点总位移:
∆C = ∆C y + ∆C x = 1.47mm
2 2
C0
Cx
(此问题若用圆弧精确求解) 此问题若用圆弧精确求解)
∆C x = 0.278mm ∆C y = 1.44mm
第二节 圆轴的扭转变形及相对扭转角
为 dx 的两个相邻截面之间有相对转角dϕ 的两个相邻截面之间有相对转角d
800 π × 0.04 4 80 ×109 32 = 0.03978rad / m
综合两段, 综合两段,最大单位扭转角应在BC 段 为 0.03978 rad/m
例4-5 图示一等直圆杆, 图示一等直圆杆,已知 d =40mm a =400mm G =80GPa, ϕ DB=1O , 求 : 1) 最大切应力 2)ϕ AC
C3
C0
[解 ]
1)分析节点C,求AC和BC的轴力(均预 分析节点C,求AC和BC的轴力 的轴力( 先设为拉力) 先设为拉力)
FAC C2
30
F
C1
FBC
C
FAC sin 30° − F = 0 FAC = 2 F = 80kN 拉
− FBC − FAC cos 30° = 0 FBC = −40 3kN
压
伸长 缩短
[解 ]
2)求AC和BC杆分别的变形量 AC和BC杆分别的变形量
∆l AC
FAC l AC = CC1 = E1 A1
C2
C1
80 × 10 3 × 1000 / cos30° = 0.481mm = 3 200 × 10 × 960
∆l BC
FBC l BC = CC 2 = E 2 A2
− 40 3 × 10 3 × 1000 = = −0.277mm 3 10 × 10 × 25000
[解 ]
3)分别作AC1和BC2的垂线交于C0 分别作AC 的垂线交于C
∆C x = CC2 = 0.277mm ∆C y = CC1 / sin30° + CC 2 cot30°
C2
= 1.44mm
第三节 梁的变形
1、梁的变形 梁在平面内弯曲时,梁轴线从原来沿 x 轴方向的直线变 梁在平面内弯曲时, 挠曲线。 平面内的曲线,该曲线称为挠曲线 成一条在 xy 平面内的曲线,该曲线称为挠曲线。 某截面的竖向位移,称为 某截面的竖向位移, 该截面的挠度 该截面的挠度 某截面的法线方向与x 某截面的法线方向与x轴 的夹角称为该截面的转角 的夹角称为该截面的转角 挠度和转角的大小和截面所处的 x 方向的位 置有关, 的函数。 置有关,可以表示为关于 x 的函数。 挠度方程(挠曲线方程) w = f1 ( x)或y = f1 ( x ) 挠度方程(挠曲线方程) 转角方程
1)求出轴力,并画出轴力图 求出轴力, 2)求伸长量
∆l = ∆l AB + ∆l BC
40 × 10 3 × 400 FNAB l AB = = 0.1 mm 伸长 ∆l AB = 3 200 × 10 × 800 EAAB FNBC l BC − 20 × 10 3 × 400 ∆l BC = = = −0.167mm 缩短 3 EABC 200 × 10 × 240 ∆l = ∆l AB + ∆l BC = 0.1 − 0.167 = −0.067mm 缩短
N ( x )d x ∆ (dx ) = EA ( x ) N ( x )dx dL = ∫ ∆ (dx ) = ∫ L L EA ( x )
dL =
∑
n
i =1
N iLi E i Ai
3、单向应力状态下的弹性定律
∆ (dx ) 1 N ( x) 1 ε = = = σ dx E A( x ) E
1 即: ε = σ E
4、泊松比(或横向变形系数) 泊松比(或横向变形系数)
ε′ ν = ε
或 : ε ′ = −νε
泊松比ν 泊松比ν 、弹性模量 E 、切变模量G 都是材料的弹性常数, 切变模量G 都是材料的弹性常数, 可以通过实验测得。对于各向同性材料, 可以通过实验测得。对于各向同性材料,可以证明三者之间存 在着下面的关系
“ 胡:请问, 弛其弦,以绳缓援之”
是什么意思 ? 郑:这是讲测量弓力时,先将弓的弦 松开,另外用绳子松松地套住弓 的两端,然后加重物,测量。 胡:我明白了。这样弓体就没有初始应力,处于自然状态。
Байду номын сангаас
郑:后来,到了唐代初期,贾公彦对我的注释又作了注疏,他说: 郑又云假令弓力胜三石,引之 中三尺者,此即三石力弓也。 必知弓力三石者,当弛其弦以绳缓擐之者,谓不张之,别以 一条 绳系两箭,乃加物一石张一尺、二石张二尺、三石张三 其中 “ 两萧” 就是指弓的两端。 尺。 胡:郑老先生讲“每加物一石,则张一尺”。和我讲的完全是同一 个意思。您比我早1500 中就记录下这种正比关系,的确了不起, 真是令人佩服之至』我在1686 年《关于中国文字和语言的研究 和推测》一文中早就推崇过贵国的古代文化: 目前我们还只 是刚刚走到这个知识领域的边缘,然而一旦对它有了充分的认 识,就将会在我们面 前展现出一个迄今为止只被人们神话般 地加以描述的知识王国”。
“
例题4 例题4-1: 如图所示阶梯形直杆,已知该杆AB段横截面面积 段横截面面积A 如图所示阶梯形直杆,已知该杆AB段横截面面积A1=800mm2, BC段横截面面积A2=240mm2,杆件材料的弹性模量E=200GPa, BC段横截面面积 段横截面面积A 杆件材料的弹性模量E=200GPa, 求该杆的总伸长量。 求该杆的总伸长量。
第四章 杆件的变形计算
第一节 拉(压)杆的轴向变形
直杆在其轴线的外力作用下,纵向发生伸长或缩短变形, 直杆在其轴线的外力作用下,纵向发生伸长或缩短变形,而其横 向变形相应变细或变粗 横截面
1、杆的纵向总变形: 杆的纵向总变形:
a c a´ c´
b d
∆x
d L = L1 − L
2、线应变: 线应变: 单位长度的线变形 P
分析 通过节点C的受力分析可以判断AC 通过节点C的受力分析可以判断AC 杆受拉而BC杆受压 AC杆将伸长 杆受压, 杆将伸长, 杆受拉而BC杆受压,AC杆将伸长,而 BC杆将缩短。 BC杆将缩短 杆将缩短。
C1
因此,C节点变形后将位于C3点 因此, 节点变形后将位于C 由于材料力学中的小变形假设 由于材料力学中的小变形假设,可 小变形假设, 以近似用C 以近似用C1和C2处的圆弧的切线来代替 圆弧(以切代弧法),得到交点C ),得到交点 圆弧(以切代弧法),得到交点C0
在一段轴上,对单位长度扭转角公式进行积分, 在一段轴上,对单位长度扭转角公式进行积分, 就可得到两端相对扭转角ϕ 。
l M dϕ Mx θ= ϕ = ∫ x dx = 0 GI dx GI p p Mx Mxl ϕ= 为常数时: 当 为常数时: GI p GI p
同种材料阶梯轴扭转时: 同种材料阶梯轴扭转时: 相对扭转角的单位: 相对扭转角的单位: rad
E G= 2(1+ν )
公式的适用条件
Fl ∆l = N EA
1)线弹性范围以内,材料符合胡克定律 线弹性范围以内, 2)在计算杆件的伸长时,l 长度内其FN、A、l 均应 在计算杆件的伸长时, 长度内其F 为常数,若为变截面杆或阶梯杆, 为常数,若为变截面杆或阶梯杆,则应进行分段计 算或积分计算。 算或积分计算。
σ = Eε = 200 ×103 × 7.41×10−4 = 148.2 MPa
2) 螺栓横向变形
ε' = − = −2.22 ×10−4 νε
∆d = ε' di = −0.0034 mm
螺栓直径缩小 0.0034 mm
例4-3 节点位移问题 如图所示桁架,钢杆AC的横截面面积 的横截面面积A 如图所示桁架,钢杆AC的横截面面积A1=960mm2,弹性模量 E1=200GPa。木杆BC的横截面面积A2=25000mm2,长1m,弹性模 =200GPa。木杆BC的横截面面积 的横截面面积A 1m, =10GPa。求铰接点C的位移。 kN。 量E2=10GPa。求铰接点C的位移。F = 80 kN。
1)画出扭矩图 2)求最大切应力 首先要求出M 首先要求出M 的数值
ϕ DB = ϕ DC + ϕCB
180° M xDC l DC M xCB lCB = + π GI p GI p
180° 3Ma = = 1° π GIp πGIp M= 540a
πGIp M= 540a
∆l = ∫
l
FNdx EA(x)
FNili ∆l = ∑ i=1 EA i
n
是谁首先提出弹性定律 弹性定律是材料力学等固体力学一个非常重要的基础。一般 认为它是由英国科学家胡克(1635一1703)首先提出来的,所以通 常叫做胡克定律。其实,在胡克之前1500年,我国早就有了关于 力和变形成正比关系的记载。 东汉经学家郑玄(127—200)对《考工记·弓人》中“量其力, 有三均”作了 这样的注释:“假令弓力胜三石,引之中三尺,弛 其弦,以绳缓擐之,每加物一石,则张一尺。” (图)
