人教版八年级数学上册10月月考试卷附答案
四川省德阳市中江县2024-2025学年八年级上学期10月月考数学试题[含答案]
![四川省德阳市中江县2024-2025学年八年级上学期10月月考数学试题[含答案]](https://img.taocdn.com/s3/m/87d11da509a1284ac850ad02de80d4d8d15a0138.png)
A.4
3
S V ABP ,其中正确的个数是(
2
B.3
C.2
第 II 卷
)
D.1
非选择题(102 分)
二、填空题(本大题共 7 个小题,每小题 4 分,本大题满分 28 分)
13.如图,在 V ABC 中, D 是 BC 边上一点, E 是边上一点.在 △ACE 中, Ð CAE 的对
边是
.
14.正十边形的每个外角等于
从点 B 出发,在直线 BC 上以 2cm/ s 的速度移动,过点 E 作 BC 的垂线交直线 CD 于点 F ,当
点 E 运动
s 时, CF
= AB .
19.如图,在 V ABC 中, ÐA = 20°, ÐEBC , ÐDCB 为 V ABC 的外角, ÐEBC 与 ÐDCB 的平分
线交于点 A1 , ÐEBA1 与 ÐDCA1 的平分线交于点 A2 , ¼,ÐEBAn -1 与 ÐDCAn -1 的平分线相交于点
的内角和为(
A. 1800°
)
B. 1440°
C. 1080°
试卷第 2 页,共 7 页
D. 720°
8.如图,在 V ABC 中,点 E 是 BC 的中点, AB = 7 , AC = 10 , △ACE 的周长是 25,则 V ABE
的周长是( )
A.18
B.22
C.28
D.32
9.如图,在 8 ´ 8 的正方形网格中, V ABC 的顶点和线段 EF 的端点都在小正方形的顶点上,
.
15.如图,四边形 ABCD 中,点 M、N 分别在 AB、BC 上,将 V BMN 沿 MN 翻折得 V FMN ,
若 MF∥AD,FN∥DC ,则 ÐB =
八年级(上)月考数学试卷(10月份)附答案
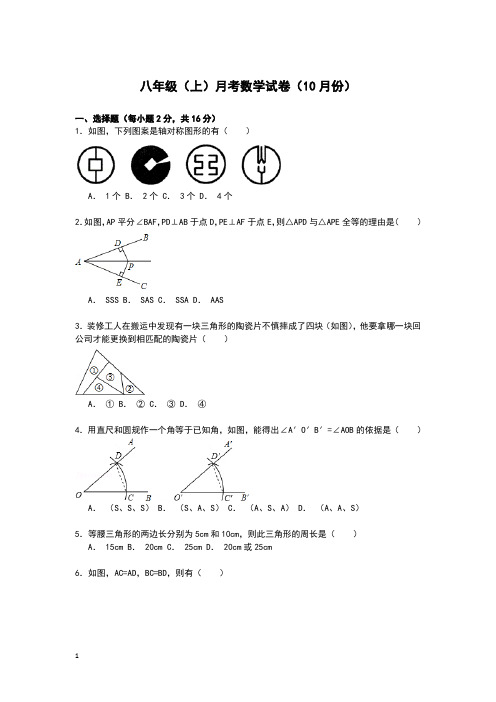
八年级(上)月考数学试卷(10月份)一、选择题(每小题2分,共16分)1.如图,下列图案是轴对称图形的有()A. 1个 B. 2个 C. 3个 D. 4个2.如图,AP平分∠BAF,PD⊥AB于点D,PE⊥AF于点E,则△APD与△APE全等的理由是()A. SSS B. SAS C. SSA D. AAS3.装修工人在搬运中发现有一块三角形的陶瓷片不慎摔成了四块(如图),他要拿哪一块回公司才能更换到相匹配的陶瓷片()A.① B.② C.③ D.④4.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是()A.(S、S、S) B.(S、A、S) C.(A、S、A) D.(A、A、S)5.等腰三角形的两边长分别为5cm和10cm,则此三角形的周长是()A. 15cm B. 20cm C. 25cm D. 20cm或25cm6.如图,AC=AD,BC=BD,则有()A. AB垂直平分CD B. CD垂直平分ABC. AB与CD互相垂直平分 D. CD平分∠ACB7.如图,△ABC中,∠ACB=90°,∠B=30°,AD是角平分线,DE⊥AB于E,AD、CE相交于点H,则图中的等腰三角形有()A. 2个 B. 3个 C. 4个 D. 5个二、填空题(每小题2分,共20分)8.角的对称轴是.9.若等腰三角形的顶角为50°,则它的底角为.10.如图,△ABC≌△DEF,由图中提供的信息,可得∠D= °11.如图8,点C、D在BE上,BC=DE,∠1=∠2,要使得△ABD≌△AEC,还需要添加一个条件,你添加的条件是.12.工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用.13.如图,AB⊥AC,点D在BC的延长线上,且AB=AC=CD,则∠ADB= °.14.如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若△ADE的周长为9,△ABC的周长是14,则BC= .15.已知,如图,AD=AC,BD=BC,O为AB上一点,那么,图中共有对全等三角形.16.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有个.17.如图所示,AOB是一钢架,且∠AOB=10°,为了使钢架更加坚固,需在其内部添加一些钢管EF,FG,GH…,添加的钢管长度都与OE相等,则最多能添加这样的钢管根.三、作图题(每小题5分,共10分)18.如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)19.利用网格线作图:在BC上找一点P,使点P到AB和AC的距离相等.然后,在射线AP 上找一点Q,使QB=QC.四、解答题20.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于()A. 30° B. 40° C. 45° D. 36°21.已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.求证:△ABC≌△CDE.22.如图,已知:AD和BC相交于O,∠1=∠2,∠3=∠4.试判断AD和BC的关系,并说明理由.23.已知:如图,等边三角形ABC中,D为AC边的中点,过C作CE∥AB,且AE⊥CE,那么∠CAE=∠ABD吗?请说明理由.24.已知:如图,AD、BC相交于点O,AO=BO,∠C=∠D=90°.求证:AD=BC.25.已知:如图,AB=AD,∠ABC=∠ADC.试说明:CB=CD.26.如图,在△ABC中,AB=AC,∠BAC=120°.AB的垂直平分线交AB于E,交BC于M; AC 的垂直平分线交AC于F,交BC于N.连接AM、AN.(1)∠MAN的大小;(2)求证:BM=CN.27.如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN 于E.易得DE=AD+BE(不需证明).(1)若直线CE绕C点旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时DE、AD、BE之间的数量关系,并说明理由;(2)若直线CE绕C点旋转到图3的位置时,其余条件不变,请直接写出此时DE、AD、BE 之间的数量关系(不需证明).28.如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程证明△ABD≌△ACD的理由.∵AD平分∠BAC,∴∠BAD=∠(角平分线的定义).在△ABD和△ACD中,∴△ABD≌△ACD .参考答案与试题解析一、选择题(每小题2分,共16分)1.如图,下列图案是轴对称图形的有()A. 1个 B. 2个 C. 3个 D. 4个考点:轴对称图形.分析:根据轴对称图形的概念对各图形分析判断即可得解.解答:解:第1个图形是轴对称图形,第2个图形不是轴对称图形,第3个图形是轴对称图形,第4个图形是轴对称图形,综上所述,轴对称图形有3个.故选C.点评:本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.2.如图,AP平分∠BAF,PD⊥AB于点D,PE⊥AF于点E,则△APD与△APE全等的理由是()A. SSS B. SAS C. SSA D. AAS考点:全等三角形的判定.分析:求出∠PDA=∠PEA=90°,∠DAP=∠EAP,根据AAS推出两三角形全等即可.解答:解:∵PD⊥AB,PE⊥AF,∴∠PDA=∠PEA=90°,∵AP平分∠BAF,∴∠DAP=∠EAP,在△APD和△APE中∴△APD≌△APE(AAS),故选D.点评:本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.3.装修工人在搬运中发现有一块三角形的陶瓷片不慎摔成了四块(如图),他要拿哪一块回公司才能更换到相匹配的陶瓷片()A.① B.② C.③ D.④考点:全等三角形的应用.分析:假定选择哪块,再对应三角形全等判定的条件进行验证.解答:解:②、③、④块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,只有第①块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.故选:A.点评:本题主要考查三角形全等的判定,看这4块玻璃中哪个包含的条件符合某个判定.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.4.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是()A.(S、S、S) B.(S、A、S) C.(A、S、A) D.(A、A、S)考点:全等三角形的判定与性质;作图—基本作图.分析:利用SSS可证得△OCD≌△O′C′D′,那么∠A′O′B′=∠AOB.解答:解:易得OC=0′C',OD=O′D',CD=C′D',那么△OCD≌△O′C′D′,可得∠A′O′B′=∠AOB,所以利用的条件为SSS,故选A.点评:考查全等三角形“边边边”的判定以及全等三角形的对应角相等这个知识点.5.等腰三角形的两边长分别为5cm和10cm,则此三角形的周长是()A. 15cm B. 20cm C. 25cm D. 20cm或25cm考点:等腰三角形的性质;三角形三边关系.分析:分5cm是腰长和底边两种情况讨论求解即可.解答:解:5cm是腰长时,三角形的三边分别为5cm、5cm、10cm,∵5+5=10,∴不能组成三角形,10cm是腰长时,三角形的三边分别为5cm、10cm、10cm,能组成三角形,周长=5+10+10=25cm,综上所述,此三角形的周长是25cm.故选C.点评:本题考查了等腰三角形的性质,三角形的三边关系,难点在于分情况讨论并利用三角形的三边关系判断是否能够组成三角形.6.如图,AC=AD,BC=BD,则有()A. AB垂直平分CD B. CD垂直平分ABC. AB与CD互相垂直平分 D. CD平分∠ACB考点:线段垂直平分线的性质.专题:压轴题.分析:由已知条件AC=AD,利用线段的垂直平分线的性质的逆用可得点A在CD的垂直平分线上,同理,点B也在CD的垂直平分线上,于是A是符合题意的,是正确的,答案可得.解答:解:∵AC=AD,BC=BD,∴点A,B在线段CD的垂直平分线上.∴AB垂直平分CD.故选A.点评:本题考查的知识点为:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上;两点确定一条直线.分别应用垂直平分线性质定理的逆定理是解答本题的关键.7.如图,△ABC中,∠ACB=90°,∠B=30°,AD是角平分线,DE⊥AB于E,AD、CE相交于点H,则图中的等腰三角形有()A. 2个 B. 3个 C. 4个 D. 5个考点:等腰三角形的判定.分析:根据等腰三角形的判定,运用直角三角形的两个锐角互余和角平分线的性质,证得∠CAD=∠BAD=30°,CD=ED,AC=AE,即△ABD、△CDE、△ACE、△BCE是等腰三角形.解答:解:∵∠ACB=90°,∠B=30°,∴∠BAC=60°,∵AD是角平分线,∴∠CAD=∠BAD=30°,∴AD=BD.∴△ABD是等腰三角形.∵AD是角平分线,∠ACB=90°,DE⊥AB,∴CD=ED∴AC=AE∴△CDE、△ACE是等腰三角形;又△CEB也是等腰三角形显然此图中有4个等腰三角形.故选C.点评:本题考查了等腰三角形的判定;要综合运用直角三角形的两个锐角互余和角平分线的性质,找到相等的线段,来判定等腰三角形.二、填空题(每小题2分,共20分)8.角的对称轴是角平分线所在的直线.考点:轴对称图形.分析:关于某条直线对称的图形叫轴对称图形.解答:解:沿角平分线所在的直线折叠后直线两旁的部分能够完全重合,所以角的对称轴是角平分线所在的直线.点评:注意:对称轴必须说成直线.9.若等腰三角形的顶角为50°,则它的底角为65°.考点:等腰三角形的性质.分析:等腰三角形中,给出了顶角为50°,可以结合等腰三角形的性质及三角形的内角和直接求出底角,答案可得.解答:解:∵三角形为等腰三角形,且顶角为50°,∴底角=(180°﹣50°)÷2=65.故填65.点评:本题主要考查了等腰三角形,的性质;等腰三角形中只要知道一个角,就可求出另外两个角,这种方法经常用到,要熟练掌握.10.如图,△ABC≌△DEF,由图中提供的信息,可得∠D= 70 °.考点:全等三角形的性质.分析:根据三角形的内角和定理求出∠A,再根据全等三角形对应角相等可得∠D=∠A.解答:解:在△ABC中,∠A=180°﹣∠B﹣∠C=180°﹣50°﹣60°=70°,∵△ABC≌△DEF,∴∠D=∠A=70°.故答案为:70.点评:本题考查了全等三角形的性质,根据对应边确定出∠A和∠D是对应角是解题的关键.11.如图8,点C、D在BE上,BC=DE,∠1=∠2,要使得△ABD≌△AEC,还需要添加一个条件,你添加的条件是∠B=∠C(答案不唯一).考点:全等三角形的判定.专题:开放型.分析:添加的条件:∠B=∠C,根据等式的性质可得∠BAD=∠EAC,DB=CE,可根据AAS判定△ABD≌△AEC.解答:解:添加的条件:∠B=∠C,∵∠1=∠2,∴∠1+∠CAD=∠2+∠CAD,即∠BAD=∠EAC,∵CB=DE,∴CB+CD=DE+CD,即DB=CE,在△ABD和△AEC中,∴△ABD≌△AEC(AAS),故答案为:∠B=∠C.点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.12.工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用三角形的稳定性.考点:三角形的稳定性.分析:三角形具有稳定性,其它多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变.解答:解:这是利用三角形的稳定性.点评:本题考查三角形稳定性的实际应用,三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.13.如图,AB⊥AC,点D在BC的延长线上,且AB=AC=CD,则∠ADB= 22.5 °.考点:等腰三角形的性质;三角形的外角性质.专题:计算题.分析:由已知可得到∠B=∠ACB=45°,∠CAD=∠CDA,再根据三角形外角的性质可得到∠ACB 与∠ADB之间的关系,从而不难求解.解答:解:∵AB=AC=CD,AB⊥AC,∴∠B=∠ACB=45°,∠CAD=∠CDA∵∠ACB=∠CAD+∠CDA=2∠ADB=45°∴∠ADB=22.5°.故答案为:22.5°.点评:此题主要考查等腰三角形的性质及三角形的外角的性质的综合运用.14.如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若△ADE的周长为9,△ABC的周长是14,则BC= 5 .考点:等腰三角形的判定与性质;平行线的性质.分析:由BO平分∠ABC,CO平分∠ACB,过点O作DE∥BC,易得△BOD与△COE是等腰三角形,又由△ADE的周长为9,可得AB+AC=9,又由△ABC的周长是14,即可求得答案.解答:解:∵BO平分∠ABC,CO平分∠ACB,∴∠ABO=∠OBC,∠ACO=∠OCB,∵DE∥BC,∴∠BOD=∠OBC,∠COE=∠OCB,∴∠ABO=∠BOD,∠ACO=∠COE,∴BD=OD,CE=OE,∵△ADE的周长为29,∴AD+DE+AE=AD+OD+OE+AE=AD+BD+CE+AE=AB+AC=9,∵△ABC的周长是14,∴AB+AC+BC=14,∴BC=5.故答案为:5.点评:此题考查了等腰三角形的性质与判定.此题难度适中,注意掌握数形结合思想的应用.15.已知,如图,AD=AC,BD=BC,O为AB上一点,那么,图中共有 3 对全等三角形.考点:全等三角形的判定.分析:由已知条件,结合图形可得△ADB≌△ACB,△ACO≌△ADO,△CBO≌△DBO共3对.找寻时要由易到难,逐个验证.解答:解:∵AD=AC,BD=BC,AB=AB,∴△ADB≌△ACB;∴∠CAO=∠DAO,∠CBO=∠DBO,∵AD=AC,BD=BC,OA=OA,OB=OB∴△ACO≌△ADO,△CBO≌△DBO.∴图中共有3对全等三角形.故答案为:3.点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.16.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有 5 个.考点:利用轴对称设计图案.分析:利用轴对称图形的性质分别得出符合要求的答案即可.解答:解:如图所示:与△ABC成轴对称的有△ACG、△AFE、△BFD、△CHD、△CGB一共有5个.故答案为:5.点评:此题主要考查了利用轴对称设计图案,根据已知得出所有符合要求的答案注意不要漏解.17.如图所示,AOB是一钢架,且∠AOB=10°,为了使钢架更加坚固,需在其内部添加一些钢管EF,FG,GH…,添加的钢管长度都与OE相等,则最多能添加这样的钢管8 根.考点:等腰三角形的性质.专题:应用题;压轴题.分析:根据已知利用等腰三角形的性质及三角形外角的性质,找出图中存在的规律,根据规律及三角形的内角和定理不难求解.解答:解:∵添加的钢管长度都与OE相等,∠AOB=10°,∴∠GEF=∠FGE=20°,…从图中我们会发现有好几个等腰三角形,即第一个等腰三角形的底角是10°,第二个是20°,第三个是30°,四个是40°,五个是50°,六个是60°,七个是70°,八个是80°,九个是90°就不存在了.所以一共有8个.故答案为:8.点评:此题考查了三角形的内角和是180度的性质和等腰三角形的性质及三角形外角的性质;发现并利用规律是正确解答本题的关键.三、作图题(每小题5分,共10分)18.如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)考点:作图—应用与设计作图.分析:根据点P到∠AOB两边距离相等,到点C、D的距离也相等,点P既在∠AOB的角平分线上,又在CD垂直平分线上,即∠AOB的角平分线和CD垂直平分线的交点处即为点P.解答:解:如图所示:作CD的垂直平分线,∠AOB的角平分线的交点P即为所求,此时货站P到两条公路OA、OB的距离相等.P和P1都是所求的点.点评:此题主要考查了线段的垂直平分线和角平分线的作法.这些基本作图要熟练掌握,注意保留作图痕迹.19.利用网格线作图:在BC上找一点P,使点P到AB和AC的距离相等.然后,在射线AP 上找一点Q,使QB=QC.考点:作图—复杂作图;角平分线的性质;线段垂直平分线的性质.分析:根据网格特点先作出∠A的角平分线与BC的交点就是点P,再作BC的垂直平分线与AP的交点就是点Q.解答:解:如图,点P就是所要求作的到AB和AC的距离相等的点,点Q就是所要求作的使QB=QC的点.点评:本题主要考查了利用网格结构作角的平分线,线段的垂直平分线,找出相应的点是解题的关键.四、解答题20.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于()A. 30° B. 40° C. 45° D. 36°考点:等腰三角形的性质.分析:题中相等的边较多,且都是在同一个三角形中,因为求“角”的度数,将“等边”转化为有关的“等角”,充分运用“等边对等角”这一性质,再联系三角形内角和为180°求解此题.解答:解:∵BD=AD∴∠A=∠ABD∵BD=BC∴∠BDC=∠C又∵∠BDC=∠A+∠ABD=2∠A∴∠C=∠BDC=2∠A∵AB=AC∴∠ABC=∠C又∵∠A+∠ABC+∠C=180°∴∠A+2∠C=180°把∠C=2∠A代入等式,得∠A+2•2∠A=180°解得∠A=36°故选:D.点评:本题反复运用了“等边对等角”,将已知的等边转化为有关角的关系,并联系三角形的内角和及三角形一个外角等于与它不相邻的两个内角的和的性质求解有关角的度数问题.21.已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.求证:△ABC≌△CDE.考点:全等三角形的判定.专题:证明题.分析:首先根据AC∥DE,利用平行线的性质可得:∠ACB=∠E,∠ACD=∠D,再根据∠ACD=∠B证出∠D=∠B,再由∠ACB=∠E,AC=CE可根据三角形全等的判定定理AAS证出△ABC≌△CDE.解答:证明:∵AC∥DE,∴∠ACB=∠E,∠ACD=∠D,∵∠ACD=∠B,∴∠D=∠B,在△ABC和△EDC中,∴△ABC≌△CDE(AAS).点评:此题主要考查了全等三角形的判定,关键是熟练掌握判定两个三角形全等的方法:SSS、SAS、ASA、AAS,选用哪一种方法,取决于题目中的已知条件,22.如图,已知:AD和BC相交于O,∠1=∠2,∠3=∠4.试判断AD和BC的关系,并说明理由.考点:全等三角形的判定与性质;等腰三角形的判定与性质.分析:根据ASA证△ABD≌△ACD,推出AB=AC,根据等腰三角形的性质得出即可.解答:解:AD⊥BC,AD平分BC,理由是:∵在△ABD和△ACD中∴△ABD≌△ACD(ASA)∴AB=AC,∵∠1=∠2,∴AD⊥BC,AD平分BC(等腰三角形三线合一性质).点评:本题考查了全等三角形的性质和判定,等腰三角形的性质和判定的应用,注意:等腰三角形顶角的平分线,底边上的高,底边上的中线互相重合.23.已知:如图,等边三角形ABC中,D为AC边的中点,过C作CE∥AB,且AE⊥CE,那么∠CAE=∠ABD吗?请说明理由.考点:等边三角形的性质.分析:根据△ABC为等边三角形,D为AC边上的中点得到AC=BA,∠BAC=∠BCA=60°,BD ⊥AC,求出∠BDA=90°,由CE∥AB得∠ACE=∠BAD,利用90°﹣∠ACE=90°﹣∠BAD得出∠CAE=∠ABD.解答:解:∠CAE=∠ABD,理由如下:∵△ABC为等边三角形,D为AC边上的中点,∴AC=BA,∠BAC=∠BCA=60°,BD⊥AC,∴∠BDA=90°,∵AE⊥CE,∴∠AEC=∠BDA=90°,又∵CE∥AB,∴∠ACE=∠BAD,∴90°﹣∠ACE=90°﹣∠BAD,即∠CAE=∠ABD.点评:本题主要考查等边三角形的性质的知识点,解答本题的关键是熟练掌握等边三角形边角之间的关系,此题难度不大.24.已知:如图,AD、BC相交于点O,AO=BO,∠C=∠D=90°.求证:AD=BC.考点:全等三角形的判定与性质.专题:证明题.分析:利用等角对等边以及全等三角形的判定与性质得出即可.解答:证明:∵AO=BO,∴∠OAB=∠OBA,在△ABC和△BAD中,∴△ABC≌△BAD(AAS).∴AD=BC.点评:此题主要考查了全等三角形的判定与性质等知识,根据已知得出△ABC≌△BAD是解题关键.25.已知:如图,AB=AD,∠ABC=∠ADC.试说明:CB=CD.考点:等腰三角形的判定与性质.专题:证明题.分析:连接BD,由AB=AD,根据等边对等角,可得∠ADB=∠ABD,由∠ABC=∠ADC,根据等式的基本性质,可得∠CBD=∠CDB,根据等角对等边,所以CD=CB.解答:证明:连接BD,∵AB=AD,∴∠ADB=∠ABD,∵∠ABC=∠ADC,∴∠ABC﹣∠ABD=∠ADC﹣∠ADB,即∠CBD=∠CDB,∴CD=CB.点评:此题考查了等腰三角形的判定与性质,用角相等来求边相等是本题的解题思路.26.如图,在△ABC中,AB=AC,∠BAC=120°.AB的垂直平分线交AB于E,交BC于M; AC 的垂直平分线交AC于F,交BC于N.连接AM、AN.(1)∠MAN的大小;(2)求证:BM=CN.考点:线段垂直平分线的性质;等腰三角形的性质.分析:(1)由在△ABC中,AB=AC,∠BAC=120°,可求得∠B与∠C的度数,又由AB的垂直平分线交AB于E,交BC于M;可得AM=BM,继而求得∠MAB的度数,则可求得∠AMN的度数,继而求得答案;(2)易得△AMN为等边三角形,则可得AM=AN=MN,又由BM=AM,CN=AN,即可证得结论.解答:(1)解:∵AB=AC,∠A=120°,∴∠B=∠C=30°,∵直线ME垂直平分AB,∴BM=AM,∴∠B=∠MAB=30°,∴∠AMN=∠B+∠MAB=60°,同理可得:∠ANM=60°.∴∠MAN=180°﹣60°﹣60°=60°;(2)证明:∵在△AMN中,∠AMN=∠ANM=∠MAN=60°,∴△AMN为等边三角形.即 AM=AN=MN,又∵BM=AM,CN=AN,∴BM=CN.点评:此题考查了线段垂直平分线的性质以及等边三角形的判定与性质.此题难度不大,注意掌握转化思想与数形结合思想的应用.27.如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN 于E.易得DE=AD+BE(不需证明).(1)若直线CE绕C点旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时DE、AD、BE之间的数量关系,并说明理由;(2)若直线CE绕C点旋转到图3的位置时,其余条件不变,请直接写出此时DE、AD、BE 之间的数量关系(不需证明).考点:旋转的性质;全等三角形的判定与性质.专题:探究型.分析:(1)DE、AD、BE之间的数量关系是DE=AD﹣BE,理由如下:由∠ACB=90°,BE⊥CE,AD⊥CE,则∠ACD+∠CAD=90°,又∠ACD+∠BCE=90°,得到∠CAD=∠BCE,可证得△ACD≌△CBE,得到AD=CE,CD=BE,即有DE=AD﹣BE;(2)DE、AD、BE之间的关系是DE=BE﹣AD.证明的方法与(1)一样.解答:解:(1)不成立.DE、AD、BE之间的数量关系是DE=AD﹣BE,理由如下:如图2,∵∠ACB=90°,BE⊥CE,AD⊥CE,∴∠ACD+∠CAD=90°,又∠ACD+∠BCE=90°,∴∠CAD=∠BCE,在△ACD和△CBE中,∵AC=CB,∠CAD=∠BCE,∠ADC=∠CEB=90°∴∴△ACD≌△CBE,∴AD=CE,CD=BE,∴DE=AD﹣BE;(2)DE、AD、BE之间的关系是DE=BE﹣AD.点评:本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心连线段的夹角等于旋转角.也考查了三角形全等的判定与性质.28.如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程证明△ABD≌△ACD的理由.∵AD平分∠BAC,∴∠BAD=∠CAD (角平分线的定义).在△ABD和△ACD中,∴△ABD≌△ACD SAS .考点:全等三角形的判定.专题:证明题.分析:首先根据角平分线定义可得到∠BAD=∠CAD,再利用SAS定理可证明△ABD≌△ACD.解答:证明:∵AD平分∠BAC(已知).∴∠BAD=∠CAD(角平分线定义),在△ABD和△ACD中,,∴△ABD≌△ACD (SAS).故答案为CAD,SAS.点评:本题主要考查了全等三角形的判定,判定两个一般三角形全等的方法有四种:AAS,SAS,SSS,ASA.。
人教版八年级上册数学月考考试卷【含答案】

人教版八年级上册数学月考考试卷【含答案】 班级: 姓名:一、选择题(本大题共10小题,每题3分,共30分)1.12-的相反数是( ) A .2- B .2 C .12- D .122.若点1(),6A x -,2(),2B x -,32(),C x 在反比例函数12y x=的图像上,则1x ,2x ,3x 的大小关系是( ) A .123x x x << B .213x x x << C .231x x x << D .321x x x <<3.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )A .108°B .90°C .72°D .60°4.已知a b 3132==,,则a b 3+的值为( ) A .1 B .2 C .3 D .275.已知1x 、2x 是一元二次方程220x x -=的两个实数根,下列结论错误..的是( )A .12x x ≠B .21120x x -=C .122x x +=D .122x x ⋅=6.一个整数815550…0用科学记数法表示为8.1555×1010,则原数中“0”的个数为( )A .4B .6C .7D .107.下列四个图形中,线段BE 是△ABC 的高的是( )A .B .C .D .8.如图,直线AB ∥CD ,∠C =44°,∠E 为直角,则∠1等于( )A .132°B .134°C .136°D .138°9.将一副三角板和一张对边平行的纸条按如图摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )A .15°B .22.5°C .30°D .45°10.已知:如图,∠1=∠2,则不一定能使△ABD ≌△ACD 的条件是 ( )A .AB =AC B .BD =CD C .∠B =∠C D .∠BDA =∠CDA二、填空题(本大题共6小题,每小题3分,共18分)1.若22(3)16x m x +-+是关于x 的完全平方式,则m =__________.2.已知222246140x y z x y z ++-+-+=, 则()2002x y z --=_______.3.当直线()223y k x k =-+-经过第二、三、四象限时,则k 的取值范围是________.4.如图,在ABC 中,点A 的坐标为()0,1,点B 的坐标为()0,4,点C 的坐标为()4,3,点D 在第二象限,且ABD 与ABC 全等,点D 的坐标是______.5.如图:在△ABC 中,∠ABC ,∠ACB 的平分线交于点O ,若∠BOC =132°,则∠A 等于_____度,若∠A =60°时,∠BOC 又等于_____。
人教版八年级上册数学《月考》试卷(完整)

人教版八年级上册数学《月考》试卷(完整) 班级: 姓名: 一、选择题(本大题共10小题,每题3分,共30分)1.已知243m -m-10m -m -m 2=+,则计算:的结果为( ).A .3B .-3C .5D .-52.在平面直角坐标系中,点(3,2)关于x 轴对称的点的坐标为( )A .(3,2)-B .(2,3)-C .(2,3)-D .(3,2)- 3.等式33=11x x x x --++成立的x 的取值范围在数轴上可表示为( ) A .B .C .D . 4.把38a 化为最简二次根式,得 ( )A .22a aB .342aC .322aD .24a a 5.直线y =23x +4与x 轴、y 轴分别交于点A 和点B ,点C ,D 分别为线段AB ,OB 的中点,点P 为OA 上一动点,PC +PD 值最小时点P 的坐标为( )A .(-3,0)B .(-6,0)C .(-52,0)D .(-32,0) 6.下列长度的三条线段能组成直角三角形的是( )A .3, 4,5B .2,3,4C .4,6,7D .5,11,127.如图,某小区计划在一块长为32m ,宽为20m 的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m 2.若设道路的宽为xm ,则下面所列方程正确的是( )A .(32﹣2x )(20﹣x )=570B .32x+2×20x=32×20﹣570C .(32﹣x )(20﹣x )=32×20﹣570D .32x+2×20x ﹣2x 2=5708.如图,在平行四边形ABCD 中,∠DBC=45°,DE ⊥BC 于E ,BF ⊥CD 于F ,DE ,BF 相交于H ,BF 与AD 的延长线相交于点G ,下面给出四个结论:①2BD BE =; ②∠A=∠BHE ; ③AB=BH ; ④△BCF ≌△DCE , 其中正确的结论是( )A .①②③B .①②④C .②③④D .①②③④9.如图将直尺与含30°角的三角尺摆放在一起,若120∠=︒,则2∠的度数是( )A .30B .40︒C .50︒D .60︒10.如图,已知某广场菱形花坛ABCD 的周长是24米,∠BAD =60°,则花坛对角线AC 的长等于( )A .3米B .6米C .3D .3米二、填空题(本大题共6小题,每小题3分,共18分)1.若△ABC 三条边长为a ,b ,c ,化简:|a -b -c |-|a +c -b |=__________.2.已知222246140x y z x y z ++-+-+=, 则()2002x y z --=_______.3.若214x x x++=,则2211x x ++= ________. 4.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是__________(用a 、b 的代数式表示).5.如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,点E 、F 分别是AO 、AD 的中点,若AB=6cm ,BC=8cm ,则AEF 的周长=______cm .6.如图,已知直线y =ax +b 和直线y =kx 交于点P ,则关于x ,y 的二元一次方程组y kx y ax b =⎧⎨=+⎩的解是________.三、解答题(本大题共6小题,共72分)1.解方程组:2313424()3(2)17x y x y x y ⎧-=⎪⎨⎪--+=⎩2.先化简()222a 2a 1a 1a 1a 2a 1+-÷++--+,然后a 在﹣1、1、2三个数中任选一个合适的数代入求值.3.已知方程组713x y m x y m+=--⎧⎨-=+⎩的解满足x 为非正数, y 为负数. (1)求m 的取值范围;(2)化简:||32m m --+;(3)在m 的取值范围内,当m 为何整数时,不等式221mx x m +<+的解为1x >.4.如图,Rt △ABC 中,∠C=90°,AD 平分∠CAB ,DE ⊥AB 于E ,若AC=6,BC=8,CD=3.(1)求DE 的长;(2)求△ADB 的面积.5.如图,某市有一块长为()3a b +米,宽为()2a b +米的长方形地块,规划部门计划将阴影部分进行绿化,中间修建一座雕像,求绿化的面积是多少平方米?并求出当3,2a b ==时的绿化面积?6.一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)若降价3元,则平均每天销售数量为________件;(2)当每件商品降价多少元时,该商店每天销售利润为1200元?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、A2、D3、B4、A5、C6、A7、A8、A9、C10、A二、填空题(本大题共6小题,每小题3分,共18分) 1、2b-2a2、03、84、ab5、96、12x y =⎧⎨=⎩.三、解答题(本大题共6小题,共72分)1、 1.52x y =-⎧⎨=-⎩2、53、(1)23m -<≤;(2)12m -;(3)1m =-4、(1)DE=3;(2)ADB S 15∆=.5、(5a 2+3ab )平方米,63平方米6、(1)26;(2)每件商品降价10元时,该商店每天销售利润为1200元.。
云南省曲靖市麒麟区第四中学2024--2025学年八年级上学期10月第一次月考数学试卷(含答案)

云南省曲靖市麒麟区第四中学2024-2025学年八年级上学期10月第一次月考数学试卷八年级 数学(人教版) 试卷范围:八上11.1~12.2(全卷三个大题,共27个小题,共8页;满分100分,考试用时120分钟)注意事项:1.本卷为试题卷.答题前请在答题卡指定位置填写学校、班级、姓名等信息。
答案书写在答题卡相应位置上,答在试题卷或草稿纸上的答案无效。
2.考试结束后,请将试题卷和答题卡一并交回。
一、选择题(本大题共15小题,每个小题只有一个正确选项,每小题2分,共30分)1.下列长度的三条线段能组成三角形的是( )A.3,8,4B.5,10,6C.4,4,8D.3,7,112.下列各组图形中,两个图形属于全等图形的是( )A. B. C. D.3.直角三角形的一个锐角是,则它的另一个锐角是( )A. B. C. D.或4.下列说法正确的是( )A.三角形的外角和为 B.面积相等的两个三角形全等C.周长相等的两个三角形全等D.两条边及其一角相等的两个三角形全等5.如图,为了使自行车稳定停放,停放时常常放下它的脚架,这里所运用的几何原理是( )A.两点之间,线段最短B.三角形具有稳定性C.两点确定一条直线D.垂线段最短6.已知图中的两个三角形全等,则等于()60︒30︒60︒120︒30︒60︒360︒1∠A. B. C. D.7.如图,在中,,,则( )A. B. C. D.8.如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形.他的依据是( )A.SASB.ASAC.AASD.SSS9.如图,的边上的高是( )A.线段B.线段C.线段D.线段10.如图,如果,那么下列结论不正确的是( )A. B. C. D.11.小刚要将一块如图所示的三角形纸板分成面积相同的两部分,则图中他所作的线段应该是的()50︒58︒60︒72︒ABC △55B ︒∠=40C ︒∠=DAC ∠=75︒85︒95︒100︒ABC △BC AF BD BF BEABC FED △≌△BD EC =//AB EF //AC FD BD DF=AD ABC△A.高线B.中线C.角平分线D.以上都不是12.如图,已知,下列所给条件不能证明的是( )A. B. C. D.13.多边形的每个内角均为,则这个多边形是( )A.四边形B.五边形C.六边形D.八边形14.下列尺规作图的语句正确的是( )A.残长射线到点B.延长线段至点,使得C.作直线D.以为圆心,任意长为半径画弧15.如图,是的角平分线,,交于点,,交于点,若,则的度数为( )A. B. C. D.二、填空题(本大题共4小题,每小题2分,共8分)16.一个七边形的内角和度数为________.17.已知的三条边长均为整数,其中两边长分别是2和5,第三边长为奇数,则此三角形的周长为________.18.如图,,,若,则的度数为________.ABC DCB ∠=∠ABC DCB △≌△A D ∠=∠AB DC =AC DB =ACB DBC∠=∠120︒AB C AB C AC BC =3cmAB =O AD ABC △//DE AC AB E //DF AB AC F 150︒∠=2∠40︒45︒50︒60︒ABC △AB AC =BD CD =70B ︒∠=DAC ∠19.如图,先将两个全等的直角三角形、重叠在一起,再将三角形沿方向平移,、相交于点.若,,则阴影部分的面积为________.三、解答题(本大题共8小题,共62分)20.(6分)一个多边形的内角和是外角和的3倍,求这个多边形的边数.21.(6分)如图,,,求证:.22.(7分)如图,在与中,点、、、在一条直线上,,,.(1)求证::(2)若,,求线段的长.23.(7分)为了测量一栋6层楼的高度,在旗杆与楼之间选定一点,测得旗杆顶的视线与地面的夹角,测得楼顶的视线与地面的夹角,测各点到楼底的距离与旗仠的高度都等于12米,测得旗杆与楼之间的距离米.求这栋6层楼的高度.ABC DEF DEF CA 2cm AB EF G 8cm BC =3cm GE =2cm 90B D ︒∠=∠=AB AD =ABC ADC △≌△ABC △DEF △B E C F //AC DF AC DF =A D ∠=∠ABC DEF △≌△7BF =3CE =BE CD P C PC 33DPC ︒∠=A PA 57APB ︒∠=P PB CD 30BD =24.(8分)如图,是的高,、是的角平分线,且.(1)求的度数;(2)若,求的度数.25.(8分)如图,在中,,点是的中点,点在上.(1)找出图中所有全等的三角形:(2)任选一组你写出的全等三角形进行证明.26.(8分)如图,点是的平分线与的平分线的交点.(1)若,,则________;(2)探究与的数量关系,并说明理由.27.(12分)如图,与相交于点,,,,点从点出发,沿方向以的速度运动,点同时从点出发,沿方向以的速度运动,当点到达点时,、两点同时停止运动,设点的运动时间为.AD ABC △AE BF ABC △30CBF ︒∠=BAD ∠70AFB ︒∠=DAE ∠ABC △AB AC =D BC E AD D CBE ∠CAB ∠60BAC ︒∠=40D ︒∠=DBE ∠=︒C ∠D ∠AE BD C AC EC =BC DC =8cm AB =P A A B A →→2cm /s Q D D E →1cm /s P A P Q P s t(1)当点在运动时,________;(用含的代数式表示)(2)求证:;(3)当,,三点共线时,求的值.P A B →BP =t AB ED =P Q C t2点·教学评——质量跟踪练习题(一)八年级 数学(人教版) 参考答案一、选择题(本大题共15小题,每小题2分,共30分)题号123456789101112131415答案BDAABACBADBCCDC二、填空题(本大题共4小题,每小题2分,共8分)16.17.1218.19.13三、解答题(本大题共8小题,共62分)20.(6分)解:设这个多边形的边数为,则,解得:,这个多边形的边数是8....................................................................................................6分21.(6分)证明:,和都是直角三角形,在和中,,.........................................................................................6分22.(7分)(1)证明:,在和中,,;...........................................................................................4分(2),,,,,,...................................................................................................................7分23.(7分)解:由题意可得:,,,900︒20︒n (2)1803603n ︒︒-+=⨯8n =∴90B D ︒∠=∠= ABC ∴△ADC △Rt ABC ∴△Rt ADC △AB ADAC AC =⎧⎨=⎩Rt Rt (HL)ABC ADC ∴△≌△//AC DF ACB F∴∠=∠ABC △DEF △A DAC DF ACB F ∠=∠⎧⎪=⎨⎪∠=∠⎩(ASA)ABC DEF ∴△≌△ABC DEF △≌△BC EF ∴=BE CE CF CE ∴+=+BE CF ∴=7BF = 3CE =2BE CF ∴==90CDP PBA ︒∠=∠⇒57APB ︒∠= 33PAB ︒∴∠=,米,米,米,在和中,,,米,这栋6层楼高18米.........................................................................................................7分24.(8分)解:(1)平分,,,是的高,,,...........................................................................................4分(2),,,,平分,,..............................................................8分25.(8分)解:(1),,;....3分(2),点是的中点,,在和中,,,,33PAB CPD ︒∴∠=∠=30BD = 12PB =18DP BD PB ∴=-=BAP △DPC △CDP PBA PAB CPD CD PB ∠=∠⎧⎪∠=∠⎨⎪=⎩(AAS)BAP DPC ∴△≌△18AB DP ∴==∴BF ABC ∠30CBF ︒∠=260ABC CBF ︒∴∠=∠=AD ABC △90ADB ︒∴∠=906030BAD ︒︒︒∴∠=-=AFB FBC C ∠=∠+∠ 70AFB ︒∠=703040C ︒︒︒∴∠=-=18080BAC ABC C ︒︒∴∠=-∠-∠=AE BAC ∠40BAE ︒∴∠=403010DAE BAE BAD ︒︒︒∴∠=∠-∠=-=ABE ACE △≌△BDE CDE △≌△ABD ACD △≌△AB AC = D BC BD CD ∴=ABD △ACD △AB AC AD AD BD CD =⎧⎪=⎨⎪=⎩(SSS)ABD ACD ∴△≌△BDE CDE ∴∠=∠在和中,,,,在和中,,.................................................................................................8分(答案不唯一,推理正确即可得分)26.(8分)解:(1)70;..................................................................................................3分(2),理由如下:,平分,平分,,,,,,......................................................................................................................8分27.(12分)解:(1);........................................................................................3分(2)在和中,,,;.....................................................................................................................7分(2)根据题意得:,,则,,,在和中,BDE △CDE △BD CD BDE CDE DE DE =⎧⎪∠=∠⎨⎪=⎩(SAS)BDE CDE ∴△≌△BE CE ∴=ABE △ACE △AB AC AE AE BE CE =⎧⎪=⎨⎪=⎩(SSS)ABE ACE ∴△≌△2C D ∠=∠CBE CAB C ∠=∠+∠ AD CAB ∠BD CBE ∠12CBD CBF ∴∠=∠12CAD CAB ∠=∠12CBD CAD C ∴∠=∠+∠CBD D CAD C ∠+∠=∠+∠ 12CAD C D CAD C ∴∠+∠+∠=∠+∠2C D ∴∠=∠82t -ABC △EDC △AC EC ACB ECD BC DC =⎧⎪∠=∠⎨⎪=⎩(SAS)ABC EDC ∴△≌△AB ED ∴=DQ t =2AP t =8EQ t =-ABC EDC △≌△A E ∴∠=∠8cmDE AB ==ACP △ECQ △,,,当时,,解得:,当时,,,解得:,综上所述,当、、三点共线时,的值为或.......................................12分A E AC ECACP ECQ ∠=∠⎧⎪=⎨⎪∠=∠⎩(ASA)ACP ECQ ∴△≌△AP EQ ∴=∴04t ……28t t =-83t =48t <…162AP t =-1628t t ∴-=-8t =∴P C Q t 8s 8s 3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版八年级数学上册10月月考试卷附答案
一、选择题(共7小题;共42分)
1. 下列各组数分别表示三条线段的长度,不能组成三角形的是
A. ,,
B. ,,
C. ,,
D. ,,
2. 下列说法中错误的是
A. 三角形三条角平分线都在三角形的内部
B. 三角形三条中线都在三角形的内部
C. 三角形三条高都在三角形的内部
D. 三角形三条高至少有一条在三角形的内部
3. 如图,的角平分线,相交于点,,则
A. B. C. D.
4. 下列图形中有稳定性的是
A. 平行四边形
B. 正方形
C. 长方形
D. 直角三角形
5. 下面四个图形中,线段是的高的图是
A. B.
C. D.
6. 下列各组条件,不能判定的一组是
A. ,,
B. ,,
C. ,,
D. ,,
7. 已知图中的两个三角形全等,则的度数是
A. B. C. D.
二、填空题(共7小题;共42分)
8. 已知一个多边形的内角和与外角和之比为,则它的边数是.
9. 是的中线,,,和的周长的差
是.
10. 如图,是的角平分线,于点,若,
,则的度数是.
11. 如图,已知,,,则.
12. 如图所示,,,的大小关系是(用“”将它们连接起
来).
13. 点,,,在同一直线上,且,.请你只添加一个边
相等或角相等的条件(不再加辅助线),使.你添加的条件是:.
14. 如图,已知,且,,则
.
三、解答题(共5小题;共66分)
15. 如图,已知于点交于点,,,求
的度数.
16. 如图,,,为上两点,且,
.求证:.。
