材料科学基础二元相图
材料科学基础---二元相图

微分整理,得: 微分整理,
dG = −SdT +VdP + ∑µidni
µi =
∂G ∂ni T,P,r
(代表体系内物质传输的驱动力; 代表体系内物质传输的驱动力; 等温、 等温、等压及其它组元数量不变 的情况下,每增加单位摩尔i 的情况下,每增加单位摩尔 组 体系自由能的变化) 元,体系自由能的变化)
组织结构 相图 加工处理 特性 性能
相图热力学的基本要点
— 相平衡条件
设有一多元系,含组元 为 摩尔,组元2为 摩尔, 设有一多元系,含组元1为n1 摩尔,组元 为n2 摩尔 ……,则体系 , 吉布斯自由能 :
G = G(T, P, n1, n2,...)
(温度T、压力 、各组元物质量 i 的函数) 温度 、压力P、各组元物质量n 的函数)
相图提供的信息
某一成分的合金, 一定温度下 所处的状态、 某一成分的合金,在一定温度下,所处的状态、相组成 状态 合金在冷却过程中 发生了哪些反应或转变, 合金在冷却过程中,发生了哪些反应或转变,以及其开始与终了温度 冷却过程 一定成分的合金,在室温下具有什么样的平衡组织, 一定成分的合金,在室温下具有什么样的平衡组织,可以根据组织与 平衡组织 性能的关系,预测材料的性能 性能的关系,预测材料的性能 相图与材料的加工工艺性能 如流动性) 相图与材料的加工工艺性能(如流动性)存在一定的对应关系 新材料研发、材料加工过程中 过程中, 在新材料研发、材料加工过程中,都起着十分重要的作用
相图热力学的基本要点
— 吉布斯相律 Gibbs phase rule
相律:在平衡条件下,一个系统的组元数、相数、 相律:在平衡条件下,一个系统的组元数、相数、自由度数之
间的关系规律,相律的数学表达式: 间的关系规律,相律的数学表达式:
材料科学-二元相图

相图5.1 二元相图基本概念5.1.1 相平衡和相律1) 相平衡条件各组元在各相中的化学势相等。
在c个组元组成的系统中若有ρ个相则:μ1α=μ1β=μ1γ=....=μ1ρμ2α=μ2β=μ2γ=....=μ2ρ..........μcα=μcβ=μcγ=......=μcρ。
2) 相律系统的自由度与组元数和相数之间的关系f=C-P+2 其中:f:系统自由度数;C:系统组元数;P:系统相数在衡压的系统中(∆P=0),相律可写成:f=C-P+15.1.2相图的表示方法1. 单元系的相图相图:反映组织(相组成)和系统变量参数之间关系的一种工具对于单元系,若∆P≠0,则:f=C-P+2=3-p,最多可出现三相平衡。
例1:水的相图:水的相图纯铁的相图此图(a)反映了在确定的温度和压力下H2O的相组成,也反映温度和压力变化时相组成的变化。
若压强不变,相图是一条直线(b)。
例2:纯铁的相图-反映固态下的相转变可以看到纯铁在不同温度和压强下发生的相转变。
2. 二元系的相图1) 二元系的自由度根据相律:f=C-P+2,一般情况下P=0f=C-P+1=3-P系统最大的自由度是2(单相平衡)分别是:T (温度)W (一个组元的浓度)因此二元相图中,横坐标是成分(组元浓度),纵坐标是温度.2) 成分表示法设两组元(A,B)在二元系中的质量百分数为:w A、w B,摩尔百分数为:x A、x B,两者之间是可以相互转换的。
设:R A 、R B 为组元的原子量, 则:100%x R x R x R w B B A A A A A ⨯+=, %100⨯+=BB A A BB B x R x R x R w ;%100⨯+=BBA A A A A R w R w R w x , %100⨯+=BBA AB B B R w R w R w x3. 相图的建立可以从理论和实验两条途径获得相图实验:测临界点 理论:计算G-x 曲线测定临界点的方法:热分析、X 射线、热膨胀、磁性方法等。
材料科学基础——二元系相图

拓扑学形成空间利用率很高配位数大的一类结 构。利用两种尺寸不同原子的配合,尽是成四 面体堆垛(为主)。密堆结构配位数很高,都大 于12,可为14、15、16。
拓扑密堆结构可用配位多面体来描述:原子为 中心,周围原子用直线连接构成的多面体。多 面体的面为三角形,称为三角形配位多面体, 如此类推……
补充: 固溶体的微观不均匀性
(1) 晶格畸变
溶质溶剂原子大小不同--局部晶格畸变-- 弹性应力场--晶格常数变化。
(2) 偏聚与有序
固溶体中的溶质原子分布可分为无序分布、偏 聚分布和短程有序分布。
(3) 有序固溶体
溶质原子和溶剂原子分别占居固定位置,而 且晶胞中溶质和溶剂原子之比都是一定的, 又称有序固溶体。
当二组元的电负性差别较大时,可能形成正常价化合 物。 当电子浓度是控制因素,并达到21/12、21/13、 21/14时,可能形成电子化合物。
当尺寸因素为主要因素时,还要看电子浓度因素与电 化学因素:
1.当二组元的原子半径差Δr<8-15%,结构类型相同、 电负性相差很小、价电子数相等时,可能形成无限固 溶体;如果,Δr<15%,但结构不同,或 15%<Δr<20%,均可能形成有限固溶体。
合金相结构总结
当尺寸因素为主要因素时,还要看电子浓 度因素与电化学因素: 2. 30%<Δr<41%,电负性相差较大,可 能形成间隙化合物。 3.Δr>41%,电负性相差较大,可能形成 间隙相。 4. Δr>41%,电负性相差不大,可能形成 间隙固溶体。
3.3 二元相图的建立
由一种元素或化合物构成的晶体称为单组元晶体或 纯晶体,该体系称为单元系。
材料科学基础-6二元相图

2
Ω=0,>0,G-x曲线也有一最小值;
Ω>0, G-x曲线也有2个最小值,拐点内<0。
6.3.2 多相平衡的公切线原理
6.3.3 混合物的自由能和杠杆法则
6.3.4 从自由能—成分曲线推测相图
6.3.5 二元相图的几何规律
★相图中所有的相界线代表相变的温度和平衡相 成分,即平衡相成分沿着相界线随温度变化而变 化; ★两单相区之间必定有这两相的两相区-相区接 触法则; ★二元相图的三相平衡区为一水平线,其与三个 单相区的交点确定平衡相的浓度; ★两相区与单相区的分界线与三相等温线相交, 分界线的延长线进入另一两相区。
(1)单相区:3个, L、 α 、β (2)两相区: 3个, L+α 、L+β 、α +β 相区:1个, L+α+β (3)三
5.与匀晶和共晶相图的区别
(1)相同处
PDC线以上区域; PDC线以下、DF以右区域的
分析方法以及结晶过程与匀晶相同;
BPDF以内区域,与共晶线MEN线以下区域相同,
按照固ห้องสมุดไป่ตู้度线分析。 (2)不同处 包晶线PDC及包晶反应:L+α→β
6.10 铁碳合金相图 6.11 二元合金的凝固理论
第6章 二元合金相图及合金凝固
由一种元素或化合物构成的晶体称为单组元晶体或纯晶体,
该体系称为单元系。两个组元的为二元系,n个组元都是独立
的体系称为n元系。对于纯晶体材料而言,随着温度和压力的 变化,材料的组成相会发生变化。
从一种相到另一种相的转变称为相变。由不同固相之间的
2.非平衡共晶组织
a
非平衡共晶组织(成分位于a点稍左)一般分布在初晶α 的相界上,或者在枝晶间。可以通过扩散退火来消除,最终得
材料科学基础-8-二元相图(2)
第二节 二元相图
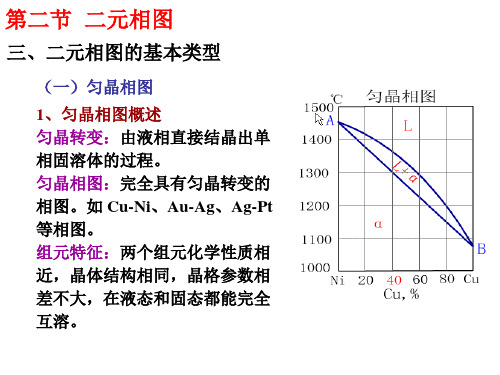
(一)匀晶相图
2、固溶体的平衡凝固
(3)固溶体的结晶规律
c.固溶体的凝固过程与纯金
属一样,也包括形核与长大
两个阶段
e. 平衡凝固得到的固溶体显
微组织和纯金属相同,除了
晶界外,晶粒之间和晶粒内
部的成分却是相同的。
d.合金结晶形核时需要能量
起伏和成分起伏
a. 固溶体的结晶与纯金属不同,它不在
(2)压力加工性:压力加工合金通常是相图上单相固溶体
成分范围内的单相合金或含有少量第二相的合金。
——单相固溶体合金切削加工性能
不够好,而具有两相组织的合金切
削加工性一般比较好。
(4)热处理性:
相图上无固态相变或固溶度变化的
合金不能进行热处理。
孔等缺陷。
——我国20世纪60年代开始研制Pt-Ag合金,但至今无法批量
稳定发展
——国内外通过添加Pd(钯)制成Pt-Pd-Ag三元合金,虽综合
性能不如Pt-Ag合金,但加工性能得以改善。
第二节 二元相图
(三)包晶相图
2、包晶合金的凝固及其平衡组织
(1)ω (Ag)为42.4%的Pt-Ag合金(合金I)
′
% =
× %
第二节 二元相图
1186℃
A
LP+αC ↔ βD
(三)包晶相图
f=2-3+1=0
包晶点
• 1、包晶相图
• 包晶转变:由一个固相与
液相作用生成另一个固相
的过程。
• 包晶相图:两组元在液态
无限互溶,固态下有限互
溶,并发生包晶反应的二
元系相图。
第二节 二元相图
2、包晶合金的凝固及其平衡组织
材料科学基础4-2二元相图及其类型

2016
液相线:
2020
组成
2017
凝固过程:
2021
后退
2018
合金1:
下页
01
04
02
03
如图所示
后退
下页
伪共晶 在非共晶成分处获得100%的共晶组织,只能在非平衡条件下得到。
不平衡凝固
后退 下页
不平衡共晶
m点以左,n点以右合金不平衡凝固时出现的共晶组织 。
01.
后退
02.
后退
下页
(2)共晶转变 在三相共存水平线men上,两条液相线汇交于e点。e点以上是液相区,e点下方是α+β两相共存区。这说明,相当于e点成分的液相,当冷至三相共存线men时会同时结晶出成分为m的α相与成分为n的β相。
三个单相区:
三个两相区:
后退
下页
共晶反应:
固相线:
2019
水的状态示意图
P
T
水
冰
气
其中f为系统的自由度数,C为组元数,P为自由度数等于组元数与相数之差再加上2。所谓自由度,即指独立可变的因
素,包括各组成相的成分、数量及温度、压力等。在金属及合金的制造和应用过程中,一般都是在常压下进行的,因此常把压力看成一个常数,相律的表达式可写成
相图基本知识
利用相图可以获取的信息 不同成分的材料在不同温度下存在哪些变化 各稳定相的相对量是多少 成分与温度变化时所可能发生的变化
第二节 二元相图及其类型
了解相图的分析和使用方法后,就可以了解合金的组织状态,进而预测合金的性能。另外,可以根据相图来制订合金的锻造和热处理工艺。
组元——组成材料最基本的、独立的物质。
二元相图【材料科学基础】

13
¾ α相: Cu-Ni合金形成的置换固溶体。 ¾ 在两相区中: 9 f =C-P+1=2-2+1= 1,两个相的成分和温度
变量中只有一个可以独立变化,其中一个固定后, 另一个也随之固定。 9 例如,温度一定,在此温度下两个平衡相成分固 定,由该温度水平线与该两相区边界线相交的两点 决定(杠杆定律)。
33
• 共晶反应:在一定的温度下,由一定成分的液相同 时结晶出成分一定且不相同的两个固相的转变过 程,也称共晶转变。其反应式为:
共晶温度
• 发生共晶反应时,根据相律 f = C – P + 1 = 2-3+1=0,所以三个相的成分不能变化,温度也 不能变化,因此共晶线为水平线,三个相在此线上 有确定的成分点。
以Cu-40%Ni合金为例
16
t0
●
t1
●
t2
●
t3
●
● ●
●
●
17
平衡结晶过程
形核和核长大
¾ 形核:过冷、结构起伏、能量起伏、成分起伏(微 小区域内成分偏离平均成分的现象)。
¾ 长大:建立平衡 界面前沿液相中溶质原子扩散 破坏平衡 晶体长大 恢复平衡 重
新建立平衡。
18
19
20
结晶特点: ¾ 结晶在一个温度范围内进行,f =1,平衡结晶过
共晶区如此。 • 组成共晶体的两相均为金属
型液固界面,两个相的长大 速度与过冷度关系的差别不 大,伪共晶区对称地扩大。
53
9 (2)伪共晶区偏向一边扩大
• 两个组元熔点差别大,共晶点偏向低熔点组元,伪共晶 区偏向高熔点组元。
材料科学基础--二元合金相图

均匀指微观尺度上的均匀,而非一般意义上的均匀。 化学成分允许连续变化 相与相之间有界面,可以用物理或机械办法分开。 相可以是单质,也可以是溶液、化合物等
气体:一般是一个相,如空气。
固体:物理性质和化学性质符合相均匀性的要求,几 个组分可以形成一个相,也可能出现多相。 液体:视其混溶程度而定。
(3)相平衡
W W L W 0 W eb W L ea W 0 eo
将(1)代入(2)式,移项可得
W ob WL oa
即杠杆定律。
杠杆定律的常用形式
改写W ob WL oa为比例的形式 W oa WL ob W0 ab 两边加 ,上式成为 ; 1 WL ob WL ob ob 取倒数, ;即L重量百分数L% 100% W0 ab ab W ao ao 同理, ;即相重量百分数 % 100% W0 ab ab
dG dG dG (i i )dn
在平衡时,显然dG=0 因为dn不等于0,所以相平衡条件为
i i
任意一组元在各相当中的化学位均相等相平衡的条件。
5.1.3 相律
吉布斯相律:f=c-p+2 C:系统的独立组元数 P:共存的平衡相数 f:自由度的数目,指给定合金系在平衡相数不变的前 提下,可独立改变变量(如温度、压力、浓度等)的 数目。 对于不含气相的凝聚系统,可视为恒压条件,相律表 述为: f=C-P+1
相互作用系数
(2)溶液的混合熵
S Mix N! k ln ; N N A N B 1m ol N B ! N A!
利用Stirring公式, N ! N ln N N ln S Mix Nk x A ln x A xB ln xB ; S Mix Rx A ln x A xB ln xB ;
材料科学基础-二元相图

相图的构成:
LE→( αC + βD)
相图的构成:线
AE和BE为两液相线; AC和BD为两固相线; CG和DH:(固溶度曲线) 固溶体α、β的溶解度线; CED:水平共晶线。
三个单相区: L、α、β; 三个双相区:L+α、L+β、
α+β 一个三相区:L+α+β,
CED共晶线。 29
连接转变开始点 和终了点
冷却过程中,不同相的热容量不同,冷却曲线上的斜率 不同, 曲线的转折点对应温度就是相变温度。
相图的测定: 二元相图:4000个(81%)(4950); 三元相图:8000(5%)(161700)。工作量巨大。 四元相图:1000(0.1%)(3921225) 问题:成分难控制,高熔点,难以达到相平衡
室温组织:α+βII +(α+β)
(α+β)%=L%=c2/ce, (α+βII)%=e2/ce
α%=c’g/fg× e2/ce,
βII%=fc’/fg × e2/ce
41
相: α+β
α初 :暗黑色粗大树枝状, βII :白色颗粒。
(α+β)
亚共晶组织:
α+βII +(α+β)
④合金Ⅳ:过共晶合金 L→L+β→β+(α+β)→β+αII+ (α+β)
4. 偏晶转变相图 fdc Ld→αf +Lc
偏晶转变:
L36→Cu +L87
72
5、具有合晶转变的相图
Lc+Ld→f
6、熔晶转变相图
→ +L
♣ 6.3.5 二元相图的几何规律
材料科学基础5-二元相图

第四节 二元包晶相图及合金凝固
2 平衡结晶过程及其组织
(2)成分在d-p之间合金的结晶
结晶过程:α剩余 ( 量的计算 ) ;
室温组织:α+β+αⅡ+βⅡ。
第四节 二元包晶相图及合金凝固
2 平衡结晶过程及其组织
第二节 二元匀晶相图
第二节 二元匀晶相图
第三节 二元共晶相图及合金凝固
共晶转变:由一定成分的液相同时结晶出两个一定 成分固相的转变。 共晶相图:具有共晶转变特征的相图(液态无限互 溶、固态有限互溶或完全不溶,且发生共晶反应)。 共晶组织:共晶转变产物。(是两相混合物)
第三节 二元共晶相图及合金凝固
第二节 二元匀晶相图
5 成分过冷及对生长形态的影响 (3)成分过冷形成的条件和影响 因素 条件:G/R<mC0(1-k0)/Dk0 合金固有参数: m( 液相线斜率 ), k0; 实 验 可 控 参 数 : G( 温 度 梯 度 ), R(凝固速度)。 (4)成分过冷对生长形态的影响 (正温度梯度下)G越小,成分 过冷 越大-生长形态:平面状 -胞状-树枝状。
2 合金的平衡结晶及其组 织(以Pb-Sn相图为例) (3)共晶合金 ① 凝固过程(冷却曲线、 相变、组织示意图)。 ② 共晶线上两相的相对 量计算。 ③ 室温组织 (α+β+αⅡ+βⅡ)及其 相对量计算。
第三节 二元共晶相图及合金凝固
2 合金的平衡结晶及其组 织(以Pb-Sn相图为例) (4)亚共晶合金 ① 凝固过程(冷却曲线、 相变、组织示意图)。 ② 共晶线上两相的相对 量计算。 ③ 室温组织 (α+βⅡ+α+β)及其相 对量计算。
b. 冷却速度非常慢→有扩散和对流→固相不混合、液 相完全混合。 c. 冷却速度很大→仅有扩散→固相不混合、液相完全 不混合。
材料科学基础_第5章_二元相图

Cu
18 20
30 40
66 60 80
Ni 相对质量为1/4。溶体合金的平衡凝固及组织
➢ 平衡凝固是指凝固过程中每个阶段都能达到平衡,因此 平衡凝固是在极其缓慢的冷速下实现的。现以30%Ni和 70%Cu的铜镍合金为例来说明固溶体的平衡冷却过程及其 组织的。
11
冷却曲线 t Ⅱ
23
X2合金结晶过程分析
L
(共晶合金)
T,C
183
L
L+
L+
c
d
e
+
T,C
(+ )
围内凝固,具有变温凝固的特征 ②还需要成分起伏
15
5.3.2 二元共晶相图 两组元在液态无限互溶,固态有限溶解,通过共晶反
应形成两相机械混合物的二元合金称为二元共晶相图。共 晶反应是液相在冷却过程中同时结晶出两个结构不同的固
相的过程。 L
16
Ta,tb分别是Pb,Sn的熔点 M:锡在铅中的最大溶解度。N:铅在锡中的最大溶解度 E:为共晶点,具有该点成分的合金在恒温183℃发生共 晶转变LE→aM+ΒN,共晶转变是具有一定成分的液相在恒 温下同时转变为两个具有一定成分和结构的固相的过程。 F:室温时锡在铅中的溶解度;G:室温时铅在锡中的溶 解度
之间一定是由这两个相组成的两相区。如铁区(线)区(
材料科学基础4-2二元相图及其类型
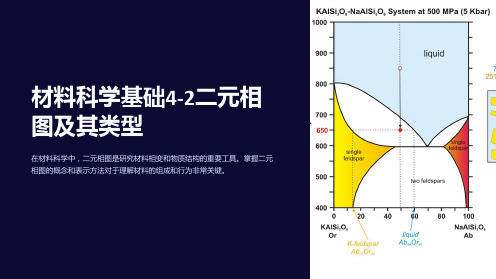
在材料科学中,二元相图是研究材料相变和物质结构的重要工具。掌握二元 相图的概念和表示方法对于理解材料的组成和行为非常关键。
二元相图的概念和基本原理
二元相图是描述两种组分在不同温度和组成条件下的相变行为的图表。它由 相平衡曲线、相区、反应区和相组成等基本元素组成。
总结和结论
二元相图是材料科学中重要的工具,它能够帮助我们理解材料的相变行为和 结构特点。掌握二元相图的基本原理和应用是进行材料研究和开发的关键。
不平衡相图描述的是在非平衡条件下的相变行为。它们可以是偏离平衡相图 的曲线,或者是描述非平衡相变过程的相图。
常见的二元相图实例
常见的二元相图实例包括铜-锌、铁-碳、铝-硅等。通过研究这些实例,我们 可以更好地理解不同材料的相变行为和结构特点。
二元相图在材料科学中的应用
二元相图在材料科学中具有广泛的应用,包括合金设计、材料制备和性能优 化等方面。通过研究相图,我们可以更好地控制和改进材二元相图通常由实验数据和计算结果得出。它们可以用等温截面、等组分截面和等压截面等方式进行表 示,以便更好地理解相变的规律和行为。
平衡相图的类型和特点
平衡相图分为几种类型,如共晶、共饱和、共晶点偏离、共析和不共晶等。每种类型都有其特定的特点 和相变行为。
不平衡相图的类型和特点
材料科学基础.第四章
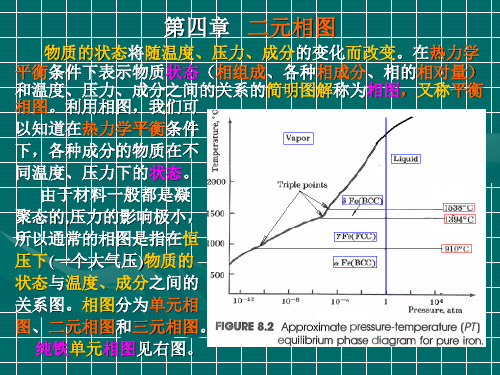
(1)平衡凝固溶质分布 冷却时固相的溶质分布
这种情况下,冷速极其缓慢, 固体、液体中溶质原子充
分扩散。凝固结束时,各部分成分都为Co,无偏析产生,如图
中的Co水平线。
(2)实际凝固(正常凝固)溶质分布 溶质分布及表达式见图。 ①液体中溶质完全混合--偏析严重,左端纯化; ②液体中溶质完全不混合—比较符合实际凝固; ③液体中溶质部分混合。
f=c-p+1(←f=c-p+2,温度、压力) 自由度数是指在木改变系统平衡相的数目的条件厂,可独立改变
的,不影响(影响/决定体系状态)合金状态的因素(如温度、压 力、平衡相成分)的数目。
自由度数的最小值为零,f =0时发生恒温转变,例如纯金属结 晶、二元合金的三相平衡转变、三元合金的四相平衡转变等。
1
4( 3
h2 hk k 2 a2
)(
l c
)2
六方系
对复杂点阵(体心立方,面心立方等),要考虑晶面层数的增加。 体心立方(001)面之间还有一同类的晶面(002),因此间距减半。
1.2.4 晶体的极射赤面投影
通过投影图可将立体图表现于平面上。晶体投影方法很多, 包括球面投影和极射赤面投影。
不平衡凝固的冷速越快,平均成分线的偏离越大。合金内部成分
不均匀现象称为偏析,晶粒内部成分不均匀称为“晶内偏析”, 树
枝晶内的偏析称为“枝晶偏析”。生产中用扩散退火(均匀化退 火)
4.固溶体合金凝固时的溶质量分布 合金凝固时的溶质重新分布,导致宏观偏析和微观偏析并对 晶体的生长形态产生很大影响。 匀晶合金冷却时,固相浓度CS与液相浓度CL的比值K0= CS/CL, 称为平衡分配系数,如图示。 讨论图4.7水平放置的圆 棒容器中,合金液体的定
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LC
+
αP
→ β 1186℃
D
1186℃—包晶温度,此温度下三相平衡,f =c-
p+1=0,
自由度为0,包晶转变是恒温转变;
4.相区
(1)单相区:3个, L、 α 、β
(2)两相区: 3个, L+α 、L+β 、α +β (3)三 相区:1个, L+α+β
5.与匀晶和共晶相图的区别 (1)相同处
PDC线以上区域; PDC线以下、DF以右区域的 分析方法以及结晶过程与匀晶相同;
L
L+A
L+B
A+B
6.4 匀晶相图
6.4.1相图分析
B A
1.点:A、B分别是Cu和Ni的熔点; 2.相:2个,L 、α相; 3.线:2条,液相线和固相线; 4.相区: 2个单相区,分别是L、 α的单相区;
1个两相区,L +α; 单相区和两相区被液相线和固相线隔开。
α2
固溶体结晶时需要成分起伏:液态金属中 存在有偏离合金平均成分的区域,一定条件下 该区域此起彼伏的现象。
1.相 (1)L相: Pb、Sn的熔体 , (2)α相、β相分别是以Pb( Sn)为溶剂、 Sn ( Pb )
为溶质的固溶体;
2.点 (1)tA 、tB分别是纯金属Pb、Sn的熔点; (2)M、N分别是共晶温度下α( β)相的最大溶解度点; (3)F、G分别是室温下α( β)相的最大溶解度点;
3.线 (1)液相线: tA E: L→ α, tB E: L→ β( 此处析出的α和 β称为初
❖ 偏析-合金内部成分不均匀; ❖ 晶内偏析-晶粒内部成分不均匀; ❖ 枝晶偏析-树枝晶内的偏析; ❖ 枝晶偏析对铸件影响很大,可在低于固相线
温度下进行均匀化退火或进行热轧、锻造降 低枝晶偏析; ❖ 不平衡凝固偏离固相线、液相线,但液、固 相界面仍然符合相图的平衡关系。
6.5 共晶相图
在T1温度下,L相中必须有α1成分的区域 才能结晶,即满足结晶时的成分条件(还必须 包括结构起伏和能量起伏)。
开始结晶时,成分为L 1的液相与成分为α1 的固相平衡。
有极大点和极小点的匀晶相图
6.4.2 固溶体的平衡凝固
利用杠杆定律计算两平衡相的相对量
在T2温度下,合金x (成分O)由液相(成分xL) 和重固Wl相,(固成相分重xWα)α,组有成:,令合金重W0,液相
1.伪共晶组织
(a)伪共晶区对称:两组元熔点相近;
(b)伪共晶区不对称:两组元熔点相差较大,共晶点偏向低 熔点组元,伪共晶区偏向高熔点组元。
不平衡凝固条件下,非共晶成分的合金可全部得到伪共晶 组织,共晶成分的合金则可能得到亚共晶或过共晶组织。
2.非平衡共晶组织
a
非平衡共晶组织(成分位于a点稍左)一般分布在初晶α 的相界上,或者在枝晶间。可以通过扩散退火来消除,最终得 到均匀的α单相固溶体组织 。
6.3.1固溶体的自由能—成分曲线
G=G0-T△Sm+△Hm △Hm=ΩxAxB
Ω=NAz[eAB-(eAA+eBB)/2]
d2G=-2+RT 1
dx2
xAxB
Ω<0,>0,G-x曲线有一最小值; Ω=0,>0,G-x曲线也有一最小值; Ω>0, G-x曲线也有2个最小值,拐点内<0。
6.3.2 多相平衡的公切线原理
6.3.3 混合物的自由能和杠杆法则
6.3.4 从自由能—成分曲线推测相图
6.3.5 二元相图的几何规律
★相图中所有的相界线代表相变的温度和平衡相 成分,即平衡相成分沿着相界线随温度变化而变 化; ★两单相区之间必定有这两相的两相区-相区接 触法则; ★二元相图的三相平衡区为一水平线,其与三个 单相区的交点确定平衡相的浓度; ★两相区与单相区的分界线与三相等温线相交, 分界线的延长线进入另一两相区。
成部分。 室温下,共晶合金的相组成物为α和β;组织组成物为
(α+β )。 相组成物相对量计算: α%= ( E1G/ FG )×100% ; β%=(FE1/ FG)×100% 组织组成物: 为100%的共晶组织(α+β )
3.亚共晶合金(亚共晶:Sn%=19~61.9%)
1以上,液相冷却;
1→2,L →α初; 2 点, α初+ L → α初+ ( αM +βN ) , 2以下,α沿着MF线变化,α→ βⅡ
β沿着NG线变化,β→αⅡ 室温组织: α初+ βⅡ + ( α+β )或
α初+ ( α+β ) (共晶组织中的二次相看不见)。
T
1 2 2′
3 τ
共晶温度下:亚共晶合金的相对量
(Sn%=19~61.9%)之间的亚共晶合金,其相组成物都为α 、β,组织组 成物都为α+ (α+β) ;但是其相对量随Sn含量的改变而改变。
(3)三相区:1个, L+α+β
5.与匀晶相图的区别 相同点: MEN线以上区域,分析方法以及结晶过程
与匀晶相同;
不同点: 共晶线MEN线及以下区域,需要重点关
注。
6.5.2共晶合金的平衡凝固
1.固溶体合金(183℃时,Pb%≤19%;Sn%≥97.5)
T
1 2 3
1以上,液相冷却; 1→2,L →α; 2→3,α冷却; 3以下,α→βⅡ。 室温组织:α初+βⅡ
晶或先共晶相等) ; (2)固相线:tA M: L→ α, tB N: L→ β ; (3)固溶度线:不同温度下固溶体最大溶解度的连线(t1 — M1 ;
t2— M2 ; t3 — M3 …… ) ,随温度降低,固溶体沿此线变化,
析出第二相(根据析出次序而称之,相对于从液相中析出的初 晶而言,指的是从固相中析出);
W0= Wl + Wα 溶质含量为:
W0 × x = Wl × xL + Wα × xα (Wl + Wα)× x = Wl × xL + Wα × xα Wl × ( x - xL)= Wα ×(xα-x) Wl ×OL2= Wα ×α2 O
Wl / Wα = α2 O/ OL2% 两平衡相的相对量与其在相图上平衡成分
t1 t2 t3
M1 M2 M3
。
6.5.1相图分析
★共晶相图——液态下无限互溶,固态下有限溶解, 且具有共晶转变的相图; ★共晶转变—— 一定温度下,一个一定成分的液相 同时转变为两个各具有一定成分固相的反应; L→α+β ★共晶合金—— 铸铁,Al-Si, Al-Cu, Pb-Sn, Pb-Sb, Ag-Cu等具有共晶转变的合金; ★共晶合金有优良的铸造性能;
1.相 (1)L相: Pt、Ag的熔体 , (2)α相、β相分别是以Pt ( Ag)为溶剂、 Ag ( Pt )
为溶质的固溶体; 2.点 (1)A 、B分别是纯金属Pt、Ag的熔点; (2)P、D分别是包晶温度下α( β)相的最大溶解度点,
C点包晶反应时的液相成分点; (3)B、F分别是室温下α( β)相的最大溶解度点;
包晶转变时, β相依附在α相形核,直至全部包住 α相。此 时, β相内部α相的Pt含量高, β相外部L相的Ag含量高, Pt原 子向外扩散, Ag原子向内扩散。新相β两侧L相和α相的成分接 近D点, β相消耗L相和α相从而长大。当L相和α相同时消耗完, 包晶转变结束,在包晶温度下只有β相。
发生包晶转变时, L相和α相的两相相对量计算如下: W(L)=DP/DC=(42.5-10.5)/(66.3-10.5)=57.3% W(α)=PC/DC=(66.3-42.5)/(66.3-10.5)=42.7% 即57.3%的液相和 42.7%的α相正好全部转变为β相
α,β (α+β)
α,β β+(α+β)+αⅡ
α,β β+αⅡ
课后练习:过共晶合金( 61.9~97.5% Sn)、N点以右合金 ( 61.9~97.5% Sn)
1.分析合金的平衡结晶过程; 2.画出金相组织示意图; 3.计算室温下相组成物和组织组成物的相对量; 4.画出冷却曲线。
6.5.3共晶合金的非平衡凝固
(α+β)
α初
Байду номын сангаас
β初
亚共晶组织
过共晶组织
共晶合金的相组成物和组织组成物
组织名称
Sn%<19% 19~61.9% Sn Pb基固溶体 亚共晶合金
61.9% Sn 共晶合金
61.9~97.5% Sn 过共晶合金
>97.5% Sn Sn基固溶体
相组成物
α,β
组织组成物 α+βⅡ
α,β α+(α+β)+βⅡ
MF: α → βⅡ, NG : β → αⅡ
(4)共晶线:MEN,位于该线内的合金,在共晶温 度下都要发生共晶转变。
LE →tE αM +βN
tE—共晶温度,此温度下三相平衡,f =c-p+1=0, 自由度为0,共晶转变是恒温转变; 4.相区
(1)单相区:3个, L、 α 、β
(2)两相区: 3个, L+α 、L+β 、α +β ( α 、 β两相为机械混合物)
T 1
D
D′
4
τ
2.合金Ⅱ
1以上,液相冷却;
1→2,L →α;
2点,包晶转变:LC +αP →βD 包晶温度: W(L)=2P/DC>57.3%,说明发生包晶反应后有液
3.离异共晶
离异共晶:条件为a点稍右,特点是初生相很 多,共晶体量很少。
离异共晶
初晶
a
6.6 包晶相图
2
4.6.1相图分析
★包晶相图——液态下无限互溶,固态下有限 溶解,且具有包晶转变的相图; ★包晶转变—— 一定温度下,一个一定成分的 液相和一个一定成分的固相同时转变另一具有 一定成分固相的反应: L+α→β 具有包晶转变的二元合金有Fe-C、Cu-Zn、AgSn、Ag-Pt等。
