材料科学基础-6二元相图
合集下载
上海交大-材料科学基础-第六章

2020/4/27
例:
(1)固溶体合金的相图所示,试根据相图确定:
a)成分为40%B的合金首 先凝固出来的固体成分; b)若首先凝固出来的固体 成分含60%B,合金的成 分为多少?
2020/4/27
c)成分为70%B的合金最 后凝固的液体成分;
d)合金成分为50%B,凝 固到某温度时液相含有 40%B,固体含有80%B, 此时液体和固体各占多少 分数?
1)由上列数据绘出Ni-Cu的相图,并标明每一区域存 在的相;
2)将50%混合物自1400℃逐渐冷却到1200℃,说明所 发生的变化,并注出开始凝固、凝固终了及1275℃互成 平衡时液相与固相的组成。
2020/4/27
(4)铋(熔点为271.5℃)和锑(熔点为630.7℃)在液 态和固态时均能彼此无限互溶,ωBi=50%的合金在 520℃时开始凝固出成分为ωSb=87%的固相。ωBi=80% 的合金在400℃时开始凝固出成分为ωSb=64%的固相。 根据上述条件,绘出Bi—Sb相图,并标出各线和相区的 名称。
2020/4/27
两组元无限互溶的条件: • 晶体结构相同 • 原子尺寸相近,尺寸差<15% • 相同的原子价 • 相似的电负性(化学亲和力)
2020/4/27
2020/4/27
具有极值的匀晶系相图
2020/4/27
有晶型转变的匀晶系相图
晶型转变曲线
2020/4/27
平衡凝固过程 指凝固过程中的每个阶段都能达到平衡。 在极其缓慢冷却条件下的凝固
2020/4/27
(2)A的熔点为300℃和B的熔点为700℃(650),A和 B在液态和固态时均能彼此无限互溶,ωA=50%的合 金在500℃时开始凝固出成分为ωB=90%(87)的固相。 ωA=80%的合金在400℃时开始凝固出成分为 ωB=60%(64)的固相。根据上述条件,要求:
例:
(1)固溶体合金的相图所示,试根据相图确定:
a)成分为40%B的合金首 先凝固出来的固体成分; b)若首先凝固出来的固体 成分含60%B,合金的成 分为多少?
2020/4/27
c)成分为70%B的合金最 后凝固的液体成分;
d)合金成分为50%B,凝 固到某温度时液相含有 40%B,固体含有80%B, 此时液体和固体各占多少 分数?
1)由上列数据绘出Ni-Cu的相图,并标明每一区域存 在的相;
2)将50%混合物自1400℃逐渐冷却到1200℃,说明所 发生的变化,并注出开始凝固、凝固终了及1275℃互成 平衡时液相与固相的组成。
2020/4/27
(4)铋(熔点为271.5℃)和锑(熔点为630.7℃)在液 态和固态时均能彼此无限互溶,ωBi=50%的合金在 520℃时开始凝固出成分为ωSb=87%的固相。ωBi=80% 的合金在400℃时开始凝固出成分为ωSb=64%的固相。 根据上述条件,绘出Bi—Sb相图,并标出各线和相区的 名称。
2020/4/27
两组元无限互溶的条件: • 晶体结构相同 • 原子尺寸相近,尺寸差<15% • 相同的原子价 • 相似的电负性(化学亲和力)
2020/4/27
2020/4/27
具有极值的匀晶系相图
2020/4/27
有晶型转变的匀晶系相图
晶型转变曲线
2020/4/27
平衡凝固过程 指凝固过程中的每个阶段都能达到平衡。 在极其缓慢冷却条件下的凝固
2020/4/27
(2)A的熔点为300℃和B的熔点为700℃(650),A和 B在液态和固态时均能彼此无限互溶,ωA=50%的合 金在500℃时开始凝固出成分为ωB=90%(87)的固相。 ωA=80%的合金在400℃时开始凝固出成分为 ωB=60%(64)的固相。根据上述条件,要求:
材料科学基础-8-二元相图(2)
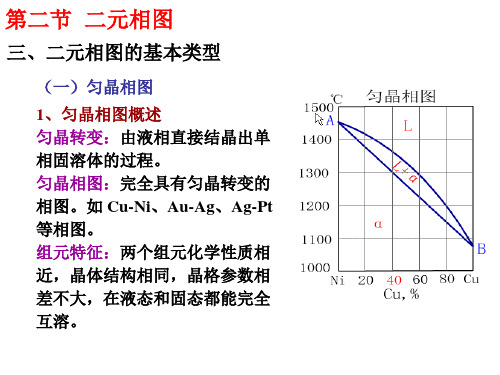
第二节 二元相图
(一)匀晶相图
2、固溶体的平衡凝固
(3)固溶体的结晶规律
c.固溶体的凝固过程与纯金
属一样,也包括形核与长大
两个阶段
e. 平衡凝固得到的固溶体显
微组织和纯金属相同,除了
晶界外,晶粒之间和晶粒内
部的成分却是相同的。
d.合金结晶形核时需要能量
起伏和成分起伏
a. 固溶体的结晶与纯金属不同,它不在
(2)压力加工性:压力加工合金通常是相图上单相固溶体
成分范围内的单相合金或含有少量第二相的合金。
——单相固溶体合金切削加工性能
不够好,而具有两相组织的合金切
削加工性一般比较好。
(4)热处理性:
相图上无固态相变或固溶度变化的
合金不能进行热处理。
孔等缺陷。
——我国20世纪60年代开始研制Pt-Ag合金,但至今无法批量
稳定发展
——国内外通过添加Pd(钯)制成Pt-Pd-Ag三元合金,虽综合
性能不如Pt-Ag合金,但加工性能得以改善。
第二节 二元相图
(三)包晶相图
2、包晶合金的凝固及其平衡组织
(1)ω (Ag)为42.4%的Pt-Ag合金(合金I)
′
% =
× %
第二节 二元相图
1186℃
A
LP+αC ↔ βD
(三)包晶相图
f=2-3+1=0
包晶点
• 1、包晶相图
• 包晶转变:由一个固相与
液相作用生成另一个固相
的过程。
• 包晶相图:两组元在液态
无限互溶,固态下有限互
溶,并发生包晶反应的二
元系相图。
第二节 二元相图
2、包晶合金的凝固及其平衡组织
无机材料科学基础 第6章 相平衡

过热晶型蒸汽压曲 线与过冷熔体蒸汽压 曲线的交点: 晶型的熔点
特点: 晶型转变温度低于二
个晶相的熔点,晶型 转变温度点处在稳定 相区之内。
G
C 晶型的熔点
转变关系为:
B
L
可逆转变
晶型和晶型 的转变点 图6-3a 可逆多晶转变的单元相图
Construction Materials
Construction Materials
6.3.1.6 形成连续固溶体的二元相图
M’高温熔体平衡冷却 特点:没有无变量点 , 系统中只存在液态溶 液和固态溶液。
液相线aL2b 以上相区为高温熔体 液态溶液与固溶体平 衡的固液二相区 固相线aS2b 以下相区为固溶体
Construction Materials
液相点在P点不 变,液相量在减 少,同时固相组 成中B晶体在不 断减少,C晶体 在不断增加,至 D点B晶体被回吸 完毕 Materials
析晶路程表示法
液相点
L LB 2 K P LP B C , f 0 f=2 f=1
L C
f=1
固相点
6.3.1.7 形成有限固溶体的二元相图
特点:组分A、B间可以形成固溶体 但溶解度有限,不能以任意比例互溶。
2个固溶体
7条线 6个相区 3个无变量点
Construction Materials
析晶路程表示法
液相点
L S B ( A) L M’ L1 E LE S A( B ) S B ( A) , f 0 f=2 f=1
f=2
L A B, f
0
I G K
A
Construction Materials
材料科学基础 -二元合金相图

1、相图分析
(1)相区 单相区:L, a, b 两相区: L+a, L+ b,a+b
(2)相变线
TAP及TBP:L→a, L→b。
TAC及TBD:初生a及b结晶终了线。
CE及DF:
a
→bII,b→
a
。
II
CDP: L+ a →b。
液相线:TAPTB
固相线:TACDTB
(3)相变点 P:包晶转变点,发生包晶反应的液相成分点。
相区
单相区:L, a, b 两相区: L+a, L+ b,a+b
相变线
TAE及TBE:初生(初晶)a及b析出线 即L→a, L→b
TAM及TBN:初生a及b结晶终了线 MF及NG: a及b溶解度变化线
即a→bII,b→aII MEN: 共晶线,即L→a+b
相变点
TA及TB:纯组元A、B的熔点 M及N:a及b的最大溶解度点 F及G:a及b室温溶解度点 E:共晶点,发生共晶反应的液相成分点
问题:假定合金分别冷却到1,2,3,4温度开始结晶,获得的组织特点有何不同?
(2)晶内偏析共晶
晶内偏析共晶: 端部固溶体合金非平衡结晶时出现共晶组织
的现象。 由于晶内偏析共晶数量较少,往往以离异
共晶形式存在。 两种情况促使离异共晶形成: ►靠近极限溶解度的端部固溶体的非平衡冷却。 ►靠近极限溶解度的亚共晶合金的平衡冷却。
(3)x2合金
组织组成物:a0+ b包+aII +bII
Wa II
DF EF
Cx2 CD
100%
相 对 量
Wb II
CE Dx2 EF CD
100%
计 算
Wa0
无机材料科学基础第六章相平衡(11)

晶型Ⅱ
晶型转变是不可逆的。
如:任意温度Tx下,稳定存在的应是具有最小蒸气压的晶型Ⅰ。 当在Tx温度下结晶时,其过程为:L→晶型Ⅱ→晶型Ⅰ。如果晶 型Ⅱ转变为晶型Ⅰ很快,则这一过程能实现;
图6-8表示晶型Ⅰ在T1温度熔融成为液相。晶型Ⅱ的蒸气压在 整个温度范围都高于晶型Ⅰ,即晶型Ⅱ处于介稳态。直接加热晶型
关系如下:
熔体(1600℃) 熔体 (1670℃)
α-石英
870℃ α-鳞石英
573℃
163℃
1470℃ α-方石英
1723℃ 熔融石英
180~270℃
急
冷
β-石英
β-鳞石英
β-方石英
石英玻璃
117℃ γ-鳞石英 重建性转变(慢)
位
移
性 转
(快)
变
26
(一)相图介绍
相图上共有六个单相区,分别表示β-石英、α-石英、α-鳞石英、α方石英、SiO2熔体及SiO2蒸气六个热力学稳定态的单相区;
第六章 相平衡 §6-1 凝聚态系统相平衡特点(相律
等基本概念、硅酸盐系统相平衡特点)
§6-2 一元系统(SiO2系统相图及应用) §6-3 二元系统(具有一个低共熔点的二元系
统相图、生成一个不一致熔融化合物的二元系统相图;
CaO-SiO2系统相图、Al2O3-SiO2系统相图及其应用)
§6-4 三元系统 §6-5 四元系统
20
(2)线
BG线:过热晶型Ⅰ的升华曲线; GH线:过热晶型Ⅰ的熔融曲线; GC线:过冷熔体的蒸发(蒸汽压)曲线; KB线:过冷晶型Ⅱ的升华曲线。
(3)点 G点:过热晶型Ⅰ、过冷熔体 和气相之间的三相介稳平衡点 ,是一个介稳三相点。
21
材料科学基础第六讲-相图

温度降到3点时,合金III全部转化为β固 溶体。
3-4点时,为单相固溶体,不发生变化。 4点以下,将从β相析出次生相αII
§4.4其它类型的二元合金相图
第五节 复杂相图
§5.1 二元合金相图的分析和使用
I 包晶反应:L+α β II 包晶反应:L+ β γ III 包晶反应:L+ ε η IV 共析反应: β α + γ V 共析反应: γ α + δ VI 共析反应: δ α + ε VII 共析反应: ζ δ + ε VIII 包析反应: γ + ε ζ IX 包析反应: γ + ζ δ X 熔晶反应: γ ε + L XI 共晶反应: L η + θ
相律:表示在平衡条件下,系统的自由度数、组元 数和相数之间的关系。它是检验、分析和使用相图 的重要工具。
F=C-P+2
F-平衡系统的自由度数 C-平衡系统的组元数 P-平衡系统的相数
当压力为常数时:F=C-P+1
J. Willard Gibbs
自由度:指平衡系统中可以独立改变的因素(如温度, 美国物理学家 压力,成分)等。纯金属的自由度最多一个,二元系 (1839-1903)
包晶转变区的特征是:反应相是液相和一个固相,其成分点位于水 平线的两端,所形成的固相位于水平线中间的下方。
典型合金的平衡结晶及组织
(一)含银量42.4%的铂银合金
当合金I自液态缓冷到1点时, 开始结晶出α相,与匀晶系 合金的结晶完全相同
当温度降到tD时,合金中 α 相的成分到P点,液相的成 分到C点。
应用相图时要注意的问题
连接线(等温线):两个平衡相成分点之间的连线
第三节 一元系相图
3-4点时,为单相固溶体,不发生变化。 4点以下,将从β相析出次生相αII
§4.4其它类型的二元合金相图
第五节 复杂相图
§5.1 二元合金相图的分析和使用
I 包晶反应:L+α β II 包晶反应:L+ β γ III 包晶反应:L+ ε η IV 共析反应: β α + γ V 共析反应: γ α + δ VI 共析反应: δ α + ε VII 共析反应: ζ δ + ε VIII 包析反应: γ + ε ζ IX 包析反应: γ + ζ δ X 熔晶反应: γ ε + L XI 共晶反应: L η + θ
相律:表示在平衡条件下,系统的自由度数、组元 数和相数之间的关系。它是检验、分析和使用相图 的重要工具。
F=C-P+2
F-平衡系统的自由度数 C-平衡系统的组元数 P-平衡系统的相数
当压力为常数时:F=C-P+1
J. Willard Gibbs
自由度:指平衡系统中可以独立改变的因素(如温度, 美国物理学家 压力,成分)等。纯金属的自由度最多一个,二元系 (1839-1903)
包晶转变区的特征是:反应相是液相和一个固相,其成分点位于水 平线的两端,所形成的固相位于水平线中间的下方。
典型合金的平衡结晶及组织
(一)含银量42.4%的铂银合金
当合金I自液态缓冷到1点时, 开始结晶出α相,与匀晶系 合金的结晶完全相同
当温度降到tD时,合金中 α 相的成分到P点,液相的成 分到C点。
应用相图时要注意的问题
连接线(等温线):两个平衡相成分点之间的连线
第三节 一元系相图
二元相图【材料科学基础】

相区: 液相区(L)、固相区 (α)、固液两相共存 区(L+α)。
13
¾ α相: Cu-Ni合金形成的置换固溶体。 ¾ 在两相区中: 9 f =C-P+1=2-2+1= 1,两个相的成分和温度
变量中只有一个可以独立变化,其中一个固定后, 另一个也随之固定。 9 例如,温度一定,在此温度下两个平衡相成分固 定,由该温度水平线与该两相区边界线相交的两点 决定(杠杆定律)。
33
• 共晶反应:在一定的温度下,由一定成分的液相同 时结晶出成分一定且不相同的两个固相的转变过 程,也称共晶转变。其反应式为:
共晶温度
• 发生共晶反应时,根据相律 f = C – P + 1 = 2-3+1=0,所以三个相的成分不能变化,温度也 不能变化,因此共晶线为水平线,三个相在此线上 有确定的成分点。
以Cu-40%Ni合金为例
16
t0
●
t1
●
t2
●
t3
●
● ●
●
●
17
平衡结晶过程
形核和核长大
¾ 形核:过冷、结构起伏、能量起伏、成分起伏(微 小区域内成分偏离平均成分的现象)。
¾ 长大:建立平衡 界面前沿液相中溶质原子扩散 破坏平衡 晶体长大 恢复平衡 重
新建立平衡。
18
19
20
结晶特点: ¾ 结晶在一个温度范围内进行,f =1,平衡结晶过
共晶区如此。 • 组成共晶体的两相均为金属
型液固界面,两个相的长大 速度与过冷度关系的差别不 大,伪共晶区对称地扩大。
53
9 (2)伪共晶区偏向一边扩大
• 两个组元熔点差别大,共晶点偏向低熔点组元,伪共晶 区偏向高熔点组元。
13
¾ α相: Cu-Ni合金形成的置换固溶体。 ¾ 在两相区中: 9 f =C-P+1=2-2+1= 1,两个相的成分和温度
变量中只有一个可以独立变化,其中一个固定后, 另一个也随之固定。 9 例如,温度一定,在此温度下两个平衡相成分固 定,由该温度水平线与该两相区边界线相交的两点 决定(杠杆定律)。
33
• 共晶反应:在一定的温度下,由一定成分的液相同 时结晶出成分一定且不相同的两个固相的转变过 程,也称共晶转变。其反应式为:
共晶温度
• 发生共晶反应时,根据相律 f = C – P + 1 = 2-3+1=0,所以三个相的成分不能变化,温度也 不能变化,因此共晶线为水平线,三个相在此线上 有确定的成分点。
以Cu-40%Ni合金为例
16
t0
●
t1
●
t2
●
t3
●
● ●
●
●
17
平衡结晶过程
形核和核长大
¾ 形核:过冷、结构起伏、能量起伏、成分起伏(微 小区域内成分偏离平均成分的现象)。
¾ 长大:建立平衡 界面前沿液相中溶质原子扩散 破坏平衡 晶体长大 恢复平衡 重
新建立平衡。
18
19
20
结晶特点: ¾ 结晶在一个温度范围内进行,f =1,平衡结晶过
共晶区如此。 • 组成共晶体的两相均为金属
型液固界面,两个相的长大 速度与过冷度关系的差别不 大,伪共晶区对称地扩大。
53
9 (2)伪共晶区偏向一边扩大
• 两个组元熔点差别大,共晶点偏向低熔点组元,伪共晶 区偏向高熔点组元。
材料科学基础(Fe-C相图)

✓ 碳在中的溶解度曲线Biblioteka ✓ 记为Acm温度。Acm
✓ 低于此温度,奥
氏体中将析出
Fe3C , 称为二次渗碳体
Fe3CII。
(3) PQ线
✓ C在F中溶解度曲线。 ✓ 727℃时,碳在F中最
大解度为0.0218%; ✓ F从727℃冷却时会析
出极少量的渗碳体, 三次渗碳体Fe3CIII。 ✓ 室温下含<0.0008%C。
1899年英国人罗伯茨-奥斯汀(W.C.RobertsAusten)制定了第一张铁碳相图;1897年完成 初稿 , 1899年彻底完成。
洛兹本 (H.W.Bakhius Roozeboom)首先在合 金系统中应用吉布斯(Gibbs)相律修订铁碳相 图 ,1900年制定出较完整的铁碳平衡图。
相图的出现,是金属学发展的一个里程碑。
过共析钢球化退火:
球状P (球状Fe3C+F)
小结:
(5)共晶白口铁(C%≈4.3%)
组织转变
L→(L+Ld) →Ld→Ld′
用量热计法测定银铜合金的凝固点,并首先用冰点曲线表示 其实验成果。
1876年与J.洛基尔一起用光谱仪作定量分析,以辅助传统的 试金法。
1885年开始研究钢的强化,研究少量杂质对金的拉伸强度的 影响。奥斯汀采用Pt/(Pt-Rh)热电偶高温计,得以测定了 高熔点物质的冷却速度,创立共晶理论。用显微镜照相研究 金属的金相形貌。
3. 三个三相区:
(1)包晶转变: HJB线: (L+)→
发生在高温, 在随后的冷却过程中 组织还会变化。 此转变不作讨论。 (简化Fe-Fe3C相图)
(2)共晶转变: ECF线:
共晶组织 (+ Fe3C)为 莱氏体, Ld(Ledeburite)
无机材料科学基础第六章-相平衡(1-1)

相图上的压力轴 为示意性的,因 为SiO2的饱和蒸 汽压极小,2000K 时仅10-7Mpa,在 相图上作了放大。
27
相图上共有九条界线,分别表示系统中的二相平衡状态:LM、 MN、ND和DO四条界线代表了相应晶型与SiO2蒸气之间的二相平 衡,即相应晶型的蒸发曲线;OC是SiO2熔体的蒸发曲线;MR、 NS、DT是晶型转变线;OU是α-方石英的熔融曲线;
19
4.虚线: 表示系统可能出现的各种介稳平衡状态。
(1)面 ECGH区: 过冷熔体的介稳单相区; FBGH区: 过热晶型Ⅰ的介稳单相区; BGC和ABK区: 过冷蒸气的介稳单相区; KFB区: 过冷晶型Ⅱ的介稳单相区。
20
(2)线
BG线:过热晶型Ⅰ的升华曲线; GH线:过热晶型Ⅰ的熔融曲线;
GC线:过冷熔体的蒸发(蒸汽压)曲线;
5
(2)独立组分数——表示构成平衡系统中各相组成所 需要的最少组分数,用“c”表示。 当不存在化学平衡时,组分数=独立组分数。 如:低温系统中CaCO3、CaO、CO2存在,组分数=独 立组分数=3; 当有独立的化学平衡存在时,组分数≠独立组分数, 独立组分数=组分数-独立的化学平衡数 如:高温系统中CaCO3、CaO、CO2存在, 有:CaCO3 CaO+CO2平衡,组分数=3; 独立组分数=3-1=2; 所以,对于单元系统,c=1;二元系统 c=2; 三元系统 c=3。
相律在凝聚系统的形式为:
f=c–p+1
注:
1——指温度因素
(1)相律是在化学位相等(平衡状态)下推导出的,所以 只能用于平衡系统。 (2)对于一元凝聚系统,为了充分反映纯物质的各种聚集 状态(超低压气相和超高压的新晶型),仍把压力取为变量。
材料科学基础-二元相图

LE→( αC + βD)
相图的构成:
LE→( αC + βD)
相图的构成:线
AE和BE为两液相线; AC和BD为两固相线; CG和DH:(固溶度曲线) 固溶体α、β的溶解度线; CED:水平共晶线。
三个单相区: L、α、β; 三个双相区:L+α、L+β、
α+β 一个三相区:L+α+β,
CED共晶线。 29
连接转变开始点 和终了点
冷却过程中,不同相的热容量不同,冷却曲线上的斜率 不同, 曲线的转折点对应温度就是相变温度。
相图的测定: 二元相图:4000个(81%)(4950); 三元相图:8000(5%)(161700)。工作量巨大。 四元相图:1000(0.1%)(3921225) 问题:成分难控制,高熔点,难以达到相平衡
室温组织:α+βII +(α+β)
(α+β)%=L%=c2/ce, (α+βII)%=e2/ce
α%=c’g/fg× e2/ce,
βII%=fc’/fg × e2/ce
41
相: α+β
α初 :暗黑色粗大树枝状, βII :白色颗粒。
(α+β)
亚共晶组织:
α+βII +(α+β)
④合金Ⅳ:过共晶合金 L→L+β→β+(α+β)→β+αII+ (α+β)
4. 偏晶转变相图 fdc Ld→αf +Lc
偏晶转变:
L36→Cu +L87
72
5、具有合晶转变的相图
Lc+Ld→f
6、熔晶转变相图
→ +L
♣ 6.3.5 二元相图的几何规律
相图的构成:
LE→( αC + βD)
相图的构成:线
AE和BE为两液相线; AC和BD为两固相线; CG和DH:(固溶度曲线) 固溶体α、β的溶解度线; CED:水平共晶线。
三个单相区: L、α、β; 三个双相区:L+α、L+β、
α+β 一个三相区:L+α+β,
CED共晶线。 29
连接转变开始点 和终了点
冷却过程中,不同相的热容量不同,冷却曲线上的斜率 不同, 曲线的转折点对应温度就是相变温度。
相图的测定: 二元相图:4000个(81%)(4950); 三元相图:8000(5%)(161700)。工作量巨大。 四元相图:1000(0.1%)(3921225) 问题:成分难控制,高熔点,难以达到相平衡
室温组织:α+βII +(α+β)
(α+β)%=L%=c2/ce, (α+βII)%=e2/ce
α%=c’g/fg× e2/ce,
βII%=fc’/fg × e2/ce
41
相: α+β
α初 :暗黑色粗大树枝状, βII :白色颗粒。
(α+β)
亚共晶组织:
α+βII +(α+β)
④合金Ⅳ:过共晶合金 L→L+β→β+(α+β)→β+αII+ (α+β)
4. 偏晶转变相图 fdc Ld→αf +Lc
偏晶转变:
L36→Cu +L87
72
5、具有合晶转变的相图
Lc+Ld→f
6、熔晶转变相图
→ +L
♣ 6.3.5 二元相图的几何规律
材料科学基础---第六章 相平衡

1、组分、独立组分
组分:组成系统的物质。必须具有相同的化学性质,
能用机械方法从系统中分离出来且能长期独立存在的
化学纯物质。组分的数目叫组分数(S)。
独立组分:构成平衡物系所有各相组成所需要的最
少数目的化学纯物质。 独立组分数:以C表示
注:只有在特殊情况下,独立组分和组分的含义才相同。
·若系统中不发生化学反应,则独立组分数=组分数; ·若系统中存在化学反应和浓度关系,则:
不一致熔融化合物:不稳定化合物,加热该化合物到
某一温度便分解,分解为一种液相和一种晶相,二者
组成与化合物组成皆不相同。
特点:化合物组成点不在其液相线范围内
1.相图分析: 点: p=3
E:
f =0
低共熔点
△
LE 冷却 A Am Bn P: 转熔点
冷却
△
LP B
Am Bn
2.
熔 体 的 冷 却 析 晶 过 程
液相点: 2 L f=2 B
K
M
H E
J
K L→B P (LP +B→C) L→C E (LE →A+C) f=1 f=1
f=0 f=0
固相点: M
F B+C D
C
J C+A
H
Q
S
液相点: 3 固相点: b
L f=2 B
Q L→B P (LP +B→C) f=1
f=0
F B+C
S
⑶固相中有化合物生成和分解的二元系统相图
七种晶型分为三个系列:石英-鳞石英-方石英
(1)重建型转变(一级变体间的转变):横向,转变 速度慢,石英-鳞石英-方石英。 (2)位移型转变(二级变体间的转变):纵向,速度 快,α -β -γ ,同一系列转变。
组分:组成系统的物质。必须具有相同的化学性质,
能用机械方法从系统中分离出来且能长期独立存在的
化学纯物质。组分的数目叫组分数(S)。
独立组分:构成平衡物系所有各相组成所需要的最
少数目的化学纯物质。 独立组分数:以C表示
注:只有在特殊情况下,独立组分和组分的含义才相同。
·若系统中不发生化学反应,则独立组分数=组分数; ·若系统中存在化学反应和浓度关系,则:
不一致熔融化合物:不稳定化合物,加热该化合物到
某一温度便分解,分解为一种液相和一种晶相,二者
组成与化合物组成皆不相同。
特点:化合物组成点不在其液相线范围内
1.相图分析: 点: p=3
E:
f =0
低共熔点
△
LE 冷却 A Am Bn P: 转熔点
冷却
△
LP B
Am Bn
2.
熔 体 的 冷 却 析 晶 过 程
液相点: 2 L f=2 B
K
M
H E
J
K L→B P (LP +B→C) L→C E (LE →A+C) f=1 f=1
f=0 f=0
固相点: M
F B+C D
C
J C+A
H
Q
S
液相点: 3 固相点: b
L f=2 B
Q L→B P (LP +B→C) f=1
f=0
F B+C
S
⑶固相中有化合物生成和分解的二元系统相图
七种晶型分为三个系列:石英-鳞石英-方石英
(1)重建型转变(一级变体间的转变):横向,转变 速度慢,石英-鳞石英-方石英。 (2)位移型转变(二级变体间的转变):纵向,速度 快,α -β -γ ,同一系列转变。
第六章二元合金相图PPT课件

1. 形态:此类共晶形态有:片层状、棒状、短棒状. 如:Pb-Sn、Pb-Cd、Cd-Zn、Sn-Zn、Ag-Cu等
(a)片层状
(b)短棒状
(c)球状
30
(f)菜花状层片 (c)纤维状
立体形态
(d) 六角螺旋状
(a)片层状
(b)短棒状
(c)球状
31
2.共晶组织金相形态形成原因:共晶组织的形态与 两相的本质、两相的相对量、两相凝固时固液界面形 貌及其冷却速度有关。 从热力学分析,共晶组织中两相的形态和分布,应 尽量使其界面积最小,界面能最低。
26
室温组织中组织组成物的相对重量为α初+(α+β) : (二次相忽略)
W 6 61 1..9 9 1 59 0100% 27.74% W ( )6 5 1 0 .9 1 1 9 91 0 0 % 7 2 .2 6 %
27
室温组织中相组成物的相对重量为α+β (近似值):
W 101 00 050100% 50%
b’表示50%Cu合金结晶完成;
bb’线段上的点表示合金正在结晶过程中,处于L和
α两相区;
3.确定合金的相变温度;
4.杠杆定律:
成分为b的合金在温度T1时处于两相共存,两相的重
量比是一定的,wL、wS分别为T1温度时的剩余的液
相及结晶出的固相。
9
(1)利用杠杆定律可确定平衡两相区内平衡两相成分 CL 及Cα
的降低由α→βⅡ (二次相)。 NG线-A组元在β固溶体中的溶解度曲线。随着温度
的降低由β→αⅡ 。(二次相)。 22
二、共晶系典型合金的平衡结晶过程
合金分类: 共晶合金-E点成分合金; 亚共晶合金- M~E间合金; 过共晶合金- E ~ N间合金; 端部固溶体合金-M、N以外
(a)片层状
(b)短棒状
(c)球状
30
(f)菜花状层片 (c)纤维状
立体形态
(d) 六角螺旋状
(a)片层状
(b)短棒状
(c)球状
31
2.共晶组织金相形态形成原因:共晶组织的形态与 两相的本质、两相的相对量、两相凝固时固液界面形 貌及其冷却速度有关。 从热力学分析,共晶组织中两相的形态和分布,应 尽量使其界面积最小,界面能最低。
26
室温组织中组织组成物的相对重量为α初+(α+β) : (二次相忽略)
W 6 61 1..9 9 1 59 0100% 27.74% W ( )6 5 1 0 .9 1 1 9 91 0 0 % 7 2 .2 6 %
27
室温组织中相组成物的相对重量为α+β (近似值):
W 101 00 050100% 50%
b’表示50%Cu合金结晶完成;
bb’线段上的点表示合金正在结晶过程中,处于L和
α两相区;
3.确定合金的相变温度;
4.杠杆定律:
成分为b的合金在温度T1时处于两相共存,两相的重
量比是一定的,wL、wS分别为T1温度时的剩余的液
相及结晶出的固相。
9
(1)利用杠杆定律可确定平衡两相区内平衡两相成分 CL 及Cα
的降低由α→βⅡ (二次相)。 NG线-A组元在β固溶体中的溶解度曲线。随着温度
的降低由β→αⅡ 。(二次相)。 22
二、共晶系典型合金的平衡结晶过程
合金分类: 共晶合金-E点成分合金; 亚共晶合金- M~E间合金; 过共晶合金- E ~ N间合金; 端部固溶体合金-M、N以外
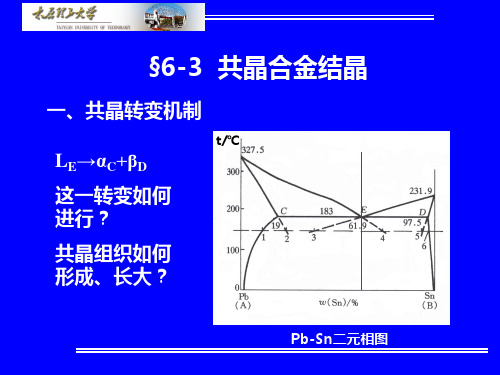
材料科学基础-材料科学基础-§6-3 共晶合金的结晶
§6-5
一、定向凝固
凝固技术
定向凝固是使铸件全部沿同一方向生长。 由此产生有相同取向的柱状、片层状及棒状所 构成的单相或双相组织,它的纵向性能明显高 于横向性能。 高温涡轮叶片以成功应用该技术。这种叶 片工作中常沿与主应力相垂直的横向晶界发生 沿晶断裂。通过定向凝固可使叶片中的晶界与 主应力相平行,从而显著提高叶片使用寿命。
b)
a)片层状交替形核生长
b)片层状共晶分离扩散
片层状共晶的形核与生长
二、共晶组织形貌
1.共晶组织及分类
(1)按微观特征分: 层片状,棒状,球状,针状,螺旋状等。 当两个固相都是金属性较强相时,共晶体 一般生长成层片状。当两相的相对数量比相差 悬殊时,在界面能的作用下,数量较小的相将 收缩为条、棒状,更少时为纤维状,甚至为点 (球)状。
一、铸锭三晶区及其形成机制
铸锭三晶区: 表层细晶区-强过冷,非均匀形核。 柱状晶区-纯金属:过冷度减小,形核困难,沿散 热方向生长; 合金:成分过冷,一次轴发达,沿散热 方向生长。 中心等轴晶区-均匀散热、液相区成分过冷、 熔体对流导致细晶漂移或枝晶破碎。
铸锭三晶区示意图 1-细晶区 2-柱现出较强的各向异性,不同方向 的生长速度不同,并且有特定的角度关系, 同时生长过程要求的过冷度也有差异,往往 有一个相在生长中起主导作用,决定了两相 的分布,共晶体的形态也具有独特性,这时 常见的形态有针状、骨肋状、蜘蛛网状、螺 旋状等。
共晶组织形貌
汽轮机叶片的宏观组织 a) 定向凝固 b) 非定向凝固
二、单晶制取
单晶材料是与半导体、压电、光电、生 光、热电、红外遥感等技术密切相关的功能 材料。 单晶是由一个晶核生长成的具有宏观尺 寸的晶体材料。
常见制备方法有两种:垂直提拉法,尖 端形核法。
材料科学基础课件第六章--相平衡与相图

F = C-P+n
自由 度数
独立组 元数
F = C-P+2
对凝聚态体系, 压力恒定或影响 较小,其相律为:
F = C-P+1
组元数C多,自 由度F大;相数P 多,自由度小
6.1.3 相平 衡研究方法
动态法
静态法 (淬冷法)
热分 析法
差热分 析法
T/℃
(1ቤተ መጻሕፍቲ ባይዱ 热分析法
1
2
3
原理:根据系统在冷却
ab c
100 80Bi 60Bi 20Bi 100 Bi 20Cd 40Cd 80Cd Cd
T/℃
ab c d e
t/s
Bi-Cd合金冷却曲线
546.15K
596.15K
L
L+Bi(s) ●
L+Cd(s)
20 40 Bi(s)+Cd(s) 80
0 Bi
WCd/%
100 Cd
Bi-Cd系统相图
液相线:由凝固开始温度连接起来的相界线 固相线:由凝固终结温度连接起来的相界线
元系统相图
P ●:熔点
■:转变点
2
L
●
Ⅱ
3
■
1
●
Ⅰ
O T0 T2 T1 T3
T
图 6-7 具有不可逆多晶转变的
单元系统相图
晶体I T3 晶体II
晶体Ⅰ 晶体Ⅱ 液相
(1) 晶体I、Ⅱ有稳定区 (2) 转变温度T3<T1 、T2(熔点)
T1 液 相 T2
(1)晶体Ⅱ无稳定区 (2)T3>T1、T2
6.2.2 单元系统专业相图
G
E
H
A+B
A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
Ω=0,>0,G-x曲线也有一最小值;
Ω>0, G-x曲线也有2个最小值,拐点内<0。
6.3.2 多相平衡的公切线原理
6.3.3 混合物的自由能和杠杆法则
6.3.4 从自由能—成分曲线推测相图
6.3.5 二元相图的几何规律
★相图中所有的相界线代表相变的温度和平衡相 成分,即平衡相成分沿着相界线随温度变化而变 化; ★两单相区之间必定有这两相的两相区-相区接 触法则; ★二元相图的三相平衡区为一水平线,其与三个 单相区的交点确定平衡相的浓度; ★两相区与单相区的分界线与三相等温线相交, 分界线的延长线进入另一两相区。
(1)单相区:3个, L、 α 、β (2)两相区: 3个, L+α 、L+β 、α +β 相区:1个, L+α+β (3)三
5.与匀晶和共晶相图的区别
(1)相同处
PDC线以上区域; PDC线以下、DF以右区域的
分析方法以及结晶过程与匀晶相同;
BPDF以内区域,与共晶线MEN线以下区域相同,
按照固ห้องสมุดไป่ตู้度线分析。 (2)不同处 包晶线PDC及包晶反应:L+α→β
6.10 铁碳合金相图 6.11 二元合金的凝固理论
第6章 二元合金相图及合金凝固
由一种元素或化合物构成的晶体称为单组元晶体或纯晶体,
该体系称为单元系。两个组元的为二元系,n个组元都是独立
的体系称为n元系。对于纯晶体材料而言,随着温度和压力的 变化,材料的组成相会发生变化。
从一种相到另一种相的转变称为相变。由不同固相之间的
2.非平衡共晶组织
a
非平衡共晶组织(成分位于a点稍左)一般分布在初晶α 的相界上,或者在枝晶间。可以通过扩散退火来消除,最终得
到均匀的α单相固溶体组织 。
3.离异共晶
离异共晶:条件为a点稍右,特点是初生相很
多,共晶体量很少。
离异共晶
初晶
a
6.6 包晶相图
2
4.6.1相图分析
★包晶相图——液态下无限互溶,固态下有限
6.6.2 包晶合金的平衡凝固
P点以左,C点以右的合金与匀晶相图相似,分析方法相同。
1.合金Ⅰ
1以上,液相冷却; 1→2,L →α; 2点,包晶转变:LC +α P →β D 2点以下,β沿DF线变化,析出二次相, β → αⅡ; 室温组织: β +αⅡ
包晶转变时, β相依附在α相形核,直至全部包住 α相。此 时, β相内部α相的Pt含量高, β相外部L相的Ag含量高, Pt原
子向外扩散, Ag原子向内扩散。新相β两侧L相和α相的成分接
近D点, β相消耗L相和α相从而长大。当L相和α相同时消耗完, 包晶转变结束,在包晶温度下只有β相。
发生包晶转变时, L相和α相的两相相对量计算如下: W(L)=DP/DC=(42.5-10.5)/(66.3-10.5)=57.3%
W(α)=PC/DC=(66.3-42.5)/(66.3-10.5)=42.7%
材料科学基础
第6章 二元相图及合金凝固
合肥工业大学材料学院 宣天鹏
6.1二元相图的表示和测定方法 6.2 相图热力学的基本要点 6.3 匀晶相图 6.4 共晶相图 6.5 包晶相图
6.6溶混间隙相图与调幅分解
6.7 其他类型的二元相图 6.8 复杂二元相图的分析方法
6.9 根据相图推测合金的性能
(3)三相区:1个, L+α+β
5.与匀晶相图的区别
相同点: MEN线以上区域,分析方法以及结晶过程
与匀晶相同;
不同点: 共晶线MEN线及以下区域,需要重点关
注。
6.5.2共晶合金的平衡凝固
1.固溶体合金(183℃时,Pb%≤19%;Sn%≥97.5)
T
1 2 3 τ
1以上,液相冷却; 1→2,L →α; 2→3,α冷却; 3以下,α→βⅡ。 室温组织:α初+βⅡ
即57.3%的液相和 42.7%的α相正好全部转变为β相
T 1 D 4 D′
τ
2.合金Ⅱ
1以上,液相冷却; 1→2,L →α; 2点,包晶转变:LC +αP →βD 包晶温度: W(L)=2P/DC>57.3%,说明发生包晶反应后有液 相过剩。 2→3,过剩的液相成分沿CB线变化, β沿DB线变化, L过剩→ β 3→4, β冷却 4点以下,β沿DF线变化,析出二次相, β →αⅡ; 室温组织: β +αⅡ
6.4.3 固溶体的非平衡凝固
偏析-合金内部成分不均匀;
晶内偏析-晶粒内部成分不均匀;
枝晶偏析-树枝晶内的偏析;
枝晶偏析对铸件影响很大,可在低于固相线
温度下进行均匀化退火或进行热轧、锻造降 低枝晶偏析;
不平衡凝固偏离固相线、液相线,但液、固
相界面仍然符合相图的平衡关系。
L L+A L+B
A+B
6.4 匀晶相图
6.4.1相图分析
B
A
1.点:A、B分别是Cu和Ni的熔点;
2.相:2个,L 、α相;
3.线:2条,液相线和固相线; 4.相区: 2个单相区,分别是L、 α的单相区;
1个两相区,L +α;
单相区和两相区被液相线和固相线隔开。
α2
固溶体结晶时需要成分起伏:液态金属中 存在有偏离合金平均成分的区域,一定条件下 该区域此起彼伏的现象。
α
βⅡ
2.共晶合金(183℃,Sn%=61.9) tE以上,液相冷却;
tE, 共晶转变:LE → αM +βN ,
tE以下,α沿着MF线变化,析出βⅡ,α→ βⅡ
β沿着NG线变化,析出αⅡ, β→αⅡ
室温组织:α+β(二次相看不见)
T
tE
E1
τ
共晶温度下:共晶合金的相对量
( α+β )
相组成物:构成显微组织的基本相; 组织组成物:由基本相构成并具有独特组织形态的组 成部分。 室温下,共晶合金的相组成物为α和β;组织组成物为 (α+β )。 相组成物相对量计算: α%= ( E1G/ FG )×100% ;
(4)共晶线:MEN,位于该线内的合金,在共晶温 度下都要发生共晶转变。
LE → αM +βN
tE—共晶温度,此温度下三相平衡,f =c-p+1=0, 自由度为0,共晶转变是恒温转变; 4.相区
tE
(1)单相区:3个, L、 α 、β
(2)两相区: 3个, L+α 、L+β 、α +β
(α、
β两相为机械混合物)
(2)P、D分别是包晶温度下α( β)相的最大溶解度点, C点包晶反应时的液相成分点;
(3)B、F分别是室温下α( β)相的最大溶解度点;
3.线
(1)液相线: AC: L→ α, CB: L→ β ;
(2)固相线:AP: L→ α, DB: L→ β ;
(3)固溶度线:不同温度下固溶体最大溶解度的连线,
随温度降低,固溶体沿此线变化,析出第二相; PB: α → βⅡ, DF : β → αⅡ
(4)包晶线:PDC,位于该线内的合金,在包晶温 度下都要发生共晶转变。
LC + αP → βD
1186℃—包晶温度,此温度下三相平衡,f =cp+1=0, 自由度为0,包晶转变是恒温转变;
1186℃
4.相区
β%=(FE1/ FG)×100%
组织组成物:
为100%的共晶组织(α+β )
3.亚共晶合金(亚共晶:Sn%=19~61.9%) 1以上,液相冷却; 1→2,L →α初; 2 点, α初+ L → α初+ ( αM +βN ) , 2以下,α沿着MF线变化,α→ βⅡ β沿着NG线变化,β→αⅡ 室温组织: α初+ βⅡ + ( α+β )或 α初+ ( α+β ) (共晶组织中的二次相看不见)。
Wl / Wα = α2 O/ OL2%
两平衡相的相对量与其在相图上平衡成分 线段长度成反比。 因为:Wl / (W0 - Wl )= α2 O/ OL2 % 所以: Wl / W0= α2 O/α2L2 % Wα / W0= 1- Wl / W0 = OL2/α2L2 % 上式就是二元系中的杠杆定律,杠杆的支 点是合金成分点,杠杆的两端点是两平衡相的 平衡成分点。
晶或先共晶相等) ;
(2)固相线:tA M: L→ α, tB N: L→ β ; (3)固溶度线:不同温度下固溶体最大溶解度的连线(t1 — M1 ; t2— M2 ; t3 — M3 …… ) ,随温度降低,固溶体沿此线变化, 析出第二相(根据析出次序而称之,相对于从液相中析出的初 晶而言,指的是从固相中析出); MF: α → βⅡ, NG : β → αⅡ
(α+β)
课后练习:过共晶合金( 61.9~97.5% Sn)、N点以右合金 ( 61.9~97.5% Sn) 1.分析合金的平衡结晶过程; 2.画出金相组织示意图; 3.计算室温下相组成物和组织组成物的相对量; 4.画出冷却曲线。
6.5.3共晶合金的非平衡凝固
1.伪共晶组织
(a)伪共晶区对称:两组元熔点相近; (b)伪共晶区不对称:两组元熔点相差较大,共晶点偏向低 熔点组元,伪共晶区偏向高熔点组元。 不平衡凝固条件下,非共晶成分的合金可全部得到伪共晶 组织,共晶成分的合金则可能得到亚共晶或过共晶组织。
溶解,且具有包晶转变的相图;
★包晶转变—— 一定温度下,一个一定成分的
液相和一个一定成分的固相同时转变另一具有
一定成分固相的反应:
L+α→β 具有包晶转变的二元合金有Fe-C、Cu-Zn、AgSn、Ag-Pt等。
1.相
