材料科学基础相图部分参考
材料科学基础 第5章 相 图剖析

由于 所以
dni dni
dG (i i )dni
在 相和 相处于平衡时,dG=0 ,故:
i i
即两相平衡的条件是两相中同一组元的化学 位相等。此时,在两相之间转移趋于平衡。 若多元系中有C个组元,P个相,则它们的相 平衡条件可以写成:
由热力学原理可知,当组元在不同相间转 移时,将引起体系自由能的变化。对于一个多 元系,这种自由能变化可用下式表示:
dG Vdp SdT
dn
i
i
在等温等压条件下,可简化为:
dG
dn
i
i
如果体系中只有 和 两相,当极少量(d n i)的 i 组元从 相转移到 相中,则B
Pb
10
20
30
40
50
60
70
80
90
500 400 tA 300 327.5℃ 231.9℃ M α +L 183℃ 19 α +β F Pb 10 20 30 40 50 60 70 80 90 G Sn E 61.9 L+β N β 97.5 L
200 α 100
tB
W W1 W2
2的质量 Wx W1 x1 体系中相 W21 x 体系中相 的质量 体系中物质的总质量 2
t1 t2 M R P Q
L1
L2 L E x x2 20 40 K S N B 100
由上两式可得:
体系中 相1 相 中 B2 组元的含量 B 中 组元的含量 B组元的含量
W1 (x x1 ) W2 (x 2 x)
1083
时间
Cu 0
30
材料科学基础-8-二元相图(2)
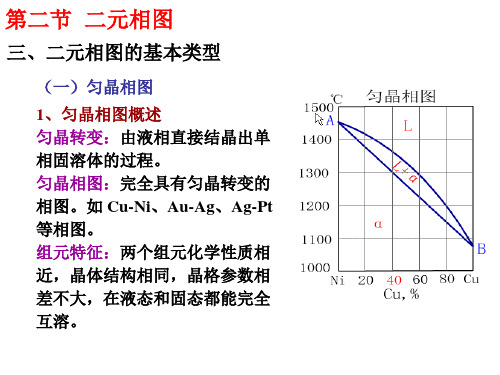
第二节 二元相图
(一)匀晶相图
2、固溶体的平衡凝固
(3)固溶体的结晶规律
c.固溶体的凝固过程与纯金
属一样,也包括形核与长大
两个阶段
e. 平衡凝固得到的固溶体显
微组织和纯金属相同,除了
晶界外,晶粒之间和晶粒内
部的成分却是相同的。
d.合金结晶形核时需要能量
起伏和成分起伏
a. 固溶体的结晶与纯金属不同,它不在
(2)压力加工性:压力加工合金通常是相图上单相固溶体
成分范围内的单相合金或含有少量第二相的合金。
——单相固溶体合金切削加工性能
不够好,而具有两相组织的合金切
削加工性一般比较好。
(4)热处理性:
相图上无固态相变或固溶度变化的
合金不能进行热处理。
孔等缺陷。
——我国20世纪60年代开始研制Pt-Ag合金,但至今无法批量
稳定发展
——国内外通过添加Pd(钯)制成Pt-Pd-Ag三元合金,虽综合
性能不如Pt-Ag合金,但加工性能得以改善。
第二节 二元相图
(三)包晶相图
2、包晶合金的凝固及其平衡组织
(1)ω (Ag)为42.4%的Pt-Ag合金(合金I)
′
% =
× %
第二节 二元相图
1186℃
A
LP+αC ↔ βD
(三)包晶相图
f=2-3+1=0
包晶点
• 1、包晶相图
• 包晶转变:由一个固相与
液相作用生成另一个固相
的过程。
• 包晶相图:两组元在液态
无限互溶,固态下有限互
溶,并发生包晶反应的二
元系相图。
第二节 二元相图
2、包晶合金的凝固及其平衡组织
材料科学基础第五章 材料的相结构及相图

SCHOOL OF CHEMISTRY AND MATERIAL SCIENCE OF GUIZHOU NORMAL UNIVERSITY
贵州师范大学
化学与材料科学学院
SCHOOL OF CHEMISTRY AND MATERIAL SCIENCE OF GUIZHOU NORMAL UNIVERSITY
贵州师范大学
化学与材料科学学院
第一节 材料的相结构
THE PHASE STRUCTURE OF MATERIALS
固溶体
中间相
SCHOOL OF CHEMISTRY AND MATERIAL SCIENCE OF GUIZHOU NORMAL UNIVERSITY
贵州师范大学
化学与材料科学学院
相:合金中具有同一聚集状态、同一晶体结构和性质 并以界面相互隔开的均匀组成部分。
SCHOOL OF CHEMISTRY AND MATERIAL SCIENCE OF GUIZHOU NORMAL UNIVERSITY
贵州师范大学
化学与材料科学学院
3)电负性差因素
电负性:衡量原子吸引电子能力的参数,电负性越强,吸引 电子的能力越强。
电负性差ΔX>0.4时,易于形成较稳定的金属间化合物;
贵州师范大学
化学与材料科学学院
4)电子浓度因素
电子浓度:合金中各组成元素的价电子数总和与原子总数 的比值,记为e/a。
C电 合金中价电子数之和 原子数之和
例:合金含有摩尔分数为x、原子价为VB的溶质原子,溶剂 的原子价为VA,则合金的电子浓度为:
e V A 1 x V B x a
材料科学基础-三元相图习题

3、根据所示的投影用热分析曲线表示图中成分为I、II、III的材料 在平衡冷却过程中发生的组织转变,并写出室温下的平衡组织;
答案 I
答案 II
答案 III
1. 根据所示Fe-W-C三元系的低碳部分的液相面的投影图,试标出 所有四相反应。
图中标出了单变 量线起始温度
答案:四相反应如下: 2755~2400℃时:L+W5C3→WC+W2C, ~2400℃时:L+ W2C→WC+W, ~1700℃时:L+ WC+ W→M6C ~1500℃时:L+ W→M6C+Fe3W2 1380℃时:L+ Fe3W2→M6C+α 1335℃时:L+α→γ+ M6C ~1200℃时:L+ M6C→WC+γ 1085℃时:L→γ+Fe3C+ WC 其液相成分变温线的温度走向如图所示:
Al
Mg→ α θ ET
S
P1
Q T
P2
Eu β
γ
2013-6-17
1、根据下图,指出成分位于△mEp中(不在边、角处)的合金在 室温下可能有哪几种组织,并画出相应的冷却曲线的示意图。
答案 可能出现的组织: (1)
答案 可能出现的组织: (2)
答案 可能出现的组织: (3)
2、在所示的三元相图的垂直截面中写出三个四相平衡反应的反应 式
C1
1150℃
C2 b C3
Fe-13%Cr-2%C合金:
L + γ+ C1
— Cr12成分点c,位于γ+ C2两 相区,
作近似连线acb可求相对量。
Fe p363图8.34(a)
材料科学基础-第8章-三元相图

L
α C A B L1 S1 L+α L+α n L o L2
7
m
α S2
C
A
第五章 材料的变形与再结晶 L
4、变温截面(垂直截面)图 变温截面(垂直截面) (1)通过成分三角形顶点的截面
α
★ 位于该截面上的所有合金含另外两 顶点组元量之比w 相同。 顶点组元量之比wA/wC相同。 ★ 此图可反映合金在不同温度时所存 在相的种类; 在相的种类;
α
β
γ
L+α L+α+β、α+β+γ 一个四相平衡区:L+α 一个四相平衡区:L+α+β+γ
19
20
2、投影图
E1 A B
o
E E3 E2
C
合金o冷却过程中的相变: 合金o冷却过程中的相变:
L+α L+(α )+α→L+(α )+(α )+α L→ L+α→ L+(α+β)+α→L+(α+β+γ)+(α+β)+α→ )+(α )+α (α+β+γ)+(α+β)+α
A C L L+α α
α B
9
第五章 材料的变形与再结晶
5、投影图
L
α A B
C
10
第五章 材料的变形与再结晶
第二节 固态互不溶解的三元共晶相图
1、相图分析 每个侧面为组元固态下互不溶的二 元共晶相图。 三个共晶点。 元共晶相图。E1、E2、E3三个共晶点。 三个液相面: ★ 三个液相面: tAE1EE3tA、 tBE1EE2tB、 tCE2EE3tC。 三元四相共晶点E ★ 三元四相共晶点E:L→A+B+C ★ 重要的线: 重要的线: 三元三相共晶线E 三元三相共晶线E1E:L→A+B 三元三相共晶线E 三元三相共晶线E2E:L→B+C 三元三相共晶线E 三元三相共晶线E3E:L→A+C
《材料科学基础教学课件》第一章-相图

在化学工业中的应用
化工过程控制
相图可以用来预测不同成分和温 度下的相态和物性,为化工过程 的控制提供依据,确保生产过程
的稳定性和安全性。
化学反应研究
相图可以用来研究化学反应过程中 物质的状态和性质变化,有助于深 入理解化学反应机理和反应条件的 选择。
分离技术应用
相图可以用来指导分离技术的选择 和应用,例如利用相图的溶解度曲 线进行萃取分离或结晶分离。
04
相图的应用
在材料科学中的应用
合金设计
相图是合金设计的基础,通过相 图可以确定合金的成分范围以及 各相的组成和性质,从而优化合 金的性能。
热处理工艺制定
利用相图可以确定合金在不同温 度下的相变过程,从而制定合理 的热处理工艺,优化材料的显微 组织和力学性能。
新材料研发
相图为新材料研发提供了理论指 导,通过研究不同成分和温度下 的相变规律,可以发现具有优异 性能的新型材料。
实验法是绘制相图最直接和可靠的方 法,但需要耗费大量的时间和资源。
实验法通常需要使用精密的实验仪器 和设备,如热分析仪、X射线衍射仪、 扫描电子显微镜等,以获得精确的数 据。
计算法
计算法是根据物质的分子或原 子模型,通过计算机模拟计算 物质之间的相平衡关系。
计算法可以快速地预测物质的 相平衡关系,但需要建立准确 的分子或原子模型,且对计算 资源的要求较高。
在冶金工业中的应用
钢铁冶金
01
钢铁冶金过程中涉及大量的相变和相分离,相图是指导钢铁冶
金工艺的重要工具,有助于优化炼钢和连铸连轧工艺。
有色金属冶金
02
在有色金属冶金中,相图可以用来确定合金的成分和温度范围,
优化熔炼、浇注和凝固工艺,提高产品的质量和性能。
材料科学基础第六讲-相图

3-4点时,为单相固溶体,不发生变化。 4点以下,将从β相析出次生相αII
§4.4其它类型的二元合金相图
第五节 复杂相图
§5.1 二元合金相图的分析和使用
I 包晶反应:L+α β II 包晶反应:L+ β γ III 包晶反应:L+ ε η IV 共析反应: β α + γ V 共析反应: γ α + δ VI 共析反应: δ α + ε VII 共析反应: ζ δ + ε VIII 包析反应: γ + ε ζ IX 包析反应: γ + ζ δ X 熔晶反应: γ ε + L XI 共晶反应: L η + θ
相律:表示在平衡条件下,系统的自由度数、组元 数和相数之间的关系。它是检验、分析和使用相图 的重要工具。
F=C-P+2
F-平衡系统的自由度数 C-平衡系统的组元数 P-平衡系统的相数
当压力为常数时:F=C-P+1
J. Willard Gibbs
自由度:指平衡系统中可以独立改变的因素(如温度, 美国物理学家 压力,成分)等。纯金属的自由度最多一个,二元系 (1839-1903)
包晶转变区的特征是:反应相是液相和一个固相,其成分点位于水 平线的两端,所形成的固相位于水平线中间的下方。
典型合金的平衡结晶及组织
(一)含银量42.4%的铂银合金
当合金I自液态缓冷到1点时, 开始结晶出α相,与匀晶系 合金的结晶完全相同
当温度降到tD时,合金中 α 相的成分到P点,液相的成 分到C点。
应用相图时要注意的问题
连接线(等温线):两个平衡相成分点之间的连线
第三节 一元系相图
材料科学基础 第五章 5.1-5.4相图

5.2.3 杠杆定律
设成份为 X的合金的总重量为1,液相的相对重量为 QL,其 成份为 X1,固相相对重量为Qα,其成份为X2,则 :
5.2.4 相图的类型和结构 根据组元的多少,可分为单元系、二元系、三元 系 …. 相图。
二元系相图的类型有:
① 液态无限溶解,固态无限溶解 -匀晶相图; ②液态无限溶解,固态有限溶解 -共晶相图和包晶
共晶组织:共晶转变产物。(是两相混合物)
共晶合金的特殊性质: ①比纯组元熔点低,简化了熔化和铸造的操作; ②共晶合金比纯金属有更好的流动性,其在凝固之 中防止了阻碍液体流动的枝晶形成,从而改善铸造 性能; ③恒温转变(无凝固温度范围)减少了铸造缺陷, 例如偏聚和缩孔; ④共晶凝固可获得多种形态的显微组织,尤其是规 则排列的层状或杆状共晶组织可能成为优异性能的 原位复合材料(in-situ composite )。
5.2.2 相律
相律(phase rule)是表示在平衡条件下,系统的自 由度数、组元数和相数之间的关系,是系统的平 衡条件的数学表达式。 相律数学表达式:f = C – P + 2 式中 P—平衡相数 C—体系的组元数 f—体系自由度(degrees of freedom) 数 2-温度和压力 自由度数 f:是指不影响体系平衡状态的独立可 变参数(温度、压力、浓度等)的数目。 在恒压下,相律表达式: f = C – P + 1
相律的应用
① 利用它可以确定系统中可能存在的最多平衡相数 单元系,因f ≥0,故 P≤1-0+1=2,平衡相最大为二个。 注意:这并不是说,单元系中能够出现的相数不能超过二 个,而是说,某一固定 T下,单元系中不同的相只能有两 个同时存在,而其它相则在别的条件下存在。
材料科学基础I__第七章__(相图)

二、相图的建立
建立相图的方法有两种: 利用已有的热力学参数,通过热力学计算和分析建立相图; 依靠实验的方法建立相图。
目前计算法还在发展之中,实际使用的相图都是实验法建立的。
实验法建立相图的原理和步骤:
以A-B二元合金相图的建立为例。
➢首先,将A-B二元合金系分成 若干种不同成分的合金。 1) 合金成分间隔越小,合金数目 越多,测得的相图越精确; 2) 合金成分间隔不需要相等。
设计合金的成分
➢将上述合金分别熔化后,以 非常缓慢的速度冷却到室温, 测出各合金的(温度-时间)冷 却曲线。合金在冷却过程中 发生转变(如:结晶)的起始温 度和结束温度,对应着冷却 曲线上的折点(如:L1、L2 和 S1、S 2等),即临界点。
测量合金的冷却曲线
1) 冷却速度越慢,越接近平衡条件,测量结果越准确; 2) 纯金属在恒温下结晶,冷却曲线应有一段水平线。Le c ຫໍສະໝຸດ c f Ⅱ d g Ⅱwc
ed100% cd
h
I
j
ce
wd
100% cd
fh
jg
wmax
10% 0 fg
wmax
10% 0 fg
edfh
ww cwm
10% 0 an cdfg
cejg
wwdwm
10% 0 an cdfg
③亚共晶合金 合金Ⅲ w(Sn)=50%
F = 0的含义是:在保持系统平衡状态不变的条件下,
没有可以独立变化的变量。即,任何变量的变化都会造 成系统平衡状态的变化。
二元系统(C=2)
压力不变的二元合金系统(以后所涉及的二元合金系统都是压 力不变的,不再特别说明),C = 2,F = 0时,P = 3。 这说明,当二元合金系统同时出现三个相时,就没有可以独立 变化的因素了。 也就是说,只有在一定的温度、成分所确定的某一点才会出现 三相同时存在的状态。
材料科学基础部分参考

L (75%B)
(15%B) (95%B)
(1) 试求含50%B的合金完全结晶后,初晶α与共 晶 (α+β) 的重量%, α 相与 β 相的重量%;共 晶体中α相与β相的重量%。 (2) 若测出显微组织中 β 初晶与 (α+β) 共晶各占一 半时,试求该合金成分。
共晶体中α相和β相的重量%
0.95 0.75 % ( )共晶 % 14.58% 0.95 0.15 % ( )共晶 % % 58.33% 14.58% 43.75%
(2) 设该合金中B的重量%为wB,则
wB 0.75 初 % 100% 50% 0.95 0.75 解得 wB 0.85,即该合金成分为含B85%
0.60% C:合金在1~2间按匀晶转变结晶出A,在2点结晶结束,全部转变为奥氏体。冷到3点时开
始析出F,3~4点A成分沿GS线变化,铁素体成分沿GP线变化,当温度到4点时,奥氏体的成分达到 S点成分(含碳0.77%),便发生共析转变,形成珠光体,此时,原先析出的铁素体保持不变,称为 先共析铁素体,其成分为0.0218%C,所以共析转变结束后,合金的组织为先共析铁素体和珠光体, 当温度继续下降时,铁素体的溶碳量沿PQ线变化,析出三次渗碳体,同样Fe3CIII量很少,可忽略。 所以含碳0.40%的亚共析钢的室温组织为:F+P 1.0% C:合金在1~2点间按匀晶转变结晶出奥氏体,2点结晶结束,合金为单相奥氏体,冷却到
0.40 0.20 A% 100% 50% 0.40 0 ( A )共晶 % 1 A% 50%
3. 试根据含碳量3.5%亚共晶白口铁的平衡组织, 计算其中各组织组成物的相对含量。
材料科学基础-第五章-材料的相结构及相图-PPT

Mg2Si
Mg—Si相图
(2)电子化合物
由ⅠB族或过渡金属元素与ⅡB,ⅢB,ⅣB族元素
形成的金属化合物。
不遵守化合价规律,晶格类型随化合物电子浓度而
变化。
电子浓度为3/2时: 呈体心立方结构(b相);
电子浓度为21/13时:呈复杂立方结构(g相);
电子浓度为21/12时。呈密排六方结构(e相);
体。
III. 电负性差因素
IV. 两元素间电负性差越小,越易形成固溶体,且形
成的固溶体的溶解度越大;随两元素间电负性差
增大,固溶度减小。
1)电负性差值ΔX<0.4~0.5时,有利于形成固溶体
2)ΔX>0.4~0.5,倾向于形成稳定的化合物
IV. 电子浓度因素
V. 电子浓度的定义是合金中各组成元素的价电子数总
子的价电子数恰好使负离子具有稳定的电子层
结构。
金属元素与周期表中的ⅣA,ⅤA,ⅥA元素
形成正常价化合物。
有较高的硬度,脆性很大。
例如:Mg2Si、Mg2Sn、Mg2Pb、MgS、MnS等
(1)正常价化合物
正常价化合物的分子式只有AB,A2B或AB2两种。
常见类型:
NaCl型
CaF2型
Cu原子形成四面体(16个)。
每个镁原子有4个近邻镁原子和12个近邻铜原子;
每个铜原子有6个近邻的铜原子和6个近邻的镁原子
。
Cu
Mg
II. 拉弗斯(Laves)相
②MgZn2型:六方晶系。
Mg原子形成硫锌矿结构;Zn原子形成四面体。
每个Mg原子有4个近邻Mg原子和12个近邻Zn原
子。
每个Zn原子有6个近邻Zn原子和6个近邻Mg原子
材料科学基础第九章三元合金相图

三.等温截面图(水平截面图) (一)等温截面图
(二)等温截面图的应用 1.可确定在某一温度时任意三元合金所处
的状态。
2.用杠杆定律在共轭线mon上可确定在任
意温度时平衡相的成分及其相对重量。
L% mo 100% mn
% no 100% mn
四.变温截面图(垂直截面图)
1. 通过成分三角形某一顶点Bg平面截取的Bg变温截面 2. 通过平行于成分三角形一边的ef平面截取的ef变温截面
4. 投影图的应用 ①确定任意合金的浇铸温度和凝固终了温度。
如:合金O低于t3温度开始结晶,低于t5温度结晶终了。 ②可以运用杠杆定律求平衡相的成分及相对重量。
固 态
一.相图分析
完1.点:
全 (1)熔点:tA、tB、Tc;
不 (2)二元共晶点:E1、E2、E3
溶 的 三
LE1 噲 垐TE垎1垐 (A + B) LE2 噲 垐TE垎2垐 (B + C)
第九章
二.固溶体合金的平衡结晶过程及组织
在T1时,固相成分为S1,L相为L1 ; 在T2时,固相成分为S2,L相为L2 ; 在T3时,固相成分为S3,L相为L3 ; 在T4时,固相成分为S4,L相为L4 ,
液相结晶完毕。 固相成分点S1 S2 S3 S4和液相将S1 S2 S3 S4和L1 L2 L3 L4 各点分别投影到成分三角形ABC 上,便得到“蝴蝶形轨迹。”最后 得到与合金组成完全相同、成分 均匀的三元固溶体α。
% Nf 100% Ff
§9-2 匀晶相图 一.相图分析
1.点:a、b、c分别表示三组元A、B、C的熔点。 2.面:底面ABC是浓度三角形,三个侧面分别是A-B、
B-C、C-A三个二元系匀晶相图。两个空间的上 曲面abc为液相面,下曲面abc为固相面。 3.相:L和α相,α相为A、B、C三组元组成的无限 固溶体;α为A(B、C)。 4.相区: 单相区:L相区(液相面以上)和α相区(固相面以下) 双相区: L+α(液、固相面之间)
材料科学基础-三元相图

2.三元相图分析 法 总 结 --- 三 相 平 衡 -- 三 相
反应的判定--:
投影图判断三 相反应
液相单变量线穿 过两旁固相成分点连 线的为二元共晶型, 而单变线穿过两旁 固相成分点连线延 长线为二元包晶反 应,且靠近单变线 的为生成相
3.三元相图分析法总结---四相平衡
面、液相面呈曲线变化,每一个温度下的固、液相成分连线在浓度三角形中 投影呈蝴蝶状
3.匀晶三元系的等温截面
匀晶三元系两相区中的共轭线,等温截面中两相区平
衡两相的成分连线
共轭线的确定:实验确定,测定两平衡相中任一相的一
个组元含量
匀晶三元系等温截面作用:
1. 该温度下三元系中各合金的相态
2.杠杆定律计算平衡相的相对量
反应及四相平衡点的反应
2. Al-Cu-Mg系
(a)固相面投影图 (b)不同温度下固溶度变化
Al-Cu-Mg合金热处理依据
3.W-C-Co系 --液相面投影图,四相反应部分
W-C-Co系变温截面:分析 W-Co硬质合金生产工
艺
相图
示例-
--
4.Mg OAl2O3SiO2系
四相平 衡反应
5. Fe-Cr-C系-- 三相区1-6-- 及四相平衡转变
4. 固态有限溶解三元共晶合金的变温截面
xy变温截面
x1:L→α+β,L→α+β+γ x2:L→α,L→α+β+γ x3:L→α,L→α+γ,L→α+β+γ x4:L→α,L→α+γ, α → β
γ
x5:L→α,L→α+γ,α → γ
OP变温截面
六、有包共晶反应的三元相图
5 《材料科学基础》第五章 相平衡和相图

( p -T 图)
自由
一、水的相图
冰的熔融曲线 水的饱和蒸汽压曲线(蒸发曲线)
3个相区:
p=1, f=2 ,双变量系统(T、P) 3条界线: p=2 , f= 1,单变量系统(T或P) 1个无变量点(三相点):
T
p=3 , f=0 ,无变量系统
冰的饱和蒸汽压曲线(升华曲线)
??
注意:
•冰点和三相点O
第五章
第五章
§5.1
相平衡和相图
基本知识
§5.2
§5.3
单元系统
二元系统
§5.4
三元系统
§5.1
相平衡与相图的基本知识
一、相平衡的基本概念 二、相律 三、相平衡的研究方法
一、相平衡的基本概念
相平衡:是研究一个多组分(或单组分)多相系统中相的平
衡问题,即多相系统的平衡状态(包括相的个数、各相的状态、
二、二元凝聚系统相图的基本类型
三、复杂二元相图的分析步骤
四、二元系统专业相图
要求
一、二元系统相图的表示方法及杠杆规则
1、作为特种陶瓷的重要原料
由于7%~9%的体积效应,常加适量CaO或Y2O3稳定剂。
在>1500℃以上与四方型ZrO2形成立方晶型固溶体,称稳定
化立方ZrO2 。
2、熔点高(2680℃),作耐火材料 3、利用导氧导电性能,作氧敏传感器元件 4、利用体积效应,对陶瓷材料进行相变增韧。
增韧机理: 微裂纹增韧
实线部分: 四个单相区: 五条界线:
两个无变量点:
晶体的升华曲线(或延长线)与液体的蒸发曲线(或延长线) 的交点是该晶体的熔点。 两种晶型的升华曲线(或延长线)的交点是两种晶型的晶型转 变点。
材料科学基础07-相图-1

Invariant:无变量点
11
The Eutectic Reaction
Disappear:消失
•When the composition falls within A and B, the final liquid disappears at the eutectic point •If the composition is outside of A and B, the final liquid doesn‟t disappear at the eutectic point
液相线: liquidus 固相线: solidus 最低共熔点: eutectic point
6
Definitions of Phase Diagrams
•MgOss represents a MgO-rich solid solution with CaO as the solute •Similarly, CaOss represents a CaO-rich solid solution with MgO as the solute
• Single Phase Region
– Composition = overall composition
Overall (总) composition = C0
• Two Phase Region
– Draw a horizontal line at temperature of interest – “tie line” – Intersection of the tie line and phase boundaries gives composition Horizontal: 水平的 Intersection: 交叉点
材料科学基础 第四章 相图(3)
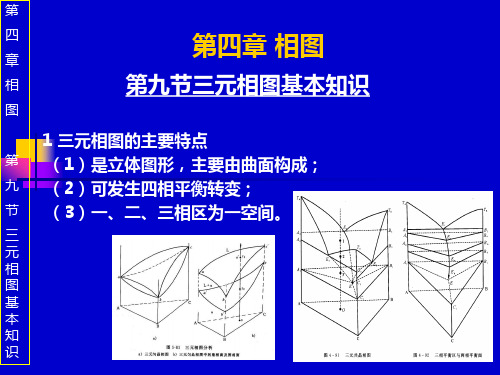
第 十 一 节 三 元 共 晶 相 图
25
第 四 章 相 图
第十一节 三元共晶相图
二 组元在固态有限溶解的共晶相图
(3)变温截面 ) 3个三相区 个三相区 共晶相图特征: 共晶相图特征:水平线 ;两相共晶区特征:曲边三角形。 两相共晶区特征:曲边三角形。 1个三相区 个三相区 应用:分析合金结晶过程,确定组织变化. 应用:分析合金结晶过程,确定组织变化 局限性:不能分析成分变化。 成分在单变量线上,不在垂直截面上) 局限性:不能分析成分变化。(成分在单变量线上,不在垂直截面上)
第十一节 三元共晶相图
一 组元在固态互不相溶的共晶相图 (1)相图分析 ) 熔点;二元共晶点;三元共晶点。 点:熔点;二元共晶点;三元共晶点。 两相共晶线 液相面交线 两相共晶面交线 液相单变量线
液相区与两相共晶面交线
第 十 一
线:EnE
节 三 元 共 晶 相 图
14
第 四 章 相 图 第 十 一 节 三 元 共 晶 相 图
第十一节 三元共晶相图
一 组元在固态互不相溶的共晶相图 (1)相图分析 ) 液相面 固相面 面: 两相共晶面 三相共晶面 两相区: 个 两相区:3个 单相区: 个 区: 单相区:4个 三相区: 个 三相区:4个 四相区: 个 四相区:1个
15
第 四 章 相 图 第 十 一 节 三 元 共 晶 相 图
第 十 一 节 三 元 共 晶 相 图
26
第 四 章 相 图
第十一节 三元共晶相图
二 组元在固态有限溶解的共晶相图 合金结晶过程分析; 合金结晶过程分析; 相组成物相对量计算(杠杆定律、重心定律) (4)投影图 相组成物相对量计算(杠杆定律、重心定律) ) 组织组成物相对量计算(杠杆定律、 组织组成物相对量计算(杠杆定律、重心定律)
材料学基础第5章三元相图

材料科学基础
第五章
5.6三元相图小结
材料科学基础
第五章
一、单相状态 f=3-1+1=3,而一个温度变量和两个成分变量之间没有任何
相互制约的关系,因此,不论是等温截面还是变温截面,单相区可能具 有多种多样的形状。 二、两相平衡 立体图:共轭曲面。 成分变化:蝶形规则。 等温图:共轭曲线(可用杠杆定律) 变温截面:判定转变温度范围和相转变过程,不能用杠杆定律。 三、三相平衡 立体图:三棱柱,棱边是三个平衡相单变量线。
二、投影图
材料科学基础
第五章
投影图的作用:合金结晶过程分析、相组成物相对量计算、组织组成 物相对量计算。
图8.17 三元共晶相图的投影区
表8.2 各典型区域合金的凝固组织过程及室温组织
材料科学基础
第五章
区
凝固过程
室温组织
Ⅰ
L→α
α
Ⅱ
L→α ,α→βⅡ
α+βⅡ
Ⅲ
L→α ,α→βⅡ,α β
α+βⅡ+γⅡ
(1)当给定合金在一定温度下处于两相平衡状态时,若其中一相的成分 给定,则根据直线法则,另一相的成分点必位于两已知成分点连线的 延长线上。 (2)如果两个平衡相的成分点已知,则合金的成分点必然位于两平衡相 成分点的连线上,根据两平衡相的成分,可用杠杆定律求出合金的成 分。
5.2.2重心定律
x,y,z分别为α,β,γ成分点,则
材料科学基础
第五章
投影图有两种。一种是把空间相图中所有相区间的交线部投影到浓度 三角形中,借助对立体图空间构造的了解,可以用投影图来分析合 金的冷却和加热过程。另一种是把一系列水平截面中的相界线投影 到浓度三角形中。每一条线上注明相应的温度,这样的投影图叫等 温线投影图。等温线可反映空间相图中各种相界面的变化趋势,等 温线越密,表示这个相面越陡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
参考答案 第4章 相 图范莉:p.4问题 讲义中说:“压力平衡最容易,温度平衡次之,化学势平衡最难达到”,为什么? 答:从三个层次考虑,力(压力) 能量(温度) 物质(化学势),平衡越来越难。
p.8问题 从图4-1看出,自由能G 随温度T 的增加而下降。
能不能据此做如下判断:低温物质不如高温物质稳定,因为前者的G 高,而后者低。
答:不可以。
用G 判据判定体系是否稳定需在同一温度下比较,否则无意义。
问题 pG S T ∂⎛⎫=- ⎪∂⎝⎭表明,G T -曲线的斜率一定是负的。
除此之外,G T -曲线还有另一个特点,请问是什么?答:温度越高熵值越大,曲线斜率越来越负,即曲线随温度的增加越降越快。
问题 在图4-1中,设有一个温度m T T <。
证明:若T 与m T 相差不大,则 ()T T T L G G G m mm L S V -=-=∆ 答:提示:(1)局部线性 (2)m m /T L S =pG S T ∂⎛⎫=- ⎪∂⎝⎭,m m m T L T )-T S T G (=∙∆=∆问题 当压力不变时,某种纯金属处于两种不同的状态:一是理想晶体;二是含晶界的多晶体。
请说明两种不同状态下该金属的G T -曲线有什么差异? 答:含晶界的多晶体的熵值比理想晶体大,故曲线更陡。
问题 当压力不变时,某种纯金属处于两种不同的状态:一是非晶体;二是含晶界的多晶体。
请说明两种不同状态下该金属的G T -曲线有什么差异?在横坐标中注明熔点位置。
答:(1)非晶体的熵值比含晶界的多晶体大,故曲线更陡。
(2)按照纯金属的自由能-温度曲线标出熔点。
问题 从图4-2看出,固-气、液-气两相平衡的温度范围比较大,而固-液两相平衡仅在很窄的温度范围存在,请分析原因。
答:根据m d d L p T T V=∆ ,主要看V ∆的大小。
问题 对图4-2中的亚稳平衡线,克拉贝龙方程还适用吗?为什么?答:适用,克拉贝龙适用于两相平衡。
P12~13问题 为什么“应变能因素总是使固溶体中A 组元的化学势高于纯A ”?注意,不能用公式回答,而要用文字表述。
答:应变能永远为正,使得体系能量增大,A 组元的化学势高于纯A.(位错等缺陷带来影响也是使体系自由能增大,与之类似。
)问题 从()x T k Z x G -+Ω+=1ln B 2A A μ看出,当1x →时,A μ→-∞。
请从物理概念角度分析这一问题。
注意:负无穷大总是不合理的。
答:考虑在纯B 中加入一个A 的情况,此时熵的变化很大而内能变化很小,此时G-X 的曲线做切线时斜率很大,A d d G G x xμ=-,故A μ→-∞问题 讲义中说:规则溶液模型既可以用于液体,也可以用于固溶体。
问:具体应用时,两者的主要差异是什么?答:两者的是主要差异在于线性项,参见教材P14问题 讲义中说:忽略e AB 、e AA 、e BB 随温度和成分的变化,其中忽略e AB 、e AA 、e BB 随成分的变化容易理解,但为什么忽略e AB 、e AA 、e BB 随温度的变化?答:e AB 、e AA 、e BB 均随温度发生同向变化,则()2/BB AA AB e e e +-=Ω几乎不变。
问题 1.规则溶液模型中,m S ∆只考虑了组态熵,为什么不考虑振动熵和平动熵呢?2.固溶体合金中有自由电子,而自由电子对应电子热容。
因此,有无自由电子熵?在规则溶液模型中为什么不考虑这份熵?答:(1)规则溶液模型考虑的主要是固溶体由于原子尺度的混合而带来的熵的变化。
纯A 或纯B 的组态熵均为零。
当形成固溶体时,n A 个A 原子与n B 个B 原子能排列出许许多多花样,所以组态熵很大。
振动熵和平动熵受温度影响较大受混合影响较小,在温度不变的情况下,不考虑变化很小的振动熵和平动熵。
( 2 )有自由电子熵(3)规则溶液模型最小的尺度为原子量级,不考虑原子内部情况。
问题 既然固溶体中需要考虑应变能对化学势的影响,那么晶界能、位错能对化学势有无影响?请给予简要说明。
答:参考问P12问题1问题 1.组态熵与相互作用参数有什么关系?2.组态熵与温度有什么关系?答:(1)相互作用参数会影响组态熵。
0Ω=时,组态熵最大;0Ω>和0Ω<造成原子偏聚和有序化,使得AB 原子能排列出花样减小,故组态熵变小。
(2)温度越高,组态熵越大。
问题 1.规则溶液模型能应用到VC-TiC 这样的置换固溶体中吗?2.此时的内能项如何计算?只要说明思路即可,不用具体写出计算式。
答:可以用。
此时的内能考虑Ω和应变能。
P16~17问题 讲义中说:“L Ω与s Ω一般具有相同的正负号,为什么?答:Ω表示形成一个A-B 键所引起的能量变化,固液中键的种类没有区别,只是液相中平均原子比固相中稍大一些,故L Ω与s Ω有相同的符号。
问题 液相与固溶体相的自由能-成分曲线(式4-16A)的主要差异来源于什么?答:L G 与s G 是出现差异的主要原因。
问题 随着温度从高温降到低温,式4-16A 中两条自由能-成分曲线的整体关系会发生什么样的变化?为什么?答:两条线均下降,从无交点到有交点再到无交点。
问题 讲义中说:“()B A 01xG G x G +-=代表一条直线(图4-4a 、b 、c),它表示成分为x 时,纯A 、纯B 机械混合的自由能。
由于机械混合不是原子尺度的混合过程,所以自由能可线性叠加”。
为什么不是原子尺度混合,自由能就可以线性叠加?事实上,这个问题与下面的问题相关:不是原子尺度,那么到底应该是什么尺度?提示:如果能够画图,分析起来容易些。
答:机械混合满足条件:(1)Ω=0(键的种类不变)(2)熵要发生变化一定要原子尺度的混合,大块的机械混合熵变很小很小,忽略不计。
所以机械混合不引起内能和熵的变化,可以进行线性叠加。
机械混合是晶粒尺度的混合。
问题 固溶体稳定与否的分析思路是什么?请用文字简要回答。
答:利用自由能成分曲线,比较成分为x 0的固溶体的自由能和由它分解为成分为x 1和x 2的两个固溶体机械混合后的自由能的高低,从而确定固溶体的稳定性。
问题 1.固溶体的混合熵m S ∆由式4-9确定。
但是,该式仅适用于溶质原子随机分布。
当溶质原子偏聚或有序化时,混合熵相对于式4-9会发生什么样的变化?为什么?2.类似的问题还可以针对m U ∆,问偏聚或有序化时,固溶体的混合热(m U ∆)会发生什么变化? 答:问题 规则溶液模型反映的是固溶体的自由能-成分关系,请问这里的固溶体含晶界吗?含位错吗?如何含有这些缺陷,自由能-成分曲线会发生什么样的变化?为什么?答:(1)不含。
因为固溶体的自由能-成分关系时未考虑这些缺陷带来的内能和熵的变化。
(2)整体都抬高。
问题 Fe-C 固溶体的自由能-成分曲线显然不能用规则溶液模型。
问此时应该如何分析,最终的自由能-成分关系式是什么样的?(假定C 含量很低)答:(1)C 原子的融入引起应变能,应变能使得内能发生变化,因此()()X -1X KV X E U m ε==∆.(2)C 含量很低,且随机分布,仍参考平衡空位浓度推导的方式求熵变,将C 原子看成空位,八面体空隙看成N.吕佳:P20问题 s F x -曲线是针对固溶体的。
1.从理论上讲,这里的固溶体中有晶界吗?有位错吗?请简要说明;2.如果有晶界、位错等缺陷,s F x -会如何变化?特别是它与L F x -的关系有什么变化,对相图中的两相区有何影响?答:1.没有。
2.s F x -曲线将会上抬,而LF x -无变化。
两相区会向固相区移动。
固相区能量高了,所存在的区域就小了。
它所对应的另一相的区域就多了(也可由G-x 曲线作切线研究)。
问题 假定Ni-Cu 相图中的固溶体含较多的位错、晶界等缺陷,问其中的固相线和液相线会发生什么变化?请根据自由能-成分曲线的公切线理论给予分析。
答:同上。
问题 讲义中说:“在保持体系成分的前提下,可以任意假设体系的具体存在方式,然后比较各种不同方式的自由能,其中自由能最低者就是能够稳定存在的方式”,其中隐含了有些状态下自由能不是最低,请问这些状态的存在性与稳定性应该如何描述?答:这些状态可以存在但不是最稳定的,为亚稳状态。
P25问题 讲义中说:“温度越低,0Ω>的作用越强(即U ∆项的作用相对越大),s F x -曲线上凸的部分越宽越高”,为什么温度越低,上凸部分“越宽越高”?答:由式(4-16A )知,温度越低,熵的作用越小,相对来说,0Ω>的作用越强(即U ∆项的作用相对越大)。
由右图可知,曲线上抬,致使sF x -曲线上凸的部分越宽越高。
问题 1.具体写出Pb-Sn 相图的共晶反应的化学势条件;2.能不能说,共晶反应属于三相平衡?答:1.βαμμμb b b P L P P ==;βαμμμn n n S L S S ==; 2.能。
问题 在略低于183℃的条件下(如182.5℃),Sn 在Pb 中的溶解度约为19%,而Pb 在Sn 中仅为2.5%。
请解释溶解度差异为什么如此之大。
答:Pb 原子的半径大于Sn ,因此Pb 溶于Sn(压缩)引起的点阵畸变比较大,应变能较大,较难溶。
问题 讲义中说:“在T 3温度下,当Sn 的含量小于10wt%时,由于熵的作用占主导地位,α固溶体能稳定存在;当Sn 的含量大于10wt%时,由于内能的作用占主导地位,α固溶体不再稳定,它的一部分开始分解,形成具有A5结构的β固溶体”,请结合图4-8的s F x -曲线进一步分析。
答:由右图可知,当Sn 的含量小于10wt%时, sF x -曲线下凹,单相固溶体较稳定。
而当Sn 的含量大于10wt%时, s F x -曲线上凸,两相机械混合较稳定。
问题 图4-8中,s F x -曲线从高温到低温发生了怎样的变化?答:温度较高时,s F x -曲线下凹,随着温度的降低,曲线出现上凸,且上凸部分越来越宽。
问题 图4-9(a)的最后两个图,哪有个更加稳定,为什么?答:前者较稳定。
因为β相偏析到晶界,应变能减小,体系能量降低。
问题 H 2O-NaCl 相图中,NaCl 在水中的溶解度曲线类似于图4-7中的MF 曲线,即随着温度的增加,NaCl 在水中的溶解度增大。
由于NaCl 溶入水中会分解为离子,且水分子是有极性的,所以每个离子周围有很多水分子。
在上述背景下,NaCl 在水中饱和的微观含义是什么?换言之,NaCl 浓度超过了溶解度曲线,NaCl 从水中析出的微观含义是什么?答:没有更多的“自由”的水分子去抓它们。
问题 画出固相完全不互溶的简单共晶相图的自由能-成分曲线。
以图4-58中的Au-Ge 相图为例。
答:问题 纯金属A 、B 在液态完全互溶而在固态完全不溶,它们的熔点分别是A T = 800K 、B T =945K ,熔化热分别是A m L = 2.5KJ/mol 、B mL = 4KJ/mol 。
