凸轮机构设计及运动分析
机械原理凸轮机构设计
凸轮机构的设计一、简介凸轮机构是由凸轮,从动件和机架三个基本构件组成的高副机构。
凸轮是一个具有曲线轮廓或凹槽的构件,一般为主动件,作等速回转运动或往复直线运动。
与凸轮轮廓接触,并传递动力和实现预定的运动规律的构件,一般做往复直线运动或摆动,称为从动件。
凸轮机构在应用中的基本特点在于能使从动件获得较复杂的运动规律。
因为从动件的运动规律取决于凸轮轮廓曲线,所以在应用时,只要根据从动件的运动规律来设计凸轮的轮廓曲线就可以了。
凸轮机构广泛应用于各种自动机械、仪器和操纵控制装置。
凸轮机构之所以得到如此广泛的应用,主要是由于凸轮机构可以实现各种复杂的运动要求,而且结构简单、紧凑。
二、凸轮机构的工作原理由凸轮的回转运动或往复运动推动从动件作规定往复移动或摆动的机构。
凸轮具有曲线轮廓或凹槽,有盘形凸轮、圆柱凸轮和移动凸轮等,其中圆柱凸轮的凹槽曲线是空间曲线,因而属于空间凸轮。
从动件与凸轮作点接触或线接触,有滚子从动件、平底从动件和尖端从动件等。
尖端从动件能与任意复杂的凸轮轮廓保持接触,可实现任意运动,但尖端容易磨损,适用于传力较小的低速机构中。
为了使从动件与凸轮始终保持接触,可采用弹簧或施加重力。
具有凹槽的凸轮可使从动件传递确定的运动,为确动凸轮的一种。
一般情况下凸轮是主动的,但也有从动或固定的凸轮。
多数凸轮是单自由度的,但也有双自由度的劈锥凸轮。
凸轮机构结构紧凑,最适用于要求从动件作间歇运动的场合。
它与液压和气动的类似机构比较,运动可靠,因此在自动机床、内燃机、印刷机和纺织机中得到广泛应用。
但凸轮机构易磨损,有噪声,高速凸轮的设计比较复杂,制造要求较高。
一、工作过程和参数在凸轮机构中最常见的运动形式为凸轮机构作等速回转运动,从动件往复移动。
以图6-8为例(对心外轮廓盘形凸轮机构)。
首先介绍一下本图中各构件的名称。
1,运动分析:停CA4ϕ2、参数①推程(升程)-- 从动件自最低位置升到最高位置的过程 ②推程角(升程角)--推动从动件实现推程时的凸轮转角(ϕ1) ③回程 -- 从动件自最高位置升到最低位置的过程 ④回程角 --从动件从最高位置回到最低位置时的 凸轮转角(ϕ3)⑤远停角(远休止角)从动件在最高位置停止不动,与此对应的凸轮转角。
机械设计中的凸轮机构设计

机械设计中的凸轮机构设计在机械设计领域中,凸轮机构是一种重要的动力传输装置,被广泛应用于各种机械设备中。
凸轮机构通过凸轮的旋转运动,驱动其他部件产生直线或曲线的往复运动。
它具有紧凑、高效、稳定等特点,在汽车发动机、机床、纺织机械等领域发挥着重要作用。
然而,在设计凸轮机构时,需要考虑多个因素,包括凸轮形状、凸轮轮廓设计、轴承选择等,才能实现理想的设计效果。
一、凸轮机构的设计要素及原理凸轮机构设计的首要任务是确定凸轮形状和凸轮轮廓。
凸轮的形状直接影响着凸轮机构的运动特性。
常见的凸轮形状包括圆形凸轮、球面凸轮、椭圆凸轮、平面凸轮等。
每种形状都有其适用的场合,需要根据具体应用和设计要求进行选择。
凸轮的轮廓设计是凸轮机构设计的核心之一。
凸轮轮廓的设计需要满足工作机构的要求,确保凸轮和从动件之间能够实现精确的接触和运动匹配。
凸轮轮廓可以根据从动件的运动学要求来确定,可以是简单的直线、圆弧,也可以是复杂的曲线轮廓。
凸轮机构的设计还需要考虑力学特性及材料选择。
凸轮与从动件之间的接触处会产生接触力和摩擦力,需要确保设计中的力学强度和刚度满足要求。
此外,凸轮的材料也需要考虑其耐磨性和耐久性,以保证长时间的可靠运行。
二、凸轮机构的设计流程凸轮机构的设计是一个系统工程,需要进行详细的规划和流程设计。
以下是一般的凸轮机构设计流程:1. 确定设计要求:包括凸轮机构的运动周期、速度、力学要求等。
2. 凸轮轮廓设计:根据从动件的运动要求,确定凸轮轮廓。
可以通过计算方法、图形方法或CAD软件进行设计。
3. 凸轮形状选择:根据具体要求和应用场景,选择合适的凸轮形状。
可以进行形状优化设计和分析,以得到最佳的设计方案。
4. 轴承选择:选择合适的轴承类型和尺寸,确保凸轮机构的运动平稳和耐久可靠。
5. 强度和刚度分析:进行力学分析,评估凸轮机构的强度和刚度是否满足要求。
可以通过有限元分析等方法进行验证。
6. 材料选择和热处理:根据设计要求选择适当的材料,并进行必要的热处理,提高材料的力学性能和耐久性。
凸轮机构的设计和计算详解

凸轮机构的设计和计算详解1. 引言凸轮机构是一种常见的机械传动装置,通过凸轮的运动来实现对其他部件的控制和驱动。
凸轮机构广泛应用于发动机、机械加工、自动化设备等领域。
在本文中,我们将详细介绍凸轮机构的设计和计算方法。
2. 凸轮机构的基本原理凸轮机构由凸轮、从动件和控制件组成。
凸轮通过旋转或移动的方式,驱动从动件进行线性或旋转运动。
不同凸轮形状和运动方式将实现不同的功能。
3. 凸轮的设计要点凸轮的设计涉及凸轮形状、凸轮面积、凸轮运动规律等方面。
在进行凸轮设计时,需要考虑以下要点:•运动要求:根据从动件需要的运动类型(线性或旋转)、速度和加速度要求,确定凸轮的形状和运动规律。
•动态负载:凸轮在运动过程中所承受的动态负载应被考虑在内,以确保凸轮的强度和耐久性。
•材料选择:根据凸轮的工作条件和负载要求,选择适当的材料来制造凸轮,以保证其可靠性和寿命。
4. 凸轮机构的计算方法4.1 凸轮剖面的计算凸轮剖面的计算是凸轮机构设计中的重要一环。
根据凸轮的运动规律和从动件的运动要求,可以进行凸轮剖面的计算。
常用的凸轮剖面计算方法有:•凸轮剖面生成法:根据从动件的运动要求,通过几何构造和插值计算,生成凸轮剖面。
•凸轮运动分析法:通过分析凸轮的运动规律和从动件的运动要求,推导出凸轮剖面的数学表达式。
4.2 凸轮机构的运动学分析凸轮机构的运动学分析是确定凸轮机构各部件的运动规律和参数的过程。
通过运动学分析,可以计算凸轮机构的几何关系、速度和加速度等。
常用的凸轮机构运动学分析方法有:•图形法:通过绘制凸轮机构的运动示意图和运动曲线,分析凸轮机构的运动规律。
•解析法:通过建立凸轮机构的运动学方程,推导出各部件的运动参数,并进行计算。
4.3 凸轮机构的强度计算凸轮机构的强度计算是为了确定凸轮所承受的载荷是否安全,并选择适当的材料和结构来满足设计要求。
在强度计算中,需要考虑凸轮的静载荷、动载荷和疲劳载荷等。
常用的凸轮机构强度计算方法有:•静态强度计算:通过分析凸轮在静态载荷下的应力和变形情况,确定凸轮的强度和刚度。
凸轮机构运动模型和受力分析
• 凸轮机构的磨损形式有:点蚀、粘着磨损、疲劳磨损等。 • 磨损分三个阶段:跑合期、稳定磨损期、剧烈磨损期。磨损量
U(磨损尺寸、体积或重量)与时间的关系曲线如图 • 磨损速度也即磨损率,它的定义为在单位时间内材料的磨损量,
记为q。针对磨损的三个阶段,分别对磨损量和磨损速度作近似 数学描述。 • 跑合阶段:
• 2fMT/H的值大小影响挺杆和移动副之间的磨 损,即接触点位置离中心线越远,MT值越 大,而 2f/H为定值,所以磨损越大;F值的
大小变化影响凸轮表面和平底从动件之间
的磨损,并使凸轮转动副受到垂直方向的 附加压力而产生额外径向磨损; Fh、 Ff、 Fg 、a 的值越大,凸轮机构的接触力F越大, 凸轮—挺杆副磨损越严重。
凸轮机构磨损形式和三个阶段
• 凸轮以不同速度旋转时,其接触应力是变化的。低速时, 由于气门弹簧压缩量最大,凸轮桃尖的载荷最大;高速时, 在负加速度区,即在凸轮桃尖附近,由于往复运动的惯性 力抵消了一部分气门弹簧力,凸轮桃尖的载荷降低了,因 此发动机速度较高时点蚀磨损减少。而在最大正加速度区, 接触应力分布幅度小,不易产生点蚀磨损,偶尔会出现金 属间的直接接触,因此会出现擦伤现象。实际上,由于气 门传动机构零件不是刚性的并可产生振动,从而改变了凸 轮桃尖附近的接触压力,高速时这些振动力就会使凸轮— 挺杆副产生点蚀。由于凸轮和挺杆都是硬而脆的材料,若 都是经淬火处理的白口铸铁,其疲劳损坏出现在拉应力最 大的区域,即出现在表面上。这些疲劳损坏向内扩展,形 成松散的鳞屑并产生凹坑(点蚀)。一般金属裂纹的扩展方 向与凸轮转动方向相反,即与滑动方向相反。
凸轮机构运动模型和受力分析
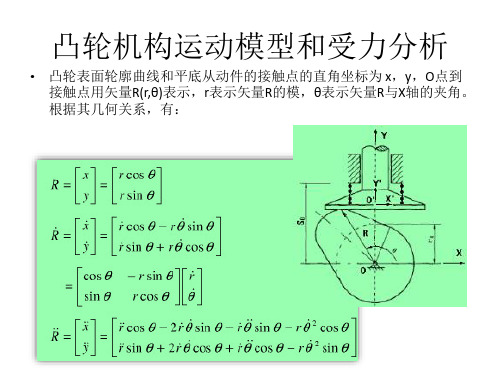
• 凸轮表面轮廓曲线和平底从动件的接触点的直角坐标为 x,y,O点到 接触点用矢量R(r,θ)表示,r表示矢量R的模,θ表示矢量R与X轴的夹角。 根据其几何关系,有:
凸轮机构运动原理解析

凸轮机构运动原理解析凸轮机构是一种机械传动装置,广泛应用于各种机械系统中,例如汽车发动机、工业机械和机床等。
本文将对凸轮机构的运动原理进行解析,以帮助读者更好地理解其工作原理。
一、凸轮机构的定义和构成凸轮机构是由凸轮和从动件(如滑块、摇臂等)组成的传动装置。
凸轮是一种特殊形状的轮轴,其外形常为椭圆或心形,具有多个凸起部分。
从动件则通过与凸轮接触,实现凸轮机构的运动传动。
二、凸轮机构的工作原理凸轮机构的工作原理基于凸轮的运动和从动件的运动响应之间的关系。
一般来说,凸轮的运动可以是旋转、往复或其他特殊的轨迹形式,这取决于具体的应用场景。
旋转运动的凸轮机构:当凸轮进行旋转运动时,从动件跟随凸轮的轨迹做往复运动。
这种机构常用于各类发动机的气门传动系统中。
例如,汽车发动机中的凸轮轴通过凸轮的旋转来驱动气门的开闭。
往复运动的凸轮机构:当凸轮进行往复运动时,从动件以一定的轨迹做复杂运动。
这种机构常用于机床和工业机械中。
例如,磨床的主轴就是通过往复运动的凸轮来驱动的。
其他特殊形式的凸轮机构:除了旋转和往复运动,凸轮还可以设计成其他特殊的轨迹形式,以满足特定的运动需求。
例如,摇杆机构中的摇杆就是一种特殊的凸轮,它通过摇杆的旋转运动来驱动从动件。
三、凸轮机构的优缺点凸轮机构具有以下几点优点:1. 可实现复杂的运动传动:由于凸轮可以设计成各种复杂的轨迹形式,因此凸轮机构可以实现各种复杂的运动传动需求。
2. 传动精度高:凸轮机构的传动精度高,能够满足精密机械装置的要求。
3. 结构简单可靠:凸轮机构的结构相对简单,不容易出现故障,具有较高的可靠性。
然而,凸轮机构也存在一些缺点:1. 摩擦和磨损问题:由于凸轮和从动件之间的接触,会产生摩擦和磨损,这可能会限制凸轮机构的使用寿命。
2. 噪音和振动:凸轮机构在工作时可能会产生噪音和振动,这对于要求低噪音和低振动的装置来说可能是一个问题。
四、凸轮机构的应用领域凸轮机构广泛应用于各种机械系统中,包括但不限于以下几个领域:1. 汽车工业:凸轮机构被广泛应用于汽车发动机的气门传动系统,实现气门的开闭控制。
凸轮机构的动态分析与设计研究

凸轮机构的动态分析与设计研究凸轮机构的动态分析与设计研究摘要:凸轮机构作为一种常见的机械传动装置,在工业应用中起到了重要的作用。
本文通过对凸轮机构的动态分析与设计进行研究,探讨了凸轮机构的工作原理、动力学特性以及设计方法等方面。
通过理论分析和计算模拟,本文旨在提供凸轮机构设计与优化的参考依据,以提高其性能和可靠性。
1. 引言凸轮机构是一种将旋转运动转变为直线运动的机械传动结构,广泛应用于各类机械设备中。
其工作原理是通过凸轮与其上的凸轮跟随件的相互作用,实现运动的传递和控制。
在许多机械装置中,凸轮机构常用于实现定制的运动轨迹和动作周期。
因此,对凸轮机构的动态分析与设计进行深入研究,对于提高机械装置的性能和可靠性具有重要意义。
2. 动态分析凸轮机构的动态分析是研究凸轮运动学和动力学特性的过程。
其中,凸轮运动学是分析凸轮运动轨迹和运动速度的研究,而凸轮动力学则是研究凸轮运动过程中产生的力学特性。
从运动学的角度来看,凸轮的运动轨迹可以通过凸轮的几何形状和旋转运动参数来描述。
而从动力学的角度来看,凸轮机构中的摩擦、惯性和弹性等因素对系统的运动性能和机构的稳定性都有重要影响。
3. 动力学模型为了更深入地研究凸轮机构的动态特性,需要建立凸轮机构的动力学模型。
动力学模型可以通过建立凸轮和跟随件之间的力学关系来描述凸轮机构的运动过程。
在建立动力学模型时,需要考虑凸轮与跟随件之间的接触力、惯性力和弹性力等因素。
通过求解动力学模型,可以获得凸轮机构在不同工况下的运动特性和力学特性。
4. 设计方法凸轮机构的设计是指根据给定的工作要求和运动轨迹,确定凸轮和跟随件的几何形状和运动参数的过程。
凸轮机构的设计方法不仅需要满足凸轮运动学和动力学的要求,还要考虑制造工艺和可靠性等因素。
在设计凸轮机构时,可以采用计算机辅助设计软件进行模拟和优化,以提高设计效率和设计质量。
5. 优化分析为了提高凸轮机构的性能和可靠性,需要对凸轮机构的设计进行优化分析。
凸轮机构运动分析的原理

凸轮机构运动分析的原理凸轮机构是一种常见的机构,用于将旋转运动转化为直线运动或者变化其运动轨迹。
其基本原理是通过凸轮的几何形状和凸轮与其它运动部件的相对位置,实现运动传递和控制。
凸轮机构的运动分析是通过分析凸轮的几何特性和与其它机构部件的作用关系,推导出机构的运动规律和性能参数,包括凸轮的运动学状态、凸轮轮廓的设计,以及机构的运动周期和速度等。
凸轮机构的关键是确定凸轮的几何特性和轮廓形状。
凸轮的几何形状通常是由其运动部位(如凸轮轴)和运动部件(如滑块、摇臂等)的相对位置关系来确定。
在运动分析过程中,可以通过几何图形的绘制和计算,以及几何和尺寸的转换,来确定凸轮的轮廓和运动状态。
其中,常见的凸轮形状有圆形凸轮、椭圆凸轮、伞形凸轮和曲线凸轮等。
凸轮机构的运动分析主要包括以下几个方面的内容:第一,凸轮的转动及滚动运动分析。
根据凸轮与其它运动部件的相对运动关系,可以推导出凸轮的转动规律和速度,并确定凸轮是否有滚动条件。
滚动条件是指凸轮与其它运动部件接触点的相对速度为零,这样可以避免由于滑动产生的摩擦和磨损等问题。
第二,凸轮轮廓的设计与绘制。
通过运动分析和计算,可以确定凸轮的运动规律和性能参数,然后根据这些参数来设计凸轮的轮廓形状。
常用的方法有图解法、计算法和仿真法等。
其中,图解法是最简单直观的方法,通过手绘几何图形来确定凸轮的轮廓形状;计算法则是通过数学模型和计算公式,来计算凸轮的几何参数和轮廓形状;仿真法主要是利用计算机辅助设计(CAD)或仿真软件,来模拟凸轮的运动状态和绘制轮廓图形。
第三,凸轮机构的运动周期与传动比分析。
凸轮机构通常是用来实现特定的工作循环或运动行程,所以需要分析凸轮的运动周期和传动比。
运动周期是指凸轮从一个状态到另一个状态所需的时间,可以通过几何图形和时距图来表示和计算;传动比是指输入轴和输出轴的转速之比,可以通过几何和动力学分析来计算。
第四,凸轮机构的运动状态分析与优化。
通过运动分析,可以得到凸轮机构的运动规律和性能参数,如加速度、速度和位置等。
机械原理第9章凸轮机构及其设计

第二十一页,编辑于星期日:十四点 分。
②等减速推程段:
当δ =δ0/2 时,s = h /2,h/2 = C0+C1δ0/2+C2δ02/4 当δ = δ0 时,s = h ,v = 0,h = C0+C1δ0+C2δ02
0 = ωC1+2ωC2δ ,C1=-2 C2δ0 C0=-h,C1= 4h/δ0, C2=-2h/δ02
如图所示,选取Oxy坐标系,B0 点为凸轮廓线起始点。当凸轮转过δ 角度时,推杆位移为s。此时滚子中 心B点的坐标为
x (s0 s) sin e cos
y
(s0
s) cos
A7
C8 A6 C7
w
A8
-w
A9
C9 B8 B9 B7 r0
C10
B12100 ° B0
O
B1 a B2
C1 L C2φ1φ0
A10 A0
φ
Φ
o
2
1
2 3 456
180º
7 8 9 10
60º 120º
δ
(1)作出角位移线图;
(2)作初始位置;
A5
C6
B6 B1580°B4
C4
C5
φ3
φC23
A1
↓对心直动平底推杆盘形凸 轮机构
↑偏置直动尖端推杆盘形凸轮机 构
第十一页,编辑于星期日:十四点 分。
↑尖端摆动凸轮机构
↓平底摆动凸轮机构
↑滚子摆动凸轮机构
第十二页,编辑于星期日:十四点 分。
(4)按凸轮与从动件保持接触的方式分
力封闭型凸轮机构
利用推杆的重力、弹簧力或其他外力使推杆与凸轮保持接
触的
此外,还要考虑机构的冲击性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
凸轮机构设计及运动分析
问题描述:
如图1所示为以对心直动尖顶盘形凸轮机构。
从动杆位移s随时间变化曲线如图2所示。
要求设计凸轮机构并分析从动件速度v,加速度a随时间变化的规律,及应力、应变随时间变化的规律。
任务与要求
1.设计满图2运动规律的凸轮机构;(要有设计计算步骤)
2.对所设计的机构运用ansys软件分析从动件速度、加速度随时间变化的规律;
3.查阅资料、了解所给机构的在生产、生活中的应用,说明其工作原理,并附相应的图片或视频。
凸轮机构设计及运动分析指导书
一、设计的目的
通过设计,训练学生机构设计的能力,掌握运用ANSYS Workbench进行瞬态动力学分析的方法、步骤和过程,提高学生解决实际问题的能力。
二、设计报告的主要要求
设计报告包括设计报告书Word文档和Powerpoint演示文稿两部分。
1.设计报告书内容包括目录、任务书、正文、参考文献、组员工作内容表。
(1)文档格式严格遵守设计书文档规范要求。
(2)目录必须层次清楚,并标有页码数。
(3)正文按章节编写,按照任务书要求合理安排内容,并附有参考文献。
2.Powerpoint演示文稿要求内容简洁,重点突出。
三、人员要求:1人
四、时间安排
1.布置任务、准备、查阅资料:2天;
2.机构设计及动画:6天;
3.Ansys分析:6天;
4.编写报告书、Powerpint演示文稿、验收:2天。
5.答辩。
五、成绩形成:
设计报告书:50分;答辩:50分
组内成员按实际完成工作量评定每位学生最终成绩;不参加答辩的学生没有答辩成绩。
六、参考资料:机械原理的平面机构,ansys机械工程应用精华59例。
