(完整版)高频电子线路张肃文第五版_第2章习题答案
高频电子线路习题答案(第五版)张肃文(完整资料).doc

【最新整理,下载后即可编辑】高频电子第五版(pF)).(L C H)(.QR则L Ω取R Δf f Q (kHz)Δf MHz解:f..159101*********1159********10010100101010121010990101211362620603670036700=⨯⨯⨯⨯===⨯⨯⨯====⨯⨯===⨯-⨯==--ωμω时,产生并联谐振。
C L 或ωC L )当(时,产生串联谐振。
C L 或ωC L )当(时,产生并联谐振。
C L 或ωC L )当解:(22021101220211012202110111311211123======-ωωωR R C L R )LC ωL(j ωR )LC ωLR(j ωC L R C j ωR L j ωR )C j ωL)(R j ω(R 证明:Z =+=-+-++=+++++=-2112111133220020020000)()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C L 故采用后一个不合理舍去pF -得C C C 由pF得C C C 由解:=⨯+⨯⨯⨯⨯='+==+=⨯+=+=⨯+--ω。
L C C ’()()()()mV V Q V V mA .R V I μH ..C L ..R C 解:Q-Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=⨯⨯====⨯===⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯==-ωω()()()()()()Ωj ..j .C jR Z Ω.....Q LQ L R pFC pF .L C C C C .V V Q μH .C 解:L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620-=⨯⨯⨯⨯-=-==⨯⨯⨯⨯-⨯⨯⨯⨯=-==→=⨯⨯⨯⨯==+⋅====⨯⨯⨯⨯==------ωωωωω()()()。
高频电子线路(第五版) 张素文
M
2 22
2 2 22
R X
R22
X 22
M
2 22
2 2 22
R X
X 22
R22 20
1 X 22 10 L2 6 10 C2
6
2-16:①:
Rf 1
M
R2
2
20
R总 R f 1 R1 25
6
L 100 10 Z ab 40 K 12 RC 25 100 10
②:音量位于最上端:
R R1 R2 // ri 2
R R 0.3 R R1 R2
③:不产生惰性失真:
验证是否产生负峰切割失 真,否则改变R1,R2
max RC 1.5
④:CC耦合300HZ ~ 3000HZ
C
取 : C1 C2 0.01或0.005
1 f 0 10 5 10 : V0 m 25 0.7 2 1 6 4 f 0 10 10 : V2 m 25 0.3 2
6 3
f 0 10 : V0 m 25
6
Vmax V0 m峰 V0
V0 Vmin m谷 V0
Vm 251 0.7 cos t 0.3 cos 2t
20 40 5 C Ci C1 // C2 18.3PF 20 40
C1 Ci Ri L
C'2 R'0
RP ②: Q0 100 0 L Q0 ③: QL RP RP 1 Ri R0
④:
RP 20.9K
Q0 28.1 20.9 20.9 1 10 45
高频电子线路课后习题答案第五版张肃文.doc

高频电子第五版(pF)).(L C H)(.QR则L Ω取R Δf f Q (kHz)Δf MHz解:f..159101*********11591014321010010100101010121010990101211362620603670036700=⨯⨯⨯⨯===⨯⨯⨯====⨯⨯===⨯-⨯==--ωμω时,产生并联谐振。
C L 或ωC L )当(时,产生串联谐振。
C L 或ωC L )当(时,产生并联谐振。
C L 或ωC L )当解:(22021101220211012202110111311211123======-ωωωR R C L R )LC ωL(j ωR )LC ωLR(j ωC L R C j ωR L j ωR )C j ωL)(R j ω(R 证明:Z =+=-+-++=+++++=-2112111133220020020000)()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C L 故采用后一个不合理舍去pF -得C C C 由pF得C C C 由解:=⨯+⨯⨯⨯⨯='+==+=⨯+=+=⨯+--ω。
L C C ’()()()()mV V Q V V mA .R V I μH ..C L ..R C 解:Q-Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=⨯⨯====⨯===⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯==-ωω()()()()()()Ωj ..j .C jR Z Ω.....Q LQ L R pF C pF .L C C C C .V V Q μH .C 解:L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620-=⨯⨯⨯⨯-=-==⨯⨯⨯⨯-⨯⨯⨯⨯=-==→=⨯⨯⨯⨯==+⋅====⨯⨯⨯⨯==------ωωωωω()()()。
高频电子线路 张肃文 第五版 课后答案

第二章选频网络注意:①有部分答案有差异;②3-1题是2-1题;③只有计算题答案和部分问答题;④答案不齐全。
(pF)).(L C H)(.QR L ΩR Δf f Q (kHz)Δf MHz:f ..159101*********11591014321010010100101010121010990101211362620603670036700=××××===×××====××===×−×==−−ωµω, .C L ωC L ) (, .C L ωC L ) ( , .C L ωC L ) :(22021101220211012202110111311211123======−ωωωR R C L R )LCωL(jωR )LC ωLR(jωC L R C jωR L jωR )C jωL)(R jω(R :Z =+=−+−++=+++++=−2112111133220020020000)()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C LpF - C C CpFC C C:=×+××××=′+==+=×+=+=×+−−ω。
L C C ’()()()()mV V Q V V mA .R V I μH ..C L ..R C :Q -Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=××====×===××××===××××××==−ωω()()()()()()Ωj ..j .C j R Z Ω.....Q L Q L R pF C pF .L C C C C .V V Q μH .C :L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620−=××××−=−==××××−××××=−==→=××××==+⋅====××××==−−−−−−ωωωωω()()().21kΩ0.5R,R , 0.5Q Q , f 22f 2Δ320105105552310023100101501052220105010514321173000.70.7660036700012620电阻所以应并上=′=′∆×=′=××−××===××===×××××==−−.f Δf Q ξΔf f Q μH ..C ω :L .∑===−g QCωΔf f C πf C πΔf :..070007022483()()()()()()()()MHz ...Q f Δf .....L ωR Q kΩ..R C C C C R R R kΩ..C LQ R MHz ....LC πf pF .C C C C C C C :C L .L P i P i 4812281064122281080106411432108858855202020209201092010202010801006411031810801432121318202020202020593607066302211021261201260102102=×===××××××===×⎠⎞⎜⎝⎛++=⎟⎟⎠⎞⎜⎜⎝⎛++==×+××===××××===++++=++++=−−∑∑−−−−)))RZ 30Z 20Z 1123f1f1f1===−解:)()()()())()()()()()()))())()()()()()()Ω.j .j ..Z M Z j ..j C L j R Z pF .L C kHz .R ρf Q f Δf .R R L Q kΩC R R L Z Ω..R M Z μH ..ηR M pF .L C C μH .ρL L :f .f f f P 8437680100201018310143210020101771014321101591014322011771015910950143211522810201022224252020101591014323251015920201015920201018310143221831014322011591015910143211159101432101133266222011126662*********2322022361100706611101112611112662201160116261201216301121−=+××××==+=⎟⎠⎞⎜⎝⎛××××−××××+=⎟⎟⎠⎞⎜⎜⎝⎛′−+==×××××=′=′=××====+××××=+==××+×=+==××××===×××===××××====××===−−−−−−−−−−ωωωωωωωωω()100101410222002010159105010159153367.00111236=×=∆==→=∴=Ω=××××==−−−f f Q M R R C R L R f P ∵解:)()()()()()()()))013.02001122211222005101001032510102402051010010205101011632207.067101671012671120126722011=×−×+=⋅−+=∆=××===×==Ω=+××=+=Ω=×==−−−−−Q f f R L Q R M k R RL R R M R :f ab f ηηωωηωω5.75.22303021103001010112118.111020*********.325.22115.2225.111030010101121117323320012302332=−=′−=→=⎟⎟⎠⎞⎜⎜⎝⎛××+=⎟⎟⎠⎞⎜⎜⎝⎛∆+==××××××===′→=⎟⎟⎠⎞⎜⎜⎝⎛××′+=⎟⎟⎠⎞⎜⎜⎝⎛∆′+=−−Q Q Q Q f f Q I I C Q R Q Q f f Q I I :ω()⎩⎨⎧==→⎪⎪⎩⎪⎪⎨⎧+==−μL μH L CL L ω C L ω :12537511218321212第三章高频小信号放大器5102501050501501 ,5012.1102501020501501 ,20491025010501501 ,154266200266200266200=⎟⎟⎠⎞⎜⎜⎝⎛×××+=⎟⎟⎠⎞⎜⎜⎝⎛+===⎟⎟⎠⎞⎜⎜⎝⎛×××+=⎟⎟⎠⎞⎜⎜⎝⎛+===⎟⎟⎠⎞⎜⎜⎝⎛××+=⎟⎟⎠⎞⎜⎜⎝⎛+==−TT T f f ββMHz f f f ββMHz f f f ββMHz f βββ当当解:当()()()()()()()()()()()()()()()()()()()()mS j .j .j b a jb a g r C j b a jb a C j g g r C j g y mS j .j b a jb a g y mS j .j .j b a jb a C j g y mS .j ..j .j b a jb a C j g y ..r ωC b .g r a pF ..πf g C mS ..r βg mS .βI g m b b c b c b c b m b b c b ce oe m fe c b c b re e b e b ieb b e b e b b b T m eb eb m E e b 68.0049.01011.01107.377011031014321733.3327.371011.01107.37187.00187.01011.0110310143241189501011.01102410143210754.010701024101432110754070112410250143210737273710754050754015026112674223127222222322221272222127322127363300+=⎟⎠⎞⎜⎝⎛+−×××+××××≈⎟⎠⎞⎜⎝⎛+−+≈+−+++=−=+−××=+−=−−=+−×××××−≈+−+−=+=+−×××××+×=+−+=≈×××××==≈××+=+==××××===××===+×=+=−−−′′′′′′−−′′−−′′−′′−′′−′−′′ωωωωω解:()()()()4124142701010042104010041704070121101241104221104210124212422124284−−=⎟⎟⎠⎞⎜⎜⎝⎛−⎟⎟⎠⎞⎜⎜⎝⎛−==⋅⎟⎟⎠⎞⎜⎜⎝⎛−==⎟⎟⎠⎞⎜⎜⎝⎛+=⎟⎟⎠⎞⎜⎜⎝⎛⋅⎟⎟⎠⎞⎜⎜⎝⎛−==⎟⎟⎠⎞⎜⎜⎝⎛+=⎠⎞⎜⎜⎝⎛−m mm m ...r m .m.m vo v m .m.mvo v Δf Δf K Q f Δf f ΔfQ A A Q f Δf f Δf Q A A 故得令得解:令()()()()()()()()()1103101045952110830081020010286021830082501020025010237952258854tan 2tan 431100316116570316107102316104107102105228113151********5228104525025052281028604110200411023723710410010710211250205250205943326662262621222206070666022632162626222166001345213231>>××+×+×××=+′++=××+×=+=′−=−−=+==⎟⎠⎞⎜⎝⎛−=⎟⎟⎠⎞⎜⎜⎝⎛−==×===××××××======××××===××+××+×=++==×××××========−−−−−−−−−−−−−−−−−∑−...y y ξg g g g S μS ....p g p g g ..ξ..Q Q K MH ...Q f Δf ..π.L ωg Q ..A A ....g y p p A μS ..g p g p g g μS ..πL Q ωg .N N p .N N p refe L oe ie s ie p L oo re fe L Z L .ΣL vo po Σfe vo ie oe p p ϕϕ解:()()()()()()()()()()()()()()()()()()()()7221698266804238225025668042479479610444454782122259044546104422610441222565197445412212243822502578213445410158010410710143222782115802438303015801503008203010037010370104107101432100111104444447070707041707041704147044436260070222122222156600..-.A A ..A A ....f ΔΔf A A kHz ...Δf f ΔkHz .Δf f ΔkHz ..Δf Δf ..A A kHz ....f Lg ωΔf .....g y p p A mS .......g p g p R g g mS ...L ωQ g vo vo vo vo ..vo vo ......vo vo .fe vo ie oe p p ==′−==′=′=×=′=′=−=−′=−=′=×−=⋅−=====×××××××===+××===×+×++=+++==××××××==−−−∑∑∑−解:()()()()不能满足解:9.1K 522106250110511432121625011830500114r0.1122620221<=×××××===×+=+=−−∑∑μH ....C πf L pF ..C p C C oe ()74.73.05.24.364.265.2144220=×+==−refeS vo C y A ω解:()()()()()()()163910601046522260104910100410465274104921040574513114910010100010465210620574513491001010001046521020100440574513100010044100012051373118607311873118118101000104652111741030706123121206321123320202236123601012222236112563423612231201.K kH .Q f Δf πg C ωQ ..g y p p A μS π...Q C ωg p g μS πQ C ωg g pF ..C p C C pF C C C .L L L L μH πC ωL .r Z L .L fe vo i o i o ==××===×××××===×××××===∴=××××+××⎟⎠⎞⎜⎝⎛=+==××××+×=+==×⎟⎠⎞⎜⎝⎛+=+==+=+==×+×+=++==××××==−−−−−−−−−−,则。
高频电子线路第二章习题

2.1 已知高频晶体管3CG322A ,当I EQ =2mA ,f 0=30MHz 时测得Y 参数如下:(2.8 3.5);(0.080.3)(3627);(0.22)ie re fe oe y j mS y j mS y j mS y j mS=+=--=+=+试求,,,,,,,ϕϕie ie oe oe fe fe re re g C g C y y 的值。
解:(2.8 3.5) 2.8; 3.518.5(0.22)0.2;210.6(0.080.3)0.311050.31;105(3627)453745;37ie ie ie oe oe oe re re re fe fe fe y j m S g m S C pF y j m S g m S C pFy j m S y m S y j m S y m S ϕϕ=+====+====--=∠-==-=+=∠-==-由得:由得:由得:由得:2.2 在题图2.2所示调谐放大器中,工作频率f 0=10.7MHz ,L 1~3=4μH ,Q 0=100, N 1~3=20匝, N 2~3=5匝, N 4~5=5匝。
晶体管3DG39在I EQ =2mA ,f 0=10.7MHz 时测得:2860,18,200,μμ===ie ieoe g S C pF g S7,45,0===oe fe re C pF y m S y 。
试求放大器的电压增益A u0和通频带BW 0.7。
解:Y 参数等效电路:10234512131300132221200130020.7013(1)11;44137228.2512.3(2)1220.66ωωωππ∑∑∑∑=======++=∴==⎫=⎪⇒⎬⎪=⎭===eo o e ie eo feu e e n n n n n n g u SQ L g n g n g g m S n n y A g Q g L f B W f Q f g L M H z2.3 题图2.3是中频放大器单级电路图。
高频电路原理与分析(第五版) 第2章

还有一种以P型、N型和本征(I)型三种半导体构成的 PIN二极管,它具有较强的正向电荷储存能力。它的高频等 效高 频及微波电路中可以用作电可控开关、限幅器、电调衰减 器或电调移相器。
2. 晶体管与场效应管(FET) 在高频中应用的晶体管仍然是双极晶体管和各种场效应 管, 这些管子比用于低频的管子性能更好,在外形结构方 面也有所不同。
图2-2 电容器的高频等效电路 (a) 电容器的等效电路; (b) 电容器的阻抗特性
理想电容器的阻抗为1/(jωC),如图2-2(b)虚线所示, 其中,f 为工作频率,ω=2πf。但实际的电容器在高频运用 时的阻抗频率特性如图2-2(b)实线所示,呈V形特性,而 且其具体形状与电容器的种类和电容量的不同有关。由此 可知,每个电容器都有一个自身谐振频率SRF(Self Resonant Frequency)。当工作频率小于自身谐振频率时, 电容器呈正常的电容特性,但当工作频率大于自身谐振频 率时,电容器将等效为一个电感。
若工作频率更高,电感内线圈匝与匝之间及各匝与地之 间的分布电容的作用就十分明显,等效电路应考虑电感两端 总的分布电容,它应与电感并联。
与电容器类似,高频电感器也具有自身谐振频率SRF。 在SRF上,高频电感的阻抗的幅值最大,而相角为零,如图 2-3所示。
图 2-3 高频电感器的自身谐振频率SRF
高频晶体管有两大类型: 一类是作小信号放大的高频小功 率管,对它们的主要要求是高增益和低噪声; 另一类为高频功 率放大管,除了增益外,要求其在高频有较大的输出功率。 目前双极型小信号放大管,工作频率可达几千兆赫兹,噪声 系数为几分贝。小信号的场效应管也能工作在同样高的频率, 且噪声更低。一种称为砷化镓的场效应管,其工作频率可达 十几千兆赫兹以上。在高频大功率晶体管方面,在几百兆赫 兹以下频率,双极型晶体管的输出功率可达十几瓦至上百瓦。 而金属氧化物场效应管(MOSFET),甚至在几千兆赫兹的频 率上还能输出几瓦功率。
高频电子线路第五版课后答案张肃文

?
?45.97(mhz)
(2)rl折合到回路两端时的接入系数p为
1?c2c11p???
c1?c22?12
c1?c2
则
11?0.52??0.05?10?3?s? 3rl5?10
电感l的损耗电导g0为
p2
g0?
11
?
?0lq02??45.97?106?0.8?10?6?100
?43.30?10?6?s? 1121总电导g???g0?p??0.0433?10?3?0.05?10-3 3rrl10?10
2?l?3?
1
2
2
??100?c?535得c?-1pf?不合理舍去
。
?
1
?0?c?c??
?2?3.14
?535?10
32
?
??450?40??10
?12
?
3?5解:q
?
1
?0c0r1
2
?
1
2?3.14?1.5?10
1
?100?10
-12
?5
?212
l0?
?0c0vomr
?
?
?2?3.14
-3
?1.5?10
?0.1933?10
?3
?s?
谐振电阻rp?g??5.17?k??
========================================================================================
第四章高频小信号谐振放大器
1.高频小信号放大器的主要技术指标有、_________、________、__________。(谐振频率、增益、通频带、选择性)
高频电子线路课后习题及答案
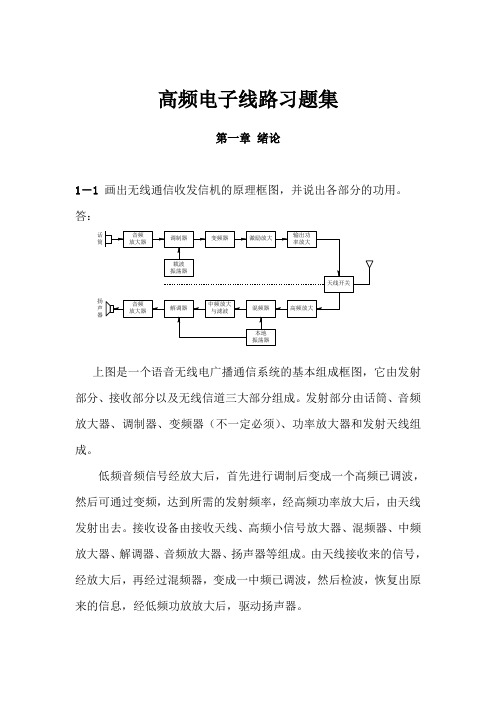
高频电子线路习题集第一章 绪论1-1 画出无线通信收发信机的原理框图,并说出各部分的功用。
答:上图是一个语音无线电广播通信系统的基本组成框图,它由发射部分、接收部分以及无线信道三大部分组成。
发射部分由话筒、音频放大器、调制器、变频器(不一定必须)、功率放大器和发射天线组成。
低频音频信号经放大后,首先进行调制后变成一个高频已调波,然后可通过变频,达到所需的发射频率,经高频功率放大后,由天线发射出去。
接收设备由接收天线、高频小信号放大器、混频器、中频放大器、解调器、音频放大器、扬声器等组成。
由天线接收来的信号,经放大后,再经过混频器,变成一中频已调波,然后检波,恢复出原来的信息,经低频功放放大后,驱动扬声器。
话筒扬声器1-2 无线通信为什么要用高频信号?“高频”信号指的是什么?答:高频信号指的是适合天线发射、传播和接收的射频信号。
采用高频信号的原因主要是:(1)频率越高,可利用的频带宽度就越宽,信道容量就越大,而且可以减小或避免频道间的干扰;(2)高频信号更适合电线辐射和接收,因为只有天线尺寸大小可以与信号波长相比拟时,才有较高的辐射效率和接收效率,这样,可以采用较小的信号功率,传播较远的距离,也可获得较高的接收灵敏度。
1-3无线通信为什么要进行凋制?如何进行调制?答:因为基带调制信号都是频率比较低的信号,为了达到较高的发射效率和接收效率,减小天线的尺寸,可以通过调制,把调制信号的频谱搬移到高频载波附近;另外,由于调制后的信号是高频信号,所以也提高了信道利用率,实现了信道复用。
调制方式有模拟调调制和数字调制。
在模拟调制中,用调制信号去控制高频载波的某个参数。
在调幅方式中,AM普通调幅、抑制载波的双边带调幅(DSB)、单边带调幅(SSB)、残留单边带调幅(VSSB);在调频方式中,有调频(FM)和调相(PM)。
在数字调制中,一般有频率键控(FSK)、幅度键控(ASK)、相位键控(PSK)等调制方法。
高频电子线路(第五版) 张肃文主编课后练习题.
绪论 选频网络练习题一、选择题1、在调谐放大器的LC 回路两端并上一个电阻R ,可以 C 。
A .提高回路的Q 值B .提高谐振频率C .加宽通频带D .减小通频带2、在高频放大器中,多用调谐回路作为负载,其作用不包括 ( D )A .选出有用频率B .滤除谐波成分C .阻抗匹配D .产生新的频率成分3、并联谐振回路的通频带是指其输出电压下降到谐振电压的 所对应的频率范围, 用7.02f ∆表示。
( D )A 、1/2B 、1/3C 、1/3D 、1/24、LC 并联谐振回路具有选频作用。
回路的品质因数越高,则 ( A )A 、回路谐振曲线越尖锐,选择性越好,但通频带越窄。
B 、回路谐振曲线越尖锐,选择性越好,通频带越宽。
C 、回路谐振曲线越尖锐,但选择性越差,通频带越窄。
D 、回路谐振曲线越尖锐,但选择性越差,通频带越宽。
5、地波传播时,传播的信号频率越高,损耗 。
( B )A 、越小B 、越大C 、不变D 、无法确定6、并联谐振回路谐振时,电纳为零,回路总导纳为 。
( B )A .最大值B .最小值C .零D .不能确定7、谐振回路与晶体管连接时,常采用部分接入方式实现阻抗匹配,控制品质因数以达到对通频带和选择性的要求,图示电路中Is 信号源的接入系数s p 为 。
( D )s iA .12L LB .21L LC .112L L L +D .212L L L +8、电路与上题同,晶体管基极与谐振回路的接入系数L p 为 。
( C )A .12C CB .21C C C .112C C C +D .212C C C +9、考虑信号源内阻和负载后,LC 选频回路的通频带变 ,选择性变 。
( D )A 、小、好B 、大、好C 、小、差D 、大、差10、LC 组成并联谐振回路,谐振频率LC f o π21=,把它串接在电路中,就能阻止频率为多少的信号通过。
( A ) A . 不为o f B .o f C .大于o f D .小于o f11、如图所示,将负载L R 等效到ab 两端L R '= 。
高频电子线路第2章参考答案

所 以 : RL (
1) R 0
Q0 Q L
答:回路电感为0.586mH,有载品质因数为58.125,这时需要并 联236.66kΩ的电阻。
高频电子线路习题参考答案
2-2 图示为波段内调谐用的并联振荡回路,可变电容 C的变化 范围为 12~260 pF,Ct为微调电容,要求此回路的调谐 范围为 535~1605 kHz,求回路电感L和Ct的值,并要求 C的最大和最小值与波段的最低和最高频率对应。
4
2
df 1
arctan( 2 fC R ) 10 8
6
4C R
4 10 200 10
125 kH z
高频电子线路习题参考答案
输出噪音电压均方值为 U 4 kTG B n H
2 n 2 0
4 kT
23
1 R
B n R 4 kTR B n
2 4 3 2
4 1.37 10
2 2
2
R R R1 R 3 0 s Rs R3
2
高频电子线路习题参考答案
2.解П型网络
R s R1 R2 R3 R1 R s R 2 R s R1 R 2 R 3 R s R1 输 出 电 阻 为 : R0 R s R1 ( R 2 R 3 )( R s R1 ) R s R1 R2 R3 R s R1
100 1.546 199 3.125
答:回路电感为0.317mH,有载品质因数为1.546
高频电子线路习题参考答案
2-4 石英晶体有何特点?为什么用它制作的振荡器的频率稳 定度较高? 答2-4 石英晶体有以下几个特点 1. 晶体的谐振频率只与晶片的材料、尺寸、切割方式、几 何形状等有关,温度系数非常小,因此受外界温度影响 很小 2. 具有很高的品质因数 3. 具有非常小的接入系数,因此受外部电路的影响很小。 4. 在工作频率附近有很大的等效电感,阻抗变化率大,因 此谐振阻抗很大 5. 构成振荡器非常方便,而且由于上述特点,会使频率非 常稳定。
(完整版)高频电子线路第2章习题答案

第2章 小信号选频放大器2.1 已知并联谐振回路的1μH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW . [解] 90-612110.035610Hz 35.6MHz 2π2π102010f LCH F-===⨯=⨯⨯6312640.71010022.4k 22.361022.36k 201035.610Hz35.610Hz 356kH z100p HR Q Ff BW Q ρρ--===Ω=⨯Ω=Ω⨯⨯===⨯=2.2 并联谐振回路如图P2.2所示,已知:300pF,390μH,100,C L Q ===信号源内阻s 100k ,R =Ω负载电阻L 200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解] 011465kHz 2π2π390μH 300PFf LC≈==⨯0.70390μH100114k Ω300PF////100k Ω//114.k Ω//200k Ω=42k Ω42k Ω42k Ω371.14k Ω390μH/300 PF /465kHz/37=12.6kHzp e s p Le e e R Q R R R R R Q BWf Q ρρ=========== 2.3 已知并联谐振回路的00.710MHz,C=50pF,150kHz,f BW ==求回路的L 和Q 以及600kHz f ∆=时电压衰减倍数。
如将通频带加宽为300 kHz ,应在回路两端并接一个多大的电阻? [解] 6262120115105μH (2π)(2π1010)5010L H f C --===⨯=⨯⨯⨯⨯ 6030.7101066.715010f Q BW ⨯===⨯2236022*********.78.11010p oU f Q f U ••⎛⎫⎛⎫∆⨯⨯=+=+= ⎪ ⎪⨯⎝⎭⎝⎭ 当0.7300kHz BW =时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f C ρ-⨯===⨯====⨯Ω=Ω⨯⨯⨯⨯而471266.72.131021.2k 2π105010p R Q ρ-===⨯Ω=Ω⨯⨯⨯ 由于,p e pRR R R R =+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω⨯Ω===Ω-Ω-Ω2。
高频电子线路(第五版) 张肃文主编课后练习题解析
绪论 选频网络练习题一、选择题1、在调谐放大器的LC 回路两端并上一个电阻R ,可以 C 。
A .提高回路的Q 值B .提高谐振频率C .加宽通频带D .减小通频带2、在高频放大器中,多用调谐回路作为负载,其作用不包括 ( D )A .选出有用频率B .滤除谐波成分C .阻抗匹配D .产生新的频率成分3、并联谐振回路的通频带是指其输出电压下降到谐振电压的 所对应的频率范围,用7.02f ∆表示。
( D )A 、1/2B 、1/3C 、1/3D 、1/24、LC 并联谐振回路具有选频作用。
回路的品质因数越高,则 ( A )A 、回路谐振曲线越尖锐,选择性越好,但通频带越窄。
B 、回路谐振曲线越尖锐,选择性越好,通频带越宽。
C 、回路谐振曲线越尖锐,但选择性越差,通频带越窄。
D 、回路谐振曲线越尖锐,但选择性越差,通频带越宽。
5、地波传播时,传播的信号频率越高,损耗 。
( B )A 、越小B 、越大C 、不变D 、无法确定6、并联谐振回路谐振时,电纳为零,回路总导纳为 。
( B )A .最大值B .最小值C .零D .不能确定7、谐振回路与晶体管连接时,常采用部分接入方式实现阻抗匹配,控制品质因数以达到对通频带和选择性的要求,图示电路中Is 信号源的接入系数s p 为 。
( D )s iA .12L LB .21L LC .112L L L +D .212L L L +8、电路与上题同,晶体管基极与谐振回路的接入系数L p 为 。
( C )A .12C CB .21C C C .112C C C +D .212C C C +9、考虑信号源内阻和负载后,LC 选频回路的通频带变 ,选择性变 。
( D )A 、小、好B 、大、好C 、小、差D 、大、差10、LC组成并联谐振回路,谐振频率LCfoπ21=,把它串接在电路中,就能阻止频率为多少的信号通过。
( A )A.不为of B.of C.大于of D.小于of11、如图所示,将负载LR等效到ab两端LR'= 。
高频电子线路第五版课后的答案(28页)

1)如果将次级线圈短路,这时反射到初级的阻抗等于什么?
初级等效 电路 (并联型)应该怎么画?
2)如果将次级线圈开路,这时反射阻抗等于什么?
初级冬
该怎么画?
3) 如 果
,反射到初级的阻抗等于什么?
解:如2.5(a), 利用戴维南定理将互感耦合并联型回路等效 为互感耦合串联联型回路的形式。图中,
V=1z. ,
S
(1)、由等效电路图4 . 1c, 知
从而
;
::
G¹
P₂
I=P₁y V
图3.1a 图3.1b 图3.1c
4)、∴.
(5)、
例3.3.3中 频 放 大 器 设 计 ( 单 调 谐 回 路 )
步骤:(已知中心频率和通频带f、B₇ )
1、 直流偏置:(1)、直流偏置电阻R,R₂ (几千欧姆), 满足放大状态(2)、旁路电容C,C(μF), 静态工作条做 (3)、射级电阻R(几百欧姆),
解:由题知 0(t)=10⁷πt+10*πt²,
1、 当t=0时 ,o(0)=10'π
2、o (1)随t成正比例关系变化
第10章习题
· 8 . 2求 v(t)=5cos(10⁶t+sin5×10³t) 率 解 :由 题 知
θ(t)=10⁶t+sin5×10³t,
当t=0 时, o(0)=(10⁶+5×10²)rad/s
在t=0 时的瞬时频
习题
· 8.9 调制信号为正弦波,当频率为500 Hz、 振 幅 为 1V 时 , 调角波的最大频移□fi=200Hz, 若调制信号振幅仍为IV, 但调制频率增大为1kHz 时 , 要 求 将 频 偏 增 加 为f₂=20kHz 。 试问:应倍频多少次? (计算调频和调相两种情况)
高频电子线路习题答案第五版张肃文

看不惯那些家伙。
高频电子第五版(pF)).(L C H)(.QR则L Ω取R Δf f Q (kHz)Δf MHz解:f..159101*********11591014321010010100101010121010990101211362620603670036700=⨯⨯⨯⨯===⨯⨯⨯====⨯⨯===⨯-⨯==--ωμω时,产生并联谐振。
C L 或ωC L )当(时,产生串联谐振。
C L 或ωC L )当(时,产生并联谐振。
C L 或ωC L )当解:(22021101220211012202110111311211123======-ωωωR R C L R )LC ωL(j ωR )LC ωLR(j ωC L R C j ωR L j ωR )C j ωL)(R j ω(R 证明:Z =+=-+-++=+++++=-2112111133220020020000 )()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C L 故采用后一个不合理舍去pF -得C C C 由pF得C C C 由解:=⨯+⨯⨯⨯⨯='+==+=⨯+=+=⨯+--ω。
L C C ’()()()()mV V Q V V mA .R V I μH ..C L ..R C 解:Q-Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=⨯⨯====⨯===⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯==-ωω()()()()()()Ωj ..j .C jR Z Ω.....Q LQ L R pF C pF .L C C C C .V V Q μH .C 解:L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620-=⨯⨯⨯⨯-=-==⨯⨯⨯⨯-⨯⨯⨯⨯=-==→=⨯⨯⨯⨯==+⋅====⨯⨯⨯⨯==------ωωωωω()()()。
高频电子线路张肃文第五版Chapter2_选频网络

1 L = 特性阻抗: r = wp L = wpC C
2013-7-29
品质因数: Q = r
R
14
谐振时的阻抗特性:
并联谐振时,回路呈纯电阻性, 且阻抗为最大值; w < wp , 呈感性 . I L C G w > wp , 呈容性 因此回路谐振时:
s
|Z|,Re,X e
Re 0 wp
|Z| w
Chapter 2 选频网络
1.选频的基本概念
所谓选频,就是选出需要的频率分量并且滤 除不需要的频率分量。
2.选频网络的分类
单谐振回路
选 振荡回路(由L、C组成) 耦合谐振回路 频 LC集中参数滤波器 网 石英晶体滤波器 络 各种滤波器 陶瓷滤波器
声表面波滤波器
2013-7-29 1
Chapter 2 选频网络
例3 设一放大器以简单并联振荡回路为负载,信号中心频率 fs=10MHz,回路电容C=50pF. ⑴ 试计算所需的线圈电感值; ⑵ 若线圈的品质因数为Q=100,试计算回路谐振电阻及回 路带宽;⑶若放大器所需带宽B=0.5MHz,则应在回路上并 联多大的电阻才能满足放大器所需带宽要求? 1 1 解:⑴ f = = 5.07μH \ L= 0 2 2 2p LC 4p f0 C ⑵ R p = Qw0 L = 2πf 0QL = 31.8k W
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高频电子线路(用于学习之间交流,不得用于出版等商业用途!)第2章习题答案2-1已知某一并联谐振回路的谐振频率f 0=1MHz,要求对990kHz 的干扰信号有足够的衰减,问该并联回路应如何设计?解 为了有效滤除990kHz 的干扰信号,应使它位于通频带之外。
若取BW 0.7=20kHz ,则由通频带与回路Q 值之间的关系有502010007.00===BW f Q因此应设计Q >50的并联谐振回路.2-2试定性分析题图2—2所示的电路在什么情况下呈现串联谐振或并联谐振状态.解 题图2-2(a )中L 1C 1或L 2C 2之一呈并联谐振状态,则整个电路即为并联谐振状态。
若L 1C 1与L 2C 2呈现为容抗,则整个电路可能成为串联谐振。
题图2-2(b)只可能呈现串联谐振,不可能呈现并联谐振状态.题图2-2(c)只可能呈现并联谐振,不可能呈现串联谐振状态。
2—3有一并联回路,其电感、电容支路中的电阻均为R 。
当C L R =时(L 和C 分别为电感和电容支路的电感值和电容值),试证明回路阻抗Z 与频率无关。
解 ()()()⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛+=⎪⎭⎫⎝⎛-++⎪⎭⎫ ⎝⎛-+=C L j R R C R LR j C L R R C j R L j R C j R L j R Z abωωωωωωωω11121112212121 要想使Z ab 在任何频率下,都呈现纯阻性,就必须使分子与分母的相角相等,亦即必须有2121121R R C L CL R R C R LR +-==-ωωωω 上式化简得C R C L LR C L 2122222-=⎪⎪⎭⎫ ⎝⎛-ω 要使上式在任何频率下都成立,必有0222=-LR C L 或 C L R =2 0212=-C R C L 或 CL R =1 因此最后得CL R R ==212-4有一并联回路在某频段内工作,频段最低频率为535kHz ,最高频率为1605kHz 。
现有两个可变电容器,一个电容器的最小电容量为12pF ,最大电容量为100pF ;另一个电容量的最小电容量为15pF ,最大电容量为450pF 。
试问:(1)应采用哪一个可变电容器,为什么? (2)回路电感应等于多少? (3)绘出实际的并联回路图。
解 (1)35351605min max min max ==''=C C f f因而9minmax=''C C但912100<, 93015450>=因此应采用C max =450pF ,C min =15pF 的电容器。
但因为30minmax=C C ,远大于9,因此还应在可变电容器旁并联一个电容C X ,以便3min max =++XXC C C C ,解之得C X ≈40pF 。
(2)将pF C C C X 490max max=+='代入CL 21ω=,kHz 5352⨯=πω解之得回路电感L =180μH 。
(3)见解题图2-42-5给定串联谐振回路的f 0=1.5MHz ,C 0=100pF ,谐振时电阻r =5Ω。
试求Q 0和L 0。
又若信号源电压振幅V sm =1mV ,求谐振时回路中的电流I 0以及回路元件上的电压V L0和V C0。
解 21210100105.12511126000=⨯⨯⨯⨯⨯==-πωC r Q()H H C L μπω11310100105.121112260200≈⨯⨯⨯⨯==-谐振时回路电流mA mVr V I sm 2.0510=Ω==V L0=Q 0V s =212mV V C0=V L0=212mV2—6串联电路如题图2—6所示。
信号源频率f 0=1MHz ,电压振幅V sm =0。
1V 。
将11端短路,电容C 调到100pF 时谐振,此时,电容C 两端的电压为10V.如11端开路,再串接一阻抗Z X (电阻与电容串联),则回路失谐,C 调到200pF 时重新谐振,电容两端电压变成2.5V ,试求线圈的电感量L 、回路品质因数Q 0值以及未知阻抗Z X .解 11端短路时,C =100pF 谐振,因此求得()H H C L μπω2531010010211122620=⨯⨯⨯==- 1001.01000===sm C V V Q11端开路,加入XX X C jR Z 01ω-=后,要恢复谐振,原电容C 应调至200pF 。
而C 与C X 串联后的总电容量仍应等于100pF 。
因此,C X =200pF 。
此时回路的Q 值降为 251.05.2==L Q 因而100250=+=X L R r r Q Q 于是求得 Ω=Ω⨯⨯⨯⨯=⨯==-7.47100102531023336600πωQ Lr R X因而未知阻抗是由47.7Ω的电阻与200pF 的电容串联组成。
2—7给定并联谐振回路的f 0=5MHz,C =50pF ,通频带BW 0。
7=150kHz 。
试求电感L 、品质因数Q 0以及对信号源频带为5.5MHz 的失调。
又若把BW 0。
7加宽到300kHz,应在回路两端再并联上一个阻值多大的电阻?解 回路电感值为()H H C L μπω2.2010501052116620=⨯⨯⨯⨯==- 又 07.0Q f BW =因此 3.3310150105367.000=⨯⨯==BW f Q 当信号源频率为5.5MHz 时36.65.5555.53.33000=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=ωωωωξQ 要使BW 0。
7加宽为300kHz ,则Q 值应减半,即7.16210==Q Q L 设回路的并联等效电导为g p ,则由Lg Q p 001ω=可以求出 S S LQ g p 666001047102.2010523.3311--⨯=⨯⨯⨯⨯⨯==πω 当Q 0下降为Q L 后,g p 变为g ∑=2×47×10-6S.因而并联电导值为g =g ∑-g p =47×10-6S即并联电阻值为Ω==k gR 3.2112-8并联谐振回路如题图2-8所示。
已知通频带BW 0.7,电容C.若回路总电导为()L p s G G g g g ++=∑∑,试证明CBW g 7.02π=∑若给定C =20pF ,BW 0.7=6MHz,R p =10k Ω,R s =10k Ω,求R L 。
解 由Lp Q Cg ω=∑、Lp Q f BW =7.0二式可得CBW BW f C f g p p 7.07.022ππ=∑=将已知数据代入上式,得s S g 61261075410201062--∑⨯=⨯⨯⨯⨯=πG L =g ∑-g s -G pS ⎪⎭⎫ ⎝⎛⨯-⨯-⨯=-336101011010110754 =554×10-6S即Ω==k G R LL 8.112-9如题图2—9所示,已知L =0。
8μH,Q 0=100,C 1=C 2=20pF ,C i =5pF ,R i =10 k Ω。
C o =20pF ,R o =5k Ω。
试计算回路谐振频率、谐振阻抗(不计R o 与R i 时)、有载Q L 值和通频带。
解 ()pF pF C C C 40202020=+=+=' 所以接入系数 3120402011=+=+'=C C C p将R o 折合到回路两端,得Ω=Ω⨯=Ω⨯⨯=='k pR R o o4510459105332 跨接入回路两端的总电容为pF pF C C C C C C i 3.184020402051=⎪⎭⎫ ⎝⎛⨯⨯+='+'+=∑ 谐振频率为MHz Hz LC f p 6.41103.18108.02121126=⨯⨯⨯==--∑ππ谐振阻抗为Ω=Ω⨯⨯⨯⨯⨯==-k L Q R p p 9.20108.0106.412100660πω总电导为po i R R R g 111+'+=∑S 633310170109.2011045110101-⨯≈⎪⎭⎫ ⎝⎛⨯+⨯+⨯= 因而 Ω≈=∑∑k g R 88.51最后得 1.28108.0106.4121017011666≈⨯⨯⨯⨯⨯⨯==--∑πωLg Q p L通频带为MHz MHz Q f BW Lp 48.11.286.417.0===2-10为什么耦合回路在耦合大到一定程度时,谐振曲线会出现双峰?解 出现双峰的原因是由反射阻抗()222Z M ω所引起的。
当耦合弱,即M ω小时,反射阻抗值也小,因此对初级电路的影响小.初级回路在谐振点为串联谐振。
初级电流随频率的变化为串联谐振曲线(单峰曲线),因而次级电流的谐振曲线也是单峰。
随着M ω的增加,反射阻抗对初级回路的影响逐渐加大。
当M ω达到某一临界值,次级电流可达到最大值。
当M ω超过此临界值后,由于反射电阻大,导致初级与次级电流下降。
而在左右偏离谐振点处,由于反射电抗与初级电路的电抗符号相反,二者可以抵消,因而初级电流可出现两个峰值.进而引起次级电流也出现双峰.2—11如何解释0201ωω=,Q 1=Q 2时,耦合回路呈现下列物理现象:(1)η<1时,I 2m 在ξ=0处是峰值,而且随着耦合加强,峰值增加; (2)η>1时,I 2m 在ξ=0处是谷值,而且随着耦合加强,谷值下降; (3)η>1时,出现双峰,而且随着η值增加,双峰之间距离加大.解 (1)η<1是欠耦合状态,次级回路反射到初级回路的反射阻抗小,初级回路呈串联谐振状态。
在谐振点ξ=0处,初级回路与次级回路电流均达到峰值。
随着耦合因数η的增加,次级回路的感应电流也增加。
(2)η>1为过耦合状态,此时次级回路电流在谐振点出现谷值的原因,已如题2-10所解释。
随着耦合的加强,次级回路反射至初级回路的反射阻抗加大,因而谷值下降.(3)η>1,次级回路电流出现双峰,已如题2—10所解释。
随着耦合的加强,次级回路反射阻抗的电抗部分与初级回路电抗相抵消的点偏离谐振点越远,因而双峰之间距离增大。
2-12假设有一中频放大器等效电路如题图2-12所示。
试回答下列问题:(1)如果将次级线圈短路,这时反射到初级的阻抗等于什么?初级等效电路(并联型)应该怎么画? (2)如果次级线圈开路,这时反射阻抗等于什么?初级等效电路应该怎么画? (3)如果221C L ωω=,反射到初级的阻抗等于什么?解 (1)次级线圈短路后,反射到初级的阻抗为()222212L M jL j M Z ωωω-==这是一个与L 1串联的容性阻抗⎪⎪⎭⎫⎝⎛-=-C j L M j ωω122。
为了变为并联型,可利用串、并联转换公式,将L 1与C 的串联形式改为并联形式,其值未变。
