A单考单招数学试卷完整版
全国2023年单独招生考试数学卷(含答案) (5)

全国2023年单独招生考试数学卷(满分120分,考试时间90分钟)一、选择题:(本题共15小题,每小题3分,共45分)1.若四面体的六条棱中,有五条棱长为a ,则该四面体的体积的最大值为( ) A .381aB .383a C .3121a D .3123a 2.不等式043)4(2≥---x x x 的解集是( )A. )4[}1{∞+⋃-,B. )4[∞+,C. (])4[1,∞+-∞-,D. (]1,-∞- 3.数列}{n a 满足()()⎪⎩⎪⎨⎧<≤-<≤=+121,12210,21n n n n n a a a a a ,若761=a ,则2004a =( ) A.76 B. 75 C. 73 D.71 4.nx x ⎪⎪⎭⎫⎝⎛+31的各项系数之和大于8,小于32,则展开式中系数最大的项是( ) 36.x A xB 4.64.x x C 644.x x xD 或5.已知f (x )=x 2,则f -1(21)=( )(A )2 (B )-1 (C )22(D )416.一个单位职工150人,其中有业务人员110人,管理人员15人,后勤服务人员25人。
为了了解职工的某种情况,要从中抽取一个容量为30的样本,则应抽取管理人员 ( ) A 、15人 B 、5人 C 、3人 D 、2人7.已知22cb ca >,则下列不等式一定成立的是( )(A )a 2>b 2 (B )ln a >ln b (C )ab11> (D )b )31(>a )31( 8.长方体1111ABCD A B C D -中,O 是AB 的中点,且1OD OB =,则( ) A .1AB CC = B .AB=BC C .145CBC ∠=︒ D.145BDB ∠=︒ 9.已知集合{}{}0,2,1,1,0,1,2A B ==-,则A B ⋂=( )A .{0,2}B .{1,2}C .{0}D .{-2,-1,0,1,2}10.圆224230x y x y ++-+=的圆心坐标为( ) A .(4,-2) B .(2,1) C .(-2,1) D .(2,1) 11. 已知平行四边形ABCD ,则向量AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ =( ) A. BD ⃗⃗⃗⃗⃗ B. DB ⃗⃗⃗⃗⃗ C. AC ⃗⃗⃗⃗⃗ D. CA ⃗⃗⃗⃗⃗ 12. 下列函数以π为周期的是( )A.y =sin (x −π8) B. y =2cos x C. y =sin x D. y =sin 2x13. 本学期学校共开设了20门不同的选修课,学生从中任选2门,则不同选法的总数是( ) A. 400 B. 380 C. 190 D. 40 14. 已知直线的倾斜角为60°,则此直线的斜率为( ) A. −√33B. −√3C. √3D. √3315. 若sin α>0且tan α<0,则角α终边所在象限是( )A. 第一象限B. 第二象限C. 第三象限D.第四象限 二、填空题:(本题共5小题,每小题6分,共30分.) 1. 用描述法表示集合{}=10,8,6,4,2 ______; 2.{m,n }的真子集共有__________个;3. 如果一个集合恰由5个元素组成,它的真子集中有两个分别是B={a,b,c },C={a,d,e },那么集合A=____ ;4.{}{},13),(,3),(=+==-=y x y x B y x y x A 那么=B A _____;5、如图,在平面直角坐标系中,点A 的坐标为(-2,0),点 B 在y 轴正半轴上,以点B 为圆心,BA 长为半径作弧, 交x 轴正半轴于点C ,则点C 的坐标为_____.三、解答题:(本题共4小题,每小题10分,共40分.解答应写出文字说明、证明过程或演算步骤.)1、已知等差数列}{n a 满足23=a ,前3项和293=S .求}{n a 的通项公式;2、已知等差数列}{n a 满足2103421=-=+a a a a ,.求}{n a 的通项公式。
2023年高职单独招生考试数学试卷(答案) (4)

2023年对口单独招生统一考试数学试卷(满分120分,考试时间90分钟)一、选择题:(本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.若O 为⊿ABC 的内心,且满足(OB -OC )•(OB +OC -2OA )=0()A.等腰三角形B.正三角形C.直角三角形D.以上都不对2.设有如下三个命题()甲:m∩l =A,m、l ⊂,m、l ⊄;乙:直线m、l 中至少有一条与平面相交;丙:平面与平面相交。
当甲成立时,乙是丙的条件。
A.充分而不必要B.必要而不充分C.充分必要D.既不充分又不必要3.⊿ABC 中,3sinA+4cosB=6,3cosA+4sinB=1,则∠C 的大小为()A.6πB.65πC.6π或65πD.3π或32π4.等体积的球和正方体,它们的表面积的大小关系是()A.S 球>S 正方体B.S 球<S 正方体C.S 球=S 正方体D.S 球=2S 正方体5.若连结双曲线22a x -22by =1与其共轭双曲线的四个顶点构成面积为S 1的四边形,连结四个焦点构成面积为S 2的四边形,则21S S 的最大值为()A.4B.2C.21D.416.若干个正方体形状的积木按如图所示摆成塔形,上面正方体中下底的四个顶点是下面相邻正方体中上底各边的中点,最下面的正方体的棱长为1,平放在桌面上,如果所有正方体能直接看到的表面积超过7,则正方体的个数至少是()A.2B.3C.4D.67.关于x 的不等式0ax b ->的解集为(1,)+∞,则关于x 的不等式02ax bx +>-的解集为()A.()2,1-B.(,1)(2,)-∞-⋃+∞C.(1,2)D.(,2)(1,)-∞-⋃+∞8.长方体1111ABCD A B C D -中,O 是AB 的中点,且1OD OB =,则()A.1AB CC =B.AB=BC C.145CBC ∠=︒D.145BDB ∠=︒9.已知集合{}{}0,2,1,1,0,1,2A B ==-,则A B ⋂=()A.{0,2}B.{1,2}C.{0}D.{-2,-1,0,1,2}10.圆224230x y x y ++-+=的圆心坐标为()A.(4,-2)B.(2,1)C.(-2,1)D.(2,1)二、填空题:(本题共3小题,每小题10分)1、已知双曲线(a>0,b>0)的两个焦点为、,点P 是第一象限内双曲线上的点,且,tan∠PF2F1=﹣2,则双曲线的离心率为_______.2、记Sk=1k+2k+3k+……+nk,当k=1,2,3,……时,观察下列等式:S1n2n,S2n3n2n,S3n4n3n2,……S5=An6n5n4+Bn2,…可以推测,A﹣B=_______.三、解答题:(本题共3小题,共50分.解答应写出文字说明、证明过程或演算步骤.)1.提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v (单位:千米/小时)是车流密度x (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当20020≤≤x 时,车流速度v 是车流密度x 的一次函数.(1)当2000≤≤x 时,求函数)(x v 的表达式;(2)当车流密度x 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时))()(x v x x f ⋅=可以达到最大?求出最大值.(精确到1辆/小时)2.如图,已知三棱柱111ABC A B C -,平面11A ACC ⊥平面ABC ,90ABC ∠=︒,1130,,,BAC A A A C AC E F ∠=︒==分别是AC ,A 1B 1的中点.(1)证明:EF BC ⊥;(2)求直线EF 与平面A 1BC 所成角的余弦值.3.设等差数列{}n a 的前n 项和为n S ,34a =,43a S =,数列{}n b 满足:对每个12,,,n n n n n n n S b S b S b *++∈+++N 成等比数列.(1)求数列{},{}n n a b 的通项公式;(2)记,n c n *=∈N证明:12+.n c c c n *++<∈N 参考答案:一、选择题1-5题答案:ACABC 6-10题答案:BBCAC 二、填空题1.∵△PF1F2中,sin∠PF1F2═,sin∠PF1F2═,∴由正弦定理得,…①又∵,tan∠PF2F1=﹣2,∴tan∠F1PF2=﹣tan(∠PF2F1+∠PF1F2),可得cos∠F1PF2,△PF1F2中用余弦定理,得2PF1•PF2cos∠F1PF23,…②①②联解,得,可得,∴双曲线的,结合,得离心率故答案为:2.根据所给的已知等式得到:各等式右边各项的系数和为1,最高次项的系数为该项次数的倒数,∴A,A1,解得B ,所以A﹣B.故答案为:.三、解答题1.(1)解:因为当20020≤≤x 时,车流速度是车流密度x 的一次函数,故设b kx v +=则⎩⎨⎧+=+=bk b k 20602000⎪⎪⎩⎪⎪⎨⎧=-=∴320031b k 320031+-=∴x v 故⎪⎩⎪⎨⎧≤≤+-<≤=20020,320031200,60)(x x x x v (2)由(1)得⎪⎩⎪⎨⎧≤≤-<≤=20020,)200(31200,60)(x x x x x x f 当200<≤x 时,)(x f 为增函数,1200)(<x f 当20020≤≤x 时,310000)100(31)200(31)(2+--=-=x x x x f 当100=x 时,最大值3333=即当车流密度为100辆/千米时,车流量可以达到最大,最大约为3333辆/小时)(x g 的减区间为)0,(-∞2.如图,已知三棱柱111ABC A B C -,平面11A ACC ⊥平面ABC ,90ABC ∠=︒,1130,,,BAC A A A C AC E F ∠=︒==分别是AC ,A 1B 1的中点.(1)证明:EF BC ⊥;(2)求直线EF 与平面A 1BC 所成角的余弦值.本题主要考查空间点、线、面位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力。
单招数学考试题及答案带解释

单招数学考试题及答案带解释一、选择题(每题5分,共20分)1. 下列函数中,哪一个是奇函数?A. \( y = x^2 \)B. \( y = x^3 \)C. \( y = \sin(x) \)D. \( y = e^x \)答案:C解释:奇函数的定义是对于所有x,都有\( f(-x) = -f(x) \)。
选项A是偶函数,因为\( (-x)^2 = x^2 \);选项B是奇函数,因为\( (-x)^3 = -x^3 \);选项C是奇函数,因为\( \sin(-x) = -\sin(x) \);选项D既不是奇函数也不是偶函数。
2. 计算极限\( \lim_{x \to 0} \frac{\sin(x)}{x} \)的值是多少?A. 0B. 1C. 2D. \( \infty \)答案:B解释:根据极限的性质,我们知道\( \lim_{x \to 0}\frac{\sin(x)}{x} = 1 \),这是一个基本的极限公式。
3. 以下哪个不等式是正确的?A. \( 2x + 3 > 5 \)B. \( 3x - 2 < 7 \)C. \( x^2 - 4x + 4 \leq 0 \)D. \( x^2 - 2x + 1 \geq 0 \)答案:D解释:选项A简化为\( x > 1 \),选项B简化为\( x < 3 \),选项C 简化为\( (x-2)^2 \leq 0 \),只有当\( x = 2 \)时成立,而选项D 简化为\( (x-1)^2 \geq 0 \),对于所有实数x都成立。
4. 计算定积分\( \int_0^1 x^2 dx \)的值是多少?A. 0B. \( \frac{1}{3} \)C. 1D. 2答案:B解释:根据定积分的计算公式,\( \int_0^1 x^2 dx =\left[ \frac{x^3}{3} \right]_0^1 = \frac{1^3}{3} -\frac{0^3}{3} = \frac{1}{3} \)。
单招试卷数学试题及答案

单招试卷数学试题及答案一、选择题(每题4分,共40分)1. 若函数f(x)=2x+3,则f(-1)的值为:A. 1B. -1C. -5D. 52. 已知集合A={1,2,3},B={2,3,4},则A∩B为:A. {1}B. {2,3}C. {3,4}D. {1,2,3,4}3. 直线y=2x+1与x轴的交点坐标为:A. (0,1)B. (-1/2, 0)C. (1/2, 0)D. (0, -1)4. 函数y=x^2-4x+4的最小值是:A. 0B. 1C. 4D. 85. 等比数列{a_n}中,a_1=2,公比q=2,则a_3的值为:A. 4B. 8C. 16D. 326. 已知向量a=(1,2),b=(2,3),则向量a·b的值为:A. 5B. 6C. 7D. 87. 圆的方程为(x-2)^2+(y-3)^2=9,该圆的半径为:A. 3B. 6C. 9D. 128. 已知三角形ABC中,a=3,b=4,c=5,则cosA的值为:A. 1/2B. 1/3C. 1/4D. 1/59. 函数y=sin(x)的周期为:A. 2πB. πC. 3πD. 4π10. 已知双曲线方程为x^2/a^2 - y^2/b^2 = 1,其中a=2,b=1,则该双曲线的渐近线方程为:A. y=±x/2B. y=±2xC. y=±xD. y=±1/2x二、填空题(每题4分,共20分)11. 已知等差数列{a_n}中,a_1=1,d=2,则a_5的值为______。
12. 函数y=cos(x)的值域为______。
13. 已知向量a=(3,-1),b=(-1,3),则向量a与b的夹角为______。
14. 已知椭圆方程为x^2/16 + y^2/9 = 1,则该椭圆的离心率为______。
15. 函数y=ln(x)的定义域为______。
三、解答题(每题20分,共40分)16. 已知函数f(x)=x^3-3x^2+2,求f(x)的导数f'(x)。
2023年对口单独招生考试数学试卷(答案)

2023年对口单独招生统一考试数学试卷(满分120分,考试时间120分钟)一、选择题:(本题共20小题,每小题3分,共60分.)1、下列计算正确的是()A .(a3)2=a9B .log36-log32=1C .12a -·12a =0D .log3(-4)2=2log3(-4)2、三个数a =0.62,b =log20.3,c =30.2之间的大小关系是()A .a<c<bB .a<b<cC .b<a<cD .b<c<a3、8log 15.021+-⎪⎭⎫⎝⎛的值为()A .12 B.72C .16 D.374、下列各式成立的是()A.()52522n m n m +=+B .(b a)2=12a 12b C.()()316255-=- D.31339=5、设2a =5b =m ,且1a +1b =3,则m 等于()A.310B .12C.20D.156、已知函数f(x)的图象与函数y=sinx的图象关于y轴对称,则f(x)=()(A)-cosx(B)cosx(C)-sinx(D)sinx7、已知平面向量,则与的夹角是()8、函数y=(x≠-5)的反函数是()(A)y=x-5(x∈R)(B)y=-+5(x≠0)(C)y=x+5(x∈R)(D)y=(x≠0)9、不等式的解集是()(A){x|0<x<1}(B){x|1<x<∞}(C){x|-∞<x<0}(D){x|-∞<x<0}10、已知函数之,则F(x)是区间()(A)()上的增函数(B)上的增函数(C)上的增函数(D)上的增函数11、已知直线L过点(-1,1),且与直线x-2y-3=0垂直,则直线L的方程是()(A)2x+y-1=0(B)2x+y-3=0(C)2x-y-3=0(D)2x-y-1=012、已知圆锥曲线母线长为5,底面周长为6π,则圆锥的体积是()(A)6π(B)12π(C)18π(D)36π13、是等差数列{}的前n项合和,已知=-12,=-6,则公差d=()(A)-1(B)-2(C)1(D)214、将3名教练员与6名运动员分为3组,每组一名教练员与2名运动员,不同的分法有()(A)90中(B)180种(C)270种(D)360种15、吉林松花石有“石中之宝”的美誉,用它制作的砚台叫松花砚,能与中国四大名砚媲美。
单招考试数学卷+答案 (8)

单独招生考试招生文化考试数学试题卷(满分120分,考试时间120分钟)一、选择题:(本题共25小题,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的)1、有四个关于三角函数的命题:1p :∃x ∈R,2sin 2x +2cos 2x =122p :,x y R ∃∈,sin()sin sin x y x y -=-3p :∀x ∈[]0,πsin x=4p :sin cos 2x y x y π=⇒+=其中假命题的是()(A)1p ,4p (B)2p ,4p (3)1p ,3p (4)2p ,3p 2、已知圆1C :2(1)x ++2(1)y -=1,圆2C 与圆1C 关于直线10x y --=对称,则圆2C 的方程为()(A)2(2)x ++2(2)y -=1(B)2(2)x -+2(2)y +=1(C)2(2)x ++2(2)y +=1(D)2(2)x -+2(2)y -=13、设,x y 满足24,1,22,x y x y x y +≥⎧⎪-≥⎨⎪-≤⎩则z x y =+()(A)有最小值2,最大值3(B)有最小值2,无最大值(C)有最大值3,无最小值(D)既无最小值,也无最大值4、已知()()3,2,1,0a b =-=-,向量a b λ+与2a b -垂直,则实数λ的值为()(A)17-(B)17(C)16-(D)165、等比数列{}n a 的前n 项和为n S ,已知2110m m m a a a -++-=,2138m S -=,则m =()(A)38(B)20(C)10(D)96、如图,正方体1111ABCD A B C D -的棱线长为1,线段11B D 上有两个动点E,F,且12EF =,则下列结论中错误的是()(A)AC BE ⊥(B)//EF ABCD平面(C)三棱锥A BEF -的体积为定值(D)AEF BEF ∆∆的面积与的面积相等7、如果执行右边的程序框图,输入2,0.5x h =-=,那么输出的各个数的和等于()(A)3(B)3.5(C)4(D)4.58、一个棱锥的三视图如图,则该棱锥的全面积(单位:2cm )为()(A)48+(B)48+(C)36+(D)36+9、用min{a,b,c}表示a,b,c三个数中的最小值。
高职2023年单招考试《数学》样卷二及参考答案

2023年单独招生考试《数学》试卷(样卷)一、单项选择题(本题共15小题,每题3分,共45分) 1.下列属于必然事件的是( )A.三角形中,任意两边之和大于第三边B.明天下雨C.任意买一张电影票,座位号是单号D.公鸡下蛋 2.=︒60cos ( ) A.0 B.21 C.23 D.1 3.数集N 表示( )A.有理数集B.实数集C.自然数集D.整数集 4.大于2且小于11的偶数组成的集合( ) A.}10,8,6{B.}8,64{,C.}8,6{D.}10,8,64{, 5.函数3)(x x f =的奇偶性是( )A.奇函数B.偶函数C.非奇非偶函数D.不确定 6.不等式92>x 的解集为( ) A.}3|{<x xB.}33|{>-<x x x 或C.}3|{->x xD.}33|{<<-x x7.不等式3||≤x 的解集为( ) A.}3|{≤x xB.}3|{-≥x xC.}33|{≤≤-x xD.}33|{≥-≤x x x 或 8.下列选项中,最小的数是( )A.-3B.-πC.-3.14D.-4139.等差数列:-6、-18、 、-42、…,则空白处应填( )A.-27B.-30C.-24D.-3610.下列为对数函数的是( )A.x y 2=B.2x y =C.x y πlog =D.x y 3= 11.圆柱的俯视图是( )A.长方形B.三角形C.梯形D.圆 12.三角函数诱导公式:=+)sin(πα( )A.αsinB.αsin -C.αcosD.αcos - 13.已知 ()0 ,2-=→a ,()1 ,2=→b ,则 =⋅→→b a ( )A.1-B. 2-C.3-D.4- 14.5log 25( )=A.2B.3C.4D.5 15.下列调查中,须用普查的是( )A.了解某市学生的视力情况B.了解我某中学生课外阅读的情况C.了解某市百岁以上老人的健康情况D.了解某市老年人参加晨练的情况 二、是非判断题(正确写A ,错误写B ,本题共10小题,每题3分,共30分) 16.两点之间直线最短。
单招数学试卷 (1)

单招招生全国统一考试数学试卷(满分150分,考试时间120分钟)一、选择题:(本题共12小题,每小题5分,共60分)1.在圆:22670x y x +--=内部的点是()A.(0) B.(7,0) C.(-2,0) D.(2,1)2.函数2()|1|f x x =+的定义域为()A.[-2,+∞)B.(-2,+∞)C.[-2,-1)∪(-1,+∞)D.(-2,-1)∪(-1,+∞)3.命题p :a=1,命题q :2(1)0a -=.p 是q 的()A.充要条件 B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件4.在△ABC 中,向量表达式正确的是()A.AB BC CA +=B.AB CA BC -=C.AB AC CB-= D.0AB BC CA ++= 5.z y x >>且2=++z y x ,则下列不等式中恒成立的是C(A )yzxy >(B )yz xz >(C )xz xy >(D )|||||y z y x >6.已知直线1l 的方程为y x =,直线2l 的方程为0ax y -=(a 为实数).当直线1l 与直线2l 的夹角在(0,12π)之间变动时,a 的取值范围是A(A,1)∪(1)(B)(C )(0,1)(D )(1)7.函数1232)(3+-=x x x f 在区间[0,1]上是()(A )单调递增的函数.(B )单调递减的函数.(C )先减后增的函数(D )先增后减的函数.8.有80个数,其中一半是奇数,一半是偶数,从中任取两数,则所取的两数和为偶数的概率为()(A)7939.(B)801.(C)21.(D)8141.9.已知函数x x f )21()( ,其反函数为)(x g ,则2)(x g 是()A.奇函数且在(0,+∞)上单调递减B.偶函数且在(0,+∞)上单调递增C.奇函数且在(-∞,0)上单调递减D.偶函数且在(-∞,0)上单调递增10.以下四个命题:①过一点有且仅有一个平面与已知直线垂直;②若平面外两点到平面的距离相等,则过这两点的直线必平行于该平面;③两条相交直线在同一平面内的射影必为相交直线;④两个互相垂直的平面,一个平面内的任一直线必垂直于另一平面的无数条直线.其中正确的命题是()A.①和②B.②和③C.③和④D.①和④11.从单词“education ”中选取5个不同的字母排成一排,则含“at ”(“at ”相连且顺序不变)的概率为()A.181 B.3781 C.4321 D.756112.已知正二十面体的各面都是正三角形,那么它的顶点数为()A.30B.12C.32D.10二、填空题(共4小题,每小题5分;共计20分)1.函数)1,0(20182018≠>+=+a a a y x 的图象恒过定点.2.=⋅⋅9log 22log 25log 532.3.=⋅+2lg 5log 2lg 22.4.若对数式)5(log )2(a a --有意义,则实数a 的取值范围是.三、大题:(满分70分)1.求不定积分⎰+dxx x x x )ln 1ln (2.求定积分⎰+-4011dxx x 3.求微分方程x x y xy sin 2'=-的通解4.求二重积分⎰⎰==D xy x y D xdxdy 2,2和是由曲线其中所围成的区域。
单招考试数学卷+答案 (3)

单独招生考试招生文化考试数学试题卷(满分120分,考试时间120分钟)一、选择题:(本题共10小题,每小题6分,共60分)1.已知函数f(x)的图象关于直线x=1对称,当x2>x1>1时,[f(x2)﹣f(x1)](x2﹣x1)<0恒成立,设a=f(−12),b=f(2),c=f(e),则a,b,c的大小关系为()A.c>a>bB.c>b>aC.a>c>bD.b>a>c2.已知函数y=f(x)在区间(﹣∞,0)内单调递增,且f(﹣x)=f(x),若a=f(log123),b=f(2﹣1.2),c=f(12),则a,b,c的大小关系为()A.a>c>bB.b>c>aC.b>a>cD.a>b>c3.设函数f(x)=ex+x﹣2,g(x)=lnx+x2﹣3.若实数a,b满足f(a)=0,g (b)=0,则()A.g(a)<0<f(b)B.f(b)<0<g(a)C.0<g(a)<f(b)D.f(b)<g(a)<04.已知函数f(x)=−x2+2x−1,x≤1|x−1|,x>1,若f(a2﹣4)>f(3a),则实数a的取值范围是()A.(﹣4,1)B.(﹣∞,﹣4)∪(1,+∞)C.(﹣1,4)D.(﹣∞,﹣1)∪(4,+∞)4.已知等比数列{an}中,a5=3,a4a7=45,则的值为()A.3B.5C.9D.256.下列函数中,在定义域内单调递增且是奇函数的是()A.y =log 2(x 2+1−x)B.y =sinxC.y =2x ﹣2﹣xD.y =|x ﹣1|7.设函数f (x )=x (ex+e ﹣x ),则对f (x )的奇偶性和在(0,+∞)上的单调性判断的结果是()A.奇函数,单调递增B.偶函数,单调递增C.奇函数,单调递减D.偶函数,单调递减8.若函数f (x )=xln (x +a +x 2)为偶函数,则a 的值为()A.0B.1C.﹣1D.1或﹣19.设函数f (x )=ln|2x+1|﹣ln|2x ﹣1|,则f (x )()A.是偶函数,且在(12,+∞)单调递增B.是奇函数,且在(−12,12)单调递增C.是偶函数,且在(−∞,−12)单调递增D.是奇函数,且在(−∞,−12)单调递增10.已知函数f (x )是定义在R 上的偶函数,且在[0,+∞)上单调递增,则三个数a =f (﹣log313),b =f (2cos 2π5),c =f (20.6)的大小关系为()A.a >b >cB.a >c >bC.b >a >cD.c >a >b二、填空题:(共30分.)1.若圆锥曲线15222=++-k y k x 的焦距与k 无关,则它的焦点坐标是__________.2.定义符号函数⎪⎩⎪⎨⎧-=101sgn x 000<=>x x x ,则不等式:x x x sgn )12(2->+的解集是__________.3.若数列}{n a ,)(*N n ∈是等差数列,则有数列)(*21N n na a ab n n ∈+++= 也为等差数列,类比上述性质,相应地:若数列}{n C 是等比数列,且)(0*N n C n ∈>,则有=n d __________)(*N n ∈4.若n S 是数列}{n a 的前n 项的和,2n S n =,则=++765a a a ________.三、解答题:(本题共3小题,每小题10分,共30分.解答应写出文字说明、证明过程或演算步骤.)1.圆C 的圆心在x 轴上,并且过点A(-1,1)和B(1,3),求圆C 的方程。
2023年高职单独招生考试数学试卷(含答案) (1)

2023年对口单独招生统一考试数学试卷(满分120分,考试时间90分钟)一、选择题:(本题共20小题,每小题2.5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设A ∈0, 则满足}1,0{=B A 的集合A , B 的组数是 ( )A .1组B .2组C .4组D .6组2.若|log |)(,10x x f a a =<<且函数, 则下列各式中成立的是( )A .)41()31()2(f f f >>B .)31()2()41(f f f >>C .)2()31()41(f f f >>D .)41()2()31(f f f >>3.在ABC ∆中, 如果1019cos ,23sin ==B A , 则角A 等于 ( )A .3πB .32π C .3π或32π D .656ππ或 4.已知数列)(lim ,131}{242n n n n n a a a a S a +++-=∞→ 那么满足的值为 ( )A .21B .32 C .1 D .-25.直线0601210122=+--++=y x y x mx y 与圆有交点, 但直线不过圆心, 则∈m ( ) A .)34,1()1,43(B .]34,1()1,43[C .]34,43[D .)34,43(6.如图, 在正三角形ABC ∆中, D 、E 、F 分别为各边的中点, G 、H 、I 、J 分别为AF , AD , BE , DE 的中点, 将ABC ∆沿DE ,EF , DF 折成三棱锥以后, GH 与IJ 所成角的度数为 ( ) A .90° B .60° C .45°D .0°7.已知以y x ,为自变量的目标函数)0(>+=k y kx ω的可行域如图阴影部分(含边界), 若使ω取最大值时的最优解有无穷 多个, 则k 的值为( ) A .1B .23C .2D .48. 已知集合A={-1,0,1},集合B={x|x <3,x ∈N},则A ∩B=( ) A. {-1,1,2} B. {-1,1,2,3} C. {0,1,2} D. {0,1}9. 已知数列:23456 34567,,,,,…按此规律第7项为( )A. 78B. 89C.78D.8910. 若x ∈R ,下列不等式一定成立的是( )A. 52x x<B. 52x x >C. 20x > D. 22(1)1xx x >11、已知f(12x -1)=2x +3,f(m)=8,则m 等于( )A 、14B 、-14C 、32D 、-32 12、函数y =lg x +lg(5-2x)的定义域是( )A 、)25,0[B 、⎥⎦⎤⎢⎣⎡250,C 、)251[,D 、⎥⎦⎤⎢⎣⎡251,13、函数y =log2x -2的定义域是( )A 、(3,+∞)B 、[3,+∞)C 、(4,+∞)D 、[4,+∞)14、函数12--=x x y 的图像是 ( ) A.开口向上,顶点坐标为)(45,21-的一条抛物线; B.开口向下,顶点坐标为)(45,21-的一条抛物线; C.开口向上,顶点坐标为)(45,21-的一条抛物线; D.开口向下,顶点坐标为)(45,21-的一条抛物线;15、函数()35x x x f +=的图象关于( )A 、y 轴对称B 、直线y =-x 对称C 、坐标原点对称D 、直线y =x 对称16、下列函数中,在区间(0,+∞)上为增函数的是( ) A 、y =x +1 B 、y =(x -1)2 C 、y =2-x D 、y =log0.5(x +1)17、已知函数x x f =)(,点),4(b P 在函数图像上,则=b ( ) A 、-4 B 、3 C 、-2 D 、2 18、不等式532≤-x 的解集是( )A 、()4,1-B 、()()∞+-∞-,,41 C 、[]4,1- D 、 ()()∞+--∞-,,14 19、不等式()()073>+x x -的解集是( )A 、 ()73,-B 、 ()7,3-C 、 ),3()7,(+∞--∞D 、 ),7()3,(+∞--∞ 20、不等式31<-x 的解集是( )A 、(-2,4)B 、(-1,3)C 、 ),4()2,(+∞--∞D 、 ),1()3,(+∞--∞ 一、填空题:(本题共2小题,每小题10分,共20分.)1、若实数y x .满足不等式组⎪⎩⎪⎨⎧≥-≤-≥+0422y x y x y x , 则y x +2的最小值是2、在等差数列{}n a 中,已知172,35a S ==,则等差数列{}n a 的公差d =_______.二、解答题:(本题共3小题,共50分.解答应写出文字说明、证明过程或演算步骤.) 1.设)(x f 是定义在),0(+∞上的增函数,当),0(,+∞∈b a 时,均有)()()(b f a f b a f +=⋅,已知1)2(=f .求:(1))1(f 和)4(f 的值;(2)不等式2()2(4)f x f <的解集 . 2.已知函数1)6sin(cos 4)(-+=πx x x f ,求求)(x f 的最小正周期;(2)求)(x f 在区间]4,6[ππ-上的最大值和最小值.3. 已知函数b b x a x x f 2)1()(22--++=,且)2()1(x f x f -=-,又知x x f ≥)(恒成立. 求:(1) )(x f y =的解析式;(2)若函数[]1)(log )(2--=x x f x g ,求函数g(x)的单调区间. 4、在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c . (1)若a =3c ,b =,cosB =,求c 的值;(2)若=,求sin (B+)的值.参考答案: 一、选择题1-5:DCACB 6-10:BADBB 二、填空题 1.参考答案.4 【解析】试题分析:根据题意可知,实数y x .满足不等式组⎪⎩⎪⎨⎧≥-≤-≥+0422y x y x y x 对应的区域如下图,当目标函数z=2x+3y 在边界点(2,0)处取到最小值z=2×2+3×0=4. 故答案为:4考点:简单线性规划的运用。
2023年高职单独招生考试数学试卷(含答案) (6)

2023年对口单独招生统一考试数学试卷(满分120分,考试时间120分钟)一、选择题:(本题共10小题,每小题3分,共60分)1.若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y=x2,值域为{1,4}的“同族函数”共有()A.9个B.8个C.5个D.4个2.球面上有三点,其中任意两点的球面距离都等于球的大圆周长的经过这三点的小圆的周长为4π,则这个球的表面积为()A.64πB.48πC.24πD.12π3.要将两种大小不同的钢板截成A、B、C 三种规格,每张钢板可同时截得三种规格的小钢板块数如下表:A 规格B 规格C 规格第一种钢板211第二种钢板123今需A、B、C 三种规格的成品各15、18、27块,所需两种规格的钢板的张数分别为m、n(m、n 为整数),则m+n 的最小值为()A.10B.11C.12D.134.如果直线y=kx+1与圆x2+y2+kx+my-4=0交于M、N 两点,且M、N 关于直线x+y=0对称,则不等式组:表示的平面区域的面积是()A.B.C.1D.25.有一条生产流水线,由于改进了设备,预计第一年产量的增长率为150%,以,61⎪⎩⎪⎨⎧≥≤-≥+-0001y my kx y kx 4121后每年的增长率是前一年的一半,同时,由于设备不断老化,每年将损失年产量的10%,则年产量最高的是改进设备后的()A.第一年B.第三年C.第四年D.第五年6.设ΔABC的三边a、b、c满足an+bn=cn(n>2),则ΔABC是()A.钝角三角形B.锐角三角形C.等腰直角三角形D.非等腰的直角三角形7.已知集合A={x|x2-11x-12<0},集合B={x|x=2(3n+1),n Z},则A∩B等于()A.{2}B.{2,8}C.{4,10}D.{2,4,8,10}8.展开式中不含项的系数的和为(B)A.-1B.0C.1D.29.函数的定义域是(B)A. B. C. D.10.展开式中不含项的系数的和为(B)A.-1B.0C.1D.2二、填空题(共10小题,每小题3分;共计30分)1.设α、β为互不重合的平面,m,n是互不重合的直线,给出下列四个命题:①若m∥n,则m∥α;②若m⊂α,n⊂α,m∥β,n∥β,则α∥β;③若α∥β,m⊂α,n⊂β,则m∥n;④若α⊥β,α∩β=m,n⊂α,m⊥n,则n ⊥β;其中正确命题的序号为_______.2.已知函数f(x),若关于x 的方程f(x)=kx 有两个不同的实根,则实数k 的取值范围是_______.3.已知关于x 的不等式(ax﹣a2﹣4)(x﹣4)>0的解集为A,且A 中共含有n 个整数,则当n 最小时实数a 的值为_______.4、不等式2340x x --+>的解集为______.(用区间表示)5、不等式422<-xx的解集为______..(用区间表示)6、函数()35lg -=x y 的定义域是______.(用区间表示)7、函数y=)9(log 2-x 的定义域是______.(用集合表示)8、不等式062<--x x 的解集是______.(用集合表示)9、不等式0125>--x 的解集为______.(用集合表示)10、已知函数)1(log )(2-=x x f ,若f(α)=1,则α=______.三、大题:(满分30分)1、如下图,四棱锥P ABCD -中侧面PAB 为等边三角形且垂直于底面ABCD ,AB BC ⊥,//BC AD ,12AB BC AD ==,E 是PD 的中点.(1)证明:直线//CE 平面PAB ;(2)求二面角B PC D --的余弦值.2、记△ABC 的内角A,B,C 的对边分别为a.,b.,c,已知b 2=ac,点D 在边AC 上,BDsin∠ABC=asinC.(1)证明:BD =b:(2)若AD =2DC .求cos∠ABC.参考答案:1-5题答案:ABCAD 6-10题答案:BBBBB 二、填空题:1、④;2、(0,12);3、﹣2;4、(-4,1);5、(-1,2);6、⎪⎭⎫⎢⎣⎡∞+,54;7、}9{>x x ;8、{}32<<-x x ;9、}32{><x x x 或;10、3。
安徽单招数学试题及答案

安徽单招数学试题及答案一、选择题(每题4分,共40分)1. 下列函数中,哪一个是奇函数?A. \( f(x) = x^2 \)B. \( f(x) = \sin(x) \)C. \( f(x) = e^x \)D. \( f(x) = \ln(x) \)答案:B2. 计算极限 \(\lim_{x \to 0} \frac{\sin(x)}{x}\) 的值是多少?A. 0B. 1C. 2D. ∞答案:B3. 已知等差数列的首项为2,公差为3,求第10项的值。
A. 29B. 30C. 31D. 32答案:A4. 以下哪个选项是不等式 \(x^2 - 4x + 4 \leq 0\) 的解集?A. \(x \in (-\infty, 0) \cup (4, +\infty)\)B. \(x \in [0, 4]\)C. \(x \in (-\infty, 4) \cup (4, +\infty)\)D. \(x \in [2, 2]\)答案:D5. 计算定积分 \(\int_0^1 x^2 dx\) 的值。
A. 1/3B. 1/2C. 1D. 2答案:A6. 计算 \(\sqrt{16}\) 的值。
A. 2B. 4C. -4D. ±4答案:B7. 已知向量 \(\vec{a} = (2, 3)\) 和 \(\vec{b} = (-1, 2)\),求向量 \(\vec{a} + \vec{b}\)。
A. (1, 5)B. (1, 1)C. (3, 5)D. (-1, 5)答案:A8. 已知函数 \(y = x^3 - 3x^2 + 2\),求导数 \(y'\)。
A. \(3x^2 - 6x\)B. \(x^2 - 3x\)C. \(3x^2 - 6x + 2\)D. \(x^3 - 3x^2\)答案:A9. 计算复数 \(z = 3 + 4i\) 的模。
A. 5B. √41C. 7D. √29答案:A10. 计算二项式 \((1 + x)^5\) 的展开式中 \(x^3\) 的系数。
2023年单招考试数学卷+答案 (7)

2023年单独招生考试招生文化考试数学试题卷(满分120分,考试时间90分钟)一、选择题:(本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.关于函数()sin |||sin |f x x x =+有下述四个结论:()①f(x)是偶函数②f(x)在区间(2π,π)单调递增③f(x)在[,]-ππ有4个零点④f(x)的最大值为2其中所有正确结论的编号是A.①②④B.②④C.①④D.①③2.设命题3:|23|1,:01x p x q x --<≤-,则p 是q 的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.已知函数2sin 1(0)y x ωω=+>的最小正周期是2π,则ω的值为()A.1B.2C.12D.44.椭圆223(0)x ky k k +=>的一个焦点与抛物线212y x =的焦点重合,则该椭圆的离心率是()A.2B.2C.3D.35.如果命题“⌝(p 或q )”为假命题,则()(A)p ,q 均为真命题(B)p ,q 均为假命题(C)p ,q 中至少有一个为真命题(D)p ,q 中至多有一个为真命题6.设ax x f x ++=)110lg()(是偶函数,xx bx g 24)(-=是奇函数,那么b a +的值为()(A)1(B)-1(C)21-(D)217.计算机是将信息转换成二进制进行处理的.二进制即“逢二进一”,如2(1101)表示二进制数,将它转换成十进制形式是321012120212⨯+⨯+⨯+⨯=13,那么将二进制数216111111个()转换成十进制形式是().A.1722-B.1622-C.1621-D.1521-(改编)8.5个人站成一排,若甲乙两人之间恰有1人,则不同站法有()A.18种B.24种C.36种D.48种9.等差数列{}n a 的通项公式为21,n a n =+其前n 项和为n S ,则数列n s n ⎧⎫⎨⎬⎩⎭的前10项为和()A.120B.70C.75D.10010.已知函数32()3f x x ax x c =+-+是奇函数.则函数()f x 的单调减区间是()A.[-1,1] B.(1,+∞) C.(-∞,1)D.(-,)∞+∞11、已知54cos ,0,2=⎪⎭⎫⎝⎛-∈x x π,则x tan =()A、34B、34-C、43D、43-12、在∆ABC 中,AB=5,BC=8,∠ABC=︒60,则AC=()A、76B、28C、7D、12913、直线012=+-y x 的斜率是();A、-1B、0C、1D、214、点P(-3,-2)到直线4x-3y+1=0的距离等于()A、-1B、1C、2D、-215、过两点A (2,)m -,B(m ,4)的直线倾斜角是45︒,则m 的值是()。
2023年高职单独招生考试数学试卷(含答案) (7)

2023年对口单独招生统一考试数学试卷(满分120分,考试时间120分钟)一、选择题:(本题共20小题,每小题3分,共60分)1.若]0,2[π-∈x ,则函数x x x x f cos 3)6cos(6cos()(+--+=ππ的最小值是()A.1B.-1C.3-D.-22.一个正四面体外切于球O 1,同时又内接于球O 2,则球O 1与球O 2的体积之比为()A.33:1B.36:1C.8:1D.27:13.给出两个命题:p:|x|=x 的充要条件是x 为正实数;q:存在反函数的函数一定是单调函数,则下列哪个复合例题是真命题()A.p 且q B.p 或qC.¬p 且qD.¬p或q4.设集合M={x|x2-x<0,x∈R},N={x||x|<2,x∈R},则()A.M∪N=M B.M∩N=MC.(CRM)∩N=ØD.(CRN)∩N=R5.设有四个命题:①底面是矩形的平行六面体是长方体②棱长都相等的直四棱柱是正方体③侧棱垂直于底面两条边的平行六面体是直平行六面体④对角线相等的平行六面体是直平行六面体,其中真命题的个数是()A.1B.2C.3D.46.如图是150辆汽车通过某路段时速度的频率分布直方图,则速度在[60,70)的汽车大约有()A.100辆B.80辆C.60辆D.45辆7.设抛物线y2=2px(p>0)的准线为l,将圆x2+y2=9按向量=(2,1)平移后恰与l 相切,则p的值为()A.0.5B.2C.0.25D.48.若,且a为第四象限角,则的值等于()A.B. C.D.9、设集合M={O,1,2},N={O,1},则M∩N=()A.{2}B.{0,1}c.{0,2}D.{0,1,2}10、不等式|x-1|<2的解集是()A.x<3B.x>-1C.x<-1或x>3D.-1<x<311、函数y=-2x+1在定义域R内是()A.减函数B.增函数C.非增非减函数D.既增又减函数a12、设则a,b,c的大小顺序为()A、a>b>cB、a>c>bC、b>a>cD、c>a>b13、已知a=(1,2),b=(x1),当a+2b与2a-b共线时,x值为()A.5B.3C、1/3D、0.514、已知{an}为等差数列,a2+a:=12,则as等于()A.1B.8C.6D.515、已知向量a=(2,1),b=(3,入),且a丄b,则入=()A.-6B.5C.1.5D、-1.516、点(0,5)到直线y=2x的距离为()A、2.5B.C.1.5D、17、将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有()A.12种B.16种C.18种D.8种18、设集合M={x|0<x<1},集合N={x|-1<x<1},则()(A)M∩N=M(B)MUN=N(C)M∩N=N(D)M∩N=M∩N19、已知函数f(x)的图象与函数y=sinx的图象关于y轴对称,则f(x)=()(A)-cosx(B)cosx(C)-sinx(D)sinx20.圆的一般方程为x2+y2-8x+2y+13=0,则其圆心和半径分别为()A.(1,-1),4B.(4,-1),2C.(-4,1),4D.(-1,1),2二、填空题(共10小题,每小题3分;共计30分)1.记复数z=a+bi(i 为虚数单位)的共轭复数为,已知z=2+i,则_____.2.已知集合U={1,3,5,9},A={1,3,9},B={1,9},则∁U(A∪B)=_____.3.某校共有师生1600人,其中教师有1000人,现用分层抽样的方法,从所有师生中抽取一个容量为80的样本,则抽取学生的人数为_____.4、已知51cos sin =+αα,则=⋅ααcos sin ______.5、在等比数列{}n a 中,若673=a a ,则=⋅⋅⋅8642a a a a ______.6、已知角α终边上一点)1,1(P ,则=+ααcos sin ______.7、函数2()13sin f x x =-的最小正周期为______.8、若“[0,],tan 4x x mπ∀∈≤”是真命题,则实数m 的最小值为______.9、已知角α终边上一点P(3,-4),则=+ααan t sin ______.10、过点P(-2,-3),倾斜角是45°的直线方程是______.三、大题:(满分30分)1、甲、乙两名篮球运动员,甲投篮的命中率为0.6,乙投篮的命中率为0.7,两人是否投中相互之间没有影响,求:(1)两人各投一次,只有一人命中的概率;(2)每人投篮两次,甲投中1球且乙投中2球的概率.2、已知数列{a n }满足a 1=1,a n+1{a n +1,n 为奇数a n +2,n 为偶数(1)记b n =a 2n ,写出b 1,b 2,并求数列{b n }的通项公式;(2)求{a n }的前20项和参考答案:一、选择题:1-5题答案:ADDBA 6-10题答案:CBDBD 11-15题答案:ABDCA 16-20题答案:BABCB 二、填空题:1、3﹣4i;2、{5};3、30;4、2512-;5、36;6、2;7、π;8、1;9、1532-;10、x-y-1=0。
2023年单独招生考试数学+英语试卷(答案) (4)
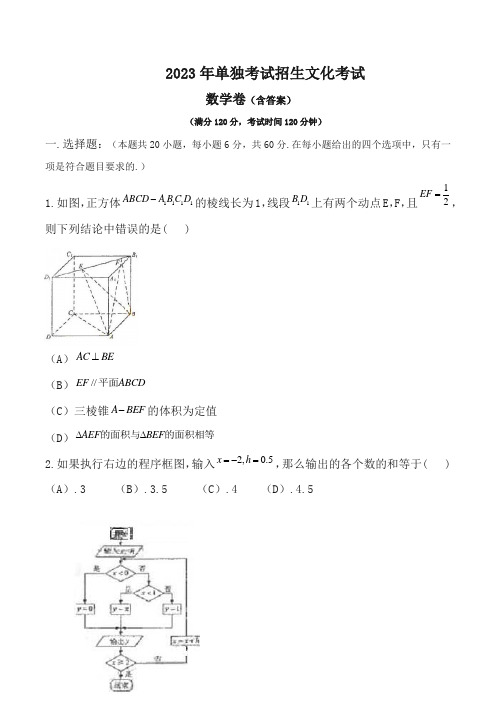
2023年单独考试招生文化考试数学卷(含答案)(满分120分,考试时间120分钟)一.选择题:(本题共20小题,每小题6分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.如图,正方体1111ABCD A B C D -的棱线长为1,线段11B D 上有两个动点E ,F ,且12EF =,则下列结论中错误的是( )(A )AC BE ⊥ (B )//EF ABCD 平面(C )三棱锥A BEF -的体积为定值 (D )AEF BEF ∆∆的面积与的面积相等2.如果执行右边的程序框图,输入2,0.5x h =-=,那么输出的各个数的和等于( ) (A ).3 (B ).3.5 (C ).4 (D ).4.53.已知集合A{}12x x =-<<,{03}B x x =<<,则A B = ( )A.(1,3)-B.(1,0)-C.(0,2)D.(2,3) 4.已知集合A {}2,1,0,1,2=--,{}(1)(2)0B x x x =-+<,则A B ( )A.{}0,1-B.{}1,0C.{}1,0,1-D.{}2,1,05.若集合}25|{<<-=x x A ,}33|{<<-=x x B ,则=B A ( ) A.}23|{<<-x x B.}25|{<<-x x C.}33|{<<-x x D.}35|{<<-x x6.在等差数列中,已知,且,则与 的值分别为 ( )A.-2,3B.2,-3C.-3,2D.3,-2 7.设,“”是“”的 ( )A.充分非必要条件B.必要充分条件C.充要条件D.既充分又必要条件 8.函数的图象如图所示,则最大.最小值分别为 ( )A. B.C.D.9.设 ,,,其中 为自然对数的底数,则 ,, 的大小关系是 ( ) A.B.C.D.10.设 ,,, 都为正数,且不等于 ,函数,,,在同一坐标系中的图象如图所示,则 ,,, 的大小顺序是 ( )B.C.D.11.“1=x ”是“0122=+-x x ”的 ( ) A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件12.“2)1(+=n n a n ”是“0)2(log 21<+x ”的 ( )A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件13.设b a ,为正实数,则“1>>b a ”是“0log log 22>>b a ”的( ) A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件 14.0=b 是直线b kx y +=过原点的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件方程的解为( )A. B. C. D.16.设b a ,是实数,则“0>+b a ”是“0>ab ”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件17.已知,则与的积为( )A.5B.3C.10D.818.“ααcos sin =”是“02cos =α”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件19.函数)32(log )(22-+=x x x f 的定义域是( ) A.[]1,3- B.()1,3- C.(][)+∞-∞-,13, D.()()+∞-∞-,13,20.设,6.0,6.05.16.0==b a 6.05.1=c ,则c b a ,,的大小关系是( ) A.c b a << B.b c a << C.c a b << D.a c b <<二.填空题:(本题共6小题,每小题5分,共30分.) 1.(2x-y)6展开式的第5项为_____.2.圆柱的轴截面是边长为3的正方形,则圆柱的体积等于_____.43)22(log =x 4=x 2=x 2=x 21=x x x x f 2)(2+=)2(f )21(f3.如图所示,函数y=f(x)的图象关于直线x=8对称,则f(6)_____f(13) (填,“>”.“<”或“=”).4.在中,,,,则______.5.若向量,的夹角为,,,则——————随机抽取名年龄在,,,年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于岁的人中按年龄段分层抽样的方法随机抽取 8人,则在 [50,60)年龄段抽取的人数为_____.圆锥的表面积是底面积的 3 倍,则该圆锥的侧面展开图扇形的圆心角的弧度数为____.三.解答题:(本题共3小题,每小题10分,共30分.解答应写出文字说明.证明过程或演算步骤.)1.圆C 的圆心在x 轴上,并且过点A(-1,1)和B(1,3),求圆C 的方程。
2023年高职单独招生考试数学试卷(答案) (1)

数学试卷
(满分 120 分,考试时间 120 分钟)
一、选择题:(本题共 20 小题,每小题 3 分,共 60 分)
(
OB
OC ) (OB OC 2OA) 0 , 则 ABC 的形状为
ABC
1、若 O 为
D. 内必存在直线与 m 平行, 不一定存在直线与 m 垂直。
2
S n 1 an
3 , 则其各项和 S(
3、已知数列 an 的前 n 项和 Sn 满足
Hale Waihona Puke A.13B. 2
5
C. 3
)
2
D. 3
4、当圆锥的侧面积与底面积的比值是 2 时, 圆锥的轴截面的顶角是(
A. 30
B. 45
C. 90
积的最小值是____.
3、过点 p(2,1) 且与直线 x 2 y 10 0 平行的直线方程是______
4、在 ABC 中,已知 B= 30 , C= 135 ,AB=4,则 AC=______
1
7
y sin x b
3
5、已知函数
的最大值是 9 ,则 b=______
A. A′C⊥平面 DBC′
B. 平面 AB′D′//平面 BDC′
C. BC′⊥AB′
D. 平面 AB′D′⊥平面 A′AC
13. 已知集合 A={-1,0,1},集合 B={-3,-1,1,3},则 A∩B=(
)
)
A. {-1,1}
B. {-1}
14. 不等式 x2-4x≤0 的解集为(
A. [0,4]
当 t>1 时,S′>0,当 0<t<1 时,S′<0,
2023年单招考试数学、英语试卷+答案 (3)

2023年单独招生考试招生文化考试数学试题卷(满分120分,考试时间120分钟)一、选择题:(本题共15小题,每小题3分,共45分)1.若6π=x 是x x x f ωωcos sin 3)(+=的图象的一条对称轴,则ω可以是( )(A)4 (B) 8 (C) 2 (D)12.已知(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨>⎩是(,)-∞+∞上的减函数,则a 的取值范围是( )(A)(0,1) (B)1(0,)3 (C)11[,)73 (D)1[,1)7 3.给定函数:①21x y =,②)1(log 21+=x y ,③1-=x y ,④12+=x y ,其中在区间(0,1)上单调递减的函数的序号是( )(A)①② (B) ②③ (C) ③④ (D)①④4.设.0,0>>b a 若3是a 3与b 23的等比中项,则b a 12+的最小值为( ) (A)8 (B) 4 (C) 1 (D)415.在进行一项物理实验中,要先后实施6个程序,其中程序A 只能出现在第一或最后一步,程序B 和C 在实施时必须相邻,则实验顺序的编排方法共有( )(A)34 (B) 48 (C) 96 (D)1446.已知命题p :存在1cos ),2,2(≥-∈x x ππ; 命题x x x q 32),0,(:<-∞∈∀ , 则下列命题为真命题的是( )(A)q p ∧ (B) q p ∧⌝)( (C) q p ∨⌝)( (D) q p ⌝∧7.若p :z k k ∈+=,2ππϕ,)0)(sin()(:≠+=ωϕωx x f q 是偶函数,则p 是q 的( )(A)充分必要条件 (B)充分不必要条件 (C) 必要不充分条件 (D) 既不充分也必要条件8、已知集合}{{}1,3,5,7,9,0,3,6,9,12A B ==,则A B =( )(A) }{3,5 (B) }{3,6(C) }{3,7 (D) }{3,99、复数3223i i +=-( )(A )1 (B )1- (C )i (D)i -10、对变量,x y 有观测数据(1x ,1y )(1,2,...,10i =),得散点图1;对变量,u v 有观测数据(1u ,1v )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。
单独招生《数学》试卷及答案

单独招生考试数学试卷请考生认真阅读如下事项:1.本试卷共四大题13小题,总分为150分,考试时间45分钟。
2.请将所有答案填写在答题纸上,在试卷上答题无效。
.......................3.本试卷可能用到的数学公式:sin()sin cos cos sin αβαβαβ±=±111sin sin sin 222sin sin sin ABC ABC S ab C ac B bc Aa b cA B C∆∆=====中一、是非选择题(本大题共5个小题,每小题10分,共50分,对每小题的命题作出判断,对的选A ,错的选B )1.如果集合A={1,Φ},B={0,1},那么A∩B=Φ.(A ,B )2.55log 20log 41-=.(A ,B )3.函数sin cos y x x =-的最大值为1.(A ,B )4.椭圆2212516x y +=的焦点是(5,0)±.(A ,B )5.直线y 3+1x =-的斜率为k 1=.(A ,B )二、单项选择题(本题共3个小题,每小题10分,共30分)6.等比数列{}n a 的各项为正数,若351,9a a ==,则{}n a 的公比()q =.A 、2B、3C 、-2D 、-37.若平面向量(3,)a x = ,(4,3)b =- 且a b ⊥,则x 的值等于().A 、1B 、2C 、3D 、48.由0,1,2,3能组成()个没有重复数字的二位数.A 、6B 、18C 、4D 、9三、填空题(本大题3个小题,每小题10分,共30分)9.sin13cos17cos13sin17 +=.10.5(1)x -展开式中的第3项是.11.已知正四棱锥底面正方形边长为3,高是4,则正四棱锥的体积是.四、求解题(本大题共2个小题,第12小题15分,第13小题25分,共40分)12.求不等式组122132x x x x +⎧>-⎪⎨⎪->-+⎩的解集.13.如图1在ABC ∆中,4,30,120a B C ===(1)求边c ;(2)求ABC ∆的面积.BCAbca图1数学试卷(样卷)参考答案一、是非选择题题号12345答案BABBB二、单项选择题题号678答案BDD三、填空题9、12;10、210x ;11、12三、求解题12、解:122x x+>-的解集为5x <……………………5′132x x ->-+的解集为34x >……………………10′∴原不等式的解集为3{5}4xx <<……………………15′13、解:(1)30,120,3054,30,120,,sin sin 43151(2)sin 2021443sin 3043252据公式∆∆'==∴====='∴='='∴=⨯⨯⨯= ABC ABC B C A a ca A C A Cc S ac B S。
2023年单独招生考试数学卷(含答案) (3)
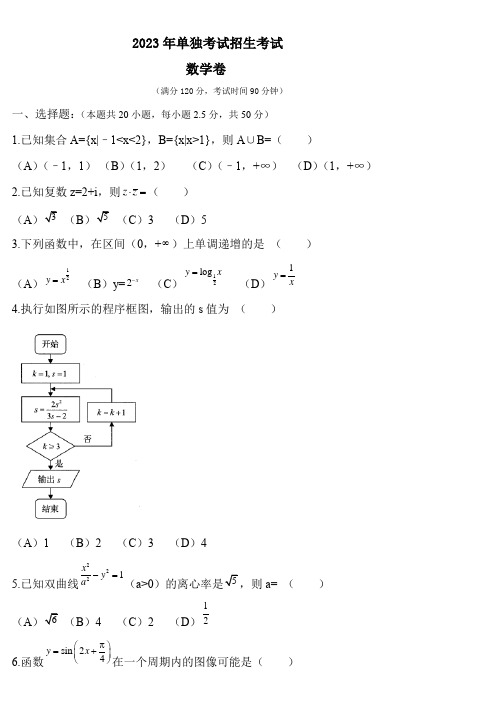
2023年单独考试招生考试数学卷(满分120分,考试时间90分钟)一、选择题:(本题共20小题,每小题2.5分,共50分)1.已知集合A={x|–1<x<2},B={x|x>1},则A ∪B=( )(A )(–1,1) (B )(1,2) (C )(–1,+∞) (D )(1,+∞)2.已知复数z=2+i ,则z z ⋅=( )(A (B (C )3 (D )53.下列函数中,在区间(0,+∞)上单调递增的是 () (A )12y x = (B )y=2x - (C )12log y x = (D )1y x =4.执行如图所示的程序框图,输出的s 值为 ( )(A )1 (B )2 (C )3 (D )45.已知双曲线2221x y a -=(a>0a= ()(A (B )4 (C )2 (D )126.函数sin 24y x π⎛⎫=+ ⎪⎝⎭在一个周期内的图像可能是( )GD31GD34GD32GD33 7.在ABC △中,若2AB BC CA ===,则AB BC ⋅等于()A. -B. C.-2 D.28.如图所示,若,x y 满足约束条件0210220x x x y x y ⎧⎪⎪⎨--⎪⎪-+⎩≥≤≤≥则目标函数z x y =+的最大值是( )A.7B.4C.3D.19.已知α表示平面,,,l m n 表示直线,下列结论正确的是( )A.若,,l n m n ⊥⊥则l m ∥B.若,,l n m n l ⊥⊥⊥则mC.若,,l m l αα∥∥则∥mD.若,,l m l αα⊥⊥∥则m10.已知椭圆22126x y +=的焦点分别是12,F F ,点M 在椭圆上,如果120FMF M ⋅=,那么点M 到x 轴的距离是()A.B.C. 2D. 111、已知54cos ,0,2=⎪⎭⎫ ⎝⎛-∈x x π,则x tan =( )A 、34B 、34-C 、43D 、43-12、在∆ABC 中,AB=5,BC=8,∠ABC=︒60,则AC=( )A 、76B 、28C 、7D 、12913、直线012=+-y x 的斜率是( );A 、-1B 、0C 、1D 、214、点P(-3,-2)到直线4x -3y+1=0的距离等于( )A 、-1B 、1C 、 2D 、-215、过两点A (2,)m -,B(m ,4)的直线倾斜角是45︒,则m 的值是()。
2023年单招考试数学+英语试卷及含答案 (3)

2023年单独招生考试招生文化考试数学卷(含答案)(满分120分,考试时间90分钟)一.选择题:(共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.下列各对函数中,是同一函数的是()A .x y =与2x y =B .()()131-+-=x x x y 与3+=x y C .2x y =与xx y =D .1)(2+=x x f 与1)(2+=v v f 2.函数)(x f 满足13)2()(=+⋅x f x f ,若2)1(=f ,则)99(f 等于()A .13B .2C .213D .1323.若集合{}{}M a ,a x x N ,,,M ∈===2210,则=N M ()A.{}0 B.{}10, C.{}21, D.{}20,4.函数)20(4)(2≤≤-=x x x x f 的反函数是()A.[]()2,1422∈--=x x y B.[]()2,0422∈--=x x y C.[]()2,1422∈-+=x x y D.[])2,0422∈-+=x x y 5.设数列{}n a 是等差数列,则()A.5481a a a a +<+B.5481a a a a +=+C.5481a a a a +>+D.5481a a a a =6.函数4cos 3sin +-=x x y 的最大值是()A.21-B.156212-- C.34-D.156212+-7.函数x sin y 2=的图象按向量a 平移后,得到的函数解析式为12+=x cos y ,则a 等()A.⎪⎭⎫ ⎝⎛41,π B.⎪⎭⎫ ⎝⎛4-1,π C.⎪⎭⎫ ⎝⎛-12,π D.⎪⎭⎫ ⎝⎛12,π8.到椭圆192522=+y x 右焦点的距离与到定直线6=x 距离相等的动点轨迹方程是()A.)5(42--=x y B.)5(42-=x y C.xy 42-= D.xy 42=9.在航天员进行的一项太空实验中,先后要实施6个程序,其中程序A 只能出现在第一步或最后一步,程序B 和C 实施时必须相邻,则实验顺序的编排方法共有()A.24种B.48种C.96种D.144种10.若ABC ∆的三个顶点C ,B ,A 及平面内一点P 满足0=++PC PB P A ,且实数λ满足:AP AC AB λ=+,则实数λ的值是()A.2B.23C.3D.611.设集合M={1,2,3,4,5},集合N={1,4,5},集合T={4,5,6},则N T M )(=()A.{2,4,5,6}B.{1,4,5}C.{1,2,3,4,5,6}D.{2,4,6}12.已知集合{|3A x x n ==+2,N n ∈,},{6,8,10,12,14}B =,则集合A B 中的元素个数为()A.5B.4C.3D.213.已知集合A{}12x x =-<<,{03}B x x =<<,则A B = ()A.(-1,3)B.(-1,0)C.(0,2)D.(2,3)14.已知集合A {}2,1,0,1,2=--,{}(1)(2)0B x x x =-+<,则A B =()A.{-1,0}B.{0,1}C.{-1,0,1}D.{0,1,2}15.若集合}25|{<<-=x x A ,}33|{<<-=x x B ,则=B A ()A.}23|{<<-x x B.}25|{<<-x xC.}33|{<<-x xD.}35|{<<-x x 16.已知集{1,2,3},B {1,3}A ==,则A B = ()A.{3}B.{1,2}C.{1,3}D.{1,2,3}17.已知集合{}{}3,2,3,2,1==B A ,则()A.A=BB.=B A ∅C.B A ⊆D.A B ⊆18.若集合{}1,1M =-,{}2,1,0N =-,则M N = ()A.{0,-1}B.{1}C.{-2}D.{-1,1}19.设A,B 是两个集合,则“A B A = ”是“A B ⊆”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件20.设集合A={0,2,a},B={1,a2},若A∪B={0,1,2,5,25},则a 的值为()A.0B.1C.2D.5二.填空题:(共20分.)1.若实数a,b 均不为零,且)0(12>=x x x b a ,则9)2(b a x x -展开式中的常数项等于________.2.代号为“狂飙”的台风于某日晚8点在距港口的A 码头南偏东60°的400千米的海面上形成,预计台风中心将以40千米/时的速度向正北方向移动,离台风中心350千米的范围都会受到台风影响,则A 码头从受到台风影响到影响结束,将持续多少小时________.3.给出下列4个命题:①函数m ax x x x f ++=||)(是奇函数的充要条件是m=0:②若函数)1lg()(+=ax x f 的定义域是}1|{<x x ,则1-<a ;③若2log 2log b a <,则1lim =+-∞→nn n n n b a b a (其中+∈N n );④圆:0541022=-+-+y x y x 上任意点M 关于直线25=--a y ax 的对称点,M '也在该圆上.填上所有正确命题的序号是________. 4.已知:=2,=2,与的夹角为45°,要使与垂直,则λ__________.三.解答题:(本题共3小题,共50分.解答应写出文字说明.证明过程或演算步骤.)1.提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v (单位:千米/小时)是车流密度x (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当20020≤≤x 时,车流速度v 是车流密度x 的一次函数.(1)当2000≤≤x 时,求函数)(x v 的表达式;(2)当车流密度x 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时))()(x v x x f ⋅=可以达到最大?求出最大值.(精确到1辆/小时)2.已知集合A={}{}B A B A x x B x x ,,71,40求<<=<<.观察下列三角形数表,假设第n 行的第二个数为),2(+∈≥N n n a n(1)依次写出第六行的所有6个数;(2)试猜想1+n a 与n a 的关系式,并求出{}n a 的通项公式.设c b a ,,分别是ABC ∆的三个内角A .B .C 所对的边,S 是ABC ∆的面积,已知4,5,3a b S ===(1)求角C ;(2)求c 边的长度.3.解:(1)由题知5,4,35===b a S 设c b a ,,分别是ABC ∆的三个内角A .B .C 所对的边,S 是ABC ∆的面积,已知4,5,3a b S ===.(1)求角C ;(2)求c 边的长度.参考答案:一.选择题1-5:DCDBB 6-10:DAACC 11-15:BDAAA 16-20:CDBCD 二.填空题1.-6722.2.5小时3.①,④4.2三.解答题1.(1)解:因为当20020≤≤x 时,车流速度是车流密度x 的一次函数,故设b kx v +=则⎩⎨⎧+=+=b k b k 20602000⎪⎪⎩⎪⎪⎨⎧=-=∴320031b k 320031+-=∴x v 故⎪⎩⎪⎨⎧≤≤+-<≤=20020,320031200,60)(x x x x v (2)由(1)得⎪⎩⎪⎨⎧≤≤-<≤=20020,)200(31200,60)(x x x x x x f 当200<≤x 时,)(x f 为增函数,1200)(<x f 当20020≤≤x 时,310000)100(31)200(31)(2+--=-=x x x x f 当100=x 时,最大值3333=即当车流密度为100辆/千米时,车流量可以达到最大,最大约为3333辆/小时)(x g 的减区间为)0,(-∞2.题,参考答案:(1,4);(0,7)3.题:参考答案:C ab S sin 21=Csin 542135⨯⨯=∴23sin =∴C 又 C 是ABC ∆的内角3π=∴C 或32π=C (2)当3π=C 时,3cos 2222πab b a c -+=215422516⨯⨯⨯-+=21=21=∴c 当32π=C 时,22222cos 3c a b ab π=+-215422516⨯⨯⨯++==6161=∴c2023年高职对口单独招生统一考试英语试卷(含答案)(满分120分,考试时间90分钟)一.选择题:(本题共20小题,每小题3分,共60分)1.There is_______“W〞in the word“woman〞,and_______“M〞is the third letter of the word.A.a;anB.an;/C.an;theD.a;the提示:冠词的用法测试:多记,勤思。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A单考单招数学试卷 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】
2015年浙江省高等职业技术教育招生考试
数学试卷A 卷
姓名 准考证号
一、单项选择题(本大题共18小题,每小题2分,共36分)
(在每小题列出的四个备选答案中,只有一个是符合题目要求的。
错涂、多涂或未涂均无分。
)
1.已知集合M={}032=++x x x ,则下列结论正确的是 A.集合M 中共有2个元素 B.集合M 中共有2个相同元素 C.集合M 中共有1个元素 D.集合M 为空集
2.命题甲""b a <是命题乙"0"<-b a 成立的 A.充分不必要条件 B.必要不充分条件 C.充分且必要条件 D.既不充分也不必要条件
3.函数x
x x f )2lg()(-=的定义域是
A.[)+∞,3
B.),3(+∞
C.),2(+∞
D.[)+∞,2 4.下列函数在定义域上为单调递减的函数是 A.x x f )2
3()(= B.x x f ln )(= C.x x f -=2)( D.x x f sin )(=
5.已知角4
π
α=,将其终边按顺时针方向旋转2周得角β,则β=C
A.
4
9π B.
4
17π C.4
15π-
D.4
17π-
6.已知直线04=-+y x 与圆,17)4()2(22=++-y x 则直线和圆的位置关
系是
A .相切 B.相离 C.相交且不过圆心 D. 相交且过圆心 7.若),,0(πβ∈则方程1sin 22
=+βy x
所表示的曲线是 D
A.圆
B.椭圆
C.双曲线
D.椭圆或圆
8.在下列命题中,真命题的个数是 ①
b a b a ⊥⇒⊥αα,//
② b a b a ////,//⇒αα
③b a b a //,⇒⊥⊥αα ④αα⊥⇒⊂⊥a b b a , 个 个 个 个
9.若6
2)4cos()4cos(=+-θπθπ,则=θ2cos
A .
3
2 . B
3
7 C .6
7
D .
6
34
10.在等比数列{}n a 中,若,1221-=+++n n
a a a 则++2
221a a ……=+2n
a A.2)12(-n B.2)12(3
1-n C.14-n D.)14(3
1-n 11.下列计算结果不正确的是 A.39
494
10
C
C C
=- B. 910
1010
P
P
=
!=1 D.!
86
868
P C =
12.直线
020153=++y x 的倾斜角为
A.6
π B.3π C.
3
2π D.
6
5π
13.二次函数34)(2-+=x ax x f 的最大值为5,则=)3(f A. 2 B.2- C.2
9 D.2
9- 14.已知5
3sin =α,且),,2
(ππα∈则=+)4
tan(π
α
A.7-
B.7
C.71-
D.7
1
15.在ABC ∆中,若三角之比,4:1:1::=C B A 则=C B A sin :sin :sin A.4:1:1 B.3:
1:1 C. 2:1:1 D .3:1:1
16.已知0)2)(2(2=++-y x x ,则3xy 的最小值为 C A.2- B.2 C.6- D.26
-
17.下列各点中与点)0,1(-M 关于点)3,2(H 中心对称的是 A.)1,0( B )6,5( C. )1,1(- D. )6,5(- 18.焦点在x 轴上,焦距为8的双曲线,其离心率e=2.则双曲线的标准方程为
A. 112422=-y x
B.141222=-y x
C.112422=-x y
D.14
122
2=-x y
二.填空题:(本大题共8小题,每小题3分,共24分) 19.不等式772>-x 的解集为 (用区间表示)
20.若),0(tan ≠=a a
b
α则=+αα2sin 2cos b a a
21.已知=()7,0-,=- 28 22.当且仅当∈x 时,三个数4,9,1-x 成等比数列 23.在“剪刀、石头、布”游戏中,两个人分别出“石头”与“剪刀”的概率=P 2/9
24.二项式12
3
32)2(x
x +展开式为
Y
25.体对角线为3cm 的正方=V
o X
26.如图所示,在所给的直角坐标系中,半径为2,
且与两坐标轴相切的圆的标准方为
三.解答题:(本大题共8小题,共60分) (题26图) (解答题应写出文字说明及演算步骤)
27.(本题满分7分)平面内,过点)6,(),,1(n B n A -的直线与直线012=-+y x 垂直,求n 的值.
28.( 本题满分7分)已知函数{
=)(x f 0
,230
,12<-≥-x x x x ,求值:
(1))21
(-f ;(2分)
(2))2(5.0-f ;(2分) (3))1(-t f .(3分)
29 (本题满分7分)课外兴趣小组共有15人,其中9名男生,6名女生,其中1名为组长,现要选3人参加数学竞赛,分别求出满足下列各条件的不同选法数. (1)要求组长必须参加;(2分)
(2)要求选出的3人中至少有1名女生;(2)
(3)要求选出的3人中至少有1名女生和1名男生.(3分)
30.(9分)根据表中所给的数字填空格,要求每行的数成等差数列,每列的数成等比数列.
求:(1)c b a ,,的值;(3分)
(2)按要求填满其余各空格中的数;(3分) (3)表格中各数之和.(3分)
(题30表格)
31.( 本题满分6分)已知2)3cos(4)sin(3)(+-+-=ππax ax x f (0≠a )
的最小正周期为
3
2
, (1)求a 的值;(4分) (2))(x f 的值域.(2分)
32.( 本题满分7分)在ABC ∆中,若,2
3
,3
,1=
=
∠=∆ABC S B BC π
,求角C . 33. (本题满分7分)如图所示, 在棱长为a 正方体D C B A ABCD -中,平面
C A
D 1把正 方体分成两部分求:(1)直线B C 1与平面C AD 1所成的角; (2
(2)平面D C 1与平面C AD 1所成二面角的
平面角的余弦值; (3分)
(3)两部分中体积大的部分的体积. (2分)
(题33图) 34.( 本题满分10分)已知抛物线y x 42= ,斜率为k 的直线L 过其焦点F 且与抛
物线相交于点)(),,(2,211y x B y x A .
(1)求直线L 的一般式方程;(3分) (2)求AOB ∆的面积S ;(4分)
(3)由(2)判断:当直线斜率k
k 为何值时AOB ∆的面积S 有最小值
X
参考答案 一、选择题
1.D 17.B
二、填空题19.(-∞,0)∪(7,+∞) 20.A 22.{7,-5} 23.9
2
24.5
612
672-=x C T 25.33 26.4)2()2(22=+++y x 三、27.
3
4
n 4(,216==+-分),n n (3分) 28.⑴4;⑵-2
1
⑶当t -1≥0,即t ≥1时,f(t-1)=2t -2t ;t 《1时,f(t-1)= -2t+5 29.⑴2
14C =91;⑵39315C C -=371;⑶16292619C C C C +=351
31.⑴y=-5sin(ax+θ)+2;(2分) a=±3π(2分)⑵[-3,7] 32.AB=2,(2分) AC=3;(2分);C= 90 33.⑴ 0;⑵
33⑶36
5
a 34.⑴焦点F(0,1) (1分) 直线kx-y+1=0 (2分)
⑵点到直线距离公式求高2分,弦长公式求底1分,面积表示1分。
