小学二年级奥数讲义之精讲精练第10讲 学习一笔画含答案
小学二年级数学奥数 第10讲 学习一笔画(1)

第10讲学习一笔画【专题简析】一笔画,就是从图形某点出发,笔不离开纸,而且每条线段都只画一次不重复。
它是一种有趣的数学游戏。
那么,哪些图形不能一笔画成,哪些图形可以一笔画成呢?一个图形能否一笔画成,关键在于单数点的多少,有2个或0个单数点的图形就能够一笔画成,单数点在一笔画中只能作为起点和终点。
【例题1】一些平面图形是由点和线构成的,这里的“线”可以是线段,也可以是一段曲线,请自己画一些图研究每个点和线的连接情况。
思路导航:请小朋友仔细观察下列各图中的点,他们分别与几条线相连。
①②③④(1)与一条线段相连的点有:(2)与两条线段相连的点有:(3)与三条线段相连的点有:(4)与四条线段相连的点有:归纳:把和一条、三条、五条等单数条线连得点叫做单数点;把和两条、四条、六条、八条等双数条线连的点叫双数点,每个图中的点要么是单数点,要么是双数点。
1.任意找一个平面图形,数一数图中有几个单数点,几个双数点。
2.下面图形中有哪几个单数点?B3.数一数下面图形中有几个双数点,分别是哪些点?B【例题2】下面的图形能不能一笔画成?如果能,应该怎样画?(1) O(2)B D(3)【思路导航】图(1)中A 、B 、C 、D 、O 五个点都是双数点,所以这个图形可以一笔画成。
画时可以从任意一点出发。
图(2)中A 、C 、D 、F 四个点都是双数点,B 和E 两个点是单数点,所以这个图形也可以一笔画成。
画时要从单数点出发,最后回到另一个单数点。
图(3)中A 、D 是双数点,B 、C 、E 和F 四个点是单数点,单数点的个数超过了两个,这个图形不能一笔画成。
1.下面的图形能不能一笔画成,如果能,请说明画法,如果不能,请说明理由(1)(2)2.下列图形能一笔画成吗?为什么?3.观察下列图形,哪个图形可以一笔画成?怎么画?【例题3】下图是某地区所有街道的平面图,甲、乙两人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达C.那么两人谁先到达?C思路导航:题中要求两人必须走遍所有街道,最后到达C.仔细观察,可以发现图中有两个单数点:A 、C 。
小学二年级奥数第10讲 学习一笔画带答案(含答案)

第10讲学习一笔画【专题简析】一笔画,就是从图形某点出发,笔不离开纸,而且每条线段都只画一次不重复。
它是一种有趣的数学游戏。
那么,哪些图形不能一笔画成,哪些图形可以一笔画成呢?一个图形能否一笔画成,关键在于单数点的多少,有2个或0个单数点的图形就能够一笔画成,单数点在一笔画中只能作为起点和终点。
【例题1】一些平面图形是由点和线构成的,这里的“线”可以是线段,也可以是一段曲线,请自己画一些图研究每个点和线的连接情况。
思路导航:请小朋友仔细观察下列各图中的点,他们分别与几条线相连。
①②③④(1)与一条线段相连的点有:(2)与两条线段相连的点有:(3)与三条线段相连的点有:(4)与四条线段相连的点有:归纳:把和一条、三条、五条等单数条线连得点叫做单数点;把和两条、四条、六条、八条等双数条线连的点叫双数点,每个图中的点要么是单数点,要么是双数点。
练习11.任意找一个平面图形,数一数图中有几个单数点,几个双数点。
2.下面图形中有哪几个单数点?B答案:A D3.数一数下面图形中有几个双数点,分别是哪些点?B 答案:A BCDE F【例题2】下面的图形能不能一笔画成?如果能,应该怎样画?AC C(1) O (2)B DF(3)D【思路导航】图(1)中A 、B 、C 、D 、O 五个点都是双数点,所以这个图形可以一笔画成。
画时可以从任意一点出发。
图(2)中A 、C 、D 、F 四个点都是双数点,B 和E 两个点是单数点,所以这个图形也可以一笔画成。
画时要从单数点出发,最后回到另一个单数点。
图(3)中A 、D 是双数点,B 、C 、E 和F 四个点是单数点,单数点的个数超过了两个,这个图形不能一笔画成。
练习21.下面的图形能不能一笔画成,如果能,请说明画法,如果不能,请说明理由(1)(2)答案:图(1)可以一笔画成,因为单数点有两个图(2)不能一笔画成,因为单数点大于两个2.下列图形能一笔画成吗?为什么?答:图(1)可以一笔画成,因为单数点个数为零图(2)不可以画成,因为单数点只有一个图(3)不可以画成,单数点个数大于两个3.观察下列图形,哪个图形可以一笔画成?怎么画?图(1)单数点个数为0,可以一笔画出图(2)单数点个数为4个,不可以一笔画出图(3)单数点2个,可以画出【例题3】下图是某地区所有街道的平面图,甲、乙两人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达C.那么两人谁先到达?AC思路导航:题中要求两人必须走遍所有街道,最后到达C.仔细观察,可以发现图中有两个单数点:A 、C 。
人教版小学数学二年级专题训练第10讲 学习一笔画(1)

第10讲学习一笔画【专题简析】一笔画,就是从图形某点出发,笔不离开纸,而且每条线段都只画一次不重复。
它是一种有趣的数学游戏。
那么,哪些图形不能一笔画成,哪些图形可以一笔画成呢?一个图形能否一笔画成,关键在于单数点的多少,有2个或0个单数点的图形就能够一笔画成,单数点在一笔画中只能作为起点和终点。
【例题1】一些平面图形是由点和线构成的,这里的“线”可以是线段,也可以是一段曲线,请自己画一些图研究每个点和线的连接情况。
思路导航:请小朋友仔细观察下列各图中的点,他们分别与几条线相连。
①②③④(1)与一条线段相连的点有:(2)与两条线段相连的点有:(3)与三条线段相连的点有:(4)与四条线段相连的点有:归纳:把和一条、三条、五条等单数条线连得点叫做单数点;把和两条、四条、六条、八条等双数条线连的点叫双数点,每个图中的点要么是单数点,要么是双数点。
练习11.任意找一个平面图形,数一数图中有几个单数点,几个双数点。
2.下面图形中有哪几个单数点?B3.数一数下面图形中有几个双数点,分别是哪些点?B【例题2】下面的图形能不能一笔画成?如果能,应该怎样画?AC C(1) O (2)B DF(3)D【思路导航】图(1)中A 、B 、C 、D 、O 五个点都是双数点,所以这个图形可以一笔画成。
画时可以从任意一点出发。
图(2)中A 、C 、D 、F 四个点都是双数点,B 和E 两个点是单数点,所以这个图形也可以一笔画成。
画时要从单数点出发,最后回到另一个单数点。
图(3)中A 、D 是双数点,B 、C 、E 和F 四个点是单数点,单数点的个数超过了两个,这个图形不能一笔画成。
练习21.下面的图形能不能一笔画成,如果能,请说明画法,如果不能,请说明理由(1)(2)2.下列图形能一笔画成吗?为什么?3.观察下列图形,哪个图形可以一笔画成?怎么画?【例题3】下图是某地区所有街道的平面图,甲、乙两人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达C.那么两人谁先到达?C思路导航:题中要求两人必须走遍所有街道,最后到达C.仔细观察,可以发现图中有两个单数点:A、C。
小学奥数 奇妙的一笔画 精选练习例题 含答案解析(附知识点拨及考点)

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答【解析】 奇点: D H J O 偶点:A B C E F G I 【答案】奇点: D H J O 偶点:A B C E F G I【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.【考点】一笔画问题 【难度】2星 【题型】填空例题精讲知识点拨4-1-5.奇妙的一笔画【关键词】华杯赛,六年级,初赛,第10题【解析】最少需要3种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。
二年级奥数:第10讲 学习一笔画(1)

第10講學習一筆劃【專題簡析】一筆劃,就是從圖形某點出發,筆不離開紙,而且每條線段都只畫一次不重複。
它是一種有趣的數學遊戲。
那麼,哪些圖形不能一筆劃成,哪些圖形可以一筆劃成呢?一個圖形能否一筆劃成,關鍵在於單數點的多少,有2個或0個單數點的圖形就能夠一筆劃成,單數點在一筆劃中只能作為起點和終點。
【例題1】一些平面圖形是由點和線構成的,這裏的“線”可以是線段,也可以是一段曲線,請自己畫一些圖研究每個點和線的連接情況。
思路導航:請小朋友仔細觀察下列各圖中的點,他們分別與幾條線相連。
①②③④(1)與一條線段相連的點有:(2)與兩條線段相連的點有:(3)與三條線段相連的點有:(4)與四條線段相連的點有:歸納:把和一條、三條、五條等單數條線連得點叫做單數點;把和兩條、四條、六條、八條等雙數條線連的點叫雙數點,每個圖中的點要麼是單數點,要麼是雙數點。
練習11.任意找一個平面圖形,數一數圖中有幾個單數點,幾個雙數點。
2.下麵圖形中有哪幾個單數點?B3.數一數下麵圖形中有幾個雙數點,分別是哪些點?B【例題2】下麵的圖形能不能一筆劃成?如果能,應該怎樣畫?A C AB C(1)OB DD E FA B CC(3)DE F【思路導航】圖(1)中A、B、C、D、O五個點都是雙數點,所以這個圖形可以一筆劃成。
畫時可以從任意一點出發。
圖(2)中A、C、D、F四個點都是雙數點,B和E 兩個點是單數點,所以這個圖形也可以一筆劃成。
畫時要從單數點出發,最後回到另一個單數點。
圖(3)中A、D是雙數點,B、C、E和F四個點是單數點,單數點的個數超過了兩個,這個圖形不能一筆劃成。
練習21.下麵的圖形能不能一筆劃成,如果能,請說明畫法,如果不能,請說明理由(1)(2)2.下列圖形能一筆劃成嗎?為什麼?3.觀察下列圖形,哪個圖形可以一筆劃成?怎麼畫?【例題3】下圖是某地區所有街道的平面圖,甲、乙兩人同時分別從A、B出發,以相同的速度走遍所有的街道,最後到達C.那麼兩人誰先到達?C B思路導航:題中要求兩人必須走遍所有街道,最後到達C.仔細觀察,可以發現圖中有兩個單數點:A、C。
二年级奥数 学习一笔画(1)

第10讲学习一笔画【专题简析】一笔画,就是从图形某点出发,笔不离开纸,而且每条线段都只画一次不重复. 它是一种有趣的数学游戏. 那么,哪些图形不能一笔画成,哪些图形可以一笔画成呢?一个图形能否一笔画成,关键在于单数点的多少,有2个或0个单数点的图形就能够一笔画成,单数点在一笔画中只能作为起点和终点.【例题1】一些平面图形是由点和线构成的,这里的“线”可以是线段,也可以是一段曲线,请自己画一些图研究每个点和线的连接情况.思路导航:请小朋友仔细观察下列各图中的点,他们分别与几条线相连.①②③④(1)与一条线段相连的点有:(2)与两条线段相连的点有:(3)与三条线段相连的点有:(4)与四条线段相连的点有:归纳:把和一条、三条、五条等单数条线连得点叫做单数点;把和两条、四条、六条、八条等双数条线连的点叫双数点,每个图中的点要么是单数点,要么是双数点.练习11.任意找一个平面图形,数一数图中有几个单数点,几个双数点.2.下面图形中有哪几个单数点?B3.数一数下面图形中有几个双数点,分别是哪些点?B【例题2】下面的图形能不能一笔画成?如果能,应该怎样画?AC C (1) O (2)B DF (3)D【思路导航】图(1)中A 、B 、C 、D 、O 五个点都是双数点,所以这个图形可以一笔画成.画时可以从任意一点出发. 图(2)中A 、C 、D 、F 四个点都是双数点,B 和E 两个点是单数点,所以这个图形也可以一笔画成. 画时要从单数点出发,最后回到另一个单数点. 图(3)中A 、D 是双数点,B 、C 、E 和F 四个点是单数点,单数点的个数超过了两个,这个图形不能一笔画成.练习21.下面的图形能不能一笔画成,如果能,请说明画法,如果不能,请说明理由(1)(2)2.下列图形能一笔画成吗?为什么?3.观察下列图形,哪个图形可以一笔画成?怎么画?【例题3】下图是某地区所有街道的平面图,甲、乙两人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达C.那么两人谁先到达?C思路导航:题中要求两人必须走遍所有街道,最后到达C.仔细观察,可以发现图中有两个单数点:A、C. 这就是说:甲可以从A点出发,不重复地走遍所有街道,最后到达C.而B点是双数点,从B点出发的乙则不行. 因此,甲所走的路程正好等于所有街道的总和,而乙所走的路程一定比这个总和多,所以甲最先到达C.解:甲最先到达C.练习3A1.下图是某新村小区主干道平面图. 甲、乙两人同时分别从A 、B 出发,以相同的速度走遍所有的主干道,最后到达C.问谁能最先到达C?2. 甲、乙两辆车同时以相同的速度分别从A 、B 出发,哪辆车能最先行驶完所有的路程?B3.一只蚂蚁分别从A 点和B 点出发,爬遍所有的小路. 如果每次爬行的速度相同,那么从哪一点出发所用的时间少?【例题4】下图(图1)能否一笔画成,若不能,你能用什么方法把它改成能够一笔画成的图形?(1) (2)思路导航:此图共有9个点,其中5个点是双数点,4个点是单数点,由于超过两个单数点,因此不能一笔画成. 要想改为一笔画成,关键在于减少单数点数目(把单数点的个数减少到0或2),所以只要在任意两个单数点间连上线,就可以一笔画,有时也可以将多余的两个单数点间的连线去掉,改成一笔画.解:图(1)有4个单数点,不能一笔画成. 要改成一笔画成,如图(2) 练习41.将下图改成一笔画.1. 2.3.在一个小区中有一些路,每个圆柱表示邮筒(如下图),邮递员叔叔每次送信时,总是没法走过每一条路而又不重复,你知道为什么吗?如果请你给小区加一条路来解决这个问题,你准备把这条路加在哪儿?请你动手画一画.【例题5】邮递员叔叔要给一个居民小区送信(如图),怎么走才能少走重复路,使每天走的路尽可能短?AGH D BF思路导航:图中一共有九个点,其中单数点有2个(点D 和点F ),因此能一次不重复走过所有的路,但必须从这两个单数点中的一个出发,再回到另一个单数点.解:邮递员叔叔只能从点D (或点F )出发,走过所有的路后,再回到点F(或点D) . 练习51.下图是以个小区的中心花园的平面图,你能一次不重复地走完所有的路吗?入口和出口应该设在哪儿呢?2.园林工人在花园里浇花,怎样才能不重复地走遍每条小路?3. 下图是“儿童乐园”平面图,出、入口应分别设在哪里才能不重复地走遍每条路?可以怎么走?D CAB【拓展提高】1、下面的图形能不能一笔画成?为什么?如果能,应该怎样画?2、给下面的图形添一条线,使它能够一笔画成.3、小明和玲玲玩“过木桥”的游戏(如下图),他们谁能不走重复的路?小明玲玲4、在王大爷家的花园中有一些路(如下图),王大爷每次给花浇水时,总是没法走过每一条路而又不重复,你知道为什么吗?如果请你给花园加一条路来解决这个问题,你准备把这条路加在哪儿?请你动手画一画.间隔趣谈【专题简析】两根绳子结起来只要打一个结,两根绳子结成一个圆需要打两个结,一根绳子剪4次被剪成了5段等等,这是日常生活中的比较特殊的问题. 想要做好这类题,需要我们多动脑筋,多动笔画画,才能找到正确的答案. 这一讲是有关绳子打结和剪绳子的问题. 给绳子打结如果不练成一个圆,打结的次数比绳子的根数少1;如果结成1个圆,打结的次数与绳子的根数同样多. 同样,如果是剪绳子,那么剪成的段数比剪得次数多1.【例题1】小刚把4根绳子连起来成一条绳子,一共需要打几个结?思路导航:解这种题,可以画图解答. 如图:打结打结打结从上图中可以看出,4根绳子要结起来成一根绳子,只要打3次结就可以了,可见,打结的次数比绳子的根数少1.解:4-1=3(个)答:小刚把4根绳子连起来成一条绳子,一共需要打3个结练习11.小明把5根绳子连起来成一根长绳,一共需要打几个结?2.把8根绳子连接起来成一根绳子,一共需要打几个结?【例题2】把几根绳子打7个结就能成一个圆?思路导航:根据题意,如图所示:打了7个结,就把一些绳子结成了一个圆,这些绳子应该有7根. 因此,如果把绳子结成圆时,绳子的根数与打结的次数相等.解:把7根绳子打7个结就能成一个圆练习21.丽丽打了8个结就把一些绳子结成一个圆,你知道丽丽拿了几根绳子吗?2.小红拿10根绳子结成一个圆,她打了几个结?3.把20根绳子连接起来成一根绳子,一共需要打几个结?如果要结成一个圆,需要结几次?【例题3】一根10米长的绳子剪了4次,平均每段长多少米?思路导航:10米长的绳子剪了4次,应该剪成了5段. 求平均每段长多少米,也就是要把10平均分成5份,求每份是多少. 210=÷(米),因此平均每段长2米5解:4+1=5(段)210=÷(米)5答:平均每段长2米练习31.一根8米长的绳子,剪了3次,平均每段长多少米?2.一根9分米长的绳子,剪了2次,平均每段长多少分米?3.一根绳子剪了5次后,平均每段长3米,这根绳子原来长多少米?【例题4】一根10米长的绳子,把它剪成2米长的一段,可以剪多少段?要剪几次?思路导航:(1)10米长的绳子,剪成每段2米长,要求可剪多少段,这里求10里面有几个2, ÷(段),可以剪5段.10=52(2)要求剪几次,可以用线段图分析:2米从图中可以看出每一段剪一次,剪最后一次还可以有2段,因此剪的次数比剪得段数少1.即剪得次数=段数-1.解:5÷(段) 5-1=4(次)10=2答:可以剪5段,要剪4次.练习41.一根木材长8米,把它锯成2米长的小段,可以锯成多少段?要锯几次?2.一根12米长的铁丝,把它剪成3米长的小段,可以剪成多少段?要剪多少次?3.一根25米长的电线,剪了4次,可以剪成多少段?平均每段长多少米?【例题5】小兰在桌上摆小棒,先摆了1根,然后每隔7厘米放1根,在距离第一根42厘米处,共放了几根?思路导航:每隔7厘米放一根,42里有几个7就有几段,42÷7=6(段),小棒的根数比段数多1,6+1=7(根).解 :42÷7+1=7(根)答:共放了7根.练习51.小灰灰把贝壳放在桌上,先放一个,然后每隔4厘米放一个,从第1个到20厘米处,一共可以放多少个?2.小红把几枝铅笔放在桌上,每两枝之间相隔8厘米,从第一根到最后一根之间相隔64厘米,你知道放了几枝铅笔吗?3.小美在桌上摆了1颗珠子,然后每隔5厘米放1颗,在距第一颗35厘米处放的是第几颗?练习题答案练习11.4个2.7个练习21.8根2.10个3.19个 20次练习31.2米2.3分米3.18米练习41.8÷2=4(段)4-1=3(次)2.12÷3=4(段) 4-1=3(次)3.4+1=5(段) 25÷5=5(米)练习51.20÷4+1=6(个)2.64÷8+1=9(枝)3.35÷5+1=8(颗)。
小学数学《一笔画》练习题(含答案)精选全文

可编辑修改精选全文完整版小学数学《一笔画》练习题(含答案)什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.所谓一笔画,就是从图形上的某点出发,笔不离开纸,而且每条线都只画一次不准重复.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点.判断图形能否一笔画的规律:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点.以另一个奇点作为终点;(4)奇点个数超过两个的图形,一定不能一笔画.(一) 一笔画以及多笔画【例1】 观察下面的图形,说明哪些图可以一笔画完,哪些不能,为什么?对于可以一笔画的图形,指明画法.(f)(e)(d)JIH G F ED C BAJ K IHGFED CB A分析:(a )图:可以一笔画,因为只有两个奇点A 、B ;画法为A →头部→翅膀→尾部→翅膀→嘴. (b )图:不能一笔画,因为此图不是连通图.(c )图:不能一笔画,因图中有四个奇点:A 、B 、C 、D.(d )图:可以一笔画,因为只有两个奇点;画法为:A →C →D →A →B →E →F →G →H →I →J →K →B. (e )图:可以一笔画,因为没有奇点;画法可以是:A →B →C →D →E →F →G →H →I →J →B →D →F →H →J →A.(f )图:不能一笔画出,因为图中有八个奇点.[注意]在上面能够一笔画出的图中,画法并不是惟一的.事实上,对于有两个奇点的图来说,任一个奇点都可以作为起点,以另一个奇点作为终点;对于没有奇点的图来说,任一个偶点都可以作为起点,最后仍以这点作为终点.[巩固]判断下列图a、图b、图c能否一笔画.E分析:图a是一个连通的图形,图中只有点A和点F两个奇点,所以它能一笔画,其中一种画法如下:A —M—N—A—F—B—C—B—K—C—D—E—D—L—E—F.‘图b是一个不连通的图形,所以不能一笔画.图c是连通图,图中所有点都是偶点,所以能一笔画.其中一种画法如下:A—B—C—D—E—F—D—A—F —C—A.【例2】右图是某地区所有街道的平面图.甲、乙二人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达 C.如果允许两人在遵守规则的条件下可以选择最短路径的话,问两人谁能最先到达C?分析:本题要求二人都必须走遍所有的街道最后到达C,而且两人的速度相同.因此,谁走的路程少,谁便可以先到达C.容易知道,在题目的要求下,每个人所走路程都至少是所有街道路程的总和.仔细观察上图,可以发现图中有两个奇点:A和C.这就是说,此图可以以A、C两点分别作为起点和终点而一笔画成.也就是说,甲可以从A出发,不重复地走遍所有的街道,最后到达C;而从B出发的乙则不行.因此,甲所走的路程正好等于所有街道路程的总和,而乙所走的路程则必定大于这个总和,这样甲先到达C.[巩固]在六面体的顶点B和E处各有一只蚂蚁(见右图),它们比赛看谁能爬过所有的棱线,最终到达终点D.已知它们的爬速相同,哪只蚂蚁能获胜?分析:许多同学看不出这是一笔画问题,但利用一笔画的知识,能非常巧妙地解答这道题.这道题只要求爬过所有的棱,没要求不能重复.可是两只蚂蚁爬速相同,如果一只不重复地爬遍所有的棱,而另一只必须重复爬某些棱,那么前一只蚂蚁爬的路程短,自然先到达D点,因而获胜.问题变为从B到D与从E到D哪个是一笔画问题.图中只有E,D两个奇点,所以从E到D可以一笔画出,而从B到D却不能,因此E点的蚂蚁获胜.[数学小游戏] 用一笔画成四条线段把所有的点连起来,怎样画?分析:通过试画,似乎不可以画,但通过仔细观察,对照一笔画的规律,便可发现,若添上两个辅助点,就可画成.如右图:FE DCB ADCBA我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.公式如下: 奇点数÷2=笔画数,即2n ÷2=n.【例3】 判断下列图形能否一笔画.若能,请给出一种画法;若不能,请加一条线或去一条线,将其改成可一笔画的图形.IH G FED CBA 图aH G I KLJ F EDCBA 图b DC HG EFBA图c分析:图a :原图有四个奇点,所以不能一笔画,在B,D 两点之间加一条线后,图中只有两个奇点,故可以一笔画出,如图d 所示.画法:H →A →B →C →D →E →F →I →D →B →I →H →G →F .图b :原图有四个奇点,所以不能用一笔画.去掉K ,L 两点之间的连线,图中只有两个奇点,故 可以一笔画出,如图e 所示.画法:B →C →D →E →F →→J →H →G →I →A →B →K →I →L →E .图c :原图有四个奇点,所以不能用一笔画.在B ,C 两点之间加一条线后,图中只有两个奇点, 故可以一笔画出,如图f 所示.画法:A →E →D →H →A →B →F →C →G →B →C →D注意:a 、b 、c 三个图都是连通的图形,但由于每个图的奇点个数均超过两个,所以都不能一笔画.图dA BCD EFG H IH GI KLJ F EDCB A 图eDC HG EFBA图f[前铺]观察下面的图,看各至少用几笔画成?分析:(1)图中有8个奇点,因此需用4笔画成. (2)图中有12个奇点,需6笔画成. (3)图是无奇点的连通图,可一笔画成.DC BA(2)(1)FEC DB A分析:图(1)中有6个奇点,因此可添上两条(或3条)边后可改为一笔画;又因为这个图中,把这6个奇点任意分为3对后,最多只有两对奇点间有边相连,因此,可去掉两条边后改为一笔画,举例如图(3)~(6).图(2)中有4个奇点,因此,可添上2条(或1条)边后改为一笔画;又因为把奇点按A 与B ,C 与D (或A 与D ,B 与C )分为两对后,每对间均有边相连,因此,可去掉两条(或1条)边后改为一笔画.举例如图(7)~(8).说明:图(6)运用了两种方法,去掉边BC ,添上边AD 与EF.(二)一笔画的实际应用【例5】 18世纪的哥尼斯堡城是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛A 和一座半岛D ,人们在这里建了一座公园,公园中有七座桥把河两岸和两个小岛连接起来(如图a).如果游人要一次走过这七座桥,而且对每座桥只许走一次,问如何走才能成功?:这个有趣的问题引起了著名数学家欧拉的注意,他证明了七桥问题中提到的走法根本不存在. 下面,我们考虑如下两个问题:(1)如果再架一座桥,游人能否走遍所有这八座桥?若能,这座桥应架在何处?若不能,请说明理由. (2)架设几座桥可以使游人走遍所有的桥回到出发地?而得到一个由四个点和七条线组成的图形(如图b).在图b 中,点A ,B ,C ,D 四个点均为奇点,显然不能一笔画出这个图形.若将其中的两个奇点改成偶点,即在某两个奇点之间连一条线,这样奇点个数由四个变为两个,此时,图形可以一笔画出.如我们可以选择奇点B ,D ,在B ,D 之间连一条线(架一座桥),如图c .在图c 中只有点A 和C 两个奇点,那么我们可以以A 为起点,C 为终点将图形一笔画出.其中一种画法为:A →C →A →B →A →D →B →D →C所以,如果在河岸B 与小岛D 之间架一座桥,游人就可以不重复地走遍所有的桥.(2)在(1)的基础上,再在另外两个奇点A 与C 之间连一条线(即架一座桥),使这两个奇点也变成偶点,如图d .那么A ,B ,C ,D 四个点均为偶点,所以图d 可以一笔画出,并且可以以任意点为起点,最后 仍回到这个点.其中一种画法为:A →C →A →C →D →A →B →D →B →A这表明:在河岸B 与小岛D 之间架一座桥后,再在小岛A 与河岸C 之间架一座桥,共架设两座桥,就可以使游人不重复地走遍所有的桥并回到出发地.[巩固]如图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一次不重复地走遍这七座桥?分析:用点表示小岛与河岸,用连接两点的线表示连接相应两地的桥,如图,有2个奇点,所以该图可以一笔画,即可以一次不重复地走遍这七座桥.例如右下图的走法.EDCBA【例6】 有一个邮局,负责21个村庄的投递工作,右图中的点表示村庄,线段表示道路.邮递员从邮局出发,怎样才能不重复地经过每一个村庄,最后回到邮局?分析:图中有两个奇点,所以该图可以一笔画,但因为邮局所在点为奇点,所以要一笔画就不可能回到邮局.又图中A,B,C,D,E,F,G,H,I,J十点均有4条线段与之相连,如果我们将上图一笔画的话,就要经过以上十点各两次,这也不满足题目的要求,所以要将这些点相连的线段去掉一些,使得与这些点相连的线段均只有两条,并且将两个奇点也变成只有两条线段与之相连,这样得到的图形即可一笔画,又只经过每个点一次,并且可以回到邮局,一种可行路线如下:邮局I JHGF E D C B A 邮局邮局【例7】 右图是某博物馆的平面图,相邻两个展厅之间有一扇门相通,每一个展厅都有一门通往馆外.问参观者能否不重复地一次穿过每一扇门?若能,请找出一条可行路径;若不能,请说明理由.如果允许关闭某一扇门,问参观者能否不重复地穿过每一扇开着的门?分析:我们把展厅A,B,C,D,E 及馆外F 看成某个图中的点,把两个展厅之间的门看作是连接表示这两个展厅的点的线.根据题中条件知,馆外F 与A ,B ,C ,D ,E 各展厅相通,这样将点F 与点A ,B ,C ,D ,E 用线连接;展厅A 与展厅B ,C ,D 相通,将点A 与点B ,C ,D 用线连接;展厅B 除与A 相通外,它还与D ,E 展厅相通,将B 与D ,E 连接;除此之外,展厅C ,D 相通,展厅D ,E 相通,将点C ,D 连接,再将点D ,E 连接(如图a).于是本题要解决的问题就变成了能否将图a 一笔画的问题.可以看出:图a 中共有六个点,其中有四个奇点,它们分别为C ,D ,E ,F ,由一笔画的规律可知,图a 不能一笔画.也就是说,参观者不能够不重复地一次穿过每一扇门.如果允许关闭某一扇门,这相当于在图a 中去掉一条线,那么参观者就有可能不重复地一次穿过每一扇门.我们知道,在图a 中有四个奇点C ,D ,E ,F 为了把图a 改成一笔画图形,我们设法减少奇点个数,使奇点数变为两个.为此,我们可以去掉一条连接两个奇点的线,如去掉E 与F 间的连线,相应的图a 就变成了图b .在图b 中,除了原来的C 和D 是奇点外,其余点全部是偶点,故图b 可以一笔画.其中一种画法为:C →F →D →E →B →F →A →B →D →A →C →D .上面的分析表明,如果关闭连接E 、F 两展厅之间的门,参观者就可以不重复地一次穿过每一扇开着的门. 本题与七桥问题类似,只是将行人过桥换成了参观者穿过每一扇门.我们将这个问题转化为一笔画问题来研究.[前铺]右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走? FFF F E C D BA EB A分析:我们将每个展室看成一个点,室外看成点E ,将每扇门看成一条线段,两个展室间有门相通表示两个点间有线段相连,于是得到下图.能否不重复地穿过每扇门的问题,变为下图是否一笔画问题.EDC BA图中只有A ,D 两个奇点,是一笔画,所以答案是肯定的,应该从A 或D 展室开始走. 【例8】 已知长方体木块的长是80厘米,宽40厘米,高80厘米(如右图),并且要求蜘蛛在爬行过程中只能前进,不能后退,同一条棱不能爬两次.请问这只蜘蛛最多要爬行多少厘米?分析:图中八个顶点均为奇点,所以不能一笔画,要使其能一笔画,至少要去掉三条棱,使上图只有两个奇点,就可以满足一笔画的条件.长方体的棱长总和一定,(80+80+40)×4=800(厘米),因此去掉的三条棱越短,蜘蛛爬过的距离就越远.所以我们去掉三条棱长为40厘米的棱,于是可知,蜘蛛爬行的最远距离为: 800-40×3=680(厘米).蜘蛛的爬行路径为:G →F →C →D →G →H →A →B →E →H(如右图).[注意]这是一个立体图形,它有八个顶点,我们把长方体的棱看作顶点与顶点之间的连线,蜘蛛只能前进不能后退,并且每一条棱不能爬两次,这实质上是一个一笔画问题.【例9】 右图是某小区的街道分布图,街道长度如图所示(单位:公里),图中各点表示不同楼的代号.一辆垃圾清扫车从垃圾站(垃圾站位于C 楼与D 楼之间的P 处)出发要清扫完所有街道后仍回到垃圾站,问怎样走路线最短,最短路线是多少公里?分析:为了少走冤枉路和节省时间,题目中要求最短路线,根据一笔画原理,我们知道一笔画路线就是最短路线.本题要求清扫车从P点出发,仍回到P 点.通过观察上图可知,图中有六个奇点,根据一笔画规律可知,清扫车想清扫完所有街道而又不走重复的路是不可能的.要使清扫车从P 点出发,最后仍回到P 点,就必须把图中所有的奇点都变成偶点,即在两奇点之间添加一条线.在实际问题中,就是清扫车在哪些街道上重复走的问题,由于每条街道的长度不同,因此需要我们考虑清扫车重复走哪条街道才使总路线最短.为使六个奇点都变成偶点,我们可以有下图中的四种方法表示清扫车所走的重复路线,其中填虚线的地方表示的是重复路线.重复的路程分别为:图a :2×2+3=7;图b :3+4×2=11;图C :3×3=9; 图d :3+6×2=15.显然,重复走的路线最短,总路程就最短.从上述计算中就可找到最短路线图,即下面四个图中的图a .408080H G F ED C BA804080H GFED CBA图b 图a图d图c在图a 中,所有点均为偶点,是一笔画图形.清扫车可按如下路径走:P →D →G →D →E →F →G →H →L →H →C →B →L →M →A →B →C →P ,全程为:(1+2+4+2)×2+3×5+2×2+3=40(公里).【例10】 邮递员李文投送邮件的街道以及街道的长度如右图所示(单位:千米),每天小李要从邮局出发,走遍所有街道后回到邮局.请你帮他设计一条最短路线,并计算出这条路线有多少千米?分析:本题仍可以用一笔画图形的方法来解决.在图a 中共有六个奇点E ,F ,G ,H ,I ,J ,把这些奇点配对,每对之间用虚线连接(如图a),其中要用到D 点,这样图中就没有奇点了,从而可以不重复地走遍所有的街道.由于邮递员李文要重复走一些路段,因此重复走的路越短越好,即添上去的重复线段的总长度越短越好.在图a 中H 与E 之间有重叠,这样势必会增加李文所走路程的长度,应作调整.经调整后,将重叠部分去掉便得图b .在图b 的圈形闭路IHGJI 中,I ,J ,G ,H 各点没有连线时是奇点,连线后变成偶点,增加长度为50×2=100千米.而如果连IJ 和HG ,增加的长度仅为10×2=20,由此可知图b 需继续作调整,改成图c ,这种连接方法是最好的,它使李文行走的路线最短.根据以上分析,为了保证添上去的线段之和最短,应遵循下面的两条原则:(1)连线不能有重叠的线段;(2)在每一个圈形闭路上,连线长度之和不能超过 这个闭路总圈长的一半.经过分析可以知道,图c 的连接方法能使邮递员李文行走路线最短,而且能保证李文从邮局出发又回到邮局.这时他的行走路线为:邮局→A →I →J →I →H →G →H →E →D →F →D →G →J →B →C →D →E →邮局 他行走的全程为: (50+15)×4+20×4+10×6+20×2=440(千米).图a图b图c[小结]本题中采用的方法叫做“奇偶点图上作业法”,用这种方法来确定最短路线比较简便实用.此方法可以用下面的口诀来描述:画出路线图,确定奇偶点;奇点对对连,连线不重叠;闭路添连线.不得过半圈.[巩固]右图是某地区街道的平面图,图上的数字表示那条街道的长度.清晨,洒水车从A 出发,要洒遍所有的街道,最后再回到A.问:如何设计洒水路线最合理? 分析:这又是一个最短路线的问题.通过分析可以知道:在洒水路线中,K 是中间点,因此必须成为偶点,这样洒水车必须重复走KC 这条边(如下左图).至此,奇点的个数并未减少,仍是6个.容易得出,洒水车必须重复走的路线有:GF 、IJ 、BC.即洒水路线如下右图.全程45+3+6=54(里).1. (例1)判断下列各图能否一笔画.图aG I H F ECD BA图bF ED CBA分析:图a 中九个点全是偶点,因此可以一笔画,其中一种画法为:A →F →B →G →C →H →D →E →H →l →→F →G →l →E →A .图b 中A ,B ,C ,D 四个点均为奇点,故不可以一笔画.图c 中,只有A,C 为奇点,故可一笔画.其中一种画法为:A →D →E →C →H →N →G →M →F →A →B →C .2. (例3)下列各图至少要用几笔画完?分析:(1)4笔;(2)4笔;(3)2笔;(4)1笔;(5)1笔;(6)1笔.3.(例6)右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?分析:把每个展室看作一个结点,整个展厅的外部也看作一个点,两室之间有门相通,可以看作两点之间有边相连.这样,展厅的平面图就转化成了我们数学中的图,一个实际问题也就转化为这个图(如下图)能否一笔画成的问题了,即能否从A出发,一笔画完此图,最后再回到A.上图(b)中,所有的结点都是偶点,因此,一定可以以A作为起点和终点而一笔画完此图.也即游人可以从入口进,一次不重复地穿过所有的门,最后从出口出来.下面仅给出一种参观路线:A→E→B→C→E→F→C→D→F→A.4.(例7)一辆清洁车清扫街道,每段街道长1公里,清洁车由A出发,走遍所有的街道再回到A.怎样走路程最短,全程多少公里?分析:清洁车走的路径为: ABCNPBCDEFMNEFGHOLMHOIJKPLJKA. 即:清洁车必须至少重复走4段1公里的街道,如下图.最短路线全程为28公里.5.(例10)一个邮递员的投递范围如右图,图上的数字表示各段街道的长度.请你设计一条最短的投递路线,并求出全程是多少?分析:邮递员的投递路线如下图,即:路线为:ABCDEDOBOMNLKLGLNEFGHIMOJIJA.最短路线的全程为39+9=48.。
苏教版二年级下册奥数培优 第10讲 一笔画成
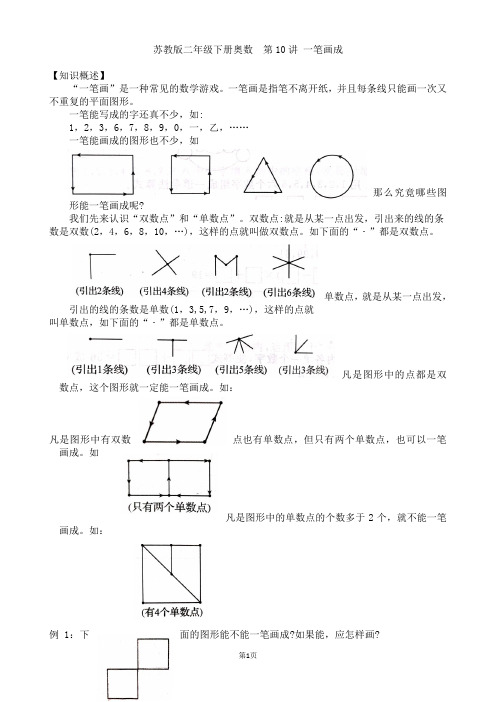
苏教版二年级下册奥数第10讲一笔画成【知识概述】“一笔画”是一种常见的数学游戏。
一笔画是指笔不离开纸,并且每条线只能画一次又不重复的平面图形。
一笔能写成的字还真不少,如:1,2,3,6,7,8,9,0,一,乙,……一笔能画成的图形也不少,如那么究竟哪些图形能一笔画成呢?我们先来认识“双数点”和“单数点”。
双数点:就是从某一点出发,引出来的线的条数是双数(2,4,6,8,10,…),这样的点就叫做双数点。
如下面的“・”都是双数点。
单数点,就是从某一点出发,引出的线的条数是单数(1,3,5,7,9,…),这样的点就叫单数点,如下面的“・”都是单数点。
凡是图形中的点都是双数点,这个图形就一定能一笔画成。
如:凡是图形中有双数点也有单数点,但只有两个单数点,也可以一笔画成。
如凡是图形中的单数点的个数多于2个,就不能一笔画成。
如:例1:下面的图形能不能一笔画成?如果能,应怎样画?练习一:1.下面两个图形能一笔画成吗?如果能,请一笔画成功。
2.下面的图形能不能一笔画成?如果能,应怎样画?3.下面的图形能不能一笔画成?为什么?例2:下面的图形能不能一笔画成?如果能,应该怎样画?练习二:1.下面的图形能不能一笔画成?如果能,应该怎样画?如果不能,请说明理由。
2.下面的图形能不能一笔画成?如果能,应该怎样画?3.下面的图形能不能一笔画成?如果能,应该怎样画?例3:有一条河,河中有两个小岛,河上有7座桥,把这两个岛与河岸联系起来,能不能不重复地走遍七座桥,最后又回到出发点?练习三:1.下图是一个迷阵图,箭头指出了迷阵的入口和出口。
请你画线表示从入口进入迷阵,从出口走出来。
能不能走通?2.下图是某展览馆的平面图,相邻两个展室之间有一个门相通,每个展室都有一扇门通往馆外。
一个参观者怎样走才能不重复地走过每一扇门?如果这种走法不存在,应关闭展览室的哪扇门才能实现上述走法?3.下图中有11个邮递员的投递点,邮递员叔叔要向这11个地点送信,邮递员能不能不重复地一次走遍各个点?如果能应怎样走?例4:下面的图形中有6个单数点,因此不能一笔画成功。
第10讲 一笔画成(数学游戏)-二年级奥数下册同步精讲精练(西师大版)

191第十讲 一笔画成(数学游戏)ʌ知识概述ɔ一笔画 是一种常见的数学游戏㊂一笔画是指笔不离开纸,并且每条线只能画一次又不重复的平面图形㊂一笔能写成的字还真不少㊂如:1㊁2㊁3㊁6㊁7㊁8㊁9㊁0㊁一㊁乙㊁ 一笔能画成的图形也不少,如:那么究竟哪些图形能一笔画成呢?我们先来认识 双数点 和 单数点 ㊂双数点:就是从某一点出发,引出来的线的条数是双数(2,4,6,8,10, ),这样的点就叫双数点㊂如下面的 ㊃ 都是双数点㊂单数点,就是从某一点出发,引出的线的条数是单数(1,3,5,7,9, ),这样的点就叫单数点,如下面的 ㊃ 都是单数点㊂凡是图形中的点都是双数点,这个图形就一定能一笔画成㊂如:凡是图形中有双数点也有单数点,但只有两个单数点,也可以一笔画192成㊂如:凡是图形的单数点的个数多于2个,就不能一笔画成㊂如:例题精学例1 下面的图形能不能一笔画成?如果能,应怎样画?ʌ思路点拨ɔ 图中共有7个交点,其中有6个点是2条线段的交点,1个点是4条线段的交点,因此都是双数点,可以一笔画成㊂画法如下图㊂同步精练1.下面两个图形能一笔画成吗?如果能,请一笔画成功㊂2.下面的图形能不能一笔画成?如果能,应怎样画?3.下面的图形能不能一笔画成?为什么?193194例2 下面的图形能不能一笔画成?如果能,应该怎样画?ʌ思路点拨ɔ 这个图形中有6个交点,其中A ,B ,C ,D 四个点都是双数点,都有4条线相交;E ,F 这两个点都是单数点,都有3条线相交㊂这个图形的单数点不多于2个,所以能一笔画成㊂画法:从一个单数点开始,到另一个单数点结束㊂E ңD ңA ңB ңC ңD ңC ңF ңB ңA ңE ңF F ңB ңC ңD ңA ңB ңA ңE ңD ңC ңF ңE同步精练1.下面的图形能不能一笔画成?如果能,应该怎样画?如果不能,请说明理由㊂2.下面的图形能不能一笔画成?如果能,应该怎样画?3.下面的图形能不能一笔画成?如果能,应该怎样画?195例3 有一条河,河中有两个小岛,河上有7座桥,把这两个岛与河岸联系起来,能不能不重复地走遍七座桥,最后又回到出发点?ʌ思路点拨ɔ 我们可以把这个七桥图形中的岸和岛看作点,而桥可以看作连接这些点的一条线㊂问题 能不能不重复地走遍这七座桥 ,实际上是 下面的图形能不能一笔画成功㊂A 点是左边的岛,D 点是右边的岛,C 点是北岸,B 点是南岸,C D 上有两座桥,B D 上有两座桥㊂图中的4个点都是单数点,不能一笔画成,所以不能不重复地走遍这七座桥㊂同步精练1.下图是一个迷阵图,箭头指出了迷阵的入口和出口㊂请你画线表示从入口进入迷阵,从出口走出来㊂能不能走通?1962.下图是某展览馆的平面图,相邻两个展室之间有一个门相通,每个展室都有一扇门通往馆外㊂一个参观者怎样走才能不重复地走过每一扇门?如果这种走法不存在,应关闭展览室的哪扇门才能实现上述走法?3.下图中有11个邮递员的投递点,邮递员叔叔要向这11个地点送信,邮递员能不能重复地一次走遍各个点?如果能应怎样走?197例4 下面的图形中有6个单数点,因此不能一笔画成功㊂但只要给下图加两条线,这个图形就能一笔画成功了㊂怎样加线?ʌ思路点拨ɔ 由于图中有6个单数点,因此不能一笔画成,如果只有两个单数点就能一笔画成了㊂在两个单数点之间连线,这两个单数点就成为双数点,画两条线就可以使4个单数点变为4个双数点,只剩下两个单数点了㊂加线方法如下:同步精练1.下图中九个点代表9棵果树,一个园丁推着水车从A 点出发,能不能给每一棵树浇上水而不走重复路线?(B 点㊁C 点为灌水的地点)2.下面的图形能不能用一笔画成功?如果能,应该怎样画?3.奥运会五环图能不能一笔画成功?如果能,可以怎样画?198练习卷一㊁填空题㊂1.下面的交点是单数点还是双数点?2.下图中有( )个交点,( )个双数点,( )个单数点,( )一笔画出(填 能 或 不能 )㊂3.下图中有( )个交点,( )个双数点,( )个单数点,( )一笔画出(填 能 或 不能 )㊂二㊁问答题㊂1.下图能不能一笔画出?如果能,应该怎样画?2.一只小虫从A 点出发,能不能不走重复路线一次走到B 点?如果能,应该怎样走?1993.小华和爸爸分别从公园的两个入口进入,谁能一次不重复地走完所有的路?4.下面的图形能不能一笔画成?为什么?如果能一笔画成,请标出起点和终点㊂三㊁解决问题㊂1.一个居民小区有四幢楼房,围墙把四幢楼房围起来,只有东㊁南㊁西㊁北四个门进出小区,小区的路有3横3竖,有一幢楼还有一条过道,把这幢楼分成两部分,人可以从过道通过㊂一个人能不能从东门进入小区,不走重复路线,一次把每条路都走遍?如果能,应该怎样走?如果不能,应从哪个门进去?200 2.园林里浇花的王大叔要到下图中的各点(字母处)浇花,他怎样走才能不重复地一次走遍每条小路?四㊁操作题㊂给下图加最少的线,使这个图形能一笔画成功㊂练习卷1.4鸡鹅兔(后三空或填鹅鸭兔)2.(1)小猴36(2)小兔18(3)23.4.(1)卡通人物唐老鸭米老鼠蝙蝠侠孙悟空哪吒喜欢人数/人2312159 (2)孙悟空唐老鸭蝙蝠侠第十讲一笔画成(数学游戏)例1图中的7个交点都是双数点,所以能一笔画成㊂[同步精练]1.(1)10个交点都是双数点,可以一笔画成㊂307308(2)有4个单数点,不能一笔画成㊂2.只有2个单数点,能一笔画成,画法是:从一个单数点出发,到另一个单数点为终点㊂3.有4个单数点,不能一笔画成㊂例2 这个图形只有两个单数点,所以能一笔画成㊂画法为从一个单数点开始,到另一个单数点结束㊂如:E ңD ңA ңB ңC ңD ңC ңF ңB ңA ңE ңF[同步精练]1.有4个单数点,不能一笔画成㊂2.如下图,只有2个单数点,能一笔画成,从一个单数点出发,以另一个单数点为终点㊂3.都是双数点,能一笔画成㊂例3 用A 点表示左边的岛,D 点表示右边的岛,C 点表示北岸,B 点表示南岸,把题目转化成下图㊂因为图中4个交点都是单数点,不能一笔画成,所以不能不重复地走遍这七座桥㊂309[同步精练]1.能走通,图略㊂2.走法不存在㊂如果关闭C ㊁D 间,D ㊁E 间及D ㊁F 间这三个门,参观者就可无重复地走过每扇门㊂下面是其中的一种走法:F ңC ңA ңD ңB ңA ңB ңE ңF ㊂3.图中只有两个单数点,能一笔画成㊂画法:③ң④ң②ң①ң③ң⑩ңң⑨ң⑩ң⑧ң⑨ң⑦ң⑧ң⑤ң⑦ң⑥ң⑤ң②例4 把左上角两个单数点连线,把右下角两个单数点连线,这4个单数点都成为双数点㊂图中只剩下2个单数点,就能一笔画成了㊂[同步精练]1.能不走重复路线,方法不唯一,如:2.4个点都是双数点,能一笔画成㊂3.8个点都是双数点,能一笔画成㊂310练习卷一㊁1.双数单数双数单数2.1266不能3.770能二㊁1.有4个双数点,没有单数点,能一笔画成㊂2.只有两个单数点,能一笔画成㊂从AңB走法如下:3.图中只有两个单数点,能一笔画成,爸爸的进入点是双数点,不能一次不重复地走完所有的路,小华的进入点是单数点,能一次不重复地走完所有的路㊂4.(1)能(2)不能(3)不能三㊁1.东门处是双数点,不能不走重复路线一次把每条路都走遍㊂从西北㊁北门进去都可以㊂2.可以从A点出发,以E点为终点;也可以从E点出发,以A点为终点㊂四㊁最少加2条线,A E和B E,就可以一笔画成㊂311第十一讲 操作图形(图形的切㊁拼)例1[同步精练]1.方法很多㊂如2.3.例2[同步精练]1.。
二年级奥林匹克数学 一笔画问题习题

二年级一笔画问题习题及答案1.下面的各个小图形都是由点和线组成的。
请你仔细观察后回答:①与一条线相连的有哪些点?②与二条线相连的有哪些点?③与三条线相连的有哪些点?④与四条线或四条以上的线相连的有哪些点?2.若把与奇数条线相连的点叫做奇点,把与偶数条线相连的点叫偶点,那么请你回答:①有0个奇点(即全部是偶点)的图形有哪些?②有2个奇点的图形有哪些?③有4个或4个以上奇点的图形有哪些?用心爱心专心1④连通图形有哪些?不连通图形有哪些?3.如果笔在纸上连续不断、又不重复地一笔画成的图形叫一笔画,自己动笔实际画画看,然后回答:①哪些图形能够一笔画成?②哪些图形不能一笔画成?4.把以上各向联系起来看,进行归纳,找出规律然后回答:①如果把各部分连结在一起的图形叫做连通图形,那么能一笔画出的图形必定是连通图形;而不是连通图形必定不能一笔画出。
这句话说得对吗?②有0个奇点(即全部是偶点)的连通图形一定可以一笔画出来(画时可以以任一点为起点,最后必能回到该点),这句话对吗?③只有两个奇点的连通图形也能一笔画出来,但要注意画时必须以一个奇点为起点,而以另一个奇点为终点,这句话对吗?④奇点个数超过两个的图形不能一笔画出来。
这句话对吗?5.从画图过程的角度,进一步理解所发现的一些规律。
解答1.解:见下图①与一条线相连的点有:(在图中画成黑点,下同。
)用心爱心专心2②与两条线相连的点有:③与三条线相连的点有:④与四条及四条以上的线相连的点有:5)、()、();10 0 2.解:①有个奇点(即全部是偶点)的图形是:(1 2 ②有个奇点的图形是:7);)、()、()、(( 236用心爱心专心3③有4个奇点的图形是:(4)、(9)有6个奇点的图形是:(8)。
④(1)~(10)是连通图形,(11)不是连通图形。
3.解:①一笔画有:(1)、(5)、(10)、(2)、(3)、(6)、(7)。
②不能一笔画出的图形是:9)、()、(11)。
小学奥数教程:奇妙的一笔画_全国通用(含答案)

知识点拨所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次, 不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢? 下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏. 我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1) 能一笔画出的图形必须是连通的图形;( 2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; ( 3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; ( 4)奇点个数超过两个的图形,一定不能一笔画.多笔画问题: 我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于 任意的连通图来说,如果有 2n 个奇点 ( n 为自然数 ) ,那么这个图一定可以用 n 笔画成.例题精讲模块一、判断奇偶点例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些 点是偶点?9 个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜, 要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出 发,不走重复路线就 (填“能”或“不能 ”)完成任务 .考点】一笔画问题 【难度】 2 星 关键词】华杯赛,六年级,初赛,第 解析】 最少需要 3 种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要 使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。
不走重复路线不能完 成插旗的任务,因为本题共有 6 各奇点。
答案】 3 种颜色,不能4-1-5. 奇妙的一笔画考点】一笔画问题 解析】 奇 点: D 答案】奇点: D 【难度】 2星HJ 【题型】解答 偶点: A B 偶点: A B CE FGI CE FGI哪些点是奇点?例 2】 同学们野营时建了 【题型】填空10考点】一笔画问题 难度】 2 星 【题型】解答 例 3】 判断下列图 a 、图 b 、图 c 能否一笔画.解析】 第 1 个能, 2、3 不能 答案】第 1个能, 2、3 不能例 6 】 右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个 进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?考点】一笔画问题 【难度】 2 星 【题型】解答解析】 将图形中的 6个区域看成 6 个点,每个门看成连结他们的线段,显然 6个点都是偶点,所以有人能一次不重复的走过所有的门.答案】能巩固】右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走? 考点】 解答案】一笔画问题 【难度】 2 星图 a 能,因为有 2 个奇点, 图 a 能 b 不能,因为图形不是连通的, 图c 能,因为因为图中全是奇点 a 能,a 能, c 能例 4】 下面图形能不能一笔画成?若果能,应该怎样画?考点】一笔画问题 【难度】 2 星 解析】 图 1 能 因为图中全是偶点; 图2能 因为图中全是偶点;图 3 不能因为有 4 个奇点。
小学奥数教程:奇妙的一笔画_全国通用(含答案)

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答 【解析】 奇点: D H J O 偶点:A B C E F G I 【答案】奇点: D H J O 偶点:A B C E F G I【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.【考点】一笔画问题 【难度】2星 【题型】填空 【关键词】华杯赛,六年级,初赛,第10题 【解析】 最少需要3种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。
小学二年级奥数 一笔画

小学奥数:一笔画【专题简析】1.概念:一笔画是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。
2.图中的点可分两大类:(1)双数点:从这点出发的线的数目是双数的,叫双数点。
(2)单数点:从这点出发的线的数目是单数的,叫单数点。
3.规律----一个图形能否一笔画成,关键在于图中单数点的多少。
(1)凡是图形中没有单数点的一定可以一笔画成。
(2)凡是图形中只有两个单数点,一定可以一笔画成,画时必须从一个单数点为起点,最后以另一单数点为终点。
(3)凡是图形中单数点的个数多于两个时,此图肯定是不能一笔画成。
【题目】1 判断下面图形中哪些点是单数点哪些点是双数点。
单数点( ) ( ) ( ) ( ) ( ) ( ) ( )双数点( ) ( ) ( ) ( ) ( ) ( ) ( )单数点( ) ( ) ( )双数点( ) ( ) ( )ABEA BCB单数点( ) ( ) ( ) 双数点( ) ( ) ( )单数点( ) ( ) ( )双数点( ) ( ) ( )单数点( ) ( ) ( )双数点( ) ( ) ( )由以上图形可以得出:BCAC单数点()()()双数点()()()单数点()()()双数点()()()由以上图形可以得出:C DEF单数点()()()双数点()()()单数点()()()双数点()()()由以上图形可以得出:欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习资料等等打造全网一站式需求。
小学二年级奥数--一笔画问题(1)

二年级奥数一笔画问题(1)知识定位一笔画的问题源于著名的“哥德斯堡七桥问题,故事发生在18世纪的哥德斯堡城。
流经那里的一条河中优两个小岛,还有七座桥把这两个小岛与河岸联系起来,那里风景优美,游子众多,在这美丽的地方,人们议论着一个有趣的问题:一个游人怎样才能不重复地一次走遍七座桥,最后又回到出发点呢?一笔画问题就是从这个问题演变而来的,也是小学奥数中较为经典较为有趣的内容。
知识梳理1. 什么是一笔画?就是指能一笔画出的话,也就是说笔不离纸能一次把它画出来,图上的每条边都要画到而且不能重复。
2. 什么是奇点,什么是偶数奇点就是表示从这个点出发的线段为奇数条;偶数就是表示从这个点出发的线段为偶数条。
3.判断可以一笔画的原则:(1)图形为连通图,(2)奇数点的个数为0或者2.4. 怎么画一笔画奇数点个数为0的时候,起点与终点在任意的同一个点上。
当奇数点个数为2的时候,起点与终点分别在两个奇点上。
5. 判断几笔画笔画数=奇点数/2例题精讲【题目】你能试着用一笔把下列图形画出来吗?如果可以,说说你是怎样画的?【题目】下图中,说一说哪些点是偶点,哪些点是奇点,再画一画看看它们能不能一笔画出?【题目】下列图形能一笔画成吗?为什么?并试着画一画。
【题目】下图中的每一个图形,最少需要几笔画出?【题目】奥迪车的标志是四个环扣在一起的样子:这个图形能不能一笔画画出呢?A.能B.不能C.不确定D.以上答案都不对【题目】下图中有( )个奇点?【选项】A.7个B.6个C.5个D.4个【题目】下列图形能一笔画成吗?下面说法正确的是( )【选项】A.能一笔画出,因为有偶数个奇点。
B.能一笔画出,因为没有奇点。
C.不能一笔画出,因为有6个奇点。
D.不能一笔画出,因为有4个奇点。
【题目】下面这座小屋子能不能一笔画出呢?下面说法正确的是( )【选项】A.可以一笔画,我已经画出来啦 B.不可以一笔画,画不出来C.不清楚可不可以一笔画D.以上答案都不对【题目】( )笔才能画出?【选项】A.4 B.2 C.3 D.1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第10讲学习一笔画
【专题简析】
一笔画,就是从图形某点出发,笔不离开纸,而且每条线段都只画一次不重复。
它是一种有趣的数学游戏。
那么,哪些图形不能一笔画成,哪些图形可以一笔画成呢?
一个图形能否一笔画成,关键在于单数点的多少,有2个或0个单数点的图形就能够一笔画成,单数点在一笔画中只能作为起点和终点。
【例题1】
一些平面图形是由点和线构成的,这里的“线”可以是线段,也可以是一段曲线,请自己画一些图研究每个点和线的连接情况。
思路导航:请小朋友仔细观察下列各图中的点,他们分别与几条线相连。
①②③④
(1)与一条线段相连的点有:
(2)与两条线段相连的点有:
(3)与三条线段相连的点有:
(4)与四条线段相连的点有:
归纳:把和一条、三条、五条等单数条线连得点叫做单数点;把和两条、四条、六条、八条等双数条线连的点叫双数点,每个图中的点要么是单数点,要么是双数点。
练习1
1.任意找一个平面图形,数一数图中有几个单数点,几个双数点。
2.下面图形中有哪几个单数点?
B
3.数一数下面图形中有几个双数点,分别是哪些点?
B
【例题2】
下面的图形能不能一笔画成?如果能,应该怎样画?
A
C C (1) O (2)
B D
F (3)
D
【思路导航】图(1)中A 、B 、C 、D 、O 五个点都是双数点,所以这个图形可以一笔画成。
画时可以从任意一点出发。
图(2)中A 、C 、D 、F 四个点都是双数点,B 和E 两个点是单数点,所以这个图形也可以一笔画成。
画时要从单数点出发,最后回到另一个单数点。
图(3)中A 、D 是双数点,B 、C 、E 和F 四个点是单数点,单数点的个数超过了两个,这个图形不能一笔画成。
1.下面的图形能不能一笔画成,如果能,请说明画法,如果不能,请说明理由
(1)(2)
2.下列图形能一笔画成吗?为什么?
3.观察下列图形,哪个图形可以一笔画成?怎么画?
【例题3】
下图是某地区所有街道的平面图,甲、乙两人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达C.那么两人谁先到达?
C
思路导航:题中要求两人必须走遍所有街道,最后到达C.仔细观察,可以发现图中有两个单数点:A、C。
这就是说:甲可以从A点出发,不重复地走遍所有街道,最后到达C.而B点是双数点,从B点出发的乙则不行。
因此,甲所走的路程正好等于所有街道的总和,而乙所走的路程一定比这个总和多,所以甲最先到达C.
解:甲最先到达C.
A
1.下图是某新村小区主干道平面图。
甲、乙两人同时分别从A 、B 出发,以相同的速度走遍所有的主干道,最后到达C.问谁能最先到达C?
2. 甲、乙两辆车同时以相同的速度分别从A 、B 出发,哪辆车能最先行驶完所有的路程?
B
3.一只蚂蚁分别从A 点和B 点出发,爬遍所有的小路。
如果每次爬行的速度相同,那么从哪一点出发所用的时间少?
【例题4】
下图(图1)能否一笔画成,若不能,你能用什么方法把它改成能够一笔画成的图形?
(1) (2)
思路导航:此图共有9个点,其中5个点是双数点,4个点是单数点,由于超过两个单数点,因此不能一笔画成。
要想改为一笔画成,关键在于减少单数点数目(把单数点的个数减少到0或2),所以只要在任意两个单数点间连上线,就可以一笔画,有时也可以将多余的两个单数点间的连线去掉,改成一笔画。
解:图(1)有4个单数点,不能一笔画成。
要改成一笔画成,如图(2) 练习4
1.将下图改成一笔画。
1. 2.
3.在一个小区中有一些路,每个圆柱表示邮筒(如下图),邮递员叔叔每次送信时,总是没法走过每一条路而又不重复,你知道为什么吗?如果请你给小区加一条路来解决这个问题,你准备把这条路加在哪儿?请你动手画一画。
【例题5】
邮递员叔叔要给一个居民小区送信(如图),怎么走才能少走重复路,使每天走的路尽可能短?
A
G
H D B
F
思路导航:图中一共有九个点,其中单数点有2个(点D 和点F ),因此能一次不重复走过所有的路,但必须从这两个单数点中的一个出发,再回到另一个单数点。
解:邮递员叔叔只能从点D (或点F )出发,走过所有的路后,再回到点F(或点D) . 练习5
1.下图是以个小区的中心花园的平面图,你能一次不重复地走完所有的路吗?入口和出口应该设在哪儿呢?
2.园林工人在花园里浇花,怎样才能不重复地走遍每条小路?
3. 下图是“儿童乐园”平面图,出、入口应分别设在哪里才能不重复地走遍每条路?可以怎么走?
D C
A
B
【拓展提高】
1、下面的图形能不能一笔画成?为什么?如果能,应该怎样画?
2、给下面的图形添一条线,使它能够一笔画成。
3、小明和玲玲玩“过木桥”的游戏(如下图),他们谁能不走重复的路?
小明
玲玲
4、在王大爷家的花园中有一些路(如下图),王大爷每次给花浇水时,总是没法走过每一条路而又不重复,你知道为什么吗?如果请你给花园加一条路来解决这个问题,你准备把这条路加在哪儿?请你动手画一画。
