01-1 分析力学基础
合集下载
[物理]分析力学基础
![[物理]分析力学基础](https://img.taocdn.com/s3/m/cff17a52f46527d3240ce040.png)
若主动力为有势力，须将势能 V 表示为广义坐标的函数。
4. 建立拉氏方程并加以整理，得出N个二阶常微分方程。
5. 求出上述一组微分方程的积分。
质量为m1、半径 为 r 的均质圆轮在水平面 上纯滚，轮心与刚性系数 为k 的弹簧相连。均质杆 AB长度为l ，质量为m2 。 求：系统的运动微分方程。 解：1、系统的约束为完整约束， 主动力为有势力。
V Qk 0 qk
d T T V ( ) 0 k dt q qk qk
称为拉格朗日函数（动势）
引入
L T V
因为势能只是广义坐标的函数，故
d L k dt q
L 0 q k
此即为主动力为有势 力的拉格朗日方程。
于是，虚位移原理的表达式成为
V 0
上式说明，在势力场中，具有理想约束的质点系的平 衡条件为质点系的势能在平衡位置处一阶变分为零。 如果用广义坐标 q1，q2， ，qN 表示质点系的位置, 则质点系的势能可以写成广义坐标的函数，即
V V q1，q2， ，qN
根据广义力表达式，在势力场中可将广义力 QN 写成 用势能表达的形式，即
V Qk 0 (k 1， 2， ，N ) qk
在势力场中具有理想约束的质点系的平衡条件 是势能对于每个广义坐标的偏导数分别等于零。
杆OA和AB以铰链相 连，O端悬挂于圆柱铰链
上，杆长OA=a ， AB=b
。杆重和铰链的摩擦都忽
略不计。今在点A和B分
别作用向下的铅锤力 FA 和 FB ，又在点B作用一 水平力 F 。试求平衡时 j1，j 2 与 F ，FA，FB
3、用广义坐标表示虚位移——广义虚位移
ri ri q1 , q2 ,, qN , t i 1,2, ,n
4. 建立拉氏方程并加以整理，得出N个二阶常微分方程。
5. 求出上述一组微分方程的积分。
质量为m1、半径 为 r 的均质圆轮在水平面 上纯滚，轮心与刚性系数 为k 的弹簧相连。均质杆 AB长度为l ，质量为m2 。 求：系统的运动微分方程。 解：1、系统的约束为完整约束， 主动力为有势力。
V Qk 0 qk
d T T V ( ) 0 k dt q qk qk
称为拉格朗日函数（动势）
引入
L T V
因为势能只是广义坐标的函数，故
d L k dt q
L 0 q k
此即为主动力为有势 力的拉格朗日方程。
于是，虚位移原理的表达式成为
V 0
上式说明，在势力场中，具有理想约束的质点系的平 衡条件为质点系的势能在平衡位置处一阶变分为零。 如果用广义坐标 q1，q2， ，qN 表示质点系的位置, 则质点系的势能可以写成广义坐标的函数，即
V V q1，q2， ，qN
根据广义力表达式，在势力场中可将广义力 QN 写成 用势能表达的形式，即
V Qk 0 (k 1， 2， ，N ) qk
在势力场中具有理想约束的质点系的平衡条件 是势能对于每个广义坐标的偏导数分别等于零。
杆OA和AB以铰链相 连，O端悬挂于圆柱铰链
上，杆长OA=a ， AB=b
。杆重和铰链的摩擦都忽
略不计。今在点A和B分
别作用向下的铅锤力 FA 和 FB ，又在点B作用一 水平力 F 。试求平衡时 j1，j 2 与 F ，FA，FB
3、用广义坐标表示虚位移——广义虚位移
ri ri q1 , q2 ,, qN , t i 1,2, ,n
分析力学基础(1)
只要ρ ≠ 0，则detP ≠ 0。因此存在反函数 detP 因此存在反函数
曲线坐标系
曲线坐标系的定义
y ρ = x + y , ϕ = arctan , z = z x
2 2
三族坐标曲面： 三族坐标曲面： 1. ρ = 常数，以 z轴为中心线的圆柱面 常数， 2. ϕ = 常数，包含 z轴的垂直于oxy平面的半平面 常数， 3. z = 常数，与oxy平面平行的平面 常数，
比较两式得到
P P =H
T
2
曲线坐标系
正交曲线坐标系 正交曲线坐标系
P P =H 两点注意： 两点注意：
T
2
1. PT P一般不等于单位矩阵 I。 一般不等于单位矩阵 2. 只有 H 2=I ，此时 e 是单位正交基向量时， 单位正交基向量时， 正交基向量时 P才是正交矩阵。
第1章 分析力学的基本概念
约 束
约
束
约 束－物体运动所受到的限制 定常约束与非定常约束
定常约束－约束方程中不显含时间的约束： 定常约束－约束方程中不显含时间的约束：
fα ( ri ) =0,i =1,2,⋅⋅⋅, n( 质点数)；α =1,2,⋅⋅⋅, s( 约束数)
非定常约束－约束方程中显含时间的约束： 非定常约束－约束方程中显含时间的约束：
i2
曲线坐标系
曲线坐标系的定义
基向量
∂r ei = ∂q ∂qi
(i =1,2,3)
ei 过M点沿坐标曲线[qi]的切线方向 沿坐标曲线[ ei 是单位向量吗？ 是单位向量吗？ ei (i = 1, 2, 3)在空间任意点M处构成局部坐标架 3)在空间任意 在空间任意点
曲线坐标系
曲线坐标系的定义
曲线坐标系
曲线坐标系的定义
y ρ = x + y , ϕ = arctan , z = z x
2 2
三族坐标曲面： 三族坐标曲面： 1. ρ = 常数，以 z轴为中心线的圆柱面 常数， 2. ϕ = 常数，包含 z轴的垂直于oxy平面的半平面 常数， 3. z = 常数，与oxy平面平行的平面 常数，
比较两式得到
P P =H
T
2
曲线坐标系
正交曲线坐标系 正交曲线坐标系
P P =H 两点注意： 两点注意：
T
2
1. PT P一般不等于单位矩阵 I。 一般不等于单位矩阵 2. 只有 H 2=I ，此时 e 是单位正交基向量时， 单位正交基向量时， 正交基向量时 P才是正交矩阵。
第1章 分析力学的基本概念
约 束
约
束
约 束－物体运动所受到的限制 定常约束与非定常约束
定常约束－约束方程中不显含时间的约束： 定常约束－约束方程中不显含时间的约束：
fα ( ri ) =0,i =1,2,⋅⋅⋅, n( 质点数)；α =1,2,⋅⋅⋅, s( 约束数)
非定常约束－约束方程中显含时间的约束： 非定常约束－约束方程中显含时间的约束：
i2
曲线坐标系
曲线坐标系的定义
基向量
∂r ei = ∂q ∂qi
(i =1,2,3)
ei 过M点沿坐标曲线[qi]的切线方向 沿坐标曲线[ ei 是单位向量吗？ 是单位向量吗？ ei (i = 1, 2, 3)在空间任意点M处构成局部坐标架 3)在空间任意 在空间任意点
曲线坐标系
曲线坐标系的定义
分析力学基础
牛顿的《原理》只提供了分析质点受力与运动的原型，对于复杂的力学系 统，甚至对一个简单的刚体的运动方程也还没有弄清楚。刚体的运动方程是 1765年由欧拉（Euler）最后弄清楚的。 按照当时已有的力学知识,要分析一个稍许复杂的机构,例如一个有五级 齿轮的传动系统的运动,也还是无能为力的.如果拿这个问题去请教牛顿,牛顿 只会处理自由质点运动,不会处理刚体运动,何况还是带约束的呢.而转去请教 欧拉呢?他不得不将整个系统化归为五个”隔离体”即五个刚体,分别列出五个 刚体的运动方程,而不同刚体之间又有作用力和反作用力的耦合,所以得面对 数十个方程联立的微分方程组.这样处理问题是太复杂了. 拉格朗日自有他的高招,他将这个系统简化为一个广义坐标的系统,因 为这个虽然有五个轮子的系统只要有一个参数便可以描述它的例如随便以 其中某一个轮子的转角为参数,这个参数知道了,整个齿轮系统的状态也便 知道了.然后再计算当系统动起来后系统的动能.这时便可以列出一个广义 坐标满足的二阶方程,这是何等的简便啊! 拉格朗日是怎么作到这一点的呢?
O
x
1
自由度： 2
a A
2
广义坐标： 1 2
二、受力分析：
y
b
B
F
计算广义坐标 1 、 2 对应 的 广义力
FA
FB
以下分两种方法进行计算
O
x
1
第一种方法： 解析法
xi yi zi Qk X i q Yi q Z i q i 1 k k k
即用质点系的平衡条件是： 所有的广义力都等于零
利用广义坐标表示的平衡条件求解实际问题时，关健在 于如何表达其广义力。
通常求广义力的方法有两种：
方法一：是采用公式计算
分析力学基础第一章(3,4节)
1 3
m2 2l 2q
m2lxcosq
m2 gl
sinq
0
FI a
F
MIC FI
MIC Ra FI
受力分析 FI ma
M IC
1 2
m R2
虚位移分析 x R
x
解：运动分析，系统自由度N=1
a R
动力学普遍方程
n
Fi FIi
ri 0
i 1
Fx 3FIx 2M IC 0
Fx 3max max 0
F 4ma x 0 x 0 F 4ma 0
3、系统的动能：T 1 m x2 y2 z2 2
4、系统的广义力：
z
mg y
W Qxx Qyy Qzz x
x 0 y z 0 y 0 x z 0 z 0 x y 0
W 0 Qx 0 W 0 Q y 0
W mgz
d dt
T qj
T q j
Qj
j 1, , k
B
O mg
C
A
mg
§ 1-3 动力学普遍方程
解：加速度分析，添加惯性力 建立动力学普遍方程
M IO
1 2
m R2O
O O aO
mg
B
AO
C
A
aCt mgaO
M IC
1 12
m
l
2
AO
B
M IO
FIO FIC mRO
FItC
m
l 2
AO
FIO O
FItC
FIC C
M IC
A
mg
mg
§ 1-3 动力学普遍方程
A
M
C1
Oq
q 90 30
分析力学基础
➢ 系统的动能
分析力学基础
T 1 {q}T [M ]{q} 2
✓在定常约束情况下，动能T是广义速度的二次齐次函 数（或称二次型） ✓系统的动能T除了广义速度全等于零外，它总是大于 零，因此动能T具有恒正的性质。 ✓在线性代数里称T这样的函数为正定二次型，相应地 称它的系数矩阵[M]是正定的。
✓对于正定的矩阵，它的全部主子行列式的值都大于零。
k
mk rk rk
动能T将是广义速度的零次、一次和二次函数
➢ 动能和势能
分析力学基础
讨论约束和时间t无关的定常约束情况，各点的坐标
只是广义坐标的函数而不显含t
rk
rk
(q1
,
q
2
,,
qn
)
rk rk
n il
n
rk
j1 qi
rddk rtk
in1rkqrki
n
qi
i 1
rk q j
qi q j
n
mij qi q j
j 1
由于系数mij仅是广义座标的函数，由上式可见，在定 常约束的情况下，动能T是广义速度的二次齐次函数。
在微振动理论中，若广义座标一律按平衡位置取作原
点，则振动过程中qi是偏离平衡位置的小量，将系数 mij在平衡位置附近按台劳级数展开得
mij
mij
0
n s 1
mij qs
✓ 但这一方法是按照各质点或刚体的运动来建立方程的，为此常 常要引入那些未知的约束反力。
✓ 对于某些复杂的系统，采用这样的方法来建立力或力矩同速度、 加速度等运动量之间的矢量关系不仅显得复杂，而且引入了那些 我们不必知道的未知约束反力。
➢ 引言
分析力学基础
第一章 分析力学的基本概念
xC
C点的速度：
y1 y2 x2 x1 x1 x2 y2 y1
第25页
应用力学研究所
李永强
§1.1 分析力学的研究对象&约束
几何约束&运动约束 运动约束
n
i Ai i Bi j Ci k
i 、Ai 、 Bi 、Ci 、A均为各质点速度和位臵的函数
约束方程 可积分的运动约束
不可积分的运动约束
其他类型的运动约束
应用力学研究所 李永强 第22页
§1.1 分析力学的研究对象&约束
几何约束&运动约束 运动约束
可积分的运动约束
应用力学研究所 李永强 第8页
§1.1 分析力学的研究对象&约束
分析力学的研究对象__ 分析力学的研究对象
质点系力学：质点个数n=1,2,…,∞。 故研究对象包括质点力学和刚体力学 近代把分析力学的研究方法扩充到研究流体力学、
固体力学形成连续介质分析力学。
应用力学研究所
李永强
第9页
§1.1 分析力学的研究对象&约束
分析力学的研究对象__ 分析力学的研究方法
运用纯粹数学分析的方法研究质点系的机械运动。
数学分析：高等数学、常微分方程、微分几何、拓扑学、实变函数、… 1788年，Lagrange：《Mé canique Analylique》
拉格朗日在书的序言中曾自豪地说“本书中无一图，在我所要阐明的
方法既不需要作图，也不需要任何几何或力学的论述，而仅需要按照统一 规定的步骤进行代数运算。爱好分析的人将会高兴地看到并感谢我使力学
应用力学研究所 李永强 第21页
§1.1 分析力学的研究对象&约束
C点的速度：
y1 y2 x2 x1 x1 x2 y2 y1
第25页
应用力学研究所
李永强
§1.1 分析力学的研究对象&约束
几何约束&运动约束 运动约束
n
i Ai i Bi j Ci k
i 、Ai 、 Bi 、Ci 、A均为各质点速度和位臵的函数
约束方程 可积分的运动约束
不可积分的运动约束
其他类型的运动约束
应用力学研究所 李永强 第22页
§1.1 分析力学的研究对象&约束
几何约束&运动约束 运动约束
可积分的运动约束
应用力学研究所 李永强 第8页
§1.1 分析力学的研究对象&约束
分析力学的研究对象__ 分析力学的研究对象
质点系力学：质点个数n=1,2,…,∞。 故研究对象包括质点力学和刚体力学 近代把分析力学的研究方法扩充到研究流体力学、
固体力学形成连续介质分析力学。
应用力学研究所
李永强
第9页
§1.1 分析力学的研究对象&约束
分析力学的研究对象__ 分析力学的研究方法
运用纯粹数学分析的方法研究质点系的机械运动。
数学分析：高等数学、常微分方程、微分几何、拓扑学、实变函数、… 1788年，Lagrange：《Mé canique Analylique》
拉格朗日在书的序言中曾自豪地说“本书中无一图，在我所要阐明的
方法既不需要作图，也不需要任何几何或力学的论述，而仅需要按照统一 规定的步骤进行代数运算。爱好分析的人将会高兴地看到并感谢我使力学
应用力学研究所 李永强 第21页
§1.1 分析力学的研究对象&约束
1.1分析力学基本概念
⑥ 1834年，哈密顿提出哈密顿正则方程。
⑦ 1843年，哈密顿提出哈密顿原理。
分析力学的特点
牛顿力学 1、真实空间、一般坐标 2、侧重“力”，“加速 度” 3、以牛顿三定律为基础 分析力学 1、数学空间、广义坐标 2、能量（L函数、H函数） 3、哈密顿原理(公理)为基础
4、运用微积分
4、运用变分
几何约束方程的一般形式为
2 2 xA yA r 2 ＯＡ，ＡＢ距离一定 2 2 2 ( xB x A ) ( y B y A ) l yB 0
f r ( x1 , y1 , z1 , , xn , yn , zn ) 0
y
B( xB , yB ) v r B
x x A A
yA yA zA 0 xB xA l sin q cos yB y A l sin q sin z l cosq
B
广义坐标对时间的导数称为与该广义坐标对应的广义速度, 写成
a dqa dt q
7.位形空间：
牛顿方程是描述物体机械运动的唯一方式吗？
ma F
牛顿方程
d 2x m 2 Fx dt
Hamilton方程 px 2 H T V V ( x) 2m H H x , px px x
Lagrange方程
L T V 1 2 mx V ( x) 2 d L L 0 dt x x
三、双面约束与单面约束 同时限制质点某方向及相反方向运动的约束称为双面约束（不可解约束）。 只能限制质点某方向的运动，而不能限制相反方向运动的约束称为单面约束 （可解约束）。并非约束面是单面还是双面。约束是对运动方向而言的。
此方向不受限制，可缩短
⑦ 1843年，哈密顿提出哈密顿原理。
分析力学的特点
牛顿力学 1、真实空间、一般坐标 2、侧重“力”，“加速 度” 3、以牛顿三定律为基础 分析力学 1、数学空间、广义坐标 2、能量（L函数、H函数） 3、哈密顿原理(公理)为基础
4、运用微积分
4、运用变分
几何约束方程的一般形式为
2 2 xA yA r 2 ＯＡ，ＡＢ距离一定 2 2 2 ( xB x A ) ( y B y A ) l yB 0
f r ( x1 , y1 , z1 , , xn , yn , zn ) 0
y
B( xB , yB ) v r B
x x A A
yA yA zA 0 xB xA l sin q cos yB y A l sin q sin z l cosq
B
广义坐标对时间的导数称为与该广义坐标对应的广义速度, 写成
a dqa dt q
7.位形空间：
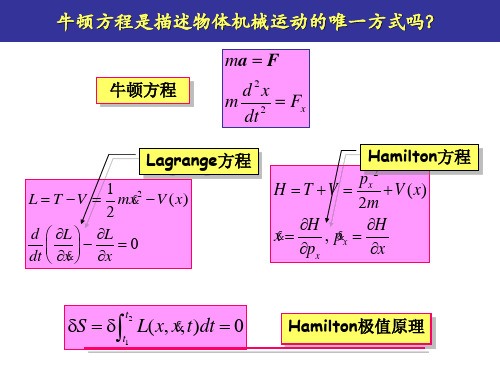
牛顿方程是描述物体机械运动的唯一方式吗？
ma F
牛顿方程
d 2x m 2 Fx dt
Hamilton方程 px 2 H T V V ( x) 2m H H x , px px x
Lagrange方程
L T V 1 2 mx V ( x) 2 d L L 0 dt x x
三、双面约束与单面约束 同时限制质点某方向及相反方向运动的约束称为双面约束（不可解约束）。 只能限制质点某方向的运动，而不能限制相反方向运动的约束称为单面约束 （可解约束）。并非约束面是单面还是双面。约束是对运动方向而言的。
此方向不受限制，可缩短
§1.1分析力学
第一章分析力学到现在为止，我们所研究的力学问题，基本上是用牛顿运动定律来求解的。
但用牛顿运动运动定律来求质点组的运动问题时，常常需要求解大量的微分方程组。
如果质点组受到约束，则因约束反力都是未知的，所以并不能因此而减少，甚至是增加了问题的复杂性。
十八、十九世纪，随着工业革命的迅速发展，在工程技术上迫切需要解决的又正好是这一类问题。
因此迫切需要寻求另外的方法来处理这一问题。
1788年，拉格朗日写了一本大型著作《分析力学》，在这一本著作中，完全用数学分析的方法来解决所有的力学问题，而无需借助以往常用的几何方法，全书一张图也没有。
在此基础上逐步发展成为一系列处理力学问题的新方法，称之为分析力学。
分析力学以拉格朗日和哈密顿等所建立的变分原理为基础，将力学的基本定律表示为分析数学的形式。
通过分析的方法来解决任意力学体系的运动问题，它所涉及的量是标量。
而牛顿力学涉及的量如力、速度、加速度等多为矢量。
由此看来，分析力学和牛顿力学只是同一个力学领域应用不同的数学描述而已。
对于自由质点和简单问题，两种方法无优劣（lie）之分，对复杂问题，分析力学的优越性就体现出来了。
分析力学是从能量的观点来研究力学问题，因而具有更广泛的应用价值。
它广泛的应用于结构分析、机器动力学与振动、航天力学、多刚体系统、机器人动力学以及各种工程技术领域，也可推广应用于连续介质力学和相对论力学。
许多新兴学科，如量子力学、相对论、电动力学、连续介质力学、天体力学、统计力学等等，都可以用到分析力学的理论和方法。
但是，由于分析力学中的数学推理较多，在历史上也发生过一些不良倾向，容易使人忘记力学的物理实质，对此我们应当引以为戒。
§1.1 广义坐标一、基本概念1、力学体系n 个相互作用着的质点构成的集合体。
2、 位形质点系各质点在空间的位置的有序集合，它决定了质点的位置和形状，也就是位形是质点系在空间的位置状态。
3、约束限制质点自由运动的条件。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1.1 分析力学基础 1.1.1 直角坐标与广义坐标
燕山大学
Yanshan University
平面直角坐标：用平面上的长度值表示平面上一点位置的坐标。 平面直角坐标系oxy。 三维直角坐标：在二维直角坐标系（oxy）的基础上,再添加一个 垂直于x轴、y轴的坐标轴，称为z轴。x轴、y轴、z轴满足右手定 则，则坐标系oxyz为三维直角坐标。 广义坐标：能决定系统几何位置的彼此独立的量。
Q2 P L sin t cos 0
(3)系统运动微分方程
d L dt q j L Qj q j j 1, 2, , n
燕山大学
Yanshan University
Q1 P sin t 0 Q2 P L sin t cos 0
两个相互啮合的光滑表面所构成的约束
燕山大学
Yanshan University
两曲面相互啮合的约束条件：两曲面不能脱
开，也不能相互嵌入；则有： δrN1=δrN2
N1与N2两者互为作用力与反作用力：
N1= -N2 由于δrT1及δrT2与约束力N1及N2相垂直，因 而约束力在该方向不做功。在虚位移下，约 束力所做的虚功为：
x1 l1 x2 l2
特点：从运动的观点来研究系统的静力平衡问题。 优点：只考虑外力，不必考虑支反力，应用方便。
虚位移
燕山大学
Yanshan University
虚位移：约束允许的微小位移。 (1)虚位移是微小的、即时发生的，即不考虑它们发生的过程。
(2)独立的虚位移数等于系统的自由度数。
对于图示杠杆系统，杠杆两端的虚位移δx1和δx2。由于杠杆是单自 由度系统，因此δx1和δx2只有一个是独立的。
理想约束
质点上的合力必然为零：
燕山大学
Yanshan University
设具有N个质点的系统处于静力平衡状态，则作用在其中每一个
Ri=0，i=1，2，…N
合力Ri可分解为两部分： 主动力Fi——主动施加的外力以及质点之间主动作用的内力；
力所做虚功之和为零：δW= －kxδx＋mgδy=0
(1)
此系统为单自由度系统，取θ角为广义坐标，由几何关系可 得：x=L(1-cosθ) y=Lsinθ。 取微分：
x L sin
y L cos
代入(1)式整理得:
mg (1 cos ) t g kL
广义坐标下的虚位移原理
燕山大学
Yanshan University
根据机械系统自由度数目，刚性构件机械系统可以划分为： 单自由度机械系统； 多自由度机械系统。
机械系统的组成、研究内容
燕山大学
Yanshan University
原 动 机
传动机构
执行机构
机 械 系 统
驱 动 力 工作阻力
运动规律？
研究内容：研究刚性构件机械系统在力作下的运动规律。
N N n
ri 上式求全微分，得： ri qj j 1 q j
n
i=1,2,,N
N Fi ri 交换求和次序： W q j j 1 i 1
n
q j 0
r 令： Q j Fi i q j i 1
N
j 1, , = 2, n
只有δqj≠0，其它广 义坐标的虚位移都 为0，非保守力所做 的虚功。
Qj——非保守力所对应的广义力。 根据虚位移相互独立的特点， Qj 为： Q j
W j
qj
j 1, 2, , n
Lagrange方程应用实例 例1 图示线性弹簧、光滑平面的质 块——单摆系统。列出图示系统运 动微分方程。 解：不考虑滑块、摆杆的弹性变形； 不考虑弹簧质量，则该系统为两自由 度数。取滑块位移x、 摆杆摆角θ作 为广义坐标。 (1)系统势能、动能、Lagrange函数
d L dt q j L 0 q j j 1, 2, , n
燕山大学
Yanshan University
L为Lagrange函数：L=T－V (2)非保守力系统Lagrange方程
d L dt q j L Qj q j j 1, 2, , n
燕山大学
Yanshan University
具有N个质点的系统。设其自由度为n，广义坐标q1，q2，…，qn。 各质点向量表示为：ri=ri(q1，q2，…，qn) i=1,2,…,N。
ri qj 0 由虚位移原理： W Fi ri Fi i 1 i 1 j 1 q j
F l1 F2l2 1
Bernoulli采用一种新的观点来研究这一问题，他假 定杠杆在F1、F2作用下已处于静力平衡状态，然后 让它产生一个约束条件所允许的微小位移，即绕O点 转过一个微小角度θ，杠杆两端位移分别为：
F1、F2两力所作的功： F1 x1 F2 x2 Fl1 F2l 2 0 1
W Q j q j 0
j 1
n
由于各广义坐标的取值是相互独立的和任意的，上式成立条件是： j=1,2,…,n
δqj的所有系数为零：Qj=0
广义坐标下的虚位移原理
静平衡的必要和充分条件是其n个广义力均为零，即： Qj=0 j=1,2,…,n。
广义力定义为: Q j
燕山大学
Yanshan University
(2)广义力
燕山大学
Yanshan University
点M坐标：
xM x s l sin yM l cos
广义坐标x的虚位移为δx
Q1 x P sin t x 0
广义坐标θ的虚位移为δθ
Q1 P sin t 0
Q2 P sin tL cos 0
L MLx cos ML2 L kx x
d L 2 x ML cos x sin ML dt
L MLx sin MgL sin
( M m) ML( cos 2 sin ) kx P sin t x 2 ML MLx cos MgL sin PL sin t cos
1 1 1 2 MLx cos ML2 2 kx 2 MgL cos L T V ( M m) x 2 2 2 L d L ( M m) x ML cos ( M m) ML cos 2 sin x x dt x
第1章 刚性构件机械系统动力学 刚性构件机械系统：由刚性构件所构成的机械系统。 假设： (1)忽略运动副间隙的影响； (2)忽略运动副中的摩擦。 当机械系统各构件的刚度 较大且运转速度较低时，将 机械系统简化为刚性系统是 合理的；对于一般的非精密 机械系统，忽略运动副间隙 和摩擦能够满足实际应用的 要求。
系统广义坐标数＝系统自由度数。
例如 双摆系统 用广义坐标表示双摆系统质点的直 角坐标。 系统自由度数：2。 取θ1，θ2作为广义坐标。 质点m1，m2的直角坐标x1，y1， x2，y2可以用θ1、θ2表示。
燕山大学
Yanshan University
x1 L1 sin 1 y1 L1 cos 1
燕山大学
Yanshan University
取滑块质心为重力势能零点。 系统势能：
1 2 V kx MgL cos 2
系统动能
摆锤坐标x，y： xM x s l sin
yM l cos
燕山大学
Yanshan University
摆锤速度：
xM x l cos yM l sin
x2 L1 sin 1 L2 sin 2 y2 L1 cos 1 L2 cos 2
1.1.2 虚位移原理
燕山大学
Yanshan University
虚位移原理是J.Bernoulli于1717年提出的用于确定系统静平衡条件 的准则。 杠杆静力平衡条件: 例如：杠杆系统
约束力fi——由约束产生的被动力，包括支反力和约束产生的内力。
Ri = Fi + fi = 0， i=1，2，…N 合力Ri在虚位移δri下所做虚功为零：
δW= Ri•δri=0，i=1，2，…N
Fi•δri +fi•δri=0，i=1，2，…N 对下标i求和，得 质点系静力 平衡条件！
F r f r
虚位移原理应用实例
燕山大学
Yanshan University
例1 如图所示，不考虑刚性杆的质量，线性弹簧原长为x0。当弹簧 未伸长时，刚性杆处于水平位置，如图中虚线所示。试以虚位移原
理确定其处于静平衡位置时的θ角。
解：系统组成：连杆、重物mg、弹簧 外力：弹簧恢复力与重力。 在平衡位置附近，令系统产生虚位移δx、δy。弹性力与重
燕山大学
Yanshan University
两个光滑表面1、2在o点相互接触，如 果不考虑摩擦力，则两曲面之间的作用 力N1，N2沿接触点的公法线方向。 N1——曲面2对曲面1的作用力； N2——曲面1对曲面2的作用力； δr1、δr2——两曲面的虚位移； δrT1、δrT2——虚位移δr1、δr2的切向分 量； δrN1、δrN2——虚位移δr1及δr2的法向分 量。
广义坐标下的虚位移原理：在理想约束情况下，n自由度系统处于
ri Fi q i 1 j
N
j 1, , = 2, n
W Q j q j 0
j 1
n
(1)广义力Qj的量纲与广义坐标qj的量纲有关。由于Qjδqj的乘积为功