7.2动生电动势感生电动势感生电场普遍环路定理
电磁感应与麦克斯韦方程组汇总

o
x x+dx X 电动势i.
解:设定回路的正方向如图,此即i的正方向.
任意时刻t的磁通:
m
BdS
BdS 2a 0I bdx 0Ib ln 2
a 2 x
2
感生电动势:
i
dm dt
0b ln 2
2 dI dt
0bI0ln 2 sin t 2
[思考] 若金属框以速率v右移,在t时刻正处于
频率
1022
1015 1T HZ 1012 1G HZ 109 1M HZ 106 1K HZ 103
射线
X 射线 紫外线 可见光 红外线
微波 雷达
高频电视 调频广播
无线电射频 电力传输
波长
10 13
0
1A 10 9 1nm
10 6 1μ m
10 2 1cm 100 1m
103 1km 105
法拉第麦克斯韦之后,人类进入电气化时代
磁通量变化引起的电动势: 感应电动势
典型情形:
①
B 不变,回路变.
(动生)
②回路不变, B 变. (感生)
法拉第定律
i
dm dt
n
B
L, i
计算:设定回路L的方向(此即i的正方向)
右手螺旋 法线方向n
m>0
法拉第定律 i (>0, 则实际方向与所
设方向一致;<0, 则相反)
Note:
N匝线圈:
⑵自感电动势
i
dm dt
L
dI dt
(i与I两者正方向一致)
B~
I~,i
Notes: ①上式仅适用于无铁磁介质 (L不随I 变化)的情形.
② L i
大学物理电磁学公式总结汇总

大学物理电磁学公式总结汇总普通物理学教程大学物理电磁学公式总结,下面给大家整理了关于大学物理电磁学公式总结,方便大家学习大学物理电磁学公式总结1定律和定理1. 矢量叠加原理:任意一矢量可看成其独立的分量的和。
即:=∑ (把式中换成、、、、、就分别成了位置、速度、加速度、力、电场强度和磁感应强度的叠加原理)。
2. 牛顿定律:=m (或= );牛顿第三定律:′= ;万有引力定律:3. 动量定理:→动量守恒:条件4. 角动量定理:→角动量守恒:条件5. 动能原理:(比较势能定义式:)6. 功能原理:A外+A非保内=ΔE→机械能守恒:ΔE=0条件A 外+A非保内=07. 理想气体状态方程:或P=nkT(n=N/V,k=R/N0)8. 能量均分原理:在平衡态下,物质分子的每个自由度都具有相同的平均动能,其大小都为kT/2。
克劳修斯表述:不可能把热量从低温物体传到高温物体而不产生其它影响。
开尔文表述:不可能从单一热源吸取热量,使之完全变为有用的功而不产生其它影响。
实质:在孤立系统内部发生的过程,总是由热力学概率小的宏观状态向热力学概率大的状态进行。
亦即在孤立系统内部所发生的过程总是沿着无序性增大的方向进行。
9. 热力学第一定律:ΔE=Q+A10.热力学第二定律:孤立系统:ΔS0(熵增加原理)11. 库仑定律:(k=1/4πε0)12. 高斯定理:(静电场是有源场)→无穷大平板:E=σ/2ε013. 环路定理:(静电场无旋,因此是保守场)θ2Ir P o Rθ1I14. 毕奥—沙伐尔定律:直长载流导线:无限长载流导线:载流圆圈:,圆弧:电磁学1. 定义:= /q0 单位:N/C =V/mB=Fmax/qv;方向,小磁针指向(S→N);单位:特斯拉(T)=104高斯(G)① 和:=q( + × )洛仑兹公式②电势:电势差:电动势:( )③电通量:磁通量:磁通链:ΦB=NφB单位:韦伯(Wb)Θ ⊕-q +qS④电偶极矩:=q 磁矩:=I =IS⑤电容:C=q/U 单位:法拉(F)乘自感:L=Ψ/I 单位:亨利(H)乘互感:M=Ψ21/I1=Ψ12/I2 单位:亨利(H)⑥电流:I = ; 乘位移电流:ID =ε0 单位:安培(A)⑦乘能流密度:2. 实验定律① 库仑定律:②毕奥—沙伐尔定律:③安培定律:d =I ×④电磁感应定律:ε感= –动生电动势:感生电动势:( i为感生电场)乘⑤欧姆定律:U=IR( =ρ )其中ρ为电导率3. 乘定理(麦克斯韦方程组)电场的高斯定理:( 静是有源场)( 感是无源场)磁场的高斯定理:( 稳是无源场)( 感是无源场)电场的环路定理:(静电场无旋)(感生电场有旋;变化的磁场产生感生电场)安培环路定理:(稳恒磁场有旋)(变化的电场产生感生磁场)4. 常用公式①无限长载流导线:螺线管:B=nμ0I② 带电粒子在匀强磁场中:半径周期磁矩在匀强磁场中:受力F=0;受力矩③电容器储能:Wc= CU2 乘电场能量密度:ωe= ε0E2 电磁场能量密度:ω= ε0E2+ B2乘电感储能:WL= LI2 乘磁场能量密度:ωB= B2 电磁场能流密度:S=ωV④ 乘电磁波:C= =3.0×108m/s 在介质中V=C/n,频率f=ν=波动学大学物理电磁学公式总结2概念(2113定义和相关公式)1. 位置矢量:,其5261在直角坐标系中:; 角位置:4102θ16532. 速度:平均速度:速率:( )角速度:角速度与速度的关系:V=rω3. 加速度:或平均加速度:角加速度:在自然坐标系中其中(=rβ),(=r2 ω)4. 力:=m (或= ) 力矩:(大小:M=rFcosθ方向:右手螺旋法则)5. 动量:,角动量:(大小:L=rmvcosθ方向:右手螺旋法则)6. 冲量:(= Δt);功:(气体对外做功:A=∫PdV)mg(重力) → mgh-kx(弹性力) → kx2/2F= (万有引力) → =Ep(静电力) →7. 动能:mV2/28. 势能:A保= –ΔEp不同相互作用力势能形式不同且零点选择不同其形式不同,在默认势能零点的情况下:机械能:E=EK+EP9. 热量:其中:摩尔热容量C与过程有关,等容热容量Cv 与等压热容量Cp之间的关系为:Cp= Cv+R10. 压强:11. 分子平均平动能:;理想气体内能:12. 麦克斯韦速率分布函数:(意义:在V附近单位速度间隔内的分子数所占比率)13. 平均速率:方均根速率:;最可几速率:14. 熵:S=KlnΩ(Ω为热力学几率,即:一种宏观态包含的微观态数)15. 电场强度:= /q0 (对点电荷:)16. 电势:(对点电荷);电势能:Wa=qUa(A= –ΔW)17. 电容:C=Q/U ;电容器储能:W=CU2/2;电场能量密度ωe=ε0E2/218. 磁感应强度:大小,B=Fmax/qv(T);方向,小磁针指向(S→N)。
动生电动势感生电动势感生电场普遍环路定理

THANKS FOR WATCHING
感谢您的观看
感应加热
感应加热器利用动生电动势对金属进 行加热。当金属在变化的磁场中时, 会在金属内部产生动生电动势,从而 产生电流并加热金属。
02 感生电动势
定义与产生机制
定义
当磁场发生变化时,会在导体中产生电动势。这个电动势被 称为感生电动势。
产生机制
磁场的变化会在导体中激发出电场,这个电场驱动导体中的 自由电荷移动,从而产生感生电动势。
感生电场的应用实例
电磁感应
当线圈中的磁场发生变化时,会在线 圈中产生感生电动势,进而产生电流。
磁记录
利用感生电场可以记录磁场的变化, 从而实现信息的存储和读取。
04 普遍环路定理
定理的表述与证明
表述
在磁场中,如果闭合回路的磁通量发生变化,那么就会产生电动势。这个电动势的大小等于回路的磁通量变化率 与回路的长度成正比。
证明
根据法拉第电磁感应定律和安培环路定律,通过引入磁场线穿过闭合回路的磁通量概念,可以推导出普遍环路定 理。
普遍环路定理的应用场景
电机工程
普遍环路定理是电机设计中的重 要理论依据,用于计算和预测电 机在不同工作状态下的电动势和
电流。
电力系统
在电力系统中,普遍环路定理用于 分析和计算电力传输过程中的电压 和电流变化,以确保电力供应的稳 定性和可靠性。
感生电动势的计算公式
公式
E = -dΦB/dt,其中E是感生电动势,ΦB是磁通量。
解释
这个公式表示,当磁通量发生变化时,就会产生感生电动势。负号表示电动势的 方向与磁通量变化的方向相反。
感生电动势的应用实例
01
02
03
感应炉
大学物理B-第十二章 电磁感应

电磁感应
产 生 机 理
i
d m dt
楞次定律 动生电动势
感生电动势
自感电动势
i (v B ) dl L B i dS S t
工业生产
12-3 自感和互感
互感电动势
一、自感电动势
自感系数 I(t) Φm
1.自感现象与自感系数 由于回路自身电流的变化,在回 路中产生感应电动势的现象。
N
ab a
I NIl a b ldr ln 2r 2 a
N B dS
s
dr
I
r
由互感系数定义可得互感为: Nl ab M ln I 2 a
l
a
b
I I I I
0
0
12-4磁场的能量与能量密度
I (t )
L
R
0
充电过程曲线
τ
t
I (t)
K2
麦克斯韦提出全电流的概念
I 全 I 传导 I D
全电流连续不中断的,构成闭合回路
ID
全电流安培环路定理
L H dl I 传导 I D dD d D dS D dS 位移电流 I D S t dt dt S
讨论: 1. 传导电流:电荷定向运动 2. 若传导电流为零
L
L
穿过S1 面 电流
穿过S2 面 电流
S1
I
+ + + +
S2
D
电流不连续 -
二、 全电流安培环路定理 S2 面电位移通量 D DS
极板间电位移矢量 D 位移电流
动生电动势和感生电动势

§6-2 动生电动势和感生电动势动生电动势:回路或其一部分在磁场中的相对运动所产生的感应电动势。
感生电动势:仅由磁场的变化而产生的感应电动势。
一 动生电动势图6 - 5 动生电动势动生电动势的产生可以用洛伦兹力来解释。
长为l 的导体棒与导轨构成矩形回路abcd 平放在纸面内,均匀磁场B 垂直纸面向里。
当导体棒ab 以速度v 沿导轨向右滑动时,导体棒内自由电子也以速度v 随之一起向右运动。
每个自由电子受到的洛伦兹力为B v F ⨯-)(=e ,方向从b 指向a ,在其作用下自由电子向下运动。
如果导轨是导体,在回路中将形成沿着abcd 逆时针方向的电流。
如果导轨是绝缘体,则洛伦兹力将使自由电子在a 端累积,从而使a 端带负电,b 端带正电,在ab 棒上产生自上而下的静电场。
当作用在自由电子上的静电力与洛伦兹力大小相等时达到平衡,ab 间电压达到稳定值,b 端电势比a 端高。
这一段运动导体相当于一个电源,它的非静电力就是洛伦兹力。
电动势定义为单位正电荷从负极通过电源内部移到正极的过程中,非静电力K 所作的功,即B v F K ⨯=-=e.动生电动势为ε⎰⎰+-⋅⨯=⋅=l B v l K d )(d ba .(6.4)均匀磁场情况:若v ⊥ B , 则有ε = B l v ;若导体顺着磁场方向运动,v // B ,则有 v ⨯ B = 0,没有动生电动势产生。
因此,可以形象地说,只有当导线切割磁感应线而运动时,才产生动生电动势。
普遍情况:在任意的恒定磁场中,一个任意形状的导线线圈L (闭合的或不闭合的)在运动或发生形变时,各个线元d l 的速度v 的大小和方向都可能是不同的。
这时,在整个线圈L 中产生的动生电动势为ε l B v d )()(⋅⨯=⎰L .(6.5)图6 - 6 洛伦兹力不作功洛伦兹力对电荷不作功:洛伦兹力总是垂直于电荷的运动速度,即v ⊥F v ,因此洛伦兹力对电荷不作功。
大学物理 马文蔚 课堂笔记15

已知 R, h, , B, dB/dt, 求 I 解 如图取一半径为r ,宽度为dr的圆环, 则
dB dB i E k dl dS dS L S dt S dt dB 因 和 S 平行 dt
圆环中的感生电动势的大小为
R
h
B
L
+ +
1 BL2 2
上海师范大学
i 方向
(点 P 的电势高于点 O 的电势) 4 /15
例2 一导线矩形框的平面与磁感强度为 B 的均匀磁场相垂直.在此矩形框
上,有一质量为 m 长为
§8.2
动生电动势和感生电动势
其值较之导线的电阻值要大得很多. 若开始时, 细导体棒以初速度 v0 沿如图
场方向垂直的平面上绕棒的一端转动;
解 如图所示,铜棒绕O点转动,
线元上产生的动生电动势为
+ + +
+ + + +B+ + + + +
d i ( v B) dl vBdl
L
整段铜棒上的电动势为
o v + + +
+ + O P
i
0
vBdl 0 lBdl
上海师范大学
14 /15
§8 -3
自感和互感
例1 如图是一长直密绕螺线管,长度为l, 横截面积为S, 线圈的总匝数为N,
管中均匀磁介质的磁导率为, 试求其自感L. (忽略边缘效应)
解 一般方法: 先设通有电流 I
螺线管密度(单位长度的线圈数) n=N/l,
求得 B
大学物理动生电动势和感生电动势

电场力 洛仑兹力
不存在 不存在
只可能是一种新型的电场力
10 - 2 动生电动势和感生电动势
第十三章电磁感应
1861年,麦克斯韦提出了感生电场的假设 变化的磁场在周围空间要激发电 场,称为感生电场。感生电流的产 生就是这一电场作用于导体中的自 由电荷的结果。
感生电场充当着产生感应电动势 的非静电力。
O
L
v
B
BvL sin
10 - 2 动生电动势和感生电动势
第十三章电磁感应
BvL sin
特例
L
B
v
v
B
v
B
0
BvL
10 - 2 动生电动势和感生电动势
第十三章电磁感应
非均匀磁场
例3
平动
一直导线CD在一无限长直电流磁场中作
切割磁力线运动。求:动生电动势。 解:方法一
R
10 - 2 动生电动势和感生电动势
第十三章电磁感应
例5. 匀强磁场B,导体棒OP绕OZ轴旋转,角 速度 , OP=b, 为已知 OZ轴∥ B 。求PO两端的电势差?
思路:d ( v B ) dl
vB cos dl
rB sin d l
e
f Ek v B e b Ek dl (v B) dl
a
平衡时
f Fe eEk
+ + + -+ + +
+ + + a+ +
+ + + f --
+ v
大学物理常用公式(电场磁场-热力学)
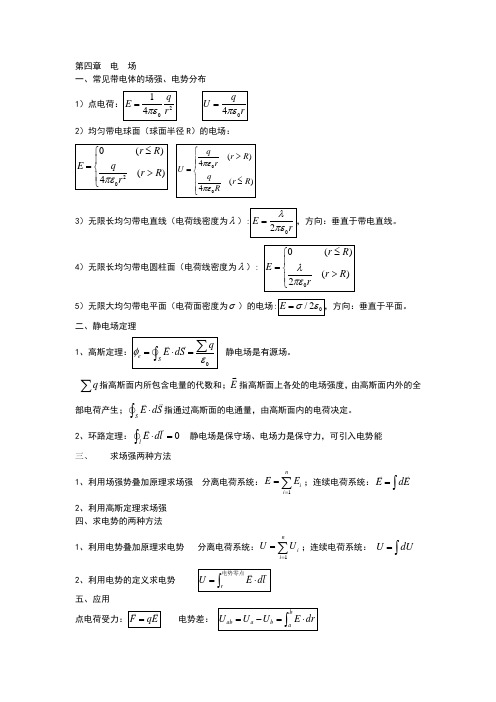
第四章 电 场一、常见带电体的场强、电势分布 1)点电荷:2014q E r πε=04q U rπε=2)均匀带电球面(球面半径R )的电场:200()()4r R E qr R r πε≤⎧⎪=⎨>⎪⎩00()4()4qr R r U q r R R πεπε⎧>⎪⎪=⎨⎪≤⎪⎩3)无限长均匀带电直线(电荷线密度为λ):02E rλπε=,方向:垂直于带电直线。
4)无限长均匀带电圆柱面(电荷线密度为λ): 00()()2r R E r R rλπε≤⎧⎪=⎨>⎪⎩5)无限大均匀带电平面(电荷面密度为σ)的电场:0/2E σε=,方向:垂直于平面。
二、静电场定理 1、高斯定理:0e Sq E dS φε=⋅=∑⎰静电场是有源场。
q ∑指高斯面内所包含电量的代数和;E指高斯面上各处的电场强度,由高斯面内外的全部电荷产生;SE dS ⋅⎰指通过高斯面的电通量,由高斯面内的电荷决定。
2、环路定理:0lE dl⋅=⎰ 静电场是保守场、电场力是保守力,可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统:1ni i E E ==∑;连续电荷系统:E dE =⎰2、利用高斯定理求场强 四、求电势的两种方法1、利用电势叠加原理求电势 分离电荷系统:1nii U U==∑;连续电荷系统: U dU =⎰2、利用电势的定义求电势 rU E dl =⋅⎰电势零点五、应用点电荷受力:F qE = 电势差: bab a b aU U U E dr =-=⋅⎰a由a 到b六、导体周围的电场1、静电平衡的充要条件: 1)、导体内的合场强为0,导体是一个等势体。
2)、导体表面的场强处处垂直于导体表面。
E ⊥表表面。
导体表面是等势面。
2、静电平衡时导体上电荷分布: 1)实心导体: 净电荷都分布在导体外表面上。
2)导体腔内无电荷: 电荷都分布在导体外表面,空腔内表面无电荷。
3)导体腔内有电荷+q ,导体电量为Q :静电平衡时,腔内表面有感应电荷-q ,外表面有电荷Q +q 。
高中物理动生电动势和感生电动势汇总

动生电动势和感生电动势法拉第电磁感应定律:只要穿过回路的磁通量发生了变化,在回路中就会有感应电动势产生。
而实际上,引起磁通量变化的原因不外乎两条:其一是回路相对于磁场有运动;其二是回路在磁场中虽无相对运动,但是磁场在空间的分布是随时间变化的,我们将前一原因产生的感应电动势称为动生电动势,而后一原因产生的感应电动势称为感生电动势。
注意:动生电动势和感生电动势的名称也是一个相对的概念,因为在不同的惯性系中,对同一个电磁感应过程的理解不同: (1)设观察者甲随磁铁一起向左运动:线圈中的自由电子相对磁铁运动,受洛仑兹力作用,作为线圈中产生感应电流和感应电动势的原因。
-动生电动势。
(2)设观察者乙相对线圈静止:线圈中的自由电子静止不动,不受磁场力作用。
产生感应电流和感应电动势的原因是运动磁铁(变化磁场)在空间产生一个感应(涡旋)电场,电场力驱动使线圈中电荷定向运动形成电流。
-感生电动势一、动生电动势导体或导体回路在磁场中运动而产生的电动势称为动生电动势。
动生电动势的来源:如图,运动导体内每个电子受到方向向上的洛仑兹力为:;正负电荷积累在导体内建立电场;当时达到动态平衡,不再有宏观定向运动,则导体 ab 相当一个电源,a 为负极(低电势),b 为正极(高电势),洛仑兹力就是非静电力。
可以使用法拉第定律计算动生电动势:对于整体或局部在恒定磁场中运动的闭合回路,先求出该回路的磁通F 与t 的关系,再将对t 求导,即可求出动生电动势的大小。
(2)动生电动势的方向可由楞次定律确定。
二、感生电动势处在磁场中的静止导体回路,仅仅由磁场随时间变化而产生的感应电动势,称为感生电动势。
感生电场:变化的磁场在其周围空间激发一种电场,称之为感生电场。
而产生感生电动势的非静电场正是感生电场。
感生电动势: 回路中磁通量的变化仅由磁场变化引起,则电动势为感生电动势 .若闭合回路是静止的,它所围的面积S 也不随时间变化。
感生电场与变化磁场之间的关系:(1)变化的磁场将在其周围激发涡旋状的感生电场,电场线是一系列的闭合线。
感生、动生电动势
v dx
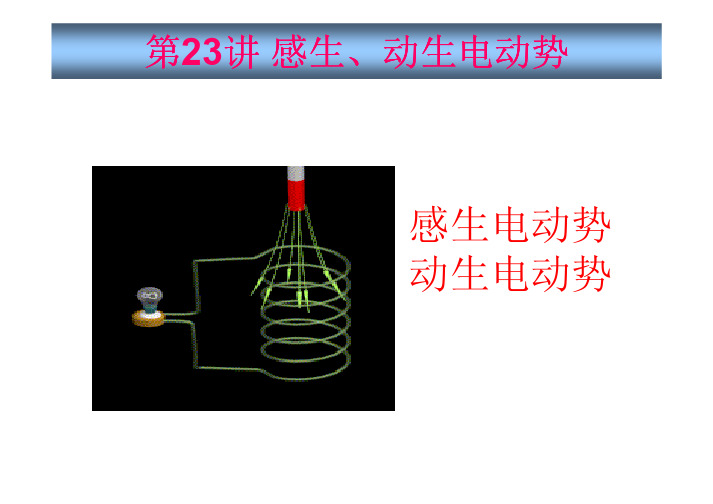
v 和 B 的夹角: θ1 = π / 2, V × B 与dx 的夹 的夹角:
二、动生电动势
r r r r r r fL r 由 f L = − e ( v × B ) 得: E k = =v×B −e + r r + r r r 代入 ε = ∫ Ek ⋅dl 得: ε = ∫ ( v × B ) ⋅d l
−
−
大小: 大小: ε =
r r − θ 1为 v与B的夹角; 的夹角;
dε i = E感dl cos θ
× × × × × × R × × × × × × × o h× × × r × θ × × ×θ B dl × L ×
r dB E感 = 由上题结果, 由上题结果,圆形区域内部的感生电场: 圆形区域内部的感生电场: 2 dt
−
ε i = ∫ dε i = ∫ E感dl cosθ
∫
L
动生电动势的求解可以采用两种方法: 动生电动势的求解可以采用两种方法:一是利用 一是利用 “动生电动势”的公式来计算; 的公式来计算;二是设法构成一种合理 的闭合回路以便于应用“法拉第电磁感应定律”求解。 求解。
三、应用动生电动势的解题方法
公式: 公式: ε
= ∫ vBdl sin θ1 cosθ 2
∫ vB dl sin θ
+
1
r r r θ 2为 v × B 与 d l 的夹角。 的夹角。
cos θ 2
方向: 方向:电动势方向从负极到正极。 电动势方向从负极到正极。 以上结论普遍成立。 以上结论普遍成立 。 如果整个回路都在磁场中运动, ,则在回路中产生的总 如果整个回路都在磁场中运动 r r r 的电动势为: 的电动势为: ε = ( v × B ) ⋅ d l
大学物理知识点归纳

大学物理第十一章:真空中的静电场一、电场强度:数值上等于单位正电荷在该点受到的电场力的大小,也等于单位面积电通量的大小(即电场线密度);方向与该点的受力方向(或者说电场线方向)一致。
二、电场强度的计算:a)点电荷的电场强度:b)电偶极子中垂线上任意一点的电场强度:(表示点到电偶极子连线的距离)c)均匀带电直棒:i.有限长度:ii.无限长(=0,):iii.半无限长:(,或者,)或三、电通量a)电场线:电场线上任意一点的切线方向与该点的电场强度E的方向一致,曲线的疏密程度表示该点电场强度的大小,即该点附近垂直于电场方向的单位面积所通过的电场线条数满足:电场中某点的电场强度大小等于该处的电场线密度,即该点附近垂直于电场方向的单位面积所通过的电场线条数。
b)静电场电场线的特点:1.电场线起于正电荷(或无穷远),终于负电荷(或伸向无穷远),在无电荷的地方不会中断;2.任意两条电场线不相交,即静电场中每一点的电场强度只有一个方向;3.电场线不形成闭合回路;4.电场强处电场线密集,电场弱处电场线稀疏。
c)电通量i.均匀电场E穿过任意平面S的电通量:ii.非均匀电场E穿过曲面S的电通量:四、高斯定理a)b)表述:真空中任何静电场中,穿过任一闭合曲面的电通量,在数值上等于该闭合曲面内包围的电荷的代数和除以;c)理解:1.高斯定理表达式左边的E是闭合面上处的电场强度,他是由闭合面内外全部电荷共同产生的,即闭合曲面外的电荷对空间各点的E有贡献,要影响闭合面上的各面元的同量。
2.通过闭合曲面的总电量只决定于闭合面内包围的电荷,闭合曲面外部的电荷对闭合面的总电通量无贡献。
d)应用:1.均匀带电球面外一点的场强相当于全部电荷集中于球心的点电荷在该点的电场强度。
2.均匀带电球面内部的电场强度处处为零。
五、电势a)静电场环路定理:在静电场中,电场强度沿任意闭合路径的线积分等于零。
b)电场中a点的电势:1.无穷远为电势零点:2.任意b点为电势零点:六、电势能:电荷在电场中由于受到电场作用而具有电荷中的电荷比值决定位置的能叫做电势能,七、电势叠加定理:点电荷系电场中任意一点的电势等于各点电荷单独存在该点所产生的电势的代数和。
气体动理论公式总结
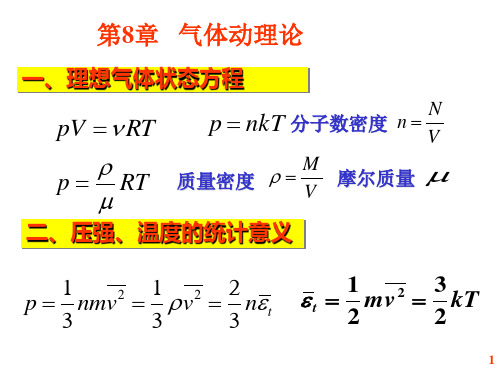
1.自由度i=t+r
单原子分子 i=t=3
刚性双原子 i=t+r=3+2 刚性三原子i=t+r=3+3
2.分子平均平动动能
t
t 2
kT
3 2
kT
3.分子平均转动动能
r
r 2
kT
4.分子平均动能
k
i kT 2
5.气体内能
E
i RT
2
i pV 2
2
四、麦克斯韦速率分布律
1.速率分布函数: f (v) dN Ndv
3、均匀带电无限长直导线
E 2 0 r
4.半径为R的均匀带电球面
E外
q
4 0r 2
E内 0
q
q
U外 4 0r U内 40R
5.无限大均匀带电平面
E
2 0
15
七、静态平衡时的导体 1. 导体内部场强为0。导体表面附近场强方向与导
体表面垂直。 2.导体为等势体(电势处处相等)。
3. 导体内无电荷,所有电荷分布于表面。
(1)
D dS q0 电场的高斯定律
(2)
E dl
L
S
B
d
S
电 场 的
环路定理
t
(变化的磁场激发电场)
(3) B d S 0
磁场的高斯定律
(4)
S
H dl
L
Ic
d D
dt
Ic
D dS t
磁 场 的 环 路 定 理 (变化的电场激发磁场)
27
第13 章量子物理
一、黑体辐射
v2 b v2 f (v)dv / b f (v)dv
a
大学物理电磁学部分总结

电磁学部分总结 静电场部分第一部分:静电场的基本性质和规律电场是物质的一种存在形态,它同实物一样也具有能量、动量、质量等属性。
静电场的物质特性的外在表现是:(1)电场对位于其中的任何带电体都有电场力的作用(2)带电体在电场中运动,电场力要作功——电场具有能量1、描述静电场性质的基本物理量是场强和电势,掌握定义及二者间的关系。
电场强度 电势2、反映静电场基本性质的两条定理是高斯定理和环路定理要掌握各个定理的内容,所揭示的静电场的性质,明确定理中各个物理量的含义及影响各个量的因素。
重点是高斯定理的理解和应用。
3、应用(1)、电场强度的计算a)、由点电荷场强公式 及场强叠加原理 计算场强q FE =⎰∞⋅==aa ar d E q W U 0∑⎰⎰=⋅=ΦiSe qS d E 01ε ⎰=⋅0r d E L 02041r rq E πε=iiE E ∑=一、离散分布的点电荷系的场强二、连续分布带电体的场强其中,重点掌握电荷呈线分布的带电体问题b)、由静电场中的高斯 定理计算场源分布具有高度对称性的带电体的场强分布一般诸如球对称分布、轴对称分布和面对称分布,步骤及例题详见课堂笔记。
还有可能结合电势的计算一起进行。
c)、由场强和电势梯度之间的关系来计算场强(适用于电势容易计算或电势分布已知的情形),掌握作业及课堂练习的类型即可。
(2)、电通量的计算2041i ii i i i r r q E E πε∑=∑=⎰⎰π==0204d r rq E d E εUgradU E -∇=-=)(k zU j y U i x U ∂∂+∂∂+∂∂-=a)、均匀电场中S 与电场强度方向垂直b)、均匀电场,S 法线方向与电场强度方向成q 角c)、由高斯定理求某些电通量(3)、电势的计算a)、场强积分法(定义法)——根据已知的场强分布,按定义计算b)、电势叠加法——已知电荷分布,由点电荷电势公式,利用电势叠加原理计算第二部分:静电场中的导体和电介质 一、导体的静电平衡状态和条件导体内部和表面都没有电荷作宏观定向运动的状态称为静电平衡状态。
大物公式
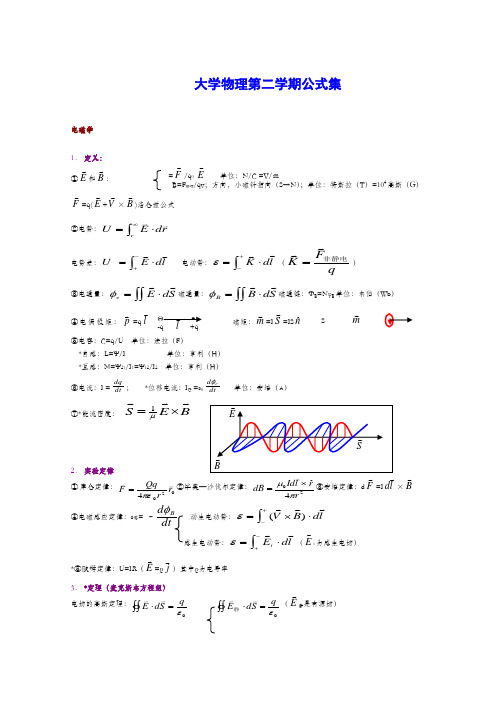
大学物理第二学期公式集电磁学1. 定义:①E 和B :F =q(E +V ×B)洛仑兹公式②电势:⎰∞⋅=rr d E U电势差:⎰-+⋅=l d E U电动势:⎰+-⋅=l d K ε(qF K 非静电 =)③电通量:⎰⎰⋅=S d E eφ磁通量:⎰⎰⋅=S d B Bφ磁通链:ΦB =N φB 单位:韦伯(Wb ) 磁矩:m =I S=IS nˆ ④电偶极矩:p=q l⑤电容:C=q/U 单位:法拉(F )*自感:L=Ψ/I单位:亨利(H ) *互感:M=Ψ21/I 1=Ψ12/I 2 单位:亨利(H )⑥电流:I =dt dq; *位移电流:I D =ε0dt d e φ 单位:安培(A )⑦*能流密度: B E S ⨯=μ12. 实验定律① 库仑定律:0204r r Qq F πε=②毕奥—沙伐尔定律:204ˆr r l Id B d πμ⨯=③安培定律:d F =I l d ×B ④电磁感应定律:ε感= –dtd Bφ 动生电动势:⎰+-⋅⨯=l d B V)(ε感生电动势:⎰-+⋅=l d E iε(E i 为感生电场)*⑤欧姆定律:U=IR (E =ρj)其中ρ为电导率3. *定理(麦克斯韦方程组)电场的高斯定理:⎰⎰=⋅0εq S d E ⎰⎰=⋅0εq S d E 静(E静是有源场)=F /q 0 E单位:N/C =V/mB=F max /qv ;方向,小磁针指向(S →N );单位:特斯拉(T )=104高斯(G )Θ ⊕ -q l +qSm⎰⎰=⋅0S d E感 (E 感是无源场) 磁场的高斯定理:⎰⎰=⋅0S d B⎰⎰=⋅0S d B(B 稳是无源场)⎰⎰=⋅0S d B(B 感是无源场)电场的环路定理:⎰-=⋅dtd l d E B φ ⎰=⋅0l d E静(静电场无旋) ⎰-=⋅dtd l d E Bφ 感(感生电场有旋;变化的磁场产生感生电场) 安培环路定理:d I I l d B 00μμ+=⋅⎰⎰=⋅I l d B 0μ稳(稳恒磁场有旋) dtd l d Be φεμ00⎰=⋅ 感(变化的电场产生感生磁场) 4. 常用公式①无限长载流导线:r I B πμ20= 螺线管:B=nμ0I② 带电粒子在匀强磁场中:半径qB mV R =周期qB m T π2=磁矩在匀强磁场中:受力F=0;受力矩B m M⨯=③电容器储能:W c =21CU 2 *电场能量密度:ωe =21ε0E 2 电磁场能量密度:ω=21ε0E 2+021μB 2*电感储能:W L =21LI 2 *磁场能量密度:ωB =021μB 2电磁场能流密度:S=ωV④ *电磁波:C=001εμ=3.0×108m/s 在介质中V=C/n,频率f=ν=021εμπ波动学1. 定义和概念简谐波方程: x 处t 时刻相位 振幅ξ=Acos(ω简谐振动方程:ξ=Acos(ωt+φ) 波形方程:ξ=Acos(2πx/λ+φ′)相位Φ——决定振动状态的量振幅A ——振动量最大值 决定于初态 x0=Acos φ 初相φ——x=0处t=0时相位 (x 0,V 0) V 0= –A ωsin φ 频率ν——每秒振动的次数圆频率ω=2πν 决定于波源如: 弹簧振子ω=m k /周期T ——振动一次的时间 单摆ω=l g /波速V ——波的相位传播速度或能量传播速度。
最新人教版高中物理高考必备知识点感生电动势和动生电动势
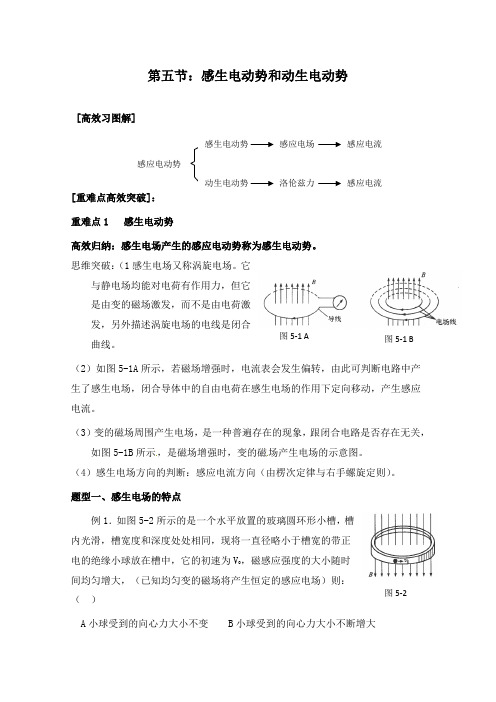
第五节:感生电动势和动生电动势[高效习图解][重难点1 感生电动势高效归纳:感生电场产生的感应电动势称为感生电动势。
思维突破:(1感生电场又称涡旋电场。
它与静电场均能对电荷有作用力,但它是由变的磁场激发,而不是由电荷激发,另外描述涡旋电场的电线是闭合曲线。
(2)如图5-1A 所示,若磁场增强时,电流表会发生偏转,由此可判断电路中产生了感生电场,闭合导体中的自由电荷在感生电场的作用下定向移动,产生感应电流。
(3)变的磁场周围产生电场,是一种普遍存在的现象,跟闭合电路是否存在无关,如图5-1B 所示,是磁场增强时,变的磁场产生电场的示意图。
(4)感生电场方向的判断:感应电流方向(由楞次定律与右手螺旋定则)。
题型一、感生电场的特点例1.如图5-2所示的是一个水平放置的玻璃圆环形小槽,槽内光滑,槽宽度和深度处处相同,现将一直径略小于槽宽的带正电的绝缘小球放在槽中,它的初速为V 0,磁感应强度的大小随时间均匀增大,(已知均匀变的磁场将产生恒定的感应电场)则:( )A 小球受到的向心力大小不变B 小球受到的向心力大小不断增大图5-1 A 图5-1 B 图5-2 感应电流感应电场 感应电流 洛伦兹力磁场力对小球做了功 D 小球受到的磁场力大小与时间成正比 思路分析:由楞次定律,此电场与小球初速度方向相同,由于小球带正电,电场力对小球做正功,小球的速度应该逐渐增大,向心力也会随着增大。
另外洛仑兹力永远对运动电荷不做功,故错。
带电小球所受洛仑兹力F=qvB,随着速率的增大而增大,同时,B 也正比于时间,则F 于不成正比,故D 错误。
答案:B规律技巧总结:本题的关键是要判断出磁感应强度的方向,感应电场对小球做正功,使带电小球的动能不断增大,带电小球既受到电场力又受到磁场力的作用。
题型一、求感生电荷量例2.有一面积为S=100c 2的金属环,电阻R=01Ω,环中磁场变规律如图5-3所示,磁场方向垂直环面向里,从1至2过程中,通过金属环的电荷量为多少?思路分析:因为B-图象为一直线,故△ф也是均匀变,△ф=△BS=(B 2-B 1)·S[。
法拉第电磁感应定律(6)

r E
r r F = qEk k r r +r r = ∫ F ⋅dr =q∫ Ek ⋅ dr k 非
−
r E
r r ε = ∫ Ek ⋅dr
+
⇒
导体回路中的感应电动势 小与穿过导体回路的磁通量 化率成正比. 化率成正比.
ε
dΦ = −k dt
r n Φ>0
L
国际单位制中 k =1 单位:1V=1Wb/s 单位 V=1Wb/s
Id无电荷流动。高 无电荷流动。
L
r r H ⋅dr = I + I d
r r J ⋅ dS ∫
S
I全
r r r ∂D J全 = J + ∂t
r ∂D r ) ⋅ dS
r r H • dr = ∫∫
r r r ∂D r J d ⋅ dS = ∫S ⋅ dS ∂t
r (J + S
well 的新思想:
—磁场变化使导线中 磁场变化使导线中
生电动势
边的直导线以v的速度 边的直导线以 的速度 滑动,回路磁通量增加, 滑动,回路磁通量增加, 感应电动势。 感应电动势。
感应电动势的大小是多
n
B X θ
d Φ ε = dt
v
=
d(B co Lx = dt
x
BdScosθ
dx =B L co dt
- F=-ev×B
1、法拉第电磁感应定律 2 、动生电动势
3、 感生电动势和感生电场 4、自感与互感 5、磁场能量
、电磁感应现象
过一个闭合回路的磁通量 过一个闭合回路的磁通量 变化时 生变化时, 回路中就有感 电流产生——该现象称为 电流产生 该现象称为 磁感应现象。产生的电流 磁感应现象。 为感应电流,相应的电动 感应电流, 为感应电动势。
(专)《大学物理下》模拟题2及参考答案

(高起专)大学物理下模拟题2一、填空题1,载有一定电流的圆线圈在周围空间产生的磁场与圆线圈半径R有关,当圆线圈半径增大时,(1)圆线圈中心点(即圆心)的磁场__________________________。
(2)圆线圈轴线上各点的磁场______________________________。
2,有一长直金属圆筒,沿长度方向有稳恒电流I流通,在横截面上电流均匀分布。
筒内空腔各处的磁感应强度为________,筒外空间中离轴线r处的磁感应强度为__________。
3,如图所示的空间区域内,分布着方向垂直于纸面的匀强磁场,在纸面内有一正方形边框abcd(磁场以边框为界)。
而a、b、c三个角顶处开有很小的缺口。
今有一束具有不同速度的电子由a缺口沿ad方向射入磁场区域,若b、c两缺口处分别有电子射出,则此两处出射电子的速率之比vb/vc=________________。
dabc4,如图,在一固定的无限长载流直导线的旁边放置一个可以自由移动和转动的圆形的刚性线圈,线圈中通有电流,若线圈与直导线在同一平面,见图(a),则圆线圈将____________;若线圈平面与直导线垂直,见图(b),则圆线圈将___________________________。
II⊙(a)(b)5,一个绕有500匝导线的平均周长50cm的细环,载有0.3A电流时,铁芯的相对磁导率为600。
(0=4×10-1)-7T·m·A(1)铁芯中的磁感应强度B为__________________________。
(2)铁芯中的磁场强度H为____________________________。
6,一导线被弯成如图所示形状,acb为半径为R的四分之三圆弧,直线段Oa长为R。
若此导线放在匀强磁场B中,B的方向垂直图面向内。
导线以角速度在图面内绕O点cB匀速转动,则此导线中的动生电动势i=___________________,电势最高b 的点是________________________。
动生电动势和感生电动势

动生电动势和感生电动势
d d 感应电动势 N dt dt 引起磁通量变化的原因 ?
磁场恒定,导体运动
导体不动,磁场变化
P.1
1、电动势定义
I
Ek
+
-
Ek : 非静电电场强度.
Ek dl
P.2
2、感应电动势的分类: (1)动生电动势 稳恒磁场中的导体运动 , 或者回路面积 变化、取向变化等。 (2)感生电动势: 导体不动,磁场变化。
OP
P.5
动生
OP
(v B) dl
混合积:(a b ) c
× × P ×
(vB sin ) cosdl
OP
×
× × ×
×
(v × B) ×
× ×
×
特例 B均匀,杆 l水平运动:
l×
×
× v×
× B
× O ×
OP
l
l (vB sin 900 )cos00 dl (v B) dl 0
vBl
vBdl vBl
0
P.6
2、计算方法
d动生 (v B) dl
动生
×
×
× P× B × dl
× ×
OP
(v B) dl
1 2 d BL 2 dt 1 2 BL 2
×
×
× P × × × ×
× ×
B ×
×
×
×
o
×
×
×
×
×
×
×
7.2动生电动势感生电动势感生电场普遍环路定理

dΦ ε =− = ε动 + ε感 dt
7.2.1 动生电动势 非静电力: 非静电力:磁场作用在运动电荷上的洛伦兹 力。导体在恒定磁场 B 中运动,自由电子随导 中运动, 运动, 体以速度 v 运动,所受洛伦兹力为 −ev×B,单 × , 位正电荷受到的非静电力: 位正电荷受到的非静电力: r r r − ev × B r r K= = v× B −e 运动导体中的动生电动势: 运动导体中的动生电动势: r r r r r r ε = ∫ (v × B) ⋅ dl , ε = ∫ (v × B ) ⋅ dl(导体回路) 导体回路) L
1 BωL2 ε = ∫ dε = −ωB∫ ldl = − 0 2
L
方向是由A指向 : 是正极 方向是由 指向O: O是正极,A是负极。 指向 是正极, 是负极 是负极。
1 BωL2 两端的电势差 : ϕO − ϕ A = 2
7.2.2 感生电动势 感生电场 普遍情况下电场 的环路定理 1. 感生电动势 感生电场 感生电动势的非静电力 麦克斯韦感生电场 非静电力? 感生电动势的非静电力 麦克斯韦 感生电场 假设: 假设: 变化的磁场会在周围空间激发电场 感 感 引起感生电动势的非静电力 引起感生电动势的非静电力: 生电场 引起感生电动势的非静电力: r r ε = ∫ Ei ⋅ dl (1)
7.2 动生电动势 感生电动势 感生电场 普遍情 况下电场的环路定理 7.2.1 动生电动势 7.2.2 感生电动势 感生电场 普遍情况下电场 的环路定理
磁场恒定、回路运动: 磁场恒定、回路运动: 动生电动势 磁场变化、回路静止: 磁场变化、回路静止:感生电动势 磁场变化、回路运动,感应电动势: 磁场变化、回路运动,感应电动势:
L
大学物理常用公式(电场磁场-热力学)

⼤学物理常⽤公式(电场磁场-热⼒学)第四章电场⼀、常见带电体的场强、电势分布 1)点电荷:2014q E r πε=04q U rπε=2)均匀带电球⾯(球⾯半径R )的电场:200()()4r R E qr R r πε≤??=?>??00()4()4qr R r U q r R R πεπε?>??=??≤??3)⽆限长均匀带电直线(电荷线密度为λ):02E rλπε=,⽅向:垂直于带电直线。
4)⽆限长均匀带电圆柱⾯(电荷线密度为λ): 00()()2r R E r R rλπε≤??=?>??5)⽆限⼤均匀带电平⾯(电荷⾯密度为σ)的电场:0/2E σε=,⽅向:垂直于平⾯。
⼆、静电场定理 1、⾼斯定理:0 e SqE dS φε==∑?v v ? 静电场是有源场。
q ∑指⾼斯⾯内所包含电量的代数和;E ?指⾼斯⾯上各处的电场强度,由⾼斯⾯内外的全部电荷产⽣;S E dS ??vv ?指通过⾼斯⾯的电通量,由⾼斯⾯内的电荷决定。
2、环路定理:0lE dl ?=?vv ? 静电场是保守场、电场⼒是保守⼒,可引⼊电势能三、求场强两种⽅法1、利⽤场强势叠加原理求场强分离电荷系统:1n i i E E ==∑v v ;连续电荷系统:E dE =?v v2、利⽤⾼斯定理求场强四、求电势的两种⽅法1、利⽤电势叠加原理求电势分离电荷系统:1nii U U==∑;连续电荷系统: U dU =?2、利⽤电势的定义求电势 rU E dl =??v v 电势零点五、应⽤点电荷受⼒:F qE =v v 电势差: bab a b aU U U E dr =-=??a由a 到b六、导体周围的电场1、静电平衡的充要条件: 1)、导体内的合场强为0,导体是⼀个等势体。
2)、导体表⾯的场强处处垂直于导体表⾯。
E ⊥v 表表⾯。
导体表⾯是等势⾯。
2、静电平衡时导体上电荷分布: 1)实⼼导体:净电荷都分布在导体外表⾯上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r r r ∂B r 麦克斯韦方程组中 ∫LE ⋅ dl = −∫S ∂t ⋅ dS 的一个方程
的圆柱形体积内, 【 例 7.6】 在一半径为 的圆柱形体积内 , 充 】 在一半径为R的圆柱形体积内 满磁感应强度为B的匀强磁场 的匀强磁场, 满磁感应强度为 的匀强磁场, dB/dt =K>0。 > 。 求感生电场的分布。 求感生电场的分布。 解 磁 场 轴对 称 → 感 生 电场轴对称 由感生电场的环路定理: 由感生电场的环路定理: r ∂B r 2 2πrEi = − ∫ ⋅ dS = − π r K S ∂t 2 1 1 KR 圆柱内: 圆柱内: i = − rK E 圆柱外: 圆柱外: i = − E 2 2 r 方向都与回路的绕向相反。 方向都与回路的绕向相反。
dΦ ε =− = ε动 + ε感 dt
7.2.1 动生电动势 非静电力: 非静电力:磁场作用在运动电荷上的洛伦兹 力。导体在恒定磁场 B 中运动,自由电子随导 中运动, 运动, 体以速度 v 运动,所受洛伦兹力为 −ev×B,单 × , 位正电荷受到的非静电力: 位正电荷受到的非静电力: r r r − ev × B r r K= = v× B −e 运动导体中的动生电动势: 运动导体中的动生电动势: r r r r r r ε = ∫ (v × B) ⋅ dl , ε = ∫ (v × B ) ⋅ dl(导体回路) 导体回路) L
ε >0:方向与 L 的绕向相同;ε <0:方向与 的绕向相同; : :方向与L
的绕向相反。 的绕向相反。
的桐棒在磁感应强度为B的 【例7.4】长度为 的桐棒在磁感应强度为 的 】长度为L的桐棒在磁感应强度为 绕棒的O端逆时针转动 端逆时针转动。 匀强磁场中以角速度ω绕棒的 端逆时针转动。 求铜棒中的动生电动势和铜棒两端的电势差。 求铜棒中的动生电动势和铜棒两端的电势差。 解 线元 方向沿半径向外 , 线元dl方向沿半径向外 方向沿半径向外, 运动速度 v 为ωl r r r dε = (v × B ) ⋅ dl = −ωlBdl 铜棒中的动生电动势: 铜棒中的动生电动势:
L
感生电场E 的环流不为零,等于感生电动势。 感生电场 i的环流不为零,等于感生电动势。 感生电场是有旋场,称做涡旋电场 涡旋电场。 感生电场是有旋场,称做涡旋电场。 根据法拉第电磁感应定律: 根据法拉第电磁感应定律: r d r r ∂B r dΦ = − ∫ B ⋅ dS = −∫ ⋅ dS (2) ε =− S ∂t dt S dt
r r r ∂B r ∫L Ei ⋅ dl = − ∫S ∂t ⋅ dS
电子感应加速器: 电子感应加速器: 交变电流 → 交磁场 B →感生电场 Ei → 加速电子 洛伦兹力F: 洛伦兹力 : 使电子沿圆 形轨道回转
2. 普遍情况下电场的环路定理 环流等于零的电场,称为势场 势场。 环流等于零的电场,称为势场。静电场就是 r r 一种势场: 一种势场: E ⋅ dl = 0
1 BωL2 ε = ∫ dε = −ωB∫ ldl = − 0 2
L
方向是由A指向 : 是正极 方向是由 指向O: O是正极,A是负极。 指向 是正极, 是负极 是负极。
1 BωL2 两端的电势差 : ϕO − ϕ A = 2
7.2.2 感生电动势 感生电场 普遍情况下电场 的环路定理 1. 感生电动势 感生电场 感生电动势的非静电力 麦克斯韦感生电场 非静电力? 感生电动势的非静电力 麦克斯韦 感生电场 假设: 假设: 变化的磁场会在周围空间激发电场 感 感 引起感生电动势的非静电力 引起感生电动势的非静电力: 生电场 引起感生电动势的非静电力: r r ε = ∫ Ei ⋅ dl (1)
7.2 动生电动势 感生电动势 感生电场 普遍情 况下电场的环路定理 7.2.1 动生电动势 7.2.2 感生电动势 感生电场 普遍情况下电场 的环路定理
磁场恒定、回路运动: 磁场恒定、回路运动: 动生电动势 磁场变化、回路静止: 磁场变化、回路静止:感生电动势 磁场变化、回路运动,感应电动势: 磁场变化、回路运动,感应电动势:
r r ε = ∫ Ei ⋅ dl (1) L r ∂B r ε = −∫ ⋅ dS (2) S ∂t 对比(1)、 得 感生电场满足的环路定理: 对比 、(2)得 感生电场满足的环路定理:
r r r ∂B r ∫L Ei ⋅ dl = − ∫S ∂t ⋅ dS
表明变化的磁场如何激发电场 表明变化的磁场如何激发电场 S:以回路 L 为边界的任意曲面。 为边界的任意曲面。 : 的绕向后, 的法线取在由L 设定 L 的绕向后,面元 dS 的法线取在由 的绕向按右手定则决定的 面的同一侧。 的绕向按右手定则决定的 S 面的同一侧。
∫
L
e
任何矢量场都可分解成势场和涡旋场, 任何矢量场都可分解成势场和涡旋场,电场 r r r 可表示为: 可表示为: 其中
普遍情况下电场的环路定理: 普遍情况下电场的环路定理: 普遍情况下电场的环路定理
r r r ∂B r ∫L Ei ⋅ dl = −∫S ∂t ⋅ dS
E = E e + Ei
