实验一梁结构静力有限元分析(精)
悬臂梁—有限元ABAQUS线性静力学分析实例

线性静力学分析实例——以悬臂梁为例线性静力学问题是简单且常见的有限元分析类型,不涉及任何非线性(材料非线性、几何非线性、接触等),也不考虑惯性及时间相关的材料属性。
在ABAQUS中,该类问题通常采用静态通用(Static,General)分析步或静态线性摄动(Static,Linear perturbation)分析步进行分析。
线性静力学问题很容易求解,往往用户更关系的是计算效率和求解效率,希望在获得较高精度的前提下尽量缩短计算时间,特别是大型模型。
这主要取决于网格的划分,包括种子的设置、网格控制和单元类型的选取。
在一般的分析中,应尽量选用精度和效率都较高的二次四边形/六面体单元,在主要的分析部位设置较密的种子;若主要分析部位的网格没有大的扭曲,使用非协调单元(如CPS4I、C3D8I)的性价比很高。
对于复杂模型,可以采用分割模型的方法划分二次四边形/六面体单元;有时分割过程过于繁琐,用户可以采用精度较高的二次三角形/四面体单元进行网格划分。
悬臂梁的线性静力学分析1.1 问题的描述一悬臂梁左端受固定约束,右端自由,结构尺寸如图1-1所示,求梁受载后的Mises应力、位移分布。
ν材料性质:弹性模量3=E=,泊松比3.02e均布载荷:F=103N图1-1 悬臂梁受均布载荷图1.2 启动ABAQUS启动ABAQUS有两种方法,用户可以任选一种。
(1)在Windows操作系统中单击“开始”--“程序”--ABAQUS 6.10 --ABAQUS/CAE。
(2)在操作系统的DOS窗口中输入命令:abaqus cae。
启动ABAQUS/CAE后,在出现的Start Section(开始任务)对话框中选择Create Model Database。
1.3 创建部件在ABAQUS/CAE顶部的环境栏中,可以看到模块列表:Module:Part,这表示当前处在Part(部件)模块,在这个模块中可以定义模型各部分的几何形体。
有限元受力分析--结构梁-力-计算

有限元受力分析–结构梁-力-计算1. 前言受力分析是工程设计中至关重要的一环,能够帮助工程师完善设计并避免安全事故的发生。
在此,我们将介绍有限元受力分析在结构梁设计中的应用。
本文将重点讲解有限元受力分析的相关理论和计算方法。
2. 有限元受力分析有限元分析是数值计算的一种方法,可用于解决工程中的受力分析问题。
它把结构离散为有限个单元,然后对每个单元进行分析。
有限元分析可分为线性有限元分析和非线性有限元分析两种类型。
本文我们只讨论线性有限元分析。
在有限元分析中,结构被分解为离散的单元,每个单元都是基于解析解的一部分。
有限元的形状、尺寸和材料属性可以通过计算机程序进行定义。
使用数学模型和有限元方法,可以计算单元的应力、变形和应变,从而进行结构的受力分析。
3. 结构梁结构梁相信大家应该都知道,它是工程中最为常用的结构之一。
它具有一定的强度和刚度,可以支撑和传递载荷。
一般来说,结构梁通常由简单的杆件单元组成。
在进行结构梁受力分析时,我们需要考虑弯曲、剪切和挤压等不同形式的载荷,以及结构在工作条件下的应变和应力分布情况。
有限元受力分析对于这些问题的研究提供了很好的解决方案。
4.力的分析在受力分析中,载荷是非常关键的参数。
载荷可以是点载荷、均布载荷、集中荷载等。
在本文中,我们将分别介绍这些载荷类型的有限元分析方法。
4.1 点载荷分析点载荷通常是一个单点受到的载荷。
对于点载荷的有限元分析,我们可以通过构建一个网格模型,然后将点载荷作用在网格的节点上。
此外,还需要设定材料的弹性模量和截面的截面面积,以计算结构的应力和变形。
需要注意的是,点载荷分析过程中的网格划分应当尽量精细,以达到更为优秀的数值精度。
4.2 均布载荷分析均布载荷是沿着梁的长度方向均匀分布的载荷,例如一根梁的自重、荷载等。
在进行均布载荷的有限元分析时,我们可以在网格的中央位置放置均布载荷,然后将梁的边缘节点设置为固定的约束条件。
同样,需要设定材料的弹性模量和截面的截面面积以计算结构的应力和变形。
有限元分析中的结构静力学分析怎样才能做好精选全文

可编辑修改精选全文完整版有限元分析中的结构静力学分析怎样才能做好1 概述结构有限元分析中,最基础、最根本、最关键、最核心同时也是最重要的一种分析类型就是“结构静力学分析”。
静力学分析可用于与结构相关、与流体相关、与电磁相关以及与热相关的所有产品;静力学分析是有限元分析的根基,是有限元分析的灵魂。
2 基础理论结构静力学按照矩阵的形式可表示为微分方程:[K]{x}+{F}=0其中,[K]代表刚度矩阵,{x}代表位移矢量,{F}代表静载荷函数。
由此可知,结构静力学有限元分析过程就是求解微分方程组的过程。
2.1 三个矩阵的说明静力学分析微分方程组三个矩阵进一步说明:[K]代表刚度矩阵。
举例说明,如果用手折弯一根筷子,假设筷子是钢材料的,比较硬,很难折断;假设筷子是常规木材的,比较脆,基本上都能折断。
这里筷子断与不断的本质并不是钢或者木材,而是钢或者木材表在筷子上表现出来的刚度(或者叫硬度),这里刚度用计算机数值分析的方式来描述,就是刚度矩阵。
{x}代表位移矢量。
举例说明,一把椅子,如果有人偏瘦,坐在椅子上,椅面基本不下沉;如果有人偏胖,坐在椅子上,椅面会有明显下沉(谁坐谁知道...),此时,椅面的下沉量,可用位移矢量来表示。
{F}代表静载荷函数,也是静力学分析的关键。
举例说明,上面筷子例子中,手腕对筷子的作用,就是一种载荷(或者叫外力、荷载、负荷、承重等);上面椅子例子中,人对椅子表面的作用,也是一种载荷。
这些载荷在大多数情况下,没有明显的快慢效应,就可用静载荷函数来表示。
2.2 静力学分析中的载荷说明静载荷函数本质说明:假设1,相同一根筷子,又假设筷子比较粗(或者说是几根筷子捆绑在一起):双手慢慢用1 / 5力,筷子难断;双手快速用力,筷子难断,此时慢慢折弯的效果就可以理解为静力学过程。
假设2,相同椅子:慢慢坐下去,椅子没有明显晃动;快速坐下去,椅子没有明显下沉与晃动,此时慢慢坐在椅子上的过程就可以理解为静力学过程。
有限元-结构静力学分析

03
结果优化
如果结果不满足设计要求,需要对有 限元模型进行优化设计,如改变梁的 截面尺寸、增加支撑等。
THANKS
谢谢您的观看
结构静力学的求解方法
解析法
解析法是通过数学方法求解结构在静载荷作用下的响应的求解方法。它通常 适用于具有简单几何形状和载荷条件的结构,如梁、板、壳等。
数值法
数值法是一种通过数值计算方法求解结构在静载荷作用下的响应的求解方法 。它通常适用于具有复杂几何形状和载荷条件的结构,如飞机、汽车等。
结构静力学的基本假设和简化
问题描述和基本方程
问题描述
弹性地基梁是支撑在弹性地基上的梁,受到垂直荷载的作用。该问题可描述为求 解地基反力和梁的挠度。
基本方程
该问题的基本方程包括梁的平衡方程、几何方程和物理方程。这些方程描述了梁 在受力后的变形和应力分布情况。
利用有限元法进行每个单元之间通过节点相连。每个节点具有三个自由度:沿 x、y、z方向的移动。
系统方程的建 立
将所有单元的平衡方程 和变形协调方程组合起 来,得到整个结构的系 统方程。
求解系统方程
利用数值方法(如高斯 消元法)求解系统方程 ,得到每个节点的位移 和应力。
结果分析和讨论
01
结果输出
输出每个节点的位移、应力、应变和 弯矩等结果。
02
结果评估
根据输出结果,对框架结构的强度、 刚度和稳定性进行评估,判断是否满 足设计要求。
连续性假设
结构静力学的基本假设是结构的材料是连续的, 即结构的内部没有空隙和缺陷。
各向同性假设
结构静力学的基本假设是结构的材料是各向同性 的,即结构的各个方向具有相同的材料性质。
均匀性假设
结构静力学的基本假设是结构的材料是均匀的, 即结构的各个部分具有相同的材料性质。
梁的有限元分析原理

梁的有限元分析原理梁的有限元分析原理是一种工程结构分析方法,广泛应用于建筑、桥梁、航空航天、汽车等领域。
它通过将连续的结构离散化为有限数量的小单元,通过数学模型进行计算,得出结构的力学性能和响应情况。
梁的有限元分析原理是有限元分析的基础,下面将对其进行详细介绍。
首先,梁的有限元分析原理基于梁理论,即在横向较小、纵向较长的情况下,结构可以近似为一维梁。
梁的有限元分析原理通过将梁划分为多个单元,每个单元内部可以看作两个节点之间的一段杆件,通过建立节点之间的力学关系方程,得到整个结构的力学性能。
其次,梁的有限元分析原理利用了变分原理,即将结构的势能取极小值,建立了结构的力学方程。
通过对于梁的弯曲、剪切和轴向力等方面的力学模型进行合理的假设与简化,可以得到结构的位移与力的关系,从而解决结构的力学问题。
在梁的有限元分析中,需要进行以下几个步骤:1.几何离散化:将梁结构划分为多个单元,每个单元具有相同的形状与尺寸,通常为矩形或三角形。
2.模型建立:根据梁理论以及力学方程的简化假设,建立节点的力学关系方程,包括位移、应力、应变等参数。
3.材料性能定义:确定梁材料的力学性能参数,如弹性模量、截面惯性矩等。
这些参数对梁结构的力学性能具有重要影响。
4.边界条件施加:根据实际问题设定边界条件,包括固定支座、约束条件等。
这些条件对于解决梁结构的位移、应力等问题至关重要。
5.方程求解:通过数学方法求解得到节点之间的力学关系方程,利用数值计算技术进行迭代求解,得到梁结构的位移、应力等参数。
6.结果分析:根据求解得到的结果,进行力学性能分析,如最大应力、挠度、模态分析等。
根据分析结果评估结构的强度与稳定性。
总结起来,梁的有限元分析原理是一种基于梁理论的工程结构分析方法,通过将结构离散化为多个小单元,利用力学关系方程和数值计算技术求解得到结构的力学性能。
通过梁的有限元分析原理,工程师可以更加准确地评估结构的强度与稳定性,对结构进行优化设计。
梁模型有限元计算_ANSYS Workbench有限元分析实例详解(静力学)_[共7页]
![梁模型有限元计算_ANSYS Workbench有限元分析实例详解(静力学)_[共7页]](https://img.taocdn.com/s3/m/ba2491b227d3240c8547ef2c.png)
4.2 梁单元静力学分析当结构长度对横截面的比率超过10:1,沿长度方向的应力为主要分析对象,且横截面始终保持不变时,即应用梁单元。
梁单元可用于分析主要受侧向或横向载荷的结构,如建筑桁架、桥梁、螺栓等。
在WB中默认为铁摩辛柯(Timoshenko)梁单元,即Beam188和Beam189,可计算弯曲、轴向、扭转和横向剪切变形。
其中Beam188采用线性多项式作为形函数,Beam189采用二次多项式作为形函数,当WB的Mesh设置中Mesh-Element Midside Nodes为Dropped 时,即为Beam188;Mesh-Element Midside Nodes为Kept时,即为Beam189。
有限元对单元特性的描述包括单元形状、节点数目、自由度和形函数。
表4-2-1为Beam 单元的对比。
在WB中默认设置为二次单元。
一般来说,线性单元需要更多的网格数才能达到二次单元的精度。
选用二次单元可提高计算精度,这是因为二次单元的曲线或曲面边界能够更好地逼近结构的曲线和曲面边界,且二次插值函数可更高精度地逼近复杂场函数,所以当结构形状不规则、应力分布或变形很复杂时可以选用高阶单元。
但高阶单元的节点数较多,在网格数量相同的情况下由高阶单元组成的模型规模要大得多,计算内存消耗也多,因此,在使用时应权衡考虑计算精度和时间。
表4-2-1 Beam单元对比4.2.1 梁模型有限元计算用ProE建立一桁架模型,导入WB进行分析计算。
(1)ProE建模。
在草绘界面绘制一边长为30mm、40mm、50mm的三角形,然后选择投影命令将草绘图形投影到基准面上,另存为x_t文件(其他3D软件操作方法类似)。
(2)导入模型。
如图4-2-1所示,在Import设置中,Operation设为Add Frozen,Line Bodies 设为Yes。
– 65 –– 66 – 图4-2-1 Import ProE模型文件设置(3)梁截面赋值,并定义截面方向,最后用Form New Part将三根梁合并为一个部件,如图4-2-2所示。
AnsysWorkbench工程实例之——梁单元静力学分析
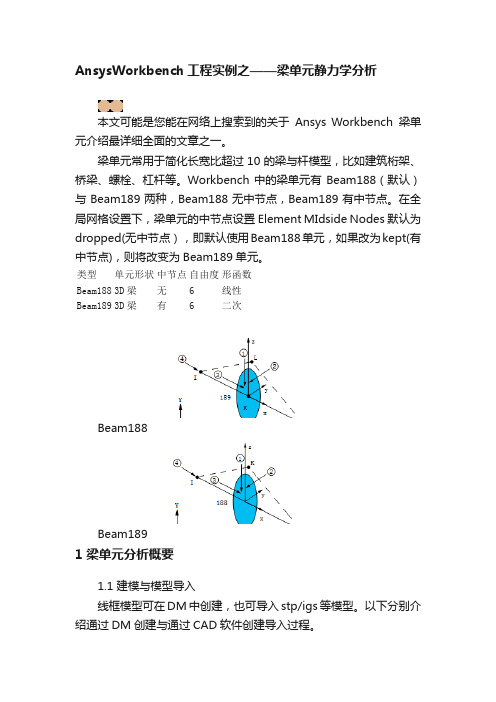
AnsysWorkbench工程实例之——梁单元静力学分析本文可能是您能在网络上搜索到的关于Ansys Workbench梁单元介绍最详细全面的文章之一。
梁单元常用于简化长宽比超过10的梁与杆模型,比如建筑桁架、桥梁、螺栓、杠杆等。
Workbench中的梁单元有Beam188(默认)与Beam189两种,Beam188无中节点,Beam189有中节点。
在全局网格设置下,梁单元的中节点设置Element MIdside Nodes默认为dropped(无中节点),即默认使用Beam188单元,如果改为kept(有中节点),则将改变为Beam189单元。
类型单元形状中节点自由度形函数Beam188 3D梁无 6 线性Beam189 3D梁有 6 二次Beam188Beam1891 梁单元分析概要1.1 建模与模型导入线框模型可在DM中创建,也可导入stp/igs等模型。
以下分别介绍通过DM创建与通过CAD软件创建导入过程。
1.1.1 梁线体的创建方法1,简单的线体模型可以在DM中创建,一般在XY平面绘制草图或点,再通过Concept——Lines From Sketches、Lines From Points或3D Curve等创建。
区别在于Lines From Sketches是提取草图所有的线条,如果线条是相连接的,提取的结果为一个线几何体。
Lines From Points或3D Curve用于将草图的点(可以是草图线条的端点)连接成为线体,结合Add Frozen选项,可以创建多个线几何体。
操作3次后多个线条可以通过From New Part功能组合为一个几何体,组合后两条线共节点,相当于焊接在一起。
选中后右击方法2,通过CAD软件创建后导入。
如果读者使用的是creo建模,可在草图中创建点,退出草图后选择基准——曲线——通过点的曲线。
操作3次后输出时需要注意,可另存为stp或igs格式,在输出对话框中必须勾选基准曲线和点选项。
悬臂梁—有限元ABAQUS线性静力学分析报告实例

线性静力学分析实例——以悬臂梁为例线性静力学问题是简单且常见的有限元分析类型,不涉及任何非线性(材料非线性、几何非线性、接触等),也不考虑惯性及时间相关的材料属性。
在ABAQUS 中,该类问题通常采用静态通用(Static ,General )分析步或静态线性摄动(Static ,Linear perturbation )分析步进行分析。
线性静力学问题很容易求解,往往用户更关系的是计算效率和求解效率,希望在获得较高精度的前提下尽量缩短计算时间,特别是大型模型。
这主要取决于网格的划分,包括种子的设置、网格控制和单元类型的选取。
在一般的分析中,应尽量选用精度和效率都较高的二次四边形/ 六面体单元,在主要的分析部位设置较密的种子;若主要分析部位的网格没有大的扭曲,使用非协调单元(如CPS4I、C3D8I)的性价比很高。
对于复杂模型,可以采用分割模型的方法划分二次四边形/ 六面体单元;有时分割过程过于繁琐,用户可以采用精度较高的二次三角形/ 四面体单元进行网格划分。
悬臂梁的线性静力学分析1.1 问题的描述一悬臂梁左端受固定约束,右端自由,结构尺寸如图1-1 所示,求梁受载后的Mises 应力、位移分布。
材料性质:弹性模量 E 2e3 ,泊松比0.3均布载荷:F=103N图1-1 悬臂梁受均布载荷图1.2 启动ABAQUS启动ABAQUS有两种方法,用户可以任选一种1)在Windows 操作系统中单击“开始” -- “程序” --ABAQUS 6.10 -- ABAQUS/CA。
E(2)在操作系统的DOS窗口中输入命令:abaqus cae 。
启动ABAQUS/CA后E ,在出现的Start Section (开始任务)对话框中选择Create Model Database 。
1.3 创建部件在ABAQUS/CA顶E 部的环境栏中,可以看到模块列表:Module:Part ,这表示当前处在Part (部件)模块,在这个模块中可以定义模型各部分的几何形体。
梁结构静力有限元分析论文

梁结构静力有限元分析论文摘要:本文比较典型地介绍了如何用有限元分析工具分析梁结构受到静力时的应力的分布状态。
我们遵循对梁结构进行有限元分析的方法,建立了一个完整的有限元分析过程。
首先是建立好梁结构模型,然后进行网格划分,接着进行约束和加载,最后计算得出结论,输出各种图像供设计时参考。
通过本文,我们对有限元法在现代工程结构设计中的作用、使用方法有个初步的认识。
关键字:ANSYS ,梁结构,有限元,静力分析。
0引言在现代机械工程设计中,梁是运用得比较多的一种结构。
梁结构简单,当是受到复杂外力、力矩作用时,可以手动计算应力情况。
手动计算虽然方法简单,但计算量大,不容易保证准确性。
相比而言,有限元分析方法借助计算机,计算精度高,且能保证准确性。
另外,有限元法分析梁结构时,建模简单,施加应力和约束也相对容易,能分析梁结构应力状况的具体分布、最大变形量以及中性面位置,优势明显。
以下介绍一种常见梁的受力状况,并采用有限元法进行静力分析,得出了与手动计算基本吻合的结论。
以下为此次分析对象。
梁的截面形状为梯形截面,各个截面尺寸相同。
两端受弯矩沿中性面发生弯曲,如图2-1所示。
试利用ANSYS 软件对此梯形截面梁进行静力学分析,以获得沿梁AA 截面的应力分布情况。
rθAAMMA -A 截面D,B 1#面2#面CA B DC,A1 有限元模型的建立首先进入ANSYS中,采用自下而上的建模方式,创建梁结构有限元分析模型,同时定义模型的材料单元为Brick 8-node 45,弹性模量为200e9,泊松比为0.3。
由于分析不需要定义实常数,因此可忽略提示,关闭Real Constants菜单。
建立的切片模型如下:(1)定义实常数定义材料属性定义几何参数定义关键点生成切片模型划分网格①设定网格划分参数。
设定L1、L3、L6和L10网格参数设定L2、L4、L8和L12网格参数设定L7、L9、L11网格参数设定L5网格参数划分网格。
梁的有限元分析原理

j
·
x
i·
Chapter 5 Bernoulli-Euler Beam
z
27
福州大学研究生课程-有限元程序设计
平面桁架杆单元(2D LINK1)
空间杆单元(3D
LINK8)
平面刚架,BEAM3 空间梁单元(BEAM4)
Chapter 5 Bernoulli-Euler Beam
28
福州大学研究生课程-有限元程序设计
举例说明
Chapter 5 Bernoulli-Euler Beam
18
福州大学研究生课程-有限元程序设计
这种高斯积分阶数低于被积函数所有项次精确 积分所需要阶数的积分方案称之为减缩积分。 实际计算表明:采用缩减积分往往可以取得较 完全积分更好的精度。这是由于: 精确积分常常是由插值函数中非完全项的 最高方次要求,而决定有限元精度的是完全多 项式的方次。这些非完全的最高方次项往往不 能提高精度,反而可能带来不好的影响。取较 低阶的高斯积分,使积分精度正好保证完全多 项式方次的要求,而不包括更高次的非完全多 项式的要求,其实质是相当用一种新的插值函 数替代原来的插值函数,从而一定情况下改善 19 Chapter 5 Bernoulli-Euler Beam 了单元的精度。
福州大学研究生课程-有限元程序设计
有限元程序设计
——梁单元,静力问题
谷 音 福州大学土木工程学院
2012
1
福州大学研究生课程-有限元程序设计
§1. 介绍. 框架结构,例如桁架、桥梁 轴力构件 axial elements 杆 受弯构件 flexural elements 梁 平面梁单元 plane beam element
Chapter 5 Bernoulli-Euler Beam
有限元分析实验报告

有限元分析实验报告有限元分析实验报告一、实验基本要求根据实验指导书的要求能够独立的使用ANSYS 软件操作并在计算机上运行,学会判断结果及结构的分析,学会建立机械优化设计的数学模型,合理选用优化方法,独立的解决机械优化设计的实际问题。
二、实验目的1. 加深对机械优化设计方法的理解2. 掌握几种常用的最优化设计方法3. 能够熟练使用ANSYS 软件操作,培养学生解决案例的能力4. 培养学生灵活运用优化设计方法解决机械工程中的具体实例三、实验软件及设备计算机一台、一种应用软件如ANSYS四、实验内容实验报告例题实训1——衍架的结构静力分析图2-2所示为由9个杆件组成的衍架结构,两端分别在1,4点用铰链支承,3点受到一个方向向下的力F y , 衍架的尺寸已在图中标出,单位: m。
试计算各杆件的受力。
其他已知参数如下: 弹性模量(也称扬式模量)E=206GPa;泊松比μ=0.3;作用力F y =-1000N;杆件的2横截面积A=0.125m.一、 ANSYS8.0的启动与设置图2-2 衍架结构简图1.启动。
点击:开始>所有程序> ANSYS8.0> ANSYS ,即可进入ANSYS 图形用户主界面。
图2-4 Preference 参数设置对话框2.功能设置。
电击主菜单中的“Preference ”菜单,弹出“参数设置”对话框,选中“Structural ”复选框,点击“OK ”按钮,关闭对话框,如图2-4所示。
本步骤的目的是为了仅使用该软件的结构分析功能,以简化主菜单中各级子菜单的结构。
3.系统单位设置。
由于ANSYS 软件系统默认的单位为英制,因此,在分析之前,应将其设置成国际公制单位。
在命令输入栏中键入“/UNITS,SI ”,然后回车即可。
(注:SI 表示国际公制单位)二单元类型,几何特性及材料特性定义1.定义单元类型。
2.定义几何特性。
3.定义材料特性。
三衍架分析模型的建立1.生成节点。
梁结构静力有限元分析

机械工程有限元法学号:姓名:专业:年月日引言有限元方法发展到今天。
已经成为一门相当复杂的实用工程技术。
有限元分析的最终目的是还原一个实际工程系统的数学行为特征。
即分析必须针对一个物理原型准确的数学模型。
模型包括所有节点、单元、材料属性、实常数、边界条件以及其他用来表现这个物理系统的特征。
ANSYS(analysis system)是一种融结构、热、流体、电磁和声学于一体的大型CANE通用有限元分析软件,可广泛应用于航空航天、机械、汽车交通、电子等一般工业及科学研究领域。
该软件提供了不断改进的功能清单,具体包括:结构高度非线性分析、电磁分析、计算流体力学分析、设计优化、接触分析、自适应网格划分及利用ANSYS参数设计语言扩展宏命令功能。
ANSYS的学习、应用是一个系统、复杂的工程。
由于它涉及到多方面的知识,所以在学习ANSYS的过程中一定要对ANSYS所涉及到的一些理论知识有一个大概的了解,以加深对ANSYS的理解。
目录引言一、实验目的 (1)二、ANSYS软件应用介绍 (1)三、实验内容 (3)四、实验步骤 (3)1. 建立有限元模型 (3)2. 施加载荷并求解 (9)3、查看实验结果 (11)五、实验结果分析 (13)六、实验总结 (14)参考文献梁结构静力有限元分析一、实验目的1、熟悉有限元建模、求解及结果分析步骤和方法。
2、能利用ANSYS软件对梁结构进行静力有限元分析。
3、加深有限元理论关于网格划分概念、划分原则等的理解。
二、ANSYS软件应用介绍ANSYS是一种广泛的商业套装工程分析软件。
所谓工程分析软件,主要是在机械结构系统受到外力负载所出现的反应,例如应力、位移、温度等,根据该反应可知道机械结构系统受到外力负载后的状态,进而判断是否符合设计要求。
一般机械结构系统的几何结构相当复杂,受的负载也相当多,理论分析往往无法进行。
想要解答,必须先简化结构,采用数值模拟方法分析。
(一)ANSYS软件主要特点1. 唯一能实现多场及多场耦合分析的软件2.唯一实现前后处理、求解及多场分析统一数据库的一体化大型FEA软件3.唯一具有多物理场优化功能的FEA软件4.唯一具有中文界面的大型通用有限元软件5.强大的非线性分析功能,多种求解器分别适用于不同的问题及不同的硬件配置6.支持异种、异构平台的网络浮动,在异种、异构平台上用户界面统一、数据文件全部兼容;强大的并行计算功能支持分布式并行及共享内存式并行;多种自动网格划分技术7. 良好的用户开发环境(二)、ANSYS的分析研究过程1、前处理(1)建模有限元分析的最终目的是还原一个实际工程系统的数学行为特征,即分析必须针对一个物理原型准确的数学模型,模型包括所有节点、单元、材料属性、实常数、边界条件以及其他用来表现这个物理系统的特征。
梁的受力分析及静态试验1

第一章绪论LI引言随着现代社会的进展,经济的提高和科技的进步,我们我国的土木工程建设项目正处于新的高潮期,重大的工程结构,如超大跨桥梁、超高层建筑、大型场馆和大型水利工程等正在不断建成,桥梁工程的进展如今更是突飞猛进。
梁是由支座支撑的主要承受弯矩和剪力的构件。
在机械,建筑等工程中存在大量受弯曲的杆件,例如起重机大梁,火车轮轴等,主要承受的外力以横向力为主。
社会的飞速进展给人们带来了诸多的便利,同时,也使我们我国的建筑土木行业得到了空前的进展,在建筑结构中,不管从它的承载力还是构造等,梁的地位显得尤为重要,由于在建筑结构中,梁是最具有典型特征的元素,它以多种形态展现在人们面前,以线性受力体系为主要的特征。
1. 2国内外梁受力分析讨论的现状20世纪以来,世界各地也相继兴建了很多以斜拉桥、悬索桥为主的大跨桥粱结构。
斜拉桥的主跨也从当时的100米左右进展到了现在的上千米。
90年月到现在,仅我们我国建筑的主跨在400米以上的斜拉桥也已有几十座。
现在世界上跨度超过IOOO米的悬索桥则更是不计其数。
由于这些大跨桥梁不仅可以满意更大流量的交通要求,并且造型轻快美观。
一般都是作为城市交通运输的重要枢纽工程和标志性建筑,投资特别巨大,对国民经济持续、稳定的进展有着特别重要的作用,这些结构假如一旦发生损坏,就会造成特别重大的人员伤亡和经济损失,并且也会产生极坏的社会影响,桥梁损坏造成的严峻损失也将是难以估量的。
桥梁在长期运营过程中也不行避开的会受到环境和有害化学物质的侵蚀,并要承受车辆,风暴、地震、破坏、爆炸、疲惫等因素的作用,这些因素使桥梁的自身性能不断退化,从而导致结构的各部分在没有达到设计年限就发生不同程度的损伤和劣化。
其中,循环荷载作用下的疲惫损伤累积和有损结构在动力荷载作用下的裂纹失稳扩展是造成很多桥梁发生灾难性事故的主要缘由,据美国土木工程协会(ASCE)统计斟,80%〜90%钢结构的破坏与疲惫损伤有关。
有限元实验报告

有限元实验报告有限元实验报告引言:有限元方法是一种数值分析方法,广泛应用于工程领域中的结构力学、流体力学、电磁场等领域。
本实验旨在通过有限元分析软件进行一系列模拟实验,以深入了解有限元方法的原理和应用。
实验一:静力分析静力分析是有限元分析中最基本的一种分析方法。
通过对静力平衡方程的求解,可以得到结构的应力分布和变形情况。
本实验以一个简单的悬臂梁为例,通过有限元软件建立模型,并施加外力,观察梁的变形和应力分布。
实验结果表明,悬臂梁的最大应力出现在悬臂端,而中间部分的应力较小。
此实验验证了有限元分析的准确性和可靠性。
实验二:动力分析动力分析是有限元分析中的另一种重要方法。
它可以用于研究结构在动态荷载下的响应情况,如振动、冲击等。
本实验以一个简单的弹簧质量系统为例,通过有限元软件建立模型,并施加动态荷载,观察系统的振动情况。
实验结果表明,系统的振动频率与质量和弹簧刚度有关,而与外力的大小无关。
此实验验证了有限元分析在动力学问题中的应用价值。
实验三:热力分析热力分析是有限元分析中的另一个重要分析方法。
它可以用于研究结构在热荷载下的温度分布和热应力情况。
本实验以一个简单的热传导问题为例,通过有限元软件建立模型,并施加热荷载,观察结构的温度分布和热应力情况。
实验结果表明,结构的温度分布与热源的位置和强度有关,而热应力与材料的热膨胀系数和热传导系数有关。
此实验验证了有限元分析在热力学问题中的应用能力。
实验四:优化设计优化设计是有限元分析的一个重要应用领域。
通过对结构的几何形状、材料参数等进行优化,可以使结构在给定的约束条件下具有最佳的性能。
本实验以一个简单的梁结构为例,通过有限元软件进行形状优化,以使梁的最大应力最小化。
实验结果表明,通过优化设计可以显著降低结构的应力,提高结构的安全性和可靠性。
此实验展示了有限元分析在工程设计中的重要作用。
结论:通过一系列有限元实验,我们深入了解了有限元方法的原理和应用。
静力分析、动力分析、热力分析和优化设计是有限元分析的主要应用领域,它们在工程设计和分析中发挥着重要的作用。
梁的有限元分析

定义单元类型:1)梁单元;2)弹簧单元
选择弹簧单元后,按“Option”按钮,在K3项 中选择如图所示:
定义实常数
定义材料常数(梁)
创建模型
划分网格:“Mesh”,“Set”
在“Mesh”菜单点击“line”,选择表示梁的二直线, “OK”,在弹出的菜单中的单元长度输入0.25,“OK”。
2.梁、弹簧——2D问题
有一水平梁,全长4米,左端固定,右端3米 处有一弹簧悬吊,弹簧刚度为5000N/m,右 端点受大小为3000kg的向下载荷,梁的截面 尺寸为30mmX20mm,梁的弹性模量为 2X1011 Pa,泊松比为0.3。求梁的变形。
0.5
3
1
计算性矩=B*H3/12=4.5*10-8m4 截面高H=3*10-2m 弹簧刚度K=5000N/m E=2e11Pa Pxy=0.3
梁的有限元分析
2006年10月
梁的有限元分析——2D问题
1.有一简支梁,载荷和边界条件如图所示, L=6m,梁的截面面积A=0.0072m2,高 H=0.42m,惯性矩=0.00021m4,材料弹性模 量E=2.06e11N/m2,P=10000N。求支反力 和挠度。
要点 1)实常数 2)分网密度控制 3)如何加载:左:UX,UY,右UY 4)后处理结果的观察
在“Mesh”菜单中按“Mesh”,选择表示梁的二
直线,“OK”,进行显示控制,标出各节点号。
对弹簧进行网格划分
在“Mesh”菜单点击“line”,选择表示弹簧的直线, “OK”,在弹出的菜单中的单元等分数输入“1”, (如果二等分表示两弹簧串联),“OK”。
在“Mesh”菜单中按“Mesh”,选择表示弹簧的
利用有限元仿真软件ansys对3D梁进行静力学分析
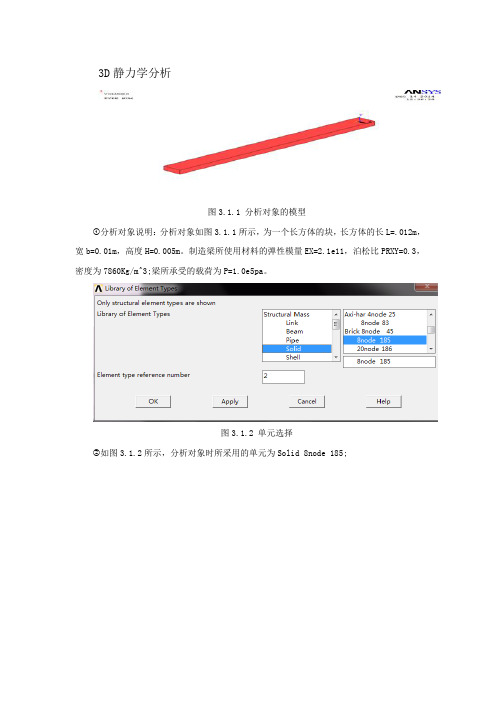
3D静力学分析
图3.1.1 分析对象的模型
①分析对象说明:分析对象如图3.1.1所示,为一个长方体的块,长方体的长L=.012m,宽b=0.01m,高度H=0.005m。
制造梁所使用材料的弹性模量EX=2.1e11,泊松比PRXY=0.3,密度为7860Kg/m^3;梁所承受的载荷为P=1.0e5pa。
图3.1.2 单元选择
②如图3.1.2所示,分析对象时所采用的单元为Solid 8node 185;
图3.1.3 划分网格后的模型
如图3.1.2所示,建立模型并对模型划分网格,经统计节点数量为286,单元数量为272。
图3.1.4施加约束后的模型
④模型网格划分完成后,在模型的左端施加UX、UY、UZ的约束,并在模型的上表面施加大小P=100000Pa的均布载荷,如图3.1.4所示。
图3.1.5 模型的变形图
⑤约束和载荷施加完成后,对模型进行计算分析的到模型快在均布载荷下各部分的变形状况,如图3.1.5所示。
以及X、Y、Z三个方向的应力分别如图3.1.6、图3.1.7、图3.1.8所示。
图3.1.6 X-方向上的应力图
图3.1.7 Y-方向上的应力图
图3.1.8 Z-方向上的应力图
通过分析X、Y、Z三个方向的应力图可以看出,由约束边界自远而近三个方向的力的变化都是逐渐增大的,越靠近约束边界,应力集中越是明显。
实验一梁结构静力有限元分析(精)
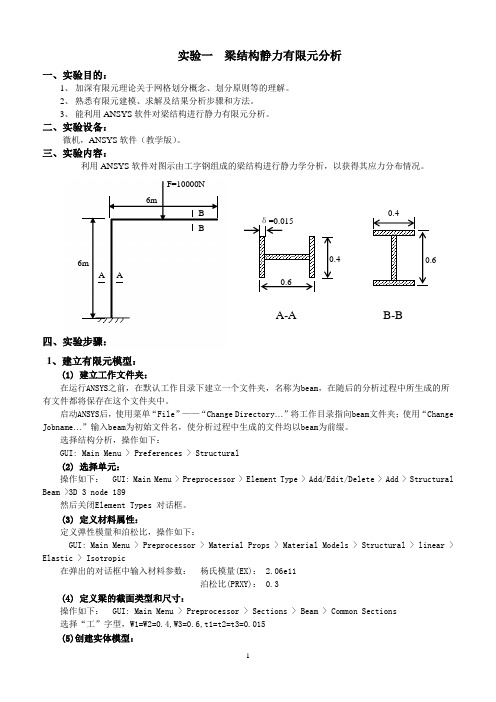
实验一 梁结构静力有限元分析一、实验目的:1、 加深有限元理论关于网格划分概念、划分原则等的理解。
2、 熟悉有限元建模、求解及结果分析步骤和方法。
3、 能利用ANSYS 软件对梁结构进行静力有限元分析。
二、实验设备:微机,ANSYS 软件(教学版)。
三、实验内容:利用ANSYS 软件对图示由工字钢组成的梁结构进行静力学分析,以获得其应力分布情况。
A-A B-B四、实验步骤:1、建立有限元模型:(1) 建立工作文件夹:在运行ANSYS 之前,在默认工作目录下建立一个文件夹,名称为beam ,在随后的分析过程中所生成的所有文件都将保存在这个文件夹中。
启动ANSYS 后,使用菜单“File ”——“Change Directory …”将工作目录指向beam 文件夹;使用“Change Jobname …”输入beam 为初始文件名,使分析过程中生成的文件均以beam 为前缀。
选择结构分析,操作如下:GUI: Main Menu > Preferences > Structural(2) 选择单元:操作如下: GUI: Main Menu > Preprocessor > Element Type > Add/Edit/Delete > Add > Structural Beam >3D 3 node 189然后关闭Element Types 对话框。
(3) 定义材料属性:定义弹性模量和泊松比,操作如下:GUI: Main Menu > Preprocessor > Material Props > Material Models > Structural > linear > Elastic > Isotropic在弹出的对话框中输入材料参数: 杨氏模量(EX): 2.06e11泊松比(PRXY): 0.3(4) 定义梁的截面类型和尺寸:操作如下: GUI: Main Menu > Preprocessor > Sections > Beam > Common Sections选择“工”字型,W1=W2=0.4,W3=0.6,t1=t2=t3=0.015(5)创建实体模型:F=10000N 6m6m A A B B首先定义3个关键点,然后通过关键点生成梁实体模型。
有限元程序设计-梁单元静力问题共56页文档

31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
Hale Waihona Puke 有限元程序设计-梁单元静力 问题
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
静力结构的有限元分析
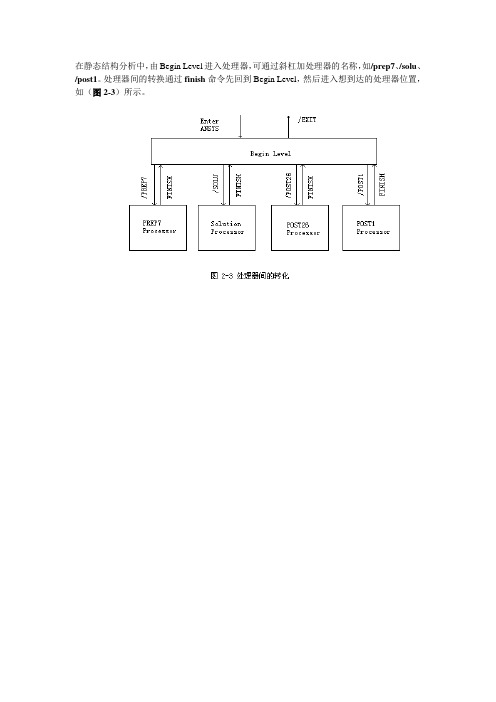
在静态结构分析中,由Begin Level进入处理器,可通过斜杠加处理器的名称,如/prep7、/solu、/post1。
处理器间的转换通过finish命令先回到Begin Level,然后进入想到达的处理器位置,如(图2-3)所示。
【例2-1】考虑悬臂梁如图2-2,求x=L变形量。
已知条件:杨氏系数E=200E9;截面参数:t=0.01m, w=0.03m, A=3E-4,I=2.5E-9;几何参数:L=4m, a=2m, b=2m;边界外力F=2N,q=0.05N/m.使用ANSYS解决该问题的命令如下:/FILNAM,EX2-1 ! 定义文件名/TITLE,CANTILEVER BEAM DEFLECTION !定义分析的标题/UNITS,SI !定义单位制(注意观察输出窗口的单位)/PREP7 !进入前置处理ET,1,3 !定义元素类型为beam3MP,EX,1,200E9 ! 定义杨氏模量R,1,3E-4,2.5E-9,0.01 !定义实常数(要严格根据该元素类型的说明文档所给出的实常数格式)N,1,0,0 !定义第1号节点X坐标为0,Y坐标为0N,2,1,0 !定义第2号节点X坐标为1,Y坐标为0N,3,2,0 !定义第3号节点X坐标为2,Y坐标为0N,4,3,0 !定义第4号节点X坐标为3,Y坐标为0N,5,4,0 !定义第5号节点X坐标为4,Y坐标为0E,1,2 !把1、2号节点相连构成单元,系统将自定义为1号单元E,2,3 !把2、3号节点相连构成单元,系统将自定义为2号单元E,3,4 !把3、4号节点相连构成单元,系统将自定义为3号单元E,4,5 !把4、5号节点相连构成单元,系统将自定义为4号单元FINISH !退出该处理层/SOLU !进入求解处理器D,1,ALL,0 !对1节点施加约束使它X,Y向位移都为0F,3,FY,-2 !在3节点加集中外力向下2NSFBEAM,3,1,PRES,0.05 !在3 号元素的第1个面上施加压力(beam3有四个面可通过命令help,beam3查看,任何一个命令都可以通过help,命令查看帮助文档)SFBEAM,4,1,PRES,0.05 !同上在4号元素的第1个面加压力SOLVE !计算求解FINISH !完成该处理层/POST1 !进入后处理SET,1,1 !查看子步1,在有限元中复杂的载荷可以看做简单的载荷相互叠加,在ANSYS 中每施加一类载荷都可以进行一次求解,可以查看它对结构的影响,称为子步。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 梁结构静力有限元分析
一、实验目的:
1、 加深有限元理论关于网格划分概念、划分原则等的理解。
2、 熟悉有限元建模、求解及结果分析步骤和方法。
3、 能利用ANSYS 软件对梁结构进行静力有限元分析。
二、实验设备:
微机,ANSYS 软件(教学版)。
三、实验内容:
利用ANSYS 软件对图示由工字钢组成的梁结构进行静力学分析,以获得其应力分布情况。
A-A B-B
四、实验步骤:
1、建立有限元模型:
(1) 建立工作文件夹:
在运行ANSYS 之前,在默认工作目录下建立一个文件夹,名称为beam ,在随后的分析过程中所生成的所有文件都将保存在这个文件夹中。
启动ANSYS 后,使用菜单“File ”——“Change Directory …”将工作目录指向beam 文件夹;使用“Change Jobname …”输入beam 为初始文件名,使分析过程中生成的文件均以beam 为前缀。
选择结构分析,操作如下:
GUI: Main Menu > Preferences > Structural
(2) 选择单元:
操作如下: GUI: Main Menu > Preprocessor > Element Type > Add/Edit/Delete > Add > Structural Beam >3D 3 node 189
然后关闭Element Types 对话框。
(3) 定义材料属性:
定义弹性模量和泊松比,操作如下:
GUI: Main Menu > Preprocessor > Material Props > Material Models > Structural > linear > Elastic > Isotropic
在弹出的对话框中输入材料参数: 杨氏模量(EX): 2.06e11
泊松比(PRXY): 0.3
(4) 定义梁的截面类型和尺寸:
操作如下: GUI: Main Menu > Preprocessor > Sections > Beam > Common Sections
选择“工”字型,W1=W2=0.4,W3=0.6,t1=t2=t3=0.015
(5)创建实体模型:
F=10000N 6m
6m A A B B
首先定义3个关键点,然后通过关键点生成梁实体模型。
定义关键点操作如下:
GUI: Main Menu > Preprocessor > Modeling > Create > Keypoints > In Active CS
关键点坐标参数如下:
1#关键点 X=0,Y=0,Z=0
2#关键点 X=0,Y=6,Z=0
3#关键点 X=6,Y=6,Z=0
连线操作如下:
GUI: Main Menu > Preprocessor > Modeling > Create > Lines > Lines > Straight Line 将1和2、2和3连成直线。
(6)划分网格
①首先要设定各梁的截面方向,操作如下:
GUI: Main Menu > Preprocessor > Meshing > Mesh Attributes > Picked Lines
选中12线后点“OK”,在弹出对话框中“Pick Orientation Keypoint”项选为Yes,选中第3点为参考点。
同样,选中23线后以第1点为参考点。
②划分网格为10份,操作如下:
GUI: Main Menu > Preprocessor > Meshing > MeshTool > Lines set (NDIV处输入10) > Mesh
③划分完后显示出截面可看得更清楚,操作如下:
菜单“Plotctrls” > Style > Size and Shape … > Display of element 项为 On Ctrl键+鼠标右键可调角度。
④保存数据库。
GUI: Toolbar >SAVE_DB
2、施加载荷并求解:
(1)定义约束
定义1#关键点的约束,操作如下:
GUI: Main Menu > Solution > Define Loads > Apply > Structural > Displacement > On Keypoints 选择1#关键点,单击OK按钮。
在被约束自由度(DOFs to be constrained)列表中选”All DoF”限制所有,单击OK按钮。
这时在图形窗口中可看到1#关键点处出现箭头,表示此点已被约束,箭头表示被约束的方向。
(2) 施加载荷
在梁的上边中间施加向下的载荷Fy=-10000N,操作如下:
GUI:Solution > Define Loads > Apply > Structural > Force/ Moment > On Nodes
弹出Apply F/M on Nodes 对话框,键入Fy载荷值-10000,单击OK按钮。
(3) 求解
GUI:Solution > Solve > Current LS
3、查看分析结果:
(1)查看模型变形前后图
GUI: Main Menu > General Postproc > Plot Results > Deformed Shape> Def+undeformed
保存图使用菜单“PlotCtrls” > Hardcopy > To file…
(2)查看等效应力
显示等效应力等值线图,操作如下:
GUI: Main Menu > General Postproc > Plot Results > Nodal Solu > Stress > von Mises stress
单击OK按钮。
保存图使用菜单“PlotCtrls” > Hardcopy > To file…
(3)查看变形过程动画
菜单PlotCtrls > Animate > Deformed Results > Stress > von Mises SEQV
动画内容自动在工作目录下保存为avi格式。
