二次函数与一元二次方程的关系(通用)解析
初中数学一元二次方程与二次函数的关系

一元二次方程与二次函数的关系方程与函数有着密切的联系,我们可以利用方程(组)解决函数问题,也可以利用函数解决方程(组)问题.我们知道,二次函数的一般形式是,而一元二次方程的一般形式是.显然当二次函数中时就能得到一元二次方程,所以一元二次方程与二次函数是特殊与一般的关系.一、知识链接透彻理解数学概念,提升你的数学内涵!1.利用一元二次方程解决二次函数问题:(1)对于二次函数来说,当时,就得一元二次方程,因此我们可以利用一元二次方程求二次函数图像与轴的交点坐标.进一步我们还可以探讨一元二次方程的取值与二次函数图像与轴的交点坐标的情况之间的关系:①当时,一元二次方程有两个不相等的实数根,抛物线与轴有两个交点;②当时,一元二次方程有两个相等的实数根,抛物线与轴有唯一交点(这个唯一交点就是抛物线的顶点);③当时,一元二次方程没有实数根,抛物线与轴没有交点(抛物线要不全部在轴上方,要不全部在轴下方).c bx ax y ++=2)0(≠a 02=++c bx ax )0(≠a c bx ax y ++=2)0(≠a 0=y 02=++c bx ax )0(≠a c bx ax y ++=2)0(≠a 0=y 02=++c bx ax )0(≠a x ac b 42-=∆x 042>-=∆ac b 02=++c bx ax c bx ax y ++=2x 042=-=∆ac b 02=++c bx ax c bx ax y ++=2x 042<-=∆ac b 02=++c bx ax c bx ax y ++=2x x x(2)我们还可以利用一元二次方程根与系数的关系解决有关二次函数图像与轴交点横坐标的有关求值问题:当一元二次方程有两个不相等的实数根、时,抛物线与轴交于两点A(,0)、B(,0),此时有,·.此时抛物线与轴两交点的距离为: AB==(公式①). (3)推广:我们可以利用一元二次方程来研究抛物线与与直线(当时为一次函数的图像,当时为平行于轴或与轴重合的一条直线)的交点情况.2.利用二次函数解决一元二次方程问题一方面,反过来,我们可以根据抛物线与x 轴的交点情况去判断一元二次方程的根的情况.另一方面,我们还可以利用二次函数图像比较直观地去解决有关一元二次方程的解的问题以及有关系数的值的问题.二、典例精讲参与数学解题过程,品味数学内在魅力! 例1(福州市中考题)已知二次函数的图象如图10-1所示,则下列结论正确的是()A .a >0B .c <0C .b 2-4ac <0D .a +b +c >0 x 02=++c bx ax 1x 2x c bx ax y ++=2x 1x 2x a bx x -=+211x ac x =2x 21x x -221)(x x -212214)(x x x x -+=224a ac b -=a ∆=c bx ax y ++=2b kx y +=0≠k 0=k x x b y =c bx ax y ++=202=++c bx ax c bx ax y ++=2分析:a决定抛物线的开口方向,c决定抛物线与y轴的交点情况,抛物线的对称轴由a、b共同决定,b2-4ac决定抛物线与x轴的交点情况.本题中,由于抛物线开口方向向下,因此a<0;抛物线与y轴的交点(0,c)在x轴上方,因此c>0;由于抛物线对称轴在y轴右侧,所以x=-b2a>0,所以b>0;由于抛物线与x轴有两个交点,所以b2-4ac>0.a+b+c是x=1时的函数值,而图像上点(1,a+b+c)在x轴上方,所以a+b+c>0.答案:D.技巧提升:本题是二次函数图像信息探究问题.解决这类问题就应熟练掌握a、b、c、x=-b2a、a+b+c、b2-4ac等与抛物线的位置特征之间的关系.例2(徐州市中考题)平面直角坐标系中,若平移二次函数y=(x-2009)(x-2008)+4的图象,使其与x轴交于两点,且此两点的距离为1个单位,则平移方式为()A.向上平移4个单位B.向下平移4个单位C.向左平移4个单位D.向右平移4个单位分析:因为二次函数y=(x-2009)(x-2008)的图象与x轴交于点(2008,0)和(2009,0),这两点间的距离为1,而二次函数y=(x-2009)(x-2008)的图象可由二次函数y=(x-2009)(x-2008)+4的图象向下平移4个单位得到. 答案:B .技巧提升:本题也可以倒过来想,容易知道抛物线y=(x-2009)(x-2008)+4经过点(2009,4)、(2008,4),这两点的距离围为1,要将这两点平移到x 轴上,应将图像向下平移4个单位.研究抛物线平移问题,一般我们要抓住特征对应点来分析.例3(镇江市中考题)已知实数x ,y 满足x 2+3x +y -3=0,则x +y 的最大值为.分析:可以利用二次函数最值方法来求,由x 2+3x +y -3=0得,x +y =-x 2-2x +3=-(x +1)2+4,所以当x =-1时,x +y 最大值为4;也可以尝试用换元法解决,设,则原方程可化为,因为这个关于必有实数根,所以,解得,所以(即x +y )的最大值为4.答案:4.技巧提升:第一种分析方法,由等式是一个关于x 的二次方程,也是关于y 的一次方程,所以可以联想到把式子转化为“x +y ”关于x 的二次函数,利用函数知识求解;第二种分析方法将问题转化为求关于x 的一元二次方程的参数的取k y x =+0322=-++k x x x 0)3(44≥--=∆k 4≤k k k值范围问题来解决,有异曲同工之效.例4(日照市中考题)如图10-2,是二次函数y =ax 2+bx+c 图象的一部分,其对称轴为直线x =1,若其与x 轴一交点为A(3,0),则由图象可知,不等式ax 2+bx+c <0的解集是.分析:由于已知了抛物线与x 轴的一交点为A (3,0),且与对称轴x =1的距离为2,所以根据抛物线的轴对称性可知抛物线与x 轴的另一交点应在对称轴左侧,且与直线x =1的距离也为2,其坐标应为(-1,0).观察图像可知,当-1<x <3时,抛物线在x 轴下方,所以不等式ax 2+bx +c <0的解集是-1<x <3答案:-1<x <3.技巧提升:不等式ax 2+bx +c >0(或<0)的解集就是二次函数y =ax 2+bx+c 的图象在x 轴上(下)方的点所对应的x 的取值范围,因此不等式ax 2+bx +c >0(或<0)的解集与抛物线与x 轴的交点的横坐标有关,所以解决一般这类问题要先利用一元二次方程求出抛物线与x 轴的交点坐标. 例5(咸宁市中考题)已知二次函数的图象与轴两交点的坐标分别为(,0),(,0)().(1)证明;(2)若该函数图象的对称轴为直线,试求二次函数的最小值. 分析:本题是二次函数问题,可借助一元二次方程与二次函2y x bx c =+-x m 3m -0m ≠243c b =1x =数的关系来解决.解:(1)证明:法一:依题意,,是一元二次方程的两根. 根据一元二次方程根与系数的关系,得,. ∴,,∴.法二:由题意得,①—②得,因为,所以.代入①得,所以,所以,,所以.法三:由抛物线的轴对称性可知其对称轴为,可得(下同法二).(2)解:法一:依题意,,∴. 由(1)得. ∴.∴二次函数的最小值为.法二:因为函数图象与轴两交点的坐标分别为(,0),(,0),所以由抛物线的轴对称性可知抛物线的对称轴是直线, 所以,所以,故抛物线与x 轴的两交点为、,所以抛物线的解析式为,当时,,∴二次函数的最小值为.技巧提升:本题两小题都给出了不同的解法,应注意体会不同解法的异同.一题多解,多中选优,平时解题的思考会带来解题能力的提升.例6(杭州市中考题)定义[]为函数的特征数,m 3m -20x bx c +-=(3)m m b +-=-(3)m m c ⨯-=-2b m =23c m =224312c b m ==⎩⎨⎧=--=-+039022c bm m c bm m 0482=+-bm m 0m ≠m b 2=0222=-+c m m 23m c =2124m c =22123m b =243b c =2)3(2m m b x -+=-=m b 2=12b -=2b =-2233(2)344c b ==⨯-=2223(1)4y x x x =--=--4-x m 3m -m x -=1=-m 1-=m )0,1(-)0,3(32)3)(1(2--=-+=x x x x y 1=x 4321-=--=最小y 4-,,a b c 2y ax bx c =++下面给出特征数为[2m,1-m,-1–m]的函数的一些结论:①当m =-3时,函数图象的顶点坐标是(,);②当m>0时,函数图象截x 轴所得的线段长度大于;③当m<0时,函数在x>时,y 随x 的增大而减小;④当m ≠0时,函数图象经过同一个点.其中正确的结论有()A .①②③④B .①②④C .①③④D .②④分析:把m =-3代入[2m ,1–m,–1–m],得a =-6,b =4,c =2,函数解析式为y =-6x 2+4x+2,易求出其图像顶点为(,),故①正确;当a=2m 、b=1-m 、c=-1-m 时,△=b 2-4ac =(1-m)2-4×2m ×(-1-m)=(3m+1)2,根据公式①可知函数图象截x 轴所得的线段长度为=,当m >0时,=>,故②正确;∵m <0,∴抛物线开口向下.∵抛物线对称轴为x =-==,∴在对称轴左侧,即当时,y 随x 的增大而增大,对称轴右侧,即当时,y 随x 的增大而减小.在∵<,所以当x>时,图像有可能一部分在对称轴左侧,一部分在对称轴右侧,故③不正确;对于抛物线31382341313821x x -a ∆=m m 2)13(2+=m m 213+21x x -m m m 2123213+=+322b a 122m m--⨯1144m -m x 4141-<m x 4141->141144m -41y=2mx 2+(1-m)x-1-m 时,当x=1时,y=2m+1-m+(-1-m)=0,∴当m ≠0时,抛物线一定经过(1,0)这个点,故④正确. 答案:B.技巧提升:本题综合考查了二次函数的各个方面的知识,比如二次函数图像顶点公式、二次函数的增减性、函数图像上的顶点问题、抛物线与x 轴交点之间的距离等.其中第③个问题体现了一元二次方程与二次函数关系的核心知识,应引起重视.例7(2008年扬州市中考题改编)若关于x 的一元二次方程的两根在1与2之间(不含1和2),则a 的取值范围是.分析:这是一个一元二次方程问题,如果直接用一元二次方程的根来列不等式组,需要列5个不等式,也就是:、、、 、,这样将会很麻烦.那么如何解才能比较简单呢?如果我们利用二次函数图像来帮助分析,0522=++ax x 0402>-=∆a 04402>-+-a a 14402<-+-a a 04402>---a a 14402<---a a解法将简单得多.令,如图10-3我们可以画出这个函数的大致图像.根据图像对称轴在y 轴右侧,可知,解得.再根据可得.根据图像特征可知图像上横坐标为1和2的两个点的纵坐标都是正数,所以可得,可解得.这样就能得到a 的取值范围是.答案:.技巧提升:利用一元二次方程解决二次函数问题,这种题型比较多,也容易想到.而反过来,利用二次函数解决一元二次方程问题,这种题型就比较少了,遇到的时候也不容易想到.以后遇到一元二次方程问题,用方程知识不好解决时,可以尝试用用二次函数.例8(潍坊市中考题)已知函数y 1=x 2与函数y 2=-12x +3的图象大致如图10-4,若y 1<y 2,则自变量x 的取值范围是()A .-12 <x <2B .x >2或x <-32C .-2<x <32D .x <-2或x >32分析:当y 1<y 2时,在图象中反映的是直线在抛物线的上方,522++=ax x y 04>-a 0<a 0402>-=∆a 102-<a ⎩⎨⎧>+⋅+⨯>+⋅+⨯052220511222a a 213->a 102213-<<-a 102213-<<-a也就是两函数图像两个交点之间的部分,所以我们要求出这两个函数图像的交点.由解得、,因此满足要求的自变量x 的取值范围应该是-2<x <32. 答案:C .技巧提升:作为选择题,解答本题时,也可以不解方程组.先根据直线在抛物线的上方排除答案B 、D ,再根据两函数图像的右交点更靠近对称轴(y 轴)可排除答案A .例9(2007年“《数学周报》杯”全国初中数学竞赛试题)已知点A ,B 的坐标分别为(1,0),(2,0).若二次函数的图象与线段AB 恰有一个交点,则的取值范围是.分析:要注意抛物线与线段AB 恰有一个交点应包含两种情况:⑴抛物线与x 轴只有一个交点,这个交点恰好在线段AB 上.由判别式解得.当时,,不合题意;当时,,符合题意.⑵抛物线与x 轴有两个交点,其中只有一个在线段AB上.设抛物线与x 轴的两个交点为C ()、D (),则.若只有点D 在线段AB 上,则,,显然,不合题意;若只有点C 在线段AB 上,则⎪⎩⎪⎨⎧+-==3212x y x y ⎩⎨⎧=-=4211y x ⎪⎩⎪⎨⎧==492322y x ()233y x a x =+-+a ()233y x a x =+-+()233y x a x =+-+012)3(2=--=∆a 0∆=323a =±323a =+123x x ==-323a =-123x x ==()233y x a x =+-+0,1x )0,(2x 21x x <321=x x 101<<x 212≤≤x 321<x x,.当点D 与点A 、B 都不重合时,函数如图10-5所示,从图像可以看出,图像上横坐标为1的点在x 轴上方,横坐标为2的点在x 轴下方,所以,解得.当当点D 与点A 重合时,由,得,此时,,符合题意;当点D 与点B 都重合时,由,得,此时,,不符合题意.综上所述,的取值范围是≤,或者.答案:≤,或者技巧提升:本题中要注意对不同情况进行分类讨论,既要考虑到一般情况,还要考虑到特殊情况.例10(全国初中数学联合竞赛试题)设是大于2的质数,k 为正整数.若函数的图象与x 轴的两个交点的横坐标至少有一个为整数,求k 的值.分析:函数图象与x 轴两交点的横坐标就是方程的两根,可考虑利用一元二次方程根与系数的关系来解决.解:由题意知,方程的两根中至少有一个为整数.由根与系数的关系可得,从而有①211≤≤x 22>x ⎩⎨⎧<+-+>+-+03)3(2403)3(1a a 112a -<<-031)3(12=+⨯-+a 1a =-11=x 32=x 032)3(22=+⨯-+a 12a =-21=x 232=x a 1-12a <-3a =-1-12a <-3a =-p 4)1(2-+++=p k px x y 04)1(2=-+++p k px x 04)1(2=-+++p k px x 21,x x 4)1(,2121-+=-=+p k x x p x x p k x x x x x x )1(4)(2)2)(2(212121-=+++=++(1)若,则方程为,它有两个整数根和.(2)若,则.因为为整数,如果中至少有一个为整数,则都是整数.又因为为质数,由①式知或.不妨设,则可设(其中m 为非零整数),则由①式可得,故,即.又,所以,即② 如果m 为正整数,则,,从而,与②式矛盾. 如果m 为负整数,则,,从而,与②式矛盾.因此,时,方程不可能有整数根. 综上所述,.技巧提升:由于方程两根之和为质数,所以只要有一个根是整数,则另一个根也必然是整数.我们也可以从方程根的1k =0)2(22=-++p px x 2-2p -1k >01>-k 12x x p +=-21,x x 21,x x p 2|1+x p 2|2+x p 2|1+x p 12x mp +=212k x m-+=121(2)(2)k x x mp m-+++=+1214k x x mp m-++=+12x x p +=-14k p mp m--+=+41)1(=-++mk p m (1)(11)36m p +≥+⨯=10k m->1(1)6k m p m-++>(1)0m p +<10k m-<1(1)0k m p m-++<1>k 04)1(2=-+++p k px x 1=k p特征来分析.根据一元二次方程求根公式可知方程的根应为,要使得其根为整数,根的判别式的值必须是完全平方数.由于是质数,因此当的值是完全平方数时,关于的二次三项式必然等于(为非负整数),也就是说应成为关于的一个完全平方式,因此可得其,可解得,(舍去).三.学力训练检测自己能力,体验成功乐趣! 1.选择题:(1)(天津市中考题)已知二次函数()的图象如图10-6所示,有下列结论:①;②;③;④.其中,正确结论的个数是() A .1B .2C .3D .4(图10-6)(图10-7)(图10-8)(2)(百色市中考题)二次函数y=-x2+bx +c的图象如图10-7所示,下列几个结论:①对称轴为x=2;②当y≤0时,x <0或x >4;③函数解析式为y =-x(x -4);④当04)1(2=-+++p k pxx216)1(42++-±-=p k p p x 16)1(42++-p k p p 16)1(42++-p k p p 16)1(42++-p k p 2)(n p ±n 16)1(42++-p k p p 064)1(162=-+=∆k 11=k 32-=k 2y ax bx c =++0a ≠240bac ->0abc >80a c +>930a b c ++<x ≤0时,y 随x 的增大而增大.其中正确的结论有() A .①②③④ B .①②③ C .①③④ D .①③(3)(“《数学周报》杯”2008年全国初中数学竞赛试题)把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m ,n ,则二次函数的图象与x 轴有两个不同交点的概率是()A .B .C .D .(4)(2008年全国初中数学竞赛浙江赛区初赛试题)在平面直角坐标系中,如果横坐标与纵坐标都是整数的点称为整点,将二次函数y =-x2+6x -274的图象与x 轴所围成的封闭图形染成红色,则在此红色区域内部及其边界上的整点的个数是( ) A .5B .6 C .7 D .82.填空题:(1)(新疆维吾尔自治区中考题)抛物线y =-x 2+bx+c 的部分图象如图所示,若y >0,则x 的取值范围是_______.(2)(玉溪市中考题)如图10-9是二次函数在平面直角坐标系中的图象,根据图形判断①>0;②++<0;③2-<0;④2+8>4中正确的是(填写序号).(3)(2006年全国初中数学联合竞赛辽宁卷)函数y =x 2-2006|x |+2008的图象与x 轴交点的横坐标之和等于2y x mx n =++51249173612)0(2≠++=a c bx ax y c a b c a b b a a c__________.(4)(全国初中数学联合竞赛题)二次函数的图象与轴正方向交于A ,B 两点,与轴正方向交于点C .已知,,则.3.(佛山市中考题)(1)请在坐标系中画出二次函数的大致图象;(2)根据方程的根与函数图象的关系,将方程的根在图上近似的表示出来(描点); (3)观察图象,直接写出方程的根.(精确到0.1)(图10-10)4.(长沙市中考题)已知:二次函数的图象过点(1,0),一次函数图象经过原点和点(1,-b ),其中a>b>0且a 、b 为实数.(1)求一次函数的表达式(用含b 的式子表示); (2)试说明:这两个函数的图象交于不同的两点; (3)设(2)中的两个交点的横坐标分别为、,求的范围.c bx x y ++=2x y AC AB 3=︒=∠30CAO c =xx y 22-=122=-x x 122=-x x22y ax bx =+-1x 2x 12||x x -5.(肇庆市中考题)已知二次函数的图象过点(2,1).(1)求证:; (2)求的最大值;(3)若二次函数的图象与轴交于点,,,,的面积是,求.6.(2007年全国初中数学联合竞赛试题)设为正整数,且,二次函数的图象与轴的两个交点间的距离为,二次函数的图象与轴的两个交点间的距离为.如果对一切实数恒成立,求的值.7.(2009年“《数学周报》杯”全国初中数学竞赛试题)已知抛物线与动直线有公共点,,且.(1)求实数t 的取值范围;(2)当t 为何值时,c 取到最小值,并求出c 的最小值. 8.(全国初中数学联合竞赛试题)已知二次函数的图象经过两点P ,Q .(1)如果都是整数,且,求的值. (2)设二次函数的图象与轴的交点为A 、B ,与轴的交点为C.如果关于的方程的两个根都是整12+++=c bx x y P 42--=b c bc x 1(x A )02(x B )0ABP ∆43b n m ,2≠m mt x mt x y 3)3(2--+=x 1d nt x n t x y 2)2(2+-+-=x 2d 21d d ≥t n m ,2y x =c x t y --=)12(),(11y x ),(22y x 3222221-+=+t t x x 2y x bx c =+-(1,)a (2,10)a ,,a b c 8c b a <<,,a b c 2y x bx c =+-x y x 20x bx c +-=数,求△ABC 的面积.第10讲.一元二次方程与二次函数的关系参考答案 1.选择题:(1)D ;(2)C ;(3)C ;(4)C ;2.填空题:(1)-3<x <1;(2)②、④;(3)0;(4).3.解:(1)如图所示;(2)如图所示,抛物线与直线y=1的两个交点的横坐标就是方程的两根,也就是x 轴上点C 、点D 所表示的数; (3)方程的根为-0.4、 2.4.4.解:(1)设一次函数的表达式为y =kx(k 为常数,k ≠0).∵一次函数图象经过原点和点(1,-b ),∴把点(1,-b ),代入y =kx ,得-b =k,即k =-b . ∴一次函数的表达式为y =-bx . (2)∵y=ax 2+bx -2过(1,0)即a+b=2 由得①∵△=19x x y 22-=122=-x x 122=-x x≈1x ≈2x 2(2)2y bxy b x bx =-⎧⎨=-+-⎩22(2)20ax a x +--=224(2)84(1)120a a a -+=-+>∴方程①有两个不相等的实数根,∴方程组有两组不同的解, ∴两函数有两个不同的交点.(3)∵两交点的横坐标x 1、x 2分别是方程①的解 ∴ ∴或由求根公式得出∵a>b>0,a+b=2,∴2>a>1 令函数,∵在1<a<2时y 随a 增大而减小, ∴,∴. 5.解:(1)∵的图象过点(2,1) ∴ ∴(2) 当时,此时, ∴当时,有最大值,最大值为2。
二次函数与一元二次方程的关系

(5)a+b+c的符号:因为x=1时,y=a+b+c,所以 a+b+c的符号由x=1时,对应的y值决定。 当x=1时,y>0,则a+b+c>0 当x=1时,y<0,则a+b+c<0 当x=1时,y=0,则a+b+c=0 (6)a-b+c的符号:因为x=-1时,y=a-b+c,所以a-b+c 的符号由x=-1时,对应的y值决定。 当x=-1,y>0,则a-b+c>0 当x=-1,y<0,则a-b+c<0 当x=-1,y=0,则a-b+c=0
快速回答:
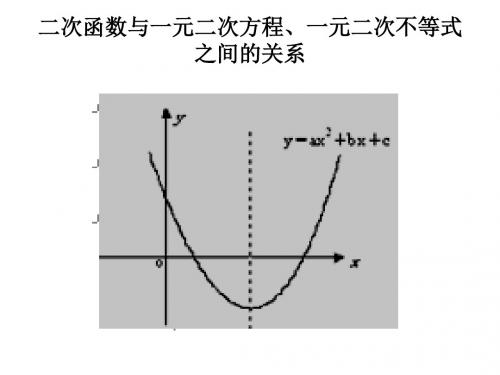
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的 符号: y
根据图像可得: 1、a>0
o
x
b 2、>0 2a
3、△=b² -4ac=0 4、C>0
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的 符号: y
根据图像可得: 1、a>0
o
b 2、=0 2a
x
3、△=b² -4ac=0 4、C=0
若抛物线y=ax2+bx+c与x轴有交点,则
b2 – 4ac ≥0
例(1)如果关于x的一元二次方程 x2-2x+m=0有两个 1 相等的实数根,则m=____ ,此时抛物线 y=x21 2x+m与x轴有 8x +c的顶点在 x轴 16 上,则c=____ .
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的 符号: y
根据图像可得: 1、a>0
《二次函数与一元二次方程》资料二次函数与一元二次方程知识点

二次函数与一元二次方程知识点
1.二次函数与一元二次方程的关系(二次函数与x 轴交点情况):
一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况.
图像与x 轴的交点个数:
① 当240b ac ∆=->时,图像与x 轴交于两点()()1200A x B x ,
,,12()x x ≠,其中12x x ,是一元二次方程()200ax bx c a ++=≠的两根. 12x x ,和的一半恰好是对称轴的横坐标.
② 当0∆=时,图像与x 轴只有一个交点;
③ 当0∆<时,图像与x 轴没有交点.
当0a >时,图像落在x 轴的上方,无论x 为任何实数,都有0y >;
当0a <时,图像落在x 轴的下方,无论x 为任何实数,都有0y <.
2. 抛物线2y ax bx c =++的图像与y 轴一定相交,交点坐标为(0,)c ;
3. 二次函数常用解题方法总结:
(1)求二次函数的图像与x 轴的交点坐标,需转化为一元二次方程;
(2)求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;或者依据函数特点确定自变量能使函数取得最大值的值,并将其带入到表达式中求出最值;
(3)根据图象的位置判断二次函数2y ax bx c =++中a ,b ,c 的符号,或由二次函数中a , b ,c 的符号判断图象的位置,要数形结合;
(4)二次函数与一次函数的交点,可通过联立方程求解,从而求出交点坐标。
二次函数与一元二次方程

二次函数与一元二次方程【知识梳理】(一)二次函数与一元二次方程的关系一元二次方程ax 2+bx+c=0(a ≠0)的解的情况等价于抛物线y=ax 2+bx+c(c ≠0)与直线y=0(即x 轴)的公共点的个数。
抛物线y=ax 2+bx+c(a ≠0)与x 轴的公共点有三种情况:两个公共点(即有两个交点),一个公共点,没有公共点,因此有:(1)抛物线y=ax 2+bx+c 与x 轴有两个公共点(x 1,0)(x 2,0)即:一元二次方程ax 2+bx+c=0有两个不等实根△=b 2-4ac >0。
(2)抛物线y=ax 2+bx+c 与x 轴只有一个公共点时,此公共点即:为顶点(2b a -,0)一元二次方程ax 2+bx+c=0有两个相等实根,122bx x a ==-240b ac -=(3)抛物线y =ax 2+bx +c 与x 轴没有公共点一元二次方程ax 2+bx+c=0没有实数根△=b 2-4ac <0.(二)二次函数关系式的确定⑴设一般式:y =ax 2+bx +c(a≠0).若已知条件是图象上三个点的坐标,则设一般式y =ax 2+bx +c (a ≠0),将已知条件代入,求出a ,b ,c 的值.⑵设顶点式:y =a(x -h)2+k(a≠0).若已知条件是图象顶点及另一点,则设顶点式y =a (x -h )2+k (a ≠0).,将已知条件代人,求解并化为一般形式.:⑶设交点式(或两点式):y =a(x -x 1)(x -x 2)(a ≠0).若已知条件是图象与x 轴的两个交点及另一点,则设交点式y =a (x -x 1)(x -x 2)(a ≠0).将已知条件代人,求解并化为一般形式.【考点剖析】考点一 二次函数与方程例1.小兰画了一个函数y=x 2+ax+b 的图象如图,则关于x 的方程x 2+ax+b=0的解是( )A . 无解B .x=1C .x=-4D .x=-1或x=4例2.已知抛物线y=x 2﹣4x +m ﹣1.(1)若抛物线与x 轴只有一个交点,求m 的值;(2)若抛物线与直线y=2x ﹣m 只有一个交点,求m 的值.例3.如图,二次函数y=x 2﹣6x+5的图象交x 轴于A 、B 两点,交y 轴于点C ,则△ABC 的面积为 .例3图 变1图【变式练习】1.已知二次函数y=-x 2+2x+m 的部分图象如图所示,则关于x 的一元二次方程022=++-m x x 的解为 。
例析二次函数与一元二次方程的转化

例析二次函数与一元二次方程的转化山东 于秀坤二次函数y=ax2+bx+c(a ≠0)与一元二次方程ax2+bx+c=0〔a ≠0〕密切相关,当函数值y=0时,可得到一元二次方程ax2+bx+c=0.从图象上看,二次函数y=ax2+bx+c 的图象与x 轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根.对于二次函数y=ax2+bx+c 的图象和一元二次方程ax2+bx+c=0:当图象与x 轴有一个公共点时,方程有两个相等实数根,即Δ=b2-4ac=0;当图象与x 轴有两个公共点时,方程有两个不等的实数根,即Δ=b2-4ac>0;当图象与x 轴没有公共点时,方程没有实数根,即 Δ=b2-4ac<0.例1 〔2019•宿迁〕假设二次函数y=ax2-2ax+c 的图象经过点〔-1,0〕,那么方程ax2-2ax+c=0的解为〔 〕x1=-3,x2=-1 B 、x1=1,x2=3 C 、x1=-1,x2=3 D 、x1=-3,x 2=1解析:∵二次函数y=ax2-2ax+c 的图象经过点〔-1,0〕,∴方程ax2-2ax+c=0一定有一个解为x=-1,∵抛物线的对称轴是x=-22a a-=1, ∴二次函数y=ax2-2ax+c 的图象与x 轴的另一个交点为:〔3,0〕. ∴方程ax2-2ax+c=0的解为x1=-1,x2=3.应选C 、例2〔2016•徐州〕假设二次函数y=x2+2x+m 的图象与x 轴没有公共点,那么m 的取值范围是______.解析:∵二次函数y=x2+2x+m 的图象与x 轴没有公共点,∴方程x2+2x+m=0没有实数根.∴∆=22-4×1×m <0,解得m >1.例3〔2019•南通〕关于x 的一元二次方程ax2-3x-1=0的两个不等的实数根都在-1和0之间〔不包括-1和0〕,那么a 的取值范围是__________解析:∵关于x 的一元二次方程ax2-3x-1=0的两个不相等的实数根,∴ =〔-3〕2-4×a×〔-1〕>0,解得a>−9 4.设y=ax2-3x-1,如图,∵实数根都在-1和0之间,[来源:学+科+网]∴-1<−-32a<0,解得a<−32.当x=-1时,y<0,即a×〔-1〕2-3×〔-1〕-1<0. 解得a<-2.[来源:1ZXXK]综上可得−94<a<-2.[来源:1ZXXK]。
《二次函数与一元二次方程的关系》PPT赏析

有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac<0
深入理解
1.一个足球被从地面向上踢出,它距地面的高度h(m) 可以用公式 h=-4.9t2+19.6t 来表示.其中t(s) 表示足球被踢出后经过的时间. (1)t=1时,足球的高度是多少? (2)t为何值时,h最大? (3)球经过多长时间球落地? (4)方程-4.9t2+19.6t=0的根的实际意义是什么? 你能在图上表示吗? (5)方程14.7=-4.9t2+19.6t 的根的实际意义是 什么?你能在图上表示吗?
解:(1)t=1时,h=14.7 (2)∵h=-4.9(t-2) 2+19.6 ∴当t=2时,h最大
(3)对于h=-4.9t2+19.6t 球落地意味着h=0, 即 -4.9t2+19.6t=0,解得t1=0(舍去),t2=4 . 即足球被踢出后经过4s后球落地.
(4) 方程-4.9t2+19.6t =0的根的实际意义是球离地 和落地的时间,图上表示为抛物线与x轴交点的横坐标.
二次函数y=ax2+bx+c何时为一元二次方程?它们 的关系如何 ?
一般地,当y取定值时,二次函数即为一元二次方程.
2. 已知二次函数y=kx2-7x-7的图象与x轴有交 点,求k的取值范围.
错解: 由△=(-7)2-4×k×(-7) =49+28k>0, 得k>- 9 . 4
正确解法:
此函数为二次函数,
二次函数与一元二次方程的关系
情境导入
我们已经知道,竖直上抛物体的高 度h(m)与运动时间t(s)的关系可用公式 h=-5t2+v0t+h0 表示, 其中h0(m) 是抛出 时的高度, v0(m/s)是抛出时的速度.
九年级数学二次函数与一元二次方程

二次函数与一元二次方程知识点一:二次函数与一元二次方程的关系二次函数)0(2=/++=a c bx ax y 中,当y 等于某一实数h 时,二次函数便转化成一元二次方程h c bx ax =++2,即02=-++h c bx ax ,解这个一元二次方程,得到的根即为二次函数c bx ax y ++=2当函数值为h 时自变量的取值。
若此时该方程有两个不相等的实数根,则说明有两个自变量的值使得h c bx ax =++2成立。
特别地,当h =0时,方程就变为02=++c bx ax ,此时方程的根为二次函数的图象与x 轴交点的横坐标。
例题1、红星中学九年级(1)班的同学去野营露宿,第三小组的同学们一齐动手搭了一个横截面为抛物线型的帐篷,小明是个爱动脑筋的孩子,他建立了如图所示的直角坐标系后,得抛物线的表达式为.2212+-=x y (1)若小明的身高为1.60 m ,他在不弯腰的情况下,横向活动的范围是几米(精确到百分位)? (2)帐篷的宽度是多少? (3)帐篷的最高点离地面几米?变式训练1、在建设社会主义新农村的过程中,中央加大了对农村投入力度,不少农村建上了自动喷灌设备,如图所示,AB 表示水管,在B 处有一个自动旋转的喷水头,一瞬间喷出的水呈抛物线状,建立如图所示的平面直角坐标系后,抛物线的表达式为.5.12212++-=x x y (1)当x =1时,喷出的水离地面多高?(2)你能求出水落地点的最远距离吗?(3)水管有多高?例3 函数132++-=x x ax y α的图象与x 轴有且只有一个交点,那么a 的值和交点坐标分别为多少?点拨:解答本题的关键是首先由系数的值确定函数是哪种函数,然后再求交点坐标。
拓展:抛物线与x 轴两交点之间的距离公式:⋅∆=-||||21a x x 此公式可由21,x x 满足的一元二次方程中根与系数之间的关系式acx x a b x x =-=+2121,推导出来。
二次函数与一元二次方程不等式关系
• 如果方程ax2+bx+c=0 (a≠0)没有 实数根,那么 • 函数y=ax2+bx+c的图像与 x轴有 0 ______ 个交点; • 不等式ax2+bx+c<0的解集是______
(1)当a>0时, ax2+bx+c<0无解 (2)当a<0时, ax2+bx+c<0的解集是一切实数。
思考4:
x1 1, x2 3 x1 0, x2 2 x1 x2 1
x 1或x 3
1 x 3
1 x 3且x 1
<
<
>
>
=
>
<
x1 3, x2 1
3 x 1
x 3或x 1
x 0或x 4
x 0或x 4
0 x4
是一个 。
X1 =X2 =-b/2a
x ≠ x1的一切实 数
没有实数根
x<x1或x>x2 x1<x<x2
所有实数 无解
人教版数学九年级上册22.2 二次函数和一元二次方程课件(共55张PPT)

例如,已知二次函数 y = -x2+4x 的值为3,求自变量 x 的值, 可以解一元二次方程-x2+4x=3 ( 即x2-4x+3=0 ). 反过来,解方程 x2-4x+3=0 又可以看作已知二次函数 y = x2-4x+3 的值为0,求自 变量x的值,还可以看做y = -x2+4x 和y=3的交点
x
-1
-2
-3
-4 -5
当x1=x2=-3时,函数值为0.
二、利用一元二次方程讨论二次函数与x轴的交点
思考
问题1 不解方程,判断下列一元二次方程根的情况. (1)x2+x-2=0; ∵∆ = b2-4ac=9>0,∴方程有两个不相等的实数根. (2)x2-6x+9=0; ∵∆ = b2-4ac=0,∴方程有两个相等的实数根. (3)x2-x+1=0. ∵∆ = b2-4ac=-3<0,∴方程有没有实数根.
公共点的坐标.
(1)y=x2+x-2;
y
两个(-2,0),(1,0)
2 1
-2 -1 O 1 2 x
-1
-2
(2)y=x2-6x+9;
y 4
一个(3,0)
3
2
1
-1 O 1 2 3 4
x
(3)y=x2-x+1
y 4
没有公共点
3
2 1
-1 O 1 2
x
二次函数图象与x轴的公共点我们也可以通过平移来观察,发现最多有两 个公共点,最少没有公共点.
O
二次函数与一元二次方程关系知识点及练习

二次函数与一元二次方程关系知识点及练习一、二次函数与一元二次方程关系1、对于二次函数c bx ax y ++=2)0(≠a 来说,当0=y 时,就得一元二次方程02=++c bx ax )0(≠a ,抛物线y=ax 2+bx+c 与x 轴交点的横坐标,就是一元二次方程ax 2+bx+c=0的根;2、二次函数y=ax 2+bx+c (a ≠0)的图象与x 轴的交点有三种情况(也即一元二次方程ax 2+bx+c=0根的情况)①抛物线y=ax 2+bx+c (a ≠0)的图象与x 轴有两个交点(x 1,0)(x 2,0) <=>当△>0时,一元二次方程ax 2+bx+c=0 (a ≠0)有两个不相等的实数根x 1,x 2,x 1,2=a ac b 24b -2-±; ②抛物线y=ax 2+bx+c (a ≠0)与x 轴有一个交点,恰好就是抛物线的顶点(-a 2b ,0)<=>当△=0时,方程ax 2+bx+c=0有两个相等的实数根x 1=x 2= -a 2b ③抛物线y=ax 2+bx+c (a ≠0)与x 轴没有交点<=>当△<0时,方程ax 2+bx+c=0没有实数根。
二、解读二次函数与一元二次方程关系1、二次函数与一元二次方程关系,其实就是一元二次方程的根和二次函数的图象与x 轴的交点横坐标之间的关系;2、若一个二次函数的图象与x 轴总有交点,则其对应的一元二次方程的判别式△≥0.反之亦然;3、若抛物线y=ax 2+bx+c (a ≠0)的图象与x 轴有两个交点A (x 1,0)B(x 2,0),则抛物线的对称轴为直线x=2x 21x +,线段AB 的距离=21x x -=221)(x x -212214)(x x x x -+=224a ac b -=a ∆=,对称轴与x 轴的交点恰为线段AB 的中点。
4、推广:我们可以利用一元二次方程来研究抛物线与c bx ax y ++=2与直线b kx y +=(当0≠k 时为一次函数的图像,当0=k 时为平行于x 轴或与x 轴重合的一条直线b y =)的交点情况.三、二次函数与一元二次方程关系应用1、若已知二次函数y=ax 2+bx+c (a ≠0)的函数值m ,求自变量x 的值,就是解一元二次方程ax 2+bx+c=m ;反之亦然。
二次函数与一元二次方程及解决实际问题(解析版)

第5天二次函数与一元二次方程及解决实际问题【知识回顾】1.抛物线与x轴的交点求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c =0,解关于x的一元二次方程即可求得交点横坐标.(1)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系.△=b2﹣4ac决定抛物线与x轴的交点个数.△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.(2)二次函数的交点式:y=a(x﹣x1)(x﹣x2)(a,b,c是常数,a≠0),可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).2.图象法求一元二次方程的近似根利用二次函数图象求一元二次方程的近似根的步骤是:(1)作出函数的图象,并由图象确定方程的解的个数;(2)由图象与y=h的交点位置确定交点横坐标的范围;1(3)观察图象求得方程的根(由于作图或观察存在误差,由图象求得的根一般是近似的).3.根据实际问题列二次函数关系式根据实际问题确定二次函数关系式关键是读懂题意,建立二次函数的数学模型来解决问题.需要注意的是实例中的函数图象要根据自变量的取值范围来确定.△描点猜想问题需要动手操作,这类问题需要真正的去描点,观察图象后再判断是二次函数还是其他函数,再利用待定系数法求解相关的问题.△函数与几何知识的综合问题,有些是以函数知识为背景考查几何相关知识,关键是掌握数与形的转化;有些题目是以几何知识为背景,从几何图形中建立函数关系,关键是运用几何知识建立量与量的等式.4.二次函数的应用(1)利用二次函数解决利润问题在商品经营活动中,经常会遇到求最大利润,最大销量等问题.解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围.(2)几何图形中的最值问题几何图形中的二次函数问题常见的有:几何图形中面积的最值,用料的最佳方案以及动态几何中的最值的讨论.(3)构建二次函数模型解决实际问题利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.23一.选择题(共10小题)1.(2019·北京市十一学校月考)已知二次函数23y x x m =-+(m 为常数)的图象与x 轴的一个交点为(1,0),则关于x 的一元二次方程230x x m -+=的两实数根分别是( )A .121,1x x ==-B .121,2x x ==C .121,0x x ==D .121,3x x ==【答案】B【解析】方法一:△二次函数23y x x m =-+图象与x 轴的一个交点为(1,0),△013m =-+,解得2m =.△一元二次方程为2320x x -+=,即(1)(2)0x x --=,解得121,2x x ==.故选B .方法二:△二次函数图象与x 轴的交点横坐标即为对应一元二次方程的实数根, △二次函数图象的对称轴是直线32x =,△二次函数的图象与x 轴的另一个交点为(2,0),4 △关于x 的一元二次方程230x x m -+=的两实数根分别是121,2x x ==.故选B .2.(2019·广东郁南月考)已知二次函数y 1=ax 2+bx+c (a≠0)与一次函数y 2=kx+m (k≠0)的图象交于点A (﹣2,4),B (8,2),如图所示,则能使y 1>y 2成立的x 的取值范围是( )A .x <﹣2B .x >8C .﹣2<x <8D .x <﹣2或x >8【答案】D【解析】 △A (﹣2,4),B (8,2),△能使y 1>y 2成立的x 的取值范围是x <﹣2或x >8.故答案选D .3.(2020·天津南开期末)抛物线y =x 2﹣5x +6与x 轴的交点情况是( )A .有两个交点B .只有一个交点C .没有交点D .无法判断【答案】A【解析】△y=x2﹣5x+6=(x﹣2)(x﹣3),△当y=0时,x=2或x=3,即抛物线y=x2﹣5x+6与x轴的交点坐标为(2,0),(3,0),故抛物线y=x2﹣5x+6与x轴有两个交点,故选A.4.(2020·浙江杭州一模)已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程23=0 2ax bx c+++的根的情况是()A.无实数根B.有两个相等实数根C.有两个异号实数根D.有两个同号不等实数根【答案】D【解析】解:函数y=ax2+bx+c向上平移32个单位得到232y ax bx c'+++=,5而y′顶点的纵坐标为﹣2+32=﹣12,故23 2y ax bx c'+++=与x轴有两个交点,且两个交点在x轴的右侧,故23=0 2ax bx c+++有两个同号不相等的实数根,故选:D.5.(2020·安徽瑶海·合肥38中月考)由下表可知方程ax2+bx+c=0(a≠0,a、b、c为常数)一个根(精确到0.01)的范围是()A.6<x<6.17B.6.17<x<6.18C.6.18<x<6.19D.6.19<x<6.20【答案】C【解析】由表可以看出,当x取6.18与6.19之间的某个数时,y=0,即这个数是ax2+bx+c=0的一个根.△ax2+bx+c=0的一个解x的取值范围为6.18<x<6.19.故选:C.67 6.(2020·福建厦门一中月考)二次函数y =x 2+mx ﹣n 的对称轴为x =2.若关于x 的一元二次方程x 2+mx ﹣n =0在﹣1<x <6的范围内有实数解,则n 的取值范围是( ) A .﹣4≤n <5B .n ≥﹣4C .﹣4≤n <12D .5<n <12 【答案】C【解析】解:△抛物线的对称轴x =-2m =2, △m =-4,则方程x 2+mx -n =0,即x 2-4x -n =0的解相当于y =x 2-4x 与直线y =n 的交点的横坐标, △方程x 2+mx -n =0在-1<x <6的范围内有实数解,△当x =-1时,y =1+4=5,当x =6时,y =36-24=12,又△y =x 2-4x =(x -2)2-4,△在-1<x <6的范围,-4≤y <12,△n 的取值范围是-4≤n <12,故选:C .7.(2020·安徽合肥三模)若无论x 取何值,代数式()()13x m x m +--的值恒为非负数,则m 的值为( )A .0B .12C .13D .1【答案】B【解析】解:(x+1−3m)(x−m)=x2+(1−4m)x+3m2−m,△无论x取何值,代数式(x+1−3m)(x−m)的值恒为非负数,△△=(1−4m)2−4(3m2−m)=(1−2m)2≤0,又△(1−2m)2≥0,△1−2m=0,△m=12.故选:B.8.(2020·山东岱岳二模)将抛物线y=﹣13x2﹣13x+2(x≤0)沿y轴对折,得到如图所示的“双峰”图象.若直线y=x+b与该“双峰”图象有三个交点时,b的值为()A.2,73B.2C.73D.0【答案】A89【解析】将抛物线y =﹣13x 2﹣13x +2(x ≤0)沿y 轴对折,得到抛物线为y =﹣13x 2+13x +2(x >0), 由抛物线y =﹣13x 2﹣13x +2(x ≤0)可知抛物线与y 轴的交点为(0,2), 把点(0,2)代入y =x +b 求得b =2, 由﹣13x 2+13x +2=x +b 整理得x 2+2x +3b ﹣6=0, 当△=4﹣4(3b ﹣6)=0,即b =73时,直线y =x +b 与该“双峰”图象有三个交点, 由图象可知若直线y =x +b 与该“双峰”图象有三个交点时,b 的值是2和73, 故选:A .9.(2020·全国)从地面竖直向上抛出一小球,小球的高度h (单位:m )与小球运动时间t (单位:s )之间的函数关系如图所示.下列结论:△小球在空中经过的路程是40m ;△小球抛出3秒后,速度越来越快;△小球抛出3秒时速度为0;△小球的高度30h m =时, 1.5t s =.其中正确的是( )10A .△△B .△△C .△△△D .△△ 【答案】D【解析】△由图象知小球在空中达到的最大高度是40m ;故△错误; △小球抛出3秒后,速度越来越快;故△正确;△小球抛出3秒时达到最高点即速度为0;故△正确; △设函数解析式为:()2340h a t =-+,把()0,0O 代入得()200340a =-+,解得409a =-,△函数解析式为()2403409h t =--+,把30h =代入解析式得,()240303409t =--+,解得: 4.5t =或 1.5t =,△小球的高度30h m =时, 1.5t s =或4.5s ,故△错误; 故选D .10.(2020·全国)如图,两条抛物线y1=-12x2+1,y2=-12x2-1与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为()A.8B.6C.10D.4【答案】A【解析】如图,过,y2=-12x2-1的顶点(0,-1)作平行于x轴的直线与y1=-12x2+1围成的阴影,同过点(0,-3)作平行于x轴的直线与y2=-12x2-1围成的图形形状相同,故把阴影部分向下平移2个单位即可拼成一个矩形,因此矩形的面积为4×2=8.故选A二.填空题(共5小题)11.(2019·北京市十一学校月考)二次函数y1=ax2+bx+c与一次函数y2=mx+n的图象如图所示,则满足ax2+bx+c≥mx+n的x的取值范围是_____.11【答案】﹣3≤x≤0.【解析】解:由图可知,-3<x<0时二次函数图象在一次函数图象上方,所以,满足ax2+bx+c≥mx+n的x的取值范围是﹣3≤x≤0.故答案为:﹣3≤x≤012.(2020·北京市昌平区第四中学期中)二次函数y=﹣x2+bx+c的部分图象如图所示,由图象可知,不等式﹣x2+bx+c<0的解集为______.【答案】x<−1或x>5.【解析】抛物线的对称轴为直线x=2,而抛物线与x轴的一个交点坐标为(5,0),所以抛物线与x轴的另一个交点坐标为(−1,0),1213所以不等式−x 2+bx +c <0的解集为x <−1或x >5.故答案为x <−1或x >5.13.(2020·四川南充月考)已知抛物线21y ax x =--与x 轴交于A ,B 两点,顶点为C ,如果ABC ∆为直角三角形,则a =________. 【答案】34【解析】出这两个距离,列方程求解,检验得出答案.【详解】解:△抛物线y=ax 2-x -1与x 轴交于A ,B 两点,△b 2-4ac >0,即1+4a >0,也就是14a >- △抛物线y=ax 2-x -1与x轴交点的横坐标为x =414a y a --=, △AB 的距离为|x 1-x 2|= ,顶点C 到x 轴距离CD 为414a a --, △当△ABC 为直角三角形,根据对称性可知它是一个等腰直角三角形,此时AB=2CD ,4124a a--=⨯14两边平方得:224144a a --⎛⎫=⨯ ⎪⎝⎭⎝⎭ 整理得:16a 2-8a -3=0 解得:1231,44a a ==- △14a >- △34a = 14.(2020·湖北武汉月考)二次函数y =ax 2+bx+c 的图象如图所示,下列结论:△ab >0;△a+b ﹣1=0;△a >1;△关于x 的一元二次方程ax 2+bx+c =0的一个根为1,另一个根为﹣1a.其中正确结论的序号是_____.【答案】△△△【解析】解:△由二次函数的图象开口向上可得a >0,对称轴在y 轴的右侧,b <0,△ab <0,故△错误;△由图象可知抛物线与x 轴的交点为(1,0),与y 轴的交点为(0,﹣1),△c=﹣1,△a+b﹣1=0,故△正确;△△a+b﹣1=0,△a﹣1=﹣b,△b<0,△a﹣1>0,△a>1,故△正确;△△抛物线与y轴的交点为(0,﹣1),△抛物线为y=ax2+bx﹣1,△抛物线与x轴的交点为(1,0),△ax2+bx﹣1=0的一个根为1,根据根与系数的关系,另一个根为﹣1a,故△正确;故答案为△△△.15.(2020·全国)如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加______m.【答案】-41516【解析】建立平面直角坐标系,设横轴x 通过AB ,纵轴y 通过AB 中点O 且通过C 点,则通过画图可得知O 为原点,抛物线以y 轴为对称轴,且经过A ,B 两点,OA 和OB 可求出为AB 的一半2米,抛物线顶点C 坐标为()0,2.通过以上条件可设顶点式22y ax =+,其中a 可通过代入A 点坐标()2,0.- 代入到抛物线解析式得出:0.5a =-,所以抛物线解析式为20.52y x =-+,当水面下降2米,通过抛物线在图上的观察可转化为:当2y =-时,对应的抛物线上两点之间的距离,也就是直线2y =-与抛物线相交的两点之间的距离,可以通过把2y =-代入抛物线解析式得出: 220.52x -=-+,解得:x =±17所以水面宽度增加到4.故答案是:4.三.解析题(共5小题)16.(2020·福建省连江第三中学月考)已知抛物线y =x 2-2x -8与x 轴的两个交点为A ,B (A 在B 的左侧),与y 轴交于点C .(1)直接写出点A ,B ,C 的坐标;(2)求△ABC 的面积.【答案】(1)A (-2,0),B (4,0),C (0,-8);(2)S △ABC =24【解析】(1)在y =x 2-2x -8,令0x =,可得8y =-,即C 点坐标为(0,8)C -令0y =,得2280x x =-- 解得122,4x x =-=△A 在B 的左侧△(2,0),(4,0)A B -(2)△(2,0),(4,0),(0,8)A B C --△6,8AB OC ==18S △ABC =12AB OC ⋅=1682⨯⨯=24 17.(2020·福建省连江第三中学月考)已知抛物线y =-x 2+4x -3.(1)用配方法求出它的顶点坐标和对称轴;(2)若抛物线与x 轴的两个交点为A 、B ,求线段AB 的长.【答案】(1)(2,1),直线x=2;(2)2【解析】解:(1)△y=-x 2+4x -3=-(x 2-4x+4)+1=-(x -2)2+1,△抛物线的顶点坐标为(2,1)、对称轴为直线x=2;(2)令y=0得-x 2+4x -3=0,解得:x=1或x=3,则抛物线与x 轴的交点坐标为(1,0)和(3,0),△线段AB 的长为2.18.(2020·全国)如图,抛物线2y x bx c =++与x 轴交于A ,B 两点,其中点A 的坐标为(3,0)-,与y 轴交于点C ,点(2,3)D --在抛物线上.19(1)求抛物线的解析式;(2)抛物线的对称轴上有一动点P ,求出PA PD +的最小值;(3)若抛物线上有一动点Q ,使ABQ △的面积为6,求点Q 的坐标.【答案】(1)223y x x =+-;(2)3)点Q 的坐标为(0,3)-或(2,3)--或(1-+或(1--【解析】解:(1)△抛物线2y x bx c =++经过点(3,0),(2,3)A D ---,△930,423,b c b c -+=⎧⎨-+=-⎩解得2,3,b c =⎧⎨=-⎩△抛物线的解析式为223y x x =+-.(2)由(1)得抛物线223y x x =+-的对称轴为直线1,(0,3)x C =--.△(2,3)D --,△C ,D 关于抛物线的对称轴对称,连接AC ,可知,当点P 为直线AC与20对称轴的交点时,PA PD +取得最小值,△最小值为AC ==(3)设点()2,23Q m m m +-, 令2230y x x =+-=,得3x =-或1,△点B 的坐标为(1,0), △4AB =.△6QAB S =, △2142362m m ⨯⨯+-=, △2260m m +-=或220m m +=,解得:1m =-+1--或0或2-,△点Q 的坐标为(0,3)-或(2,3)--或(1-+或(1--.19.(2020·山东日照·中考真题)如图,某小区有一块靠墙(墙的长度不限)的矩形空地ABCD ,为美化环境,用总长为100m 的篱笆围成四块矩形花圃(靠墙一侧不用篱笆,篱笆的厚度不计).(1)若四块矩形花圃的面积相等,求证:AE =3BE ;(2)在(1)的条件下,设BC 的长度为xm ,矩形区域ABCD 的面积为ym 2,求y 与x 之间的函数关系式,并写出自变量x 的取值范围.21【答案】(1)见解析;(2)2610040053⎛⎫=-+<< ⎪⎝⎭y x x x ,见解析. 【解析】解:(1)证明:△矩形MEFN 与矩形EBCF 面积相等,△ME =BE ,AM =GH .△四块矩形花圃的面积相等,即S 矩形AMDND =2S 矩形MEFN ,△AM =2ME ,△AE =3BE ;(2)△篱笆总长为100m ,△2AB +GH +3BC =100, 即1231002AB AB BC ++=, △6405AB BC =-设BC 的长度为xm ,矩形区域ABCD 的面积为ym 2,22 则266404055y BC AB x x x x ⎛⎫=⋅=-=-+ ⎪⎝⎭, △6405AB BC =-, △402035EB x =->, 解得1003x <, △2610040053⎛⎫=-+<< ⎪⎝⎭y x x x . 20.(2020·云南一模)大学毕业生小李自主创业,开了一家小商品超市.已知超市中某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价必须低于34元,设每件商品的售价上涨x 元(x 为非负整数),每个月的销售利润为y 元.(1)求y 与x 的函数关系式,并直接写出自变量x 的取值范围;(2)利用函数关系式求出每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?(3)利用函数关系式求出每件商品的售价定为多少元时,每个月的利润恰好是1920元?这时每件商品的利润率是多少?【答案】(1)y=80x+1800x 4,≤<(0且x 为整数);(2)每件商品的售价为33元时,商品的利润最大为1950元;(3)售价为32元时,利润为1920元.每件商品的利润率是60%.23【解析】(1)2y=3020+x)(180-10x)=-10x =80x+18000x 4,x -≤<((且为整数);(2)()2y 1041960x =--+,100-<,当x 4<时y 随x 的增大而增大,由0x 4≤<, 且x 为整数可得当x 3=时,y =1950最大答:每件商品的售价为33元时,商品的利润最大为1950元; (3)2192010x 80x 1800=-++,2x 8x 120-+=,即()2(6=0x x )-- 解得x 2=或x 6=,0x 4≤<,x 2∴=,()322020100%60%-÷⨯=∴售价为32元时,利润为1920元.每件商品的利润率是60%.。
43.二次函数与一元二次方程的关系(一)

问题探究
从上面发现,二次函数y=ax2+bx+c何时为一元二次方程?
一般地,当y取常数(定值)时,二次函数为一元二次方程.
如:y=5时,则5=ax2+bx+c就是一个一元二次方程.
所以二次函数与一元二次方程联系密切 已知二次函数y = -x2+4x的值为3,求自变量x的值,可以看作解一元二 次方程-x2+4x=3(即x2-4x+3=0). 反过来,解方程x2-4x+3=0 又可以看作已知二次函数 y = x2-4x+3 的值 为0,求自变量x的值. 既然联系密切,我们可以运用二次函数y=ax2+bx+c深入讨论 一元二次方程ax2+bx+c=0
0个 1个
2个 y = x2-x+1
3
-2, 1
y = x2+x-2
1
知识梳理
以上是运用二次函数y=ax2+bx+c深入讨论一元二次方程ax2+bx+c=0
反过来,由一元二次方程根的情况,也可以确定相应的二次函数的图象
与x轴的位置关系.
二次函数y=ax2+bx+c的图象与x轴交点的坐标与 一元ห้องสมุดไป่ตู้次方程ax2+bx+c=0根的关系
问题2.下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是 多少?当x取公共点的横坐标时,函数值是多少?由此,你能得出相应的一 元二次方程的根吗?
(1)y=x2+x-2;
(2)y=x2-6x+9;
(3)y=x2-x+1.
观察图象,完成下表 二次函数 y = x2-x+1 y = x2-6x+9 y = x2+x-2 抛物线与x轴 公共点 公共点个数 横坐标 当x取公共点横坐标 相应的一元二次方 程的根 时,函数值是多少? x2-x+1=0没有实数根 0 x2-6x+9=0,x1=x2=3 x2+x-2=0,x1=-2,x2=1 0 y = x2-6x+9
二次函数与一元二次方程ppt课件

2.5 二次函数与一元二次方程
▍考点集训/夯实基础
■考点 1 二次函数与一元二次方程的关系 1. 一位篮球运动员跳起投篮,篮球运行的高度 y(m)关于篮球运动的水
平距离 x(m)的函数解析式是y= - (x-2.5)2+3.5.已知篮圈中心到地面 的距离 3.05 m,如果篮球运行高度达到最高点之后能准确投入篮圈,那么 篮球运行的水平距离为 ( )
■考点二 二次函数与 x 轴的交点 1. 函数 y=ax2+bx+c(a≠0),当 y=0 时,得到一元二次方程 ax2+bx+c
=0(a≠0).因此,一元二次方程的解就是二次函数的图象与 x 轴交点的横坐 标,所以二次函数 y=ax2+bx+c(a≠0)的图象与 x 轴的交点情况决定了一元 二次方程 ax2+bx+c=0(a≠0)根的情况.具体关系如下:
次函数分别进行讨论.
答案:解:分两种情况:
(1)m+6=0,此时 m=-6,y=-14x-5,此直线与 x 轴必有交点;
(2)m+6≠0,此时关于 x 的二次函数 y=(m+6)x2+2(m-1)x+m+1 的图
象与x 轴总有交点,
∴Δ=b2-4ac=4(m-1)2-4(m+6)(m+1)≥0,解得 m≤
x
6.17
6.18
6.19
6.20
y
-0.03
-0.01
0.02
0.04
-10-
2.5 二次函数与一元二次方程
解析:由表格中的数据看出-0.01 和 0.02 更接近于 0, 故 x 应取对应的范围. 答案:6.18<x<6.19 易错:6.17<x<6.18 错因:不明白“用图象法求一元二次方程的近似根,解题的关键是找到 y 由正(负)变为负(正)时,自变量的取值”. 满分备考:根据表格数据确定一元二次方程的近似解(或范围),重点在 函数值符号发生变化时刻取 x 的值(或范围).
二次函数与一元二次方程的关系

解:(1)-1 x 3.
(2)设y=x2 -1,则y是x的二次函数.
a=1 0,抛物线开口向上.
又 当y=0时,x2 -1=0,
∴
>0
∴△>0,
∴无论 m取何值,抛物线总与x轴有两个交点.
温馨提示:为更好地满足您的学习和使用需求,课件在下载后可以自由编辑,请您根据实际情况进行调整!Thank you for
能力提升
5.已知二次函数 y kx2 6x 7 的图像与X轴
ห้องสมุดไป่ตู้
有两个不同的交点.
(1) 求k的取值范围
(2) 当k为何值时,这两个交点横坐标的平方和等
可由一元二次方程的根的判别式来判定二次函数图象与x 轴的交点的情况,由根与系数的关系来解决相关问题。
在函数问题中,往往需要解方程:反过来也可以利用函 数图象解方程。
课后练习
1.已知抛物线y x2 6x a与x轴有两个交点,则a的取值范围是多少? 2.已知抛物线y=x2 px q与x轴的两个交点为(2, 0), (3, 0),则p、q的 值分别是多少? 3.已知二次函数y x2 kx k 2. (1)判别上述抛物线与x轴的交点情况; (2)设抛物线与x轴交点之间的距离为2 5,求k的值. 4.设二次函数的图象与x轴交于A, B两点,与y轴交点点C,线段OA与OB 的长的积等于60(点O是坐标原点), 求m的值.
解得x =-1,x =1.
1
2
由此得抛物线的大致图象如图所示:
观察函数图象可知:
当x -1或x 1时,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的图象如图所示。
y x2 x 2
y x2 6x 9
y x2 x 1
(1).每个图象与x轴有几个交点? 答:2个,1个,0个 (2).一元二次方程? x2+x-2=0 , x2 - 6x +9=0有几个根?
验证一下一元二次方程x2 – x+ 1 =0有根吗?
2.2个根,2个相等的根 ,无实数根.
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.已知二次函数y 2 x2 mx m2.
(1)求证: 对于任意实数m,该二次函数的图象与x轴总有公共点;
(2)若该二次函数的图象与x轴有两个公共点A、B, 且A点坐标
为(1,0),求B点坐标.
(1)证明 : 令y 0,得2 x2 mx m2 0 (m)2 4 2 m2 9m2 0
1、学习二次函数与一元二次方程的关系
2、会用一元二次方程解决二次函数图象 与x轴的交点问题
复习.
1、一元二次方程ax2+bx+c=0的根的情 况可由 b2- 4ac 确定。
>0
有两个不相等的实数根
=0
有两个相等的实数根
<0
没有实数根
2、在式子h=50-20t2中,如果h=15,那么
50-20t2= 15 ,如果h=20,那50-20t2= 20 , 如果h=0,那50-20t2= 0 。如果要想求t的值,那么我 们可以求 方程 的解。
二次函数与一元二次方程
2、二次函数y=ax2+bx+c的图象和x轴交点
情况如何?(b2-4ac如何)
(1)有两个交点
b2 – 4ac > 0
(2)有一个交点
b2 – 4ac= 0
(3)没有交点
b2 – 4ac< 0
思考:若抛物线y=ax2+bx+c与x轴有交点,则 b2-4ac ≥0 .
练习:看谁算的又快又准。
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与
一元二次方程ax2+bx+c=0的根有什么关系?
2、二次函数y=ax2+bx+c的图象和x轴交 点,则b2-4ac的情况如何。
b2 – 4ac <0
Y
b2 – 4ac =0
.
O
b2 – 4ac >0
X
二次函数与一元二次方程
一般地,从二次函数y a x2 bx c的图象可知, (1)如果抛物线y a x2 bx c与x轴有公共点,公共点 的横坐标是x x0时,函数的值是0,因此x x0 就是 方程a x2 bx c 0的一个根.
4.抛物线y=x2-3x+2 与y轴交于点__(0_,2_) ,与x轴交
于点_(1_,0_) (2,0_) .
K≠0 5图.如象图知,,抛关物于线x的y=方ax程2+abxx2++bcx的+对c=称0的b轴2两-是4个a直c根线≥分0x别=-是1,由
x1=1.3 ,x2=_-_3.3_
6.已知抛物线y=kx2-7x-7的图象和x轴有交点,则 k的取值范围( B )
一般地,当y取定值时,二次函数为一元 二次方程。
如:y=5时,则5=ax2+bx+c就 是一个一元二次方程。
练习一:
如图设水管AB的高出地面2.5m,在B处有一自动旋
转的喷水头,喷出的水呈抛物线状,可用二次函数
y=-0.5x2+2x+2.5描述,在所有的直角坐标系中,求
水流的落地点D到A的距离是多少?
A
:
k
4 7
B
:
k
4 7
且k
0
B
C
ቤተ መጻሕፍቲ ባይዱ
:
k
4 7
D:k
4 7
且k
0
(1)抛物线y x2 2x 3与x轴的交点个数有( C ) .
A.0个 B.1个 C.2个 D.3个
(2)抛物线y m x2 3x 3m m2 经过原点,则其顶点
顶点坐标为___(_1_,_3_)___.
24
(3)关于x的一元二次方程x2 x n 0没有实数根,则 抛物线y x2 x n的顶点在( A ) .
1.不与x轴相交的抛物线是( D )
A y=2x2 – 3
B y= - 2 x2 + 3
C y= - x2 – 2x D y=-2(x+1)2 - 3
2.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实
数根,则m=_1_,此时抛物线 y=x2-2x+m与x轴有_1 个
交点.
3.已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=_1_6 .
不论m取何值,抛物线与 x轴总有公共点 .
(2) A(1,0)在抛物线y 2x2 mx m2 上 0 212 m 1 m2 即m2 m 2 0, (m 2)(m 1) 0 m1 2, m2 1 B点坐标为(2,0)
5.在ABC中, B 90,点P从点A开始沿AB边向点B 以1cm / s的速度移动,点Q从点B开始沿BC的边向点C
以2cm / s的速度移动,设PBQ的面积为y cm2 运动
时间为xs,如果P、Q分别从A、B同时出发: (1)写出y与x的函数关系式;
(2)几秒后PBQ的面积等于8c m2?
6.已知抛物线y x2 ax a 2与x轴交于A、B两点,与y轴交于点D(0,8),
分析:根据图象可知,水流的
y
落地点D的纵坐标为0,横坐
标即为落地点D到A的距离。
B
即:y=0 。
解:根据题意得 -0.5x2+2x+2.5 = 0, -1 A 0
Dx
解得x1=5,x2=-1(不合题意舍去) 答:水流的落地点D到A的距离是5m。
边观察边思考
1、二次函数y = x2+x-2 , y = x2 - 6x +9 , y = x2 – x+ 1
(20)=h球=20的0飞t 行– 5高t度2 能否达到 20 m ? 若能,需要多少时间?
(3)球的飞行高度能否达到 20.5 m ? 若能,需要多少时间?
(4)球从 飞出到落地 要用多少时间 ?
h t
为一个常数 (定值)
那么从上面,二次函数y=ax2+bx+c何时为 一元二次方程?它们的关系如何?
问题1:如图,以 40 m /s的速度将小球沿与地面成 30度
角的方向击出时,球的飞行路线是一条抛物线,如果不考虑
空气阻力,球的飞行高度 h (单位:m)与飞行时间 t (单
位:s)之间具有关系:h=
考虑下列问题:
20 2t0=2–02.15055=t=2t–02250ttt–2 –55t2t2
(1)球的飞行高度能否达到 15 m ? 若能,需要多少时间?
