单缝和圆孔的夫琅禾费衍射
圆孔的夫朗和费衍射
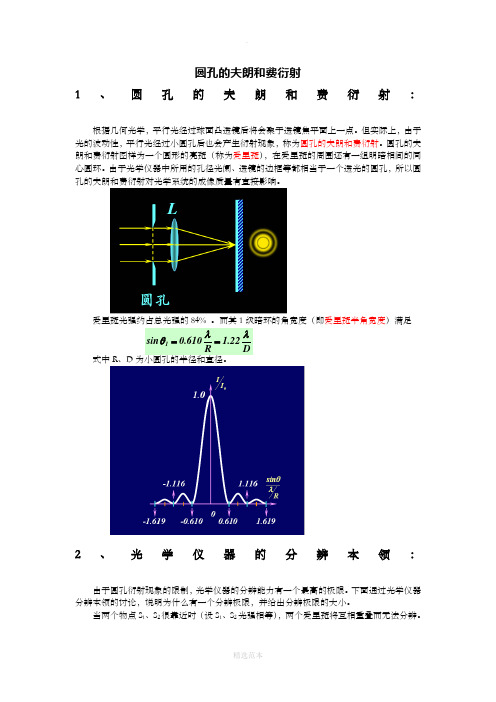
圆孔的夫朗和费衍射1、圆孔的夫朗和费衍射:根据几何光学,平行光经过球面凸透镜后将会聚于透镜焦平面上一点。
但实际上,由于光的波动性,平行光经过小圆孔后也会产生衍射现象,称为圆孔的夫朗和费衍射。
圆孔的夫朗和费衍射图样为一个圆形的亮斑(称为爱里斑),在爱里斑的周围还有一组明暗相间的同心圆环。
由于光学仪器中所用的孔径光阑、透镜的边框等都相当于一个透光的圆孔,所以圆孔的夫朗和费衍射对光学系统的成像质量有直接影响。
爱里斑光强约占总光强的84% 。
而其1级暗环的角宽度(即爱里斑半角宽度)满足D 22.1R610.0sin 1λλθ==式中R 、D 为小圆孔的半径和直径。
2、光学仪器的分辨本领:由于圆孔衍射现象的限制,光学仪器的分辨能力有一个最高的极限。
下面通过光学仪器分辨本领的讨论,说明为什么有一个分辨极限,并给出分辨极限的大小。
当两个物点S 1、S 2很靠近时(设S 1、S 2光强相等),两个爱里斑将互相重叠而无法分辨。
对一个光学仪器来说,若一个点光源产生的爱里斑的中央刚好与另一个点光源产生的爱里斑瑞的1级暗环相重合,这时两个爱里斑重合部分的光强约为单个爱里斑中央光强的80%左右,一般人眼刚好能分辨出这是两个光点的像。
因此,满足上述条件的两个点光源恰好能被该光学仪器所分辨。
这一条件称为瑞利分辨判据。
(见下图)恰能分辨时两光源发出的光线对透镜光心的夹角Δθ 称为最小分辨角,用δθ表示。
由上讨论可知,最小分辨角δθ等于爱里斑的半角宽度θ1:)D 22.1arcsin(1λθδθ==尤其当θ1 ~ 0D 22.1λδθ≈(或称分辨率),用R 表示:λδθ22.1D 1R ==讨论:⑴ 增大透镜的直径D 可提高镜头的分辨率。
光学天文望远镜的镜头孔径可达数米! ⑵ 设r 、d 为爱里斑的半径和直径,则:f 2d f r D 22.1===λδθ即:D f44.2d λ=f D称为镜头的相对孔径(越大越好)。
如照相机镜头上所标示的502:1字样,即表示镜头的焦距mm 50f =,而镜头的孔径mm 25D =。
单缝和圆孔夫琅禾费衍射介绍

三、入射光非垂直入射时光程差的计算
DB BC A
b(si n sin ) b
(中央明纹向下移动)
D
B
C
BC DA
b(si n sin )
(中央明纹向上移动)
D A
b
C
B
例1 在单缝衍射中,=600nm, a=0.60mm, f=60cm, 则(1)中央明纹宽度为多少?(2)两 个第三级暗纹之间的距离?
单缝和圆孔的夫琅 禾费衍射介绍
一、单缝夫琅禾费衍射
1.衍射装置及图样
单缝 透镜
衍射角
f
衍射屏
I
衍射图样
(1) 衍射条纹与狭缝平行。 (2)中心条纹很亮,两侧明条纹对称分布, 亮度减弱。 (3)中央亮斑的宽度为其他亮斑的两倍。
由惠更斯——菲涅耳原理:
单缝处波面看作无穷多个相干波源,屏上一点是 (无穷)多光束干涉的结果。
解 ⑴ 中央明纹的宽度
⑵第三级暗纹在屏上的位置
x3ftanf3a3l0
两个第三级暗纹之间的距离
x6l 7.2mm 0
例2 已知:一雷达位于路边d =15m处,射束与公路成 15°角,天线宽度a =0.20m,射束波长=30mm。
求:该雷达监视范围内公路长L =?
L
d
a
θ1
β
150
解:将雷达波束看成是单缝衍射的0级明纹
越大,
越大,衍射效应越明显.
1
二、用振幅矢量推导光强公式
1.振幅矢量法 将缝AB的面积S等分成N(很大)个等宽的窄带,
每个窄带宽度a/N.
每个窄带发的子波在P点振
A
幅近似相等,设为A1,相邻
窄带所发子波在P点引起的振
夫琅禾费单缝衍射光强分布的研究

夫琅禾费单缝衍射光强分布的研究(Research Of Fraunhofer Single Slot Diffraction Of LightIntensity Distribution)摘要:我们在光学中学习了有关夫琅禾费单缝衍射和圆孔衍射的内容,本文主要是对夫琅禾费单缝衍射光强的计算公式进行数学推导以及拓展,并且根据推导的数学公式对夫琅禾费单缝衍射光强分布情况进行讨论,对夫琅禾费单缝衍射的特点进行分析介绍。
关键词:夫琅禾费单缝衍射(Fraunhofer single slot diffraction)、光强(Light intensity)、光强分布(Light intensity distribution)、最大值(Maximum)引言:光的衍射是光的波动性的重要现象之一。
衍射现象即波在传播过程中不沿直线传播,而是向各方向绕射的现象。
而光绕过障碍物偏离直线传播而进入几何阴影,并在屏幕上出现光强分布不均匀的现象,称为光的衍射。
在衍射现象中,把平行光束的衍射现象,称为夫琅禾费衍射。
夫琅禾费衍射在光学研究中有着重要意义,它主要包括单缝衍射、圆孔衍射。
这里我重点介绍夫琅禾费单缝衍射的光强分布特点。
一、夫琅禾费单缝衍射实验装置与衍射图样的特点。
所谓夫琅禾费衍射是指光源、衍射屏和观察屏三者之间都是相距无限远的衍射情况。
即相当于入射光和衍射光都是平行的情况。
在这种情况下计算衍射花样中光强的分布时,数学运算就比较简单。
所谓光源在无限远,实际上就是把光源置于第一个透镜的焦平面上,使之成为平行光束;所谓观察角在无限远,实际上是在第二个透镜的焦平面上观察衍射花样。
由于透镜的会聚,衍射花样的光强将比菲涅耳衍射花样的光强大大增加。
夫琅禾费单缝衍射包含着衍射现象的许多主要特征。
夫琅禾费单缝衍射光路图如下图所示:夫琅禾费单缝衍射图样的主要特点如下:(1)中央有一条特别明亮的亮条纹,其宽度是其他亮条纹的两倍;其他亮条纹的宽度相等,亮度逐渐下降。
第43讲光的衍射现象单缝夫琅禾费衍射光学仪器的分辨本领

教学要求了解菲涅耳衍射、夫琅和费衍射、惠更斯-菲涅耳原理;理解光的衍射现象;单缝的夫琅和费衍射;圆孔的夫琅和费衍射、瑞利准则、分辨律;理解光学仪器的分辨本领。
15.1光的衍射现象惠更斯——菲涅耳原理15.1.1光的衍射现象及分类在讨论第六章时就已知道:孔隙(或障碍物)的线度与波长的比值直接影响着衍射现象,当孔隙(或障碍物)的线度与波长的数量级接近时,才能观察到明显的衍射现象。
对于光波,由于波长远小于一般孔隙(或障碍物)的线度,所以光的衍射现象通常不易观察到。
而光的直线传播却给人们留下了深刻的印象。
图15-1 光的衍射现象实验在实验室中,采用高亮度的激光或是普通的强点光源,同时屏幕的面积也足够大,则可以将光的衍射现象演示出来。
如图15-1(a)所示,E为屏幕,K是一个可调节的狭缝,S 为一单色点光源。
实验发现,当E,K,S三者位置固定的情况下,光通过宽缝时,是沿直线传播的,如图(a)所示。
若将缝的宽度减小到约10 4m及更小时,缝后几何阴影区的光屏上将出现衍射条纹,如图(b)所示,光斑的亮度也由原来的均匀分布变成一系列的明暗条纹(单色光源)或彩色条纹(白光光源),条纹的边缘也失去了明显的界限,变得模糊不清,这就是光的衍射现象。
衍射系统是由光源、衍射屏和接收屏组成,通常是根据三者相对位置的大小,把衍射现象分为两类。
一类是光源、接收屏(或两者之一)与衍射物之间的距离有限远。
这种衍射叫做菲涅耳衍射(或近场衍射),如图15-2(a )所示。
另一类是光源、接收屏与衍射物的距离都是无限远。
这种衍射称为夫琅禾费衍射(或远场衍射),如图15-2(b )所示。
在实验室中产生的夫琅禾费衍射通常利用两个会聚透镜来实现,如图15-2(c )。
由于夫琅和费衍射在实际应用和理论上都十分重要,而且这类衍射的分析与计算都比菲涅耳衍射简单,因此本节只讨论只讨论夫琅和费衍射。
15.1.2惠更斯——菲涅耳原理惠更斯原理指出:波阵面上的每一点都可以看成是发射子波的新波源,任何时刻子波的包迹即为新的波阵面。
2—3 夫琅和费单缝衍射

3、狭缝上所有次波在P 的叠加
积分过程见(附录2-1) b sinu u sin A A A0 sincu 令 p 0 u
2 sin u 2 2 2 2 Ap A0 A sin c u 0 2 u
I p I 0 sinc 2 u P点光强随θ的分布
16
三、强度公式的讨论 1、最大最小位置:
y2 = u
-
·
-2.46
·
-1.43
· 0
0
+1.43
+2.46
解得 :
相应 :
u 1.43, 2.46, 3.47, „
b sin 1.43 , 2.46 , 3.47 ,„
19
前几个次最大的位置
次最大序号 次最大位置 相对强度
u
1.43 2.46
(k 1, 2, ) 暗纹 (k 1, 2, ) 明纹 中央明纹
•正、负号表示衍射条纹对称分布于中央明纹的两侧 •对于任意衍射角,单缝不能分成整数个半波带,
在屏幕上光强介于最明与最暗之间。
方法一、菲涅耳半波带法
I / I0
明纹宽度
中央明条纹的角宽度 为中央两侧第一暗条纹 之间的区域:
3.47
4.48
sin
3 2b 5 2.46 b 2b 7 3.47 b 2b 9 4.48 b 2b 1.43 b
I I 0
1 2 3 4
0.047
0.017
0.008
0.005
1 sin k0 k 2 b
b
0
sin (2k 1)
2b
9.2光的衍射190415

d
d
解得
400 10 9
4
k - (700 400 ) 10 9 3
可见,只有第一级光栅光谱是完整的。
本次课知识点: 1 光的衍射不易察觉,是因为?
2 衍射条纹特征:中央明纹最亮最宽,两侧明纹 宽度是中央明纹的一半,亮度逐渐减小。
3
明暗纹条件:
a sin
9.2 光的衍射
一 单缝夫琅禾费衍射(掌握) 二 圆孔衍射(了解) 三 光栅衍射(掌握)
光的衍射:光绕过障碍物边缘传播,并形成明暗相间条 纹的现象。
屏幕
屏幕
阴
影
缝较大时,光沿直线传播 缝很小时,发生衍射
一、单缝夫琅禾费衍射
衍射角
f
P
a
o
(衍射角 :向上为正,向下为负 )
衍射角:衍射光线与狭缝面法线之间的夹角
公式
δ (2k 1) λ 2
k 1,2 ,
明纹 暗纹
2 衍射图样的特征
各次级亮纹的宽度为中央明纹的一半
各级亮纹的亮度随k 的增大而减小
asin (2k 1)
2
抵消后剩余的 半波带的面积 逐渐减小,光 强逐渐减弱。
3 条纹宽度
S
a
Px
fO
•第k级暗纹到O点的距离
2
两个半波带发出的子波在P点干涉相消,剩 下一个半波带发出的子波在P点叠加,结果 为亮纹。
B
a C
A
思考1: 若AC a sin
2
对应的是明纹还是暗纹?
若AC a sin λ
没有完全抵消,是亮纹,但不是亮 纹中心。
B
基于MATLAB的矩孔、单缝、圆孔夫琅和费衍射概诉

课程设计任务书学生姓名:专业班级:指导教师:工作单位:信息工程学院题目: 夫琅和费矩孔、单缝、圆孔衍射图样一、设计目的了解MA TLAB软件的基本知识,基本的程序设计,软件在高等数学和工程数学中的应用,学会使用软件进行数值计算和控制工程中的应用。
二、设计内容和要求1.绘制弗朗禾费矩孔、单缝和圆孔衍射图样,可以是二维的或三维的,也可以两种都有。
改变矩孔、单缝和圆孔的参数,比较衍射条纹的变化。
2. 学习Matlab语言的概况和Matlab语言的基本知识。
3.学习Matlab语言的程序设计。
三、初始条件计算机;Matlab软件。
四、时间安排1、2015年01月19日,任务安排,课设具体实施计划与课程设计报告格式的要求说明。
2、2015年01月20日,查阅相关资料,学习Matlab语言的基本知识,学习MATLAB语言的应用环境、调试命令,绘图功能函数等。
3、2015年01月21日至2015年01月22日,Matlab课程设计制作和设计说明书撰写。
4、2015年01月23日,上交课程设计成果及报告,同时进行答辩。
指导教师签名:2015年01 月19日系主任(或负责教师)签名:2015年01 月19日目录摘要 (I)1.设计的内容及要求 (1)1.1设计的目的 (1)1.2设计任务要求 (1)2.设计原理及设计思路 (1)2.1夫琅和费干涉理论 (1)2.1.1夫琅和费圆孔衍射 (2)2.1.2夫琅和费矩孔衍射 (2)2.1.3夫琅和费单缝衍射 (2)2.2设计思路 (3)3.仿真及分析 (4)4.心得和体会 (8)参考文献 (8)摘要物理光学理论较为复杂抽象,实验现象的演示对条件要求高。
采用MATLAB7.0强大的函数作图功能对矩孔、单缝、圆孔的夫琅和费衍射进行模拟,建立直观形象并且精确完整的理论模型,并附上程序代码,将干涉理论联系起来,分析衍射和干涉的本质。
从而加深对夫琅和费原理、概念、和图像的理解。
通过使用MATLAB编写程序,不仅理解了物理思想,而且了解了运用软件解决物理问题的方法。
夫琅禾费衍射

夫琅禾费衍射摘要:运用数学方法推导了不同孔径夫琅禾费衍射的振幅和光强分布,并作出计算机模拟图,定性定量的研究夫朗禾费衍射的光强分布和图样。
引言光学中的衍射分为近场衍射和远场衍射,而我们在实验室见到的多是远场衍射,即夫琅禾费衍射,所以本文对其进行了进一步研究。
夫琅禾费衍射是平行光入射,所以可以较容易的用数学方法对其研究论证。
本文对不同孔径的夫琅禾费衍射进行了研究,掌握了他们的成像规律才能将其更好的应用在实际生活中。
关键词:夫朗禾费衍射 光强分布 计算机模拟 惠更斯-菲涅耳原理 傅里叶变换 1夫琅禾费单缝衍射光强及分布的研究衍射花样的光强分布B'M Bx FP 0PI/I 0光强振幅-3π-2π-ππ2π3π-3π-2π-ππ2π3πy=tguuuy图1 图2当光屏放置在透镜2L 的焦平面上时,屏上出现衍射花样,光强的分布可由u c I I 20sin =式决定,不同的衍射角θ对应于光屏上不同的观察点,首先来决定衍射花样中光强最大值和最小值的位置,即求出满足光强的一阶导数为零的那些点:()2222sin cos sin sin 0u u u u d u du u u -⎛⎫== ⎪⎝⎭ 由此得sin 0,u u tgu ==分别解以上两式,可得出所有的极值点。
1)单缝衍射中央最大值的位置:由sin 0u =,解得满足()00sin /u b πθλ=的那个方向,即0sin θ=0 (中央最大值的位置) (1)也就是在焦点0P 处,200p I =A ,光强为最大。
这里,叠加的各个次波位相差为零,所以振幅叠加相互加强。
2)单缝衍射最小值的位置由sin u =0 ,解得满足 2(s i n )/2k k u b k πθλπ== 的一些衍射方向,即sin k kbλθ=(最小值位置)()1,2,3,k =±±± (2)时,p A 为零,屏上这些点是暗的。
3)单缝衍射次最大的位置在每两个相邻最小值之间有一最大值,这些最大值的位置可由u tgu =这一超越方程解得,我们可以用图解法求得u 的值,作直线y u =和正切曲线y tgu =(图3的下半部),它们的诸交点就是这个超越方程的解:12340, 1.43, 2.463.47, 4.48,u u u u u ππππ==±=±=±=±由此可得分列于中央主最大两边的其他最大值(称为次最大)的位置为()1020300003sin 1.4325sin 2.4627sin 3.4721sin 21,2,k bb bbbbk b k λλθλλθλλθλθ=±≈±=±≈±=±≈±⎛⎫≈±+ ⎪⎝⎭=3) 把这些θ值代入u c I I 20sin =式,可得各最大值光强的比值,若以中央最大的光强20A 为1,即使振幅归一化,则对于10θ,20θ,30θ…处,次最大光强依次为2221230.0472,0.0165,0.0083,A =A =A = 衍射花样最大值与最小值位置沿着垂直于缝长的方向分S(图 3)布,(图3),并由(1)、(2)和(3)三式决定,在居间位置,光强也介乎最大值与最小值之间。
4_1光的衍射

2.
没有民主的形式,就没有民主的内涵
费曼《科学的价值》:
“古往今来,人们一直都在试图测度人生的意义。他们想,如有某种 方向或意义指导行动,人类定会释放出巨大的力量。于是乎,很多很 多的答案应运而生。可是,这些答案彼此太不同了,一种答案的倡导 者,会把信奉另一种答案的行动者视为洪水猛兽。他们很可怕,因为, 换一个角度看,那就是人类的所有潜能都被引入一条狭隘 的死胡同。 历史告诉我们,虚妄信仰产生巨大恶行。
一、惠更斯原理
Optics 任何时刻波面上的每一点都可作为次波的波源,各 自发出球面波;在以后的任何时刻,所有这些次波波面 的包络面形成整个波在该时刻的新波面。
ut
平 面 波 球 面 波
R1
O
R2
直线传播规律 Optics
成功之处
较好的解释光的
反射折射规律
双折射现象
定性的解释光的干涉、衍射现象
不涉及波的空间周期特性-波长、振幅和相位
没有爱因斯坦的相对论也许是可惜的,或者有爱因斯 坦的相对论是必然的,这都不重要,重要的科学的范 式引导着人们前赴后继,创造出了如此丰富的科学技 术。
每一个领域什么样的问题都有人深入研究,真是太美 妙了!这是科学的范式带给我们的,其美妙程度远远 超过某一个理论的美妙。
Education is what remains after one has forgotten what one has learned in school. 所以作为要教导学生科学精神,关键不是要他们学 会哪些具体知识,或者掌握什么具体技能,没有哪 一个科学知识或者技术会是独门绝技,祖传秘方, 是学生学会之后就可以安身立命的。即使背完了整 本百科全书,你也不能成为科学家。 关键是学会怎样由未知到已知的、科学的求知方法; 或者通过尝试和纠错,学会一种有普遍意义的自由 探索和创造精神……也就是对科学的范式的理解和 掌握。 当然,我们需要通过知识的学习和技能的训练来达 到这一目的,但是如果我们不能达到这一目的,这 些知识和技能还有什么用处呢?
单孔衍射和圆孔衍射

显然,菲涅尔衍射是普遍情况,夫琅禾费衍射只是它的特例。
大学物理实验中心
实验目的:
1.观察单缝衍射和圆孔衍射现象; 2.学习掌握单缝和圆孔衍射规律,证明极小值
的位置与理论值一致。
大学物理实验中心
大学物理实验中心
数据记录:
表1 0.08mm单缝衍射
狭缝到屏幕的距离(D)=_________ (激光波长λ=532 × 10-6mm)
第一级(m=1)
第二级(m=2)
第三级(m=3)
条纹宽度(暗纹)
中心到暗条纹的距离y
计算狭缝宽度
|a - a0|/a0×100%
大学物理实验中心
数据记录:
表2 a=0.20mm圆孔衍射
圆孔到屏幕的距离(D)=_________ (激光波长λ=532 × 10-6mm)
第一级(m=1)
第二级(m=2)
第三级(m=3)
暗环直径(mm) (每级测3次)
暗环半径ym(mm)
ym=(直径3平均值) ×(1/2)
计算圆孔直径d(mm) (公式①②③)
|a - a0|/a0×100%
大学物理实验中心
数据处理:
1.利用各级别干涉条纹的数据,依据公式
d m D (m 1,2,3)
y
分别计算出狭缝距离d ,并计算出相对误差(表一)。
2.利用数据求出各级次的暗环直径平均值,再求出其相应的暗环半径 ymi
利用公式①、②、③分别计算出圆孔的直径d1,d2,d3;并求出其相对 误差。
大学物理实验中心
2.圆孔衍射 当光通过圆孔发生圆孔衍射,衍射图样是一组明暗相同 的圆环。中央明亮的圆斑——艾里斑,它集中了衍射光能的 83.5%。 如图,第一级暗环所对应的衍射角
光的衍射现象

P
衍射图象不变!
(在光栅中用到,请记住!)
留一思考:若光源在原平面内上下平行移动, 在双缝实验中干涉条纹如何变化? 2.若光线斜入射,则屏上条纹如何?
例1:单色平行光斜射到宽为a的 单缝,求各级暗纹的衍射角.
A C B D
解:如图AC、BD分别为入射、反射光的波面 光束中的最大光程差
AD BC a sin a sin
暗条纹应有 a sin a sin k 得
1
k=1,2,3,...
k sin sin a
五、圆孔夫琅禾费衍射
1
2r
f
图样,爱里斑
与单缝夫琅禾费衍射唯一的不同是衍射物不同。
不能分辨
恰能分辨
能分辨
瑞利准则 :一个点光源的衍射图样的主极大正
好与另一点光源的第一极小 刚好重合时,这两个 点光源恰好能被光学仪器分辨。
S2
1
S1
两物点对衍射中心所张的角度正好等于爱里斑的 半角宽时为最小分辨角
R 1 sin 1 1.22
分辨本领为最小分辨角的倒数
哈勃太空望远镜 电子显微镜
回忆: 惠更斯原理:在波的传播过程中,波阵 面(波前)上的每一点都可看作是发射 子波的波源,在其后的任一时刻,这些 子波的包迹就成为新的波阵面。
思考:衍射条纹与干涉
条纹的相像之处? 菲涅耳的补充假设—子波的干涉 在波的传播过程中,从同一波阵面上的各点发出的子 波,经传播在空间某点相遇时,这些次级子波要相干 叠加,这一点的振动即是相干叠加的结果。
作业
要求对光的干涉内容,按所讲的四个重点去总结主 要的五个干涉实验,并分析改变光程差的手段。 对光的衍射内容,要求理解菲涅耳半波带法,掌握 衍射明暗纹公式。
夫琅禾费单缝衍射
(A) 2m (B) 1m (C) 0.5m (D) 0.2m (E) 0.1m
[B]
矩形孔的夫琅禾费衍射
两个正交迭置的狭缝(设宽度分别为a、b) 衍射光在x, y方向的衍射角分别为
x, y
衍射光场:两个按正交方向展开的单缝衍射场的乘积
I(P)
I
0
s i n
2
s i n
2
远去的汽车头灯
最小分辨角:
S1
D
*
1
1.22
D
* S2
0 I
表达式中的波长 是指衍射光场在像方空间所处介质
中的波长
眼睛(正常人眼) a=D/2=1mm,n=1,n'=1.336,
0=550nm,f '=2.2cm
角分辨极限: m=0.610/n'a ≈2.511×10-4 rad
线分辨极限:
0m=0.610/na ≈3.355×10-4 rad
分辨本领:
1 R
min
光学系统对被观察对象微小细节的分辨能力
These photographs of an automobile’s headlights were taken at the greater and greater distances from the camera.
远去的汽车头灯
两个按正交方向展开的单缝衍射场的乘积衍射光在xy方向的衍射角分别为其中矩形远场衍射振幅三维图矩形孔的夫琅禾费衍射图样矩形远场衍射强度三维图24设圆孔的直径为d与p点对应的衍射角为衍射屏观察屏中央亮斑爱里斑变小第一暗圈所包围的中央亮斑叫做爱里斑airydisk线半径
2.3 夫琅禾费单缝衍射
bsin j
夫琅和费衍射实验

课程名称:物理光学实验
实验名称:夫琅禾费衍射实验
'0'0E()a a P C C ==⎰⎰,利用贝塞尔
消像差透镜
图4 夫琅禾费衍射光路图
使其探测面与透镜的距离为透镜焦距f(探测器靶面的位置与滑块
17.3mm,透镜距离滑块刻度为6mm);
“相机图像”预览功能,预览衍射图案。
调整CCD
光强适中(不饱和,也不过弱)。
记录CCD处的衍射图案;
打开软件,点击“圆孔方孔衍射”→“捕获衍射图案”,获取夫琅禾费圆孔衍射的实
图5
图6
图7 图8
图9 2.当D=300μm时的夫琅禾费圆孔衍射
图10
图11 图12
图13 L=500μm时的夫琅禾费方孔衍射
图14
图16
图17 L=300μm时的夫琅禾费方孔衍射
图18
图19 图20
图21
六、数据处理
同数据记录
七、结果陈述:
实验得到了夫琅禾费圆孔衍射和夫琅禾费方孔衍射的实验图像。
测量了夫琅禾费圆孔衍射和夫琅禾费方孔衍射的光强分布,发现实验值和理论值符合的很好,说明夫琅禾费衍射公式的正确性。
实验得到了夫琅禾费圆孔衍射和夫琅禾费方孔衍射虚焦时的图像。
夫琅禾费衍射
2 106 0.5 5000 1010
2
光的衍射 习题课
一、基本要求
1.了解惠更斯—菲涅耳原理
2.掌握单缝夫琅禾费衍射的条纹分布,以 及缝宽,波长等对衍射条纹的影响
3.理解光栅衍射方程,会分析光栅常数,
光栅缝数N等对条纹的影响
二、基本内容
1.单缝夫琅禾费衍射
(1)半波带法的基本原理
(2)明暗条纹的条件
(3)缺级条件,当
(b b)sin k k 0,1,2,
bsin k k' 1,2,
同时成立时,衍射光第 k 级缺
级且 k b b' k' b
3.光学仪器的分辩率
最小分辨角 0
1,22
D
三、讨论 1.由下列光强分布曲线,回答下列问题 (1)各图分别表示几缝衍射 (2)入射波长相同,哪一个图对应 的缝最宽
可见到17条(实际15条)
(3)此时屏上条纹不再对称, 在一侧有
(b b) sin 30 (b b) sin k
当 90时,k 15
另一侧有 (b b)(sin 30 sin ) k
90时,k 5
考虑到第4,8,12及-4
i
为缺级以及实际效果,共
观察到15条明纹,全部级
Nd
由图,有: k Nk 1 ( )
d
Nd
得 R Nk 1 Nk,(k 0)
(N >>1)
N k
R
例如:
N = 4 I 0级 1级
sin -2(/d)-(/d) 0 /d 2/d
3
4d 2d 4d
N 4, k 1 : 设
sin Nk 1 ( )
a
5000
夫琅禾费衍射实验报告

一、单缝衍射 计算光强比: 背景光: I p
I 3 I 4 4 15 9.5 2 2
I1 I 2 175 172 1.83%( 10%) . 对称性要求: I I 172 175 1 2 Ip 9.5 2 2
4
主极强位置与缝数目 N 无关,但 N 越大,主极强宽度越小;相 邻主极强之间有 N-1 个暗纹和 N-2 个次极强;光强分布的外部轮廓 (包络线型)与单缝衍射的形状相同,这是单缝衍射因子的作用。
[实验仪器]
毫米刻度尺 2 个(最小分度值 1mm) 、光学平台、He-Ne 激光 器(λ=632.8nm)、平面镜、衍射元件、光探测器、光栅尺、微机。
2
2
表示衍射光场任意方向的相对光强。
单缝衍射光强分布的特点: 单缝的夫琅禾费衍射图样的中心有一 个主极强(零级衍射斑),两侧都有一系列次极强和暗斑。主极强出现 在 sin
0 的地方, 原因是到这里的各条衍射光线有相同的
相位,它们相干叠加的结果具有最大的光强。 几何光学中的光线就是零级衍射线, 几何光学中的象点就是零级 衍射斑的中心。 在单缝衍射因子具有极大值的地方, 即在
光的衍射和偏振-1

40
Summary
•光的衍射的概念和原理 •夫琅禾费单缝衍射原理和性质
•夫琅禾费圆孔衍射 •光栅衍射的原理和性质
相关习题:习题7:7-2,7-5,7-6
41
光的偏振
Polarization
42
光的偏振 Polarization
一、光的偏振态、马吕斯定律 二、玻片堆 三、双折射 四、偏振光的产生和检验 五、旋光性
3
一、概述
1、定义:
光偏离直线传播的现象称为光的衍射 (diffraction)现象。 衍射显著的条件: 障碍物尺寸与波长大得不多 衍射系统通常包括:光源、衍射屏、接收屏三部 分。
4
圆孔
单缝
方孔
几种典型的衍射图样
5
正三边形孔
正四边形孔
正六边形孔
6
正八边形孔 衍射图样
单缝
6
2、 光的衍射分类 1.菲涅耳衍射
极大 极小
(a)
(b)
(c)
(d)
(e)
自然光和偏振光的光矢量分布
46
1、线偏振光 linear polarized light
定义:只含单一振动方向的光称为线偏振光。
光矢量只在一个方向上振动 线偏振光的表示法
(光振动平行板面)
(光振动垂直板面)
47
2、自然光 Natural light
普通光源如太阳、白炽灯、钠灯等发光时,组成 光源的原子自发或受激辐射的光波列是随机的, 各光波列振动方向、频率和位相不尽相同,光矢 量在垂直于光传播方向的平面上取各方向的几率 相等。
L2后会聚在屏上P处。屏上出现单缝衍射图样。 10
光强分布
衍射图样
特点:明暗相间的衍射条纹
单缝和圆孔的夫琅禾费衍射介绍

二、用振幅矢量推导光强公式
1.振幅矢量法 将缝AB的面积S等分成N(很大)个等宽的窄带,
每个窄带宽度a/N.
每个窄带发的子波在P点振
A
幅近似相等,设为A1,相邻
窄带所发子波在P点引起的振
动的光程差
δ = (asin)/N
B
相位差 2 2 asin
N
屏上P点的合振幅 AP就是各子波的振幅矢量和的 模,这是多个同方向、同频率,同振幅、初相依 次差一个恒量的简谐振动的合成。
对于屏中心o点
衍射角为零,各子波的相位相同
A
1
…
A 0
o点的合振动振幅 A0 = N A1
中央明纹的光强 I0 A02
对于屏上其它点P,由
于屏上位置不同,对应的衍
射角就不同,Ap的大小也
单缝和圆孔的夫琅 禾费衍射介绍
一、单缝夫琅禾费衍射
1.衍射装置及图样
单缝 透镜
衍射角
f
衍射屏
I
衍射图样
(1) 衍射条纹与狭缝平行。 (2)中心条纹很亮,两侧明条纹对称分布, 亮度减弱。 (3)中央亮斑的宽度为其他亮斑的两倍。
由惠更斯——菲涅耳原理:
单缝处波面看作无穷多个相干波源,屏上一点是 (无穷)多光束干涉的结果。
由 a sin1
有
sin1
a
30 mm 0.20 m
0.15
d
a
θ1
L
β
150
1 8.63°
如图: 15°1 23.63° 15°1 6.37°
L d(ctg ctg )
