中科大数学系本科专业必读科目及参考
中国科学技术大学数学科学学院;培养方案整理与课程简介;

大三上学期:数理统计 大三下学期:回归分析、应用随机过程
1
二、专业方向课程(数院各方向的选修课程,8 credits)
修读任一方向的学生,需要从对应计划选修课程中修读至少 8 学分
基础数学(8/25 credits)
夏季学期:纯粹数学前沿(1 学分) 秋季学期:组合学、高等实分析*、微分流形*、代数拓扑*、代数学* 春季学期:应用随机过程
修读任一方向的学生,需要从对应计划选修课程中修读 8 学分
基础数学(8/20 credits)
秋季学期:高等实分析*、微分流形*、代数拓扑*、代数几何引论*、交换代数* 春季学期:李代数及其表示*、应用随机过程、黎曼几何*
计算数学(8/26 credits)
秋季学期:数值代数、符号计算软件、数学实验、有限元方法*、偏微分方程数值解 春季学期:数值分析、计算机图形学、算法基础、小波分析
夏季学期: 计算与应用类课程:间断有限元简介*(1 credits)、计算机图形学前沿(2 credits) 基础数学类课程:纯粹数学前沿(1 credit)
3
四、华罗庚数学科技英才班培养计划
通修课程(80.5 credits)
同数学科学学院培养计划
学科群基础课(11 credits)
大一上学期:代数学基础(3 学分)、解析几何 大二上学期:微分方程 I
5
四、大学物理实验(3 credits):
中国科学技术大学数学科学学院
培养方案整理与课程简介
整理人:章俊彦 2013 级数学科学学院‐基础数学方向 PB13001112
目录
必修课程………………………………………………………1
·全校通修课程、学科群基础课(数院必修)、专业核心课(方向必修)
数学专业参考材料书汇总整编推荐

学数学要多看书,但是初学者很难知道那些书好,我从网上收集并结合自己的经验进行了整理:从数学分析开始讲起:数学分析是数学系最重要的一门课,经常一个点就会引申出今后的一门课,并且是今后数学系大部分课程的基础。
也是初学时比较难的一门课,这里的难主要是对数学分析思想和方法的不适应,其实随着课程的深入会一点点容易起来。
当大四考研复习再看时会感觉轻松许多。
数学系的数学分析讲三个学期共计15学分270学时。
将《数学分析》中较难的一部分删去再加上常微分方程的一些最简单的内容就是中国非数学专业的《高等数学》,或者叫数学一的高数部分。
记住以下几点:1,对于数学分析的学习,勤奋永远比天分重要。
2,学数学分析不难,难得是长期坚持做题和不遗余力的博览群书。
3,别指望第一遍就能记住和掌握什么,请看第二遍,第三遍,…,第阿列夫遍。
4,看得懂的仔细看,看不懂的硬着头皮看。
5,课本一个字一个字的看完,至少再看一本参考书,尽量做一本习题集。
6,开始前三遍,一本书看三遍效果好于三本书看一遍;第四遍开始相反。
7,经常回头看看自己走过的路以上几点请在学其他课程时参考。
数学分析书:初学从中选一本教材,一本参考书就基本够了。
我强烈推荐11,推荐1,2,7,8。
另外建议看一下当不了教材的16,20。
中国人自己写的:1《数学分析》陈传璋,金福临,朱学炎,欧阳光中著(新版作者顺序颠倒)应该是来自辛钦的《数学分析简明教程》,是数学系用的时间最长,用的最多的书,大部分学校考研分析的指定教材。
我大一用第二版,现在出了第三版,但是里面仍有一些印刷错误,不过克可以一眼看出来。
网络上可以找到课后习题的参考答案,不过建议自己做。
不少经济类工科类学校也用这一本书。
里面个别地方讲的比较难懂,而且比其他书少了一俩个知识点,比如好像没有讲斯托尔滋(stolz)定理,实数的定义也不清楚。
不过仍然不失为一本好书。
能广泛被使用一定有它自己的一些优势。
2《数学分析》华东师范大学数学系著师范类使用最多的书,课后习题编排的不错,也是考研用的比较多的一本书。
适合中科大的强基教材

适合中科大的强基教材
中科大作为一所拥有优秀师资和研究基础的高水平综合性大学,拥有一系列适合的强基教材。
以下是一些适合中科大的强基教材推荐:
1. 《线性代数》(大一下学期):中科大的工科及理科专业都会开设这门课程,具有重要的基础地位。
适合外行转行或者刚入门的学生,逻辑清晰,内容丰富,包括向量、矩阵、线性方程组、行列式等基本概念和常用的运算方法。
推荐教材:《线性代数及其应用》(第5版)- Gilbert Strang。
2. 《概率论与数理统计》(大二上学期):该课程是中科大的数学基础课程之一,对于理解概率与统计的基本原理、理论和方法具有重要作用。
推荐教材:《概率论与数理统计》(第6版)- 胡庆余大、王成文。
3. 《高等数学》:作为中科大的首要数学基础课程,高等数学涵盖了微积分和数学分析的基本概念、原理和应用。
推荐教材:《高等数学》(第7版)- 同济大学数学系。
4. 《离散数学》:该课程是计算机科学和信息工程等专业的必修课,主要涉及逻辑、集合论、图论、布尔代数等内容。
适合培养学生的数学思维和逻辑推理能力。
推荐教材:《离散数学及其应用》(第7版)- Kenneth H. Rosen。
5. 《计算方法》:作为计算机科学、数学和物理等专业的必修课,计算方法教授数值计算的基本方法和算法。
推荐教材:
《数值计算方法》(第4版)- 田文俊。
当然,以上仅是一些基础课程的推荐,针对不同专业的具体需求还需结合实际情况进行选择教材。
另外,中科大的教师团队也在不断创新教学方法,可能会有具体的内部教材和教学资源。
因此,在选用教材时,还需要关注学校或教师对教材的要求和建议。
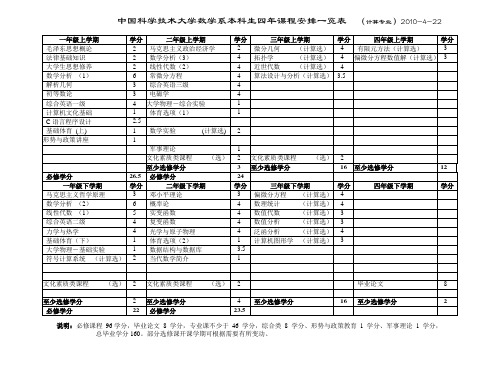
中国科学技术大学数学系本科生计算四年课程安排一览
至少选修学分
4
至少选修学分
16
至少选修学分
2
必修学分
22
必修学分
23.5
说明:必修课程96学分,毕业论文8学分,专业课不少于46学分,综合类8学分、形势与政策教育1学分、军事理论1学分,
总毕业学分160。部分选修课开课学期可根据需要有所变动。
3
综合英语二级
4
复变函数
4
数值分析(计算选)
3
力学与热学
4
光学与原子物理
4
泛函分析(计算选)
4
基础体育(下)
1
体育选项(2)
1
计算机图形学(计算选)
3
大学物理-基础实验
1
数据结构与数据库(选)
3.5
符号计算系统(计算选)
2
当代数学简介
1
文化素质类课程(选)
2
文化素质类课程(选)
2
毕业论文
8
至少选修学分
2
文化素质类课程(选)
2
至少选修学分
3
至少选修学分
16
至少选修学分
12
必修学分
26.5
必修学分
24
一年级下学期
学分
二年级下学期
学分
三年级下学期
学分
四年级下学期
学分
马克思主义哲学原理
3
邓小平理论
3
偏微分方程(计算选)
4
数ቤተ መጻሕፍቲ ባይዱ分析(2)
6
概率论
4
数理统计(计算选)
4
线性代数(1)
5
实变函数
4
数值代数(计算选)
2
线性代数(2)
大学本科数学与应用数学专业所学课程

大学本科数学与应用数学专业所学课程第一篇:大学本科数学与应用数学专业所学课程专业选修运筹与优化组合数学开关电路与布尔代数数理统计初等数论统筹法与图论初步数学史选讲点集拓扑学计算机辅助教学中学数学高考及竞赛课外活动辅导公共课大学英语大学体育思想道德修养与法律基础高等数学大学物理中国近代史纲要教育心理学教育学毛泽东思想和邓小平论书法普通话马克思主义哲学大学语文计算机基础现代教育技术文献检索形势与政策人文社会科学基础军事理论就业指导专业必修数学分析空间解析几何中学学科新课标及教材剖析计算方法初等代数研究数学学科教学论近世代数概率论基础常微分方程高等代数复变函数论C语言程序设计微分几何空间解析几何数学模型与实验初等几何研究高等几何研究实变函数论基础第二篇:数学与应用数学专业数学与应用数学专业《学年论文》数学与应用数学专业《学年论文》指导书撰写人:撰写人:杨禾花审定人:审定人:毛志强一、学年论文的目的与任务学年论文是学生在学年结束时完成的学术性的论文,要求学生在教师指导下,运用已有知识进行学术研究,分析解决所属专业领域的问题,并能准确表达自己的研究成果。
其目的在于使学生初步掌握撰写学术论文的方法,巩固深化所学理论知识,培养学生缜密的思维能力和分析解决问题的能力、较强的书面表达能力及论证才能,发挥创造精神,并作为检验学生一学年学习成绩和研究成果的重要手段。
学年论文是学生在完成公共课、专业基础课和大部分专业课学习后的一个教学环节,是学生整理已学到的理论知识的一次训练,并为撰写毕业论文奠定基础。
本学年论文的目的和任务是:1.检验学生在专业学习中的效果和收获;2.培养学生实际运用知识和获取资料的能力;3.培养学生理论创新能力;4.使学生了解期刊论文的基本格式和写作要求,并遵照要求完成论文写作;5.使学生认识遵守学术道德的重要,培养科学创造精神;二、学年论文的时间安排序号学年论文教学工作内容教学工作目标、要求论题要求明确具体,具备一定的理论价值或实用价值。
中国科学技术大学数学系课程简介

课 号:MA02006 课程名称(中文):线性代数(2) 课程名称(英文):Linear Algebra (II) 学 时:80 学 分:4 开课学期:秋 预修课程:整数与多项式、MA03003 解析几何 适用对象和学科方向:数学 主要内容:本课程讲授线性空间关于线性变换的空间分解理论和矩阵的 Jordan 标准型理论;讲授 Euclid
28
பைடு நூலகம்
热传导方程与调和方程的定解问题,解的存在性、唯一性和稳定性。适当地介绍方程线的 相应问题及柯西-柯娃列夫斯卡娅定理,对特征理论、算子理论、广义函数理论也做了适量 的讨论。通过内容的论述介绍了偏微分方程中常用的广义解及处理手段并适当地引入一些 现代化的处理方法
的微分学和积分学的基本内容以及基本的运算技巧和方法。
课 号:MA02001 课程名称(中文):数学分析(2) 课程名称(英文):Mathematical Analysis(2) 学 时:100 学 分:5 开课学期:春 预修课程:MA02000 数学分析(1) 适用对象和学科方向:数学 主要内容:本课程主要讲授数项级数,函数列与函数项级数,Fourier级数与Fourier积分;Rn的拓扑及
多变量连续函数的性质。
课 号:MA02002 课程名称(中文):数学分析(3) 课程名称(英文):Mathematical Analysis(3) 学 时:80 学 分:4 开课学期:秋 预修课程:MA02001 数学分析(2) 适用对象和学科方向:数学 主要内容:本课程讲授多变量函数的微分学和积分学,表达重积分和线面积分之间关系的 Green 公式,
Gauss 公式和 Stokes 公式;介绍数量场和向量场中几个重要的量以及它们之间的关系;讲 授用参变量积分表示的函数的性质。
中科大数学系本科专业必读科目及参考

中科大数学必读科目及参考有些科大学生,尤其是新生,抱怨科大教材偏难;而且新生通常缺乏学习方法,对如何在大学中学习还没有清楚的概念。
下面是一位科大数学系学长给科大数学专业学生的一些建议。
我转发过来,仅供参考。
1、老老实实把课本上的题目做完。
其实说科大的课本难,我以为这话不完整。
科大的教材,就数学系而言还是讲得挺清楚的,难的是后面的习题。
事实上做1道难题的收获是做10道简单题所不能比的。
2、每门数学必修课至少要看一本参考书,尽量做一本习题集。
3、数学分析别做吉米,除非你太无聊,推荐北大方企勤的习题集。
此外注意一下有套波兰的数学分析习题集,是不是搞得到中文或英文版。
4、线性代数推荐普罗斯库列科夫的<<线性代数习题集>>和法捷耶夫的<<高等代数习题集>>。
莫斯科大学要求把上面的题全做光。
建议大家在搞定亚洲第一难书的同时也把里面的题打通。
5、解析几何不要不重视。
现在有种削弱几何课的倾向,甚至有的学校把解析几何课改成只有两课时,这样一来,几何训练不足,会很吃亏的。
6、常微要看看阿诺尔德的书,打通菲利波夫的习题集。
7、数论课是很重要的,起码可以锻炼思维能力。
8、数学分析、线性代数、解析几何、泛函、拓扑、抽象代数、实变、微分几何是最重要的课,大家脱层皮也要学好。
要尽量加强这方面的工底,不然的话以后很吃亏。
9、有时间去物理系多听课,千万不要毕业了连量子力学也不懂,这样的数学家注定要被淘汰的。
读读费曼物理讲义和郎道的理论物理教程。
10、华罗庚的<<数论导引>>的前言大家好好看看,多多领会!11、想读数理统计和计算数学的要注意,统计和计算数学同样是数学类的专业,不要以为加上计算和统计就可以降低要求。
中科大基础数学修课指南

中科大基础数学修课指南
中科大基础数学修课指南如下:
1. 高等数学:这门课程是数学专业的基础课程,主要包括微积分、极限、导数、积分、级数等内容。
学生需要掌握基本的数学推导和计算方法,以及应用数学解决问题的能力。
2. 线性代数:线性代数是数学中的一门重要课程,主要涉及向量空间、矩阵、线性方程组、特征值等内容。
学生需要理解向量和矩阵的基本概念和性质,并能运用线性代数的方法解决实际问题。
3. 概率论与数理统计:概率论与数理统计是一门应用性很强的数学课程,主要包括概率、随机变量、概率分布、参数估计、假设检验等内容。
学生需要熟悉概率和统计的基本概念和方法,并能应用于实际数据分析和决策问题。
4. 数学分析:数学分析是一门较为抽象和深入的数学课程,主要包括实数理论、函数极限、连续性、一元微积分等内容。
学生需要具备较强的数学抽象和推导能力,并能运用分析方法解决复杂问题。
5. 偏微分方程:偏微分方程是数学中的一门重要研究领域,涉及到物理、工程等多个学科。
学生需要掌握偏微分方程的基本概念和求解方法,以及应用于实际问题的能力。
总的来说,中科大基础数学修课指南包括高等数学、线性代数、概
率论与数理统计、数学分析和偏微分方程等课程。
学生需要在这些课程中掌握基本的数学概念和方法,并能应用于实际问题的解决。
中科大高等数学教材

中科大高等数学教材高等数学是大学数学教学中的重要课程之一,对于培养学生的逻辑思维和数学能力具有重要意义。
中科大高等数学教材是一套针对大学本科学生编写的教材,旨在帮助学生系统学习和掌握高等数学的基本概念、原理和方法。
一、教材概述中科大高等数学教材内容丰富,涵盖了大学高等数学课程的核心内容。
教材分为上下两册,分别对应于大学高等数学的第一学期和第二学期教学内容。
每一册教材都经过精心编写和编辑,力求简明扼要、逻辑严谨,使学生能够轻松理解和掌握数学知识。
二、教材结构1. 基本概念和定义:教材第一部分主要介绍高等数学中的基本概念和定义,包括数列、极限、导数、积分等内容。
通过系统地介绍基本概念,帮助学生建立扎实的数学基础。
2. 基本原理和定理:教材第二部分重点介绍高等数学中的基本原理和定理,包括极限的性质、导数的计算法则、积分的计算法则等。
通过深入讲解各种原理和定理,提高学生的数学推理和证明能力。
3. 典型问题和案例分析:教材第三部分选取了一些典型的数学问题和案例,通过具体的例子来说明数学理论在实际问题中的应用。
通过分析解决实际问题的过程,培养学生的数学建模能力。
4. 习题和练习:教材中设有丰富的习题和练习,包括选择题、填空题、计算题以及证明题。
这些习题既能帮助学生巩固和复习知识,又能培养学生的问题解决能力和创新思维。
三、教学特点1. 系统性:教材内容根据课程安排和教学需要进行了合理的架构和编排,各章节内容之间紧密联系,层层递进,有助于学生系统地学习数学知识。
2. 规范性:教材严格按照数学分类和定义的规范,准确描述数学概念和性质。
同时,在演绎推理过程中注重逻辑推理和论证方法的规范性。
3. 实用性:教材中充分利用了实际问题和案例,通过具体问题的分析和解决,培养学生的数学建模和解决实际问题的能力。
四、教学引导中科大高等数学教材在内容安排和解题思路上给予了学生充分的引导,既注重理论和方法的解释,又注重实际问题和案例的分析。
中科大数学系课程

中科大数学系课程
中科大数学系的课程包括但不限于以下几个方向:
1. 基础数学课程:包括高等数学、线性代数、概率论与数理统计等。
2. 应用数学课程:包括偏微分方程、数值计算方法、优化理论与方法等。
3. 统计学课程:包括数理统计、时间序列分析、生存分析等。
4. 运筹学课程:包括线性规划、整数规划、图论等。
5. 金融数学课程:包括金融随机过程、金融衍生品定价等。
6. 计算数学课程:包括计算方法、数值计算线性代数、数值优化等。
7. 数学建模课程:包括数学建模与仿真、科技创新方法与实践等。
此外,中科大数学系还有一些专业方向的课程,如微分几何、抽象代数、数论等,以及培养学生实际应用能力的课程,如实变函数、泛函分析等。
具体课程设置可能因学期和教学计划有所调整,建议在官方网站或相关学术资料上查询最新信息。
大学数学专业课程有哪些整理

大学数学专业课程有哪些整理高校数学专业课程有哪些数学与应用数学,本专业同学主要学习数学和应用数学的基础理论、基本方法,受到数学模型、计算机和数学软件方面的基本训练,具有较好的科学素养,初步具备科学讨论、教学、解决实际问题及开发软件等方面的基本力量。
下面是我为大家收集的高校数学专业课程有哪些,期望能够帮忙到大家。
高校数学专业课程1、数学分析这门课是对大家从学校到高校的一门数学总结课程,也是一门从1到实数的课。
之所以这么说,是由于这门课的内容,大家可能并不生疏。
从上幼儿园我们就学会了数数,数数这个过程看上去非常简洁。
但其实里面蕴含了这门课当中特别重要的一些概念,也是后面证明许多定理必要的手段。
幼儿园的时候,我们数的数是自然数,到了学校可能就能数到整数了。
但许多人应当不知道,有理数也可以被数出来。
可能刚开头接受这样的概念的时候有点反直觉,这就是我们之后要提到的我们的直觉可能有的时候并不符合规范化的思索方式。
自从毕达哥拉斯学派发觉了根号2以后,数学就到了实数的范畴了,这算是高中的终点了。
数学分析作为讨论生的实分析的课程的基础,讨论了实数的各种性质。
在实数的性质中,最重要的可能就是实数的完备性公理,简洁来讲这个公理的一部分内容就是,假如我知道一块沙滩上的沙子的数量是有限的且肯定有沙子,那么这片沙滩的沙子数量存在一个上确界。
有了实数我们就可以连续争论实数上的数列sequence。
1,2,3,…就是一个数列,但数列不仅仅是表现的那么简洁,这实际上是一个从实数到自然数的映射。
类似的看上去不是映射的映射关系还有概率里的随机变量。
2、抽象代数抽象代数属于数学系里对人的抽象思维比较有考验的一门课了。
简洁介绍一下,信任大家对集合应当都特别了解。
整个现代数学就是建立在集合论上的学科。
那么,简洁的集合看上去非常清楚,当集合中的元素数量特别大的时候,集合是不是看上去不那么干净了呢。
同时,集合又满意了无序性,两辆元素之间没有任何关系,显得有些杂乱无章。
关于数学参考书(大学数学系本科所有课程)

关于数学参考书(大学数学系本科所有课程)来源:复旦BBS数学一、数学分析从数学分析的课本讲起吧。
复旦自己的课本应该可以从六十年代上海科技出的算起(指正式出版),那本书在香港等地翻印后反应据说非常好,似乎丘成桐先生做学生的时候也曾收益与此。
到90年代市面上还能看到的课本里面,有一套陈传璋先生等编的,可能就是上面的书的新版,交大的试点班有几年就拿该书做教材。
另外有上海科技版的欧阳光中(谷先生的连襟),秦曾复,朱学炎三位编的课本,好象后来数学系不用了,计算机系倒还在用。
那本书里面据说积分的第二中值定理的陈述有点小错。
总的说来,这些书里面都可以看到一本书的影子,就是菲赫今哥尔茨的"数学分析原理",其原因,按照秦老师的说法,是最初在搞教材建设的时候,北大选的"模本"是辛钦的"数学分析简明教程",而复旦则选了"数学分析原理"。
后来自然有欧阳先生和姚允龙老师的那本数学分析。
我不否认那是一种尝试,但是感觉上总有点别扭。
以比较新的观点来看数学分析这样经典的内容在国际上的确是一种潮流,但是从这个意义上说该书做得并不是非常好。
而且从整体的课程体系上说,在后面有实变函数这样一门课的情况下是否有必要引入Lebesgue积分值得商榷。
下面开始讲一些课本,或者说参考书:1。
菲赫今哥尔茨"微积分学教程","数学分析原理"。
前一本书,俄文版共三卷,中译本共8本;后一本书,俄文版共二卷,中译本共4本。
此书堪称经典。
"微积分学教程"其实连作者(莫斯科或者列宁格勒大学的教授,门下弟子无数,包括后来得诺贝尔经济学奖的著名数学家Kantoro vitch)都承认不太合适作为教材,为此他才给出了能够做教材的后一套书,可以说是一个精简的版本(有所补充的是在最后给出了一个后续课程的简介)。
相信直到今天,很多老师在开课的时候还是会去找"微积分学教程",因为里面的各种各样的例题实在太多了。
大学数学专业学什么课程

大学数学专业学什么课程大学数学专业是基础学科,一般人还真学不来。
于是有同学问大学数学专业学些什么课程呢?下面是由小编为大家整理的“大学数学专业学什么课程”,仅供参考,欢迎大家阅读。
大学数学专业学什么课程"数学类"专业类属于理学门类,涵盖了四个专业,分别有“数学与应用数学”、“信息与计算科学”、“数理基础科学”、“数据计算及应用”。
大学是一个从过度的过程,是以在刚进入大学大一阶段时并不会学难度系数过高的课程,通常大学数学专业学的有《解析几何》、《高等代数》、《概率论于数据统计》和《微分几何》等课程。
1、《高等数学》,主要内容是极限→导数→微积分,导数类似求曲线切线的斜率,微积分类似于求不规则图形的面积2、《线性代数》,它的研究对象是向量,向量空间(或称线性空间),线性变换和有限维的线性方程组。
学会了可以求多元方程组3、《概率论》,研究随机现象数量规律。
学会了可以研究事情发生的各种可能性4、《统计学》,主要通过建立数学模型,收集数据,进行量化的分析、总结,并进而进行推断和预测,为相关决策提供依据和参考。
概率论和统计学视专业情况而定,有些专业是不用学的。
拓展阅读:数学师范类都学啥需要学习的专业课有:《数学分析》、《高等代数》、《概率与数理统计》、《解析几何》、《复变函数》、《实变函数》、《拓扑学》、《常微分方程》、《泛函分析》等等,开设的专业课因校而异,但主要的《数学分析》和《高等代数》是都有的。
其他非专业课包括很多,同样也是因学校的不同而不同,主要有:《大学英语》、《法律基础》、《心理学》、《教育学》、《体育》等等,选修课就要看自己的爱好了。
出来以后不一定只当老师的,要看学到什么程度了。
只是本科毕业的话,主要就是从事教师行业,如果学到硕士甚至博士毕业,就可以进大型企业或者研究所之类的机构了。
数学是很有用的,学好了数学其他的学科再学起来就容易多了。
数学好上大学选择什么专业合适合适的专业:1、数学与应用数学专业:培养掌握数学科学的基本理论与基本方法,具备运用数学知识、使用计算机解决实际问题的能力,受到科学研究的初步训练,能在科技、教育和经济部门从事研究、教学工作或在生产经营及管理部门从事实际应用、开发研究和管理工作的高级专门人才。
中科大数学系课程

中科大数学系课程摘要:一、引言二、中科大数学系简介三、课程设置与培养方案四、中科大数学系在国内外的声誉与影响五、优秀毕业生及知名教授六、对有志于数学专业的学生建议正文:一、引言作为中国科学技术大学(简称中科大)的优势学科之一,数学系自成立以来,始终秉持严谨治学、求实创新的优良传统,培养了大量杰出人才。
本文将详细介绍中科大数学系的相关情况。
二、中科大数学系简介中科大数学系成立于1958年,是我国最早开展现代数学教育的院系之一。
经过几十年的发展,现已形成本科、硕士、博士及博士后完整的人才培养体系。
数学系师资力量雄厚,拥有一批国内外知名专家和学者。
三、课程设置与培养方案中科大数学系课程设置严谨、科学,涵盖了数学基础课程、专业课程及选修课程。
为培养学生的创新能力和实践能力,还设有丰富的实践课程、研讨课程和研究课程。
此外,还有国际合作项目和实践基地,为学生提供了宽广的发展空间。
四、中科大数学系在国内外的声誉与影响中科大数学系在国内外的声誉和影响力不断提高,已与多所国际知名高校建立了合作关系,为学生提供了丰富的交流和实习机会。
数学系毕业生在学术界、企业界等领域取得了骄人成绩,为国家和社会做出了巨大贡献。
五、优秀毕业生及知名教授中科大数学系培养了众多杰出人才,如著名数学家陈景润、席南华等。
此外,许多毕业生在国内外知名高校和研究机构取得了优异成绩,为数学事业做出了突出贡献。
六、对有志于数学专业的学生建议选择数学专业,需要对数学有浓厚的兴趣和扎实的基础。
在学习过程中,要注重培养自己的逻辑思维能力、分析问题和解决问题的能力。
同时,要关注国内外数学研究动态,拓宽知识面,为将来的发展打下坚实基础。
综上所述,中科大数学系作为我国数学教育的重要基地,一直发挥着举足轻重的作用。
中科大数学与应用数学专业

中科大数学与应用数学专业是一个非常重要的专业,旨在培养具有坚实的数学基础和系统的应用数学知识,能够运用所学知识解决实际问题的专门人才。
该专业的主要课程包括数学分析、高等代数、实变函数、常微分方程、近世代数、微分几何、复变函数、点集拓扑、概率论、数理统计等。
此外,该专业还开设了一系列专业选修课程,如数理逻辑、偏微分方程、泛函分析、动力系统、数学物理方程、数论导引、群与代数表示、微分流形、代数拓扑、代数几何、金融数学、多元统计分析、应用随机过程、组合数学、应用随机分析、运筹学、图论、控制论、密码学等。
该专业注重培养学生的数学素养和解决实际问题的能力,通过课程学习和实践训练,使学生能够掌握数学与应用数学的基本理论和方法,具备运用数学知识解决实际问题的能力。
此外,该专业还注重培养学生的计算机应用能力,使学生能够熟练使用计算机进行数学计算和模拟。
总之,中科大数学与应用数学专业是一个非常有前途的专业,为培养具有坚实的数学基础和系统的应用数学知识,能够运用所学知识解决实际问题的专门人才做出了重要贡献。
中科大数学系课程

中科大数学系课程
(最新版)
目录
1.中国科学技术大学数学系的简介
2.数学系的课程设置
3.数学系的教学特点
4.数学系的成就与影响
正文
中国科学技术大学数学系是中国科学技术大学的一个重要系所,该系成立于 1958 年,是中国最早设立的数学系之一。
数学系一直致力于培养具有扎实的数学基础和较强的科学研究能力的高素质数学人才。
为了达到这个目标,数学系在课程设置方面下了很大的功夫。
首先,让我们来看一下数学系的课程设置。
数学系的课程主要包括基础课程和专业课程。
基础课程主要包括高等数学、线性代数、概率论与数理统计等,这些课程旨在为学生打下扎实的数学基础。
专业课程则包括数学分析、高等代数、微分几何、拓扑学、数论、动力系统等,这些课程旨在帮助学生深入理解数学的专业知识。
此外,数学系还开设了一些选修课程,如数学建模、数学软件等,以满足学生不同的学习需求。
其次,数学系的教学特点也非常值得一提。
数学系的教学注重培养学生的独立思考能力和创新能力,鼓励学生积极参与课堂教学和学术讨论。
数学系的教师队伍实力雄厚,他们具有丰富的教学经验和学术研究经验,能够为学生提供高质量的教学服务。
最后,让我们来看一下数学系的成就与影响。
数学系自成立以来,取得了许多重要的科研成果,发表了大量的高质量学术论文,为数学科学的发展做出了重要贡献。
同时,数学系的毕业生也取得了优异的成绩,他们在国内外的学术界、企业界等领域取得了广泛的影响。
中科大各专业课表

中科大各专业课表中科大各专业课表一、计算机科学与技术专业课表1. 第一学年- 秋季学期- 高等数学- 线性代数- 大学物理- 大学英语- 计算机导论- 春季学期- 概率论与数理统计- 离散数学- 数据结构与算法分析- 面向对象程序设计2. 第二学年- 秋季学期- 计算机组成原理- 操作系统原理与设计- 计算机网络原理与应用 - 春季学期- 编译原理与技术基础- 数据库系统原理与应用3. 第三学年- 秋季学期- 软件工程基础与实践- 春季学期- 人工智能基础- 计算机图形学基础4. 第四学年秋季学期- 分布式系统原理与设计- 计算机安全技术5. 第五年春季学期- 毕业设计二、电子信息工程专业课表1. 第一学年秋季学期- 高等数学- 大学物理- 大学英语- 电路理论基础春季学期- 概率论与数理统计- 信号与系统分析2. 第二学年- 秋季学期- 数字电路与逻辑设计- 模拟电子技术基础- 春季学期- 电磁场与电磁波理论3. 第三学年- 秋季学期- 微机原理与接口技术- 春季学期- 通信原理与应用4. 第四学年- 秋季学期- 无线通信技术基础5. 第五年春季学期- 毕业设计三、化工专业课表1. 第一学年秋季学期- 高等数学- 大学物理- 大学英语2. 第二学年秋季学期- 物理化工基础春季学期- 有机化工基础3. 第三学年秋季学期- 化工热力基础春季学期- 化工原理与计算机模拟4. 第四学年秋季学期- 化工过程控制与仪表春季学期- 化工设备与流程设计5. 第五年春季学期- 毕业设计四、土木工程专业课表1. 第一学年秋季学期- 高等数学- 大学物理- 大学英语2. 第二学年秋季学期- 工程力学基础- 材料力学基础- 土力学基础春季学期- 结构力学基础3. 第三学年秋季学期- 钢筋混凝土结构设计基础 - 岩土工程基础4. 第四学年秋季学期- 桥梁工程基础5. 第五年春季学期- 毕业设计五、生物科学与技术专业课表1. 第一学年秋季学期- 高等数学- 大学物理- 大学英语2. 第二学年秋季学期- 生物化学基础春季学期- 细胞生物学基础3. 第三学年秋季学期- 分子生物学基础春季学期- 生物信息学基础4. 第四学年秋季学期- 生物工程原理与应用5. 第五年春季学期- 毕业设计六、总结以上是中科大各专业的课表安排。
中国科学技术大学数学系教材及参考书目录

中国科学技术大学数学系教材及参考书目录 [转]必修课:数学基础:教材:汪芳庭《数学基础》科学出版社初等数论:教材:冯克勤《整数与多项式》高等教育出版社参考书:潘承洞、潘承彪《初等数论》北京大学出版社数学分析:教材:常庚哲《数学分析教程》(第二版)高等教育出版社参考书:方企勤《数学分析习题集》高等教育出版社许绍浦《数学分析教程》南京大学出版社华罗庚《高等数学引论》科学出版社S. M. Nikolsky,A course of mathematical analysis,Mir Publishers库朗《微积分与分析引论》科学出版社卢丁《数学分析原理》高等教育出版社斯皮瓦克《流形上的微积分》科学出版社解析几何:教材:吴光磊《解析几何简明教程》高等教育出版社参考书:丘维声《解析几何》北京大学出版社线性代数:教材:李烔生《线性代数》中国科学技术大学出版社参考书:叶明训《线性空间引论》武汉大学出版社张贤科《高等代数学》清华大学出版社许以超《线性代数与矩阵论》高等教育出版社A.I. Kostrikin,Introduction to algebra,Springer-VerlagM. Postnikov,Linear algebra and differential geometry,Mir Publishers Lang. Serge,Linear algebra,Springer-Verlag普通物理:教材:郑永令《力学》复旦大学出版社张玉民《基础物理学教程———热学》中国科学技术大学出版社胡有秋《电磁学》高等教育出版社郭光灿《光学》高等教育出版社徐克尊《近代物理学》高等教育出版社参考书:漆安慎《力学》高等教育出版社秦允豪《热学》高等教育出版社赵凯华《电磁学》高等教育出版社赵凯华《光学》高等教育出版社杨福家《原子物理学》高等教育出版社中国科大物理教研室《美国物理试题汇编》中国科学技术大学出版社常微分方程:教材:丁同仁、李承治《常微分方程教程》高等教育出版社参考书:V.I.Arnold《常微分方程》科学出版社庞特里亚金《常微分方程》高等教育出版社袁相碗《常微分方程》南京大学出版社A. Coddington,Theory of ordinary differential equations,McGraw-HillA.Φ.菲利波夫《常微分方程习题集》上海科技出版社复变函数:教材:龚昇《简明复分析》北京大学出版社参考书:H.嘉当《解析函数论初步》科学出版社L.V.Ahlfors, Complex Analysis 3rd ed ,McGraw-Hill任尧福《应用复分析》复旦大学出版社余家荣《复变函数》高等教育出版社L.沃尔科维斯《复变函数论习题集》上海科技出版社实变函数:教材:徐森林《实变函数论》中国科学技术大学出版社(近两届改为北大教材)参考书:郑维行《实变函数与泛函分析概要》(第一册)高等教育出版社周民强《实变函数论》北京大学出版社A.N. Kolmogorov,Theory of Functions and Functional Analysis,DOVERE. Hewitt,Real and Abstract Analysis,Springer V erlag鄂强《实变函数论的定理与习题》高等教育出版社(好书!不多,好象只有两到三本,很旧)近世代数:教材:冯克勤《近世代数引论》中国科学技术大学出版社参考书:熊全淹《近世代数》武汉大学出版社莫宗坚《代数学》(上)北京大学出版社(比聂灵沼《代数学引论》好的多)聂灵沼《代数学引论》高等教育出版社N.Jacobson,Basic Algebra(1)Springer-V erlagA.I. Kostrikin,Introduction to algebra,Springer-V erlag概率论:教材:苏淳《概率论》中国科学技术大学讲义(几乎是照抄杨的,我基本不看)参考书:杨振明《概率论》科学出版社王辛坤《概率论及其应用》科学出版社微分几何:教材:彭家贵《微分几何》高等教育出版社参考书:A.T.Fomenko Differential geometry and topology,Consultants Bureau陈省身《微分几何》南开大学讲义多卡模《曲线和曲面的微分几何学》高等教育出版社吴大任《微分几何讲义》高等教育出版社A?C?菲金科《微分几何习题集》北京师范大学出版社拓扑学:教材:熊金城《点集拓扑讲义(第二版)》高等教育出版社参考书:儿玉之宏《拓扑空间论》科学出版社J.L.Kelley,General Topology,Springer-V erlagM.A.Armstrong《基础拓扑学》北京大学出版社陈肇姜《点集拓扑学》南京大学出版社陈肇姜《点集拓扑学题解与反例》南京大学出版社泛函分析:教材:张恭庆《泛函分析讲义》(上册)北京大学出版社参考书:刘培德《泛函分析基础》武汉大学出版社夏道行《实变函数与泛函分析》(下册)高等教育出版社郑维行《实变函数与泛函分析概要》(下册)高等教育出版社A.N. Kolmogorov,Theory of Functions and Functional Analysis,DOVER А.Б.安托涅维奇《泛函分析习题集》高等教育出版社偏微分方程:教材:陈祖墀《偏微分方程》中国科技大学出版社参考书:齐民友《广义函数与数学物理方程》高等教育出版社姜礼尚《数学物理方程讲义》高等教育出版社Aleksei.A.Dezin ,Partial differential equations,Springer-V erlag数理统计:教材:陈希孺《数理统计学教程》上海科技出版社参考书:陈家鼎《数理统计学讲义》高等教育出版社陆璇《数理统计基础》清华大学出版社中国科学技术大学统计与金融系《数理统计习题集》中国科学技术大学讲义数值分析:教材:奚梅成《数值分析方法》中国科学技术大学出版社参考书:林成森《数值计算方法》科学出版社C语言程序设计:教材:谭浩强《C语言程序设计》清华大学出版社数据结构:教材:黄刘生《数据结构》中国科学技术大学出版社数据库:教材:黄刘生《数据结构》中国科学技术大学出版社微机原理:教材:周佩玲《16位微机原理接口技术及其应用》中国科学技术大学出版社电子电路:教材:李翰荪《电路分析》高等教育出版社模拟电子技术:教材:刘同怀《模拟电子线路》中国科学技术大学出版社数字电子技术:教材:康华光《电子技术基础(数字部分)》高等教育出版社理论力学:教材:金尚年《经典力学》复旦大学出版社参考书:Landau,Mechanics,Heinemann电动力学:教材:郭硕鸿《电动力学》(第二版)高等教育出版社参考书:Jackson,Classical Electrodynamics热力学与统计物理学:教材:汪志诚《热力学?统计物理》高等教育出版社参考书:Landau,Statistical Physics Part1,Heinemann电动力学:教材:张永德《量子力学讲义》中国科学技术大学讲义参考书:Landau,Quantum Mechanics (Non-relatisticTheory),Heinemann最近几年,国内引进了很多不错的书,事实上,这个书单是需要修正了,首先是机械工业出版社和高等教育出版社引进了一批国外的优秀数学原版教材,其次是高等教育出版社开始翻译俄罗斯的优秀数学教材.数学分析:到夏天估计高等教育出版社翻译的V.A.Zorich的数学分析大概会出版了,所有的数学专业的新生,我都郑重的推荐他们买一本V.A.Zorich的数学分析,看看目前国际上先进的教材是怎么样的,免得坐井观天.Courant的微积分与分析引论应该说是西方最好的一套微积分教材了,里面有一堆乱七八糟的应用,而且极其简洁,读读也是颇有好处的.菲赫金哥尔兹的微积分学教程,好处是乱七八糟的例题特别多,所以也值得一看了,不过毕竟是很传统的教材了,所以如果时间不够,就算了吧.很多人会向学数学分析的学生推荐吉米多维奇,不过我不主张大家看,因为里面计算题太多,并不适合数学分析教学.除非将来想做应用的,那倒可以抽一些题目练习练习计算.解析几何:这门课,其实国内一直不重视,其实也是相当基本的课程了,我想国内可以找到的书有两本值得一提,一是Postnikov的几何讲义第一卷:解析几何,二是狄隆涅那套两卷本的解析几何,这门课关键是要掌握一切几何对象,比如说乱七八糟的二次曲线曲面之类.科大自己的书特点是简洁,不过不够详细,我们当时一天多的时间就能把上面的题目搞定,至于丘维声的书,如果找不到Postnikov的几何讲义第一卷:解析几何,也是不错的选择.线性代数:其它国内学校喜欢管这门课叫高等代数,不过国际上高等代数一般等于线性代数加初等抽象代数.线性代数,国内可以找到的书不多,图书馆里应该有Greub的线性代数,是GTM里面的,这本书是相当现代了,很容易过渡到多重线性代数,此外,估计夏天的时候,A.I. Kostrikin的Introduction to algebra第三版的中文版应该出来了,里面第一二卷都是讲线性代数的,这是一套相当好的书,A.I. Kostrikin是李群专家,俄罗斯科学院院士,以建立了模李代数理论而著称.不过实际上有一本代数书更好,可惜国内没有引进,就是E.B.Vinberg的A Course in Algebra.叶明训的《线性空间引论》其实是从一本法国的高等数学教科书的线性代数部分改编过来的,他的讲法很有趣,值得一看.许以超的《线性代数与矩阵论》有一个好处,就是课本上的题目做不出的时候,可以查这本书,因为科大的线性代数其实是从许先生的《代数学引论》改编过来的,这是科大的老教材,而《线性代数与矩阵论》是许先生后来自己写的一个改编本.抽象代数:最值得推荐的参考书就是机械工业出版社影印的M.Artin的Algebra了,这本书的好处是讲了很多课本上通常没有,又很重要的东西,如典型群,李群等等,A.I. Kostrikin的Introduction to algebra也是一本类似的书,这也算是当前代数学教材发展的潮流.熊全淹《近世代数》基本上是范德瓦尔登第一卷的简本,不过好处在于书里面的参考资料里列了一堆小文章,找来看看是蛮不错的.N.Jacobson的Basic Algebra的好处是面面俱到,可以当辞典用,而且题目不少,对于非代数专业的本科生来说,里面的东西绝对够用了.数学分析再讲一本书:Loomis的高等微积分,这本书以前是哈佛的教材,可惜太难,后来就没有人用了,不可否认,作为教材,这本书有点鸡肋的味道,按照美国的高微初微模式,读完一般的初等微积分教材肯定读不懂这本书,起码你得看过Courant的微积分与分析引论,但是如果读了Courant的微积分与分析引论,正常的想法是继续去读实变函数泛函分析之类的高级课程,谁也不会吃饱了没事干,再来学一年数学分析,不过呢,作为一本参考书这本书还是蛮好的,里面的一些讲法,一般的教材里很不容易看到.基本上这本书用了相当多的现代分析的观点来处理微积分,和V.A.Zorich的数学分析颇有异曲同工之妙,当然V.A.Zorich的数学分析比这本可接受性要好得多.。
数学系本科专业学习参考书

观点很新,最近几年很流行,不过似乎没有必要。 14《数学分析简明教程》辛钦
课后没有习题,但是推荐了《吉米多维奇数学分析习题集》里的相应习题。但是随着 习题集的更新,题已经对不上号了,不过辛钦的文笔还是不错的。 15《数学分析讲义》阿黑波夫等著
记住以下几点: 1. 对于数学分析的学习,勤奋永远比天分重要。 2. 学数学分析不难,难得是长期坚持做题和不遗余力的博览群书。 3. 别指望第一遍就能记住和掌握什么,请看第二遍,第三遍,…,第阿列夫遍。 4. 看得懂的仔细看,看不懂的硬着头皮看。 5. 课本一个字一个字的看完,至少再看一本参考书,尽量做一本习题集。 6. 开始前三遍,一本书看三遍效果好于三本书看一遍;第四遍开始相反。 7. 经常回头看看自己走过的路
师范类使用最多的书,课后习题编排的不错,也是考研用的比较多的一本书。课本最 后讲了一些流形上的微积分。虽然是师范类的书,难度比上一本有一些降低,不过还是值得 一看的。 3《数学分析》陈纪修等著
以上三本是考研用的最多的三本书。 4《数学分析》李成章,黄玉民
是南开大学一个系列里的数学分析分册,这套教材里的各本都经常被用到,总体还是 不错的,是为教学改革后课时数减少后的数学系各门课编写的教材。 5《数学分析讲义》刘玉链
个人感觉写的比较混乱,不过各个大学数学系都在用。 2《实变函数与泛函分析》夏道行
上面说过,再推荐一次,虽然有点厚。 3《实变函数与泛函分析概要》郑维行 4《泛函分析习题集》安托涅维奇 5《函数论与泛函分析初步》柯尔莫哥洛夫
好好看完会有收获。大师的经典名著,包括了实变函数,泛函分析,变分等各方面的 内容 6《泛函分析理论习题解答》克里洛夫
也是一本可以经常看到的书,作者已经去世。国家精品课程的课本。 11 许绍浦《数学分析教程》南京大学出版社
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中科大数学必读科目及参考有些科大学生,尤其是新生,抱怨科大教材偏难;而且新生通常缺乏学习方法,对如何在大学中学习还没有清楚的概念。
下面是一位科大数学系学长给科大数学专业学生的一些建议。
我转发过来,仅供参考。
1、老老实实把课本上的题目做完。
其实说科大的课本难,我以为这话不完整。
科大的教材,就数学系而言还是讲得挺清楚的,难的是后面的习题。
事实上做1道难题的收获是做10道简单题所不能比的。
2、每门数学必修课至少要看一本参考书,尽量做一本习题集。
3、数学分析别做吉米,除非你太无聊,推荐北大方企勤的习题集。
此外注意一下有套波兰的数学分析习题集,是不是搞得到中文或英文版。
4、线性代数推荐普罗斯库列科夫的<<线性代数习题集>>和法捷耶夫的<<高等代数习题集>>。
莫斯科大学要求把上面的题全做光。
建议大家在搞定亚洲第一难书的同时也把里面的题打通。
5、解析几何不要不重视。
现在有种削弱几何课的倾向,甚至有的学校把解析几何课改成只有两课时,这样一来,几何训练不足,会很吃亏的。
6、常微要看看阿诺尔德的书,打通菲利波夫的习题集。
7、数论课是很重要的,起码可以锻炼思维能力。
8、数学分析、线性代数、解析几何、泛函、拓扑、抽象代数、实变、微分几何是最重要的课,大家脱层皮也要学好。
要尽量加强这方面的工底,不然的话以后很吃亏。
9、有时间去物理系多听课,千万不要毕业了连量子力学也不懂,这样的数学家注定要被淘汰的。
读读费曼物理讲义和郎道的理论物理教程。
10、华罗庚的<<数论导引>>的前言大家好好看看,多多领会!11、想读数理统计和计算数学的要注意,统计和计算数学同样是数学类的专业,不要以为加上计算和统计就可以降低要求。
12、推荐一些参考书:B.A.卓里奇《数学分析》(第一卷有中文版,第二卷未翻译,会俄文的一定要看)S.M.Nikolsky,A course of mathematical analysis(有中文版)A.I.Kostrikin,Introduction to algebra(有中文版)M.Postnikov,Analytic geometry(有中文版)M.Postnikov,Linear algebra and differential geometry(有中文版)G.H.Hardy,An Introduction to the Theory of NumbersV.I.Arnold,Ordinary differential equation(有中文版)H.嘉当,解析函数论初步Kolmogorov,Elements of the Theory of Functions and Functional Analysis(有中文版,亚马逊上出售英文版,20美元一套)Fomenko,Differential geometry and topologyKelley,General Topology(有中文版)Bott,Differential forms in algebraic topology莫宗坚《代数学》Atiyah,Introduction to Commutative Algebra(有中文版)Riesz,Functional Analysis(有中文版)Landau,Mechanics(有中文版)Goldstein,Classical Mechanics(有中文版)Landau,The Classical Theory of Fields(有中文版)Jackson,Classical Electrodynamics(有中文版)Landau,Statistical Physics Part1(有中文版)Kerson Huang,Statistical MechanicsLandau,Quantum Mechanics(Non-relatisticTheory)(有中文版)Greiner,Quantum Mechanics:A Introduction(有中文版)黄昆《固体物理学》Kittel,Introduction to Solid State Physics(有中文版)费曼《费曼物理讲义》玻恩《光学原理》王梓坤《概率论基础及其应用》方企勤《数学分析习题集》普罗斯库列科夫《线性代数习题集》法捷耶夫《高等代数习题集》菲利波夫《常微分方程习题集》沃尔维科斯基《复变函数习题集》鄂强《实变函数的例题与习题》符拉基米诺夫《偏微分方程习题集》巴兹列夫《几何与拓扑习题集》菲金科《微分几何习题集》1,迪亚库的《天遇--混沌与稳定性的起源》,上海科技教育出版社。
这本书的内容是关于自牛顿时代以来,数学家探索一个经典的数学物理难题:三体问题的历史,很多新生可能以为数学家就是陈景润那样玩些和实际生活不相关问题的怪人,其实真正好的数学是要能够解决人类科学研究和实际生活中提出的各种数学问题的数学,数学不能离开工程和科学,现代工程技术和自然科学(也包括社会科学)是数学研究活的源泉,这本书里面的三体问题就是关于计算三个天体的运动轨道的问题,这个问题的研究就是现代动力系统理论的起源,甚至说现代的拓扑学也与此大有关系,庞加勒的经典著作《位置分析》很大程度上是为他的《天体力学讲义》提供数学工具,你们可以在这里看见很多数学大师的踪影:庞加勒,柯尔莫哥诺夫,阿诺尔德还有我国的年轻数学家夏志宏。
2,《数学——它的内容,方法和意义》,科学出版社。
这套书一共三本,是由多位俄罗斯著名数学家集体编写的,包括了二十世纪最优秀的数学家柯尔莫哥诺夫先生以及亚历山德罗夫先生、沙法列维奇先生、索伯列夫先生、盖尔范德先生等数学大师。
基本上对大学本科的基础课程都做了一个简介,还推荐了一些参考书,这些书大部分国内都可以找到。
3,外尔的《对称》,上海科技教育出版社。
外尔也是二十世纪最优秀的数学家之一,据说是懂得物理最多的数学家,这本书当然也是值得一读的了。
4,克莱因《古今数学思想》,科学出版社。
关于数学历史的名著,不过这本书对以刘徽为代表的中国古代数学的辉煌成就比较忽视3#(一)从"数学分析"的课本讲起吧。
下面开始讲一些课本,或者说参考书:1.菲赫今哥尔茨的"微积分学教程","数学分析原理"。
前一本书,俄文版共三卷,中译本共8本;后一本书,俄文版共二卷,中译本共4本。
此书堪称经典。
"微积分学教程"其实连作者都承认不太合适作为教材,为此他才给出了能够做教材的后一套书,可以说是一个精简的版本。
相信直到今天,很多老师在开课的时候还是会去找"微积分学教程",因为里面各种各样的例题实在太多了,如果想比较扎实的打基础的话,可以考虑把里面的例题当做有答案的习题来做,当然不是每道题都可以这么办的。
毫无疑问,这套书代表了以古典的方式处理数学分析内容(指不引入实变,泛函的观念)的最高水平。
2.Apostol的"Mathematical Analysis"在西方(西欧和美国),算得上相当完整的课本,里面讲了勒贝格积分,不过讲的不好。
3.W.Rudin的"rinciples of Mathematical Analysis"(中译本:卢丁"数学分析原理")是一本相当不错的书,后面我们可以看到, 这位先生写了一个系列的教材。
该书的讲法(指一些符号,术语的运用)也是很好的。
学完"高等数学"以后,可以找一本西方advanced calculus水平的书来看(特别是Rubin的书),基本上就能够达到一般数学系的要求了。
说到Advaced Calculus,在这个标题下面有一本书也是可以一看的,就是L.Loomis和S.Sternberg的Advanced Calculus。
这本书的观点还是很高的,毕竟是人家Harvard的课本.4."数学分析"(北大版)方企勤,沈燮昌等的"数学分析习题集","数学分析习题课教材"。
北大的这套课本写得还是可以的,不过最好的东西还是两本关于习题的东西。
大家知道,吉米多维奇并不是很适合数学系的学生的,毕竟大多是计算题。
相比之下北大的这本习题集就要好许多,的的确确值得一做。
那本习题课教材也是很有意思的书,包括一些相当困难的习题的解答。
5.克莱鲍尔的"数学分析"。
记得那是一本以习题的形式讲分析的书,题目也很不错。
6.张筑生的"数学分析新讲"(共三册)。
我个人认为这是中国人写的观点最新的数学分析课本,张老师写这书也实在是呕心沥血,手稿前后写了差不多五遍。
象他这样身有残疾的人做这样一件事情所付出的是比常人要多得多的,以致他自己在后记中也引了"都云作者痴,谁解其中味"。
在这套书里,对于许多材料的处理都和传统的方法不太一样.非常值得一读。
唯一的遗憾是,按照张老师本人的说法,北大出版社找了家根本不懂怎么印数学书的印刷厂,所以版面不是很好看。
下面的一些书可能是比较"新颖"的.7a.尼柯尔斯基"数学分析教程" 是清华的人翻译的,好象没翻全。
那属于80年代以后苏联的新潮流的代表,不管怎么说,人家是苏联科学院院士。
7b.V.A.zorich"数学分析",莫斯科大学的教材。
SPRINGER出了英文版,相当好的一套教材,特别是习题。
8.狄多涅"现代分析基础(第一卷)"是一套二十世纪的大家写的一整套教材的第一卷,用的术语相当"高深",可能等以后学了实变,泛函再回过头来看感觉会更好一些.9.说两句关于非数学专业的高等数学。
强烈推荐理图里面几本法国人写的数学书。
因为在法国高等教育系统里面,对于最好的学生,中学毕业以后念的是两年大学预科,这样就是不分系的,所以他们的高等数学(如J. Dixmier院士的"高等数学"第一卷)或者叫"普通数学",其水平基本上介于国内数学系和物理系的数学课之间)10.再补充个技术性的小问题.对于函数项级数收敛, 一致收敛是充分而非必要的,有一个充要条件叫"亚一致收敛性",在"微积分学教程"里面提了一句,其详细讨论,似乎仅见于鲁金(Lusin)的"实变函数论"里面。
11.华罗庚先生的"高等数学引论"第一卷。
这套书(其实没有完成最初的计划)是六十年代初华先生在王元先生的辅助下对科大学生开课时的讲义。
