结构动力学2
结构动力学第二章

∂T ∂V d ∂T ( )− + = Pncj (t ), & dt ∂u j ∂u j ∂u j
其中: T —— 体系的动能;
j = 1,2,L , N
V —— 体系的位能,包括应变能及任何保守力的势能; Pncj ——与 uj 相应的非保守力(包括阻尼力及任意外荷载)。
– 红色部分为引入动力自由度概念的目的,蓝色部分为实 现此目的的手段。 – 概念中的“全部”、“独立”两个条件非常关键。
• 严格来说,所以结构体系质量都是连续分布的,为无限自 由度体系,研究比较困难。但许多情况下,可以作一定的 简化,变为有限自由度体系。 • 简化并确定结构动力自由度最典型的方法:集中质量法
动能
1 & mu 2 转动质量 2
T =
1 &2 Jθ 2
1 2 V = ku 转动弹簧 2
1 &2 V = kθ θ 2
位能
1 1 & & &j T = ∑ ∑ mij u i u j = ∑ m j u 2 2 i j 2 j
V =
1 ∑ ∑ kij ui u j 2 i j
∫
1 体系的动能:T = mu 2 & 2
粘滞(性)阻尼力可表示为:
& f D = -cu
D — 表示阻尼(damping) c — 阻尼系数(Damping coefficient)
k c
u m
f S(t) m f D(t) f I (t)
& u — 质点的运动速度
阻尼系数 c 的确定:
• 不能像结构刚度 k 那样可通过结构几何尺寸、构件尺寸等 来获得,因为 c 是反映了多种耗能因素综合影响的系数, 阻尼系数一般是通过结构原型振动试验的方法得到。 • 粘性(滞)阻尼理论仅是多种阻尼中最为简单的一种。 • 其它常用的阻尼:
第2章 结构动力学概述(中英文)

动荷载的定义 definition of dynamic loadings
荷载在大小、方向或作用点方面随时间变化,使 得质量运动加速度所引起的惯性力与荷载相比大 到不可忽略时,则把这种荷载称为动荷载。 A dynamic load is any load of which its magnitude, direction, and/or position varies with time. In general, if the inertial forces represent a significant portion of the total load equilibrated by the internal elastic forces of the structure, then this kind of load is defined as dynamic loading.
动荷载:
Dynamic loading:any load of which its magnitude, direction
and /or position varies with time
快慢标准: 是否会使结构产生显著的加速度. criteria: Whether a remarkable acceleration is exerted on the structure
静荷载 Static load 结构体系 Structural system 位移displacement 静力响应 Responses to static loads 内力internal force 应力stress
输入 input
输出 Output
大小 magnitude 方向 direction 作用点 position
结构动力学课件PPT

my cy ky FP (t)
§2-5 广义单自由度体系:刚体集合
➢刚体的集合(弹性变形局限于局部弹性 元件中)
➢分布弹性(弹性变形在整个结构或某些 元件上连续形成)
➢只要可假定只有单一形式的位移,使得 结构按照单自由度体系运动,就可以按 照单自由度体系进行分析。
E2-1
x
p( x,t
)
=p
)
3
B'
M I1
E'
D'
F' G'
A
D
E
B
F
G
C
fD1
fI1
fS1
f D2
f I2
f S2
a
2a
a aa a
Z(t )
f S1
k1(EE')
3 4
k1Z (t )
f D1
d c1( dt
DD')
1 4
c1Z (t )
fS2
k1(GG')
1 3
k2
Z
(t
)
fD2 c2Z (t)
f
I1
m1
1 2
Z(t)
3. 有限单元法
—— 将有限元法的思想用于解决结构的动力计算问题。
要点:
▪ 先把结构划分成适当(任意)数量的单元;
▪ 对每个单元施行广义坐标法,通常取单元的节点位移作 为广义坐标;
▪ 对每个广义坐标取相应的位移函数 (插值函数);
▪ 由此提供了一种有效的、标准 化的、用一系列离散坐标 表示无限自由度的结构体系。
建立体系运动方程的方法
▪ 直接平衡法,又称动静法,将动力学问题转化为任一时刻 的静力学问题:根据达朗贝尔原理,把惯性力作为附加的 虚拟力,并考虑阻尼力、弹性力和作用在结构上的外荷载, 使体系处于动力平衡条件,按照静力学中建立平衡方程的 思路,直接写出运动方程。
结构动力学习题解答-2

====Word 行业资料分享--可编辑版本--双击可删====第一章 单自由度系统1.1 总结求单自由度系统固有频率的方法和步骤。
单自由度系统固有频率求法有:牛顿第二定律法、动量距定理法、拉格朗日方程法和能量守恒定理法。
1、 牛顿第二定律法适用范围:所有的单自由度系统的振动。
解题步骤:(1) 对系统进行受力分析,得到系统所受的合力;(2) 利用牛顿第二定律∑=F x m,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
2、 动量距定理法适用范围:绕定轴转动的单自由度系统的振动。
解题步骤:(1) 对系统进行受力分析和动量距分析;(2) 利用动量距定理J ∑=M θ,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
3、 拉格朗日方程法:适用范围:所有的单自由度系统的振动。
解题步骤:(1)设系统的广义坐标为θ,写出系统对于坐标θ的动能T 和势能U 的表达式;进一步写求出拉格朗日函数的表达式:L=T-U ; (2)由格朗日方程θθ∂∂-∂∂∂LL dt )( =0,得到系统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
4、 能量守恒定理法适用范围:所有无阻尼的单自由度保守系统的振动。
解题步骤:(1)对系统进行运动分析、选广义坐标、写出在该坐标下系统的动能T 和势能U 的表达式;进一步写出机械能守恒定理的表达式 T+U=Const(2)将能量守恒定理T+U=Const 对时间求导得零,即0)(=+dtU T d ,进一步得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。
用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法和共振法。
方法一:衰减曲线法。
求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线,并测得周期和相邻波峰和波谷的幅值i A 、1+i A 。
结构动力学(2)

4. 对称性的利用 振动体系的对称性是指:结构对称、质量分布对称,强迫振
动时荷载对称或反对称。
多自由度和无限自由度对称体系的主振型不是对称就是反对称, 可分别取半边结构进行计算。
对称荷载作用下,振动形式为对称的;反对称荷载作用下, 振动形式为反对称的,可分别取半边结构进行计算。一般荷载可 分解为对称荷载和反对称荷载两组,分别计算再叠加。
(A( j ) )(T K ωi2 M)A( i ) 0
(A( i ) )(T K ω2j M)A( j ) 0
(1)
(A( i ) )(T K T ωi2 M T )( A( j ) ) 0
(2)
又: K T K MT M
(1)式-(2)式得:
( i22 j)(源自A( i ))TM
A(
3. 动内力幅值计算 位移、惯性力、动荷载频率相同。对于无阻尼体系三者同时
达到幅值。于是可将荷载幅值和惯性力幅值加在结构上,按静力 学方法求解,即得到体系的最大动内力和最大动位移。
多自由度体系不仅位移动力系数和内力动力系数不同,而且 不同截面上的位移动力系数和内力动力系数也各不相同,不能采 用统一动力系数计算动力反应。
由式(14-38)可知,此时式(14-47)得到位移为无穷大。所以, 一般情况下,n个自由度体系有n个共振点。
对于两个自由度体系,稳态振动时的位移幅值方程为
(11m1
1
2
)
y10
12 m2
y20
1P
2
0
21m1 y10 (22m2
1
2
)
y20
2P
2
0
D m1 11 2 1 12m2 2 21m1 2 m2 22 2 1
结构动力学第二章 单自由度系统的振动2

0.39 0.66 0.73 1.00 1.05 1.20 1.42 1.55 1.69 1.76 2.00
23
24
解: 水塔的自振频率和周期分别为
k 29.4106 N / m 31.305rad / s
m
30103 kg
T 2 0.2007s
取微小时段 0.01s ,约相当于水塔自振
同理,积分项 B(t) 可用相同的方法进行计算。
16
因此,无阻尼体系动力响应的数值解: y(t) A(t) sin t B(t) cost
同理,也可求得有阻尼体系动力响应。 注:数值积分解答的精确度与计算中选择和微 小时段 有关,一般可取小于系统自振周期 的十分之一,便可得到较好的结果。
17
A yst
1
2
t1
2
( 1 cost1
) 2
t1
1/ 2
sint1
t1 T
0.371
动力系数只与 t1 有关,即只与 t1 T 有关
下表列出不同 t1 T 值时的动力系数。
表 不同 t1 T 值时的动力系数表
t1/T 0.125 0.20 0.25 0.371 0.40 0.50 0.75 1.00 1.50 2.00
用下式进行计算。
无阻尼:
( 0)
y(t) 1 t p( ) sin (t )d
m 0
有阻尼: y(t) 1
( 0)
md
t 0
p(
)e (t )
sin d
(t
)d
2)对于许多实际情况,如果荷载的变化规律是 用一系列离散数据表示(如试验数据),此时 的响应计算就必须借助于数值分析方法。
11
结构动力学_2

初相位
4、振幅C和初相位
x0 C sin
x0 Ccos
C
x02
x02
2
arctan x0
x0
——振幅 ——初相位
第2章 单自由度系统
x
3
x02
x02
2
sin(t
)
x
x02 2
x02
T 2
x0 0
t
图2.7 无阻尼系统自由振动位移曲线
-3
0
3
第2章 单自由度系统
x x02 x022 cos(t )
mx cx kx 0
设:
x Aept
第2章 单自由度系统
mp2 cp k 0
p1,2 c
c2 4mk 2m
c2 4mk
1、过阻尼系统
0 x A1e p1t A2e p2t
第2章 单自由度系统
2、临界阻尼系统
0
c2 4mk 0
cc 2 mk 2m
x
e
c 2m
t
第2章 单自由度系统
3、解的形式
x Asint x Bcost x Asint Bcost
x A2 B2 ( A sint B cost)
A2 B2
A2 B2
A2 B2 (cos sint sincost)
C sin(t )
第2章 单自由度系统
x C sin(t )
振幅
剪切变形
第2章 单自由度系统
3EI
ml 3
——弯曲频率
2 3EI
ml 3
——剪切频率
第2章 单自由度系统
图2.5 框架的剪切变形
第2章 单自由度系统
③摆问题
结构动力学(克拉夫) 第二章 分析动力学基础

第二章 分析动力学基础2.1 基本概念 2.1.1 约束• 定义:对非自由系各质点的位置和速度所加的几何或 运动学的限制。
N 个质点的约束方程: → → 为mi 的位置向量及速度 **弹簧支座不是约束。
• 约束的分类:*稳定(不含t → 左图) 与非稳定(含t → 右图)* 完整(不含 → )几何约束(有限约束) 与非完整(含 → )运动约束(微分约束) • 约束条件:zc=a (水平面绝对光滑)一个完整约束 *水平面粗糙,仅滚动无滑动,A 点速度为零 。
两个完整约束*若为刚性圆球,三个约束(A点两个水平方向速度为零,可证明约束微分方程不能积分成有限形式)非完整约束单向(约束方程为不等式):柔索 与双向(约束方程为等式):刚杆 工程力学中研究对象:稳定的、完整的、双 向约束• 质点系约束方程:→ (N :质点数;M 约束数) 2.1.2 自由度与广义坐标 广义坐标定义:能决定体系几何位置的、彼此独立的量广义坐标个数→空间质点系:n=3N-k;平面质点系: n=2N-k0),,,,,,(11=⋅⋅⋅⋅⋅⋅N N r r r r t f 0),,(=i i r r t f i i r r ,0),(=i i rr f 0),,(=i i rr t f Ai r0),(=i r t f i r 0),,(=i i rr t f ϕϕa x a x v C C A =⇒=−=)(0积分 lr ≤l r =0),,(1=⋅⋅⋅N k r r f )~1;~1(0)(M k N i r f i k ===x双连刚杆双质点系的约束方程:广义坐标数:广义坐标:独立参数→角度→ 振型等(见下页) 梁的挠度曲线用三角级数表示: 广义坐标→*自由度定义:在固定时刻,约束许可条件下能自由变更的 独立的坐标数目(对完整约束=广义坐标数)• 自由度数→空间质点系:n=3N-k 平面质点系:n=2N-k (N :质点数;k: 约束数) 非完整约束:(广义坐标数>系统自由度数)2.1.3 功的定义元功:A →B 过程中力作的功:对摩擦传动轮的例,由于力未移动,位移=? • 功的新定义:(传动齿轮)• 功率:2.1.4 有势力和体系的势能有势力:(1)大小和方向只决定于体系质点的位置(2)体系从位置A 移动到位置B ,力作功只决定于位置而与路径无关取体系的任意位置为“零位置O ”,从位置A 移动到零位置O 各力作的功为体系在位置A 时的势能UA(位能)。
《结构力学》结构动力学(2)

为最大的动力位移与静力位移之比,称为位移动力系数。
简谐荷载作用下, 与 之间关系曲线分析。
1、无阻尼条件
(1) 0 时, 5.0
1, ymax ( t ) yst。
4.0
(2)0 1 0 时,
随着 增加 增大,
3.0
0
FP ( t ) FP sint。 y( t ) yst sint。
(3)当ξ=1时的阻尼称为临界阻尼;相应的 值称为
临界阻尼系数,用cr 表示,则
cr 2mk 2m ,
k 2mk 2m cr
阻尼比 即为阻尼系数 与临界阻尼系数 cr 之比。
§14-4 单自由度结构在简谐荷载作用下的强迫振动
当干扰力 F(t) 直接作用在质点上,质点的受力将如图14-10所示,
且 y( t )与FP ( t ) 同步。
2.0
(3) 1 时, 1.0
, ymax ( t ) , 共振。
(4)1 时,
1.0 2 2.0
3.0
随着 增加 减小,且 y( t )与 FP ( t ) 反向。
(5) 时, 0, 在静平衡位置附近作微小
振动 。
y0
cos 't
y0
ky0
'
sin
't
y bekt sin( 't ')
其中
b
y02
(ห้องสมุดไป่ตู้
y0
ky0
'
)2
tan ' ' y0
/ 为有阻尼自振频率。
y0 ky0
令 k ,称为阻尼比。
' 2 k2 1 ( k )2 1 2
通常当ξ<0.1时,则 ' 和 的差别很小。
于开平-结构动力学第二讲

(2) 阻尼力的功:
Wd A cos t dt c 2 / 1 cos 2 t cA2 2 dt 0 2 1 2 1 2 2 2 / cA2 2 cA cos 2 t dt 0 2 2
5 稳态响应振幅和相位
5.2 初始相位角 根据初相位角表达式
2 tg 1 2
可以画出初相位角随频率比的变化曲线,简称相频曲线:
在共振点,不管阻尼比多大,初相位角均为90度。
6 稳态响应复数解法及频响函数
之前将外载荷假设为正弦形式,其运动控制方程为:
������������ሷ 1 + ������������ሶ 1 + ������������1 = ������0 sin������������ 简谐激励的另一种典型形式为余弦形式,其运动控制方程写作: ������������ሷ 2 + ������ ������ሶ 2 + ������������2 = ������0 cos������������ (2) (1)
o o o
o
1 2 Fo A sin Fo A sin 2
6 稳态响应复数解法及频响函数
令方程特解为������ ������ = ������������ ������ ������������������ ,代入运动控制方程得: (−������2 ������������������ + ������������������������������ + ������������������ )������ ������������������ = ������0 ������ ������������������ 方程对任意时刻t恒等,则方程两边指数函数������ ������������������ 前系数相等,由此可得: ������������ = ������0 ������ − ������������ 2 + ������������������
高等结构动力学2_模态综合法(动态子结构方法)

Φ
a p b Φ J b {0} p
[C ]{ p} {0}
d行
(n1+n2)个 p a
所以,有:
[C dd ]1[C dI ] { p} { p I } [ S ]{q} [I ]
独立的模态坐标
(n1+n2-d)个
[ M ]* [ S ]T [ M ][ S ], [ K ]* [ S ]T [ K ][ S ]
对于一般的动力学分析问题,也可以得到缩聚方程为:
} [C ]*{q } [ K ]*{q} {R}* [ M ]*{q
[C ]* [ S ]T [C ][ S ], {R}* [ S ]T {R}
动态子结构方法的基本思想:
按照工程的观点或结构的几何轮廓,遵循某些原则要求,把完整的大型复 杂结构人为地抽象成若干个子结构。首先对自由度少得多的各个子结构进 行动态分析,然后经由各种方案,把它们的主要模态信息予以保留,以综 合总体结构的动态特性 总系统(n个自由度) 子结构1 dd ]1[C dI ] [S ] [ I ]
uJ uI
uI
a b u u a b I I {u } a , {u } b u J u J {u a } [Φ ]a { p a }, {u b } [Φ ]b { p b }
{ p} b p d个 pd 设{p}中独立广义坐标为{pI},非独立广义坐标为{pd}: { p} p I (n1+n2-d)个 pd { pd } [C dd ]1[C dI ]{ p I } 可写为: [C dd ] [C dI ] {0} pI
结构动力学-2(哈工大结构动力学)

m y(t)
cy(t)
my(t) k11 y(t )
运动方程 my cy k11y 0
令 c / 2m y 2y 2 y 0
设 y(t) Aet
2 2 2 0 特征方程
根为 i 1 2 由初始条件
小阻尼情况
y(0) y0 , y(0) v0
1 (c 2m)
c1 (v0 y0 ) / D , c2 y0
k
k
k
PROBLEMS:
3.A mass m is at rest,partially supported by a spring and partially by stops.In the position shown,the spring force is mg/2. At time t=0 the stops are rotated,suddenly releasing the mass.Determine the motion of the mass.
第二章单自由度体系的振动分析
§2.1 自由振动
一. 无阻尼体系 运动方程
y(t) 11[my(t)] k11y(t) my(t) 令 2 k11 1
m m11
y(t) 2 y(t) 0
二阶线性齐次常微分方程
m
my(t)
y(t)
l EI
km
运动方程的通解 y(t) c1 cost c2 sin t
令 D 1 2
方程的通解为
y(t) Aet sin( Dt D )
A
y02
( v0
y0 D
)2
y(t) et (c1 sin Dt c2 cosDt) tan D y0D /(v0 y0 )
结构力学 动力学第2章3

单元的杆端力和杆端位移之间的关系是通过单元刚 单元的杆端力和杆端位移之间的关系是通过单元刚 杆端力 之间的关系是通过 度方程反映出来的 反映出来的; 度方程反映出来的; 重点掌握单元刚度矩阵中每个刚度系数的物理意义, 刚度系数的物理意义 重点掌握单元刚度矩阵中每个刚度系数的物理意义, 由此求得不同杆单元的刚度矩阵。 由此求得不同杆单元的刚度矩阵。
ui = 1 :
矩阵表示: 矩阵表示: Fxi EA 0 l F 0 0 yi = − EA 0 l Fxj Fyj 0 0
− EA l 0 EA l 0
0
0 0
0
ui v i u j v j
(1)单元刚度方程
单元的刚度方程: 单元的刚度方程:
F(e) = K (e) δ (e)
单元的刚度方程给出了单元 杆端位移 单元的刚度方程 给出了单元杆端位移 δ(e) 与 杆端力 F(e) 给出了单元 之间的关系. 之间的关系 K(e) 称为 单元刚度矩阵 。 它是一个方阵 。 如杆端位移 称为单元刚度矩阵 它是一个方阵。 单元刚度矩阵。 δ(e)和杆端力F(e)为6阶向量,则K(e)为6X6方阵。 阶向量, 方阵。 阶向量 方阵
端为刚结点, 若单元 i 端为刚结点, j 端为铰结点, 端为铰结点 则单元刚度 矩阵为: 矩阵为
=K δ
(e)
y
(e)
θ
i
j
vi
其中: 其中:
δ
F
(e)
(e)
= { i vi θi u j v j θ j} u
Fyi
FQi
T
ui
i y
最新克拉夫《结构动力学》习题答案汇总

第二章自由振动分析2-1(a )由例2 2W Tgk22()W K Tg 因此max()()D t kT 其中k=0、1、2……T D =0.64sec如果很小,T D =T222200()49.9/0.64sec 386/sec kips k kips inin 50/k kips in(b )211ln ln n n v v v v 222121()11.2ln0.3330.86210.05292()10.33320.053025.3%(a ’)21D2T21D TT 249.950/1kkips in(c)2c mW mg2T4cTg21D T T 241WcTg2240.05292000.64sec 386/sec 10.0529kipsc in 0.539sec/ckips inT=T D 0.538sec/ckips in 0.54sec/ckips in2-22k m40 4.472(1/sec )(0)(0)()sin(0)costDDDv v t et v t(0)(0)()sin(0)(0)(0))costDDDv v t et v v v t22(0)(0)()(0)cossinDtDDDv v t ev tt21D()(0)cos(0)(0)sintDDDt ev t v v t2(0)(0)()(0)c o s s i n1tD D v v t ev tt 0.055922(2)(4.47)c c cm(a) c=00D5.6(1)sin 4.470.7cos4.47 1.384.47v t in(1) 5.6cos 4.47 4.47(0.7)sin 4.47 1.69/secv t in (1) 1.4v in ,(1) 1.7/secv in (b) c=2.80.0559(2.8)0.15724.4710.1574.41D(1/sec )(0.157)(4.41)5.60.7(0.157)(4.47)(1)sin 4.410.7cos 4.414.41t e(1)0.764t in(0.157)(4.41)20.157(5.6) 4.41(0.7)(1) 5.6cos 4.41sin 4.4110.157t e (1) 1.10/sect in (1)0.76v in ,(1) 1.1/secv in 第三章谐振荷载反应3-1根据公式有21sin sin 1R t wt wt0.8w w2.778sin 0.8sin1.25R twt wt将t 以80°为增量计算)(t R 并绘制曲线如下:0 80°160°240°320°400°480°560°640°720°800°00.5471.71 -0.481 -3.214 0.357 4.33-0.19 -4.9244.9241.25w wt)(t R3-2解:由题意得:22mkips s in ,20kkips in ,(0)(0)0v v ,w w20 3.162sec2k w rad m8wt(a )0c1sin cos 2R twt wt wt将8wt 代入上式得:()412.566R t (b )0.5ck s in0.50.0395222 3.162cc c c mw1exp1cos exp sin 2R twtwtwt wt将8wt 代入上式得:()7.967R t (c ) 2.0ck s in2.00.158222 3.162cc c c mw1exp1cos exp sin 2R twtwtwt wt将8wt 代入上式得:() 3.105R t 3-3解:(a ):依据共振条件可知:1003860.0810.983sec4000k kg wwrad m W由2LTVw 得:10.9833662.96022wL V ft s(b ):122max2221212tgovv 1w w 0.41.2gov in 代入公式可得:max1.921tv in(c ):2L T Vw45m i n 66Vhf t s226611.51336V wrad secL11.513 1.04810.983w w0.4代入数据得:122max22212=1.85512t govv in3-4解:按照实际情况,当设计一个隔振系统时,将使其在高于临界频率比2下运行,在这种情况下,隔振体系可能有小的阻尼。
结构力学:第十章结构动力学2
ae-ξωt t
低阻尼y- t曲线
t
无阻尼y- t曲线
②阻尼对振幅的影响.
振幅ae- ξω t 随时间衰减,相邻两个振幅的比
yk1 eT 常数 yk
振幅按等比级数递减.
经过一个周期后,相邻两振幅yk和yk+1的比值的对数为:
ln yk lneT T 2 称为振幅的对数递减率.
yk1
r
如 0.2 则 r 1, 1 r ln yk 1 ln yk
令
k m
,
c 2m ( 阻尼比)
y 2 y 2 y 0(15.16)
k m y
cy ky
c y
my
设解为:y(t) Celt 特征方程为:l2 2l 2 0
1)ξ<1(低阻尼)情况
l ( ± 2 1)
l ir 其中 r 1 2
y et C1 cosrt C2 sinrt
低阻尼体系的自振圆频率
平稳阶段:后来只按荷载频率振动的阶段。(由于阻尼的存在)
平稳阶段:
y
yst
1
1
3)ξ>1 强阻尼:不出现振动,实际问题不常见。
§10-3 单自由度体系的受迫振动
受迫振动(强迫振动):结构在动力荷载作用下的振动。
弹性力-ky、惯性力 my
和荷载P(t)之间的平衡方程为:
y(t)
k
m
m
P(t ) P(t )
myky P(t)(a)
y 2 y P(t) (15.24)
m
一、简谐荷载:
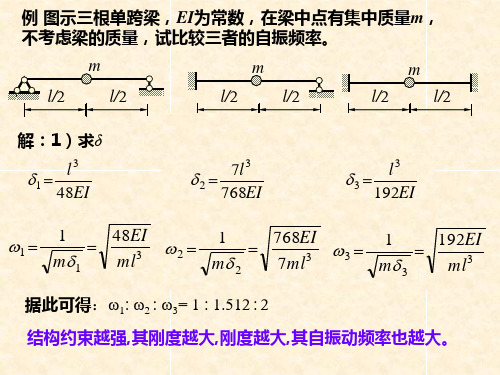
77613m86l El3I2l
5l3 )
32
71l 3
7m68E3I
192EI ml3
清华大学结构动力学2-1

2.2 运动方程的建立 4. Hamilton原理
可以应用变分法(原理)建立结构体系的运动方程。 体系的平衡位置是体系的稳定位置,在稳定位置,体系 的能量取得极值,一般是极小值。 Hamilton原理是动力学中的变分法(原理)。
2.2 运动方程的建立 4. Hamilton原理(积分形式的动力问题的变分方法)
∫
t2 t1
用 Hamilton 原理推导 Lagrange 方程 对于有 N 个自由度的结构体系,体系的动能和位能分别为:
& & & T = T ( u1 , u 2 , L u N , u1 , u 2 , L u N ) V = V ( u1 , u 2 ,L u N )
(a) (b)
因此动能和位能的变分为:
∫
∫
t2 t1
t2
t1
& & & [ muδu − cuδu − kuδu + p(t )δu]dt = 0
对上式中的第一项进行分部积分
& & & muδudt = ∫ mu(δ
t2 t1 t t t t d d & & & && && u )dt = ∫ mu (δu )dt = ∫ mud (δu ) = muδu tt − ∫ δu ⋅ mudt = − ∫ muδudt t t t t dt dt
结构动力学
(2004秋)
结构动力学
第二章
运动方程的建立
运动方程: 描述结构中力与位移关系的数学表达式 (有时称动力方程) 运动方程是进行结构动力分析的基础 运动方程的建立是结构动力学的重点和难点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.1 基本动力体系
2. 弹簧的恢复力(Resisting Force of Spring)
对弹性体系,弹簧的恢复力也被称为弹性恢复力 弹性恢复力:大小等于弹簧刚度与位移(弹簧变形)的乘积, 方向指向体系的平衡位置。
f s = ku
s— 表示弹簧(Spring) k— 弹簧的刚度(Spring Stiffness) u— 质点位移
分析单自由度体系的意义: 第一,单自由度系统包括了结构动力分析中涉及的所有物理量及基本概念。 第二,很多实际的动力问题可以直接按单自由度体系进行分析计算。
图2.1 结构动力分析中常用的单自由度体系力学模型
2.1 基本动力体系
两个典型的单自由度体系 物理元件: 集中质量 阻尼系数 弹簧刚度
(a)单层框架结构
转动质量
T=
1 ɺ2 Jθ 2
1 V = ku 2 位能:拉伸弹簧 2
多自由度体系:
1 V = kθθ 2 转动弹簧 2
动能
T=
1 2
ɺ ɺ ∑∑ m u u
ij i i j
j
=
1 2
ɺ ∑ m u 位能 V = 2 ∑∑ k u u
2 j j
ij i
1
j
j
i
j
2.2 运动方程的建立 4. Hamilton原理(用Hamilton原理建立单自由度弹簧-质量体系的运动方程)
F = ma
F = p(t ) − f D − f s
ma + f D + f s = p(t )
图2.7单质点体系的受力分析
ɺɺ a=u
ɺ f D = cu
f s = ku
ɺɺ ɺ mu + cu + ku = p(t )
单质点体系运动时要满足的控制方程—运动方程
2.2 运动方程的建立 利用牛顿第二定律的优点: 牛顿第二定律是基于物理学中已有知识的直接应用 以人们最容易接受的知识建立体系的运动方程
ɺɺ f I = mu
ɺ f D = cu
f s = ku
图2.8 单质点体系的受力分析
ɺɺ ɺ mu + cu + ku = p(t )
2.2 运动方程的建立 2. D’Alembert原理(直接动力平衡法)
D’Alembert原理的优点:静力问题是人们所熟悉的,有了D’Alembert
原理之后,形式上动力问题就变成了静力问题,静力问题中用来建立控 制方程的方法,都可以用于建立动力问题的平衡方程,使对动力问题的 思考有一定的简化。对很多问题,D’Alembert原理是用于建立运动方程 的最直接、最简便的方法。
ɺ 非保守力:Pnc = −cu + p(t )
结构动力学
(2003春)
结构动力学
第二章 运动方程的建立
运动方程:描述结构中力与位移关系的数学表达式 (有时称动力方程) 运动方程是进行结构动力分析的基础 运动方程的建立是结构动力学的重点,也是难点
2.1 基本动力体系
单自由度体系:SDOF(Single-Degree-of-Freedom-System) 结构的运动状态仅需要一个几何参数即可以确定
(a) (b)
因此动能和位能的变分为:
δT =
ɺ ∑ ∂u δu + ∑ ∂u δu ɺ
j j j j j
N
∂T
N
∂T
j
(c)
δV =
∑ ∂u δu
j j
N
∂V
j
(d)
δ (T − V ) dt +
t2
t1
nc
同时,非保守力所做功的变分为:
δWnc =
∑P
j
N
ncj δu j
(e)
将式(c)、(d)和(e)代入 Hamilton 原理式(2.11)得:
=
∂T δu j ɺ ∂u j
| −∫
∑∫
j N
t2
d ∂T ( )δu j dt = − ɺ dt ∂u j
∫
t2
t1
式 (g)代入式 (f)得:
t2
t1
(−
d ∂T ∂T ∂V ( )+ − + Pncj )δu j dt = 0 ɺ dt ∂u j ∂ u j ∂u j
(h)
由 δu j 的任意性,可知式 (h)中括号内的项恒为零,这样就得到了 Lagrange 方程:
2.2 运动方程的建立 4. Hamilton原理(积分形式的动力问题的变分方法)
Hamilton原理的优点:不明显使用惯性力和弹性力,而分别用 对动能和位能的变分代替。因而对这两项来讲,仅涉及处理 纯的标量,即能量。 而在虚位移中,尽管虚功本身是标量,但用来计算虚功的力和 虚位移则都是矢量。
1 ɺ 动能:集中质量 T = 2 mu 2
∫
t2
t1
δ (T − V ) dt +
∫
t2
t1
δWnc dt = 0
∫
∫
t2
t2
t1
ɺ ɺ ɺ [ muδu − cuδu − kuδu + p(t )δu]dt = 0
对上式中的第一项进行分部积分
t1
ɺ ɺ muδudt =
∫
t2
t1
ɺ mu (δ
d u ) dt = dt
∫
t2
t1
ɺ mu
d (δu ) dt = dt
∫
t2
t1
δ (T − V )dt +
∫
t2
t1
δWnc dt = 0
δWnc =
∑P
j
ncjδu j
其中: T —— 体系的总动能; V —— 体系的位能,包括应变能及任何保守力的势能; Wnc—— 作用于体系上非保守力(包括阻尼力及任意外荷载)所做的功; δ —— 指(在指定时间段内)所取的变分。
∫ ∑
t1 j
t2 N
(
∂T ∂V − + Pncj )δu j dt + ∂u j ∂u j
∑∫
j
N
t2
t1
∂T ɺ δu j dt = 0 ɺ ∂u j
(f)
对式 (f)的第二项进行分部积分:
d ∂T ∂T ∂V ( )− + = Pncj (t ) , ɺ dt ∂u j ∂u j ∂u j
∫
阻尼:引起结构能量的耗散,使结构振幅骤渐变小的一种作用 阻尼来源(物理机制):
(1)固体材料变形时的内摩擦,或材料快速应变引起的热耗散; (2)结构连接部位的摩擦,结构构件与非结构构件之间的摩擦; (3)结构周围外部介质引起的阻尼。例如,空气、流体等。
粘滞(性)阻尼力可表示为:
ɺ f D = cu
D — 阻尼(damping) c — 阻尼系数(Damping coefficient) ù — 质点的运动速度
2.2 运动方程的建立 5.运动的Lagrange方程
∫ δW dt = 0 用: ∫ Hamilton原理 推导: Lagrange方程
t1 t2
对于有 N 个自由度的结构体系,体系的动能和位能分别为:
ɺ ɺ ɺ T = T (u1 , u 2 ,⋯ u N , u1 , u 2 ,⋯ u N ) V = V (u1 , u 2 ,⋯ u N )
d ∂T ∂T ∂V ( )− + = Pncj (t ) , ɺ dt ∂u j ∂u j ∂u j j = 1, 2, ⋯, N
其中: T —— 体系的动能; V —— 体系的位能,包括应变能及任何保守力的势能; Pncj——与uj相应的非保守力(包括阻尼力及任意外荷载)。
用 Hamilton 原理推导 Lagrange 方程
m c k
两个力学模型完全等效 两个体系的运动方程相同
(b)弹簧―质点体系
2.1 基本动力体系
1. 惯性力(Inertial Force)
惯性:保持物体运动状态的能力 惯性力: 大小等于物体的质量与加速度的乘积, 方向与加速度的方向相反。
ɺɺ f I = mu
I — 惯性(Inertial); m— 质量(mass) ; ü — 质点的加速度。
2.1 基本动力体系 5. 非弹性体系 (Inelastic System)
结构构件的力—变形关系为非线性关系,结构刚度不再为常数 构件(或弹簧)的恢复力可表示为
ɺ f s = f s (u , u )
fs是位移和速度的非线性函数。
图2.6 非弹性体系中结构构件的力与位移关系
2.2 运动方程的建立 1. 利用牛顿(Newton)第二定律
2.2 运动方程的建立 4. Hamilton原理
应用变分法来建立结构体系的运动方程。 动力学中广泛应用的变分法是Hamilton原理 体系的平衡位置是体系的稳定位置,在稳定位置,体系的能量取得极值, 一般是极小值。 Hamilton原理:在任意时间区段[t1, t2]内,体系的动能和位能的变分加上 非保守力做功的变分等于0。
2.1 基本动力体系 4. 线弹性体系和粘弹性体系 (Linearly Elastic System and Viscous Elastic System)
线弹性体系:由线性弹簧(或线性构件)组成的体系。 — —最简单的理想化力学模型。 粘弹性体系:当线弹性系统中进一步考虑阻尼的影响时的体系。 —结构动力分析中的最基本力学模型。
d ∂T ∂T ∂V ( )− + = Pncj (t ) , ɺ dt ∂u j ∂u j ∂u j
j = 1, 2, ⋯ , N
2.2 运动方程的建立 5.运动的Lagrange方程
用Lagrange方程方程建立体系的运动方程
体系的动能: = T
