工程力学第17讲 弯曲应力：正应力 惯性矩(完整)
合集下载
工程力学第17讲 弯曲应力：正应力 惯性矩(完整)
第 11 章 弯曲应力
本章主要研究：
单辉祖:工程力学
对称弯曲正应力 对称弯曲切应力 梁的强度分析与设计 非对称弯曲应力
1
§1 §2 §3 §4 §5 §6 §7
引言 对称弯曲正应力 惯性矩与平行轴定理 对称弯曲切应力 梁的强度条件 梁的合理强度设计 双对称截面梁的非对称弯曲
单辉祖:工程力学
Ai yCi AyC
yC
i 1
n
A y
i 1
n
i Ci
21
A
A1 yC 1 A2 yCb 2 2
bd db
0.045 m
3. 惯性矩计算
I z I z1 I z 2
2
bd 3 d 3.0210 -6 m4 I z1 bd yC 12 2
d b3 b I z2 db d yC 5.8210 -6 m4 12 2
I z I z 1 I z 2 8.8410 6 m 4
2
4. 最大弯曲正应力
M B yC 30.5 MPa Iz M ( b d yC ) s c,max B 64.5 MPa Iz
dA 0 (b) F x 0 , s A M z 0, A ysdA M (c)
10
物理方面:
s ( y ) E ( y )
单辉祖:工程力学
s E
y
(a)
sdA 0 A
(b)
A ysdA M
yC y dA A 0 A
(c)
(a)(b)
A ydA 0
2
§1 引 言
弯曲应力与对称弯曲 本章内容
本章主要研究：
单辉祖:工程力学
对称弯曲正应力 对称弯曲切应力 梁的强度分析与设计 非对称弯曲应力
1
§1 §2 §3 §4 §5 §6 §7
引言 对称弯曲正应力 惯性矩与平行轴定理 对称弯曲切应力 梁的强度条件 梁的合理强度设计 双对称截面梁的非对称弯曲
单辉祖:工程力学
Ai yCi AyC
yC
i 1
n
A y
i 1
n
i Ci
21
A
A1 yC 1 A2 yCb 2 2
bd db
0.045 m
3. 惯性矩计算
I z I z1 I z 2
2
bd 3 d 3.0210 -6 m4 I z1 bd yC 12 2
d b3 b I z2 db d yC 5.8210 -6 m4 12 2
I z I z 1 I z 2 8.8410 6 m 4
2
4. 最大弯曲正应力
M B yC 30.5 MPa Iz M ( b d yC ) s c,max B 64.5 MPa Iz
dA 0 (b) F x 0 , s A M z 0, A ysdA M (c)
10
物理方面:
s ( y ) E ( y )
单辉祖:工程力学
s E
y
(a)
sdA 0 A
(b)
A ysdA M
yC y dA A 0 A
(c)
(a)(b)
A ydA 0
2
§1 引 言
弯曲应力与对称弯曲 本章内容
梁的弯曲应力
Iz=πD4/64 Iz=π(D4-d4)/64 若设圆环的直径比d/D=α，则相
应的截面抗弯系数为
Wz
=
π D3 32
Wz
=
π D3 32
(1−α 4 )
y 第10章 梁的弯曲应力 C Dz
y
O
z
d D
工程力学
q=60kN/m
A
1m
C
l = 3m
FS 90kN
(+ ) (− )
M ql2 / 8 = 67.5kN⋅ m
T形截面外伸梁尺寸及受载如图，截面对形心轴z的惯性矩
Iz=86.8cm4，yl=3.8cm。求梁横截面上的最大拉应力和最大压应力。
解 1)由静力平衡
2kN
0.8kN
y1 y2 6cm
方程求出梁的支反力
FA=0.6kN，FB=2.2kN A
C
BD
zC
作弯矩图。 得最大正弯矩在截面
1m 1m 1m
FA
FB
=
−
E ρ
I
z
1 ρ
=
Mz EIz
重要公式 σ = − Mz y Iz
工程力学
σ = − My Iz
第10章 梁的弯曲应力
M AZ y
x
y 横截面上正应力分布规律: (1)中性轴是过横截面形心的一条直线。中性轴上，正应力为零。 (2)以中性轴为界，横截面上的一侧受拉，一侧受压。 (3)离中性轴越远，正应力的绝对值越大。在横截面上离中性轴 最远的边或点上有最大的拉应力和最大的压应力。
几何关系 ( 平截面假定 )
正应变与中性层曲率间的关系
物理关系 ( Hooke 定律 )
正应力与中性层曲率间的关系
工程力学(静力学与材料力学)第二篇第11章弯曲应力精品PPT课件
2. 应力计算
M M e 2.0 0 km N s
max
M Wz
10.18MPa
3. 变形计算
1 M
EI z 16m 6
EI z
M
单辉祖,材料力学教程
13
§2 惯性矩与平行轴定理
静矩与惯性矩 简单截面惯性矩 平行轴定理 例题
单辉祖,材料力学教程
14
静矩与惯性矩
静矩
Sz
ydA
Iz Ay2dA IzAy0a2dA
Iz A y 0 2 d A 2 a A y 0 d A A 2a
Iz0 Ay02dA Ay0dA0
Iz Iz0 Aa2
同理得： IyIy0Ab2
Cy0z0－形心直角坐标系 Oyz －任意直角坐标系
二者平行
单辉祖,材料力学教程
17
例题
例 2-1 已知：F=15 kN, l=400 mm, b=120mm, d=20mm 试计算：截面 B-B 的最大拉应力st,max与压应力sc,max
中性轴与形心轴
中性轴－横截面受拉与受压区的分界线 形心轴－通过横截面形心的坐标轴
截面弯曲刚度与抗弯截面系数
弯曲刚度EI－代表梁截面抵抗弯曲变形的能力
抗弯截面系数Wz－代表梁截面几何性质对弯曲强度 的影响
单辉祖,材料力学教程
11
例题
例 1-1 梁用№18 工字钢制成，Me=20 kN•m, E=200 GPa。
单辉祖,材料力学教程
2
§1 对称弯曲正应力
引言 弯曲试验与假设 对称弯曲正应力公式 例题
单辉祖,材料力学教程
3
引言
弯曲应力 弯曲正应力
梁弯曲时横截面上的s
弯曲切应力
弯曲正应力
dA
y
z
y
x
A
y 2 dA M
已知
A
y 2 dA I z
横截面对 z 轴的惯性矩
得到：
M EI z
1
Ey 代入： E
(b)
得到：
My Iz
弯曲正应力计算公式
横截面上的最大正应力Leabharlann max令： 得：
M ymax Iz
M
max
抗弯截面系数
Iz Wz ymax
尚有两个问题?
1、
?
2、中性层的位置？
三、静力关系
F
Ey
A
x
0
dA 0
A
dA
E
M
A
ydA 0
得： 而
A
A
ydA 0
z
ydA S z A y
是横截面对 z 轴的静矩
M
y
z
y
dA
x
y 0
中性轴 z 通过横截面的形心
中性轴必为形心轴
M
E
y
0
z
已知:
a 50mm
2a A
a
F C
140MPa
求: F力的最大许可值 解: 作出梁的弯矩图 梁的危险截面为B截面 B截面的弯矩为:
B
M
Fa
M B M max Fa
梁的危险截面为B截面 M B M max Fa B截面的尺寸如图
30 203 14 203 12 Iz 10 12 12 1.07 108 m 4
《工程力学》教学课件第十二章弯曲应力
简支梁
在均布载荷或集中力作用下，简支梁横截面上的正应力呈线 性分布，最大正应力出现在梁的中性层上。
悬臂梁
在自由端受到集中力或均布载荷作用时，悬臂梁横截面上的 正应力呈非线性分布，最大正应力出现在固定端附近。
叠加原理在复杂载荷下梁正应力计算中应用
叠加原理
当梁受到多个载荷作用时，可以将每个载荷单独作用时产生的弯曲变形和正应力进行叠加，从而得到梁在复杂载 荷作用下的总弯曲变形和正应力。
提高构件的弯曲疲劳强度。
06 弯曲应力实验测定方法
电阻应变片法测量原理及操作步骤
测量原理
基于电阻应变效应，通过测量应变片电阻值变化来推算 出试件应变，进而得到弯曲应力。
操作步骤
粘贴应变片、连接测量电路、加载试件、记录数据。
光弹性法测量原理及优缺点分析
01
02
03
测量原理
利用某些透明材料在偏振 光场中受力产生应力双折 射现象，通过光弹性仪器 分析得到应力分布。
其他截面形状（圆形、工字形等）梁剪应力计算方法
圆形截面梁
对于圆形截面梁，可以采用极坐标方法进行剪应力计算，或者将其等效为矩形截面进行 计算。
工字形截面梁
对于工字形截面梁，由于其截面形状复杂，一般采用数值方法进行剪应力计算，如有限 元法等。
剪应力对梁强度和稳定性影响分析
对强度的影响
剪应力过大会导致梁截面发生剪切破坏 ，从而降低梁的承载能力。
《工程力学》教学课件第十二章弯 曲应力
contents
目录
• 弯曲应力基本概念与原理 • 梁弯曲时正应力计算与分析 • 梁弯曲时剪应力计算与分析 • 弯曲变形与位移计算 • 弯曲强度条件与校核方法 • 弯曲应力实验测定方法
01 弯曲应力基本概念与原理
在均布载荷或集中力作用下，简支梁横截面上的正应力呈线 性分布，最大正应力出现在梁的中性层上。
悬臂梁
在自由端受到集中力或均布载荷作用时，悬臂梁横截面上的 正应力呈非线性分布，最大正应力出现在固定端附近。
叠加原理在复杂载荷下梁正应力计算中应用
叠加原理
当梁受到多个载荷作用时，可以将每个载荷单独作用时产生的弯曲变形和正应力进行叠加，从而得到梁在复杂载 荷作用下的总弯曲变形和正应力。
提高构件的弯曲疲劳强度。
06 弯曲应力实验测定方法
电阻应变片法测量原理及操作步骤
测量原理
基于电阻应变效应，通过测量应变片电阻值变化来推算 出试件应变，进而得到弯曲应力。
操作步骤
粘贴应变片、连接测量电路、加载试件、记录数据。
光弹性法测量原理及优缺点分析
01
02
03
测量原理
利用某些透明材料在偏振 光场中受力产生应力双折 射现象，通过光弹性仪器 分析得到应力分布。
其他截面形状（圆形、工字形等）梁剪应力计算方法
圆形截面梁
对于圆形截面梁，可以采用极坐标方法进行剪应力计算，或者将其等效为矩形截面进行 计算。
工字形截面梁
对于工字形截面梁，由于其截面形状复杂，一般采用数值方法进行剪应力计算，如有限 元法等。
剪应力对梁强度和稳定性影响分析
对强度的影响
剪应力过大会导致梁截面发生剪切破坏 ，从而降低梁的承载能力。
《工程力学》教学课件第十二章弯 曲应力
contents
目录
• 弯曲应力基本概念与原理 • 梁弯曲时正应力计算与分析 • 梁弯曲时剪应力计算与分析 • 弯曲变形与位移计算 • 弯曲强度条件与校核方法 • 弯曲应力实验测定方法
01 弯曲应力基本概念与原理
[PPT]材料力学课件之弯曲应力
![[PPT]材料力学课件之弯曲应力](https://img.taocdn.com/s3/m/e793bed90b1c59eef9c7b47c.png)
1.计算公式 2.分布规律
s M.y
Iz
横截面上任一点处的正应力大小，与该点至中性轴的距
离成正比，即正应力沿截面宽度均匀分布，沿高度呈线性分 布。中性轴的一侧为拉应力，另一侧为压应力。
3.正应力公式讨论：
1）适用于均匀连续、各向同性材料，在线弹性范围小变 形时的等截面直杆。
2）在纯弯曲时，横截面在弯曲变形后保持平面，公式为精 确解；横力弯曲时，横截面不再保持平面，公式为近似
M z
(s dA) y
A
Ey2 dA E
A
y2dA EIz M
A
依此确定正应力计算公式。
3.弯曲中心的确定
P
M x A (t dA)d力臂 0,
O
依此确定x轴到杆轴的距离e。
z
ts
非对称截面梁发生平面弯曲的条件：外力必
x
须作用在主惯性面内，中性轴为形心主轴，
y
若是横向力，还必须过弯曲中心。
P
zP
M
V
s
x
y
翼缘上t1VA 2Iz;单肢合力为V1。腹板上t
VS
z
;合力为V
P
bI z
M x A (t dA)d力臂 0
e e V1h
V
6-6 考虑材料塑性时的极限弯矩
s
ss
ss
ss ss
ss
ss
理想弹塑性材料的
s图
弹性极限 分布图
塑性极限 分布图
全面屈服后,平面假设不再成立;仍做纵向纤维互不挤压假设。
]
时,
D
1.67
D1
Wz3
D3
32
(1- 0.8 4 )
2.75Wz1
工程力学：弯曲应力
Q 的4 A3
倍。
b.薄壁圆截面
最大剪应力发生在中性轴上各点处：
max
2
Q A
最大剪应力是平均剪应力 平
Q A
的2倍。
4. 剪应力强度条件
梁内最大剪应力一般发生在剪力最大的横截面的中性轴
上ቤተ መጻሕፍቲ ባይዱ若以
S
* z
m
a
x
表示中性轴以下（或以上）部分面积对中性轴
的静矩，则梁的剪应力强度条件为：
m axQ m aI xz S b z *m ax 79
拉应力强度足够。
A截面
C截面
2．压应力强度校核
A截面下部受压 ：
Amax
MA y2 Iz
C截面上部受压 ：
Cmax
MC y1 Iz
由于 M Ay2M Cy1，最大压应力发生在A截面的下边缘
m a x A m a x M I A z y 2 6 9 M P a 1 0 0 M P a
2
max
3Q 2bh
3Q 2A
最大剪应力是平均剪应力 平
Q A
的 1.5倍。
2. 工字型截面梁的剪应力 主要考虑工字型截面梁腹板上的剪应力计算。
可按照矩形截面梁的剪应力公式计算：
Q
S
* z
I zd
式中：d —腹板宽度
S
* z
—图中因阴影部分面积对中性轴之
静矩。
图 7-5
IQ zdb 2(h 42h 4 12)d 2(h 4 12y2)
二、纯弯曲时的正应力
（由实验观察得如下现象：）
a. 变形后，所有横向线仍保持为直 线，只是相对倾斜了一个角度。
b. 变形后，所有纵向线变成曲线， 仍保持平行;上、下部分的纵向线分 别缩短和伸长 。
工程力学-弯曲应力PPT文档62页
工程力学-弯曲应力
11、战争满足了，或曾经满足过人的 好斗的 本能， 但它同 时还满 足了人 对掠夺 ，破坏 以及残 酷的纪 律和专 制力的 欲望。 ——查·埃利奥 特 12、不应把纪律仅仅看成教育的手段 。纪律 是教育 过程的 结果， 首先是 学生集 体表现 在一切 生活领 域—— 生产、 日常生 活、学 校、文 化等领 域中努 力的结 果。— —马卡 连柯(名 言网)
拉
60、生活的道路一旦选定，就要勇敢地 走到底 ，决不 回头。 ——左
13、遵守纪律的风气的培养，只有领 导者本 身在这 方面以 身作则 才能收 到成效 。—— 马卡连 柯 14、劳动者的组织性、纪律性、坚毅 精神以 及同全 世界劳 动者的 团结一 致，是 取得最 后胜利 的保证 。—— 列宁 摘自名言网
15、机是生活，而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次，但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许，为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处， 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
11、战争满足了，或曾经满足过人的 好斗的 本能， 但它同 时还满 足了人 对掠夺 ，破坏 以及残 酷的纪 律和专 制力的 欲望。 ——查·埃利奥 特 12、不应把纪律仅仅看成教育的手段 。纪律 是教育 过程的 结果， 首先是 学生集 体表现 在一切 生活领 域—— 生产、 日常生 活、学 校、文 化等领 域中努 力的结 果。— —马卡 连柯(名 言网)
拉
60、生活的道路一旦选定，就要勇敢地 走到底 ，决不 回头。 ——左
13、遵守纪律的风气的培养，只有领 导者本 身在这 方面以 身作则 才能收 到成效 。—— 马卡连 柯 14、劳动者的组织性、纪律性、坚毅 精神以 及同全 世界劳 动者的 团结一 致，是 取得最 后胜利 的保证 。—— 列宁 摘自名言网
15、机是生活，而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次，但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许，为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处， 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
工程力学弯曲应力教学课件PPT
截面对轴的惯性矩等于该截面各部分对同一轴的 惯性矩之和。
n
I y I yi i 1
n
Iz Izi i 1
第九页，共81页。
· 型钢截面
可以查阅有关工程手册（型钢表）得到。
第十页，共81页。
四、平行移轴定理
I y
z 2dA
A
A (zC a)2dA
A zC2dA 2a A zCdA a2
2max
M2 Wz 2
M2
d23
32
ห้องสมุดไป่ตู้
d2
3
32 M 2
3
32 4.55103
140106
0.018m
第三十七页，共81页。
例：T 形截面铸铁梁的载荷和截面尺寸如图示。铸铁的抗拉许用应力为 [σ t] = 30MPa，抗压许用应力为[σ c] = 160MPa，试校核梁的强度。
解：⑴ 求支座约束力，作弯矩图
第三十页，共81页。
max
FS
S* z max
Iz
FS
8Iz
[bh02
(b )h2 ]
min
FS
8Iz
[bh02
bh2 ]
腹板厚度 远小于翼缘宽度 b 时， b -， ≈ b
τmax ，≈τ可m认in 为腹板上的切应力均匀分布
FS
A
腹板的面积
2.翼缘的切应力
翼缘部分切应力分布复杂且数值很小，一般不作计算，认为 翼缘主要承受截面的弯矩。
第七页，共81页。
· 圆环截面 （内径为d ，外径为D ，y、z轴过圆心）
Iz
Iy
(D4 d4)
64
D4
64
(1 4 )
工程力学---弯曲正应力
例1：求1-1截面上A、B两点的正应力。
解：（1）1-1截面上的弯矩
F=1kN
M z F 1 q 1 0.5
q=600N/m
20
1300N m
1
A
（2）惯性矩Iz
Iz
bh3 12
0.1 0.153 12
1
1m
2m
B 40
100 y
z 150
2.81105 m4
F l a Fl a
M max 2 2 4
A
max
M max W1
Fl a [ ]
4W1
F
4W1[ ]
l a
A
F
a
B
l
（b）
F/2
F/2
a
B
即
[F ]2
4W1[ ]
l a
l
F l a
横力弯曲与纯弯曲
横力弯曲 —— 剪力FS不为零
（ Bending by transverse force ）
例如AC, DB段
FS
纯弯曲 —— 剪力FS ＝0且 弯矩为常数
（ Pure bending ）
例如CD段
变形几何关系的建立
研究对象：等截面直梁
研究方法：实验——观察——假定
纯弯曲试验: 取对称截面梁，例如矩形截面梁，在其侧表
—— 梁横截面上正应力计算公式
纯弯曲时梁的正应力
关于中性轴的概念
由静力平衡关系： dA A
FNx
0
z
得： dA E ydA
A
A
x y
E
工程力学-弯曲应力
6 弯曲应力1、平面弯曲梁横截面上的正应力计算。
正应力公式是在梁纯弯曲情况下导出的，并被 推广到横力弯曲的场合。
横截面上正应力公式为j zM y I σ=横截面上最大正应力公式为 max zM W σ=2、横力弯曲梁横截面上的切应力计算，计算公式为*2z QS I bτ= 该公式是从矩形截面梁导出的，原则上也适用于槽形、圆形、工字形、圆环形截面梁横截面切应力的计算。
3、非对称截面梁的平面弯曲问题，开口薄壁杆的弯曲中心。
4、梁的正应力强度条件和切应力强度条件为[]max σσ≤[]max ττ≤根据上述条件，可以对梁进行强度校核、截面设计和容许荷载的计算，与此相关的还要考虑梁的合理截面问题。
5、梁的极限弯矩6.1图6-6所示简支梁用其56a 号工字钢制成，试求此梁的最大切应力和同一截面腹板部分在与翼板交界处的切应力。
图 6.1[解] 作剪力图如图(c).由图可知，梁的最大剪力出现在AC 段，其值为max 7575000Q kN N ==利用型钢表查得，56a 号工字钢*247.7310z z S I m -=⨯,最大切应力在中性轴上。
由此得以下求该横截面上腹板与翼板交界处C 的切应力。
此时*z S 是翼板面积对中性轴的面积矩，由横截面尺寸可计算得*3435602116621()9395009.401022z S mm m -=⨯⨯-==⨯ 由型钢表查得465866z I cm =,腹板与翼板交界处的切应力为*max max max max23*max7500012600000126.47.731012.510z a z z z Q S Q MP I I dd S τ--=====⨯⨯⨯⨯a MP 6.12解题范例483750009.40108.6658661012.510fc a MP τ---⨯⨯==⨯⨯⨯6.2长为L 的矩形截面悬臂梁，在自由端作用一集中力F ，已知b ＝120mm ，h ＝180mm 、L ＝2m ，F ＝1.6kN ，试求B 截面上a 、b 、c 各点的正应力。
梁的弯矩和应力关系式【最新】
第17讲教学方案——弯曲正应力第七章弯曲应力§7-1纯弯曲正应力梁的横截面上同时存在剪力和弯矩时，这种弯曲称为横弯曲。
剪力Q是横截面切向分布内力的合力；弯矩M是横截面法向分布内力的合力偶矩。
所以横弯梁横截面上将同时存在剪应力τ和正应力σ。
实践和理论都证明，其中弯矩是影响梁的强度和变形的主要因素。
因此，我们先讨论Q = 0，M = 常数的弯曲问题，这种弯曲称为纯弯曲。
图6-1所示梁的CD段为纯弯曲；其余部分则为横弯曲。
与扭转相似，分析纯弯梁横截面上的正应力，同样需要综合考虑变形、物理和静力三方面的关系。
1．变形关系——平面假设考察等截面直梁。
加载前在梁表面上画上与轴线垂直的横线，和与轴线平行的纵线，如图6-2a所示。
然后在梁的两端纵向对称面内施加一对力偶，使梁发生弯曲变形，如图图6-2b所示。
可以发现梁表面变形具有如下特征：（1）横线（m-m和n-n）仍是曲线，只是发生相对转动，但仍与纵线（如a-a，b-b）正交。
（2）纵线（a-a和b-b）弯曲成曲线，且梁的一侧伸长，另一侧缩短。
根据上述梁表面变形的特征，可以作出以下假设：梁变形后，其横截面仍保持平面，并垂直于变形后梁的轴线，只是绕着梁上某一轴转过一个角度。
与扭转时相同，这一假设也称平面假设。
此外，还假设：梁的各纵向层互不挤压，即梁的纵截面上无正应力作用。
根据上述假设，梁弯曲后，其纵向层一部分产生伸长变形，另一部分则产生缩短变形，二者交界处存在既不伸长也不缩短的一层，这一层称为中性层。
如图6-3所示。
中性层与横截面的交线为截面的中性轴。
横截面上位于中性轴两侧的各点分别承受拉应力或压应力；中性轴上各点的应力为零。
下面根据平面假设找出纵向线应变沿截面高度的变化规律。
考察梁上相距为dx 的微段（图6-4a ），其变形如图6-4b 所示。
其中x 轴沿梁的轴线，y 轴与横截面的对称轴重合，z 轴为中性轴。
则距中性轴为y 处的纵向层a-a 弯曲后的长度为θρd y )(+，其纵向正应变为ρθρθρθρεy d d d y =-+=)( （a ） 式（a ）表明：纯弯曲时梁横截面上各点的纵向线应变沿截面高度线性分布。
工程力学-9(2)弯曲应力
25
§9(2). 弯曲应力
弯曲正应力及正应力强度条件
3. 全梁上最大正应力
M x Fx
0 x l
工 程 力 学
全梁上最大弯矩的大小为 M max Fl 40 kN m
max
M max ymax 40 103 90 103 11.1MPa 2 9 Iz 120 180 10 12
30
§9(2). 弯曲应力
弯曲正应力及正应力强度条件
讨论：承载能力相同情况下，比较两种设计方案：
工 程 力 学
1 2 π 2 A实 πD 40 1256mm 2 4 4
A空
1 π 2 π D02 d 2 482 48 0.8 675mm 2 4 4
工 程 力 学
B
b
BH 3 bh3 Iz 12 12
C
z
HB hb Iy 12 12
3
3
y
BH 3 bh3 Wz 6H
21
§9(2). 弯曲应力
弯曲正应力及正应力强度条件 惯性矩I与抗弯截面系数W的计算
惯性矩的平行移轴公式
工 程 力 学
z O C
dA
y yc a ,
平面假设：纯弯曲梁的横截面变形前后保持为平面且与轴线正交。
工 程 力 学
从对称截面A－A处将 杆件截开。 截开后的杆段，其结 构、受力和变形仍然是对 称的，所以杆段的对称面 同样保持平面。 无限分割下去，就可 以证明所有横截面都将保 持平面。
5
§9(2). 弯曲应力
弯曲正应力及正应力强度条件 变形的几何关系
解：取x截面右段梁为研究对象。
弯曲应力-材料力学
已知：弯矩M、横截面的惯性矩Iz、许用应力[]。求：判断不等号。
max
Mymax Iz
工程力学 Engineering Mechanics
典型例题
例1 图示矩形截面梁，梁上载荷q=100kN/m，梁跨度l=6m，截面尺寸：
b=400mm，h=600mm，材料许用应力[]=100MPa，试判断该梁是否安全。
弹性力学精确分析表明，当跨度l与横截面高度h之比l/h>5（细长梁）时， 纯弯曲正应力公式对于横力弯曲近似成立。
横力弯曲最大正应力
max
M max ymax Iz
弯曲正应力适用范围 细长梁的纯弯曲或横力弯曲 横截面惯性积Iyz=0 弹性变形阶段
工程力学 Engineering Mechanics
YA
2m
2m YB
B 2m
20 b
90
c
z
a
50
解：（3）求解正应力
My Iz
惯性矩
Iz
1 12
50 903
3.0375106 mm4
弯矩
M 10kN.m
典型例题
例1 求图示矩形截面梁指定截面上对应点的正内力。
10kN
1
A
YA
2m
2m YB
B 2m
20 b
90
c
z
a
50
解：（3）求解正应力
M max
1 8
ql 2
1 8
q
62
q
533.3kN/m
练习1
受均布载荷作用的简支梁如图，求 ① 1-1截面上1、2两点的正应力； ② 1-1截面上的最大正应力； ③ 全梁的最大正应力； ④ 已知E=200GPa，求1-1截面的曲率半径。
max
Mymax Iz
工程力学 Engineering Mechanics
典型例题
例1 图示矩形截面梁，梁上载荷q=100kN/m，梁跨度l=6m，截面尺寸：
b=400mm，h=600mm，材料许用应力[]=100MPa，试判断该梁是否安全。
弹性力学精确分析表明，当跨度l与横截面高度h之比l/h>5（细长梁）时， 纯弯曲正应力公式对于横力弯曲近似成立。
横力弯曲最大正应力
max
M max ymax Iz
弯曲正应力适用范围 细长梁的纯弯曲或横力弯曲 横截面惯性积Iyz=0 弹性变形阶段
工程力学 Engineering Mechanics
YA
2m
2m YB
B 2m
20 b
90
c
z
a
50
解：（3）求解正应力
My Iz
惯性矩
Iz
1 12
50 903
3.0375106 mm4
弯矩
M 10kN.m
典型例题
例1 求图示矩形截面梁指定截面上对应点的正内力。
10kN
1
A
YA
2m
2m YB
B 2m
20 b
90
c
z
a
50
解：（3）求解正应力
M max
1 8
ql 2
1 8
q
62
q
533.3kN/m
练习1
受均布载荷作用的简支梁如图，求 ① 1-1截面上1、2两点的正应力； ② 1-1截面上的最大正应力； ③ 全梁的最大正应力； ④ 已知E=200GPa，求1-1截面的曲率半径。
弯曲正应力PPT课件
横截面 不再保持为平面 且由于切应力的存在，也不能保证纵向纤维之间没有正应力
二 横力弯曲正应力
纯弯曲正应力公式 My
IZ
弹性力学精确分析表明：
对于跨度 L 与横截面高度 h 之比 L / h > > 5的细长
梁， 用纯弯曲正应力公式计算横力弯曲正应力， 误差<<2%
满足工程中所需要的精度。
例1：某车间欲安装简易吊车，大梁选用工字钢。已知电葫芦 自重 F1 6.7kN, 起重量F2 50kN,跨度 l 9.5m,材料的许用应力
140MPa, 试选择工字钢的型号。
分析
（1）简化为力学模型
（2）确定危险截面
（3）截面为关于中性轴对称
（4）应力计算公式 max
M max Wz
（5）计算 M max
（6）计算 Wz ，选择工字钢型号
（1）计算简图
F=F1+F2
FF F FL/4
M
（4）强度计算
max
M max Wz
（5）选择工字钢型号
（2）绘弯矩图 （3）危险截面
F1 6.7kN, F2 50kN,
l 9.5m, 140MPa
应用公式 My
Iz
t,max
4
103 52103 7.64 106
27.2MPa
t
c,max
4103 88103 7.64 106
46.1MPa
c
9KN
A FA 1m M
CB
1m
F1B m
2.5KNm
4KN
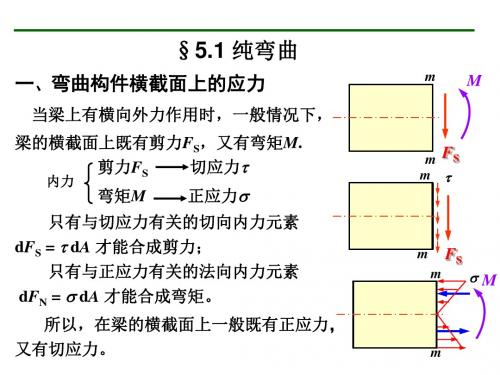
二 横力弯曲正应力
纯弯曲正应力公式 My
IZ
弹性力学精确分析表明：
对于跨度 L 与横截面高度 h 之比 L / h > > 5的细长
梁， 用纯弯曲正应力公式计算横力弯曲正应力， 误差<<2%
满足工程中所需要的精度。
例1：某车间欲安装简易吊车，大梁选用工字钢。已知电葫芦 自重 F1 6.7kN, 起重量F2 50kN,跨度 l 9.5m,材料的许用应力
140MPa, 试选择工字钢的型号。
分析
（1）简化为力学模型
（2）确定危险截面
（3）截面为关于中性轴对称
（4）应力计算公式 max
M max Wz
（5）计算 M max
（6）计算 Wz ，选择工字钢型号
（1）计算简图
F=F1+F2
FF F FL/4
M
（4）强度计算
max
M max Wz
（5）选择工字钢型号
（2）绘弯矩图 （3）危险截面
F1 6.7kN, F2 50kN,
l 9.5m, 140MPa
应用公式 My
Iz
t,max
4
103 52103 7.64 106
27.2MPa
t
c,max
4103 88103 7.64 106
46.1MPa
c
9KN
A FA 1m M
CB
1m
F1B m
2.5KNm
4KN
梁的弯曲计算—弯曲正应力的计算(工程力学课件)
x(轴线)
横截面上σ的分布规律
My
Iz
横截面对中性轴的惯性矩
bh3 Iz 12
横截面对中性轴的惯性矩
bh3 Iz 12
Iz
D4 64
(14 )
My
Iz
式中各量均以绝对值代入！ σ的正负自己判断
【例 1】求梁固定端A的右侧截面上的指定点的正应力
40kN.m
c 0
A
B
a
M ya Iz
40 106 N mm 300 2
33.75 107 mm4
mm 17.78 MPa
（拉应力）
b
M yb Iz
40 106 N mm 75 mm 33.75107 mm4
8.88
MPa
（拉应力）
d
M yd Iz
40 106 N mm 300
2 33.75 107 mm4
mm 17.78 MPa
a
M ya Iz
76106 90 48.6 106
140.74MPa
（拉应力）
b
M yb Iz
76106 50 48.6 106
78.19MPa
（拉应力）
d
M yd Iz
76106 90 48.6 106
140.74MPa （压应力）
c 0
（压应力）
习题1：求悬臂梁固定端A的右侧截面上各点的正应力
76kN.m
20kN/m
18kN
58kN
（1）求支座反力 （2）画弯矩图
76
28
A
M图(kN m) B
习题1：求悬臂梁固定A
B
（3）求正应力
Iz
100 1803
横截面上σ的分布规律
My
Iz
横截面对中性轴的惯性矩
bh3 Iz 12
横截面对中性轴的惯性矩
bh3 Iz 12
Iz
D4 64
(14 )
My
Iz
式中各量均以绝对值代入！ σ的正负自己判断
【例 1】求梁固定端A的右侧截面上的指定点的正应力
40kN.m
c 0
A
B
a
M ya Iz
40 106 N mm 300 2
33.75 107 mm4
mm 17.78 MPa
（拉应力）
b
M yb Iz
40 106 N mm 75 mm 33.75107 mm4
8.88
MPa
（拉应力）
d
M yd Iz
40 106 N mm 300
2 33.75 107 mm4
mm 17.78 MPa
a
M ya Iz
76106 90 48.6 106
140.74MPa
（拉应力）
b
M yb Iz
76106 50 48.6 106
78.19MPa
（拉应力）
d
M yd Iz
76106 90 48.6 106
140.74MPa （压应力）
c 0
（压应力）
习题1：求悬臂梁固定端A的右侧截面上各点的正应力
76kN.m
20kN/m
18kN
58kN
（1）求支座反力 （2）画弯矩图
76
28
A
M图(kN m) B
习题1：求悬臂梁固定A
B
（3）求正应力
Iz
100 1803
第十章 工程力学之弯曲应力
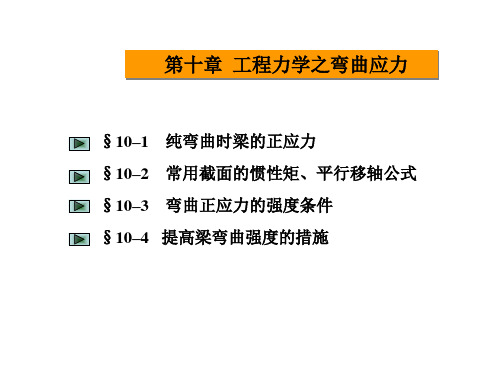
max拉MWm1ax [拉] ； max压MWm2ax [压]
式中W1和W2分别是相应于最大拉应力 max拉和最大压应力 max压 的抗弯截面模量，[ 压 ] 为材料的许用拉应力，[ 拉 ]为
材料的许用压应力。
例10-1 某冷却塔内支承填料用的梁，可简化为受均布载荷 的简支梁，如图10-8所示。已知梁的跨长为3m，所受均布
加载之前，先在梁的侧面，分别画上与梁轴线垂直的横线mn、 m1n1，与梁轴线平行的纵线ab、a1b1，前二者代表梁的横截面；
后二者代表梁的纵向纤维。如图10-2（a）所示。
在梁的两端加一对力偶，梁处于纯弯曲状态，将产生如图 10-2（b）、图10-2（c）所示的弯曲变形，可以观察到以下 现象：
•两条横线仍为直线，仍与纵线垂直，只是横线间作相对 转动，由平行线变为相交线。
2. 梁的变形规律
可以证明，纯弯曲梁变形后的轴线为一段圆弧。将图10-2(b)
中代表横截面的线段mn和m1n1延长，相交于C点，C点就是梁轴 弯曲后的曲率中心。若用 表示这两个横截面的夹角， 表
示中性层 故有
O
1
O
2
的曲率半径，因为中性层的纤维长度
O
1
O
2
不变，
O1O2
在如图10-2所示的坐标系中，y轴为横截面的对称轴，z轴为
如图10-1（a）所示的简支梁，其剪 力图如图10-1（b）所示，弯矩图如图 10-1（c）所示。可以看出梁中间一段 的剪力为零，而弯矩为常数，即为纯
弯曲； AC 和DB 段上既有剪力，又有
弯矩，为横力弯曲。
一、变形的几何关系
1. 梁的变形特点
如图10-2（a）所示，取梁的纵向对称面为xy平面。梁上的 外载荷就作用在这个平面内，梁的轴线在弯曲变形后也位于这 个平面内。
材料力学：弯曲正应力
σ Eε E
y
ρ
M
中性轴
弯曲正应力
3. 静力学方面 在横截面上法向内力元素 dA
dA
1 dA
M
Z
构成了空间平行力系。
y
O
x
dA
dA Z
y
该空间平行力系简化为 x 轴方向的主矢
FN dA
A
dA
1 dA
M
O
Z
x
dA
对y 轴和 z 轴主矩
M y A z (dA)
y
M M C
Z
中性轴 中性轴 Z
C
y
y
My Iz
（3）最大正应力发生在横截面上离中性轴最远的点处
中性轴为对称轴
tmax
拉 M
yt max
Z
C
压
yc max
Cmax
y
My Iz
用 ymax 表示最大 拉（压）
应力点到中性轴的距离。
tmax
拉 M
yt max
Z
C
y t max y c max y max
My Iz
4. 讨论 （1）应用公式时，一般将 M ，y 以绝对值代入。根据梁变形
的实际情况直接判断 的正，负号。
以中性轴为界
梁变形后凸出边的应力为拉应力（ 为正号）
梁变形后凹入边的应力为压应力（ 为负号）
My Iz
（2）横截面 中性轴上 各点的正应力最小。且 min = 0
压
yc max
Cmax
y
max
M y max Iz
tmax
拉 M
yt max
Z
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ymax
D d 0.701 m 2 2
285 MPa
3. 弯矩计算
M EI z
单辉祖:工程力学
1
E bd 3 1.141 N m M 12
EI z
24
8
推 论 梁内存在一长度不变的过渡层－中性层 中性层与横截面得交线－中性轴
中性轴⊥截面纵向对称轴
横截面间绕中性轴相对转动
单辉祖:工程力学 9
对称弯曲正应力公式
公式的建立
几何方面:
( y)
( y )d d y d
s ( y) E
y
(a)
静力学方面:
( y)
y
s ( y ) E ( y )
sdA 0 ysdA M A A
结论 中性轴位置：中性轴过截面形心 中性层曲率：
M （ I z － 惯性矩） EI z （EI z － 截面弯曲刚度） 1
M My 正应力公式： s ( y) s max Iz Wz （Wz － 抗弯截面系数）
§2 对称弯曲正应力
弯曲试验与假设 对称弯曲正应力公式 例题
单辉祖:工程力学
6
弯曲试验与假设
弯 曲 试 验
单辉祖:工程力学
7
试验现象 （纯弯与正弯矩作用） 横线为直线, 仍与纵线正交 靠顶部纵线缩短, 靠底部纵 线伸长 纵线伸长区,截面宽度减小 纵线缩短区, 截面宽度增大 弯曲假设 横截面变形后保持平面，仍与纵线正交－弯曲平 面假设 各纵向“纤维”处于单向受力状态－单向受力假 设 单辉祖:工程 力学
s t,max
单辉祖:工程力学
22
例 3-2 已知：钢带厚 d = 2mm, 宽 b = 6mm, D=1400mm, E=200GPa。试计算：带内的 smax 与 M
解：1. 问题分析
已知钢带的变形（轴线曲率 半径），求钢带应力与内力 应力～变形关系：
s E
y
s max E
单辉祖:工程力学
应用条件： s max s p , 对称弯曲 , 纯弯与非纯弯
12
一些易混淆的概念 对称弯曲与纯弯曲 对称弯曲－对称截面梁，在纵向对称面承受横向外 力时的受力与变形形式 纯 弯 曲－梁或梁段各横截面的剪力为零弯矩为常 数的受力状态 中性轴与形心轴 中性轴－横截面受拉与受压区的分界线 形心轴－通过横截面形心的坐标轴 截面弯曲刚度与抗弯截面系数 弯曲刚度EI－代表梁截面抵抗弯曲变形的能力 抗弯截面系数Wz－代表梁截面几何性质对弯曲强度 的影响
E
中性轴通过横截面形心
(a)(c)
A
y 2 dA M
1
Iz
A
y2dA －惯性矩
M (d) EI z
(d)(a)
My s max max Iz
My s ( y) Iz
Iz Wz －抗弯截面系数 ymax
单辉祖:工程力学
M s max Wz
11
总 结 假设 平面假设，单向受力假设 综合考虑三方面
ymax
内力～变形关系：
M EI z
单辉祖:工程力学
1
M
EI z
23
带厚 d=2 mm, 宽 b= 6mm, D = 1400mm, E = 200GPa，求 smax 与 M
2. 应力计算
s max E
ymax
ymax
s max E
d 3 1.0 10 m 2
Ai yCi AyC
yC
i 1
n
A y
i 1
n
i Ci
21
A
A1 yC 1 A2 yC 2 yC A1 A2
bd
d db d b 2 2
bd db
0.045 m
3. 惯性矩计算
I z I z1 I z 2
2
bd 3 d 3.0210 -6 m4 I z1 bd yC 12 2
ห้องสมุดไป่ตู้
d b3 b I z2 db d yC 5.8210 -6 m4 12 2
I z I z 1 I z 2 8.8410 6 m 4
2
4. 最大弯曲正应力
M B yC 30.5 MPa Iz M ( b d yC ) s c,max B 64.5 MPa Iz
3. 变形计算
M EI z
1
EI z 166 m M
15
单辉祖:工程力学
§3 惯性矩与平行轴定理
惯性矩
简单截面惯性矩 平行轴定理 例题
单辉祖:工程力学
16
惯性矩
惯性矩
I z A y dA
2
[L]4
－截面对 z 轴的惯性矩
I y z dA
2 A
Iz Iz i
第 11 章 弯曲应力
本章主要研究：
单辉祖:工程力学
对称弯曲正应力 对称弯曲切应力 梁的强度分析与设计 非对称弯曲应力
1
§1 §2 §3 §4 §5 §6 §7
引言 对称弯曲正应力 惯性矩与平行轴定理 对称弯曲切应力 梁的强度条件 梁的合理强度设计 双对称截面梁的非对称弯曲
单辉祖:工程力学
I p A dA A ( y z )dA
2
2 2
Ip I z I y
I p d 4 Iz 2 64
单辉祖:工程力学
Ip 2I z
d 2 d Wz 64 d 32
4 3
19
平行轴定理
平行轴定理
建立 I z 与 I z0 的关系
I z A y 2dA
dA 0 (b) F x 0 , s A M z 0, A ysdA M (c)
10
物理方面:
s ( y ) E ( y )
单辉祖:工程力学
s E
y
(a)
sdA 0 A
(b)
A ysdA M
yC y dA A 0 A
(c)
(a)(b)
A ydA 0
i 1
n
n
单辉祖:工程力学
Iy
I
i 1
yi
17
简单截面惯性矩
矩形截面惯性矩
bh I z A y dA - h/2 y bdy 12
2
h/ 2 2
3
2 I z bh bh Wz ymax 12 6 h 2
单辉祖:工程力学 18
3
简单截面惯性矩
圆形截面惯性矩
例 题
例 3-1 已知：F=15 kN, l=400 mm, b=120mm, d=20mm 试计算：截面 B-B 的最大拉应力st,max与压应力sc,max
解：1. 弯矩计算 2. 形心位置计算
Sz
单辉祖:工程力学
M B Fl 6000 N m
由矩形 1 与矩形 2 组成的组合截面
单辉祖:工程力学 13
例 题
例 2-1 梁用№18 工字钢 制成，Me=20 kN•m, E=200 GPa。
试计算：最大弯曲正应力smax ，梁轴曲率半径
解：1. 工字钢（GB 706-1988） 一种规范化、系列化的工字形截面的标准钢材 №18 工字钢：
I z 1.66 10 5 m 4
I z A y0 a dA
2
2 I z A y0 dA 2a A y0 dA Aa2
2 I z0 A y0 dA
A y0dA 0
Cy0z0－形心直角坐标系 Oyz －任意直角坐标系 二者平行
20
I z I z0 Aa 2
同理得：
单辉祖:工程力学
I y I y0 Ab2
2
§1 引 言
弯曲应力与对称弯曲 本章内容
单辉祖:工程力学
3
弯曲应力与对称弯曲
弯曲应力
弯曲正应力 梁弯曲时横截面上的s
弯曲切应力 梁弯曲时横截面上的t 对称弯曲
对称截面梁，在纵向对称面承受横向 外力时的受力与变形形式－对称弯曲
单辉祖:工程力学 4
变形形式与本章内容
变形形式
基本变形形式－轴向拉压，扭转，弯曲 组合变形形式－两种或三种不同基本变形形式的组合
弯拉（压）组合，弯扭组合，弯拉（压）扭组合
本章主要内容
对称弯曲正应力 对称弯曲切应力 弯曲强度计算与合理强度设计 双对称截面梁非对称弯曲 应力与强度
5
弯拉（压）组合应力与强度
单辉祖:工程力学
单辉祖:工程力学
Wz 1.85 10 4 m 3
14
I z 1.66 10 5 m 4
Wz 1.85 10 4 m 3
Me=20 kN•m，E=200 GPa，求 smax 与
2. 应力计算
M M e 20.0 kN m
M s max 108.1 MPa Wz
D d 0.701 m 2 2
285 MPa
3. 弯矩计算
M EI z
单辉祖:工程力学
1
E bd 3 1.141 N m M 12
EI z
24
8
推 论 梁内存在一长度不变的过渡层－中性层 中性层与横截面得交线－中性轴
中性轴⊥截面纵向对称轴
横截面间绕中性轴相对转动
单辉祖:工程力学 9
对称弯曲正应力公式
公式的建立
几何方面:
( y)
( y )d d y d
s ( y) E
y
(a)
静力学方面:
( y)
y
s ( y ) E ( y )
sdA 0 ysdA M A A
结论 中性轴位置：中性轴过截面形心 中性层曲率：
M （ I z － 惯性矩） EI z （EI z － 截面弯曲刚度） 1
M My 正应力公式： s ( y) s max Iz Wz （Wz － 抗弯截面系数）
§2 对称弯曲正应力
弯曲试验与假设 对称弯曲正应力公式 例题
单辉祖:工程力学
6
弯曲试验与假设
弯 曲 试 验
单辉祖:工程力学
7
试验现象 （纯弯与正弯矩作用） 横线为直线, 仍与纵线正交 靠顶部纵线缩短, 靠底部纵 线伸长 纵线伸长区,截面宽度减小 纵线缩短区, 截面宽度增大 弯曲假设 横截面变形后保持平面，仍与纵线正交－弯曲平 面假设 各纵向“纤维”处于单向受力状态－单向受力假 设 单辉祖:工程 力学
s t,max
单辉祖:工程力学
22
例 3-2 已知：钢带厚 d = 2mm, 宽 b = 6mm, D=1400mm, E=200GPa。试计算：带内的 smax 与 M
解：1. 问题分析
已知钢带的变形（轴线曲率 半径），求钢带应力与内力 应力～变形关系：
s E
y
s max E
单辉祖:工程力学
应用条件： s max s p , 对称弯曲 , 纯弯与非纯弯
12
一些易混淆的概念 对称弯曲与纯弯曲 对称弯曲－对称截面梁，在纵向对称面承受横向外 力时的受力与变形形式 纯 弯 曲－梁或梁段各横截面的剪力为零弯矩为常 数的受力状态 中性轴与形心轴 中性轴－横截面受拉与受压区的分界线 形心轴－通过横截面形心的坐标轴 截面弯曲刚度与抗弯截面系数 弯曲刚度EI－代表梁截面抵抗弯曲变形的能力 抗弯截面系数Wz－代表梁截面几何性质对弯曲强度 的影响
E
中性轴通过横截面形心
(a)(c)
A
y 2 dA M
1
Iz
A
y2dA －惯性矩
M (d) EI z
(d)(a)
My s max max Iz
My s ( y) Iz
Iz Wz －抗弯截面系数 ymax
单辉祖:工程力学
M s max Wz
11
总 结 假设 平面假设，单向受力假设 综合考虑三方面
ymax
内力～变形关系：
M EI z
单辉祖:工程力学
1
M
EI z
23
带厚 d=2 mm, 宽 b= 6mm, D = 1400mm, E = 200GPa，求 smax 与 M
2. 应力计算
s max E
ymax
ymax
s max E
d 3 1.0 10 m 2
Ai yCi AyC
yC
i 1
n
A y
i 1
n
i Ci
21
A
A1 yC 1 A2 yC 2 yC A1 A2
bd
d db d b 2 2
bd db
0.045 m
3. 惯性矩计算
I z I z1 I z 2
2
bd 3 d 3.0210 -6 m4 I z1 bd yC 12 2
ห้องสมุดไป่ตู้
d b3 b I z2 db d yC 5.8210 -6 m4 12 2
I z I z 1 I z 2 8.8410 6 m 4
2
4. 最大弯曲正应力
M B yC 30.5 MPa Iz M ( b d yC ) s c,max B 64.5 MPa Iz
3. 变形计算
M EI z
1
EI z 166 m M
15
单辉祖:工程力学
§3 惯性矩与平行轴定理
惯性矩
简单截面惯性矩 平行轴定理 例题
单辉祖:工程力学
16
惯性矩
惯性矩
I z A y dA
2
[L]4
－截面对 z 轴的惯性矩
I y z dA
2 A
Iz Iz i
第 11 章 弯曲应力
本章主要研究：
单辉祖:工程力学
对称弯曲正应力 对称弯曲切应力 梁的强度分析与设计 非对称弯曲应力
1
§1 §2 §3 §4 §5 §6 §7
引言 对称弯曲正应力 惯性矩与平行轴定理 对称弯曲切应力 梁的强度条件 梁的合理强度设计 双对称截面梁的非对称弯曲
单辉祖:工程力学
I p A dA A ( y z )dA
2
2 2
Ip I z I y
I p d 4 Iz 2 64
单辉祖:工程力学
Ip 2I z
d 2 d Wz 64 d 32
4 3
19
平行轴定理
平行轴定理
建立 I z 与 I z0 的关系
I z A y 2dA
dA 0 (b) F x 0 , s A M z 0, A ysdA M (c)
10
物理方面:
s ( y ) E ( y )
单辉祖:工程力学
s E
y
(a)
sdA 0 A
(b)
A ysdA M
yC y dA A 0 A
(c)
(a)(b)
A ydA 0
i 1
n
n
单辉祖:工程力学
Iy
I
i 1
yi
17
简单截面惯性矩
矩形截面惯性矩
bh I z A y dA - h/2 y bdy 12
2
h/ 2 2
3
2 I z bh bh Wz ymax 12 6 h 2
单辉祖:工程力学 18
3
简单截面惯性矩
圆形截面惯性矩
例 题
例 3-1 已知：F=15 kN, l=400 mm, b=120mm, d=20mm 试计算：截面 B-B 的最大拉应力st,max与压应力sc,max
解：1. 弯矩计算 2. 形心位置计算
Sz
单辉祖:工程力学
M B Fl 6000 N m
由矩形 1 与矩形 2 组成的组合截面
单辉祖:工程力学 13
例 题
例 2-1 梁用№18 工字钢 制成，Me=20 kN•m, E=200 GPa。
试计算：最大弯曲正应力smax ，梁轴曲率半径
解：1. 工字钢（GB 706-1988） 一种规范化、系列化的工字形截面的标准钢材 №18 工字钢：
I z 1.66 10 5 m 4
I z A y0 a dA
2
2 I z A y0 dA 2a A y0 dA Aa2
2 I z0 A y0 dA
A y0dA 0
Cy0z0－形心直角坐标系 Oyz －任意直角坐标系 二者平行
20
I z I z0 Aa 2
同理得：
单辉祖:工程力学
I y I y0 Ab2
2
§1 引 言
弯曲应力与对称弯曲 本章内容
单辉祖:工程力学
3
弯曲应力与对称弯曲
弯曲应力
弯曲正应力 梁弯曲时横截面上的s
弯曲切应力 梁弯曲时横截面上的t 对称弯曲
对称截面梁，在纵向对称面承受横向 外力时的受力与变形形式－对称弯曲
单辉祖:工程力学 4
变形形式与本章内容
变形形式
基本变形形式－轴向拉压，扭转，弯曲 组合变形形式－两种或三种不同基本变形形式的组合
弯拉（压）组合，弯扭组合，弯拉（压）扭组合
本章主要内容
对称弯曲正应力 对称弯曲切应力 弯曲强度计算与合理强度设计 双对称截面梁非对称弯曲 应力与强度
5
弯拉（压）组合应力与强度
单辉祖:工程力学
单辉祖:工程力学
Wz 1.85 10 4 m 3
14
I z 1.66 10 5 m 4
Wz 1.85 10 4 m 3
Me=20 kN•m，E=200 GPa，求 smax 与
2. 应力计算
M M e 20.0 kN m
M s max 108.1 MPa Wz