耦合电感的等效电路
电路分析基础课件第8章耦合电感和变压器电路分析

耦合电感在电路中的应用
信号传输
耦合电感在电路中可以用于传输信号,由于其电磁耦 合的特性,信号可以在不同的电路之间传递。
滤波器
耦合电感可以组成各种滤波器,如高通、低通、带通 等,用于对信号进行筛选和过滤。
振荡器
在振荡电路中,耦合电感与电容配合使用,可以形成 振荡信号。
变压器在电路中的应用
电压转换
01
电路分析基础课件第8章耦合电感 和变压器电路分析
目 录
• 耦合电感电路分析 • 变压器电路分析 • 耦合电感和变压器在电路中的应用 • 习题与思考
01 耦合电感电路分析
耦合电感基本概念
耦合电感定义
由两个或多个线圈通过磁场相互耦合而构成的电路元件。
耦合系数
描述耦合电感线圈之间耦合程度的一个参数,其值在0到1之间 。
习题2
计算变压器初级和次级线圈的电压和电流, 以及变压器的变比。
习题3
分析一个具有变压器和耦合电感的电路,计 算各元件的电压和电流。
习题4
设计一个变压器,满足特定的电压和电流要 求,并计算所需的匝数和线径。
思考题
思考题1
如何理解耦合电感和变压器在 电路中的作用?
思考题2
如何分析具有耦合电感和变压 器的电路?
02
变压器在电力系统、电子设备和 工业自动化等领域有着广泛的应 用,是电力传输和分配的关键设 备之一。
变压器的工作原理
当交流电通过变压器的一次绕组时, 会在铁芯中产生交变磁场,这个磁场 会感应出电动势,从而在二次绕组中 产生电压和电流。
变压器的工作原理基于电磁感应定律 和全电流定律,通过改变绕组匝数实 现电压和电流的变换。
根据耦合系数和线圈的匝数比,可以确定电压和电流的幅值关系。
耦合电感的去耦等效电路
ห้องสมุดไป่ตู้
Lb )
di1 dt
Lb
di2 dt
u2
Lb
di1 dt
(Lb
Lc )
di2 dt
图10-11 由此解得: 图10-11(d)
例10-3 用去耦等效电路求图(a)单口网络的等效电感。
图10-12
解:若将耦合电感 b、d两端相连,其连接线中的电流为零,不会 影响单口网络的端口电压电流关系,此时可用图
u2
Lb
di1 dt
(Lb
Lc )
di2 dt
La L1 M
Lb M
L c L 2 M
L1 La Lb
L2
Lb
L
c
M L b
La L1 M
Lb M
L c L 2 M
u1
L1
di1 dt
M
di2 dt
u2
M
di1 dt
L2
di2 dt
u1
(La
10.3 耦合电感的去耦等效电路
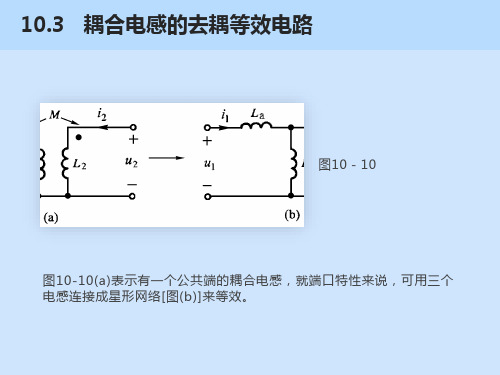
图10-10
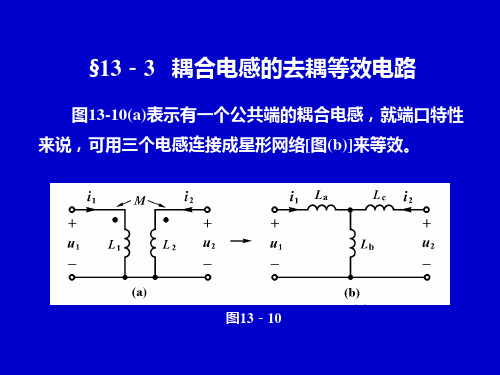
图10-10(a)表示有一个公共端的耦合电感,就端口特性来说,可用三个 电感连接成星形网络[图(b)]来等效。
u1
L1
d i1 dt
M
di2 dt
u2
M
d i1 dt
L2
di2
dt
u1
(La
Lb )
di1 dt
Lb
di2 dt
u2
Lb
di1 dt
(Lb
Lc )
di2 dt
列出图(a)和(b)电路的电压、电流关系方程: 图10-10
令以上两式 各系数分别 相等,得到:
电路第十章含有耦合电感的电路
.. . . .. .. . . .. 一致,故1,4是同名端,(不2是,同名端,1,4是同名端,
3也是同名i1 端) i2 (2,3也是同名端i1 ) i2
1 23 4
1 23 4
同名端只与线圈的绕向有关,与电流方向无关。 只要知道线圈的绕向,就能标出同名端。
L L1L2 M2 L1 L2 2M
M2 L1L2
M L1L2 M L1 L2
2
几何平均值(小) 算术平均值(大)
除非两电感相同,一般:几何平均值< 算术平均值
∴用几何平均值求M更严格
∴互感M必须满足 M L1L2 的要求 ∴ M的最大值 Mmax L1L2
3.耦合系数 k M M max
最大值
i(t)
••
u ( t ) L1 L2
i(t)
u(t)
L1 -
di
M
dt +
L2
+
M
di
- dt
utL1d d ti Md d ti L2d d ti Md dti
L1
L2
2Mdi
dt
L
di dt
反接时,串联电感值为
LL1L22M
电感贮能 WL 12LiL2 0
即L一定为正值
L1L22M
M L1 L2 2
实际值
M L1 L 2
0k1
k 反应了磁通相耦合的程度
k=1 k→1 k<0.5 k=0
全耦合
线圈中电流产生的磁通全部与另一个线 圈交链达到使M无法再增加
紧耦合,强耦合
松耦合,弱耦合
无耦合
4.耦合电感的T型等效
耦合电感的去耦等效电路
(10 17)
两端相连, 也可将耦合电感 b、c两端相连,所求得的等效电感与 、 两端相连 相同。 式(10-17)相同。 - 相同
所示单口网络的等效电路。 例10-4 试求图 - 试求图10-13(a)所示单口网络的等效电路。 所示单口网络的等效电路
图10-13 -
解:先化简电路。将2 电阻合并到 电阻成为 电阻合并到3 电阻成为5 ,将端 先化简电路。 电感的理想变压器等效为5H电感 接50mH电感的理想变压器等效为 电感,再将耦合电感 电感的理想变压器等效为 电感, 去耦以得到图(b)所示等效电路 所示等效电路。 去耦以得到图 所示等效电路。最后用电感串并联公式求 得总电感为
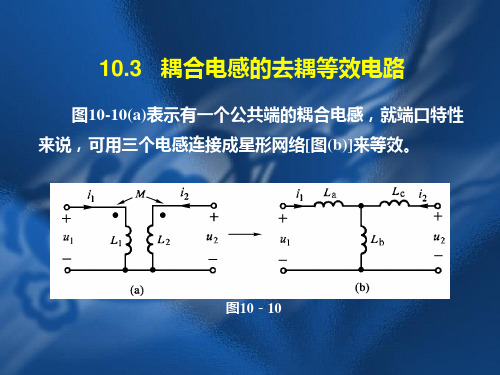
10.3 耦合电感的去耦等效电路
表示有一个公共端的耦合电感, 图10-10(a)表示有一个公共端的耦合电感,就端口特性 表示有一个公共端的耦合电感 来说,可用三个电感连接成星形网络 图 来等效。 来说,可用三个电感连接成星形网络[图(b)]来等效。 来等效
图10-10 -
图10-10 -
列出图(a)和(b)电路的电压、电流关系方程: 电路的电压、 列出图 和 电路的电压 电流关系方程:
图10-12 -
解:若将耦合电感 b、d两端相连,其连接线中的电流为零, 两端相连, 、 两端相连 其连接线中的电流为零, 不会影响单口网络的端口电压电流关系, 不会影响单口网络的端口电压电流关系,此时可用图 (b)电路来等效。再用电感串并联公式求得等效电感 电路来等效。 电路来等效
M ( L2 M ) M2 Lab = L1 M + = L1 M + L2 M L2
L1 = La + Lb L2 = Lb + Lc M = Lb
图10-11(d) -
14-2 耦合电感的等效电路

14-2 耦合电感的等效电路
耦合电感的等效电路包括两个不同的电路:主电路和耦合电路。
主电路指的是两个电感器分别与各自的电源相连的电路,而耦合电路则是两个电感器之间通过磁场相互耦合的电路。
主电路的等效电路可以通过简单的串联电路或并联电路来表示。
耦合电路可以表示为一个电感器和一个磁芯之间的电路,其中磁芯通过磁场将电感器之间的电能耦合在一起。
当两个耦合电感器之间有运动时,它们之间的磁场也会随之改变。
这种变化会导致电感器之间的电能转移,从而影响它们的电流和电压。
耦合电感的等效电路可以通过电容器、变压器、晶体管等电子元件来实现。
这些元件可以用于设计各种类型的电路,从而满足不同的需求。
7.3耦合电感的连接及等效变换 7.4耦合电感的T型连接及等效变换
İ1
İ2
I 1 11 .3 81 .87 A
I 2 4 216 .87 A
P 160W
(2)K=1,M = 1H,有
解:去耦等效电路
(1)K=0.5,M = 0.5H,有
j5 I1 j5( I1 I 2 ) 10 0
j 5 I 2 j 5 ( I 1 I 2 ) 10 I 2 0
顺接:
反接:
3
有缘学习更多+谓ygd3076或关注桃报:奉献教育(店铺)
7-4 耦合电感的T型连接及等效变换
一、 T型连接
同侧T型连接
异侧T型连接
4
二、去耦等效电路
İ1
同侧T型连接
U 13 j L1 I 1 j M I 2
j L1 I 1 j M ( I 3 M I 3
7
有缘学习更多+谓ygd3076或关注桃报:奉献教育(店铺)
İ2 İ3
LL22+-MM
M-M
5
小结: 同侧T型
L1 - M L2 - M M
异侧T型
L1 + M L2 + M -M
6 有缘学习更多+谓ygd3076或关注桃报:奉献教育(店铺)
例1: 图示电路,=10rad/s。 分别求K=0.5和K=1时,电路中的电流 İ1和İ2 以及电阻R=10时吸收的功率.
U 23 j L 2 I 2 j M I 1
jL2 I 2 jM ( I 3 I 2 )
j (L2 M ) I 2 jM I 3
LL11+-MM
异侧T型连接 有缘学习更多+谓ygd3076或关注桃报:奉献教育(店铺)
U 13 j ( L1 M ) I 1 j M I 3
U 23 j ( L 2 M ) I 2 j M I 3
20170420-实际变压器的耦合电感等效电路

vp (t ) Lp vs (t ) = LM
LM d ip (t ) Ls dt − is (t )
(3)
这个耦合电感原边和副边的自感及互感分别为:
Lp = Lmp + Llp
Ls = ( Ns 2 ) Lmp + Lls Np Ns Lmp Np
(4) (5)
LM =
(6)
对于耦合电感而言, 当原边和副边的漏感为零时, 其原副边的匝数比与原副边的自感有下述
1
关系:
Ns = Np
Ls Lp
(7)
同样的我们可将(7)定义为变压器在不能忽略漏感时的等效匝数比,这个等效匝数比可以 通过测量原边和副边的自感后,再用计算获得。在测量原边的自感时,应先将副边开路,然 后用电感测量表测得其原边的电感;在测量副边的电感时,应先将原边开路,然后用电感测 量表测得其副边的电感。除了等效匝数比外,特征耦合电感性能好坏的参数还有一个,那就 是耦合系数,如下式定义:
实际变压器的耦合电感等效电路
普高(杭州)科技开发有限公司 张兴柱 博士
ip
Llp ( Ns / Np )is
Lls
is
ip
vs
LM
vp
Lp
vp
imp
Lmp
变比
Np : Ns
vs
(b)
Ls
is
(a)
图 1: 变压器的耦合电感等效电路
前面已经介绍过变压器的实际等效电路模型,如图 1(a)。如对该等效电路用方程加以表示的 话,则它的端口电压电流将满足:
k=
LM LpLs
(8)
当一个实际的变压器用图 1 所示的等效电路等效时, 表示其好坏的参数除了漏感和激磁电感 这种方法外,还可用等效匝比和耦合系数的办法。一般情况下,希望变压器的耦合系数越高 越好, 希望变压器的等效匝比与真实的匝比越接近越好。 对于原边和副边电压差不多的变压 器,其能实现的耦合系数就越大,对于原边和副边电压相差很大的变压器,其能实现的耦合 系数就较低。
耦合电感并联等效电感公式推导

耦合电感并联等效电感公式推导
在电路中,电感是一种用来存储电能的元件,而耦合电感则是指两个或多个电感之间存在一定的磁耦合关系。
当两个电感之间存在磁耦合时,它们的等效电感将会发生变化。
本文将介绍耦合电感并联时的等效电感公式推导过程。
假设有两个耦合电感L1和L2,它们之间存在一定的磁耦合。
当这两个耦合电感并联在一起时,它们的等效电感记为Leq。
根据电路理论,耦合电感并联时的等效电感可以通过以下公式进行推导:
1. 首先,我们可以利用电感的互感系数M来描述两个电感之间的磁耦合关系。
互感系数M的取值范围在0到1之间,当M等于1时,表示两个电感之间完全磁耦合,而当M等于0时,表示两个电感之间没有磁耦合。
2. 根据耦合电感的定义,我们可以得到Leq与L1和L2之间的关系:Leq = L1 + L2 + 2M√(L1L2)。
这个公式表示了当两个耦合电感并联时,它们的等效电感与它们本身的电感值以及互感系数之间的关系。
3. 通过上述公式,我们可以看到,耦合电感并联时的等效电感不仅与两个电感的电感值有关,还与它们之间的磁耦合程度有关。
当M 接近1时,Leq的值将会显著大于L1和L2之和,这是因为磁耦合会增加电感的存储能量。
耦合电感并联时的等效电感公式可以通过电感的互感系数M来描述两个电感之间的磁耦合关系。
通过合理选择互感系数M的取值,我们可以控制并联电路的等效电感值,从而满足电路设计的需求。
通过深入理解耦合电感并联的等效电感公式推导过程,我们可以更好地应用这一原理于实际电路设计中,提高电路性能和稳定性。
耦合电感的等效电路

端联接在一起,该联接方式称为同向串联(顺接);图6-42( a )中L 1和L 2的同名端连接在l_2 M :u'u 2—(b )L 1 ■ L2 - 2M_____ ■■- __________________________4 U -(c) 图6-41 串联耦合电路的去耦顺接时,支路的电压电流关系为uM 色)(L 2d M di ) dt dt dt dt-J: -J: -J:= (L j M )匕(L 2 M )2 = (L 1L 2 2M )d -dt dtdt根据等效变换的概念,该顺接耦合电感可用一个(L j • M )的电感和一个 (L 2M )的电感相串联的电路等效替代,或用一个(J • L 2• 2M )的电感等效替代。
如图6-41 ( b )所示。
反接时,支路的电压电流关系为八 di R” didi di u =馆 M ) (L 2M ) dt dtdtdt-J:-J:-J:=(L i - M )—— (L 2- M )——=(L iL 2- 2M )—dt dtdtdi根据等效变换的定义, 该反接耦合电感可用一个(L r -M )的电感和一个 (L 2- M )的电感相串联的电路等效替代, 或用一个 (J • L 2-2M )的电感等效替代。
如图6-42 ( b )所示。
6.5.2耦合电感的等效电路 1.耦合电感的去耦等效电路 (1)串联电路去耦图6-41 (a )和图6-42( a )即为耦合电感的串联电路。
图6-41 (a )中J 和L 2的异名起,该连接方式称为反向串联(反接)(a )l_1 ::;U 1+u. M ,L1 一、L2比 _ - u2-L2「MU2 -M亠U1(a)(c )图6-42 串联耦合电路的去耦(2) T 型电路去耦图6-43 ( a )和图6-44 (a )即为耦合电感的T 型连接电路,其中图 6-43 ( a )中耦合电感的联接形式称为同侧联接,图6-44 (a )的联接形式称为异侧联接。
耦合电感的电路分析10

第十三章 含耦合电感的电路分析
磁耦合线圈在电子工程、通信工程和测量仪器等方面得到了广泛应用。 为了得到实际耦合线圈的电路模型,现在介绍一种动态双口元件——耦合电 感,并讨论含耦合电感的电路分析。
在介绍耦合电感元件以前,下面先用示波器观察磁耦合线圈初级和次 级的波形。
在环形磁芯上用漆包线绕一个耦合电感,初级60匝,次级30匝,如图所示。
在前面的实验中已经测量出上图所示耦合电 感初级线圈自电感L1=0.66mH和耦合电感线圈次 级的等效自电感L2=0.17mH。由此可以计算出该 耦合线圈的耦合系数为
k M 0.26 0.776 L1L2 0.66 0.17
该耦合线圈接近紧耦合,其原因是磁环的导磁系数很高。
例13-2 图13-9电路原已稳定。已知R=20, L1=L2=4H, k=0.25, US=8V。t=0时开关闭合,求t>0时的i(t)和 u(t)。
图13-1(a)
对于图(a)的情况,根据电磁感应定律可以得到:
u1
d 1
dt
d 11
dt
d 12
dt
L1
di1 dt
M
di2 dt
u2
d 2
dt
d 21
dt
d 22
dt
M
di1 dt
L2
di2
dt
(13 3)
图13-1(b)
与此相似,对于图(b)情况可以得到:
u1
d 1
dt
d 11
dt
d 12
di dt
M
di dt
M
di dt
L2
di dt
( L1
L2
2M )
di dt
耦合电感的等效电路

11
并联去耦等效(异名端共一节点)
M
L1
L2
-M L1+M
L2+M
电磁耦合
-jωM
电耦合
jω(L1+M)
jω(L2+M)
正弦稳态模型
12
Lc
di2 dt
6
皮肌炎图片——皮肌炎的症状表现
• 皮肌炎是一种引起皮肤、肌肉、 心、肺、肾等多脏器严重损害的, 全身性疾病,而且不少患者同时 伴有恶性肿瘤。它的1症状表现如 下:
• 1、早期皮肌炎患者,还往往伴 有全身不适症状,如-全身肌肉酸 痛,软弱无力,上楼梯时感觉两 腿费力;举手梳理头发时,举高 手臂很吃力;抬头转头缓慢而费 力。
M
i2
+
+
u1
L1
L2
u2
-
-
+ i1 L1+M
u1 -
L2+M i2
+
-M
u2
-
3
3.耦合电感的顺接串联等效
i
.+
M
+
u1 L1 L2
u-
_
KVL:u=u1+u2
u2
u1=
L1
di dt
M udi2=
dt
L2
di dt
M di dt
+
∴u=
L1
L2
2 M= di
dt
L di dt
i
L=L1+L2+2M — 等效电路
+
u
L
_
4
4.反接串联
i
+ + u1 L1
耦合电感电路的等效6种模型

耦合电感电路的等效6种模型
耦合电感电路的等效模型有以下6种:
1. 互感耦合模型:将耦合电感电路分解为两个互感元件(互感电感),通过互感系数来描述电感之间的耦合程度。
2. 理想变压器模型:将耦合电感电路看作是一个理想变压器,将互感耦合转化为变压器变比。
3. T模型:将耦合电感电路通过一根传输线分为两段,在传输线的中心位置连接一个串联电感,表示耦合电感。
4. π模型:将耦合电感电路通过一根传输线分为两段,在传输线的中心位置连接一个并联电感,表示耦合电感。
5. 串联模型:将耦合电感电路看作是一个串联电感,将多个电感元件串联连接。
6. 并联模型:将耦合电感电路看作是一个并联电感,将多个电感元件并联连接。
以上是耦合电感电路的常见等效模型,根据具体情况选择适合的模型进行分析和计算。
记得具体情况具体分析,如果需要更详细的解答,可以提供具体的电路图等信息。
§13-3 耦合电感的去耦等效电路
di1 di2 u1 = (La + Lb ) + Lb dt dt di1 di2 u2 = Lb + (Lb + Lc ) dt dt
令以上两式各系数分别相等,得到: 令以上两式各系数分别相等,得到:
L = La + Lb 1 L2 = Lb + Lc M = Lb
La = L M 1 由此解得: b 由此解得: L = M Lc = L2 M
郁 金 香
M(L2 M) M2 Lab = L1 M + = L1 M + L2 M L2
(13 17)
两端相连, 也可将耦合电感 b、c两端相连,所求得的等效电感与 、 两端相连 相同。 式(13-17)相同。 - 相同
所示单口网络的等效电路。 例13-4 试求图 - 试求图13-13(a)所示单口网络的等效电路。 所示单口网络的等效电路 解:先化简电路,将2 先化简电路 将 电阻合并到3 电阻合并到 电阻成为 5 。 将端接50mH电感的理 电感的理 将端接
名 称 1 3 5 7 9 耦合线圈的电压波形 耦合线圈的同名端 耦合线圈参数测量 铁心变压器的电路模型 铁心变压器的阻抗变换
时间 0:49 2:32 2:48 4:21 2:35 2 4 6 8
名
称
时间 2:04 1:20 3:37 4:01
同名端的实验确定 耦合线圈的实验 耦合线圈的反映阻抗 铁心变压器的输入阻抗
di1 di2 u1 = L1 M dt dt di1 di2 u2 = M + L2 dt dt
di1 di2 u1 = (La + Lb ) + Lb dt dt di1 di2 u2 = Lb + (Lb + Lc ) dt dt
多线圈耦合电感等效_概述及解释说明

多线圈耦合电感等效概述及解释说明引言是一篇长文的开端,通过简明扼要地介绍文章的主题、结构和目的,帮助读者对接下来的内容有一个整体的把握。
在本篇文章中,引言部分分为三个方面进行阐述:概述、文章结构以及目的。
1.1 概述多线圈耦合电感是电子领域中一个重要且广泛应用的概念。
它是指通过磁场耦合实现电感元件之间能量传输和信号传递的一种技术。
相比于单线圈电感,多线圈耦合电感能够提供更高的电感值,并具备更复杂的工作原理和更广泛的应用领域。
1.2 文章结构本文将分为五个部分进行阐述多线圈耦合电感等效模型及参数计算方法。
首先,在第二部分中,我们将详细介绍多线圈耦合电感的基本概念与原理,包括定义、工作原理以及应用领域。
在第三部分中,我们将探讨多线圈耦合电感等效模型及参数计算方法,主要包括串联和并联多线圈耦合电感等效模型以及参数计算方法,并举例进行实例分析。
接下来,在第四部分,将介绍多线圈耦合电感的设计原则和优化方法,这包括了设计要求以及实现优化的方法和策略,并通过实例验证与性能评估来验证。
最后,在第五部分中,我们将进行总结回顾,概括文章的主要内容,并展望未来研究方向。
1.3 目的本文旨在系统地介绍多线圈耦合电感等效模型及参数计算方法,展示其在电子领域中的重要性和广泛应用。
通过本文的阐述,读者可以对多线圈耦合电感有一个整体而清晰的认识,并了解其设计原则、优化方法以及相关参数计算。
希望本文能够为相关领域工作者提供指导和参考,促进多线圈耦合电感技术的广泛应用和进一步发展。
2. 多线圈耦合电感的基本概念与原理:2.1 多线圈耦合电感的定义:多线圈耦合电感是指由多个线圈相互耦合而形成的电感器件。
它由两个或多个线圈组成,其中有一个主要线圈和其他附属线圈通过磁场相互连接。
这种耦合可以通过将附属线圈绕在主要线圈周围或与主要线圈共享磁芯来实现。
2.2 多线圈耦合电感的工作原理:多线圈耦合电感利用了磁场的作用,当通过主要线圈施加交流电源时,会在主要线圈中产生变化的磁场。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.5.2 耦合电感的等效电路 1. 耦合电感的去耦等效电路 (1)串联电路去耦
图6-41(a )和图6-42(a )即为耦合电感的串联电路。
图6-41(a )中1L 和2L 的异名端联接在一起,该联接方式称为同向串联(顺接);图6-42(a )中1L 和2L 的同名端连接在一起,该连接方式称为反向串联(反接)。
1
+-
2
u
M L +i
M
L +1
+-
2
u
(a ) (b )
M
L L 2++-
+
u
(c )
图6-41 串联耦合电路的去耦
顺接时,支路的电压电流关系为
dt
di M L L dt di
M L dt
di M L dt di M
dt di L dt di M dt di L u )
2()
()()
()(21212
1
++=+++=+++=
根据等效变换的概念,该顺接耦合电感可用一个)(1M L +的电感和一个)(2M L +的电感相串联的电路等效替代,或用一个)2(21M L L ++的电感等效替代。
如图6-41(b )所示。
反接时,支路的电压电流关系为
dt
di M L L dt di M L dt
di M L dt di M
dt di L dt di M dt di L u )
2()()()
()(21212
1
-+=-+-=-+-=
根据等效变换的定义,该反接耦合电感可用一个)(1M L -的电感和一个)(2M L -的电感相串联的电路等效替代,或用一个)2(21M L L -+的电感等效替代。
如图6-42(b )所示。
1
+-
2
u
M L -i
M
L -1+-
2
u
(a ) (b )
M L L 2-+i
-
+
u
(c )
图6-42 串联耦合电路的去耦
(2)T 型电路去耦
图6-43(a )和图6-44(a )即为耦合电感的T 型连接电路,其中图6-43(a )中耦合电感的联接形式称为同侧联接,图6-44(a )的联接形式称为异侧联接。
T 型电路的等效去耦网络分别如图6-43(b )和图6-44(b )所示(证明从略)。
请特别注意等效变换前后O 点的位置。
(a ) (b )
图6-43 T 型电路的去耦
(a ) (b )
图6-44 T 型电路的去耦
2. 耦合电感的等效受控源电路
耦合电感上的互感电压是可以用电流控电压源CCVS 表示出来的,所以耦合电感的另一种等效电路就是含CCVS 的无互感电路。
图6-45(b )就是图6-45(a )所示的耦合电感的等效受控源电路。
(a ) (b ) 图6-45 耦合电感的等效受控源电路。
