2022-2023学年山西省太原市部分学校九年级上学期12月月考数学试卷
山西省太原市外国语学校2021-2022学年九年级上学期12月月考数学试卷(含答案解析)

山西省太原市外国语学校2021-2022学年九年级上学期12月月考数学试卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列关系式中,表示y 是x 的反比例函数的是()A .21y x =B .3x y =C .21y x=+D .3y x=2.如图所示的礼品盒的主视图是()A .B .C .D .3.已知ABC DEF :△△,相似比为1:2,且DEF 的面积为12,则ABC 的面积为()A .48B .48C .6D .34.如图,小树AB 在路灯O 的照射下形成投影BC .若树高AB=2m ,树影BC=3m ,树与路灯的水平距离BP=4.5m .则路灯的高度OP 为()A .3mB .4mC .4.5mD .5m5.如图,阴影部分是一个菱形剪去一个平行四边形后所剩下的,要想知道阴影部分的周长,需要测量线段()的长度.A .AB 与BC B .AB 与DE C .AFD .AB6.数学兴趣小组在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制了如图所示的频率分布散点图,则符合这一结果的试验可能是()A .抛掷一枚硬币,正面向上的概率B .抛掷一枚骰子,朝上一面的点数为3的倍数的概率C .从装有3个红球、2个黄球的袋子中,随机摸出1个球为红球的概率D .一副去掉大、小王的普通扑克牌洗匀后,从中任抽一张,牌的花色是红桃的概率7.《九章算术》是我国古代数学的经典著作,它的出现标志着中国古代数学形成了完整的体系,其“勾股”章中记载了一个数学问题:“今有户高多于广六尺,两隅相去适一丈,问户高、广各几何?”译文为:“已知有一扇矩形门的高比宽多6尺,门的对角线长为1丈(1丈=10尺),那么门的高和宽各是多少?”如果设门的宽为x 尺,则可列方程为()A .x 2+(x +6)2=102B .x 2+(x +6)2=12C .x 2+(x ﹣6)2=102D .x 2+(x ﹣6)2=128.如图,矩形ABCD 的对角线AC BD 、相交于点O ,过点O 的直线EF 分别交AD BC 、于点E F 、.若6,10AB BC ==则图中阴影部分的面积为()A .24B .30C .48D .609.在平面直角坐标系中,点()1,4A ,()2,3B -,()2,C m 分别在三个不同的象限,若反比例函数()0ky k x=≠的图像经过其中两点,则m 的值为()A .2B .3-C .2或3D .2-或3-10.如图,直线y x k =-+与反比例函数()0k y x x=>的图像交于A ,B 两点,则下列结论错误的是()A .OA OB=B .当A ,B 两点重合时,4k =C .当6k =时,OA =D .不存在这样的k 使得AOB 是等边三角形二、填空题11.反比例函数()0ky x x=<的图像如图所示,则k 的值可能是______.12.如图,正方形ABCD 中,OAC ODA ∠=∠,则AOD ∠=_____.13.如图,四边形OABC 和四边形BDEF 都是正方形,反比例函数my x=在第一象限的图像经过点E ,若两正方形的面积差为3,则m 的值为______.14.如图,OAB 与OCD 是以点O 为位似中心的位似图形,相似比为3:4,30AOB ∠=︒,OB AB =,若点B 的坐标是()3,0,则点D ,点C 的坐标分别是_______.15.如图,ABC 中,,,BD AB BD AC ⊥相交于点D ,4,2,1503AD AC AB ABC ==∠=︒,则点C 到AB 的距离为_____.三、解答题16.(1)解方程:()21x x -=;(2)如图,在ABC 中,AB AC =,点E ,F 在边BC 上,EAF B ∠=∠,求证:ABF ECA ∽△△.17.如图,在矩形ABCD 中,对角线AC 和BD 相交于点O ,过点B 作BE AC ⊥于点F ,点E 在BF 的延长线上,且ADE ADB ∠=∠.(1)求证:DE AC ∥.(2)若4AC =,F 是AO 的中点,求BC 的长.18.在创建全国卫生文明城市期间,小明同学收集到了4张外形一样的卡片,卡片上分别标有四种垃圾分类图标,它们分别为厨余垃圾(A )、可回收物(B )、其他垃圾(C )、有害垃圾(D ).他将卡片背面朝上,洗匀放好.(1)从中随机抽取一张,抽到的卡片上的图表是可回收物是.A .不可能事件;B .必然事件;C .随机事件(2)从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图法求抽到的两张卡片上的图表恰好都是抽对称图形的概率.19.如图,直线y =3x +3与x 轴交于点A ,与反比例函数()0ky x x=>的图像交于点B (1,m ).(1)求反比例函数的表达式.(2)若C 是反比例函数图像上一点,连接AC ,若45CAO ∠=︒,求直线BC 的表达式.20.阅读下列材料,并按要求完成相应的任务:清虚阁,位于山西省晋中市榆次老城中,俗称南阁,建成于明代成化五年(1469),是榆次区境内仅见的,也是晋中地区稀有的古代阁楼式建筑杰作,如图,某中学数学实践小组利用节假日时间到现场测量清虚阁AB 的高度.步骤一:在地面BC 上取E G 、两点,分别竖立高为2m 的标杆EF 和GH ,两标杆间隔23m ,并且清虚阁AB ,标杆EF 和GH 在同一竖直平面内,从标杆EF 后退2m 到D 处,从D 处观察A 点,,,A F D 三点成一线;步骤二:从标杆GH 后退4m 到C 处,从C 处观察A 点,,,A H C 三点也成一线.下面是某同学根据测量结果,计算清虚阁AB 的高度时的部分过程:解:∵,,AB BC EF BC GH BC ⊥⊥⊥,∴90,90ABD FED ABD HGC ∠=∠=︒∠=∠=︒,∴,AB FE AB GH ∥∥,∴,FED ABD HGC ABC ∆~∆∆~∆,∴,EF ED GH CGAB ED BE AB CG EG BE==+++,......任务:(1)请根据上面的思路,补充剩余的解答过程.(2)该小组在制定方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳,你认为其原因可能是什么?(写出一条即可)21.某面粉车间安装了粉尘检测仪,工人加工4h 后粉尘检测仪开始报警,工人立即停止加工并对车间进行自然通风除尘.如图,线段DE 表示工人加工时粉尘检测仪显示的数据()3ug /m y 与时间x (h )之间的函数关系(04x ≤≤),反比例函数()0ky x x=>对应曲线EF ,表示通风除尘期间粉尘检测仪显示的数据()3ug /m y 与时间x (h )之间的函数关系.根据图像解答下列问题:(1)求粉尘检测仪在工人加工前显示的数据.(2)当车间内粉尘指数在50~1003ug /m 之间时,室内空气质量为良,求该车间空气质量保持良的时间.22.感知∶(1)数学课上,老师给出了一个模型∶如图1,∠BAD =∠ACB =∠AED =90°,由∠1+∠+2+∠BAD =180°,∠2+∠D +∠AED =180°,可得∠1=∠D ;又因为∠ACB =∠AED =90°,可得△ABC ∽△DAE ,进而得到BCAC= .我们把这个数学模型称为“一线三等角”模型.应用∶(2)实战组受此模型的启发,将三等角变为非直角,如图2,在△ABC 中,点D 在边BC 上,并且DA=DE ,∠B =∠ADE =∠C .若BC =a ,AB=b ,求CE 的长度(用含a ,b 的代数式表示).拓展∶(3)创新组突发奇想,将此模型迁移到平行四边形中,如图3,在平行四边形ABCD 中,E 为边BC 上的一点,F 为边AB 上的一点.若∠DEF =∠B .求证∶AB ·FE =BE ·DE .23.如图,直线y x m =-+与反比例函数ky x=的图像相交于点()2,A n -,与x 轴交于点()2,0B .(1)求m 和k 的值.(2)点C 在x 轴的负半轴上,直线AC 与反比例函数ky x=的图像交于点D ,若D 是AC 的中点,求AOC 的面积.(3)若点P与点O关于直线AB对称,连接AP.①求点P的坐标;②若点M在反比例函数kyx的图像上,点N在x轴上,以点A,P,M,N为顶点的四边形能否为平行四边形?若能,直接写出点M的坐标;若不能,请说明理由.参考答案:1.D【分析】根据反比例函数定义:形如()=0ky k x≠的函数是反比例函数,即可得到答案.【详解】解:A 、21y x =,分母中的x 的指数是2,所以不是反比例函数,故本选项不符合题意;B 、3xy =是正比例函数,故本选项不符合题意;C 、21y x=+,没有加1才是反比例函数,故本选项不符合题意;D 、3y x=是反比例函数,故本选项符合题意;故选:D .【点睛】本题考查了反比例函数的定义,熟记正比例函数,反比例函数以及一次函数的定义是解题的关键,是基础题,难度不大.2.B【分析】找出从几何体的正面看所得到的图形即可.【详解】解:从礼品盒的正面看,可得图形:故选:B .【点睛】此题主要考查了简单几何体的三视图,关键是掌握主视图所看的位置.3.D【分析】根据相似三角形的面积比等于相似比的平方即可求解.【详解】解:∵ABC DEF :△△,相似比为1:2,∴ABC 与DEF 的面积比为1:4,∵DEF 的面积为12,∴ABC 的面积为3,故选:D .【点睛】本题考查了相似三角形的性质,掌握相似三角形的性质是解题的关键.4.D【分析】根据在同一灯光照射下任何物体的高度与其影子的比值不变建立等量关系即可求解.【详解】解:在同一灯光照射下任何物体的高度与其影子的比值不变:∵当树高AB=2m ,树影BC=3m ,且BP=4.5m ∴OP ABPC BC =,代入得:27.53OP =∴5OP =m 故选:D【点睛】本题考查利用相似三角形测高,掌握同一灯光照射下任何物体的高度与其影子的比值不变是解题关键.5.C【分析】如图,延长AB ,ED 交于点H ,证明BC DH =,CD BH =,再利用菱形的性质证明:阴影部分的周长4AB BC CD DE EF AF AF =+++++=,从而可得答案.【详解】解:如图,延长AB ,ED 交于点H ,四边形BCDH 是平行四边形,BC DH ∴=,CD BH =,四边形AFEH 是菱形,AF EF EH AH ∴===,∴阴影部分的周长4AB BC CD DE EF AF AF =+++++=,故需要测量AF 的长度,故选:C .【点睛】本题考查的是平行四边形的性质,菱形的性质,证明阴影部分的周长4AF =是解本题的关键.6.C【分析】根据统计图可知,试验结果在0.6附近波动,即其概率P ≈0.6,计算四个选项的概率,约为0.6者即为正确答案.【详解】解:A 、掷一枚硬币,出现正面朝上的概率为12,故此选项不符合题意;B 、抛掷一枚骰子,朝上一面的点数为3的倍数的概率为21=63,故此选项不符合题意;C .从装有3个红球、2个白球袋子中,随机摸出一球为红球的概率为33=3+25,故此选项符合题意;D .一副去掉大、小王的普通扑克牌洗匀后,从中任抽一张,牌的花色是红桃的概率为14,故此选项不符合题意;故选:C .【点睛】考查了利用频率估计概率的知识,解题的关键是能够分别求得每个选项的概率,然后求解.7.A【分析】直接利用勾股定理进而得出等式方程即可.【详解】解:设门的宽为x 尺,那么这个门的高为(x +6)尺,根据题意得方程:x 2+(x +6)2=102,故选:A .【点睛】此题主要考查了勾股定理的应用及由实际问题抽象出一元二次方程的知识,正确应用勾股定理是解题关键.8.B【分析】根据矩形的性质证明AOE COF △≌△,得出阴影部分面积等于矩形的面积的一半即可求解.【详解】解: 四边形ABCD 是矩形,OA OC AEO CFO ∴=∠=∠,;AOE COF ∴ ≌,AOE BOF COD COF BOF COD BCD S S S S S S S S ∴=++=++= 阴影;303012BCD S BC CD S ==⨯= 阴影,.故选:B .【点睛】本题考查了矩形的性质,掌握矩形的性质是解题的关键.9.B【分析】利用点过反比例函数图象,将点坐标代入求出反比例解析式,再求出m 即可.【详解】解:根据反比例函数图像性质,若k >0,则反比例函数图象过第一、三象限;若k <0,则反比例函数图象过第二、四象限.若点A (1,4)在反比例函数(0)k y k x=≠图象上,则4=1k ,解得k =4,反比例函数图象过第一、三象限.故点C 需在第三象限,与点C 横坐标为2矛盾,若点B (-2,3)在反比例函数(0)k y k x=≠图象上,则3=2k -,解得k =-6,反比例函数图象过第二、四象限.故点C 需在第四象限,将点C (2,m )代入反比例函数解析式6y x =得6=32m -=-,符合题意,综上,m 的值为-3.故选B .【点睛】本题考查了反比例函数图像性质,能熟练掌握反比例函数k 值影响图象所在象限是解题的关键.10.D 【分析】先联立联立y x k k y x =-+⎧⎪⎨=⎪⎩得到20x kx k -+=,设A 点坐标为(1x ,1x k -+),B 点坐标为(2x ,2x k -+),然后分别求出OA ,OB ,即可判断A ;根据A 、B 重合,则方程20x kx k -+=只有一个实数根,即()240k k ∆=--=,由此即可判断B ;把6k =代入222OA k k =-中即可判断C ;若△AOB 是等边三角形,则OA =AB ,然后求出AB 的长,令AB =OA ,求出k 的值,即可判断D .【详解】解:联立y x k k y x =-+⎧⎪⎨=⎪⎩得到20x kx k -+=,设A 点坐标为(1x ,1x k -+),B 点坐标为(2x ,2x k -+),∴()22222111122OA x x k x kx k =+-+=-+,()22222222222OB x x k x kx k =+-+=-+,∵A 、B 是直线与反比例函数的两个交点,∴2110x kx k -+=,2220x kx k -+=,∴211x kx k -=-,222x kx k -=-,∴2222OA k k OB =-=,∴OA OB =,故A 选项不符合题意;∵A 、B 重合,则方程20x kx k -+=只有一个实数根,∴()240k k ∆=--=,解得4k =或0k =(舍去),故B 选项不符合题意;当6k =时,222361224OA k k =-=-=,∴OA =C 选项不符合题意;若△AOB 是等边三角形,则OA =AB ,∵12x x k +=,12x x k=∴()()()2221212AB x x x k x k =-+-+--+⎡⎤⎣⎦,()2122x x =-()2121228x x x x =+-228k k =-,∴22282k k k k -=-,解得6k =或0k =(舍去),∴存在6k =,使得△AOB 是等边三角形,故D 选项符合题意;故选D【点睛】本题主要考查了反比例函数与一次函数综合,两点距离公式,等边三角形的性质,一元二次方程根于系数的关系,一元二次方程根的判别式等等,解题的关键在于能够熟练掌握相关知识进行求解.11.-2(答案不唯一)【分析】利用反比例函数的性质得到k <0,然后在此范围内取一个值即可.【详解】解:∵双曲线的一支分别位于第二象限,∴k <0,∴k 可取-2.故答案为-2(答案不唯一).【点睛】本题考查了反比例函数的性质:反比例函数y =k x k ≠0)的图象是双曲线;当k >0,双曲线的两支分别位于第一、第三象限,在每一象限内y 随x 的增大而减小;当k <0,双曲线的两支分别位于第二、第四象限,在每一象限内y 随x 的增大而增大.12.135︒##135度【分析】根据正方形的性质得出45DAC ∠=︒,根据已知条件可得45ODA DAO ∠+∠=︒,进而根据三角形内角和定理即可求解.【详解】解:∵四边形ABCD 是正方形,∴45DAC ∠=︒,∵OAC ODA ∠=∠,∴45ODA DAO OAC DAO DAC ∠+∠=∠+∠=∠=︒,∴()180********AOD ODA DAO ∠=︒-∠+∠=︒-︒=︒.故答案为:135︒.【点睛】本题考查了正方形的性质,三角形内角和定理,掌握正方形的性质是解题的关键.13.3【分析】设E 点坐标为(a ,b ),正方形OABC 的边长为s ,正方形BDEF 的边长为t ,根据图形可知s t b s t a+=⎧⎨-=⎩,再由两个正方形的面积的差值为3,得到223s t -=,即()()3s t s t +-=,由此求解即可.【详解】解:设E 点坐标为(a ,b ),正方形OABC 的边长为s ,正方形BDEF 的边长为t ,∴s t b s t a +=⎧⎨-=⎩,∵两个正方形的面积的差值为3,∴223m n -=,∴()()3s t s t +-=,∴3ab =,∵E 在反比例函数m y x=上,∴3m ab ==,故答案为:3.【点睛】本题主要考查了反比例函数比例系数的几何意义,平方差公式,解题的关键在于能够根据题意得到s t b s t a+=⎧⎨-=⎩.14.()()4,0,6,23【分析】分别过A C AE OB CF OB ⊥⊥、作,,根据已知条件求得点D 的坐标,进而解Rt CDF △,即可求解.【详解】解:分别过A C 、作AE OB CF OB ⊥⊥,,垂足分别为,E F ,∵30AOB ∠=︒,OB AB=∴AOB ∠=OAB ∠=30︒,60ABF ∠=︒∵OAB 与OCD 是以点O 为位似中心的位似图形相似比为34:,点B 的坐标为()3,0,∴()40D ,,则4DO CD ==,∴3sin 604232CF CD ︒=⋅=⨯=,2DF =故点C 的坐标是:(6,23).故答案为:()()4,0,6,23.【点睛】本题考查了位似图形的性质,坐标与图形,解直角三角形,数形结合是解题的关键.15.32【分析】过点C BD 作的垂线,交BD 的延长线于点E ,证明ABD CED ∽△△,根据已知条件求得32CE =,进而根据15090ABC ABD ∠=︒∠=︒,,得出60CBE ∠=︒,勾股定理即可求解.【详解】解:如图,过点C BD 作的垂线,交BD 的延长线于点E ,90E ∠=︒BD AB CE BD⊥⊥,Q AB ∴90CE ABD ∠=︒∥,,∴ABD CED∽△△AD AB BD CD CE DE==∴ 43AD AC =,∴43AD CD =243AB BD CE CE DE===∴32CE ∴=15090ABC ABD ∠=︒∠=︒,,Q 60CBE ∴∠=︒,∴32BE CE ==,∴C 到AB【点睛】本题考查了相似三角形的性质与判定,勾股定理,含30度角的直角三角形的性质,掌握以上知识是解题的关键.16.(1)11x =21x =;(2)见解析【分析】(1)先去括号,然后移项,最后利用开平方法解一元二次方程即可;(2)由三角形外角的性质可得AEC B BAE ∠=∠+∠,再由BAF EAF BAE ∠=∠+∠,EAF B ∠=∠即可得到AEC BAF ∠=∠,再由等腰三角形的性质得到B C ∠=∠,即可证明ABF ECA ∽△△.【详解】解:(1)()21x x -=整理得221x x -=.则22111x x -+=+,即()212x -=,∴1x -=∴11x =,21x =(2)证明:∵AEC B BAE ∠=∠+∠,BAF EAF BAE ∠=∠+∠,EAF B ∠=∠.∴AEC BAF ∠=∠,又∵AB AC =,∴B C ∠=∠.∴ABF ECA ∽△△.【点睛】本题主要考查了等腰三角形的性质,相似三角形的判定,解一元二次方程,三角形外角的性质等等,解题的关键在于能够熟练掌握相关知识.17.(1)见解析;(2)【分析】(1)由矩形的性质得OA OD =,即可得到ADO DAO ∠=∠,从而可以推出ADE DAO ∠=∠,由此即可证明;(2)由F 是AO 的中点,BF AC ⊥,得到AB OB =,则122AB OB OA AC ====,然后利用勾股定理求解即可.【详解】解:(1)证明:∵四边形ABCD 是矩形.∴OA OD =,∴ADO DAO ∠=∠,∵ADE ADB ∠=∠,∴ADE DAO ∠=∠,∴DE AC ∥;(2)∵F 是AO 的中点,BF AC ⊥,∴AB OB =,∵四边形ABCD 是矩形,∴122AB OB OA AC ====,∴BC ==.【点睛】本题主要考查了矩形的性质,勾股定理,等腰三角形的性质与判定,平行线的判定等等,解题的关键在于能够熟练掌握矩形的性质.18.(1)C ;(2)16.【分析】(1)随机事件是可能发生也可能不发生的事件;必然事件是一定会发生或一定不会发生的事件;由定义即可得出答案;直接得出答案;(2)根据题意先画树状图列出所有等可能的结果数,两张卡片恰好是“厨余垃圾(A )”和“有害垃圾(D )”的结果数为2,根据概率公式求解.【详解】解:(1)从中随机抽取一张,抽到的卡片上的图表可能是可回收物,也可能不是可回收物,故该事件是随机事件,故选C ;(2)画树状图如下:共有12中等可能的结果,抽到的两张卡片上的图标恰好都是轴对称图形的结果有2种,∴抽到的两张卡片上的图标恰好都是抽对称图形的概率为21126=【点睛】此题考查了用列表法或树状图法求概率,解题时要注意此题是放回试验还是不放回试验,用到的知识点为:概率=所求情况数与总情况数之比。
山西省太原市某校2021-2022学年-有答案-九年级上学期数学12月月考试卷

山西省太原市某校2021-2022学年九年级上学期数学12月月考试卷一、单选题(共10题;共16分)1. sin30∘的值为()A.√22B.12C.1D.√322. 在△ABC中,∠ACB=90∘,若AC=8,BC=6,则sinA的值为()A.53B.35C.45D.543. 在下列y关于x的函数中,一定是二次函数的是()A.y=x2B.y=3x+1C.y=ax2+bx+cD.y=1x4. 一个圆柱体钢块,正中央被挖去了一个长方体孔,其俯视图如图所示.则此圆柱体钢块的主视图可能是下列选项中的()A. B. C. D.5. 在平面直角坐标系中,把抛物y=x2−2x+5线,向右平移4个单位,再向下平移3个单位得到的抛物线的为()A.y=(x−5)2+4B.y=(x+3)2+8C.y=(x+3)2+1D.y=(x−5)2+16. 已知反比例函数y=6x,下列说法中正确的是()A.该函数的图象分布在第二、四象限B.点(−4,−3)在函数图象上C.y随x的增大而减小D.若点(−2,y1)和(−1,y2)在该函数图象上,则y1>y27. 如图,已知一次函数y=ax+b与反比例函数y=kx图象交于M、N两点,则不等式ax+b>kx解集为()A.x>2或−1<x<0B.−1<x<0C.−1<x<0或0<x<2D.x>28. 如图,ΔABC的三个项点均在格点上,则tanA的值为()A.12B.√55C.2D.2√559. 如图,在△ABC中,点D是AB边上的一点,∠ACD=∠B,AD=1,AC=2,若△ADC的面积为2,则△BCD的面积为()A.5B.6C.7D.810. 如图,将直角三角板ABC放在平面直角坐标系中,点A,B的坐标分别为(2,1),(7,1).将三角板ABC沿x轴正方向平移,点B的对应点B′刚好落在反比例函数y=10(x>0)的图像上,则点C平移的距离CC′=()xA.3B.5C.7D.10二、填空题(共8题;共6分)将二次函数y=x2−6x+11化为y=a(x−ℎ)2+k的形式为________,此抛物线的开口方向为:________,顶点坐标为:________.如图,正比例函数y=ax的图象与反比例函数y=k的图象相交于点A,B,若点A的x坐标为(−2, 3),则点B的坐标为________.大自然巧夺天工,一片小小树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP>PB),如果AP的长度为8cm,那么AB的长度是________cm.如图,点A是反比例函数y=k的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为xy轴上的一点,连接AC,BC.若△ABC的面积为4,则k的值是________.如图,在平面直角坐标系中,以原点O 为位似中心,相似比为3:1,将ΔABC 放大为ΔDEF ,已知C(1,√2),则点F 的坐标为________.已知点(−1,y 1),(2,y 2),(−3,y 2)都在函数y =3(x +1)2−m 的图象上,则y 1,y 2,y 3的大小关系是________.平面直角坐标系xOy 中,若抛物线y =ax 2上的两点A 、B 满足OA =OB ,且tan∠OAB =12,则称线段AB 为该抛物线的通径.那么抛物线y =12x 2的通径长为________.如图,正方形ABCD 的对角线AC ,BD 相交于点O ,AB =5√2,E 为OC 上一点,OE =2,连接BE ,过点A 作AF ⊥BE 于点F ,与BD 交于点G ,则EF 的长是________.三、解答题(共5题;共50分)计算:2sin45∘−32tan30∘cos30∘+sin 260∘(1)如图①,BE ,DF ,MN 是三根直立于地面的木杆在同一灯光下的影子,请画出第三根木杆,(画出示意图,不用写画法)(2)如图②,小明在阳光下利用标杆AB 测量校园内一棵小树CD 的高度,在同一时刻测得标杆的影长BE 为2m ,小树的影长落在地面上的部分DM 为3m ,落在墙上的部分MN为1m,若标杆AB的长为1.5m,求小树的高度CD.某气球内充满了一定质量的气体,当温度不变时,气球内的气压p(kpa)是气体体积v(m3)的反比例函数,其图象如图所示.(1)写出这一函数的表达式.(2)当气球体积1.5m3为时,气压是多少?(3)当气球内的气压大于144kpa时,气球会爆炸,为了安全起见,气球的体积应不小于多少?如图,学校某数学兴趣小组想测量操场对面旗杆AB的高度,他们在E处测得旗杆顶部A的仰角为65∘,再向旗杆相方方向走了4米达到D处,再继续沿着坡度为1:2的楼梯向上走了3√5米达到C处,在C处测得旗杆顶部A的仰角为35∘,求旗杆的高度AB为多少米?(结果精确到0.1米,参考数据:sin35∘≈0.6,cos35∘≈0.8,tan35∘≈0.7,sin65∘≈0.9,cos65∘≈0.4,tan65∘≈2.1).如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于点A,点B,与y轴交于点C,其中A(−4,0),B(2,0),C(0,−4).(1)求该抛物线的函数表达式:(2)若点D是y轴上的点,且以A,C,D为顶点的三角形与△ABC相似,求点D的坐标.(3)点P是抛物线y=ax2+bx+c的对称轴上的一点,点S是坐标平面内一点,若以A,C,P,S为顶点的四边形是菱形,请直接写出所有符合条件的点P的坐标.参考答案与试题解析山西省太原市某校2021-2022学年九年级上学期数学12月月考试卷一、单选题(共10题;共16分)1.【答案】B【考点】特殊角的三角函数值【解析】直接根据特殊角的三角函数值进行选择.【解答】解:sin30∘=12故答案为:B.2.【答案】B【考点】锐角三角函数的定义【解析】利用勾股定理求出AB的长,再利用正弦计算方法求解即可.【解答】在△ABC中,∠ACB=90∘,AC=8,BC=6AB=√AC2+BC2=√82+62=10sinA=BCAB=610=35故答案为:B.3.【答案】A【考点】二次函数的定义【解析】根据二次函数的定义逐项判定即可.【解答】解:A、是二次函数,故此选项符合题意;B、是一次函数,故此选项不合题意;C、当a=0时,不是二次函数,故此选项不合题意;D、是反比例函数,故此选项不合题意;故答案为:A.4.【答案】简单几何体的三视图【解析】根据三视图的定义求解即可.【解答】解:此圆柱体钢块的主视图可能是:故答案为:C.5.【答案】D【考点】二次函数图象与几何变换二次函数图象的平移规律轴对称图形【解析】先写出顶点式然后根据左加右减,上加下减求出结果即可.【解答】解:抛物线y=x2−2x+5化为顶点式得:y=(x−1)2+4向右平移4个单位,再向下平移3个单位得到的抛物线的为:y=(x−1−4)2+4−3,化简得:y=(x−5)2+1故答案为:D.6.【答案】D【考点】反比例函数的性质反比例函数的图象【解析】利用反比例函数的图形、性质与其系数的关系逐项判定即可.【解答】解:A、k=6>0,函数的图象在第一、三象限,故说法不符合题意;B、因为−3×(−4)=12≠6,所以点(−4,−3)不在函数图象上,故说法不符合题意;c、k=6>0,在每个象限内,y随着х的增大而减小,故说法不符合题意;D、k=6>0,在每个象限内,y随着х的增大而减小,因为−2<−1<0,则y1>y2,故说法符合题意;故答案为:D.7.【答案】A【考点】反比例函数与一次函数的综合【解析】根据函数图象写出一次函数图象在反比例函数图象上方部分的x的取值范围即可.【解答】.由图可知,x>2或−1<x<0时,ax+b>kxA【考点】解直角三角形【解析】连接格点BD,根据勾股定理可求得BD=CD的值,在直角三角形ABD中,根据tanA=BDAD可求解.【解答】解:如图所示,连接格点BD,根据勾股定理可得BD=CD=√2,BC=2∴ 2DC=90∘,故△ABD为在直角三角形,且AD=2√2tanA=BDAD=√22√2=12故答案为:A.9.【答案】B【考点】相似三角形的性质与判定【解析】根据∠ACD=∠B,∠A=∠A,证明△ACD−4ABC,再根据相似三角形的性质:面积之比等于相似之比的平方求解即可.【解答】解:∠ACD=∠B,∠A=∠A△ACD−△ABCS△ACD S△ABC =(ADAC)2=14S△ACD=2S△ABC=8S△BCD=S△ABC−S△ACD=6故答案为:B.10.【答案】A【考点】反比例函数图象上点的坐标特征平移的性质【解析】利用反比例函数求出B′的坐标,求出BB′的长度即可算出CC【解答】由平移可知B的纵坐标为1,,得B(10,1)代入y=10x平移的距离为BB′=10−7=3=CC故答案为:A.二、填空题(共8题;共6分)【答案】y=(x−3)2+2,向上,(3,2)【考点】二次函数的三种形式二次函数的性质待定系数法求二次函数解析式【解析】利用配方法将二次函数一般式转化为顶点式,再结合函数图象与系数的关系求解即可.【解答】解:y=λ2−6x+11=(x−3)2+2a=1>0:.抛物线开口向上,顶点坐标为(3,2)故答案是:y=(x−3)2+2;向上;③(3,2)【答案】(2, −3)【考点】反比例函数与一次函数的综合反比例函数图象的对称性【解析】反比例函数的图象是中心对称图形,则经过原点的直线的两个交点一定关于原点对称.【解答】解:根据题意,知点A与B关于原点对称,∵点A的坐标是(−2, 3),∴B点的坐标为(2, −3).故答案为:(2, −3).【答案】(4√5+4)【考点】黄金分割【解析】根据黄金分割点的性质可得AP=√5−12AB,计算求解即可.【解答】解:∵P为AB的黄金分割点(AP>PB)AP=√5−12ABAB=√5−1=√5−18=(4√5+4)c故答案是:(4√5+4)【答案】−8【考点】反比例函数系数k的几何意义【解析】连结OA,如图,利用三角形面积公式得到S△OAB=S△ABC=4,再根据反比例函数的比例系数k的几何意义得到12|k|=4,然后去绝对值即可得到满足条件的k的值.【解答】解:连接OA,如图.∵AB⊥x轴,∴OC // AB,∴S△OAB=S△ABC=4.而S△OAB=12|k|,∴12|k|=4.∵k<0,∴k=−8.故答案为:−8.【答案】(3,3√2)【考点】位似变换【解析】根据题意,由位似变换的性质,将C点的横坐标和纵坐标乘以3,即可得到答案.【解答】=3,解:由题意得:△ABC−△DEF,DFAC又.△ABC与△DEF位似,且两个图形在位似中心的同侧,C(1√2)F(3,3√2)故答案为:(3√2)【答案】y2>y3>y1【考点】二次函数图象上点的坐标特征一次函数图象上点的坐标特点反比例函数图象上点的坐标特征【解析】先求出二次函数的对称轴,将所有点放到对称轴的一边,再利用二次函数的性质求解即可.【解答】解:y=3(x+1)2−m;.图象的开口向上,对称轴是直线x=−1(2,y2)关于对称轴的对称点为(−4,y2)−4<−3<−1y2>y3>y1故答案为:y2>y3>y1【答案】2【考点】二次函数图象上点的坐标特征解直角三角形【解析】根据题意可以设出点A的坐标,从而可以求得通径的长.【解答】设点A的坐标为(−2a, a),点A在x轴的负半轴,×(−2a)2,则a=12,解得,a=0(舍去)或a=12∴点A的横坐标是−1,点B的横坐标是1,∴AB=1−(−1)=2,【答案】14√2929【考点】正方形的性质相似三角形的性质与判定【解析】根据正方形的性质求出AO=BO=CO=5,证明ABO−AF,得到EFOE =AEBE,求解即可.【解答】解::四边形ABCD是正方形,AB=5√2∠AOB=90∘OA=OB=OC=OD2OA2=AB2AO=BO=CO=5AF⊥BE∠EBO=∠EAF△EBO−△EAF,即EFOE =AEBEOE=2,OB=OA=5 BE=√29,AE=7∴EE2=√29EF=14√2929故答案为:14√2929三、解答题(共5题;共50分)【答案】解:原式=2×√22−32×√33×√32+(√32)2=√2−34+34=√2【考点】特殊角的三角函数值【解析】利用特殊角的三角函数值化简,再计算即可.【解答】此题暂无解答【答案】解:连接EA与FC相交于一点,连接该点与点N,过点M作MP垂直于这条直线于点P,如图,PM为第三根木杆.解:解:由题意可知,MNMP =ABBE.即1MP =1.52.解得,MP=43,由CDDP =ABBE,得CD 3+43=1.52.解得CD=3.25.答:小树的高度CD为3.25m.【考点】中心投影相似三角形的应用作图-相似变换【解析】(1)连接EA,FC,延长EA,FC交于点S,连接SN,过点M作PM⊥MN加SN于点P,即可求出点P;(2)作直线CN交DM于P,根据物长与影长成正比,构建方程求解即可.【解答】此题暂无解答【答案】解:(1)设P与V的函数关系式为P=kv,则k0.8=120,解得k=96,∴函数关系式为P=96V;(2)当气球内气体的体积是1.5m3时,P=961.5=64,∴气球内气体的气压是64kPa.(3)当P>144KPa时,气球将爆炸,∴P≤144,即96v≤144,解得V≥1.5(m3).故为了安全起见,气体的体积应不小于1.5(m3).【考点】反比例函数的应用待定系数法求反比例函数解析式【解析】(1)设函数解析式为P=kv,把点(0.8, 120)的坐标代入函数解析式求出k值,即可求出函数关系式;(2)把V=1.5代入求得的函数关系式即可求出P值;≤144,解不等式即可.(3)依题意P≤144,即96v【解答】,解:(1)设P与V的函数关系式为P=kv=120,则k0.8解得k=96,∴函数关系式为P=96;V(2)当气球内气体的体积是1.5m3时,=64,P=961.5∴气球内气体的气压是64kPa.(3)当P>144KPa时,气球将爆炸,≤144,∴P≤144,即96v解得V≥1.5(m3).故为了安全起见,气体的体积应不小于1.5(m3).【答案】解:如图:作CG⊥AB于G,DH⊥CG于H,则HG=DB,BG=DH,∵ 楼梯CD的坡度为1:2,CD=3√5,∴ BG=DH=3,CH=6,=tan35∘≈0.7,在Rt△ACG中,∠ACG=35∘,tan∠ACG=AGCG∴ AG≈0.7CG,∴ AB=AG+BG=0.7CG+3,∵ DB=HG=CG−CH=CG−6,∴ EB=DB−DE=CG−6−4=CG−10,=tan65∘≈2.1,在Rt△AEB中,∠AEB=65∘,tan∠AEB=ABEB∴ AB=2.1EB,∴ 0.7CG+3=2.1(CG−10),解得:CG=17.14,∴ AB=0.7×17.14+3=15.0,即旗杆的高度AB约为15.0米.【考点】解直角三角形的应用-仰角俯角问题【解析】作CG⊥AB子=G,DH⊥CG+H,则HG=DB,BG=DH,然后求出BG=DH= 3,CH=6,在RtΔAC中解直角三角形可得AG,然后根据线段的和差计算即可.【解答】此题暂无解答【答案】解:∵A(−4, 0),B(2, 0),设抛物线解析式为y=a(x+4)(x−2),∵ 抛物线过C(0, −4)∴−8a=−4,∴ a=12,∴ 此抛物线解析式为y=12x2+x−4解:∵A(−4, 0),B(2, 0),C(0, −4)∴ OA=OC=4,BO=2,∴ AB=6∴ △ACO为等腰直角三角形①当△ABC∽△CAD时则CDAC =ACAB∴4√2=4√26,∴ CD=163∴ OD=CD−OC=163−4=43∴D1(0, 4 3 )②当△ABC∽△CDA时则CDAB =ACAC∴CD6=√24√2,∴ CD=6∴ OD=CD−OC=6−4=2∴D2(0, 2)解:∵抛物线对称轴为直线x=−1,设点P(−1, y),∵A(−4, 0),C(0, −4),AP2=(−1+4)2+y2=y2+9,CP2=(0+1)2+(y+4)2=(y+4)2+1 AC2=(0+4)2+(0+4)2=32①若AP=CP,则y2+9=(y+ 4)2+1,解得y=−1,∴P1(−1, −1),②若AP=AC,则y2+9=32,解得:y1=√23,y2=−√23,∴P2(−1, √23),P3(−1, −√23)③若CP=AC,则(y+ 4)2+1=32,解得:y1=−4+√31,y2=−4−√31,∴P4(−1, −4+√31),P5(−1, −4−√31)P1(−1, −1),P2(−1, √23),P3(−1, −√23),P4(−1, −4+√31),P5(−1, −4−√31)【考点】待定系数法求二次函数解析式相似三角形的性质与判定【解析】(1)设二次函数为交点式,再将点C代入解析式求解即可;(2)分两种情况讨论:①当△ABC−△CAD时;②当△ABC−△CDA时,求点D的坐标即可;(3)根据菱形是四边都相等的平行四边形,分情况讨论即可.【解答】此题暂无解答。
2023-2024学年山西省太原市迎泽区五育中学九年级(上)月考数学试卷(12月份)+答案解析

一、选择题:本题共9小题,每小题3分,共27分。
在每小题给出的选项中,只有一项是符合题目要求2023-2024学年山西省太原市迎泽区五育中学九年级(上)月考数学试卷(12月份)的。
1.的值是( )A. B.C.D.2.二次函数的顶点坐标是( )A. B.C.D. 3.如果是锐角,且,那么( )A. B. C.D.4.抛物线过,两点,那么抛物线对称轴为( )A. 直线B. y 轴C. 直线D. 直线5.在平面直角坐标系中,将抛物线先向上平移3个单位长度,再向左平移2个单位长度,所得的抛物线的解析式是( )A.B.C.D.6.如图所示,过y 轴正半轴上的任意一点P ,作x 轴的平行线,分别与反比例函数和的图象交于点A 和点B ,若点C 是x 轴上任意一点,连接AC ,BC ,则的面积为( )A. 6B. 7C. 8D. 147.反比例函数的图象在第二、四象限,点、、是图象上的三点,则,,的大小关系是( )A.B.C.D.8.如图所示,网格中的每个小正方形的边长都是1,的顶点都在交点处,则的正弦值为( )A.B.C.D.9.已知二次函数的图象如图所示,则下列结论正确的是( )A.B.C.D.二、填空题:本题共6小题,每小题3分,共18分。
10.如图,在平面直角坐标系中,矩形ABCD的顶点A,C分别在x轴,y轴的正半轴上,点,,若反比例函数的图象经过点B,则k的值为______.11.在中,,,,则的值是______.12.小明在某次投篮中刚好把球打到篮板的点D处后进球.已知小明与篮框内的距离米,眼镜与底面的距离米,视线AD与水平线的夹角为,已知,则点D到底面的距离CD是______米.13.已知抛物线与x轴交于A,B两点,点A的坐标为,抛物线的对称轴为直线,则线段AB的长为______.14.如图所示,抛物线与x轴交于A,B两点,与y轴交于点C,M为第一象限抛物线上一点,且,则点M的坐标为______.15.如图,矩形ABCD中,点E,F分别在AD,BC上,且,,连接EF,将矩形ABCD沿EF折叠,点A恰好落在BC边上的点G处,则的值为______.三、解答题:本题共8小题,共64分。
山西省太原 九年级(上)月考数学试卷(12月份)
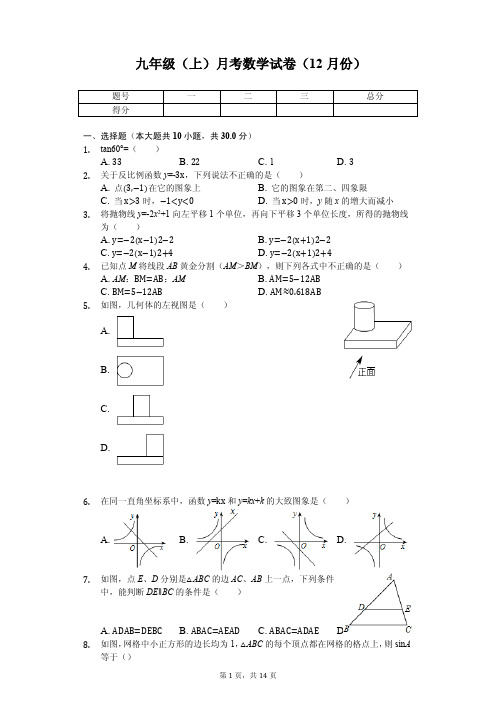
15. 如图,DE 是△ABC 的中位线,F 是 DE 的中点,CF 的延 长线交 AB 于点 G,若△CEF 的面积为 18cm2,则 S△DGF 的值为______cm2.
第 2 页,共 14 页
三、解答题(本大题共 7 小题,共 56.0 分) 16. 计算
(1)(-2)2⋅sin60°-(12)-1×12 (2)(-5)0+48cos230°-(22)2
交于点 O,若 S△AOB:S△DOE=25:9,则 CE:BC 等于( )
A. 2:5
B. 3:5
C. 16:25
10. 如图,二次函数 y=ax2+bx+c(a≠0)的图象与 x 轴 交于 A、B 两点,与 y 轴交于点 C,且对称轴为直
线 x=1,点 B 的坐标为(-1,0).则下面的五个结
17. 在如图的方格中,△OAB 的顶点坐标分别为 O(0,0)、A(-2,-1)、B(-1,-3), △O1A1B1 与△OAB 是关于点 P 为位似中心的位似图形. (1)在图中标出位似中心 P 的位置,并写出点 P 的坐标及△O1A1B1 与△OAB 的相 似比; (2)以原点 O 为位似中心,在 y 轴的左侧画出△OAB 的一个位似△OA2B2,使它与 △OAB 的位似比为 2:1,并写出点 B 的对应点 B2 的坐标.
A. ADAB=DEBC B. ABAC=AEAD C. ABAC=ADAE D. ACAE=ADAB
8. 如图,网格中小正方形的边长均为 1,△ABC 的每个顶点都在网格的格点上,则 sinA 等于()
第 1 页,共 14 页
A. 23
B. 55
C. 255
D.
12 9. 如图,在菱形 ABCD 中,E 为 CD 上一点,连接 AE、BD,
山西省2022版九年级上学期数学12月月考试卷(I)卷

山西省 2022 版九年级上学期数学 12 月月考试卷(I)卷姓名:________班级:________成绩:________一、 单选题 (共 10 题;共 20 分)1. (2 分) (2020 九上·江阴月考) 如果,则下列各式中不正确的是( )A.B.C.D.2. (2 分) (2017 九上·武昌期中) 把抛物线 y=﹣ 解析式为( )x2 向下平移 3 个单位长度再向左平移 2 个单位长度的A . y=﹣ (x+2)2+3B . y=﹣ (x+2)2﹣3C . y=﹣ (x+3)2﹣2D . y=﹣ (x﹣3)2+2 3. (2 分) (2016 九上·平潭期中) 如图,AB 是⊙O 的直径, 数是( ),∠COD=32°,则∠AEO 的度A . 48°B . 51°C . 56°D . 58°4. (2 分) 如图是一些卡片,它们的背面都一样,先将它们背面朝上,从中任意摸一张卡片,则摸到奇数卡片的概率是( )第 1 页 共 22 页A.B.C.D. 5. (2 分) 下列条件,不能判定△ABC 与△DEF 相似的是( )A . ∠C=∠F=,∠A=,∠D=B . ∠C=∠F=,AB=10,BC=6,DE=15,EF=9C . ∠C=∠F=,D . ∠B=∠E=,6. (2 分) (2018 九上·绍兴期中) 已知二次函数 y=ax2+bx+c 的图象如图所示,有以下结论:①a+b+c<0;②a-b+c>1;③abc>0;④4a-2b+c<0;⑤c-a>1.其中正确的结论的个数是( )A . 2个B . 3个C . 4个D . 5个7. (2 分) (2020 八下·侯马月考) 在平面直角坐标系中,正方形的对称中心为坐标原点,其中点 的坐标为,点按逆时针顺序排列,则点 的坐标为( )A.B.第 2 页 共 22 页C.D.8. (2 分) (2019·太仓模拟) 在平面直角坐标系中,直线 经过点,且直线轴.若直线 与二次函数的图像交于 , 两点,与二次函数的图像交于 , 两点,其中 , 为整数.若,.则的值为( )A.9B . 11C . 16D . 249. (2 分) (2016 七下·盐城开学考) 一个由小菱形组成的装饰链,断去了一部分,剩下部分如图所示,则断去部分的小菱形的个数可能是( )A . 2016 个B . 2015 个C . 2014 个D . 2013 个10. (2 分) (2018·沙湾模拟) 二次函数值是( )A.B.C.D.二、 填空题 (共 6 题;共 7 分)11. (1 分) (2020 九上·株洲期中) 如图,,,则的长为________.在的范围内有最小值 ,则 的,点 在 上, 与 交于点 ,12. (2 分) (2020 九上·讷河月考) 将二次函数第 3 页 共 22 页,化为的形式,结果为________,该函数图象不经过第________象限. 13. (1 分) (2019 九上·滕州期中) 已知线段 AB 的长为 2cm , 点 P 是线段 AB 的黄金分割点(AP>BP),那么线段 PB 的长等于________(结果保留根号). 14. (1 分) 如图,长方形 OABC 的边 OC、OA 分别在 x 轴、y 轴上,点 B 的坐标为( ,1)点 D 是 AB 边上一个动点(与点 A 不重合),沿 OD 将△OAD 对折后,点 A 落到点 P 处,并满足△PCB 是等腰三角形,则 P 点坐标为 ________.15. (1 分) (2020 九上·温州月考) 不透明的袋中装有 2 个红球和 3 个黑球,它们除颜色外没有任何其他区 别,小红搅匀后从中随机摸出 1 个球,摸出红球的概率是________.16. (1 分) (2021 九下·东坡开学考) 如图,正方形 ABCD 中,AB=4,E 为 BC 中点,两个动点 M 和 N 分别在 边 CD 和 AD 上运动且 MN=2,若△ABE 与以 D、M、N 为顶点的三角形相似,则 DM=________.三、 解答题 (共 7 题;共 76 分)17. (10 分) (2017·慈溪模拟) 如图所示,在⊙O 中, = ,弦 AB 与弦 AC 交于点 A,弦 CD 与 AB 交于点 F,连接 BC.(1) 求证:AC2=AB•AF; (2) 若⊙O 的半径长为 2cm,∠B=60°,求图中阴影部分面积. 18. (5 分) 如图,AD 是 Rt△ABC 斜边上的高,若 AB=4cm,BC=10cm,求 BD 的长.第 4 页 共 22 页19. (15 分) 如图,抛物线 y=ax2+bx﹣1(a≠0)经过 A(﹣1,0),B(2,0)两点,与 y 轴交于点 C.(1) 求抛物线的解析式及顶点 D 的坐标; (2) 点 P 在抛物线的对称轴上,当△ACP 的周长最小时,求出点 P 的坐标; (3) 若点 M 为抛物线第四象限内一点,连接 BC、CM、BM,求当△BCM 的面积最大时点 M 的坐标. 20. (6 分) (2019·扬州) 只有 1 和它本身两个因数且大于 1 的正整数叫做素数.我国数学家陈景润哥德巴赫 猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于 2 的偶数都表示为两个素数的和”.如 20=3+17. (1) 从 7、11、19、23 这 4 个素数中随机抽取一个,则抽到的数是 7 的概率是________; (2) 从 7、11、19、23 这 4 个素数中随机抽取 1 个数,再从余下的 3 个数中随机抽取 1 个数,用画树状图或 列表的方法,求抽到的两个素数之和等于 30 的概率. 21. (10 分) 如图 (1),已知△ABC 是等边三角形,以 BC 为直径的⊙O 交 AB、AC 于 D、E.求证:(1) △DOE 是等边三角形.(2) 如图(2),若∠A=60°,AB≠AC , 则(1)中结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.22. (15 分) (2019 九上·崇明期末) 如图,在平面直角坐标系 xOy 中,二次函数(a、b都是常数,且 a<0)的图像与 x 轴交于点、,顶点为点 C.第 5 页 共 22 页(1) 求这个二次函数的解析式及点 C 的坐标;(2) 过点 B 的直线交抛物线的对称轴于点 D , 联结 BC , 求∠CBD 的余切值;(3) 点 P 为抛物线上一个动点,当∠PBA=∠CBD 时,求点 P 的坐标.23. (15 分) (2020 九上·六安期末) 如图,直线 y= x+ 与 x 轴交于点 A,与 y 轴交于点 C,以 AC为直径作⊙M,点 D 是劣弧 AO 上一动点(D 点与 A,C 不重合).抛物线 y=- 于另一点 B,x²+bx+c 经过点 A、C,与 x 轴交(1) 求抛物线的解析式及点 B 的坐标; (2) 在抛物线的对称轴上是否存在一点 P,是︱PA—PC︱的值最大;若存在,求出点 P 的坐标;若不存在, 请说明理由. (3) 连 CD 交 AO 于点 F,延长 CD 至 G,使 FG=2,试探究当点 D 运动到何处时,直线 GA 与⊙M 相切,并请说 明理由.第 6 页 共 22 页一、 单选题 (共 10 题;共 20 分)答案:1-1、 考点:参考答案解析: 答案:2-1、 考点: 解析:答案:3-1、 考点: 解析:第 7 页 共 22 页答案:4-1、 考点:解析: 答案:5-1、 考点: 解析:答案:6-1、 考点: 解析:第 8 页 共 22 页答案:7-1、 考点:解析: 答案:8-1、 考点: 解析:第 9 页 共 22 页答案:9-1、 考点: 解析:答案:10-1、 考点: 解析:第 10 页 共 22 页二、填空题 (共6题;共7分)答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共7题;共76分)答案:17-1、答案:17-2、考点:解析:答案:18-1、考点:解析:答案:19-1、答案:19-2、答案:19-3、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、答案:21-2、考点:解析:答案:22-1、答案:22-2、答案:22-3、考点:解析:答案:23-1、答案:23-2、答案:23-3、考点:解析:。
2022-2023年山西省某校初三(上)月考数学试卷

2022-2023年山西省某校初三(上)月考数学试卷一、选择题1. 一元二次方程2x 2−3x −1=0的二次项系数是2,则一次项系数是( ) A.3 B.−3 C.1 D.−12. 一元二次方程x 2+3x −1=0的解的情况是( ) A.没有实数根B.有两个不相等的实数根C.有两个相等的实数根D.只有一个根3. 关于x 的方程(a −1)x 2+√a +1x +2=0是一元二次方程,则a 的取值范围是( ) A.a ≠1 B.a ≥−1且a ≠1 C.a >−1且a ≠1 D.a ≠±14. 已知关于x 的一元二次方程kx 2−2x +3=0有两个不相等的实数根,则k 的取值范围是( ) A.k <13且k ≠0B.k >−13C.k >−13且k ≠0D.k <135. 一个三角形的两边长分别为2和6,第三边是方程x 2−8x +15=0的一根,则这个三角形的周长为( ) A.5 B.3或5C.13D.11或136. 二次函数y =2(x +2)2−1的图象是( )A.B.C. D.7. 在一幅长80cm ,宽50cm 的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm 2,设金色纸边的宽为xcm ,那么x 满足的方程是( )A.x 2+65x −350=0B.x 2+130x −1400=0C.x 2−130x −1400=0D.x 2−65x −350=08. 同一坐标系中,抛物线y =(x −a)2与直线y =a +ax 的图象可能是( )A. B.C.D.9. 2021年10月16日晚,大同南城墙关城流光溢彩、星光璀璨,第六届成龙国际动作电影周入城仪式暨闭幕式隆重举行.自从2018年电影频道“星光行动”从黄花地迈出了第一步,成龙等中国电影人就一直共同见证参与着“小黄花成为大产业”的历程.据统计,2019年∼2021年之间,我市黄花种植面积从22万亩增至26.5万亩.设黄花种植面积年平均增长率为x ,则由题意所列方程正确的是( ) A.22(1+x%)2=26.5 B.22(1+x )2=26.5C.22(1+x )+22(1+x )2=26.5D.22+22(1+x )+22(1+x )2=26.510. 如图,是由三个边长分别为6,9,x 的正方形所组成的图形,若直线AB 将它分成面积相等的两部分,则x 的值是( )A.1或9B.3或5C.4或6D.3或6二、填空题抛物线y=12(x+1)2的顶点坐标为________已知x=1是方程x2+bx−2=0的一个根,则方程的另一个根是________.定义新运算®:对于任意实数a、b都有:a®b=a2+ab,如果3®4=32+3×4=9+12=21,那么方程x®2=0的解为________.九年级学生在毕业前夕,某班每名同学都为其他同学写一段毕业感言,全班共写了2256段毕业感言,如果该班有x名同学,根据题意列出方程为________.设α,β是一元二次方程x2+3x−7=0的两个根,则α2+5α+2β=________.三、解答题解方程:(1)5x2=3x;(2)x2−5x−6=0;(3)(x−2)(x−5)=−1;(4)4x(2x+1)=3(2x+1);已知关于x的方程x2+ax+a−2=0.(1)当该方程的一个根为1时,求a的值及该方程的另一个根;(2)求证:不论a取任何实数,该方程都有两个不相等的实数根.某商店购进一批小玩具,每个成本价为20元,经调查发现售价为32元时,每天可售出20个,若售价每增加5元,每天销售量减少2个;售价每减少5元,每天销售量增加2个,商店同一天内售价保持不变.(1)若售价增加x元,则销售量是________个(用含x的代数式表示);(2)某日商店销售该玩具的利润为384元,求当天的售价是多少元?(利润=售价-进价)如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1, −4).(1)求二次函数的图象与x轴的交点A,B的坐标;(2)在二次函数的图象上是否存在点P,使S△PAB=54S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.(1)当售价为22万元/辆时,求平均每周的销售利润.(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.如图,有一矩形空地,一边是长为20米的墙,另三边由一根长为34米的铁丝围成,且与墙平行的一边有个1米宽的小门.已知矩形空地的面积是125平方米,求矩形空地的长和宽.我们知道,解一元二次方程,可以把它转化为两个一元一次方程来解,其实用“转化”的数学思想,我们还可以解一些新的方程,例如一元三次方程x3+x2−2x=0可以通过因式分解把它转化为x(x2+x−2)=0,通过解方程x=0和x2+x−2=0,可得方程x3+x2−2x=0的解.(1)方程x3+x2−2x=0的解是x1=0,x2=________,x3=________.(2)用“转化”的思想求方程√2x+3=x的解.(3)试直接写出方程组{x2−4y2=0,x+y=1的解.随着新冠病毒在全世界蔓延,口罩成为紧缺物资,甲、乙两家工厂积极响应政府号召,准备跨界投资生产口罩.根据市场调查,甲、乙两家工厂计划每天各生产6万片口罩,但由于转型条件不同,其生产的成本不一样,甲工厂计划每生产1万片口罩的成本为0.6万元,乙工厂计划每生产1万片口罩的成本为0.8万元.(1)按照计划,甲、乙两家工厂共生产2000万片口罩,且甲工厂生产口罩的总成本不高于乙工厂生产口罩,求甲工厂最多可生产多少万片的口罩?的总成本的34(2)实际生产时,甲工厂完全按计划执行,但乙工厂的生产情况发生了一些变化.乙工厂实际每天比计划少生产0.5m万片口罩,每生产1万片口罩的成本比计划多0.2m万元,最终乙工厂实际每天生产口罩的成本比计划多1.6万元,求m的值.参考答案与试题解析2022-2023年山西省某校初三(上)月考数学试卷一、选择题 1. 【答案】 B【考点】一元二次方程的一般形式 【解析】 此题暂无解析 【解答】解:由题意可知,该一元二次方程的一次项系数为:−3. 故选B . 2. 【答案】 B【考点】 根的判别式 【解析】由题意计算b 2−4ac 的值,根据一元二次方程的根的判别式”①当b2−4a >0时,方程有两个不相等的实数根;②当b2−4c =0时,方程有两个相等的实数根;③当b2−4a <0时,方程没有实数根”即可判断求解. 【解答】解:∵ Δ=b 2−4ac =9−(−4)=13>0, ∴ 方程有两个不相等的实数根. 故选B . 3. 【答案】 B【考点】一元二次方程的定义 二次根式有意义的条件 【解析】根据一元二次方程的一般形式是ax 2+bx +c =0(且a ≠0),以及二次根式有意义的条件是:被开方数是非负数,即可求解. 【解答】解:根据题意得:{a −1≠0,a +1≥0,解得:a ≥−1且a ≠1. 故选B . 4.【答案】 A【考点】 根的判别式一元二次方程的定义 【解析】要使一元二次方程有两个不相等的实数根,判别式必须大于0,得到k 的取值范围,因为方程是一元二次方程,所以k 不为0. 【解答】解:∵ 关于x 的一元二次方程kx 2−2x +3=0有两个不相等的实数根, ∴ △=4−12k >0,且k ≠0 ∴ k <13且k ≠0, 故选A . 5. 【答案】 C【考点】解一元二次方程-因式分解法 三角形三边关系 【解析】利用因式分解法求出方程的解确定出第三边,即可求出周长. 【解答】解:方程x 2−8x +15=0,分解因式得:(x −3)(x −5)=0, 解得:x =3或x =5,当x =3时,三角形三边分别为2,3,6,不能构成三角形,舍去; 当x =5时,三角形三边分别为2,5,6,周长为2+5+6=13. 故选C . 6. 【答案】 C【考点】二次函数的图象 【解析】先根据解析式确定抛物线的顶点坐标、对称轴,然后对图象进行讨论选择. 【解答】解:∵ a =2>0,∴ 抛物线开口方向向上;∵ 二次函数解析式为y =2(x +2)2−1, ∴ 顶点坐标为(−2, −1),对称轴x =−2. 故选C . 7.【答案】A【考点】一元二次方程的应用——几何图形面积问题由实际问题抽象出一元二次方程【解析】此题暂无解析【解答】解:依题意得:(80+2x)(50+2x)=5400,即4000+260x+4x2=5400,化简为:4x2+260x−1400=0,即x2+65x−350=0.故选A.8.【答案】D【考点】二次函数的图象一次函数的图象【解析】可先根据一次函数的图象判断a、b的符号,再判断二次函数图象与实际是否相符,判断正误.【解答】解:A,由一次函数y=a+ax的图象可得:a<0或a>0,此时二次函数y=(x−a)2的顶点(a, 0),a<0,矛盾,故错误;B,由一次函数y=a+ax的图象可得:a<0,此时二次函数y=(x−a)2的顶点(a, 0),a>0,矛盾,故错误;C,由一次函数y=a+ax的图象可得:a<0或a>0,此时二次函数y=(x−a)2的顶点(a, 0),a<0,矛盾,故错误;D,由一次函数y=a+ax的图象可得:a>0,此时二次函数y=(x−a)2的顶点(a, 0),a>0,故正确.故选D.9.【答案】B【考点】由实际问题抽象出一元二次方程一元二次方程的应用——增长率问题【解析】此题暂无解析【解答】B10. 【答案】D【考点】正方形的性质面积相等问题一元二次方程的应用——几何图形面积问题【解析】根据题意列方程,即可得到结论.【解答】解:如图,∵若直线AB将它分成面积相等的两部分,∴12×(6+9+x)×9−x×(9−x)=12×(62+92+x2),解得x=3,或x=6.故选D.二、填空题【答案】(−1, 0)【考点】二次函数的性质二次函数图象上点的坐标特征二次函数的三种形式【解析】直接根据抛物线的解析式写出顶点坐标即可.【解答】解:∵抛物线y=12(x+1)2,∴顶点坐标为(−1,0),故答案为:(−1,0).【答案】x=−2【考点】根与系数的关系【解析】根据根与系数的关系得出x1x2=ca=−2,即可得出另一根的值.【解答】解:∵x=1是方程x2+bx−2=0的一个根,∴x1x2=ca=−2,∴1×x2=−2,则方程的另一个根是:x=−2,故答案为:x=−2.【答案】x1=0,x2=−2【考点】解一元二次方程-因式分解法定义新符号【解析】根据新定义得到x2+2x=0,然后利用因式分解法解方程即可.【解答】解:方程x®2=0化为x2+2x=0,则x(x+2)=0,所以x1=0,x2=−2.故答案为:x1=0,x2=−2.【答案】(x−1)x=2256【考点】一元二次方程的应用——其他问题【解析】根据题意得:每人要写(x−1)条毕业感言,有x个人,然后根据题意可列出方程.【解答】根据题意得:每人要写(x−1)条毕业感言,有x个人,…全班共写:(x−1)x=2256故答案为:(x−1)x=2256【答案】1【考点】根与系数的关系【解析】此题暂无解析【解答】1三、解答题【答案】解:(1)x1=0,x2=35.(2)x1=6,x2=−1.(3)x1=(7+√5)2,x2=(7−√5)2.(4)x1=34,x2=−12.【考点】解一元二次方程-因式分解法解一元二次方程-配方法解一元二次方程-直接开平方法解一元二次方程-公式法【解析】此题暂无解析【解答】解:(1)x1=0,x2=35.(2)x1=6,x2=−1.(3)x1=(7+√5)2,x2=(7−√5)2.(4)x1=34,x2=−12.【答案】解:(1)设方程的另一个根为x,则由根与系数的关系得:x+1=−a,x⋅1=a−2,解得:x=−32,a=12,即a=12,方程的另一个根为−32;(2)证明:∵Δ=a2−4(a−2)=a2−4a+8=a2−4a+4+4=(a−2)2+4>0,∴不论a取任何实数,该方程都有两个不相等的实数根.【考点】根与系数的关系根的判别式【解析】(1)设方程的另一个根为x,则由根与系数的关系得:x+1=−a,x⋅1=a−2,求出即可;(2)写出根的判别式,配方后得到完全平方式,进行解答.【解答】(1)解:设方程的另一个根为x,则由根与系数的关系得:x+1=−a,x⋅1=a−2,解得:x =−32,a =12,即a =12,方程的另一个根为−32;(2)证明:∵ Δ=a 2−4(a −2)=a 2−4a +8=a 2−4a +4+4=(a −2)2+4>0, ∴ 不论a 取任何实数,该方程都有两个不相等的实数根. 【答案】 20−0.4(2)(32−20+x )(20−0.4x )=384, 化简得x 2−36x +360=0, x 1=20,x 2=18,当x 2=18时,20−0.4x =20−0.4×18=12.8(不符合实际,舍去), 当x 1=20时,售价为:32+20=52(元). 答:当天的售价为52元. 【考点】一元二次方程的应用——利润问题 【解析】(1)每增加5元,销售量减少2个,则售价增加x 元,销售量减少2×π5,则可得出售价增加x 元,销售量是20−0.4x(2)用“单个玩具的利润×销售玩具的数量=销售玩具的利润”这一等量关系,列出方程然后求解即可. 【解答】解:(1)由题意可知:每增加5元,销售量减少2个,则售价增加x 元, 销售量减少2×x5,则可得出售价增加x 元,销售量是20−0.4x .(2)(32−20+x )(20−0.4x )=384, 化简得x 2−36x +360=0, x 1=20,x 2=18,当x 2=18时,20−0.4x =20−0.4×18=12.8(不符合实际,舍去), 当x 1=20时,售价为:32+20=52(元). 答:当天的售价为52元. 【答案】解:(1)∵ 抛物线解析式为y =(x +m)2+k 的顶点为M(1, −4), ∴ y =(x −1)2−4.令y =0得(x −1)2−4=0, 解得x 1=3,x 2=−1, ∴ A(−1, 0),B(3, 0).(2)∵ △PAB 与△MAB 同底,且S △PAB =54S △MAB , ∴ |y P |=54|y M |=54×4=5,即y P =±5.又∵ 点P 在y =(x −1)2−4的图象上,∴ y P ≥−4, ∴ y P =5,则(x −1)2−4=5,解得x 1=4,x 2=−2,∴ 存在合适的点P ,坐标为(4, 5)或(−2, 5).【考点】 三角形的面积二次函数图象上点的坐标特征 【解析】(1)由条件可先求得二次函数的解析式,再令y =0可求得A 、B 两点的坐标; (2)由条件可先求得P 点的纵坐标,再代入解析式可求得P 点坐标. 【解答】解:(1)∵ 抛物线解析式为y =(x +m)2+k 的顶点为M(1, −4), ∴ y =(x −1)2−4.令y =0得(x −1)2−4=0, 解得x 1=3,x 2=−1, ∴ A(−1, 0),B(3, 0).(2)∵ △PAB 与△MAB 同底,且S △PAB =54S △MAB , ∴ |y P |=54|y M |=54×4=5,即y P =±5.又∵ 点P 在y =(x −1)2−4的图象上,∴ y P ≥−4, ∴ y P =5,则(x −1)2−4=5, 解得x 1=4,x 2=−2,∴ 存在合适的点P ,坐标为(4, 5)或(−2, 5). 【答案】(1)由题意,可得当售价为22万元/辆时,平均每周的销售量是:25−220.5×1+8=14)(辆)则此时,平均每周的销售利润是:(22−15)×14=98(万元); (2)设每辆汽车降价x 万元,根据题意得:(25−x −15)(8+2x )=90 解得x 1=1,x 2=5当x =1时,销售数量为8+2×1=10(辆); 当x =5时,销售数量为8+2×5=18(辆),为了尽快减少库存,则x =5,此时每辆汽车的售价为25−5=20(万元), 答:每辆汽车的售价为20万元. 【考点】 列代数式求值一元二次方程的应用——利润问题 【解析】(1)根据售价计算销售量,即可求出利润;(2)设每辆汽车降价x 万元,根据已知条件列出方程解答即可. 【解答】(1)由题意,可得当售价为22万元/辆时,平均每周的销售量是:25−220.5×1+8=14)(辆)则此时,平均每周的销售利润是:(22−15)×14=98(万元);(2)设每辆汽车降价x万元,根据题意得:(25−x−15)(8+2x)=90解得x1=1,x2=5当x=1时,销售数量为8+2×1=10(辆);当x=5时,销售数量为8+2×5=18(辆),为了尽快减少库存,则x=5,此时每辆汽车的售价为25−5=20(万元),答:每辆汽车的售价为20万元.【答案】解:设矩形空地靠墙的一边长为x米,x⋅34−(x−1)2=125,解得:x1=25,x2=10,∵25>20,∴x=10,∴34−(x−1)2=12.5.故矩形空地的长为12.5米,宽为10米.【考点】一元二次方程的应用一元二次方程的应用——几何图形面积问题【解析】设AB边的长为x米,则BC边的长为(20−2x)米,利用矩形的面积公式列出方程求解即可;【解答】解:设矩形空地靠墙的一边长为x米,x⋅34−(x−1)2=125,解得:x1=25,x2=10,∵25>20,∴x=10,∴34−(x−1)2=12.5.故矩形空地的长为12.5米,宽为10米.【答案】1,−2(2)∵√2x+3=x,∴2x+3=x2(x≥0),即x2−2x−3=0,∴(x+1)(x−3)=0,则x+1=0或x−3=0,解得x1=−1(舍去,不合题意),x2=3. (3){x2−4y2=0①,x+y=1②,由②得y=1−x,代入①得:x2−4(1−x)2=0,化简得:−3x2+8x−4=0,解得:x=2或x=23,故y=−1或y=13.方程组的解为{x1=2,y1=−1,{x2=23,y2=13.【考点】一元二次方程的解解一元二次方程-配方法二元二次方程组【解析】此题暂无解析【解答】解:(1)∵x3+x2−2x=0,∴x(x2+x−2)=0,∴x(x−1)(x+2)=0,则x=0或x−1=0或x+2=0,解得x1=0,x2=1,x3=−2.故答案为:1;−2.(2)∵√2x+3=x,∴2x+3=x2(x≥0),即x2−2x−3=0, ∴(x+1)(x−3)=0,则x+1=0或x−3=0,解得x1=−1(舍去,不合题意),x2=3. (3){x2−4y2=0①,x+y=1②,由②得y=1−x,代入①得:x2−4(1−x)2=0,化简得:−3x2+8x−4=0,解得:x=2或x=23,故y =−1或y =13.方程组的解为{x 1=2,y 1=−1,{x 2=23,y 2=13.【答案】解:(1)设甲工厂生产x 万片口罩,则乙工厂生产(2000−x )万片口罩, 由题意得:0.6x ≤0.8(2000−x )×34 解得:x ≤1000答:甲工厂最多可生产1000万片的口罩. (2)由题意得:(6−0.5m )(0.8+0.2m )=6×0.8+1.6 整理得:m 2−8m +16=0 解得:m 1=m 2=4 答:m 的值为4.【考点】一元二次方程的应用——工程问题 一元一次不等式的实际应用 【解析】 此题暂无解析 【解答】解:(1)设甲工厂生产x 万片口罩,则乙工厂生产(2000−x )万片口罩, 由题意得:0.6x ≤0.8(2000−x )×34 解得:x ≤1000答:甲工厂最多可生产1000万片的口罩. (2)由题意得:(6−0.5m )(0.8+0.2m )=6×0.8+1.6 整理得:m 2−8m +16=0 解得:m 1=m 2=4 答:m 的值为4.。
2021-2022学年太原市五中12月月考九年级数学答案

太原五中龙城校区2021-2022学年第一学期九年级数学测试一、选择题(本大题共10小题,共30分钟) 1.若,3,4,6346x y zx k y k z k ======,则x z y +的值为( ) A .94B67C .34D .103【答案】A 【解析】设346x y zk ===,求出3,4,6x k y k z k ===,再代入求出答案即可. ,故选A2.方程(1)10x x x -+-=的解是( )A .122,1x x ==B .120,1x x ==-C .120,1x x ==D .121,1x x =-=【答案】D【解析】利用因式分解法求解即可,故选D3.如图,已知点(4,2),(2,2)E F ---,以O 为位似中心,按比例尺1:2,把EFO ∆缩小,则点E 的对应点E '的坐标为( )A .()2,1-B .()8,4-C .()2,1-或()2,1-D .()8,4-或()8,4--【答案】C【解析】根据平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k ,那么位似图形对应点的坐标的比等于k 或﹣k 解答,故选C4.图2是图1中长方体的三视图,用S 表示面积,223,3,S x x S x x =+=+主左则S =俯( )A .232x x ++B .221x x ++C .243x x ++D .224x x +【答案】C【解析】由主视图和左视图的宽为x ,结合两者的面积得出俯视图的长和宽,从而得出答案,故选C5.在一个不透明的袋子里装有5个红球和若干个白球,它们除颜色外其余完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在0.2附近,则估计袋中的白球大约有( )个 A .25B .20C .15D .10【答案】B【解析】由摸到红球的频率稳定在0.2附近得出口袋中得到红色球的概率,进而求出白球个数即可,故选B6.已知m <0,则函数my x=的图象大致是( ) A . B .C .D .【答案】B【解析】根据反比例函数的性质,分别分析x >0和x <0时图象所在象限,故选B7.对于反比例函数4y x-=,①这个函数图象的两个分支分别位于第二、四象限,②这个函数的图象既是轴对称图形又是中心对称图形,③点()2,2--不在这个函数图象上,④若点(),A a b 和点()2,B a c +在该函数图象上,则c >b .上述四个判断中,不正确的个数是( ) A .3B .2C .1D .0【答案】C【解析】根据反比例函数的图象和性质一一进行判断即可,故选C8.为增强学生体质,丰富学生的课外生活,为同学们搭建一个互相交流的平台,学校要组织一次篮球联赛,赛制为单循环(参赛的每两队间比赛一场),根据场地和时间等条件,学校计划安排15场比赛.-设学校应邀请x 个队参赛,根据题意列方程为( ) A .(1)15x x += B .(1)15x x -= C .1(1)152x x += D .1(1)152x x -= 【答案】D【解析】利用安排比赛的场次数=邀请参赛的队伍数×(邀请参赛的队伍数﹣1)÷2,即可得出关于x 的一元二次方程,此题得解,故选D9.如图,在菱形ABCD 中,P 是对角线AC 上一动点,过点P 作PE BC ⊥于点E .PF AB ⊥于点F .若菱形ABCD 的周长为20,面积为24,则PE PF +的值为( )A .4B .245C .6D .485【答案】B 【解析】连接BP ,如图,根据菱形的性质得5BA BC ==,12ABC S ∆=,然后利用三角形面积公式,得到11551222PE PF ⨯⨯+⨯⨯=,再整理即可得到PE PF +的值,故选B 10.如图,在ABC ∆中,,10==AC AB ,2tan =A ,AC BE ⊥于点E ,D 是线段BE 上的一个动点,则BD CD 55+的最小值是( )A.22 B.54 C.35 D.10【答案】B【解析】如图,作AB DH ⊥于H ,AB CM ⊥于MAC BE ⊥ ︒=∠∴90AEB2tan ==AEBEA ,设a =AE ,a 2=BE , 则有22a 4a 100+=,20a 2=∴,(舍弃)或52a 52a -==∴,54a 2==∴BE ,AB CM AC BE AC AB ⊥⊥=,, ,54==∴BE CM (等腰三角形两腰上的高相等) BEA BHD ABE DBH ∠=∠∠=∠, , 55sin ===∠∴AB AE BD DH DBH , DH CD BD CD BD DH +=+∴=∴55,55, CM DH CD ≥+∴5455≥+∴BD CD 二、填空题(本大题共5道小题,共15分) 11.已知,在ABC R ∆t 中,︒=∠90C ,若35sin =A ,则=B tan . 【答案】552 【解析】35sin =A ,3k AB k 5==∴,则设BC , 则k 222=+=BC AB BC 552k5k 2tan ===∠∴BC AC B 12.在不透明的口袋里装有4个黑色棋子和若干白色棋子,每个棋子除颜色外完全相同.从口袋里随机摸出一个棋子,摸到黑棋的概率是52,则白色棋子个数为 . 【答案】613.如图,已知点A ,B 分别在反比例函数)>(0x x 2y =,)>(0x x3y -=的图象上,OB OA ⊥,则OBOA的值为 .【答案】36 【解析】过点A 作y ⊥AM 轴于点M ,过B 作y ⊥BN 轴于点N ,︒=∠+∠∴︒=∠=∠∴90,90OAM AOM BNO AMO , ︒=∠+∠∴⊥90,BON AOM OB OA , OBM ∆∆∴∠=∠∴相似AOM BON OAMB A ,点 分别在反比例函数)>(),>(0x x3y 0x x 2y -==的图像上,3632S 2=∴=∆∆=⎪⎭⎫⎝⎛∴OB OA BON S AOM OB OA 14.如图,某小型水库栏水坝的横断面是四边形ABCD ,AB DE ∥,测得迎水坡的坡角︒=30α,已知背水坡的坡比为1:2.1,坝顶部宽为2m ,坝高为6m ,则坝底AB 的长为 .【答案】()m 367+【解析】如图所示,过点C 作AB DF AB CE ⊥⊥,,垂足分别为F E ,,坝顶部宽2m ,坝高为6m ,3630tan 30m 6m 2=︒=∴︒=====∴ECBE DF EC EF DC α ,背水坡的坡比1.2:1,)m 5,12.12.1(=∴==∴AF AF AF DF mBE EF AF AB )3673625+=++=++=∴(15.如图,在ABC R ∆t 中,︒=∠90ACB ,AB CD BC AC ⊥==,4,3,垂足为D ,E 为BC 的中点,AE 与CD 交于点F ,则DF 的长为 .【答案】1730【解析】如图,过点F 作H AC FH 于⊥BC FH AC BC ACB ∥∴⊥∴︒=∠,,90 BC E BC 是点,4= 中点,2==∴CE BEAEC AFH BC FH ∆∝∆∴∥FH AH EC AC FH AH 23,23=∴==∴, 设FH 为x ,则x 23=AH ,由勾股定理得53432=+=ABCD AB BC AC ABC S ⨯=⨯=∆2121 ,512=∴CD ,则5922=-=CD AC ADACD FCH CDA FHC ∠=∠︒=∠=∠,90 ,CDCHAD FH CAD CFH =∴∆∝∆∴,, 1718x 512x23359x =-=∴,解得,AD CF FH AC AFC S FH ⨯=⨯=∆=∴2121,1718 , 1730=∴CF 三、计算题(本大题共1小题,共10分) 16.(1)计算:0120192020(30tan 323)21()π++︒----; 【答案】1【解析】原式=11333322=+⨯---)( (2)解方程:121x 8x -=++))(( 【答案】5x 4x 21-=-=,【解析】:方程化简为020x 9x 2=++, 因式分解得:()()05x 4x =++5x 4x 05x 04x 21-=-=∴=+=+∴,,或四、解答题(本大题共7小题,共65分)17.某商场在去年底以每件80元的进价购进一批同型号的服装,一月份以每件150元的售价销售了320件,二、三月份该服装畅销,销量持续走高,在售价不变的情况下,三月底统计知三月份的销量达到了500件.(1)求二、三月份服装销售量的平均月增长率;(2)从四月份起商场因换季清仓采用降价促销的方式,经调查发现,在三月份销量的基础上,该服装售价每降价5元,月销售量增加10件,当每件降价多少元时,四月份可获利12000元? 【答案】(1)%25 (2)降价50元【解析】(1)设二,三月份服装销售量得平均月增长率为x ,得:500x 13202=+)(,解得(舍去),25.2x %2525.0x 21-===答:设二,三月份服装销售量得平均月增长率为%25(2)设每件降价y 元,则四月份可销售出)(5y10500⨯+件 依题意:120005y 10500y 80150=⨯+--))(( 整理011500y 180y 2=-+,解的(舍去),230y 50y 21-==答:每件降价50元,则四月份可获利12000元18.为庆祝中国共产党成立100周年,在中小学生心中厚植爱党情怀,我市开展“童心向党”教育实践活动,某校准备组织学生参加唱歌,舞蹈,书法,国学诵读活动,为了解学生的参与情况,该校随机抽取了部分学生进行“你愿意参加哪一项活动”(必选且只选一种)的问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:(1)这次抽样调查的总人数为人,扇形统计图中“舞蹈”对应的圆心角度数为;(2)若该校有1400名学生,估计选择参加书法的有多少人?(3)学校准备从推荐的4位同学(两男两女)中选取2人主持活动,利用画树状图或表格法求恰为一男一女的概率.【答案】:(1)200108︒.(2)560人.(3)2 3 .【解析】(1)这次抽样调查的总人数为:3618%200÷=(人),则参加舞蹈的学生人数为:20036802460﹣﹣﹣=(人),∴扇形统计图中“舞蹈”对应的圆心角度数为:60 360108200︒⨯︒=,故答案为:200108︒,.(2)801400560200⨯=(人),故答案为:560人.(3)画树状图如图:共有12种等可能的结果,恰为一男一女的结果有8种, ∴恰为一男一女的概率为82123= 故答案为2319.如图,一次函数1y k x b =+与反比例函数2(0)k y x x=>的图象交于(1,6)A ,(3,)B n 两点. (1)求反比例函数的解析式和n 的值; (2)根据图象直接写出不等式21k k x b x+<的x 的取值范围; (3)求AOB ∆的面积.【答案】 (1)6y x=,n 2=. (2)01x <<或3x >. (3)8. 【解析】 (1)(1,6)A ,(3,)B n 在2k y x=的图象上, 26k ∴=,∴反比例函数的解析式是6y x=. 623n ∴==; 故答案为:6y x=,n 2=. (2)当01x <<或3x >时,21k k x b x+<; 故答案为:01x <<或3x >. (3)(1,6)A ,(3,2)B 在函数1y k x b =+的图象上,∴11632k b k b +=⎧⎨+=⎩,解得:128k b =-⎧⎨=⎩,则一次函数的解析式是28y x =-+,设直线28y x =-+与x 轴相交于点C ,C 的坐标是(4,0). 11(|||)822AOB AOC BOC A B S S S OC y OC y ∆∆∆=-=-=.故答案为:8.20.如图,在平面直角坐标系中,已知12OA cm =,6OB cm =,点P 从点O 开始沿OA 边以1/cm s 的速度向点A 移动,点Q 从点B 开始沿BO 边以1/cm s 的速度向点O 移动,如果P Q 、同时出发,用()t s 表示移动的时间(06)t ,那么当t 为何值时,POQ ∆与AOB ∆相似?【答案】t 4=或t 2=. 【解析】①若POQ AOB ∆∆∽时,OQ OPOB OA=,即6612t t -=, 整理得t 4=②若POQ BOA ∆∆∽时,OQ OPOA OB=,即6126t t -=, 解得t 2=.所以当t 4=或t 2=时,POQ ∆与AOB ∆相似.21.越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A 处安置测倾器,测得点M 的仰角33MBC ∠=︒,在与点A 相距3.5米的测点D 处安置测倾器,测得点M 的仰角45MEC ∠=︒(点A ,D 与N 在一条直线上),求电池板离地面的高度MN 的长.(结果精确到1米;参考数据sin330.54︒≈,cos330.84︒≈,tan330.65)︒≈【答案】8米.【解析】解:延长BC 交MN 于点H , 3.5AD BE ==,设MH x =米,45MEC ∠=︒,EH x ∴=米,在Rt MHB ∆中,tan 0.653.5MHxMBH HE EB x ∠==≈++,解得 6.5x =,则 1.6 6.58.18MN =+=≈(米),∴电池板离地面的高度MN 的长约为8米.22.阅读与思考下面是小明同学记录的一节数学活动课的部分内容,请仔细阅读,并完成相应的任务.【课堂实录】提出问题:如图1,请在ABCD 中画出一个矩形并证明.下面是小明、小亮的作法.小明的作法如图2,分别作AE BC ⊥于点E ,CF AD ⊥于点F ,则四边形AECF 是矩形;证明:AE BC⊥,⊥、CF AD∴∠=∠=︒.90AEC AFC四边形ABCD是平行四边形,//∴,AD CB∴∠+∠=︒,180AEC EAF∴∠=︒.90EAF∴∠=∠=∠=︒.AEC AFC EAF90∴四边形AECF是矩形.小亮的作法如图3,连接对角线AC,取AC的中点O,以点O为圆心,OA的长为半径画弧交AD于F,连接FO并延长FO交BC于点E,连接CF、AE,则四边形AECF是矩形.证明:四边形ABCD是平行四边形,∴.//AD BC∴∠=∠,FAO ECA∠=∠,AFO CEO⋯(1)小明作法的证明依据是是是矩形.(2)请按照上面小亮的证明思路,写出该证明的剩余部分;(3)如图3,若小亮作出的矩形AECF恰好是正方形,已知5<,请直接写出ABCD的BC=,且BE CFAB=,7面积为.【解析】解:(1)小明根据90=∠=∠=︒.判定四边形AECF是矩形,AEC AFC EAF∴小明作法的证明依据是三个角是直角的四边形是矩形,故答案为:三个角是直角的四边形是;(2)证明的全部过程是:连接对角线AC,取AC的中点O,以点O为圆心,OA的长为半径画弧交AD于F,连接FO并延长FO交BC于点E,连接CF、AE,则四边形AECF是矩形.证明:四边形ABCD是平行四边形,∴.//AD BC∠=∠.∴∠=∠,FAO ECAAFO CEOO是AC的中点,∴=,AO CO在AFO∆中,∆和CEOAFO CEO FAO ECA AO CO ∠=∠⎧⎪∠=∠⎨⎪-⎩,()AFO CEO AAS ∴∆≅∆,FO EO ∴=,AO FO =,AO CO FO EO ===,AC EF ∴=,∴四边形AECF 是矩形;(3)矩形AECF 是正方形,AE EC CF AF ∴===,90AEB ∠=︒设AE EC CF AF x ====,7BC =,7BE x ∴=-,222AB AE BE =+,2225(7)x x ∴=+-,解得:13x =,24x =,BE CE <,4AE ∴=,7428ABCD S BC AE ∴=⋅=⨯=.故答案为:28.23.数学活动——求重叠部分的面积.问题情境:数学活动课上,老师出示了一个问题:如图1,将两块全等的直角三角形纸片ABC ∆和DEF ∆叠放在一起,其中90ACB E ∠=∠=︒,6BC DE ==,8AC FE ==,顶点D 与边AB 的中点重合,DE 经过点C ,DF 交AC 于点G .求重叠部分()DCG ∆的面积.(1)独立思考:请回答老师提出的问题.(2)合作交流:“希望”小组受此问题的启发,将DEF ∆绕点D 旋转,使DE AB ⊥交AC 于点H ,DF 交AC 于点G ,如图2,你能求出重叠部分()DGH ∆的面积吗?请写出解答过程.(3)提出问题:老师要求各小组向“希望”小组学习,将DEF ∆绕点D 旋转,再提出一个求重叠部分面积的问题. “爱心”小组提出的问题是:如图3,将DEF ∆绕点D 旋转,DE ,DF 分别交AC 于点M ,N ,使DM MN =,求重叠部分()DMN ∆的面积.任务:①请解决“爱心”小组提出的问题,直接写出DMN ∆的面积是 .②请你仿照以上两个小组,大胆提出一个符合老师要求的问题,并在图4中画出图形,标明字母,不必解答(注:也可在图1的基础上按顺时针旋转).【解析】解:(1)【独立思考】 90ACB ∠=︒,D 是AB 的中点,DC DA DB ∴==,B DCB ∴∠=∠.又ABC FDE ∆≅∆,FDE B ∴∠=∠.FDE DCB ∴∠=∠,//DG BC ∴.90AGD ACB ∴∠=∠=︒,DG AC ∴⊥.又DC DA =,G ∴是AC 的中点, 118422CG AC ∴==⨯=,116322DG BC ==⨯=,1143622DGC S CG DG ∆∴=⋅=⨯⨯=.(2)【合作交流】解法一:如下图所示:ABC FDE ∆≅∆,1B ∴∠=∠.90C ∠=︒,ED AB ⊥,90A B ∴∠+∠=︒,290A ∠+∠=︒,2B ∴∠=∠,12∴∠=∠,GH GD ∴=.290A ∠+∠=︒,1390∠+∠=︒,3A ∴∠=∠,AG GD ∴=,AG GH ∴=,即点G 为AH 的中点. 在Rt ABC ∆中,22228610AB AC BC =+=+=, D 是AB 中点,152AD AB ∴==.在ADH ∆与ACB ∆中,A A ∠=∠,90ADH ACB ∠=∠=︒,ADH ACB ∴∆∆∽, ∴AD DHAC CB =,即586DH=,解得154DH =, 1111157552224416DGH ADH S S DH AD ∆∆∴==⨯⨯⋅=⨯⨯=. 解法二:同解法一,G 是AH 的中点. 连接BH ,DE AB ⊥,D 是AB 中点,AH BH ∴=.设AH x =,则8CH x =-. 在Rt BCH ∆中,222CH BC BH +=即:22(8)36x x -+=,解得254x =.11257562244ABH S AH BC ∆∴=⋅=⨯⨯=.111175752224416DGH ADH ABH S S S ∆∆∆∴==⨯=⨯=. 解法三:同解法一,12∠=∠.连接CD ,由(1)知,1B DCB ∠=∠=∠, 12B DCB ∴∠=∠=∠=∠.DGH BDC ∴∆∆∽.过点D 作DM AC ⊥于点M ,CN AB ⊥于点N .D 是AB 的中点,90ACB ∠=︒,CD AD BD ∴==,∴点M 是AC 的中点, 116322DM BC ∴==⨯=. 在Rt ABC ∆中,22228610AB AC BC =+=+=,1122AC BC AB CN ⋅=⋅,8624105AC BC CN AB ⋅⨯∴===.DGH BDC ∆∆∽,∴2()DGHBDC S DM S CN∆∆=,221()()2DGH BDC DMDM S S BD CN CN CN ∆∆∴=⋅=⋅⋅2312475()52425165DGH S ∆∴=⨯⨯⨯=.(3)【提出问题】①解决“爱心”小组提出的问题.如答图4,过点D 作DK AC ⊥于点K ,则//DK BC , 又点D 为AB 中点,132DK BC ∴==.DM MN =,MND MDN ∴∠=∠,由(2)可知MDN B ∠=∠, MND B ∴∠=∠,又90DKN C ∠=∠=︒,DKN ACB ∴∆∆∽, ∴KN DK BC AC =,即368KN =,得94KN =. 设DM MN x ==,则94MK x =-. 在Rt DMK ∆中,由勾股定理得:222MK DK MD +=,即:2229()34x x -+=,解得258x =, 112575322816DMN S MN DK ∆∴=⋅=⨯⨯=. ②此题答案不唯一,示例:如答图5,将DEF ∆绕点D 旋转,使DE BC ⊥于点M ,DF 交AC 于点N ,求重叠部分(四边形DMCN )的面积.。
2023-2024学年山西省太原市小店区新时代双语学校九年级(上)月考数学试卷(12月份)+答案解析

一、选择题:本题共11小题,每小题3分,共33分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.如果,则等于( )A.B.C. D.2.用配方法解一元二次方程,将其化成的形式,则变形正确的是( )A.B.C.D.3.菱形、矩形、正方形都具有的性质是2023-2024学年山西省太原市小店区新时代双语学校九年级(上)月考数学试卷(12月份)( )A. 对角线相等 B. 对角线互相垂直C. 对角线互相平分D. 对角线平分一组对角4.画如图所示物体的俯视图,正确的是( )A.B.C.D.5.如图,在离铁塔150米的A 处,用测倾仪测得塔顶的仰角为,测倾仪高AD 为米,则铁塔的高BC为( )A. 米B. 米C.米D.米6.如图,在平行四边形ABCD 中,的平分线交AC 于点E ,交AD 于点F ,交CD 的延长线于点G ,若,则的值为( )A. B. C. D.7.函数和在同一平面直角坐标系中的大致图象可能是( )A. B.C. D.8.如图,在平面直角坐标系中,菱形ABCD 的顶点A 、B 的坐标分别为、,点D 在y 轴正半轴上,则点C 的坐标为( )A. B. C. D.9.如图,已知梯形ABCO的底边AO在x轴上,,,过点C的双曲线交OB于D,且OD::2,若的面积等于3,则k的值( )A. 等于2B. 等于C. 等于D. 无法确定10.古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段MN分为两线段MG,GN,使得其中较长的一段MG是全长MN与较短的一段GN的比例中项,即满足,后人把这个数称为“黄金分割”数,把点G称为线段MN的“黄金分割”点.如图,在中,已知,,若D,E是边BC的两个“黄金分割”点,则的面积为( )A. B. C. D.11.已知,,三点都在反比例函数的图象上,则,,,的大小关系是( )A. B. C. D.二、填空题:本题共4小题,每小题3分,共12分。
山西省太原市小店区第三中学校 2022-2023学年九年级上学期12月月考数学试题

任务三:直接写出方程(x - 5)3 - 4(x - 5)2 = 0 的根 .
A
A
D
B
C
D
C
x
F
B
(第 14 题图)
18.(本题 10 分)
如图 1,一个质地均匀的正六面体,其六个面上分别标有 1,2,3,4,5,6;如图 2,正方
形 ABCD 的四个顶点处各有一个小圆圈 . 张华和李辉玩跳圈游戏,游戏规则为:游戏
3. 答案全部在答题卡上完成,答在本试卷上无效。
B. -4
B. x2 - 7x = -1
7. 某企业通过扩大规模 ,改进生产技术 ,降低产品成本 . 某品牌产品的成本原来为
2. 答卷前,
考生务必将自己的姓名、
准考证号填写在本试卷相应的位置。
A. 4
D. 线段
A. x2 - x - 1 = 0
(
1. 本试卷共 6 页,满分 120 分,考试时间 120 分钟。
2
小华同学的解法是:将 x - 3 移到等号左边,得到 ( x - 3) 2 -(x - 3)=0,
提公因式,得(x - 3)(x - 3 - 1)= 0 即 x - 3 = 0 或 x - 4 = 0,进而得到原
x
连接 OA,OB,则 △AOB 的面积为 ▲ .
14. 如图,在平面直角坐标系 xoy 中,点 B(2,4),若四边形 ABCD 关于点 O 的位似图形为
四边形 A′B′C′D′,且四边形 A′B′C′D′ 与四边形 ABCD 的面积比为 1:2,则点 B′ 的坐标为
▲ .
(
)
y B
A
O D
山西省太原市第五中学2022-2023学年九年级上学期月考数学试题

山西省太原市第五中学2022-2023学年九年级上学期月考数
学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
A.1
5
B.
1
6
C.
1
12
7.如图,AP是ABC
的角平分线,MN垂直平分AP,且交
A.2.5B.
二、填空题
11.如表记录了一名球员在罚球线上投篮的结果.那么,这名球员投篮一次,投中的概
15.如图所示,在菱形ABCD中,∠
出发,以相同的速度分别向终点B,C
为.
三、解答题
16.解方程:
(1)x2+4x﹣1=0;
(2)2(x﹣3)2=x2﹣9.
17.下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.
(1)求证:四边形ABDF 是矩形;
(2)若4BC =,3DF =,求四边形20.“共和国勋章”是中华人民共和国的最高荣誉勋章,在八位杰出人物中,有于敏、孙家栋、袁隆平、黄旭华四位院士,如图是四位院士(依次
2。
太原市第十二中学校2023届九年级上学期月考数学试卷(含解析)

数学试卷一、选择题1. 将一元二次方程(x+3)(2x﹣1)=﹣4化为一般形式,结果是()A. 2x2+5x﹣7=0B. 2x2+5x+1=0C. 2x2﹣5x+1=0D. x2﹣7x﹣1=0答案:B解析:详解:解:(x+3)(2x﹣1)=﹣4故选B2. 若关于的一元二次方程的一个根是,则的值为()A. B. C. D.答案:A解析:详解:解:把代入方程得,解得,,而,所以.故选:A.3. 用配方法解方程时,应将其变形()A. B.C D.答案:C解析:详解:解:,,,,故选:C.4. 如图,在中,对角线与交于点,添加下列条件不能判定为矩形的只有()A. B. ,,C. D.答案:C解析:详解:A. ,对角线相等,可以判定为矩形B. ,,,可知△ABC为直角三角形,故∠ABC=90°,故可以判定为矩形C. ,对角线垂直,不能判定为矩形D. ,可得AO=BO,故AC=BD,可以判定为矩形故选C.5. 如图,在中,,P为边上一动点,于E,于F,动点P从点B出发,沿着匀速向终点C运动,则线段的值大小变化情况是()A. 一直增大B. 不变C. 先减小后增大D. 先增大后减小答案:C解析:详解:解:如图所示,连接.∵,∴,∵,∴四边形是矩形,∴,由垂线段最短可得当时,最短,则线段的值最小,∴动点P从点B出发,沿着匀速向终点C运动,则线段的值大小变化情况是先减小后增大.故选:C.6. 如图,在平面直角坐标系中,的斜边OA在第一象限,并与x轴的正半轴夹角为30度,C为OA的中点,BC=1,则A点的坐标为()A. B. C. D.答案:B解析:详解:解:如图,过A点作轴于D点,的斜边在第一象限,并与轴的正半轴夹角为.,,为的中点,,,,则点的坐标为:,.故选:.7. 若直角三角形的两边长分别是方程的两根,则该直角三角形的面积是()A. 6B. 12C. 12或D. 6或答案:D解析:详解:解方程得,当3和4分别为直角三角形的直角边时,面积为;当4为斜边,3为直角边时根据勾股定理得另一直角边为,面积为;则该直角三角形的面积是6或,故选:D.8. 如图,矩形中,于,且::,则的度数为()A. B. C. D.答案:C解析:详解:解:∵矩形中,∴∵::,∴∵,∴∵∴∴故选C.9. 《代数学》中记载,形如的方程,求正数解的几何方法是:“如图1,先构造一个面积为的正方形,再以正方形的边长为一边向外构造四个面积为的矩形,得到大正方形的面积为,则该方程的正数解为.”小聪按此方法解关于的方程时,构造出如图2所示的图形,已知阴影部分的面积为36,则该方程的正数解为()A. 6B.C.D.答案:B解析:详解:x2+6x+m=0,x2+6x=-m,∵阴影部分的面积为36,∴x2+6x=36,4x=6,x=,同理:先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为x的矩形,得到大正方形的面积为36+()2×4=36+9=45,则该方程的正数解为.故选:B.10. 正方形ABCD,正方形CEFG如图放置,点B、C、E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M.有下列结论:①EC=BP;②AP=AM:③∠BAP=∠GFP;④AB2+CE2=AF2;⑤S正方形ABCD+S正方形CGFE=2S△APF,其中正确的是( )A. ①②③B. ①③④C. ①②④⑤D. ①③④⑤答案:D解析:详解:①∵∠EPF+∠APB=90°,∠APB+∠BAP=90°,∴∠EPF=∠BAP.在△EPF和△BAP中,有,∴△EPF≌△BAP(AAS),∴EF=BP,∵四边形CEFG为正方形,∴EC=EF=BP,即①成立;②无法证出AP=AM;③∵FG∥EC,∴∠GFP=∠EPF,又∵∠EPF=∠BAP,∴∠BAP=∠GFP,即③成立;④由①可知EC=BP,在Rt△ABP中,AB2+BP2=AP2,∵PA=PF,且∠APF=90°,∴△APF为等腰直角三角形,∴AF2=AP2+EP2=2AP2,∴AB2+BP2=AB2+CE2=AP2=AF2,即④成立;⑤由④可知:AB2+CE2=AP2,∴S正方形ABCD+S正方形CGFE=2S△APF,即⑤成立.故成立的结论有①③④⑤.故选D.11. 如图,菱形ABCD中,,AB=4,则以AC为边长的正方形ACEF的周长为()A. 14B. 15C. 16D. 17答案:C解析:详解:∵四边形ABCD是菱形,∴AB=BC.∵∠B=60°,∴△ABC是等边三角形.∴AC=AB=4.∴正方形ACEF的周长是AC+CE+EF+AF=4×4=16.故选C.二、填空题12. 已知关于的方程有两个不相等的实数根,则的取值范围是___.答案:且解析:详解:由关于的方程有两个不相等的实数根得,解得则且故答案为且13. 如图,在菱形中,,取大于的长为半径,分别以点,为圆心作弧相交于两点,过此两点的直线交边于点(作图痕迹如图所示),连接,,则的度数为_________.答案:45°解析:详解:∵∴∴故答案为:45°.14. 如图,O为坐标原点,四边形为矩形,,点D是的中点,点P在上运动,当是以为腰的等腰三角形时,则P点的坐标为______答案:或或解析:详解:解:∵四边形为矩形,,∴,,∵点D是的中点,∴;①当时,在中,,∴;②当,点P在点D的左侧时,过点作于点,则,∵,∴四边形是矩形,∴,在中,由勾股定理得:,∴,∴此时点P坐标为;当,点P在点D的右侧时,同法可得:,∴;∴此时点P坐标为;综上:或或.故答案为:或或.15. 如图,在中,,,分别以,为边向外作正方形,.若,则______.答案:解析:详解:解:过点E作EM⊥AD垂足为M,EN⊥CD垂足为N,则∠DME=90°,在正方形ABCD中,∠ADC=∠MDC =90°,,∴四边形DMEN为矩形,∵∠CDE=45°,∴∠ADE=135°,∴∠MDE=45°,∴∠MED=45°,∴DM=EM,∴矩形DMEN为正方形,设DM=EM=DN=EN=x,则AM=x+1,在Rt△AME中,AE2=AM2+EM2,AE=BD,∴2=(x+1)2+x2,∴或(负值舍去),∴,∴,∵正方形,∴EF=CE,在Rt△CNE中,CE2=CN2+NE2,∴∴三、解答题16. 解下列方程;(1);(配方法)(2)(因式分解法)答案:(1),(2).解析:小问1详解:解:方程整理得:,配方得:,即,开方得:,解得:,;小问2详解:解:,,,,,.17. 小明在解方程时发现了错误,解答过程如下:(第一步)(第二步)(第三步)(第四步)(1)小明解答过程是从第_____步开始错误的,其错误原因是_____.(2)第三步所使用的公式是______.(3)写出此题正确的解答过程.答案:(1)一,方程没有化成一般式(2)(3),正确的解答过程见解析解析:小问1详解:解:小明解答过程是从第一步开始出错的,其错误原因是方程没有化成一般式,故答案为:一,方程没有化成一般式;小问2详解:解:第三步所使用的公式是,故答案为:;小问3详解:解:方程化为:,,,,.18. 如图,在四边形中,,对角线交于点平分角,过点作交的延长线于点,连接.(1)求证:四边形是菱形;(2)若,求的长.答案:(1)见解析(2)解析:小问1详解:证明:∵,∴,∵平分,∴,∴,∴,∵,∴四边形是平行四边形,∵,∴四边形是菱形;小问2详解:解:∵四边形是菱形,∴,∵,∴,∵,∴,在中,,∴,∴.19. 由多项式乘法:,将该式从右到左使用,即可得到“十字相乘法”进行因式分解公式:.示例:分解因式:(1)尝试:分解因式:____________)(2)应用:请用上述方法解方程:.(3)拓展:请用上述方法解方程:.答案:(1)2,4(或4,2)(2),;(3),.解析:小问1详解:解:故答案为:2,4(或4,2);小问2详解:解:∵,或,解得:,;小问3详解:解:,∴,∴或,∴,.20. 如图①,在正方形中,点分别在上且.(1)试探索线段的大小关系,写出你的结论并说明理由;(2)连接,分别取的中点,顺次连接,得到四边形:①请在图②中补全图形;②四边形是什么特殊平行四边形?请说明理由.答案:(1),说明理由见解析(2)①请在图②中补全图形见解析;②四边形是正边形,说明理由见解析解析:小问1详解:解:.∵是正方形,∴,∵,∴,∴;小问2详解:解:①补全图形如图,②四边形是正方形.∵H、I、J、K分别是的中点,∴,∵,∴,∴四边形是菱形,∵,∴,∵,∴,∴,∴,∴四边形是正方形.21. 邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第次余下的四边形是菱形,则称原平行四边形为阶准菱形,如图,中,若,,则为1阶准菱形:中,若,,则为3阶准菱形.(1)判断与推理:邻边长分别为2和3的平行四边形是______阶准菱形;(2)操作、探究、计算:①已知的边长分别为1,且是3阶准菱形,请画出及裁剪线的示意图,并在下方写出的值.②已知的邻边长分别为,,满足,,请写出是______阶准菱形.答案:(1)2;(2)①画图见解析;,,,;②6.解析:详解:(1)邻边长分别为2和3的平行四边形是2阶准菱形;故答案为2.(2)①如图a=4×1=4;a=2×1+1÷2=a=1+1÷3=;②6阶准萎形.如图所示:故答案为6.22. (1)如图1,将矩形折叠,使落在对角线上,折痕,点落在点处,若,则º;(2)小丽手中有一张矩形纸片,,.她准备按如下两种方式进行折叠:①如图2,点在这张矩形纸片的边上,将纸片折叠,使点落在边上的点处,折痕为,若,求的长;②如图3,点在这张矩形纸片的边上,将纸片折叠,使落在射线上,折痕为,点,分别落在,处,若,求的长.答案:(1)12;(2)①AG=;②解析:详解:解:(1)∵∠DAC=66°,∴∠CAB=24°∵将矩形ABCD折叠,使AB落在对角线AC上,∴∠BAE=∠CAE=12°故答案为12;(2)如图2,过点F作FH⊥AB于H,∵∠D=∠A=90°,FH⊥AB∴四边形DFHA是矩形∴AD=FH=4,∵将纸片ABCD折叠∴DF=D1F=5,DG=D1G,∴D1H=,∴AD1=2∵AG2+D1A2=D1G2,∴AG2+4=(4−AG)2,∴AG=;②∵DK=,CD=9,∴CK=9−=,∵四边形ABCD是矩形,∴DC∥AB,∴∠CKH=∠AHK,由翻折不变性可知,∠AHK=∠CHK,∴∠CKH=∠CHK,∴CK=CH=,∵CB=AD=4,∠B=90°,∴在Rt△CDF中,BH=,∴AH=AB−BH=,由翻折不变性可知,AH=A1H=,∴A1C=CH−A1H=3.。
太原市九年级上学期数学12月月考试卷

太原市九年级上学期数学12月月考试卷姓名:________ 班级:________ 成绩:________一、选择题(本题有10小题,每小题4分,共40分。
) (共10题;共40分)1. (4分)二次函数y=x2-2x+2与y轴交点坐标为()A . (0,1)B . (0,2)C . (0,-1)D . (0,-2)2. (4分)(2020·沈北新模拟) 点P(4,3)关于y轴的对称点所在的象限是()A . 第一象限B . 第二象限C . 第三象限D . 第四象限3. (4分) (2019九上·瑞安月考) 已知一个扇形的半径为3,弧长为2π,那么它所对的圆心角度数为()A . 240°B . 120°C . 90°D . 60°4. (4分) (2019九上·瑞安月考) 将抛物线y=2x2先向右平移1个单位,再向上平移3个单位后所得抛物线的解析式为()A . y=2(x-1)2+3B . y=2(x-1)2-3C . y=2(x+1)2+3D . y=2(x+1)2-35. (4分) (2019九上·瑞安月考) 如图A是某公园的进口,B,C,D是三个不同的出口,小明从A处进入公园,那么从B,C,D三个出口中恰好在C出口出来的概率为()A .B .C .D .6. (4分) (2019九上·瑞安月考) 已知点A(-2,a),B(2,b),C(4,c)是抛物线y=x2-4x上的三点,则a,b,c的大小关系为()A . b>c>aB . b>a>cC . c>a>bD . a>c>b7. (4分) (2019九上·瑞安月考) 如图,下面图形及各个选项均是由边长为1的小方格组成的网格,三角形的顶点均在小方格的顶点上。
下列四个选项中哪一个阴影部分的三角形与已知△ABC相似。
2022-2023年山西省某校初三(上)月考数学试卷(含答案)123300

2022-2023年山西省某校初三(上)月考数学试卷试卷考试总分:125 分 考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )1. 方程的二次项系数,一次项系数,常数项分别是( )A.,,B.,,C.,,D.,,2. 若关于的一元二次方程=有解,则的值可为( )A.B.C.D.3. 下列关于的方程中,一定是一元二次方程的是( )A.B.C.D.4. 若关于的方程有实数根,则的取值范围是( )A.且B.且C.D.5. 三角形的两边长分别为和,第三边是方程的解,则第三边的长为( )A.B.C.或D.无法确定3=x+2x 23123−123−1−231−2x −3x+m x 20m 2345x (m−3)−x−2x 23–√x+5k +6=0k 2−x−=02–√x 22–√4123+−2=0x 21x x 4x−1=kx 2k k <4k ≠0k ≤4k ≠0k ≤−4k ≤427−10x+21=0x 273736. 已知抛物线的部分图象如图所示,若,则的取值范围是( )A.B.C.或D.或7. 用米长的铝材制成一个矩形窗框,使它的面积为平方米.若设它的一条边长为米,则根据题意可列出关于的方程为( )A.B.C.D.8. 二次函数=,,为常数,且的图象如图所示,则一次函数=在直角坐标系中的大致图象是( ) A. B. C. D.9. 某校年学生数比年增长了,年新学期开学统计,该校学生数又比年增长了,,这两年该校学生数平均增长率为,则满足的方程是( )A.B.y =+bx+c x 2y <0x −1<x <4−1<x <3x <−1x >4x <−1x >3106x x x(5+x)=6x(5−x)=6x(10−x)=6x(10−2x)=6y a +bx+c(a x 2b c a ≠0)y bx+ac 201720168.5%201820179.6%20172018x x 2x =8.5%+9.6%2(1+x)=(1+8.5%)(1+9.6%)2(1+x =(1+8.5%+9.6%))2C.D.10. 如图,在中,,则的长为( )A.B.C.D.二、 填空题 (本题共计 5 小题 ,每题 3 分 ,共计15分 )11. 抛物线的顶点坐标为________.12. 已知方程的一个根是,则它的另一个根是________.13. 在实数范围内,对于任意实数, 规定一种新运算:.例如: .若,则________.14. 小明发明了一个魔术盒,当任意实数对进入其中时,会得到一个新的实数:,例如把放入其中,就会得到=现将实数对放入其中,得到实数,则=________.15. 已知、是方程=的两个实数根,则的值为________.三、 解答题 (本题共计 8 小题 ,每题 10 分 ,共计80分 )16. 解下列方程:;;;;(用配方法).17. 已知一元二次方程,求证:当时,方程总有两个不相等的实数根.18. 某企业设计了一款工艺品,每件的成本是元,为了合理定价,投放市场进行试销.据市场调查,销售单价是元时,每天的销售量是件,而销售单价每降低元,每天就可多售出件,但要求销售单价不得低于成本.求每天的销售利润(元)与销售单价(元)之间的函数关系式;求销售单价为多少元时,每天的销售利润最大?最大利润是多少元?如果该企业要使每天的销售利润不低于元,那么销售单价应控制在什么范围内?19. 如图,直线与轴交于点,与轴交于点.2(1+x =(1+8.5%+9.6%))2(1+x =(1+8.5%)(1+9.6%))2△ABC ∠A =,tanB =,AC =230∘3–√23–√AB 3+3–√2+23–√592y =2−3(x+2)2+mx−2=0x 22m n(m≠0)m ⊗n =+mn−3m n 4⊗2=+4×2−3=2142x ⊗2=−3x =(a,b)+b −1a 2(3,−2)+(−2)−132 6.(m,−2m)2m a b +2x−5x 20+ab +2a a 2(1)7(2x−3=28)2(2)−2y−99=0y 2(3)2+1=4x x 2(4)4x(2x−3)=3(2x−3)(5)−4x+1=0x 2a +bx+c =0(a ≠0)x 2−4ac >0b 2501005015(1)y x (2)(3)4000AB x A(1,0)y B(0,−2)求直线的解析式;若直线上的点在第一象限,且,求点的坐标.20. 某服装店出售某品牌的棉衣,进价为元/件,当售价为元/件时,平均每天可卖件;为了增加利润和减少库存,商店决定降价销售.经调查,每件每降价元,则每天可多卖件.若每件降价元,则平均每天可卖________件.现要想平均每天获利元,且让顾客得到实惠,求每件棉衣应降价多少元?21. 某社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为米,宽为米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为平方米.求通道的宽是多少米?该停车场共有车位个,据调查分析,当每个车位的月租金为元时,可全部租出;当每个车位的月租金每上涨元,就会少租出个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为元?22. 已知关于的方程的一个根是,请求出力程力一个枢,开水.以此方程的两根为边长的直角三角形的周长. (23. 随着新冠病毒在全世界蔓延,口罩成为紧缺物资,甲、乙两家工厂积极响应政府号召,准备跨界投资生产口罩.根据市场调查,甲、乙两家工厂计划每天各生产万片口罩,但由于转型条件不同,其生产的成本不一样,甲工厂计划每生产万片口罩的成本为万元,乙工厂计划每生产万片口罩的成本为万元.(1)按照计划,甲、乙两家工厂共生产万片口罩,且甲工厂生产口罩的总成本不高于乙工厂生产口罩的总成本的,求甲工厂最多可生产多少万片的口罩?(2)实际生产时,甲工厂完全按计划执行,但乙工厂的生产情况发生了一些变化.乙工厂实际每天比计划少生产万片口罩,每生产万片口罩的成本比计划多万元,最终乙工厂实际每天生产口罩的成本比计划多万元,求的值.(1)AB (2)AB C =4S △BOC C 1001503012(1)20(2)20005228640(1)(2)6420010114400π−(m+2)x+(2m−1)=0x 2x =1610.610.820000.5m 10.2m 1.6m参考答案与试题解析2022-2023年山西省某校初三(上)月考数学试卷试卷一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )1.【答案】C【考点】一元二次方程的一般形式【解析】先将已知方程转化为一般形式,然后求方程的二次项系数,一次项系数,常数项.【解答】解:由已知方程得到:,所以方程的二次项系数,一次项系数,常数项分别是,、.故选:.2.【答案】A【考点】根的判别式【解析】根据判别式的意义得到=,然后解不等式求出的范围后对各选项进行判断.【解答】根据题意得:=,解得.3.【答案】C【考点】一元二次方程的定义【解析】根据一元二次方程的定义解答.一元二次方程必须满足四个条件:未知数的最高次数是;二次项系数不为;是整式方程;含有一个未知数.由这四个条件对四个选项进行验证.【解答】解:、是多项式,故错误;、时是一元一次方程,故错误;3=x+2x 23−x−2=0x 23=x+2x 23−1−2C △(−3−4m≥0)2m △(−3−4m≥0)2m≤94(1)2(2)0(3)(4)A A B k =0B、是一元二次方程,故正确;、是分式方程,故错误;故选:.4.【答案】D【考点】一元二次方程的定义根的判别式【解析】分和两种情况考虑,当时可以找出方程有一个实数根;当时,根据方程有实数根结合根的判别式可得出关于的一元一次不等式,解不等式即可得出的取值范围.结合上面两者情况即可得出结论.【解答】解:当时,原方程可化为,解得,所以符合题意;当时,原方程可化为,方程有实数根,,解得且,综上可知,的取值范围是.故选.5.【答案】A【考点】解一元二次方程-因式分解法三角形三边关系【解析】将已知的方程左边分解因式,利用两数相乘积为,两因式中至少有一个为转化为两个一元一次方程,求出一次方程的解得到原方程的解为或,利用三角形的两边之和大于第三边进行判断,得到满足题意的第三边的长.【解答】解:,因式分解得:,解得:,,∵三角形的第三边是的解,∴三角形的第三边为或,当三角形第三边为时,,不能构成三角形,舍去;当三角形第三边为时,三角形三边分别为,,,能构成三角形,则第三边的长为.故选.6.【答案】BC C CD C k =0k ≠0k =0k ≠0m k k =04x−1=0x =14k =0k ≠0k −4x+1=0x 2∵∴Δ=−4k ≥0(−4)2k ≤4k ≠0k k ≤4D −10x+21=0x 20037−10x+21=0x 2(x−3)(x−7)=0=3x 1=7x 2−10x+21=0x 23732+3<772777A【考点】二次函数的图象【解析】根据图象,已知抛物线的对称轴,与轴的一个交点,可求另一交点,观察图象得出时的取值范围.【解答】解:因为抛物线的对称轴,与轴的一个交点;根据抛物线的对称性可知,抛物线与轴的另一交点为,因为抛物线开口向上,当时,.故选.7.【答案】B【考点】由实际问题抽象出一元二次方程一元二次方程的应用——几何图形面积问题【解析】一边长为米,则另外一边长为:,根据它的面积为平方米,即可列出方程式.【解答】解:一边长为米,则另外一边长为:,由题意得:.故选.8.【答案】D【考点】一次函数的图象二次函数的图象【解析】首先得出,,的符号,进而利用一次函数的性质得出答案.【解答】由二次函数开口向上可得:,对称轴在轴的右侧可得,,异号,则,图象与轴交于负半轴,可得:,则,故一次函数=经过二、三、四象限.9.【答案】D【考点】x =1x (−1,0)y <0x x =1x (−1,0)x (3,0)y <0−1<x <3B x 5−x 6x 5−x x(5−x)=6B a b c a >0x a b b <0y c <0ac <0y bx+ac一元二次方程的应用——增长率问题由实际问题抽象出一元二次方程【解析】此题暂无解析【解答】解:,这两年该校学生数平均增长率为,所以从年到年的增长了,又因为年学生数比年增长了,年新学期开学统计,该校学生数又比年增长了,所以.故选.10.【答案】C【考点】正方形的性质勾股定理【解析】此题暂无解析【解答】此题暂无解答二、 填空题 (本题共计 5 小题 ,每题 3 分 ,共计15分 )11.【答案】【考点】二次函数的性质二次函数的三种形式二次函数图象上点的坐标特征【解析】此题暂无解析【解答】解:抛物线符合顶点式,∴顶点坐标为:.故答案为:.12.【答案】20172018x 20162018(1+x)2201720168.5%201820179.6%(1+x =(1+8.5%)(1+9.6%))2D (−2,−3)y =2−3(x+2)2(−2,−3)(−2,−3)−1设方程的另一根为,可将该方程的已知根和设的根一起代入两根之积公式列出方程,解方程即可求出方程的另一根.【解答】解:设方程的两根分别为,,且,根据根与系数的关系可得,∴.故答案为:.13.【答案】或【考点】定义新符号解一元二次方程-因式分解法【解析】根据定义的运算可得一个关于的一元二次方程,进一步解放即可求出的值.【解答】解:根据题意,得.∴.解方程,得,.故答案为:或.14.【答案】或【考点】一元二次方程的应用——其他问题【解析】【解把实数对.代入中得移项得因式分解得解得或,故答案为或.【解答】此题暂无解答15.【答案】x 12x 1x 2=2x 1⋅=2=−2x 1x 2x 2=−1x 2−1−20x x x ⊗2=+2x−3x 2+2x−3=−3x 2=−2x 1=0x 2−203−1.317(m,−2m)+b−|=2a 2−2m−1=2m 2|−2m−3=0,m 2(m−3)(m+1)=0m=3−13−10由、是方程=的两个实数根,可得=,=,推出=,由此即可解决问题;【解答】∵、是方程=的两个实数根,∴=,=,∴=,∴==,三、 解答题 (本题共计 8 小题 ,每题 10 分 ,共计80分 )16.【答案】解:,两边除以,,开方得,解得,;,因式分解得,解得,;,移项可得,,则该方程有两个不相等的实数根,则,;,移项可得,解得,;,移项可得,配方得,即,解得,则,.【考点】解一元二次方程-因式分解法解一元二次方程-公式法解一元二次方程-配方法解一元二次方程-直接开平方法【解析】此题暂无解析【解答】解:,两边除以,,开方得,解得,;,因式分解得,解得,;,移项可得,,则该方程有两个不相等的实数根,则,;a b +2x−5x 20ab −5+2a −5a 20+2a a 25a b +2x−5x 20ab −5+2a −5a 20+2a a 25+ab +2a a 25−50(1)7(2x−3=28)27(2x−3=4)22x−3=±2=x 152=x 212(2)−2y−99=0y 2(x+9)(x−11)=0=−9x 1=11x 2(3)2+1=4x x 22−4x+1=0x 2Δ=(−4−4×2×1=8>0)2==x 1−(−4)+8–√2×22+2–√2==x 2−(−4)−8–√2×22−2–√2(4)4x(2x−3)=3(2x−3)(4x−3)(2x−3)=0=x 134=x 232(5)−4x+1=0x 2−4x =−1x 2−4x+4=−1+4x 2(x−2=3)2x =±+23–√=2+x 13–√=2−x 23–√(1)(1)7(2x−3=28)27(2x−3=4)22x−3=±2=x 152=x 212(2)−2y−99=0y 2(x+9)(x−11)=0=−9x 1=11x 2(3)2+1=4x x 22−4x+1=0x 2Δ=(−4−4×2×1=8>0)2==x 1−(−4)+8–√2×22+2–√2==x 2−(−4)−8–√2×22−2–√2,移项可得,解得,;,移项可得,配方得,即,解得,则,.17.【答案】证明:,即,化简得,则当时,方程总有两个不相等的实数根,分别为,.【考点】根与系数的关系根的判别式【解析】此题暂无解析【解答】证明:,即,化简得,则当时,方程总有两个不相等的实数根,分别为,.18.【答案】解:.∵,∴抛物线开口向下.∵,此抛物线的对称轴是直线.∴当时,答:销售单价为元时,每天的销售利润最大,最大利润为元.当时,即,解得.∴当时,,答:销售单价应控制在元至元范围内.【考点】一元二次方程的应用——利润问题【解析】(4)4x(2x−3)=3(2x−3)(4x−3)(2x−3)=0=x 134=x 232(5)−4x+1=0x 2−4x =−1x 2−4x+4=−1+4x 2(x−2=3)2x =±+23–√=2+x 13–√=2−x 23–√a +bx+c =a(+x)+c x 2x 2b a=a(x++c −=0b 2a )2b 24a a(x+=b 2a )2−4ac b 24a x =−b ±−4ac b 2−−−−−−−√2a −4ac >0b 2=x 1−b +−4ac b 2−−−−−−−√2a =x 2−b −−4ac b 2−−−−−−−√2a a +bx+c =a(+x)+c x 2x 2b a =a(x++c −=0b 2a )2b 24a a(x+=b 2a )2−4ac b 24a x =−b ±−4ac b 2−−−−−−−√2a −4ac >0b 2=x 1−b +−4ac b 2−−−−−−−√2a =x 2−b −−4ac b 2−−−−−−−√2a (1)y =(x−50)[50+5(100−x)]=−5+800x−27500(50≤x ≤100)x 2(2)y =−5+800x−27500=−5+4500x 2(x−80)2−5<0y =−5+800x−27500x 250≤x ≤100x =80x =80=4500y 最大804500(3)y =4000−5+800x−27500=4000x 2=70,=90x 1x 270≤x ≤90y ≥40007090此题暂无解析【解答】解:.∵,∴抛物线开口向下.∵,此抛物线的对称轴是直线.∴当时,答:销售单价为元时,每天的销售利润最大,最大利润为元.当时,即,解得.∴当时,,答:销售单价应控制在元至元范围内.19.【答案】解:设直线的解析式为,直线过点,点,代入直线解析式可得: 解得∴直线的解析式为.设点的坐标为,∵,∴,解得,∴,∴点的坐标是 .【考点】一次函数图象上点的坐标特点待定系数法求一次函数解析式三角形的面积【解析】答案未提供解析。
山西省太原市第三十七中学校2023-2024学年九年级上学期月考数学试题
山西省太原市第三十七中学校2023-2024学年九年级上学期月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题二、填空题15.如图,在矩形ABCD 中,12AB BC ==,,得到折痕AE ,则BE 的长为.三、解答题16.解方程:(1)25210x x +-=(2)(3)4(3)0x x x ---=17.如图,菱形ABCD 中的对角线AC BD ,相交于点O ,BE AC ∥,CE BD ∥.求证:四边形OBEC 是矩形.18.组织一次排球邀请赛,参赛的每两个队都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,则比赛组织者应邀请多少个队参赛?19.在学校组织的国学比赛中,小明晋级了总决赛,比赛过程分两个环节,参赛选手须在每个环节中抽取一道题目.第一环节:写字注音、成语故事、国学常识、成语接龙(分别用1234A A A A ,,,表示):第二环节:成语听写、诗词对句、经典诵读(分别用123B B B ,,表示)求小明参加总决赛抽取题目都是成语题目(成语故事,成语接龙,成语听写)的概率.20.如图,在ABC 中,CD 平分ACB ∠,CD 的垂直平分线分别交AC ,DC ,BC 于点E ,F ,G ,连接DE ,DG ,求证:四边形DGCE 是菱形.21.口罩在预防流感时起着非常重要的防护作用,主要是保护呼吸道,预防呼吸道飞沫的传播,减少病毒或细菌的侵袭,预防感染的作用,同时还可以预防有害物质的入侵,极大地减少交叉感染的概率,某药店新购进一批口罩进行销售,平均每天可售出500个,每个盈利0.6元,为了让利于民,药店决定采取适当的降价措施,根据以往的经验,如果每个口罩的售价每降低0.1元,那么平均每天可多售出100个,该药店要想通过销售这种口罩,每天盈利达到240元,则每个口罩的售价应降价多少元?22.如图1,在正方形ABCD 中,O 是对角线的交点,P 是线段AO 上任一点(不与点A ,O 重合),过点P 作PE PB ⊥,PE 交边CD 于点E .(1)PCE ∠的度数为_______________.(2)求证:PB PE =.(3)如图2,若正方形ABCD 的边长为4,过点E 作EF AC ⊥于点F ,在点P 运动的过程中,PF 的长度是否发生变化?若不发生变化,直接写出这个不变的值;若发生变化,请说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2022-2023学年山西省太原市部分学校九年级上学期12月月考数学试卷
1.剪纸艺术是最古老的中国民间艺术之一,其内容丰富题材广泛,以特有的概括和夸张手
法将吉事祥物.美好愿望表现得淋漓尽致.下列剪纸的图案既是轴对称图形,又是中心对称图形的是()
A.B.C.D.
2.用配方法解一元二次方程时,需要将原方程化为()
A.B.
C.D.
3.一个不透明的袋子里有3个白球,7个黑球,这些球除颜色外完全相同.如果从袋子里随
机摸出一个球,那么摸到白球的概率是()
A.3 B.C.D.
4.下列二次函数中,其图象的顶点坐标为(-3,-1)的是()
A.B.C.D.
5.向空中发射一枚炮弹,经过秒后高度为米,且时间与高度的关系式为
,若炮弹在第6秒与第14秒时的高度相等,则炮弹所在高度最高的时间是()
A.第8秒B.第9秒C.第10秒D.第11秒
6.如图,内接于,是的直径,平分,交于点,连接,
则下列结论错误的是()
A.B.C.D.
7.在某次冠状病毒感染中,有5只动物被感染,后来经过两轮感染后,共有605只动物被
感染.若设每轮感染中平均一只动物会感染x只动物,则可列方程为()
A.B.
C.D.
8.如图,将绕点顺时针旋转角,得到,若点恰好在的延长线上,则
等于()
A.B.C.D.
9.一次函数和二次函数,在同一平面直角坐标系中的图象不可能是()
A .
B .
C .D.
10.
如图,AB 是的直径,的弦DC 的延长线与AB 的延长线相交于点P ,于点E ,,,则阴影部分的面积为()
A.B.C.D.
11.方程的解为 _____.
12.在平面直角坐标系中,点关于原点对称的点的坐标是______.
13.如图,在中弦的长为,点在圆上,且,则的半径为
________.
14.抛物线与x轴有两个不同的交点,则m的取值范围是 _____.
15.如图,在Rt中,,,,点是的中点,以为直径
作,分别与、交于点、,过点作的切线,交于点,则的长为________.
16.解方程:
(1) ;
(2).
17.如图,平面直角坐标系中,网格中的每个小正方形的边长为1个单位长度;已知,
请画出绕点顺时针旋转得到的三角形.并求出旋转过程中,点所经过的路径的长.
18.中华人民共和国第二届青年运动会在太原举办,会议期间,太原市某高校选拔了10名优
秀志愿者,每位志愿者都将通过抽取卡片的方式决定去以下四个场馆中的两个场馆进行颁奖礼仪服务,四个场馆分别为:太原学院足球场.太原市沙滩排球场、山西省射击射箭训练基地.太原水上运动中心,这四个场馆分别用字母A、B、C、D表示,现把分别印有A、B、C、D的四张卡片(除字母外,其余都相同)背面朝上,洗匀放好.志愿者小玲从中随机抽取一张卡片(不放回),再从中随机抽取一张请你用列表或画树状图的方法求小玲抽到的两张卡片恰好是“A”和“B”的概率.
19.某商店以每件50元的价格购进若干件衬衫,第一个月以单价80元销售,售出200件,第
二个月为增加销售量,且能够让顾客得到更大的实惠,决定降价处理,经市场调查,,如何定价,才能使以后每个月的利润达到7920元?
解:设……
根据题意,得
……
根据上面所列方程,完成下列任务:
(1)数学问题中括号处短缺的条件是;
(2)所列方程中未知数x的实际意义是;
(3)请写出解决上面的数学问题的完整的解题过程.
20.如图,直线与抛物线交于、两点(在的左侧)
(1)求、两点的坐标;
(2)直接写出时,的取值范围;
(3)抛物线的顶点为A,求的面积.
21.我们知道:利用公式法解方程的求根公式为,
根据公式可进一步推导出根与系数的关系:,.
(1)已知二次函数的图象与x轴交于,两点,试求两
点间的距离.
(2)我们继续探究:如果二次函数的图象,与x轴的两个交点为
,,利用根与系数的关系,可以得到A、B两个交点间的距离为:
,若
二次函数与x轴的两个交点为,利用上述结论,求出两点间的距离.
22.综合与实践
问题情境:
如图①,在中,,,四边形为正方形,当点D、F分别在AC,BC边上时,显然有,.
(1)操作发现:
将正方形绕点C顺时针旋转到如图②的位置时,是否成立?若成立,请给出证明;若不成立,请说明理由.
(2)将正方形绕点C顺时针旋转到如图③的位置(点E在线段上)时,延长交
于点H,交于点M,求证:.
问题解决:
(3)在(2)的条件下,当,时,求的长.
23.综合与探究
如图二次函数与直线交于A、C两点,已知:,二次函数的图象与x轴的另一个交点为点B,点D在直线上方的抛物线上运动,过点D做y轴的平行线交于点E.
(1)求直线与抛物线的解析式;
(2)求线段的最大值,及此时点D的坐标.
(3)在x轴上找一点P,使为等腰三角形,请直接写出点P的坐标.。
