高中数学必修2第二章(免费)
高中数学必修2《点、直线、平面之间的位置关系》知识点
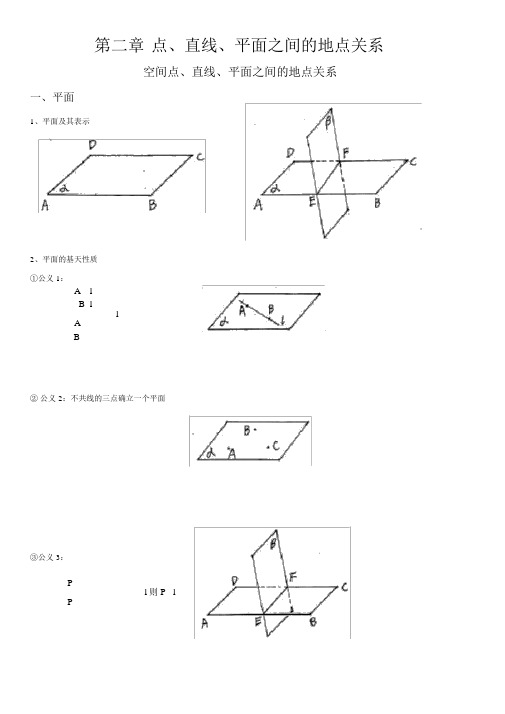
第二章点、直线、平面之间的地点关系空间点、直线、平面之间的地点关系一、平面1、平面及其表示2、平面的基天性质①公义 1:A lB llAB②公义 2:不共线的三点确立一个平面③公义 3:Pl 则 P lP二、点与面、直线地点关系1、 A1、点与平面有 2 种地点关系2、 B2、点与直线有1、 A l2 种地点关系l2、 B三、空间中直线与直线之间的地点关系1、异面直线2、直线与直线的地点关系订交共面平行异面3、公义 4 和定理公义 4:l1 Pl3l1 Pl 2l 2 Pl3定理:空间中假如两个角的两边分别对应平行,那么这两个角相等或互补。
4、求异面直线所成角的步骤:① 作:作平行线获得订交直线;② 证:证明作出的角即为所求的异面直线所成的角;③ 结构三角形求出该角。
提示: 1、作平行线常有方法有:直接平移,中位线,平行四边形。
2、异面直线所的角的范围是000 ,90。
四、空间中直线与平面之间的地点关系地点关系直线 a在平面内直线 a与平面订交直线 a与平面平行公共点有无数个公共点有且只有一个公共点没有公共点符号表示a a IA a P图形表示五、空间中平面与平面之间的地点关系地点关系两个平面平行两个平面订交公共点没有公共点有一条公共直线符号表示P I a图形表示直线、平面平行的判断及其性质一、线面平行1、判断:ba b Pb Pa(线线平行,则线面平行)2、性质:a Pa a Pbb(线面平行,则线线平行)二、面面平行1、判断:aba b P Pa Pb P(线面平行,则面面平行)2、性质 1:PI a a PbI b(面面平行,则线面平行)性质 2:Pm Pm(面面平行,则线面平行)说明( 1)判断直线与平面平行的方法:① 利用定义:证明直线与平面无公共点。
② 利用判断定理:从直线与直线平行等到直线与平面平行。
③ 利用面面平行的性质:两个平面平行,则此中一个平面内的直线必平行于另一个平面。
(2)证明面面平行的常用方法①利用面面平行的定义:此法一般与反证法联合。
数学必修二第二章知识点总结

数学必修二第二章知识点总结(实用版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的实用范文,如演讲致辞、合同协议、条据文书、策划方案、总结报告、简历模板、心得体会、工作材料、教学资料、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this store provides various types of practical sample essays, such as speeches, contracts, agreements, documents, planning plans, summary reports, resume templates, experience, work materials, teaching materials, other sample essays, etc. Please pay attention to the different formats and writing methods of the model essay!数学必修二第二章知识点总结数学必修二第二章知识点总结通用4篇社会学科的知识能够让我们更好地了解社会,理解人性。
高中数学必修2第二章点直线平面之间的位置关系211平面及其表示法(含习题课)PPT课件

1,2,3(1)(2)
21
补充练习金太:阳教育网
l 1、A为直线 l上的点,又点A不在平面
与 的公共点最多有 _______1个.
品质来自专业 信赖源于诚信
内,则
2、四条直线过同一点,过每两条直线作一个平
面,则可以作_____1_或___4_或___6个不同的平面 .
22
金太阳教育网
品质来自专业 信赖源于诚信
2
金实太阳教例育网引入
品质来自专业 信赖源于诚信
观察活动室里的地面,它呈现出怎样的形象?
3
一.平面金太的阳教育概网 念:
品质来自专业 信赖源于诚信
光滑的桌面、平静的湖面等都是我们
熟悉的平面形象,数学中的平面概念是现
实平面加以抽象的结果。
二.平面的特征:
平面没有大小、厚薄和宽窄,平面在空 间是无限延伸的。
文字语金言太阳:教育网 公理1.如果一条直线上两点品信质赖在来源自于专诚一业信 个平面内,那么这条直线在此平
面内(即这条直线上的所有的点
23
点、线金、太阳面教之育网间的位置关系及语言表达
品质来自专业
信赖源于诚信
文字语言表达 图形语言表达 符号语言表达
点A在直线a上 点A不在直线a上
A
a
A
a
A∈a A∈a
点A在平面α上 点A不在平面α上 直线a在平面α内
α
A
α
α
A
a a
A∈α A∈ α
aα
a b∩α=A
直线a在平面α外 α
A α
a∩α=φ 或 a∥α24
B A
B
CαA
C
公理2.过不在同一直线上的三点,有且只有一个平面.
高中数学必修二第二章第一节课件

k y2 y1 x1 x2 .
x2 x1
如果x1 x2,那么直线PQ的斜率不
存在(图2 1 22).
图2 1 2
y
l
第 2章 平面解析几何初步
如 果 代 数 与 几 何 各 自 分开 发 展, 那 它 的 进 步 将 十 分 缓 慢,而 且 应 用 范 围 也 很 有 限.但 若 两 者 互 相 结 合 而 共同 发 展, 则 就 会 互 相加 强, 并 以 快速 的 步 伐 向 着 完 美 化 的 方 向 猛 进.
点的集合是一条曲线.
我 们 知 道, 直 线 和 圆 是 基 本 的 几 何图 形.那 么 如何建立它们的方程? 如何通过方程来研究它们的性质?
2.1 直线与方程
高二(19)
直 线 是 最 常 见 的 图 形, 过 一 点 沿 着 确 定 的 方 向 就 可 以 画 出 一 条 直 线.
为 什 么?
在直角坐标系中, 对于一条与x 轴相交的直线,把 x 轴所在 的 直 线 绕 着 交 点 按 逆 时针 方 向 旋 转 到 和 直 线 重合 时 所 转
过的最小正角称为这条直线的倾 斜 角(inclination),并规定:
y B
A
O
N
图2 1 51
与 x 轴 平 行 或 重 合 的 直 线 的倾 斜 角 为00 . 由定义可知,直线的倾斜角 的取值范 围是00 1800 . 当 直 线 的 斜 率 为 正 时, 直 线 的 倾 斜 角
x 为锐角图2 1 51,此时,
k y BN tan .
数学必修二第二章知识点总结

数学必修二第二章知识点总结第二章是数学必修二课程中的重要章节,主要涵盖了函数的概念、函数图像与性质、函数的运算以及反函数等内容。
本文将对这一章节的知识点进行总结,以帮助读者更好地掌握相关知识。
1. 函数的概念函数是数学中的一个重要概念,它描述了两个集合之间的一种特殊关系,即每个自变量对应唯一的因变量。
函数可用符号表示为 y = f(x),其中 x 为自变量,y 为因变量,f 表示函数。
2. 函数的图像与性质函数的图像是函数在坐标系中的几何表示,通常是曲线或直线。
函数的性质包括定义域、值域、单调性、奇偶性等。
定义域是函数能够取值的自变量的范围,值域是函数实际取到的因变量的范围。
函数的单调性描述了函数在定义域上的增减情况,可以是增函数、减函数或常函数。
奇偶性是函数的一种对称性质,一个函数可分为奇函数或偶函数,或者既不是奇函数也不是偶函数。
3. 函数的运算函数的运算主要包括四则运算、复合函数与反函数。
四则运算即加减乘除运算,可以对函数进行加减乘除操作。
复合函数指的是将一个函数的结果作为另一个函数的输入,也就是将两个函数逐步嵌套使用。
反函数是指与原函数具有互逆关系的函数,即输入和输出对换的函数。
4. 一次函数与二次函数一次函数是指次数为一的多项式函数,它的图像是一条直线。
一次函数的一般式为 y = kx + b,其中 k 表示斜率,b 表示与 y 轴交点。
二次函数是指次数为二的多项式函数,它的图像是一个抛物线。
二次函数的一般式为 y = ax^2 + bx + c,其中 a 表示开口方向和抛物线开口的大小,b 表示抛物线位置的水平偏移量,c 表示抛物线位置的垂直偏移量。
5. 绝对值函数与倒数函数绝对值函数是指函数的结果取绝对值的函数,它的图像是一个 V 字形曲线。
绝对值函数的一般式为 y = |x|,其中 x 为自变量,y 为因变量。
倒数函数是指与原函数相乘等于 1 的函数,也就是结果取其倒数的函数。
6. 对数函数与指数函数对数函数是指函数的结果通过指数变换得到的函数,常见的对数函数有自然对数函数和常用对数函数。
数学书必修二第二章知识点

数学书必修二第二章知识点第二章:函数与方程1. 函数的定义及表示法- 函数是指一种具有特定性质的对应关系,将一个自变量的值映射到一个因变量的值上。
- 函数通常用 f(x) 或 y 表示,其中 x 是自变量,f(x) 或 y 是因变量。
- 函数也可以用图像、表格或公式表示。
2. 基本初等函数- 常数函数:f(x) = a,其中 a 是常数。
- 一次函数:f(x) = kx + b,其中 k 和 b 是常数,且 k ≠ 0。
- 幂函数:f(x) = x^n,其中 n 是常数,且 n ≠ 0。
- 指数函数:f(x) = a^x,其中 a 是常数且 a > 0,且 a ≠ 1。
- 对数函数:f(x) = log_a(x),其中 a 是正常数且 a ≠ 1。
3. 函数的性质- 定义域:函数的自变量的取值范围。
- 值域:函数的因变量的取值范围。
- 奇偶性:f(x) = f(-x) 时,函数为偶函数;f(x) = -f(-x) 时,函数为奇函数。
- 单调性:函数在定义域上递增或递减。
- 有界性:函数在某个区间上有上界或下界。
4. 复合函数- 复合函数是由一个函数作为另一个函数的自变量而得到的函数。
- 复合函数的表示法为 (f ∘ g)(x) = f(g(x))。
5. 反函数- 若函数 f 和 g 是互逆的,则 f(g(x)) = x,g(f(x)) = x。
- 如果函数 f 的反函数存在,记为 f^(-1)(x),则有 f(f^(-1)(x)) = x。
6. 方程的根与解集- 方程是含有未知数的等式。
- 方程的根是使方程成立的值。
- 解集是使方程成立的所有值的集合。
7. 一元一次方程- 一元一次方程是形如 ax + b = 0 的方程。
- 一元一次方程的解为 x = -b/a。
8. 一元二次方程- 一元二次方程是形如 ax^2 + bx + c = 0 的方程,其中 a ≠ 0。
- 一元二次方程的解可以通过公式 x = (-b ±√(b^2 - 4ac))/(2a) 求得。
北师大版高中数学必修二第二章1.1直线的倾斜角和斜率.docx

§1直线与直线的方程1.1 直线的倾斜角和斜率问题导学1.求直线的倾斜角活动与探究1已知直线l1的倾斜角是30°,直线l2⊥l1,试求直线l2的倾斜角.迁移与应用1.如图,有三条直线l1,l2,l3,倾斜角分别是α1,α2,α3,则下列关系正确的是( ).A.α1>α2>α3 B.α1>α3>α2C.α2>α3>α1 D.α3>α2>α12.直线l过原点,且倾斜角为150°,若将直线l绕原点逆时针方向旋转30°,得到直线l1,那么l1的倾斜角为__________.求直线的倾斜角,主要是根据题意画出图形,根据倾斜角的定义,找出直线向上的方向与x轴正半轴所成的角,即为倾斜角,注意平面几何中相关知识的应用.2.求直线的斜率活动与探究2(1)已知两条直线的倾斜角α1=30°,α2=45°,求这两条直线的斜率;(2)如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,AC的斜率;(3)求经过两点A(a,2),B(3,6)的直线的斜率.迁移与应用1.(1)若直线l 的倾斜角为60°,则该直线的斜率为__________;(2)经过两点A (3,2),B (4,7)的直线的斜率是__________.2.经过下列两点的直线的斜率是否存在?如果存在,求其斜率.①(1,1),(-1,-2);②(1,-1),(-2,4);③(2,2),(10,2);④(-2,-3),(-2,3).1.求直线的斜率通常有两种方法:一是已知直线的倾斜角α时,可根据斜率的定义,利用k =tan α求得;二是已知直线上经过的两点时,可利用两点连线的斜率公式计算求得.2.使用斜率公式k =y 2-y 1x 2-x 1时,要注意前提条件x 1≠x 2.若x 1=x 2,则斜率不存在.当两点的横坐标含有字母时,要先讨论横坐标是否相等再确定直线的斜率.3.直线的倾斜角和斜率的关系活动与探究3a 为何值时,过点A (2a,3),B (2,-1)的直线的倾斜角是锐角?钝角?直角?迁移与应用已知直线l经过点P(5,10),Q(m,12),若l的倾斜角θ≥90°,则实数m的取值范围是__________.根据斜率与倾斜角的关系(即当倾斜角0°≤α<90°时,斜率是非负的;当倾斜角90°<α<180°时,斜率是负的)来解答直线的倾斜角是锐角还是钝角问题.4.运用斜率公式解决三点共线问题活动与探究4已知三点A(a,2),B(3,7),C(-2,-9a)在同一条直线上,求实数a的值.迁移与应用已知三点A(1,-1),B(3,3),C(4,5),求证:三点在同一直线上.三点共线问题的证明(1)用斜率法证明三点共线问题.(2)三点共线问题也可利用线段长度之间的关系来证明,即若|AB |+|BC |=|AC |,则可判定A ,B ,C 三点共线.当堂检测1.对于下列命题:①若θ是直线l 的倾斜角,则0°≤θ<180°;②若k 是直线l 的斜率,则k ∈R ;③任一条直线都有倾斜角,但不一定都有斜率;④任一条直线都有斜率,但不一定有倾斜角.其中正确命题的个数是( ).A .1B .2C .3D .42.若直线l 的斜率k =-1,则其倾斜角等于( ).A .0° B.45° C.90° D.135°3.过点P (-2,m ),Q (m,4)的直线的斜率为1,则m 的值为( ).A .1B .4C .1或3D .1或44.已知A (3,0),B ⎝ ⎛⎭⎪⎫32,-3,C (a ,2a )三点共线,求实数a 的值. 5.已知直线l 的倾斜角为30°,且过点P (1,2)和Q (x,0),求该直线的斜率和x 的值.答案:课前预习导学预习导引1.一个点 方向2.(1)逆时针 倾斜角 0° 0°≤α<180°预习交流1 提示:任何一条直线都有唯一的倾斜角;倾斜角相同的直线不是唯一的,它们是一组平行线;不同的直线其倾斜角可能是相同的.(2)正切 tan α预习交流2 提示:并非每一条直线都有斜率,当直线与x 轴垂直时,即倾斜角为90°时,该直线的斜率不存在;当倾斜角0°≤α<90°时,斜率k ≥0;当90°<α<180°时,斜率k <0,故可知斜率k 的取值范围为(-∞,0)∪[0,+∞),即k ∈R .预习交流3 提示:斜率和倾斜角之间的关系是“数与形”的关系,斜率是个实数,倾斜角则是一个角;每条直线都有唯一的倾斜角与之对应,但并不是每条直线都有斜率,当倾斜角0°≤α<90°时,斜率是非负的,倾斜角越大,直线的斜率就越大;当倾斜角90°<α<180°时,斜率是负的,倾斜角越大,直线的斜率也越大.3.y 2-y 1x 2-x 1(x 2≠x 1) 预习交流4 提示:不能.斜率公式的适用条件是x 1≠x 2,当两点的横坐标相同时,不能用斜率公式,因为此时直线与x 轴垂直,其倾斜角为90°,斜率不存在.预习交流5 提示:无关,即k =y 2-y 1x 2-x 1=y 1-y 2x 1-x 2. 课堂合作探究问题导学活动与探究1 思路分析:由l 1⊥l 2知两直线与x 轴可构成直角三角形,因此可利用三角形内角和定理以及倾斜角的定义求出l 2的倾斜角.解:如图所示,由于l 2⊥l 1,所以△MAB 是直角三角形,而l 1的倾斜角等于30°,即∠MAB =30°,于是∠MBA =60°,从而∠MBx =180°-60°=120°,即直线l 2的倾斜角等于120°.迁移与应用 1.D2.0° 解析:将l 绕原点旋转30°后,直线与x 轴重合,其倾斜角为0°.活动与探究2 思路分析:利用斜率公式k =tan α和k =y 2-y 1x 2-x 1(x 1≠x 2)来解决. 解:(1)k 1=tan 30°=33,k 2=tan 45°=1. (2)直线AB 的斜率k AB =1-2-4-3=17; 直线BC 的斜率k BC =-1-10-(-4)=-24=-12; 直线AC 的斜率k AC =2-(-1)3-0=33=1. (3)当a =3时,斜率不存在.当a ≠3时,直线的斜率k =43-a . 迁移与应用 1.(1) 3 (2)52.解:①k =-2-1-1-1=32;②k =4-(-1)-2-1=-53;③k =2-210-2=0;④∵x 1=x 2=-2,∴斜率不存在.活动与探究3 思路分析:根据倾斜角与斜率的关系解决本题.若直线的倾斜角是锐角,则k >0,若为钝角,则k <0,若为直角,则斜率不存在.解:当过点A ,B 的直线的倾斜角是锐角时,k AB >0,根据斜率公式得k AB =3+12a -2=2a -1>0, ∴a >1;同理,当倾斜角为钝角时,k AB <0,即2a -1<0, ∴a <1.当倾斜角为直角时,A ,B 两点的横坐标相等.即2a =2,∴a =1.迁移与应用 m ≤5 解析:当θ=90°时,直线l 的斜率不存在,故m =5;当θ>90°时,倾斜角为钝角,l 的斜率k <0,即2m -5<0,解得m <5.综上m 的取值范围是m ≤5. 活动与探究4 思路分析:先用k AB =k BC 建立关于a 的方程,然后解方程求实数a 的值. 解:∵A ,B ,C 三点共线,且3≠-2,∴BC ,AB 的斜率都存在,且k AB =k BC .又∵k AB =7-23-a =53-a ,k BC =-9a -7-2-3=9a +75, ∴9a +75=53-a ,解得a =2或a =29. 迁移与应用 证明:∵k AB =3+13-1=2,k BC =5-34-3=2, ∴k AB =k BC .又直线AB 和BC 有公共点B ,∴A ,B ,C 三点共线.当堂检测1.C 2.D 3.A4.解:∵A ,B ,C 三点共线,3≠32, ∴AB ,AC 的斜率都存在,且k AB =k AC .∴-3-032-3=2a -0a -3,解得a =2. 5.解:由斜率的计算公式得,该直线的斜率k =tan 30°=33. 又l 过点P (1,2)和Q (x,0),则k =2-01-x =33,解得x =1-2 3.。
高中数学必修2第二章知识点+习题+答案

第二章 直线与平面的位置关系2.1空间点、直线、平面之间的位置关系1 平面含义:平面是无限延展的2 平面的画法与表示 〔1〕平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长〔如图〕〔2〕平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等. 3 三个公理:〔1〕公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内 符号表示为A ∈LB ∈L => L α A ∈αB ∈α公理1作用:判断直线是否在平面内〔2〕公理2:过不在一条直线上的三点,有且只有一个平面. 符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α,使A ∈α、B ∈α、C ∈α.公理2作用:确定一个平面的依据.〔3〕公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线. 符号表示为:P ∈α∩β =>α∩β=L,且P ∈L公理3作用:判定两个平面是否相交的依据2.1.2 空间中直线与直线之间的位置关系1 空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点; 平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点. 2 公理4:平行于同一条直线的两条直线互相平行. 符号表示为:设a 、b 、c 是三条直线a ∥bc ∥b强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用. 公理4作用:判断空间两条直线平行的依据.3 等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补4 注意点:① a'与b'所成的角的大小只由a 、b 的相互位置来确定,与O 的选择无关,为了简便,点O 一般取在两直线中的一条上; ② 两条异面直线所成的角θ∈<0, >;③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a ⊥b ; ④ 两条直线互相垂直,有共面垂直与异面垂直两种情形;D C B A α A·α C ·B· A · α P · α Lβ 共面直线=>a ∥c 2⑤计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角.— 2.1.4 空间中直线与平面、平面与平面之间的位置关系1、直线与平面有三种位置关系:〔1〕直线在平面内——有无数个公共点〔2〕直线与平面相交——有且只有一个公共点〔3〕直线在平面平行——没有公共点指出:直线与平面相交或平行的情况统称为直线在平面外,可用a α来表示a α a∩α=A a∥α2.2.直线、平面平行的判定与其性质2.2.1 直线与平面平行的判定1、直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.简记为:线线平行,则线面平行.符号表示:a αb β => a∥αa∥b平面与平面平行的判定1、两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行.符号表示:a βb βa∩b = P β∥αa∥αb∥α2、判断两平面平行的方法有三种:〔1〕用定义;〔2〕判定定理;〔3〕垂直于同一条直线的两个平面平行.— 2.2.4直线与平面、平面与平面平行的性质1、定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行. 简记为:线面平行则线线平行.符号表示:a∥αa β a∥bα∩β= b作用:利用该定理可解决直线间的平行问题.2、定理:如果两个平面同时与第三个平面相交,那么它们的交线平行.符号表示:α∥βα∩γ= a a∥bβ∩γ= b作用:可以由平面与平面平行得出直线与直线平行2.3直线、平面垂直的判定与其性质2.3.1直线与平面垂直的判定1、定义如果直线L与平面α内的任意一条直线都垂直,我们就说直线L与平面α互相垂直,记作L⊥α,直线L叫做平面α的垂线,平面α叫做直线L的垂面.如图,直线与平面垂直时,它们唯一公共点P叫做垂足.Lpα2、判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.注意点: a>定理中的"两条相交直线〞这一条件不可忽视;b>定理体现了"直线与平面垂直〞与"直线与直线垂直〞互相转化的数学思想.平面与平面垂直的判定1、二面角的概念:表示从空间一直线出发的两个半平面所组成的图形A梭 l βBα2、二面角的记法:二面角α-l-β或α-AB-β3、两个平面互相垂直的判定定理:一个平面过另一个平面的垂线,则这两个平面垂直.2.3.3—2.3.4直线与平面、平面与平面垂直的性质1、定理:垂直于同一个平面的两条直线平行.2性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.第二章点、直线、平面之间的位置关系A组一、选择题1.设,为两个不同的平面,l,m为两条不同的直线,且l⊂,m⊂β,有如下的两个命题:①若∥,则l∥m;②若l⊥m,则⊥.那么< >.A.①是真命题,②是假命题B.①是假命题,②是真命题C.①②都是真命题D.①②都是假命题2.如图,ABCD-A1B1C1D1为正方体,下面结论错误..的是< >.A.BD∥平面CB1D1B.AC1⊥BDC.AC1⊥平面CB1D1D.异面直线AD与CB1角为60°<第2题> 3.关于直线m,n 与平面,,有下列四个命题:①m ∥,n ∥且∥,则m∥n;②m ⊥,n ⊥且⊥,则m⊥n;③m ⊥,n ∥且∥,则m⊥n;④m ∥,n ⊥且⊥,则m∥n.其中真命题的序号是< >.A.①②B.③④C.①④D.②③4.给出下列四个命题:①垂直于同一直线的两条直线互相平行②垂直于同一平面的两个平面互相平行③若直线l1,l2与同一平面所成的角相等,则l1,l2互相平行④若直线l1,l2是异面直线,则与l1,l2都相交的两条直线是异面直线其中假.命题的个数是<>.A.1B.2C.3D.45.下列命题中正确的个数是< >.①若直线l 上有无数个点不在平面内,则l ∥②若直线l 与平面平行,则l 与平面内的任意一条直线都平行③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行④若直线l 与平面平行,则l 与平面内的任意一条直线都没有公共点A.0个B.1个C.2个D.3个6.两直线l1与l2异面,过l1作平面与l2平行,这样的平面< >.A.不存在B.有唯一的一个C.有无数个D.只有两个7.把正方形ABCD沿对角线AC折起,当以A,B,C,D四点为顶点的三棱锥体积最大时,直线BD和平面ABC所成的角的大小为< >.A.90°B.60°C.45°D.30°8.下列说法中不正确的....是<>.A.空间中,一组对边平行且相等的四边形一定是平行四边形B .同一平面的两条垂线一定共面C .过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内D .过一条直线有且只有一个平面与已知平面垂直 9.给出以下四个命题:①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面 ③如果两条直线都平行于一个平面,那么这两条直线互相平行 ④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直 其中真命题的个数是<>.A .4B .3C .2D .110.异面直线a ,b 所成的角60°,直线a ⊥c ,则直线b 与c 所成的角的X 围为<>. A .[30°,90°] B.[60°,90°] C.[30°,60°]D.[30°,120°] 二、填空题11.已知三棱锥P -ABC 的三条侧棱PA ,PB ,PC 两两相互垂直,且三个侧面的面积分别为S 1,S 2,S 3,则这个三棱锥的体积为.12.P 是△ABC 所在平面外一点,过P 作PO ⊥平面,垂足是O ,连PA ,PB ,PC .<1>若PA =PB =PC ,则O 为△ABC 的心; <2>PA ⊥PB ,PA ⊥PC ,PC ⊥PB ,则O 是△ABC 的心;<3>若点P 到三边AB ,BC ,CA 的距离相等,则O 是△ABC 的心; <4>若PA =PB =PC ,∠C =90º,则O 是AB 边的点; <5>若PA =PB =PC ,AB =AC ,则点O 在△ABC 的线上. 13.如图,在正三角形ABC 中,D ,E ,F 分别为各边的中点,G ,H ,I ,J 分别为AF ,AD ,BE ,DE 的中点,将△ABC 沿DE ,EF ,DF 折成三棱锥以后,GH 与IJ 所成角的度数为.14.直线l 与平面所成角为30°,l ∩=A ,直线m∈,则m 与l 所成角的取值X 围是.15.棱长为1的正四面体内有一点P ,由点P 向各面引垂线,垂线段长度分别为d 1,d 2,d 3,d 4,J<第13题>则d 1+d 2+d 3+d 4的值为.16.直二面角-l -的棱上有一点A ,在平面,内各有一条射线AB ,AC与l 成45°,AB ⊂,AC ⊂,则∠BAC =.三、解答题17.在四面体ABCD 中,△ABC 与△DBC 都是边长为4的正三角形. <1>求证:BC ⊥AD ;<2>若点D 到平面ABC 的距离等于3,求二面角A -BC -D 的正弦值;<3>设二面角A -BC -D 的大小为,猜想为何值时,四面体A -BCD 的体积最大.<不要求证明>18. 如图,在长方体ABCD —A 1B 1C 1D 1中,AB =2,BB 1=BC =1,E 为D 1C 1的中点,连结ED ,EC ,EB 和DB .<1>求证:平面EDB ⊥平面EBC ; <2>求二面角E -DB -C 的正切值.19*.如图,在底面是直角梯形的四棱锥S-ABCD 中,AD ∥BC ,∠ABC =90°,SA ⊥面ABCD ,SA =AB =BC =1,AD =21.<1>求四棱锥S —ABCD 的体积;<2>求面SCD 与面SBA 所成的二面角的正切值. <提示:延长 BA ,CD 相交于点 E ,则直线 SE 是 所求二面角的棱.><第19题>20*.斜三棱柱的一个侧面的面积为10,这个侧面与它所对棱的距离等于6,求这个棱柱的体积.<提示:在 AA 1 上取一点 P ,过 P 作棱柱的截面,使 AA 1 垂直于这个截面.><第20题>第二章 点、直线、平面之间的位置关系参考答案<第18题><第17题>一、选择题1.D 解析:命题②有反例,如图中平面∩平面=直线n ,l ⊂,m ⊂,且l ∥n ,m ⊥n ,则m ⊥l ,显然平面不垂直平面,<第1题>故②是假命题;命题①显然也是假命题, 2.D 解析:异面直线AD 与CB 1角为45°.3.D 解析:在①、④的条件下,m ,n 的位置关系不确定.4.D 解析:利用特殊图形正方体我们不难发现①②③④均不正确,故选择答案D . 5.B 解析:学会用长方体模型分析问题,A 1A 有无数点在平面ABCD 外,但AA 1与平面ABCD 相交,①不正确;A 1B 1∥平面ABCD ,显然A 1B 1不平行于BD ,②不正确;A 1B 1∥AB ,A 1B 1∥平面ABCD ,但AB ⊂平面ABCD 内,③不正确;l 与平面α平行,则l 与无公共点,l 与平面内的所有直线都没有公共点,④正确,应选B . <第5题>6.B 解析:设平面 过l 1,且 l 2∥,则 l 1上一定点 P 与 l 2 确定一平面,与的交线l 3∥l 2,且 l 3 过点 P . 又过点 P 与 l 2 平行的直线只有一条,即 l 3 有唯一性,所以经过 l 1 和 l 3 的平面是唯一的,即过 l 1 且平行于 l 2 的平面是唯一的.7.C 解析:当三棱锥D -ABC 体积最大时,平面DAC ⊥ABC ,取AC 的中点O ,则△DBO 是等腰直角三角形,即∠DBO =45°.8.D 解析:A .一组对边平行就决定了共面;B .同一平面的两条垂线互相平行,因而共面;C .这些直线都在同一个平面内即直线的垂面;D .把书本的书脊垂直放在桌上就明确了.9.B 解析:因为①②④正确,故选B .10.A 解析:异面直线a ,b 所成的角为60°,直线c ⊥a ,过空间任一点 P ,作直线 a ’∥a , b ’∥b , c ’∥c . 若a ’,b ’,c ’ 共面则 b ’ 与 c ’ 成 30°角,否则b ’与c ’所成的角的X 围为<30°,90°],所以直线b 与c 所成角的X 围为[30°,90°].二、填空题 11.313212S S S .解析:设三条侧棱长为a ,b ,c .则21ab =S 1,21bc =S 2,21ca =S 3 三式相乘:∴ 81a 2 b 2 c 2=S 1S 2S 3,∴ abc =23212S S S . ∵ 三侧棱两两垂直,∴ V =31abc ·21=313212S S S .12.外,垂,内,中,BC 边的垂直平分.解析:<1>由三角形全等可证得O 为△ABC 的外心;<2>由直线和平面垂直的判定定理可证得,O 为△ABC 的垂心; <3>由直线和平面垂直的判定定理可证得,O 为△ABC 的内心; <4>由三角形全等可证得,O 为 AB 边的中点;<5>由<1>知,O 在 BC 边的垂直平分线上,或说O 在∠BAC 的平分线上.13.60°.解析:将△ABC 沿DE ,EF ,DF 折成三棱锥以后,GH 与IJ 所成角的度数为60°. 14.[30°,90°].解析:直线l 与平面所成的30°的角为m 与l 所成角的最小值,当m 在内适当旋转就可以得到l ⊥m ,即m 与l 所成角的的最大值为90°. 15.36.解析:作等积变换:4331⨯×<d 1+d 2+d 3+d 4>=4331⨯·h ,而h =36. 16.60°或120°.解析:不妨固定AB ,则AC 有两种可能. 三、解答题17.证明:<1>取BC 中点O ,连结AO ,DO . ∵△ABC ,△BCD 都是边长为4的正三角形, ∴AO ⊥BC ,DO ⊥BC ,且AO ∩DO =O, ∴BC ⊥平面AOD .又AD ⊂平面AOD , ∴BC ⊥AD .<第17题>解:<2>由<1>知∠AOD 为二面角A -BC -D 的平面角,设∠AOD =,则过点D 作DE ⊥AD ,垂足为E .∵BC ⊥平面ADO ,且BC ⊂平面ABC ,∴平面ADO ⊥平面ABC .又平面ADO ∩平面ABC =AO , ∴DE ⊥平面ABC .∴线段DE 的长为点D 到平面ABC 的距离,即DE =3.又DO =23BD =23, 在Rt △DEO 中,sin =DODE =23,故二面角A -BC -D 的正弦值为23. <3>当=90°时,四面体ABCD 的体积最大.18.证明:<1>在长方体ABCD -A 1B 1C 1D 1中,AB =2,BB 1=BC =1,E 为D 1C 1的中点.∴△DD 1E 为等腰直角三角形,∠D 1ED =45°.同理∠C 1EC =45°.∴︒=∠90DEC ,即DE ⊥EC .在长方体ABCD -1111D C B A 中,BC ⊥平面11DCC D ,又DE ⊂平面11DCC D ,∴BC ⊥DE .又C BC EC = ,∴DE ⊥平面EBC .∵平面DEB 过DE ,∴平面DEB ⊥平面EBC . <2>解:如图,过E 在平面11DCC D 中作EO ⊥DC 于O .在长方体ABCD -1111D C B A 中,∵面ABCD⊥面11DCC D ,∴EO ⊥面ABCD .过O 在平面DBC 中作OF ⊥DB 于F ,连结EF ,∴EF ⊥BD .∠EFO 为二面角E -DB -C 的平面角.利用平面几何知识可得OF =51,<第18题> 又OE =1,所以,tan ∠EFO =5.19*.解:<1>直角梯形ABCD 的面积是M 底面=AB AD BC ⋅)(+21=43=1221+1⨯, ∴四棱锥S —ABCD 的体积是V =31·SA ·M 底面=31×1×43=41.<2>如图,延长BA ,CD 相交于点E ,连结SE ,则SE 是所求二面角的棱. ∵AD ∥BC ,BC =2AD , ∴EA =AB =SA ,∴SE ⊥SB∵SA ⊥面ABCD ,得面SEB ⊥面EBC ,EB 是交线. 又BC ⊥EB ,∴BC ⊥面SEB ,故SB 是SC 在面SEB 上的射影,∴CS ⊥SE ,∠BSC 是所求二面角的平面角. ∵SB =22+AB SA =2,BC =1,BC ⊥SB ,∴tan ∠BSC =22=SB BC ,<第19题> 即所求二面角的正切值为22. 20*.解:如图,设斜三棱柱ABC —A 1B 1C 1的侧面BB 1C 1C 的面积为10,A 1A 和面BB 1C 1C 的距离为6,在AA 1上取一点P 作截面PQR ,使AA 1⊥截面PQR ,AA 1∥CC 1,∴截面PQR ⊥侧面BB 1C 1C ,过P 作PO ⊥QR 于O ,则PO ⊥侧面BB 1C 1C ,且PO =6.∴V 斜=S △PQR ·AA 1=21·QR ·PO ·AA 1 =21·PO ·QR ·BB 1 =21×10×6 =30.<第20题>。
高中数学 第二章《2.2 直线、平面平行的判定及其性质》课件3 新人教A版必修2

说明理由.
(2)设E、F分别是A1B和B1C的中点,求证直线
EF//平面ABCD.
D1
C1
M A1
D
E
A
G
B1 F C
H B
小结
直线与平面平行的判定定理可简述为
“线线平行,则线面平行”
思想方法
通过直线间的平行,推证直线与平面平 行,即将直线与平面的平行关系(空间问题) 转化为直线间的平行关系(平面问题).
A α
M βB
C
N E
D
l
练习1
如果三个平面两两相交,那么它们的交线 位置如何?
bβ
γ l
α
β γα
ab l a
相交于一条交线 三条交线两两平行
三条交线相交 于一点
应用举例
练习2 一条斜线和两个平行平面相交,求证它和两
个平面所成的角相等.
小结
1. 知识小结 几个结论和性质的应用
2. 思想方法
面面平行
( )-网校通名校系列资料上,下精品资料! •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/62021/9/62021/9/6Sep-216-Sep-21
•12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/62021/9/62021/9/6Monday, September 06, 2021 13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/62021/9/62021/9/62021/9/69/6/2021
D′
数学必修二第二章知识点总结

数学必修二第二章知识点总结一、函数的概念与表示方法1. 函数定义:一个从集合A到集合B的映射,记为$f: A\rightarrow B$。
2. 函数的表示方法:- 公式法:$y = f(x)$- 图像法:通过坐标平面上的点集表示函数- 表格法:列出一系列的$(x, f(x))$值对二、函数的性质1. 单调性:- 单调递增:对于任意$x_1 < x_2$,有$f(x_1) \leq f(x_2)$ - 单调递减:对于任意$x_1 < x_2$,有$f(x_1) \geq f(x_2)$ 2. 奇偶性:- 奇函数:满足$f(-x) = -f(x)$- 偶函数:满足$f(-x) = f(x)$3. 周期性:存在正数T,使得对于任意x,有$f(x + T) = f(x)$三、函数的基本类型1. 一次函数:$y = ax + b$,其中a和b为常数2. 二次函数:$y = ax^2 + bx + c$,其中a、b和c为常数3. 指数函数:$y = a^x$,其中a>0且a≠14. 对数函数:$y = \log_a(x)$,其中a>0且a≠15. 三角函数:- 正弦函数:$y = \sin(x)$- 余弦函数:$y = \cos(x)$- 正切函数:$y = \tan(x)$四、函数的运算1. 函数的加法、减法、乘法和除法:- $(f + g)(x) = f(x) + g(x)$- $(f - g)(x) = f(x) - g(x)$- $(f \cdot g)(x) = f(x) \cdot g(x)$- $(f / g)(x) = \frac{f(x)}{g(x)}$,要求$g(x) \neq 0$ 2. 复合函数:$(f \circ g)(x) = f(g(x))$五、函数的图像1. 一次函数图像:直线2. 二次函数图像:抛物线3. 指数函数图像:指数曲线4. 对数函数图像:对数曲线5. 三角函数图像:- 正弦函数:波形曲线- 余弦函数:波形曲线- 正切函数:周期性波动曲线六、函数的应用1. 实际问题的建模与解决2. 优化问题中的最值求解3. 物理和工程问题中的应用请将以上内容复制到Word文档中,并根据实际需要进行格式设置,如标题加粗、分点符号的使用、段落缩进等,以确保文档的专业性。
人教版高中数学必修二第2章2.22.2.3直线与平面平行的性质

223直线与平面平行的性质学习目标1. 了解直线与平面平行的性质定理的探究以及证明过 程.2. 理解直线与平面平行的性质定理的含义并能应用.(重点) 3. 能够综合应用直线与平面平行的判定定理和性质定 理进行线面平行的相互转化.(难点) 自主预习。
播新和 zizHi jyt xi口新知初探I直线与平面平行的性质定理 文字语言一条直线与一个平面平行, 面的交线与该直线平行• 过该直线的任意一个平面与已知平符号语言a // a, a? 3, aA b? a /b 图形语言思考:若a // a b? a,则直线a 一定与直线b 平行吗?[提示]不一定.由a / a,可知直线a 与平面a 无公共点,又b? a,,所以a 与b 无公共点,所以直线a 与直线b 平行或异面.口初试身^□1. 如图,过正方体 ABCD-A'B C 'D 的棱BB '作一平面交平面 CDD'C 于EE : 则BB 与EE 的位置关系是()核心素养通过学习直线与平面 平行的性质,提升直观 想象、逻辑推理的数学 素养•A .平行B .相交C•异面D .不确定A [因为BB'// 平面CDD C ;BB 7 平面BB'E'E,平面BB'E^G 平面CDD C=EE 所以BB ' // EE '.]2. 设m、n是平面a外的两条直线,给出以下三个论断:①m// n;②m// a;③n// a以其中两个为条件,余下的一个为结论,构造三个命题,写出你认为正确的一个命题:________ .(用序号表示)①②?③(或①③?②)[设过m的平面B与a交于I •因为m//a,所以m//l,因为m // n,所以n // I,因为n?a, I? a,所以n // a]合作探究。
I星驀养直线与平面平行性质定理的应用[探究问题]1. 直线与平面平行性质定理的条件有哪些?[提示]线面平行的性质定理的条件有三个:(1) 直线a与平面a平行,即a / a;(2) 平面a、B相交于一条直线,即aG b;(3) 直线a在平面B内,即a? B三个条件缺一不可.2. 直线与平面平行的性质定理有什么作用?[提示]定理的作用:(1) 线面平行?线线平行;(2) 画一条直线与已知直线平行.3. 直线与平面平行的判定定理和性质定理有什么联系?[提示]经常利用判定定理证明线面平行,再利用性质定理证明线线平行.【例1】 如图,用平行于四面体 ABCD 的一组对棱AB , CD 的平面截此 四面体•求证:截面 MNPQ 是平行四边形.[证明] 因为AB //平面 MNPQ ,平面 ABC A 平面 MNPQ = MN ,且 AB?平面 ABC ,所以由线面平行的性质定理,知AB / MN ,同理,AB//PQ ,所以MN // PQ.同理可得 MQ // NP.所以截面MNPQ 为平行四边形.对蕊凍吭 将本例变为:如图所示,四边形 ABCD 是矩形,P ■ 平面ABCD , 过BC 作平面BCFE 交AP 于E ,交DP 于F.[证明]因为四边形ABCD 为矩形,所以BC / AD ,因为AD?平面PAD , BC?平面PAD ,所以BC /平面PAD.因为平面BCFE G 平面FAD = EF ,所以 BC //EF. 求证:四边形因为AD = BC, AD托F,所以BC M EF,所以四边形BCFE是梯形.1.利用线面平行性质定理解题的步骤:2 •证明线线平行的方法:(1) 定义:在同一个平面内没有公共点的两条直线平行.(2) 平行公理:平行于同一条直线的两条直线平行.a //a(3) 线面平行的性质定理:a? B ? a//b,应用时题目条件中需有线面aA b平行.【例2】如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA=3,点F在棱RA上,且AF = 1,点E在棱PD上,若CE//平面BDF,求PE : ED 的值.B[解]过点E作EG // FD交AP于点G,连接CG,连接AC交BD于点O, 连接FO.因为EG// FD , EG?平面BDF, FD?平面BDF ,所以EG//平面BDF ,又EG A CE= E, CE//平面BDF, EG?平面CGE, CE?平面CGE,所以平面CGE//平面BDF,又CG?平面CGE,所以CG//平面BDF,又平面BDF A平面PAC= FO, CG?平面PAC,所以FO // CG,又O为AC的中点,所以F为AG的中点,所以FG = GP= 1,所以E为PD的中点,PE : ED= 1 : 1.利用线面平行的性质定理计算有关问题的三个关键点:(1) 根据已知线面平行关系推出线线平行关系.(2) 在三角形内利用三角形中位线性质、平行线分线段成比例定理推出有关线段的关系.(3) 利用所得关系计算求值.働跟礙训练I如图所示,在棱长为6的正方体ABCD-A i B i C i D i 中,点E, F 分别是棱C i D i , B i C i 的中点,过A , E , F 三点作该正方体的截面,则截面的周长为 ____________ .6 13+ 3 2 [如图所示,延长EF ,A i B i 相交于点M ,连接AM ,交BB i 于 点H ,连接FH ,延长FE , A i D i 相交于点N ,连接AN 交DD i 于点G ,连接EG ,可得截面五边形AHFEG ,因为几何体ABCD-A i B i C i D i 是棱长为6的正方体,且ii E 、F 分别是棱 C i D i , B i C i 的中点,所以 EF = 3 2,易知 B i M = C i E = QC i D i = 2 A i B i ,又 B i H //AA i ,所以 B i H = iAA i = 2, J 则 BH = 4,易知 AG = AH = 62 + 42= 2 i3, EG = FH =、32 + 22= i3,所以截面的周长为 6 i3+ 3,2]i •在遇到线面平行时,常需作出过已知直线与已知平面相交的辅助平面, 以便运用线面平行的性质.2 •要灵活应用线线平行、线面平行的相互联系、相互转化•在解决立体几 何中的平行问题时,一般都要用到平行关系的转化.转化思想是解决这类问题的 最有效的方法.当堂达标科固观基1 •如图,在三棱锥SABC中,E, F分别是SB SC上的点,且EF //平面ABC,则()A. EF与BC相交B. EF // BCC. EF与BC异面D. 以上均有可能B [因为平面SBC n平面ABC= BC,又因为EF //平面ABC,所以EF // BC.]2 .直线a//平面a, a内有n条直线交于一点,则这n条直线中与直线a平行的直线有()A. 0条B . 1条C. 0条或1条 D .无数条C [过直线a与交点作平面B,设平面B与a交于直线b,则a// b,若所给n 条直线中有1条是与b重合的,则此直线与直线a平行,若没有与b重合的,则与直线a平行的直线有0条.]3. 过正方体ABCD-A1B1C1D1的三顶点A1, C1, B的平面与底面ABCD所在的平面的交线为I,则I与A1C1的位置关系是__________ .平行[因为A1C1 /平面ABCD,A1C1?平面A1C1B,平面ABCD n平面A1C1B= I,由线面平行的性质定理,所以A1C1//IJ4. 如图,在三棱柱ABC-A1B1C1中,D是棱CC1上的一点,P是AD的延长线与A1C1延长线的交点,且PB1//平面BDA1,求证:CD = C1D.[证明]如图,连接AB1与BA1交于点0,连接0D,因为PB i // 平面BDA i, PB i?平面AB i P,平面AB i P n平面BDA i = OD,所以OD // PB i, 又AO= B i O,所以AD = PD,又AC// C i P,所以CD = C i D.。
高中数学第二章平面解析几何初步22直线的方程223两条直线的位置关系课件新人教B版必修2

∴n=-1,
∴所求直线方程为 x+2y-1=0.
2021/4/17
高中数学第二章平面解析几何初步22直线的方
25
程223两条直线的位置关系课件新人教B版必修
【知识点拨】 (1)与定直线 Ax+By+C=0(A2+B2≠0)垂直 的直线方程为 Bx-Ay+m=0;
(2)与定直线 Ax+By+C=0(A2+B2≠0)平行的直线方程为 Ax+By+n=0(n≠C).
已知两直线 l1:x+my+3=0,l2:(m-
1)x+2my+2m=0,若 l1∥l2,则 m 为( )
A.0
B.-1 或12
C.3
D.0 或 3
解析:由 1·2m-m(m-1)=0,得 m=0 或 m=3.
当 m=3 时,l1:x+3y+3=0,l2:2x+6y+6=0,
l1 与 l2 重合,∴m≠3;
根据下列条件,分别求直线方程: (1)经过点 A(3,0)且与直线 2x+y-5=0 垂直的直线方程; (2)经过直线 x-y-1=0 与 2x+y-2=0 的交点,且平行于 直线 x+2y-3=0 的直线方程.
2021/4/17
高中数学第二章平面解析几何初步22直线的方
23
程223两条直线的位置关系课件新人教B版必修
A.2
B.-2
C.12
D.-12
【解析】 由 l1⊥l2,得 m+2×(-1)=0,∴m=2.故选 A.
【答案】 A
2021/4/17
高中数学第二章平面解析几何初步22直线的方
20
程223两条直线的位置关系课件新人教B版必修
直线 y=kx 与直线 y=2x+1 垂直,则 k
等于( )
A.-2
数学必修二第二章知识点总结

数学必修二第二章知识点总结第二章一元二次函数1. 一元二次函数的概念一元二次函数的一般形式为y = ax^2 + bx + c(其中a≠0),其中x为自变量,y为因变量,a、b、c为常数且a ≠ 0。
一元二次函数一般表示为y = f(x),其中x ∈ R,f(x) = ax^2 + bx + c。
这个函数是二次函数,其中x的最高幂为2,也称为二次方程。
2. 一元二次函数的图像特征一元二次函数的图象是平面直角坐标系xy平面内的一个二次曲线。
若a>0,则抛物线开口朝上;若a<0,则抛物线开口朝下。
(1)当a > 0时,抛物线的最低点为最小值;(2)当a < 0时,抛物线的最高点为最大值;(3)当a = 0时,函数为一次函数。
3. 一元二次函数的性质(1)顶点坐标:对于一元二次函数y = ax^2 + bx + c,其中,顶点的横坐标为x = -b/2a,纵坐标为y = f(-b/2a);(2)对称轴:一元二次函数的图像关于直线x = -b/2a对称;(3)奇偶性:当a为偶数时,函数为偶函数,对称于y轴;当a为奇数时,函数为奇函数,对称于原点;(4)增减性:a > 0时,函数y = ax^2 + bx + c在(-∞,-b/2a)上是递减的,在(-b/2a,+∞)上是递增的;a < 0时,函数在(-∞,-b/2a)上是递增的,在(-b/2a,+∞)上是递减的。
4. 一元二次函数的应用一元二次函数在现实生活中有着广泛的应用,比如抛物线的运动、建筑工程、生产成本等,都可以用一元二次函数进行建模和分析。
5. 一元二次函数的解析式与图像之间的关系通过一元二次函数的解析式,我们可以推断出函数的开口方向、最值、零点、对称轴等图像特征,并通过这些特征来对一元二次函数进行分析和应用。
6. 一元二次函数的图像绘制方法(1)结合曲线的开口方向、顶点坐标、对称轴等特征来绘制;(2)通过利用多个点来构造函数的图象(如顶点、零点、对称轴等)。
高中数学必修2(人教B版)第二章平面解析几何初步2.2知识点总结含同步练习题及答案

|a| = |b|
⋯⋯②
由 ①② 解得 a = b = 5 或 a = −1 ,b = 1 ,所以直线方程为 x + y − 5 = 0 或 x − y + 1 = 0. (ii)当 a = b = 0 时,直线过原点和 P (2, 3) ,所以直线方程为 3x − 2y = 0 . 综上可知,所求直线方程为 x + y − 5 = 0 或 x − y + 1 = 0 或 3x − 2y = 0 . 已知三角形的顶点是 A(−5, 0) ,B(3, −3) ,C (0, 2) ,求 AC 边所在直线的方程,以及该边上的 中线所在直线的方程. 解:过点 A(−5, 0) ,C (0, 2) 的两点式方程为
直线的基本量与方程 直线与直线的位置关系 直线的相关计算
三、知识讲解
1.直线的基本量与方程 描述: 直线的倾斜角 当直线l 与x 轴相交时,我们取 x 轴作为基准,x 轴正向与直线 l 向上方向之间所成的角α叫做直 线l 的倾斜角(angle of inclination).直线倾斜角α 的取值范围为0 ∘ ≤ α < 180 ∘ .
2 y − (−3) x−3 由两点式得直线 BD 的方程为 ,整理可得 8x + 11y + 9 = 0 ,这就是 = 1 − (−3) −5 − 3 2 AC 边上的中线所在直线的方程.
⎪ ⎩
2.直线与直线的位置关系 描述: 直线 l 1 :y = k1 x + b 1 ,l 2 :y = k2 x + b 2 . 当 l 1 与 l 2 平行时,则 k1 = k2 且 b 1 ≠ b 2 ; 当 l 1 与 l 2 重合时,则 k1 = k2 且 b 1 = b 2 ; 当 l 1 与 l 2 相交时,则 k1 ≠ k2 ,特别地,若两直线垂直,则 k1 ⋅ k2 =#43; B 1 y + C1 = 0, A 2 1 + B 1 ≠ 0 ,l 2 :A 2 x + B 2 y + C2 = 0, A 2 + B 2 ≠ 0 . 当 l 1 与 l 2 平行时,则 A 1 B 2 = A 2 B 1 且 B 1 C2 ≠ B 2 C1 ; 当 l 1 与 l 2 重合时,则 A 1 B 2 = A 2 B 1 且 B 1 C2 = B 2 C1 ; 当 l 1 与 l 2 相交时,则 A 1 B 2 ≠ A 2 B 1 ,特别地,若两直线垂直,则 A 1 A 2 + B 1 B 2 = 0 . 例题: 直线 3x − 2y + m = 0 和 (m 2 + 1)x + 3y − 3m = 0 的位置关系是( A.平行 B.重合 C.相交 D.不确定 解:两直线的斜率分别为 交. )
数学必修二第二章知识点

数学必修二第二章知识点第二章是数学必修二中的一个重要章节,主要涉及到函数及其运算。
函数是数学中一个非常重要的概念,它描述了一种输入和输出之间的关系。
在本章中,我们将学习函数的定义、图像、性质以及函数的运算。
1. 函数的定义函数是一种将每个输入值映射到唯一的输出值的关系。
我们通常用字母表示函数,例如 f(x)、g(x)。
在函数中,x被称为自变量(输入值),f(x)被称为因变量(输出值)。
函数可以通过几何图形(如曲线)或表格来表示。
2. 函数的图像函数的图像是函数在平面坐标系上的表示,横轴表示自变量,纵轴表示因变量。
函数的图像可以帮助我们直观地了解函数的特征,如增减性、奇偶性、周期性等。
我们可以通过观察函数的图像来获取函数的一些主要信息。
3. 函数的性质函数有很多重要的性质,包括定义域、值域、单调性、奇偶性等。
- 定义域:函数的定义域是自变量的取值范围,也就是使函数有意义的自变量的集合。
- 值域:函数的值域是因变量的取值范围,也就是函数所有可能的输出值的集合。
- 单调性:如果函数在定义域内的任意两个点x1、x2满足x1<x2时,f(x1)<f(x2),则函数是递增的;如果f(x1)>f(x2),则函数是递减的。
- 奇偶性:如果对于任意x,有f(-x)=f(x),则函数是偶函数;如果对于任意x,有f(-x)=-f(x),则函数是奇函数。
4. 函数的运算函数之间可以进行运算,主要包括加法、减法、乘法和除法。
这些函数的运算可以通过图像或公式来表达。
- 加法:设f(x)和g(x)是两个函数,则它们的和是h(x)=f(x)+g(x)。
函数h(x)的图像是函数f(x)和g(x)图像之间对应点的纵坐标相加。
- 减法:设f(x)和g(x)是两个函数,则它们的差是h(x)=f(x)-g(x)。
函数h(x)的图像是函数f(x)和g(x)图像之间对应点的纵坐标相减。
- 乘法:设f(x)和g(x)是两个函数,则它们的积是h(x)=f(x)g(x)。
高中人教版必修2数学课件第二章2.1.2精选ppt课件

() A.2 对
B.3 对
C.6 对
D.12 对
解析:选 C.如图所示,在长方体 AC1 中,与对角线 AC1 成异面 直线位置关系的是:A1D1、BC、BB1、DD1、A1B1、DC,所以 组成 6 对异面直线.
3.如图,点 G、H、M、N 分别是三棱柱的顶点或所在棱的中 点,则表示直线 GH,MN 是异面直线的图形是________.
(1)判断两直线平行仍是立体几何中的一个重要组成部分,除了 平面几何中常用的判断方法以外,公理 4 也是判断两直线平行的 重要依据. (2)证明角相等,利用空间等角定理是常用的思考方法;另外也 可以通过证明两个三角形全等或相似来证明两角相等.在应用等 角定理时,应注意说明这两个角同为锐角、直角或钝角.
(2)异面直线所成的角 两条异面直线所成的角是由两条相交直线所成的角扩充而成的, 由平移原理可知,当两条异面直线在空间的位置确定后,它们所 成的角的大小也就随之确定了.
1.分别在两个平面内的两条直线间的位置关系是( )
A.异面
B.平行
C.相交
D.以上均有可能
答案:D
2.长方体的一条体对角线与长方体的棱所组成的异面直线有
章 点、直线、面之间的位置关系
2.1.2 空间中直线与直线之间的位置关系
第二章 点、直线、平面之间的位置关系
1.会判断空间两直线的位置关系. 2.理解两异面直线的 定义,会求两异面直线所成的角. 3.能用公理 4 解决一些简单的相关问题.
1.空间直线的位置关系 (1)异面直线 ①定义:把不同在_任__何__一__个__平面内的两条直线叫做异面直线. ②画法:(通常用平面衬托)
A.6 C.5 答案:B
B.4 D.8
3.若正方体 ABCD-A1B1C1D1 中∠BAE=25°.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章点、直线、平面之间的位置关系A组一、选择题1.设α,β为两个不同的平面,l,m为两条不同的直线,且l⊂α,m⊂β,有如下的两个命题:①若 α∥β,则l∥m;②若l⊥m,则 α⊥β.那么().A.①是真命题,②是假命题B.①是假命题,②是真命题C.①②都是真命题D.①②都是假命题2.如图,ABCD-A1B1C1D1为正方体,下面结论错误..的是().A.BD∥平面CB1D1B.AC1⊥BDC.AC1⊥平面CB1D1D.异面直线AD与CB1角为60°(第2题) 3.关于直线m,n与平面 α,β,有下列四个命题:①m∥α,n∥β 且 α∥β,则m∥n;②m⊥α,n⊥β 且 α⊥β,则m⊥n;③m⊥α,n∥β 且 α∥β,则m⊥n;④m∥α,n⊥β 且 α⊥β,则m∥n.其中真命题的序号是().A.①②B.③④C.①④D.②③4.给出下列四个命题:①垂直于同一直线的两条直线互相平行②垂直于同一平面的两个平面互相平行③若直线l1,l2与同一平面所成的角相等,则l1,l2互相平行④若直线l1,l2是异面直线,则与l1,l2都相交的两条直线是异面直线其中假.命题的个数是().A.1 B.2 C.3 D.45.下列命题中正确的个数是().①若直线l上有无数个点不在平面 α 内,则l∥α②若直线l与平面 α 平行,则l与平面 α 内的任意一条直线都平行③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行④若直线l与平面 α 平行,则l与平面 α 内的任意一条直线都没有公共点A.0个B.1个C.2个D.3个6.两直线l1与l2异面,过l1作平面与l2平行,这样的平面().A.不存在B.有唯一的一个C.有无数个D.只有两个7.把正方形ABCD沿对角线AC折起,当以A,B,C,D四点为顶点的三棱锥体积最大时,直线BD和平面ABC所成的角的大小为().A.90°B.60°C.45°D.30°8.下列说法中不正确的....是().A.空间中,一组对边平行且相等的四边形一定是平行四边形B.同一平面的两条垂线一定共面C.过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内D.过一条直线有且只有一个平面与已知平面垂直9.给出以下四个命题:①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面③如果两条直线都平行于一个平面,那么这两条直线互相平行④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直其中真命题的个数是().A.4 B.3 C.2 D.110.异面直线a,b所成的角60°,直线a⊥c,则直线b与c所成的角的范围为().A.[30°,90°]B.[60°,90°]C.[30°,60°]D.[30°,120°]二、填空题11.已知三棱锥P-ABC的三条侧棱P A,PB,PC两两相互垂直,且三个侧面的面积分别为S1,S2,S3,则这个三棱锥的体积为.12.P是△ABC所在平面 α 外一点,过P作PO⊥平面 α,垂足是O,连P A,PB,PC.(1)若P A=PB=PC,则O为△ABC的心;(2)P A ⊥PB ,P A ⊥PC ,PC ⊥PB ,则O 是△ABC 的 心;(3)若点P 到三边AB ,BC ,CA 的距离相等,则O 是△ABC 的 心; (4)若P A =PB =PC ,∠C =90º,则O 是AB 边的 点; (5)若P A =PB =PC ,AB =AC ,则点O 在△ABC 的 线上. 13.如图,在正三角形ABC 中,D ,E ,F 分别为各边的中点,G ,H ,I ,J 分别为AF ,AD ,BE ,DE 的中点,将△ABC 沿DE ,EF ,DF 折成三棱锥以后,GH 与IJ 所成角的度数为 .14.直线l 与平面 α 所成角为30°,l ∩α=A ,直线m ∈α,则m 与l 所成角的取值范围 是 .15.棱长为1的正四面体内有一点P ,由点P 向各面引垂线,垂线段长度分别为d 1,d 2,d 3,d 4,则d 1+d 2+d 3+d 4的值为 .16.直二面角 α-l -β 的棱上有一点A ,在平面 α,β 内各有一条射线AB ,AC 与l 成45°,AB ⊂α,AC ⊂β,则∠BAC = .三、解答题17.在四面体ABCD 中,△ABC 与△DBC 都是边长为4的正三角形. (1)求证:BC ⊥AD ;(2)若点D 到平面ABC 的距离等于3,求二面角A -BC -D 的正弦值;(3)设二面角A -BC -D 的大小为 θ,猜想 θ 为何值时,四面体A -BCD 的体积最大.(不要求证明)J(第13题)(第17题)18. 如图,在长方体ABCD —A 1B 1C 1D 1中,AB =2,BB 1=BC =1,E 为D 1C 1的中点,连结ED ,EC ,EB 和DB .(1)求证:平面EDB ⊥平面EBC ; (2)求二面角E -DB -C 的正切值.19*.如图,在底面是直角梯形的四棱锥S-ABCD 中,AD ∥BC ,∠ABC =90°, SA ⊥面ABCD ,SA =AB =BC =1,AD =21. (1)求四棱锥S —ABCD 的体积;(2)求面SCD 与面SBA 所成的二面角的正切值. (提示:延长 BA ,CD 相交于点 E ,则直线 SE 是 所求二面角的棱.)(第19题)(第18题)20*.斜三棱柱的一个侧面的面积为10,这个侧面与它所对棱的距离等于6,求这个棱柱的体积.(提示:在AA1上取一点P,过P作棱柱的截面,使AA1垂直于这个截面.)(第20题)第二章点、直线、平面之间的位置关系参考答案A组一、选择题1.D解析:命题②有反例,如图中平面 α∩平面 β=直线n,l⊂α,m⊂β,且l∥n,m⊥n,则m⊥l,显然平面 α 不垂直平面β, (第1题)故②是假命题;命题①显然也是假命题,2.D解析:异面直线AD与CB1角为45°.3.D解析:在①、④的条件下,m,n的位置关系不确定.4.D解析:利用特殊图形正方体我们不难发现①②③④均不正确,故选择答案D.5.B解析:学会用长方体模型分析问题,A1A有无数点在平面ABCD外,但AA1与平面ABCD相交,①不正确;A1B1∥平面ABCD,显然A1B1不平行于BD,②不正确;A1B1∥AB,A1B1∥平面ABCD,但AB⊂平面ABCD内,③不正确;l与平面α平行,则l与 α 无公共点,l与平面 α 内的所有直线都没有公共点,④正确,应选B.(第5题) 6.B解析:设平面α 过l1,且l2∥α,则l1上一定点P与l2确定一平面β ,β 与α 的交线l3∥l2,且l3 过点P. 又过点P与l2平行的直线只有一条,即l3有唯一性,所以经过l1和l3的平面是唯一的,即过l1且平行于l2的平面是唯一的.7.C解析:当三棱锥D -ABC 体积最大时,平面DAC ⊥ABC ,取AC 的中点O ,则△DBO 是等腰直角三角形,即∠DBO =45°.8.D解析:A .一组对边平行就决定了共面;B .同一平面的两条垂线互相平行,因而共面;C .这些直线都在同一个平面内即直线的垂面;D .把书本的书脊垂直放在桌上就明确了.9.B解析:因为①②④正确,故选B . 10.A解析:异面直线a ,b 所成的角为60°,直线c ⊥a ,过空间任一点 P ,作直线 a ’∥a , b ’∥b , c ’∥c . 若a ’,b ’,c ’ 共面则 b ’ 与 c ’ 成 30° 角,否则 b ’ 与 c ’ 所成的角的范围为(30°,90°],所以直线b 与c 所成角的范围为[30°,90°] .二、填空题 11.313212S S S .解析:设三条侧棱长为 a ,b ,c . 则 21ab =S 1,21bc =S 2,21ca =S 3 三式相乘: ∴81a 2 b 2 c 2=S 1S 2S 3, ∴ abc =23212S S S . ∵ 三侧棱两两垂直,∴ V =31abc ·21=313212S S S .12.外,垂,内,中,BC 边的垂直平分.解析:(1)由三角形全等可证得 O 为△ABC 的外心;(2)由直线和平面垂直的判定定理可证得,O 为△ABC 的垂心; (3)由直线和平面垂直的判定定理可证得,O 为△ABC 的内心; (4)由三角形全等可证得,O 为 AB 边的中点;(5)由(1)知,O 在 BC 边的垂直平分线上,或说 O 在∠BAC 的平分线上. 13.60°.解析:将△ABC 沿DE ,EF ,DF 折成三棱锥以后,GH 与IJ 所成角的度数为60°.14.[30°,90°].解析:直线l 与平面 α 所成的30°的角为m 与l 所成角的最小值,当m 在 α 内适当旋转就可以得到l ⊥m ,即m 与l 所成角的的最大值为90°.15.36. 解析:作等积变换:4331⨯×(d 1+d 2+d 3+d 4)=4331⨯·h ,而h =36. 16.60°或120°.解析:不妨固定AB ,则AC 有两种可能. 三、解答题17.证明:(1)取BC 中点O ,连结AO ,DO . ∵△ABC ,△BCD 都是边长为4的正三角形, ∴AO ⊥BC ,DO ⊥BC ,且AO ∩DO =O , ∴BC ⊥平面AOD .又AD ⊂平面AOD ,∴BC ⊥AD . (第17题)解:(2)由(1)知∠AOD 为二面角A -BC -D 的平面角,设∠AOD =θ,则过点D 作DE ⊥AD ,垂足为E .∵BC ⊥平面ADO ,且BC ⊂平面ABC ,∴平面ADO ⊥平面ABC .又平面ADO ∩平面ABC =AO , ∴DE ⊥平面ABC .∴线段DE 的长为点D 到平面ABC 的距离,即DE =3. 又DO =23BD =23, 在Rt △DEO 中,sin θ=DODE =23,故二面角A -BC -D 的正弦值为23. (3)当 θ=90°时,四面体ABCD 的体积最大.18.证明:(1)在长方体ABCD -A 1B 1C 1D 1中,AB =2,BB 1=BC =1,E 为D 1C 1的中点.∴△DD 1E 为等腰直角三角形,∠D 1ED =45°.同理∠C 1EC =45°.∴︒=∠90DEC ,即DE ⊥EC .在长方体ABC D -1111D C B A 中,BC ⊥平面11DCC D ,又DE ⊂平面11DCC D ,∴BC ⊥DE .又C BC EC = ,∴DE ⊥平面EBC .∵平面DEB 过DE ,∴平面DEB ⊥平面EBC .(2)解:如图,过E 在平面11DCC D 中作EO ⊥DC 于O .在长方体ABCD -1111D C B A 中,∵面ABCD ⊥面11DCC D ,∴EO ⊥面ABCD .过O 在平面DBC 中作OF ⊥DB 于F ,连结EF ,∴EF ⊥BD .∠EFO 为二面角E -D B -C 的平面角.利用平面几何知识可得OF =51, (第18题) 又OE =1,所以,tan ∠EFO =5.19*.解:(1)直角梯形ABCD 的面积是M 底面=AB AD BC ⋅)(+21=43=1221+1⨯, ∴四棱锥S —ABCD 的体积是V =31·SA ·M 底面=31×1×43=41.(2)如图,延长BA ,CD 相交于点E ,连结SE ,则SE 是所求二面角的棱. ∵AD ∥BC ,BC =2AD , ∴EA =AB =SA ,∴SE ⊥SB∵SA ⊥面ABCD ,得面SEB ⊥面EBC ,EB 是交线. 又BC ⊥EB ,∴BC ⊥面SEB ,故SB 是SC 在面SEB 上的射影,∴CS ⊥SE ,∠BSC 是所求二面角的平面角. ∵SB =22+AB SA =2,BC =1,BC ⊥SB , ∴tan ∠BSC =22=SB BC , (第19题)即所求二面角的正切值为22. 20*.解:如图,设斜三棱柱ABC —A 1B 1C 1的侧面BB 1C 1C 的面积为10,A 1A 和面BB 1C 1C 的距离为6,在AA 1上取一点P 作截面PQR ,使AA 1⊥截面PQR ,AA 1∥CC 1,∴截面PQR ⊥侧面BB 1C 1C ,过P 作PO ⊥QR 于O ,则PO ⊥侧面BB 1C 1C ,且(第20题)第 11 页 共 11 页 PO =6. ∴V 斜=S △PQR ·AA 1=21·QR ·PO ·AA 1 =21·PO ·QR ·BB 1 =21×10×6=30.。
