课时跟踪训练九答案
人教版高中物理选修3-1第二章第8、9节课时跟踪训练(含答案解析).docx

高中物理学习材料桑水制作[课时跟踪训练](满分50分时间30分钟)一、选择题(本大题共8个小题,每小题4分,共计32分。
每小题至少有一个选项正确,把正确选项前的字母填在题后的括号内)1.下列说法中正确的是( )A.欧姆表的每一挡测量范围都是0到∞B.欧姆表只能用来粗略地测量电阻C.用欧姆表测电阻,指针越接近刻度中央误差越大D.用欧姆表测电阻,指针越靠近刻度右边误差越小解析:从欧姆表的使用,我们知道用每一挡测量前都要进行电阻调零,而两表笔断开时,相当于电阻为无穷大,故每一挡测量范围都是从0到∞,故A正确;因欧姆表电阻刻度线不均匀,即电流随电阻非线性变化,故测量出的电阻不可能是准确值,只能用来粗测,故B正确;欧姆表测电阻,中值附近最准确,越靠近两侧误差越大,故C、D错误。
答案:AB2.欧姆表电路及刻度盘如图1所示,现因表头损坏,换用一个新表头。
甲表头满偏电流为原来表头的2倍,内阻与原表头相同;乙表头满偏电流与原表头相同,内阻为原表头的2倍,则换用甲表头和换用乙表头后刻度盘的中值电阻分别为( )A.100 Ω,100 ΩB.200 Ω,100 ΩC.50 Ω,100 ΩD.100 Ω,200 Ω图 1解析:由欧姆表改装原理及闭合电路欧姆定律可得,甲表头满偏电流为原表头的2倍,内阻与原表头相同,在电动势不变的情况下,其中值电阻变为原来的1/2,即50 Ω;乙表头满偏电流与原表头相同,内阻为原表头的2倍,在电动势不变的情况下,其中值电阻仍然不变,即100 Ω。
答案:C3.用多用电表测直流电压U和测电阻R时,若红表笔插入正(+)插孔,则( )A.测电压U时红表笔电势高,测电阻R时电流从红表笔流出电表B.不管测电压U还是测电阻R,都是红表笔电势高C.测电压U时电流从红表笔流入电表,测电阻R时电流从红表笔流入电表D.测电压U时电流从红表笔流出电表,测电阻R时电流从红表笔流出电表解析:用多用电表测直流电压U时,多用电表就是电压表,电流从红表笔流入电表,从黑表笔流出电表;用多用电表测电阻R时,多用电表内部有电源,电流也是从红表笔流入电表,从黑表笔流出电表,故C正确,D错误;测电压时,电流源于外电路的电压,红表笔电势高;测电阻时,电流源于内电路的电压,红表笔电势低,A、B错误。
语文同步优化指导(人教版必修4)课时跟踪训练9+Word版含解析

课时跟踪训练(九)父母与孩子之间的爱A组:基础达标(建议用时20分钟)一、基础积累1.下列加点字的注音全都正确的一项是()A.诞.生(dàn)刹.那(shà)撕.碎(sī)缺陷.(xiàn)B.怀孕.(yùn)挑.选(tiāo)典型.(xínɡ)履.行(lǔ)C.求援.(yuán)专横.(hénɡ)辜.负(ɡū)罪孽.(niè)D.仁慈.(cí)赢.得(yínɡ)渊.源(yuān)秩.序(zhì)解析:A项,“刹”应读chà;B项,“履”应读lǚ;C项,“横”应读hènɡ。
答案:D2.下列词语中书写完全正确的一项是()A.恐惧辩认给予综合B.哭泣空虚因素严厉C.遵徇愿望鉴于树立D.幼稚惩罚阻碍慨念解析:A项,辩—辨;C项,徇—循;D项,慨—概。
答案:B3.依次填入下列横线处的词语,最恰当的一组是()①深入贯彻全军政治工作会议精神,________推进依法治军、从严治军,全面加强部队革命化现代化正规化建设。
②15日,香港警方________完持续近80天的“占领中环”非法集会后,各种商铺便纷纷打出节日促销广告。
③高兴了________躺在洁白的雪堆里面,仰望浩瀚的苍穹,静观疏林水墨画,夕阳下的雪山,任风雪亲近你的脸颊,任白云飘荡蓝天,一种世外桃源________的清静感觉,痛痛快快享受那种畅游后的快感。
A.切实处理随意超凡脱俗B.扎实处置任意超尘出世C.扎实处理随意超尘出世D.切实处置任意超凡脱俗解析:“扎实”侧重于过程的踏实、牢固。
“处置”包含惩罚性的处理。
“任意”是不经心的意思,更符合语境。
“超尘出世”指超脱尘世,到了另外的境界。
“超凡脱俗”指超脱凡俗,成为一个清高的人。
答案:B4.下列各句中加点成语的使用,全部不正确的一组是()①“徒步三千,流亡万里”,这是中华民族历史上硕果仅存....的一次悲壮的师生长征,堪称我国教育史上一次可歌可泣的文化长征。
2019鲁科版高中化学选修五练习:第2章 课时跟踪检测(九) 糖类 Word版含答案

课时跟踪检测(九)糖类1.下列说法中正确的是()A.凡符合通式C n(H2O)m的化合物一定属于糖类,不符合此通式的不属于糖类B.凡能溶于水且具有甜味的化合物都属于糖类C.葡萄糖是一种单糖的主要原因是它是一种多羟基醛D.葡萄糖分子中含有醛基,它具有还原性解析:选D有些符合通式C n(H2O)m的物质不属于糖类,如乙酸(CH3COOH)、甲酸甲酯(HCOOCH3),有些不符合通式C n(H2O)m的物质属于糖类,如鼠李糖(C6H12O5);能溶于水且具有甜味的物质不一定是糖类,如糖精;葡萄糖是单糖的主要原因是它不能水解成更简单的糖;葡萄糖分子中含有醛基,它具有还原性。
2.下列关于葡萄糖与蔗糖的比较错误的是()A.分子式不同,蔗糖的分子式是C12H22O11B.分子结构不同,蔗糖不含醛基C.它们不是同分异构体,但互为同系物D.蔗糖能水解,葡萄糖不能解析:选C葡萄糖的分子式为C6H12O6,蔗糖的分子式为C12H22O11,二者不是同分异构体,也不互为同系物,蔗糖可以水解,葡萄糖为单糖,不能水解,C项错误。
3.关于淀粉和纤维素的下列说法中,正确的是()A.两者都能水解,且水解的最终产物不相同B.两者实验式相同,且互为同分异构体C.两者都属于糖类,且都没有甜味D.两者都属于高分子化合物,且遇碘单质都显蓝色解析:选C淀粉和纤维素都属多糖,都能水解,且水解的最终产物都是葡萄糖;淀粉和纤维素既无甜味,也无还原性;两者尽管能用同一分子通式(C6H10O5)n表示,但由于n值不同,因而不是同分异构体的关系;两者都是天然高分子化合物,但只有淀粉能与碘单质作用显蓝色。
4.青苹果汁遇碘溶液显蓝色,熟苹果汁能还原银氨溶液,这说明()A.青苹果中只含淀粉不含糖类B.熟苹果中只含糖类不含淀粉C.苹果转熟时淀粉水解为单糖D.苹果转熟时单糖聚合成淀粉解析:选C青苹果汁中含淀粉较多,熟苹果汁中含葡萄糖较多。
5.某食品厂由葡萄糖制备葡萄糖酸钙的过程中,葡萄糖的氧化可用以下某种试剂,其中最适合的是()A.O2/葡萄糖氧化酶B.酸性KMnO4溶液C.新制Cu(OH)2悬浊液D.[Ag(NH3)2]OH溶液解析:选A新制Cu(OH)2悬浊液、[Ag(NH3)2]OH溶液氧化性较弱,且反应需要在碱性条件下进行,不利于葡萄糖的氧化;而酸性高锰酸钾溶液氧化性较强,不能得到葡萄糖酸;可在葡萄糖氧化酶催化作用下用氧气氧化葡萄糖生成葡萄糖酸,A项正确。
2019地理同步新一线选修三中图版精练第四章第一节课时跟踪检测九旅行业的进展及其对区域的阻碍

课时跟踪检测(九)旅行业的进展及其对区域的阻碍一、选择题1.参观农业是最近几年来兴起的一种旅行与农业交叉的新兴产业,它既是农业生产的一部份,又具有旅行业休闲娱乐、提供旅行效劳的功能。
进展参观农业( )①有利于扩大农业经营范围②有利于农业产业结构调整③便于大量销售农产品④幸免环境污染⑤增强城乡交流,增进科技兴农A.①③⑤B.①②④C.②③⑤D.①②⑤解析:选D参观农业不是以销售农产品为要紧目的,而是以销售农业旅行资源获取经济效益;农业参观游览一样会造成环境污染。
2.“旅行一动百业兴”表现旅行活动的作用是()A.知足人类的需求B.促进经济的发展C.扩大交流D.保护环境解析:选B“旅行一动百业兴”说明旅行业能够带动酒店、餐饮、交通运输、邮电通信、金融贸易等第三产业的进展,增进农副产品加工、建材、交通机械等工业部门的进展。
3.“我爷爷小的时候,常在那个地址玩耍,高高的前门恍如挨着我的家……”一曲《前门情思大碗茶》唱出了北京“胡同文化”的深厚文化底蕴,“胡同游”吸引了大量外国旅行者,其踊跃阻碍主若是()A.提供大量就业机遇B.促进国民素质提高C.提高我国人民生活质量D.促进文化交流解析:选D北京“胡同文化”底蕴深厚,国外旅行者的大量到来极大地增进了东西方文化的交流。
以下四幅图表现的是我国部份少数民族的风俗、节日活动。
据此完成4~5题。
4.以下文化特色旅行项目与其民族对应正确的选项是()A.①—壮族B.②—藏族C.③—苗族D.④—彝族5.文化特色旅行项目进展对旅行接待地文化环境的不利阻碍要紧表现为()A.不同民族和文化接触增多,增加了一些社会、民族成见B.在原先风俗文化的基础上经整合而创新了一些新的文化特色旅行项目C.民族文化与外来文化融合,民族文化的特色与吸引力下降D.风俗、节庆、宗教活动作为旅行项目来开发,其本身的传统文化价值有所下降解析:4.A 5.D第4题,四幅图表示的风俗、节日活动与其民族对应依次为:上刀山—壮族,那达慕大会—蒙古族,泼水节—傣族,芦笙节—苗族。
高中地理总复习 中图版 课时跟踪训练9 气压带和风带 含答案
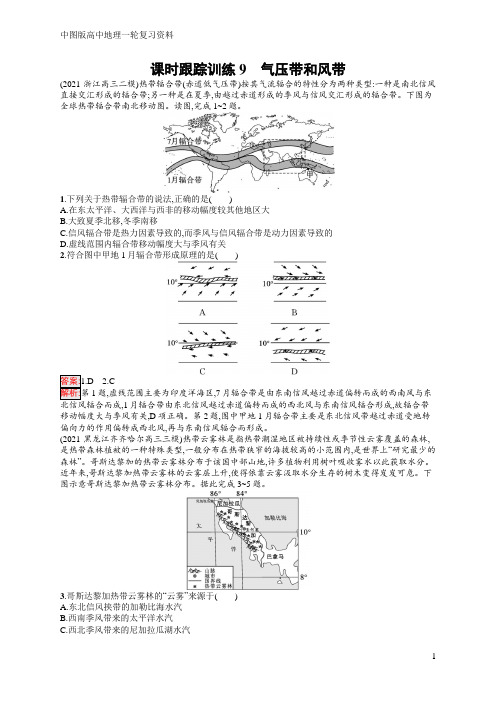
课时跟踪训练9气压带和风带(2021·浙江高三二模)热带辐合带(赤道低气压带)按其气流辐合的特性分为两种类型:一种是南北信风直接交汇形成的辐合带;另一种是在夏季,由越过赤道形成的季风与信风交汇形成的辐合带。
下图为全球热带辐合带南北移动图。
读图,完成1~2题。
1.下列关于热带辐合带的说法,正确的是()A.在东太平洋、大西洋与西非的移动幅度较其他地区大B.大致夏季北移,冬季南移C.信风辐合带是热力因素导致的,而季风与信风辐合带是动力因素导致的D.虚线范围内辐合带移动幅度大与季风有关2.符合图中甲地1月辐合带形成原理的是()2.C1题,虚线范围主要为印度洋海区,7月辐合带是由东南信风越过赤道偏转而成的西南风与东,1月辐合带由东北信风越过赤道偏转而成的西北风与东南信风辐合形成,故辐合带移动幅度大与季风有关,D项正确。
第2题,图中甲地1月辐合带主要是东北信风带越过赤道受地转偏向力的作用偏转成西北风,再与东南信风辐合而形成。
(2021·黑龙江齐齐哈尔高三三模)热带云雾林是指热带潮湿地区被持续性或季节性云雾覆盖的森林,是热带森林植被的一种特殊类型,一般分布在热带狭窄的海拔较高的小范围内,是世界上“研究最少的森林”。
哥斯达黎加的热带云雾林分布于该国中部山地,许多植物利用树叶吸收雾水以此获取水分。
近年来,哥斯达黎加热带云雾林的云雾层上升,使得依靠云雾汲取水分生存的树木变得岌岌可危。
下图示意哥斯达黎加热带云雾林分布。
据此完成3~5题。
3.哥斯达黎加热带云雾林的“云雾”来源于()A.东北信风挟带的加勒比海水汽B.西南季风带来的太平洋水汽C.西北季风带来的尼加拉瓜湖水汽D.盛行西风带来的太平洋水汽4.热带云雾林成为世界上“研究最少的森林”主要是因为()①人体舒适度差②植被破坏严重③分布范围较小④大气含氧量少A.①②B.③④C.①③D.②④5.哥斯达黎加热带云雾林生存面临巨大威胁的原因可能是()A.乱砍滥伐B.病虫危害D.全球气候变暖4.C5.D3题,哥斯达黎加地处北半球低纬地区,主要是东北信风从加勒比海带来的水汽受山地阻挡, ,故选A项。
语文同步优化指导(人教版必修4)课时跟踪训练9+Word版含解析【KS5U+高考】.doc

课时跟踪训练(九)父母与孩子之间的爱A组:基础达标(建议用时20分钟)一、基础积累1.下列加点字的注音全都正确的一项是()A.诞.生(dàn)刹.那(shà)撕.碎(sī)缺陷.(xiàn)B.怀孕.(yùn)挑.选(tiāo)典型.(xínɡ)履.行(lǔ)C.求援.(yuán)专横.(hénɡ)辜.负(ɡū)罪孽.(niè)D.仁慈.(cí)赢.得(yínɡ)渊.源(yuān)秩.序(zhì)解析:A项,“刹”应读chà;B项,“履”应读lǚ;C项,“横”应读hènɡ。
答案:D2.下列词语中书写完全正确的一项是()A.恐惧辩认给予综合B.哭泣空虚因素严厉C.遵徇愿望鉴于树立D.幼稚惩罚阻碍慨念解析:A项,辩—辨;C项,徇—循;D项,慨—概。
答案:B3.依次填入下列横线处的词语,最恰当的一组是()①深入贯彻全军政治工作会议精神,________推进依法治军、从严治军,全面加强部队革命化现代化正规化建设。
②15日,香港警方________完持续近80天的“占领中环”非法集会后,各种商铺便纷纷打出节日促销广告。
③高兴了________躺在洁白的雪堆里面,仰望浩瀚的苍穹,静观疏林水墨画,夕阳下的雪山,任风雪亲近你的脸颊,任白云飘荡蓝天,一种世外桃源________的清静感觉,痛痛快快享受那种畅游后的快感。
A.切实处理随意超凡脱俗B.扎实处置任意超尘出世C.扎实处理随意超尘出世D.切实处置任意超凡脱俗解析:“扎实”侧重于过程的踏实、牢固。
“处置”包含惩罚性的处理。
“任意”是不经心的意思,更符合语境。
“超尘出世”指超脱尘世,到了另外的境界。
“超凡脱俗”指超脱凡俗,成为一个清高的人。
答案:B4.下列各句中加点成语的使用,全部不正确的一组是()①“徒步三千,流亡万里”,这是中华民族历史上硕果仅存....的一次悲壮的师生长征,堪称我国教育史上一次可歌可泣的文化长征。
高中英语Unit3 课时跟踪检测九Project含解析牛津译林版选修9

课时跟踪检测(九) ProjectⅠ.单词拼写1.The choice of the players for the team seems completely arbitrary (任意的).2.You should exercise extreme caution (小心) when driving in fog.3.You’ve not very consistent (一致的):first you condemn me, then you praise me.4.Chemicals in the factory’s sewage system have changed the ecology (生态) of the whole area.5.Our perception of things is often influenced by subjective (主观的) factors, such as tiredness.6.When grandmother died they went into mourning (哀悼).7.He was touched by the warmth (热情) of their welcome.8.He wears a garment (衣服) that had once been a jacket.Ⅱ.完成句子1.我们必须谨慎行事。
We must proceed with_caution.2.这个老农场主把农场转让给他的孙子。
The old farmer conveyed_his_farm_to his grandson.3.我总是将他和速度快的汽车联系起来。
I always associate_him_with fast cars.4.这条新的法律没有提及农用土地。
The new law does not refer_to_land used for farming.5.如果你想坐公共汽车去,那对我也合适。
【人教版】高中英语选修9 全册精品课时跟踪检测(含答案)

课时跟踪检测(一)Warming Up & Reading — Language Points Ⅰ.单词拼写1.Can you tell me the approximate number of athletes who will participate in the Brazil Olympic Games?2.They accomplished their mission ahead of time.3.Having no motivation to study may be the most dangerous thing for a student.4.What good does it do a man if he gains the whole world but loses his soul?5.We are working under extreme pressure at the moment.6.He doubted the reality (真实性) of what he had heard.7.He is rather conventional(传统的) in his daily life.8.You will have to make adjustments (调整) to your thinking if you are to get promoted.9.I urged (催促) him to set out early.10.At the meeting we showed our devotion (忠诚) to our leader.Ⅱ.选词填空come through,ahead of,approximate to,urge ... on,make adjustments1.She could hear him urging her on as she ran past.2.What has been reported in the newspaper is approximate_to the truth.3.Our company is ahead_of_ other makers of spare parts for the airplane.4.We're still waiting for our exam results tocome_through.5.Since everything develops, we have to make_adjustments to the changing situation.Ⅲ.完成句子1.This is inconvenient in_the_extreme (极其).2.You like tennis, while_I'd_rather (而我愿意) read.3.The fine view from the tower fascinated_us (把我们迷住了).4.There_is_a_limit_to (对……来说是有限的) the amount of money I can afford.5.She came_third (得了第三) in the English oral competition.Ⅳ.句型转换1.He is unfit for the work.He is not_fit_to_do the work.2.It took her a while to get used to living alone after the divorce.It took her a while to adjust_to living alone after the divorce.3.Officially he is in charge, but actually his secretary does all the work.Officially he is in charge, but in_reality his secretary does all the work.4.Their team won the second place in the match.Their team came_second in the match.5.I urged Tony to stay away from computer games.I urged that Tony_(should)_stay_away_from_computer_games.Ⅴ.阅读理解AEvery day, in all kinds of weather, thousands of men and women jog.Why has jogging —running slowly for long distances —become so popular?Most joggers begin because they hear it is a very good exercise.Jogging makes the heart stronger and helps people lose weight.It can also help them feel better about themselves.Donald Robbins, who is forty-two years old and works in anoffice, began jogging a few years ago because he felt he was toofat.At first he could only run about 100 yards.It took him threemonths to be able to run a mile.But two years later, he ran in amarathon over twenty-six miles.Many joggers, like Donald Robbins,feel that if they can succeed in jogging, they can succeed in other things, and quite often this feeling helps them in their jobs.Should you jog too?If you do, be sure to ask your doctor for advice.Jogging may be too much exercise for you.Does jogging cost much?No, it costs almost nothing.But it is very important to have a good pair of shoes that are made especially for jogging.They protect your feet and legs from the shock of running on the hard surface.How fast should you go?Jog with a friend and talk to each other as you run.If you have difficulty in talking, you're going too fast.How far should you jog?Remember not to go too far too soon.In fact, you should walk, not run, the first few times.Then do some short jogs, but no more than what you can do comfortably.After that, increase your distance a quarter or half a mile every two weeks or so.Maybe in a few years, you can run in a marathon too.A.jogging as a sportB.jogging as an exerciseC.jogging in a safe wayD.jogging as a way to the marathon解析:选B主旨大意题。
高中语文 课时跟踪检测(九)雪落在中国的土地上(含解析)新人教版选修《中国现代诗歌散文欣赏》(202

2017-2018学年高中语文课时跟踪检测(九)雪落在中国的土地上(含解析)新人教版选修《中国现代诗歌散文欣赏》编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017-2018学年高中语文课时跟踪检测(九)雪落在中国的土地上(含解析)新人教版选修《中国现代诗歌散文欣赏》)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017-2018学年高中语文课时跟踪检测(九)雪落在中国的土地上(含解析)新人教版选修《中国现代诗歌散文欣赏》的全部内容。
课时跟踪检测(九)雪落在中国的土地上一、诗歌阅读鉴赏(一)课内阅读阅读《雪落在中国的土地上》一诗,完成1~3题。
1.全诗写了什么内容?表达了诗人什么样的心情?答:________________________________________________________________________ ________________________________________________________________________参考答案:抒写了残暴的侵略战争使中国人民蒙受的苦难,表达了诗人忧国忧民的沉重心情.2.在诗中,诗人也提到了自己,把诗人表现自我的一段文字找出来.这样写有什么作用?答:________________________________________________________________________ ________________________________________________________________________________________________________________________________________________参考答案:“告诉你/我也是农人的后裔—-……我的生命/也像你们的生命/一样的憔悴呀。
2017-2018学年高中语文 课时跟踪检测(九)雪落在中国的土地上(含解析)新人教版选修《中国

课时跟踪检测(九)雪落在中国的土地上一、诗歌阅读鉴赏(一)课内阅读阅读《雪落在中国的土地上》一诗,完成1~3题。
1.全诗写了什么内容?表达了诗人什么样的心情?答:________________________________________________________________________ ________________________________________________________________________ 参考答案:抒写了残暴的侵略战争使中国人民蒙受的苦难,表达了诗人忧国忧民的沉重心情。
2.在诗中,诗人也提到了自己,把诗人表现自我的一段文字找出来。
这样写有什么作用?答:________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ 参考答案:“告诉你/我也是农人的后裔——……我的生命/也像你们的生命/一样的憔悴呀。
”诗人把自己的苦难和广大农民还有祖国的苦难命运联系在一起,使对祖国的苦难抒写得更加深刻而真切。
3.“中国,/我的在没有灯光的晚上/所写的无力的诗句/能给你些许的温暖么”,请从抒情方式的角度赏析其表达效果。
答:________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ 参考答案:结尾的这几行诗是直接抒情,是战栗的呼喊,是为祖国急切献身的心声。
高中英语人教版选修9课时跟踪检测(九) Using Language Word版含解析

课时跟踪检测(九)Using Language Ⅰ.单词拼写1.The Great Wall winds (蜿蜒) its way from west to east until to the sea.2.The economy is at last beginning to recover.3.Hold on to that bag, or someone in the crowd may snatch (抢走) it.4.This wounded soldier was unconscious (无意识的)from his loss of blood.5.I put another steak on the barbecue.Ⅱ.单句改错1.Sunshine, fresh air, and rest often accelerate a person's recovery from sick.sick_→sickness2.We haven't yet recovered in the shock.in→from3.She is unconscious in the effect she has on people.in→of4.The boy talked his mother into bought him a home computer.bought→buying5.The medicine had a good effort on me.effort→effectⅢ.阅读理解AThe koala is Australia's second most famous animal.Thisgentle, slow-moving animal has lived in the forests of Australiafor over half a million years.In the first quarter of the century,early settlers killed about ten million koalas for their fur.Today,the koala is strictly protected.Gum leaves are the koala's only food.And instead of a tail the animal has a pad that enables it to sit comfortably for hours in the fork of a gum tree.The Aborigines named this animal koala meaning “I don't drink”.The gum leaves supply all the moisture it requires.So Koala is an aboriginal word.The koala lives in trees in forests.It doesn't eat any meat and it doesn't drink any water.The koala is active at night and during the day it sleeps in the fork of a tree.The koala has long arms and sharp curved claws for climbing trees and for grasping branches.It has a large hairless nose and it hasn't got a tail.The koala usually has only one baby a year.At birth the baby is very small.At first it cannot see and it hasn't got any fur.The female koala has a pouch on her stomach.Inside thispouch the mother produces milk for her baby.The baby stays in its mother's pouch until it is about six months old.Then it clings to its mother's back for another six months.After this the young koala starts to live a solitary (单独的) life.1.The name “Koala” has something to do with______.A.food B.sandC.water D.grass解析:选C细节理解题。
2024届高考语文一轮总复习课时跟踪练9

课时跟踪练9(40分钟32分)一、阅读下面的文字,完成1~4题。
(16分)滚烫的土地阎秀丽秋阳很毒,像针,扎在爹的脊背上。
娘抬头看了看天,说:“歇一会儿吧,这日头忒毒,晒得人脱层皮。
”爹没有言语,只是把镐头抡得更高了些,然后再使劲儿让它落下。
坚硬的山土在他的镐头下只是蹦出了一个亮晃晃的镐印,几块细碎的土坷垃蹦在他裸着的胸膛和脸上,和脸上的汗珠混合在一起,变成浑浊的小溪淌下来。
娘便生了气,叨咕着说:“非得刨那点儿地,不知道能种几粒粮食!”爹回了头,擦了把汗,眼睛一横,说:“你懂啥!这片小山包荒着也是荒着,我刨出来就能有用,要不种地,要不栽几棵树,咋了?”娘说:“咱家的粮食也不是不够吃,你费那大劲儿刨这点儿地有啥用?乐意干你干!”我在旁边看了看爹,娘能扔镐头耍脾气,我可不敢。
爹那火爆脾气,不敢拿我娘撒气,要是有个不小心,那火准定得烧到我身上。
爹头也没抬,只是把手里的镐头更加用力地刨下去。
我心里是极不愿意爹到处“开荒”的,但是我不敢反抗。
爹的工作在县里,他是机关里一个科室的科长,是村里人人羡慕的“公家人”。
周六回家,爹换上一身旧衣裳,扛了镐头就往山里走,娘阻拦不住。
村里人也说,不值当,吃公家饭的,还差那点儿地?正儿八经的庄稼人都没人弄。
为这,爹和娘吵了一架。
娘没有去地里,爹也没有喊我,一个人扛着镐头下了地。
娘并没有想象中清闲,反而在家里走来走去。
娘把地扫了一遍又一遍,屋里的那几件简陋的家具,也被娘擦得泛了光,映着娘有些魂不守舍的神情。
娘还时不时地扒着后门,一遍又一遍地望着爹去干活儿的山沟沟。
我心想,再怎么望,也看不到那个小山包,何况是一个人。
到了中午,爹还是没有回来,娘让我去地里看看,喊爹回来吃饭。
我有些不情愿,又不敢违拗娘的意思,只能慢腾腾地向着那山沟走去。
太阳火辣辣地悬在天空,不知名的虫儿有气无力地鸣叫着,连风都是热的。
我心里暗暗气着:这么热的天,不好好在家待着,连带着我也跟着遭罪,刨了那点儿山边子,还能富了?气归气,还得去,这么热的天,爹要是中暑了,那可就糟了。
高中英语人教版高二选修6课时跟踪检测(九)

课时跟踪检测(九)Warming Up & Reading — Language Points Ⅰ.单句语法填空1.Our visitors arrived at the appointed (appoint) time.2.At the railway station, the mother waved to her daughter until the train was out of sight.3.A year passed by, but she didn’t find a suitable (suit) job.4.A sudden fire burnt the building to the ground, and now it lay in ruins.5.There being (be) no bus, we had to walk home.6.He asked whether I could share a bedroom with an English speaker.7.He has always been enthusiastic about sports.8.Having_been_persuaded (persuade) to change my attitude, I finally got the right way to rid myself of carelessness and gained confidence as well.9.We were about to give up when they came to help us out.10.It is important for us to_keep (keep) on trying.Ⅱ.完成句子1.I have_an_appointment_with the doctor at 10:30.我和医生在10:30有个约定。
第二章 函数、导数及其应用 课时跟踪检测(九) 指数与指数函数 Word版含答案

课时跟踪检测(九) 指数与指数函数一抓基础,多练小题做到眼疾手快 1.函数y =2x与y =2-x的图象关系是( ) A .关于x 轴对称 B .关于y 轴对称 C .关于原点对称D .关于直线y =x 对称解析:选B 作出y =2x 与y =2-x=⎝ ⎛⎭⎪⎫12x 的图象(图略),观察可知其关于y 轴对称.2.设a =22.5,b =2.50,c =⎝ ⎛⎭⎪⎫12 2.5,则a ,b ,c 的大小关系是( )A .a >c >bB .c >a >bC .b >a >cD .a >b >c解析:选D a >1,b =1,0<c <1,所以a >b >c . 3.已知f (x )=3x -b(2≤x ≤4,b 为常数)的图象经过点(2,1),则f (x )的值域为( )A .B .C .D .上是增函数,所以f (x )min =f (2)=1,f (x )m ax=f (4)=9.故f (x )的值域为.4.不等式222x x-+>⎝ ⎛⎭⎪⎫12x +4的解集为________. 解析:不等式222x x-+>⎝ ⎛⎭⎪⎫12x +4可化为⎝ ⎛⎭⎪⎫1222x x ->⎝ ⎛⎭⎪⎫12x +4,等价于x 2-2x <x +4,即x 2-3x -4<0,解得-1<x <4.答案:{x |-1<x <4}5.若函数f (x )=a x-1(a >0,a ≠1)的定义域和值域都是,则实数a =________. 解析:当a >1时,f (x )=a x-1在上为增函数, 则a 2-1=2,∴a =± 3.又∵a >1,∴a = 3. 当0<a <1时,f (x )=a x-1在上为减函数, 又∵f (0)=0≠2,∴0<a <1不成立. 综上可知,a = 3. 答案: 3二保高考,全练题型做到高考达标 1.化简4a 23·b -13÷⎝ ⎛⎭⎪⎫-23a -13b 23的结果为( ) A .-2a3bB .-8abC .-6a bD .-6ab解析:选C 原式=4÷⎝ ⎛⎭⎪⎫-23a ⎛⎫⎪⎝⎭1233——b -1323—=-6ab -1=-6ab,故选C.2.(2017·贵州适应性考试)函数y =a x +2-1(a >0且a ≠1)的图象恒过的点是( )A .(0,0)B .(0,-1)C .(-2,0)D .(-2,-1)解析:选C 法一:因为函数y =a x(a >0,a ≠1)的图象恒过点(0,1),将该图象向左平移2个单位,再向下平移1个单位得到y =ax +2-1(a >0,a ≠1)的图象,所以y =ax +2-1(a >0,a ≠1)的图象恒过点(-2,0),选项C 正确.法二:令x +2=0,x =-2,得f (-2)=a 0-1=0,所以y =a x +2-1(a >0,a ≠1)的图象恒过点(-2,0),选项C 正确.3.已知函数y =kx +a 的图象如图所示,则函数y =ax +k的图象可能是( )解析:选B 由函数y =kx +a 的图象可得k <0,0<a <1,又因为与x 轴交点的横坐标大于1,所以k >-1,所以-1<k <0.函数y =a x +k的图象可以看成把y =a x的图象向右平移-k个单位得到的,且函数y =a x +k是减函数,故此函数与y 轴交点的纵坐标大于1,结合所给的选项,故选B.4.若函数f (x )=⎩⎪⎨⎪⎧a x, x >1,-3a x +1,x ≤1是R 上的减函数,则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫23,1B.⎣⎢⎡⎭⎪⎫34,1C.⎝ ⎛⎦⎥⎤23,34 D.⎝ ⎛⎭⎪⎫23,+∞解析:选C 依题意,a 应满足⎩⎪⎨⎪⎧0<a <1,2-3a <0,-3a +1≥a 1,解得23<a ≤34.5.已知函数f (x )=⎩⎪⎨⎪⎧1-2-x,x ≥0,2x-1,x <0,则函数f (x )是( )A .偶函数,在时,不等式(m 2-m )·4x-2x<0恒成立,则实数m 的取值范围是________.解析:原不等式变形为m 2-m <⎝ ⎛⎭⎪⎫12x ,因为函数y =⎝ ⎛⎭⎪⎫12x在(-∞,-1]上是减函数,所以⎝ ⎛⎭⎪⎫12x ≥⎝ ⎛⎭⎪⎫12-1=2,当x ∈(-∞,-1]时,m 2-m <⎝ ⎛⎭⎪⎫12x 恒成立等价于m 2-m <2,解得-1<m <2.答案:(-1,2) 9.化简下列各式:(1)⎝ ⎛⎭⎪⎫2790.5+0.1-2+⎝ ⎛⎭⎪⎫21027-32-3π0+3748;(2)3a 72·a -3÷3a -3·a -1.解:(1)原式=⎝ ⎛⎭⎪⎫25912+10.12+⎝ ⎛⎭⎪⎫6427-23-3+3748=53+100+916-3+3748=100. (2)原式=3a 72·a-32÷3a-32·a-12=3a 72÷3a-12=a 76÷a -16=a 86=a 43.10.已知函数f (x )=a |x +b |(a >0,b ∈R).(1)若f (x )为偶函数,求b 的值;(2)若f (x )在区间时,函数y =12x 2与y =a x(a >0)的图象有交点,则a 的取值范围是( )A.⎣⎢⎡⎦⎥⎤12,2B.⎣⎢⎡⎦⎥⎤12,2C.⎣⎢⎡⎦⎥⎤14,2D.⎣⎢⎡⎦⎥⎤14,2解析:选B 当a >1时,如图①所示,使得两个函数图象有交点,需满足12·22≥a 2,即1<a ≤2;当0<a <1时,如图②所示,需满足12·12≤a 1,即12≤a <1,综上可知,a ∈⎣⎢⎡⎦⎥⎤12,2.2.已知定义在R 上的函数f (x )=2x-12|x |.(1)若f (x )=32,求x 的值;(2)若2tf (2t )+mf (t )≥0对于t ∈恒成立,求实数m 的取值范围. 解:(1)当x <0时,f (x )=0,无解; 当x ≥0时,f (x )=2x-12x ,由2x-12x =32,得2·22x-3·2x-2=0,将上式看成关于2x的一元二次方程, 解得2x =2或2x=-12,∵2x>0,∴x =1.(2)当t ∈时,2t ⎝⎛⎭⎪⎫22t-122t +m ⎝⎛⎭⎪⎫2t -12t ≥0,即m (22t -1)≥-(24t-1),∵22t-1>0, ∴m ≥-(22t+1), ∵t ∈,∴-(22t+1)∈,故实数m 的取值范围是[-5,+∞).。
2021-2022学年高中语文语文版必修三课时跟踪检测(九) 宝黛初会 Word版含答案

课时跟踪检测(九)宝黛初会(时间:40分钟分值:49分)一、语言表达专练(24分,选择题每小题3分)1.下列句子中的成语使用不恰当的一项是( )A.不少观众认为,新版《红楼梦》电视剧中的林黛玉稍显丰腴,其扮演者也缺少一种顾盼神飞....的灵气。
B.曹雪芹写贾府的众人在贾母面前的敛声屏气....是为了更好地衬托王熙凤这个人物的特点。
C.胡适特殊强调属于神怪不经之谈....的《西游记》的妙处在于“荒唐而有情思,诙谐而有庄意”。
D.有评论家认为,超人气天王在上海的演唱会引起十室九空....的现象,在很大程度上是自上而下炒作的结果。
解析:选D D项,“十室九空”,形容天灾人祸使得人民流离失所的凄惨景象。
2.下列句子中没有语病的一项是( )A.我校校庆徽标设计大赛的参赛者大多是以高一班级的师生为主,其他班级的师生也有,但为数不多。
B.我们体育老师取得成果的关键在于他擅长动员和启发同学们参与体育活动的乐观性。
C.曹雪芹晚年完成了《石头记》的写作,但却无力付梓印刷。
D.假如说中华民族的文化是一部雄浑壮丽的交响乐,那么中华节日文化便是其中一组亮丽的乐章。
解析:选D A项,句式杂糅。
“大多是……”与“以……为主”杂糅,去掉一个。
B项,搭配不当。
不能说“启发……乐观性”。
C项,“印刷”与“付梓”词义重复。
3.(浙江高考)填入下面空缺处的语句,最恰当的一项是( )贾母因要带着刘姥姥散闷,遂携了刘姥姥至山前树下盘桓了半晌,又说与他这是什么树,这是什么石,这是什么花。
刘姥姥一一的领悟,又向贾母道:“谁知城里不但人尊贵,连雀儿也是尊贵的。
____________。
”众人不解……刘姥姥道:“那廊上金架子上站的绿毛红嘴是鹦哥儿,我是认得的。
那笼子里黑老鸹子,怎么又长出凤头来,也会说话呢。
”众人听了,又都笑将起来。
A.这雀儿到了你们这里,变得既俊又会说话了B.偏这雀儿到了你们这里,他会说话了,也变俊了C.偏这雀儿到了你们这里,他也变俊了,也会说话了D.这雀儿到了你们这里,变得既会说话又俊了解析:选C 依据下文“笼子里黑老鸹子,怎么又长出凤头来,也会说话呢”,确定在A、C项间选择,C 项中的“偏”是“偏偏”的意思,强调城里不同于乡下,据此可确定答案为C项。
高中英语 课时跟踪练(九)Lesson 2Lesson 3Lan

号顿市安谧阳光实验学校课时跟踪练(九) Lesson 2 & Lesson 3—Language Points一、全练语言点,基稳才能楼高Ⅰ.单词拼写1.Her careful makeup hid the signs of age beneath (在底下).2.Try to grasp (理解) what the writer is going to tell you in the book as a whole.3.The government had already committed (投入) itself to a wide range of reforms.4.After he had given an account of the difficulties, he went on to suggest ways to overcome (克服) them.5.In some countries, it is illegal (非法的) to use the cellphone while driving.6.I reminded him of the appointment (约会), but he didn't make any response.7.The children were jumping constantly (不断地) to keep warm.8.We should inspect (检查) the goods to see if there is any damage.9.We were determined to explore the surrounding (附近的) countryside.10.He hesitated_(犹豫)for a while before he made the phone call.Ⅱ.单句语法填空1.Do you believe the existence of ghosts? Perhaps they only exist in the minds of some people.(exist)2.There's enough time left. You can go into details at the moment.3.If you do know the answer, speak up so everyone can hear you.4.I'm constantly (constant) telling him to behave himself.5.Stave has a good grasp of the European legal system.6.Having_committed (commit) herself to this line of action, there was no retreating for bad weather.7.The boy ran away quickly the instant his father turned his back.8.It's suggested that I should have an appointment with the interviewer.9.The officer, surrounded (surround) by these noises, was moved and a little embarrassed.10.It is illegal (legal) to sell tobacco to someone under 16.Ⅲ.完成句子1.我现在不能细说面试的事,太费工夫。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时跟踪检测(九) 正弦函数、余弦函数的周期性与奇偶性
一、基础知识训练:
1.函数f (x )=sin(-x )的奇偶性是( )
A .奇函数
B .偶函数
C .既是奇函数又是偶函数
D .非奇非偶函数
解析:选A 由于x ∈R ,且f (-x )=sin x =-sin(-x )=-f (x ),所以f (x )为奇函数. 2.函数y =-x cos x 的部分图象是下图中的( )
解析:选D 因为函数y =-x cos x 是奇函数,图象关于原点对称,所以排除A ,C ;当x ∈⎝⎛⎭
⎫0,π
2时,y =-x cos x <0,故排除B. 3.已知函数f (x )=sin ⎝
⎛⎭⎫πx -π
2-1,则下列命题正确的是( ) A .f (x )是周期为1的奇函数 B .f (x )是周期为2的偶函数 C .f (x )是周期为1的非奇非偶函数 D .f (x )是周期为2的非奇非偶函数 解析:选B f (x )=sin ⎝⎛⎭⎫πx -π2-1=-cos πx -1,从而函数为偶函数,且T =2π
π=2. 4.函数y =4sin(2x +π)的图象关于( )
A .x 轴对称
B .原点对称
C .y 轴对称
D .直线x =π
2
对称
解析:选B y =4sin(2x +π)=-4sin 2x ,奇函数图象关于原点对称. 5.函数y =cos ⎝⎛⎭
⎫-x 2+π
2的奇偶性是( ) A .奇函数 B .偶函数 C .非奇非偶函数
D .即是奇函数也是偶函数
解析:选A cos ⎝⎛⎭⎫-x 2+π2=cos ⎝⎛⎭⎫π2-x 2=sin x
2,故为奇函数. 6.函数y =cos ⎝⎛⎭
⎫12x +π
6的周期为________.答案:4π 7.函数ƒ(x )是以2为周期的函数,且ƒ(2)=3,则ƒ(6)=________.答案:3 8.函数ƒ(x )=3cos ⎝⎛⎭⎫ωx -π3(ω>0)的最小正周期为2π
3
,则ƒ(π)=________. 解析:由已知2πω=2π
3得ω=3,∴ƒ(x )=3cos ⎝⎛⎭⎫3x -π3,∴ƒ(π)=3cos ⎝⎛⎭⎫3π-π3 =3cos ⎝⎛⎭⎫π-π3=-3cos π3=-3
2
.
9.判断下列函数的奇偶性.
(1)ƒ(x )=cos ⎝⎛⎭⎫π2+2x cos(π+x ); (2)ƒ(x )=1+sin x +1-sin x . 解:(1)x ∈R ,ƒ(x )=cos ⎝⎛⎭⎫π
2+2x cos(π+x )=-sin 2x ·(-cos x )=sin 2x cos x . ∴ƒ(-x )=sin(-2x )cos(-x )=-sin 2x cos x =-ƒ(x ).∴该函数ƒ(x )是奇函数. (2)对任意x ∈R ,-1≤sin x ≤1,∴1+sin x ≥0,1-sin x ≥0.∴ƒ(x )=1+sin x +
1-sin x 的定义域为R. ∵ƒ(-x )=
1+sin (-x )+
1-sin (-x )=
1-sin x +
1+sin x =ƒ(x ),
∴该函数是偶函数.
10.已知函数y =12sin x +1
2
|sin x |,
(1)画出函数的简图;(2)此函数是周期函数吗?若是,求其最小正周期.
解:(1)y =12sin x +1
2|sin x |=⎩
⎪⎨⎪⎧
sin x ,x ∈[2k π,2k π+π](k ∈Z ),0,x ∈[2k π-π,2k π](k ∈Z ),
图象如图所示:
(2)由图象知该函数是周期函数,且周期是2π.
二 、能力提高训练:
1.下列函数中最小正周期为π且为偶函数的是( )
A .y =cos ⎝⎛⎭⎫2x -π2
B .y =sin ⎝⎛⎭⎫2x +π2
C .y =sin ⎝⎛⎭
⎫x +π2 D .y =cos ⎝⎛⎭
⎫x -π
2 解析:选B 对于A ,y =cos ⎝⎛⎭⎫2x -π2=cos ⎝⎛⎭⎫π
2-2x =sin 2x 是奇函数;对于B ,y =sin ⎝⎛⎭⎫2x +π2=cos 2x 是偶函数,且最小正周期T =2π
2=π;对于C ,y =sin ⎝⎛⎭⎫x +π2=cos x 是偶函数,但最小正周期T =2π;对于D ,y =cos ⎝⎛⎭⎫x -π
2=sin x 是奇函数,故选B. 2.函数ƒ(x )=3sin ⎝⎛⎭⎫
23
x +15π2是( ) A .周期为3π的偶函数 B .周期为2π的偶函数 C .周期为3π的奇函数
D .周期为
4π
3
的偶函数
解析:选A ∵ƒ(x )=3sin ⎝⎛⎭⎫23x +3π2=-3cos 23x ,∴ƒ(x )为偶函数,且T =2π
2
3=3π,.
3.函数y =cos ⎝⎛⎭
⎫k 4x +π
3(k >0)的最小正周期不大于2,则正整数k 的最小值应是( ) A .10 B .11 C .12
D .13
解析:选D ∵T =2πk 4=8π
k ≤2,∴k ≥4π,又k ∈Z ,∴正整数k 的最小值为13.
4.函数ƒ(x )=sin(2x +φ)为R 上的奇函数,则φ的值可以是( )
A .π4
B .π2
C .π
D .3π2
解析:选C 要使函数ƒ(x )=sin(2x +φ)为R 上的奇函数,需φ=k π,k ∈Z.故选C. 5.若函数f (x )的定义域为R ,最小正周期为3π
2
,且满足f (x )=⎩⎪⎨⎪⎧
cos x ,-π2≤x <0,sin x ,0≤x <π,
则f ⎝⎛⎭⎫
-15π4=________.
解析:∵T =3π2,∴f ⎝⎛⎭⎫-15π4=f ⎝⎛⎭⎫-15π4+3π2×3=f ⎝⎛⎭⎫3π4=sin 3π4=22. 6.函数y =⎪⎪⎪
⎪sin x
2的最小正周期是________. 解析:∵y =sin x 2的最小正周期为T =4π,而y =⎪⎪⎪⎪sin x 2的图象是把y =sin x
2的图象在x 轴下方的部分翻折到x 轴上方,∴y =⎪⎪⎪
⎪sin x
2的最小正周期为T =2π. 7.已知ƒ(x )是以π为周期的偶函数,且x ∈⎣⎡⎦⎤0,π2时,ƒ(x )=1-sin x ,当x ∈⎣⎡⎦⎤5π
2,3π时,求ƒ(x )的解析式.
解:x ∈⎣⎡⎦⎤5π2,3π时,3π-x ∈⎣⎡⎦⎤0,π2,因为x ∈⎣⎡⎦⎤0,π
2时,ƒ(x )=1-sin x ,所以ƒ(3π-x )=1-sin(3π-x )=1-sin x .又ƒ(x )是以π为周期的偶函数,
所以ƒ(3π-x )=ƒ(-x )=ƒ(x ),所以ƒ(x )的解析式为ƒ(x )=1-sin x ,x ∈⎣⎡⎦⎤5π
2,3π. 8.已知函数ƒ(x )对于任意实数x 满足条件ƒ(x +2)
=-
1
ƒ(x )
(ƒ(x )≠0). (1)求证:函数ƒ(x )是周期函数. (2)若ƒ(1)=-5,求ƒ(ƒ(5))的值.
解:(1)证明:∵ƒ(x+2)=-
1
ƒ(x)
,∴ƒ(x+4)=-1
ƒ(x+2)
=-1
-1
ƒ(x)
=ƒ(x),
∴ƒ(x)是周期函数,4就是它的一个周期.
(2)∵4是ƒ(x)的一个周期.∴ƒ(5)=ƒ(1)=-5,∴ƒ(ƒ(5))=-1
ƒ(1)
=1
5.。
