非寿险精算答案整理
非寿险精算课后习题答案(中精-主编-韩天雄)

第一章 1T0.09811S ==2T5.6569σ== 3T[]{}()14%,25%, 1.1,()12.5%,20.2%, 2.6%()0.1036()0.456()()0.0051p p p m m F p Fp p Fpp F p m F E R E R R E R R Treynor E R R Sharpe Jensen s alpha E R R E R R σβσβσβ======-==-=='=-+-=度量值度量值度量值4T[]{}()0.099()0.4091()()()()0m Fm m Fmm F m m F m m E R R Treynor E R R Sharpe Jensen s alpha E R R E R R E R E R βσβ-==-=='=-+-=-=度量值度量值度量值5T[]{}()() 1.2%p F p m F Jensen s alpha E R R E R R β'=-+-=-度量值 6T0.950.90.810,10,0ξξξ===7T0.990.990.990.990.99()0.9933330.99109109330.99109332.326109286.53P X X P ξξξξξ≤=--⎛⎫≤= ⎪⎝⎭-⎛⎫Φ= ⎪⎝⎭-== 8T222()331()109(1)(2)39.65992.2018E X r r Var X r r r θθθ⎧==⎪-⎪⎨⎪==⎪--⎩=⎧⎨=⎩ 0.950.950.990.99()110.95114.9510.99281.48rrrF x x Q Q Q Q θθθθθθ⎛⎫=- ⎪+⎝⎭⎛⎫-= ⎪+⎝⎭=⎛⎫-= ⎪+⎝⎭=9T()[]011()11p prQ Q p r pE X QF x dx dx x r Q θθθθθ-⎛⎫∧=-= ⎪+⎝⎭⎡⎤⎛⎫⎢⎥=- ⎪ ⎪-+⎢⎥⎝⎭⎣⎦⎰⎰111()()111111111p p p r p pr p pCTE Q E X E X Q p Q p r r Q Q p r Q θθθθθθθ--⎡⎤=+-∧⎣⎦-⎧⎫⎡⎤⎛⎫⎪⎪⎢⎥=+-- ⎪⎨⎬ ⎪---+⎢⎥⎪⎪⎝⎭⎣⎦⎩⎭⎛⎫=+••⎪ ⎪--+⎝⎭0.950.990.950.9939.66, 2.20,114.95,281.48243.60548.70r Q Q CTE CTE θ====∴==Q15T()222212112212|111111p p p p p p x Q x x Q Q Q CTE E X X Q dxp dx dx p p pμσμμσσμσμ-⎛⎫-+∞⎪⎝⎭--⎛⎫⎛⎫--+∞+∞ ⎪ ⎪⎝⎭⎝⎭-⎛⎫- ⎪ ⎪⎝⎭⎡⎤=>⎣⎦=-⎡⎤⎢⎥=+-⎢⎥⎣⎦=+--⎰⎰⎰ 0.950.950.950.950.95()0.95330.9510933 1.645109212.29257.89P X Q Q Q Q CTE ≤=-⎛⎫Φ= ⎪⎝⎭-==∴=第二章 2T(1)从表中可以得出索赔额组中值i i f X 和索赔频率1841600121610122101====∑∑=-=i i i i i i f x X f x X由题知)(~2σ,u LN X ,对数正态分布的期望和方差如下:()()()122222-==++σσσeeX Var X E u u根据矩估计法可知:()2222248.605)(111216222=--=-=++X X n ne e eu u σσσ由此可以求得:47.099.6==∧∧σu(2)()()%27.0748.214000ln 4000ln =-=⎪⎪⎭⎫⎝⎛->-=>φσσu u P P x x3T每份保单赔款次数X 服从泊松分布,X 的概率密度函数为: ())32,10(!,,==-k k ex f kλλ由极大似然估计可以得到:X nXni ==∑=∧1iλ而且1965.01==∑=ni i i f x X所以1965.0=∧λ 5T韦伯分布的分布函数为:()rcx e X F --=1令7.012.01=-=---rrcx cx ee解得韦伯分布的20%和70%分位数:()()rrc x c x 17.012.03.0ln 8.0ln ⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-=根据观测数据可以知道 :8.02.07.02.0==x x令()()8.03.0ln 2.08.0ln 11=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-rrc c 解得12.135.1==r c7T指数分布的概率密度函数为()xex f λλ-=,由极大似然估计得到220011==∧Xλ 2x 分布检验的检验假设:0H :赔款额分布服从参数22001=λ的指数分布 1H :赔款额分布不服从参数22001=λ的指数分布显著水平005.0=α,查自由度为41161=--=--k n 的2x 分布表, 得到分位数14.86,所以拒绝域为86.142≥x 赔款额落在0~100的理论概论为:()3653.0220011000022001000==≤≤-⎰dx e X P x同理可得8.2312=E 2.1473=E 4.934=E 3.595=E 1036=E()86.1489.3316122≥=-=∑=i ii i E E Q x在拒绝域范围内,所以拒绝原假设0H ,不能用指数分布模拟个别理赔分布。
2021精算师考试《非寿险精算》真题模拟及答案(4)

2021精算师考试《非寿险精算》真题模拟及答案(4)1、在一个7年的投资期中,前3年的实际利率为10%,随后2年的实际利率为8%,再随后1年的实际利率为6%,最后1年的利息强度为4%。
则一笔1000元的投资在这7年中所得的总利息为()元。
(单选题)A. 710.2B. 711.4C. 712.8D. 715.6E. 717.5试题答案:C2、假设每次事故的损失服从参数为λ的指数分布,而每份保单规定的免赔额为1/λ,则保险公司对每张保单的期望赔款为()。
(单选题)A. λB. 1/λC. 1D. 1/λ2E. λ2试题答案:B3、假设损失X服从正态分布N(33,1092),99%CTE为()。
(单选题)A. 320B. 324C. 328D. 332试题答案:B4、10000元的系列债券在以后5年每半年赎回本金1000元,票息率为每半年一次计息的年复利为10%,若每年计息2次的年名义收益率为6%,投资者购买此债券的价格是()元。
(单选题)A. 8350B. 10000C. 10980D. 11320E. 12460试题答案:C5、假设基本危险单位为车年,现有一车于2009年10月1日参加保险,期限为6个月,则该车在2010年的已签危险量、已承担危险量和在2010年1月1日的有效危险量分别为()。
(单选题)A. 1.00,0.50,0.50B. 0.00,0.50,0.50C. 0.00,0.25,0.25D. 0.00,0.25,0.50E. 0.00,0.50,0.25试题答案:D6、设某人有1000元财产,潜在损失在[0,100]上服从均匀分布,其效用函数为u(x)=,保单均以纯保费出售。
若此人愿付20元保险费购买具有免陪额的保单,则当免赔额为()时使其获最大期望效用。
(单选题)A. 32.40B. 33.28C. 34.26E. 36.75试题答案:E7、某保险公司有关机动车辆险的信息如下:2011年7月1日家庭轿车的费率为1900元2008年~2010年家庭轿车的保单数如下:2008年3570;2009年4230;2010年5100以2011年费率作为当前费率,用危险扩展法求2008~2010年均衡已赚保费为()万元。
CAA非寿险精算

CAA非寿险精算(A6)真题回忆汇总2014秋季非寿险精算(A6 )真题回忆单选题回忆:1、Jansen's alpha公式带数计算;2、简单的贝叶斯公式应用题;3、概念题:风险异质时,总的方差是多少?条件期望的方差和条件方差的期望之和;4、Bulmann和Bulmann-Straub根据表格数据计算下一年保费各一题;5、已知X为损失额,其分布满足f(x|b)=2x/b(0<x<无穷),b服从均匀分布,g(b)=1/b(1<b<无穷),若第一次损失额为2,求第二次的期望值是多少?6、给了各种保费、损失数据,求损失率法的调整因子;7、NCD四道选择题:转移矩阵,第一年后各水平人数,第二年后各水平人数,稳定人数;8、S-B法求预期损失率,P236例题;9、P232,再保费公式带数计算;10、2道ULAE准备金,略难;11、链梯法求ALAE准备金;12、有免赔额的保险,求期望最大效用;13、判断三种效用函数的性质;14、已知基准费率及费率等级,青年/老年,普通车/豪华车,以及3年各级别的投保人数,第一问用危险扩展法(!!!!书上就提了1句啊!)求均衡已赚保费,第二问补充了经验损失信息,求经验损失率。
多选题回忆:1、损失率法和纯保费法的区别;2、先验信息、后验信息、信度因子的定义;3、再保险、财务再保险的各种概念辨析;4、模拟理赔次数的分布:泊松、二项、几何。
大题回忆:1、完全信度理论的假设、定义、公式推导。
(神坑!)2、级别相对数、冲销因子书上的符号推导。
(又一神坑!!)3、贝叶斯保费证明:P=E(Xn+1|x1...xn)=E(u(瑟塔)|x1...xn)其中,u(瑟塔)=E(X|塞塔)。
4、叙述预算IBNR方法的原理、计算步骤并举例。
5、劳合社比例法:(1)解释公式中各部分含义;⑵书上例题计算15000~25000 这一层的分保费。
2014春季非寿险精算(A6 )真题回忆考到的知识点:1、间接理赔费用有哪些;2、再保险按照不同的标准可以分为哪些类别;3、保费的分类;4、费率必须满足哪些条件,也就是费率特点;5、均匀进展因子,链梯法预测最终损失;6、求准备金的ced比率、po比率;7、ncd系统的要素以及数学模型;8、财务再保险的分类;9、BF推导未决赔款准备金估计;10、sharp 比率;11、IBNR ;12、buhlmann信度估计,考了好几个题,这个精算模型里就有;13、分位数估计求韦伯分布的参数。
中国精算师考试《非寿险精算》试题网友回忆版一

中国精算师考试《非寿险精算》试题(网友回忆版)一[单选题]1.根据保险公司风险资本比率所在的不同范围,监管部门会采取相应的措施。
(江南博哥)当风险资本比率()时,属于授权控管水准,监管部门可以对保险公司采取重整或清算的行动。
A.大于200%B.介于150%至200%之间C.介于100%至150%之间D,介于70%至100%之间E低于70%参考答案:D参考解析:风险资本比率=总调整资本/最低风险资本XIOo除比率越大,则风险越小。
200%以上——无行动水准150%-200%——公司行动水准100%-150%——监管行动水准70%-100%——授权控管水准70%以下——强制控管水准[单选题]2.某公司承保业务如下表所示:()OA.0.148B.0.168C.0.188D.0.208E.0.228参考答案:B参考解析:财务稳定性系数K是保险赔付随机变量的标准差Q与所收保费P的比值,即K=Q∕P°K越小,财务越稳定。
设n个独立的危险单位,每个保额a元,损失概率为p,损失变量服从二项分布B(n,p),则保险赔付的标准差Q=Tnp(1-p),纯保费p=em q,则财务稳定系数n=Q= ------------------- - --------= ------Pαnq√⅞α设有n类业务,第i类有ni个独立的危险单位,每个保额ai元,损失概率pi,则赔付的方差DXi=a⅛Mi-PJ,则所有业务的财务稳定系数为QJD,Ei1D)-JXg E1DXiJ比J4n<Pι(i-P。
】-F-Σ{1ιi n i p i^∑11⅝n i p j^∑1ι⅜∏iPi因此,业务一和业务三合并的财务稳定系数为_Q_√M∏1p1(i-PJ+申a p aα-p・)3nd>,+a√⅛¾⅛____________κ_√5000z×6000×003×0.97÷1000001×300×0.03×0.97二SOOOX6000×0J3+100000×300×0.03=0.168[单选题]3.一组样本数据满足以下条件:(1)均值=35,000(2)标准差=75,000(3)中值二10,000(4)90%分位数=Io0,000(5)样本服从WeibUI1分布用分位数估计法估计WeibU11分布的参数丫,估计结果0。
非寿险精算期末试题及答案

非寿险精算期末试题及答案一、选择题1. 下列哪个选项不属于非寿险精算的核心任务?A. 产品设计与定价B. 统计分析与风险管理C. 声誉评估与市场运营D. 赔付分析与预测答案:C2. 以下哪个指标可以衡量一个非寿险公司的风险承受能力?A. 经济附加值B. 投资收益率C. 赔付率D. 保费收入增长率答案:A3. 非寿险公司在产品设计阶段通常会使用什么方法来确定保费?A. 风险调整净保费法B. 赔付预测法C. 统计估计法D. 客户需求调查法答案:B4. 下列哪个风险不属于非寿险精算中常见的核心风险?A. 市场风险B. 操作风险C. 微观经济风险D. 利率风险答案:C5. 假设某个非寿险产品的保费为100万,赔款率为60%,则该产品的赔款金额为多少?A. 40万B. 60万C. 100万D. 160万答案:B二、简答题1. 请简要介绍非寿险精算的定义和作用。
非寿险精算是指利用数学和统计方法对非寿险业务进行风险评估、保费定价、赔付分析等分析和计算的过程。
其作用是帮助保险公司控制风险、确定合理的保费、评估赔付能力,从而保障公司的经营稳定性和盈利能力。
2. 请列举非寿险精算中常见的核心风险。
非寿险精算中常见的核心风险包括但不限于以下几个方面:- 赔款风险:即由于保险事故引起的赔付金额不确定性。
- 市场风险:即由于市场变动而导致的投资收益波动风险。
- 操作风险:即由于业务操作不当引起的风险。
- 法律风险:即由于法律法规变化导致的风险。
- 自然风险:即由于自然灾害等不可抗力因素引起的风险。
- 战争风险:即由于战争等社会因素引起的风险。
3. 请简述非寿险产品的定价方法。
非寿险产品的定价通常使用风险调整净保费法。
该方法首先根据历史数据和统计模型对风险进行评估,确定赔付率和赔款金额的期望值。
然后通过对期望赔款金额进行风险调整计算得出净保费,并加上预期利润和费用进行最终定价。
定价过程需要综合考虑市场需求、竞争状况等因素,以确保产品的竞争力和盈利能力。
保险精算考试题及答案

保险精算考试题及答案1. 保险精算中,用于计算未来现金流的现值的公式是:A. 未来值 = 现值× (1 + 利率)^期数B. 现值 = 未来值÷ (1 + 利率)^期数C. 未来值 = 现值× (1 - 利率)^期数D. 现值 = 未来值× (1 - 利率)^期数答案:B2. 在非寿险精算中,用于计算纯保费的公式是:A. 纯保费 = 预期损失 + 预期费用B. 纯保费 = 预期损失 - 预期费用C. 纯保费 = 预期损失× 预期费用D. 纯保费 = 预期损失÷ 预期费用答案:A3. 以下哪项是寿险精算中的生命表的主要组成部分?A. 死亡率表B. 疾病率表C. 残疾率表D. 以上都是答案:A4. 寿险精算中,计算年金现值的公式是:A. 年金现值 = 年金支付额× 利率× (1 - 1/(1 + 利率)^期数)B. 年金现值 = 年金支付额÷ 利率× (1 - 1/(1 + 利率)^期数)C. 年金现值 = 年金支付额× 利率÷ (1 - 1/(1 + 利率)^期数)D. 年金现值 = 年金支付额÷ 利率÷ (1 - 1/(1 + 利率)^期数) 答案:A5. 保险精算中,用于评估保险公司财务稳定性的指标是:A. 偿付能力比率B. 资产负债比率C. 投资回报率D. 以上都是答案:A6. 在精算评估中,用于计算保单持有人未来利益的现值的贴现率是:A. 预定利率B. 市场利率C. 法定利率D. 以上都不是答案:A7. 以下哪项是精算师在评估寿险保单的死亡率风险时常用的方法?A. 蒙特卡洛模拟B. 敏感性分析C. 精算表分析D. 以上都是答案:C8. 保险精算中,用于计算保单持有人未来利益的现值的公式是:A. 未来利益现值 = 未来利益× 利率× (1 - 1/(1 + 利率)^期数)B. 未来利益现值 = 未来利益÷ 利率× (1 - 1/(1 + 利率)^期数)C. 未来利益现值 = 未来利益× 利率÷ (1 - 1/(1 + 利率)^期数)D. 未来利益现值 = 未来利益÷ 利率÷ (1 - 1/(1 + 利率)^期数) 答案:B9. 在保险精算中,用于计算保单的准备金的公式是:A. 准备金 = 未来利益现值 - 已收保费B. 准备金 = 未来利益现值 + 已收保费C. 准备金 = 未来利益现值× 已收保费D. 准备金 = 未来利益现值÷ 已收保费答案:A10. 以下哪项是保险精算中用于评估保单持有人未来利益的不确定性的方法?A. 精算评估B. 风险评估C. 敏感性分析D. 以上都是答案:C。
黑龙江 2023年精算师考试《非寿险精算》真题模拟汇编(共92题)

黑龙江 2023年精算师考试《非寿险精算》真题模拟汇编(共92题)1、已知经验总损失15万元,已经风险单位600,与保费直接相关因子为12%,利润因子为4%,每风险单位固定费用为10元,由纯保费法得到的指示费率为()元。
(单选题)A. 250.0B. 279.5C. 309.5D. 412.5E. 512.5试题答案:C2、设某保险人经营某种车辆险,对过去所发生的1000次理赔情况作了记录,平均赔款额为2200元,又按赔款额分为5档,各档中的记录次数如表1所示。
表1利用χ2分布检验,假设置信水平为99.5%,则拒绝域形式是____,判断能否用指数分布拟合个别赔款额的分布的结论是____。
()(单选题)A. ,能B. ,不能C. ,能D. ,能E. ,不能试题答案:B3、某地区每次台风对农作物所造成的损失Y(单位万公斤)服从参数α=3.0,β=2.0的对数伽玛分布,则每次台风对农作物造成的平均损失为()万公斤。
(单选题)A. 7B. 8C. 9D. 10E. 11试题答案:B4、保险公司有2000份机动车辆车身险保险单,按照预期的赔款频率分别属于由表所示的三类A、B、C,现从这2000份保险单中随机地抽取一份并发现在过去的一年中未发生索赔,则这份保险单分别属于A、B、C类的概率分别是()。
(假定赔款次数服从泊松分布)。
表风险分布(单选题)A. 0.539,0.341,0.120B. 0.439,0.441,0.120C. 0.541,0.339,0.120D. 0.341,0.539,0.120E. 0.539,0.120,0.341试题答案:A5、设p的先验分布为(0,1)上的均匀分布,已知x1,x2,…,x n是来自总体分布为二点分布的样本,二点分布的参数为p,并且已知后验分布的均值为1/4,以下结论正确的一项为()。
(单选题)A. ∑X i=1,n=2B. ∑X i=1,n=4C. ∑X i=0,n=2D. ∑X i=0,n=4E. ∑X i=0,n=6试题答案:C6、某火险的损失经验数据按赔款规模分级统计如表所示。
非寿险精算杨静平答案

非寿险精算杨静平答案【篇一:精算师】xt>(一)申请准精算师资格应满足的条件: 1、具有本科(国家承认同等学历)以上学历; 2、通过a1-a8全部科目的考试。
(二)申请准精算师资格应满足的条件:1、具备中国准精算师资格;2、满足以下要求之一:(1 )寿险方向:通过f1(寿险方向)、f2(寿险方向)、f3和f8科目,并在f4、f9和f10这3门科目中至少通过1门科目。
(2 )非寿险方向:通过f1(非寿险方向)、f6、f7和f8科目,并在f2(非寿险方向)、f5、f9和f10这4门科目中至少通过1门科目。
(3 )特别说明:2010年12月31日(含12月31日)之前获得中国准精算师资格的考生可按照如下要求申请精算师资格:寿险方向:通过f1(寿险方向)、f2(寿险方向)和f3科目,并在f4、f8、f9和f10这4门科目中至少通过2门科目。
非寿险方向:通过f1(非寿险方向)、f6和f7科目,并在f2(非寿险方向)、f5、f8、f9和f10这5门科目中至少通过2门科目。
3、拥有三年精算相关工作经验。
中国精算师资格考试辅导用书数学方面:从最基础的高等数学线性代数开始看然后看概率论与数理统计计量经济学金融方面:从金融学概论开始要看会计学(相当于中级)金融理论与应用数量金融(这里推荐一个教材paul willmott的数量金融介绍)经济方面:由于考到后面会考经济学知识所以宏微观经济学是必需的知识以上就是知识储备了关于精算师的书国内都大同小异第i 部分中国精算师资格考试 01 数学基础Ⅰ参考书目: 1. 《高等数学讲义》(第二篇数学分析)樊映川编著高等教育出版社 2. 《线性代数》胡显佑四川人民出版社 3. 《运筹学》(修订版) 1990 年《运筹学》教材编写组清华大学出版社除以上参考书外,也可参看其他同等水平的参考书。
02 数学基础Ⅱ参考书目: 1、《概率论与数理统计》茆诗松,周纪芗编著,中国统计出版社 1996 年7 月第 1 版。
《非寿险精算》试题及答案

《非寿险精算》试题及答案(解答仅供参考)第一套一、名词解释1. 非寿险精算:非寿险精算是研究非寿险业务中风险评估、保费定价、准备金评估、损失分布分析等领域的数学和统计方法。
2. 损失概率:损失概率是指在一定时间内,某一特定风险事件发生的可能性。
3. 纯保费:纯保费是指保险公司为了覆盖预期的损失成本而收取的保费。
4. 保险准备金:保险准备金是保险公司为应对未来可能发生的索赔而储备的资金。
5. 责任年限法:责任年限法是一种计算未决赔款准备金的方法,基于假设所有未决赔款将在一定年限内结案。
二、填空题1. 非寿险精算的主要内容包括风险评估、______、准备金评估和损失分布分析。
答案:保费定价2. 在非寿险业务中,______是决定保费水平的重要因素。
答案:损失概率和损失程度3. 如果实际赔付金额超过已收取的保费和投资收益之和,就需要动用______来支付。
答案:保险准备金4. 在非寿险精算中,______是一种常用的损失分布模型。
答案:泊松分布或帕累托分布5. 在责任年限法中,如果假设所有未决赔款将在一年内结案,那么这就是______责任年限法。
答案:一年三、单项选择题1. 非寿险精算主要应用于哪种类型的保险业务?A. 寿险B. 健康险C. 财产险D. 意外险答案:C. 财产险2. 下列哪一项不属于非寿险精算的内容?A. 风险评估B. 保费定价C. 投资管理D. 准备金评估答案:C. 投资管理3. 在非寿险精算中,用来衡量风险大小的指标是?A. 损失概率B. 损失程度C. 风险暴露D. 风险溢价答案:A. 损失概率4. 下列哪种方法可以用来计算非寿险业务的未决赔款准备金?A. 综合比例法B. 平均估算法C. 责任年限法D. 追溯法答案:C. 责任年限法5. 在非寿险精算中,如果某风险事件的发生概率为0.1,且每次发生时的平均损失为1000元,则该风险的期望损失为?A. 10元B. 100元C. 1000元D. 10000元答案:B. 100元四、多项选择题1. 非寿险精算的主要内容包括:A. 风险评估B. 保费定价C. 准备金评估D. 损失分布分析E. 投资管理答案:ABCD2. 下列哪些因素会影响非寿险业务的保费定价?A. 损失概率B. 损失程度C. 营运费用D. 目标利润E. 法律法规答案:ABCD3. 下列哪些方法可以用来计算非寿险业务的未决赔款准备金?A. 综合比例法B. 平均估算法C. 责任年限法D. 追溯法E. 预测法答案:ABCD4. 在非寿险精算中,以下哪些是常用的损失分布模型?A. 正态分布B. 泊松分布C. 帕累托分布D. 对数正态分布E. 卡方分布答案:BC5. 下列关于非寿险精算的陈述中,哪些是正确的?A. 非寿险精算是研究非寿险业务中的风险评估和管理的学科。
非寿险精算课后习题答案(中精-主编-韩天雄)

1.0041
1391×1.0041=1396.7
2008
1.0764
1364×1.0764=1468.21
2009
1.3
1224×1.3=1591.2
6T
G=40000/500000=0.08
V=(200000+20000+50000)/1000000+45000/900000=0.32
Q=0.05
9/32×1.1+22/32×1.188+1/32×1.3068=1.1669625
1.3068/1.1669625=1.1198
所以2006年至2008年近似均衡已赚保费总额为:
20469×1.30273+23543×1.2161+28300×1.11983=86987.39元
4T
相邻年间的损失进展因子如下所示:
2T
(1)2006年至2008年在2009年7月1日费率下各年均衡已赚保费分别为:
2006年:1.9×3570+3.2×1620+1.2×5820+2.3×1280=21895元
2007年:1.9×4230+3.2×1910+1.2×6320+2.3×1320=24769元
2008年:1.9×5100+3.2×2200+1.2×6930+2.3×1500=28496元
赔款额落在0~100的理论概论为:
同理可得
在拒绝域范围内,所以拒绝原假设 ,不能用指数分布模拟个别理赔分布。
8T
假设实际赔款平均额为 ,正态分布假设检验:
:
:
为: ,假定
则 ,拒绝域为
中国精算师非寿险精算第8章 经验模型综合练习与答案

中国精算师非寿险精算第8章经验模型综合练习与答案一、单选题(一)、【题干】:从t=0开始观察一个由8人组成的团体,直到他们全部死亡,仅记录发生死亡的时间(以天为单位)。
假设t=0的初始事件发生在一天的中点,死亡事件也发生在那天的中点,那么,所有的生存期限均为整数。
所观察的生存期限为3,4,5,5,7,10,10,12。
So(t)是观察的样本空间的经验生存函数。
1、利用So(t)估计S(t),则S(5)、S(12)的估计量分别为()。
A.0.125,0B.0.125,0.125C.0.375,0D.0.375,0.125E.0.500,0【参考答案】:E【试题解析】:由于So(t)是右连续的,t=5时,而t8=12是最后一次死亡事件发生的时间,则So(12)=0。
So(t)的图形如图所示。
(二)、【题干】:考察一个在t=0处有20个个体的样本,所有的个体均在5周内死亡,并只记录每周的死亡人数,所观察的结果为:2人第1周死亡,3人第2周死亡,8人第3周死亡,6人第4周死亡,1人第5周死亡。
1、计算和的估计值分别为()。
A.0.05,0.0024B.0.10,0.0045C.0.15,0.0064D.0.30,0.0105E.0.40,0.0120【参考答案】:D【试题解析】:由已知得:,故2、计算和的估计值分别为()。
A.1.14286,0.02381B.1.14286,0.14286C.1.94591,0.14286D.1.94591,0.85714E.1.94591,0.94591【参考答案】:D【试题解析】:由已知可得:,所以在死动恒定假设下3、运用上述数据估计(1)2q0为____;(2)S(3)为____;(3)q3为____。
()A.0.35,0.40,0.8571B.0.40,0.35,0.8571C.0.40,0.8571,0.40D.0.8571,0.35,0.40E.0.8571,0.40,0.35【参考答案】:B【试题解析】:由已知作图,如下:4、若样本的生存分布为区间(0,5]上的均匀分布,则的值分别为()。
最新非寿险精算答案作业
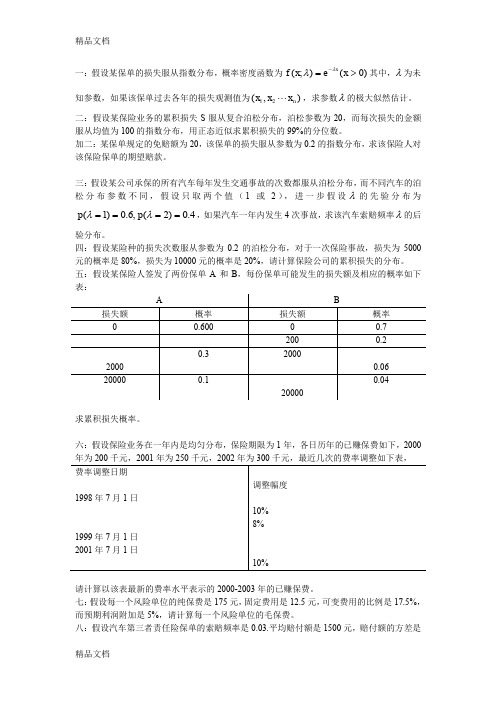
一:假设某保单的损失服从指数分布,概率密度函数为)0();(>=-x ex f xλλ其中,λ为未知参数,如果该保单过去各年的损失观测值为),(21n x x x ,求参数λ的极大似然估计。
二:假设某保险业务的累积损失S 服从复合泊松分布,泊松参数为20,而每次损失的金额服从均值为100的指数分布,用正态近似求累积损失的99%的分位数。
加二:某保单规定的免赔额为20,该保单的损失服从参数为0.2的指数分布,求该保险人对该保险保单的期望赔款。
三:假设某公司承保的所有汽车每年发生交通事故的次数都服从泊松分布,而不同汽车的泊松分布参数不同,假设只取两个值(1或2),进一步假设λ的先验分布为4.0)2(,6.0)1(====λλp p ,如果汽车一年内发生4次事故,求该汽车索赔频率λ的后验分布。
四:假设某险种的损失次数服从参数为0.2的泊松分布,对于一次保险事故,损失为5000元的概率是80%,损失为10000元的概率是20%,请计算保险公司的累积损失的分布。
五:假设某保险人签发了两份保单A 和B ,每份保单可能发生的损失额及相应的概率如下表:求累积损失概率。
六:假设保险业务在一年内是均匀分布,保险期限为1年,各日历年的已赚保费如下,2000年为200千元,2001年为250千元,2002年为300千元,最近几次的费率调整如下表,请计算以该表最新的费率水平表示的2000-2003年的已赚保费。
七:假设每一个风险单位的纯保费是175元,固定费用是12.5元,可变费用的比例是17.5%,而预期利润附加是5%,请计算每一个风险单位的毛保费。
八:假设汽车第三者责任险保单的索赔频率是0.03.平均赔付额是1500元,赔付额的方差是360000元,试问当保单组合的索赔次数为多大时就可以赋予完全可信性?保单组合应该包含多少份保单?(k=0.1,p=0.9)384)(2=ky p十:假设某险种的保险期限为1年,新费率的生效日期是2005年7月1日,目标赔付率为60%,如果每年按5%的速度增长,请根据下表计算费率的调整幅度。
非寿险精算(孟生旺)课后答案

2.15 X 的矩母函数为 M x ( z ) = ∫ e
0
N 的母函数为 PN ( z ) = [1 − β ( z − 1) ]
kh da w. co m
案 网
zx 5 ni Ai2 n A2 + 0.04∑ i i = 1.7072 × 109 4 i =1 12
1
θ
e
− x /θ
dx =
1
θ
n
2.5 2.6
M x (t ) = E(etx ) = ∫ etx ∑ ai λi e − λi x dx = ∑ ai (1 −
0 i =1 i =1
E ( S ) = λ E ( X ) = 20 × 100 = 2000
Var ( S ) = Var ( X ) E ( N ) + Var ( N ) [ E ( X ) ] = λ Var ( X ) + [ E ( X ) ]
课后答案网
《非寿险精算学》
(孟生旺 刘乐平 编著,中国人民大学出版社 2007 版)
参考答案
(2008 年 2 月)
0, x ≤ 0 ⎧ ⎪ f (x + d ) 其密度函数为 f Y ( x ) = ⎨ ,x > 0 ⎪ ⎩ 1 − F (d )
w.
=
1⎞ ⎛ f ⎜x+ ⎟ ∞ ∞ ∞ f (x + d) λ⎠ E (Y ) = ∫ xfY ( x )dx = ∫ x ⋅ dx = ∫ x ⎝ dx 0 0 0 1− F (d ) ⎛1⎞ 1− F ⎜ ⎟ ⎝λ⎠
+∞
1 16 −2 λ 4 −λ e , P ( x = 4 λ = 1) = e−1 , P (x = 4 λ = 2) = e 24 4! 24
非寿险精算答案整理

一:假设某保单的损失服从指数分布,概率密度函数为)0();(>=-x e x f x λλ其中,λ为未知参数,如果该保单过去各年的损失观测值为),(21n x x x ,求参数λ的极大似然估解:利用极大似然估计的方法,可以得到xxnni i1ˆ1==∑=λ二:假设某保险业务的累积损失S 服从复合泊松分布,泊松参数为20,而每次损失的金额服从均值为100的指数分布,用正态近似求累积损失的99%的分位数。
解:[]400000)100100(20)()()()()(200010020)()(222=+=+==⨯==X E N VAR N E X VAR S VAR X E S E λ分位数=3471)(326.2)(=⨯+S VAR S E加二、某保单规定的免赔额为20,该保单的损失服从参数为0.2的指数分布,求该保险人对该保险保单的期望赔款。
解: 令⎩⎨⎧≥-≤=2020200X X X Y ,,为保险人的赔款随机变量4202.052.0)20()2020()(-∞-=-=>-=⎰e dx e x X X E Y E x三、假设某公司承保的所有汽车每年发生交通事故的次数都服从泊松分布,而不同汽车的泊松分布参数不同,假设只取两个值(1或2),进一步假设λ的先验分布为4.0)2(,6.0)1(====λλp p ,如果汽车一年内发生4次事故,求该汽车索赔频率λ的后验分布。
解:λλλ-==e x P !4)4(41241)14(-===e x P λ 22416)24(-===e x P λ 2031.04.024166.0246.024)41(211=⨯+⨯⨯===---e e e x P λ7969.04.024166.0246.02416)42(212=⨯+⨯⨯===---e e e x P λ=)(λE 1)41(⨯==x P λ+2)42(⨯==x P λ=1.7969四:假设某险种的损失次数服从参数为0.2的泊松分布,对于一次保险事故,损失为5000元的概率是80%,损失为10000元的概率是20%,请计算保险公司的累积损失的分布 解:为简化计算,假设一个货币单位为5000元,解:818731.0)0(2.0===--e e f s λ ,130997.08.02.0)0()1()1(2.0=⨯⨯==-e f f f S X s λ043229.0))0()2(2)1()1((2)2(=+=S X S X s f f f f f λ五:假设某保险人签发了两份保单六:假设保险业务在一年内是均匀分布,保险期限为1年,各日历年的已赚保费如下,2000解:如果把1998年生效的相对费率看做是1,则1999年生效的相对费率为1.08,2001年生效的相对费率为1772.19.01*8.01=,2000年的相对费率为7.01.5%87*8.01.5%12*1=+,2001年的相对费率为1.08*12.5%+1.1772*12.5%=1.09215,2002年的相对费率为1.08*12.5%+1.1772*87.5%=1.16505,将所有年费的已赚保费调整到2002年的水平,可得等水平已赚保费为3100*1.1772/1.07+3200*1.1772/1.09215+3500*1.1772/1.16505=10396.28 八:某险种当年的相对费率和保费收入、过去三年的等水平已赚保费和经验损失数据如下表所示,假设A 为基础类别,经验数据的可信度为40%,如果整体保费需要上调15%,请计算调整后的相对费率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一:假设某保单的损失服从指数分布,概率密度函数为)0();(>=-x e x f x λλ其中,λ为未知参数,如果该保单过去各年的损失观测值为),(21n x x x ,求参数λ的极大似然估解:利用极大似然估计的方法,可以得到xxnni i1ˆ1==∑=λ二:假设某保险业务的累积损失S 服从复合泊松分布,泊松参数为20,而每次损失的金额服从均值为100的指数分布,用正态近似求累积损失的99%的分位数。
解:[]400000)100100(20)()()()()(200010020)()(222=+=+==⨯==X E N VAR N E X VAR S VAR X E S E λ分位数=3471)(326.2)(=⨯+S VAR S E加二、某保单规定的免赔额为20,该保单的损失服从参数为0.2的指数分布,求该保险人对该保险保单的期望赔款。
解: 令⎩⎨⎧≥-≤=2020200X X X Y ,,为保险人的赔款随机变量4202.052.0)20()2020()(-∞-=-=>-=⎰e dx e x X X E Y E x三、假设某公司承保的所有汽车每年发生交通事故的次数都服从泊松分布,而不同汽车的泊松分布参数不同,假设只取两个值(1或2),进一步假设λ的先验分布为4.0)2(,6.0)1(====λλp p ,如果汽车一年内发生4次事故,求该汽车索赔频率λ的后验分布。
解:λλλ-==e x P !4)4(41241)14(-===e x P λ 22416)24(-===e x P λ 2031.04.024166.0246.024)41(211=⨯+⨯⨯===---e e e x P λ7969.04.024166.0246.02416)42(212=⨯+⨯⨯===---e e e x P λ=)(λE 1)41(⨯==x P λ+2)42(⨯==x P λ=1.7969四:假设某险种的损失次数服从参数为0.2的泊松分布,对于一次保险事故,损失为5000元的概率是80%,损失为10000元的概率是20%,请计算保险公司的累积损失的分布 解:为简化计算,假设一个货币单位为5000元,解:818731.0)0(2.0===--e e f s λ ,130997.08.02.0)0()1()1(2.0=⨯⨯==-e f f f S X s λ043229.0))0()2(2)1()1((2)2(=+=S X S X s f f f f f λ五:假设某保险人签发了两份保单六:假设保险业务在一年内是均匀分布,保险期限为1年,各日历年的已赚保费如下,2000解:如果把1998年生效的相对费率看做是1,则1999年生效的相对费率为1.08,2001年生效的相对费率为1772.19.01*8.01=,2000年的相对费率为7.01.5%87*8.01.5%12*1=+,2001年的相对费率为1.08*12.5%+1.1772*12.5%=1.09215,2002年的相对费率为1.08*12.5%+1.1772*87.5%=1.16505,将所有年费的已赚保费调整到2002年的水平,可得等水平已赚保费为3100*1.1772/1.07+3200*1.1772/1.09215+3500*1.1772/1.16505=10396.28 八:某险种当年的相对费率和保费收入、过去三年的等水平已赚保费和经验损失数据如下表所示,假设A 为基础类别,经验数据的可信度为40%,如果整体保费需要上调15%,请计算调整后的相对费率。
解:有实际赔付经验可知1500m (k 因此完全可信性所需的索赔次数不能小于445).401(3842=+=F n又由于每份保单的索赔频率为0.03,所以发生445次索赔所需要的保单数为445/0.03=14848 十、假设某险种的保险期限为1年,新费率的生效日期是2005年7月1日,目标赔付率为60%,如果每年按5%的速度增长,请根据下表计算费率的调整幅度。
解:20032005年7月1日签发的保单,其赔款平均在2006年7月1日支出。
因此把2003年的保单年度的最终赔款调整到2006年7月1日得水平即为3.711295.011000.52=⨯,同样把2004年保单年度的最终赔款调整到2006年7月1日的.51费率上调幅度=0.6716/0.6=12%十一:已知两个风险A 和B 的损失金额服从下述分布,,其中风险A 发生损失的概率是风险B 的两倍,如果已知某个风险在某次事故的损失额为300元,求该风险下次损失额的BL 解:7.12726))2((31)1()32()(==Θ+=Θ⨯=x E x E x E 56.10795755)7.127268080(31)7.1272615050(3222=-+-=a756242500)1505070000(2.0)150503000(3.0)15050300(5.0)1(222=-+-+-⨯==ΘX VAR 427467600)808070000(1.0)80803000(3.0)8080300(6.0)2(222=-+-+-⨯==ΘX VAR 7.6466508664274676003175624250032=⨯+⨯=ν 899.59==a k ν 01642.0=+=kn n z 信度估计值为65.12522)1(=-+μz X z十二、已知有四个风险等级的被保险人,每人可能发生的损失为2或者4,其分布如下表所示,随机选定某一风险等级,并且从中选取四个被保险人,总的损失为4,如果从同一风险等级中再抽取一个被保险人,请用bl-s 信度模型估计这5个被保险人的总损失。
2675.085.2)6.336.22.2(41.705.8222222=-+++===a ,,νμ6011.02675.071.044=+=+=kn nz 738.1)1(ˆ=-+=μz X z x69.8ˆ5=x十三、假设不同被保险人的索赔频率相互独立,每个被保险人在每月的索赔次数服从泊松分布,不同被保险人的泊松参数互不相同,泊松参数服从伽马分布,其密度函数为λλλλ120)100()(1006-=e f ,假设保险人在过去4个月份的经验数据如下表所示,请应用bl-s模型估计保险人在下个月的索赔次数。
十四十六:已知 100个人投保,这些投保的个体有相互独立的索赔,索赔的均值和方差按照性设S 为总的索赔量,总的保险费按照)(2)(S D S E +收取,这100个成员中,男女性别个数未知,设男性有N 个人,N 服从二项分布,)4.0,100(b 。
求总保费为多少?解:设X 表示男性索赔,Y 表示女性索赔,N 表示男性个数,)4.0,100(~b N ,则总索赔为男、女之和,即1002121Y Y Y X X X S N N N +++++++=++ 4)(2)(==X D X E , 10)(4)(==Y D Y E ,则))(()(N S E E S E =))()100()((Y E N X NE E -+= )(2400N E -==320D(S)=))(())((N S E D N S D E +))()100()(())()100()((Y E N X NE D Y D N X ND E -++--= 85696760=+=所以总保费为)(2)(S D S E +=378.5十七、设2=λ,4,3,2,1,1.0)(==x x x p ,计算总索赔S 的分布4,3,2,1,0),(==x x S f 的概率。
一:一般解法: )()()()(0n N P n N x S P x S P x f n ======∑∞=)()(0*n N P x Pn n==∑∞=方法二:44332211其中,i N 服从参数为i p λ的泊松分布,4,3,2,1,1.0)(==x x x p十八:由解:设损失变量为∑==1000001i iXL ,则理赔变量为==L S 8.0∑=10000018.0i iX,又设安全附加费为θ,则保费总额为)()1(S E G θ+=则根据题意1000005439120)(100000*1060)(⨯==S D S E有))()(()()()()(S D S E S D S E S D S E S P θφθ≈⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤- 所以安全附加保费为1.645*100000*5439120=1213193.9将收取纯保费的)1(θ+倍为保费,求相对附加保费θ使得05.0))()1((=+≥S E S P θ成立。
解:设i X 代表第i 类得个体索赔变量,i I 为0-1变量,{}1=i I 表示第i 类索赔发生,{}0=i I 表示第i 类索赔不发生,i B 代表在索赔发生的条件下,索赔的大小。
则根据个体索赔量得定义,i i i B I X =,且i i q I P ==)1(,i q 为索赔概率。
则i i i i i i i i i q q q X D q X E 22)1()(,)(σμμ+-==其中)1(),1(2====i i i i i i I B D I B E σμ,且根据已知2i i σμ=成立 所以150075.05001.0100025.0500)(31=⨯+⨯+⨯==∑=i iiiqn S E μ∑==31)(i i n S D ))1((22i i i i i q q q σμ+-=12687.5查表的到:645.1)()(=S D S E θ所以1235.0=θ二十:某保险公司规定赔款最高限额是3000元时,超过部分由投保人自己支付,随机变量X 即一笔赔款的分布函数是)(x F ,而)(x F 遵从于01)(001.0≥-=-X e x F x试计算对一笔赔款应由保险人支付平均额度。
解:赔款额的概率密度是⎪⎩⎪⎨⎧≥==-0)0(,001.0)()(001.0x e x F dx dx f x因此根据赔偿限额的规定,我们得到二十一:假设汽车保险的损失分布是参数)100,3(==θα的帕累托分布:0,)100100(1)(3≥+-=x x x F 求免赔额为20时的赔偿期望值为多少?解:50131001)(=-=-=αθX E 8.215))120100(1(13100)20(13=--=∧-X E213.40)120100(1)20(3=-=F则赔款的期望值为60)20(1)20()()(=-∧-=X F X E X E Y E二十二:假设某汽车保险的损失分布是参数)100,3(==θα的帕累托分布:0,)100100(1)(3≥+-=x x x F 求免赔额为200时的赔偿期望值为多少? 解:50131001)(=-=-=αθX E 4.444))300100(1(13100)200(13=--=∧-X E解:将各进展年的因子相邻相除,得到相邻进展因子。
