完全平方公式
完全平方公式经典例题

完全平方公式经典例题
【原创实用版】
目录
1.完全平方公式的定义和基本形式
2.经典例题解析
3.完全平方公式的应用场景和技巧
正文
一、完全平方公式的定义和基本形式
完全平方公式,又称平方差公式或完全平方差公式,是指两个数的平方和与这两个数的乘积的二倍之间的关系。
其基本形式为:(a+b)=a+2ab+b 和 (a-b)=a-2ab+b。
二、经典例题解析
例题 1:求解 (3x+2y) 的值。
解答:根据完全平方公式,(3x+2y)= (3x) + 2*3x*2y + (2y) = 9x + 12xy + 4y。
例题 2:求解 (x-3y+2z) 的值。
解答:根据完全平方公式,(x-3y+2z)= x - 2*x*3y + (3y) - 2*x*2z + (2z) = x - 6xy + 9y - 4xz + 4z。
三、完全平方公式的应用场景和技巧
完全平方公式在代数运算中具有广泛的应用,例如求解平方和、平方差、完全平方等。
在解题过程中,熟练掌握完全平方公式可以简化运算过程,提高解题效率。
技巧 1:注意符号。
在运用完全平方公式时,要特别注意符号。
例如,(a+b) 中的 + 号,在展开后应分别与 a 和 b 相乘。
技巧 2:化简表达式。
利用完全平方公式,可以将复杂的平方和或平方差表达式化简为更容易计算的形式。
技巧 3:结合其他代数公式。
在解题过程中,完全平方公式可以与其他代数公式相结合,如乘法公式、分配律等,以达到更快速地解决问题。
完全平方公式知识讲解

完全平方公式知识讲解
假设方程的两个解是x1和x2,那么根据求根公式的推导,可以得到
完全平方公式的一般形式如下:
x1 = (-b + √(b^2 - 4ac)) / (2a)
x2 = (-b - √(b^2 - 4ac)) / (2a)
首先,将 ax^2+bx+c=0 变形为 x^2 + (b/a)x + c/a = 0。
然后,将方程右侧的常数项移动到方程左侧,得到x^2+(b/a)x=-c/a。
接着,我们将方程左侧的平方项和一次项组合成一个完全平方,即(x + (b/2a))^2 = (1/4a^2)(b^2 - 4ac)。
继续变形,得到x + (b/2a) = √((b^2 - 4ac)/(4a^2))。
再将方程左侧的二次项系数变为1,即 x = -b/(2a) ± √((b^2 -
4ac)/(4a^2))。
最后,简化形式,得到 x = (-b ± √(b^2 - 4ac)) / (2a)。
通过上述推导过程,我们得到了完全平方公式。
使用这个公式,可以
快速而准确地求解一元二次方程的解。
需要注意的是,完全平方公式适用于任意实数系数的二次方程。
但在
实际应用中,可能会遇到无实数解或有重复解的情况。
因此,在使用完全
平方公式求解一元二次方程时,需要根据情况进行判断和处理。
完全平方公式

完全平方公式1、完全平方公式:()2222b ab a b a ++=+; ().2222b ab a b a +-=-即:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的两倍。
2、深入理解: 完全平方公式的条件:⑴二项式的平方。
完全平方公式的结论:⑴ 三项式 ;⑵有两项平方项,且是正的;另一项是二倍项,符号看前面。
口诀记忆:“头平方,尾平方,头尾两倍在中央”;3、逆运算:()2222b a b ab a ±=+±例1:计算下列各式: (1)、2)52(y x +(2)、2)221(y x -例2:(1)()212-+b a (2)5z)4y -(x 5-4++)(z y x例3:如果多项式92+-mx x 是一个完全平方式,则m 的值是。
例4:计算:()()_________22=--+b a b a ;()__________222-+=+b a b a 练习:1、如果多项式k xy x ++82是一个完全平方式,则k 的值是。
2、已知。
y ,xy y x 的值求22x 60,17+==+3、若13a a +=,求221a a +的值。
课下练习:1、下列计算中正确的是()A.222)(b a b a +=+B. 222)(b a b a -=-C.22224)2(y xy x y x +-=-D.25541)521(22++=+x x x 2、下列各式计算结果为2xy -x 2-y 2的是()A .(x -y )2B .(-x -y )2C .-(x+y )2D .-(x -y )23、已知,,,则代数式的值为( ) A.12 B.13 C.25 D.264、计算下列各式:(1)(3m-n)(m-2n) (2)()()()()()222312-+++--+x x x x x(3)、()2101684212⨯⨯⨯⨯-(4)、22)(2)())((b a b a b a b a --++-+5、如图15-2-3,AB =a ,P 是线段AB 上一点,分别以AP 、BP 为边作正方形.图15-2-3(1)设AP =x ,则两个正方形的面积之和S =__________;(2)当AP 分别为13a 和12a 时,两个正方形的面积的和分别为S 1和S 2,比较S 1和S 2的大小:__________.。
完全平方公式20种变形

完全平方公式20种变形【最新版】目录1.完全平方公式的基本形式2.完全平方公式的 20 种变形3.变形实例及解题方法正文【1.完全平方公式的基本形式】完全平方公式是指一个二次多项式的平方可以表示为两个一次多项式的平方和。
其基本形式为:(a+b)^2 = a^2 + 2ab + b^2(a-b)^2 = a^2 - 2ab + b^2【2.完全平方公式的 20 种变形】在实际解题过程中,完全平方公式可以衍生出 20 种变形,具体如下:1.(a+b)^2 = a^2 + 2ab + b^22.(a-b)^2 = a^2 - 2ab + b^23.(a+2b)^2 = a^2 + 4ab + 4b^24.(a-2b)^2 = a^2 - 4ab + 4b^25.(a+3b)^2 = a^2 + 6ab + 9b^26.(a-3b)^2 = a^2 - 6ab + 9b^27.(a+ab)^2 = a^2 + 2ab^2 + b^28.(a-ab)^2 = a^2 - 2ab^2 + b^29.(a+b^2)^2 = a^2 + 2ab^2 + b^410.(a-b^2)^2 = a^2 - 2ab^2 + b^411.(a+2b)^2 = a^2 + 4ab + 4b^212.(a-2b)^2 = a^2 - 4ab + 4b^213.(a+3b)^2 = a^2 + 6ab + 9b^214.(a-3b)^2 = a^2 - 6ab + 9b^215.(a+ab)^2 = a^2 + 2ab^2 + b^216.(a-ab)^2 = a^2 - 2ab^2 + b^217.(a+b^2)^2 = a^2 + 2ab^2 + b^418.(a-b^2)^2 = a^2 - 2ab^2 + b^419.(a+2b)^2 = a^2 + 4ab + 4b^220.(a-2b)^2 = a^2 - 4ab + 4b^2【3.变形实例及解题方法】以第一种变形为例:(a+b)^2 = a^2 + 2ab + b^2假设 a = 3, b = 2,代入公式得:(3+2)^2 = 3^2 + 2*3*2 + 2^2= 25 = 9 + 12 + 4可见,公式左边的 (3+2)^2 等于右边的 9 + 12 + 4。
完全平方公式知识讲解

完全平方公式知识讲解二次方程的一般形式是 ax^2 + bx + c = 0,其中a,b和c是已知常数,而x是未知数。
完全平方公式的形式为 x = (-b ± √(b^2 -4ac)) / 2a。
让我们详细解释一下完全平方公式的推导过程。
首先,我们要将二次方程写成平方的形式。
我们可以通过配方来完成这一步骤。
将二次方程移项,我们得到 ax^2 + bx = -c。
接下来,我们需要创建一个完全平方。
我们可以通过将b的一半平方加入方程的两边来实现这一点。
这意味着我们需要将b/2平方并加入方程两边。
形式上写为(b/2)^2通过这样做,我们可以将方程转变为一个完全平方的形式。
现在方程变为 (ax^2 + bx + (b/2)^2) = (b/2)^2 - c。
简化方程,我们得到 (ax + b/2)^2 = (b^2/4) - c。
将方程再次移项,我们得到 (ax + b/2)^2 - (b^2/4) = -c。
注意到,左边的式子是两个平方的差。
这是一个重要的公式,称为平方差公式。
平方差公式是 (a-b)(a+b) = a^2 - b^2、应用这个公式,我们可以将方程进一步简化为 (ax + b/2)^2 - (b^2/4) = -c。
通过移项,我们得到 (ax + b/2)^2 = (b^2/4) - c。
然后,我们可以开始解方程。
首先,我们要对两边的式子开根号,可以得到ax + b/2 = ±√((b^2/4) - c)。
接下来,我们继续化简。
我们将b/2移项,得到 ax = -b/2 ±√((b^2/4) - c)。
最后,我们将x与a相除,得到 x = (-b ± √(b^2 - 4ac)) / 2a。
这就是完全平方公式的最终形式。
需要注意的是,完全平方公式只适用于二次方程。
对于高次方程,我们需要采用其他方法来求解。
总结起来,完全平方公式是一个用于求解二次方程的重要公式。
完全平方公式

完全平方公式完全平方公式是学习数学中的一个重要定理,它能够帮助我们快速求解二次方程的根。
在本文档中,我们将解释完全平方公式的原理,并给出一些例子。
定义在代数学中,完全平方是指一个数可以写成另一个数的平方。
完全平方公式是通过将二次方程转化为一个完全平方的形式,以便更轻松地求解该方程的根。
公式对于二次方程ax2+bx+c=0,其中a,b,c是实数且a eq0,完全平方公式可表示为:$$ x = \\frac{-b \\pm \\sqrt{b^2 - 4ac}}{2a} $$公式中的$\\pm$ 表示可以取正号或负号,因此,二次方程的解可以有两个根,分别对应取正号和负号。
推导过程为了推导完全平方公式,我们先从一个完全平方的观点入手。
假设有一个完全平方(x+p)2,则展开得到:(x+p)2=x2+2px+p2如果我们将二次方程的通项表示成完全平方的形式,即ax2+bx,那么我们需要寻找一个p,使得2px=bx,然后再等式两边加上常数p2,这样就能得到完全平方公式的形式。
为了寻找p的值,我们可以观察下面的等式:$$ 2px = bx \\Rightarrow 2p = b \\Rightarrow p = \\frac{b}{2} $$将这个解代入(x+p)2,得到:$$ (x + \\frac{b}{2})^2 = x^2 + bx + \\frac{b^2}{4} $$现在我们已经得到了完全平方公式,最后一步是将常数项c纳入考虑。
为此,我们将等式右边的 $\\frac{b^2}{4}$ 替换为c,得到完全平方公式的最终形式:$$ x = \\frac{-b \\pm \\sqrt{b^2 - 4ac}}{2a} $$示例让我们通过几个例子来演示完全平方公式的应用。
例子1:求解x2+6x+9=0根据完全平方公式,我们可以找到a=1,b=6,c=9。
将这些值代入公式:$$ x = \\frac{-6 \\pm \\sqrt{6^2 - 4 \\cdot 1 \\cdot 9}}{2 \\cdot 1} $$简化后得到:$$ x = \\frac{-6 \\pm \\sqrt{36 - 36}}{2} = \\frac{-6}{2} = -3 $$因此,该二次方程的解为x=−3,它是一个重根。
完全平方公式

完全平方公式具体来说,完全平方公式可以用于求解形如ax^2 + bx + c = 0的一元二次方程的解。
首先,我们来推导完全平方公式。
考虑一元二次方程ax^2 + bx + c = 0。
为了将其表示成一个平方的形式,我们可以将x的系数b除以2,并进行平方。
这样,我们得到(x + b/2a)^2展开得到(x+b/2a)^2=x^2+(b/2a)x+(b/2a)^2比较上式与原方程ax^2 + bx + c = 0,我们可以看到,如果c可以表示为(b/2a)^2,那么方程就变成了一个平方。
因此,我们可以得到完全平方公式:ax^2 + bx + c = a(x + b/2a)^2 - (b/2a)^2 + c。
根据这个公式,我们可以将一元二次方程表示成一个完全平方形式。
接下来,我们来研究如何使用完全平方公式来解一元二次方程。
假设我们有一个一元二次方程ax^2 + bx + c = 0。
我们可以使用完全平方公式将其表示成(mx + n)^2 = 0的形式。
并且,根据等式的性质,我们可以得到mx + n = 0,进一步得到x = -n/m。
因此,我们可以得到一元二次方程的根的公式:x = (-b ± √(b^2 - 4ac)) / 2a。
这就是我们通常所说的一元二次方程的根的公式。
通过这个公式,我们可以很方便地求解一元二次方程的根。
此外,完全平方公式也可以用于其他应用,如配方法、求和方法等。
在数学中,我们常常利用完全平方公式来简化计算和求解问题。
总结起来,完全平方公式是将一个一元二次多项式表示成一个平方的形式的公式。
通过完全平方公式,我们可以方便地求解一元二次方程的根。
此外,完全平方公式还有其他应用。
对于学习和理解一元二次方程以及相关数学问题具有重要的意义。
完全平方公式及其应用

完全平方公式及其应用完全平方公式是数学中一个重要的公式,利用它可以快速计算一个二次多项式的解,也可以应用于各种数学和科学领域中。
一、完全平方公式的定义完全平方公式表明,任意一个二次多项式都可以表示为一个完全平方加上一个常数项。
具体地讲,对于形如ax²+bx+c的二次多项式,其完全平方公式为:ax²+bx+c = a(x + b/2a)² - (b² - 4ac)/4a其中,x是未知数,a、b、c均为实数且a不等于0。
二、完全平方公式的应用1. 求二次函数的零点对于形如ax²+bx+c=0的二次方程,可以利用完全平方公式解出其根。
ax²+bx+c = a(x + b/2a)² - (b² - 4ac)/4a = 0解得:x = (-b ± √(b² - 4ac))/2a这就是二次函数的根,也叫做零点。
2. 计算几何中的面积利用完全平方公式,可以计算各种几何图形的面积。
比如,对于一个正方形,其对角线的长度可以表示为边长的根号2倍,即:d = a√2其中,a为正方形的边长。
根据勾股定理,任意一个直角三角形的斜边也可以用完全平方公式表示。
3. 计算概率完全平方公式还可以应用于概率计算中。
比如,正态分布的概率密度函数服从下面的公式:f(x) = 1/√(2πσ²) * e^-(x-μ)²/2σ²其中,e是自然对数的底数,μ是正态分布的均值,σ²是方差。
这个公式中的(x-μ)²可以用完全平方公式表示为一个完全平方加上一个常数项。
4. 计算物理量在物理中,完全平方公式也有巨大的应用价值。
比如,牛顿第二定律可以表示为:F = ma其中,F是物体所受的力,m是物体的质量,a是物体所受的加速度。
根据质能方程E=mc²,物体的质量也可以用能量的形式表示为E/c²。
完全平方公式8种变形

完全平方公式8种变形完全平方公式是数学中一个重要的公式,它可以帮助我们求解一元二次方程的解,进而解决一些实际问题。
在学习完全平方公式时,我们不仅要熟记其基本形式,还需要了解其一些变形,以便更灵活地应用于解题过程中。
下面将介绍完全平方公式的8种变形,希望对大家的学习有所帮助。
1. 标准形式变形:完全平方公式的标准形式是:(a+b)²=a²+2ab+b²。
我们可以将其变形为:a²= (a+b)²-2ab-b²,这种变形可以帮助我们从平方项和常数项中提取出待求解的项。
2. 差平方变形:我们可以将完全平方公式改写为:(a-b)²=a²-2ab+b²。
这种变形用于需要处理差平方的情况,可以减少计算过程中的错误。
3. 完全平方差变形:如果我们遇到一个二次方程的形式是a²-b²=0,可以利用完全平方公式的变形来求解。
变形后的形式为(a+b)(a-b)=0,我们可以得到a+b=0或a-b=0,从而求得方程的解。
4. 半平方变形:在一些问题中,我们可能会遇到一个二次方程的形式是a√x+b=0。
我们可以将其改写为:(√x)²=-(b/a),通过对等式两边开方并得到x的值,从而解决问题。
5. 配方法变形:配方法是解决一元二次方程的一种常用方法,我们可以将完全平方公式进行配方法的变形。
变形后的形式是(a+b)²-c²=(a+b+c)(a+b-c),通过将多项式相加相减从而得到解。
6. 两边取平方根变形:当我们遇到一个二次方程的形式为a²=c²时,可以将完全平方公式应用于此。
变形后的形式是:a=±√c²,通过对两边同时取平方根,我们可以得到a的值。
7. 合并同类项变形:在解决一些复杂的方程时,我们可能会遇到一些多项式的平方和。
我们可以将其中的一些同类项合并,从而简化计算过程。
完全平方公式的定义

完全平方公式的定义
完全平方公式是一种有用的数学工具,可以用来解决多个方程。
它是一个常见的抽象表示形式,由四个变量X、a、b、c和d组成,它的表达式为:X^2+aX+b=cX+d。
这里的X表示一个未知数,a、b、c和d分别表示四个常数。
如果所有变量都是定值(即a,b,c和d都是非零常数),则将上述公式视为一元二次方程(也就是完全平方方程)。
在求解它时,首先必须将它化成一般形式ax²+bx+c=0。
然后应用平方根公式(即X=−b±√b²−4ac2a)来解决这个问题。
此外,如果该方程有不止一个根(即b²-4ac是正数时),则要考虑所有根的情况。
对于复杂的多项式问题来说,使用完全平方公式能够很好地减少问题的复杂度。
例如在求解三次多项式中的根时可以将三次多项式化成三个不含x³成分的完全平方形式。
考虑到这些优势和特性,它成为了很多学生和工作者在数学中使用的一个重要工具。
完全平方公式

完全平方公式知识要点1.完全平方公式的推导: ①两数的平方:2)(b a +=))((b a b a ++=22b ab ab a +++(多项式乘法法则)=222b ab a ++(合并同类项) ②两数差的平方:2)(b a -=))((b a b a --=22b ab ab a +--(多项式乘法法则)=222b ab a +-(合并同类项) 2.完全平方公式:①2)(b a +=222b ab a ++ ②2)(b a -=222b ab a +-这就是说,两数和(或差)的平方,等于它们的平方和,加上(或者减去)它们的积的2倍,这两个公式叫做乘法的完全平方公式.3.完全平方公式的结构特征:公式的左边是一个二项式的平方;右边是三项,其中有两项是左边二项式中每一项的平方,即另一项是左边二项式中两项乘积的2倍. 4.知识的综合运用:①改变符号运用公式计算:如2)(b a --=[]2)(b a +-=2)(b a + ②根据加减法的运算律变形运用公式:如2)(b a +-=2)(a b - ③利用完全平方公式把代数式变形:如ab b a b a 2)(222-+=+=2)(b a -+ab 2;2)(b a -=ab b a 4)(2-+等④推广:[]22)()(c b a c b a ++=++=22)(2)(c c b a b a +++++=222222c bc ac b ab a +++++=bc ac ab c b a 222222+++++典型例题例1. 判断下列各式的计算是否正确,如果错了,指出错的地方,并把它改正过来. ①222)())((b a b a b a b a +=+=++ ②222)(b a b a -=-③2)3(y x -=2293y xy x +- ④222244)2()2(b ab a b a b a ---=+-=--⑤212)1(22++=+xx x x ⑥22241025)25(y xy x y x +-=--例2.计算: ①2)3(b a + ②2)3(y x +- ③2)(n m --例3.利用完全平方公式进行计算: ①2201 ②299例4.要使4142++mx x 成为一个两数和的完全平方式,则( )A 、2-=mB 、2=mC 、1=mD 、1-=m例5.已知3=+b a ,12-=ab ,求下列各式的值.①22b a + ②22b ab a +-③2)(b a -例6.计算下列各式: ①2)241(y x +- ②22)3()3(y y --+ ③2)2(b a +-例7.计算: ①2)(c b a +- ②2)312(+-y x例8.如果y x ,满足0)(22=++-y x x ,求x y 的值.1.填空:①+=-22)3(x x +9 ②+2a +4=2)2(+a ③++a a 62 =2)5(+a ④2244b ab a +-=( )22.计算: ①2)43(y x +- ②)211)(141(a a +--③2)52(n m +3.如果2642b ab M a +∙-是一个完全平方式,则M 等于( ) A 、8B 、8±C 、16±D 、32±4.用完全平方公式计算: ①2204 ②22985.若5=+y x ,2=xy ,求22y x +6.已知b a b a 42522+=++,b a 53-求的值.7.用完全平方公式计算下列各题: ①2)74(-+y x ②2)(z y x ++③2)132(+-b a ④2)7(+-n m1.填空:(1)16x 2-8x+_______=(4x -1)2; (2)_______+6x+9=(x+3)2;(3)16x 2+_______+9y 2=(4x+3y )2; (4)(a -b )2-2(a -b )+1=(______-1)2. (5)+=+229)3(n m n +2m (6)=++229124y xy x ( )2 (7)+2a +25=2)5(+a (8)x 2- 6xy+ =( )22.用简便方法计算: ①2301 ②24993.计算下列各题: ①2)65(y x - ②2)83(b a + ③2)62(-+n m4. 有个多项式的前后两项被墨水污染了看不清,已知它的中间项是12xy ,•且每一项系数均为整数,请你把前后两项补充完整,使它成为一个完全平方式,•并将它进行因式分解.你有几种方法? 多项式:■+12xy+■=( )25. 若代数式m 2+4加上一个单项式后可构成一个完全平方式,求这个单项式(要求至少写出两个).。
八年级数学完全平方公式

04
完全平方公式的应用举例
代数表达式化简
将复杂的代数表达式通过完全平方公 式进行化简,使其更易于理解和计算。
VS
例如,将$(a+b)^2$展开为 $a^2+2ab+b^2$,可以简化复杂的 代数表达式。
解决实际问题
通过完全平方公式解决一些实际问题,如计算面积、周长等。
例如,计算矩形的面积和周长,可以将矩形分成两个相同的直角三角形,然后利用完全平方公式计算 。
在数学竞赛中的应用
在数学竞赛中,完全平方公式是重要的解题工具之一。
完全平方公式在解决数学问题时 具有重要的作用,如求代数式的
值、因式分解、解方程等。
02
完全平方公式的基本形式
公式表达
$(a+b)^2 = a^2 + 2ab + b^2$ $(a-b)^2 = a^2 - 2ab + b^2$
公式的结构特点
完全平方公式由三部分组成:首平方、尾平方和两倍首尾积 的二倍。
通过大量的练习题,熟悉 公式的应用场景和变化形 式,提高解题能力和技巧。
总结归纳
将完全平方公式的应用进 行归纳总结,形成系统化 的知识体系,有助于加深 理解和记忆。
THANKS
推导方法二:通过代数运算
利用代数运算,将一个多项式表示为另一个多项式的平方 。
例如,$(a+b)^2$ 可以展开为 $a^2 + 2ab + b^2$,其中 $2ab$ 是 $a$ 和 $b$ 的两倍乘积,$b^2$ 是 $b$ 的平方。
完全平方公式知识点总结

完全平方公式知识点总结一、完全平方公式的定义在代数中,完全平方是指一个数的平方能够整除另一个数。
在一元二次方程中,如果其二次项和一次项可以写成一个完全平方的形式,那么我们就可以利用完全平方公式来求解方程的根。
二、完全平方公式的形式一元二次方程的标准形式为ax^2 + bx + c = 0,而完全平方公式的一般形式为(a+b)^2 =a^2 + 2ab + b^2,其中a、b为任意实数。
根据这个形式,我们可以进一步推导出完全平方公式的常用形式,即(a+b)^2 = a^2 + 2ab + b^2。
三、完全平方公式的推导要理解完全平方公式的推导过程,我们可以通过简单的代数运算来进行推导。
假设我们有一个二次方程x^2 + 6x + 9 = 0,我们可以将其写成完全平方的形式,即(x+3)^2 = 0。
通过这个例子,我们可以看到完全平方公式的推导过程,即将一元二次方程的一次项系数分解成两个相同的系数,然后将其写成完全平方的形式。
四、完全平方公式的应用技巧在使用完全平方公式求解一元二次方程时,我们需要注意以下几点应用技巧:1.将一元二次方程转化为完全平方的形式2.确定完全平方公式的形式,即(a+b)^2 = a^2 + 2ab + b^23.利用完全平方公式求解方程的根4.注意判断方程的解的情况,即判断判别式的正负性五、完全平方公式的拓展应用除了求解二次方程外,完全平方公式还可以在数学和科学领域的其他问题中进行拓展应用。
比如在几何学中,我们可以利用完全平方公式来求解圆的面积和周长;在物理学中,我们可以利用完全平方公式来分析物体的运动规律等。
总之,完全平方公式是求解一元二次方程的重要方法之一,它有着广泛的应用领域,对于学生来说掌握完全平方公式是十分重要的。
通过以上的知识点总结,相信大家对完全平方公式有了更深入的理解和掌握,希望能够帮助大家更好地学习和应用完全平方公式。
平方差公式和完全平方公式
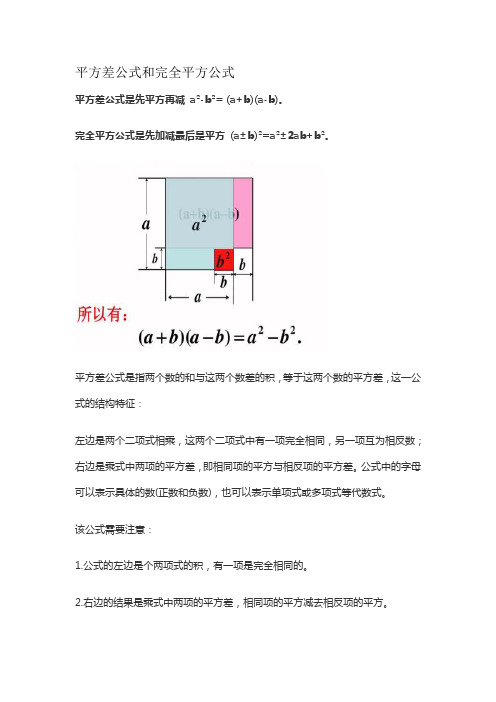
平方差公式和完全平方公式平方差公式是先平方再减a²-b²= (a+b)(a-b)。
完全平方公式是先加减最后是平方(a±b)²=a²±2ab+b²。
平方差公式是指两个数的和与这两个数差的积,等于这两个数的平方差,这一公式的结构特征:左边是两个二项式相乘,这两个二项式中有一项完全相同,另一项互为相反数;右边是乘式中两项的平方差,即相同项的平方与相反项的平方差。
公式中的字母可以表示具体的数(正数和负数),也可以表示单项式或多项式等代数式。
该公式需要注意:1.公式的左边是个两项式的积,有一项是完全相同的。
2.右边的结果是乘式中两项的平方差,相同项的平方减去相反项的平方。
3.公式中的a,b 可以是具体的数,也可以是单项式或多项式。
完全平方公式指两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
为了区别,会叫做两数和的完全平方公式,或叫做两数差的完全平方公式。
这个公式的结构特征:1.左边是两个相同的二项式相乘,右边是三项式,是左边二项式中两项的平方和,加上或减去这两项乘积的2倍;2.左边两项符号相同时,右边各项全用“+”号连接;左边两项符号相反时,右边平方项用“+”号连接后再“-”两项乘积的2倍(注:这里说项时未包括其符号在内)。
公式中的字母可以表示具体的数(正数或负数),也可以表示单项式或多项式等数学式。
该公式需要注意:1.左边是一个二项式的完全平方。
2.右边是二项平方的和,加上(或减去)这两项乘积的二倍,a和b可是数,单项式,多项式。
3.不论是(a+b)2还是(a-b)2,最后一项都是加号,不要因为前面的符号而理所当然的以为下一个符号。
4.不要漏下一次项。
5.切勿混淆公式。
6.运算结果中符号不要错误。
7.变式应用难,不易于掌握。
完全平方公式讲解

完全平方公式讲解完全平方公式是高中数学中最重要的公式之一,它能够帮助学生解决复杂的问题,因而被广泛使用。
完全平方公式的基本内容是一个多项式,它的一般形式如下:ax2 + bx + c = 0。
完全平方公式的原理很简单,它是分解多项式的系统方法,即先将多项式分解为完全平方公式的形式,然后从中求出解。
完全平方公式的分解如下:a(x + b/2a)2 = ax2 + bx + c,其中a为多项式中的系数,b为多项式中的系数,c为多项式中的常数。
现在我们来看看如何使用完全平方公式来求解多项式。
假设有一个如下形式的多项式:x2 + 6x + 9 = 0,即ax2 + bx + c = 0,其中a=1,b=6,c=9。
首先,将多项式分解为完全平方公式:(x + 3)2 = x2 + 6x + 9,即a(x + b/2a)2 = ax2 + bx + c,其中a=1,b=6,c=9。
继而,从多项式一般形式中求出解:x = -3,即x + 3 = 0,所以x = -3。
完全平方公式的应用广泛,它可以用于求解一元二次方程、求取多次方程的解等。
然而,使用完全平方公式需要注意一些重要问题,例如是否能够简化为完全平方公式形式,这得根据实际情况而定。
此外,完全平方公式也可以用于计算各种数学结果,例如计算角的正弦值、余弦值、正切值等。
一般而言,利用完全平方公式就可以快速求出解,从而节省计算时间。
最后,当我们碰到一些复杂的数学问题时,完全平方公式可以提供非常有用的帮助。
它可以帮助我们提高解决数学问题的速度,同时避免出现错误,从而减少计算错误的机会。
综上所述,完全平方公式是高中数学中最重要的公式之一,它能够帮助我们快速准确地解决复杂的数学问题,节省计算时间,减少出错的机会。
完全平方公式

(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
完全平方公式的文字叙述: 两个数的和(或差)的平方,等于 它们的平方和,加上(或减去)它们的 积的2倍。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2 (a+b)(a-b)= a2 - b2
1、完全平方公式: (a+b)2= a2 +2ab+b2 (a-b)2= a2 - 2ab+b2 2、完全平方公式的来历 3、完全平方公式的应用 ………
作业布置:
1、必做题:名校学案(第一课时) 2、选做题:(1)阅读书上“读一读”
1 1 2 已知a 10, 求(a ) 的值。 (2 ) a a
祝大家马到成功!
(2)(x -3yz)2 (a - b)2= a2 -2 ab + b2
解: (x-3yz)2= x2 -2•x •3yz+(3yz)2
x 6 xyz 9 y z
2
2 2
你难不倒我
• 每组同学出一道要求运用完全 平方公式来解的计算题。然后 其他组成员进行解答。
小结:
今天,我们学到了什么?
小游戏:
( x 3) 2 Nhomakorabea快速计算:
(1)( x y )
2
(2)( p 2)
2
(3)( 2 x 1)
2
1 2 (4)( m n) 3
例1 运用完全平方公式计算:
(1)(x+2y)2 (a +b)2= a2 + 2 ab
