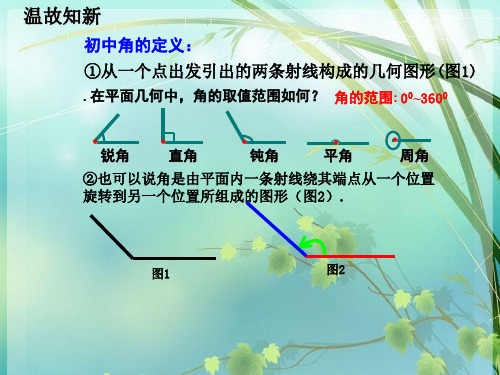
高中数学必修4任意角
人教版高中数学必修四第2讲:任意角的三角函数(学生版)

人教版高中数学 任意角的三角函数__________________________________________________________________________________ __________________________________________________________________________________1.能根据三角函数的定义导出同角三角函数的基本关系式及它们之间的联系;2.熟练掌握已知一个角的三角函数值求其它三角函数值的方法。
3.牢固掌握同角三角函数的两个关系式,并能灵活运用于解题.(一)任意角的三角函数: 任意点到原点的距离公式:=r ____________________1.三角函数定义:在直角坐标系中,设α是一个任意角,α终边上任意一点P (除了原点)的坐标为(,)x y ,它与原点的距离为2222(||||0)r r x y x y =+=+>,那么(1)比值y r 叫做α的正弦,记作sin α,即sin y r α=; (2)比值x r 叫做α的余弦,记作cos α,即cos xr α=;(3)比值y x 叫做α的正切,记作tan α,即tan yxα=;(4)比值x y 叫做α的余切,记作cot α,即cot x yα=; 正弦、余弦、正切、余切是以角为自变量,比值为函数值的函数,以上四种函数统称为三角函数。
(二)单位圆与三角函数线:1.三角函数线的定义:当角的终边上一点(,)P x y 的坐标满足____________时,有三角函数正弦、余弦、正切值的几何表示——三角函数线。
2.有向线段:____________________________规定:与坐标轴方向一致时为_____,与坐标方向相反时为______。
3.三角函数线的定义:设任意角α的顶点在原点O ,始边与x 轴非负半轴重合,终边与单位圆相交与点P (,)x y ,过P 作x 轴的垂线,垂足为M ;过点(1,0)A 作单位圆的切线,它与角α的终边或其反向延长线交与点T .由四个图看出:当角α的终边不在坐标轴上时,有向线段,OM x MP y ==,于是有sin 1y y y MP r α====_________________, cos 1x x x OM r α====_______________,tan y MP AT AT x OM OA α====_______________ 我们就分别称有向线段,,MP OM AT 为正弦线、余弦线、正切线。
高二数学必修4知识点:任意角和弧度制

高二数学必修 4 知识点:随意角和弧度制在中国古代把数学叫算术,又称算学,最后才改为数学。
小编准备了高二数学必修 4 知识点,希望你喜爱。
1.随意角(1)角的分类:①按旋转方向不一样分为正角、负角、零角.②按终边地点不一样分为象限角和轴线角.(2)终边同样的角:终边与角同样的角可写成+k360(kZ).(3)弧度制:① 1 弧度的角:把长度等于半径长的弧所对的圆心角叫做1弧度的角 .②规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零,||=, l 是以角作为圆心角时所对圆弧的长,r 为半径 .③用弧度做单位来胸怀角的制度叫做弧度制.比值与所取的r 的大小没关,仅与角的大小相关.④弧度与角度的换算:360 弧度 ;180 弧度 .⑤弧长公式: l=||r ,扇形面积公式:S 扇形 =lr=||r2.2.随意角的三角函数(1)随意角的三角函数定义:设是一个随意角,角的终边与单位圆交于点P(x, y) ,那么角的正弦、余弦、正切分别是:sin =y ,cos =x,tan =,它们都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数 .(2)三角函数在各象限内的符号口诀是:一全正、二正弦、三正切、四余弦 .3.三角函数线察看内容的选择,我本着先静后动,由近及远的原则,有目的、有计划的先安排与少儿生活靠近的,能理解的察看内容。
随机察看也是不行少的,是相当风趣的,如蜻蜓、蚯蚓、毛毛虫等,孩子一边察看,一边发问,兴趣很浓。
我供给的察看对象,注意形象传神,色彩鲜亮,大小适中,指引少儿多角度多层面地进行察看,保证每个少儿看获得,看得清。
看得清才能说得正确。
在察看过程中指导。
我注意帮助少儿学习正确的察看方法,即按次序察看和抓住事物的不一样特点重点察看,察看与说话相联合,在察看中累积词汇,理解词汇,如一次我抓住机遇,指引少儿察看雷雨,雷雨前天空急巨变化,乌云密布,我问少儿乌云是什么样子的,有的孩子说:乌云像海洋的波涛。
数学必修4第一章三角函数

第一章三角函数1.1任意角和弧度制1.1.1任意角1.B.2.C.3.C.4.-1485°=-5³360°+315°.5.{-240°,120°}.6.{α|α=k²360°-490°,k∈Z};230°;-130°;三.7.2α的终边在第一、二象限或y轴的正半轴上,α2的终边在第二、四象限.集合表示略.8.(1)M={α|α=k²360°-1840°,k∈Z}.(2)∵α∈M,且-360°≤α≤360°,∴-360°≤k²360°-1840°≤360°.∴1480°≤k²360°≤2200°,379≤k≤559.∵k∈Z,∴k=5,6,故α=-40°,或α=320°.9.与45°角的终边关于x轴对称的角的集合为{α|α=k²360°-45°,k∈Z},关于y轴对称的角的集合为{α|α=k²360°+135°,k∈Z},关于原点对称的角的集合为{α|α=k²360°+225°,k∈Z},关于y=-x对称的角的集合为{α|α=k²360°+225°,k∈Z}.10.(1){α|30°+k²180°≤α≤90°+k²180°,k∈Z}.(2){α|k²360°-45°≤α≤k²360°+45°,k∈Z}.11.∵当大链轮转过一周时,转过了48个齿,这时小链轮也必须同步转过48个齿,为4820=2.4(周),即小链轮转过2.4周.∴小链轮转过的角度为360°³2 4=864°.1.1.2弧度制1.B.2.D.3.D.4.αα=kπ+π4,k∈Z.5.-5π4.6.111km.7.π9,7π9,13π9.8.2π15,2π5,2π3,4π5.9.设扇形的圆心角是θrad,∵扇形的弧长是r θ,∴扇形的周长是2r+rθ,依题意,得2r+rθ=πr,∴θ=π-2,∴扇形的面积为S=12r2θ=12(π-2)r2.10.设扇形的半径为R,其内切圆的半径为r,由已知得l=π2R,R=2lπ.又∵2r+r=R,∴r=R2+1=(2-1)R=2(2-1)πl,∴内切圆的面积为S=πr2=4(3-22)πl2.11.设圆心为O,则R=5,d=3,OP=R2-d2=4,ω=5rad/s,l=|α|R,α=ωt=25rad,l=4³25=100(cm).1.2任意角的三角函数1.2.1任意角的三角函数(一)1.B.2.B.3.C.4.k.5.π6,56π.6.x|x≠2kπ+32π,k∈Z.7.-25.8.2kπ+π2,2kπ+π,k∈Z.9.α为第二象限角.10.y=-3|x|=-3x(x≥0),3x(x<0),若角α的终边为y=3x(x<0),即α是第三象限角,则sinα=-31010,tanα=3;若角α的终边为y=-3x(x≥0),即α是第四象限角,则sinα=-31010,tanα=-3.11.f(x)=-(x-1)2+4(0≤x≤3).当x=1时,f(x)max=f(1)=4,即m=4;当x=3时,f(x)min=f(3)=0,即n=0.∴角α的终边经过点P(4,-1),r=17,sinα+cosα=-117+417=31717.1.2.1任意角的三角函数(二)1.B.2.C.3.B.4.334.5.2.6.1.7.0.8.x|2kπ+π≤x<2kπ+32π,或x=2kπ,k∈Z.9.(1)sin100°²cos240°<0.(2)tan-11π4-cos-11π4>0.(3)sin5+tan5<0.10.(1)sin25π6=sin4π+π6=sinπ6=12.(2)cos-15π4=cos-4π+π4=cosπ4=22.(3)tan13π3=tan4π+π3=tanπ3=3.11.(1)∵cosα>0,∴α的终边在第一或第四象限,或在x轴的非负半轴上;∵tanα<0,∴α的终边在第四象限.故角α的集合为α2kπ-π2<α<2kπ,k∈Z.(2)∵2kπ-π2<α<2kπ,k∈Z,∴kπ-π4<α2<kπ,k∈Z .当k=2n(n∈Z)时,2nπ-π4<α2<2nπ,n∈Z,sinα2<0,cosα2>0,tanα2<0;当k=2n+1(n∈Z)时,2nπ+3π4<α2<2nπ+π,n∈Z,sinα2>0,cosα2<0,tanα2<0. 1.2.2同角三角函数的基本关系1.B.2.A.3.B.4.-22.5.43.6.232.7.4-22.8.α2kπ+π2<α<2kπ+3π2,或α=kπ,k∈Z.9.0.10.15.11.3+12.1.3三角函数的诱导公式(一)1.C.2.A.3.B.4.-1-a2a.5.12.6.-cos2α.7.-tanα.8.-2sinθ.9.32.10.-22+13.11.3.1.3三角函数的诱导公式(二)1.C.2.A.3.C.4.2+22.5.-33.6.13.7.-73.8.-35.9.1.10.1+a4.11.2+3.1.4三角函数的图象与性质1.4.1正弦函数、余弦函数的图象1.B.2.C.3.B.4.3;-3.5.2.6.关于x轴对称.7.(1)取(0,0),π2,1,(π,2),3π2,1,(2π,0)这五点作图.(2)取-π2,0,0,12,π2,0,π,-12,3π2,0这五点作图.8.五点法作出y=1+sinx的简图,在同一坐标系中画出直线y=32,交点有2个.9.(1)(2kπ,(2k+1)π)(k∈Z).(2)2kπ+π2,2kπ+32π(k∈Z).10.y=|sinx|=sinx(2kπ≤x≤π+2kπ,k∈Z),-sinx(π+2kπ<x<2π+2kπ,k∈Z),图象略.y=sin|x|=sinx(x≥0),-sinx(x<0),图象略.11.当x>0时,x>sinx;当x=0时,x=sinx;当x<0时,x<sinx,∴sinx=x只有一解.1.4.2正弦函数、余弦函数的性质(一)1.C.2.A.3.D.4.4π.5.12,±1.6.0或8.提示:先由sin2θ+cos2θ=1,解得m=0,或m=8.7.(1)4.(2)25π.8.(1)π.(2)π.9.32,2.10.(1)sin215π<sin425π.(2)sin15<cos5.11.342.1.4.2正弦函数、余弦函数的性质(二)1.B.2.B.3.C.4.<.5.2π.6.3,4,5,6.7.函数的最大值为43,最小值为-2.8.-5.9.偶函数.10.f(x)=log21-sin2x=log2|cosx|.(1)定义域:xx≠kπ+π2,k∈Z.(2)值域:(-∞,0]. (3)增区间:kπ-π2,kπ(k∈Z),减区间:kπ,kπ+π2(k∈Z).(4)偶函数.(5)π.11.当x<0时,-x>0,∴f(-x)=(-x)2-sin(-x)=x2+sinx.又∵f(x)是奇函数,∴f(-x)=-f(x).∴f(x)=-f(-x)=-x2-sinx.1.4.3正切函数的性质与图象1.D.2.C.3.A.4.5π.5.tan1>tan3>tan2.6.kπ2-π4,0(k∈Z).7.2kπ+6π5<x<2kπ+3π2,k∈Z .8.定义域为kπ2-π4,kπ2+π4,k∈Z,值域为R,周期是T=π2,图象略.9.(1)x=π4.(2)x=π4或54π.10.y|y≥34.11.T=2π,∴f99π5=f-π5+20π=f-π5,又f(x)-1是奇函数,∴f-π5-1=-fπ5-1 f-π5=2-fπ5=-5,∴原式=-5.1.5函数y=Asin(ωx+φ)的图象(一)1.A.2.A.3.B.4.3.5.-π2.6.向左平移π4个单位.7.y=sinx+2的图象可以看作是将y=sinx图象向上平移2个单位得到,y=sinx-1的图象可以看作是将y=sinx图象向下平移1个单位而得到.8.±5.9.∵y=sin3x-π3=sin3x-π9,∴可将y=sin3x的图象向右平移π9个单位得到.10.y=sin2x+π4的图象向左平移π2个单位,得到y=sin2x+π2+π4,故函数表达式为y=sin2x+5π4.11.y=-2sinx-π3,向左平移m(m>0)个单位,得y=-2sin(x+m)-π3,由于它关于y轴对称,则当x=0时,取得最值±2,此时m-π3=kπ±π2,k∈Z,∴m的最小正值是5π6.1.5函数y=Asin(ωx+φ)的图象(二)1.D.2.A.3.C.4.y=sin4x.5.-2a;-310a+2ka(k∈Z);-2a.6.y=3sin6x+116π.7.方法1y=sinx横坐标缩短到原来的12y=sin2x向左平移π6个单位y=sin2x+π6=y=sin2x+π3.方法2y=sinx向左平移π3个单位y=sinx+π3横坐标缩短到原来的12y=sin2x+π3.8.(1)略.(2)T=4π,A=3,φ=-π4.9.(1)ω=2,φ=π6.(2)x=12kπ+π6(k∈Z),12kπ-112π,0(k∈Z).10.(1)f(x)的单调递增区间是3kπ-5π4,3kπ+π4(k∈Z).(2)使f(x)取最小值的x的集合是x|x=7π4+3kπ,k∈Z.11.(1)M=1,m=-1,T=10|k|π.(2)由T≤2,即10|k|π≤2得|k|≥5π,∴最小正整数k 为16.1.6三角函数模型的简单应用(一)1.C.2.C.3.C.4.2sinα.5.1s.6.k²360°+212 5°(k∈Z).7.扇形圆心角为2rad时,扇形有最大面积m216.8.θ=4π7或5π7.9.(1)设振幅为A,则2A=20cm,A=10cm.设周期为T,则T2=0.5,T=1s,f=1Hz.(2)振子在1T内通过的距离为4A,故在t=5s=5T内距离s=5³4A=20A=20³10=200cm=2(m).5s末物体处在点B,所以它相对平衡位置的位移为10cm.10.(1)T=2πs.(2)12π次.11.(1)d-710=sint-1.8517.5π.(2)约为5.6秒.1.6三角函数模型的简单应用(二)1.D.2.B.3.B.4.1-22.5.1124π.6.y=sin52πx+π4.7.95.8.12sin212,1sin12+2.9.设表示该曲线的三角函数为y=Asin(ωx+φ)+b.由已知平均数量为800,最高数量与最低数量差为200,数量变化周期为12个月,所以振幅A=2002=100,ω=2π12=π6,b=800,又7月1日种群数量达最高,∴π6³6+φ=π2.∴φ=-π2.∴种群数量关于时间t的函数解析式为y=800+100sinπ6(t-3).10.由已知数据,易知y=f(t)的周期T=12,所以ω=2πT=π6.由已知,振幅A=3,b=10,所以y=3sinπ6t+10.11.(1)图略.(2)y-12.47=cos2π(x-172)365,约为19.4h.单元练习1.C.2.B.3.C.4.D.5.C.6.C.7.B.8.C.9.D.10.C.11.5π12+2kπ,13π12+2kπ(k∈Z).12.4412.13.-3,-π2∪0,π2.14.1972π.15.原式=(1+sinα)21-sin2α-(1-sinα)21-sin2α=1+sinα|cosα|-1-sinα|cosα|=2sinα|cosα|. ∵α为第三象限角,|cosα|=-cosα,∴原式=-2tanα.16.1+sinα+cosα+2sinαcosα1+sinα+cosα=sin2α+cos2α+2sinαcosα+sinα+cosα1+sinα+cosα=(sinα+cosα)2+sinα+cosα1+sinα+cosα=(sinα+cosα)·(1+sinα+cosα)1+sinα+cosα=sinα+cosα. 17.f(x)=(sin2x+cos2x)2-sin2xcos2x2-2sinxcosx-12sinxcosx+14cos2x=1-sin2xcos2x2(1-sinxcosx)-12sinxcosx+14cos2x=12+12sinxcosx-12sinxcosx+14cos2x=12+14cos2x.∴T=2π2=π,而-1≤cos2x≤1,∴f(x)max=34,f(x)min=14.18.∵Aπ3,12在递减段上,∴2π3+φ∈2kπ+π2,2kπ+3π2.∴2π3+φ=5π6,φ=π6.19.(1)周期T=π,f(x)的最大值为2+2,此时x∈x|x=kπ+π8,k∈Z;f(x)的最小值为2-2,此时x ∈x|x=kπ-38π,k∈Z;函数的单调递增区间为kπ-3π8,kπ+π8,k∈Z.(2)先将y=sinx(x∈R)的图象向左平移π4个单位,而后将所得图象上各点的横坐标缩小为原来的12,纵坐标扩大成原来的2倍,最后将所得图象向上平移2个单位.20.(1)1π.(2)5π或15.7s.(3)略.。
人教版高二数学必修四《任意角和弧度制》评课稿

人教版高二数学必修四《任意角和弧度制》评课稿一、引言《任意角和弧度制》是人教版高中数学必修四教材中的一章内容。
本评课稿旨在对该章节进行全面的评价,并提出一些建议与改进之处。
二、教材内容概述《任意角和弧度制》是高中数学中的重要概念之一。
本章主要介绍了任意角的概念,介绍了弧度制以及角度和弧度之间的相互转化等内容。
该章节主要内容包括: 1. 角的概念与表示方式; 2. 角的度量单位:弧度制; 3. 角度与弧度的转换; 4. 弧长与角度的关系; 5. 三角函数中的角度单位转换。
三、教学目标分析1.知识目标:–掌握任意角的概念和表示方式;–理解角的度量单位弧度制;–能够进行角度与弧度的相互转换;–理解弧长与角度的关系;–了解三角函数中的角度单位转换。
2.能力目标:–能够正确使用各种符号表示角度大小;–能够灵活运用弧度制进行角度单位转换;–能够运用所学知识解决实际问题。
3.情感目标:–培养学生对数学的兴趣和好奇心;–增强学生解决问题的能力;–培养学生对数学的认真态度和严谨思维。
四、教学重点和难点分析1.教学重点:–任意角的概念和表示方式;–弧度制的概念及其应用。
2.教学难点:–角度与弧度的相互转换;–弧长与角度的关系的理解。
五、教学方法1.演绎法:通过具体例子引导学生从观察实例中归纳出规律。
2.归纳法:通过总结归纳的方式帮助学生理解概念和定理。
3.实践活动法:通过实际问题解决的活动,培养学生的动手能力和创新思维能力。
4.讨论法:通过小组讨论、互动交流的方式激发学生思考和独立思维能力。
六、教学流程1.导入:通过展示一些实际生活中的角度,引起学生的兴趣,激发他们对该内容的探索欲望。
2.概念讲解:介绍任意角的概念和表示方式,引导学生认识角度的度量单位。
3.弧度制讲解:引导学生理解弧度制的定义,并通过具体例子说明弧度与角度的转换方法。
4.练习与讨论:提供多种角度单位转换的练习题,通过小组合作和全班讨论的方式,帮助学生巩固所学知识。
高中数学必修四:1.1.1《任意角》 PPT课件 图文
精讲领学
例题1 写出与下列各角终边相同的角的集合S,并把S中在 360~720范围的角写出来.
( 1 ) 6 0 ;( 2 ) 2 1 ;( 3 ) 3 6 3 1 4
解: ( 1 ) S {| k 3 6 0 6 0 , k Z }300,60,420
( 2 ) S {| k 3 6 0 2 1 , k Z }21,339,699
2、下列角中终边与330°相同的角是( ) A.30° B.-30° C.630° D.-630°
3、把-1485°转化为α+k·360° (0°≤α<360°, k∈Z)的形式是( ) A.45°-4×360° B.-45°-4×360° C.-45°-5×360° D.315°-5×360°
反馈固学
1.1.1 任意角
第一课时
(1)推广角的概念;理解并掌握正角、负角、零角的定义; (2)理解任意角以及象限角的概念; (3)掌握所有与角终边相同的角(包括角)的表示方法; (4)树立运动变化观点,深刻理解推广后的角的概念;
思考:那么工人在拧紧或拧松螺丝时,转动的角度 如何表示才比较合适?
逆时 针
4、下列结论中正确的是( ) A.小于90°的角是锐角 B.第二象限的角是钝角 C.相等的角终边一定相同 D.终边相同的角一定相等
5:任意两个角的数量大小可以相加、相减.
例如50°+80°=130°, 50°-80°=-30°, 你能解释一下这两个式子的几何意义吗?
130°是以50°角的终边为始边,逆时针旋转80°所成的角. -30°是以50°角的终边为始边,顺时针旋转80°所成的角.
注3:(1) 为任意角 (2) k Z这一条件必不可少;
(3) 终边相同的角不一定相等, 终边相等的角有无数多个,它们相差3600的整数倍.
人教版高中数学必修4全册

(2k+<<2k+
3
2
,
kZ)
第四象限角:
(2k+
3
2
<<2k+2,
kZ
或
2k-
2
<<2k,
kZ
)
②轴线角
x 轴的非负半轴: =k360º(2k)(kZ);
x 轴的非正半轴: =k360º+180º(2k+)(kZ);
y
轴的非负半轴:
=k360º+90º(2k+
2
)(kZ);
y 轴的非正半轴: =k360º+270º(2k+ 32) 或
(1) 2
(2)
3
评析: 在解选择题或填空题时,
如求角所在象限,也可以不讨论k的
几种情况,如图所示利用图形来判断.
四、什么是1弧度的角? 长度等于半径长的弧所对的圆心角。
B r
Or A
B
2r
Or A
(3)角度与弧度的换算.只要记住,就可
以方便地进行换算. 应熟记一些特殊角的
度数和弧度数. 在书写时注意不要同时
2
2
则α角属于(C ) A.第-象限; B.第二象限;
2
C.第三象限; D.第四象限.
点评: 本题先由α所在象限确定α/2所在象限,再α/2的 余弦符号确定结论.
例1 求经过1小时20分钟时钟的分针所转过的角度:
解:分针所转过的角度 1 20 360 480
60
例2 已知a是第二象限角,判断下列各角是第几象限角
知识网络结构
任意角的概念
角的度量方法 (角度制与弧度制)
新人教A版必修4 4.1 任意角的三角函数

考点2
角的象限判定
要确定角α所在象限,只要把α表示为α=2kπ+α0 (k∈Z,0≤α0<2π),由α0所在象限即可判定出α所在的象限.
例2
α 若 α 为第一象限角,则-α, 是第几象限角? 2
α 【思路分析】 写出 α 的不等式形式,变为-α 及 的不等式 2 形式,讨论 k 确定象限.
【解】 ∵ α 为第一象限角, π ∴ 2kπ< α< 2kπ+ (k∈ Z), 2 π ∴ 2(-k)π+ (- )<- α< 2(-k)π, 2 即- α 是第四象限角; α π 又 kπ< < kπ+ ,当 k 为偶数时,设 k= 2n, n∈ Z, 2 4 α π 则 2nπ< < 2nπ+ ; 2 4 当 k 为奇数时,设 k= 2n+ 1, n∈ Z, α 5π α 则 2nπ+ π< < 2nπ+ ,故 是第一或第三象限角. 2 4 2
)
4.在半径为r的圆周上,有一动点P顺时针转动弧长为4πr,所
转过的圆心角的弧度数为__________.
答案:-4π
5.弧长为3 π,圆心角为135°的扇形半径为________,面积
为________. 答案:4 6π
考点 1
角的概念与表示
这类问题主要涉及到角的定义, 角的表示以及角度与弧度的 互化和终边相同的角的概念及表示方法.还有象限角、区域 角的概念,它们的表示方法都要借助于终边相同的角的 表示形式. 在弧度制下,正角、负角、零角分别对应正数、负数、零.
2.弧度制 (1)弧度角 弧长等于半径时的弧所对的圆心角叫 1 弧度的角.规定:正角 的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度 圆心角时所对弧的长, r 是圆的半径. (2)弧长公式及扇形面积公式 |α|· r ; ①弧长公式: l= _______ 1 1 ②扇形面积公式: S 扇形 = l· r= |α|· r2. 2 2 其中, l 是弧长, r 是圆的半径, α 是弧长为 l 的圆弧所对的圆 心角的弧度数.
高中数学 必修四 1.1.1任意角和弧度制

又k∈Z,故所求的最大负角为β=-50°. (2)由360°≤10 030°+k·360°<720°, 得-9670°≤k·360°<-9310°,又k∈Z,解得k=-26. 故所求的角为β=670°.
【方法技巧】 1.在0°到360°范围内找与给定角终边相同的角的方法 (1)一般地,可以将所给的角α 化成k·360°+β 的形式(其中 0°≤β <360°,k∈Z),其中的β 就是所求的角. (2)如果所给的角的绝对值不是很大,可以通过如下方法完成:当所 给角是负角时,采用连续加360°的方式;当所给角是正角时,采用 连续减360°的方式,直到所得结果达到要求为止.
4.将35°角的终边按顺时针方向旋转60°所得的角度数为_______, 将35°角的终边按逆时针方向旋转两周后的角度数________. 【解析】将35°角的终边按顺时针方向旋转60°所得的角为35°60°=-25°,将35°角的终边按逆时针方向旋转两周后的角为 35°+2×360°=755°. 答案:-25° 755°
【解析】(1)错误.终边与始边重合的角是k·360°(k∈Z),不一定 是零角. (2)错误.如-10°与350°终边相同,但是不相等. (3)错误.如-330°角是第一象限角,但它是负角. (4)错误.终边在x轴上的角不属于任何象限. 答案:(1)× (2)× (3)× (4)×
2.下列各组角中,终边不相同的是( )
2.判断角的概念问题的关键与技巧 (1)关键:正确理解象限角与锐角、直角、钝角、平角、周角等概念. (2)技巧:判断一种说法正确需要证明,而判断一种说法错误只要举 出反例即可.
【变式训练】射线OA绕端点O顺时针旋转80°到OB位置,接着逆时针 旋转250°到OC位置,然后再顺时针旋转270°到OD位置,则 ∠AOD=________.
