三角函数-反三角函数-积分公式-求导公式
三角函数的积分与反函数公式

三角函数的积分与反函数公式在数学中,三角函数是一类经典的函数,其中包括正弦函数、余弦函数、正切函数等。
这些函数在解决几何、物理、工程等领域的问题时起到了重要的作用。
在三角函数的研究中,积分与反函数是两个重要的概念和技巧。
本文将介绍三角函数的积分与反函数公式。
一、正弦函数的积分与反函数公式正弦函数是数学中常见的三角函数之一,其函数图像是一个周期性波动的曲线。
下面是正弦函数的积分公式:∫sin(x)dx = -cos(x) + C其中C为常数。
正弦函数的反函数是反正弦函数,常用符号为arcsin(x)或sin^(-1)(x)。
下面是反正弦函数的导数公式:d/dx(arcsin(x)) = 1/√(1-x^2)二、余弦函数的积分与反函数公式余弦函数是另一个常见的三角函数,其函数图像也是一个周期性波动的曲线。
下面是余弦函数的积分公式:∫cos(x)dx = sin(x) + C其中C为常数。
余弦函数的反函数是反余弦函数,常用符号为arccos(x)或cos^(-1)(x)。
下面是反余弦函数的导数公式:d/dx(arccos(x)) = -1/√(1-x^2)三、正切函数的积分与反函数公式正切函数是三角函数中的另一个重要函数,其函数图像有无穷多个渐近线。
下面是正切函数的积分公式:∫tan(x)dx = -ln|cos(x)| + C其中C为常数。
正切函数的反函数是反正切函数,常用符号为arctan(x)或tan^(-1)(x)。
下面是反正切函数的导数公式:d/dx(arctan(x)) = 1/(1+x^2)四、其他三角函数的积分与反函数公式除了正弦函数、余弦函数和正切函数以外,还存在其他三角函数如割函数、余割函数和余切函数。
它们的积分和反函数公式如下:∫sec(x)dx = ln|sec(x) + tan(x)| + C∫csc(x)dx = ln|csc(x) - cot(x)| + C∫cot(x)dx = ln|sin(x)| + C其中C为常数。
三角函数公式及反三角函数公式 版

cos(-α)=cosα
sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα
sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα
两角和与差的三角函数公式
tan(-α)=-tanα sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα tan(3π/2-α)=cotα cot(3π/2-α)=tanα
sin(3π/2+α)=-cosα cos(3π/2+α)=sinα tan(3π/2+α)=-cotα cot(3π/2+α)=-tanα 万能公式
同角三角函数的基本关系式 倒数关系:
tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1
三角函数公式表
商的关系:
sin tan sec concs源自 con cot csc
sin
sec
平方关系:
sin2α+cos2α=1 1+tan2α=sec2α 1+cot2α=csc2α
1 tan tan
1 tan tan
2 tan( )
sin
2
1 tan2 ( )
2
2 tan
tan
2
1 tan2 ( )
2
半角的正弦、余弦和正切公式
三角函数的降幂公式
大学用三角函数公式大全

倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1cosα/sinα=cotα=cscα/secα1+cot^2(α)=csc^2(α)tan α *cot α=1一个特殊公式(sina+sinθ)*(sina-sinθ)=sin(a+θ)*sin(a-θ)二倍角公式正弦sin2A=2sinA·cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a) 正切tan2A=(2tanA)/(1-tan^2(A))万能公式sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))半角公式sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 两角和公式tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=(tanα-tanβ)/(1+tanαtanβ)cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ -cosαsinβ双曲函数sh a = [e^a-e^(-a)]/2ch a = [e^a+e^(-a)]/2th a = sin h(a)/cos h(a)sin(π/2+α)= cosαcos(π/2+α)= -sinαtan(π/2+α)= -cotαcot(π/2+α)= -tanαsin(π/2-α)= cosαcos(π/2-α)= sinαtan(π/2-α)= cotαcot(π/2-α)= tanα三角函数的诱导公式(六公式)公式一sin(-α) = -sinαtan (-α)=-tanα公式二sin(π/2-α) = cosαcos(π/2-α) = sinα公式三sin(π/2+α) = cosαcos(π/2+α) = -sinα公式四sin(π-α) = sinαcos(π-α) = -cosα公式五sin(π+α) = -sinαcos(π+α) = -cosα公式六tanA= sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+(tan(α/2))²]cosα=[1-(tan(α/2))²]/[1+(tan(α/2))²]tanα=2tan(α/2)/[1-(tan(α/2))²]其它公式(1) (sinα)^2+(cosα)^2=1(平方和公式)(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2;+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)(seca)^2+(csca)^2=(seca)^2(csca)^2和差化积及积化和差用还原法结合上面公式可推出(换(a+b)/2与(a-b)/2)两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)反三角函数公式arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x ∈〔—π/2,π/2〕时,有arcsin(sinx)=x当x ∈〔0,π〕,arccos(cosx)=xx ∈(—π/2,π/2),arctan(tanx)=xx ∈(0,π),arccot(cotx)=xx 〉0,arctanx=π/2-arctan1/x,arccotx 类似若(arctanx+arctany)∈(—π/2,π/2),则arctanx+arctany=arctan(x+y/1-xy) 三角函数求导:(sinx)'=cosx(cosx)'=-sinx(tanx)'=(secx)^2(secx)'=secxtanx(cotx)'=-(cscx)^2(cscx)'=-csxcotx(arcsinx)'=1/√(1-x^2)(arccosx)'=-1/√(1-x^2)(arctanx)'=1/(1+x^2)(arccotx)'=-1/(1+x^2)基本求导公式⑴ 0)(='C (C 为常数)⑵ 1)(-='n n nx x ;一般地,1)(-='αααx x 。
三角函数导数表大全

ห้องสมุดไป่ตู้
比如说,对于正弦函数 y=sinx,都知道导数 dy/dx=cosx, 那么 dx/dy=1/cosx, 而 cosx=√(1-(sinx)^2)=√(1-y^2),所以 dx/dy=√(1-y^2), y=sinx 可知 x=arcsiny,而 dx/dy=1/√(1-y^2),所以 arcsiny 的导数就是 1/√(1-y^2), 再换下元 arcsinx 的导数就是 1/√(1-x^2)。
三角函数反三角函数积分公式求导公式

三角函数反三角函数积分公式求导公式三角函数是数学中常见的一类函数,包括正弦函数、余弦函数、正切函数等。
而反三角函数则是三角函数的逆运算,用于解决三角方程和计算角度值。
三角函数与反三角函数的积分求导公式在数学中有着重要的应用,下面将介绍这些公式以及其推导。
一、正弦函数与反正弦函数的积分求导公式:1.正弦函数的积分求导公式:∫sin(x) dx = -cos(x) + C该公式可以通过求导得到,即对右边的-cos(x) + C对x求导,由导数的链式法则可得到sin(x)。
2.反正弦函数的积分求导公式:∫arcsin(x) dx = x * arcsin(x) + sqrt(1 - x^2) + C这个公式可以通过对右边的表达式求导来验证,即对x * arcsin(x) + sqrt(1 - x^2)对x求导,应用链式法则和反正弦函数的导数即可得到1 / sqrt(1 - x^2)。
二、余弦函数与反余弦函数的积分求导公式:1.余弦函数的积分求导公式:∫cos(x) dx = sin(x) + C可以通过对右边的sin(x) + C求导来验证,由导数的链式法则可得到cos(x)。
2.反余弦函数的积分求导公式:∫arccos(x) dx = x * arccos(x) - sqrt(1 - x^2) + C可以通过对右边的x * arccos(x) - sqrt(1 - x^2)求导来验证,应用链式法则和反余弦函数的导数即可得到-1 / sqrt(1 - x^2)。
三、正切函数与反正切函数的积分求导公式:1.正切函数的积分求导公式:∫tan(x) dx = -log,cos(x), + C可以通过对右边的-log,cos(x), + C求导来验证,应用对数函数的导数和链式法则即可得到sec^2(x) = 1/cos^2(x)。
2.反正切函数的积分求导公式:∫arctan(x) dx = x * arctan(x) - 1/2 * log(1 + x^2) + C可以通过对右边的x * arctan(x) - 1/2 * log(1 + x^2)求导来验证,应用对数函数的导数和链式法则即可得到1 / (1 + x^2)。
三角函数的积分和反三角函数的计算

三角函数的积分和反三角函数的计算积分是微积分中的重要概念之一,而三角函数的积分及反三角函数的计算是积分中的常见类型。
本文将从三角函数的积分开始,然后讨论反三角函数的计算方法。
一、三角函数的积分1. 正弦函数的积分正弦函数的积分公式为:∫sin(x)dx = -cos(x) + C其中,C为常数。
2. 余弦函数的积分余弦函数的积分公式为:∫cos(x)dx = sin(x) + C同样,C为常数。
正切函数的积分公式为:∫tan(x)dx = -ln|cos(x)| + C这里的ln表示自然对数,C为常数。
4. 余切函数的积分余切函数的积分公式为:∫cot(x)dx = ln|sin(x)| + C同样,ln表示自然对数,C为常数。
5. 正割函数的积分正割函数的积分公式为:∫sec(x)dx = ln|sec(x) + tan(x)| + C其中,ln为自然对数,C为常数。
余割函数的积分公式为:∫csc(x)dx = ln|csc(x) - cot(x)| + C这里,ln为自然对数,C为常数。
二、反三角函数的计算1. 反正弦函数的计算反正弦函数的计算公式为:asin(x) = y其中,x为正弦函数的值,y为对应的角度值。
2. 反余弦函数的计算反余弦函数的计算公式为:acos(x) = y其中,x为余弦函数的值,y为对应的角度值。
3. 反正切函数的计算反正切函数的计算公式为:atan(x) = y其中,x为正切函数的值,y为对应的角度值。
4. 反余切函数的计算反余切函数的计算公式为:acot(x) = y其中,x为余切函数的值,y为对应的角度值。
5. 反正割函数的计算反正割函数的计算公式为:asec(x) = y其中,x为正割函数的值,y为对应的角度值。
6. 反余割函数的计算反余割函数的计算公式为:acsc(x) = y其中,x为余割函数的值,y为对应的角度值。
总结:通过上述介绍,我们可以了解到三角函数的积分和反三角函数的计算方法。
三角函数公式大全(很详细)
高中三角函数公式年夜全[图]之老阳三干创作创作时间:二零二一年六月三十日1 三角函数的界说1.1 三角形中的界说图1 在直角三角形中界说三角函数的示意图在直角三角形ABC,如下界说六个三角函数:•正弦函数•余弦函数•正切函数•余切函数•正割函数•余割函数1.2 直角坐标系中的界说图2 在直角坐标系中界说三角函数示意图在直角坐标系中,如下界说六个三角函数:•正弦函数r•余弦函数•正切函数•余切函数•正割函数•余割函数2 转化关系2.1 倒数关系2.2 平方关系2 和角公式3 倍角公式、半角公式3.1 倍角公式3.2 半角公式3.3 万能公式4 积化和差、和差化积4.1 积化和差公式证明过程首先,sin(α+β)=sinαcosβ+sinβcosα(已证.证明过程见《和角公式与差角公式的证明》)因为sin(α+β)=sinαcosβ+sinβcosα(正弦和角公式)则sin(α-β)=s in[α+(-β)]=sinαcos(-β)+sin(-β)cosα=sinαcosβ-sinβcosα于是sin(α-β)=sinαcosβ-sinβcosα(正弦差角公式)将正弦的和角、差角公式相加,获得sin(α+β)+sin(α-β)=2sinαcosβ则sinαcosβ=sin(α+β)/2+sin(α-β)/2(“积化和差公式”之一)同样地,运用诱导公式cosα=sin(π/2-α),有cos(α+β)=sin[π/2-(α+β)]=sin(π/2-α-β)=sin[(π/2-α)+(-β)]=sin(π/2-α)cos(-β)+sin(-β)cos(π/2-α)=cosαcosβ-sinαsinβ于是cos(α+β)=cosαcosβ-sinαsinβ(余弦和角公式)那么cos(α-β)=cos[α+(-β)]=cosαcos(-β)-sinαsin(-β)=cosαcosβ+sinαsinβcos(α-β)=cosαcosβ+sinαsinβ(余弦差角公式)将余弦的和角、差角公式相减,获得cos(α+β)-cos(α-β)=-2sinαsinβ则sinαsinβ=cos(α-β)/2-cos(α+β)/2(“积化和差公式”之二)将余弦的和角、差角公式相加,获得cos(α+β)+cos(α-β)=2cosαcosβ则cosαcosβ=cos(α+β)/2+cos(α-β)/2(“积化和差公式”之三)这就是积化和差公式:sinαcosβ=sin(α+β)/2+sin(α-β)/2sinαsinβ=cos(α-β)/2-cos(α+β)/2cosαcosβ=cos(α+β)/2+cos(α-β)/24.2 和差化积公式部份证明过程:sin(α-β)=sin[α+(-β)]=sinαcos(-β)+sin(-β)cosα=sinαcosβ-sinβcosαcos(α+β)=sin[90-(α+β)]=sin[(90-α)-β]=sin(90-α)cosβ-sinβcos(90-α)=cosαcosβ-sinαsinβcos(α-β)=cos[α+(-β)]=cosαcos(-β)-sinαsin(-β)=cosαcosβ+sinαsinβtan(α+β)=sin(α+β)/cos(α+β)=(sinαcosβ+sinβcosα)/ (cosαcosβ-sinαsinβ)=(cosαtanαcosβ+cosβtanβcosα)/(cosαcosβ-cosαtanαcosβtanβ)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=tan[α+(-β)]=[tanα+tan(-β)]/[1-tanαtan(-β)]=(tanα-tanβ)/(1+tanαtanβ)诱导公式•sin(-a)=-sin(a)•cos(-a)=cos(a)•sin(pi/2-a)=cos(a)•cos(pi/2-a)=sin(a)•sin(pi/2+a)=cos(a)•cos(pi/2+a)=-sin(a)•sin(pi-a)=sin(a)•cos(pi-a)=-cos(a)•sin(pi+a)=-sin(a)•cos(pi+a)=-cos(a)•tgA=tanA=sinA/cosA两角和与差的三角函数•sin(a+b)=sin(a)cos(b)+cos(α)sin(b)•cos(a+b)=cos(a)cos(b)-sin(a)sin(b)•sin(a-b)=sin(a)cos(b)-cos(a)sin(b)•cos(a-b)=cos(a)cos(b)+sin(a)sin(b)•tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))•tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))三角函数和差化积公式•sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)•sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)•cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)•cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)积化和差公式•sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]•cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]•sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]二倍角公式•sin(2a)=2sin(a)cos(a)•cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)半角公式•sin^2(a/2)=(1-cos(a))/2•cos^2(a/2)=(1+cos(a))/2•tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))万能公式•sin(a)= (2tan(a/2))/(1+tan^2(a/2))•cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))•tan(a)= (2tan(a/2))/(1-tan^2(a/2))其它公式•a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中,tan(c)=b/a]•a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中,tan(c)=a/b]•1+sin(a)=(sin(a/2)+cos(a/2))^2•1-sin(a)=(sin(a/2)-cos(a/2))^2其他非重点三角函数•csc(a)=1/sin(a)•sec(a)=1/cos(a)双曲函数•sinh(a)=(e^a-e^(-a))/2• cosh(a)=(e^a+e^(-a))/2 •tgh(a)=sinh(a)/cosh(a)经常使用公式表(一)1.乘法公式(1)(a+b )²=a 2+2ab+b 2(2)(a-b)²=a ²-2ab+b ²(3)(a+b)(a-b)=a ²-b ²(4)a ³+b ³=(a+b)(a ²-ab+b ²) (5)a ³-b ³=(a-b)(a ²+ab+b²)2、指数公式:(1)a 0=1 (a ≠0)(2)a P -=P a1(a ≠0)(3)a mn=mn a(4)a m a n =a n m + (5)a m ÷a n=n m a a =anm -(6)(a m )n =a mn(7)(ab )n =a n b n(8)(ba)n=n n b a (9)(a )2=a(10)2a =|a|3、指数与对数关系:(1)若a b=N,则N b a log =(2)若10b=N,则b=lgN(3)若b e =N,则b=㏑N4、对数公式:(1)b a b a =log , ㏑e b =b (2)N a aN =log ,e N ln =N(3)aNN a ln ln log =(4)ab b e a ln =(5)N M MN ln ln ln +=(6)N M N Mln ln ln-=(7)Mn M n ln ln =(8)㏑nM =Mn ln 15、三角恒等式:(1)(Sin α)²+(Cos α)²=1 (2)1+(tan α)²=(sec α)²(3)1+(cot α)²=(csc α)²(4)αααtan cos sin =(5)αααcot sin cos =(6)ααtan 1cot =(7)ααcos 1csc =(8)ααcos 1sec =6、特殊角三角函数值:7.倍角公式:(1)αααcos sin 22sin =(2)ααα2tan 1tan 22tan -=(3)ααααα2222sin 211cos 2sin cos 2cos -=-=-=8.半角公式(降幂公式):(1)(2sin α)2=2cos 1a -(2)(2cos α)2=2cos 1a +(3)2tanα=a a sin cos 1+=a a cos 1sin +9、三角函数与反三角函数关系:(1)若x=siny,则y=arcsinx (2)若x=cosy,则y=arccosx(3)若x=tany,则y=arctanx (4)若x=coty,则y=arccotx10、函数界说域求法:(1)分式中的分母不能为0,(a 1α≠0)(2)负数不能开偶次方,(a α≥0)(3)对数中的真数必需年夜于0,(N a log N>0)(4)反三角函数中arcsinx,arccosx 的x 满足:(--1≤x ≤1)(5)上面数种情况同时在某函数呈现时,此时应取其交集.11、直线形式及直线位置关系:(1)直线形式:点斜式:()00x x k y y -=-斜截式:y=kx+b 两点式:121121x x x x y y y y --=--(2)直线关系:111:b x k y l +=222:b x k y l +=平行:若21//l l ,则21k k =垂直:若21l l ⊥,则121-=⋅k k经常使用公式表(二)1、求导法则:(1)(u+v )/=u /+v /(2)(u-v )/=u /-v /(3)(cu )/=cu /(4)(uv )/=uv /+u /v (5)2v v u v u v u '-'='⎪⎭⎫ ⎝⎛2、基本求导公式:(1)(c )/=0 (2)(x a )/=ax1-a (3)(a x )/=a xlna (4)(e x )/=e x (5)(㏒a x )/=a x ln 1(6)(lnx )/=x 1(7)(sinx )/=cosx (8)(cosx )/=-sinx(9)(tanx )/=2)(cos 1x =(secx )2(10)(cotx )/=-2)(sin 1x =-(cscx )2 (11)(secx)/=secx*tanx (12)(cscx)/=-cscx*cotx(13)(arcsinx)/=211x - (14)(arccosx)/=-211x -(15)(arctanx)/=211x + (16)()211cot x x arc +-=' 3、微分(1)函数的微分:dy=y /dx(2)近似计算:|Δx|很小时,f ()x x ∆+0=f (x 0)+f /(x 0)*x ∆4、基本积分公式(1)kdx=kx+c (2)C x a dx x a a ++=+⎰111(3)c x dx x +=⎰ln 1(4)C a a dx a xx +=⎰ln(5)⎰+=c e dx e x x (6)⎰+-=Cx xdx cos sin (7)⎰+=C x xdx sin cos (8)C x dx x xdx +==⎰⎰tan cos 1sec 22(9)cx dx x xdx +-==⎰⎰cot sin 1csc 22(10)⎰+=-c x dx x arcsin 112 (11)c x dx x +=+⎰arctan 1125、定积分公式:(1)⎰⎰=b a b a dt t f dx x f )()( (2)⎰=aa dx x f 0)((3)()()dx x f dx x f a b ba ⎰⎰-=(4)⎰⎰⎰+=b ac a b c dxx f dx x f dx x f )()()((5)若f (x )是[-a,a]的连续奇函数,则⎰-=aa dx x f 0)((6)若f (x )是[-a,a]的连续偶函数,则:6、积分定理:(1)()()x f dt t f xa ='⎥⎦⎤⎢⎣⎡⎰(3)若F (x )是f (x )的一个原函数,则)()()()(a F b F x F dx x f b a ba -==⎰8.积分方法⎰ ⎰ - = a a adxx f dx x f 0 ) ( 2 ) (()()b1;设:tf+=xax+bax=()()22=;设:txf-a2x=ax sin ()22ax=;设:tf-x=x seca()22xf+=;设:txa=ax tan()3分部积分法:⎰⎰-udvuv=vdu。
三角函数-反三角函数-积分公式-求导公式
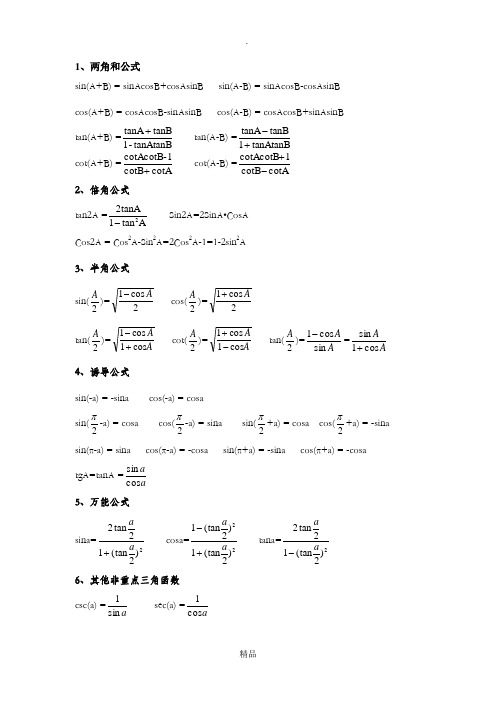
1、两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotA cotB 1cotAcotB -+ 2、倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA•CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A3、半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 4、诱导公式sin(-a) = -sina cos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aa cos sin 5、万能公式 sina=2)2(tan 12tan2a a + cosa=22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan 2a a - 6、其他非重点三角函数 csc(a) =a sin 1 sec(a) =acos 17、(a+b)的三次方,(a-b)的三次方公式(a+b)^3=a^3+3a^2b+3ab^2+b^3(a-b)^3=a^3-3a^2b+3ab^2-b^3a^3+b^3=(a+b)(a^2-ab+b^2)a^3-b^3=(a-b)(a^2+ab+b^2)8、反三角函数公式arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x∈〔—π/2,π/2〕时,有arcsin(sinx)=x当x∈〔0,π〕,arccos(cosx)=xx∈(—π/2,π/2),arctan(tanx)=xx∈(0,π),arccot(cotx)=xx〉0,arctanx=π/2-arctan1/x,arccotx类似若(arctanx+arctany)∈(—π/2,π/2),则arctanx+arctany=arctan(x+y/1-xy) 9、三角函数求导:(sinx)'=cosx(cosx)'=-sinx(tanx)'=(secx)^2(secx)'=secxtanx(cotx)'=-(cscx)^2(cscx)'=-csxcotx(arcsinx)'=1/√(1-x^2)(arccosx)'=-1/√(1-x^2)(arctanx)'=1/(1+x^2)(arccotx)'=-1/(1+x^2)10、基本求导公式⑴ 0)(='C (C 为常数)⑵ 1)(-='n n nx x ;一般地,1)(-='αααx x 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、两角和公式
sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB
cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB
1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotA
cotB 1cotAcotB -+ 2、倍角公式 tan2A =A
tan 12tanA 2- Sin2A=2SinA•CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A
3、半角公式 sin(2A )=2cos 1A - cos(2
A )=2cos 1A + tan(
2A )=A A cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 4、诱导公式
sin(-a) = -sina cos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2
π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =a
a cos sin 5、万能公式 sina=2)2(tan 12tan 2a a + cosa=22)2(tan 1)2(tan 1a a +- tana=2
)2
(tan 12tan 2a a - 6、其他非重点三角函数 csc(a) =a
sin 1 sec(a) =a cos 1
7、(a +b )的三次方,(a -b )的三次方公式
(a+b)^3=a^3+3a^2b+3ab^2+b^3
(a-b)^3=a^3-3a^2b+3ab^2-b^3
a^3+b^3=(a+b)(a^2-ab+b^2)
a^3-b^3=(a-b)(a^2+ab+b^2)
8、反三角函数公式
arcsin(-x)=-arcsinx
arccos(-x)=π-arccosx
arctan(-x)=-arctanx
arccot(-x)=π-arccotx
arcsinx+arccosx=π/2=arctanx+arccotx
sin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)
当x ∈〔—π/2,π/2〕时,有arcsin(sinx)=x
当x ∈〔0,π〕,arccos(cosx)=x
x ∈(—π/2,π/2),arctan(tanx)=x
x ∈(0,π),arccot(cotx)=x
x 〉0,arctanx=π/2-arctan1/x,arccotx 类似
若(arctanx+arctany)∈(—π/2,π/2),则arctanx+arctany=arctan(x+y/1-xy)
9、三角函数求导:
(sinx)'=cosx
(cosx)'=-sinx
(tanx)'=(secx)^2
(secx)'=secxtanx
(cotx)'=-(cscx)^2
(cscx)'=-csxcotx
(arcsinx)'=1/√(1-x^2)
(arccosx)'=-1/√(1-x^2)
(arctanx)'=1/(1+x^2)
(arccotx)'=-1/(1+x^2)
10、基本求导公式
⑴ 0)(='C (C 为常数)⑵ 1)(-='n n nx x ;一般地,1)(-='αααx x 。
特别地:1)(='x ,x x 2)(2=',21)1(x x -=',x
x 21)(='。
⑶ x x e e =')(;一般地,)1,0( ln )(≠>='a a a a a x x 。
⑷ x x 1)(ln =';一般地,)1,0( ln 1)(log ≠>='a a a
x x a 。
11、求导法则 ⑴ 四则运算法则
设f (x ),g (x )均在点x 可导,则有:(Ⅰ))()())()((x g x f x g x f '±'='±; (Ⅱ))()()()())()((x g x f x g x f x g x f '+'=',特别)())((x f C x Cf '='(C 为常数); (Ⅲ))0)(( ,)
()()()()())()((2≠'-'='x g x g x g x f x g x f x g x f ,特别21()()()()g x g x g x ''=-。
12、微分 函数()y f x =在点x 处的微分:()dy y dx f x dx ''==
13、积分公式
常用的不定积分公式:
(1) ⎰⎰⎰⎰⎰+==+=+=-≠++=+c x dx x x dx x c x xdx c x dx C x dx x 43,2,),1( 11433
221αααα
; (2) C x dx x
+=⎰||ln 1; C e dx e x x +=⎰; )1,0( ln ≠>+=⎰a a C a a dx a x x ; (3)⎰⎰=dx x f k dx x kf )()((k 为常数)
定积分:
()()|()()b
b a a f x dx F x F b F a ==-⎰
⑴ ⎰⎰⎰+=+b
a b a b a dx x g k dx x f k dx x g k x f k )()()]()([2121 分部积分法:
设u (x ),v (x )在[a ,b ]上具有连续导数)(),(x v x u '',则
⎰⎰-=b
a b a b
a x du x v x v x u x dv x u )()()()()()( 14、重要的等价无穷小替换:
当x→0时,
sinx~x tanx~x arcsinx~x arctanx~x
1-cosx~1/2*(x^2) (a^x )-1~x*lna (e^x )-1~x ln(1+x)~x (1+Bx)^a-1~aBx
[(1+x)^1/n]-1~(1/n )*x loga(1+x)~x/lna。
