波动方程PPT课件
合集下载
波动方程差分方法初步(PPT文档)

U
n1 j
(1
2 2 )U
n j
2
U
n j 1
U
n j 1
U
n1 j
U
n 0
(n
)
n,
U
n J
(n )
n,
n0
U
0 j
fj,
U
1 j
fj
gj
2
2
f j1 2 f j f j1 ,
0 jJ
h
U
1 j
2(1
2
)U
0 j
2
U
0 j 1
U
0 j 1
U
1 j
初始速度的离散
一、简单处理
初始位移
U
0 j
f
(
jh)
f
0 j
初始速度 u(xj ,tk ) u(x j ,tk ) u(x j ,tk ) O( )
t
u(x j ,tk ) u(x j ,tk ) u(x j ,tk )
U
0 j 1
U
1 j
2U
1 j
2(1
2
)U
0 j
2
U
0 j 1
U
0 j 1
2 g j
2f j 2 g j 2 f j1 2 f j f j1
U
1 j
fj
gj
波动方程和行波法剖析课件

波动方程和行波法剖析课件
目录 Contents
• 波动方程的基本概念 • 行波法的基本原理 • 波动方程的解析解法 • 波动方程的数值解法 • 行波法的应用实例
01
波动方程的基本概念
பைடு நூலகம்
波动方程的定义
波动方程
描述波动现象的基本数学模型,通常 用于描述物理场(如声场、电磁场、 水波等)随时间和空间的变化规律。
03
最后,通过迭代求解差分方程 ,得到波在每个网格点上的值 ,从而得到波的传播和演化过 程。
行波法的优缺点
优点
行波法简单易懂,易于编程实现,能够处理复杂的边界条件和初始条件,适用 于求解各种类型的波动方程。
缺点
行波法需要设定初始条件和边界条件,对于某些复杂的波动问题可能需要较高 的计算成本和精度要求。
水波传播的模拟
要点一
总结词
利用行波法模拟水波的传播,有助于研究水波的形成、演 化及对环境的影响。
要点二
详细描述
在水波传播的模拟中,行波法能够模拟水面的波动情况, 包括波浪的生成、传播和消散。通过调整参数,可以研究 不同条件下水波的传播规律,如风速、水深、地形等,对 于水文学、海洋学等领域具有重要意义。
03
波动方程的解析解法
分离变量法
将波动方程的解表示为若干个变量的 乘积或商的形式,以便分别求解。
VS
分离变量法是一种求解波动方程的常 用方法。通过假设波动方程的解可以 表示为若干个变量的乘积或商的形式 ,我们可以将一个复杂的偏微分方程 转化为若干个简单的常微分方程,从 而方便求解。
积分变换法
利用积分变换将波动方程化为易于求解的形式,再进行逆变换得到原方程的解。
地震学
用于模拟地震波的传播和反射,进行地震预 测和地球结构研究。
目录 Contents
• 波动方程的基本概念 • 行波法的基本原理 • 波动方程的解析解法 • 波动方程的数值解法 • 行波法的应用实例
01
波动方程的基本概念
பைடு நூலகம்
波动方程的定义
波动方程
描述波动现象的基本数学模型,通常 用于描述物理场(如声场、电磁场、 水波等)随时间和空间的变化规律。
03
最后,通过迭代求解差分方程 ,得到波在每个网格点上的值 ,从而得到波的传播和演化过 程。
行波法的优缺点
优点
行波法简单易懂,易于编程实现,能够处理复杂的边界条件和初始条件,适用 于求解各种类型的波动方程。
缺点
行波法需要设定初始条件和边界条件,对于某些复杂的波动问题可能需要较高 的计算成本和精度要求。
水波传播的模拟
要点一
总结词
利用行波法模拟水波的传播,有助于研究水波的形成、演 化及对环境的影响。
要点二
详细描述
在水波传播的模拟中,行波法能够模拟水面的波动情况, 包括波浪的生成、传播和消散。通过调整参数,可以研究 不同条件下水波的传播规律,如风速、水深、地形等,对 于水文学、海洋学等领域具有重要意义。
03
波动方程的解析解法
分离变量法
将波动方程的解表示为若干个变量的 乘积或商的形式,以便分别求解。
VS
分离变量法是一种求解波动方程的常 用方法。通过假设波动方程的解可以 表示为若干个变量的乘积或商的形式 ,我们可以将一个复杂的偏微分方程 转化为若干个简单的常微分方程,从 而方便求解。
积分变换法
利用积分变换将波动方程化为易于求解的形式,再进行逆变换得到原方程的解。
地震学
用于模拟地震波的传播和反射,进行地震预 测和地球结构研究。
《机械波波动方程》课件

04 机械波的应用
机械波在声学中的应用
声波传播
机械波在声学中用于描述声波的传播规律,包括声音的传播速度 、衰减和反射等。
声音合成与处理
通过控制机械波的波形和频率,可以实现声音的合成与处理,如音 频信号的调制、滤波和混响等。
声呐技术
利用机械波在介质中的传播特性,声呐技术可用于探测水下目标、 测量水深和流速等。
和计算效率。
开展跨学科的研究合作,将机 械波波动方程与流体力学、电 磁学等领域进行交叉融合,以 拓展其应用领域和研究范围。
加强机械波波动方程在各领域 的应用研究,探索其在新能源 、新材料、生物医学等领域的
应用前景。
注重人才培养和学术交流,加 强国内外学术合作与交流,推 动机械波波动方程领域的不断 发展。
通过研究机械波波动方程,可以深入理解波动现象的内在规律和机制,为 工程技术和科学研究提供重要的理论支撑。
机械波波动方程在声学、地震学、波动成像等领域有着广泛的应用,对于 这些领域的发展起着至关重要的作用。
机械波波动方程未来的研究方向和展望
深入研究机械波波动方程的求 解方法和数值模拟技术,以提 高对复杂波动现象的模拟精度
程
波动方程是通过将牛顿第二定律 应用于波的传播过程而建立的。 它描述了波在传播过程中,各点 的位移如何随时间变化。
波的传播过程
波在传播过程中,各点的振动状 态会以波的形式传播出去。这种 传播过程可以用波动方程来描述 。
波的叠加过程
当两个或多个波相遇时,它们会 相互叠加,产生干涉、衍射等现 象。这些现象也可以通过波动方 程来描述。
THANKS
波动方程的物理量
波动方程中的物理量
在波动方程中,通常包含位移、速度、加 速度、时间等物理量。这些物理量描述了 波在空间和时间中的传播和变化。
波动方程举例ppt课件

500 Hz
0.02 s 0.4 m
精品课件
15
2. x = 2 m 处
0.05 cos ( 5×2 – 100 t ) 0.05 cos ( 100 t –10 ) 初相为–10
3. x1 = 0.2 m 处的振动相位比原点处的振动相 位落后
x2 = 0.35 m 处的振动相位比原点处的振动相 位落后
解:1.
0.05 cos ( 5 x – 100 t ) 0.05 cos 100 ( t – x )
20
cosa = cosa
正向波
精品课件
14
波动方程 y = 0.05 cos ( 5 x – 100 t ) (SI)
与
y
Acos(t
x u
)
比较得 0.05 m
100
20 m ·s -1
0. 02 8
精品课件
18
(2)p点处x = 0.2m,代入上述波动方程
y0.c 0o 4 0s .[ 4t0. 2 -]
0. 02 8
0.0c4o0s.[4t]
2
方法二 设波动方程为
y
Acos(t
x u
)
A=0.04m
u=0.08m/s
2 0.4
T
?
把x=0代入上述波动方程 y Acost
31 02co4sπ[t3π] 5
精品课件
9
u
8m 5m 9m
C
B oA
Dx
点 D 的相位落后于点 A
D
A
-
x u
4t - 4 9
20
yD31 0 2co4sπt[-5 9]
31 02co4sπ[t]
第三章波动方程培训课件

在均匀、各向同性、理想弹性介质中的弹性波方程为:
2 U ( )gr a F d 2 tU 2
两边分别取散度和旋度,并且令
V P 2(2)/
VS2 /
则可得纵波方程和横波方程
2t2 VP22
2t2 VS2
5
3 波动方程的解及地震波的特点
波动方程反映了物体波动过程的普遍规律。 波动方程的求解通常是和定解问题联系起来 考虑。波动方程的解就是波函数。
12
3.2 无限大、均匀各向同性介质中的球面波
2、坐标变换和球坐标下球面纵波的传播方程解
已知球面纵波传播波动方程如下:
2t2 VP220
此式是直角坐标系中的波动方程,需转换到球 坐标系中,即
x rsic nos y rs in s in(0 r ,0 ,0 2 ) z rcos
前面是平行的。
▪ k1,k2,k3 是平面的法线方向数。有 k12k2 2k3 21
▪ 取负号时,表示随时间t的增加,波沿k方向前进,即延 迟一个时间。
▪ 取正号时,表示随时间t的增加,波沿-k方向前进,即 提前一个时间
▪ 当K是任意矢量的,则平面法向量为任意方向的。即表 示沿任意方向传播的平面简谐波。
8
二、沿X轴方向传播的平面波(即
kx
)
U Aex 2 p ik1xk2yk3zV td AieA co sisin
k1 1 ,k 2
U A exp
u A 1 exp
0 ,k 3 0
2i
x
Vt
2i
x
Vt
d
v
A 2 exp
2i
x
Vt
w
A 3 exp
2i
u rer u rr r
2 U ( )gr a F d 2 tU 2
两边分别取散度和旋度,并且令
V P 2(2)/
VS2 /
则可得纵波方程和横波方程
2t2 VP22
2t2 VS2
5
3 波动方程的解及地震波的特点
波动方程反映了物体波动过程的普遍规律。 波动方程的求解通常是和定解问题联系起来 考虑。波动方程的解就是波函数。
12
3.2 无限大、均匀各向同性介质中的球面波
2、坐标变换和球坐标下球面纵波的传播方程解
已知球面纵波传播波动方程如下:
2t2 VP220
此式是直角坐标系中的波动方程,需转换到球 坐标系中,即
x rsic nos y rs in s in(0 r ,0 ,0 2 ) z rcos
前面是平行的。
▪ k1,k2,k3 是平面的法线方向数。有 k12k2 2k3 21
▪ 取负号时,表示随时间t的增加,波沿k方向前进,即延 迟一个时间。
▪ 取正号时,表示随时间t的增加,波沿-k方向前进,即 提前一个时间
▪ 当K是任意矢量的,则平面法向量为任意方向的。即表 示沿任意方向传播的平面简谐波。
8
二、沿X轴方向传播的平面波(即
kx
)
U Aex 2 p ik1xk2yk3zV td AieA co sisin
k1 1 ,k 2
U A exp
u A 1 exp
0 ,k 3 0
2i
x
Vt
2i
x
Vt
d
v
A 2 exp
2i
x
Vt
w
A 3 exp
2i
u rer u rr r
第六章弹性波波动方程及其解ppt课件

又 • u • uS 0
2
代入纳维方程 ( )( • u ) u f u
uS f uS
2 2
VS uS f uS
2
vs
结论:在均匀各向同性弹性体内,切变扰动以速度VS向
(4)
(5)
式u j , ji (ui , jj u j ,ij ) f i ui即为位移在弹性体
内传播时所满足的方程 .称为纳维 ( Navier)方程.
纳维方程是线性弹性假设条件下得到的各向同性弹性体中
的弹性波最基本方程。
指标表示的纳维方程 ( )u j , ji ui , jj f i ui
§6.1 线性弹性动力学的基本方程
1.
基本方程
➢
➢
运动微分方程 ji , j
几何方程
1
eij (ui , j u j ,i )
2
2 ui
f i 2
t
u1
e11
x1
u2
e22
x2
u
e33 3
x3
1 u1 u2
e12 (
)
2 x2 x1
v p t
上式表示波场是以速度VP向外传播的无旋场。
转动矢量表示的横波方程
2
( )( • u ) u f u两边取旋度
2
(
u
)
( )( ( • u )) 2 ( u ) ( f )
《一维波动方程》课件

三维波动方程
描述空间波的传播
三维波动方程适用于描述在三维空间 中波的传播,例如声波、电磁波等。
物理应用广泛
三维波动方程在物理、工程等领域有 广泛的应用,如地震波传播、电磁波 传播等。
多维波动方程的解法
数值解法
对于多维波动方程,由于其复杂性, 通常采用数值解法来求解。常见的数 值解法包括有限差分法、有限元法等 。
解的物理意义
通过求解一维波动方程,可以得到波在空间中传播时的具体形式和性质,如波速、波长、振幅和相位 等。这些解具有明确的物理意义,可以用于描述和分析各种波动现象。
03
一维波动方程的解法
Chapter
分离变量法
总结词
通过将一维波动方程转化为多个常微分 方程,逐个求解,得到波动方程的解。
VS
详细描述
03
三维波动方程
描述三维空间中波的传播和变化规律,一般形式为:∂²u/∂t² = c² *
(∂²u/∂x² + ∂²u/∂y² + ∂²u/∂z²) + f(x, y, z, t)。
02
一维波动方程的建立
Chapter
一维波动方程的推导
波动现象的观察
波动现象在自然界中广泛存在,如声波、光波和水 波等。通过对这些现象的观察,可以发现波动具有 传播、干涉和衍射等特性。
有限差分法
总结词
通过将一维波动方程离散化,转化为差分方程组,然后求解差分方程组得到波 动方程的近似解。
详细描述
有限差分法是一种通过将一维波动方程离散化,转化为差分方程组的方法。在 离散化的过程中,需要考虑差分方程的稳定性和精度。然后利用数值计算方法 求解差分方程组,得到波动方程的近似解。
04
波动方程与波速ppt课件

x
上页 下页 返回 结束
第十章 波动和声
设横波沿x方向传播,体元横截面积S,密度 .
切 应 变dy dx
x 处,由胡克定律
Fx dy G ,G为切变模量 。 S dx x
yy(x,t)
Fx y(x,t) G
S
x x
xΔx处
FxΔx y(x,t) G
S
x xΔx
F xΔ xF x y(x x,t)xΔ xy(x x,t)x GS
K为媒质的体变弹性模量; 为质量密度.
在液体和气体中只能传播纵波.
上页 下页 返回 结束
第十章 波动和声
理想气体纵波波速 (声速)
v气
p
RT
为气体的摩尔质量, T为热力学温度;
R为摩尔气体常数, 是气体的比热容比.
波速与温度有关 深水波
v g 2π
浅水波
v gh
深水波的波速依赖于频率,这种现象称色散.
上页 下页 返回 结束
G
2 y x2
2 y E 2 y
t 2 x2
2 y t 2
FT
l
2 y x2
第十章 波动和声 ——横波的波动方程 ——纵波的波动方程 ——柔软弦中的横波
上页 下页 返回 结束
§10.3.2 波速色散
第十章 波动和声
对于一维简谐波
y (x ,t) A ck o (vs tx )
2 t2 yA2 kv2c ok(svtx) 2yA2 kcoks(vtx) x2
2 y t 2
v2
2 y x2
与2y t2
G
2y比较可得 x2
上页 下页 返回 结束
第十章 波动和声
在密度为,扬氏模量为E的介质传播的纵波的波
上页 下页 返回 结束
第十章 波动和声
设横波沿x方向传播,体元横截面积S,密度 .
切 应 变dy dx
x 处,由胡克定律
Fx dy G ,G为切变模量 。 S dx x
yy(x,t)
Fx y(x,t) G
S
x x
xΔx处
FxΔx y(x,t) G
S
x xΔx
F xΔ xF x y(x x,t)xΔ xy(x x,t)x GS
K为媒质的体变弹性模量; 为质量密度.
在液体和气体中只能传播纵波.
上页 下页 返回 结束
第十章 波动和声
理想气体纵波波速 (声速)
v气
p
RT
为气体的摩尔质量, T为热力学温度;
R为摩尔气体常数, 是气体的比热容比.
波速与温度有关 深水波
v g 2π
浅水波
v gh
深水波的波速依赖于频率,这种现象称色散.
上页 下页 返回 结束
G
2 y x2
2 y E 2 y
t 2 x2
2 y t 2
FT
l
2 y x2
第十章 波动和声 ——横波的波动方程 ——纵波的波动方程 ——柔软弦中的横波
上页 下页 返回 结束
§10.3.2 波速色散
第十章 波动和声
对于一维简谐波
y (x ,t) A ck o (vs tx )
2 t2 yA2 kv2c ok(svtx) 2yA2 kcoks(vtx) x2
2 y t 2
v2
2 y x2
与2y t2
G
2y比较可得 x2
上页 下页 返回 结束
第十章 波动和声
在密度为,扬氏模量为E的介质传播的纵波的波
(大学物理 课件)波动方程

表示 x1 处质点的振动方程
结束
返回
2. t = t 1 (常数) y
o y = A cos ω ( t 1 x )+j u x
表示在 t 1 时刻的波形
结束
返回
3. t 与 x 都发生变化 x t = t1 y 1 = A cos ω ( t 1 u ) + j x t = t 1+Δ t y ´= A cos ω ( t 1+Δ t u ) + j y
波 动 方 程
返回16章 结束
波动方程 一、平面简谐波的波动方程 y u x
§16-2平面简谐波
o
B
x
参考点O点的振动方程为: y = A cos ( t + j ) ω
任意点(B点)的振动方程,即波动方程为: y = A cos ω ( t x ) + j u 结束 返回
平面简谐波的波动方程为: x j y = A cos ω ( t u ) + t x j y = A cos 2π ( T l ) +
A cos 2π (x +120 t ) = 60
π
3
例2. 有一列向 x 轴正方向传播的平面简 谐波,它在t = 0时刻的波形如图所示,其波 速为u =600m/s。试写出波动方程。 y(m)
u 5 x (m)
o
12
.
结束
返回
解: o 由图可知, 在t = 0时刻
y(m)
u 5 x (m)
12
.
y1 y´ ut
.
O
x
x´
t
令 y 1= y ´
得: ´= x +uΔ t x 这表示相应于位移y1的相位,向前传播了 uΔ t的距离。 结束 返回
数学物理方法波动方程教学ppt
(0 x l;t u xl 0
0)
u t0 ( x);
ut t0 ( x)
B
II
:
utt
a 2uxx 0 ux x0
0;
(0 x u xl
l;t 0
0)
u t0 ( x);
ut t0 ( x)
DII
:
utt
a 2uxx 0 ux x0 0;
u t0 ( x); ut t0 ( x)
x [0, l]
物理解释:
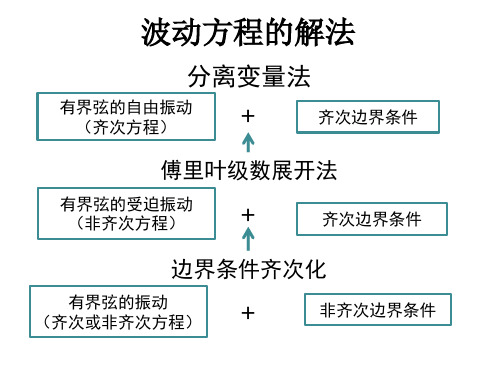
一根长为 l 的弦,两端固定,给定初始位 移和速度,在没有强迫外力作用下的振动
齐次方程+齐次边界条件
求解的基本步骤
第一步:分离变量
偏微分方 程变成常 微分方程
设 u(x,t) X (x)T (t) 代入 utt a2uxx 0
Tn (t )
An
cos
na
l
t
Bn
sin
na
l
t
T(t)的表达式
第三步:定系数
na
na
n
un ( x, t) ( An cos
l
t Bn sin
l
t ) sin( l
x)
通解:
u( x, t)
( An cos
n1
na
l
t
Bn
s
in
na
l
t)sin( n
l
x)
由初始条件确定An, Bn u t0 ( x); ut t0 ( x)
X ( x l) B sin l 0 B 0 sin l 0
l n 0 n / l (n 1,2,3,...)
II 0 X(x) A Bx A B 0
波动方程ppt课件

∴ B为原点的波动方程:
10m
5m
· · · 0
AB
x
y B
=5cosπ
t
-
x +5
20
(a)
=5cosπt- x2+05π =5cosπt - x2π0 -π4
B为原点的波动方程:
y B
=5
cos
πt
-
x2π0 -π4
=5cosπ(t - 2x0)-π4 (m)
因为是右行波,0点的振动相位超
前A点的振动相位,而且相距10m
式中A、B 、C 为正常数,求波长、波速、波 在传播方向上相距为d 的两点间的相位差。
例题:平面简谐波的波函数为:
y =A cos(Bt-Cx )
式中A、B 、C 为正常数,求波长、波速、波 在传播方向上相距为d 的两点间的相位差。
解:
y
=A cos(Bt-Cx
)
=A cosB(t-
x B
)
以上式对照波动方程的标准像
y
o
u
· A P
注意: 波动图的纵横坐标
分别为x、y。它们表示振动 状态传到的地方和振动质 x 点离开平衡位置的距离。
x
在此时间t 是隐函数,
不在波形图上。
已知振源(波源)
的振动方程为: y =A cos(ω t +j ) 0
1.时间推迟方法
1.时间推迟方法
y
u
o
· A P
x
已知振源(波源) 的振动方程为:
y(m)
0
u
5 .12
解: 上坡下行
下坡上行
x (m)
0点在t 稍>0 时
过平衡位置向y 负方向运动
10m
5m
· · · 0
AB
x
y B
=5cosπ
t
-
x +5
20
(a)
=5cosπt- x2+05π =5cosπt - x2π0 -π4
B为原点的波动方程:
y B
=5
cos
πt
-
x2π0 -π4
=5cosπ(t - 2x0)-π4 (m)
因为是右行波,0点的振动相位超
前A点的振动相位,而且相距10m
式中A、B 、C 为正常数,求波长、波速、波 在传播方向上相距为d 的两点间的相位差。
例题:平面简谐波的波函数为:
y =A cos(Bt-Cx )
式中A、B 、C 为正常数,求波长、波速、波 在传播方向上相距为d 的两点间的相位差。
解:
y
=A cos(Bt-Cx
)
=A cosB(t-
x B
)
以上式对照波动方程的标准像
y
o
u
· A P
注意: 波动图的纵横坐标
分别为x、y。它们表示振动 状态传到的地方和振动质 x 点离开平衡位置的距离。
x
在此时间t 是隐函数,
不在波形图上。
已知振源(波源)
的振动方程为: y =A cos(ω t +j ) 0
1.时间推迟方法
1.时间推迟方法
y
u
o
· A P
x
已知振源(波源) 的振动方程为:
y(m)
0
u
5 .12
解: 上坡下行
下坡上行
x (m)
0点在t 稍>0 时
过平衡位置向y 负方向运动
光电子技术基础-波动方程PPT课件

若电场为横向分布,磁场没有横向分量,则为横电 波——TE波;
若磁场为横向分布,电场没有横向分量,则为横磁
波——TM波;
-
12
2.4.2 频域波动方程
在时谐条件下,均匀简单介质中 有源矢量波动方程(2-45)化为
-
13
当然,不同条件下,上面的方程也有不同的形式, 这里就不一一列举了。
不管是什么情况下的形式,都可以用同一的格式 来表示:
满足扩散方程的电磁场不具有波动性。
-
9
不同情况下波动方程的简化 5. 恒定场(不随时间变化的场)
这种情况下,电场和磁场不发生相互作用。
-
10
一维电磁波的场解
可化简为最简单的一维齐次波动方程
-
11
上面方程的解是:
当然,情况不同,场解的形式也不同。
若电场和磁场都是横向分布,则形成横电磁波—— TEM波;
13242频域波动方程在时谐条件下均匀简单介质中有源矢量波动方程245化为14当然丌同条件下上面的方程也有丌同的形式这里就丌一一列举了
光电子技术基础
2.4 波动方程
陈晓峰-1Fra bibliotek麦克斯韦方程
-
2
对2-28a取旋度,并考虑2-28b和B=u。H,可得:
-
3
2.4.1 简单电介质中的时域波动方程
-
4
以上两个方程是均匀简单介质中电磁场有源 矢量的波动方程,也是电磁场广义波动方程 的最普遍形式。
在低频高电导介质中,有近似关系:
在高频低电导介质中,有近似关系:
-
14
另外,光场在无损介质中的传播时, 应注意一下几个重要的关系式:
-
15
没有上课经验,讲的不 好请见谅,也感谢老师
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Q
P
波函数:
y
=A
cos ω
(t-
x -x0
u
)+j
y
=A
cos ω
(t-
x
u
)
+j
y
=A cos
2π(
t T
-
x
l
) +j
l =uT
ω =2Tπ
平面简谐波波动方程的标准像
必
y
=A
cos ω
(t-
x
u
)
+j
做
须 牢
y
=A cos
2π(
t T
-
x
l
) +j
题 对
记
y
=A
cos ω
(
t-
x -x0
u
)+j
l
x
o
· A P
x
j P
=-
2π
l
x
+j
x
j P
=-
2π uT
x +j
=-ω
x u
+j
l =uT
ω =2Tπ
y =A cos(ω t +j )
P
P
=A cos (ω t -ω
x
u
)
+j
介质中任一质点(坐标为 x)相对其平衡位
置的位移(坐标为 y)随时间t 的变化关系。
波波
函 数
动 方 程
y
=A
cos ω
x
x
任何复杂的波都可以看成是由若干个频率不同简谐波叠 加而成到的,所以研究简谐波仍具有特别重要的意义。
1. 平面简谐波波动方程的推导
推导的方 时间推迟方法 法有两种: 相位比较方法
y
o
u
· A P
注意: 波动图的纵横坐标
分别为x、y。它们表示振动 状态传到的地方和振动质 x 点离开平衡位置的距离。
(
t-
x
u
)
+j
波向x 轴正方向 传播也称右行波
波向x 轴负方向 传播也称左行波
y
=A
cos ω
(
t
+
x
u
) +j
物理意义:波线上任一点(距原点为 x)处 的质点任一瞬间相对其平衡位置的位移。
当波向x 轴正方向传播而且已知 距离0点为xo的Q点振动方程为:
可理解为将Q点 作为计时原点。
y =A cos(ω t +j )
y =y(x、t)
各质点相对平 衡位置的位移
波线上各质 点平衡位置
★ 简谐波:在均匀的、无吸收的介质中,波源作简谐振 动时,其振动状态在介质中传播过程中所形成的波。
★平面简谐波:波面为平面的简谐波。
各种不同 的简谐波
y
简谐波1 0
y
简谐波2 0
y
合成 复杂波 0
合成 分解
复杂波 简谐波 的波形图
x
x
(a)
t=0时的波形图
y
0
t
(b)
质点的振动曲线图
(A)均为零
(B)均为
π
2
(C)均为-π2
(D)π2 与-π2 (E)-π2 与π2
提示:分清波动图和振动图上各点运动的方向。
y
u
y
0
0
x
t
(a)
t=0时的波形图
(b)
质点的振动曲线图
判断波动图上各 点运动的方向:上坡下行、下坡上行
(a)是波形图,注意到它 的传播方向,x =0处质点振 动是过平衡位置 ,向y 轴负 方向运动的(理由:上坡下行、 下坡上行)
上坡下行 下坡上行
传播, 画出波形曲线上 A、B 、C 、D 、E 、F 各 点的运动方向和四分之
y C· B· ·D
u
一周期后的波形曲线。
· A 0
T 4
E·
·F
x
特别要注意:波的传播方向,这是关键。
例题:图(a)中所表示的x =0 处质点振动的初相位
与图(b)所表示的振动的初相位分别为:
y
u
0
x
在此时间t 是隐函数,
不在波形图上。
已知振源(波源)
的振动方程为: y =A cos(ω t +j ) 0
1.时间推迟方法
1.时间推迟方法
y
u
o
· A P
x
已知振源(波源) 的振动方程为:
x y =A cos(ω t +j ) 0
振源的振动状态从0点以传播速度
u传送到P 点,显然时间要落后:t´=
波速
u=
B C
周期T
=ω2π
=
2π
B
初相位 j =0
l=uT
=
B C
2π
B
=
2π
C
与波源相距为d 处的振动表达式为:
y =A cos(Bt-Cx ) =A cos(Bt-Cd )
波传播方向上相距为d 的两点间的相位差:
△
j=
2lπ△
x
=
2π
2π
d =Cd
C (本题结束)
判断各点运动 方向的技巧
例题:有一列横波向右
x
u
y =A P
cos
ω
(
t-t´
)
+j
=A
cos ω
(
t-
x
u
)
+j
介质中任一质点(坐标为 x)相对其平衡位 置的位移(坐标为 y)随时间t 的变化关系。
2.相位比较方法
y
已知振源(波源)
u
的振动方程为:
o
· A P
x y =A cos(ω t +j )
0
x
P点的相位比 0点的相位落后: △ j =jP - j
照
波动方程的 另外几种形式
y
=A
cos
2π(
t-
x
l
) +j
y =A cos (ω t -kx ) +j
k =2lπ k 角波数
角波数:表示单位长度上波的相位变化,在
数值上等于2π长度上的完整波数目。
例题:平面简谐波的波函数为:
y =A cos(Bt-Cx )
式中A、B 、C 为正常数,求波长、波速、波 在传播方向上相距为d 的两点间的相位差。
平面简谐波的波函数 波动方程
Equation of wave
定量地描述前进中的波动(也称行波) ,用数学 形式描述介质中各个质点的位移随时间而变化 的规律。这样的函数式称为行波的波动方程。
§6-2 平面简谐波的波函数
一 . 平面简谐波的波函数 介质中任一质点(坐标为 x)相对其平衡位置的位移 (坐标为 y)随时间t 的变化关系,称为波函数。
(D)π2 与-π2 (E)-π2 与π2
例题:如图所示简谐
波以余弦函数表示, 求:Q、a、b、c 各点 振动相位。
y
t =0 A
u
·b
t=T/4
a
0·
c·
x
-A ·Q
Q点
A
j o
=π
0·
y
按照 上坡下行
下坡上行
Hale Waihona Puke b点j b=0
0· A y
y =A cos(ω t +j )
P
P
公式可查处: 教材P153
jP
j
=-
2π
l
x
j P
=-
2π
l
x
+j
l =uT
ω
=
2π T
j P
=-
2π uT
x +j
=-ω
x u
+j
2.相位比较方法
y =A cos(ω t +j )
P
P
P点的相位比 0点的相位落后: △ j =jP - j
y
u
j P
-
j
=-
2π
.π-2
0
y
t 稍>0时的波形图是红色曲线 由此画出旋转矢量图。
y
0
t
(b)
质点的振动曲线图
(b)是振动图 ,t =0处 质点振动是过平衡位置, 向y 轴正方向运动的。
由此画出旋转矢量图:
解题体会:做此类
.
0
π-2
y
题目,切不可盲目 判断,要加以分析!
所以取
(A)均为零
(B)均为
π
2
(C)均为-π2
例题:平面简谐波的波函数为:
y =A cos(Bt-Cx )
式中A、B 、C 为正常数,求波长、波速、波 在传播方向上相距为d 的两点间的相位差。
解:
y
=A cos(Bt-Cx
)
=A cosB(t-
x B
)
以上式对照波动方程的标准像
C 波长
y
=A
cos ω
(t-
x
u
)
+j
∴振幅=A ,角频率ω=B
