分离变量法很好的例题共26页
第二章 分离变量法

2°设λ=0,此时方程(2.5)的通解为 由条件(2.6)还是得A=B=0,所以λ也不能等于零。
3°设λ>0,并令λ=β2, β为非零实数。此时方程(2.5)得通解为 由条件(2.6)得 由于B 不能为零(否则X(x) ≡0),所以sinβl=0,即 (n为负整数可以不必考虑,因为例如n=-2,实际上还是的形式)从 而
解,它的主要步骤大体为:
一、首先将偏微分方程的定解问题通过分离变量转化为常微分方程
的定解问题,这对线性齐次偏微分方程来说是可以做到的。
二、确定特征值与特征函数。由于特征函数是要经过叠加的,所以
确定特征函数的方程与条件,当函数经过叠加之后仍旧要满足。当边界
条件是齐次时,求特征函数就是求一个常微分方程满足零边界条件的非
§2.2 有限长杆上的热传导
设有一均匀细杆,长为l,两端点的坐标分别为x=0与x=l,杆的侧 面是绝热的,且在端点x=0处的温度是零摄氏度,而在另一端x=l处杆 的热量是自由散发到周围温度是零度的介质中去(参考第一章§1.2中 第三类边界条件,并注意在杆的x=l端的截面上,外法线方向就是x轴的 正方向),已知初始温度分布为φ(x)。求杆上的温度变化规律,也就 是要考虑下列定解问题:
从上面的运算过程可以看出,用分离变量法求解定解问题的关键步 骤是确定特征函数与运动叠加原理,这些运算之所以能够进行,就是因
为偏微分方程与边界条件都是齐次的,这一点一定要注意。 例1 设有一根长为10个单位的弦,两端固定,初速度为零,初始位
移为,求弦作微小横向振动时的位移。 解 设位移函数为u(x,t),它是定解问题
数理方程第二章分离变量法

分离变量法得到的解可能不唯一,有时需要额外的条件或参数才能 确定唯一解。
数值稳定性
分离变量法在数值实现时可能存在数值稳定性问题,如数值误差的 累积和扩散等,需要采取适当的措施进行控制和校正。
06
CATALOGUE
分离变量法的改进与拓展
改进方向一:提高求解精度
数值稳定性
通过改进数值算法,提高求解过程中数值的稳定性, 减少误差的传播和累积。
原理推导
01
首先,将偏微分方程中的多个变量分离出来,使方程变为一个 关于各个变量的常微分方程。
02
然后,对每个常微分方程分别求解,得到各个变量的解。
最后,将各个变量的解代回原偏微分方程,得到整个问题的解
03 。
原理应用
在物理学中,分离变量法广泛应用于求解具有多个独立变量的偏微分方程 ,如波动方程、热传导方程等。
高阶近似方法
研究高阶近似方法,以更精确地逼近真实解,提高求 解精度。
自适应步长控制
引入自适应步长控制策略,根据解的精度要求动态调 整步长,提高求解精度。
改进方向二:拓展应用范围
复杂边界条件
研究如何处理更复杂的边界条件,使得分离变 量法能够应用于更广泛的数理方程问题。
多维问题
将分离变量法拓展到多维问题,以解决更复杂 的数学模型。
04
CATALOGUE
分离变量法的实例
实例一:一维波动方程的分离变量法
总结词
通过将一维波动方程转化为常微 分方程,分离变量法能够简化求 解过程。
详细描述
一维波动方程是描述一维波动现 象的基本方程,通过分离变量法 ,我们可以将该方程转化为多个 常微分方程,从而逐个求解,得 到波动问题的解。
数学表达式
第13讲直角坐标分离变量法例题

k = 0,±1,±2,⋅ ⋅ ⋅ 傅氏系数 ∞ r nπ nπ b = VS ( x) φ (r ) | y =b = ∑ An sin x sh a a n =1
nπ ⎛ ⎜ An sh ∑ a n =1 ⎝
∞
nπ ⎞ b ⎟ sin x = U ( x) a ⎠
26
求解
1 nπ nπ b = ∫ U ( x) sin xdx An sh a a −a a
Vs ( x) 的形式没有给出,用迭加原理和傅 立叶级数求解系数 23
迭加原理和傅立叶级数求解系数
试探解
∞ ∞ r r nπ nπ x sh y φ (r ) = ∑ φn (r ) = ∑ An sin a a n =1 n =1
y=b处B.C. ∞ r nπ nπ b = VS ( x) φ (r ) | y =b = ∑ An sin x sh a a n =1
31
解答
A= V0 sh
πb
a
域内的电位分布
r V0 πx πy φ (r ) = sin sh (V) πb a a sh a
(0 < x < a,0 < y < b)
32
例5
本例题说明如何用迭加原理求解电位问 一个在z方向无 限长的金属角 域,在y=b和 x=a的两面分别 有电位 VS1 (x ) 和 VS 2 ( y ) 。
24
延拓为周期函数
(0<x<a)定义域中的 Vs ( x ) 开拓为
(− ∞ < x < ∞ ) 定义域中的周期函数。
U (x )
V S (x )
− 2a
−a
a
2a
x
分离变量法习题课26页PPT

分离变量法习题课
46、法律有权打破平静。——马·格林 47、在一千磅法律里,没有一盎司仁 爱。— —英国
48、法律一多,公正就少。——托·富 勒 49、犯罪总以惩罚相补偿;只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
谢谢
拉普拉斯方程.分离变量法PPT文档28页

46、法律有权打破平静。——马·格林 47、在一千磅法律里,没有一盎司仁 爱。— —英国
48、法律一多,公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿;只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
▪
谢谢!
28
Hale Waihona Puke 26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
分离变量法习题课.ppt

Rm (r)<3>C* 0 (ln r ln r2 )
Cm (r m r22mr m )
Wuhan University
4
Rm (r) C0 (ln r ln r2 )
( ) 一A、m 正co交s m曲线 坐Bm标sin系m中的分离变Cm量(r m r22mr m )
[ n ]2
n
因为 a Rn () b bn
④
u(,)
n
Cn
n1
sin
n
(
)
由式<3>,得:
f
()
n
Cna
n1
sin
n
(
)
#
n
Cn a a
u(x,0) 3sin ut (x,0) 0
x
,
0
x
u(0,t) u( ,t) 0;
u(x,t) (An cos nat Bn sin nat)sin nx
n1
u(x,0) 3sin x An sin nx 3sin x
sin
x
sin
y
<1>
sin z
ut (x, y, z;0) 0 u(0, y, z;t) u(1,
y,
z;
t
)
<3> 0 <4>
Z Z 0
<10> u(x,0, z;t) u(x,1, z;t) 0 <5>
其中( )
第四章分离变量法

∵ ∴
∴
∴C=-D=0此时
∴ 不合适
若 时,方程 的特征方程为
∴
∴
∵ ∴
∵ ∴
∵ ∴
∴
∴
综上所述。
该问题的特征值为
特征函数为
Step3:将 代入关于 的微分方程求 有:
∴
∴
Step4:叠加,原方程的解为:
∵
∴
其中
(3)该问题的数字模型为:
其中
Step1:分离变量:令 ,代入齐次方程及齐次边界条件中有:
其特征根为
∴ n=0,1,2,……
∴
n=0,1,2,……
Step4:叠加:原方程的解为:
其中 得求
∵ ∴
∴
n=0,1,2,……
∵
∵
即 ∴ n=0,1,2,……
∴原方程的解为
6.长为2l的均匀细杆,被作用在两端的压力压缩式 ,在t=0时,把这个载荷移去,试证,若x=0是杆的中点,则在t时刻,坐标为x的杆的截面位移 由下式确定:
Step4:叠加
由于
所以:
∴
综上知该热传导问题的解为:
其中
(2)该问题的数字模型为
其
Step1:分离变量:令 ,并代入齐次方程及齐次边界条件中有:
由于 故上面方程可化为
所以有:
整理得
Step2:求解下面的特征值问题
讨论:若 ,则方程变为
这样
∵ 而 ∴
此时有 (取 0即可)
若 时则方程 的特征方程为
∴
解:假设细杆的左端点固定,于是该问题的数字桂型为:
其中E为细杆的杨氏模量, 为细杆的横截面积
Step1:分离变量:令 ,并代入齐次方程和齐次边界条件中有:
分离变量法
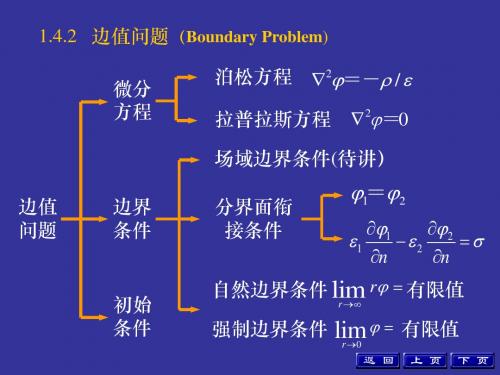
均匀电场中的介质圆柱棒
a≤ ρ <∞
ϕ1 =ϕ2 ϕ2
ρ=0
∂ϕ1 ∂ϕ2 ε0 =ε ∂ρ ∂ρ
ρ→∞
0≤ ρ ≤a
ρ =a
=0 , ϕ1
= −Ex = −Eρ cosφ
根据对称性 π ϕ(ρ,φ) = ϕ(ρ, −φ) 及 ϕ(ρ, ± ) = 0 2
返 回
上 页
下 页
分离变量, 设 ϕ(ρ,φ) = R(ρ)θ (φ) 代入微分方程
返 回 上 页 下 页
1.4.3 惟一性定理(Uniqueness Theorem) 惟一性定理 : 在静电场中,满足给定边界条件的 电位微分方程的解是惟一的。 例1.4.4 图示平板电容器的电位,哪一个解答正确?
U0 2 A. ϕ1 = x d U0 B. ϕ2 = x +U0 d U0 C ϕ3 = − . x +U0 d 答案:(C )
ρ2 d2R ρ dR 1 d2θ + + =0 2 2 R dρ R dρ θ dφ
2
d2θ dR dR 2 2 = 常数,令 ρ2 + n2θ = 0 +ρ −n R = 0 取n 2 dφ2 dρ dρ
当 n = 0 时, R0 (ρ) = A0 ln ρ + B0 , 0 (φ) = C0φ + D0 θ 当 n ≠ 0时, Rn (ρ) = Anρn + Bnρ−n, n (φ) = Cn cos nφ + Dn sin nφ θ 通解 ϕ(ρ,φ) = ( A ln ρ + B0 )(C0φ + D0 ) 0
nAnan−1 cos nφ ∑
n=1
∞
第三讲分离变量法演示文稿

要使它满足边界条件X(0)=0和 X(l)=0, X(x)也必恒为零。
第9页,共29页。
情况C 当λ>0时,方程(3.4)的通解为
要使此解满足边界条件X(0)=0,则C1=0。 再由X (l)=0,可知
为了使C2≠0,就必须有 于是可以确定λ的取值为
这样就找到了一族非零解: 特征函数
ut Duxx 0 0 x ,t 0
u(0,t) u( ,0) 0
u(x,0) sin x 2sin 3x
解:没有现成的公式可套,直接采用分离变量法求解 (1)分离变量:
则有: 即
u(x,t) X (x)T (t) X (x)T (t) DX (x)T (t)
T(t) X (x)
0
xa
0 0
x
0
a, y
0 b
y
b
u y0 f (x),u yb 0 0 x a
第19页,共29页。
§3-2 有界杆上的热传导问题
初边值问题的分离变量法
在前一章中,我们用分离变量法求得了波动方程初边值问题 的解。这一方法对热传导方程的初边值问题也是适用的。以下以 热传导方程在边界上分别取第一和第三边界条件的初边值问题为 例详细讨论其求解过程。 利用分离变量法求解如下的初边值问题
l
特征方程的实根:
可求得其通解为
k akπ i l
上式中Ak ,Bk 为任意待定常数。这样我们就得到了方程(3.1)满足边 界条件u(0,t)=0和 u(l,t)=0的分离变量形式的特解:
第12页,共29页。
现在我们设法作出这种特解的适当的线性组合,以得出初边值问 题的解。也就是说,要确定出常数Ak 和Bk 使
数学物理方程分离变量法 (2)精品

) 1, 2,3,L
)
特征值与 特征函数
数学物理方程与特殊函数
第2章分离变量法
2u t 2
a2
2u x2
,
0 x l,t 0
u(0,t) 0, u(l,t) 0,
t 0
u(x, 0) (x),
u(x, 0) (x),
0 xl
t
a2n2 2
T ''n (t) l2 Tn (t) 0
分离变量法可以求解具有齐次边界条件的齐次偏微分方程。
数学物理方程与特殊函数
第2章分离变量法
2 解的性质
un (x,t)
(Cn
cos
n
l
a
t
Dn
sin
n a t)sin
l
n
l
x
An
cos(nt
n )sin
n
l
x
其中: An Cn2 Dn2
n
n a
l
n
arctan
Dn Cn
x=x0时:
un (x0,t)
x2
2lx,
u(x, 0) t
0,
0 x l,t 0 t0 0 xl
解: u(x,t) X (x)T (t)
u(0,t) X (0)T (t) 0
X (0) 0
XT a2 X T
X X
1 a2
T T
X X 0 T a2T 0
u(l,t) X (l)T (t) 0 x
l 长,由此可见驻波的波长 2l / n。
数学物理方程与特殊函数
第2章分离变量法
n 1的驻波除两端x 0和x l外没有其他节点,它的波长2l在所有 本征振动中是最长的;相应地,它的频率a / 2l在所有本征振动中是 最低的。这个驻波叫做基波。n 1的各个驻波分别叫做n次谐波。 n次谐波的波长2l / n是基波的1/ n,频率na / 2l则是基波的n倍。
第十四章分离变量法-92页文档资料

第四步:利用本征函数的正交性定出叠加系数
l
本征函数的正交性: Xn(x)Xm(x)dx0, 0
对于
n1
Dnsinnlx(x)
nm
两端同乘以 sin m x ,并积分,得
第二步:求解本征值
当 0时,方程 X (x )X (x ) 0 为 X(x)0
方程的通解为 X (x)A x B 由边界条件 X(0)0,X(l)0知 AB0 即 X(x)0
因此, 0不是本征值。
当 0时,常微分方程的通解是 X (x ) A si n x B co x s
由边界条件 X(0)0,X(l)0知 B0,Asinl0 ∵ A0 ∴ l n即 nnl2 n1,2,3
t0
t t0
0xl
方程和边界条件是齐次的,初始条件为非齐次的。
第一步:分离变量 U (x ,t) X (x )T (t)…………………………所希望的特解
代入方程 2tU2 a22xU2 0 得 X (x ) T (t) a 2 X (x ) T (t) 0
移项,两端同除以 X(x)T(t)
有 a12T T((tt))X X((xx))
l
l (x)sinm l
0
xdx
l 0
n1
n
Dnsinl
xsinm
l
xdx
n1
Dn
l 0
sinn
l
xsinm
l
xdx
定义:本征函数的模方
l
X n(x)2
X n 2(x)d xlsi2nxd 2 lx
2.2 分离变量法(非齐次问题)

W ( x, t )的解可以直接使用分离变量法获得。 nπ a nπ a nπ W ( x, t ) = ∑ (Cn cos t + Dn sin t ) sin x (n = 1, 2,3,L) l l l n =1
∞
只需求解V ( x, t ) 即可。
数学物理方程与特殊函数
第2章分离变量法 章分离变量法
v n (0) = 0
n=0 n≠0
v0 (t )+ a 2 2 v n (t ) = 0 n l
ω
cos ωt + C
v 0 (t ) =
2 2 2n π −a t l2
1
ω
(1 − cos ωt )
vn (t ) = Ce
v n (t ) = 0
u=
1
ω
2 ∂ 2v 2 ∂ v , t >τ 2 =a 2 ∂x ∂t1 v = 0, vt1 = f ( x,τ ), t1 = 0 t1 = 0 v x =0 = 0, v x =l = 0
u2 ( x, t ) = ∫ v( x, t ;τ )dτ
0
t
t 令:1 = t − τ
数学物理方程与特殊函数
第2章分离变量法 章分离变量法
§2.3、非齐次问题
一、非齐次方程 1 齐次边界条件下非齐次发展方程 发展方程的混合问题 发展方程 (一)傅立叶级数法 (二)冲量定理法 2 齐次边界条件下非齐次场位方程 场位方程的混合问题 场位方程 (一)特解法 二、非齐次边界条件的处理
数学物理方程与特殊函数
∂u 2 ∂ u 0 < x < l, t > 0 ∂t = a ∂x 2 ∂u (0, t ) ∂u (l , t ) = = 0, t > 0 ∂x ∂x 0≤ x≤l u ( x, 0) = 0,
大学物理-分离变量法例题

相应的本征函数为
思考:n 只取正整数的原因?
3. 求解关于 T(t) 的常微分方程
将
代入(6-1-6),得到
其通解为
由此得到 u(x,t) 的特解
(6-1-9) (6-1-10)
(6-1-11)
4. 利用叠加原理,将特解进行叠加,得到通解 一般说来,un(x,t) 不可能满足初始条件,但特解的线性叠 加仍满足方程与边界条件。将特解线性叠加,得到通解:
(x) C1 x C2
而由 (7) 式有
C1a C2 0 C1a C2 0
于是有 C1= C2 = 0,从而有φ(x) = 0,所以λ≠ 0。
2. 若λ< 0,则由式 (6' ) 有
x C1e x C2e x
而由 (7) 式有 C1e x C2e x 0 C1e x C2e x 0
(k 1, 2,
)
故本征值问题 (6' ) ~ (7) 的本征值为
En
n 2 2
n2 2 2 8a2
(n 1, 2,
)
(13)
这是能量本征值,而由(10)和(12)式可得相应的本征函数为
n
(
x)
Cn
sin
n
2a
(
x
a)
(14)
这是第 n 个定态 (即不含时的) 波函数。
方法二 通过坐标平移利用已知结果来求解。 我们已看到上述求解本征值问题 (6' ) ~ (7) 的过程是相
即
i f '(t) 2 ''(x) 令 E (能量) f (t) 2 (x)
于是得
i
d f Ef dt
(5)
高中数学解题方法之分离变量法(含答案)

分离变量法分离变量法是近年来发展较快的思想方法之一.高考数学试题中,求参数的范围常常与分类讨论、方程的根与零点等基本思想方法相联系.其中与二次函数相关的充分体现数形结合及分类思想方法的题目最为常见.与二次函数有关的求解参数的题目, 相当一部分题目都可以避开二次函数,使用分离变量,使得做题的正确率大大提高.随着分离变量的广泛使用,越来越多的压轴题都需要使用该思想方法.分离变量法:是通过将两个变量构成的不等式(方程)变形到不等号(等号)两端,使两端变量各自相同,解决有关不等式恒成立、不等式存在(有)解和方程有解中参数取值范围的一种方法.两个变量,其中一个范围已知,另一个范围未知.解决问题的关键: 分离变量之后将问题转化为求函数的最值或值域的问题.分离变量后,对于不同问题我们有不同的理论依据可以遵循.以下定理均为已知x 的范围,求a 的范围:定理1不等式()()f x g a 恒成立min()()f x g a (求解()f x 的最小值);不等式()()f x g a 恒成立max()()f x g a (求解()f x 的最大值).定理2不等式()()f x g a 存在解max()()f x g a (求解()f x 的最大值);不等式()()f x g a 存在解min()()f x g a (即求解()f x 的最小值).定理3方程()()f x g a 有解()g a 的范围()f x 的值域(求解()f x 的值域).解决问题时需要注意:(1)确定问题是恒成立、存在、方程有解中的哪一个;(2)确定是求最大值、最小值还是值域.再现性题组:1、已知当x R 时,不等式a+cos2x<5-4sinx恒成立,求实数a 的取值范围。
2、若f(x)=233x x 在[1,4]x 上有()21f x x a 恒成立,求a 的取值范围。
3、若f(x)=233x x 在[1,4]x 上有2()251f x x aa 恒成立,求a 的取值范围。
分离变量法

第二章 分离变量法一 齐次偏微分方程的分离变量法1 有界弦的自由振动(1) 考虑两端固定的弦振动方程的混合问题⎪⎪⎪⎩⎪⎪⎪⎨⎧====><<∂∂=∂∂==)(|),(|0),(),0(0,0,01022222x u x u t l u t u t l x x u a t u t t φϕ ① 这个定解的特点是:偏微分方程是齐次的,边界条件是齐次的。
求解这样的方程可用叠加原理。
类似于常微分方程通解的求法先求出其所有线性无关的特解,通过叠加求定解问题的解。
所谓),(t x u 具有分离变量的形式,即)()(),(t T x X t x u =把)()(),(t T x X t x u =带入方程①中,可得到常微分方程定解为:),(t x u =∑∞=1),(n n t x u =l x n l t an D l t an C n n n πππ∑∞=+1sin )sin cos (其中:⎰=l n dx l x n x l C 0sin )(2πϕ,⎰=l n dx lx n x an D 0sin )(2πφπ 2离变量法的解题步骤可以分成三步:(一) 首先将偏微分方程的定解问题通过分离变量转化为常微分方程的定解问题。
(二) 确定特征值与特征函数。
(三) 求出特征值和特征函数后,再解其它的常微分方程,将所得的解与同一特征值报骊应的特征函数相乘得到所有分离变量的特解。
3 有限长杆上的热传导设有一均匀细杆,长为l ,比热为c ,热传导系数为k ,杆的侧面是绝缘的,在杆的一端温度保持为0度,另一端杆的热量自由散发到周围温度是0的介质中,杆与介质的热交换系数为0k ,已知杆上的初温分布为)(x ϕ,求杆上温度的变化规律,也就是要考虑下列问题:0,0,22222><<∂∂=∂∂t l x xu a t u (2.18) 0),(,0),0(=+∂∂=t l hu xt l u t u ),( (2.19) )()0,(x x u ϕ= (2.20) 其中ρc k a =2,00>=k k h注意到此定解问题中方程和边界条件均是齐次的,因此仍用分离变量法来求解。
大学物理-分 离变量法例题

数 w (x,t) 也满足与 u (x,t) 相同的方程,而所满足的边界条
件就是齐次的了。为使 v 的形式尽可能地简单,取它为 x
的线性函数 (这必定满足原来的方程) v = Ax + B, 其中常
数
A, B 由边界条件
v x0
u0 和 v q0
k
x u0 定出,即
A q0 k
B u0
所以
C
(12)
一并代入通解(10)得原定解问题(1)-(3)的解为
u(x, y) (3x y)2 3 C 3 (x y)2 3 C 3x2 y2
4 44
4
思考 若改变此例中变量y的取值范围,即将此例改变为如
下的定解问题
uxx 2uxy 3uyy 0 ( x , y y0 0)
故由 (2) 式有
f1(x) f2 (x) (x)
(5)
由 (3) 式有
a f1(x) a f2(x) (x)
即
f1(x)
f2 ( x)
1 a
x
0
(x)d
C
(6)
其中:C = f1 (0) – f2 (0)
解 (5)、(6) 式得
f1(x)
1 2
(x)
1 2a
x
0
(
)d
C 2
(0 x )
例4:求解下列定解问题
2u 24Cxy (x2 y2 a2 ) U ra 0
解 方法一:用相应齐次方程的本征函数展开的方法 设解为
u(r,) An (r)sin n Bn (r) cos n n0
将非齐次项展开,这时只有一项,即
24Cxy 12Cr2 sin 2
将它们代入原方程及边界条件,即得
