课程安排问题的数学模型及评价方法'
abcd模型课程设计

abcd模型课程设计一、教学目标本课程的教学目标是使学生掌握abcd模型的基本概念、原理和方法,能够运用abcd模型分析问题和解决问题。
具体目标如下:1.了解abcd模型的定义、结构和特点。
2.掌握abcd模型的基本原理和应用。
3.熟悉与abcd模型相关的概念和知识点。
4.能够运用abcd模型分析问题,提出解决方案。
5.能够运用abcd模型进行有效沟通和协作。
6.能够运用abcd模型进行创新思考和问题解决。
情感态度价值观目标:1.培养学生的批判性思维和创新意识。
2.培养学生的团队合作和沟通能力。
3.培养学生的自主学习和持续学习的习惯。
二、教学内容根据课程目标,教学内容主要包括abcd模型的基本概念、原理和方法。
具体安排如下:1.第一章:abcd模型概述–介绍abcd模型的定义、结构和特点。
–讲解abcd模型的发展历程和应用领域。
2.第二章:abcd模型的原理–讲解abcd模型的基本原理和逻辑。
–分析abcd模型的核心要素和相互关系。
3.第三章:abcd模型的应用–介绍abcd模型在不同领域的应用案例。
–讲解abcd模型在实际问题解决中的运用方法。
4.第四章:abcd模型的实践–引导学生进行abcd模型的实践操作。
–分析abcd模型在实际情境中的效果和反馈。
三、教学方法为了激发学生的学习兴趣和主动性,本课程将采用多种教学方法相结合的方式。
具体方法如下:1.讲授法:教师通过讲解abcd模型的基本概念、原理和应用,引导学生理解和掌握相关知识。
2.案例分析法:教师通过引入实际案例,让学生运用abcd模型进行分析,培养学生的解决问题的能力。
3.小组讨论法:学生分组进行讨论,分享对abcd模型的理解和应用经验,促进学生之间的交流和合作。
4.实验法:学生通过实践操作,亲身体验abcd模型的应用过程,增强对知识的理解和记忆。
四、教学资源为了支持教学内容和教学方法的实施,丰富学生的学习体验,我们将选择和准备以下教学资源:1.教材:选用权威、实用的abcd模型教材,为学生提供系统的学习材料。
数学建模模型案例

数学建模模型案例一、旅行商问题(TSP)旅行商问题是一个典型的数学优化问题,在旅行商问题中,旅行商需要在给定的一系列城市之间找到一条最短路径,使得他能够只经过每个城市一次并最终回到起点城市。
这个问题可以用图论和线性规划等方法来进行建模和求解,可以应用于物流配送、路径规划等领域。
二、股票价格预测模型股票价格预测是金融领域中的一个重要问题。
可以使用时间序列分析、机器学习等方法来建立股票价格预测模型。
模型需要考虑多个因素,如历史股价、经济指标、市场情绪等,以预测未来股票价格的趋势和波动。
三、疫情传播模型疫情传播模型是在流行病学领域中使用的一种数学模型,用于研究疾病在人群中的传播规律。
常见的疫情传播模型有SIR模型、SEIR 模型等,这些模型可以用来预测疫情的传播速度、感染人数以及制定相应的防控策略。
四、能源优化调度模型能源优化调度模型用于优化电力系统、能源系统等中的能源调度问题。
这种模型需要考虑电力需求、能源供应、能源转换效率等因素,以最小化成本或最大化效益,并且满足各种约束条件。
五、机器学习分类模型机器学习分类模型用于将数据集中的样本分为不同的类别。
这种模型可以使用各种机器学习算法,如逻辑回归、决策树、支持向量机等,以根据样本的特征来预测其所属的类别。
六、交通拥堵预测模型交通拥堵预测模型用于预测城市交通网络中的拥堵情况。
这种模型可以使用历史交通数据、天气数据、道路网络数据等进行建模,以预测未来某个时刻某个路段的交通状况,并提供相应的交通管理建议。
七、供应链优化模型供应链优化模型用于优化供应链中的物流和库存管理等问题。
这种模型需要考虑供应商、生产商、分销商之间的关系,以最小化库存成本、运输成本等,并满足客户需求。
八、排课调度模型排课调度模型用于学校或大学的课程安排问题。
这种模型需要考虑教室、教师、学生、课程等因素,以最大化教学效果、减少冲突,并满足各种约束条件。
九、旅行路线规划模型旅行路线规划模型用于帮助旅行者规划旅行路线。
数学建模课表安排

文理学院新校区课表安排问题编号:J4004摘要:每学期的开学初,总有许多老师对新校区的课程安排很有意见,本文选取文理学院某系某专业的师生情况、课程、教室间数为研究对象,以课程与上课时间之间的关系矩阵为目标矩阵,通过用各影响矩阵优化目标矩阵的方法,对新校区各系各专业的课表进行了重排。
在具体模型建立过程中采用了0-1矩阵法,矩阵的乘法等数学方法,建立优化类数学模型来求解有效矩阵,根据有效矩阵初排课表,结合多方面因素建立修正矩阵,对初排课表逐层修改,得出最优排课表,最后通过lingo软件加以实现。
运用我们建立的数学模型,对文理学院数学系08级信息与计算科学专业的课表进行重排,将所得新课表与现有的课表进行比较,显然新排的课表更加合理化、人性化。
根据新课表中每节课对应的相关因素(课程名称、教室、老师、班级)进行分析整合,可衍生出新的安排表(如通过对不同时间段上课老师人数的研究安排校车的接送)。
我们以学校、教师和学生对所排课表满意度作为衡量标准,以文理学院数学系08级信息与计算科学专业的课表为例,可得学校、教师和学生对我们所排课表的满意度主因素分别为校车接送次数、在新区逗留时间、专业课排在早上,计算得评价指标分别为 0.88、1、1,可见对本模型使三方的满意度基本均衡且都超过80%,即做到了三者兼顾的满意最大化。
最后,通过我们建立的模型,我们给教务处排课表问题给处了一些合理的、可行性的建议。
关键字:排课问题 0-1矩阵矩阵的乘法优化目标矩阵满意度一. 问题重述每学期的开学初,总有许多老师对对新校区的课程安排进行抱怨,还有许多老师要求调课,教务处对这一问题很是头疼。
根据文理学院院的实际情况,用数学建模的方法解决这一问题,既要让老师满意,又要让同学和学校满意。
让老师满意,就是要让每位老师在一周前往新校区上课的乘车次数尽可能少,同时还要使每位老师在新校区逗留的时间尽可能少,比如安排尽量少出现像同一天同一位老师上1-2节,7-8节;让同学们满意,可从以下几方面考虑,比如,同一班级同一门课程,至少应隔一天上一次,另外对学生感到比较难学的课程尽量安排在最好的时段;同时为避免下课楼道拥挤,对于上午有四节课的班级,在教室功能允许的情况下,应尽量避免更换教室;让学校满意,就是要节约支出,每周派往新校区的车次尽可能的少。
高中数学问题教学法教学案例分析

高中数学问题教学法教学案例分析问题教学法是一种以问题为核心,以学生为主体,以教师为引导的教学方法。
这种教学方法旨在培养学生的问题解决能力、创新思维和自主学习能力。
在高中数学教学中,问题教学法已经被广泛运用,并取得了良好的效果。
本文将以高中数学问题教学法的教学案例为分析对象,探讨问题教学法的实施策略和应用效果。
创设问题情境是问题教学法的第一步。
教师需要根据教学内容和学生实际情况,创设具有挑战性和趣味性的问题情境,激发学生的求知欲和探究欲望。
例如,在讲解“等差数列”这一概念时,教师可以创设以下问题情境:“如果你是一个银行家,你如何计算每天的利息和累计利息?如果你是一个运动员,你如何计算每天的训练量和累计训练量?”这些问题情境贴近生活,能够引起学生的兴趣,激发他们探究问题的积极性。
在问题解决过程中,教师需要发挥引导作用,帮助学生明确问题解决的目标和方法,引导学生自主解决问题。
同时,教师还需要根据学生的实际情况,采用多种教学方式,如小组合作、讨论交流等,让学生在互动中互相学习、互相启发。
例如,在讲解“不等式”这一概念时,教师可以给出一些实际生活中的不等式问题,让学生分组解决。
学生在小组合作中互相讨论、互相学习,最终得出结论。
总结评价与反思是问题教学法的最后一步。
在问题解决后,教师需要对学生的学习过程和结果进行总结评价,肯定学生的优点和进步,指出存在的问题和不足,并引导学生进行反思。
同时,教师还需要根据学生的学习情况,对教学方法进行反思和改进,提高教学质量。
例如,在讲解“三角函数”这一章时,教师可以引导学生总结评价自己在解决三角函数问题中的表现,反思自己的解题思路和方法是否得当,进而提高自己的解题能力。
下面以一个高中数学“函数单调性”的问题教学法教学案例为例进行分析。
教师首先通过多媒体展示函数图像和表格,让学生观察图像和表格的变化趋势,引导学生思考函数单调性的概念和判断方法。
然后,教师提出以下问题:“如何定义函数单调性?”,“如何判断一个函数的单调性?”,“函数单调性与生活有什么?”等问题,激发学生的探究欲望。
排课问题的数学模型及基于遗传算法的实现

时间表 问题 是一 类多元 受 限 的资源 调度 组合 优化 问题 . 列 车时 刻表 、 班时刻 表 、 市公 路运 营表 、 航 城 医院病 房 调度 表 等均
与此有关 。
c 2
e7
c q
c ^
e5
eJ
l11 时 间 表 问 题 的 相 关 定 义 _. 为 了更好 的描 述 时间表 问题 , 出以下 时间 表 问题 的相关 给 定义 : 定 义 1 时 间 集 ( i eS t : 件 发 生 时 间 构 成 的 集 合 , Tm e) 事 具 有有 序性 、 一 性 , 为 : 唯 记
摘
要 : 时 间表 问题 的 分析 论述 入手 , 从 对排课 问题 进行 合理 抽 象并 建 立 了该 问题 的数 学模 型 。在此 基础 上 . 用遗 利
传 算 法进行 问题 求解 , 出染 色体 编码 方 案和适 应度 函数 , 计 并 实现 了排 课 系统 。结 果表 明 算法 具有合 理 性 和可 给 设
第7 第 1 期 卷 l
20 年 1 08 1月
软 件 导 刊
S fwae Gud o t r ie
Vo _ l No. 1 7 1 NO . o V 2 08
排课 问题 的数 学模型及基 于遗传 算法 的实现
剥、 华 金
( 门理 工 学院 计 算机 科 学与技 术 系, 建 厦 门 3 12 ) 厦 福 6 0 4
作考简介: 孙金华( 7- , 福建三明人, 1 6 )男, 9 硕士, J-学院计算机系高级工程师, 厦门z ̄ ' 研究方向为软件工程、 e开发技术、 wb 数据库技术。
・
6 6・
软 件 导 刊
2o o 8年
教师评价数学建模

教师评价模型数学建模师评价模型一、摘要学校是一个充满着评价人的场所,每时每刻都在对各个人进行评价。
毫不夸张地说评价教师是学校里每个人的“日常功课”。
由于教师职业劳动的特殊性,它是复杂劳动。
不能仅仅用工作量来评价教师的劳动,同时评价教师的人员纷繁复杂,方式多种多样。
评价教师的标准往往束缚着学校的教学质量,教师教学的积极性。
所以教师评价的确定就显的很重要。
新课程强调:评价的功能应从注重甄别与选拔转向激励、反馈与调整;评价内容应从过分注重学业成绩转向注重多方面发展的潜能;评价主体应从单一转向多元。
那么如何公正、客观地评价教师的同时,有效地保护教师的教学积极性和帮助提高学校的办学水平呢?此模型的建立改变了以往同类模型的多种弊端,从另一角度更加合理地分析、评价,就是为了更公平,公正地对教师做出合理的评价,从而促进学生发展和教师提高。
本模型主要用了模糊数学模型和对各项评价付权重的方法进行建模分析。
从(1)教师对自己的评价,学生对教师的评价;由专家组对教师的评价的角度出发,(2)(3)通过量化,加权,得出结果。
然后确定三方面的比重来评价教师。
同时通过确定教师自评与他人评价的比值范围,而确定这次评价是否有效。
在各个方面采用的数学模型如下:1、教师对自己的评价:教师对自己的满意度,既体现教师的主人翁意识也保护教师的教学积极性。
(Q表示教师自评的得分P i 表示教师对自己各项符合度而打的分数Di表示对教师自评要求各项所加给的权重)2、学生对教师的评价:表明以学生为主体,体现了模型的客观性,公平、公开的原则。
3、由专家组成通过听课对教师的评价:表明专家对教师指导性,帮助教师提高教学水平。
体现了评价的权威性,真实性。
同时也是作为教师提拔的一个方面。
模型的缺点和推广优点:(1)采用模糊数学建模,充分考虑许多因素。
评价尽量客观,真实,全面(2)采用加权,分等。
使教师之间互相的竞争,同时也保护了教师的积极性(3)模型分为三个方面进行建模,以教师自我评价的主要方面,综合评议。
可行性分析数学模型

可行性分析数学模型可行性分析数学模型是一种用于评估项目、计划或决策的数学模型。
它通过对相关数据进行分析和运算,帮助我们在不同的情境中评估可行性,并为决策提供依据。
在进行可行性分析数学模型时,我们需要明确问题的目标,收集数据,选择适当的数学模型,并进行参数估计和推断。
以下是可行性分析数学模型的基本步骤和常用的数学方法。
第一步:明确问题目标在进行可行性分析数学模型之前,我们首先需要明确问题的目标。
这包括确定项目的目标、范围和约束条件,以便为后续的数学建模提供指导。
第二步:收集数据在进行可行性分析数学模型时,我们需要收集相关的数据来支持决策。
这包括历史数据、市场调研数据、调查问卷数据等。
数据的收集需要合理的样本设计和调查方法,以确保数据的准确性和代表性。
第三步:选择适当的数学模型在选择数学模型时,我们需要考虑问题的性质、数据的特点以及可行性分析的目标。
常见的数学模型包括线性规划、整数规划、多目标规划、动态规划、排队论、模拟等。
对于不同的问题,我们可以选择不同的数学方法来建立模型。
第四步:参数估计和推断在建立数学模型后,我们需要进行参数估计和推断以获得模型的结果。
这包括对模型中的参数进行估计,通过计算和统计分析得到模型的输出和决策。
第五步:结果分析和决策在进行可行性分析数学模型后,我们需要对结果进行分析和解释。
通过对结果的分析,我们可以评估项目的可行性,并为决策提供依据。
在做出决策时,我们需要综合考虑结果的经济、社会和环境影响,并在各种约束条件下做出最优决策。
可行性分析数学模型的应用非常广泛。
例如,在投资项目的可行性分析中,我们可以使用投资回报率模型、净现值模型和内部收益率模型来评估项目的可行性。
在生产计划的可行性分析中,我们可以使用线性规划模型和动态规划模型来确定最优的生产计划。
在市场营销策略的可行性分析中,我们可以使用市场需求预测模型和市场份额模型来评估市场潜力和制定市场策略。
总之,可行性分析数学模型是一种重要的决策分析工具。
排课数学模型

学校排课的优化模型摘要排课是学校的一项常规工作,也是学校教育教学管理过程中不可或缺的重要环节。
在学校教务管理工作中,课程的编排是一项十分复杂、棘手的工作。
它不仅关系到学校教学工作的正常运行、教学效果、学生发展及教学资源的整合和科学高效的利用,而且关系到教师的身心健康和教育教学质量。
排课需要考虑时间、课程、教学区域、教室、班级、教师等多种因素。
本文就此类问题进行讨论,并根据题目要求深入分析后,将该问题归结为优化问题,确定了“将教师、课程、教室三个因素优化组合,并并分配到课表上的不同时间段上,形成最终课表”的解决方案。
首先建立各因素间关联关系,根据各因素间约束关系的不同,将多重约束条件为硬约束(强制要求)和软约束,写出各因素间的目标函数。
其次,为课表上四个时间段随机分配课表,以0-1规划方法分别将教师、教室分配到课表上的不同时间段上。
最终,形成了一份尽可能多的满足课程、教师、教室的要求的课表。
本文采用0-1规划法、逐级优化法,并考虑多重约束条件,形成了一个良好的排课模型。
并根据题目给出的数据,通过计算机编程,进行模型验证,求出了所需课表。
且在方案合理性分析中用计算机模拟的方法分析了教室的种类对排课结果的影响,最后给出了教师、教室、课程的配置建议。
一.问题的重述在学校的教务管理工作中,课程表的编排是一项十分复杂、棘手的工作。
排课需要考虑时间、课程、教学区域、教室、班级、教师等多种因素。
经优化的排课,可以在任意一时间段内,教师不冲突,授课不冲突,授课的班级不冲突,教室占用不冲突,且综合衡量全校课表在宏观上是合理的。
如何利用有限的师资力量和有限的教学资源,排出一个合理的课程安排结果,对稳定教学秩序、提高教学质量有着积极意义。
某高校现有37个自然班,编号为1..N;教师共有79名,编号为1..M;有教室50间,编号为1..R;有课程数54.课表编排规则:1.同一自然班不在同一时候参加不同教学班的授课;2. 同一教师不能同时参加不同教学班的授课;3. 一个教室不能同时开两门课程;4. 满足课程的教室类型需求;5. 学生人数不能超过教室容量;6. 同一门课程尽量不在同一天开课两次及以上;7. 一个自然班的课程尽量分布均匀到每天;8. 教师上课尽量集中,同时一天尽量不要超过6节,最好4节10. 晚上尽量不排课。
数学建模课程设计选题背景

数学建模课程设计选题背景一、课程目标知识目标:使学生掌握数学建模的基本概念和原理,理解数学模型在解决实际问题中的应用价值;学会运用所学的数学知识和方法,构建简单的数学模型,解决实际情境中的问题。
技能目标:培养学生运用数学语言进行表达、交流的能力;提高学生运用数学工具(如计算器、计算机软件等)进行数据分析和模型构建的能力;培养学生团队协作、问题解决和创新思维的能力。
情感态度价值观目标:激发学生对数学学科的兴趣和热情,增强学生学习数学的自信心;培养学生严谨、细致、勇于探究的学习态度;引导学生认识到数学在现实生活中的广泛应用和价值,增强学生的数学应用意识。
课程性质:本课程为选修课,旨在帮助学生将所学的数学知识运用到实际问题中,提高学生的数学素养和综合能力。
学生特点:学生为八年级学生,已具备一定的数学基础和逻辑思维能力,对新鲜事物充满好奇,但部分学生对数学学习兴趣不足,需要激发和引导。
教学要求:结合学生特点和课程性质,课程目标应具有趣味性、实用性和挑战性。
在教学过程中,注重启发式教学,引导学生主动探究和解决问题,提高学生的数学建模能力和综合素质。
课程目标分解为以下具体学习成果:1. 学生能够理解并描述数学建模的基本概念和原理;2. 学生能够运用所学知识,构建简单的数学模型解决实际问题;3. 学生能够运用数学语言和工具进行数据分析和模型构建;4. 学生能够在团队协作中发挥个人优势,共同解决问题;5. 学生能够体验数学建模的乐趣,增强学习数学的自信心和兴趣。
二、教学内容本课程教学内容主要包括以下几部分:1. 数学建模基本概念:介绍数学建模的定义、意义和分类,使学生了解数学建模的广泛应用。
2. 建模方法与步骤:讲解数学建模的基本方法、步骤和技巧,如问题分析、模型假设、模型构建、模型求解和模型检验等。
3. 实际问题案例:选取与学生生活密切相关的实际问题,如人口增长、环境污染、交通规划等,引导学生运用所学知识进行数学建模。
课表的多指标数学模型及解决方法

2004年3月内蒙古大学学报(自然科学版)M ar.2004第35卷第2期A cta Scientiarum N aturalium U niversitatis N ei M ongo l V o l.35N o.2 文章编号:1000-1638(2004)022*******课表的多指标数学模型及解决方法Ξ张春梅1,行 飞1,梁治安2(1.内蒙古大学理工学院,呼和浩特010021;2.上海财经大学应用数学系,上海200433)摘要:课程表问题又称时间表问题(ti m etable p roblem),是一个多指标的优化决策问题,也是组合规划中的典型问题.对已有的时间表问题进行探讨,并研究其数学模型及解决方法.关键词:时间表问题;遗传算法;多指标决策中图分类号:O221.7 文献标识码:A1 排课问题的提出 一所学校为了保证其正常的高水平教学质量,必须制定一套严密、规范的教学计划,并严格执行.课程安排在学校教学计划中又处于核心地位.合理准确的课程表对提高教学水平至关重要.2 排课问题的实质 课程表问题又称时间表问题.课表编排是一个多指标的优化决策问题,是组合规划中的典型问题.课程表的编排就是解决对时间和空间资源争夺而引起的冲突.70年代中期,S.Eveo等人论证了课表问题是N P完全类问题〔1〕,之后很多人尝试采用各种方法对此问题求解.但由于课表问题所涉及的信息较多,并且求课表问题最佳解的时间复杂性是课表规模的指数级,所以对于有一定规模的课表问题,一般采用求较佳解的算法.3 课表的数学模型及约束条件3.1 排课问题的形式化描述在课表编排问题中涉及到班级、教师、时间、课程、教室等五个相互制约的因素.分别用以下集合表示:课程集合 s={s1,s2,…,s n};时间集合 t={t1,t2,…,t n3};班级集合 c={c1,c2,…,c n1};教室集合 r={r1,r2,…,r n4};教师集合 p={p1,p2,…,p n2}时间和教室的笛卡尔积为:N=T×R={(t1,r1),(t1,r2),…(t n3,r n4)},N中的元素称为时间—教室对.课表问题的求解过程就是对任何s i=(i=1,…,n)∈S寻找一个合适的老师P j(j=1,2,…,n2)∈P和合适的时间—教室对(t1,r m)∈N(l=…n3,m=1,…n4),在安排时不能发生冲突,同时尽量满足经验常识.3.2 课表问题的冲突情况:1)同一时间,一个教师同时上一门以上课程;2)同一时间,一个班级同时上一门以上课程;3)同一时间,一个教室同时上一门以上课程;4)选课人数大于当前指定的教室的最大容量.3.3 须满足一些经验常识1)一门课在一周内分散安排,提供可引导性学习环境;2)保留一些特殊的时间,如户外活动;3)一周多学时的同一门课应尽量安排在一个教室(方便教师及学生);4)尽量安排在好的教学时间点(如上Ξ收稿日期:2003201220基金项目:国家自然科学基金资助项目(10261005);内蒙古大学青年科学基金资助项目(ND0204)作者简介:张春梅(1970~),女,内蒙古乌盟人,内蒙古大学理工学院硕士,讲师.041内蒙古大学学报(自然科学版)2004年午比下午好);5)安排到教室中的人数应尽量和教室的大小吻合,一方面资源合理利用,另外教学效果也好,因此一个好的时间表就是一个无冲突且能更多地满足经验常识的安排.4 已有的排课问题的解决方法4.1 基于人工智能原理李明〔2〕给出一个实用的大学课表编排模型,问题模型定义如下:定义1 排课表问题中基本时间表计划问题:设“可安排教学时”集H,“课程”集L( L =n L),“学生”集S( S =n S)组成小组{S i}(i=1,2,…,n l)(S=S1∪S2∪…∪S nl,S i∩S j不一定为空集),“教师”集T,对于每个学生S ij∈S i(教师t∈T),有一个“空闲时间”集A(s ij)ΑH(A(t)ΑH);对于每门课程l∈L,有一个“可安排时间”集A(l)ΑH,并且对于每一三元组(s i,t,l)∈{S i}×T×L,有一个“要求教学时间”数目R(s i,t,l)∈Z+0 (其中Z+0表示非负整数集),求完成所有课程的时间表,即求函数f:({s i}×T×L×H)→{0,1},(其中f(s i,t,l,h)=1表示学生组s i教师t在时间h内上课程l),使得:(1)仅当h∈(∩A(s ij))∩A(t)∩A(l)时,f(s i,t,l,h)=1;(2)对于每个h∈H和s i,t∈T,至多有一个l∈L满足f(s i,t,l,h)=1;(3)对于每个h∈H和s i,lt∈L,至多有一个t∈T满足f(s i,t, l,h)=1;(4)对于每个h∈H和t∈T,l∈L,至多有一个s i满足f(s i,t,l,h)=1;(5)对于每个三元组(s i,t,l)∈{S i}×T×L,恰好有R(s i,t,l)个h∈H满足f(s i,t,l,h)=1定义2 最小时间约束条件集:称定义1中条件(1)~(5)为排课表问题须满足的最小时间约束条件集.定义3 (教室)资源分配问题:设有“教室”集C,每个教室c∈C均满足一定条件A(c),且时间表已经安排好.要求:在一定的约束条件下为每个h∈H且满足f(s i,t,l,h)=1的所有三元组(s i,t,l)∈{S i}×T×L分配教室C.算法主要思想是通过引入一个规则库(知识库),来有效地处理各种复杂约束条件,并在这个规则库的指导下,搜索满足条件的时间集.由于搜索是在规则库的指导下进行的,所以称这个算法是基于智能的.安排好时间表后,进行教室资源的分配.洪力奋〔3〕等用人工智能的原理及专家系统知识构造出了类似的数学模型及有关编排算法,对排课的死锁问题进行了处理.主要设计了两个推理机,一个推理机是根据课程模式要求,根据既定规则找出合适的时间与教室.第二个推理机解决死锁问题而设置(所谓死锁即规则遍历完,仍存在时间冲突或教室冲突).4.2 利用集合的概念及其相关运算董艳云等人〔4~5〕在分析排课所遵循的基本原则和模糊性原则的基础上,定义了课元之间关于教师的相关关系和关于自然班的相关关系.提出以课元相关运算和候选时空片计算为核心的计算机排课算法,其算法描述如下:令C cou表示排课课元的集合,令T T EA,C CL A,R ROO和S SL I分别表示参与排课的教师、班级、教室和时间片的集合.此外,用C T Y={0,1,2,…}表示课元的课程类型集合,其中类型0的课元为必修课或必选课,对同一自然班,这类课的排课时间不允许与其它课冲突,其它类型的选修课按允许时间冲突的课元子集归类.1)课元的相关关系计算.假定用F T:C COU→T T EA描述课元任课教师集合,用F C:C COU→C CL A描述课元的自然班集合,则课元的相关关系定义如下:定义 课元关于教师的相关关系R T:C COU→C COU为{v} F T(u)∩F T(v)≠ (1)R T(u)=∪v∈C COU 课元关于自然班的相关关系R C:C COU→C COU为{v} F C(u)∩F C(v)≠ (2)R C(u)=∪v∈C COU式(1)和(2)中:u∈C COU,R T(u)的物理意义表示课元u的任课教师所担任的所有课程;R C(u)的物理意义表示课元u的上课班所上的所有课程.2)候选时空片计算.假定用F CT:C COU→C T Y描述课元的课程类型集合,用F CR:C COU→R T Y描述课元可选的教室类型集合,用F CS :C COU →C S I 描述课元所需的最小教室容量,用F R T :R ROO →R T Y 描述教室的类型,用F R S :R COU →R S I 描述教室容量,用F S :C COU →S SL I 表示课元已分配到的时间片集合,用F S R :C COU →S SL I ×R ROO 表示课元已分配到的时空片的集合.由排课的基本原则(1)和(2)可知,课元u ∈C COU 可选用的时间片取决于它的相关课元已分配到的时间片及课程类型,即A S (u )=S SL I -∪v ∈R T (u )F S (v )-∪v ∈R C (u )F S (v ) F CT (u )=0∨F CT (u )≠F CT (v )(3) 由排课的基本原则(3)可知,课元u ∈C COU 可选用的教室A R (u )取决于该课元所要求的教室类型和容量,即 A R (u )=∪r ∈R TRO{r } F R T (r )∈F CR (u )∧F CS c (u )ΦF RS (r )(4) 所以,课元u ∈C COU 可选用的时空片(候选时空片)A R (u )为A S R (u )=∪s ∈A s (u )r ∈A R (u )(s ,r )-∪v ∈C COU F S R (v )(5) 本算法最后通过关系数据库实现.课元数据库T EA CH .DB F ,班级数据库CLA SS .DB F ,教室数据库ROOM .DB F .按照上述排课算法及软件实现方法,已成功地开发出高校计算机排课软件.文献〔5〕提出的算法借鉴了资源管理的思想,使用以集合为元素的矩阵建立了问题的数学模型.时间模型定义如下:排课一般以一个学期作为一个独立的阶段,假定一个学期由Z 周组成(例如Z =18),每周可以使用的授课时间为S 个单位时间(如S =24),则一学期可以使用的总授课时间为N =S ×Z .这里S 和Z 可以作为系统参数.整个有效的时间域可以定义为集合K ={1,2,…,n -1,n },教师、班级和教室被占用的任何时间是K 的一个子集.算法的实现是以集合运算为基础的.该算法是动态、次优的,但时间和空间复杂性几乎和问题规模成正比.4.3 应用专家系统〔6〕文中将传统的数据库和专家系统结合起来,充分发挥各自的长处,达到优势互补的目的.系统将拥有的几方面的知识:教室、班级、课程、教师、时间等详细资料存入数据库中,将排课中的一些限制条件放入规则库中,为了便于规则的推理和编辑,所有的规则采用统一格式:对象 属性 属性值 要求 置信度对象有教师、班级、教室;教师的属性有编号、名称、职称,班级的属性有编号、年级、系别,教室的属性有编号、名称;要求包括时间或教室要求两种;置信度是一个0~1的数,等于1表示此规则是必须满足,大于0.5表示最好满足,等于0表示一定不能,小于0.5表示最好不能这样.专家系统使用排课专家的大量排课知识策略(这里的策略指把求解过程看成对一种与或图的搜索),通过查询数据库和进行规则推理,灵活的编排出符合要求的课表.4.4 分批与或图与匈牙利算法结合从前面课表的形式化描述中可看到,课表问题可看作匹配问题.其数学模型如下:把课表看成是有n 门课,怎样分配到n 个时间2教室对中的问题.需要系数矩阵,其元素c ij >0(i ,j =1,2,…,n ),表示指派第i 门课到第j 个时间2教室对时的期望值,该期望值反映教师、学生和学校根据教育的特点对该时间上某门课的观点;解题时还需引入变量x ij ,其取值只能是1或0,即x ij =1 (当指派第i 门课到第j 时间2教室对时)x ij =0 (当不指派第i 门课到第j 时间2教室对时)问题要求极小化时,数学模型为m in Z =6n i =16n j =1c ij x ij 约束条件为6n i =1x ij =1 (j =1,2,…,n );6n j =1x ij =1 (i =1,2,…,n );x ij =1或0(i ,j =1,2,…,n ) 该问题较好的解法是用匈牙利算法.该算法的主要思想是基于下面的定理:如果系数矩阵[c ij ]的每一行元素中分别减去(或加上)一个常数u i (称为该行的位势),从每一列元素中分别减去(或加上)一个常数v j (称为该列的位势),于是得到新的矩阵[b ij ],其中,第i 行第j 列141第2期张春梅等 课表的多指标数学模型及解决方法241内蒙古大学学报(自然科学版)2004年元素为b ij=c ij-u i-v j,则结果[b ij]的最优解等价于矩阵[c ij]的最优解.甘肃工业大学的魏平等人〔7〕采用分批与或图和分批优化的匈牙利算法相给合的方法实现.如把上课时间、场地、设备和连续上课时间超过两节的具有特殊要求的课程分为一批,采用搜索算法,且优先排课,然后对余下的课采用分批优化匈牙利算法和分批与或图搜索法相结合进行排课,一批中限制条件较多时采用匈牙利算法,其他采用分批与或图算法,从而提高编排效率.4.5 分组优化决策算法和定额匹配算法在课表的编排问题中,课程、时间、教室是三个相互制约的因素,1)课程定义:课程是由开课教学单位按教学任务书的要求指派讲员构成的一个教学班,课程的记录类型由下面字段定义:〈课程〉∷=〈课号〉〈课名〉〈讲员〉〈周学时〉〈人数〉〈班集合〉〈排课要求〉设L={l l-课程},L表示待排的课程任务集合.Πl1,l2∈L,若(l1〈讲员〉)=(l2〈讲员〉)或(〈班集合〉)∩(l2〈班集合〉)≠ ,称课程l1与l2相关,记作l1・l2=1,否则称无关,记作l1・l2=0.相关课程将争夺周课表上的时间.2)时间、时间模式定义 设T={t t—周课表上的时间}表示周课表上的时间集合,且若t={Ρ1,Ρ2,…,Ρn},叫做个数为n的时间组.若t中的时间个数n及Ρi在表上的时间间隔分布符合某种上课的学时机制,则称t为周学时为n的时间模板(或时间模式).下文中用t(l)表示课程的一个时间模板.若l1・l2=1,且t(l1)∩t(k2)≠ ,则称两个相关课程的时间模板冲突,记作t(l1)・t(l2)=1,否则,为不冲突,记作t(l1)・t(l2)=0.不相关课程的时间模板恒为t(l1)・t(l2)=0.3)教室、“时间教室”定义:教室的记录类型由下面字段定义:〈教室〉∷=〈教室名〉〈房间号〉〈人数〉〈功能〉.假定周课表上任何一个时间均有k个教室可供选用.即ΠΡi∈T则时间Ρi上的k个教室为r(Ρi) ={r1(Ρi),r2(Ρi),r3(Ρi),…,r k(Ρi)},用r j(Ρi)表示时间Ρi的第j个教室,通常,排课时总是先确定课程l的时间模板,再选教室,课程l的“时间教室”记为r(t(l)),其意义为:r(t(l))={r j(Ρi) Ρi∈t(l),i=1,2,…,n;n=(l〈周学时〉);r j(Ρi)∈r(Ρi)}其中t(l)为课程的合适的时间模板,并且每个r j(Ρi)均是在时间Ρi满足课程l的人数(区间)要求的某个教室.除非时间相连,且该课要求占用同一教室,否则时间教室中的r j(Ρi)与r j+1(Ρi+1)不必相同.l1,l2∈L,若t(l1)与t(l2)有相同的时间,且在这相同时间r(t(l1))与r(t(l2))存在相同的教室,则称课程的“时间教室”选择冲突,记作:r(t(l1))・r(t(l2))=1,否则为不冲突,记为r(t(l1))・r(t(l2))=0.无论l1,l2是否相关,均必须满足r(t(l1))・r(t(l2))=0.4)课程安排、课表定义:Πl∈L,选择l的不冲突时间模板(在课程相关的意义下时间模板不冲突)和分派不冲突“时间教室”,称为构造课程l的一个课表安排,记作l(l),l(l)也是记录类型:l(l)∷=〈l〉〈t(l)〉〈r(t(l))〉课程安排集合用D={l l=l(l),l∈L}表示.l1,l2∈D,l1=l(l1),l2=l(l2),在课程l1、l2相关意义下,保证t(l1)・t(l2)=0,并且还满足r(t(l1))・r(t(l2))=0,则称D为一个合适的排课集合.即D中的课程安排,两两教室必须不冲突;若课程两两相关,D中的课程安排还必须两两时间不冲突.王祜民等人〔8~9〕将课程集合中按优等级逐次分组,每组用优化决策方法排课,这是一种在启发式准则指导下,逐次的、向前的构造性排课过程.通过分组优化决策算法,先难后易逐组编排课表.那些学时多,班数多的大合班课是最难编排的课程,要先将这些课组编排到课表中去,形成称为D e的阶段课表.而定额匹配算法是解决某些特殊课程(组)的自动编排问题.所谓的特殊课,如体育课、按水平分班的外语课等,该种课程的班集合中的班数目大,因而排课难度与大合班课类似,但班级可任意组合在一起,排课时可动态挑选班组合,这使排课有更多的选择机会.4.6 作为满意约束问题处理把排课问题当作满意约束问题,对此已有多种解决方法,如图着色〔10〕,在图着色的示例中计算时间相当长,因为一旦指定的值失败就需做大量的反跟踪,原因是没有办法避开不可行解.4.7 启发式算法用启发式算法〔11〕如禁忌搜索〔12〕、模拟类似于自然界金属的退火过程的模拟退火〔13〕、类似于自然界种群遗传的遗传算法〔14,15〕;在算法的具体实现过程中,所采用的方法有用事先做好的特殊操作去产生一个可行解;也有的在适应度函数中并入惩罚;或采用修复程序过滤不可行基因;也可采取将问题中的一些约束条件消除或弱化的方法重新对问题给出表述等几种.A .co lo rn l 在高中课表的启发式算法中以特定的高中课表为例给出了模拟退火(SA )、禁忌搜索(T S )、遗传算法(GA )三种算法的比较结果〔16〕.他认为T S 是最好的算法,GA 产生的解比SA 好.但是最终用户相对于SA 和T S 更易接收GA .4.8 遗传算法意大利的A .co lo rn i 等人用遗传算法求解高中课表的安排问题〔16〕.文中将每位老师的活动作为基因,这些活动包括上课、休息、写论文等,分别用字符0、1…9、a 、b 、…p 表示.意大利高中每周上课30h ,以时间点为列,所有老师为行组成二维染色体,适应度函数定义为最小化总代价,其中组织代价指临时教学岗位没有安排老师,个人代价指不想休息时休息,教训代价指一周的几天内同一门课集中在一起;姚新的教室安排问题,主要优化的是教室的合理利用〔15〕;另日本的Sigeru .O 采用遗传算法中加入控制约束的方法解决大学课表安排问题〔14〕;用自适应的遗传算法求解大学课表安排问题〔17〕,根据大学课程安排的特点,将课程分为必修课P 、选修课Q 两类.并对两类课分别给出其染色体编码和适应度函数.在P 类课中适应度函数考虑了两点:第一点是要使所安排的课尽可能占用好的时间点,所以我们对一天的四个时段分别给出了期望值:8:00----12:00为12;10:00----12:00为8;2:00----4:00为4;4:00----6:00为1.在这种定义下我们所涉及的20个时间点的期望值如表1所示:表1 时间的期望值Table 1 preferences of ti m eslot时间点T 1T 2T 3T 4T 5T 6T 7T 8T 9T 10T 11T 12T 13T 14......T 20期望值128411284112841128 (1) 第二点如果某一门课多于1个时间片(4学时或多于4学时),或一个教师带两门以上的课,都希望能在时间上分散安排,这样从学生接收知识和教师的教学效果上都是很好的.我们用编号相同的两课的时间差来描述这种离散度并给出相应的期望值.如表3所示:表2 课程离散度期望值Table 2 preferences of i n terval degree of courese两课时间差1,192,3,17,184,5,15,166,7,13,148,9,10,11,12期望值0241016 所以定义适应度函数f (g )=6ni =1(g (t (S i ))+h (S i ))(g ),其中g (t (s i ))表示课程所占时间片的期望值,h (s i )表示课程离散度,f 即为所有课程时间期望值与课程离散度之和.在Q 类课中主要考虑的是让教室有效合理地得到利用.因此我们的适应度函数定义为:g (x )=A ×6n i =11l (r (S i ))-Q (S i ) +1(x ) 其中Q (s i )表示课程s i 的选课人数,表示课程s i 所在教室的大小.该式分母中加1是为了避免房间大小与选课人数正好相等的情况出现,从而产生O 分母.杂交概率和变异概率的选取在相当大程度上影响算法的收敛速度和近优解的质量,为加快GA 的搜索效率和有效地防止陷于局部最优解,本文采用自适应的杂交概P c 和变异概率P c =k 1sin (Π2×f m ax -f ′c f m ax -f avg ) f ′c Εf avg k 2 f ′c <f avgPm =k 3sin (Π2×f m ax -f m f m ax -f avg ) f m Εf avg k 4 f m <f avg 其中:0<k 1、k 2、k 3、k 4≤1是群体的最大适应度函数值,f avg 是群体的平均适应度函数值,f ′c 是进341第2期张春梅等 课表的多指标数学模型及解决方法441内蒙古大学学报(自然科学版)2004年行杂交的两个染色体串中适应度函数值较大者,f m是变异串的适应度函数值.由自适应的杂交概率和变异概率的定义可以看出,定义的形式满足:0ΦP cΦ1;0ΦP mΦ1,另外,当f′c=f m ax时,P c=0;f m=f m ax时,Pm=0.这表明当前代的最优个体不经过杂交操作和变异操作而直接进入到下一代.5 结束语 该文给出了排课问题的数学模型及解决方法,其思想和方法对解决类似的优化组合问题也有一定的借鉴作用.参考文献:[1] Garey M R,Johnson D S.Co m p u te and Intractability:A Gu id e to the theory of N P co m p leteness[M].San fran2cisco:W.H,F reem an Co.,1979.[2] 李明.一个基于智能化搜索的排课表演算法及其client server实现[J].现代计算机,1997,59:21~22.[3] 洪力奋.基于人工智能原理的大学课表编排模型[J].合肥工业大学学报(自然科学版),1999,22(4),101~104.[4] 陈洁.学校教务部门排课问题的数学模型及算法[J].管理信息系统,1999,3:53~56.[5] 董艳云,钱晓群,张宇舒.基于课元相关运算的高校排课算法[J].甘肃交通大学学报,1998,33(6):670~673.[6] 周建新,王科俊等.课表编排专家系统[J].计算机应用,2000,20(5):76~78.[7] 魏平,熊伟清.计算机辅助课表编排技术的研究[J].甘肃工业大学学报,1997,23(4):76~81.[8] 王祜民,赵致格.排课表问题中的分组优化决策算法[J].控制与决策,1999,14(2):109~114.[9] 王祜民,赵致格.时间表问题中的定额匹配算法[J].清华大学学报,1998,38(6):8~11.[10] W erra D de.A n Introducti on to T i m etabling[J].E u r.J.Op nl.R cs.S oc,1985,48(11):1178~1190.[11] W righ t M.Schoo l T i m etabling using H euristic Search[J].J.Op nl.R cs.S oc,1996,47(3):347~357.[12] H ertz A.F inding a feasible course schedule using tabu search[J].D iscrete A pp lied M athe m atics,1992,35(2):250~270.[13] A bram son A.Constructing schoo l ti m etables using si m ulated annealing:Sequential and Parallel A lgo rithm s[J].M anag e m ent S cience,1991,37(1):98~113.[14] Safaai D,Sigeru O.Inco rpo rating constraint p ropagati on in genetic algo rithm fo r university ti m etable p lanning[J].E ng ineering A pp lications of A rtif icial Intellig ence,1999,35(2):241~253.[15] L uan F,Yao X.So lving real2w o rld lecture room assignm ent p roblem s by genetic algo rithm s,Comp lexity Inter2nati onal[J].A n E lectronic J ou rnal of Co m p lex S y ste m R esearch,1996,3:87~90.[16] Co lo rni A,M arco.do rigo,M aniezzo V.M etaheuristics fo r h igh schoo l ti m etabling[J].Co m p u tational Op ti2m iz ation and A pp lications,1998,(9):275~298.[17] 张春梅,行飞.用自适应的遗传算求解大学课表安排问题[J].内蒙古大学学报(自然科学版),2002,33(4):459~464.(责任编委 孙 炯) T he M u lti2target M athem atical M odeland So lu ti on of T i m etab le P rob lemZHAN G Chun2m ei1,X I N G Fei1,L I AN G Zh i2an2(1.Colleg e of S ciences and T echnology,N ei M ong ol U n iversity,H ohhot010021,P R C;2.D ep a rt m en t of A pp lied M a the m a tics,S hang ha i F inance and E cono m ics U n iversity,S hang ha i200433,P R C) Abstract:T i m etab le p rob lem is a m u lti2target op ti m ized decisi on p rob lem and typ ical p rob lem in adm in istrati on and p lann ing.Som e ex isting m athem atical m odels and so lu ti on s of the ti m etab le p rob lem are discu ssed.Key words:ti m etab le p rob lem;genetic algo rithm s;m u lti2target decisi on。
数学建模:课程安排优化问题

2012年数学建模竞赛参赛队员题目 A题:课程安排优化问题关键词排课问题,优化矩阵,有效矩阵摘要每学期的开学初,总有许多老师对阳光校区的课程安排很有意见,本文选取武汉纺织大学机械设计系的师生情况、课程、教室间数为研究对象,以课程与上课时间之间的关系矩阵为目标矩阵,通过用各影响矩阵优化目标矩阵的方法,对机械设计系的课表进行了重排。
在具体模型建立过程中采用了0-1矩阵法,矩阵的乘法等数学方法,建立优化类数学模型来求解有效矩阵,根据有效矩阵初排课表,结合多方面因素建立修正矩阵,对初排课表逐层修改,得出最优排课表。
运用我们建立的数学模型,对武汉纺织大学机械设计系的课表进行重排,将所得新课表与现有的课表进行比较,显然新排的课表更加合理化、人性化。
根据新课表中每节课对应的相关因素(课程名称、教室、老师、班级)进行分析整合,可衍生出新的安排表(如通过对不同时间段上课老师人数的研究安排校车的接送)。
我们以学校、教师和学生对所排课表满意度作为衡量标准,以···大学机械设计系的课表为例,可得学校、教师和学生对我们所排课表的满意度主因素分别为校车接送次数、在阳光校区逗留时间、专业课排在早上,可见对本模型使三方的满意度基本均衡且都超过80%,即做到了三者兼顾的满意最大化。
最后,根据我们建立的模型,分析了模型的优缺点。
一、问题重述我校现有三个校区,有在校学生近25000人,其中阳光校区在校学生人数最多。
阳光校区现有四栋教学楼,分别是3号、6号、7号和8号楼,四栋教学楼之间有较大的距离,如从3号楼到8号楼步行需要约10分钟。
我校的学生作息时间安排中,一天共有13节课,划分为5个时间段,分别是1-2节、3-5节、6-8节、9-10节、11-13节。
按学校的规定同一门课程一天中最多可集中上3节课,一周不得超过6节。
同一年级的相同课程可以合班上课,合班一般由各个院系或公共课教学部门给出具体安排。
每学期临近结束时,学校教务处根据各个专业的培养计划向各院系下达下一学期的教学任务,由各个专业将教学任务分解到具体的任课教师,然后由教务处排出下一学期的课程表。
排课问题分析

排课问题分析摘要:本题要求我们对多约束条件的典型组合进行分析,求解,并作最优化处理。
基于此种原因,我们先对各个元素间的冲突做预处理,进行约束条件的规划,再通过matlab软件将教室、教师、课程和时间间的约束条件统一化,构成R-T-C表(详见附表),再将各个元素进行优先级的计算,从而根据排课的优化模型,求出最优解。
经过对所给的表格,数据的深入分析,我们可以得知,教师明显缺少,比如课程学时要求有160个课时,然而教师能上的课时仅有116个课时,所以开始排课时,不考虑教师,向教师中安排课程。
?由于同类课程最好不要放在一起,同时根据老师的需求和教室的开放时间进行分配,经过与我们实际的课表的排课情况的分析,比如隔一天排同一课,课程类别不同的课程不在同一时间上课,我们可以大致的排出一个按教室上课的表,即R-T-C表。
通过对R-T-C表的分析,发现有很多课没老师上和老师没课上的情况,我们就对其进行相应的,合理的调整。
最后发现还是老师要外聘。
将外聘14名老师去上相应没人上的科目,具体情况见附表。
最后,我们得到了一张相对优化的,以教室为准的课表(详见附表),从而解决问题(1)的要求。
对于我们课表的安排,发现再没对晚自习有其他条件约束是不会对所排的课表有所影响。
关键词:排课问题组合规划多目标函数数据量化优先级一、问题重述对于有课程40门,教师共有25名,教室18间的条件下合理的安排课程表,而课程、教师、教室的具体属性及要求详见附表(表1,表2,表3)对于课表德编排,题目有如下规则:每周以5天为单位进行编排;每天最多只能编排8节课(上午4节,下午4节),特殊情况下可以编排10节课(晚上2节),每门课程以2节课为单位进行编排,同类课程尽可能不安排在同一时间。
要求所要解决的问题:1.请你结合实际情况建立数学模型,通过编程计算,给出较为合理的课表编排方案,分析你所给出的方案的合理性。
2.如果不准晚上排课,排课结果是否有所变化,如何变化?3.对教师聘用,教室配置给出合理化建议。
数学模型课程设计捕鱼

数学模型课程设计捕鱼一、教学目标本节课的教学目标是让学生掌握数学模型中的捕鱼问题,包括问题的背景、模型的建立和求解方法。
具体目标如下:1.知识目标:(1)了解捕鱼问题的背景和意义;(2)掌握捕鱼问题的数学模型及其求解方法;(3)理解数学模型在实际问题中的应用。
2.技能目标:(1)能够运用捕鱼问题的模型解决类似问题;(2)培养学生的逻辑思维能力和数学表达能力;(3)提高学生运用数学知识解决实际问题的能力。
3.情感态度价值观目标:(1)培养学生对数学模型的兴趣和好奇心;(2)培养学生团队协作和交流分享的良好品质;(3)引导学生认识数学模型在生活中的重要作用,培养学生的责任感和使命感。
二、教学内容本节课的教学内容主要包括以下三个方面:1.捕鱼问题的背景和意义:介绍捕鱼问题的实际背景,让学生了解数学模型在解决实际问题中的应用价值。
2.捕鱼问题的数学模型:引导学生学习捕鱼问题的数学模型,包括模型的建立、求解和分析。
3.数学模型在实际问题中的应用:通过案例分析,让学生了解数学模型在其他领域中的应用,培养学生的应用意识。
三、教学方法为了提高教学效果,本节课采用以下教学方法:1.讲授法:教师讲解捕鱼问题的背景、数学模型的建立和求解方法。
2.案例分析法:分析实际问题中的数学模型,让学生了解数学模型的应用。
3.讨论法:分组讨论,让学生分享自己的想法和解决问题的方法,培养学生的团队协作和沟通能力。
4.实验法:通过模拟实验,让学生亲身参与模型的求解过程,提高学生的实践能力。
四、教学资源为了支持本节课的教学,准备以下教学资源:1.教材:提供相关章节,让学生预习和复习;2.参考书:为学生提供更多的学习资料,拓展知识面;3.多媒体资料:制作课件,生动展示捕鱼问题的模型和应用;4.实验设备:准备模拟实验所需的器材,让学生亲身体验模型的求解过程。
五、教学评估本节课的教学评估将采用多种方式,以全面、客观地评价学生的学习成果。
评估方式包括:1.平时表现:观察学生在课堂上的参与程度、提问回答和小组讨论的表现,以了解学生的学习态度和理解程度。
最优化课程设计

最优化课程设计一、课程目标知识目标:1. 学生能理解并掌握最优化问题的基础概念,如线性规划、非线性规划等。
2. 学生能运用数学模型解决实际问题,建立最优化问题的数学模型。
3. 学生能掌握并运用求解最优化问题的方法,如单纯形法、梯度下降法等。
技能目标:1. 学生具备分析实际问题时,能够将其转化为最优化问题的能力。
2. 学生能够运用数学软件或工具解决最优化问题,并能够解释结果。
3. 学生能够通过小组合作,共同探讨并解决复杂的最优化问题。
情感态度价值观目标:1. 学生能够认识到数学在解决实际问题中的广泛应用,增强数学学习的兴趣。
2. 学生通过解决最优化问题,培养严谨、细致的科学态度。
3. 学生能够从团队合作中学会相互尊重、沟通与协作,培养团队精神。
课程性质:本课程为数学学科的一节应用性课程,旨在让学生通过解决实际最优化问题,巩固数学知识,提高数学应用能力。
学生特点:学生处于高中年级,具有一定的数学基础和分析问题的能力,但对于最优化问题的理解尚浅。
教学要求:结合学生特点,课程要求注重理论与实践相结合,强调学生的动手操作能力和团队合作能力,培养解决实际问题的能力。
通过本课程的学习,使学生能够将所学知识应用于实际生活和工作中。
二、教学内容1. 最优化问题概念:介绍最优化问题的定义、分类(线性规划、非线性规划等)及其应用场景。
教材章节:第二章第二节《最优化问题的概念》2. 数学建模:通过实例讲解如何将实际问题抽象为数学模型,包括目标函数、约束条件等要素的确定。
教材章节:第二章第三节《数学建模》3. 求解方法:讲解线性规划问题的单纯形法、非线性规划问题的梯度下降法等求解方法。
教材章节:第二章第四节《最优化问题的求解方法》4. 数学软件应用:指导学生运用数学软件(如MATLAB、Lingo等)解决最优化问题。
教材章节:第二章第五节《数学软件在优化问题中的应用》5. 实践案例分析:分析实际案例,引导学生运用所学知识解决实际问题。
人教版实际问题与方程评课

人教版《实际问题与方程》评课一、课程背景与目标《实际问题与方程》是初中数学课程中的重要内容,旨在培养学生运用方程解决实际问题的能力。
本节课的教学目标是让学生能够根据实际问题建立数学模型,运用方程解决生活中的问题,同时培养学生的创新思维和合作精神。
二、教学内容概述本节课的主要内容是让学生通过生活中的实际问题,学习如何设未知数、列方程、解方程,并能够运用所学的知识解决实际问题。
教学重点是如何设未知数和列方程,教学难点是正确理解题意,找出等量关系,并运用所学知识解决实际问题。
三、教学方法与策略本节课采用了以下教学方法和策略:1. 通过实例演示和讲解,让学生了解如何根据实际问题设未知数和列方程。
2. 运用小组合作的方式,让学生自主探究和讨论,提高他们的合作精神和解决问题的能力。
3. 通过案例分析,让学生了解如何运用所学知识解决实际问题,提高他们的应用能力。
4. 通过课堂练习和反馈,及时了解学生的学习情况,调整教学策略。
四、学生活动设计与引导思考本节课设计了以下学生活动:1. 让学生自主探究如何设未知数和列方程,通过小组合作的方式进行讨论和交流。
2. 通过案例分析,让学生了解如何运用所学知识解决实际问题,并进行课堂练习和反馈。
3. 通过思考题和拓展延伸,让学生进一步了解如何运用方程解决更为复杂的问题。
五、实际问题与方程的应用案例分析本节课通过以下案例分析,让学生了解如何运用方程解决实际问题:案例一:某学校组织春游,共有师生100人。
学校安排了两种车型接送师生,其中大巴车每辆可乘坐20人,小巴车每辆可乘坐10人。
现已知小巴车的租金是每辆100元,大巴车的租金是每辆250元。
请问如何租车才能最省钱?案例二:某市环保局对辖区内两家企业进行环保检查时发现,这两家企业一个月内排放的污染物总量分别为45吨和60吨,且都是合格的。
经调查发现,这两家企业都是新建企业,且都在近两年内完成了建设。
请问这两个企业的污染物排放量是否符合国家标准?如果是超标了,超标了多少?六、课堂评价和反馈机制本节课采用了以下评价和反馈机制:1. 通过小组合作的方式,让学生在小组内进行自我评价和互评,了解自己的学习情况和不足之处。
课表编排问题
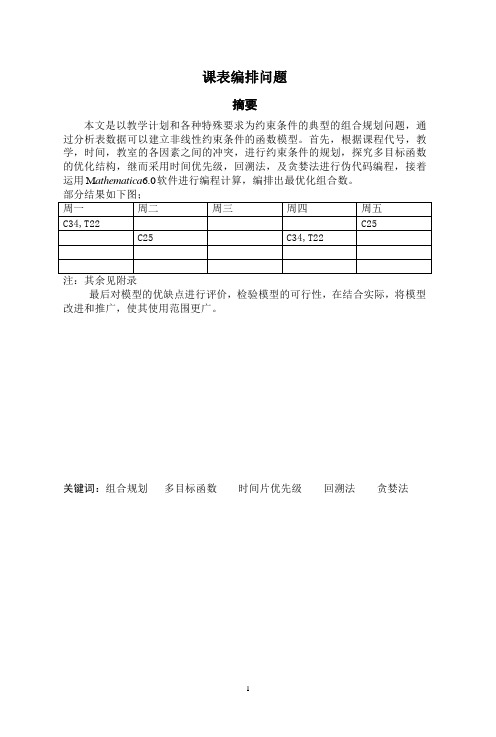
课表编排问题摘要本文是以教学计划和各种特殊要求为约束条件的典型的组合规划问题,通过分析表数据可以建立非线性约束条件的函数模型。
首先,根据课程代号,教学,时间,教室的各因素之间的冲突,进行约束条件的规划,探究多目标函数的优化结构,继而采用时间优先级,回溯法,及贪婪法进行伪代码编程,接着运用M 6.0athem atica软件进行编程计算,编排出最优化组合数。
注:其余见附录最后对模型的优缺点进行评价,检验模型的可行性,在结合实际,将模型改进和推广,使其使用范围更广。
关键词:组合规划多目标函数时间片优先级回溯法贪婪法一、问题重述1.1背景随着教学改革的进行及“211”工程的实施,新的教育体制对课表的编排提出了更高的要求。
手工排课时,信息的上通下达是极其麻烦的,而采用计算机排课,教学中的信息可以一目了然,对于优化学生的学习进程,评估每位教师对教学的贡献,领导合理决策等都具有重要的意义,必将会大大推进教学的良性循环。
现实生活中,课程编排问题屡屡皆是,从我们上小学到初中,一直到高中,我们上的课程都涉及什么时间上那一门课,上午到下午有许多课程要上。
到大学更是,不仅课目多样,而且教室、上课教师都在变化;这在教学活动中有一系列管理工作,管理者尤为头疼,其中,教学计划的实施是一个重要的教学环节。
每学期管理人员都要整理教学计划,根据教学计划下达教学任务书,然后根据教学任务书编排课程表。
在这些教学调度工作中,既有大量繁琐的数据整理工作,更有严谨思维的脑力劳动,还要填写大量的表格。
因此工作非常繁重。
当课程、教室、教师多而复杂的时候,排课问题是就课程、教师、教室和时间的多资源组合问题,问题的求解的目的是找出各个元素之间的对应关系。
这就要求我们优化方法,合理分配各个环节从而使课程有条不紊的进行。
1.2问题某学校现有课程40门,编号为C01~C40;教师共有25名,编号为T01~T25;教室18间,编号为R01~R18。
具体属性及要求见附录表1,表2,表3:课表编排规则:每周以5天为单位进行编排;每天最多只能编排8节课,上午4节,下午4节,特殊情况下可以编排10节课,每门课程以2节课为单位进行编排,同类课程尽可能不安排在同一时间。
数学与科学融合课程设计

数学与科学融合课程设计一、教学目标本课程的学习目标主要包括知识目标、技能目标和情感态度价值观目标。
知识目标要求学生掌握数学与科学融合的核心概念,理解数学模型在科学研究中的应用。
技能目标则侧重于培养学生的数学思维能力、问题解决能力和科学探究能力。
情感态度价值观目标则在于培养学生对数学与科学融合领域的兴趣和好奇心,提高他们的科学素养,培养他们积极探究、勇于创新的精神。
二、教学内容根据课程目标,我们选择和了与数学与科学融合相关的一系列教学内容。
主要涉及数学模型在物理学、生物学、化学等科学领域的应用。
具体包括:1. 数学模型在物理学中的应用,如线性方程组、微分方程等在力学、电磁学等领域的应用;2. 数学模型在生物学中的应用,如种群动力学模型、遗传概率模型等;3. 数学模型在化学中的应用,如化学反应动力学、物质传输方程等。
三、教学方法为了实现课程目标,我们采用了多样化的教学方法,包括讲授法、讨论法、案例分析法、实验法等。
在教学过程中,我们注重启发式教学,引导学生主动思考、探究问题,提高他们的数学思维能力和科学探究能力。
同时,通过小组讨论、案例分析等方法,培养学生的团队合作能力和沟通表达能力。
四、教学资源为了支持教学内容和教学方法的实施,我们选择了适当的教五、教学评估本课程的评估方式包括平时表现、作业、考试等多个方面,以全面客观地评价学生的学习成果。
平时表现主要考察学生的课堂参与度、提问回答、小组讨论等,旨在评价学生的学习态度和积极性。
作业则主要包括练习题、项目报告、研究论文等,用于评估学生对课程内容的掌握程度和应用能力。
考试则包括期中考试和期末考试,以闭卷形式进行,全面考察学生的知识掌握和问题解决能力。
评估方式将尽量公正、客观,确保全面反映学生的学习成果。
六、教学安排本课程的教学进度和时间安排将根据课程内容和目标进行合理规划。
教学时间将分配于每周的固定课时,确保在有限的时间内完成教学任务。
教学地点将选择适合教学的教室或实验室,以提供必要的学习环境和设备。
